2. 同济大学 土木工程学院,上海 200092;
3. 南京工业大学 土木工程学院,南京 211816
2. College of Civil Engineering, Tongji University, Shanghai 200092, China;
3. College of Civil Engineering, Nanjing Tech University, Nanjing 211816, China
深远海风能具有资源丰富、风力稳定、环境友好等诸多优点,近年来在全球范围内获得了广泛关注和积极发展[1]。为了降低深远海风能开发成本,发电机组采用漂浮式基础结构已成为共识[2]。当前,深远海风能开发主要面临机组服役条件十分恶劣和由于离岸较远而造成高昂维修保养费用等挑战[3-4]。此外,与陆上风能和近海风能开发相比,深远海风能开发中支撑结构的费用急剧增长[1]。上述因素使得当前浮式风机尚未完全实现商业化,限制了深远海风能的大规模开发。为此,应当采用基于整体可靠度的结构设计方法,实现兼顾浮式风机结构安全性与经济性的定量设计,为深远海风能的大规模开发提供关键技术保障。因此,浮式风机结构的整体可靠度分析具有重要意义。
当前,复杂结构的整体可靠度评估通常采用数值分析方法,主要涉及三个方面的问题:结构响应分析的数值模型、随机荷载的建模、结构可靠度分析方法[5]。浮式风机结构的精细化数值分析模型是其整体可靠度分析的关键基础[6]。由于浮式风机结构中同时存在多种复杂耦合效应[7-8],例如桨叶-机舱-塔筒-浮体-锚索等部件之间的相互作用、刚体运动与弹性变形耦合、气动-结构-机电-水动耦合、桨叶转动效应和几何非线性效应等,使得浮式风机结构的一体化动力学建模成为一项难题[9]。虽然针对该建模问题当前已有较多研究,但是在实际工程中仍主要采用分离式设计方法,难以合理考虑上述复杂的耦合效应,也难以进行结构的整体可靠度分析。一般来说,浮式风机结构的一体化建模主要基于多体动力学理论[9],采用Lagrange方法或者Kane方法建立结构的整体动力学方程,并可以进一步分为多刚体动力学模型和多柔性体动力学模型[10]。多刚体动力学模型将浮式风机中的所有部件均考虑为刚体,因而无法获得柔性部件(桨叶、塔筒等)的弹性变形和内力响应,具有较大的局限性[10]。但是,由于多刚体动力学模型建模简便、分析效率较高,因此多用于浮式风机结构的概念设计和初始设计阶段[11]。多柔性体模型能够同时考虑系统中的刚体运动和弹性变形响应,其中一般采用有限元方法或者模态叠加方法建立柔性部件的弹性模型[7]。虽然多柔性体模型能够全面反映系统的力学特性和复杂的耦合效应,但是该类模型建模较为复杂,同时存在分析效率不高的问题,难以应用于需要进行大量数值模拟分析的问题中,例如结构的可靠度评估与优化设计等[12]。
浮式风机在服役期间的主要环境荷载为风荷载和波浪荷载,且两种荷载具有相关性[13]。因此,在浮式风机结构的动力分析与可靠度评估中应当合理考虑风和波浪荷载的联合作用[14]。实测数据表明,10 min内的风速时程和20 min至3~6 h内的波浪时程均可以认为是平稳过程,并可以采用平均风速、有效波高、谱峰周期、风-浪夹角等物理量描述上述风况和海况[13]。为了刻画结构在服役期内所经历的所有工况的概率大小,可基于结构所在场址的长期观测数据建立上述物理量的联合概率分布,这也是当前海洋结构设计规范中所推荐的方法[13]。在建立风-浪参数的联合概率分布模型时,可采用条件概率分布建模方法[15]、Nataf变换方法[16]和Copula方法[17-18]。条件概率分布建模方法是当前海洋结构设计规范中推荐使用的方法[13]。该方法首先确定主导随机变量,并建立其边缘概率分布模型,然后根据主导随机变量的取值将数据划分为一系列区间,进而估计主导随机变量取不同值条件下的其他随机变量的概率分布。但是,当随机变量的个数较多时,该方法需要进行多次条件概率分布建模。此外,在某些条件下(例如高风速条件),观测数据较少,将导致该条件下的概率分布建模结果误差较大[18]。Nataf变换方法首先基于等概率变换原则,将原始随机变量变换为服从标准高斯分布的随机变量,进而利用多维高斯分布模型建立变换后的随机变量的联合概率分布,最后再利用反变换获得原始随机变量的联合概率分布[16]。该方法虽然简便易行,但是当随机变量为非线性、非高斯相关时,例如风-浪参数间的相关结构通常呈现这种特点,该方法将引入较大误差。Copula方法是近年来发展的多维随机变量联合概率分布建模的新方法,对于非线性相关问题十分有效[17]。该方法在联合概率分布建模中,将随机变量的边缘概率分布建模与变量间的概率相关结构建模分开处理,具有简便、灵活、精确等优点。该方法目前已在多个领域获得广泛关注[19],但在海洋工程中尚应用较少。
结构可靠度分析方法主要包括一次和二次可靠度方法、基于跨越过程理论的首次超越破坏可靠度方法、随机模拟方法、概率密度演化理论等[5, 20]。一次和二次可靠度方法常用于静力问题的分析,具有较高的效率,然而该方法需要将系统的极限状态函数展开为一阶或二阶形式,对于强非线性系统(例如浮式风机结构)会产生较大误差[9]。基于跨越过程理论的首次超越破坏可靠度方法适用于动力系统,但通常引入Poisson假定,具有一定的近似性,尤其对于大失效概率问题其误差较大[5]。随机模拟方法主要包括Monte Carlo模拟及其改进方法以及子集模拟等方法,这类方法不受问题的维度、非线性程度等因素的限制,应用范围较广,但通常具有随机收敛和效率不高等问题[20]。为了将这类方法应用于浮式风机的可靠度分析中,通常发展浮式风机结构分析的代理模型以提高效率,但同时也引入了新的误差[21]。概率密度演化理论给出了随机动力系统响应的概率密度函数的演化方程,揭示了系统响应随机性演化的内在物理规律[5],该方法在分析系统的可靠度时同样不受问题类型、问题维度和非线性程度等因素的影响,能给出系统响应量的概率密度函数演化过程,同时具有较高的分析效率,因此适用于浮式风机的可靠度分析,但目前在此领域的应用研究较少。
为了分析浮式风机结构的整体可靠度,首先引入结合多刚体动力学理论和有限元方法建立起来的浮式风机结构一体化分析模型(StoDRAFOWT模型)。该模型不仅能同时获得浮式风机的刚体运动和弹性变形响应,而且具有建模简便、易于求解等优点[9]。然后,基于我国南海某场址长期风-浪数据并引入Copula方法,建立风-浪联合作用的多参数非线性相关的联合概率分布模型,进而采用概率密度演化理论分析浮式风机结构的整体可靠度。由此,建立了风-浪联合作用下浮式风机结构整体可靠度分析的基本框架。针对风机结构设计中需要考虑的额定风速和极端风剪不利工况,采用上述方法进行了单柱式浮式风机结构的整体可靠度分析。
1 浮式风机一体化动力学建模 1.1 基本建模思想与坐标系统如前所述,浮式风机的多刚体动力学模型虽然分析效率较高,但是无法分析结构的弹性变形。而多柔性体动力学模型虽然能够全面分析结构的动力响应,但是建模复杂、分析效率不高。本文首先介绍将多刚体动力学模型与有限元方法相结合的建模策略,不仅能够全面分析结构响应,而且建模较为简便,分析效率较高[9]。已有研究表明[10-11],对于当前兆瓦级的浮式风机系统,结构的弹性变形对系统刚体运动响应的影响可以忽略,因此可以首先采用多刚体动力学模型分析系统的刚体运动响应。而系统的刚体运动对结构的弹性变形具有重要影响。为此,采用Kane方法[22-23]推导了考虑系统刚体运动效应的结构有限元模型,从而能够全面获得结构的动力响应。
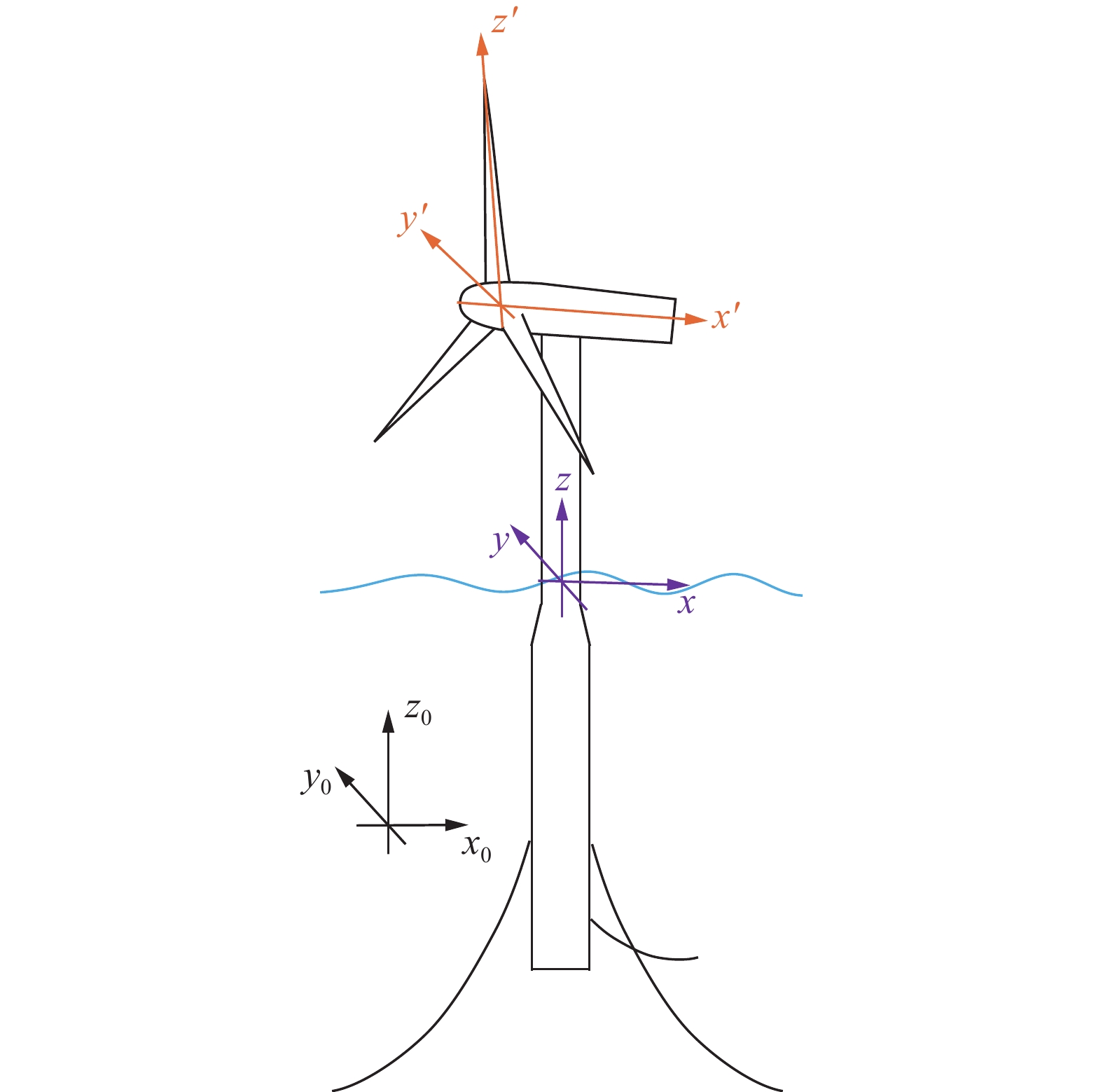
图1为单柱式浮式风机的示意图和坐标系的定义。为描述浮式风机系统的状态,定义三组笛卡尔坐标系,分别为惯性坐标系
|
图 1 单柱式浮式风机示意图与坐标系统 Fig.1 Schematic diagram of a spar-type floating offshore wind turbine and the coordinate system |
为了建立浮式风机系统的多刚体动力学模型,通常基于Lagrange方程得到考虑转子转动和浮体六自由度刚体运动的动力方程[10],即包含七个自由度。由于现代风力机通常配备桨距控制系统,为此,将变桨距控制方程与上述七自由度动力方程耦合,得到考虑变速、变桨距控制的浮式风机多刚体动力学模型[9, 24]:
| $ \left[ {\begin{array}{*{20}{c}} {{{\left[ {{{\boldsymbol{M}}_0}} \right]}_{6 \times 6}}}& {\begin{array}{*{20}{c}} 0&0&0 \\ 0&0&0 \\ 0&0&0 \\ {{I_{rx}}}&0&0 \\ 0&0&0 \\ 0&0&0 \\\end{array}}\\ {\begin{array}{*{20}{c}} 0&0&0&{{I_{rx}}}&0&0 \\ 0&0&0&0&0&0 \\ 0&0&0&0&0&0 \end{array}}& {\begin{array}{*{20}{c}} {{I_{rx}}}&0&0 \\ 0&1&0 \\ 0&0&1 \end{array}} \end{array}} \right] \left\{ \begin{gathered} {{{\dot {\boldsymbol{v}}}}_p} \\ {{\dot {\boldsymbol{\omega}} }_p} \\ {{\dot \omega }_b} \\ {\dot \varphi } \\ {\dot \beta } \\ \end{gathered} \right\} +$ |
| $ \begin{split}& \left[ {\begin{array}{*{20}{c}} {{{\left[ {{{\boldsymbol{C}}_0}} \right]}_{6 \times 6}}}&{\begin{array}{*{20}{c}} \;\;\;\;\;\;0&\;\;\;\;\;\;\;\;\;\;0&\;\;\;\;\;0 \\ \;\;\;\;\;\;0&\;\;\;\;\;\;\;\;\;\;0&\;\;\;\;\;0 \\ \;\;\;\;\;\;0&\;\;\;\;\;\;\;\;\;\;0&\;\;\;\;\;0 \\ \;\;\;\;\;\;0&\;\;\;\;\;\;\;\;\;\;0&\;\;\;\;\;0 \\ {{I_{rx}}{\omega _z}}&\;\;\;\;\;\;\;\;\;\;0&\;\;\;\;\;0 \\ { - {I_{rx}}{\omega _y}}&\;\;\;\;\;\;\;\;\;\;0&\;\;\;\;\;0 \end{array}} \\ {\begin{array}{*{20}{c}} 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 \end{array}} & {\begin{array}{*{20}{c}}\\ {{c_0}} & 0 & 0 \\ { - 1} & 0 & 0 \\ {\dfrac{G}{{{\tau _p}}}\Bigg(\dfrac{{{\tau _d}{c_0}}}{{{I_{rx}}}} - 1\Bigg)} & {\dfrac{{ - G}}{{{\tau _p}{\tau _i}}}} & {\dfrac{1}{{{\tau _p}}}} \end{array}} \end{array}} \right]\left\{ \begin{gathered} {{{{{\boldsymbol{v}}}}}_p} \\ {{{{{\boldsymbol{\omega}} }}}_p} \\ {\omega _b} \\ \varphi \\ \beta \\ \end{gathered} \right\} \\& = \left\{ {\begin{array}{*{20}{c}} {{\boldsymbol {F}_G} + {\boldsymbol {F}_D}} \\ {{\boldsymbol {M}_G} + {\boldsymbol {M}_D}} \\ {{F_M}} \\ 0 \\ { - \dfrac{{G{\omega _0}}}{{{\tau _p}}}\Bigg(1 + \dfrac{t}{{{\tau _i}}}\Bigg) + \dfrac{{G{\tau _d}{F_M}}}{{{\tau _p}{I_{rx}}}}} \end{array}} \right\} \\[-45pt] \end{split} $ | (1) |
式中,
通过求解方程式(1)即可获得浮式风机中浮体的六自由度刚体运动响应、桨叶转速和桨叶的桨距角。为了分析浮式风机中柔性部件的弹性变形,基于Kane方程分别推导得到塔筒单元和桨叶单元的有限元表达式。
在坐标系
| $ {{\boldsymbol{M}}^t}\ddot {\boldsymbol{\mu}} + {{\boldsymbol{C}}^t}{\dot {\boldsymbol{\mu}} } + {{\boldsymbol{K}}^t}{{\boldsymbol{\mu }}} = {{{\boldsymbol{F}}}^t} $ | (2) |
式中:
| $ {{\boldsymbol{C}}^t} = {\boldsymbol{C}}_0^t{\text{ + }}{\boldsymbol{C}}_d^t $ | (3) |
| $ {{\boldsymbol{K}}^t} = {\boldsymbol{K}}_0^t{\text{ + }}{\boldsymbol{K}}_d^t $ | (4) |
| $ {{{\boldsymbol{F}}}^t} = {{\boldsymbol{F}}}_0^t + {{\boldsymbol{F}}}_d^t $ | (5) |
其中:
| $ {\boldsymbol{C}}_d^t = \int_V {2\rho {{{\boldsymbol{\tilde N}}}^{\text{T}}}{\boldsymbol{\tilde {\boldsymbol{\omega }}}}} {\boldsymbol{\tilde N}}{\text{d}}V $ | (6) |
| $ {\boldsymbol{K}}_d^t = \int_V {\rho {{{\boldsymbol{\tilde N}}}^{\text{T}}}\left( {{\boldsymbol{\dot {\tilde {{\boldsymbol{\omega}}}} }} + {\boldsymbol{\tilde {{\boldsymbol{\omega}}} \tilde {{\boldsymbol{\omega}} }}}} \right)} {\boldsymbol{\tilde N}}{\text{d}}V $ | (7) |
| $ \boldsymbol {F}_d^t = - \int_V {\rho {{{\boldsymbol{\tilde N}}}^{\text{T}}}\left[ {\left( {{\boldsymbol{\dot {\tilde {\boldsymbol{\omega}}} }} + {\boldsymbol{\tilde{\boldsymbol{ \omega}} \tilde {\boldsymbol{\omega}} }}} \right){{{\boldsymbol{r}}}_k} + {{\boldsymbol{R}}^{\text{T}}}{{{\ddot {\boldsymbol{r}}}}_o}} \right]} \;{\text{d}}V $ | (8) |
式中:
类似地,在坐标系
| $ {{\boldsymbol{M}}^b}{\ddot {\boldsymbol{\mu}} } + {{\boldsymbol{C}}^b}{\dot {\boldsymbol{\mu}} } + {{\boldsymbol{K}}^b}{{\boldsymbol{\mu}} } = {{{\boldsymbol{F}}}^b} $ | (9) |
式中:
| $ {\boldsymbol{C}}_d^b\; = \int_V {2\rho {{{\boldsymbol{\tilde N}}}^{\text{T}}}\left( {{{\boldsymbol{T}}^{\text{T}}}{\boldsymbol{\tilde {\boldsymbol{\omega}} T}} + {\boldsymbol{\tilde \varOmega }}} \right)} {\boldsymbol{\tilde N}}\;{\text{d}}V $ | (10) |
| $ {\boldsymbol{K}}_d^b\; = \int_V {\rho {{{\boldsymbol{\tilde N}}}^{\text{T}}}\left[ {{{\boldsymbol{T}}^{\text{T}}}\left( {{\boldsymbol{\tilde {{\boldsymbol{\omega}}} \tilde {{\boldsymbol{\omega}}} }} + {\boldsymbol{\dot {\tilde {\boldsymbol{\omega}}} }}} \right){\boldsymbol{T}} + 2{{\boldsymbol{T}}^{\text{T}}}{\boldsymbol{\tilde {{\boldsymbol{\omega}}} T\tilde {{\boldsymbol{\omega}}} }} + \left( {{\boldsymbol{\tilde {\boldsymbol{\omega}} \tilde {\boldsymbol{\omega}} }} + {\boldsymbol{\dot {\tilde {\boldsymbol{\omega}}} }}} \right)} \right]{\boldsymbol{\tilde N}}} {\text{d}}V $ | (11) |
| $ \begin{split} \boldsymbol {F}_d^b\; =& - \int_V {\rho {{{\boldsymbol{\tilde N}}}^{\text{T}}}\left\{ {{{\boldsymbol{T}}^{\text{T}}}{{\boldsymbol{R}}^{\text{T}}}{{\boldsymbol{\ddot r}}_o} + {{\boldsymbol{T}}^{\text{T}}}\left( {{\boldsymbol{\tilde {\boldsymbol{\omega}} \tilde {\boldsymbol{\omega}} }} + {\boldsymbol{\dot {\tilde {\boldsymbol{\omega}}} }}} \right){{\boldsymbol r}_{o'}}} \right\}\;{\text{d}}V} - \\& \int_V {\rho {{{\boldsymbol{\tilde N}}}^{\text{T}}}} \left[ {{{\boldsymbol{T}}^{\text{T}}}\left( {{\boldsymbol{\tilde {\boldsymbol{\omega}} \tilde {\boldsymbol{\omega}} }} + {\boldsymbol{\dot {\tilde {\boldsymbol{\omega}}} }}} \right){\boldsymbol{T}} + 2{{\boldsymbol{T}}^{\text{T}}}{\boldsymbol{\tilde {\boldsymbol{\omega}} T\tilde {\boldsymbol{\omega}} }} + \left( {{\boldsymbol{\tilde {\boldsymbol{\omega}} \tilde {\boldsymbol{\omega}} }} + {\boldsymbol{\dot {\tilde {\boldsymbol{\omega}}} }}} \right)} \right]{\boldsymbol{r}_q}{\text{d}}V \end{split} $ | (12) |
其中:
值得注意的是,桨叶截面为非对称形状,并且桨叶截面存在沿翼展方向变化的预扭转角,同时还存在桨距控制。因此,桨叶在风轮平面内、外两个方向的振动相互耦合,在建模过程中应当合理考虑。此外,桨叶在风机正常运转工况下的变形较大,应当在桨叶的三维梁单元模型中考虑几何非线性效应。这是与塔筒有限元模型的不同之处。
基于塔筒和桨叶的有限元模型,并结合前述浮式风机的刚体运动响应,可建立浮式风机柔性构件的整体有限元模型,进而分析浮式风机结构弹性变形响应。
1.3 荷载计算在浮式风机结构的动力响应分析中,主要应考虑桨叶和塔筒的气动荷载、浮体的水动力荷载和锚泊荷载。本文采用叶素动量理论方法[25]计算桨叶的气动荷载,并考虑了Prandtl叶尖损失因子和高推力系数条件下的Glauert修正[25]。塔筒的气动荷载可基于准定常假定计算[25]。
在计算大型浮体的水动力荷载时,应当合理考虑辐射效应和绕射效应[26]。本文关注的是单柱式浮式风机,浮体的截面尺寸相对较小,因此可以简化考虑这两种效应。在实际中可采用相对形式的Morison公式计算单柱式浮体的水动力荷载[10, 26],此时,单位长度浮体的水动力荷载为[27]:
| $ \begin{split} {\boldsymbol {f}_h} =& \frac{1}{2}{\rho _w}{d_p}{C_d}\left( {{{{\boldsymbol{v}}}_w} - {{{\boldsymbol{v}}}_f}} \right)\left\| {{{{\boldsymbol{v}}}_w} - {{{\boldsymbol{v}}}_f}} \right\| + \\& \frac{1}{4}{\rho _w}{\text{π }}d_p^2\left( {1 + {C_A}} \right){{{\boldsymbol{a}}}_w} - \frac{1}{4}{\rho _w}{\text{π }}d_p^2{C_A}{{{\boldsymbol{a}}}_f} \end{split} $ | (13) |
式中:
在计算浮式风机的锚泊荷载时,需要建立锚索的力学分析模型,主要包括锚索的静力模型、拟静力模型和动力模型[28]。由于静力和拟静力模型在某些工况下会低估锚索的疲劳荷载,因此推荐采用锚索的动力模型[28]。本文采用锚索的集中质量动力模型[28]计算锚泊荷载。该模型不仅考虑锚索的受拉弹性变形,而且将锚索的动力效应和水动力效应以及与海底的接触效应等也考虑在内。锚索底部固定在海床上,锚索顶部的边界条件由浮体的位置确定。通过求解锚索的动力方程,可以获得锚索对浮体的荷载效应。
1.4 模型验证为了检验上述模型的正确性,分别利用该模型和当前风力机结构分析的常用软件FAST,分析风-浪联合作用下的海上单柱式浮式风机结构的动力响应,并进行对比。浮式风机结构参数采用美国国家可再生能源实验室(NREL)给出的5 MW海上风力发电机组参数[29]和OC3项目中海上单柱式浮式风机基础参数[30],关键参数如表1所示。
| 表 1 浮式风力发电机组关键参数 Table 1 Key parameters of the floating offshore wind turbine |
|
|
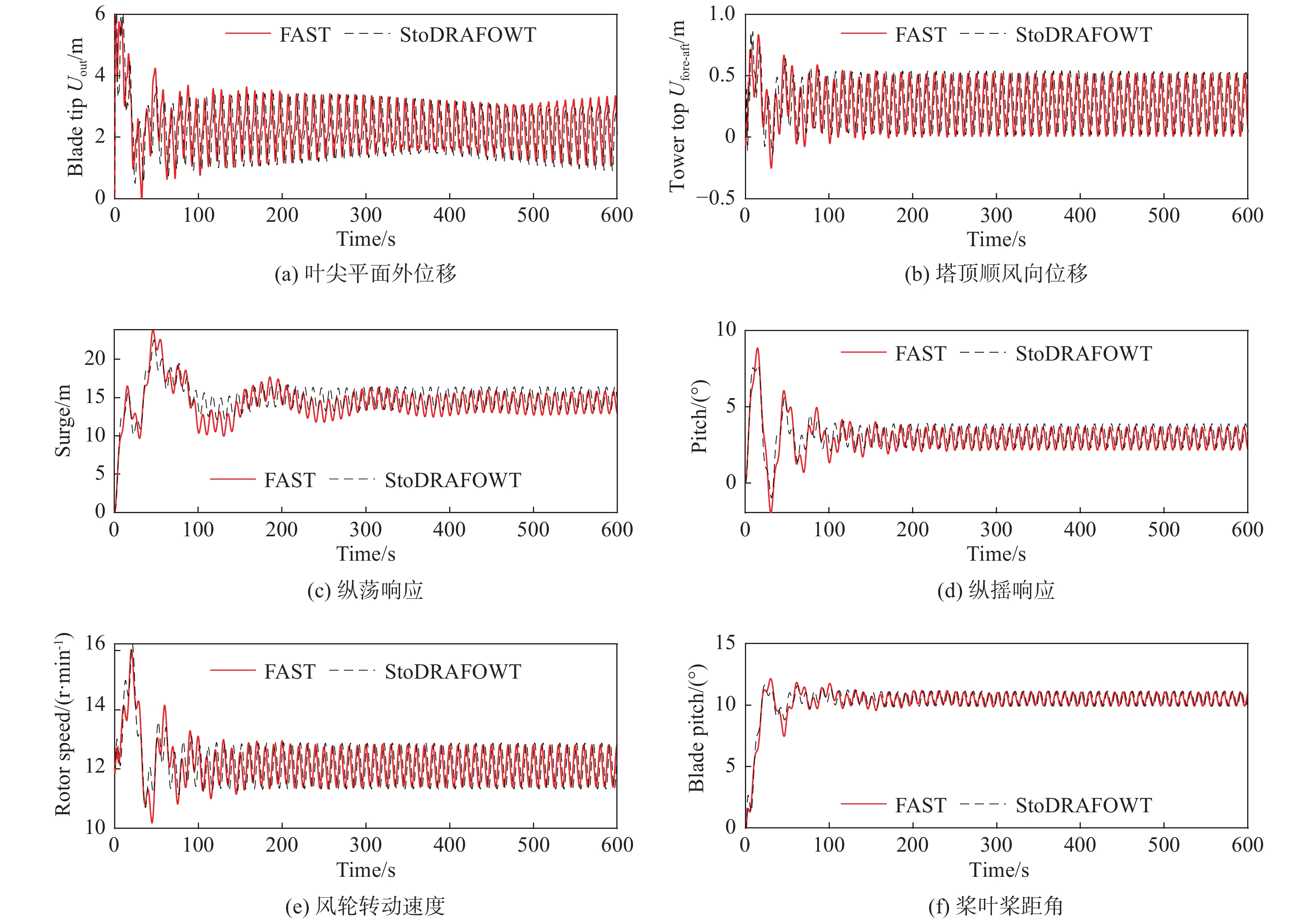
本文仅给出一种工况条件下的分析对比结果,其他工况条件下的对比结果见文献[24]。此处的工况条件为:定常风速场,且轮毂高度处的风速为15 m/s;规则波浪,波高为6 m,波浪周期为10 s。分析结果如图2所示。结果对比表明,本文模型的分析结果与FAST的分析结果吻合良好,尤其是在响应进入平稳阶段以后。因此,可以利用本文模型进行浮式风机结构的可靠度分析。
|
图 2 风-浪作用下浮式风机结构响应的对比结果 Fig.2 Comparisons of the responses of floating offshore wind turbine under wind and wave excitations |
由于浮式风机在服役期间同时受到风荷载和波浪荷载作用,因此在进行浮式风机的动力响应与可靠度分析时,应当合理考虑风-浪联合作用。如前所述,当前海洋结构的设计规范中建议采用风-浪参数的联合概率分布模型考虑风-浪联合作用[13]。本文采用Copula方法建立风-浪参数的联合概率分布模型。
在实际工程中,通常需要考虑平均风速
在建立风-浪参数的联合概率分布模型时,应当基于场址的长期风-浪观测数据。本文采用欧洲中尺度天气预报中心ERA-Interim数据库[32]提供的风-浪参数再分析数据,获取了我国南海场址(21°N,113°E)处1979年至2018年(共计40年)的风-浪再分析数据。这些数据均为30 min内观测数据的平均值,时间分辨率为6 h。通过对数据预处理,可得到轮毂处平均风速、有效波高和谱峰周期的长期数据。
为了建立额定风速条件下
根据Copula联合概率分布建模的基本理论[17],对于任意两个随机变量
| $ f\left( {{x_1},{x_2}} \right) = {c_{12}}\left( {{F_1}\left( {{x_1}} \right),{F_2}\left( {{x_2}} \right)} \right) \; {f_1}\left( {{x_1}} \right) \; {f_2}\left( {{x_2}} \right) $ | (14) |
式中:
从式(14)中可以看到,在利用Copula方法建立多维随机变量的联合概率分布模型时,需要分别建立各随机变量的边缘概率分布模型及变量间的相关结构模型。由于边缘概率分布模型及变量间的相关结构模型可以分开处理,因此该方法具有灵活、便捷、精确等优点。
基于上述681个额定风速条件下的数据点,首先采用常用的参数概率分布模型,建立
| 表 2 波浪参数概率分布建模结果 Table 2 Probabilistic modeling results of wave parameters |
|
|
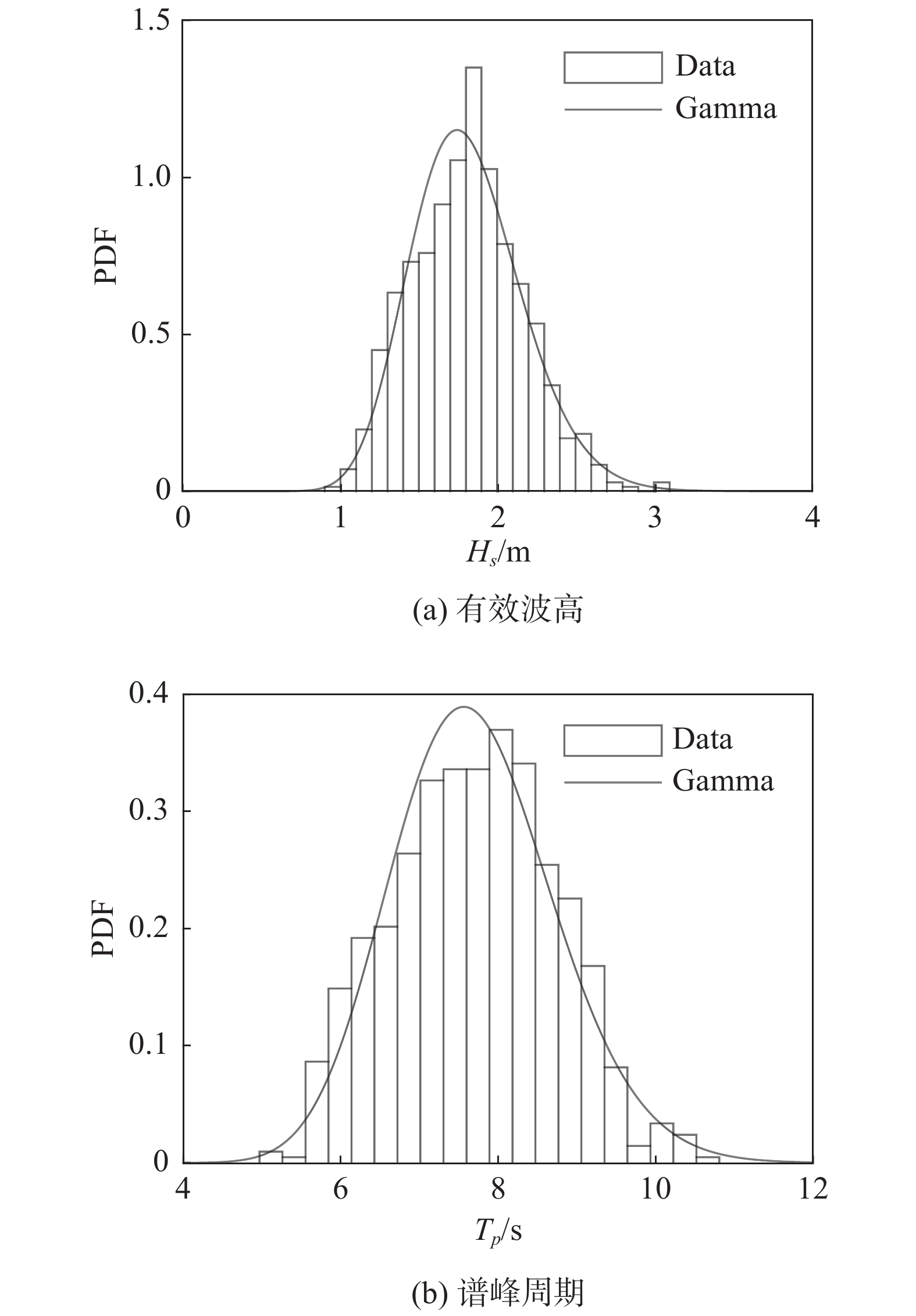
|
图 3 额定风速下有效波高和谱峰周期的边缘概率分布 Fig.3 Marginal probability distributions of Hs and Tp under the rated wind speed condition |
进一步,采用常用的Copula函数建立
| $ \bar C\left( {u,v} \right) = C\left( {{u^{{{\alpha} _0}}},{v^{{\beta _0}}};\lambda } \right) \; {u^{1 - {{\alpha} _0}}} \; {v^{1 - {\beta _0}}} $ | (15) |
式中:
在确定备选的Copula函数后,采用极大似然方法估算Copula函数中的待定参数,然后根据AIC准则选取最优Copula函数并进行拟合优度检验[17,19]。对于上述额定风速条件下的风浪数据,识别的最优结果为按照式(15)构造的非对称高斯Copula模型,见表2。表中,
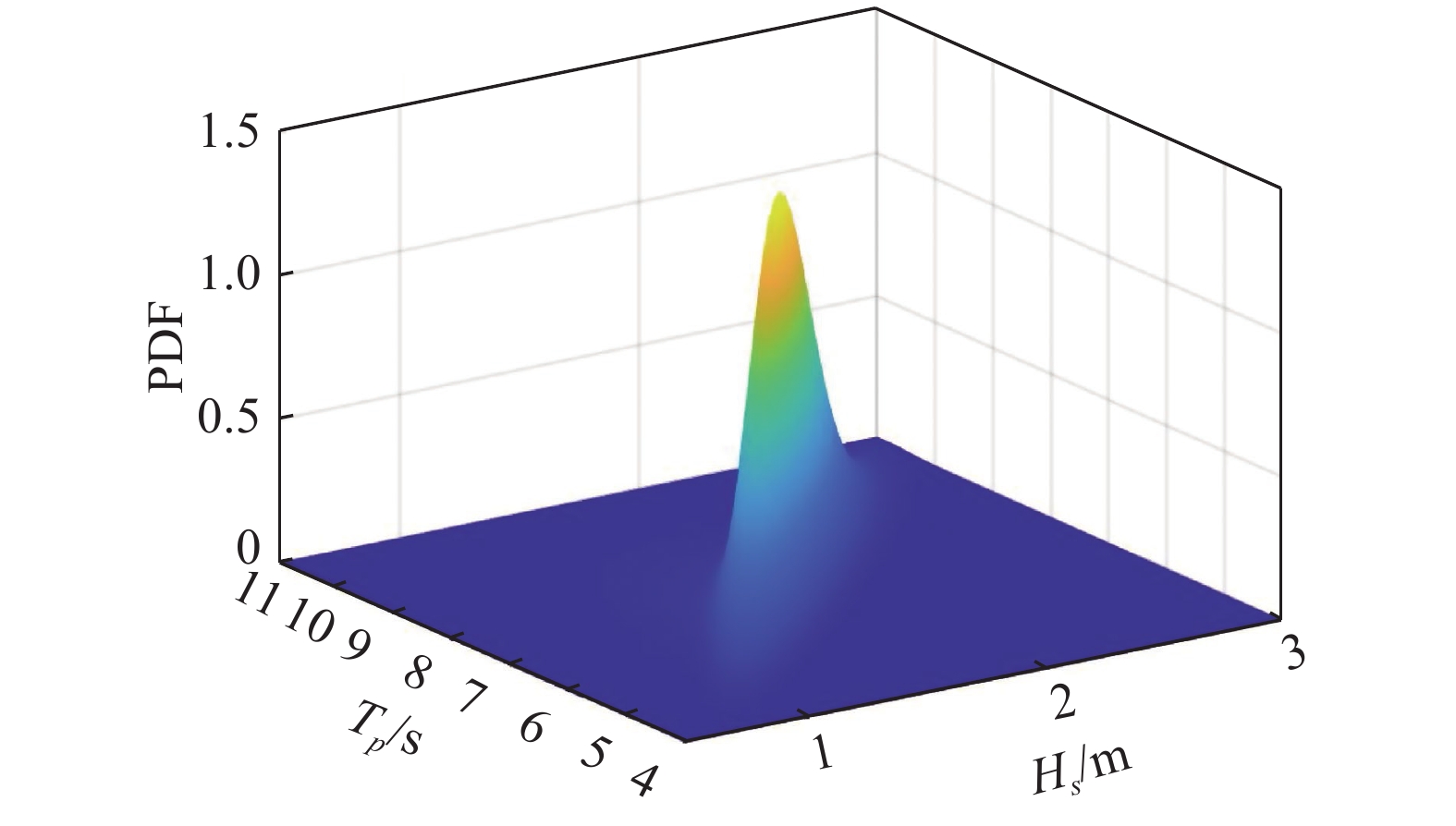
|
图 4 额定风速下有效波高和谱峰周期的联合概率密度函数 Fig.4 Joint probability density function of Hs and Tp under the rated wind speed condition |
应指出,本文采用Copula方法建立了二维随机环境变量的条件联合概率分布模型。对于高维随机环境变量,可采用C-vine Copula方法便捷地建立其联合概率分布模型[18-19]。
3 浮式风机结构整体可靠性分析 3.1 概率密度演化理论简介本文采用概率密度演化理论进行额定风速下发生极端风剪时浮式风机的可靠度分析。为此,先简要介绍概率密度演化理论。
不失一般性,对于多自由度动力系统,考虑系统的随机因素后,动力方程可写为:
| $ \dot {\boldsymbol{Y}}\left( t \right) = {\boldsymbol{G}}\left( {{\boldsymbol{Y}}\left( t \right),\;{\boldsymbol{\varTheta}} ,\;t} \right),\;\;\;\;{\boldsymbol{Y}}\left( {{t_0}} \right) = {{\boldsymbol{Y}}_0} $ | (16) |
式中:
式(16)的解可写为
| $ \frac{{\partial {p_{_{Z{{ \varTheta}} }}}\left( {z,\;{{\theta}} ,\;t} \right)}}{{\partial t}} + \dot Z\left( {{\boldsymbol{\varTheta}} ,\;t} \right)\frac{{\partial {p_{_{Z{{ \varTheta}} }}}\left( {z,\;{{\theta}} ,\;t} \right)}}{{\partial z}} = 0 $ | (17) |
且具有如下的初值条件:
| $ {p_{_{Z{{\varTheta}}} }}\left( {z,\;{{\theta}} ,\;t} \right)\left| {_{t = 0}} \right. = \delta \left( {z - {z_0}} \right) {p_{_{{\varTheta}} }}\left( {{\theta}} \right) $ | (18) |
式中:
因此,
| $ {p_{_Z}}\left( {z,\;t} \right) = \int_{{\varOmega _{{ \varTheta}} }} {{p_{_{Z{{ \varTheta}}} }}\left( {z,\;{{\theta}} ,\;t} \right){\text{d}}{{\theta}} } $ | (19) |
式中,
为了求解广义概率密度演化方程,已发展了点演化和群演化两类数值求解方法。本文采用点演化方法,具体的求解步骤可参考文献[5]。
基于概率密度演化理论发展了两种结构首次超越破坏可靠度分析方法,即,基于吸收边界条件的可靠度分析方法和基于极值分布的可靠度分析方法[5]。本文采用基于极值分布的可靠度分析方法。首先构造随机过程
| $ {Z_{{\text{ext}}}}\left( {\boldsymbol{\varTheta}} \right) = \mathop {\max }\limits_{t \in \left[ {0,T} \right]} \Big| {Z\left( {{\boldsymbol{\varTheta}} ,\;t} \right)} \Big| $ | (20) |
式中,
进而构造如下的虚拟随机过程[5]:
| $ {Z_{{\text{vir}}}}\left( {{\boldsymbol{ \varTheta}} ,\;t} \right) = {Z_{{\text{ext}}}}\left( {\boldsymbol{ \varTheta}} \right)\sin \left( {\frac{{\text{π }}}{2}t} \right),\;\;t \in \left[ {0,1} \right] $ | (21) |
由于
| $ {p_{_{Z_{\max }}}}\left( z \right) = {p_{_{Z_{{\text{vir}}}}}}\left( {z,t} \right)\left| {_{t = 1}} \right. $ | (22) |
由此,可得到结构的可靠度为:
| $ {F_s} = \int_{ - \infty }^b {{p_{_{Z_{\max }}}}\left( z \right){\text{d}}z} $ | (23) |
式中,
针对风力机结构设计规范[31]中定义的额定风速条件下发生极端风剪的工况,进行了单柱式浮式风机结构的整体可靠度分析。此处仅考虑竖直方向的正极端风剪,此时风剖面为[31]:
| $ V\left( {z,t} \right) = \left\{ \begin{array}{l} {V_{{\text{hub}}}}{\left( {\dfrac{z}{{{z_{{\text{hub}}}}}}} \right)^{\alpha} } + \left[ {1 - \cos \left( {\dfrac{{2{\text{π}}t}}{{{T_0}}}} \right)} \right] \left( {\dfrac{{z - {z_{{\text{hub}}}}}}{D}} \right) \cdot \\ \qquad \left[ {2.5 + 0.2\beta {\sigma _1}{{\left( {\dfrac{D}{{{\varLambda _1}}}} \right)}^{\frac{1}{4}}}} \right],\;\;0 \leqslant t \leqslant {T_0} \\ {V_{{\text{hub}}}}{\left( {\dfrac{z}{{{z_{{\text{hub}}}}}}} \right)^{\alpha} }\;\;\;\quad\qquad\qquad,\;\;{\text{otherwise}} \end{array} \right. $ | (24) |
式中:
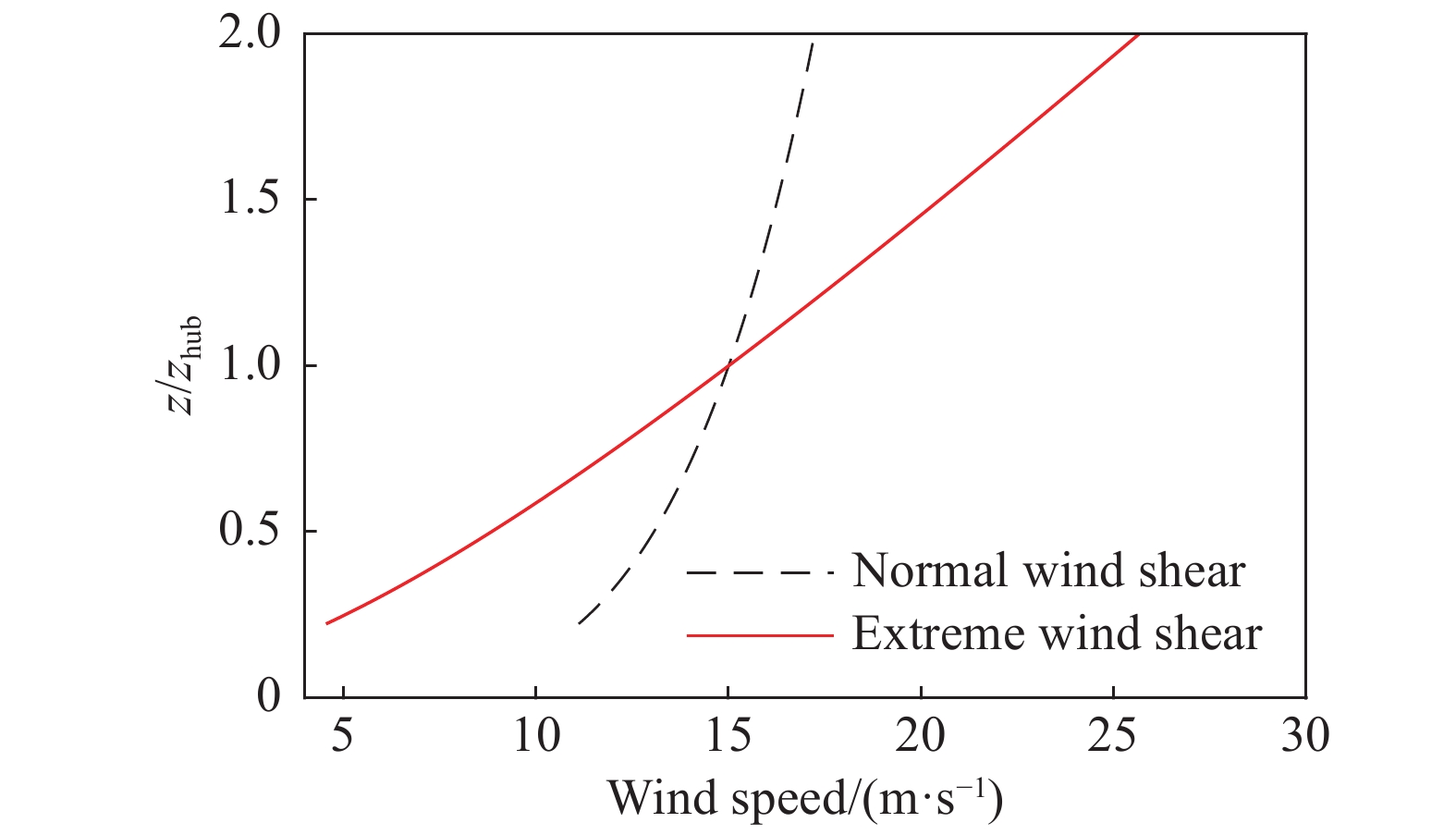
|
图 5 正常风剖面和极端风剖面对比 Fig.5 Comparison of normal and extreme wind profiles |
在分析结构的可靠度时,应当充分、合理考虑系统中的随机源。本文采用的概率密度演化理论在分析结构可靠度时能够同时全面考虑结构自身和外部激励的随机性[5]。作为示例,本文不仅将额定风速条件下的有效波高
| 表 3 随机变量的概率分布信息 Table 3 Probability distributions of random variables |
|
|
在求解广义概率密度演化方程时,首先需要将概率空间剖分为
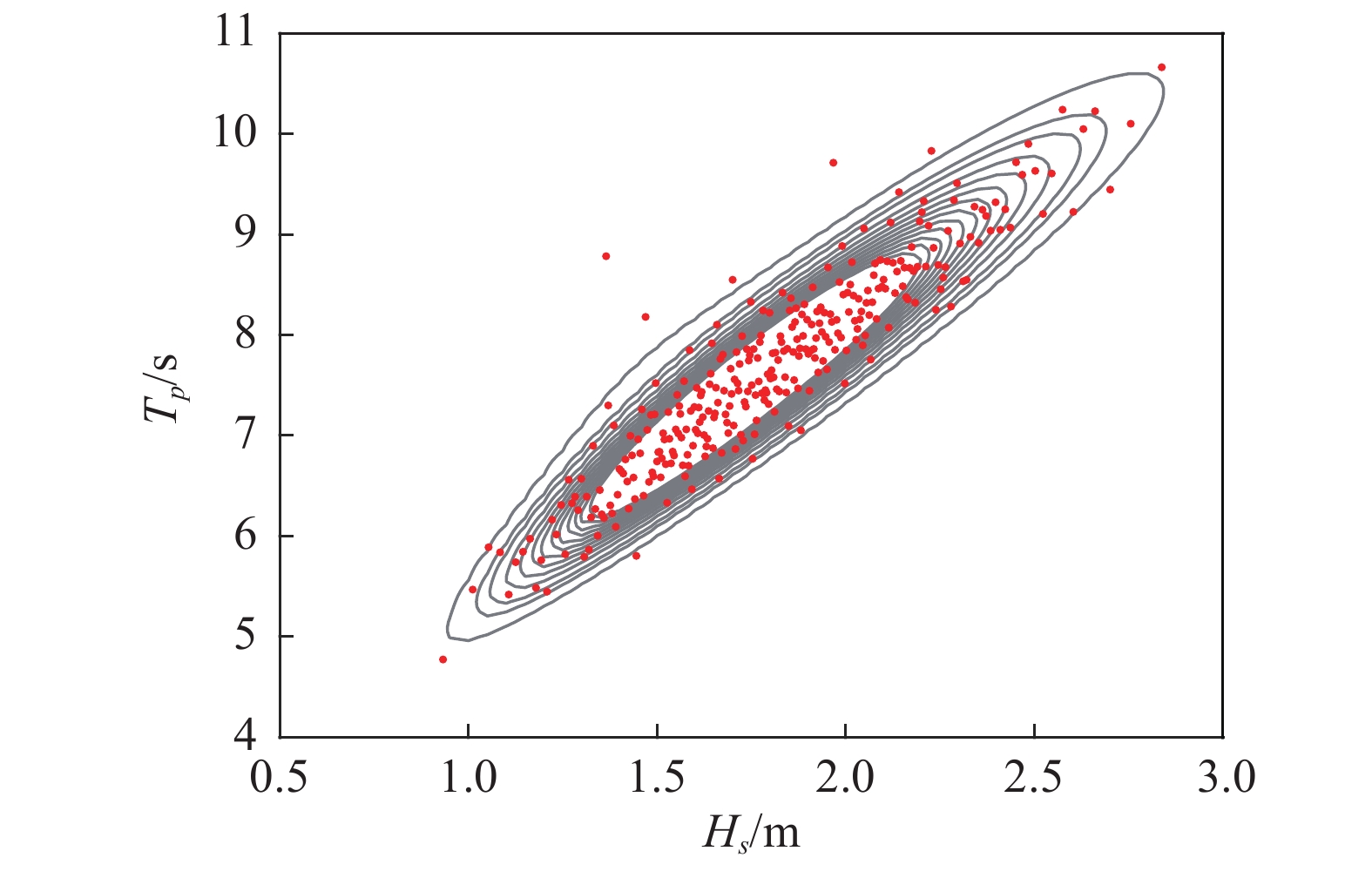
|
图 6 额定风速下随机动力分析中的波浪参数代表点 Fig.6 Representative points of wave parameters for the stochastic analysis under rated wind speed condition |
在选定代表点之后,需要模拟每种情况下的随机风场和波浪场,并分析浮式风机结构的动力响应。作为示例,图7给出了
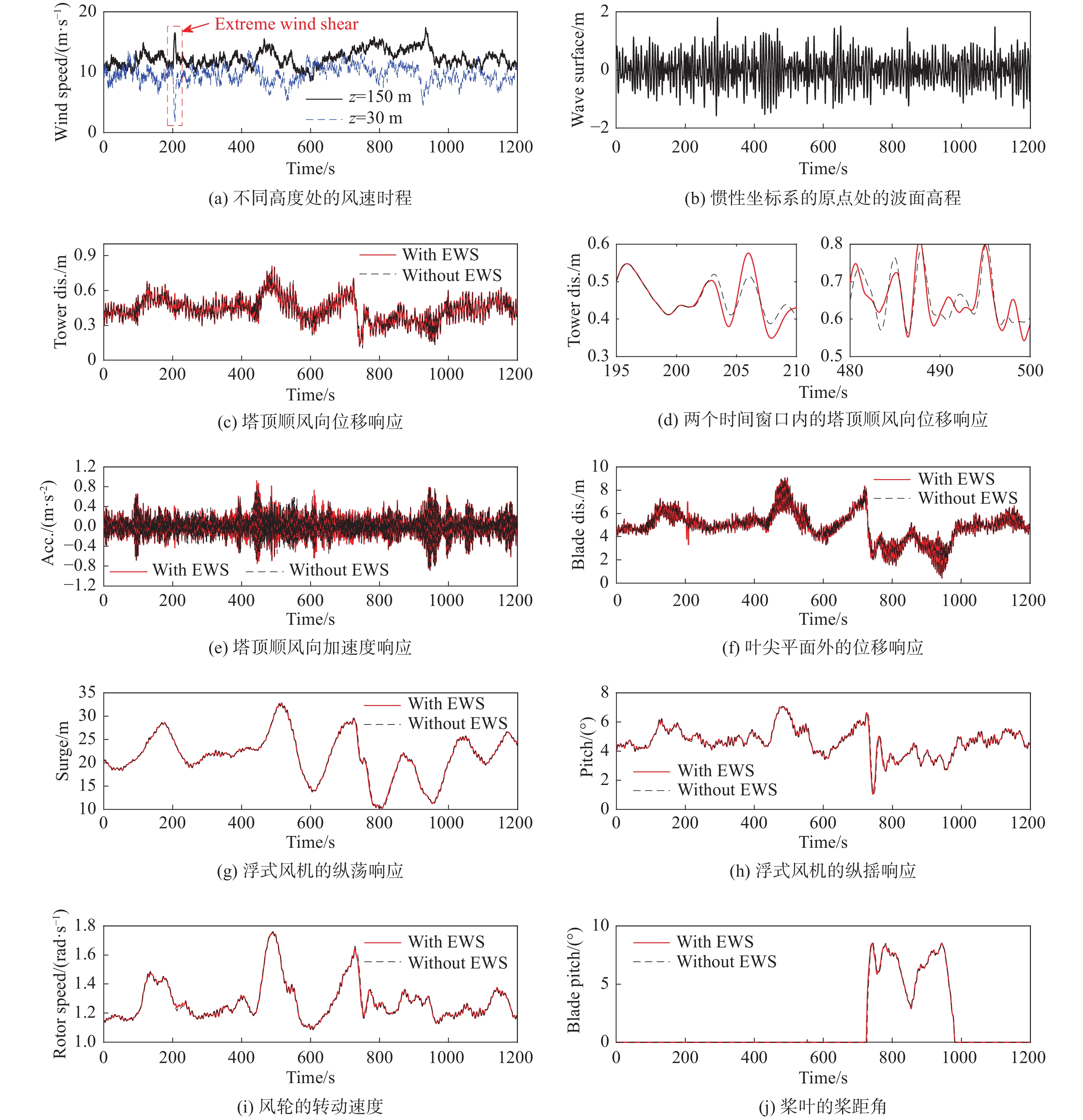
|
图 7 浮式风机结构在特定工况下的响应 Fig.7 Responses of the floating offshore wind turbine under specified load conditions |
从图7(a)可以看出,在施加极端风剪条件后,
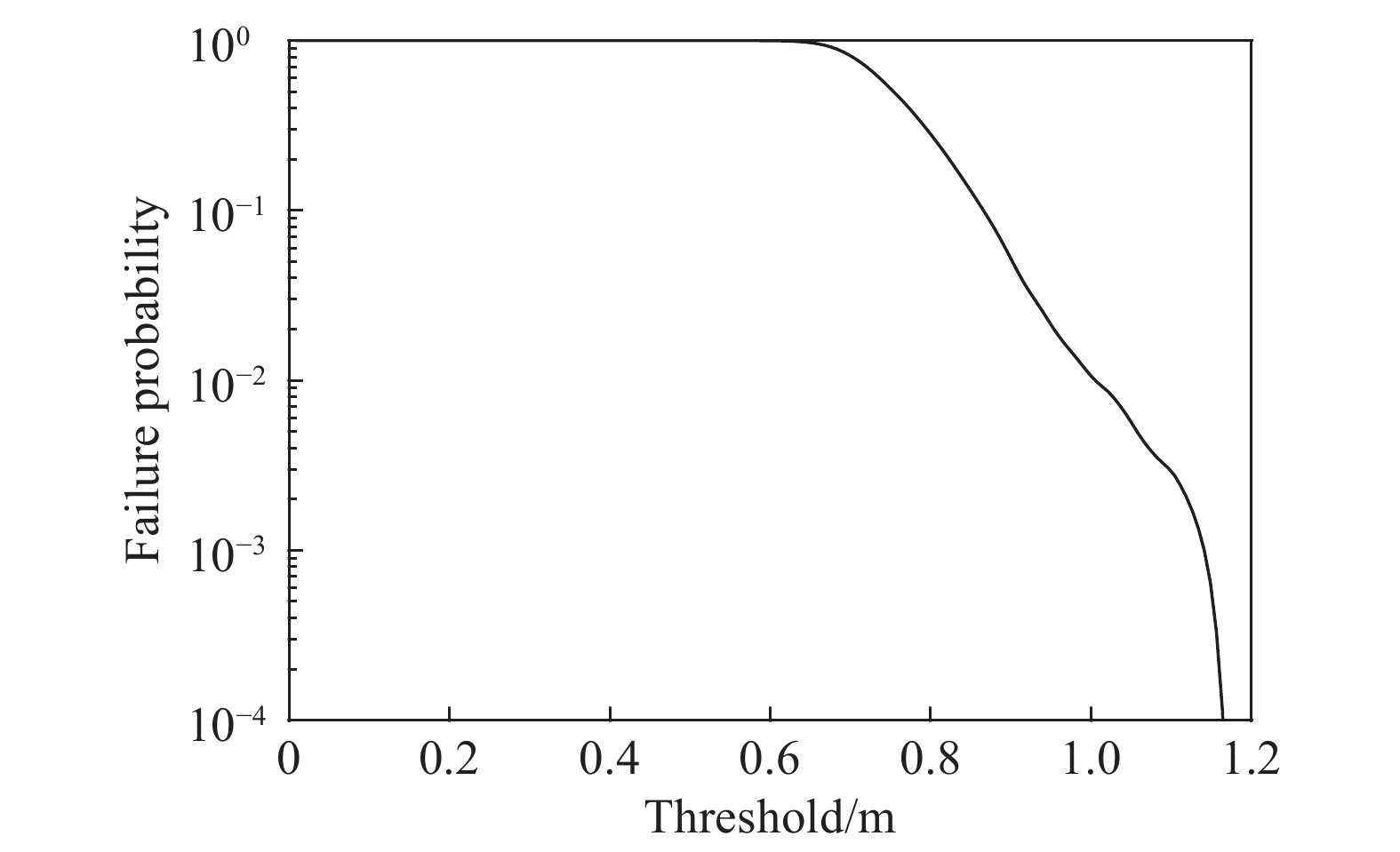
采用概率密度演化理论可以获得结构响应极值的概率分布。以塔顶顺风向位移为例,通过求解广义概率密度演化方程,得到其响应极值的概率密度函数如图8所示。在给定的失效阈值条件下,当塔顶位移响应超过该阈值时,即认为发生失效。由此可以得到不同失效阈值条件下的失效概率,如图9所示。
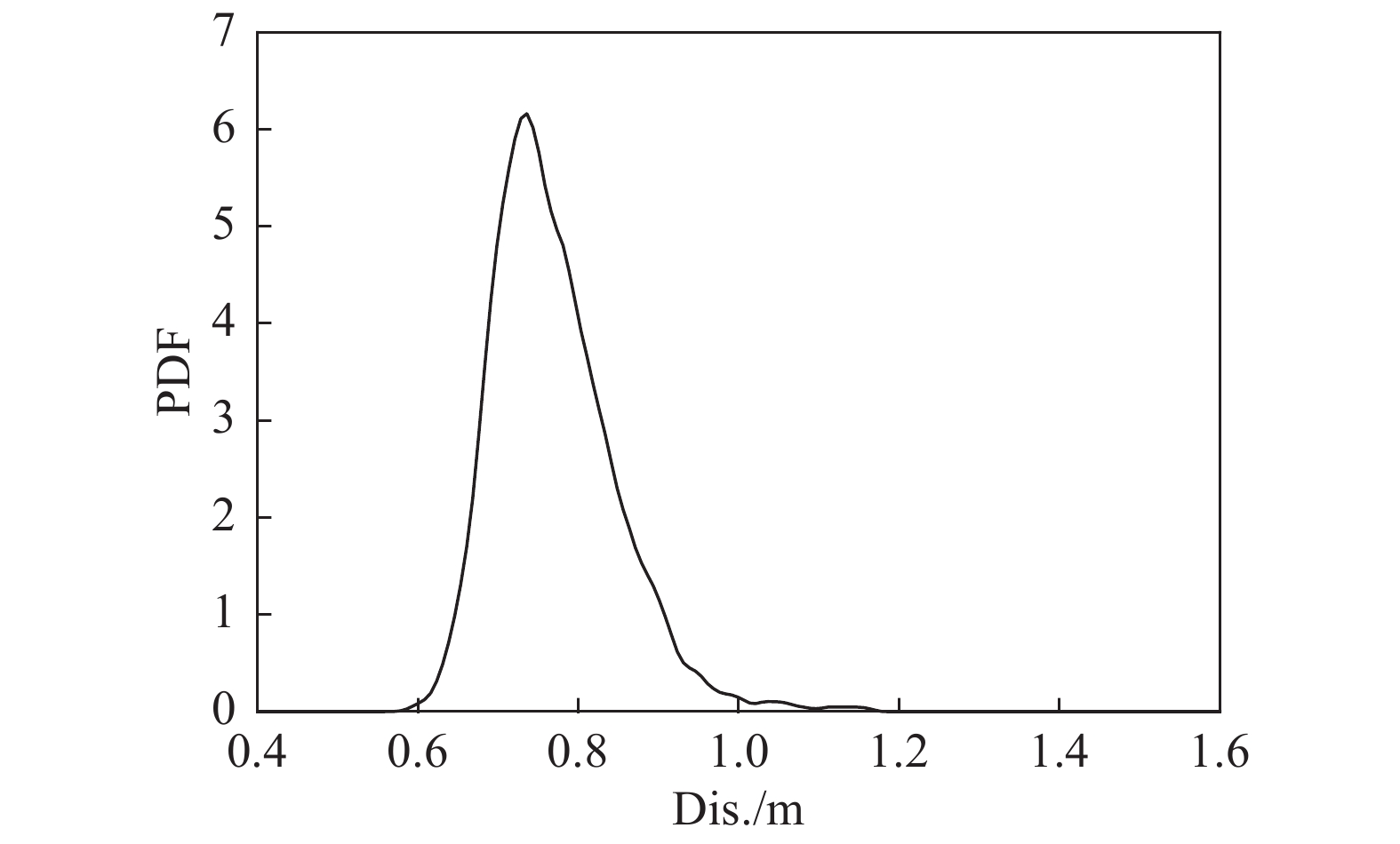
|
图 8 塔顶顺风向位移响应极值的概率密度函数 Fig.8 Probability density function of the extreme value of the fore-aft displacement response at the tower top |
|
图 9 失效概率随失效阈值变化关系 Fig.9 Relationship between failure probability and failure threshold |
作为示例,本文在分析浮式风机结构的可靠度时,仅考虑了塔顶位移。在实际中,应考虑多个指标,例如塔顶加速度、塔底应力以及浮式风机的纵摇响应等。概率密度演化理论能够同时考虑多个失效指标[5]。当同时采用多个失效指标分析时,可靠度结果可能发生变化。
4 结 论浮式风机结构的整体可靠性分析是进行基于可靠度优化设计的关键基础,对于大规模深远海风能的开发具有重要意义。本文针对海上单柱式浮式风机结构,首先介绍了一体化耦合动力学分析模型,然后建立了环境参数的联合概率分布模型以合理考虑风-浪联合作用,进而分析浮式风机结构在极端工况条件下的动力可靠度。主要研究结论如下:
1)对于当前兆瓦级浮式风机,柔性部件的弹性变形对浮式风机的刚体运动响应几乎没有影响,因此在建模过程中可以忽略这一因素,从而使建模方法与分析过程更为简便。本文基于这一思想,将多刚体动力学理论与有限元方法结合起来考察了浮式风机结构的一体化模型,不仅能够弥补一般多刚体动力学模型的不足,而且利用Kane方法便捷地考虑了系统中刚体运动对柔性部件变形的影响。虽然从理论上看,全耦合多柔性体模型(例如FAST)的建模方法考虑得更为全面,但是从实际工程应用的角度来看,本文所提的方法更为便捷。两种模型的对比分析结果表明了本文模型具有良好的精度。
2)在浮式风机结构的动力响应分析中,应当合理考虑风-浪联合作用。基于场址的长期风-浪观测数据并采用Copula方法,能够精确、便捷地建立风-浪多参数非线性相关的联合概率分布模型,从而合理地考虑风和波浪对结构的荷载效应。
3)基于概率密度演化理论的可靠度分析方法适用于海上大型浮式风机结构的整体可靠性分析。该方法不仅能够同时考虑外部激励和结构自身的随机性,而且能够获得结构响应的概率密度演化过程,同时具有很高的分析效率。
本文研究建立了海上大型浮式风机结构整体可靠性分析的基本框架,为进行基于整体可靠度的结构优化设计奠定了基础。由于我国东南海域的风电场常年遭受台风侵袭[38],因此在未来工作中需要进一步分析在台风等极端环境条件下的浮式风机结构整体可靠度,并开展基于整体可靠度的结构优化设计等研究。
| [1] |
CRUZ J, ATCHESON M. Floating offshore wind energy: the next generation of wind energy[M]. Springer, 2016. doi: 10.1007/978-3-319-29398-1
|
| [2] |
KARIMIRAD M. Offshore energy structures: for wind power, wave energy and hybrid marine platforms[M]. Springer, 2014. doi: 10.1007/978-3-319-12175-8
|
| [3] |
李嘉文, 唐友刚, 曲晓奇. 海上浮式风机运动对风机结构载荷影响研究[J]. 哈尔滨工程大学学报, 2018, 39(5): 881-888. LI J W, TANG Y G, QU X Q. Influence of motion on structural loads of offshore floating wind turbine[J]. Journal of Harbin Engineering University, 2018, 39(5): 881-888. (in Chinese) |
| [4] |
马远, 陈超核, 樊天慧, 等. Spar型浮式风机平台设计与水动力响应分析[J]. 中国海洋平台, 2020, 35(3): 1-5. MA Y, CHEN C H, FAN T H, et al. Design and hydrodynamic response analysis of spar offshore wind turbine platform[J]. China Offshore Platform, 2020, 35(3): 1-5. (in Chinese) |
| [5] |
LI J, CHEN J B. Stochastic dynamics of structures[M]. Singapore: John Wiley & Sons, Ltd, 2009. doi: 10.1002/9780470824269
|
| [6] |
陈建兵, 孙涛, 黄凯, 等. 大型海上风力发电高塔系统一体化分析建模研究[J]. 动力学与控制学报, 2017, 15(3): 268-278. CHEN J B, SUN T, HUANG K, et al. Study on integrated numerical modeling of offshore wind turbine tower systems[J]. Journal of Dynamics and Control, 2017, 15(3): 268-278. (in Chinese) |
| [7] |
ZHANG Z L, HØEG C. Dynamics and control of spar-type floating offshore wind turbines with tuned liquid column dampers[J]. Structural Control and Health Monitoring, 2020, 27(6): e2532. DOI:10.1002/stc.2532 |
| [8] |
万德成, 程萍, 黄扬, 等. 海上浮式风机气动力-水动力耦合分析研究进展[J]. 力学季刊, 2017, 38(3): 385-407. WAN D C, CHENG P, HUANG Y, et al. Overview of study on aero-and hydro-dynamic interaction for floating offshore wind turbines[J]. Chinese Quarterly of Mechanics, 2017, 38(3): 385-407. (in Chinese) |
| [9] |
SONG Y P, BASU B, ZHANG Z L, et al. Dynamic reliability analysis of a floating offshore wind turbine under wind-wave joint excitations via probability density evolution method[J]. Renewable Energy, 2021, 168: 991-1014. DOI:10.1016/j.renene.2020.12.093 |
| [10] |
AL-SOLIHAT M K, NAHON M, BEHDINAN K. Dynamic modeling and simulation of a spar floating offshore wind turbine with consideration of the rotor speed variations[J]. Journal of Dynamic Systems, Measurement, and Control, 2019, 141(8): 081014. DOI:10.1115/1.4043104 |
| [11] |
CHEN J H, HU Z Q, LIU G L, et al. Comparison of different dynamic models for floating wind turbines[J]. Journal of Renewable and Sustainable Energy, 2017, 9(6): 063304. DOI:10.1063/1.5002750 |
| [12] |
LEMMER F, YU W, LUHMANN B, et al. Multibody modeling for concept-level floating offshore wind turbine design[J]. Multibody System Dynamics, 2020, 49(2): 203-236. DOI:10.1007/s11044-020-09729-x |
| [13] |
DNVGL. Environmental conditions and environmental loads, DNVGL-RP-C205[S/OL]. 2017. https://fenix.tecnico.ulisboa.pt/downloadFile/1689468335664874/DNVGL-RP-C205_2017-Environment.pdf
|
| [14] |
贺广零, 仲政. 风浪联合作用下的海上单桩基础风力发电机组动力响应分析[J]. 电力建设, 2012, 33(5): 1-7. HE G L, ZHONG Z. Dynamic response analysis of offshore wind turbine systems with monopile foundation under combined wind & wave loads[J]. Electric Power Construction, 2012, 33(5): 1-7. (in Chinese) |
| [15] |
STEWART G M, ROBERTSON A, JONKMAN J, et al. The creation of a comprehensive metocean data set for offshore wind turbine simulations[J]. Wind Energy, 2016, 19(6): 1151-1159. DOI:10.1002/we.1881 |
| [16] |
SILVA-GONZÁLEZ F, HEREDIA-ZAVONI E, MONTES-ITURRIZAGA R. Development of environmental contours using Nataf distribution model[J]. Ocean Engineering, 2013, 58: 27-34. DOI:10.1016/j.oceaneng.2012.08.008 |
| [17] |
NELSEN R B. An introduction to copulas (2nd ed. )[M]. New York: Springer, 2006.
|
| [18] |
LI X, ZHANG W. Long-term assessment of a floating offshore wind turbine under environmental conditions with multivariate dependence structures[J]. Renewable Energy, 2020, 147: 764-775. DOI:10.1016/j.renene.2019.09.076 |
| [19] |
TAO J J, CHEN J B, REN X D. Copula-based quantification of probabilistic dependence configurations of material parameters in damage constitutive modeling of concrete[J]. Journal of Structural Engineering, 2020, 146(9): 04020194. DOI:10.1061/(asce)st.1943-541x.0002729 |
| [20] |
MELCHERS R E, BECK A T. Structural reliability analysis and prediction[M]. Chichester, UK: John Wiley & Sons Ltd, 2017.
|
| [21] |
MORATÓ A, SRIRAMULA S, KRISHNAN N. Kriging models for aero-elastic simulations and reliability analysis of offshore wind turbine support structures[J]. Ships and Offshore Structures, 2019, 14(6): 545-558. DOI:10.1080/17445302.2018.1522738 |
| [22] |
KANE T R, LEVINSON D A. Dynamics: theory and applications[M]. McGraw-Hill College, 1985.
|
| [23] |
李德源, 叶枝全, 陈严. 风力机旋转叶片的多体动力学数值分析[J]. 太阳能学报, 2005, 26(4): 473-481. LI D Y, YE Z Q, CHEN Y. Multi-body dynamics numerical analysis of rotating blade of horizontal axis wind turbine[J]. Acta Energiae Solaris Sinica, 2005, 26(4): 473-481. (in Chinese) |
| [24] |
宋玉鹏. 大型海上浮式风力发电机组结构整体动力学建模与可靠性分析[D]. 上海: 同济大学, 2021.
|
| [25] |
BURTON T, JENKINS N, SHARPE D, et al. Wind energy handbook (2nd ed. ) [M]. West Sussex: John Wiley & Sons, 2011.
|
| [26] |
JONKMAN J M. Dynamics of offshore floating wind turbines—model development and verification[J]. Wind Energy, 2009, 12(5): 459-492. DOI:10.1002/we.347 |
| [27] |
FALTINSEN O M. Sea loads on ships and offshore structures [M]. Cambridge: Cambridge University Press, 1990.
|
| [28] |
HALL M, GOUPEE A. Validation of a lumped-mass mooring line model with DeepCwind semisubmersible model test data[J]. Ocean Engineering, 2015, 104: 590-603. DOI:10.1016/j.oceaneng.2015.05.035 |
| [29] |
JONKMAN J, BUTTERFIELD S, MUSIAL W, et al. Definition of a 5-MW reference wind turbine for offshore system development[R]. NREL/TP-500-38060, 2009. https://www.nrel.gov/docs/fy09osti/38060.pdf doi: 10.2172/947422
|
| [30] |
JONKMAN J M. Definition of the floating system for phase IV of OC3[R]. NREL/TP-500-47535, 2010. https://www.nrel.gov/docs/fy10osti/47535.pdf doi: 10.2172/979456
|
| [31] |
IEC International Standard. Wind energy generation systems-Part 1: Design requirements (4th ed. ), IEC 61400-1[S]. Switzerland: International Electrotechnical Commision (IEC), 2019.
|
| [32] |
DEE D P, UPPALA S M, SIMMONS A J, et al. The ERA-Interim reanalysis: configuration and performance of the data assimilation system[J]. Quarterly Journal of the Royal Meteorological Society, 2011, 137(656): 553-597. DOI:10.1002/qj.828 |
| [33] |
FAZERES-FERRADOSA T, TAVEIRA-PINTO F, VANEM E, et al. Asymmetric copula–based distribution models for met-ocean data in offshore wind engineering applications[J]. Wind Engineering, 2018, 42(4): 304-334. DOI:10.1177/0309524x18777323 |
| [34] |
CHEN J B, SONG Y P, PENG Y B, et al. Simulation of homogeneous fluctuating wind field in two spatial dimensions via a joint wave number–frequency power spectrum[J]. Journal of Engineering Mechanics, 2018, 144(11): 04018100. DOI:10.1061/(asce)em.1943-7889.0001525 |
| [35] |
CHEN J B, SONG Y P, PENG Y B, et al. An efficient rotational sampling method of wind fields for wind turbine blade fatigue analysis[J]. Renewable Energy, 2020, 146: 2170-2187. DOI:10.1016/j.renene.2019.08.015 |
| [36] |
LI J, PENG Y B, YAN Q. Modeling and simulation of fluctuating wind speeds using evolutionary phase spectrum[J]. Probabilistic Engineering Mechanics, 2013, 32: 48-55. DOI:10.1016/j.probengmech.2013.01.001 |
| [37] |
YANG J Y, TAO J J, SUDRET B, et al. Generalized F-discrepancy-based point selection strategy for dependent random variables in uncertainty quantification of nonlinear structures[J]. International Journal for Numerical Methods in Engineering, 2020, 121(7): 1507-1529. DOI:10.1002/nme.6277 |
| [38] |
柯世堂, 徐璐. 考虑中尺度台风效应的大型风力机体系气动性能分析[J]. 东南大学学报(自然科学版), 2019, 49(2): 340-347. KE S T, XU L. Analysis on aerodynamic performance of large wind turbine system considering mesoscale typhoon effect[J]. Journal of Southeast University (Natural Science Edition), 2019, 49(2): 340-347. (in Chinese) |
 2022, Vol. 40
2022, Vol. 40


