0 引　言

化学反应流不仅广泛存在于自然界中，更在人类日常生活、工业生产、航空航天和国防建设等诸多领域发挥着越来越重要的作用^[1-3]。在化学反应流中，各类流体动力学行为和化学反应过程相互耦合，具有典型的流体力学非平衡、热力学非平衡和化学非平衡效应，表现出丰富多变的物理化学现象^[1-3]。对于此类非定常、非平衡的复杂物理化学系统，不能使用定常流场的解析方法或数值模型进行研究，而需要使用包含多物理场耦合和时空演化过程的物理模型。尤其是高超声速飞行器^[2-4]还同时面临稀薄气体效应、化学反应效应和壁面热流效应等外界因素的影响。这些极端复杂条件对如何有效模拟和预测高超声速飞行器的运行过程提出挑战。因此，高速反应流的数值建模与模拟研究在航空航天等领域具有特别重要的实际应用背景，是进一步提升航空航天工程技术的关键问题之一。

相对于高超声速飞行器，航天飞行器再入过程跨越了更加宽泛的时空尺度。具体来讲，航天飞行器以（超）高马赫数依次经历稀薄自由分子流区、过渡流区、滑移流区以及连续流区，这一经历伴随着复杂的变密度、变温度、变速度、电离和化学反应等真实飞行环境。在各个流体区域，气体物性表现出显著差异，其绕流状态具有典型的跨尺度效应。同时，几何尺寸差异明显的外形部件也会使飞行器不同区域表现出多流区共存的多尺度混合流动现象。在高超声速再入过程中，还具有强黏性、高摩阻、高熵层、强气动加热、热力学与化学非平衡相互耦合等典型特征^[5-6]。为此，需要构建准确高效、稳定可靠的跨尺度模型，用以研究分析高超声速飞行器跨流域飞行的气动力热机理，明晰复杂绕流的时空变化特点以及非平衡热化学行为表征。

然而，传统的宏观数值研究大都基于连续性假设，侧重于模拟研究系统宏观演化过程，忽略了实时伴随流体宏观行为的丰富的热力学非平衡效应，导致其应用范围不够广泛、数值仿真结果不够精确。目前，基于Boltzmann方程的动理学模型具有微介观尺度的优势，相关方法的应用研究已经成为国际国内的热点课题，包括格子气自动机（lattice gas automaton，LGA）、格子玻尔兹曼方法（lattice Boltzmann method，LBM）、离散玻尔兹曼方法（discrete Boltzmann method，DBM）、离散速度方法、离散统一气体动理论方法、气体动理论统一算法和矩方法等。

作为一种元胞自动机，LGA不仅是解方程（恢复方程）的一种全新的数值方法，更是研究各类复杂系统的一种基本工具^[7]。最初，LGA由法国的Hardy、Pomeau、De Pazzis于1973年首次提出，目标是能够模拟Navier-Stokes（N-S）方程组描述的流体系统，但是由于该模型旋转不变性的缺失，导致它具有高度各向异性^[8]。后来，Frisch、Hasslacher、Pomeau在1986年优化了LGA模型，其格子矢量具有四阶张量对称性^[9]。时至今日，LGA已经被成功应用于流体力学、化学、电磁学、热声学等领域。

LGA的基本思想是：不同的微观行为可以导致相似的宏观表征，虚拟粒子在网格上迁移和碰撞的过程保持物理量守恒，如质量、动量、能量守恒^[7]。为了提高计算效率，这种虚拟世界的微观动力学应该尽可能简单^[7]。此外，LGA可看作是LBM和DBM的鼻祖。广义上讲，LGA及其后代动力学模型被认为具有许多相似优点：1）设计方案简单易行，因此便于编写代码和检验程序。2）碰撞规则具有局部性，因此非常适合大规模并行计算。3）可通过选取合适的边界条件来模拟具有复杂几何结构的系统。然而，LGA具有统计噪声等问题，而LBM和DBM能够有效避免该问题。

近30年来，LBM被成功应用到诸多复杂流体系统^[10-12]，并且在早期就被拓展到化学反应流领域。早在1997年，欧洲院士Succi等^[13]首次提出燃烧系统的LBM，其限制条件包括：化学反应极快、流场不可压、反应热对流场没有影响。2015年，日本的Yamamoto等^[14]使用LBM模拟了三维空隙结构系统中的燃烧现象。2018年，德国Hosseini等的课题组^[15]构建了多组分系统的LBM，并解决了扩散方程误差引起的质量不守恒问题。同时，国内学者也在相关领域做出了突出贡献。华中科技大学的陈胜等^[16]把LBM应用到二维和三维低马赫数燃烧系统，将流体密度和温度场直接耦合。西安交通大学的陶文铨院士、何雅玲院士等的课题组^[17-18]使用LBM研究包含多相、多组分、化学反应的能源转换系统。另外，国内外还有许多其他优秀科研团队将LBM应用到包含溶解、沉淀、流固耦合等复杂因素的反应流系统^[19-21]。

尽管传统LBM的应用研究已经取得了巨大进步，但基本都是还原传统宏观控制方程的解法器，基本没有聚焦于详细的热力学非平衡信息，也没有实现真正意义上的化学反应和可压缩流体的耦合。作为一种新型的微介观动理学方法，近几年发展起来的DBM能够解决物理精度与计算效率之间的矛盾。DBM是玻尔兹曼方程在速度空间的特殊离散化形式，可以看作传统LBM的进一步发展或变异^[22-36]。值得说明的是，DBM继承了玻尔兹曼方程描述非平衡物理系统的主要功能。可以证明，一方面DBM在连续性极限条件下能够恢复宏观流体控制方程组；另一方面DBM还包含宏观流动方程组之外的热力学非平衡效应^[22-36]。因此，DBM可用于处理宏观模型失效、非平衡效应较为显著的微尺度物理系统、稀薄气体系统和滑移层流体区域等相关问题^[31]。

目前，DBM在化学反应流方面已经得到初步应用。2013年，DBM已被初步发展到爆轰领域，并被用于模拟分析爆轰波附近的非平衡效应^[22]。2014年，林传栋等^[23]构建并使用极坐标系DBM模拟研究了内爆和外爆过程的非平衡强度，并从动理学角度分析了粒子速度分布函数的主要特征。2015年，许爱国等^[24]构建并使用多松弛DBM模拟研究了黏性和热传导在爆轰系统中对局域和全域非平衡效应的影响。2016年，张玉东等^[26]使用DBM模拟研究了负温度系数对爆轰系统的影响机理。之后，林传栋等构建了多组分DBM用于模拟预混、非预混和部分预混反应流系统^[27]，又使用高效、准确的多松弛DBM研究了不稳定反应热流演化过程的非平衡行为^[30]。

为了在连续性极限条件下恢复N-S方程组或者更高阶的流体力学方程组，并且为了包含更准确和详实的热力学非平衡信息，要求DBM包含足够多的动理学矩关系。现有的DBM模型至少能够恢复N-S方程组，与之对应，至少包含了7个张量形式的动理学矩关系。例如，对于二维DBM，当包含额外自由度时，需要构建16速度的离散速度模型^[30]，与之对应，需要包含16组形式统一的DBM演化方程。然而，在实际的物理系统中，有时（或有些区域）物理场蕴含的非平衡效应可能较弱，不需要特精确和太费时的模拟工具，而需要使用较为简洁和高效的模型。

为此，本文首次提出并构建了简化的二维DBM。该模型只包含9个独立的动理学矩关系，并且在连续性极限条件下能够恢复带有化学反应的Euler方程组。该DBM包含9个离散速度，基于9组形式统一的DBM演化方程。相对于之前构建的16速度模型^[30]或者24速度模型^[24]，该DBM具有更高的运算效率。本项目的开展有助于推动动理学方法在化学反应流的发展应用，并进一步促进其在复杂多尺度物理系统的模拟研究。

1 二维简化DBM 1.1 离散玻尔兹曼方程

化学反应流的离散玻尔兹曼方程如下：

$ \frac{{\partial {f_i}}}{{\partial t}} + {{\boldsymbol{v}}_i} \cdot \nabla {f_i} = - \frac{1}{\tau }\left( {{f_i} - f_i^{{\rm{eq}}}} \right) + {R_i} $

(1)

式中： $ t $ 为时间， $ \tau $ 为松弛时间， $ \nabla $ 为Hamilton算子， ${f_i}$ 为离散化的速度分布函数， $f_i^{{\rm{eq}}}$ 为离散化的平衡态速度分布函数，下标 $i = 1,{\text{ }}2,{\text{ }} \cdots ,{\text{ }}N$ 用于标记离散速度，本文提出的离散速度总数 $N = 9$ 。方程右侧的 $ {R_i} $ 为化学反应源项，用于描述化学反应引起的分布函数的改变率，其表达式见式（22）。

本文构建了二维九速模型，其离散速度 $ {{\boldsymbol{v}}_i} $ 的数学形式为：

$ {{\boldsymbol{v}}_i} = \left\{ \begin{gathered} {v_a}\left( {\cos \frac{{2{\text{π}} i - 2{\text{π}} }}{3},\sin \frac{{2{\text{π}} i - 2{\text{π}} }}{3}} \right),\;\;\;\;{\text{1}} \leqslant i \leqslant 3 \hfill \\ {v_b}\left( {\cos \frac{{2{\text{π}} i - 2{\text{π}} }}{3},\sin \frac{{2{\text{π}} i - 2{\text{π}} }}{3}} \right),\;\;\;\;{\text{4}} \leqslant i \leqslant 6 \hfill \\ {v_c}\left( {\cos \frac{{2{\text{π}} i - 2{\text{π}} }}{3},\sin \frac{{2{\text{π}} i - 2{\text{π}} }}{3}} \right),\;\;\;\;{\text{7}} \leqslant i \leqslant 9 \hfill \\ \end{gathered} \right. $

(2)

式中： $ {v_a} $ 、 $ {v_b} $ 、 $ {v_c} $ 为可调参数，其数值可以是正数或负数，用于控制离散速度的大小和方向。

图1给出了两种情况下的离散速度示意图，其中图1（a）对应 $ {v_a} > 0 $ 、 $ {v_b} > 0 $ 、 $ {v_c} > 0 $ ；图1（b）对应 $ {v_a} > 0 $ 、 $ {v_b} > 0 $ 、 $ {v_c} < 0 $ 。可以看出，当 $ {v_c} $ 的正负号改变后，其对应的速度方向也随之改变。同理，当 $ {v_a} $ 或者 $ {v_b} $ 的正负号改变后，其控制的速度方向也随之改变。需要说明的是，对于控制参数 $ {v_a} $ 、 $ {v_b} $ 、 $ {v_c} $ 数值大小的选取，需要满足式（15）中的矩阵 ${\boldsymbol{M}}$ 可逆。

同时，为了描述分子转动和振动对应的内能，引入额外自由度 $I$ ，并引入变量：

$ {\eta _i} = \left\{ \begin{gathered} {\eta _a},\;\;\;\; 1 \leqslant i \leqslant 3 \hfill \\ {\eta _b},\;\;\;\; 4 \leqslant i \leqslant 6 \hfill \\ {\eta _c},\;\;\;\; 7 \leqslant i \leqslant 9 \hfill \\ \end{gathered} \right. $

(3)

与式（2）中的离散速度类似，控制参数 $ {\eta _a} $ 、 $ {\eta _b} $ 、 $ {\eta _c} $ 数值大小的选取，也需要满足式（15）中的矩阵 $ {\boldsymbol{M}} $ 可逆。另外，比热比 $\gamma $ 与额外自由度 $I$ 的关系为：

$ \gamma = \frac{{D + I + 2}}{{D + I}} $

(4)

其中 $ D = 2 $ 为物理空间的维度数。因此，该DBM可以描述不同比热比的化学反应流系统。实际上，这种内能引入方式与传统LBM势能/内能/总能模型的引入思路是一致的，此类方法均可以看作是通过改变碰撞不变量而调节比热比的一种手段。

1.2 动理学矩关系

流体的密度 $ \; \rho $ 、流速 $ {\boldsymbol{u}} $ 、能量 $ E $ 与离散速度分布函数 $ {f_i} $ 的关系式如下：

$ \rho = \sum\nolimits {{f_i}} $

(5)

$ \rho {\boldsymbol{u}} = \sum\nolimits {{f_i}{{\boldsymbol{v}}_i}} $

(6)

$ E = \frac{1}{2}\sum\nolimits {{f_i}\left( {{{\left| {{{\boldsymbol{v}}_i}} \right|}^2} + \eta _i^2} \right)} $

(7)

通过式（5）～式（7），由离散分布函数可以计算得到系统的密度、速度和能量。根据温度与能量的关系：

$ E = \frac{1}{2}\rho {\left| {\boldsymbol{u}} \right|^2} + \frac{1}{{\gamma - 1}}\rho T $

(8)

可得温度：

$ T = \left( {\gamma - 1} \right)\left( {\frac{1}{\rho }E - \frac{1}{2}{{\left| {\boldsymbol{u}} \right|}^2}} \right) $

(9)

另外，平衡态离散速度分布函数 $f_i^{{\rm{eq}}}$ 满足的动理学矩关系如下：

$ \rho = \sum\nolimits {f_i^{{\rm{eq}}}} $

(10)

$ \rho {u_{\alpha} } = \sum\nolimits {f_i^{{\rm{eq}}}{v_{i\alpha }}} $

(11)

$ \rho \left[ {{u^2} + \left( {D + I} \right)T} \right] = \sum\nolimits {f_i^{{\rm{eq}}}\left( {v_i^2 + \eta _i^2} \right)} $

(12)

$ \rho \left( {{\delta _{\alpha \beta }}T + {u_{\alpha} }{u_{\beta} }} \right) = \sum\nolimits {f_i^{{\rm{eq}}}{v_{i\alpha }}{v_{i\beta }}} $

(13)

$ \rho {u_{\alpha} }\left[ {\left( {D + I + 2} \right)T + {u^2}} \right] = \sum\nolimits {f_i^{{\rm{eq}}}\left( {v_i^2 + \eta _i^2} \right){v_{i\alpha }}} $

(14)

其中 $ u = \left| {\boldsymbol{u}} \right| $ 为流速大小， ${u_{\alpha} }$ 为流速 $ {\boldsymbol{u}} $ 在 $ \alpha $ 方向的分量， $ {v_i} = \left| {{{\boldsymbol{v}}_i}} \right| $ 为离散速度大小， $ {v_{i\alpha }} $ 为离散速度在 $ {{\boldsymbol{v}}_i} $ 在 $ \alpha $ 方向的分量。式（10）～式（14）可以统一写成以下数学形式：

$ {{\boldsymbol{\hat f}}^{{{\rm{eq}}}}} = {\boldsymbol{M}}{{\boldsymbol{f}}^{{{\rm{eq}}}}} $

(15)

上式中 $\;{{\boldsymbol{f}}^{{\rm{eq}}}} = {\left( {\begin{array}{*{20}{c}} {f_1^{{\rm{eq}}}} & {f_2^{{\rm{eq}}}} & \cdots & {f_N^{{\rm{eq}}}} \end{array}} \right)^{\text{T}}}$ 为离散化的平衡态速度分布函数 $f_i^{{\rm{eq}}}$ 组成的列矩阵； ${{\hat{\boldsymbol f}}^{{\rm{eq}}}} = {\left( {\begin{array}{*{20}{c}} {\hat f_1^{{\rm{eq}}}} & {\hat f_2^{{\rm{eq}}}} & \cdots & {\hat f_N^{{\rm{eq}}}} \end{array}} \right)^{\text{T}}}$ 为动理学矩 $\hat f_i^{{\rm{eq}}}$ 组成的列矩阵，其元素依次为： $\hat f_1^{{\rm{eq}}} = \rho$ ， $\hat f_2^{{\rm{eq}}} = \rho {u_x}$ ， $\hat f_3^{{\rm{eq}}} = \rho {u_y}$ ， $\hat f_4^{{\rm{eq}}} = \rho \left[ {\left( {D + I} \right)T + {u^2}} \right]$ ， $\hat f_5^{{\rm{eq}}} = \rho \left( {T + u_x^2} \right)$ ， $\hat f_6^{{\rm{eq}}} = \rho {u_x}{u_y}$ ， $\hat f_7^{{\rm{eq}}} = \rho \left( {T + u_y^2} \right)$ ， $\hat f_8^{{\rm{eq}}} = \rho {u_x}\left[ {\left( {D + I + 2} \right)T + {u^2}} \right]$ ， $\hat f_9^{{\rm{eq}}} = \rho {u_y}\left[ {\left( {D + I + 2} \right)T + {u^2}} \right]$ ； $ {\boldsymbol{M}} $ 为用于映射速度空间和动理学矩空间的 $ N \times N $ 方阵，其元素分别为： ${M_{1i}} = 1$ ， ${M_{2i}} = {v_{ix}}$ ， ${M_{3i}} = {v_{iy}}$ ， ${M_{4i}} = v_i^2 + \eta _i^2$ ， ${M_{5i}} = v_{ix}^2$ ， ${M_{6i}} = {v_{ix}}{v_{iy}}$ ， ${M_{7i}} = v_{iy}^2$ ， ${M_{8i}} = \left( {v_i^2 + \eta _i^2} \right){v_{ix}}$ ， ${M_{9i}} = \left( {v_i^2 + \eta _i^2} \right){v_{iy}}$ 。由公式（15）可得：

$ {{\boldsymbol{f}}^{{\rm{eq}}}} = {{\boldsymbol{M}}^{ - 1}}{{\boldsymbol{\hat f}}^{{\rm{eq}}}} $

(16)

其中 $ {{\boldsymbol{M}}^{ - 1}} $ 为矩阵 $ {\boldsymbol{M}} $ 的逆矩阵。上式即为平衡态分布函数的计算方式。

1.3 化学反应进程

对于化学反应进程的描述，可以使用（半）经验模型、简化或者详细的化学反应机理。本文采用两步化学反应模型^[37]，即使用变量 $\xi $ 描述热中性诱导区内的反应进程，使用变量 $\lambda $ 描述化学放热区内的反应进程。具体来讲，变量 $\xi $ 与 $\lambda $ 的时间改变率 $\xi ' $ 、 $\lambda ' $ 分别如下：

$ \xi ' = H{k_I}\exp \left[ {{E_I}\left( {T_s^{ - 1} - {T^{ - 1}}} \right)} \right] $

(17)

$ \lambda ' = \left( {1 - H} \right){k_R}\left( {1 - \lambda } \right)\exp \left( { - {E_R}{T^{ - 1}}} \right) $

(18)

其中 $ H $ 是 $\xi$ 的阶梯函数。 $\xi < 1$ 时， $H = 1$ ； $\xi \geqslant 1 $ 时， $H = 0$ 。参数 ${k_I}$ 和 ${k_R}$ 是速率常数， ${E_I}$ 和 ${E_R}$ 分别是点火和反应过程的活化能， ${T_s}$ 是预冲击波后的温度。

为了简单起见，本文忽略电离、热辐射、活性自由基和可逆反应等效应^[25]；同时，考虑较为一般的情况，即化学反应的时间尺度大于热力学弛豫时间，且小于流体系统的特征尺度^[25]。那么，由此可以进一步假设：化学反应引起的粒子速度分布函数的改变率近似等于平衡态速度分布函数的改变率，且在化学反应的时间尺度内，局部流体的密度和速度尚未来得及改变^[25]。

下面推导化学反应项的数学表达式。首先引入以下物理量：单位质量的反应物释放的化学能为 $Q$ ，在放热区内化学能的释放速率为 $E'$ ，相应的温度改变率为 $T'$ 。那么，化学反应项的理论表达式为：

$ R = \frac{{ - \left( {1 + D} \right)IT + I{{\left| {{\boldsymbol{v}} - {\boldsymbol{u}}} \right|}^2} + {\eta ^2}}}{{2I{T^2}}}{f^{{\rm{eq}}}}T' $

(19)

离散形式的化学反应项 $ {R_i} $ 需要满足下列关系式：

$ \iint {R\varPsi {{\rm{d}}} {\boldsymbol{v}}{{\rm{d}}} \eta } = \sum\nolimits {{R_i}} {\varPsi _i} $

(20)

其中， $\varPsi = 1$ 、 ${v_x}$ 、 ${v_y}$ 、 $v_x^2 + v_y^2 + {\eta ^2}$ 、 $v_x^2$ 、 ${v_x}{v_y}$ 、 $v_y^2$ 、 $\left( {{v^2} + {\eta ^2}} \right){v_x}$ 、 $\left( {{v^2} + {\eta ^2}} \right){v_y}$ ，与之对应 ${\varPsi _i} = 1$ 、 ${v_{ix}}$ 、 ${v_{iy}}$ 、 $v_{ix}^2 + v_{iy}^2 + \eta _i^2$ 、 $v_{ix}^2$ 、 ${v_{ix}}{v_{iy}}$ 、 $v_{iy}^2$ 、 $\left( {v_i^2 + \eta _i^2} \right){v_{ix}}$ 、 $\left( {v_i^2 + \eta _i^2} \right){v_{iy}}$ 。式（20）可以写成下列形式：

$ {\boldsymbol{\hat R}} = {\boldsymbol{MR}} $

(21)

上式中 $ {\boldsymbol{\hat R}} = {\left( {\begin{array}{*{20}{c}} {{{\hat R}_1}}&{{{\hat R}_2}}& \cdots &{{{\hat R}_N}} \end{array}} \right)^{\text{T}}} $ 为化学反应项动理学矩组成的列矩阵；其元素依次为： $ {\hat R_1} = 0 $ ， $ {\hat R_2} = 0 $ ， $ {\hat R_3} = 0 $ ， $ {\hat R_4} = 2\rho \lambda 'Q $ ， $ {\hat R_5} = {{2\rho \lambda 'Q} \mathord{\left/ {\vphantom {{2\rho \lambda 'Q} {\left( {D + I} \right)}}} \right. } {\left( {D + I} \right)}} $ ， $ {\hat R_6} = 0 $ ， $ {\hat R_7} = {{2\rho \lambda 'Q} \mathord{\left/ {\vphantom {{2\rho \lambda 'Q} {\left( {D + I} \right)}}} \right. } {\left( {D + I} \right)}} $ ， $ {\hat R_8} = {{2\rho {u_x}\lambda 'Q\left( {D + I + 2} \right)} \mathord{\left/ {\vphantom {{2\rho {u_x}\lambda 'Q\left( {D + I + 2} \right)} {\left( {D + I} \right)}}} \right. } {\left( {D + I} \right)}} $ ， ${\hat R_9} = {{2\rho {u_y}\lambda 'Q\left( {D + I + 2} \right)} \mathord{\left/ {\vphantom {{2\rho {u_y}\lambda 'Q\left( {D + I + 2} \right)} {\left( {D + I} \right)}}} \right. } {\left( {D + I} \right)}}$ 。 $ {\boldsymbol{R}} = {\left( {\begin{array}{*{20}{c}} {{R_1}}&{{R_2}}& \cdots &{{R_N}} \end{array}} \right)^{\text{T}}} $ 为化学反应项组成的列矩阵，由式（21）得：

$ {\boldsymbol{R}} = {{\boldsymbol{M}}^{ - 1}}{\boldsymbol{\hat R}} $

(22)

该式即为化学反应项的计算方式。

1.4 流体力学模型和非平衡物理量

理想气体状态方程 $ p = {n_{{\text{mol}}}}RT = {{\rho RT} \mathord{\left/ {\vphantom {{\rho RT} m}} \right. } m} $ ，其中 $ {n_{{\text{mol}}}} $ 为摩尔数密度， $ m $ 为粒子的摩尔质量， $ R = 8.31{\text{ J/(mo}}{{\text{l}}^{}} \cdot {\text{K)}} $ 为摩尔气体常量。本文采用无量纲参数，令 $ m = 1 $ 且 $ R = 1 $ ，因此 $ \rho = n $ 且 $ p = \rho T $ 。

通过Chapman-Enskog多尺度分析可以证明，在连续性极限条件下，该DBM模型可以恢复包含化学反应的Euler方程组，即：

$ \frac{{\partial \rho }}{{\partial t}} + \frac{{\partial \rho {u_{\alpha} }}}{{\partial {r_{\alpha} }}} = 0 $

(23)

$ \frac{{\partial \rho {u_{\alpha} }}}{{\partial t}} + \frac{\partial }{{\partial {r_{\alpha} }}}\left( {{\delta _{\alpha \beta }}p + \rho {u_{\alpha} }{u_{\beta} }} \right) = 0 $

(24)

$ \frac{{\partial E}}{{\partial t}} + \frac{\partial }{{\partial {r_{\alpha} }}}\left( {p{u_{\alpha} } + E{u_{\alpha} }} \right) = \rho \lambda 'Q $

(25)

式（23）～式（25）分别描述了质量守恒、动量守恒和能量守恒定律。特别是对于能量方程式（25），在化学反应过程中，化学能转化为系统其他形式的能量（转化速率为 $ \rho \lambda 'Q $ ），总能量保持不变。

需要说明的是，动理学关系式（10）～式（14）是从DBM获得Euler方程组的前提条件。对于前三个子式（10）～式（12），将方程中的 $f_i^{{\rm{eq}}}$ 替换为 ${f_i}$ ，等式依然成立；对于后面的两个子式（13）和式（14），将方程中的 $f_i^{{\rm{eq}}}$ 替换为 $ {f_i} $ ，等式不一定成立。实际上， $ {f_i} $ 动理学矩与 $f_i^{{\rm{eq}}}$ 动理学矩的偏差恰恰反映了物理系统偏离热力学平衡态的程度。也就是说，对于该模型可以计算下列非平衡量：

$ \Delta _{\alpha \beta }^* = \sum\nolimits {\left( {{f_i} - f_i^{{\rm{eq}}}} \right)v_{i\alpha }^*v_{i\beta }^*} $

(26)

$ \Delta _{\alpha} ^* = \sum\nolimits {\left( {{f_i} - f_i^{{\rm{eq}}}} \right)\left( {{v_i^*}^2 + \eta _i^2} \right)v_{i\alpha }^*} $

(27)

其中 $v_{i\alpha }^* = {v_{i\alpha }} - {u_{\alpha} }$ 为相对于流速 ${u_{\alpha} }$ 的本动速度。式（26）中的 $ \Delta _{\alpha \beta }^* $ 为非组织动量通量，包含三个独立变量 $ \Delta _{xx}^* $ 、 $ \Delta _{xy}^* $ 和 $ \Delta _{yy}^* $ ，其中 $ \Delta _{xx}^* $ 表示两倍 $x$ 自由度的内能偏离平均值的程度， $ \Delta _{yy}^* $ 表示两倍 $y$ 自由度的内能偏离平均值的程度， $ \Delta _{xy}^* $ 表示 $x$ 方向的非组织动量在 $y$ 方向的通量（或者 $y$ 方向的非组织动量在 $x$ 方向的通量）。另外，式（27）中的 $\Delta _{\alpha} ^*$ 为两倍非组织能量通量，包含两个独立变量 $ \Delta _x^* $ 和 $ \Delta _y^* $ ，其中 $ \Delta _x^* $ 表示两倍非组织能量通量在 $x$ 方向的分量， $ \Delta _y^* $ 表示两倍非组织能量通量在 $y$ 方向的分量。

可以看出，在物理描述功能方面，简化二维DBM除了具有Euler模型描述流体系统演化的功能之外，还具有描述一定热力学非平衡行为的功能。因此，该DBM动理学模型具有超越Euler模型物理描述范围的优势。也就是说，在该简化二维DBM中，DBM等价于带有化学反应的Euler方程组和包含少量非平衡效应的粗粒化模型。

需要说明的是，对于二维DBM，当对应包含额外自由度的N-S方程组时，需要构建16速度^[30]（或24速度^[24]）的离散速度模型，与之对应地需要包含16组^[30]（或24组^[24]）形式统一的DBM演化方程；当对应Burnett方程组时，至少需要26个离散速度和26组演化方程^[36]，计算量相应增大。然而，在实际的物理系统中，有时（或有些区域）物理场蕴含的非平衡效应可能较弱，不需要特精确和太费时的模拟手段，反而使用较为简洁和高效的模型更为可行。此时，仅有9个离散速度和9组演化方程的简化DBM更加可取。总之，简化DBM的优势为：离散速度数量较少、计算效率高。

另外，在已有的二维DBM中，平衡态分布函数和反应项都至少各自满足16个^[30]（或24个^[24]）独立的矩关系，DBM等价于带有化学反应的N-S方程组和包含较多非平衡效应的粗粒化模型。尤其对于文献[36]，平衡态分布函数满足26个独立的矩关系，该DBM等价于Burnett方程组和包含更多非平衡效应的粗粒化模型。在本文构建的简化模型中，平衡态分布函数和反应项都仅满足9个独立的矩关系。相比于已有的DBM，该DBM的局限性为：满足的动理学矩关系较少、物理精度较低，仅适用于热力学非平衡程度较弱的物理系统。

1.5 数值离散格式

DBM使用离散玻尔兹曼方程描述化学反应流的演化过程，该方程形式简单、易于编程。同时，该方程具有时空局域性特点，易于实现并行化，方便在高性能计算集群运行。另外，对于离散玻尔兹曼方程式（1）的时间和空间偏微分，可以借用已有的数值格式处理。本文使用的是二阶精度的Runge-Kutta格式和二阶精度的无波动、无自由参数的耗散有限差分格式（nonoscillatory and nonfree-parameter dissipation finite difference scheme，NND）^[38]分别用于处理方程式（1）的时间和空间偏微分。

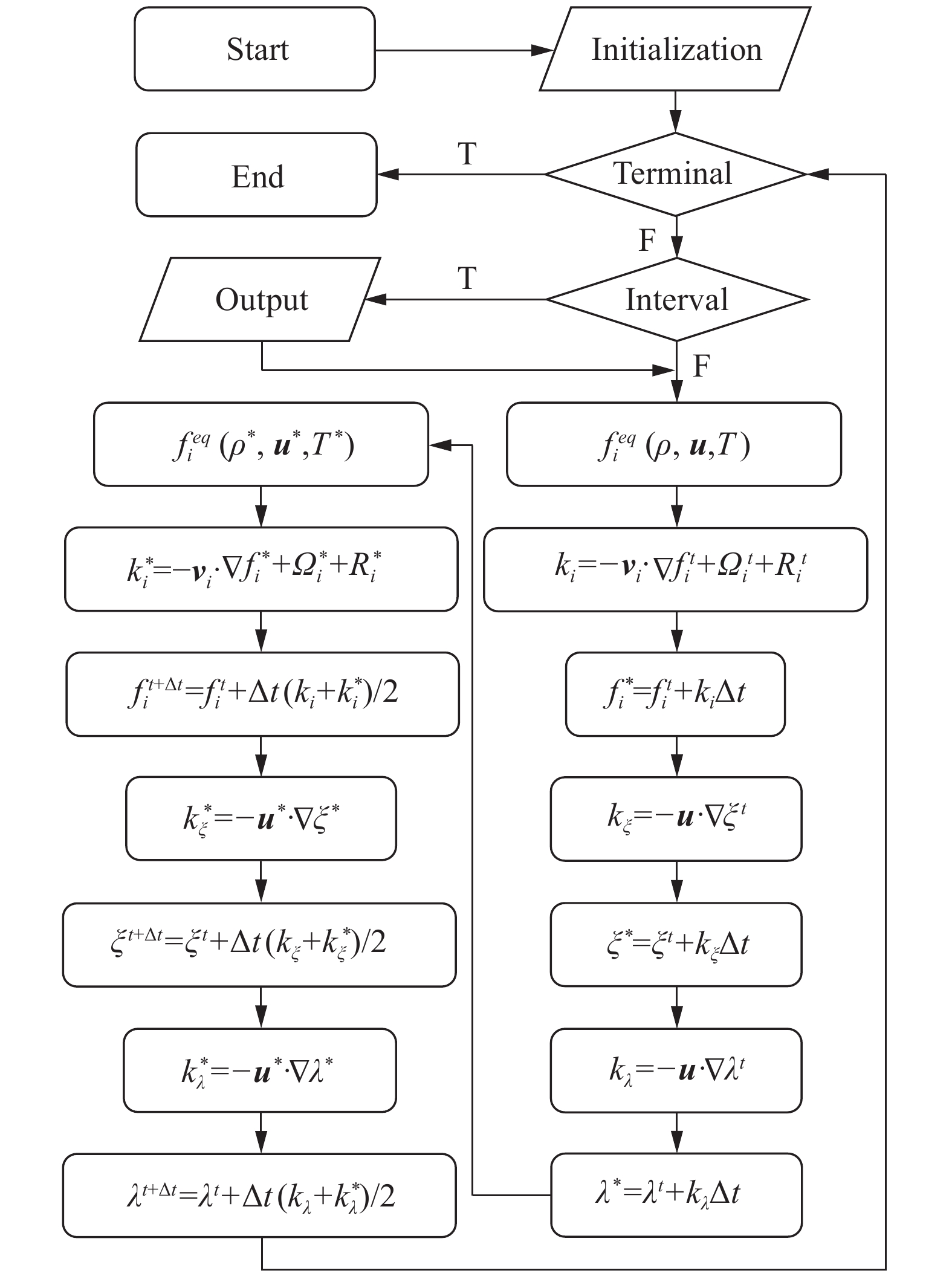
1.5.1 Runge-Kutta格式

本文采用Runge-Kutta格式处理时间离散化问题，具体计算流程见图2。

1）程序的开头是初始化，根据物理场的初始条件，输入参数；

2）根据给定的时间步数，即程序循环周期，判断是否终止运行；

3）根据给定的时间间隔，判断是否输出数值结果；

4）根据离散速度分布函数 ${f_i}$ ，计算宏观物理量（ $\rho $ ， ${\boldsymbol{u}}$ ， $ T $ ）；

5）根据宏观物理量（ $\rho $ ， ${\boldsymbol{u}}$ ， $ T $ ），计算平衡态离散速度分布函数 $f_i^{{\rm{eq}}}\left( {\rho ,{\boldsymbol{u}},T} \right)$ ；

6）根据宏观物理量（ $\rho $ ， ${\boldsymbol{u}}$ ， $ T $ ）、化学反应进程 $\lambda $ ，计算化学反应项；

7）考虑对流项、碰撞项和反应项对分布函数的改变，得到离散速度分布函数 $f_i^*$ ，同时更新化学反应进程 ${\xi ^*}$ 和 ${\lambda ^*}$ ；

8）根据离散速度分布函数 $f_i^*$ ，计算宏观物理量（ ${\rho ^*}$ ， ${{\boldsymbol{u}}^*}$ ， $ {T^*} $ ）；

9）根据宏观物理量（ ${\rho ^*}$ ， ${{\boldsymbol{u}}^*}$ ， $ {T^*} $ ），计算平衡态离散速度分布函数 $f_i^{{\rm{eq}}}\left( {{\rho ^*},{{\boldsymbol{u}}^*},{T^*}} \right)$ ；

10）根据宏观物理量（ ${\rho ^*}$ ， ${{\boldsymbol{u}}^*}$ ， $ {T^*} $ ）和化学反应进程 ${\lambda ^*}$ ，计算化学反应项；

11）考虑对流项、碰撞项和反应项对分布函数的改变，得到离散速度分布函数 $f_i^{t + \Delta t}$ ，同时更新化学反应进程为 ${\xi ^{t + \Delta t}}$ 和 ${\lambda ^{t + \Delta t}}$ 。

需要补充说明的是第4～7步依次与第8～11步相似。

1.5.2 NND格式

NND有限差分格式用于处理空间偏微分，具体如下：

$ {v_{ir}}\frac{{\partial {f_i}}}{{\partial r}} = \frac{1}{{\Delta r}}\Bigg[H\Bigg(ir + \frac{1}{2}\Bigg) - H\Bigg(ir - \frac{1}{2}\Bigg)\Bigg] $

(28)

$ H\Bigg(ir + \frac{1}{2}\Bigg) = {H_L}\Bigg(ir + \frac{1}{2}\Bigg) + {H_R}\Bigg(ir + \frac{1}{2}\Bigg) $

(29)

$\begin{split} & {H_L}\Bigg(ir + \frac{1}{2}\Bigg) = f_i^ + (ir) + \\ & \qquad\frac{1}{2}\min \,\bmod \,\Bigg[\Delta f_i^ + \Bigg(ir + \frac{1}{2}\Bigg),\Delta f_i^ + \Bigg(ir - \frac{1}{2}\Bigg)\Bigg] \end{split} $

(30)

$ \begin{split} &{H_R}\Bigg(ir + \frac{1}{2}\Bigg) = f_i^ - (ir + 1)- \\ & \qquad \frac{1}{2}\min \,\bmod \,\Bigg[\Delta f_i^ - \Bigg(ir + \frac{1}{2}\Bigg),\Delta f_i^ - \Bigg(ir + \frac{3}{2}\Bigg)\Bigg] \end{split} $

(31)

$ \Delta f_i^ + \Bigg(ir + \frac{1}{2}\Bigg) = f_i^ + (ir + 1) - f_i^ + (ir) $

(32)

$ \Delta f_i^ - \Bigg(ir + \frac{1}{2}\Bigg) = f_i^ - (ir + 1) - f_i^ - (ir) $

(33)

$ f_i^ + (ir) = \frac{1}{2}({v_{ir}} + \left| {{v_{ir}}} \right|){f_i} $

(34)

$ f_i^ - (ir) = \frac{1}{2}({v_{ir}} - \left| {{v_{ir}}} \right|){f_i} $

(35)

在式（28）～式（35）中符号 $r$ 代表 $x$ 或 $y$ ，符号 $ir$ 代表网格点 $ix$ 或 $iy$ 。函数 $ \min \bmod $ 为限制器，定义如下：

$ \begin{split}\min\mathrm{mod}[X,Y] = \left\{\begin{array}{l}X,Y中绝对值小的那个值\text{，}若XY\geqslant 0\\ 0\text{，}若XY < 0\end{array}\right. \\[-9pt]\end{split}$

(36)

需要说明的是，上述NND格式具有二阶空间精度，是二阶中心格式和二阶迎风格式的结合，是具有负系数的四阶耗散项。因此，该NND格式可以抑制奇偶失联震荡，能够有效捕捉冲击波和爆轰波^[38]。

2 数值验证

本部分通过3个典型算例对DBM进行数值验证。首先，通过均匀化学反应系统验证本模型能够将化学反应与物理场自然耦合，模型既适用于吸热反应，也适用于放热反应，并且反应流系统的比热比可调；其次，通过Sod激波管验证本模型适用于可压缩流体系统，并且能够同时捕捉稀疏波、物质界面和冲击波的时空演化；最后，通过爆轰波算例开展了网格无关性验证，并验证本模型适用于超声速可压缩化学反应流。

2.1 均匀化学反应系统

为了验证本模型能够将化学反应与物理场自然耦合，本节首先考虑均匀化学反应系统：在初始时刻，化学反应物均匀、静止分布在计算区域，初始温度为 $ {T_0} = 2 $ 。经过一段足够长的时间后，化学反应结束，反应物完全转变成产物，化学能完全释放并转变成系统内能。由于该系统为均匀系统，每处的物理量分布都相同，所以为了提高计算速度，可以只用一个网格点，即 ${N_X} \times {N_Y} = 1 \times 1$ 。松弛时间 $\tau = 4 \times {10^{ - 6}}$ ，空间步长 $\Delta x = \Delta y = 1 \times {10^{ - 4}}$ ，时间步长 $\Delta t = 2 \times {10^{ - 6}}$ ，离散参数 $ {v_a} = - 3.7 $ 、 $ {v_b} = - 2 $ 、 $ {v_c} = - 1.5 $ ， $ {\eta _a} = 4 $ 、 $ {\eta _b} = 0 $ 、 $ {\eta _c} = 0 $ 。另外，对计算区域四周都采用周期边界条件。

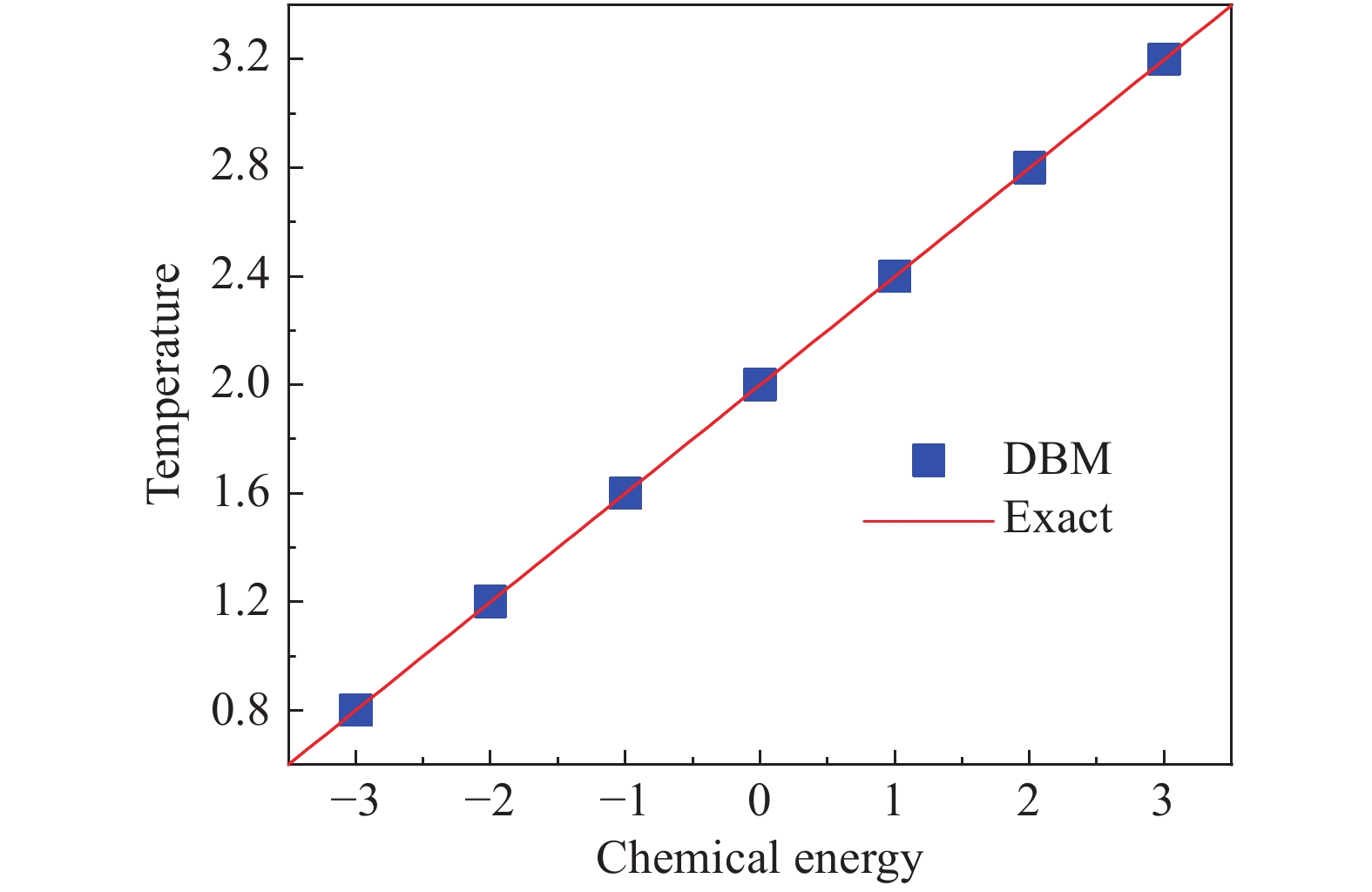
图3展示了化学反应后不同化学能对应的系统温度，其关系见式（37），此处设置比热比 $ \gamma = 1.4 $ 。符号代表DBM模拟结果，实线代表理论解：

$ T = {T_0} + \left( {\gamma - 1} \right)Q $

(37)

可以看出，DBM的模拟结果与理论解完全吻合。而且，图3中化学能的数值涵盖负值到正值的范围。其中负值区域代表化学反应吸热，正值区域代表化学反应放热。也就是说，该DBM既适用于化学吸热系统，也适用于化学放热系统。

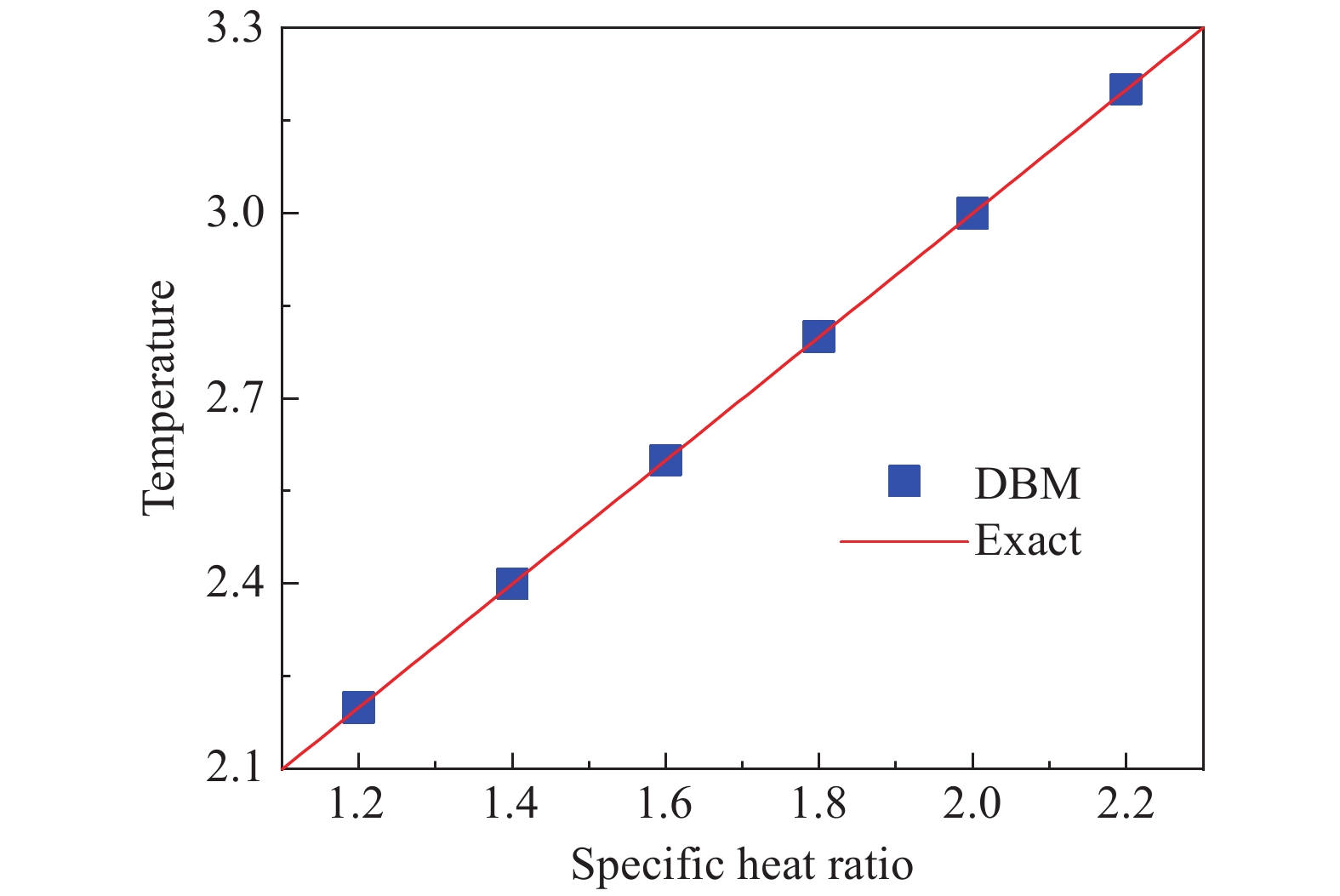
下面考虑固定化学能不变 $ Q = 1 $ ，调节比热比数值的情况。图4展示了化学反应后不同比热比对应的系统温度。符号代表DBM模拟结果，实线代表理论解（式（37））。同样，DBM给出的模拟结果与理论解完全吻合。因此，数值模拟证明该模型能够适用于不同比热比的化学反应流系统。

2.2 激波管

为了验证该DBM能够适用于可压缩流体系统，本节考虑Sod激波管的模拟。初始物理场设置如下：

$ \left\{ {\begin{array}{*{20}{l}} {{{\left( {\rho ,T,{u_x}} \right)}_L} = \left( {1,1,0} \right)} \\ {{{\left( {\rho ,T,{u_x}} \right)}_R} = \left( {{\text{0}}{\text{.125}},{\text{0}}{\text{.8}},0} \right)} \end{array}} \right. $

下标L表示左侧区域 $0 \leqslant x < 0.03$ ，下标R表示右侧区域 $0.03 \leqslant x \leqslant 0.06$ 。流速在垂直方向的分量为 $ {u_y} = 0 $ 。比热比 $\gamma = 1.4$ ，松弛时间 $\tau = 5 \times {10^{ - 6}}$ ，空间步长 $\Delta x = \Delta y = {1\times 10^{ - 4}}$ ，时间步长 $\Delta t = 2 \times {10^{ - 6}}$ ，计算网格 ${N_X} \times {N_Y} = {\text{600}} \times 1$ ，离散参数 $ {v_a} = 2.9 $ 、 $ {v_b} = 1 $ 、 $ {v_c} = 0.5 $ ， $ {\eta _a} = 4 $ 、 $ {\eta _b} = 0 $ 、 $ {\eta _c} = 0 $ 。另外，上下边界采用周期边界条件，左右边界采用出口边界条件。

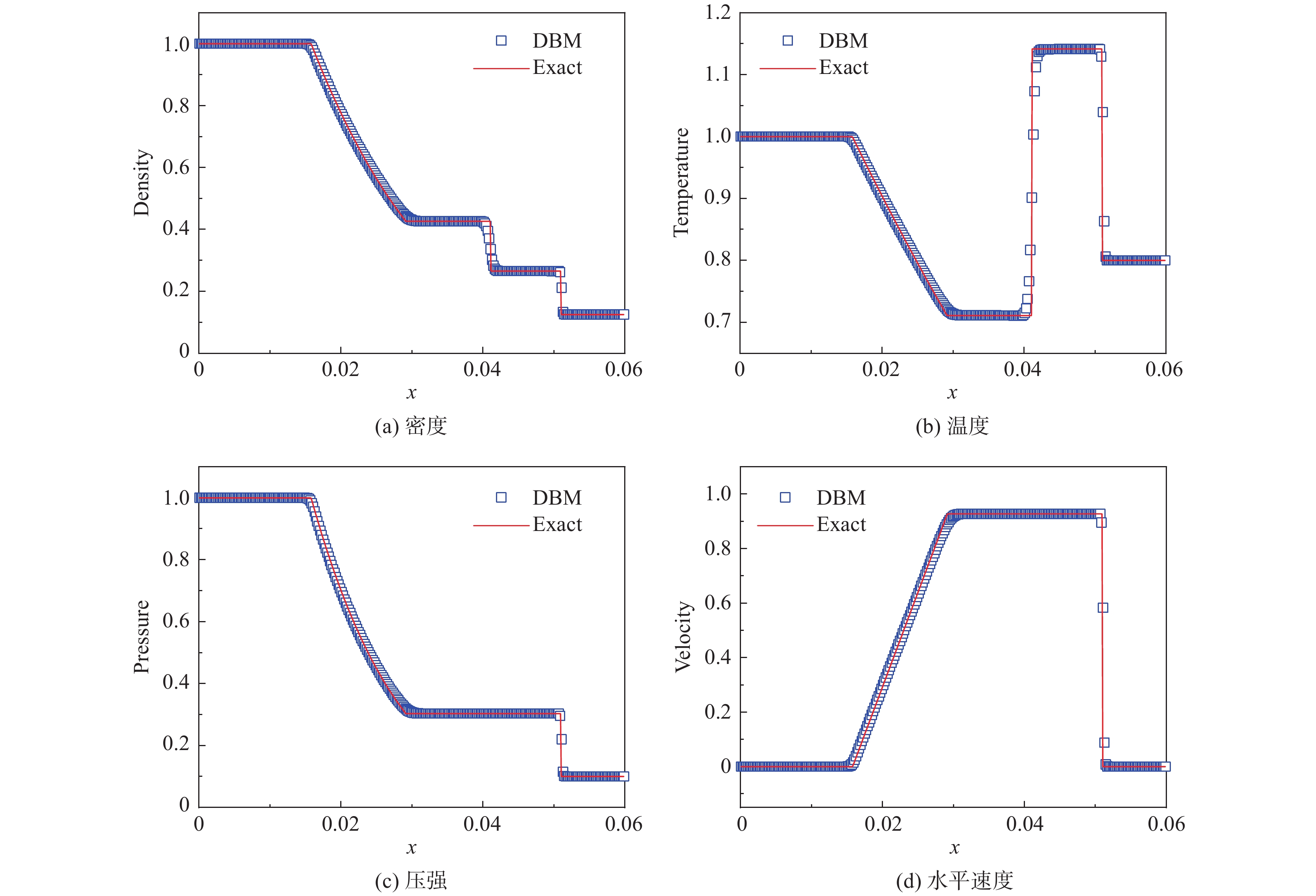
图5展示了在t = 0.02时刻激波管中的物理量分布，图5（a～d）依次是密度、温度、压强和水平速度。符号代表DBM模拟结果，实线代表理论解。可以看出：在最左侧的是稀疏波（向左传播），在中间的是物质分界面，在最右侧的是冲击波（向右传播）。其中，稀疏波在水平方向的跨度最大，各物理量都有清晰的空间梯度；在物质界面两侧，密度和温度具有明显空间梯度，而压强和速度均匀分布；在冲击波波阵面，各物理量梯度最大，具有剧烈的空间变化。在以上演化过程中，DBM与理论解具有很高的匹配度。这充分说明，DBM能够很好地捕捉稀疏波、物质界面和冲击波的空间分布。

2.3 爆轰波

爆轰是一种特殊的化学反应流现象，在其化学反应区前沿是以超声速传播的冲击波^[1]。在爆轰演化过程中，密度、温度和压强急剧上升，流场产生剧烈变化。物理量时空变化如此剧烈，在数值模拟中容易产生数值振荡，所以对爆轰波的数值模拟方法要具有较好的鲁棒性。本节将验证我们的DBM模型能够有效模拟爆轰波的传播过程。

下面考虑沿水平方向传播的爆轰波。在一个水平放置的长度为 ${l_0} = 0.06$ 的直通道内，初始物理场设置如下：

$ \left\{ {\begin{array}{*{20}{l}} {{{\left( {\rho ,p,{u_x}} \right)}_L} = \left( {1.48043,3.05433, - 1.69953} \right)} \\ {{{\left( {\rho ,p,{u_x}} \right)}_R} = \left( {1,1, - 2.51603} \right)} \end{array}} \right. $

下标L表示左侧区域 $0 \leqslant x < 0.99{l_0}$ ，下标R表示右侧区域 $0.99{l_0} \leqslant x \leqslant {l_0}$ ，左右两侧的物理量满足Hugoniot关系。设置化学反应热 $Q = 2$ ，马赫数 $Ma = 2.12643$ ，比热比 $\gamma = 1.4$ ，松弛时间 $\tau = 5 \times {10^{ - 6}}$ ，离散参数 ${v_a} = - 3.7$ 、 $ {v_b} = - 2 $ 、 $ {v_c} = - 1.5 $ ， $ {\eta _a} = 4 $ 、 $ {\eta _b} = 0 $ 、 $ {\eta _c} = 0 $ 。另外，上下采用周期边界条件，左右采用出口边界条件。

首先进行网格无关性验证。图6展示了不同空间步长的密度分布图，即 $\Delta {x_1} = 5 \times {10^{ - 5}}$ 、 $\Delta {x_2} = {1\times 10^{ - 4}}$ 、 $\Delta {x_3} = 2 \times {10^{ - 4}}$ 、 $\Delta {x_4} = 4 \times {10^{ - 4}}$ ；与之对应的水平网格点数分别是 ${N_X} = {\text{1\;200}}$ 、 $6{\text{00}}$ 、 $3{\text{00}}$ 、 $15{\text{0}}$ 。可以看出，随着空间步长的减小（网格数的增加），模拟结果之间的差异越来越小。尤其是在 $\Delta {x_1}$ 和 $\Delta {x_2}$ 下的模拟结果几乎完全重合。因此，考虑到计算效率，可以使用空间步长 $\Delta {x_2}$ 进行数值模拟。同样，可以对不同的时间步长进行数值对比。结果表明，时间步长 $\Delta t = 2 \times {10^{ - 6}}$ 和 $4 \times {10^{ - 6}}$ 之间的模拟结果差异可以忽略。

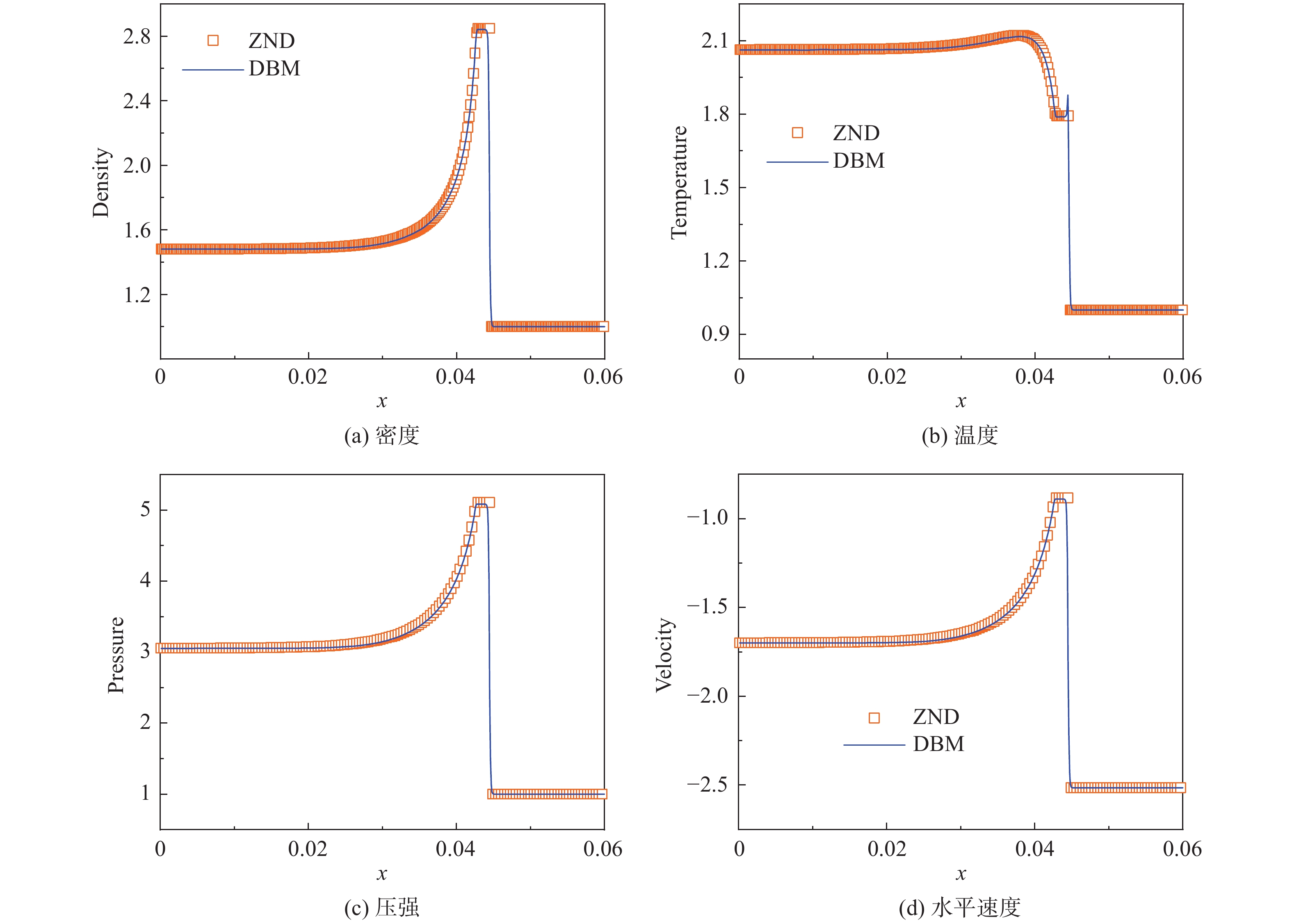
图7展示了在空间步长 $\Delta x = {1\times 10^{ - 4}}$ 、时间步长 $\Delta t = 2 \times {10^{ - 6}}$ 下爆轰波附近的模拟结果。图7（a～d）依次对应密度、温度、压强和水平速度的空间分布，其中符号代表DBM模拟结果，实线代表Zeldovich-Neumann-Doering（ZND）理论解^[1]。可以看出，DBM模拟结果与ZND 理论解具有非常好的一致性。尤其是当化学反应结束后，在爆轰波后侧形成稳定的“平台区域”，此处的DBM模拟结果为 $\;\rho = {\text{1}}{\text{.48065}}$ 、 $T = {\text{2}}{\text{.06216}}$ 、 $p = {\text{3}}{\text{.05334}}$ 、 ${u_x} = - {\text{1}}{\text{.69974}}$ 。对比ZND 理论解，相对误差依次为： $0.015\% $ 、 $0.047\% $ 、 $0.032\% $ 、 $0.012\% $ ，误差非常小。因此该DBM能够有效模拟爆轰现象。

3 结　论

基于动理学理论，本文提出了适用于超声速可压缩化学反应流的二维简化DBM。该模型具有下列特点：

1）构建并使用了仅有9个离散速度的模型，即离散速度分为3组，每组含有3个速度，各组速度的方向均匀分布、大小独立可调。由于离散速度较少，模型具有较高的运算效率。

2）为了描述分子转动和振动对应的额外自由度，引入了三组独立可调的参数用于描述额外自由度部分的内能。由此，该DBM具备了模拟比热比可调的反应流系统的功能。

3）平衡态离散速度分布函数与化学反应项各自都满足9个独立的动理学矩关系，并可以通过矩阵求逆的方式获得其数学表达式。该方法具有物理精确、运算高效的特点。

4）通过Chapman-Enskog多尺度分析可以证明，该DBM除了在连续性极限条件下可以恢复包含化学反应的Euler方程组之外，还具有描述一定热力学非平衡行为的功能。

5）使用形式统一的离散玻尔兹曼方程，方法简单、易于编程。同时，离散玻尔兹曼演化方程具有时空局域性特点，易于实现并行化，方便在高性能计算集群运行。

本文开展了3个数值算例，验证了该DBM的可靠性。首先，通过均匀反应系统验证模型能够将化学反应与物理场自然耦合，适用于吸热或放热反应，并且反应流系统的比热比可调；其次，通过激波管验证模型适用于可压缩流体系统，并且能够同时捕捉稀疏波、物质界面和冲击波的时空演化；最后，通过爆轰波算例开展了网格无关性验证，并验证模型适用于超声速可压缩化学反应流。

已有的二维DBM至少包含16个离散速度、动理学矩关系和演化方程，等价于N-S（或者Burnett）方程组和包含更多非平衡效应的粗粒化模型^[24,30,36]。与之相比，简化DBM的优势为离散速度数量较少、计算效率较高；局限性为物理精度较低，适用于热力学非平衡程度较弱的物理系统。