2. 汕头大学 智能制造技术教育部重点实验室,汕头 515063
2. Key Laboratory of Intelligent Manufacturing Technology, Shantou University, Shantou 515063, China
多相流动现象不仅与自然界、人们的日常生活息息相关,也普遍存在于工业生产领域[1-2]。对于计算流体力学(computational fluid dynamic,CFD)研究人员来说,由于多相流固有的非线性、物理性质(如密度和黏度)的巨大差异,以及因质量、动量和能量同时进行交换而产生移动界面的复杂拓扑变化[3],因此开发一个简单有效的数值模型来研究这些复杂现象在实践中面临着巨大的挑战。到目前为止,已经有许多研究学者对多相流进行了数值仿真,并针对多相流问题发展了一些数值模拟方法,包括相场方法(phase-field method,PFM)[4-6]、流体体积法(volume of fluid,VOF)[7-8]、水平集方法(level set method,LSM)[9-10]、前沿跟踪法(front-tracking method,FTM)[11-12]、光滑粒子流体动力学方法(smooth particle hydrodynamics method,SPHM)[13]。其中,相场方法是研究这类流动最常用的方法之一。在相场方法中,尖锐界面被视为有限厚度的过渡区,物理参数在其上平滑变化。
相场方法作为扩散界面方法中研究复杂界面动力学的一种,已被许多学者应用在模拟多相流问题上。相场方法主要分为两种:一种是用包含空间四阶导数的Cahn-Hilliard(C-H)方程[14]来捕捉界面变化,另一种是具有二阶精度的Allen-Cahn(A-C)界面控制方程[15]。当前,大多数描述多相流的相场方法都是基于C-H理论,其方程源自梯度流法[16]。Lee等[17-19]开发了一种基于总自由能假设的非整体相场方法;Kim[20]进一步改进了该方法,通过引入新的离散delta函数提出了广义连续表面张力公式。与非整体相场方法不同,Elliort和Luckhaus[21]提出了一种具有修正自由能公式的整体相场方法,对其引入了对称正定矩阵,其中的系数与不同流体之间的成对表面张力有关。Dong[2,22-24]使用整体相场方法进行了一系列应用。然而,我们观察到,由于总自由能随时间减少,C-H方程在保持各相体积方面的性能较差[25]。此外,当构造非线性势时,在两两表面张力不均匀的情况下很难满足还原一致性条件。
格子Boltzmann方法(lattice Boltzmann method,LBM)作为一种介观方法,自20世纪80年代末以来,已发展成为一种流行的CFD替代工具。因为它的简单性、在并行计算机上的可扩展性以及易于处理复杂几何图形,被广泛应用于模拟流体动力学[26-27]和非线性方程组[28-29]。LBM使用基于粒子的密度分布函数来演化宏观系统。最近,基于相场理论,许多研究者结合LBM来仿真研究多相流问题。Liang等[30]提出一个LB模型,通过巧妙地构建流场LB方程中的力项来进一步发展C-H动力学。Reza等[31]开发了另一个PF-LB模型,使用C-H方程跟踪三种不同流体之间的界面。然而,上述两种方法仍受到体积守恒和质量守恒的影响。在A-C方程的动力学建模中,Reza等[32]提出了一种描述三相流的守恒相场LB模型,该模型可保持良好的质量守恒性,并且满足还原一致性条件。Zheng等[33]针对不混溶多组分流体开发了另一种满足还原一致性条件的守恒PF-LB方法。Hu等[34]提出一种广义守恒PF-LB模型,其中每一相相变量满足广义eikonal方程和体积分数约束。
在本文中,我们在单松弛LB框架下提出一种简化的多相流LB方法,用于仿真具有大密度比、大黏度比的多相流问题。该模型基于Hu等[34]提出的广义守恒PF理论,其优点在于可以处理不可压、不混溶多相流,并具有良好的还原一致性以及质量和体积守恒性。此外,该方法保持了我们早期开发的用于两相流大密度比的SMLBM的良好数值稳定性[35]。与用于模拟多相流的常用单松弛和多松弛LB方法不同,简化多相流格子Boltzmann方法(simplified multiphase lattice Boltzmann method,SMLBM)在单松弛LB方法的框架内通过预测-校正策略来模拟流体系统和跟踪界面演化,其计算过程中仅需要考虑平衡分布函数的演化。因此,SMLBM大大减少了计算中对虚拟内存的需求,简化了物理边界条件的实施,而这两点往往是限制传统单松弛和多松弛LB方法应用的主要因素。最近,Li等[36]构造了一种统一的SMLBM方法来模拟大密度比、大黏度比的磁流体两相流问题,验证了此方法模拟多相磁流体流动的效率性和准确性。Khan等[37]运用SMLBM模拟研究了均匀磁场下磁流体液滴变形和气泡在磁流体中合并的动力学过程。随后,Chen等[38]发展了一种三相流SMLBM方法,并将其应用于中等雷诺数剪切流中的复合液滴数值研究,但研究中的各相流体之间的密度比和黏度比依旧较小。因此,在模拟多相流系统中,解决大密度比、大黏度比多相流问题还较为困难,尤其是三相流及以上的多相流问题。但在现实生活中,气-液多相流中的各相流体之间的密度比普遍都达到了1000以上。所以为了提高模型对大密度比多相流问题数值仿真的鲁棒性,并克服单松弛模型对黏度的敏感性,需要提高相场方程界面捕捉的稳定性和精确性。因此,我们将广义守恒PF方程中扩散项构造的源分布函数吸收到相场平衡分布函数中,这使得该方法的实现更加简单。
通过拉普拉斯定律和具有不同表面张力比的液滴透镜扩展两个基准问题的数值仿真,我们首先验证了本方法的稳定性和准确性。进一步,通过模拟不同黏度比的三相泊肃叶流问题以及不同密度比复合液滴在平板上的扩散算例,将数值结果与解析解进行比较,展示了本模型的精确性和处理大密度比、大黏度比复杂多相流问题的能力。
1 数值方法 1.1 广义守恒相场模型相场模型实质上就是一类特殊的扩散界面模型。为了准确地描述整个流体系统中多种非混溶流体共存的状态以及他们在相互作用下的运动,在相场模型中将任意位置上多种非混溶流体所占的体积分数定义为该点的相变量ϕi,显然存在如下约束:
| $ \sum\limits_{i = 1}^N {{\phi _i}} = 1,\;\;0 \leqslant {\phi _i} \leqslant 1 $ | (1) |
多相流系统的稳定演化过程主要受流体系统的总自由能驱动。在此模型中,广义总自由能泛函可表示为[34]:
| $ W\left( {\phi ,\nabla \phi } \right) = \int_\mathit{\Omega} {\left[ {\sum\limits_{i,j = 1}^N {\left( {{\alpha _{ij}}\nabla {\phi _i} \cdot \nabla {\phi _j} + {\beta _{ij}}\phi _i^2\phi _j^2} \right)} } \right]} {\text{ }}{\rm{d}}x $ | (2) |
式中,Ω代表整个流体系统,方程右边第一项表示界面能,第二项表示体自由能。其中系数αi和βi被定义为:
| $ \alpha_{i j} = -\frac{3 \xi \sigma_{i j}}{8}, \quad \beta_{i j} = \frac{6 \sigma_{i j}}{\xi} $ | (3) |
式中,
为了有效、精确地求解不可压、非混溶多相流问题,基于式(2)可以构造一种变分格式,并使用梯度流方法,将多相流界面宏观控制方程写成如下形式[34]:
| $ \frac{\partial \phi_{i}}{\partial t}+\nabla \cdot\left(\boldsymbol{u} \phi_{i}\right) = M\left\{\nabla^{2} \phi_{i}-\nabla \cdot\left[\frac{4 \phi_{i}\left(1-\phi_{i}\right)}{\xi} \hat{\boldsymbol{n}}_{i}\right]\right\}+\gamma $ | (4) |
称其为广义守恒相场方程,其中M表示迁移系数。为了满足还原一致性条件,拉格朗日算子
| $ \gamma = \frac{\chi_{i}}{\displaystyle\sum\limits_{j = 1}^{N} \chi_{j}} \displaystyle\sum\limits_{j = 1}^{N}\left\{M \nabla \cdot\left[\frac{4 \phi_{j}\left(1-\phi_{j}\right)}{\xi} \hat{\boldsymbol{n}}_{j}\right]\right\} $ | (5) |
其中N 表示流体相数。式(4)和式(5)中,
| $ {\chi _i} = \left\{ \begin{gathered} 0,\;\;\;\;{\text{ }}\int_\mathit{\Omega} {\left| {{\phi _i}\left( {\boldsymbol{x},0} \right)} \right|{\rm{d}}\boldsymbol{x} = 0} \hfill \\ 1,\;\;\;\;{\text{ }}\int_\mathit{\Omega} {\left| {{\phi _i}\left( {\boldsymbol{x},0} \right)} \right|{\rm{d}}\boldsymbol{x} > 0} \hfill \\ \end{gathered} \right. $ | (6) |
不可压缩多相流的质量守恒和动量守恒方程可用以下形式表示[39-40]:
| $ \nabla \cdot \boldsymbol{u} = 0 $ | (7) |
| $ \begin{gathered} \frac{\partial \boldsymbol{u}}{\partial t}+\nabla \cdot(\boldsymbol{u} \boldsymbol{u}) = \\ -\nabla\left(\frac{p}{\rho}\right)+\nabla \cdot\left[\upsilon\left(\nabla \boldsymbol{u}+(\nabla \boldsymbol{u})^{\mathrm{T}}\right)\right]+\frac{\boldsymbol{F}_{\text {total }}}{\rho} \end{gathered} $ | (8) |
式中,u表示流体速度,p表示压力,ρ表示流体密度,
| $ \boldsymbol{F}_{\text {total }} = \boldsymbol{F}_{p}+\boldsymbol{F}_{\upsilon}+\boldsymbol{F}_{s} $ | (9) |
其中:
| $ \boldsymbol{F}_{p} = -\frac{p}{\rho} \nabla \rho $ | (10) |
| $ \boldsymbol{F}_{\upsilon} = \upsilon\left[\nabla \boldsymbol{u}+(\nabla \boldsymbol{u})^{{\rm{T}}}\right] \cdot \nabla \rho $ | (11) |
| $ \begin{split} {F_s} =& \sum\limits_{i,j = 1}^N { - {\alpha _{ij}}\left( {{\nabla ^2}{\phi _i}\nabla {\phi _j} + {\nabla ^2}{\phi _j}\nabla {\phi _i}} \right)} +\\& {\text{ }} {\beta _{ij}}\left( {\frac{{\partial \varPsi }}{{\partial {\phi _i}}}\nabla {\phi _i} + \frac{{\partial \varPsi }}{{\partial {\phi _j}}}\nabla {\phi _j}} \right) \end{split} $ | (12) |
其中体自由能
为了求解广义守恒相场方程(4)和流体动力学方程(7)和方程(8),采用了简化多相流格子Boltzmann方法(SMLBM)。在SMLBM中,通过分步技术运用预测和校正两个步骤来重建LB方程的解[35],如下所示:
预测步:
| $ p^{*} = \rho^{*} c_{s}^{2} \sum_{\alpha} f_{\alpha}^{{\rm{e q}}}\left(\boldsymbol{x}-\boldsymbol{e}_{\alpha} \Delta t, t-\Delta t\right) $ | (13) |
| $ \boldsymbol{u}^{*} = \sum_{\alpha} \boldsymbol{e}_{\alpha} f_{\alpha}^{{\rm{e q}}}\left(\boldsymbol{x}-\boldsymbol{e}_{\alpha} \Delta t, t-\Delta t\right) $ | (14) |
| $ \phi_{i}^{*} = \sum_{\alpha} g_{\alpha}^{i, {\rm{e q}}}\left(\boldsymbol{x}-\boldsymbol{e}_{\alpha} \Delta t, t-\Delta t\right) $ | (15) |
校正步:
| $ p^{n+1} = p^{*} $ | (16) |
| $ \qquad\begin{split} \boldsymbol{u}^{n+1} = & \boldsymbol{u}^{*}+\sum_{\alpha} \boldsymbol{e}_{\alpha}\left[f_{\alpha}^{\sim}\left(\boldsymbol{x}+\frac{1}{2} \boldsymbol{e}_{\alpha} \Delta t, t-\frac{1}{2} \Delta t\right)-\right.\\ &\left.f_{\alpha}^{\sim}\left(\boldsymbol{x}-\frac{1}{2} \boldsymbol{e}_{\alpha} \Delta t, t-\frac{1}{2} \Delta t\right)\right] -\\ &\frac{\Delta t}{2} \sum_{\alpha} \boldsymbol{e}_{\alpha}\left[F_{\alpha}^{\sim}\left(\boldsymbol{x}+\boldsymbol{e}_{\alpha} \Delta t, t-\frac{1}{2} \Delta t\right)-\right.\\ &\left.F_{\alpha}^{\sim}\left(\boldsymbol{x}-\boldsymbol{e}_{\alpha} \Delta t, t-\frac{1}{2} \Delta t\right)\right]+\frac{\Delta t \boldsymbol{F}_{\text {total }}}{2 \rho^{n+1}} \end{split} $ | (17) |
| $ \qquad\begin{split} \phi_{i}^{n+1} =& \phi_{i}^{*} +\sum_{\alpha}\left(\tau_{g}-1\right)\left[g_{\alpha}^{\sim}\left(\boldsymbol{x}+\frac{1}{2} \boldsymbol{e}_{\alpha} \Delta t, t-\frac{1}{2} \Delta t\right)-\right.\\ &\left.g_{\alpha}^{\sim}\left(\boldsymbol{x}-\frac{1}{2} \boldsymbol{e}_{\alpha} \Delta t, t-\frac{1}{2} \Delta t\right)\right] \end{split} $ | (18) |
式中,cs为格子声速,Δt为时间步长,eα为格子速度;τg为关于相场的松弛参数,它与迁移系数M之间的关系是
| $ f_{\alpha}^{{\rm{e q}}} = \omega_{\alpha}\left[\frac{p}{\rho c_{s}^{2}}+\frac{\boldsymbol{e}_{\alpha} \cdot \boldsymbol{u}}{c_{s}^{2}}+\frac{\left(\boldsymbol{e}_{\alpha} \cdot \boldsymbol{u}\right)^{2}}{2 c_{s}^{4}}-\frac{|\boldsymbol{u}|^{2}}{2 c_{s}^{2}}\right] $ | (19) |
| $ g_{\alpha}^{i, {\rm{e q}}} = \omega_{\alpha} \phi_{i}\left(1+\frac{\boldsymbol{e}_{\alpha} \cdot \boldsymbol{u}}{c_{s}^{2}}\right)+\frac{\omega_{\alpha} \boldsymbol{e}_{\alpha}}{c_{s}^{2}} \cdot B $ | (20) |
其中:
| $ B = M\left[\frac{4 \phi_{i}\left(1-\phi_{i}\right)}{\xi} \cdot \hat{\boldsymbol{n}}_{i}-\frac{\chi_{i}}{\displaystyle\sum_{j = 1}^{N} \chi_{j}} \displaystyle\sum_{j = 1}^{N} \frac{4 \phi_{j}\left(1-\phi_{j}\right)}{\xi} \cdot \hat{\boldsymbol{n}}_{j}\right] $ | (21) |
此外,非平衡分布函数
| $ \begin{split}& f_{\alpha}^{\sim}\left(x+\frac{1}{2} \boldsymbol{e}_{\alpha} \Delta t, t-\frac{1}{2} \Delta t\right) = \left[\tau_{f}\left(x+\frac{1}{2} \boldsymbol{e}_{\alpha} \Delta t, t-\frac{1}{2} \Delta t\right)-1\right] \cdot \\&\qquad \left[f_{\alpha}^{{\rm{e q}}}\left(\boldsymbol{x}+\boldsymbol{e}_{\alpha} \Delta t, t\right)-f_{\alpha}^{{\rm{e q}}}(\boldsymbol{x}, t-\Delta t)\right] \end{split} $ | (22) |
| $ \begin{split}& f_{\alpha}^{\sim}\left(x-\frac{1}{2} \boldsymbol{e}_{\alpha} \Delta t, t-\frac{1}{2} \Delta t\right) = \left[\tau_{f}\left(x-\frac{1}{2} \boldsymbol{e}_{\alpha} \Delta t, t-\frac{1}{2} \Delta t\right)-1\right] \cdot\\&\qquad \left[f_{\alpha}^{{\rm{e q}}}(\boldsymbol{x}, t)-f_{\alpha}^{{\rm{e q}}}\left(\boldsymbol{x}-\boldsymbol{e}_{\alpha} \Delta t, t-\Delta t\right)\right] \end{split} $ | (23) |
| $ \begin{split}&\qquad\qquad g_{\alpha}^{\sim}\left(x+\frac{1}{2} \boldsymbol{e}_{\alpha} \Delta t, t-\frac{1}{2} \Delta t\right) = \\& \left(\tau_{g}-1\right)\left[g_{\alpha}^{i, {\rm{e q}}}\left(\boldsymbol{x}+\boldsymbol{e}_{\alpha} \Delta t, t\right)-g_{\alpha}^{i, {\rm{e q}}}(\boldsymbol{x}, t-\Delta t)\right] \end{split} $ | (24) |
| $ \begin{split}&\qquad\qquad {g_{\alpha} ^\sim}\left(x-\frac{1}{2} \boldsymbol{e}_{\alpha} \Delta t, t-\frac{1}{2} \Delta t\right) = \\& \left(\tau_{g}-1\right)\left[g_{\alpha}^{i, {\rm{e q}}}(\boldsymbol{x}, t)-g_{\alpha}^{i, {\rm{e q}}}\left(\boldsymbol{x}-\boldsymbol{e}_{\alpha} \Delta t, t-\Delta t\right)\right] \end{split} $ | (25) |
| $ \begin{split}&\qquad\qquad {F_{\alpha} ^\sim} =\tau_{f}\left(1-\frac{1}{2 \tau_{f}}\right) \frac{\omega_{\alpha}}{\rho}\cdot \\& \left[\frac{F_{\text {total }} \cdot\left(\boldsymbol{e}_{\alpha}-\boldsymbol{u}\right)}{c_{s}^{2}}+\frac{\boldsymbol{u} F_{\text {total }}: \boldsymbol{e}_{\alpha} \boldsymbol{e}_{\alpha}}{c_{s}^{4}}\right] \end{split} $ | (26) |
式中,ωα为权系数;τf为松弛参数,它与运动黏度
上述的简化多相流格子Boltzmann模型采用经典的D2Q9离散格子速度模型,在此模型中,格子速度定义如下:
| $ \boldsymbol{e}_{\alpha} = \begin{cases}0 & \alpha = 0 \\ (\pm 1,0),(0, \pm 1) & \alpha = 1,2,3,4 \\ (\pm 1, \pm 1) & \alpha = 5,6,7,8\end{cases} $ | (27) |
模型中,权系数ω0 = 4/9、ω1-4 = 1/9、ω5-8 = 1/36,格子声速
| $ \upsilon\left[\nabla \boldsymbol{u}+(\nabla \boldsymbol{u})^{{\rm{T}}}\right] = -\frac{\boldsymbol{v}}{c_{s}^{2} \Delta t}\left[\sum_{\alpha} \boldsymbol{e}_{\alpha} \boldsymbol{e}_{\alpha} \frac{f_{\alpha}^{\sim}}{\tau_{f}}\right] $ | (28) |
根据式(28)可知,黏性力计算式(11)可以直接通过平衡分布函数来求得。
显然,上述SMLBM的整个实施过程只涉及平衡分布函数,而平衡分布函数又可以直接从宏观变量计算得到。与传统的单松弛和多松弛LB方法相比,不再需要计算流场的碰撞演化过程,提高了模型的计算效率。此外,由广义守恒相场方程(4)中扩散项构造的源分布函数被吸收到式(20)中的相场平衡分布函数中,这使得该方法更加简单和稳定。
2 模拟算例本节中我们以四个二维的数值算例来验证方法的稳定性和准确性。所有的网格划分和数值离散都在笛卡尔坐标系下完成,并对时间和空间进行了无量纲化。我们将单位格子时间Δt设定为1,无量纲时间为
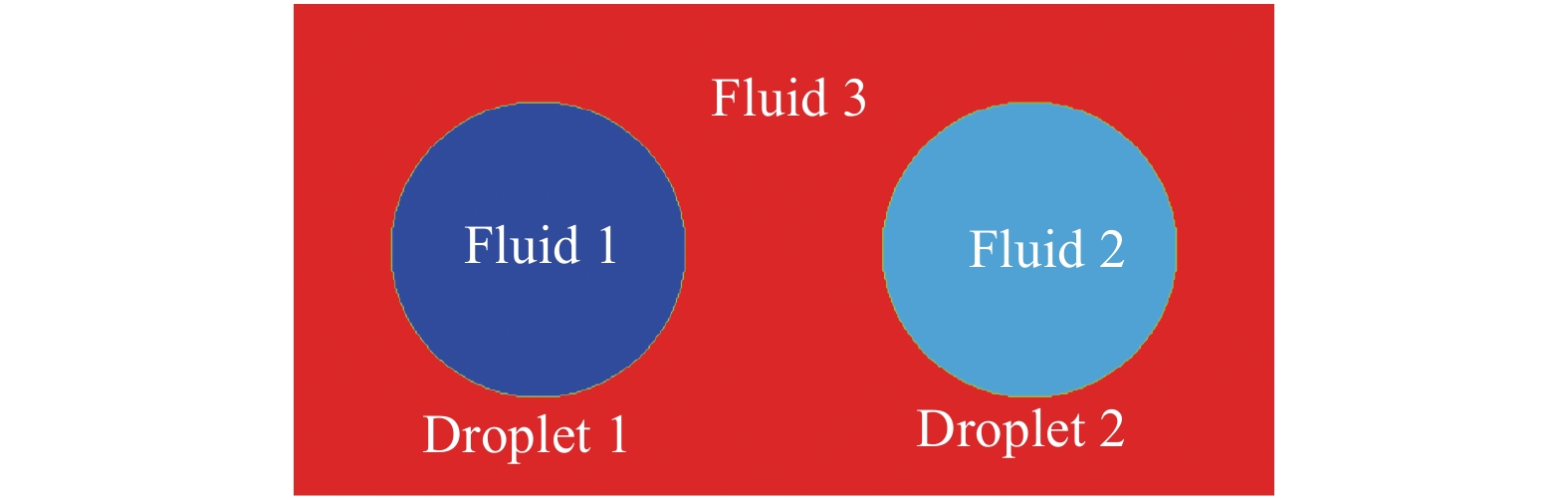
本节首先进行拉普拉斯定律的基准试验,以此来验证模型的准确性。我们将两个不同密度的液滴(流体1、流体2)同时浸入流体3中,如图1所示。在表面张力的影响下,液滴内部的压力大于液滴外部的压力,在达到平衡时,液滴会以圆形保持静止。同时液滴内外界面压力差Δpij与表面张力σij之间满足以下公式:
| $ \sigma_{i j} = \Delta p_{i j} R_{i j} $ | (29) |
其中,Rij表示为i相和j相之间相界面的曲率半径,即液滴的半径,这里我们设置两个液滴的半径是相同的。计算中对所有边界采用周期性边界条件。界面厚度
|
图 1 两个液滴浸没到另一种流体中示意图 Fig.1 Diagram of two droplets immersed in another fluid |
首先为了验证网格的收敛率,分别在计算域为x×y = 100×50、200×100、400×200和600×300时进行仿真。我们设定参考长度Lc = 2Rij,并将其分别设置为30、60、120和180。根据下述公式计算了三种相变量在不同网格大小下的数值误差:
| $ E\left(\phi_{i}\right) = \sqrt{\frac{\displaystyle\sum_{x, y}\left(\phi_{i}^{n+1}-\phi_{i}^{n}\right)^{2}}{\displaystyle\sum_{x, y}\left(\phi_{i}^{n}\right)^{2}}} $ | (30) |
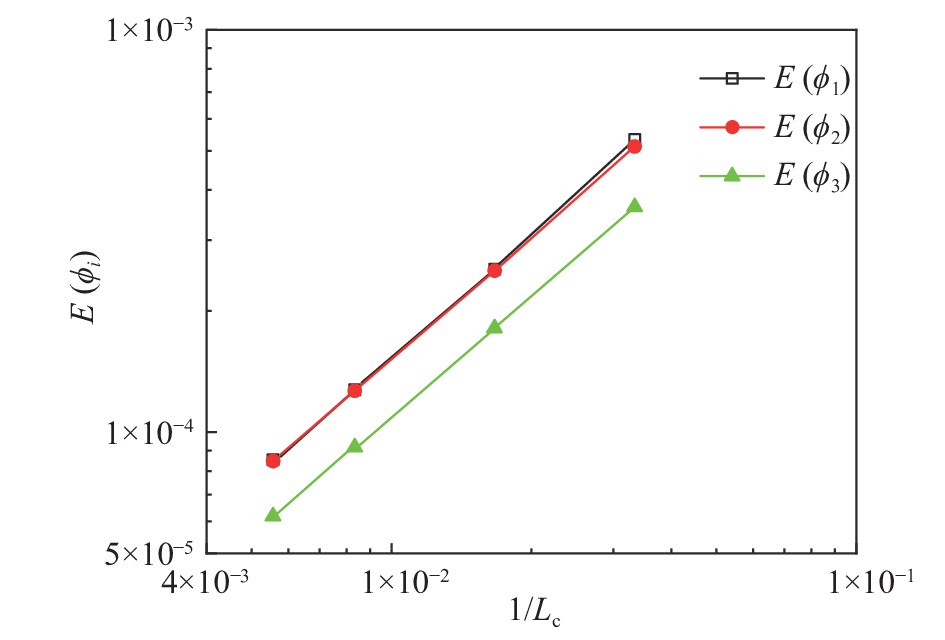
三种相变量的数值误差如图2所示。可以发现三种相变量的误差呈现相同的趋势,即网格越小,相变量的误差越小,说明模型的收敛精度与网格的大小有关。当计算域为100×50时,网格最大,其收敛精度为1×10−3;当计算域为600×300时,网格最小,收敛精度达到1×10−4,均在二阶精度以内。从图3中可以看出,400×200和600×300两种网格的误差非常接近,可以判断在这个网格数量区间内,模型的精度不会随着网格数量的增加而有较大变化,进一步证明了网格独立性。为了保证计算精度,同时尽可能地减少计算时间,我们选择计算域为400×200的网格大小。
|
图 2 当前模型的收敛误差 Fig.2 Convergence errors of the present model |
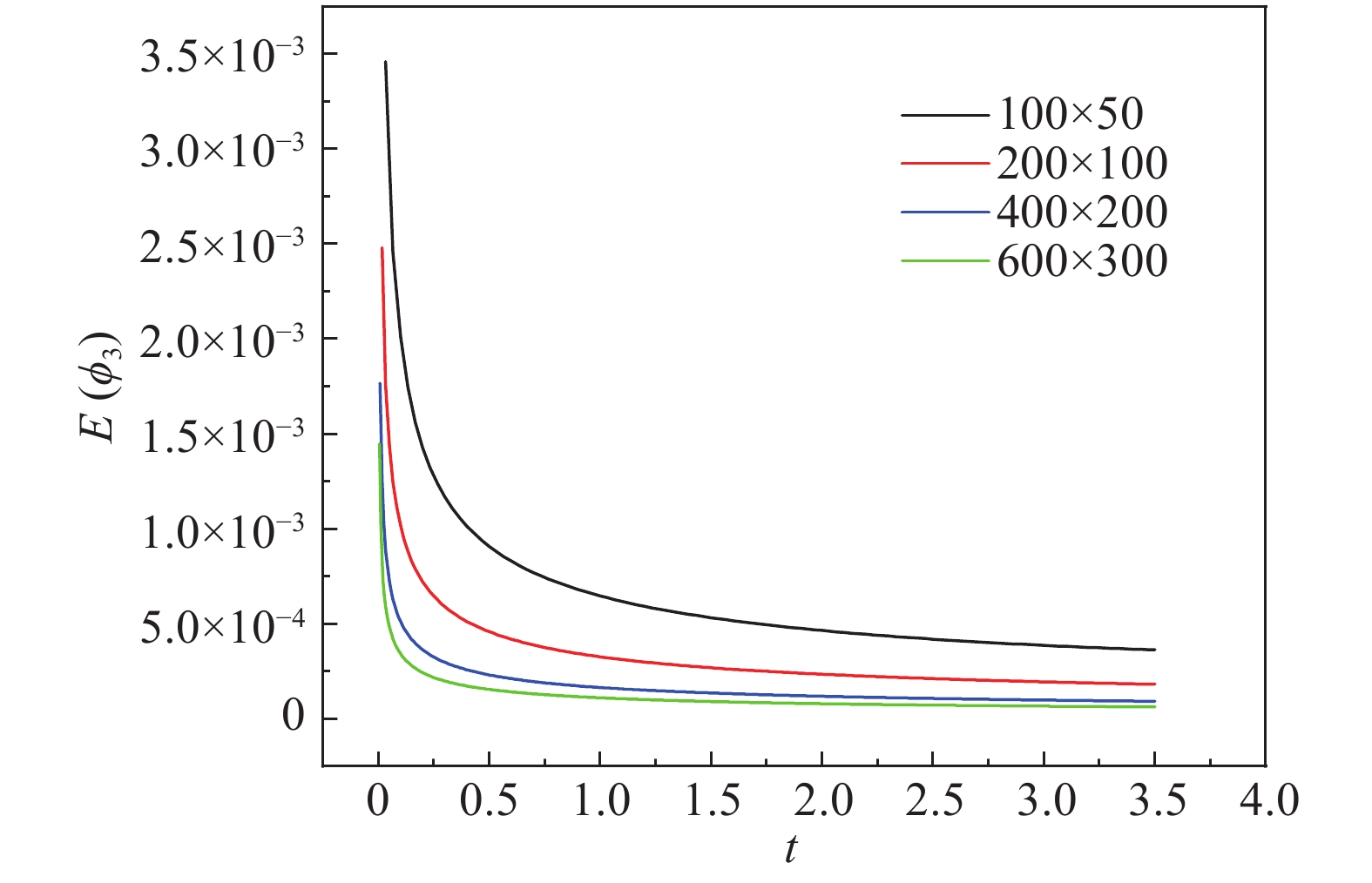
|
图 3 在不同网格大小下 |
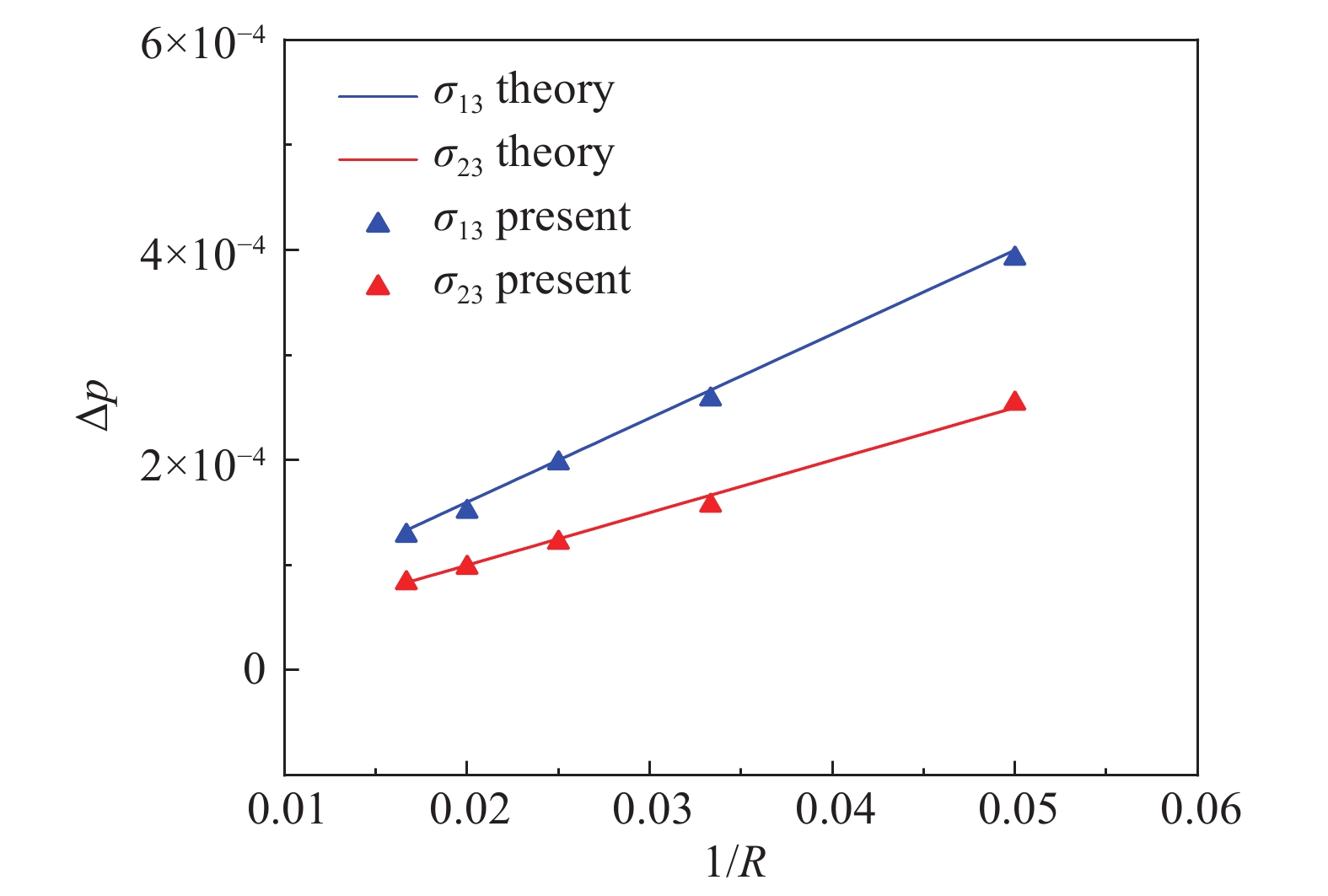
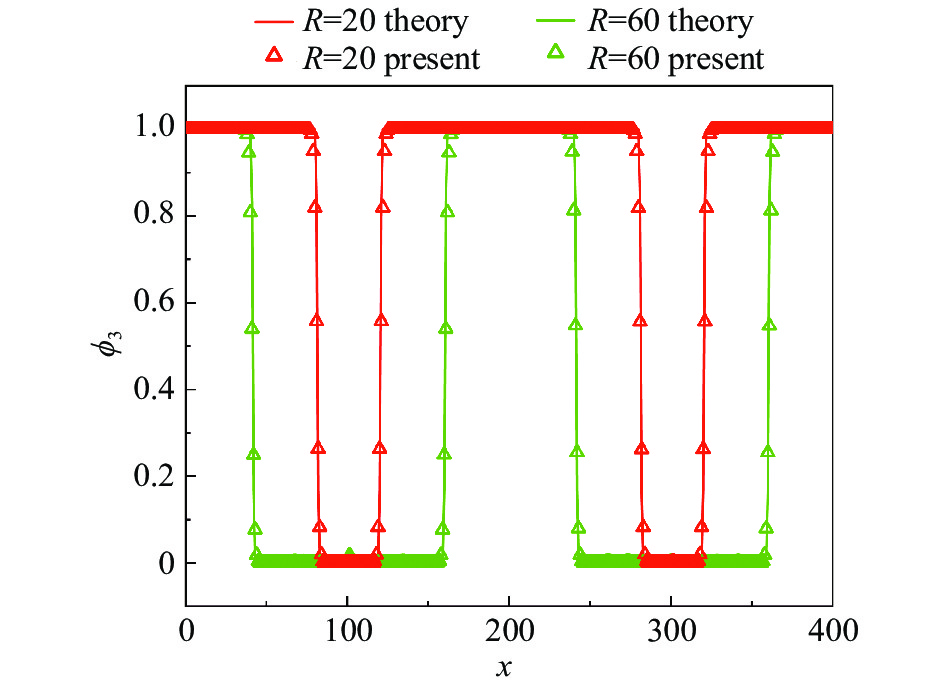
图4中列出了界面压力差在两个液滴不同的表面张力(σ13、σ23)下和不同半径(Rij = 20、30、40、50、60)下模拟值与理论值的对比。图中可以清楚地看出模拟值和理论值吻合得非常好。我们对比了两个液滴在不同半径下相变量ϕ在水平中央线的模拟值和初始值,如图5所示。从图中可以看出,在液滴半径为
|
图 4 液滴1和液滴2界面压差的模拟值和理论值对比 Fig.4 Comparison of the pressure difference across the interfaces of droplet 1 and droplet 2 between the numerical results and theoretical solutions |
|
图 5 相变量在水平中央界面分布对比图( |
本节研究了一个透镜在两层不相溶流体间的扩散运动这一经典算例,液滴透镜扩散问题在文献[10,32,41,42]中被广泛用于验证模拟多相流的数值方法。液滴透镜如果一开始存在于两相不混溶的流体之间,在表面张力的作用下透镜会发生形变,其最终的平衡状态是上下两层流体间相互作用的结果。透镜的平衡状态由三个表面张力系数决定,根据诺伊曼定律可以得出以下关系[43]:
| $ \cos \theta_{1} = \frac{\sigma_{12}^{2}+\sigma_{13}^{2}-\sigma_{23}^{2}}{2 \sigma_{12} \sigma_{13}} $ | (31) |
| $ \cos \theta_{2} = \frac{\sigma_{12}^{2}+\sigma_{23}^{2}-\sigma_{13}^{2}}{2 \sigma_{12} \sigma_{23}} $ | (32) |
其他几何参数以及接触角
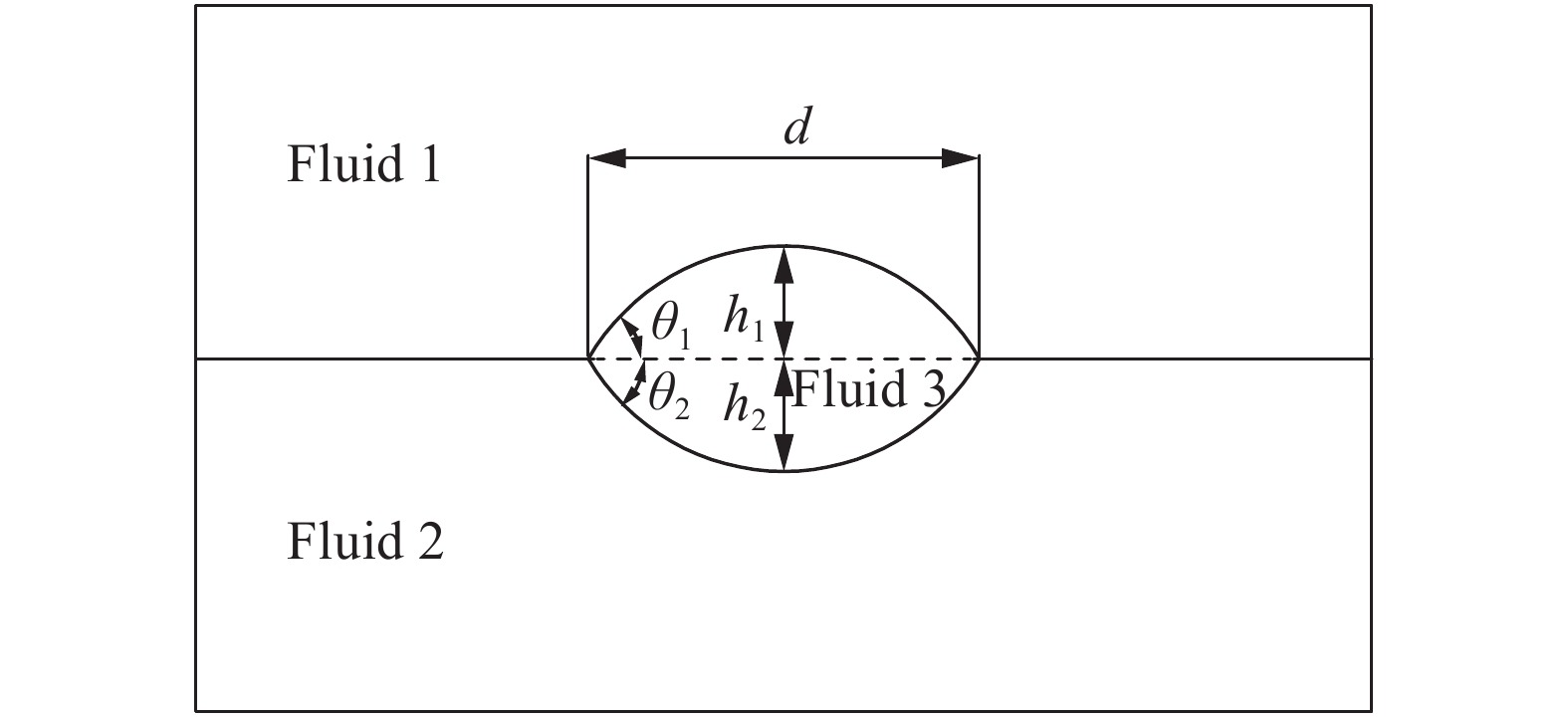
|
图 6 液滴透镜参数示意图 Fig.6 Diagram of the spreading of a liquid lens |
| $ {d} = 2\left\{\frac{\displaystyle\sum_{j = 1}^{2}\left[\dfrac{1}{\sin \theta_{j}}\left(\dfrac{\theta_{j}}{\sin \theta_{j}}-\cos \theta_{j}\right)\right]}{A}\right\}^{-\frac{1}{2}} $ | (33) |
| $ \boldsymbol h_{j} = \frac{1-\cos \theta_{j}}{\sin \theta_{j}}\frac{{d}}{2}, \quad j = 1,2 $ | (34) |
式中A是气泡在平衡状态下的面积。
我们将计算域的网格均匀划分成250×150,三种流体的密度为ρ1 = ρ2 = ρ3 = 1,黏度设为
| 表 1 液滴透镜算例中表面张力系数的设定 Table 1 Surface tension coefficients used in the simulation of spreading of a liquid lens |
|
|
4种情况下的透镜平衡状态如图7所示,显然,不同的表面张力系数比会导致透镜最后的平衡形状不同。当σ23的值增加时流体2的作用力会增大;同理,当σ13的值减小时,流体1的作用力也会相应减小。正因为上下作用力的改变形成压力差导致了透镜形变的不同。我们将平衡时透镜两个三相点之间的距离d,以及h1和h2的模拟值和理论值进行了对比,如表2所示。从表中可知,模拟值和理论值吻合得较好,最大的相对误差值为5.6%。这种微小的误差是由于在界面厚度为零的极限情况下计算了理论值。
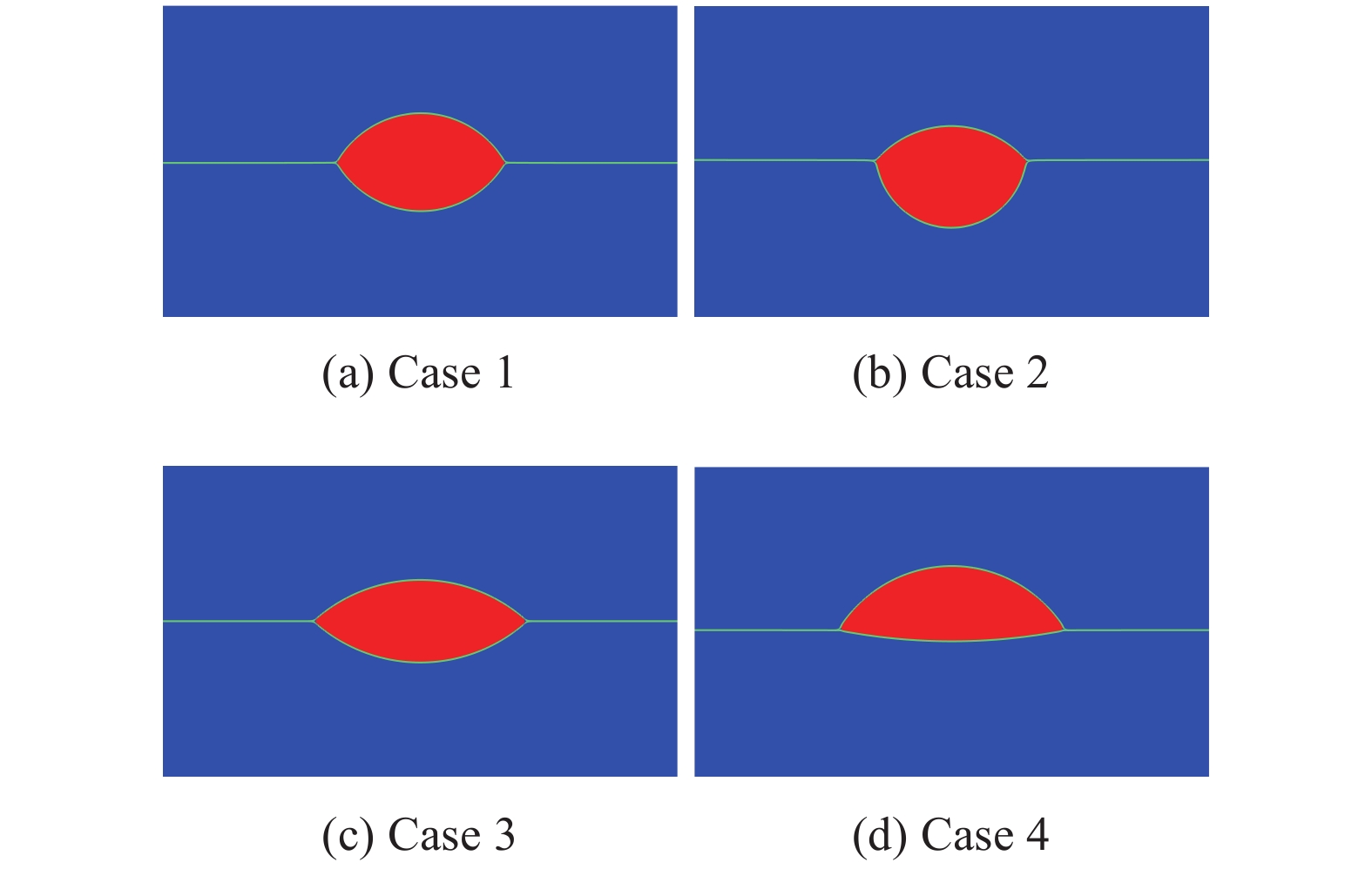
|
图 7 不同表面张力系数下液滴透镜的平衡状态 Fig.7 The equilibrium shape of the liquid lens for different surface tension coefficients |
| 表 2 液滴透镜平衡态下长度(d)和高度(h1,h2)的模拟值和理论值对比 Table 2 Comparison of the numerical results and analytical solutions of the equilibrium length (d) and height (h1, h2) in the lens spreading |
|
|
图8展示了四组不同表面张力系数下液滴透镜质量随时间的变化。在图中,以液滴透镜的初始质量(m0)为评判标准,若质量守恒,液滴透镜的初始质量和实时计算质量(m1)的比值为1。从图中可以看出,四种方案的液滴透镜在演变过程中的质量比曲线与准确质量比1的直线基本重合,质量耗散误差都在1%以内,表明本方法能够保持良好的质量守恒性。
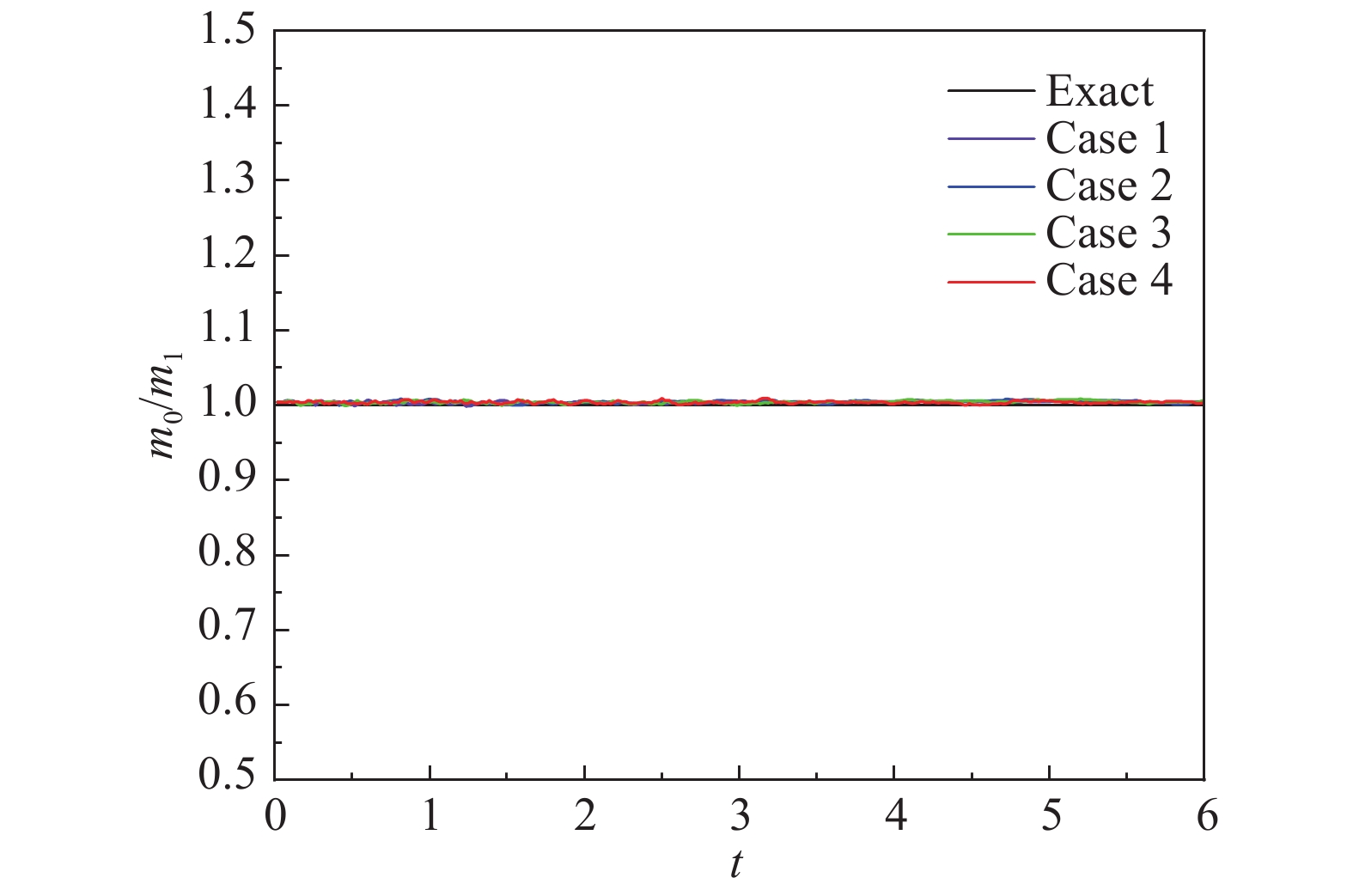
|
图 8 四种方案液滴透镜的初始质量和计算质量比值随时间的变化 Fig.8 Variations of liquid lens mass ratio with time for four cases |
泊肃叶流动问题主要用于验证黏度比对模型计算精度的影响。这里我们模拟了三相泊肃叶流动问题。假设各相流体之间的界面是光滑的,对于相场的相变量初始化使用了如下函数:
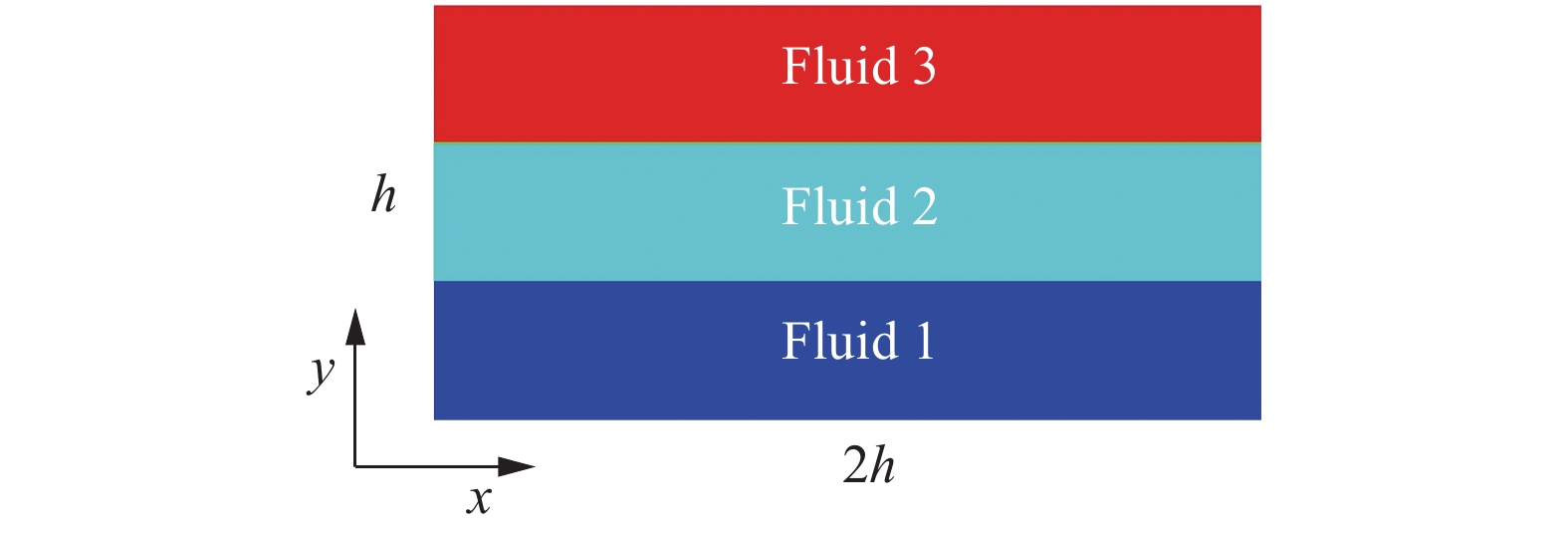
| $ \left\{\begin{array}{l} \phi_{1}(x, y) = \dfrac{1}{2}\left\{1+\tanh \left[\dfrac{2}{\xi}\left(\dfrac{1}{3} h-y\right)\right]\right\} \\ \phi_{2}(x, y) = \dfrac{1}{2}\left\{1+\tanh \left[\dfrac{2}{\xi}\left(\dfrac{2}{3} h-y\right)\right]\right\}-\phi_{1}(x, y) \\ \phi_{3}(x, y) = 1-\phi_{1}(x, y)-\phi_{2}(x, y) \end{array}\right. $ | (35) |
其中,h为矩形槽道的高度,槽道长度为2h,水平槽道内充满了三层互不混溶的流体,如图9所示。
|
图 9 三相泊肃叶流示意图 Fig.9 Diagram of Poiseuille flow with three phases |
在三相泊肃叶流动中,流体由一个体力G = ρg驱动,g是x方向的恒定加速度。因为各相的流体密度为常量,整个系统的N-S方程表述如下:
| $ \frac{{\rm{d}}}{{{\rm{d}}y}}\left( {\upsilon \frac{{{\rm{d}}{u_x}}}{{{\rm{d}}y}}} \right) + g = 0 $ | (36) |
在计算域中,设置网格大小为240×120;界面厚度为
| 表 3 三相泊肃叶流算例中密度和运动黏度的设定 Table 3 Densities and kinematic viscosities used in three-phase Poiseuille flow example |
|
|
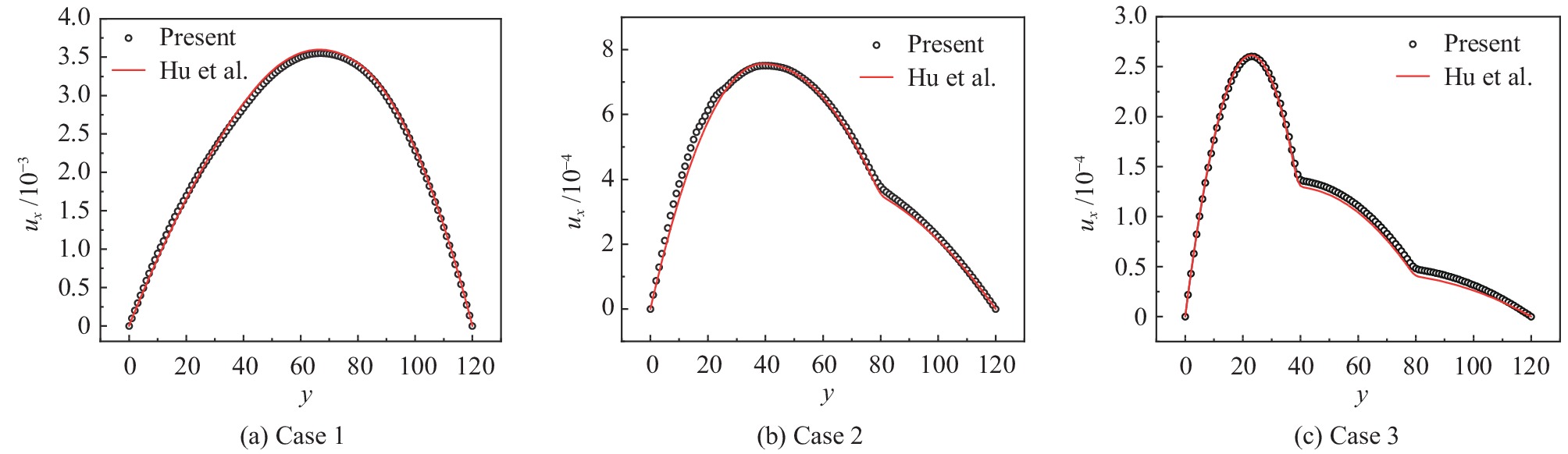
我们绘制了速度分量ux在y轴上的分布曲线,并将当前结果与Hu等的结果进行对比,如图10所示,发现三种情况下两者的曲线吻合较好。图10(a)中,由于三种流体之间的黏度比为1,沿y轴的速度剖面较为光滑。而在方案2和方案3中,黏度比增大,图10(b、c)非常好地捕捉到了因黏度变化而引起的相界面处明显的速度分量ux的跳跃。
|
图 10 当前结果与Hu等结果[34]之间速度剖面的比较 Fig.10 Comparison of velocity profiles between present results and Hu et al.[34] |
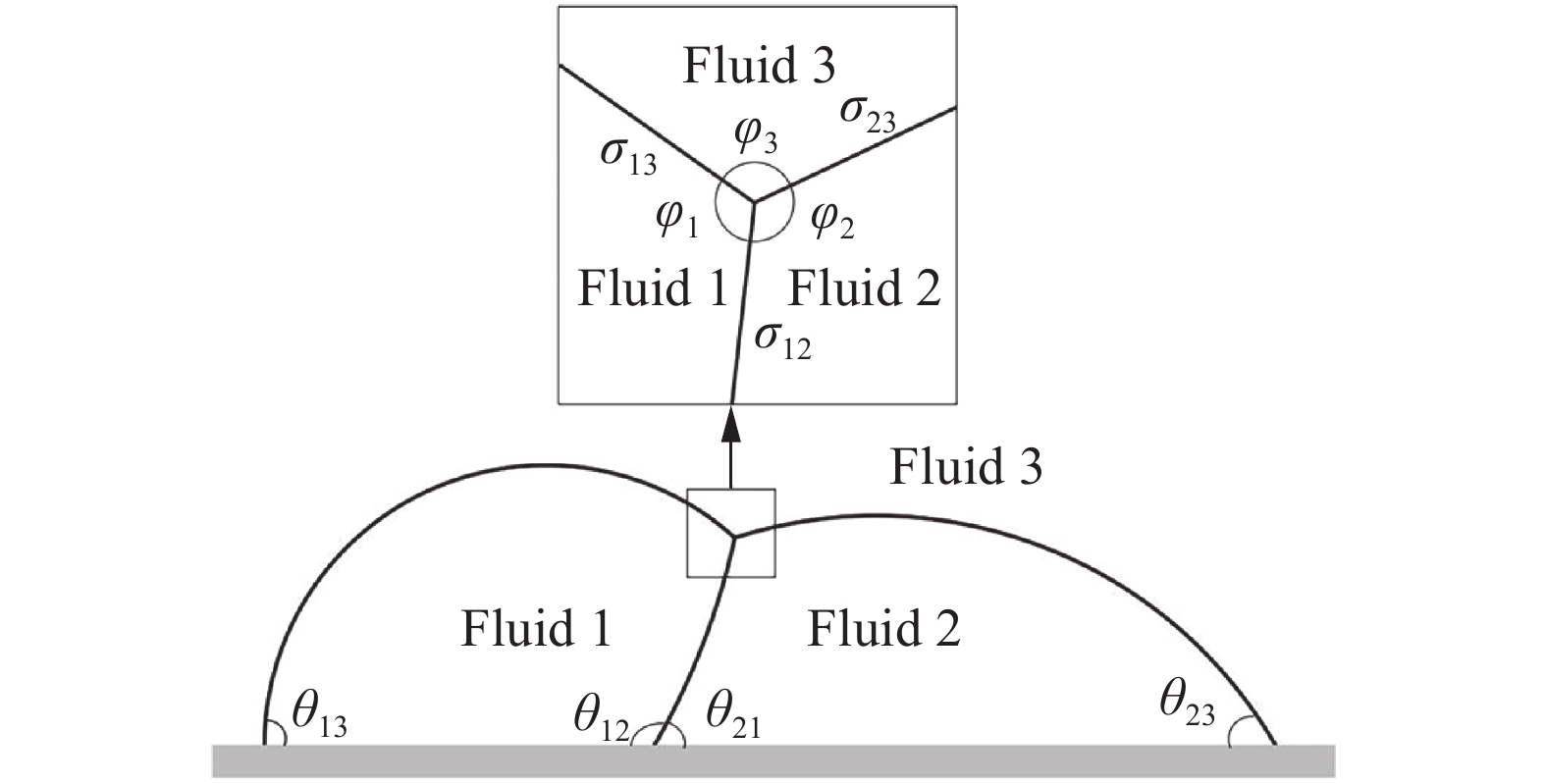
为了验证模型是否能够克服大密度比多相流交互界面处的较大压力梯度问题,这里采用一个二维复合液滴在光滑平板上的铺展问题来进行数值模拟。在这个算例中充分考虑了湿润边界条件,图11中流体1、流体2和流体3为非混溶的三种流体,与固体壁面从左至右形成的接触角分别为θ13、θ12和θ23,由几何关系可知,θ21 = π − θ12。为了满足三相表面张力系数平衡条件,流体i和流体j与光滑平面形成的接触角θij可根据Young’s法则定义如下:
|
图 11 三种流体与固体壁面接触角示意图 Fig.11 Diagram of a compound droplet on a solid substrate |
| $ \cos \theta_{i j} = \frac{\sigma_{j s}-\sigma_{i s}}{\sigma_{i j}} $ | (37) |
σis和σjs分别表示流体i和流体j与固体壁面之间的表面张力系数。
在三相流系统中,三种流体与固体壁面的接触角和三相角(φ1、φ2和φ3)具有一定的联系,基于静态平衡可得:
| $ \sin \varphi_{2} \cos \theta_{13}-\sin \varphi_{3} \cos \theta_{12}-\sin \varphi_{1} \cos \theta_{23} = 0 $ | (38) |
| $ \frac{\sin \varphi_{1}}{\sigma_{23}} = \frac{\sin \varphi_{2}}{\sigma_{13}} = \frac{\sin \varphi_{3}}{\sigma_{12}} $ | (39) |
为了解决三相流系统与固体平面接触面上接触角的不连续性问题,在湿润边界处理上设置加权接触角θ1和θ2来判定湿润度,保证界面均匀光滑地过渡。加权接触角的定义如下:
| $ {\theta _1} = \frac{{{\phi _3}}}{{{\phi _3} + {\phi _2}}}{\theta _{13}} + \frac{{{\phi _2}}}{{{\phi _3} + {\phi _2}}}{\theta _{12}} $ | (40) |
| $ {\theta _2} = \frac{{{\phi _3}}}{{{\phi _3} + {\phi _1}}}{\theta _{23}} + \frac{{{\phi _1}}}{{{\phi _3} + {\phi _1}}}{\theta _{21}} $ | (41) |
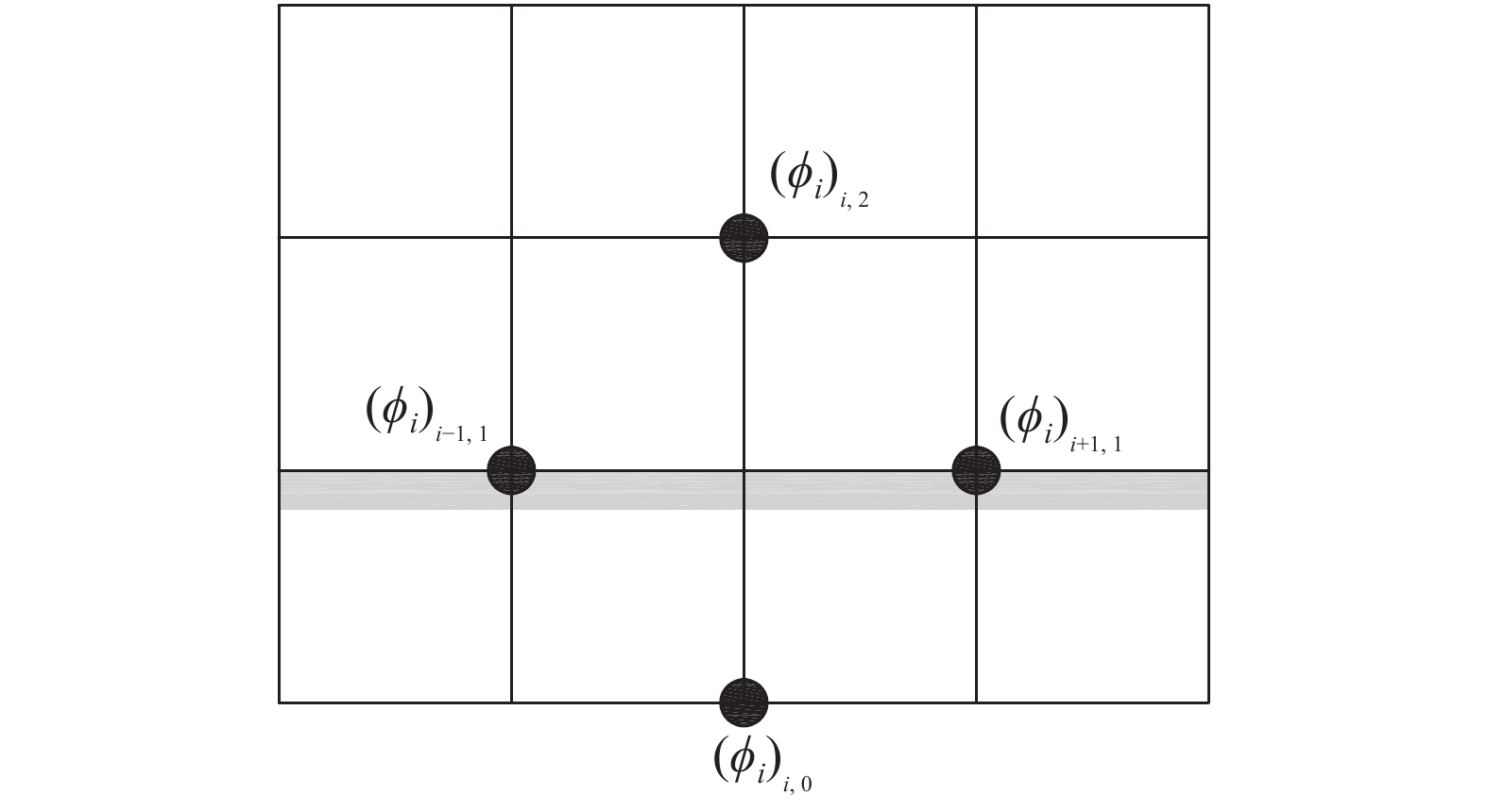
湿润边界的实施还需要人为在固体壁面下侧添加一层虚拟网格,如图12所示。使用中心有限差分格式离散单元格(i,1)后,通过相邻网格的数值近似获得虚拟网格(i,0)的值[45]:
| $ \left(\phi_{i}\right)_{i, 0} = \left(\phi_{i}\right)_{i, 2}+\tan \left(\frac{\text{π}}{2}-\theta_{i}\right)\left|\left(\phi_{i}\right)_{i+1,1}-\left(\phi_{i}\right)_{i-1,1}\right| $ | (42) |
|
图 12 湿润边界条件实施示意图 Fig.12 Diagram of the implementation of wetting boundary conditions |
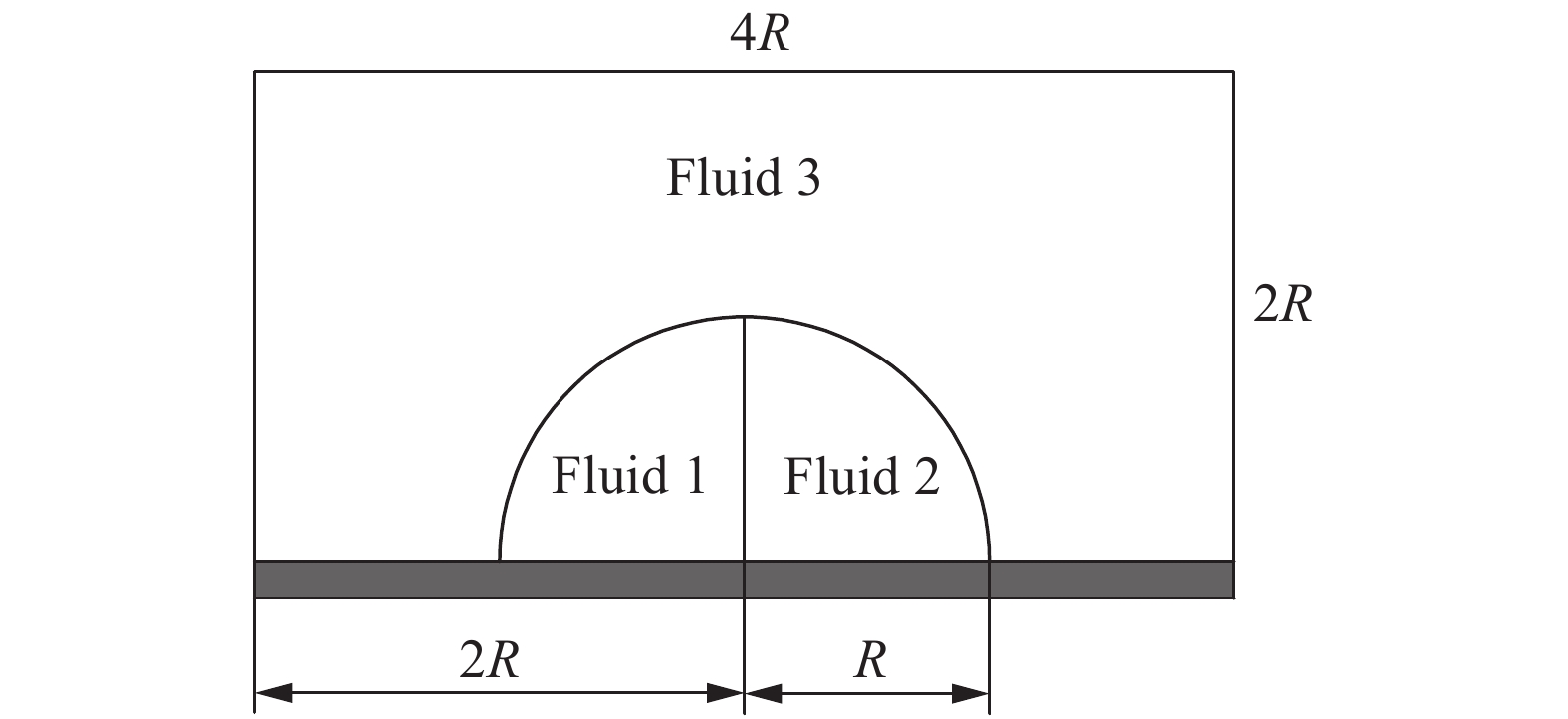
复合液滴的初始形态如图13所示,流体1和流体2分别为一个四分之一圆,它们共同组成一个半圆复合液滴,周围区域为流体3。此算例中,三相流体的运动黏度
|
图 13 复合液滴在平面上铺展初始形态 Fig.13 Initial shape of the compound droplet |
| 表 4 复合液滴铺展中三种流体的密度 Table 4 Densities used in the simulation of spreading of the compound droplet |
|
|
在该算例中将湿润边界条件接触角设置为:θ13 = 90°、θ12 = 120°、θ23 = 60°。假设任意两相界面间的表面张力系数相同,其值为0.01,则有三相角φ1 = φ2 = φ3 = 120°。整个复合液滴不考虑重力因素,主要在表面张力和黏性力作用下推动液滴形态变化。这里用无量纲参数Re和We来表征液滴的动力学特性,设置
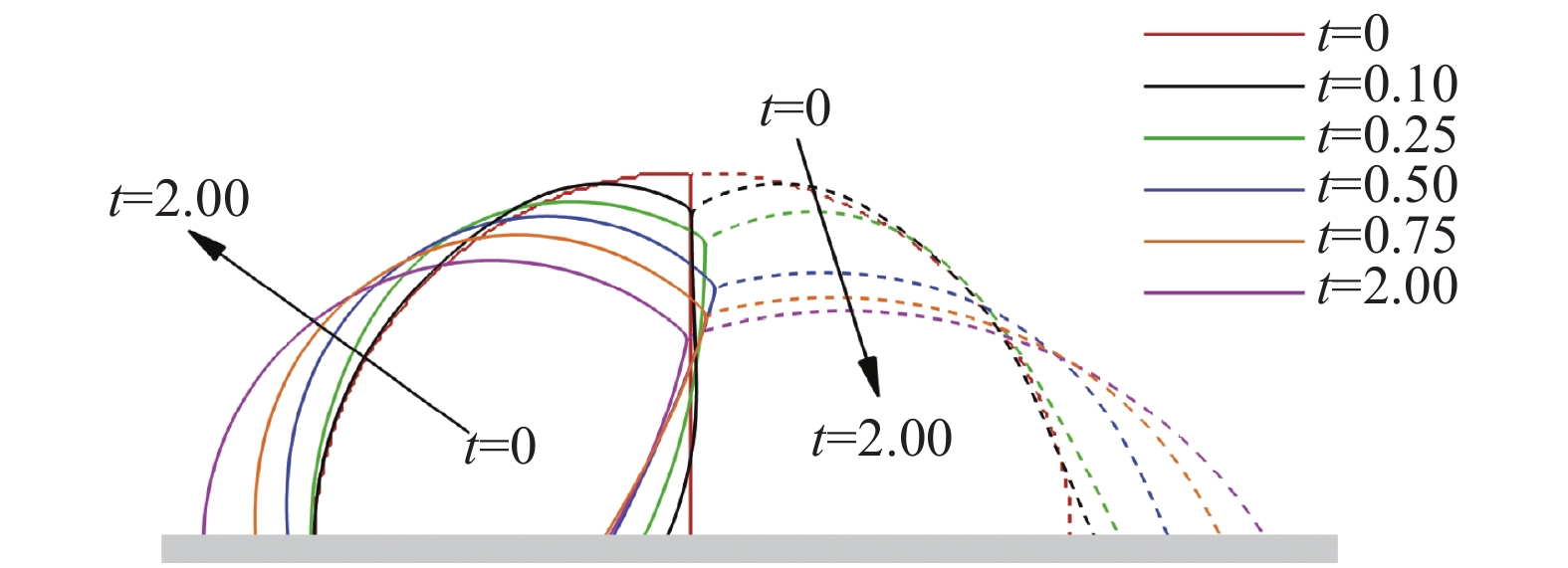
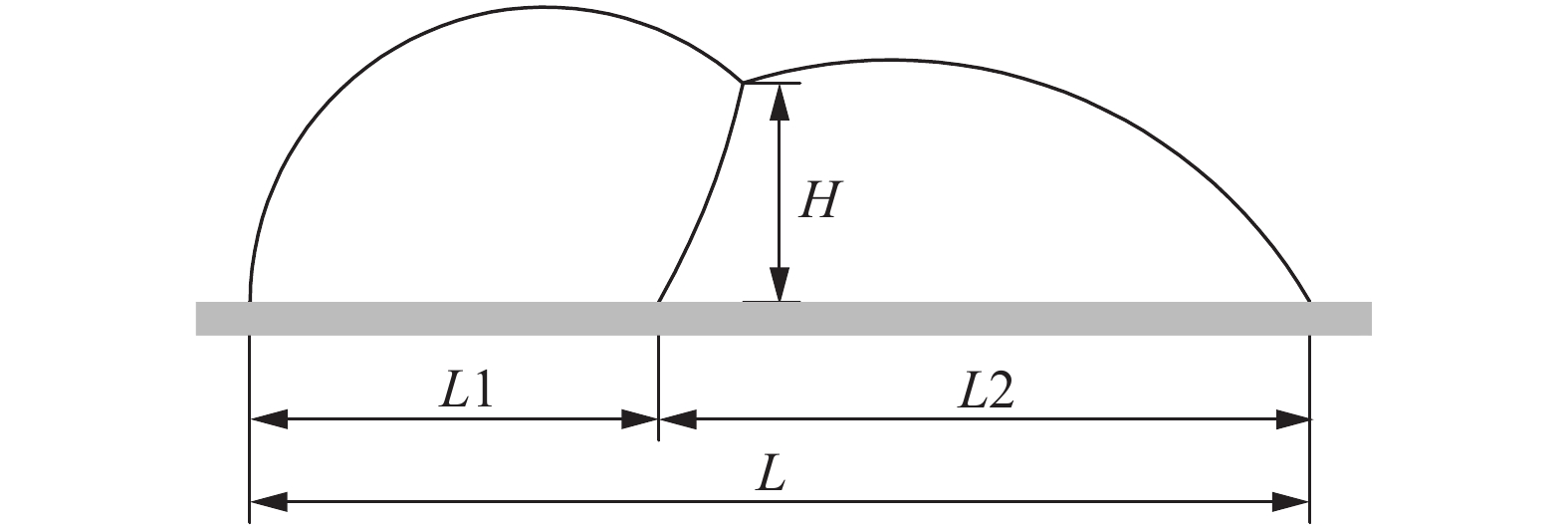
图14表示了在方案1情况下,复合液滴在光滑平板上随时间发展的状态图,不同颜色的线分别表示不同时间节点复合液滴所处状态,这里时间节点分别取t = 0、0.10、0.25、0.50、0.75、2.00。从图中可看到复合液滴随着时间的演变,慢慢地向外铺展,当复合液滴到达平衡状态时其形态会保持不变,平衡时复合液滴的形状主要由初始设置的接触角和三相角给定。这里,我们令流体1和流体2与固体平面接触的润湿长度分别为L1和L2,其总润湿长度为L,如图15所示。其中润湿长度的理论值是根据Zhang等[46]计算的结果,并与模拟值进行了对比,如表5所示。从表中可以发现误差值均小于1%,理论值与数值模拟结果非常吻合,验证了该模型的精确性。
|
图 14 方案1的复合液滴随时间演化过程示意图 Fig.14 Time evolution of the compound droplet of Case 1 |
|
图 15 方案1的复合液滴平衡状态 Fig.15 Equilibrium state of a compound droplet of Case 1 |
| 表 5 方案1的润湿长度理论值与模拟值对比 Table 5 Comparison of the numerical results and analytical solutions of wetting length in Case 1 |
|
|
方案2~方案4(如图16所示)的复合液滴的平衡形状与方案1相似。但是,随着密度比的增加,复合液滴达到平衡状态所需的时间逐渐增加。这是因为密度比的增加导致压力梯度和界面上黏性力的增加,从而进一步延迟复合液滴扩散到平衡状态。然而,即使对于密度比高达1200的方案4,本模型仍能给出稳定解。四种情况下接触角的数值结果与表6中的理论值进行了比较,其中

|
图 16 不同情况下复合液滴的平衡形态 Fig.16 The equilibrium shape of the compound droplet for different cases |
| 表 6 不同密度比复合液滴平衡状态下接触角的模拟值与理论值对比 Table 6 Comparison of the numerical results and analytical solutions of the compound droplet for different cases under equilibrium state |
|
|
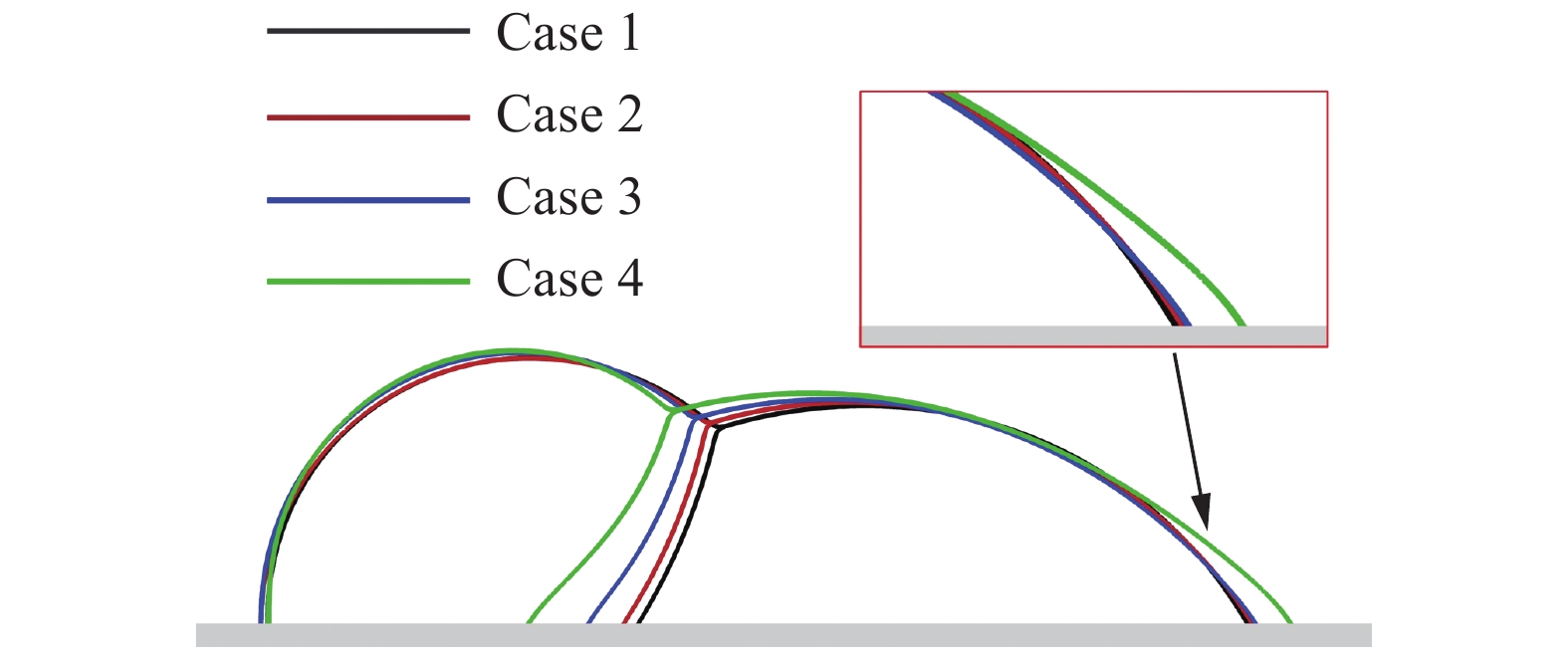
为了更清楚地观察不同密度比下复合液滴的平衡形态,将四种情况下复合液滴平衡态图绘制在一张图中,如图17所示。我们发现了一个有趣的现象,随着密度比的增加,流体1和流体2之间的交界线逐渐向左移动。此外,在较大的密度比下,润湿边界总长度L也增加,三相边界点不仅向左移动,而且随着密度比的增加向上移动。显然,在方案4中,复合液滴中流体1和流体2的形状不像方案1那样规则,从而增加了总润湿长度。有趣的是,四种情况下设置的接触角是相同的,并且由于密度比的增加,复合液滴的形状并不规则,无法计算润湿长度的理论值,但是最终平衡状态下接触角仍与预设的平衡接触角一致。
|
图 17 不同密度比下复合液滴平衡状态图 Fig.17 Equilibrium shape of compound droplets at different density ratios |
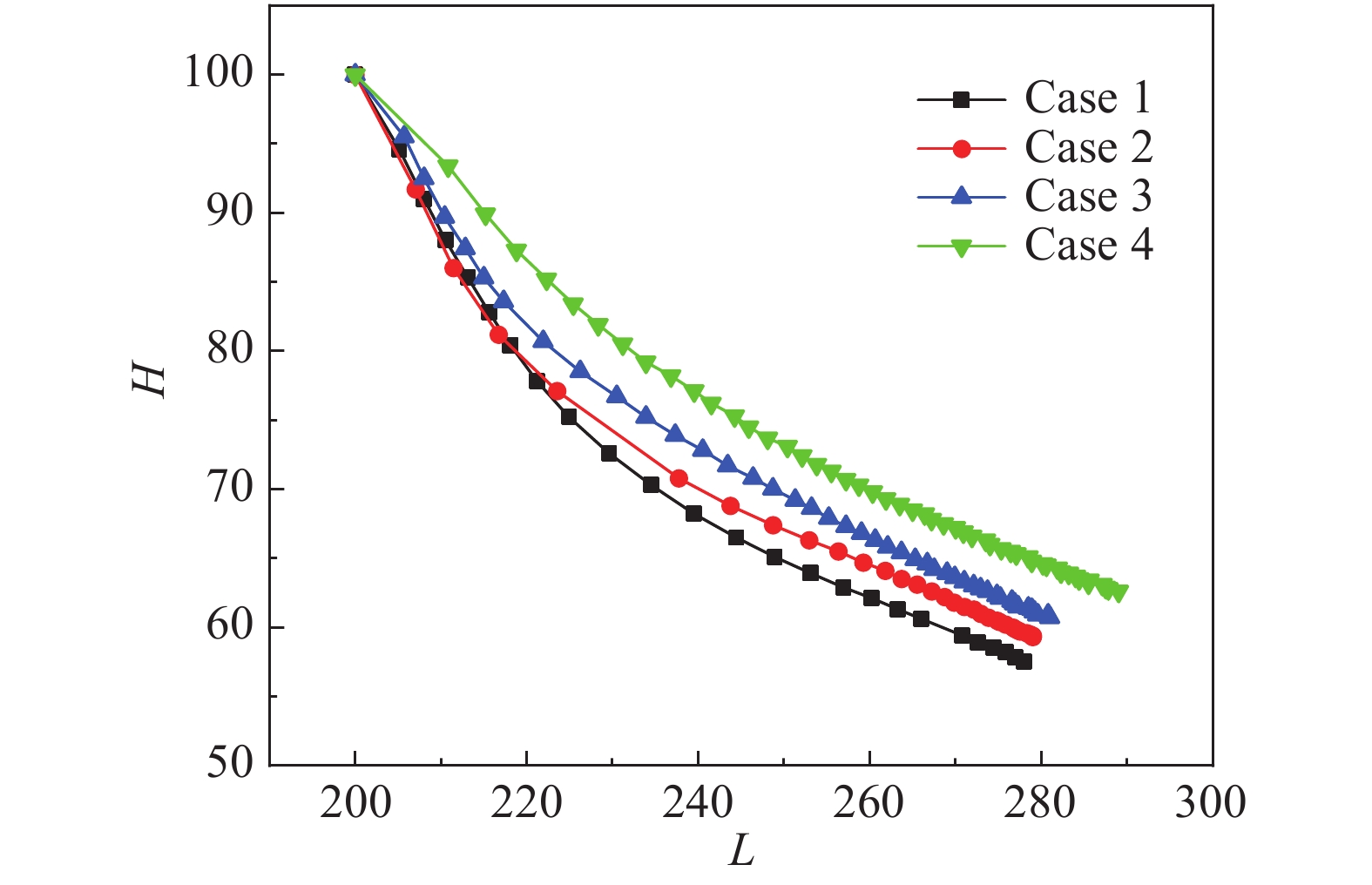
为了更加直观地观察三相交界点的变化规律,绘制了在总润湿长度L的变化过程中,不同密度比下三相交界点高度H的变化,如图18所示。首先在图中可以明显地看出,密度比增大的同时,复合液滴三相交界点的高度随之增高,并在复合液滴演化的过程中一直保持这种趋势。其次,在复合液滴到达平衡状态时,密度比越大,总湿润长度也会越长,其中方案4的L是增长最显著的。这一现象可归因于两种流体之间的作用力和压力差,它们随着密度比的增加而增加,因此复合液滴扩散得更多。
|
图 18 不同密度比下复合液滴三相交界点高度随总润湿长度的变化曲线 Fig.18 Curves of H varying with L for different cases |
本文提出了一种广义守恒相场简化多相流格子Boltzmann方法。该方法继承了Hu等推导出的广义守恒相场方程的还原一致性和质量体积守恒的优点,并结合早前提出的SMLBM用于处理大密度比、大黏度比问题,其中广义守恒相场方程的源分布函数被吸收入相场平衡分布函数中,以保持方法的良好稳定性。此外,本方法大大降低了内存的需求,这通常是限制传统单松弛或多松弛LB方法应用的一个主要因素。为了验证本方法在处理多相流时的网格独立性和精确性,我们首先模拟了拉普拉斯定律和液体透镜两个基准算例,并获得了令人满意的结果。其次,对不同黏度比下的三相泊肃叶流进行了仿真,验证了此方法能够模拟大黏度比(最高可达500)问题。最后,对不同密度比下的复合液滴在润湿基底上的扩散进行了模拟,数值结果表明,该方法能够模拟大密度比多相流问题,其中最大密度比可达1200。对此还发现在较大的密度比下,复合液滴轮廓变得不规则,导致总润湿长度增加,并且还找到了复合液滴在不同密度比下三相交界点的变化规律。以此我们可以得出结论,本文所提出的方法在模拟多相流的准静态问题上有较好的表现。
| [1] |
CHEN Z, SHU C, TAN D, et al. Simplified multiphase lattice Boltzmann method for simulating multiphase flows with large density ratios and complex interfaces[J]. Physical Review E, 2018, 98(6): 063314. DOI:10.1103/physreve.98.063314 |
| [2] |
UTADA A S, LORENCEAU E, LINK D R, et al. Monodisperse double emulsions generated from a microcapillary device[J]. Science, 2005, 308(5721): 537-541. DOI:10.1126/science.1109164 |
| [3] |
DONG S. Physical formulation and numerical algorithm for simulating N immiscible incompressible fluids involving general order parameters[J]. Journal of Computational Physics, 2015, 283: 98-128. DOI:10.1016/j.jcp.2014.11.039 |
| [4] |
YUAN X, LIANG H, CHAI Z, et al. Phase-field-based lattice Boltzmann model for immiscible incompressible N-phase flows[J]. Physical Review E, 2020, 101(6-1): 063310. DOI:10.1103/physreve.101.063310 |
| [5] |
BOYER F, LAPUERTA C, MINJEAUD S, et al. Cahn-Hilliard/Navier-Stokes model for the simulation of three-phase flows[J]. Transport in Porous Media, 2010, 82(3): 463-483. DOI:10.1007/s11242-009-9408-z |
| [6] |
GARCKE H, NESTLER B, STOTH B. A MultiPhase field concept: numerical simulations of moving phase boundaries and multiple junctions[J]. SIAM Journal on Applied Mathematics, 1999, 60(1): 295-315. DOI:10.1137/s0036139998334895 |
| [7] |
KIM J. Phase field computations for ternary fluid flows[J]. Computer Methods in Applied Mechanics and Engineering, 2007, 196(45-48): 4779-4788. DOI:10.1016/j.cma.2007.06.016 |
| [8] |
HIRT C W, NICHOLS B D. Volume of fluid (VOF) method for the dynamics of free boundaries[J]. Journal of Computational Physics, 1981, 39(1): 201-225. DOI:10.1016/0021-9991(81)90145-5 |
| [9] |
GUEYFFIER D, LI J, NADIM A, et al. Volume-of-fluid interface tracking with smoothed surface stress methods for three-dimensional flows[J]. Journal of Computational Physics, 1999, 152(2): 423-456. DOI:10.1006/jcph.1998.6168 |
| [10] |
OSHER S, SETHIAN J A. Fronts propagating with curvature-dependent speed: Algorithms based on Hamilton-Jacobi formulations[J]. Journal of Computational Physics, 1988, 79(1): 12-49. DOI:10.1016/0021-9991(88)90002-2 |
| [11] |
SMITH K, SOLIS F, CHOPP D. A projection method for motion of triple junctions by level sets[J]. Interfaces and Free Boundaries, 2002, 263-276. DOI:10.4171/ifb/61 |
| [12] |
UNVERDI S O, TRYGGVASON G. A front-tracking method for viscous, incompressible, multi-fluid flows[J]. Journal of Computational Physics, 1992, 100(1): 25-37. DOI:10.1016/0021-9991(92)90307-K |
| [13] |
TRYGGVASON G, BUNNER B, ESMAEELI A, et al. A front-tracking method for the computations of multiphase flow[J]. Journal of Computational Physics, 2001, 169(2): 708-759. DOI:10.1006/jcph.2001.6726 |
| [14] |
GINGOLD R A, MONAGHAN J J. Smoothed particle hydrodynamics: theory and application to non-spherical stars[J]. Monthly Notices of the Royal Astronomical Society, 1977, 181(3): 375-389. DOI:10.1093/mnras/181.3.375 |
| [15] |
CAHN J W, HILLIARD J E. Free energy of a nonuniform system. I. interfacial free energy[J]. The Journal of Chemical Physics, 1958, 28(2): 258-267. DOI:10.1063/1.1744102 |
| [16] |
ALLEN S M, CAHN J W. Mechanisms of phase transformations within the miscibility gap of Fe-rich Fe-Al alloys[J]. Acta Metallurgica, 1976, 24(5): 425-437. DOI:10.1016/0001-6160(76)90063-8 |
| [17] |
BAO W Z, DU Q. Multiscale modeling and analysis for materials simulation[M]. World Scientific . Imperial College Press, 2011. doi: 10.1142/8212
|
| [18] |
LEE H G, CHOI J W, KIM J. A practically unconditionally gradient stable scheme for the N-component Cahn-Hilliard system[J]. Physica A:Statistical Mechanics and Its Applications, 2012, 391(4): 1009-1019. DOI:10.1016/j.physa.2011.11.032 |
| [19] |
LEE H G, KIM J. An efficient numerical method for simulating multiphase flows using a diffuse interface model[J]. Physica A:Statistical Mechanics and Its Applications, 2015, 423: 33-50. DOI:10.1016/j.physa.2014.12.027 |
| [20] |
LEE H G, KIM J. A second-order accurate non-linear difference scheme for the N-component Cahn-Hilliard system[J]. Physica A:Statistical Mechanics and Its Applications, 2008, 387(19-20): 4787-4799. DOI:10.1016/j.physa.2008.03.023 |
| [21] |
KIM J. A generalized continuous surface tension force formulation for phase-field models for multi-component immiscible fluid flows[J]. Computer Methods in Applied Mechanics and Engineering, 2009, 198(37-40): 3105-3112. DOI:10.1016/j.cma.2009.05.008 |
| [22] |
ELLIOTT C M, LUCKHAUS S. A generalised diffusion equation for phase separation of a multi-component mixture with interfacial free energy[R]. IMA Preprints Series #2486. https://www.ima.umn.edu/sites/default/files/887.pdf
|
| [23] |
DONG S. An efficient algorithm for incompressible N-phase flows[J]. Journal of Computational Physics, 2014, 276: 691-728. DOI:10.1016/j.jcp.2014.08.002 |
| [24] |
DONG S. Wall-bounded multiphase flows of N immiscible incompressible fluids: consistency and contact-angle boundary condition[J]. Journal of Computational Physics, 2017, 338: 21-67. DOI:10.1016/j.jcp.2017.02.048 |
| [25] |
DONG S. Multiphase flows of N immiscible incompressible fluids: a reduction-consistent and thermodynamically-consistent formulation and associated algorithm[J]. Journal of Computational Physics, 2018, 361: 1-49. DOI:10.1016/j.jcp.2018.01.041 |
| [26] |
YUE P T, ZHOU C F, FENG J J. Spontaneous shrinkage of drops and mass conservation in phase-field simulations[J]. Journal of Computational Physics, 2007, 223(1): 1-9. DOI:10.1016/j.jcp.2006.11.020 |
| [27] |
KIM J, LOWENGRUB J. Phase field modeling and simulation of three-phase flows[J]. Interfaces and Free Boundaries, 2005, 435-466. DOI:10.4171/ifb/132 |
| [28] |
WANG Y, SHU C, HUANG H B, et al. Multiphase lattice Boltzmann flux solver for incompressible multiphase flows with large density ratio[J]. Journal of Computational Physics, 2015, 280: 404-423. DOI:10.1016/j.jcp.2014.09.035 |
| [29] |
CHAI Z H, SHI B C, GUO Z L. A multiple-relaxation-time lattice boltzmann model for general nonlinear anisotropic convection-diffusion equations[J]. Journal of Scientific Computing, 2016, 69(1): 355-390. DOI:10.1007/s10915-016-0198-5 |
| [30] |
WANG L, ZHAO Y, YANG X G, et al. A lattice Boltzmann analysis of the conjugate natural convection in a square enclosure with a circular cylinder[J]. Applied Mathematical Modelling, 2019, 71: 31-44. DOI:10.1016/j.apm.2019.02.012 |
| [31] |
LIANG H, SHI B C, CHAI Z H. Lattice Boltzmann modeling of three-phase incompressible flows[J]. Physical Review E, 2016, 93(1): 013308. DOI:10.1103/physreve.93.013308 |
| [32] |
HAGHANI HASSAN ABADI R, FAKHARI A, RAHIMIAN M H. Numerical simulation of three-component multiphase flows at high density and viscosity ratios using lattice Boltzmann methods[J]. Physical Review E, 2018, 97(3): 033312. DOI:10.1103/physreve.97.033312 |
| [33] |
HAGHANI HASSAN ABADI R, RAHIMIAN M H, FAKHARI A. Conservative phase-field lattice-Boltzmann model for ternary fluids[J]. Journal of Computational Physics, 2018, 374: 668-691. DOI:10.1016/j.jcp.2018.07.045 |
| [34] |
ZHENG L, ZHENG S, ZHAI Q L. Reduction-consistent phase-field lattice Boltzmann equation for N immiscible incompressible fluids[J]. Physical Review E, 2020, 101(4): 043302. DOI:10.1103/physreve.101.043302 |
| [35] |
HU Y, LI D C, HE Q. Generalized conservative phase field model and its lattice Boltzmann scheme for multicomponent multiphase flows[J]. International Journal of Multiphase Flow, 2020, 132: 103432. DOI:10.1016/j.ijmultiphaseflow.2020.103432 |
| [36] |
LI Q Z, LU Z L, ZHOU D, et al. Unified simplified multiphase lattice Boltzmann method for ferrofluid flows and its application[J]. Physics of Fluids, 2020, 32(9): 093302. DOI:10.1063/5.0021463 |
| [37] |
KHAN A, NIU X D, LI Q Z, et al. Dynamic study of ferrodroplet and bubbles merging in ferrofluid by a simplified multiphase lattice Boltzmann method[J]. Journal of Magnetism and Magnetic Materials, 2020, 495: 165869. DOI:10.1016/j.jmmm.2019.165869 |
| [38] |
CHEN Z, SHU C, LIU Y Y, et al. Ternary phase-field simplified multiphase lattice Boltzmann method and its application to compound droplet dynamics on solid surface in shear flow[J]. Physical Review Fluids, 2021, 6(9): 094304. DOI:10.1103/physrevfluids.6.094304 |
| [39] |
DING H, SPELT P D M, SHU C. Diffuse interface model for incompressible two-phase flows with large density ratios[J]. Journal of Computational Physics, 2007, 226(2): 2078-2095. DOI:10.1016/j.jcp.2007.06.028 |
| [40] |
ZU Y Q, HE S. Phase-field-based lattice Boltzmann model for incompressible binary fluid systems with density and viscosity contrasts[J]. Physical Review E, 2013, 87(4): 043301. DOI:10.1103/physreve.87.043301 |
| [41] |
LIANG H, XU J, CHEN J, et al. Phase-field-based lattice Boltzmann modeling of large-density-ratio two-phase flows[J]. Physical Review E, 2018, 97(3-1): 033309. DOI:10.1103/physreve.97.033309 |
| [42] |
KALANTARPOUR R, EBADI A, HOSSEINALIPOUR S M, et al. Three-component phase-field lattice Boltzmann method with high density ratio and ability to simulate total spreading states[J]. Computers & Fluids, 2020, 204: 104480. DOI:10.1016/j.compfluid.2020.104480 |
| [43] |
RAWLINSON J S, WIDOM B. The molecular theory of capillarity[M]. Oxford University Press, 1982.
|
| [44] |
REN F, SONG B, SUKOP M C, et al. Improved lattice Boltzmann modeling of binary flow based on the conservative Allen-Cahn equation[J]. Physical Review E, 2016, 94(2-1): 023311. DOI:10.1103/physreve.94.023311 |
| [45] |
DING H, SPELT P D M. Wetting condition in diffuse interface simulations of contact line motion[J]. Physical Review E, 2007, 75(4): 046708. DOI:10.1103/physreve.75.046708 |
| [46] |
ZHANG C Y, DING H, GAO P, et al. Diffuse interface simulation of ternary fluids in contact with solid[J]. Journal of Computational Physics, 2016, 309: 37-51. DOI:10.1016/j.jcp.2015.12.054 |
 2022, Vol. 40
2022, Vol. 40


