在过去的三十年间,LBM 已经被发展到诸多领域,除了作为可压、不可压Navier-Stokes (N-S)方程的替代工具,还可以用作其他偏微分方程的解法器。尤其是在不可压流动模拟方面,LBM 被广泛认为是一种简单高效的数值工具。标准LBM的碰撞迁移过程使得编程简单、易于并行、数值耗散低。然而,这样的求解方式也存在一些不足。例如,物理空间和离散速度空间的耦合导致标准LBM必须使用均匀笛卡尔网格,对复杂外形的几何适应性差,时间步长和空间步长必须一致,即Courant-Friedrichs-Lewy(CFL)数为1,标准的单松弛BGK(Bhatnagar-Gross-Krook)格式在高雷诺数情况下数值稳定性差。此外,尽管LBM的数值耗散低,然而它始终还是只有二阶空间精度。应用LBM进行湍流模拟往往需要大量的网格,计算效率低。提高标准LBM的精度是较为困难的,目前主要的策略是对速度空间高阶离散或者对平衡态函数高阶展开。这些不足给LBM应用到高速、复杂外形的工程问题造成了一定困难。
格子玻尔兹曼方程(LBE)可以看作是离散速度玻尔兹曼方程(DVBE)的一种差分格式。已证明,物理对称性和格子对称性可以分开处理[1],物理空间的离散可以独立于速度空间的离散,这样就可以将离散速度和计算网格进行解耦。在这一思想指导下建立起来的方法一般称为非标准格子玻尔兹曼方法(OLBM)。OLBM主要分为两大类,一类是在欧拉框架下采用传统的数值离散方法,比如利用有限差分[2]、有限体积[3]、有限元法[4]直接求解DVBE(以下称为欧拉法);另一类是在半拉格朗日(semi-Lagrangian)框架下借助插值方法实现粒子分布函数的演化(以下称为半拉格朗日法)[5-7]。早期的OLBM大多只有二阶精度,并且相比标准LBM会引入更大的数值耗散。近十多年来,高精度格式开始引起学者们的广泛关注。这类格式拥有较小的数值耗散,在多尺度流动的模拟上具有明显优势,例如湍流、气动噪声。和低精度的格式相比,高精度格式在取得相同误差条件下需要的网格要少得多,因而提高了计算效率。利用高精度格式求解N-S方程数值模拟不可压流的算法一般较为复杂,主要因为N-S方程的对流项是非线性,黏性项包含二阶偏导数,以及压强和速度的耦合。最常用的投影法或者压强修正法都需要求解压强泊松方程,该方程不容易收敛。非线性的对流项对于通过插值基函数在网格单元内构造数值解高阶多项式的高精度方法来说,还可能会产生混淆误差。而DVBE可以看成一组线性偏微分方程,它的曲线坐标形式相比N-S方程也要简洁得多,所以用高精度格式求解DVBE要容易得多。事实上,相关工作早在21世纪初就有展开。Shi等[8]采用间断伽辽金谱元法求解DVBE;Düster等[9]也发展了一种间断伽辽金格子玻尔兹曼法。然而,由于这两种方法缺少网格收敛性研究,它们的收敛阶能否取得高阶并不清楚。后来,Hejranfar和Ezzatneshan[10-11]提出了一种紧致有限差分格子玻尔兹曼法(CFDLBM)并做了收敛性分析,验证了该方法能够取得四阶精度。由于中心型的紧致有限差分格式没有数值耗散,为了确保计算的稳定,必须引入过滤器。他们将CFDLBM和标准LBM做了比较,当取得相似的误差时,CFDLBM的效率更高。为了避免过滤操作、简化计算过程,后续又有相关工作采用带有数值耗散的高阶差分格式。如利用五阶WENO格式[12]以及五阶迎风型紧致有限差分格式[13]求解DVBE。有限差分对于复杂外形的几何适应性较差,为了改进这一问题,Li[14]将高精度谱差分方法(SD)和DVBE结合,提出了SDLBM。通过坐标变换形函数,SDLBM可以应用非结构网格。Li对SDLBM做了详细的收敛性分析,证明了在被压缩性误差影响之前,SDLBM可以获得高阶精度,并且算法简单、易于并行。
以上这些方法的时间离散都采用显式格式。当雷诺数较高时,DVBE碰撞项的刚性将严重限制时间步长,大大降低计算效率。目前应对这种问题的方法主要有两种,一种是将碰撞项隐式处理,直接求解DVBE(以下称为直接法),常用的方法有Guo和Zhao[15]提出的基于半隐格式的显式方法和隐式-显式Runge-Kutta方法(IMEX)等[16];另一种是将计算分为两步(以下称为分步法),首先执行碰撞步,这和标准LBM一样,然后在迁移步采用高精度格式求解一个纯对流方程。通过这种方法学者们也提出了不同的高精度OLBM,如Min和Lee[17]提出的谱元间断伽辽金格子玻尔兹曼法以及Zadehgol等[18]提出的节点间断伽辽金格子玻尔兹曼法。然而,鲜有文献比较分步法和碰撞项隐式处理的直接法之间的数值表现。
另一种构造高精度OLBM的思路是在半拉格朗日框架下采用高阶插值[19]。由于不需要求解对流方程,没有CFL条件的限制,这种方法能在大时间步长下保持稳定,并且每个时间步空间算子(插值)只演化一次,因此这种方法计算效率较高。然而事实上,半拉格朗日法误差和时间步长是成正比的。要想获得高精度,还是需要取较小的时间步长。此外,半拉格朗日法的离散误差相比分步法要更大[20]。因此,这几种高精度OLBM的优劣依然值得进一步讨论。
本文将最近较为流行的通量重构(FR)格式引入OLBM,发展了一种高阶通量重构格子玻尔兹曼方法(FRLBM)。FR格式为多种单元内多自由度的高阶格式,如节点间断有限元(NDG)和SD,提供了一个统一的框架[21],且算法更加简单,计算效率更高[22]。在FRLBM的框架下,本文比较了直接法和分步法的精度以及稳定性,并且对比了基于半隐格式的显式方法和一阶IMEX、二阶IMEX以及三阶IMEX对不同雷诺数下CFL数取值的影响。研究结果旨在进一步加深对高精度OLBM的认识,为发展更加高效高精度的OLBM提供参考。
1 FRLBM计算方法 1.1 控制方程采用BGK近似的DVBE为:
| $ \frac{{\partial {f_{\alpha} }}}{{\partial t}} + {{\boldsymbol{e}}_{\alpha} }\cdot\nabla {f_{\alpha} } = - \frac{{\left( {{f_{\alpha} } - f_{\alpha} ^{{\text{eq}}}} \right)}}{\tau } $ | (1) |
其中,
| $ f_{\alpha} ^{{\text{eq}}} = {\omega _{\alpha} }\left[ {p + {p_0}\left( {\frac{{{{\boldsymbol{e}}_{\alpha} }\cdot{\boldsymbol{u}}}}{{c_s^2}} + \frac{{{{\left( {{{\boldsymbol{e}}_{\alpha} }\cdot{\boldsymbol{u}}} \right)}^2}}}{{2c_s^4}} - \frac{{{\boldsymbol{u}}\cdot{\boldsymbol{u}}}}{{2c_s^2}}} \right)} \right] $ | (2) |
其中,
| $ p = \sum\limits {{f_{\alpha} }} ,\quad {p_0}{\boldsymbol{u}} = \sum\limits {{{\boldsymbol{e}}_{\alpha} }} {f_{\alpha} } $ | (3) |
本文采用D2Q9离散速度模型,相应的离散速度和权系数为:
| $ {{\boldsymbol{e}}_{\alpha} } = \left\{ {\begin{array}{*{20}{l}} {(0,0),}&{\alpha = 0} \\ {( \pm 1,0),(0, \pm 1),}&{\alpha = 1 ~ 4} \\ {( \pm 1, \pm 1),}&{\alpha = 5 ~ 8} \end{array}} \right. $ | (4) |
| $ {\omega _{\alpha} } = \left\{ {\begin{array}{*{20}{l}} {4/9,}&{\alpha = 0} \\ {1/9,}&{\alpha = 1 ~ 4} \\ {1/36,}&{\alpha = 5 ~ 8} \end{array}} \right. $ | (5) |
此时,
直接法求解的方程为式(1),而分步法则先采用θ方法将式(1)在时间区间[t,t + Δt]沿特征线方向积分,得到[17]:
| $ \begin{split} &{{f}_{\alpha }|}_{\left({\boldsymbol{x}}+{{\boldsymbol{e}}}_{\alpha }\Delta t,t+\Delta t\right)}-{{f}_{\alpha }|}_{({\boldsymbol{x}},t)} = {\frac{\theta }{{\tau }^{\prime }}\left({f}_{\alpha }^{\text{eq}}-{f}_{\alpha }\right)\Bigg|}_{({\boldsymbol{x}},t)}+\\ &\qquad{\frac{1-\theta }{{\tau }^{\prime }}\left({f}_{\alpha }^{\text{eq}}-{f}_{\alpha }\right)\Bigg|}_{\left({\boldsymbol{x}}+{{\boldsymbol{e}}}_{\alpha }\Delta t,t+\Delta t\right)} \end{split}$ | (6) |
上式
| $ {\bar{f}}_{\alpha } = {f}_{\alpha }+\frac{{f}_{\alpha }-{f}_{\alpha }^{\text{eq}}}{2{\tau }^{\prime }} $ | (7) |
由上式可得:
| $ \bar f_{\alpha} ^{{\text{eq}}} = f_{\alpha} ^{{\text{eq}}} $ | (8) |
因此,式(6)可以重写为:
| $ {\bar f_{\alpha} }({\boldsymbol{x}},t) - {\bar f_{\alpha} }\left( {{\boldsymbol{x}} - {{\boldsymbol{e}}_{\alpha} }\Delta t,t - \Delta t} \right) = - {\left. {\frac{1}{{{\tau ^\prime } + 0.5}}\left( {{{\bar f}_{\alpha} } - \bar f_{\alpha} ^{{\text{eq}}}} \right)} \right|_{\left( {{\boldsymbol{x}} - {{\boldsymbol{e}}_{\alpha} }\Delta t,t - \Delta t} \right)}} $ | (9) |
对式(9)的求解分为两步,首先执行碰撞步[17]:
| $ {\hat{f}}_{\alpha } = {\bar{f}}_{\alpha }-\frac{{\bar{f}}_{\alpha }-{\bar{f}}_{\alpha }^{\text{eq}}}{{\tau }^{\prime }+0.5} $ | (10) |
接着求解以下的纯对流方程:
| $ \frac{\partial {\hat{f}}_{\alpha }}{\partial t}+{{\boldsymbol{e}}}_{\alpha }\cdot\nabla {\hat{f}}_{\alpha } = 0 $ | (11) |
本文采用高精度FR格式对式(1)和式(11)进行空间离散。
1.2 空间离散本文仅讨论四边形单元下FR格式,考虑以下的二维守恒律:
| $ \frac{\partial w}{\partial t}+\nabla \cdot {\boldsymbol{F}}(w) = 0 $ | (12) |
其中,
将空间划分为相互不重叠的四边形网格单元。为了在每个四边形单元采用统一的插值函数,简化计算过程,首先需要把不规则的单元映射到标准单元
| $ \left( {\begin{array}{*{20}{l}} {x(\xi ,\eta )} \\ {y(\xi ,\eta )} \end{array}} \right) = \sum\limits_{i = 1}^K {{M_i}} (\xi ,\eta )\left( {\begin{array}{*{20}{l}} {{x_i}} \\ {{y_i}} \end{array}} \right) $ | (13) |
式中,K表示定义该网格单元的节点数量,M为坐标转换函数。根据坐标变换关系,守恒方程(12)在标准单元下的表达形式为:
| $ \frac{\partial \tilde{w}}{\partial t}+\nabla \cdot\tilde{{\boldsymbol{F}}} = \frac{\partial \tilde{w}}{\partial t}+\frac{\partial {\tilde{F}}_{x}}{\partial \xi }+\frac{\partial {\tilde{F}}_{y}}{\partial \eta } = 0 $ | (14) |
式中,
| $ \tilde{w} = \left|{\boldsymbol{J}}\right|w \text{,}\left[ {\begin{array}{*{20}{c}} {{{\tilde F}_x}} \\ {{{\tilde F}_y}} \end{array}} \right] = |{\boldsymbol{J}}|{{\boldsymbol{J}}^{ - 1}}\left[ {\begin{array}{*{20}{l}} {{F_x}} \\ {{F_y}} \end{array}} \right] $ | (15) |
其中雅克比矩阵
| $ {\boldsymbol{J}} = \frac{\partial (x,y)}{\partial (\xi ,\eta )} = \left(\begin{array}{c}{x}_{\xi },{x}_{\eta }\\ {y}_{\xi },{y}_{\eta }\end{array}\right) $ | (16) |
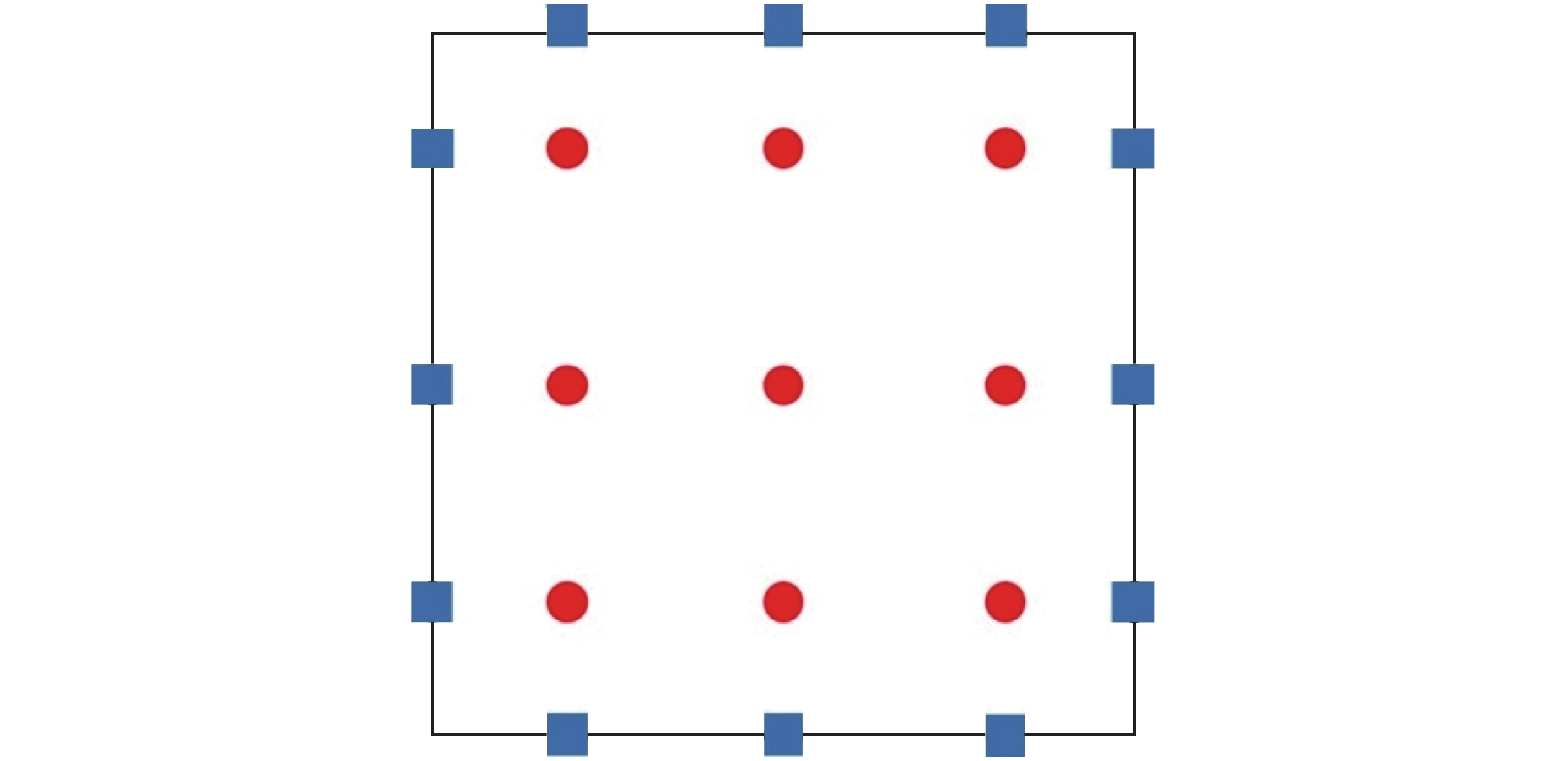
为了在单元内构造高阶的连续通量插值多项式,需要定义两类点集,即求解点和通量点。求解点本文应用Gauss-Legendre点,通量点为每个方向上的边界点。三阶FR方法的标准单元如图1所示。
|
图 1 三阶FR方法标准单元求解点(圆形)和通量点(正方形)分布 Fig.1 Arrangement of the solution points (circles) and the interface flux points (squares) in a standard element for the third-order FR method |
以
| $ {\tilde F_x}(\xi ,\eta ) = \sum\limits_{j = 1}^N {\sum\limits_{i = 1}^N {{{\tilde F}_{i,j}}} } \left[ {{l_i}(\xi ) \cdot {l_j}(\eta )} \right] $ | (17) |
其中,N为一维方向上的求解点个数,
| $ {\tilde F_x}(\xi ) = \sum\limits_{i = 1}^N {{{\tilde F}_i}} {l_i}(\xi ) $ | (18) |
以上的通量多项式并没有考虑单元间的作用,因此,它在单元边界是间断的。为了重新构造单元间连续的通量多项式,需要引入左右边界的公共通量
| $ \begin{split} \tilde F_x^{{\text{c }}}\left( \xi \right) =& {{\tilde F}_x}(\xi ) + \left[ {\left( {{{\tilde F}_x}} \right)_{i - \frac{1}{2}}^{{\text{com }}} - {{\tilde F}_x}( - 1)} \right]{g_{_{\rm{L}}}}(\xi )+ \\ & \left[ {\left( {{{\tilde F}_x}} \right)_{i{\text{ + }}\frac{1}{2}}^{{\text{com }}} - {{\tilde F}_x}(1)} \right]{g_{_{\rm{R}}}}(\xi ) \\ \end{split}$ | (19) |
其中
最终,对式(19)两边同时关于
| $ \begin{split} \frac{{{\rm{d}}\tilde F_x^{{\text{c }}}}}{{{\rm{d}}\xi }}\left( \xi \right) =& \frac{{{d}\tilde F_x^{\text{ }}}}{{{\rm{d}}\xi }}\left( \xi \right) + \left[ {\tilde F_{i - \frac{1}{2}}^{{\text{com }}} - {{\tilde F}_i}( - 1)} \right]\frac{{{\rm{d}}{g_{_{\rm{L}}}}}}{{{\rm{d}}\xi }}\left( \xi \right) +\\ &\left[ {\tilde F_{i + \frac{1}{2}}^{\text{com}} - {{\tilde F}_i}(1)} \right]\frac{{{\rm{d}}{g_{_{\rm{R}}}}}}{{{\rm{d}}\xi }}\left( \xi \right) \end{split} $ | (20) |
如果采用显式时间离散格式求解方程(1),每个单元i的时间步长受限于CFL条件以及碰撞松弛时间,如下式所示:
| $ \Delta {t_i} = \sigma \min \left( {\frac{{\sqrt {{V_i}} }}{{{\varLambda _i}}},2\tau } \right)\bigg /\left( {2N + 1} \right) $ | (21) |
其中
| $ f_{\alpha} ^{n + 1} - f_{\alpha} ^n + \Delta t{{\boldsymbol{e}}_{\alpha} }\cdot\nabla f_{\alpha} ^n = \Delta t\left[ {\theta \varOmega _{\alpha} ^{n + 1} + (1 - \theta )\varOmega _{\alpha} ^n} \right] $ | (22) |
其中,
| $ {g}_{\alpha } = {f}_{\alpha }-\frac{1}{2}\Delta t{\varOmega }_{\alpha } $ | (23) |
式(22)重写为:
| $ g_{\alpha} ^{n + 1} = f_{\alpha} ^n - \Delta t{{\boldsymbol{e}}_{\alpha} }\cdot\nabla f_{\alpha} ^n + \frac{1}{2}\Delta t\varOmega _{\alpha} ^n $ | (24) |
n+1时刻的宏观量可以对
| $ f_{\alpha} ^{n + 1} = \frac{{g_{\alpha} ^{n + 1} + \dfrac{{\Delta t}}{{2\tau }}{{\left( {f_{\alpha} ^{{\text{eq}}}} \right)}^{n + 1}}}}{{1 + \dfrac{{\Delta t}}{{2\tau }}}} $ | (25) |
其中
另一种方法是隐式-显式Runge-Kutta法,其表达形式如下:
| $ \begin{split} f_{\alpha} ^{(j)} =& f_{\alpha} ^n - \Delta t\sum\limits_{k = 1}^{j - 1} {{{\tilde m}_{jk}}} \left( {{{\boldsymbol{e}}_a}\cdot\nabla f_{\alpha} ^{(k)}} \right)- \hfill \\ & \Delta t\sum\limits_{k = 1}^j {{m_{jk}}} \frac{{f_{\alpha} ^{(k)} - f_{\alpha} ^{{\text{eq}}(k)}}}{\tau } \hfill \end{split} $ | (26) |
| $ \begin{split} f_{\alpha} ^{n + 1} =& f_{\alpha} ^n - \Delta t\sum\limits_{j = 1}^r {{{\tilde n}_j}} \left( {{e_{\alpha} }\cdot\nabla f_{\alpha} ^{(k)}} \right) - \hfill \\ & \Delta t\sum\limits_{j = 1}^r {{n_j}} \frac{{f_{\alpha} ^{(k)} - f_{\alpha} ^{{\text{eq}}(k)}}}{\tau } \hfill \end{split} $ | (27) |
其中,
| $ \Delta {t_i} = \sigma \min \left( {\frac{{\sqrt {{V_i}} }}{{{\varLambda _i}}}} \right)\bigg/\left( {2N + 1} \right) $ | (28) |
本文数值算例中涉及的无滑移壁面及远场边界处理,采用非平衡态外推的方法[27],将边界上的分布函数写成平衡态和非平衡态之和的形式:
| $ {\left( {{f_{\alpha} }} \right)_{\text{b}}} = {\left( {f_{\alpha} ^{{\text{eq}}}} \right)_{\text{b}}}{\text{ + }}{\left( {f_{\alpha} ^{{\text{neq}}}} \right)_{\text{b}}} $ | (29) |
其中,下标b表示边界,上标neq表示非平衡态。平衡态可以根据边界的宏观量直接求得,而非平衡态可以由求解点的非平衡态通过拉格朗日插值得到。一旦得到边界上的分布函数,就可以直接计算出边界通量,然后通过式(19)将边界的影响考虑进来。
2 数值算例 2.1 Taylor-Green涡Taylor-Green涡问题被广泛用来研究非定常不可压流动算法的收敛性,这个问题的解析解为:
| $ \left\{ {\begin{array}{*{20}{l}} {{u^*}(x,y,t) = - {U_0}\cos (2{\text{π}}x)\sin (2{\text{π}}y)\exp \left( { - 8{{\text{π}}^2}vt} \right)} \\ {{v^*}(x,y,t) = {U_0}\sin (2{\text{π}}x)\cos (2{\text{π}}y)\exp \left( { - 8{{\text{π}}^2}vt} \right)} \\ {{p^*}(x,y,t) = - \dfrac{{U_0^2}}{4}\big[\cos (4{\text{π}}x) + \cos (4{\text{π}}y)\big]\exp \left( { - 16{{\text{π}}^2}vt} \right)} \end{array}} \right. $ | (30) |
其中
| $ \begin{split} {L_2}\left( t \right) =& {\left\| {u(t) - {u^*}(t)} \right\|_2} \\ = & \sqrt {\frac{{\displaystyle\sum\limits_{i = 1}^{{N_{{\text{total}}}}} {{{\left[ {{u_i}(t) - u_i^*(t)} \right]}^2}} }}{{\displaystyle\sum\limits_{n = 1}^{{N_{{\text{total}}}}} {{{\left[ {u_i^*(t)} \right]}^2}} }}} \end{split} $ | (31) |
其中,Ntotal为求解点总数,
顶盖驱动方腔流因为其流动结构丰富、流场变化受雷诺数影响明显的特点,是不可压流算法的经典校核算例之一。在本算例中,计算域是一个边长L为1的方腔,顶盖驱动速度u0为0.1,其他三个边为无滑移壁面,计算的雷诺数定义为Re = u0L/
| $ \frac{{\sqrt {\displaystyle\sum\limits_{{N_{{\rm{total}}}}} {\left[ {{{\left( {u_{}^{t + \Delta t} - u_{}^t} \right)}^2} + {{\left( {v_{}^{t + \Delta t} - v_{}^t} \right)}^2}} \right]} } }}{{\sqrt {\displaystyle\sum\limits_{{N_{{\rm{total}}}}} {\left[ {{{\left( {u_{}^{t + \Delta t}} \right)}^2} + {{\left( {v_{}^{t + \Delta t}} \right)}^2}} \right]} } }} < {10^{ - 8}} $ | (32) |
| 表 1 直接法和分步法不同网格下的误差及收敛精度 Table 1 Error and convergence order of direct method and two-step method for different grid resolution |
|
|
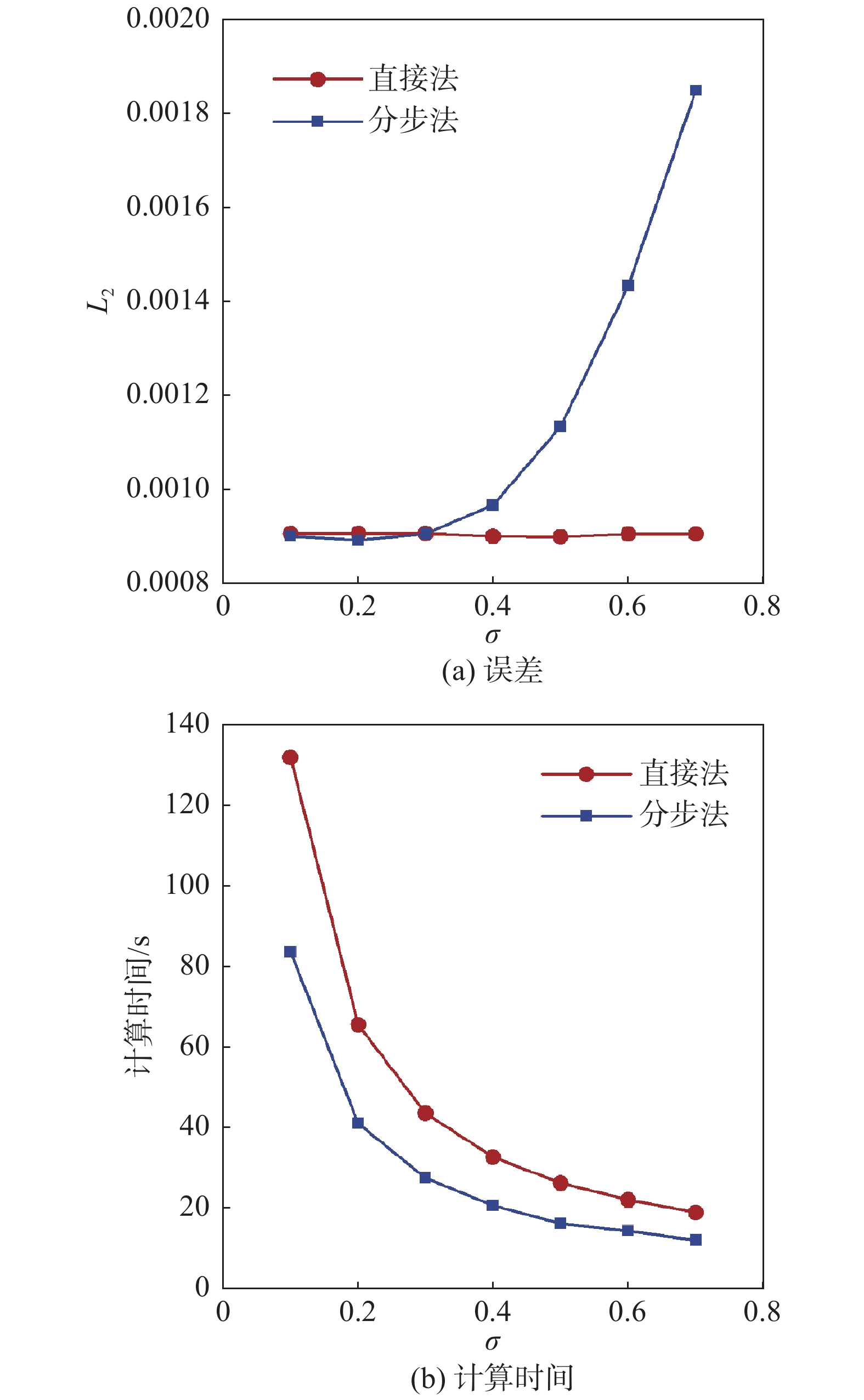
|
图 2 直接法和分步法不同CFL数下的误差和计算时间 Fig.2 Errors and computational time at different CFL numbers by direct method and two-step method |
为了更好地捕捉方腔角落处的涡,采用非均匀网格:
| $ x = \frac{1}{{2a}}[a + \tanh (\beta \xi )]\quad $ | (33) |
| $ y = \frac{1}{{2a}}[a + \tanh (\beta \eta )] $ | (34) |
其中,
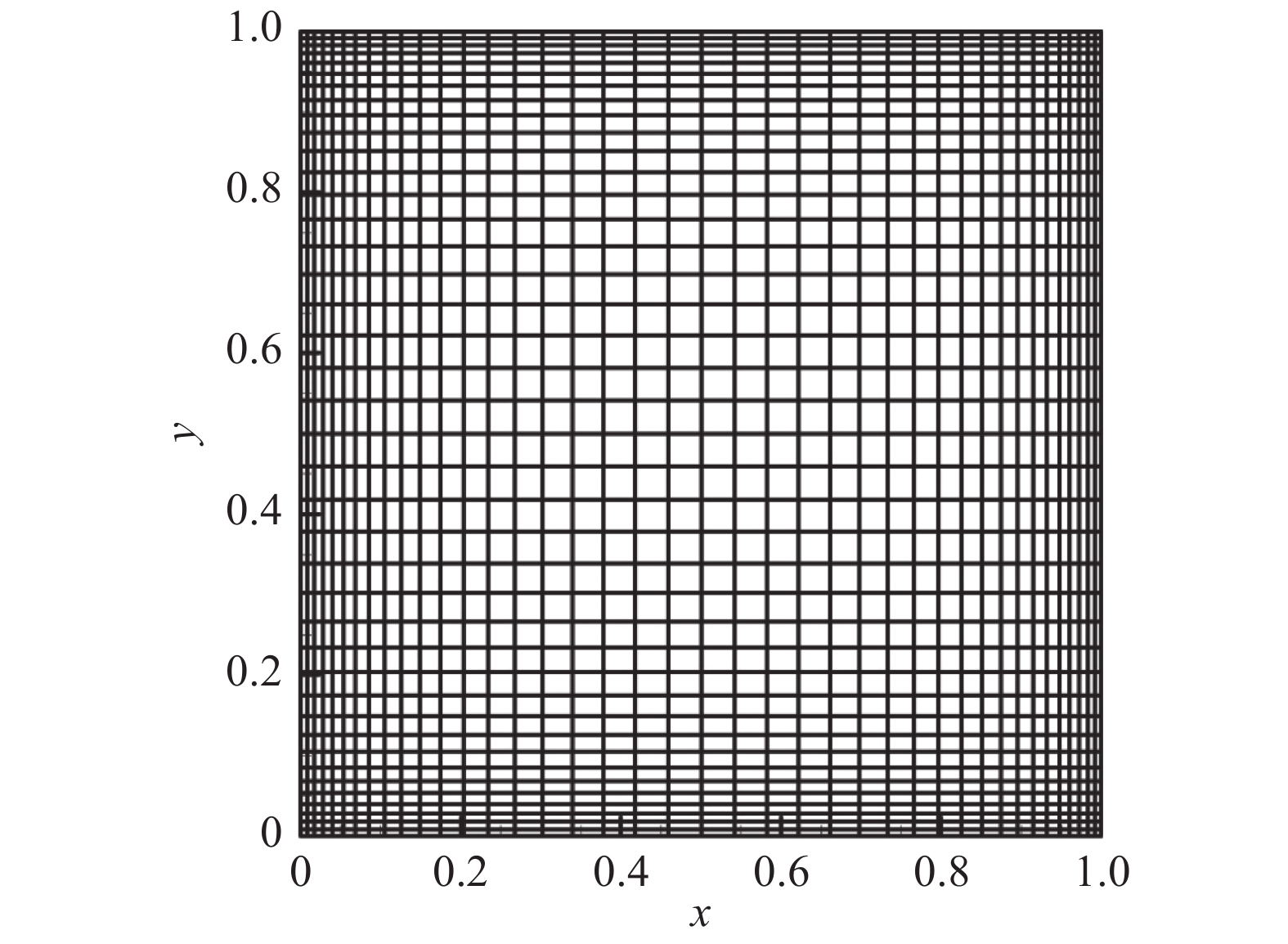
|
图 3 顶盖驱动方腔流40×40非均匀网格单元的分布 Fig.3 Non-uniform mesh distribution with 40×40 for lid-driven cavity flow |
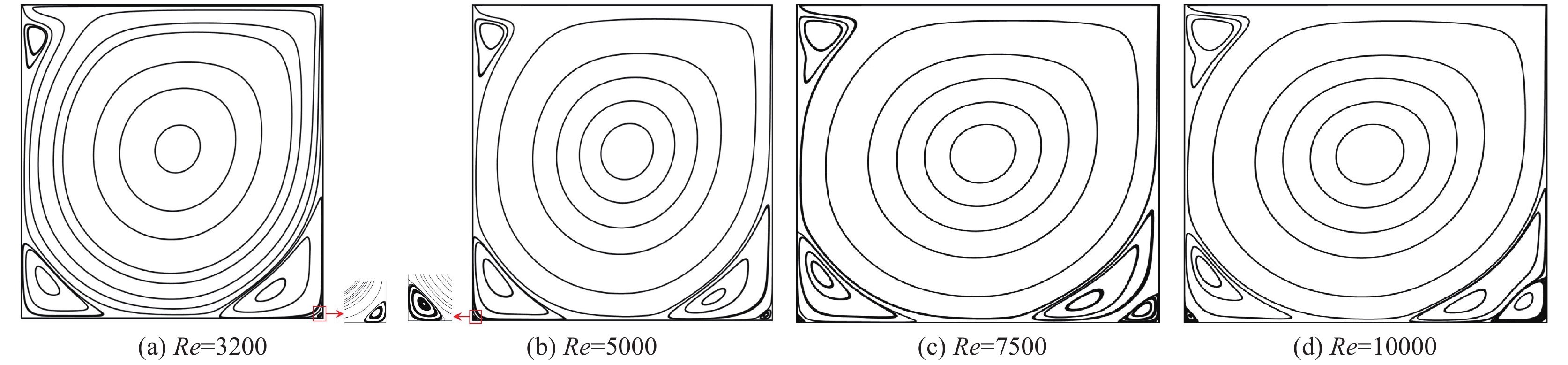
|
图 4 顶盖驱动方腔流在Re = 3200、5000、7500和10000时的流线图 Fig.4 Streamlines for lid-driven cavity flow at Re = 3200, 5000, 7500 and 10000 |
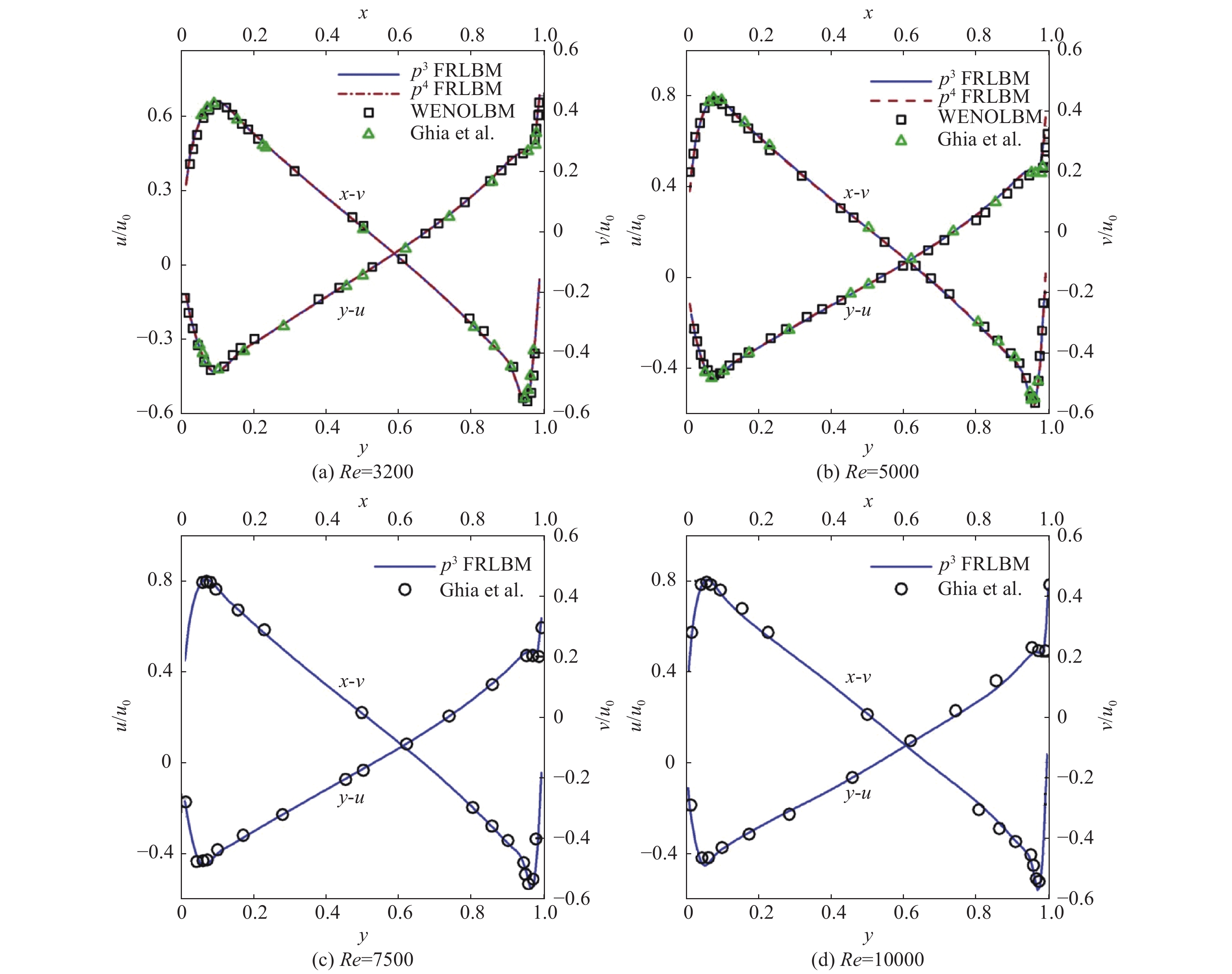
|
图 5 顶盖驱动方腔流在Re = 3200、5000、7500和10000时中线上的速度型比较 Fig.5 Comparison of centerline velocity profiles for lid-driven cavity flow at Re = 3200, 5000, 7500 and 10000 |

|
图 6 顶盖驱动方腔流在Re = 3200、5000、7500和10000时四种时间离散格式的最大CFL数比较 Fig.6 Comparison of maximum CFL numbers of the four time discretization methods for lid-driven cavity flow at Re = 3200, 5000, 7500 and 10000 |
圆柱绕流是验证算法模拟复杂外形绕流的经典算例之一,本文计算了瞬态雷诺数Re = 200的情况。采用沿径向延展的非均匀O型贴体网格,网格单元为1次曲线单元,即式(13)中的K = 8。径向延展的变化由下式确定:
| $ {r_j} = {r_1} + \left( {{r_1} - {r_0}} \right)\frac{{\tanh \left( {\beta {\eta _j}} \right)}}{{\tanh \beta }} $ | (35) |
其中,r0为圆柱的半径,取为0.5;r1为圆形计算域的半径,取为50;

|
图 7 圆柱绕流计算域及贴体网格单元的分布 Fig.7 Computational domain and body-fitted mesh distribution for flow over a circular cylinder |
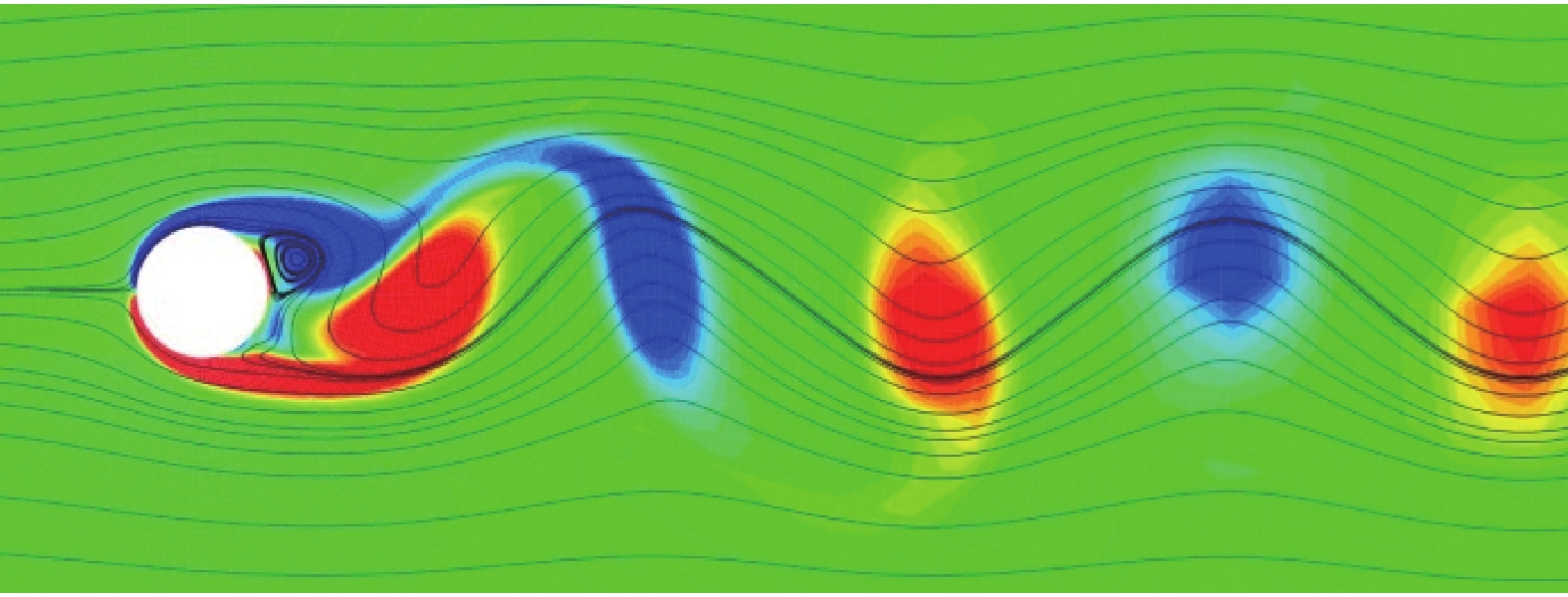
|
图 8 圆柱绕流Re = 200时的瞬时流线及涡量等值线 Fig.8 The instantaneous streamlines and vorticity contours for flow over a circular cylinder at Re = 200 |
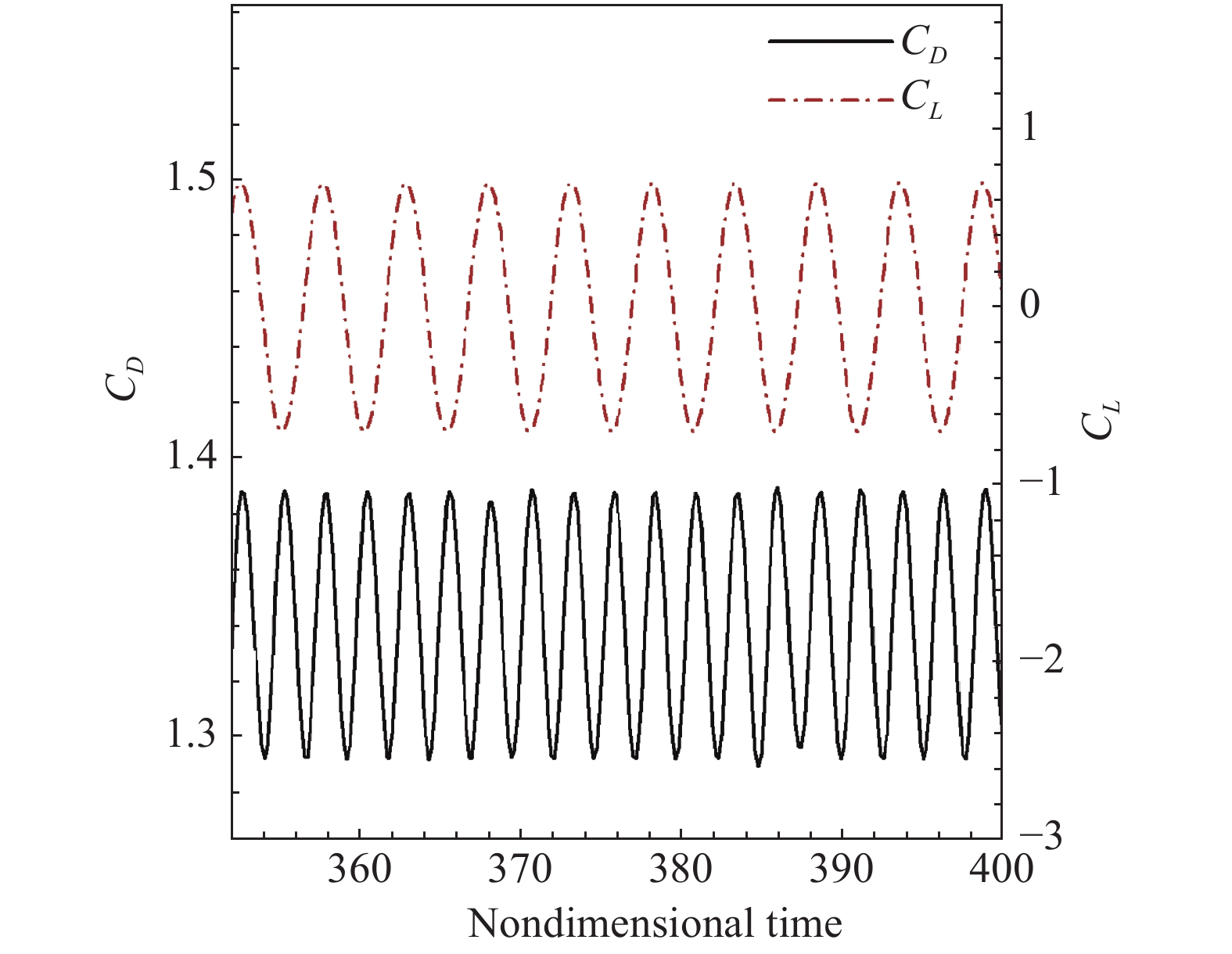
|
图 9 圆柱绕流Re = 200时升阻力随时间的周期性变化 Fig.9 Periodic variations of drag and lift coefficients for flow over a circular cylinder at Re = 200 |
| 表 2 圆柱绕流Re = 200时结果和文献比较 Table 2 Comparison of the results of flow over a circular cylinder at Re = 200 with the available results. |
|
|
OLBM可以改善标准LBM的几何适应性,本文回顾了不可压流动高精度OLBM的发展过程。相比基于N-S方程的高精度不可压流算法,基于DVBE的高精度算法要容易实现得多。本文基于高精度通量重构格式发展了一种通量重构格子玻尔兹曼方法,并在此框架下比较了直接求解DVBE和先碰撞、再求解纯对流方程这两种方法的数值表现。研究发现,在小时间步长下,这两种方法误差接近,采用高精度格式都能获得高阶的收敛阶。然而,当时间步长增大时,分步法的误差出现明显上升,而直接法误差几乎不变。数值测试显示,在取得相似误差时直接法能取更大的时间步长,运算周期较短、计算效率更高。此外,采用二阶隐式-显式Runge-kutta推进的直接法,稳定性优于分步法。接着,通过顶盖驱动方腔流算例,比较了4种碰撞项隐式处理的时间推进方法在不同雷诺数下所能取到的最大CFL数。数值结果表明,二阶IMEX是较好的时间离散方法。然而,尽管IMEX能使时间步长的选取摆脱松弛时间的限制,但由于对流项依然显式处理,在模拟壁湍流问题时较小的边界层网格厚度同样会严重限制时间步长。因此,发展低存储、全隐式的时间推进方法是OLBM的重要发展方向之一,目前已有学者开展了一些工作[32-33]。本文采用的碰撞模型是单松弛,为了增强稳定性,也可以采用更先进的碰撞模型,比如多松弛等。此外,高精度OLBM还可以直接拓展到湍流、多相流、热流等应用中[34-35],目前相关工作正在开展中。
| [1] |
HE X Y, LUO L S. Theory of the lattice Boltzmann method: from the Boltzmann equation to the lattice Boltzmann equation[J]. Physical Review E, 1997, 56: 6811-6817. DOI:10.1103/PhysRevE.56.6811 |
| [2] |
MEI R W, SHYY W. On the finite difference-based lattice Boltzmann method in curvilinear coordinates[J]. Journal of Computational Physics, 1998, 143(2): 426-448. DOI:10.1006/jcph.1998.5984 |
| [3] |
CHEN H D. Volumetric formulation of the lattice Boltzmann method for fluid dynamics: Basic concept[J]. Physical Review E, 1998, 58(3): 3955-3963. DOI:10.1103/physreve.58.3955 |
| [4] |
LEE T, LIN C L. A characteristic Galerkin method for discrete Boltzmann equation[J]. Journal of Computational Physics, 2001, 171(1): 336-356. DOI:10.1006/jcph.2001.6791 |
| [5] |
HE X Y, LUO L S, DEMBO M. Some progress in lattice Boltzmann method. Part I. Nonuniform mesh grids[J]. Journal of Computational Physics, 1996, 129(2): 357-363. DOI:10.1006/jcph.1996.0255 |
| [6] |
SHU C, NIU X D, CHEW Y T. Taylor-series expansion and least-squares-based lattice Boltzmann method: Two-dimensional formulation and its applications[J]. Physical Review E, Statistical, Nonlinear, and Soft Matter Physics, 2002, 65(3 Pt 2B): 036708. DOI:10.1103/PhysRevE.65.036708 |
| [7] |
LIN X J, WU J, ZHANG T W. A mesh-free radial basis function-based semi-Lagrangian lattice Boltzmann method for incompressible flows[J]. International Journal for Numerical Methods in Fluids, 2019, 91(4): 198-211. DOI:10.1002/fld.4749 |
| [8] |
SHI X, LIN J Z, YU Z S. Discontinuous Galerkin spectral element lattice Boltzmann method on triangular element[J]. International Journal for Numerical Methods in Fluids, 2003, 42(11): 1249-1261. DOI:10.1002/fld.594 |
| [9] |
DÜSTER A, DEMKOWICZ L, RANK E. High-order finite elements applied to the discrete Boltzmann equation[J]. International Journal for Numerical Methods in Engineering, 2006, 67(8): 1094-1121. DOI:10.1002/nme.1657 |
| [10] |
HEJRANFAR K, EZZATNESHAN E. A high-order compact finite-difference lattice Boltzmann method for simulation of steady and unsteady incompressible flows[J]. International Journal for Numerical Methods in Fluids, 2014, 75(10): 713-746. DOI:10.1002/fld.3916 |
| [11] |
HEJRANFAR K, EZZATNESHAN E. Implementation of a high-order compact finite-difference lattice Boltzmann method in generalized curvilinear coordinates[J]. Journal of Computational Physics, 2014, 267: 28-49. DOI:10.1016/j.jcp.2014.02.030 |
| [12] |
HEJRANFAR K, SAADAT M H, TAHERI S. High-order weighted essentially nonoscillatory finite-difference formulation of the lattice Boltzmann method in generalized curvilinear coordinates[J]. Physical Review E, 2017, 95(2-1): 023314. DOI:10.1103/physreve.95.023314 |
| [13] |
SUN Y X, TIAN Z F. High-order upwind compact finite-difference lattice Boltzmann method for viscous incompressible flows[J]. Computers & Mathematics With Applications, 2020, 80(7): 1858-1872. DOI:10.1016/j.camwa.2020.08.014 |
| [14] |
LI W D. High order spectral difference lattice Boltzmann method for incompressible hydrodynamics[J]. Journal of Computational Physics, 2017, 345: 618-636. DOI:10.1016/j.jcp.2017.05.039 |
| [15] |
GUO Z L, ZHAO T S. Explicit finite-difference lattice Boltzmann method for curvilinear coordinates[J]. Physical Review E, 2003, 67(6): 066709. DOI:10.1103/physreve.67.066709 |
| [16] |
PIERACCINI S, PUPPO G. Implicit-explicit schemes for BGK kinetic equations[J]. Journal of Scientific Computing, 2007, 32(1): 1-28. DOI:10.1007/s10915-006-9116-6 |
| [17] |
MIN M S, LEE T. A spectral-element discontinuous Galerkin lattice Boltzmann method for nearly incompressible flows[J]. Journal of Computational Physics, 2011, 230(1): 245-259. DOI:10.1016/j.jcp.2010.09.024 |
| [18] |
ZADEHGOL A, ASHRAFIZAADEH M, MUSAVI S H. A nodal discontinuous Galerkin lattice Boltzmann method for fluid flow problems[J]. Computers & Fluids, 2014, 105: 58-65. DOI:10.1016/j.compfluid.2014.09.015 |
| [19] |
KRÄMER A, KÜLLMER K, REITH D, et al. Semi-Lagrangian off-lattice Boltzmann method for weakly compressible flows[J]. Physical Review E, 2017, 95(2-1): 023305. DOI:10.1103/PhysRevE.95.023305 |
| [20] |
KRÄMER A, WILDE D, KÜLLMER K, et al. Lattice Boltzmann simulations on irregular grids: Introduction of the NATriuM library[J]. Computers & Mathematics With Applications, 2020, 79(1): 34-54. DOI:10.1016/j.camwa.2018.10.041 |
| [21] |
VINCENT P E, CASTONGUAY P, JAMESON A. A new class of high-order energy stable flux reconstruction schemes[J]. Journal of Scientific Computing, 2011, 47(1): 50-72. DOI:10.1007/s10915-010-9420-z |
| [22] |
YU M L, WANG Z J, LIU Y. On the accuracy and efficiency of discontinuous Galerkin, spectral difference and correction procedure via reconstruction methods[J]. Journal of Computational Physics, 2014, 259: 70-95. DOI:10.1016/j.jcp.2013.11.023 |
| [23] |
HE X Y, LUO L S. Lattice Boltzmann model for the incompressible navier-stokes equation[J]. Journal of Statistical Physics, 1997, 88(3-4): 927-944. DOI:10.1023/B:JOSS.0000015179.12689.e4 |
| [24] |
ROE P L. Approximate Riemann solvers, parameter vectors, and difference schemes[J]. Journal of Computational Physics, 1981, 43(2): 357-372. DOI:10.1016/0021-9991(81)90128-5 |
| [25] |
HUYNH H T. A flux reconstruction approach to high-order schemes including discontinuous Galerkin methods[C]//18th AIAA Computational Fluid Dynamics Conference, Miami, Florida. Reston, Virigina: AIAA, 2007: 4079. doi: 10.2514/6.2007-4079
|
| [26] |
CASTONGUAY P, WILLIAMS D M, VINCENT P E, et al. Energy stable flux reconstruction schemes for advection-diffusion problems[J]. Computer Methods in Applied Mechanics and Engineering, 2013, 267: 400-417. DOI:10.1016/j.cma.2013.08.012 |
| [27] |
GUO Z L, ZHENG C G, SHI B C. Non-equilibrium extrapolation method for velocity and pressure boundary conditions in the lattice Boltzmann method[J]. Chinese Physics, 2002, 11: 366-374. DOI:10.1088/1009-1963/11/4/310 |
| [28] |
LEE T, LIN C L. An Eulerian description of the streaming process in the lattice Boltzmann equation[J]. Journal of Computational Physics, 2003, 185(2): 445-471. DOI:10.1016/S0021-9991(02)00065-7 |
| [29] |
GHIA U, GHIA K N, SHIN C T. High-Re solutions for incompressible flow using the Navier-Stokes equations and a multigrid method[J]. Journal of Computational Physics, 1982, 48(3): 387-411. DOI:10.1016/0021-9991(82)90058-4 |
| [30] |
BERGER E, WILLE R. Periodic flow phenomena[J]. Annual Review of Fluid Mechanics, 1972, 4(1): 313-340. DOI:10.1146/annurev.fl.04.010172.001525 |
| [31] |
CHIU P H, LIN R K, SHEU T W H. A differentially interpolated direct forcing immersed boundary method for predicting incompressible Navier-Stokes equations in time-varying complex geometries[J]. Journal of Computational Physics, 2010, 229(12): 4476-4500. DOI:10.1016/j.jcp.2010.02.013 |
| [32] |
LI W D, LI W, SONG P, et al. A conservation-moment-based implicit finite volume lattice Boltzmann method for steady nearly incompressible flows[J]. Journal of Computational Physics, 2019, 398: 108882. DOI:10.1016/j.jcp.2019.108882 |
| [33] |
GHAFFARIAN A, HEJRANFAR K. An implicit dual-time stepping spectral difference lattice Boltzmann method for simulation of viscous compressible flows on structured meshes[J]. Meccanica, 2019, 54(10): 1561-1581. DOI:10.1007/s11012-019-01036-w |
| [34] |
MA C, WU J, JIANG L. A weighted essentially nonoscillatory-based phase field lattice Boltzmann method for incompressible two-phase flows with high density contrast[J]. International Journal for Numerical Methods in Fluids, 2021, 93(7): 2272-2290. DOI:10.1002/fld.4973 |
| [35] |
MA C, WU J, ZHANG T W. A high order spectral difference-based phase field lattice Boltzmann method for incompressible two-phase flows[J]. Physics of Fluids, 2020, 32(12): 122113. DOI:10.1063/5.0033204 |
 2022, Vol. 40
2022, Vol. 40


