2. 福建师范大学 福建省分析数学及应用重点实验室,福州 350117;
3. 福建师范大学 福建省应用数学研究中心,福州 350117;
4. 中山大学 中法核工程与技术学院,珠海 519082
2. Fujian Key Laboratory of Analytical Mathematics and Application, Fujian Normal University, Fuzhou 350117, China;
3. Center for Applied Mathematics of Fujian Province, Fujian Normal University, Fuzhou 350117, China;
4. Sino-French Institute of Nuclear Engineering and Technology, Sun Yat-sen University, Zhuhai 519082, China
在自然界和工程技术领域中存在三种常见的流体不稳定性:瑞利-泰勒(Rayleigh-Taylor,RT)不稳定性、瑞奇迈尔-莫西科夫(Richtmyer-Meshkov,RM)不稳定性和开尔文-亥姆霍兹(Kelvin-Helmholtz,KH)不稳定性。外力场中当重流体被轻流体加速或支撑时,两流体界面处的扰动随时间发展起来的一种流体力学不稳定性现象,被称为RT不稳定性[1-2]。RT不稳定性作为一种基本的流体不稳定现象,在科学工程的许多领域都具有重要意义。例如在惯性约束聚变点火过程中,靶丸在压缩发生内爆时会产生RT不稳定性,其诱导的湍流混合会直接影响靶丸的能量增益并导致点火失败[3]。这时发生的RT不稳定性是具有破坏作用的,我们应当尽可能减弱它。而对于超燃冲压发动机来说,RT不稳定性的存在则会使得燃料充分混合,提高其燃烧效率。RT不稳定性还广泛存在于天文领域,如旋转恒星[4]、极光斑[5]、行星状星云[6]、超新星爆炸[7]等。因此,对RT不稳定性的研究不仅具有重要的理论意义,还具有实际的应用价值。
一般的,RT不稳定性的研究方法主要有实验分析[8-9]、理论研究[10-13]和数值模拟[14-21]三种。然而,自然界的RT不稳定性现象相当复杂,本身的物理系统具有较强的非线性,绝大多数实际问题的计算均超出了现有解析求解的能力范围,理论研究需要各种简化及线性假设,所得到的结果往往较为有限。实验研究则常常会存在仪器昂贵、实验危险和无法观察短时间行为等缺点。因而对RT不稳定性的研究在理论求解和实验方法上都会遇到这样或那样的不足。数值模拟作为一种当今新兴的研究工具已然成为重要的科学研究手段。相较于实验与理论研究,数值模拟可通过计算机模拟得到复杂物理系统演化过程中的精细结构和物理机制。对于RT不稳定性现象,研究人员通过数值模拟已取得了较为丰硕的成果。例如,Gallis等[14]利用分子气体动力学的直接模拟蒙特卡罗方法,数值模拟再现了RT不稳定性混合层增长的许多定性特征,并且在线性、非线性和自相似状态下与理论和经验模型具有定量上的一致性。Wei等[15]提出了模拟二维不可压缩 RT 不稳定性的耦合格子玻尔兹曼模型和一种修正的平衡分布函数, 并利用一个简单的标度讨论了混合RT 不稳定性的区域。Liang等[16]利用格子玻尔兹曼方法研究了雷诺数(Re)对多模、互不相溶的RT不稳定性中的演化界面动力学和气泡/尖钉振幅的影响。Lyubimova等[17]在相场方法的基础上,研究了限制在水平平面内的RT不稳定性中的扩散与对流演化。Scott等[18]利用基于小波的二维可压缩直接数值模拟研究了单模RT不稳定性对涡旋动力学的影响。Li等[19]以欧拉(Euler)模拟为基础对双界面的RT不稳定性弱非线性区域内的界面耦合效应进行了数值研究。结果表明,当下界面的阿特伍德数(At)较小时,下界面的微扰增长幅度与上界面的At呈正相关;但当下界面上的At较大时,二者呈负相关。Luo等[20]利用二元混合流体模型研究了可压缩性对RT不稳定性的影响,发现可压缩性引起的初始密度分层起稳定作用,而膨胀-压缩效应起失稳作用。Livescu等[21]利用直接数值模拟研究了在重力为零或反转时RT不稳定性的演化。他们发现,当加速度改变时,一些湍流量发生了显著变化。以上列举的是不同学者利用不同数值模拟方法对RT不稳定性做出的一系列研究,他们的结论丰富了我们对RT不稳定性的认知。
在RT不稳定性的数值模拟中,根据初始扰动界面结构的设置,可以分为单模RT不稳定性(流体界面被一个具有单个频率的余弦或者正弦所扰动)和多模RT不稳定性(界面被两个及以上不同频率的余弦或者正弦所扰动)。此前,多模RT不稳定性已被许多专家学者研究,并得到了一些有意义的结论。例如,Banerjee等[22]结合不可压缩Euler方程和隐式大涡模拟方法研究初始条件对不可压缩流体的多模RT不稳定性的影响,发现RT混合的整体增长强烈依赖于初始条件。Burton等[23]使用非线性大涡模拟方法对具有超高At的多模RT不稳定性进行研究,发现尖钉的高度和混合层生长速率受到初始密度比的强烈影响。Zhang等[24]对多模烧蚀可压缩RT不稳定性的自相似非线性演化进行了二维和三维数值研究,发现气泡发展速度受到初始条件和烧蚀速度的影响。Liang等[16]使用改进的相场格子玻尔兹曼方法研究了Re对不可压缩多模非混相RT不稳定性的影响,研究表明多模RT不稳定性在不同Re下表现出不同的界面动力学情形。Yilmaz等[25]利用大涡模拟模拟了高At下的多模三维RT不稳定性,结果表明高At下RT不稳定性快速发展,尖钉的生长速率和速度增加,混合区域的不对称性增大。Hamzehloo等[26]利用相场方法研究了At、Re、表面张力和初始扰动幅值的不同组合对不可压缩流体的多模非混相RT不稳定性的影响,发现三维多模RT不稳定性在初始阶段表现出与单模RT不稳定性相似的指数界面增长率。Ding等[27]利用分子动力学方法研究了强加速度下的双模微观RT不稳定性,发现微观RT不稳定性表现出较弱的非线性性质,并且双模RT不稳定性在微观尺度上的模耦合行为与宏观尺度上的模耦合行为有明显差异。
根据上述研究方法的不同,可以将流体不稳定性的模拟工具分为以下三个层次:微观分子动力学模型、介观动理学模型和宏观流体力学模型。宏观流体力学模型主要是指基于Euler方程组或N-S方程组的各类模型,可以用于描述较大时空尺度的缓变行为。这类模型基于宏观连续性假设,无法描述小尺度上粒子随机运动对应的热涨落行为,缺乏描述微介观结构和快模式的能力。为了从更底层的基础上深入理解流体系统特征机制,需要利用其它数值模型手段,比如微观分子动力学方法[28]。虽然这种方法在纳米流等问题中得到了成功应用,但由于其对计算资源的高需求,本质上局限于小尺度问题。为了解决物理精度与计算效率的矛盾问题,可以借助动理学理论构建介观层次的数值模拟方法。
近十年,基于非平衡统计物理的离散玻尔兹曼方法(discrete Boltzmann method,DBM)被成功发展应用于研究复杂流场中热力学非平衡效应(thermodynamic non-equilibrium effect,TNE)和流体力学非平衡效应(hydrodynamic non-equilibrium effect,HNE)。作为一种粗粒化的物理建模方法,DBM可以从以下两方面弥补NS模型的不足:1)适用于模拟研究具有锐利界面的流体流动,如冲击波;2)可以描述和刻画更底层的热力学非平衡信息。事实上,我们通过查普曼-恩斯柯(Chapman-Enskog,CE)多尺度分析展开,可以得到连续极限假设条件下,介观层次的分布函数演化与宏观层次的物理量演化之间的内在联系。根据CE多尺度分析,利用克努森数(Kn)中的各阶项,可以构造不同层次的描述热力学非平衡信息的DBM。在分布函数需要满足的动理学矩中存在守恒矩和非守恒矩两种类型,利用守恒矩可得到流体的宏观物理量信息,同时利用
目前,DBM已被广泛用于模拟研究各类复杂流体流动,包括流体不稳定性[34-43]、多相流[44-45]、反应流[46-48]、激波[49]和爆轰[50-56]等。这里,我们重点关注并简要介绍一下DBM研究流体不稳定性的成果。Lai等[34]研究了可压缩性对RT不稳定性的影响,发现可压缩性在演化早期抑制了RT不稳定性的发生,在后期则促进了RT不稳定性。Li等[35]利用DBM模拟了可压缩流体系统的多模RT不稳定性,探讨了其演化机理。Chen等[36]利用多松弛时间DBM研究了黏性、热传导和普朗特数对RT不稳定性的影响。他们还模拟了二维RM不稳定性和RT不稳定性共存系统,讨论了RT与RM不稳定系统的相似和不同之处;研究了两种不稳定性的协作和竞争机制,并探讨了重力场
为了进一步从动理学角度深入研究可压缩流体RT不稳定性的演化规律和物理机制,本文使用Bhatnagar-Gross-Krook(BGK)DBM模拟分析多模RT系统中的HNE和TNE的动态演化过程和宏观表征,并通过分析流体系统中温度梯度与非平衡面积占比解释非平衡分量和全局非平衡效应的演化规律,进而从介观与宏观两方面了解多模RT不稳定性。
1 离散玻尔兹曼模型为方便起见,本文统一对物理量进行了无量纲化。包含外力作用的玻尔兹曼方程形式如下:
| $ {\partial _t}f + {\boldsymbol{v}} \cdot {\nabla _{\boldsymbol{r}}}f + {\boldsymbol{a}} \cdot {\nabla _{\boldsymbol{v}}}f = \varOmega $ | (1) |
其中,
| $ {\partial _t}{f_i} + {{\boldsymbol{v}}_i} \cdot {\nabla _{\boldsymbol{r}}}{f_i} + {\boldsymbol{a}} \cdot {\nabla _{{{\boldsymbol{v}}_i}}}{f_i} = - \frac{1}{\tau }({f_i} - f_i^{{\rm{eq}}}) $ | (2) |
其中,
DBM的构建过程是粗粒化物理建模的过程。通过CE多尺度展开,可以将上述离散玻尔兹曼方程恢复到可压缩N-S方程组:
| $ \frac{{\partial \rho }}{{\partial t}} + \nabla \cdot (\rho {\boldsymbol{u}}) = 0 $ | (3) |
| $ \frac{\partial }{{\partial t}}(\rho {\boldsymbol{u}}) + \nabla \cdot (\rho {\boldsymbol{uu}} + p{\boldsymbol{I}} + {\boldsymbol{P}}) = \rho {\boldsymbol{a}} $ | (4) |
| $ \begin{split}& \hfill \frac{\partial }{{\partial t}}\big[\rho (E + \frac{{{{\left| {\boldsymbol{u}} \right|}^2}}}{2})\big] + \nabla \cdot \big[\rho {\boldsymbol{u}}(E + T + \frac{{{{\left| {\boldsymbol{u}} \right|}^2}}}{2}) + {\boldsymbol{J}} + {\boldsymbol{P}} \cdot {\boldsymbol{u}}\big] = \rho {\boldsymbol{a}} \cdot {\boldsymbol{u}} \end{split} $ | (5) |
其中,
| $ {\boldsymbol{P}} = - \mu \left[ {\nabla {\boldsymbol{u}} + {{(\nabla {\boldsymbol{u}})}^{\text{T}}} - \frac{2}{{D + n}}(\nabla \cdot {\boldsymbol{u}}){\boldsymbol{I}}} \right] $ | (6) |
| $ {\boldsymbol{J}} = - \kappa \nabla T $ | (7) |
为了研究方便,我们可通过CE多尺度分析,恢复出对应的N-S层次的可压缩宏观流体力学方程组。此时,需要保证离散的平衡态分布函数
| $ {\boldsymbol{M}}_0^{{\rm{eq}}} = \sum\limits_i {f_i^{{\rm{eq}}}} = \rho $ | (8) |
| $ {\boldsymbol{M}}_1^{{\rm{eq}}} = \sum\limits_i {f_i^{{\rm{eq}}}} {{\boldsymbol{v}}_i} = \rho {\boldsymbol{u}} $ | (9) |
| $ {\boldsymbol{M}}_{2,0}^{{\rm{eq}}} = \sum\limits_i {f_i^{{\rm{eq}}}\left( {{{\boldsymbol{v}}_i} \cdot {{\boldsymbol{v}}_i} + \eta _i^2} \right)} = \rho \big[(D + n)T + {\boldsymbol{u}} \cdot {\boldsymbol{u}}\big] $ | (10) |
| $ {\boldsymbol{M}}_2^{{\rm{eq}}} = \sum\limits_i {f_i^{{\rm{eq}}}{{\boldsymbol{v}}_i}{{\boldsymbol{v}}_i}} = \rho \left( {T{\boldsymbol{I}} + {\boldsymbol{uu}}} \right) $ | (11) |
| $ \begin{split} {\boldsymbol{M}}_{3,1}^{{\rm{eq}}} =& \sum\limits_i {f_i^{{\rm{eq}}}\left( {{{\boldsymbol{v}}_i} \cdot {{\boldsymbol{v}}_i} + \eta _i^2} \right)} {{\boldsymbol{v}}_i} \\ =& \rho {\boldsymbol{u}}\big[(D + n + 2)T + {\boldsymbol{u}} \cdot {\boldsymbol{u}}\big] \end{split}$ | (12) |
| $ \begin{split} {\boldsymbol{M}}_3^{{\rm{eq}}} =& \sum\limits_i {f_i^{{\rm{eq}}}{{\boldsymbol{v}}_i}{{\boldsymbol{v}}_i}} {{\boldsymbol{v}}_i} = \rho \big[T({{\boldsymbol{u}}_{\alpha} }{{\boldsymbol{e}}_{\beta} }{{\boldsymbol{e}}_{\chi} }{\delta _{{\beta} {\chi} }} +\\& {{\boldsymbol{u}}_{\beta} }{{\boldsymbol{e}}_{\alpha} }{{\boldsymbol{e}}_{\chi} }{\delta _{{\alpha} {\chi} }} + {{\boldsymbol{u}}_{\chi} }{{\boldsymbol{e}}_{\beta} }{{\boldsymbol{e}}_{\alpha} }{\delta _{{\alpha} {\beta} }}) + {\boldsymbol{uuu}}\big] \end{split} $ | (13) |
| $ \begin{split} {\boldsymbol{M}}_{4,2}^{{\rm{eq}}} = &\sum\limits_i {f_i^{{\rm{eq}}}\left( {{{\boldsymbol{v}}_i} \cdot {{\boldsymbol{v}}_i} + \eta _i^2} \right)} {{\boldsymbol{v}}_i}{{\boldsymbol{v}}_i} \\ =&\rho T\big[(D + n + 2)T + {\boldsymbol{u}} \cdot {\boldsymbol{u}}\big]{{\boldsymbol{e}}_{\alpha} }{{\boldsymbol{e}}_{\beta} }{\delta _{{\alpha} {\beta} }} +\\&\rho {\boldsymbol{u}} {\boldsymbol{u}} \big[(D + n + 4)T + {\boldsymbol{u}} \cdot {\boldsymbol{u}}\big] \end{split} $ | (14) |
其中,
| $ {\boldsymbol{C}} \cdot {{\boldsymbol{f}}^{{\rm{eq}}}} = {{\boldsymbol{\hat f}}^{{\rm{eq}}}} $ | (15) |
其中:
| $ {{\boldsymbol{f}}^{{\rm{eq}}}} = {\Big[f_1^{{\rm{eq}}},f_2^{{\rm{eq}}}, \cdots ,f_N^{{\rm{eq}}}\Big]^{\text{T}}} $ | (16) |
| $ {{\boldsymbol{\hat f}}^{{\rm{eq}}}} = {\Big[\hat f_1^{{\rm{eq}}},\hat f_2^{{\rm{{\rm{eq}}}}}, \cdots ,\hat f_N^{{\rm{eq}}}\Big]^{\text{T}}} $ | (17) |
|
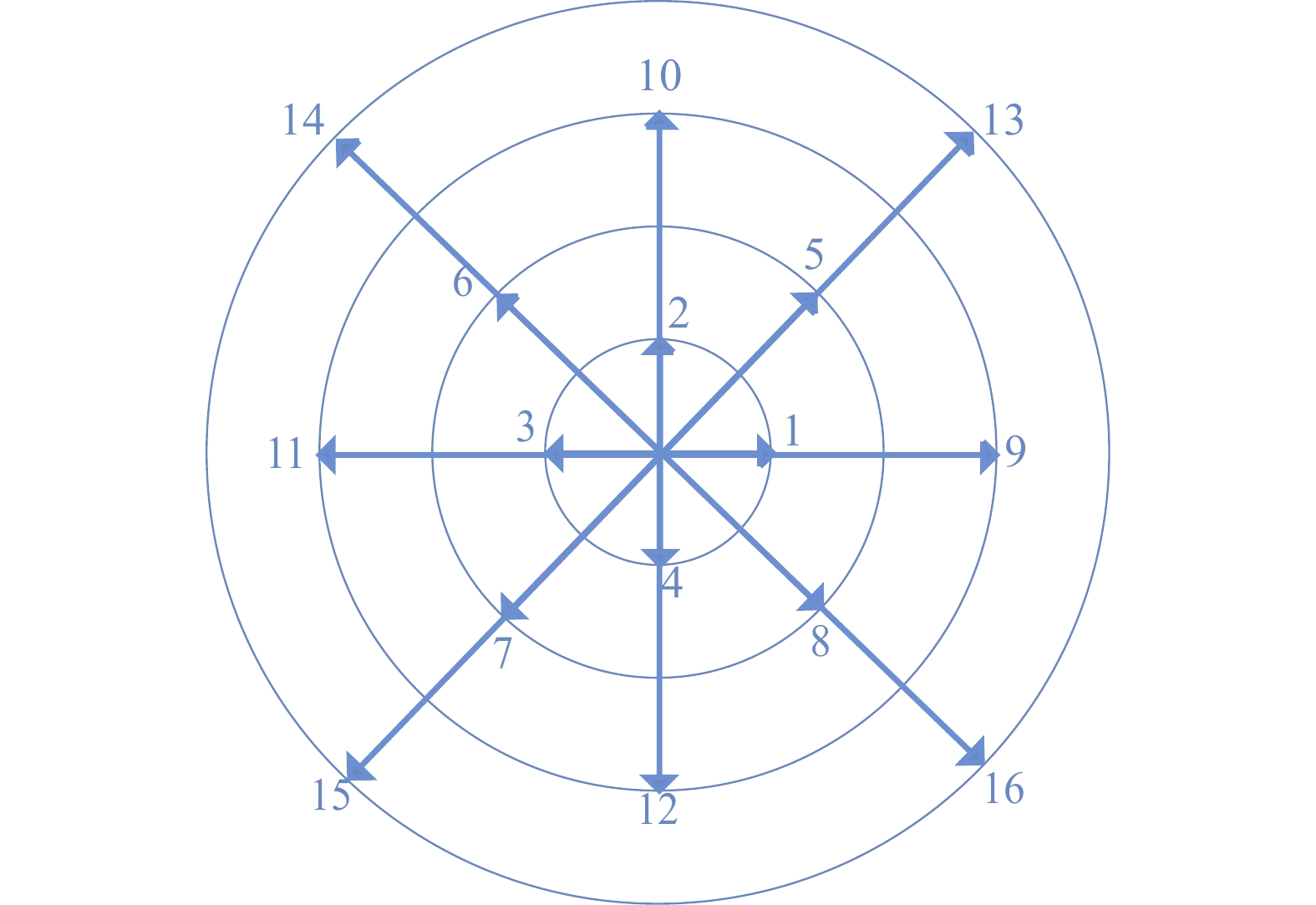
图 1 离散速度示意图 Fig.1 Schematic diagram of discrete velocities |
| $ {{\boldsymbol{v}}_i} = \left\{ {\begin{array}{*{20}{l}} {{v_a}\left[ {\cos \dfrac{{(i - 1)\text {π} }}{2},\sin \dfrac{{(i - 1)\text {π} }}{2}} \right],i = 1, \cdots ,4} \\ {{v_b}\left[ {\cos \dfrac{{(2i - 1)\text {π} }}{4},\sin \dfrac{{(2i - 1)\text {π} }}{4}} \right],i = 5, \cdots ,8} \\ {{v_c}\left[ {\cos \dfrac{{(i - 9)\text {π} }}{2},\sin \dfrac{{(i - 9)\text {π} }}{2}} \right],i = 9, \cdots ,12} \\ {{v_d}\left[ {\cos \dfrac{{(2i - 9)\text {π} }}{4},\sin \dfrac{{(2i - 9)\text {π} }}{4}} \right],i = 13, \cdots ,16} \end{array}} \right. $ | (18) |
另外,当
在上述7个矩关系中,只有在式(8)~式(10)中的平衡态分布函数
为了定性分析系统全局热力学非平衡效应,我们具体定义以下几种热力学非平衡量:
| $ \left| {{\boldsymbol{\varDelta }}_2^*} \right| = \left| {\varDelta _{2xx}^*} \right| + \left| {\varDelta _{2xy}^*} \right| + \left| {\varDelta _{2yy}^*} \right| $ | (19) |
| $ \left| {{\boldsymbol{\varDelta }}_{3,1}^*} \right| = \left| {\varDelta _{3,1x}^*} \right| + \left| {\varDelta _{3,1y}^*} \right| $ | (20) |
| $ \left| {{\boldsymbol{\varDelta }}_{4,2}^*} \right| = \left| {\varDelta _{4,2xx}^*} \right| + \left| {\varDelta _{4,2xy}^*} \right| + \left| {\varDelta _{4,2yy}^*} \right| $ | (21) |
| $ \left| {{\boldsymbol{\varDelta }}_3^*} \right| = \left| {\varDelta _{3xxx}^*} \right| + \left| {\varDelta _{3xxy}^*} \right| + \left| {\varDelta _{3xyy}^*} \right| + \left| {\varDelta _{3yyy}^*} \right| $ | (22) |
基于以上几种非平衡量,我们可进一步定义一种可以描述流体系统整体偏离平衡态程度的全局热力学非平衡量:
| $ \left| {{\boldsymbol{\varDelta }}_{}^*} \right| = \left| {{\boldsymbol{\varDelta }}_2^*} \right| + \left| {{\boldsymbol{\varDelta }}_{3,1}^*} \right| + \left| {{\boldsymbol{\varDelta }}_{4,2}^*} \right| + \left| {{\boldsymbol{\varDelta }}_3^*} \right| $ | (23) |
对流体系统中的热力学非平衡强度进行积分并求平均就可以得到以下几种热力学非平衡量的全局平均强度:
| $ \bar D = \frac{1}{{{L_x}{L_y}}}\int_0^{{L_x}} {\int_0^{{L_y}} {\left| {{{\boldsymbol{\varDelta }}^*}} \right|} } {\text{d}}x{\text{d}}y $ | (24) |
| $ {\bar D_2} = \frac{1}{{{L_x}{L_y}}}\int_0^{{L_x}} {\int_0^{{L_y}} {\left| {{\boldsymbol{\varDelta }}_2^*} \right|} } {\text{d}}x{\text{d}}y $ | (25) |
| $ {\bar D_{3,1}} = \frac{1}{{{L_x}{L_y}}}\int_0^{{L_x}} {\int_0^{{L_y}} {\left| {{\boldsymbol{\varDelta }}_{3,1}^*} \right|} } {\text{d}}x{\text{d}}y $ | (26) |
其中
另外,对于离散玻尔兹曼演化方程(2)中的时间导数采用一阶精度的向前Euler格式进行处理,空间导数采用二阶精度的无波动、无自由参数的耗散有限差分格式(nonoscillatory and nonfree-parameter dissipation finite difference scheme,NND格式)[59]。
2 数值模拟本文在
| $ {y_c}(x) = \sum\limits_{n = 21}^{30} {[{a_n}\cos ({k_n}x) + {b_n}\sin ({k_n}x)]} $ | (27) |
其中,
| $ {\partial _y}p(y) = - g\rho (y) $ | (28) |
其中
| $ \left\{\begin{array}{l}\begin{array}{l}T(y) = {T}_{u}\text{,}\rho (y) = \dfrac{{p}_{0}}{{T}_{u}}\mathrm{exp}\bigg\{\dfrac{g}{{T}_{u}}\Big[2d-{y}_{c}(x)\Big]\bigg\}\text{,}\\ \;\;\;\;\quad\qquad\qquad\qquad\qquad\qquad\qquad y > {y}_{c}(x)\end{array} \\ \begin{array}{l}T(y) = {T}_{b}\text{,}\rho (y) = \dfrac{{p}_{0}}{{T}_{b}}\mathrm{exp}\bigg\{\dfrac{g}{{T}_{u}}\Big[2d-{y}_{c}(x)\Big]-\\\qquad \dfrac{g}{{T}_{u}}\Big[y-{y}_{c}(x)\Big]\bigg\}\text{,}\\\;\;\;\;\quad\qquad\qquad\qquad\qquad\qquad\qquad y > {y}_{c}(x)\end{array} \end{array}\right. $ | (29) |
其中,
| $ T(y) = \frac{{{T_b} + {T_u}}}{2} - \frac{{{T_b} - {T_u}}}{2} \cdot \tanh \left[ {\frac{{y - {y_c}(x)}}{W}} \right] $ | (30) |
其中
需要说明的是,本文模拟的是可压缩流体系统,即由于重力的作用,系统中的压强从上到下逐层增大。因此,当设定上下层部分流体温度分别为定值
| $ {\rho _u}{T_u} = {\rho _b}{T_b} $ | (31) |
其中
数值模拟中,在满足网格无关性条件下,将模拟区域划分为
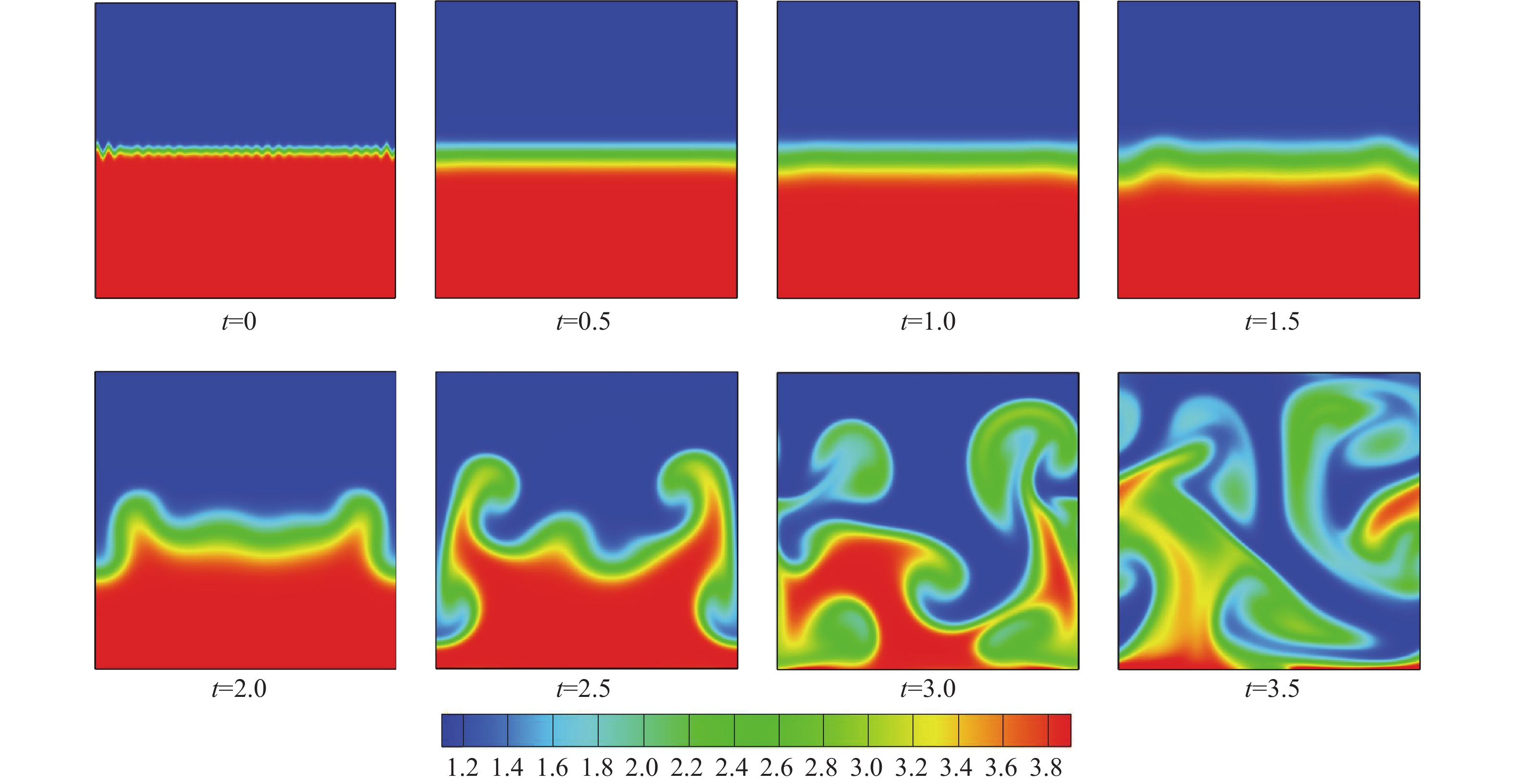
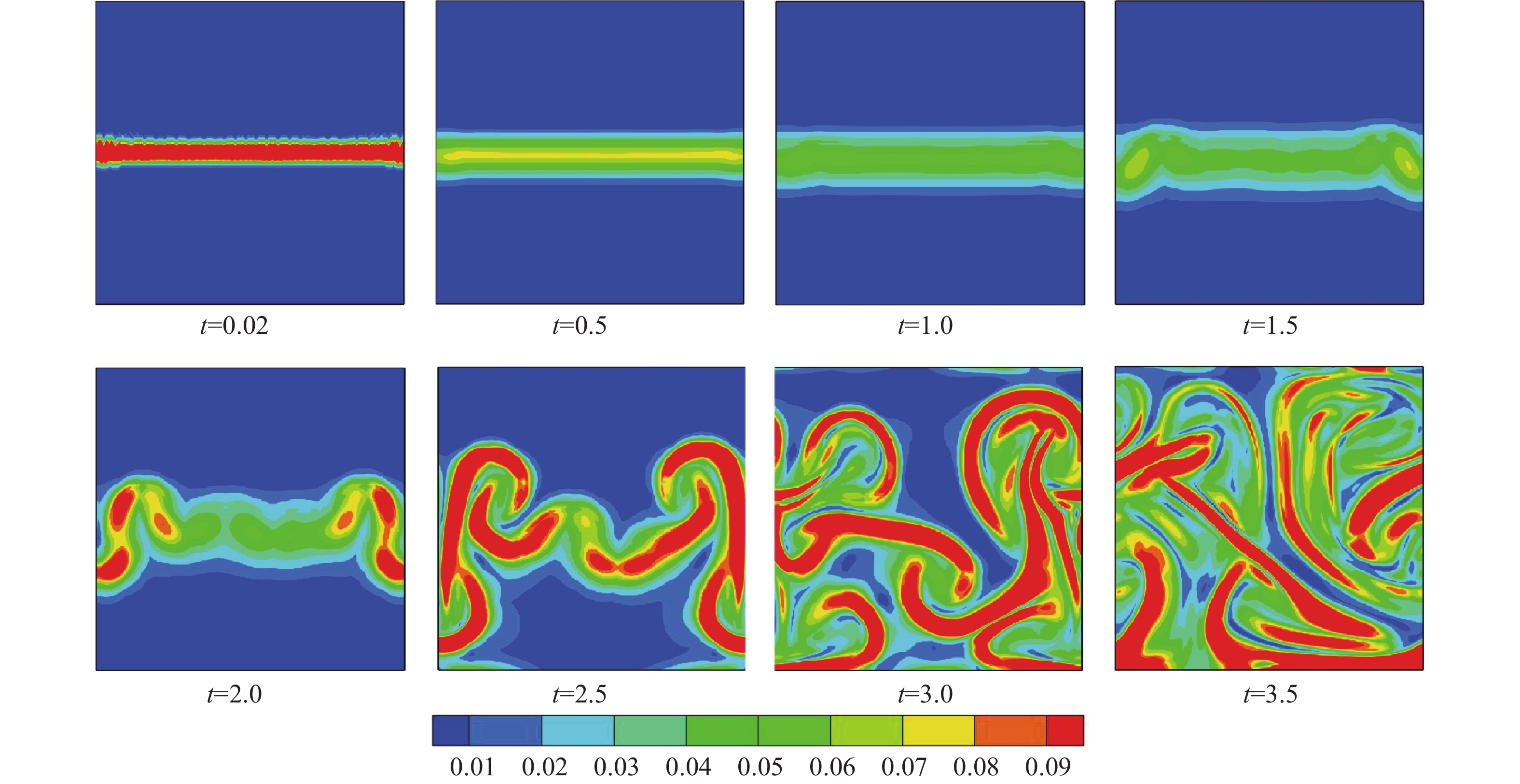
为了直观感受流体系统随时间的演化情况,图2给出了系统中不同时刻的温度云图。可以看出,初始时刻界面处存在不同振幅不同波长的微小扰动,并且由于在界面附近使用了tanh函数,因此物理场的空间梯度变化较为光滑。演化开始后,伴随着系统耗散和热传导的发生,小波长随机扰动界面变得光滑,过渡层变宽,宏观物理量梯度从尖锐转向光滑。大约
|
图 2 |
本文的模拟结果与经典多模RT不稳定性的主要特征基本一致[60-61],但同时也存在些许不同,造成这种差异的原因有以下几点:
1)随机扰动模态不同。在程序中,通过随机函数在物质界面产生随机扰动模态,不同软件平台的随机函数产生的结果往往不一致。
2)流体可压性的影响。与不可压模型不同,本文使用的可压缩DBM可以用于准确预测和研究RT不稳定性的可压缩效应。
3)与Euler、N-S等传统流体力学模型不同,本文使用的DBM不仅包含了黏性和热传导的影响,还同时包含了其他重要的非平衡效应。
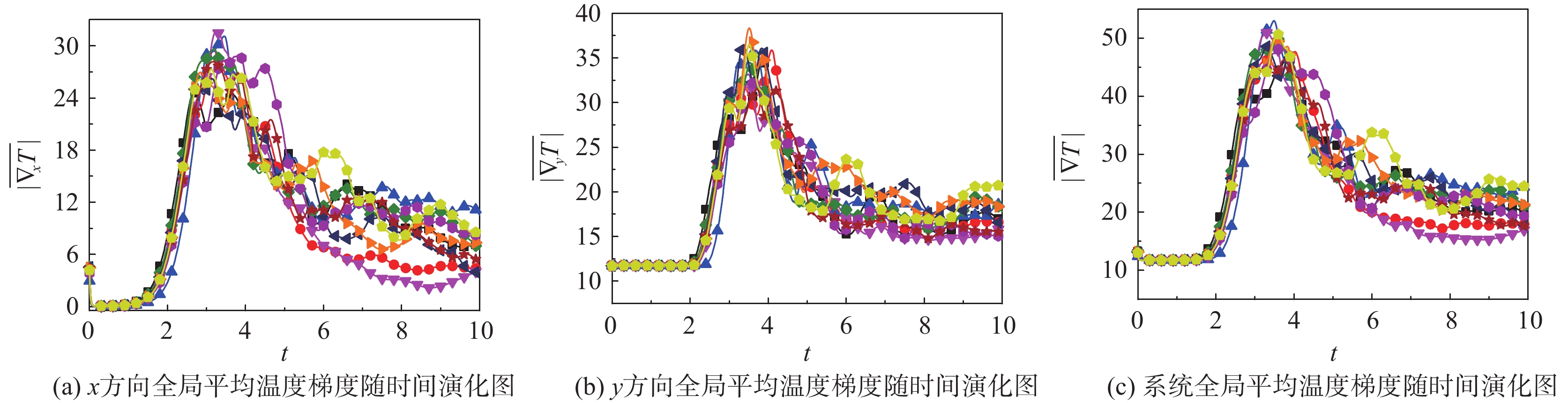
由于多模随机初始扰动中扰动种子的不确定性,我们模拟了10组不同随机扰动情况下的RT不稳定性,并根据其统计特性进行分析。首先,我们分析了RT不稳定系统中系统温度梯度的变化趋势。图3(a)为
|
图 3 在10组不同随机扰动情况下全局平均温度梯度随时间的演化图 Fig.3 Time evolution of the global average temperature gradients under ten initial conditions with different random perturbations |
第一阶段,即初始阶段(大约
第二阶段,
第三阶段(
图3(b)展示了
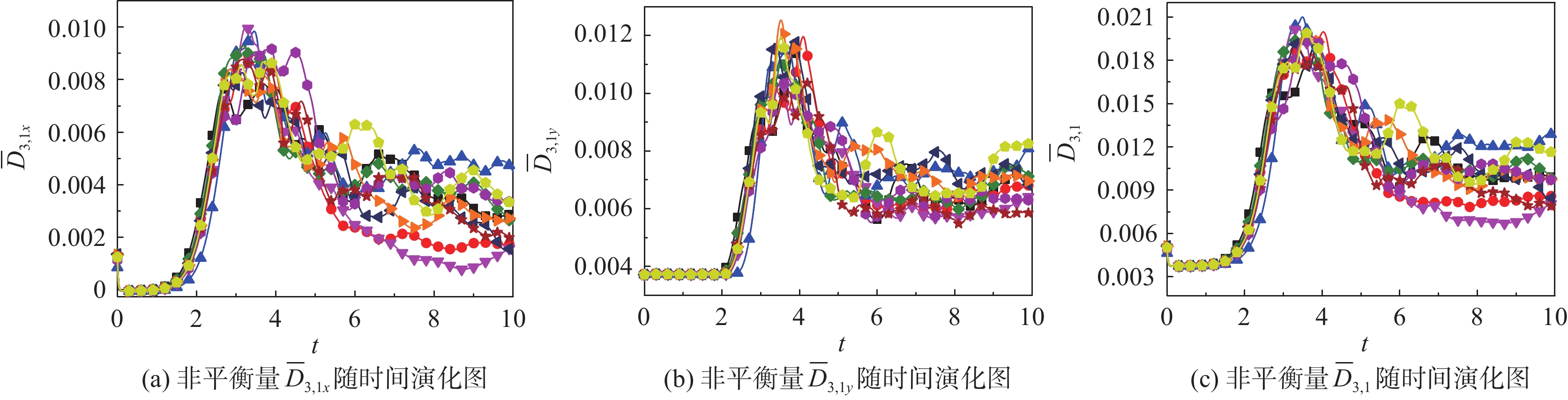
图4给出了与热传导相关的非平衡量的全局平均强度演化图,图4(a、b、c)分别对应
|
图 4 不同随机扰动下与热传导相关的非平衡量的全局平均强度演化图 Fig.4 Time evolution of the global non-organized energy flux with different initial random perturbations |
进一步可以发现,全局平均TNE强度
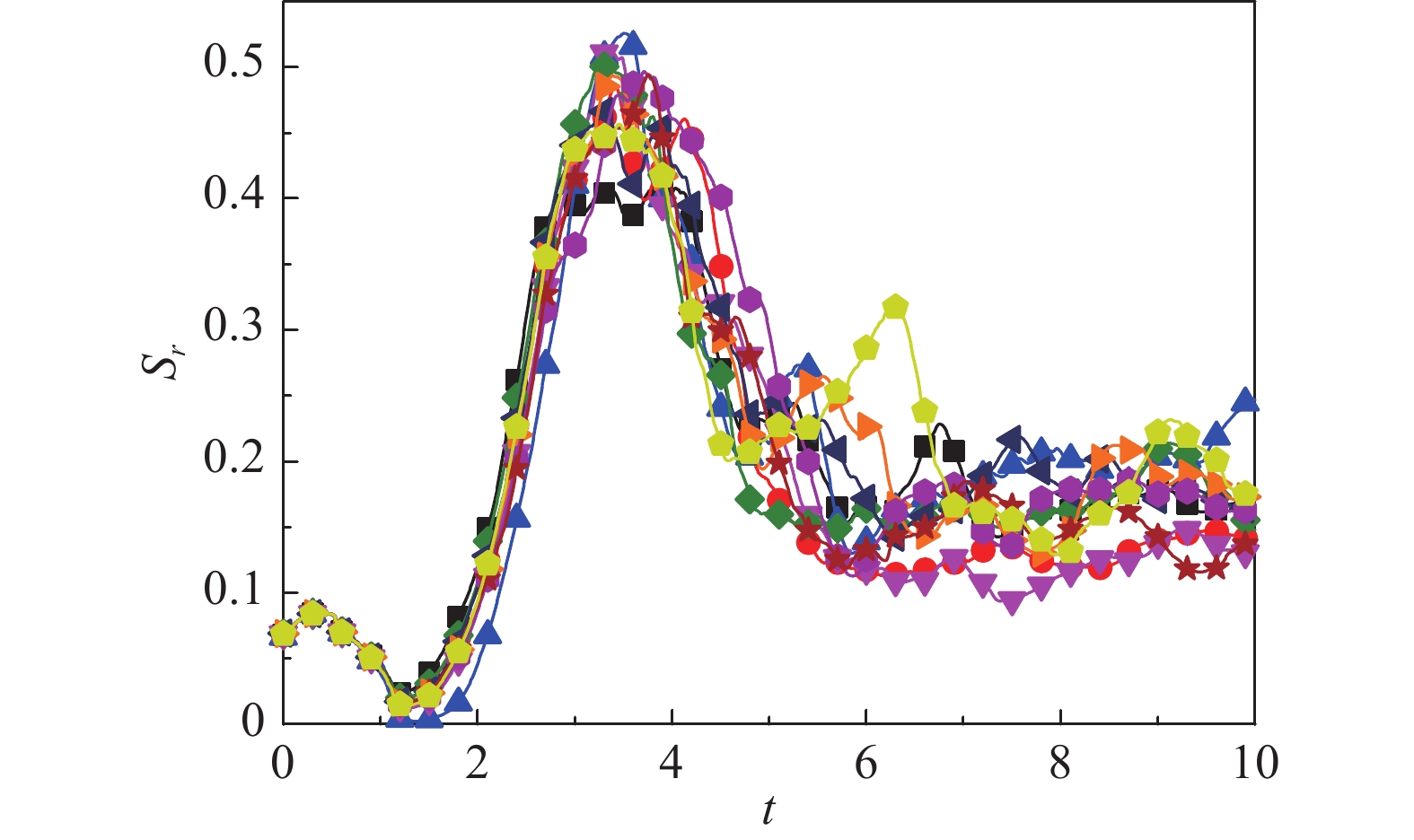
|
图 5 不同随机扰动下非平衡区域面积占比随时间演化图 Fig.5 Time evolution of the proportion of the non-equilibrium region with different initial random perturbations |
|
图 6 |
图7给出了系统全局TNE强度随时间演化图。
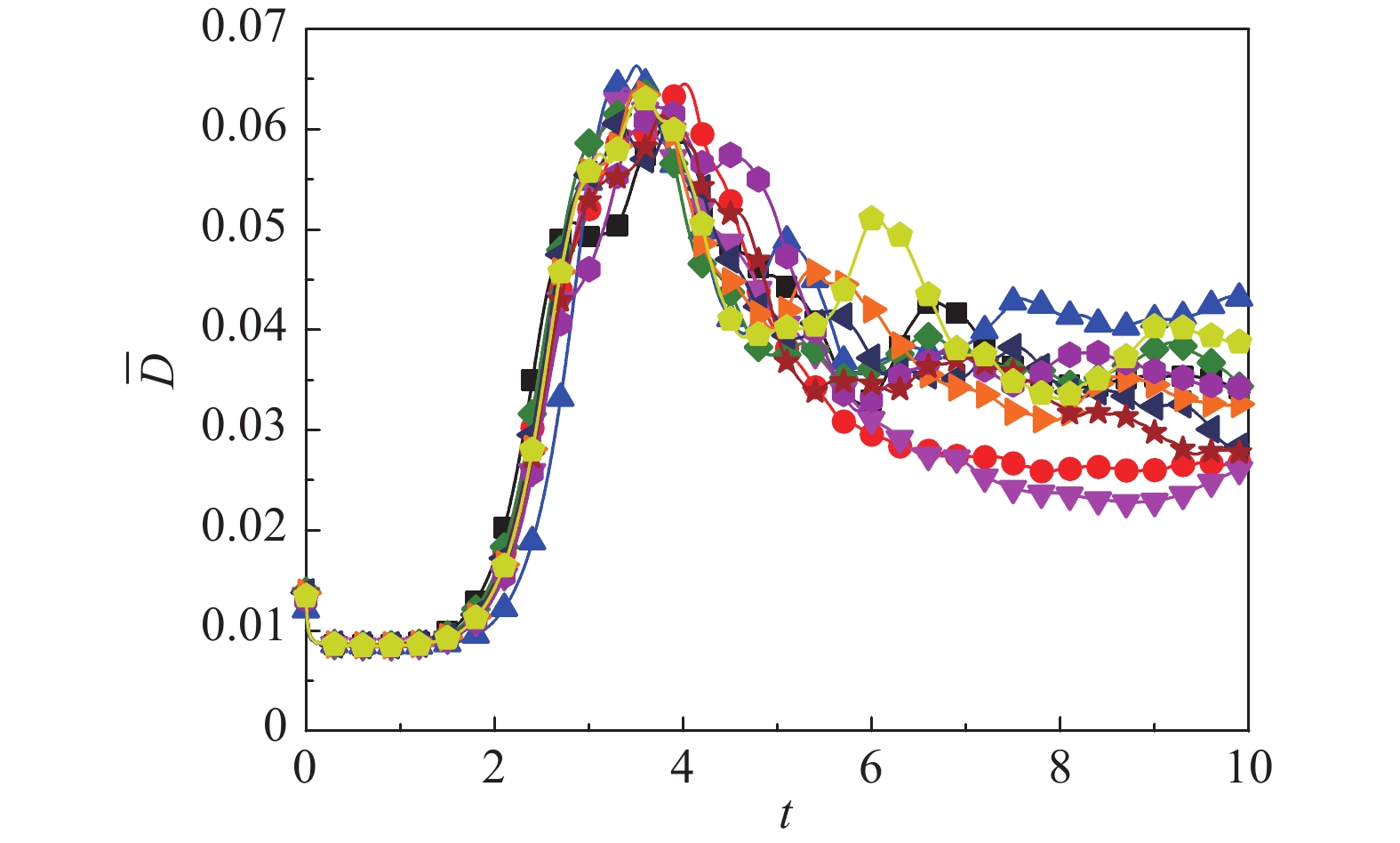
|
图 7 不同随机扰动下全局平均TNE强度随时间演化图 Fig.7 Evolution of the global average TNE intensity with different initial random perturbations |
本文利用DBM研究了可压缩流体中的多模初始扰动的RT不稳定性。首先,分析了与热通量相关的热力学非平衡分量的演化趋势,有两个物理机制起主要作用:一是温度梯度的增大使非平衡强度增大;二是两种流体接触面积的增大促进热交换,从而使非平衡区域增大。两个因素相互竞争共同影响全局非平衡强度的发展趋势。其次,分析了非平衡面积占比的变化趋势。界面热扩散作用使得界面上的局部非平衡强度有减小的趋势,同时界面的拉伸增加非平衡的区域。两种竞争机制使得非平衡区域呈现出复杂的变化趋势。最后,分析了全局平均TNE强度,全局平均TNE强度先增后减最后趋于稳定。此过程也存在两个竞争机制:非平衡区域的面积增大(减小)会增强(减弱)非平衡强度,物质界面物理梯度的增大(减小)对全局平均热力学非平衡强度有相同的影响,二者相互竞争,使其呈现出先减、后增、再减的趋势。这些现象和规律有助于我们更好地理解和分析可压缩RT不稳定性背后的物理机制和机理,为今后相关的流体不稳定性研究提供介观尺度的物理参考。
| [1] |
RAYLEIGH L. Investigation of the character of the equilibrium of an incompressible heavy fluid of variable density[J]. Proceedings of the London Mathematical Society, 1882, s1-14(1): 170-177. DOI:10.1112/plms/s1-14.1.170 |
| [2] |
TAYLOR G I. The instability of liquid surfaces when accelerated in a direction perpendicular to their planes. I[J]. Proceedings of the Royal Society of London Series A Mathematical and Physical Sciences, 1950, 201(1065): 192-196. DOI:10.1098/rspa.1950.0052 |
| [3] |
WOO K M, BETTI R, SHVARTS D, et al. Effects of residual kinetic energy on yield degradation and ion temperature asymmetries in inertial confinement fusion implosions[J]. Physics of Plasmas, 2018, 25(5): 052704. DOI:10.1063/1.5026706 |
| [4] |
MAEDER A, MEYNET G, LAGARDE N, et al. The thermohaline, Richardson, Rayleigh-Taylor, Solberg-Høiland, and GSF criteria in rotating stars[J]. Astronomy & Astrophysics, 2013, 553: A1. DOI:10.1051/0004-6361/201220936 |
| [5] |
SHIOKAWA K, NAKAJIMA A, IEDA A, et al. Rayleigh-Taylor type instability in auroral patches[J]. Journal of Geophysical Research:Space Physics, 2010, 115(A2): A02211. DOI:10.1029/2009ja014273 |
| [6] |
MARTIN J, XILOURIS K, SOKER N. The early interaction of the planetary nebula NGC 40 with the interstellar medium[J]. Astronomy & Astrophysics, 2002, 391(2): 689-692. DOI:10.1051/0004-6361:20020848 |
| [7] |
ABARZHI S I, BHOWMICK A K, NAVEH A, et al. Supernova, nuclear synthesis, fluid instabilities, and interfacial mixing[J]. Proceedings of the National Academy of Sciences, 2019, 116(37): 18184-18192. DOI:10.1073/pnas.1714502115 |
| [8] |
AKULA B, SUCHANDRA P, MIKHAEIL M, et al. Dynamics of unstably stratified free shear flows: an experimental investigation of coupled Kelvin-Helmholtz and Rayleigh-Taylor instability[J]. Journal of Fluid Mechanics, 2017, 816: 619-660. DOI:10.1017/jfm.2017.95 |
| [9] |
POLAVARAPU R, ROACH P, BANERJEE A. Rayleigh-Taylor-instability experiments with elastic-plastic materials[J]. Physical Review E, 2019, 99(5-1): 053104. DOI:10.1103/physreve.99.053104 |
| [10] |
XUE C, YE W H. Destabilizing effect of compressibility on Rayleigh-Taylor instability for fluids with fixed density profile[J]. Physics of Plasmas, 2010, 17(4): 042705. DOI:10.1063/1.3360295 |
| [11] |
ZHANG Y S, RUAN Y C, XIE H S, et al. Mixed mass of classical Rayleigh-Taylor mixing at arbitrary density ratios[J]. Physics of Fluids, 2020, 32(1): 011702. DOI:10.1063/1.5131495 |
| [12] |
MESHKOV E E, ABARZHI S I. Group theory and jelly's experiment of Rayleigh–Taylor instability and Rayleigh–Taylor interfacial mixing[J]. Fluid Dynamics Research, 2019, 51(6): 065502. DOI:10.1088/1873-7005/ab3e83 |
| [13] |
陶烨晟, 王立锋, 叶文华, 等. 任意Atwood数Rayleigh-Taylor和Richtmyer-Meshkov不稳定性气泡速度研究[J]. 物理学报, 2012, 61(7): 314-320. TAO Y S, WANG L F, YE W H, et al. The bubble velocity research of Rayleigh-Taylor and Richtmyer-Meshkov instabilities at arbitrary Atwood numbers[J]. Acta Physica Sinica, 2012, 61(7): 314-320. (in Chinese) |
| [14] |
GALLIS M A; KOEHLER T P; TORCZYNSKI J R, et al. Direct simulation Monte Carlo investigation of the Rayleigh-Taylor instability[J]. Physical Review Fluids, 2016, 1(4): 043403. DOI:10.1103/PhysRevFluids.1.043403 |
| [15] |
WEI Y K, DOU H S, QIAN Y H, et al. A novel two-dimensional coupled lattice Boltzmann model for incompressible flow in application of turbulence Rayleigh-Taylor instability[J]. Computers & Fluids, 2017, 156: 97-102. DOI:10.1016/j.compfluid.2017.07.003 |
| [16] |
LIANG H, HU X L, HUANG X F, et al. Direct numerical simulations of multi-mode immiscible Rayleigh-Taylor instability with high Reynolds numbers[J]. Physics of Fluids, 2019, 31(11): 112104. DOI:10.1063/1.5127888 |
| [17] |
LYUBIMOVA T, VOROBEV A, PROKOPEV S. Rayleigh-Taylor instability of a miscible interface in a confined domain[J]. Physics of Fluids, 2019, 31(1): 014104. DOI:10.1063/1.5064547 |
| [18] |
WIELAND S A, HAMLINGTON P E, RECKINGER S J, et al. Effects of isothermal stratification strength on vorticity dynamics for single-mode compressible Rayleigh-Taylor instability[J]. Physical Review Fluids, 2019, 4(9): 093905. DOI:10.1103/physrevfluids.4.093905 |
| [19] |
LI Z Y, WANG L F, WU J F, et al. Interface coupling effects of weakly nonlinear Rayleigh–Taylor instability with double interfaces[J]. Chinese Physics B, 2020, 29(3): 034704. DOI:10.1088/1674-1056/ab6965 |
| [20] |
LUO T F, WANG J C, XIE C Y, et al. Effects of compressibility and Atwood number on the single-mode Rayleigh-Taylor instability[J]. Physics of Fluids, 2020, 32(1): 012110. DOI:10.1063/1.5131585 |
| [21] |
LIVESCU D, WEI T, BRADY P T. Rayleigh-Taylor instability with gravity reversal[J]. Physica D:Nonlinear Phenomena, 2021, 417: 132832. DOI:10.1016/j.physd.2020.132832 |
| [22] |
BANERJEE A, ANDREWS M J. 3D Simulations to investigate initial condition effects on the growth of Rayleigh-Taylor mixing[J]. International Journal of Heat and Mass Transfer, 2009, 52(17-18): 3906-3917. DOI:10.1016/j.ijheatmasstransfer.2009.03.032 |
| [23] |
BURTON G C. Study of ultrahigh Atwood-number Rayleigh-Taylor mixing dynamics using the nonlinear large-eddy simulation method[J]. Physics of Fluids, 2011, 23(4): 045106. DOI:10.1063/1.3549931 |
| [24] |
ZHANG H, BETTI R, YAN R, et al. Self-similar multimode bubble-front evolution of the ablative Rayleigh-Taylor instability in two and three dimensions[J]. Physical Review Letters, 2018, 121(18): 185002. DOI:10.1103/physrevlett.121.185002 |
| [25] |
YILMAZ I. Analysis of Rayleigh-Taylor instability at high Atwood numbers using fully implicit, non-dissipative, energy-conserving large eddy simulation algorithm[J]. Physics of Fluids, 2020, 32(5): 054101. DOI:10.1063/1.5138978 |
| [26] |
HAMZEHLOO A, BARTHOLOMEW P, LAIZET S. Direct numerical simulations of incompressible Rayleigh-Taylor instabilities at low and medium Atwood numbers[J]. Physics of Fluids, 2021, 33(5): 054114. DOI:10.1063/5.0049867 |
| [27] |
DING J C, SUN P Y, HUANG S H, et al. Single- and dual-mode Rayleigh-Taylor instability at microscopic scale[J]. Physics of Fluids, 2021, 33(4): 042102. DOI:10.1063/5.0042505 |
| [28] |
LIU H, ZHANG Y, KANG W, et al. Molecular dynamics simulation of strong shock waves propagating in dense deuterium, taking into consideration effects of excited electrons[J]. Physical Review E, 2017, 95(2-1): 023201. DOI:10.1103/physreve.95.023201 |
| [29] |
许爱国, 张广财, 应阳君. 燃烧系统的离散Boltzmann建模与模拟研究进展[J]. 物理学报, 2015, 64(18): 35-60. XU A G, ZHANG G C, YING Y J. Progess of discrete Boltzmann modeling and simulation of combustion system[J]. Acta Physica Sinica, 2015, 64(18): 35-60. DOI:10.7498/aps.64.184701 (in Chinese) |
| [30] |
XU A G, ZHANG G C, ZHANG Y D. Discrete Boltzmann modeling of compressible flows[M]// KYZAS G Z, MITROPOULOS A C, edited. Kinetic Theory: Chapter 2. Croatia: InTech, 2018. https://www.intechopen.com/chapters/56964 doi: 10.5772/intechopen.70748
|
| [31] |
XU A G, ZHANG G C, GAN Y B, et al. Lattice Boltzmann modeling and simulation of compressible flows[J]. Frontiers of Physics, 2012, 7(5): 582-600. DOI:10.1007/s11467-012-0269-5 |
| [32] |
许爱国, 陈杰, 宋家辉, 等. 多相流系统的离散玻尔兹曼研究进展[J]. 空气动力学学报, 2021, 39(3): 138-169. XU A G, CHEN J, SONG J H, et al. Progress of discrete Boltzmann study on multiphase complex flows[J]. Acta Aerodynamica Sinica, 2021, 39(3): 138-169. DOI:10.7638/kqdlxxb-2021.0021 (in Chinese) |
| [33] |
许爱国, 宋家辉, 陈锋, 等. 基于相空间的复杂物理场建模与分析方法[J]. 计算物理, 2021, 38(6): 631-660. XU A G, SONG J H, CHEN F, XIE K, YING Y J. Modeling and analysis methods for complex fields based on phase space[J]. Chinese Journal of Computational Physics, 2021, 38(6): 631-660. DOI:10.19596/j.cnki.1001-246x.8379 (in Chinese) |
| [34] |
LAI H L, XU A G, ZHANG G C, et al. Nonequilibrium thermohydrodynamic effects on the Rayleigh-Taylor instability in compressible flows[J]. Physical Review E, 2016, 94(2): 023106. DOI:10.1103/physreve.94.023106 |
| [35] |
李德梅, 赖惠林, 许爱国, 等. 可压流体Rayleigh-Taylor不稳定性的离散Boltzmann模拟[J]. 物理学报, 2018, 67(8): 080501. LI D M, LAI H L, XU A G, et al. Discrete Boltzmann simulation of Rayleigh-Taylor instability in compressible flows[J]. Acta Physica Sinica, 2018, 67(8): 080501. DOI:10.7498/aps.67.20171952 (in Chinese) |
| [36] |
CHEN F, XU A G, ZHANG G C. Viscosity, heat conductivity, and Prandtl number effects in the Rayleigh-Taylor Instability[J]. Frontiers of Physics, 2016, 11(6): 114703. DOI:10.1007/s11467-016-0603-4 |
| [37] |
CHEN F, XU A G, ZHANG G C. Collaboration and competition between Richtmyer-Meshkov instability and Rayleigh-Taylor instability[J]. Physics of Fluids, 2018, 30(10): 102105. DOI:10.1063/1.5049869 |
| [38] |
GAN Y B, XU A G, ZHANG G C, et al. Nonequilibrium and morphological characterizations of Kelvin-Helmholtz instability in compressible flows[J]. Frontiers of Physics, 2019, 14(4): 1-17. DOI:10.1007/s11467-019-0885-4 |
| [39] |
LIN C D, LUO K H, GAN Y B, et al. Kinetic simulation of nonequilibrium Kelvin-Helmholtz instability[J]. Communications in Theoretical Physics, 2019, 71(1): 132. DOI:10.1088/0253-6102/71/1/132 |
| [40] |
CHEN F, XU A G, ZHANG Y D, et al. Morphological and non-equilibrium analysis of coupled Rayleigh-Taylor-Kelvin-Helmholtz instability[J]. Physics of Fluids, 2020, 32(10): 104111. DOI:10.1063/5.0023364 |
| [41] |
YE H Y, LAI H L, LI D M, et al. Knudsen number effects on two-dimensional Rayleigh–Taylor instability in compressible fluid: Based on a discrete Boltzmann method[J]. Entropy, 2020, 22(5): 500. DOI:10.3390/e22050500 |
| [42] |
CHEN L, LAI H L, LIN C D, et al. Specific heat ratio effects of compressible Rayleigh—Taylor instability studied by discrete Boltzmann method[J]. Frontiers of Physics, 2021, 16(5): 1-12. DOI:10.1007/s11467-021-1096-3 |
| [43] |
ZHANG G, XU A G, ZHANG D J, et al. Delineation of the flow and mixing induced by Rayleigh-Taylor instability through tracers[J]. Physics of Fluids, 2021, 33(7): 076105. DOI:10.1063/5.0051154 |
| [44] |
GAN Y B, XU A G, ZHANG G C, et al. Physical modeling of multiphase flow via lattice Boltzmann method: Numerical effects, equation of state and boundary conditions[J]. Frontiers of Physics, 2012, 7(4): 481-490. DOI:10.1007/s11467-012-0245-0 |
| [45] |
GAN Y B, XU A G, ZHANG G C, et al. Discrete Boltzmann modeling of multiphase flows: hydrodynamic and thermodynamic non-equilibrium effects[J]. Soft Matter, 2015, 11(26): 5336-5345. DOI:10.1039/c5sm01125f |
| [46] |
LIN C D, LUO K H, FEI L L, et al. A multi-component discrete Boltzmann model for nonequilibrium reactive flows[J]. Scientific Reports, 2017, 7: 14580. DOI:10.1038/s41598-017-14824-9 |
| [47] |
LIN C D, LUO K H. MRT discrete Boltzmann method for compressible exothermic reactive flows[J]. Computers & Fluids, 2018, 166: 176-183. DOI:10.1016/j.compfluid.2018.02.012 |
| [48] |
LIN C D, LUO K H. Discrete Boltzmann modeling of unsteady reactive flows with nonequilibrium effects[J]. Physical Review E, 2019, 99: 012142. DOI:10.1103/physreve.99.012142 |
| [49] |
LIN C D, SU X L, ZHANG Y D. Hydrodynamic and thermodynamic nonequilibrium effects around shock waves: based on a discrete Boltzmann method[J]. Entropy, 2020, 22(12): 1397. DOI:10.3390/e22121397 |
| [50] |
YAN B, XU A G, ZHANG G C, et al. Lattice Boltzmann model for combustion and detonation[J]. Frontiers of Physics, 2013, 8(1): 94-110. DOI:10.1007/s11467-013-0286-z |
| [51] |
LIN C D, XU A G, ZHANG G C, et al. Polar coordinate Lattice Boltzmann Kinetic modeling of detonation phenomena[J]. Communications in Theoretical Physics, 2014, 62(5): 737-748. DOI:10.1088/0253-6102/62/5/18 |
| [52] |
ZHANG Y D, XU A G, ZHANG G C, et al. Kinetic modeling of detonation and effects of negative temperature coefficient[J]. Combustion and Flame, 2016, 173: 483-492. DOI:10.1016/j.combustflame.2016.04.003 |
| [53] |
LIN C D, XU A G, ZHANG G C, et al. Double-distribution-function discrete Boltzmann model for combustion[J]. Combustion and Flame, 2016, 164: 137-151. DOI:10.1016/j.combustflame.2015.11.010 |
| [54] |
LIN C D, LUO K H. Mesoscopic simulation of nonequilibrium detonation with discrete Boltzmann method[J]. Combustion and Flame, 2018, 198: 356-362. DOI:10.1016/j.combustflame.2018.09.027 |
| [55] |
ZHANG Y D, XU A G, ZHANG G C, et al. A one-dimensional discrete Boltzmann model for detonation and an abnormal detonation phenomenon[J]. Communications in Theoretical Physics, 2019, 71(1): 117. DOI:10.1088/0253-6102/71/1/117 |
| [56] |
LIN C D, LUO K H. Kinetic simulation of unsteady detonation with thermodynamic nonequilibrium effects[J]. Combustion, Explosion, and Shock Waves, 2020, 56(4): 435-443. DOI:10.1134/S0010508220040073 |
| [57] |
GIMELSHEIN S F, WYSONG I J. Nonequilibrium air flow predictions with a high-fidelity direct simulation Monte Carlo approach[J]. Physical Review Fluids, 2019, 4(3): 033405. DOI:10.1103/physrevfluids.4.033405 |
| [58] |
ZHANG Y D, XU A G, ZHANG G C, et al. Discrete Boltzmann method for non-equilibrium flows: Based on Shakhov model[J]. Computer Physics Communications, 2019, 238: 50-65. DOI:10.1016/j.cpc.2018.12.018 |
| [59] |
ZHANG H X, ZHUANG F G. NND schemes and their applications to numerical simulation of two- and three-dimensional flows[J]. Advances in Applied Mechanics, 1991, 29: 193-256. DOI:10.1016/S0065-2156(08)70165-0 |
| [60] |
NOURGALIEV R R, THEOFANOUS T G. High-fidelity interface tracking in compressible flows: unlimited anchored adaptive level set[J]. Journal of Computational Physics, 2007, 224(2): 836-866. DOI:10.1016/j.jcp.2006.10.031 |
| [61] |
RAHMAN S, SAN O. A relaxation filtering approach for two-dimensional Rayleigh–Taylor instability-induced flows[J]. Fluids, 2019, 4(2): 78. DOI:10.3390/fluids4020078 |
 2022, Vol. 40
2022, Vol. 40


