0 引　言

在自然界和工程生产中，存在许多的对流现象，例如：地球上的大气和海洋对流，晶体生长和金属制备过程中的对流等。Rayleigh-Bénard（RB）湍流热对流模型是一种从众多自然现象中抽象出来的经典对流模型^[1-4]。Rayleigh-Bénard湍流热对流简单的描述就是在一个封闭的充满介质的对流槽内，下板加热，上板冷却，形成温差，下板附近热的流体受热膨胀在浮力作用下向上运动，上板附近冷的流体密度变大在重力作用下向下运动，由此形成了热对流。而自然界工程生产中除了上述对流现象外，还有一些其他对流现象，例如：砾石路堤中的对流^[5]，地热能回收过程中^[6-7]的热对流以及填充床反应器中的对流^[8]。这些对流现象中的不同之处在于，对流介质在发生流动时会受到其他物体的影响。砾石会影响水在对流过程中的流动方向，填充床中的填充物会影响反应效率。研究者把这些对流现象称为多孔介质自然热对流^[9-15]。

传统Rayleigh-Bénard（RB）对流系统中有三个控制参数，分别是Rayleigh数 $R a = \alpha g \Delta T H^{3} /(\upsilon \kappa)$ ，Prandtl数 $P_{r} = \upsilon / \kappa$ ，对流槽宽高比 $\varGamma = L / H$ ，其中 $ \alpha $ 为对流介质的热膨胀系数， $ g $ 为重力加速度， $ \Delta T $ 为上下板温差， $ H $ 为系统的高度， $\upsilon$ 为运动黏性系数， $\kappa $ 为热扩散系数， $L$ 为系统水平长度。本文在传统RB对流系统中加入有机玻璃实心圆球，所以在内置圆球RB对流系统中还有一个控制参数孔隙度 $\phi$ ，孔隙度^[16]的计算方法为：

$ \phi = 1-V_{S} / V $

(1)

其中， $ V_{S} $ 为加入圆球的总体积， $ V $ 为对流槽的总体积。Ra数表征的是系统无量纲化的温差；Pr数是流体本身的属性，表征的则是流体的动量扩散与热扩散之间的相对强弱。系统对流传热的响应参数是Nusselt数 $ N u = J /(\lambda \Delta T / H) $ ，其中J为热流量密度，λ为对流介质的热传导系数。Nu数表征的是对流传热的效率。

1 研究现状

为了模拟多孔介质热对流，研究者对Darcy型对流进行了各种研究，相关的数值模拟主要是基于粗粒度的宏观模型^[13,17-19]。近些年来Darcy型对流的数值研究已经扩展到非常高的Ra数，并且观察到Nu数相对于Darcy-Rayleigh数Ra^*的线性标度律^[17-18]（ $ R a^{\prime \prime} = $ $ R a D a $ ， $ D a $ 为Darcy数）。压力驱动的多孔介质流动在Darcy体系中的输运和混合过程已经取得了显著的进展。运输动力学受孔隙中速度概率密度函数的制约，尤其是在低速范围内的速度分布，这在多孔介质中异常或非定常的输运行为中起着关键作用^[20]。使用连续时间随机游走方法对非均质流场中的异常输运行为进行建模，以解释孔隙中平流时间广泛分布的影响, 大概率出现的低速度区域会导致持续的反常的non-Fickian行为^{[16, 21-23]}，即随着孔隙度提高，在相应长时间内的位移方差与Fickian行为相比会出现比较明显的偏移。Dentz^[24]等研究了三维多孔介质中层流在孔隙空间中的扩散机理。确定了两种不同的流动区域，第一个区域的特点是平流停留时间在单孔中分布很广，第二个区域的特征是随着固体颗粒向低速区的扩散传质。Souzy^[25]等测量了由随机堆积的固体球组成的各向同性多孔介质中的三维速度场。发现低速下速度值的分布是平坦的，这与Dentz等的数值结果是一致的。在粗粒多孔介质中，与流体中的流动和热长度尺度相比，固体多孔材料的长度尺度并不小，Darcy模型不再有效。Keene和Goldstein^[26]研究了以压缩氩作为饱和流体，直径为25.4 mm球形聚丙烯珠用简单立方包装排列方式填充在279 mm×279 mm×279 mm对流方腔中的系统传热。其中压力在5.6～77 bar之间变化，得到了1.68×10⁹＜Ra＜3.86×10¹¹的高Ra数区间内的传热结果，他们还结合Kladias和Prasad^[20]等的数据，分析得出，在高Ra数下，除非固相具有较高的导热性，否则多孔介质中的传热会逐渐接近均质流体层中的传热行为。2019年Iman等和Manu等^[21-22]分别用实验和数值研究了方腔中相同孔隙度下不同材料多孔介质对传热的影响，结果发现低Ra数下，对流传热会被减弱；高Ra数的渐近范围内，Nu数与粗粒多孔介质大小无关，但明显依赖于流体和多孔介质的导热性能。Liu等^{[16, 23]}通过二维数值模拟发现圆形填充物阵列在传热方面有两个相互竞争的影响。一方面，脉动温度与垂直速度的相关性增强，逆梯度对流换热受到抑制，流动变得更加一致，从而传热增强。另一方面，由于圆形填充物阵列的阻抗，对流强度降低，导致传热降低。结果表明Nu数跟孔隙度大小以及球形填充物排列方式有关。

然而，目前还没有相关实验探究在内部添加圆球填充物，通过改变圆球的排列方式、排放位置及圆球直径的大小来调节孔隙度的大小，以测定孔隙度对系统传热效率的影响，本文的目的就是完成这一项工作。

2 实验装置及方法

图1是本实验对流槽示意图，对流槽的长 $ L_{x} = $ $ 240 $ mm，宽 $ L_{y} = 60 $ mm，高H = 120 mm，对应的宽高比分别为 $ \varGamma_{x} = L_{x} / H = 2 $ ， $ \varGamma_{y} = L_{y} / H = 0.5 $ 。对流槽由上下导板和有机玻璃边壁组成。其中上下导板用紫铜制作（导热系数为400 W/(m·K)），导板表面电镀了一层很薄的镍以防止紫铜被空气氧化。有机玻璃的厚度为8mm，利用四根直径为8 mm的不锈钢柱将上下导板和有机玻璃边壁固定在一起。下导板为加热板，内部嵌入一片厚度约为1 mm，大小为240 mm×60 mm的矩形加热片，加热片与小型直流电源（GPD-3303S，最大输出电流为3 A，最大输出功率为180 W，稳定性高达99.9%）。上导板为冷却板，内部设计了可以通过水流的槽道，连接水冷机（Polyscience 9702，温度控制精度0.01℃）以使其冷却并保持温度恒定。在上下导板内分别插入直径约为2.5 mm的温度探头（OMEGA TH-44008，温度稳定性为±0.02℃），连接温度采集仪（AGIENT Keysight 34972A）采集温度探头的电阻数据并保存到电脑，利用温度探头的温度-电阻标定曲线，测定温度数据进行后续相关计算。

实验中所采用的对流介质为水，Pr数固定为5.5，我们在对流槽内部加入直径分别为D = 30 mm、20 mm的有机玻璃实心圆球，通过改变圆球大小、排列方式及排放位置来探究内置圆球填充物对传统RB热对流的湍流传热影响。需要强调的是实验中圆球采用的材料是PMMA有机玻璃，其导热系数相较于对流介质水来说要小得多，所以将圆球看作绝热填充物。另外，我们先在侧壁打一直径为2 mm的半深孔，有机圆球内部同样打孔，然后用相同材料的有机玻璃棒把圆球串起来后插入侧壁孔中，黏合对流槽时将其固定，有机玻璃棒与圆球之间、以及圆球与圆球之间是紧密接触的，所以圆球不会发生移动或者旋转。此外，为了减少系统漏热，在对流槽外测包裹两层保温棉，并且在实验过程中，保持实验室温度稳定。

3 实验结果及分析

图2为双对数坐标中不同孔隙度条件下，测得的Nu数随Ra的变化情况。当 $\phi$ = 1时，此时没有添加圆球填充物即为传统RB对流系统，Nu数与Ra数存在着Nu～Ra^0.30这一标度律关系，图2中给出了与Grossmann-Loshe（GL）理论^[27-29]中方形对流槽的数据对比结果，具有很好的吻合性，实验结果得到了很好的验证。本文中加入圆球后所测得的Nu数测量误差均不超过1%。

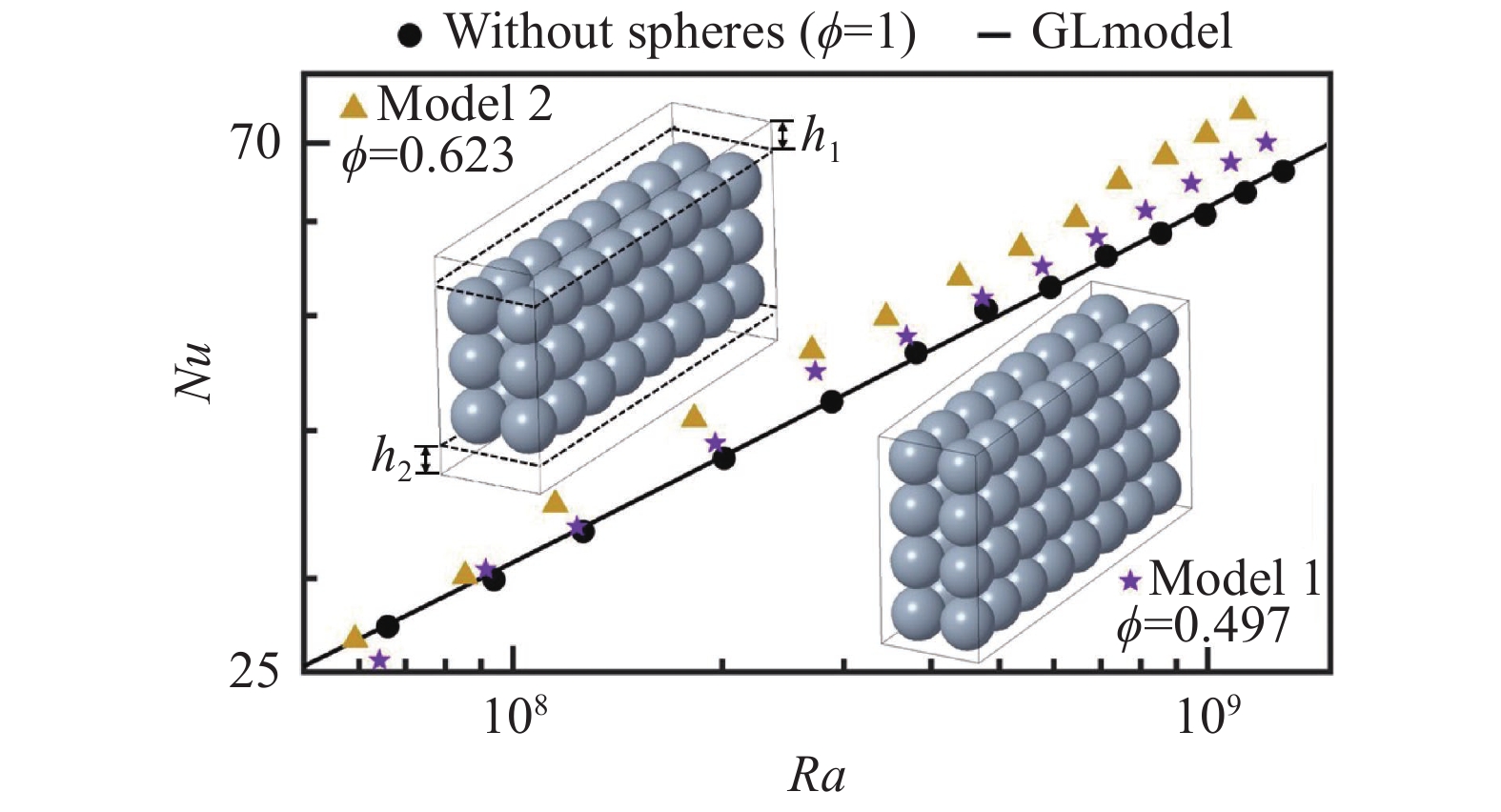
本文设置了一组对照实验，用直径相同的圆球填充物（直径D = 30 mm）填充两个大小相同的对流槽，其中工况1（ $\phi$ = 0.497）中的圆球规则填充在整个对流槽当中，圆球与上下导板均紧密接触；工况2（ $\phi$ = 0.623）中的圆球规则填充在距离上下导板为15 mm的对流槽内部。图2给出了对照实验的结果，对于工况1（ $\phi$ = 0.497），当5×10⁷＜Ra＜1×10⁸时，此时温差较低，对流槽内湍流度较低，填充圆球对整个系统的影响较小，系统的整体传热与传统RB对流的情况相当；当Ra＞1×10⁸时，上下导板附近的温度边界层变得更薄，圆球填充物之间的有序流动促进了羽流的生成与发射，系统的整体传热明显高于传统RB对流的情况。对于工况2（ $\phi$ = 0.623），当Ra＜1×10⁸时，此时系统的整体传热与传统RB对流的情况相当；当Ra＞1×10⁸时，系统的整体传热显著高于传统RB对流的传热。对比工况1 和工况2，发现 $\phi$ = 0.623工况下Nu数的增强幅度要高于 $\phi$ = 0.497工况下Nu数的增强幅度。因为前者对流槽内的流体比后者要多，在相同Ra数时，有更多的流体在对流槽内流动进行热交换因此Nu数提升的幅度更大。在较高Ra数时，两种工况下Nu数提高效率都趋于稳定。

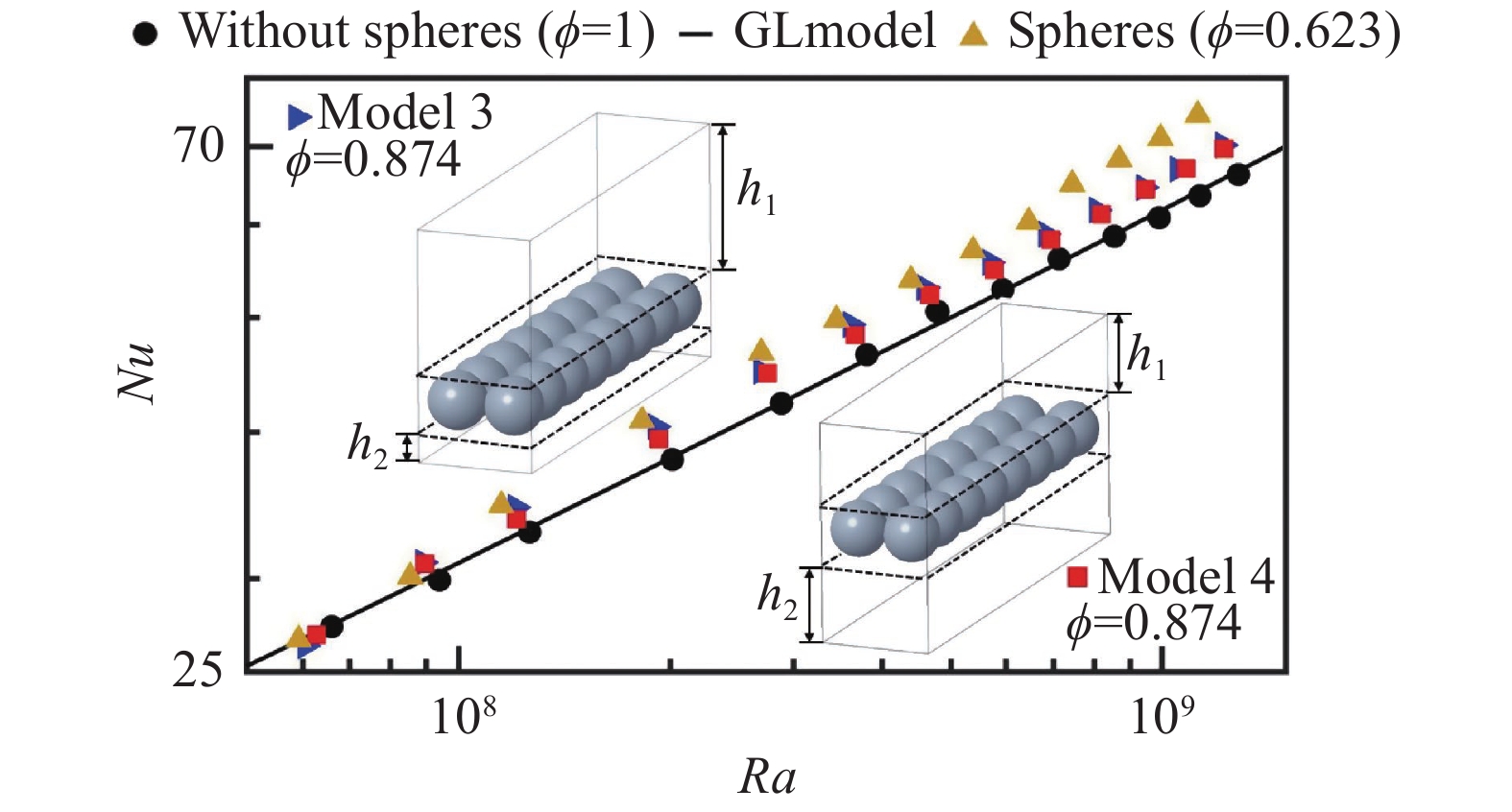
为了研究不同填充区域对系统传热的影响，本文设置了第二组对照实验，用直径相同的圆球（直径D = 30 mm）填充三个大小相同的对流槽，其中工况2（ $\phi$ = 0.623）的填充区域与上下导板距离为 $ h_{1} = $ $ h_{2} = 15 $ mm，工况3（ $\phi$ = 0.874）的填充区域与上下导板距离为 $ h_{1} = 75 $ mm， $ h_{2} = 15 $ mm，工况4（ $\phi$ = 0.874）的填充区域与上下导板距离为 $ h_{1} = h_{2} = 45 $ mm。图3给出了对照实验中不同工况Nu数随Ra数的变化关系。从图3中可以看到，当Ra＜1×10⁸时，对比传统RB对流的Nu数，三个工况的Nu数没有明显差别；当Ra＞1×10⁸时，三个工况的系统传热均高于传统RB对流的传热。这是因为在这三个工况中，圆球填充区域内部形成了稳定的对流通道，系统的整体流动更加有序，上下导板促发的羽流可以更加高效地将热量从边界层区运输到主流区。然而随着Ra数的增大，工况2传热增大的幅度逐渐高于工况3和工况4。这是因为在对照实验中，工况2的圆球填充区域大于工况3和工况4的圆球填充区域，在圆球填充区域形成的对流通道更稳定，系统的整体流动也更有序。而工况3和工况4的对流槽内部虽然也布置了圆球填充物，但数目太少且只有一层，当羽流通过圆球之间的通道后不能维持稳定有序的流动状态。从结果上看，工况3和工况4的孔隙度 $\phi$ 相同，传热增强的幅度也基本相同，说明高孔隙度 $\phi$ 下，圆球在对流槽内部的位置对传热增强效率影响不大；在高Ra数时，三种工况Nu数增大的幅度均趋于稳定。

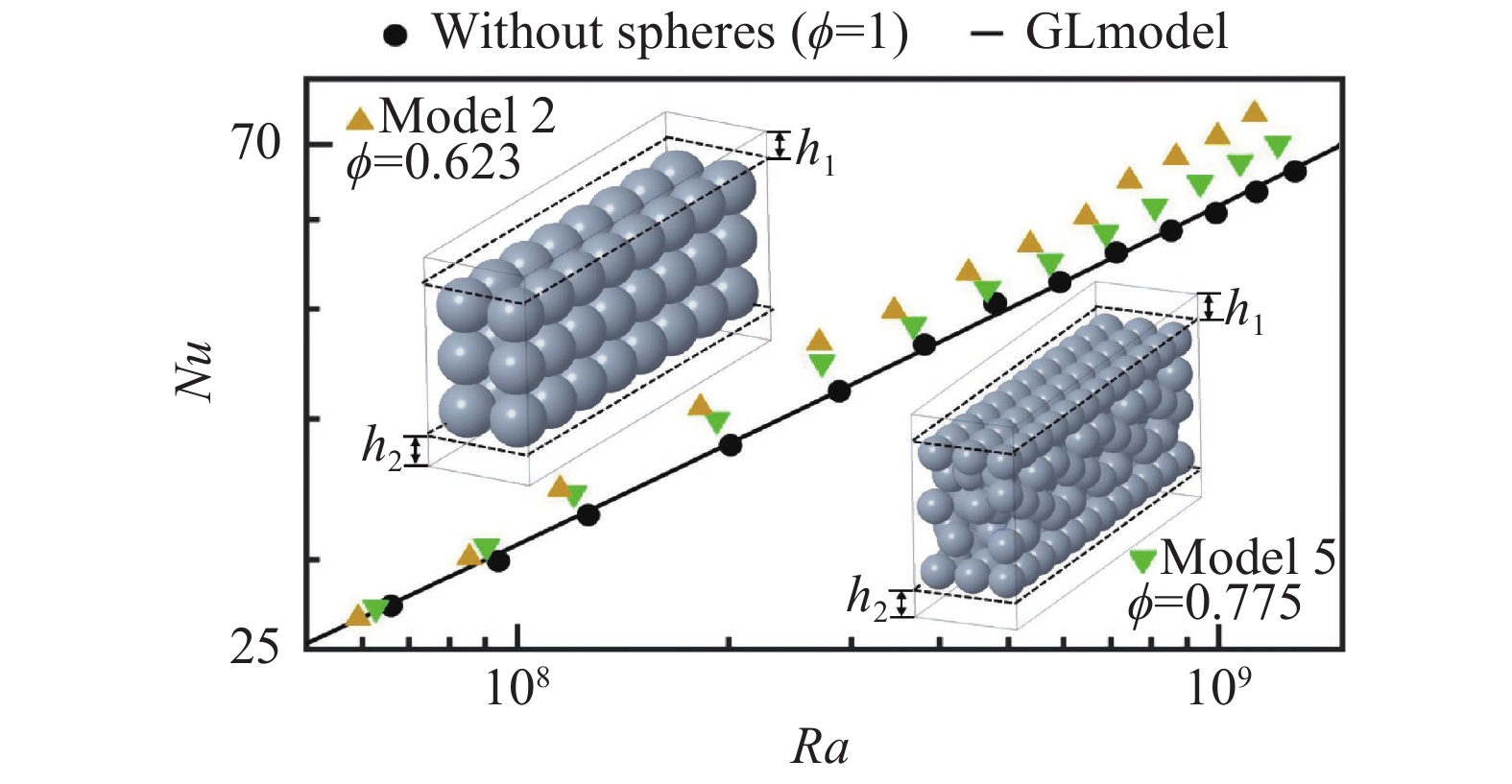
为了研究圆球填充物尺寸对系统传热的影响，我们设置了第三组对照实验，分别用两种不同直径的圆球填充大小相同的对流槽。两个工况的填充区域与上下导板间距均为 $ h_{1} = h_{2} = 15 $ mm，其中工况2（ $\phi$ = 0.623）圆球的直径为D= 30 mm，工况5（ $\phi$ = 0.775） 圆球直径为D = 20 mm。图4给出了两个工况的Nu数随Ra数的变化关系。结果显示，相较于传统RB对流，当Ra＜1×10⁸时，这两种工况下Nu数无明显变化；当Ra＞1×10⁸时，两种工况的结果均大于传统RB系统的传热。从图中可以明显地看到，工况2增大的幅度要高于工况5的幅度，这因为工况5中圆球的直径要小于工况2中圆球的直径，球与球之间形成的对流通道更加狭窄，对流通道中的流动也更加缓慢，导致羽流的热输运效率更低，因此工况5的传热Nu数要低于工况2的传热Nu数。随着Ra数的逐渐增大，两种工况下Nu数增大的幅度同样会趋于稳定。

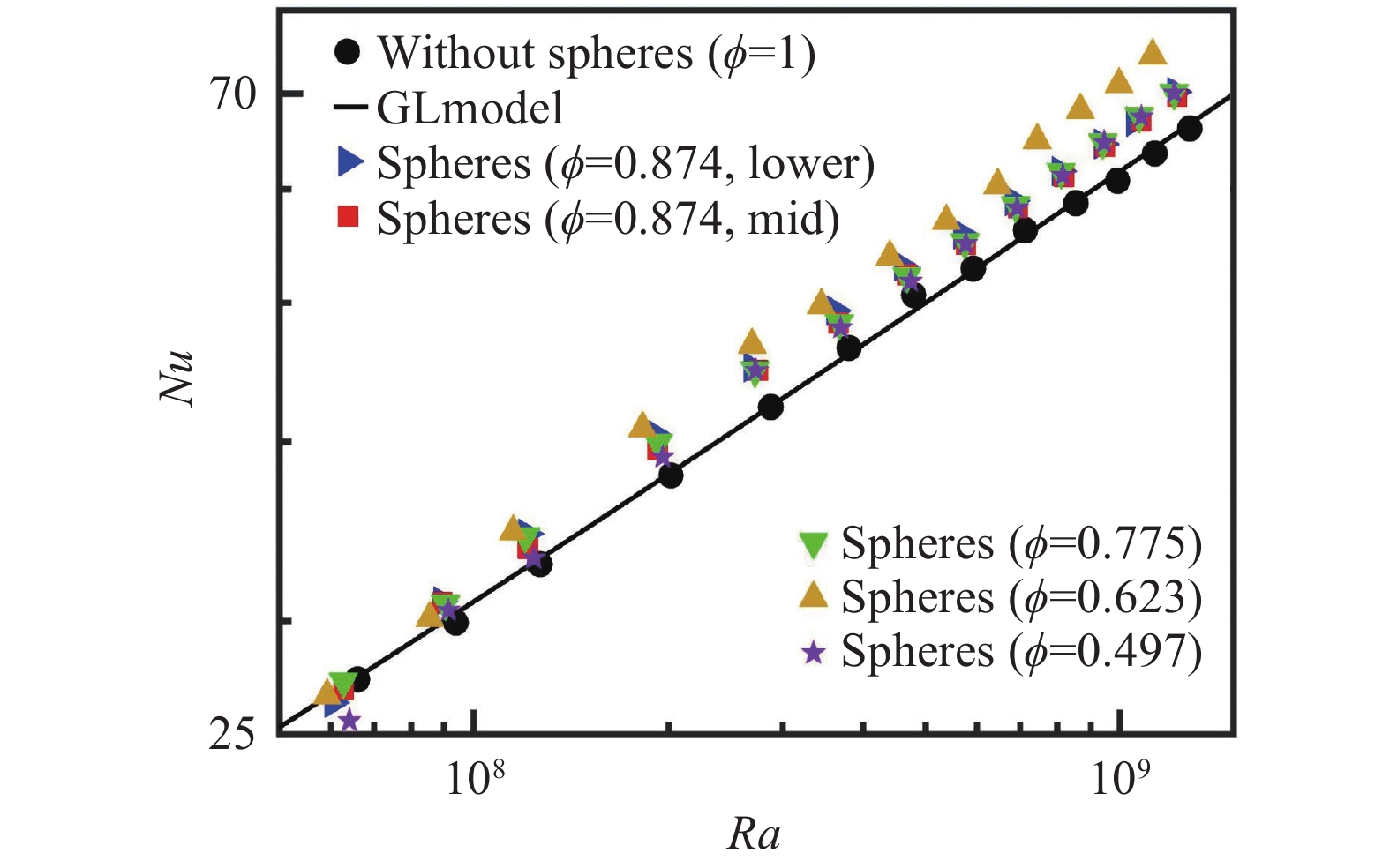
为了更清楚地说明填充物对RB对流系统传热的影响，我们将三组对照实验的五种不同工况的Nu数结果画到一起，如图5所示。从图中可以看到，在本文研究的Ra数的范围内，当Ra数较低时，所有工况的系统传热均与传统RB对流系统的传热相当；当Ra数较高时五种工况的系统传热相对于传统RB对流都有所增强，这说明在对流槽内填充圆球可以增强RB对流的系统传热。其中工况1、工况2、工况3、工况4、是采用相同大小的圆球填充对流槽，不难发现，加入圆球后，都是在高Ra数下提高系统传热，但从孔隙度的变化来看，系统传热的增强幅度并不是与孔隙度呈单调变化，当孔隙度由 $\phi$ = 0.874减小到 $\phi$ = 0.623后，系统传热的增强幅度是变大的，但当孔隙度由 $\phi$ = 0.623进一步减小到 $\phi$ = 0.497时，系统传热的增强幅度并没有继续变大，反而是降低的，这说明加入圆球调节传热是一种可行的方式 。

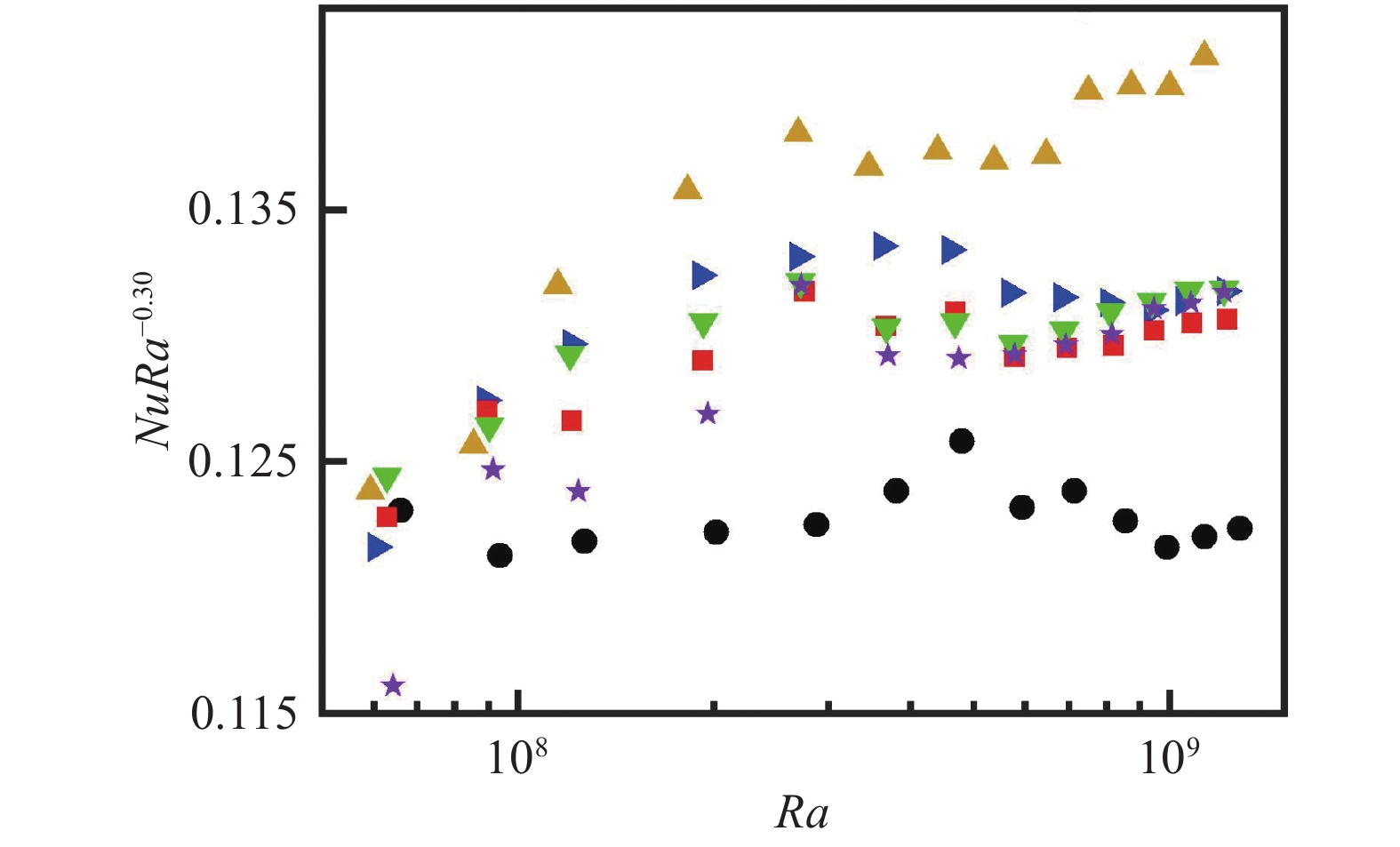
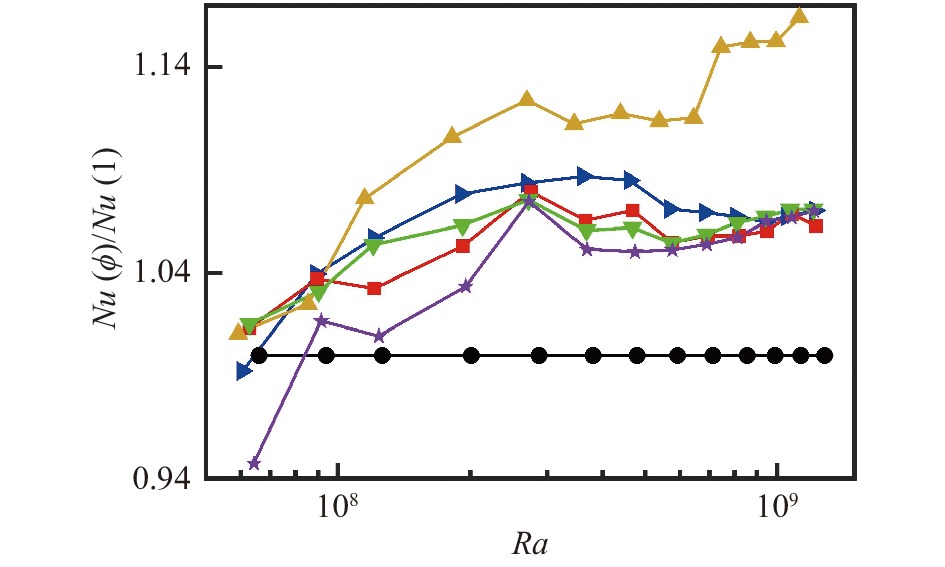
图6为五种工况下NuRa^−0.30随Ra数的变化情况，图7为五种工况下Nu( $\phi$ )/Nu(1)随Ra数的变化情况。根据图6可以发现，对比不同孔隙度 $\phi$ 下，在较低Ra数区间（5×10⁷＜Ra＜3×10⁸）内，相近Ra数下NuRa^−0.30的大小比较明显的变化，且呈逐渐增大的趋势，这意味着传热效率出现提升，且不同孔隙度 $\phi$ 的提升幅度也有差别，而在较高Ra数区间（3×10⁸＜Ra＜2×10⁹）内，NuRa^−0.30的值呈现先减小再增大的趋势，但变化幅度非常小，基本上趋于稳定。

不同孔隙度下，在Ra数由低向高的变化过程中发现，在Ra = 2.7×10⁸附近，Nu数会出现一个小峰值，此时填充圆球对系统的传热提高效果最为显著。这可能是因为在该Ra数附近，填充圆球对羽流的有序性流动影响最为明显。结合图7的结果，发现在孔隙度 $\phi$ = 0.623时，传热提高效率最为明显，Nu数的增幅可达16%，而在其余4种工况下，传热效率同样有所提升，Nu数的增幅最高可达7%。

4 结　论

本实验以长方体RB湍流热对流系统为研究对象，通过给对流槽内部加入不同数目及不同大小的圆球，调节不同的孔隙度 $\phi$ ，精确测量了新系统湍流传热效率Nu数，研究了圆球不同孔隙度对Nu数的影响。实验结果表明，在系统内部添加圆球填充物，可以改变系统的传热Nu数。在本文研究的参数范围内，主要的结论有：

1）在低Ra数的情况下，填充圆球对系统传热影响不大，系统的传热没有明显的变化。

2）在高Ra数的情况下，系统内的圆球之间会形成较为稳定的对流通道，从上（冷）下（热）导板发射的冷（热）羽流可以沿着对流通道有序流动，从而提高系统的传热效率，填充圆球起到了稳定流场的作用，这与Chong等^[30]提到的适当强度的稳定力可以通过增加流动一致性来强化传热这一结论是吻合的。

3）在高Ra数的情况下，当圆球与上下导板留有足够空间时，对于相同直径的圆球，圆球填充的区域越大，系统的传热增强的幅度越大。

4）在高Ra数的情况下，当圆球与上下导板留有足够空间时，若圆球填充的区域相同，圆球直径较大时，系统的传热增强的幅度较大。在本实验中，当孔隙度 $\phi$ = 0.623时，Nu数的提升最大达到16%。

传热效率是RB湍流热对流系统中的核心问题之一，我们通过实验发现在对流槽内部填充圆球可以增强长方体 RB 湍流热对流系统的传热，传热效率增强的幅度与填充圆球数目及填充位置有关，当圆球距离上下导板一定高度且规则填充时，增强幅度最大。本文证明了填充圆球可以调节RB湍流热对流系统的传热效率，但目前实验并未找到提高传热效率的最佳填充位置和最佳填充数目，同时改变填充圆球的材料是否也会影响系统的传热，这都是值得探索的方向。