由温差导致的热对流现象广泛存在于自然界和各种工程应用中,比如热对流在海洋对流、大气环流、地幔对流、太阳对流等自然现象以及在电子设备的冷却和凝固过程、核反应堆设计、晶体生长等工程应用中扮演着重要角色。Rayleigh-Bénard(RB)对流模型是研究热对流问题的经典物理模型之一,RB对流指流体层中下壁面加热、上壁面冷却导致的流动现象。该系统的控制参数主要是瑞利数Ra和普朗特数Pr,响应参数为努塞尔数Nu和雷诺数Re。当Ra较小时,流动由羽流主导,大尺度环流并不明显[1];随着Ra的增加,系统逐渐进入湍流状态,此时上下壁面存在很薄的温度边界层,冷热羽流在温度边界层内生成并在浮力的作用下运动并自组织形成大尺度环流。随着流动复杂性的增加,对RB对流研究的重心也转为对湍流状态下系统各物理量统计特性的研究[2-4]。
在RB对流的研究中通常使用侧壁绝热的温度边界条件,在侧壁绝热的充分发展的RB湍流中,体区的温度近似均匀,因此侧壁的温度在大部分区域近似为上下壁面温度的平均值。实际的对流换热装置中,侧壁的导热性往往不能忽略[5-9]。极端条件下,当侧壁导热系数相比流体很大时,可以认为侧壁是理想导热壁面,此时侧壁的温度为线性分布[10-22]。
前人在宽度∶深度∶高度之比为6∶2∶1[23]和6∶4∶1[24]的三维方腔内研究了低Ra下不同侧壁温度对系统流动结构的影响。Corcione[25]在二维腔体研究了侧壁温度等于底壁温度对流动和传热的影响。Stevens等[6]研究了圆筒中不同侧壁温度对Nu的影响。Moon等[26]研究了侧壁温度等于上壁面温度的立方腔体内的流动。Vasu等[27]研究了三维方腔中侧壁等温条件或等热流条件对流动模态的影响。也有研究讨论了壁面厚度、导热率对RB对流的影响,提出了侧壁修正模型并进行了分析[6-8,25,28-36]。工程应用中热对流的温度边界条件各种各样,Pandey等[37]对方腔温度边界条件方面的研究进行了详细的总结,指出侧壁温度边界条件主要分为绝热、加热、冷却、温度线性分布四种。目前,对侧壁等温且温度为上下壁面温度平均值的对流问题研究仍然不多。
本文使用直接数值模拟(DNS)研究了
腔体的高度为
| $ \nabla \cdot {{\boldsymbol{u}}} = 0 $ |
| $ \frac{\partial \boldsymbol{u}}{\partial t}+\left(\boldsymbol{u}\cdot \nabla \right)\boldsymbol{u} = -\nabla p+\frac{1}{\sqrt{Ra/Pr}}{\nabla }^{2}\boldsymbol{u}+T\boldsymbol{k} $ |
| $ \frac{\partial T}{\partial t}+\left({\boldsymbol{u}}\cdot \nabla \right)T = \frac{1}{\sqrt{Ra\cdot Pr}}{\nabla }^{2}T $ | (1) |
其中,
数值求解使用课题组自主开发的lMn2d和lMn3d程序。该程序采用交错网格,将矢量放置在网格界面上,将标量放在网格中心处,避免了速度和压力解耦。空间离散使用二阶精度的中心差分,对非线性项采用Adams-Bashforth格式,对黏性项和扩散项采用Crank-Nicolson格式。壁面附近采用拉伸网格以更好地分辨边界层。在二维方腔和三维方腔内分别在
| 表 1 不同Ra下二维数值模拟的网格数 Table 1 Grid resolutions for two-dimensional simulations with different Ra |
|
|
| 表 2 不同Ra下三维数值模拟的网格数 Table 2 Grid resolutions for three-dimensional simulations with different Ra |
|
|
热量输运规律是热对流系统中关注的重要问题。无量纲数Nu表征了对流传热的效率,其计算公式为:
| $ Nu = \frac{\hat{Q}}{\hat{k}\mathrm{\Delta }\hat{T}/\hat{H}} $ | (2) |
其中,
| $ \hat{Q} = {\hat{Q}}_{\mathrm{c}\mathrm{o}\mathrm{n}\mathrm{v}}+{\hat{Q}}_{\mathrm{c}\mathrm{o}\mathrm{n}\mathrm{d}} = {\left\langle{\hat{\rho }{\hat{c}}_{p}{\hat{u}}_{z}\hat{T}}\right\rangle}_{{\rm{A}}}- {\left\langle{\hat{k}{\partial }_{z}\hat{T}}\right\rangle}_{{\rm{A}}} $ | (3) |
则公式(2)可写为:
| $ Nu = \frac{\hat{Q}}{\hat{k}\mathrm{\Delta }\hat{T}/\hat{H}} = \frac{{\left\langle{\hat{\rho }{\hat{c}}_{p}{\hat{u}}_{z}\hat{T}}\right\rangle}_{{\rm{A}}}-{\left\langle{\hat{k}{\partial }_{z}\hat{T}}\right\rangle}_{{\rm{A}}}}{\hat{k}\mathrm{\Delta }\hat{T}/\hat{H}} $ | (4) |
其中
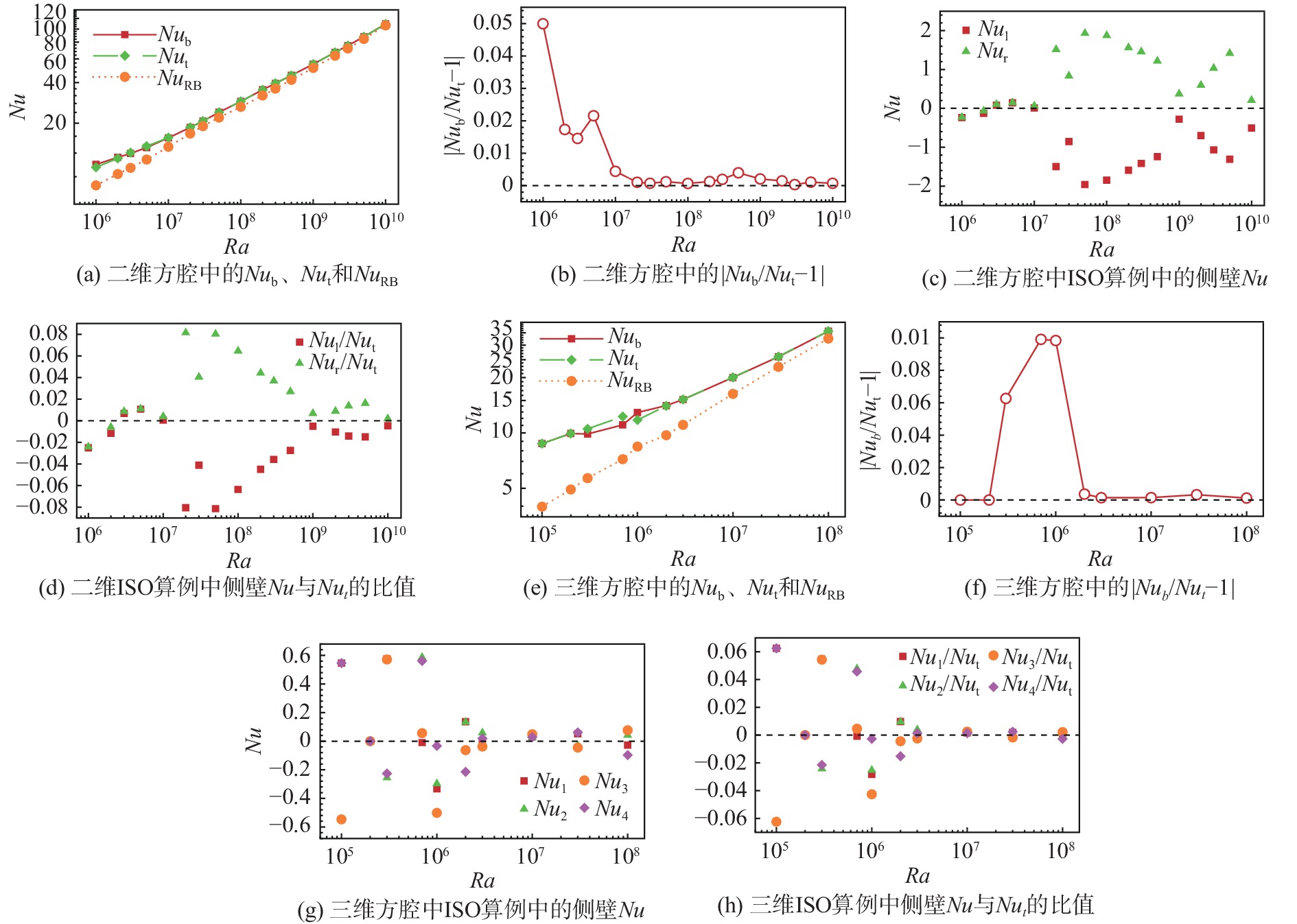
图1给出了二维和三维方腔各个壁面Nu、
|
图 1 二维和三维方腔中各Nu随Ra的变化以及Nu之间关系随Ra的变化 Fig.1 Nu numbers and the relationships between them as functions of Ra in two- and three-dimensional square cavities |
当侧壁温度固定为上下壁面温度的平均值时,由于系统存在的上下对称性,直觉告诉我们上下壁面的Nu应该相等,然而有意思的是,从图1(a、e)可以看出二维和三维方腔中上下壁面的Nu在某些比较低的Ra区间都出现了明显的偏差,即
图1(b、f)分别给出了二维方腔和三维方腔中
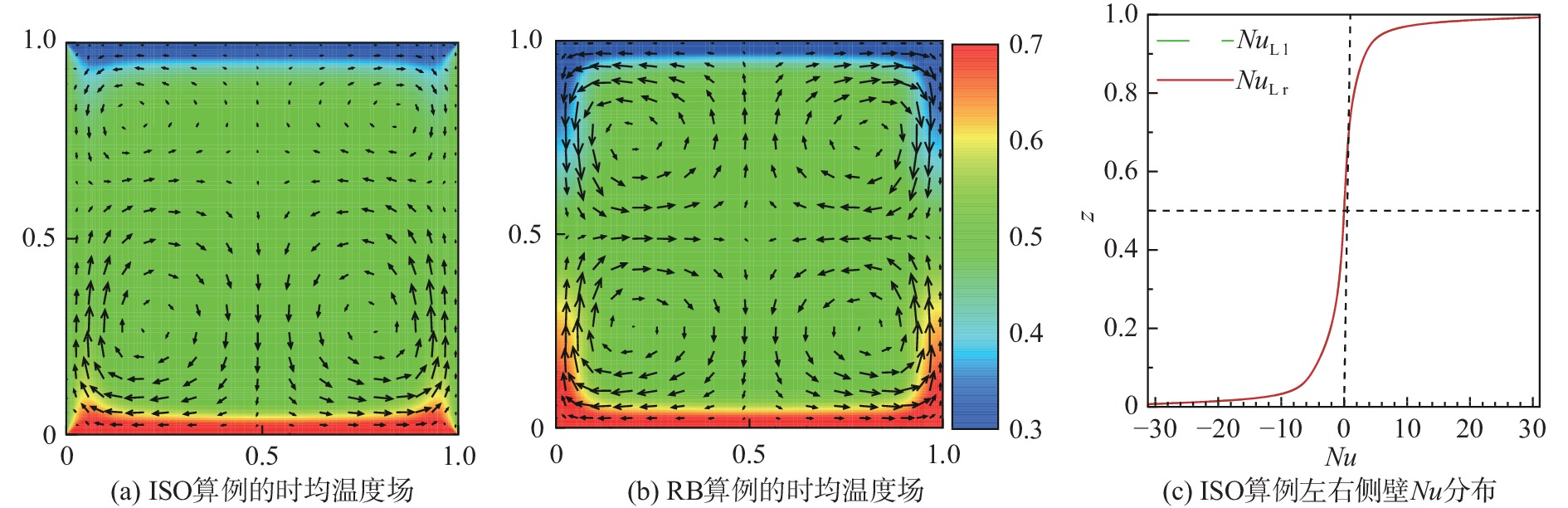
时间平均的流场可以反映系统的整体流动特性。为了探究图1中上下壁面时均Nu不相等的原因,在二维方腔中选取
图2给出了二维方腔中
|
图 2 二维数值模拟中 |
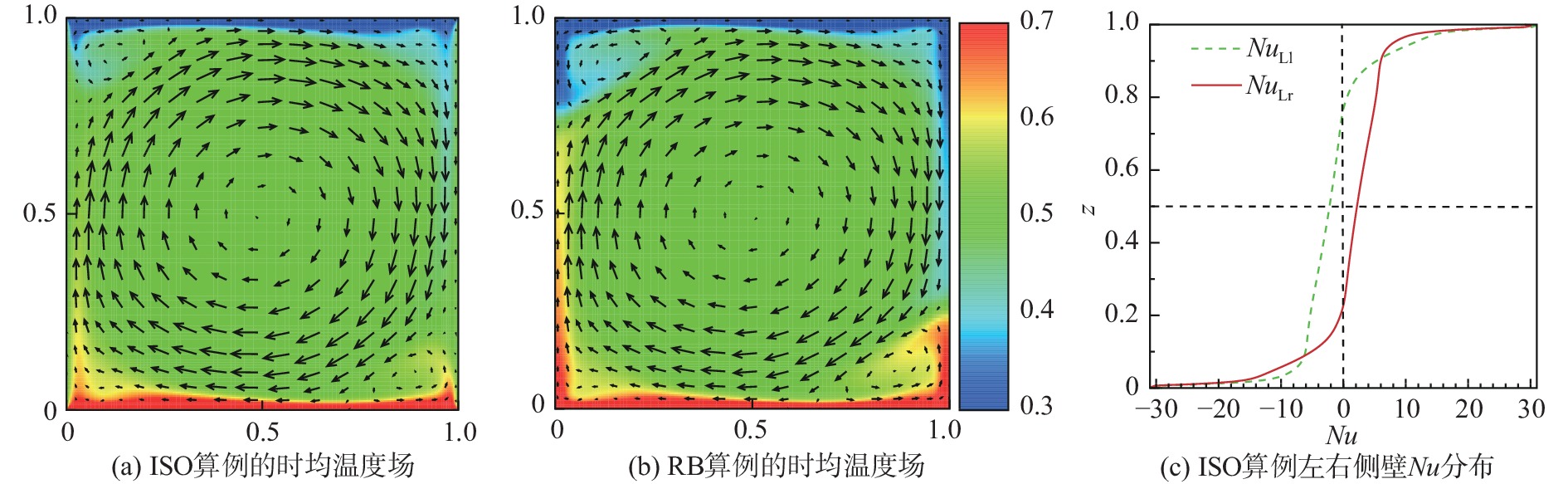
图3展示了
|
图 3 二维数值模拟中 |
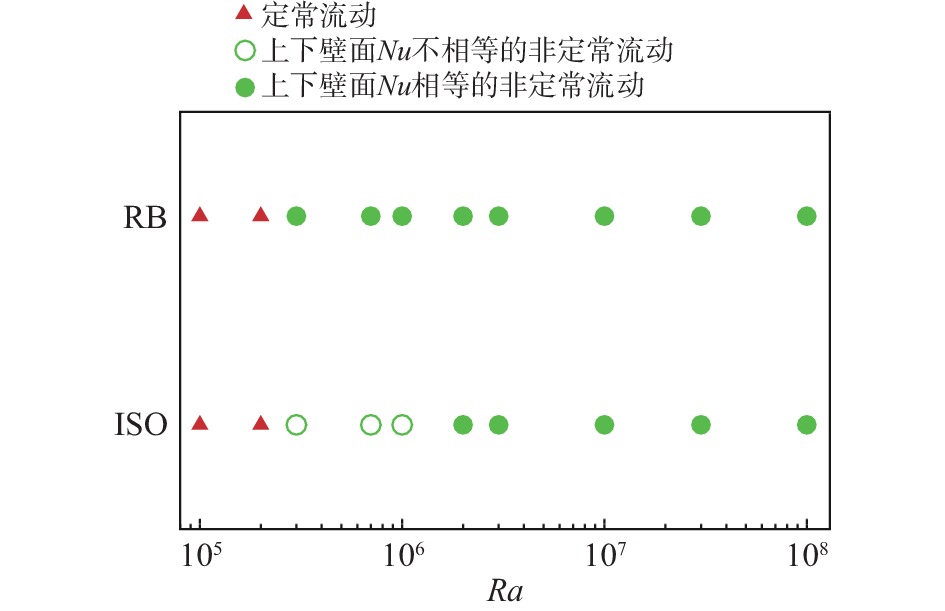
图4展示了三维RB算例和ISO算例在计算的Ra区间内定常、非定常的流动状态相图。可以发现上下壁面Nu的不相等情形主要发生在侧壁等温系统刚刚由定常转为非定常流动的区间内。
|
图 4 三维方腔内RB对流的流动状态相图 Fig.4 Phase diagram of flow states in three-dimensional RB convection |
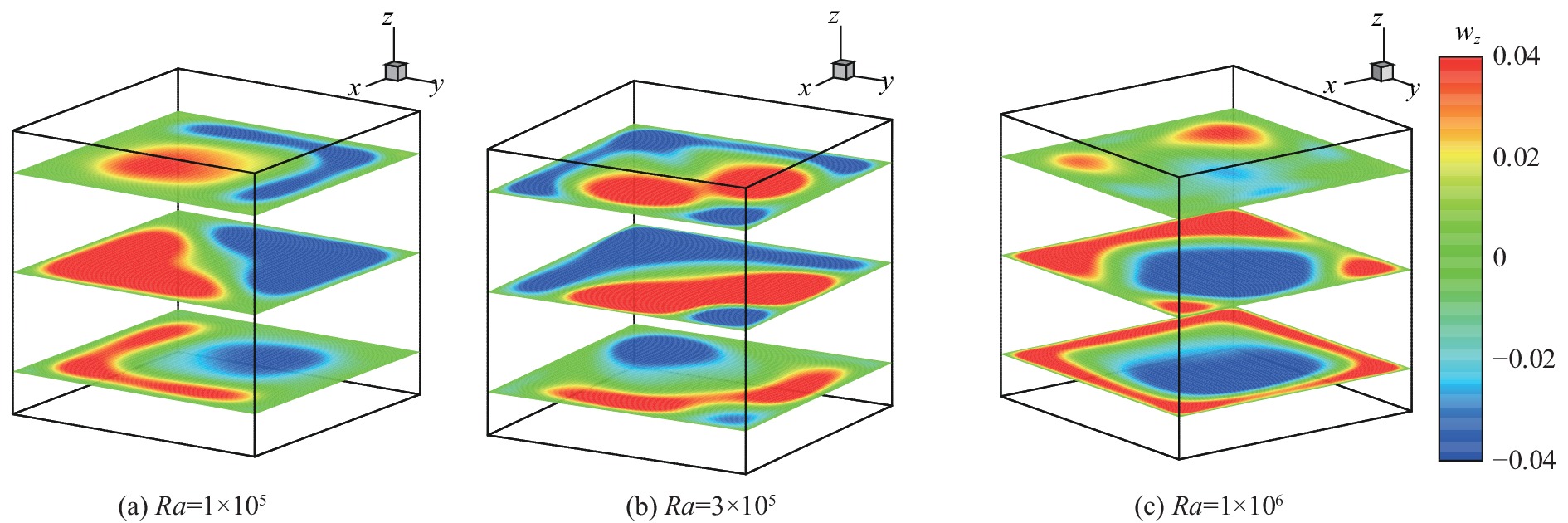
Pallares等[14]指出可以根据水平截面上竖直速度分布判断系统内的流动结构。图5是
|
图 5 侧壁等温边界条件的三维RB对流时均竖直方向速度场在水平截面高度为z = 0.15,z = 0.5和z = 0.85处的分布 Fig.5 Time-avraged vertical velocity for the three-dimensional RB convection with isothermal sidewalls at z = 0.15, 0.5, 0.85 |
雷诺数是热对流系统另一个重要的响应参数,可以用于刻画湍流的强度,其计算公式为:
| $ Re = \frac{\sqrt{{\left\langle \hat{\boldsymbol{u}}\cdot \hat{\boldsymbol{u}} \right\rangle } _{{\rm{V}},t}}\hat{H}}{\hat{\upsilon }} $ | (5) |
其中,
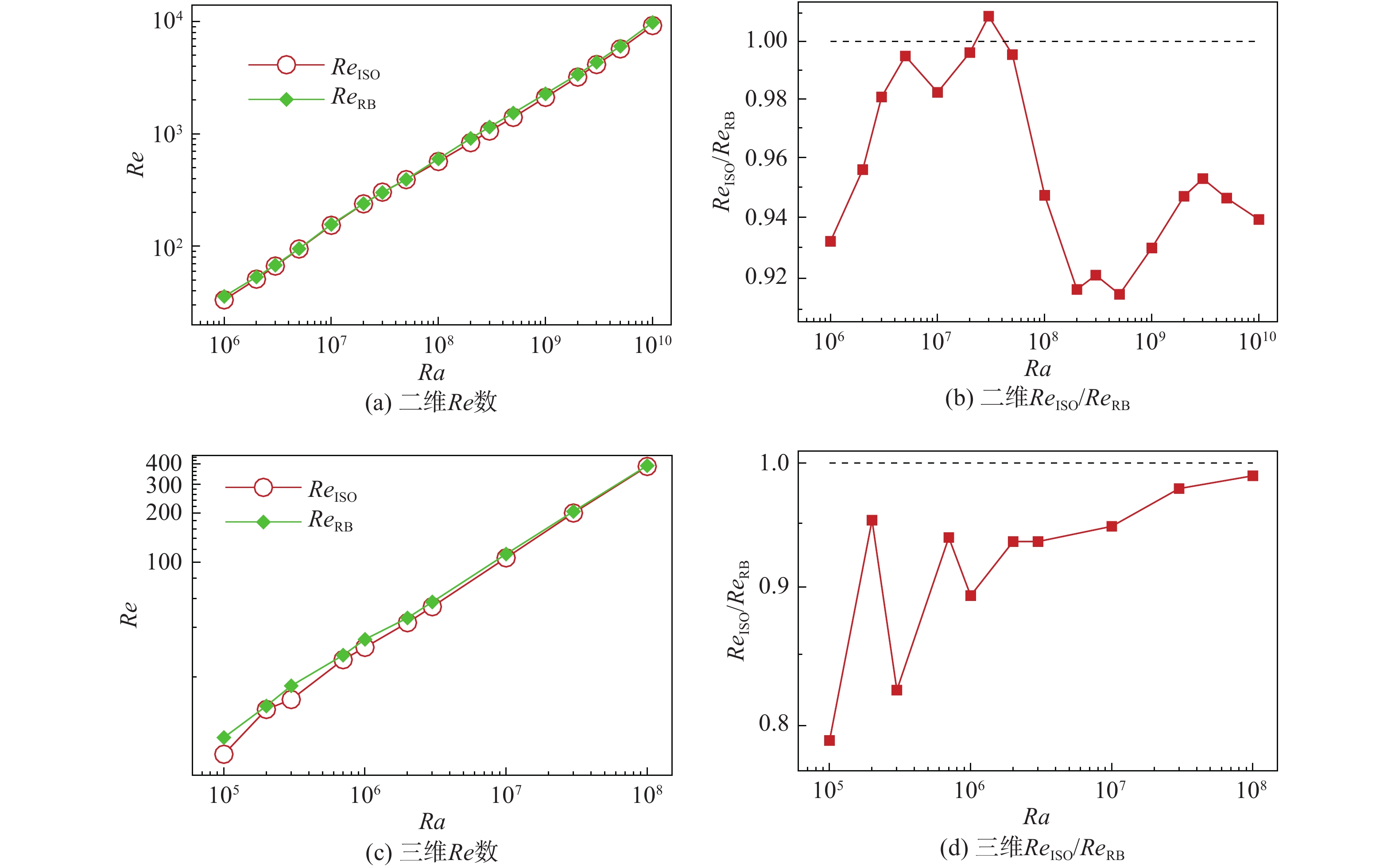
我们分别使用
|
图 6 Re和 |
本小节进一步讨论上下壁面Nu出现不相等时对应的瞬时流动状态。角动量的符号可以表征大尺度环流的瞬时流动方向,其计算公式为:
| $ L\left(t \right) = {\left\langle{-\left(z-1/2\right)v\left(\boldsymbol{x},t\right)+\left(y-1/2\right)w(\boldsymbol{x},{t})}\right\rangle}_{{\rm{V}}} $ | (6) |
其中
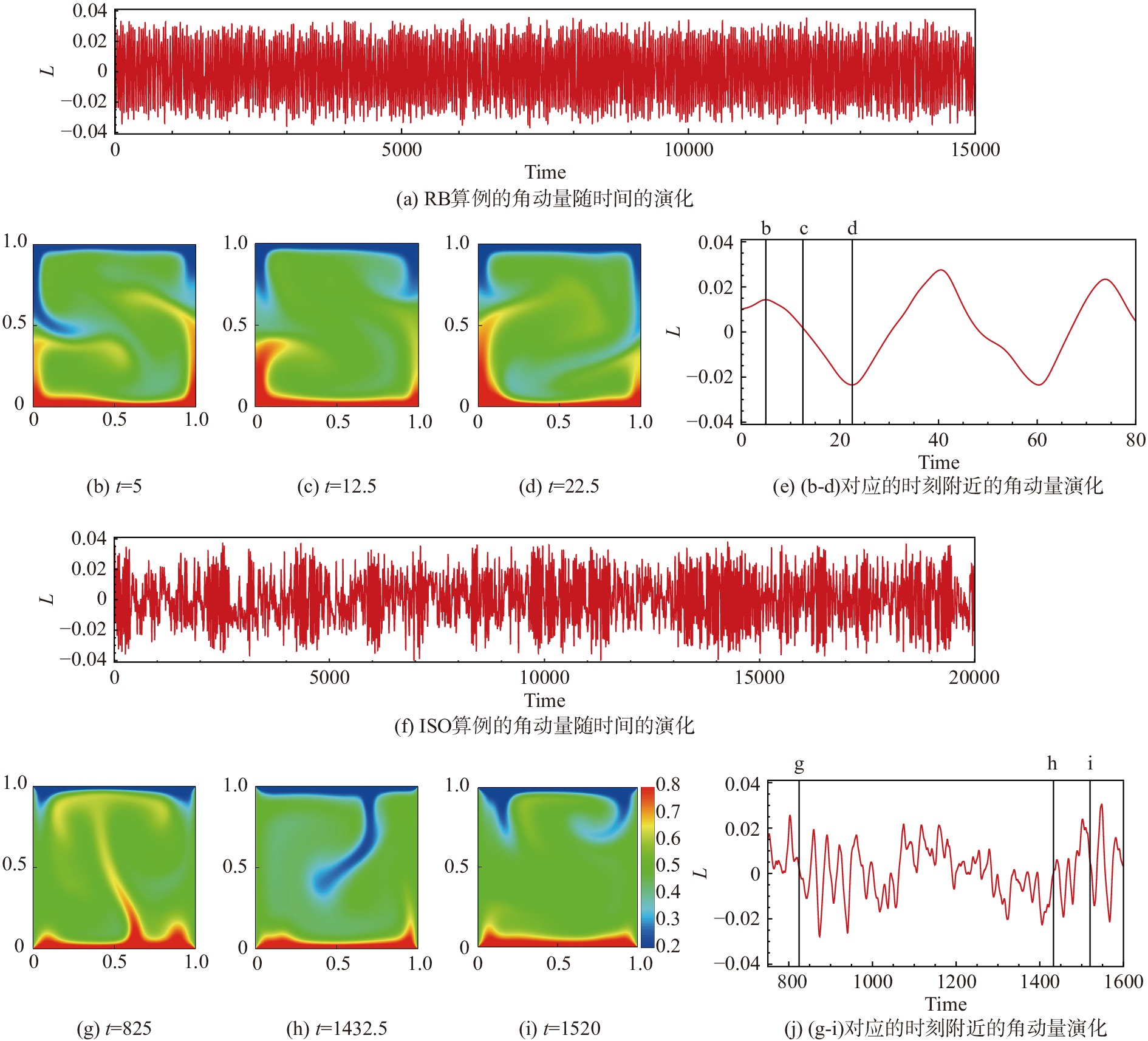
图7展示了
|
图 7 二维计算中 |
当系统处于大尺度热羽流占据中心区域并进行摆动的流动结构时,下壁面Nu小于上壁面Nu;当系统处于大尺度冷羽流占据中心区域并进行摆动的流动结构时,上壁面Nu小于下壁面Nu;当系统处于冷热羽流无序发射的流场结构时,上下壁面Nu几乎相等。由于三种流动结构持续的时间不同,导致了时均Nu和时均流场的不对称。而随着Ra的逐渐增加,系统流动加强,瞬时流场呈现出稳定的大涡结构,上述三种结构消失,此时上下壁面的Nu相等。
3 结 论本文结合二维和三维直接数值模拟方法研究了侧壁恒温且温度为上下壁面平均值的边界条件对RB对流的影响,并与传统的侧壁绝热条件下的RB对流进行了比较。宽高比
1)Ra较小时,在特定Ra区间内存在上下壁面Nu不相等的现象。该现象出现时,流场结构存在明显的上下不对称,导致侧壁的Nu之和并不为0,从而上下壁面的Nu不相等。随着Ra的增加,侧壁的Nu减小且可以忽略,此时上下壁面的Nu恢复成相等。
2)侧壁恒温时系统的传热效率要高于侧壁绝热情况,这是由于侧壁恒温条件下,一部分热量可以直接通过侧壁来传递,从而绕开温度边界层。
3)当采用恒温边界条件时,系统的Re要小于侧壁绝热条件下对应的Re,从而表明侧壁恒温边界条件会降低系统的流动强度。
| [1] |
SUGIYAMA K, NI R, STEVENS R J, et al. Flow reversals in thermally driven turbulence[J]. Physical Review Letters, 2010, 105(3): 034503. DOI:10.1103/physrevlett.105.034503 |
| [2] |
AHLERS G, GROSSMANN S, LOHSE D. Heat transfer and large scale dynamics in turbulent Rayleigh-Bénard convection[J]. Reviews of Modern Physics, 2009, 81(2): 503-537. DOI:10.1103/revmodphys.81.503 |
| [3] |
LOHSE D, XIA K Q. Small-scale properties of turbulent Rayleigh-Bénard convection[J]. Annual Review of Fluid Mechanics, 2010, 42(1): 335-364. DOI:10.1146/annurev.fluid.010908.165152 |
| [4] |
周全, 夏克青. Rayleigh-Bénard湍流热对流研究的进展、现状及展望[J]. 力学进展, 2012, 42(3): 231-251. ZHOU Q, XIA K Q. Advances and outlook in turbulent Rayleigh-Bénard convection[J]. Advances in Mechanics, 2012, 42(3): 231-251. DOI:10.6052/1000-0992-11-163 (in Chinese) |
| [5] |
VERZICCO R. Sidewall finite-conductivity effects in confined turbulent thermal convection[J]. Journal of Fluid Mechanics, 2002, 473: 201-210. DOI:10.1017/s0022112002002501 |
| [6] |
STEVENS R J A M, LOHSE D, VERZICCO R. Sidewall effects in Rayleigh–Bénard convection[J]. Journal of Fluid Mechanics, 2014, 741: 1-27. DOI:10.1017/jfm.2013.664 |
| [7] |
AHLERS G. Effect of sidewall conductance on heat-transport measurements for turbulent Rayleigh-Bénard convection[J]. Physical Review E, Statistical, Nonlinear, and Soft Matter Physics, 2001, 63(1 pt 2): 015303. DOI:10.1103/physreve.63.015303 |
| [8] |
ROCHE P E, CASTAING B, CHABAUD B, et al. Side wall effects in Rayleigh Bénard experiments[J]. The European Physical Journal B - Condensed Matter and Complex Systems, 2001, 24(3): 405-408. DOI:10.1007/s10051-001-8690-5 |
| [9] |
NIEMELA J J, SREENIVASAN K R. Confined turbulent convection[J]. Journal of Fluid Mechanics, 2003, 481: 355-384. DOI:10.1017/s0022112003004087 |
| [10] |
LEONG W H, HOLLANDS K G T, BRUNGER A P. On a physically-realizable benchmark problem in internal natural convection[J]. International Journal of Heat and Mass Transfer, 1998, 41(23): 3817-3828. DOI:10.1016/S0017-9310(98)00095-7 |
| [11] |
LEONG W H, HOLLANDS K G T, BRUNGER A P. Experimental Nusselt numbers for a cubical-cavity benchmark problem in natural convection[J]. International Journal of Heat and Mass Transfer, 1999, 42(11): 1979-1989. DOI:10.1016/S0017-9310(98)00299-3 |
| [12] |
SEZAI I, MOHAMAD A A. Natural convection in a rectangular cavity heated from below and cooled from top as well as the sides[J]. Physics of Fluids, 2000, 12(2): 432-443. DOI:10.1063/1.870321 |
| [13] |
CUESTA I, GRAU F X. Rayleigh-Bénard convection in a perfectly conducting cubical cavity at Pr = 0.7[C]//CHT'01-Advances in Comput-ational Heat Transfer II. Proceedings of a Second Symposium. Begel House Inc. , 2001.
|
| [14] |
PALLARES J, ARROYO M P, GRAU F X, et al. Experimental laminar Rayleigh-Bénard convection in a cubical cavity at moderate Rayleigh and Prandtl numbers[J]. Experiments in Fluids, 2001, 31(2): 208-218. DOI:10.1007/s003480100275 |
| [15] |
PALLARES J, CUESTA I, GRAU F X. Laminar and turbulent Rayleigh-Bénard convection in a perfectly conducting cubical cavity[J]. International Journal of Heat and Fluid Flow, 2002, 23(3): 346-358. DOI:10.1016/S0142-727X(02)00182-0 |
| [16] |
PEPPER D W, HOLLANDS K G T. Summary of benchmark numerical studies for 3-D natural convection in an air-filled enclosure[J]. Numerical Heat Transfer, Part A:Applications, 2002, 42(1-2): 1-11. DOI:10.1080/10407780290059396 |
| [17] |
PAUL M R, CHIAM K H, CROSS M C, et al. Pattern formation and dynamics in Rayleigh-Bénard convection: numerical simulations of experimentally realistic geometries[J]. Physica D:Nonlinear Phenomena, 2003, 184(1-4): 114-126. DOI:10.1016/S0167-2789(03)00216-1 |
| [18] |
PUIGJANER D, HERRERO J, SIMÓ C, et al. Bifurcation analysis of steady Rayleigh-Bénard convection in a cubical cavity with conducting sidewalls[J]. Journal of Fluid Mechanics, 2008, 598: 393-427. DOI:10.1017/s0022112007000080 |
| [19] |
BOROŃSKA K, TUCKERMAN L S. Extreme multiplicity in cylindrical Rayleigh-Bénard convection. I. Time dependence and oscillations[J]. Physical Review E, 2010, 81(3): 036320. DOI:10.1103/physreve.81.036320 |
| [20] |
HÉBERT F, HUFSCHMID R, SCHEEL J, et al. Onset of Rayleigh-Bénard convection in cylindrical containers[J]. Physical Review E, 2010, 81(4): 046318. DOI:10.1103/physreve.81.046318 |
| [21] |
HU Y P, LI Y R, LI M H, et al. Effects of enclosure geometry and thermal boundary condition on Rayleigh-Bénard convection of cold water near its maximum density[J]. International Journal of Thermal Sciences, 2017, 120: 220-232. DOI:10.1016/j.ijthermalsci.2017.06.013 |
| [22] |
YU J, GOLDFADEN A, FLAGSTAD M, et al. Onset of Rayleigh-Bénard convection for intermediate aspect ratio cylindrical containers[J]. Physics of Fluids, 2017, 29(2): 024107. DOI:10.1063/1.4976543 |
| [23] |
KOIZUMI H, HOSOKAWA I, ITO H. Effects of side-wall temperature on the flow pattern of Rayleigh-Bénard cells in an enclosure[J]. Heat Transfer - Japanese Research, 1998, 27(6): 462-471. DOI:10.1002/(sici)1520-6556(1998)27:6<462:aid-htj5>3.0.co;2-d |
| [24] |
KOIZUMI H. Effects of sidewall temperature on the flow pattern and the bifurcation to chaos of Rayleigh-Bénard cells in an enclosure (aspect ratio of enclosure: 6: 4: 1)[J]. JSME International Journal Series B, 2003, 46(3): 377-384. DOI:10.1299/jsmeb.46.377 |
| [25] |
CORCIONE M. Effects of the thermal boundary conditions at the sidewalls upon natural convection in rectangular enclosures heated from below and cooled from above[J]. International Journal of Thermal Sciences, 2003, 42(2): 199-208. DOI:10.1016/S1290-0729(02)00019-4 |
| [26] |
MOON J Y, CHUNG B J. Influence of Prandtl number, height and lateral cooling condition on laminar natural convection in a rectangular enclosure[J]. Heat and Mass Transfer, 2019, 55(6): 1593-1605. DOI:10.1007/s00231-018-02540-7 |
| [27] |
VASU U, TIWARI S, SAHU S. Effect of side wall conditions and aspect ratio on convective pattern formation in Rayleigh-Bénard convection[J]. International Journal of Thermal Sciences, 2019, 139: 246-268. DOI:10.1016/j.ijthermalsci.2019.01.031 |
| [28] |
ROCHE P E, CASTAING B, CHABAUD B, et al. Heat transfer in turbulent Rayleigh-Bénard convection below the ultimate regime[J]. Journal of Low Temperature Physics, 2004, 134(5-6): 1011-1042. DOI:10.1023/B:JOLT.0000016727.23228.78 |
| [29] |
MADANAN U, GOLDSTEIN R J. Effect of sidewall conductance on nusselt number for Rayleigh-Bénard convection: a semi-analytical and experimental correction[J]. Journal of Heat Transfer, 2019, 141(12). DOI:10.1115/1.4044659 |
| [30] |
IVANČIĆ A, OLIVA A, SEGARRA C D P, et al. Heat transfer simulation in vertical cylindrical enclosures for supercritical Rayleigh number and arbitrary side-wall conductivity[J]. International Journal of Heat and Mass Transfer, 1999, 42(2): 323-343. DOI:10.1016/S0017-9310(98)00113-6 |
| [31] |
STRINGANO G, VERZICCO R. Mean flow structure in thermal convection in a cylindrical cell of aspect ratio one half[J]. Journal of Fluid Mechanics, 2006, 548: 1. DOI:10.1017/s0022112005007378 |
| [32] |
URBAN P, HANZELKA P, MUSILOVÁ V, et al. Heat transfer in cryogenic helium gas by turbulent Rayleigh-Bénard convection in a cylindrical cell of aspect ratio 1[J]. New Journal of Physics, 2014, 16(5): 053042. DOI:10.1088/1367-2630/16/5/053042 |
| [33] |
XU M, PAUL M R. Chaotic Rayleigh-Bénard convection with finite sidewalls[J]. Physical Review E, 2018, 98(1-1): 012201. DOI:10.1103/PhysRevE.98.012201 |
| [34] |
DANILOV N I, MITIN K A, BERDNIKOV V S. Effect of conjugate heat transfer on the side and horizontal walls on the structure of convective flow in the Rayleigh-Bénard convection mode[J]. Journal of Physics:Conference Series, 2019, 1382(1): 012078. DOI:10.1088/1742-6596/1382/1/012078 |
| [35] |
MADANAN U, GOLDSTEIN R J. Thermal convection in horizontal rectangular enclosures at moderate Rayleigh numbers: Effect of sidewall conductance and aspect ratio[J]. International Journal of Heat and Mass Transfer, 2019, 136: 178-185. DOI:10.1016/j.ijheatmasstransfer.2019.02.076 |
| [36] |
WAN Z H, WEI P, VERZICCO R, et al. Effect of sidewall on heat transfer and flow structure in Rayleigh-Bénard convection[J]. Journal of Fluid Mechanics, 2019, 881: 218-243. DOI:10.1017/jfm.2019.770 |
| [37] |
PANDEY S, PARK Y G, HA M Y. An exhaustive review of studies on natural convection in enclosures with and without internal bodies of various shapes[J]. International Journal of Heat and Mass Transfer, 2019, 138: 762-795. DOI:10.1016/j.ijheatmasstransfer.2019.04.097 |
 2022, Vol. 40
2022, Vol. 40


