自20世纪60年代RBCC(Rocket-Based Combined-Cycle)发动机概念提出以来[1-2],有关其研究一直持续至今[3-8]。长期以来,美国一直主导着RBCC发动机的研究,早期研究瞄准单机入轨,先后提出ERJ[9]、SERJ[10]、A5[11]、Strutjet[12]、GTX[13]等氢燃料发动机方案。经过大量的发动机总体应用研究[14-25]后,发动机应用目标收敛为两级入轨之一级动力,并提出了ISTAR[26]煤油燃料发动机方案。除宽范围、多模态工作带来的发动机自身复杂性外,由于与飞行器总体气动/结构高度耦合,RBCC发动机研制面临很大的困难,虽然经过了五十多年的研究,RBCC发动机仍未实现工程应用。掌握飞行剖面内发动机特性,是发动机概念方案设计、总体应用论证、部件指标确定及控制规律制定的前提,因此,RBCC发动机特性分析一直是研究的重点之一。
Olds等[27-29]建立了RBCC发动机全模态性能准一维分析软件SCCREAM (Simulated Combined-Cycle Rocket Engine Analysis Module)。发动机前体考虑了斜激波/锥形激波与压缩效应,燃烧室采用响应面方法求解一维流动控制方程,燃烧过程视为化学平衡流处理,调用CEA程序计算燃气热力学参数,在引射掺混段、喷管、主火箭及冲压燃烧室引入效率系数模拟部件性能及损失。同时采用SCCREAM软件开展了氢/氧推进剂单级入轨飞行器概念方案设计[30],飞行器腹部半环形安装5台RBCC发动机,飞行器长54.56 m(179 in)、宽29.87 m(98 in)、高9.75 m(32 in),低轨有效载荷9.07 t(20000 lb),吸气式模态最高飞行马赫数10。Mckamey等[31]开发了EPSURBCC软件,采用干扰系数法求解一维连续方程、动量方程、能量方程,获得发动机推力、比冲。EPSURBCC软件仅支持H2燃料,未考虑黏性影响及部件损失,燃烧过程视为化学平衡流处理,考虑了多组分变比热影响。
国内,黄生洪等[32]建立了RBCC发动机准一维性能预估模型,燃烧采用一维模型,采用变步长半隐式多步Runge-Kuta方法求解考虑化学反应源项的一维流动方程组,化学反应源项采用基于阿累尼乌斯定律的有限化学反应速率求解,燃烧计算过程中采用掺混效率近似替代燃烧效率。引射段采用控制体法,通过引入掺混效率,求解出口参数。并对模型发动机零速引射状态进行了性能预测,给出了气流参数沿发动机轴向的变化曲线及发动机推力。
吕翔等[33-34]发展了RBCC发动机准一维性能分析方法,采用理想气体假设,考虑了前体边界层厚度对进气道流量系数的影响,通过斜激波关系式完成进气道参数计算。燃烧室采用一维模型,用MacCormack格式求解带有化学反应源项的一维流动方程组,化学反应源项采用有限速率模型计算,并采用最小吉布斯自由能方法,进一步改进了一次火箭燃烧室热力计算模型。完成了Hyperion计划RBCC发动机性能预测,并将比冲预测结果与SCCREAM软件计算结果进行了对比。
王洪信[35]采用准一维方法进行发动机性能计算,对进气道、混合段、燃烧室分别建模,通过迭代计算确保相邻部件交接面参数匹配。进气道采用激波关系式处理,混合段采用等静压模型假设,未给出燃烧室计算模型,采用理想气体假设,未考虑换热、摩擦影响。完成了模型发动机高度、速度特性计算,并将计算结果与SCCREAM软件计算结果进行了对比。
安佳宁[36]建立了RBCC发动机引射模态性能计算准一维模型。进气道总压恢复系数采用飞行马赫数单变量多项式估算,主火箭和补燃室热力计算采用化学平衡假设,并采用引射器理论,建立了等截面混合及等压混合两种构型计算模型。
此外,叶中元[37]采用一维方法,理论分析了发动机特征截面参数变化及推力比冲性能,提出了发动机设计需遵循的一些基本原则。黄伟等[38]针对概念模型发动机,通过求解理想气体总静参数关系式及状态方程,研究了气流总温及发动机出口截面直径变化对发动机推力、比冲的影响。张蒙正等[39-40]通过对发动机火箭引射模态、火箭/亚燃冲压模态、火箭/超燃冲压模态及纯火箭模态的高度及速度特性分析,指出了各模态存在的主要问题,给出了发动机应用模式的相关建议。路媛媛等[41]通过求解理想气体准一维流动控制方程,讨论了火箭推力室喷管内存在正激波的条件,并分析了正激波的存在对发动机推力、比冲性能的影响。刘昊[42]基于数值仿真结果,理论分析了RBCC发动机火箭推力增益产生的原因,并指出火箭推力增益由引射推力增益、补燃推力增益及火箭推力损失三部分组成。
从上述文献调研情况来看,近三十多年来,国内外学者对RBCC发动机性能及其分析方法持续给予关注。现有发动机性能分析模型均基于一维流动方程建立,虽然也有学者考虑了化学动力学[32-33]及化学平衡流动[27-29, 32, 34, 36]的影响,但像进气道流量系数、进气道总压恢复系数、燃烧效率、燃烧室总压恢复系数等影响发动机性能的部件关键特性均采用效率系数假设,甚至不予考虑,因此造成所发展的性能分析方法计算结果差异较大,精度难以确认。
因此,本文基于进气道风洞试验、燃烧室直连试验及发动机自由射流试验数据,结合数值仿真及理论分析,建立了发动机关键部件特性数学模型,并编写了RBCC发动机一体化性能计算代码,完成了飞行马赫数Ma0 = 0~8范围内发动机特性仿真,定量分析了不同因素对发动机特性的影响,给出的研究结论可以作为RBCC发动机总体应用论证、概念方案设计、部件参数选取及控制规律制定的参考。
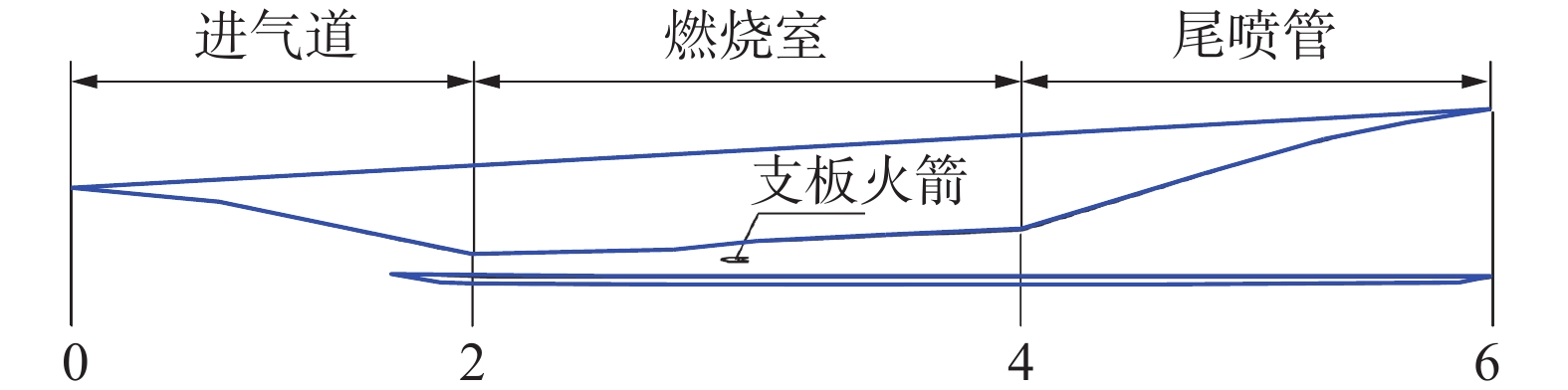
1 数学模型及验证本文采用文献[42]中的模型RBCC发动机方案,其结构示意及特征截面定义见图1。发动机由二元多楔进气道、二元单侧扩张燃烧室、支板火箭及尾喷管组成,火箭推力室采用中心支板布局方式。图1中截面0为自由来流,截面2为进气道出口(燃烧室入口),截面4为燃烧室出口(尾喷管入口),截面6为尾喷管出口。发动机进气道捕获面积A0 =1 m2,进气道、燃烧室、尾喷管根据具体工作条件均可进行调节。
|
图 1 发动机构型及截面定义 Fig.1 Schematic of the engine configuration and cross section definition |
发动机设计工作范围Ma0 = 0~8,具体工作方式为:
1)Ma0<2时,来流条件不满足冲压模态工作条件,火箭推力室最大工况工作,此时进气道出口气流为亚声速,通过火箭高能燃气的引射作用从进气道引入空气,与火箭推力室燃气掺混、燃烧,燃气通过喷管膨胀加速,产生推力,此时发动机工作模态定义为火箭引射模态。
2)2≤Ma≤6时,火箭推力室工作,发动机以大推力状态加速爬升,进气道出口气流为超声速,进气道捕获空气与燃烧室内注入燃料燃烧,并与火箭高能燃气掺混,燃气通过喷管膨胀加速,产生推力,此时发动机工作模态定义为火箭冲压模态。
3)Ma0>6时,当飞行器巡航时,火箭推力室不工作,进气道捕获空气与燃烧室内注入燃料燃烧,燃气通过喷管膨胀加速,产生推力,此时发动机工作模态定义为冲压模态;当飞行器需要爬升或机动飞行时,火箭推力室起动,并通过推力室工况与冲压燃烧室余气系数调节,满足飞行器推力需求。
1.1 进气道计算模型采用USSA-1976大气模型[43]及文献[44]给出的热完全气体计算模型完成自由流(截面0)参数计算。根据进气道风洞试验数据,完成进气道总压恢复系数
| $ {\sigma _2} = {a_0} + {a_1}\;M{a_0} + {a_2}\; \alpha + {a_3}\;M{a_0}^2 + {a_4}\;M{a_0}\;\alpha + {a_5}\;{\alpha ^2} $ | (1) |
| $ {\varphi _s} = {b_0} + {b_1} \; M{a_0} + {b_2} \; \alpha + {b_3} \; M{a_0}^2 + {b_4} \; M{a_0} \; \alpha + {b_5} \; {\alpha ^2} $ | (2) |
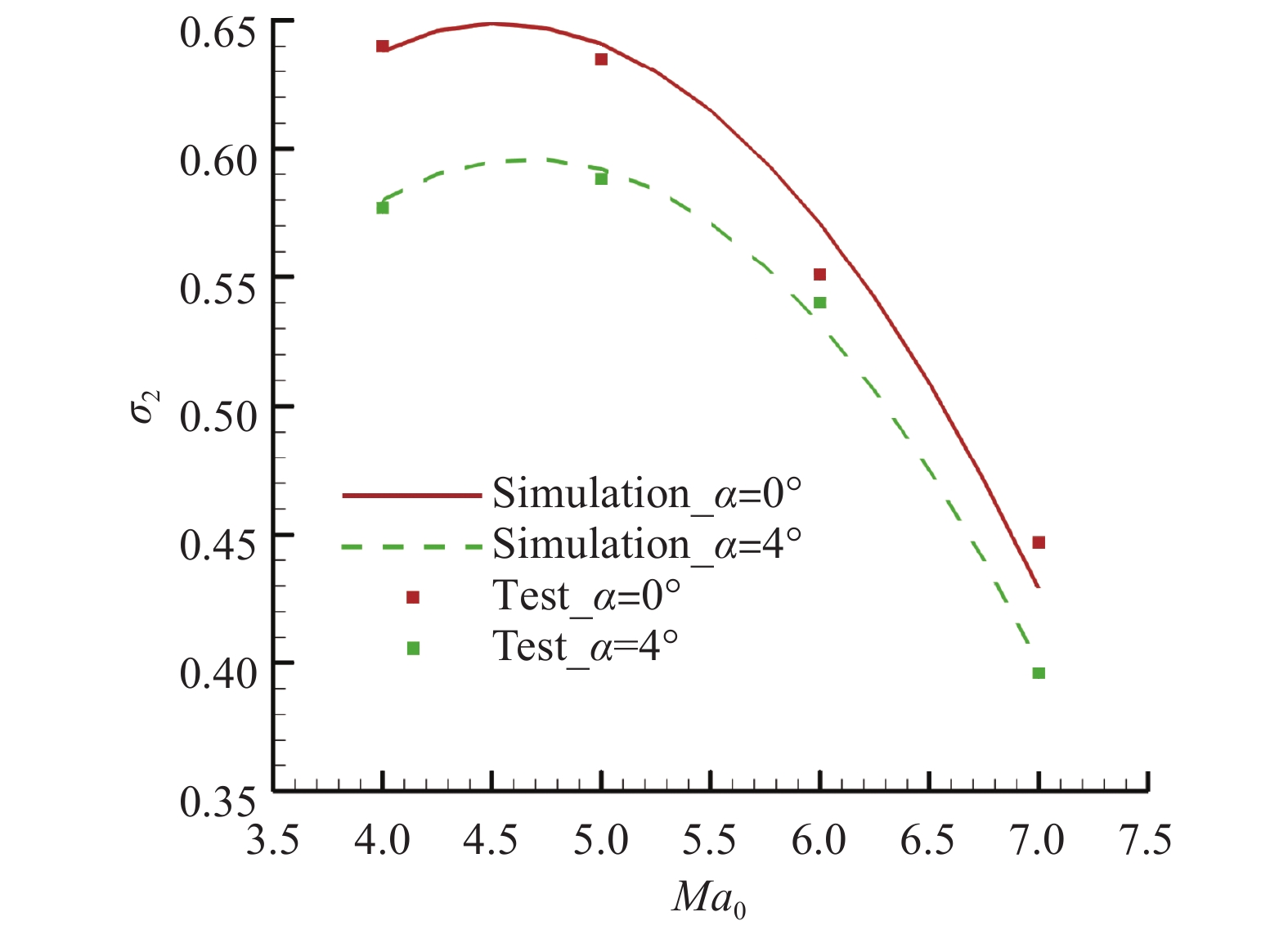
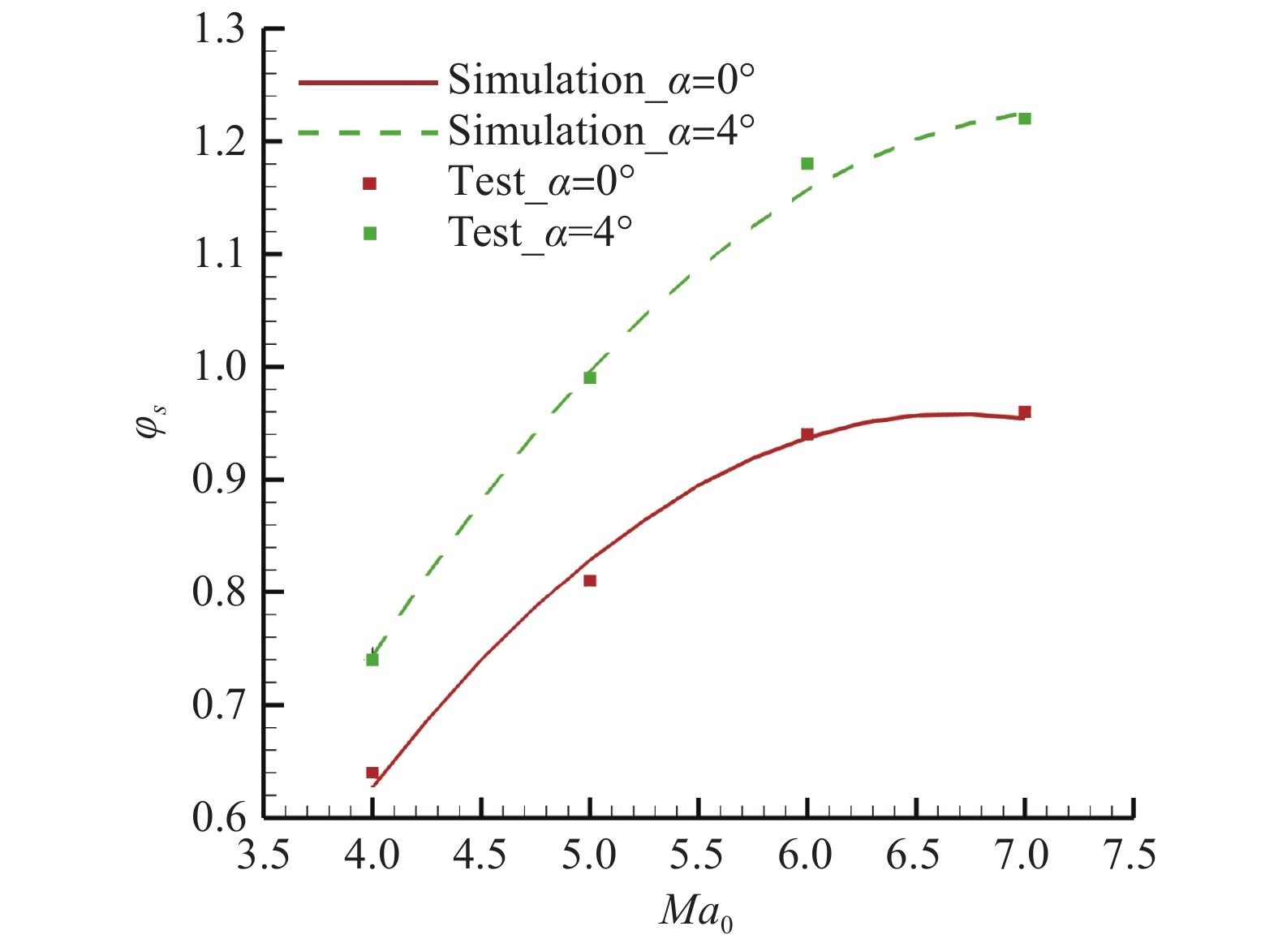
图2、图3分别给出了进气道总压恢复系数
|
图 2 进气道总压恢复系数计算与试验结果对比 Fig.2 Comparison of total pressure recovery coefficients of the air inlet between simulation and test data |
|
图 3 进气道流量系数计算与试验结果对比 Fig.3 Comparison of mass flux coefficients of the air inlet between simulation and test data |
采用控制体法进行进气道出口参数计算。具体计算过程如下:
1)根据飞行高度H,参考文献[43]中给定的大气模型,完成大气参数静温T0、静压P0、密度ρ0计算;
2)根据求出的大气参数及飞行马赫数Ma0,参考文献[44]给出的热完全气体计算模型,完成截面0滞止参数总温Tt0、总压Pt0及速度V0计算;
3)通过式(1)计算获得进气道总压恢复系数
4)冲压及火箭冲压模态下,通过式(2)计算进气道流量系数
| $ {\dot m_0} = {\varphi _s}{A_0}{\rho _0}{V_0} $ | (3) |
| $ {\dot m_0} = n {\dot m_{{\rm{rocket}}}} $ | (4) |
式(4)中
| $ n = {c_{{\rm{ej}}}} P_{t2} $ | (5) |
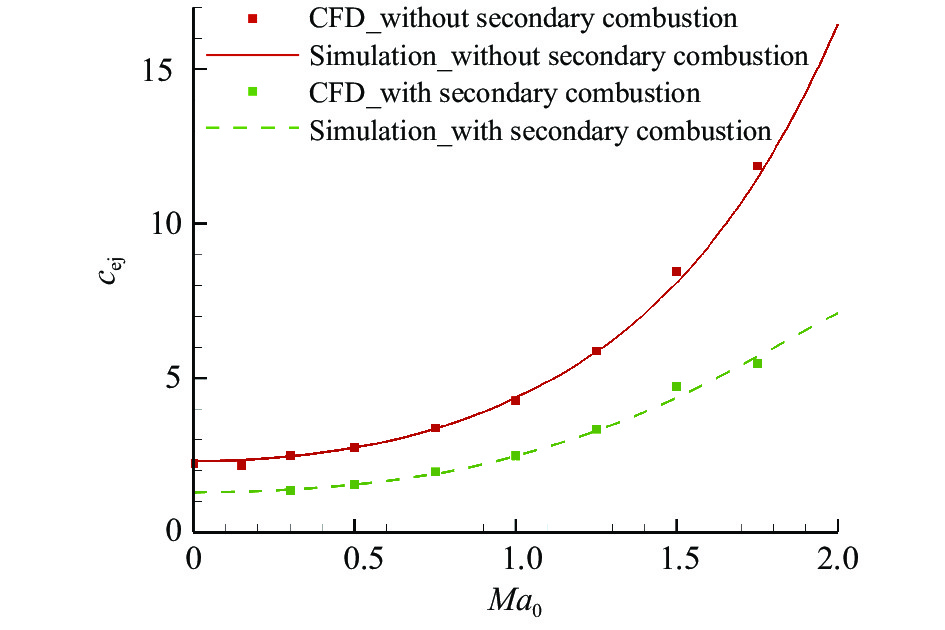
式(5)中常系数cej与发动机具体构型、火箭布局方式、火箭工作参数及是否补燃相关。图4给出了飞行高度H = 0 km时,采用式(5)计算结果与CFD仿真结果对比。图4中红色曲线及数据点为不考虑火箭富燃燃气二次燃烧时引射系数的计算结果,绿色曲线及数据点为火箭富燃燃气进行二次燃烧时引射系数的计算结果。从图4中可以看出,无论考虑火箭富燃燃气二次燃烧与否,计算模型误差均在5%以内。
|
图 4 引射系数计算与CFD结果对比 Fig.4 Comparison of injection coefficients between simulation and CFD data |
5)采用式
6)根据空气流量
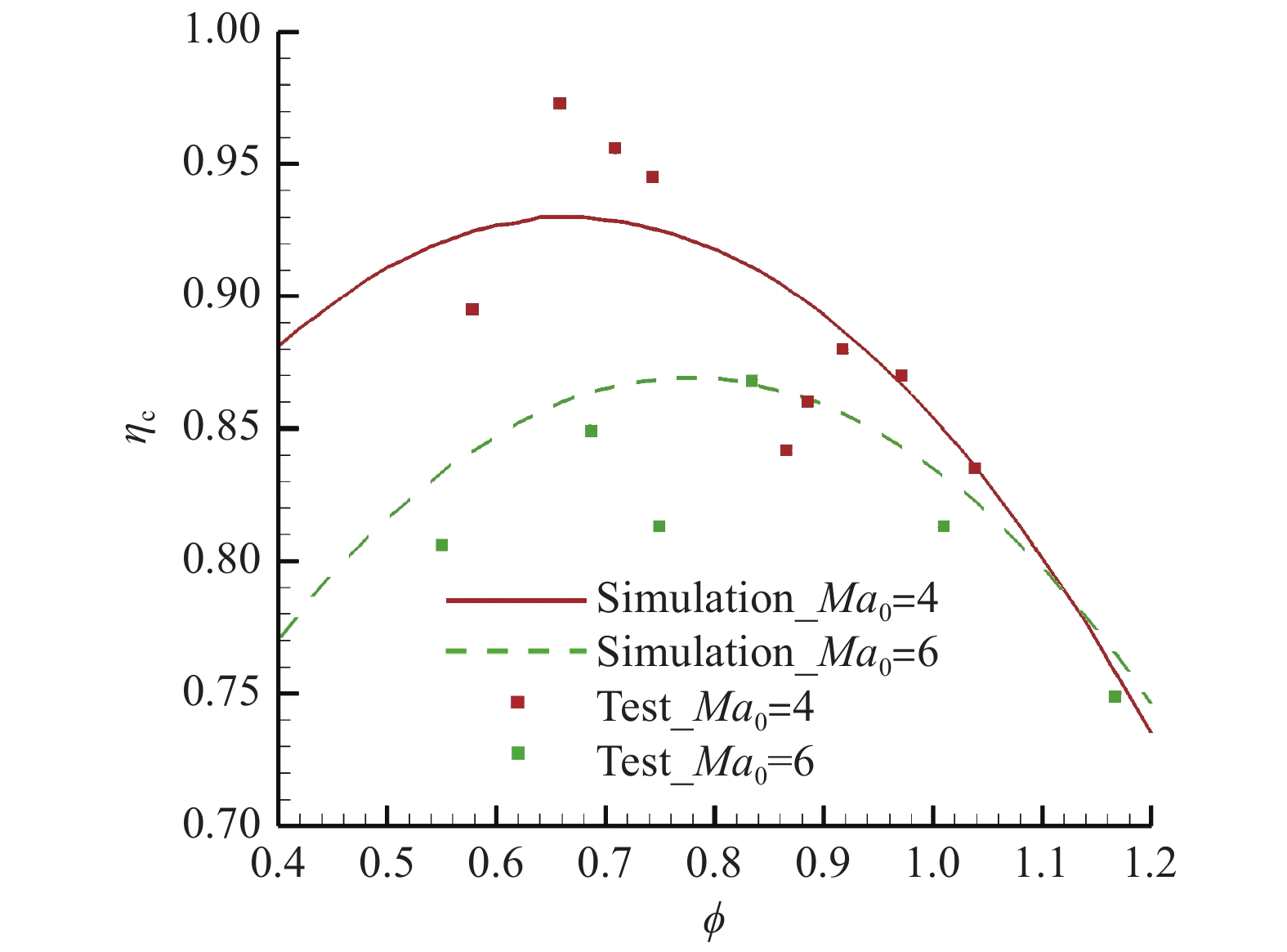
根据燃烧室直连试验数据,完成燃烧效率
| $ {\eta _c} = {c_0} + {c_1} \; M{a_0} + {c_2} \; \phi + {c_3} \; M{a_0}^2 + {c_4} \; M{a_0} \; \phi + {c_5} \; {\phi ^2} $ | (6) |
| $ \;\;\;{\sigma _4} = {d_0} + {d_1} \; M{a_0} + {d_2} \; \phi + {d_3} \; M{a_0}^2 + {d_4} \; M{a_0} \; \phi + {d_5}\;{\phi ^2} $ | (7) |
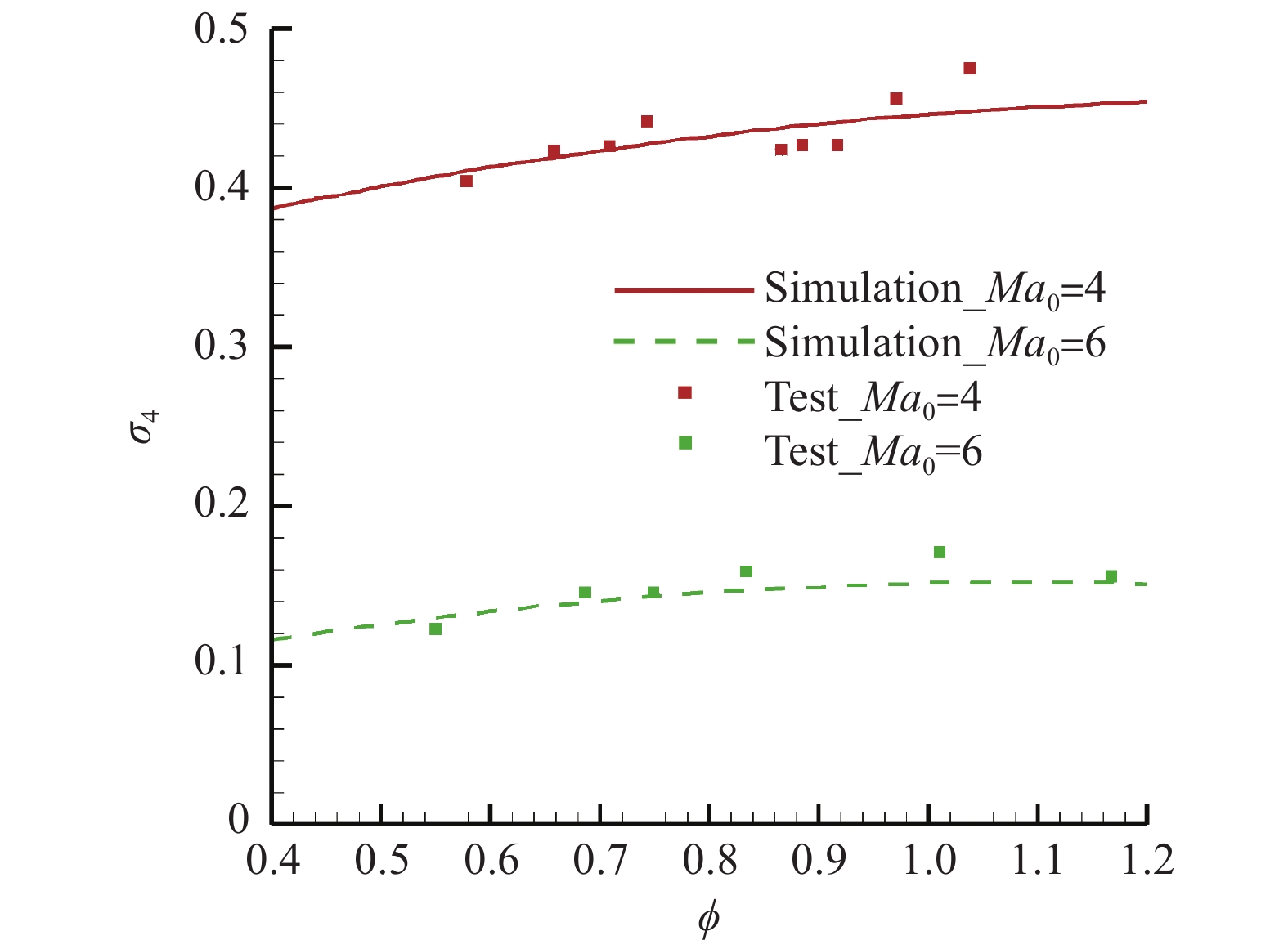
图5、图6分别给出了燃烧效率
|
图 5 燃烧效率计算与试验结果对比 Fig.5 Comparison of combustion coefficients between simulation and test data |
采用控制体法完成燃烧室出口截面参数计算。冲压模态,截面4参数具体计算过程如下:
1)根据式(6)计算燃烧效率
| $ T_{t4} = \left [T_{t2} + (T_{t{\rm{{,ide}}}} - T_{t2}) {\eta _c}\right](1 - {T_{\rm{{loss\_eff\_combustor}}}}) $ | (8) |
2)根据式(7)计算燃烧室总压恢复系数
|
图 6 燃烧室总压恢复系数计算与试验结果对比 Fig.6 Comparison of total pressure recovery coefficients of the combustor between simulation and test data |
3)采用式
4)根据燃气流量
火箭引射及火箭冲压模态,截面4参数具体计算过程如下:
1)采用上文给出的冲压模态燃烧室出口参数计算方法,完成只考虑空气与燃料燃烧时截面4燃气流量
2)采用式
3)采用式(9)~式(12)计算截面4出口燃气总温Tt4。式中,通用气体常数R= 8.314 J/(mol·K);
| $ {\gamma }_{4}=\frac{({\dot{m}}_4'{\gamma }_4'+{\dot{m}}_{{\rm{rocket}}}{\gamma }_{\rm{{rocket}}})}{{\dot{m}}_{4}} $ | (9) |
| $ {M_4} = \dfrac{{\dot m_4' + {{\dot m}_{{\rm{rocket}}}}}}{{\dfrac{{\dot m_4'}}{{M_4'}} + \dfrac{{{{\dot m}_{{\rm{rocket}}}}}}{{{M_{{\rm{rocket}}}}}}}} $ | (10) |
| $ c_{p4} = \frac{{{\gamma _4}}}{{{\gamma _4} - 1}} \cdot \frac{R}{{{M_4}}} $ | (11) |
| $ T_{t4} = \dfrac{{c_{p4}'T_{t4}' + \dfrac{{{{\dot m}_{{\rm{rocket}}}}}}{{\dot m_4'}}c_{p{\rm{{,rocket}}}}T_{t{{\rm{,rocket}}}}}}{{\dfrac{{{{\dot m}_4}}}{{\dot m_4'}}c_{p4}}} $ | (12) |
4)采用式(13)计算截面4出口总压Pt4。基于试验数据分析,式(13)中采用了冲压模态与火箭冲压模态燃烧室出口马赫数相似假设。
| $ P_{t4}=P_{t4}^{'} \dfrac{{\dot{m}}_{4}}{{\dot{m}}_{4}^{'}}\sqrt{\dfrac{T_{t4}}{T_{t4}^{'}}}\text{}\dfrac{\sqrt{\dfrac{{\gamma }_{4}^{'}{M}_{4}^{'}}{R}{\Bigg(\dfrac{2}{{\gamma }_{4}^{'}+1}\Bigg)}^{\frac{{\gamma }_{4}^{'}+1}{{\gamma }_{4}^{'}-1}}}}{\sqrt{\dfrac{{\gamma }_{4}{M}_{4}}{R}{\Bigg(\dfrac{2}{{\gamma }_{4}+1}\Bigg)}^{\frac{{\gamma }_{4}+1}{{\gamma }_{4}-1}}}} $ | (13) |
5)根据燃气流量
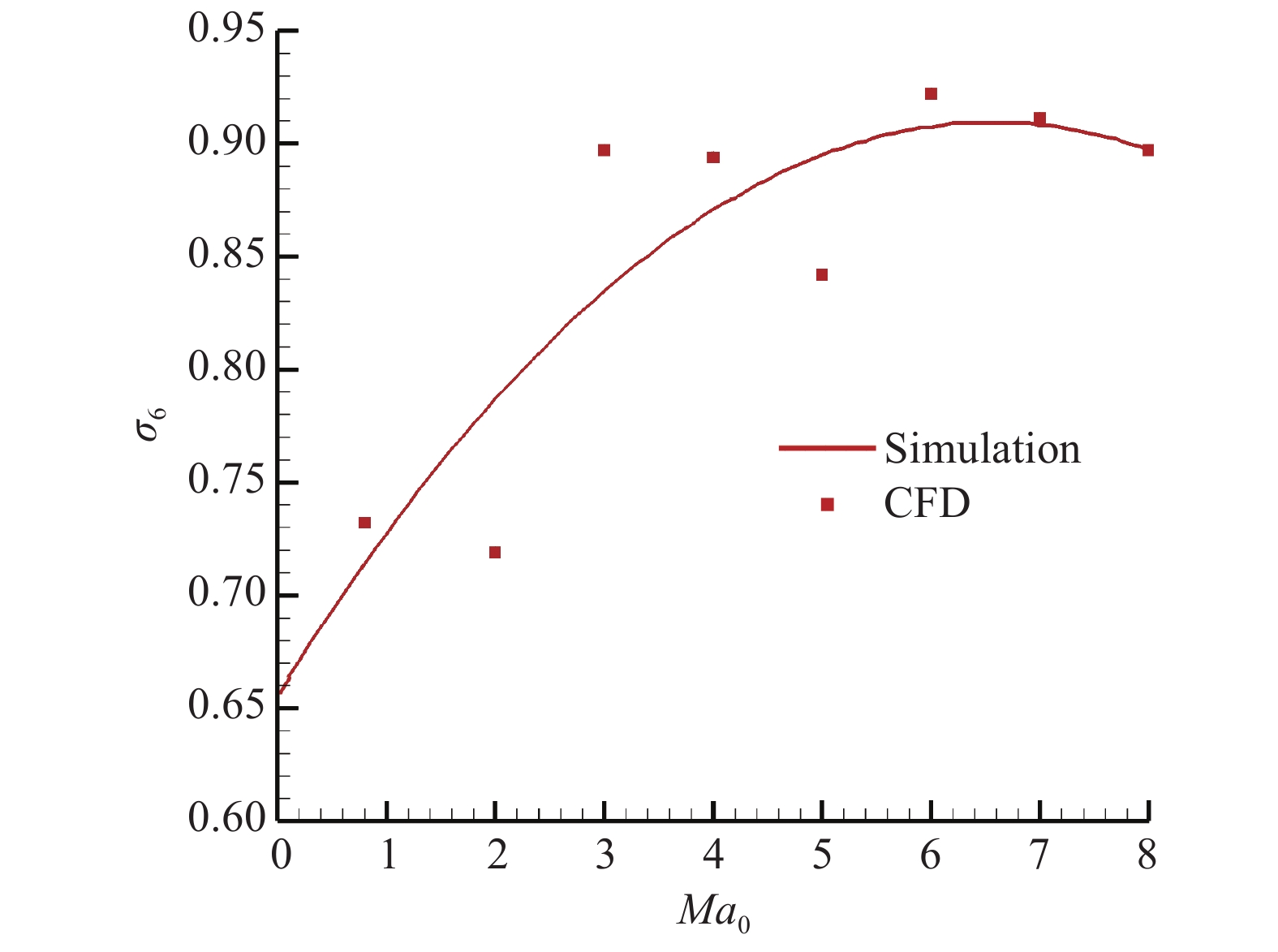
根据尾喷管流场CFD仿真结果,完成尾喷管总压恢复系数
| $ {\sigma _6} = {e_0} + {e_1} M{a_0} + {e_2} M{a_0}^2 $ | (14) |
图7给出了尾喷管总压恢复系数
|
图 7 尾喷管总压恢复系数计算与CFD结果对比 Fig.7 Comparison of total pressure recovery coefficients of the nozzle between simulation and CFD data |
采用控制体法完成尾喷管出口参数计算。具体计算过程如下:
1)采用式
2)通过式(14)计算获得尾喷管总压恢复系数
3)根据燃气流量
上文通过对进气道、燃烧室、尾喷管分别采用控制体法,基于试验及CFD仿真数据,建立了部件性能计算模型,并给出发动机特征截面参数计算方法。在完成发动机特征截面参数计算后,采用式(15)、式(16)计算,获得发动机推力F、比冲Isp。
| $ F = ({\dot m_6}{V_6} - {\dot m_0}{V_0}) + ({P_6} - {P_0}){A_6} $ | (15) |
| $ I_{{\rm{sp}}} = \frac{F}{{({{\dot m}_6} - {{\dot m}_0})}} $ | (16) |
采用本文建立的发动机性能分析方法,对文献[8]中给出的发动机构型进行了计算,并将计算结果与发动机自由射流试验结果进行对比。图8、图9分别给出了Ma0 = 4及Ma0 = 6工况下计算结果与试验结果的对比,可以看出,与试验结果相比,冲压模态及火箭冲压模态下的发动机推力、比冲计算误差均在10%以内。

|
图 8 Ma0= 4工况计算与自由射流试验结果对比 Fig.8 Comparison between simulation and test data at Ma0= 4 |
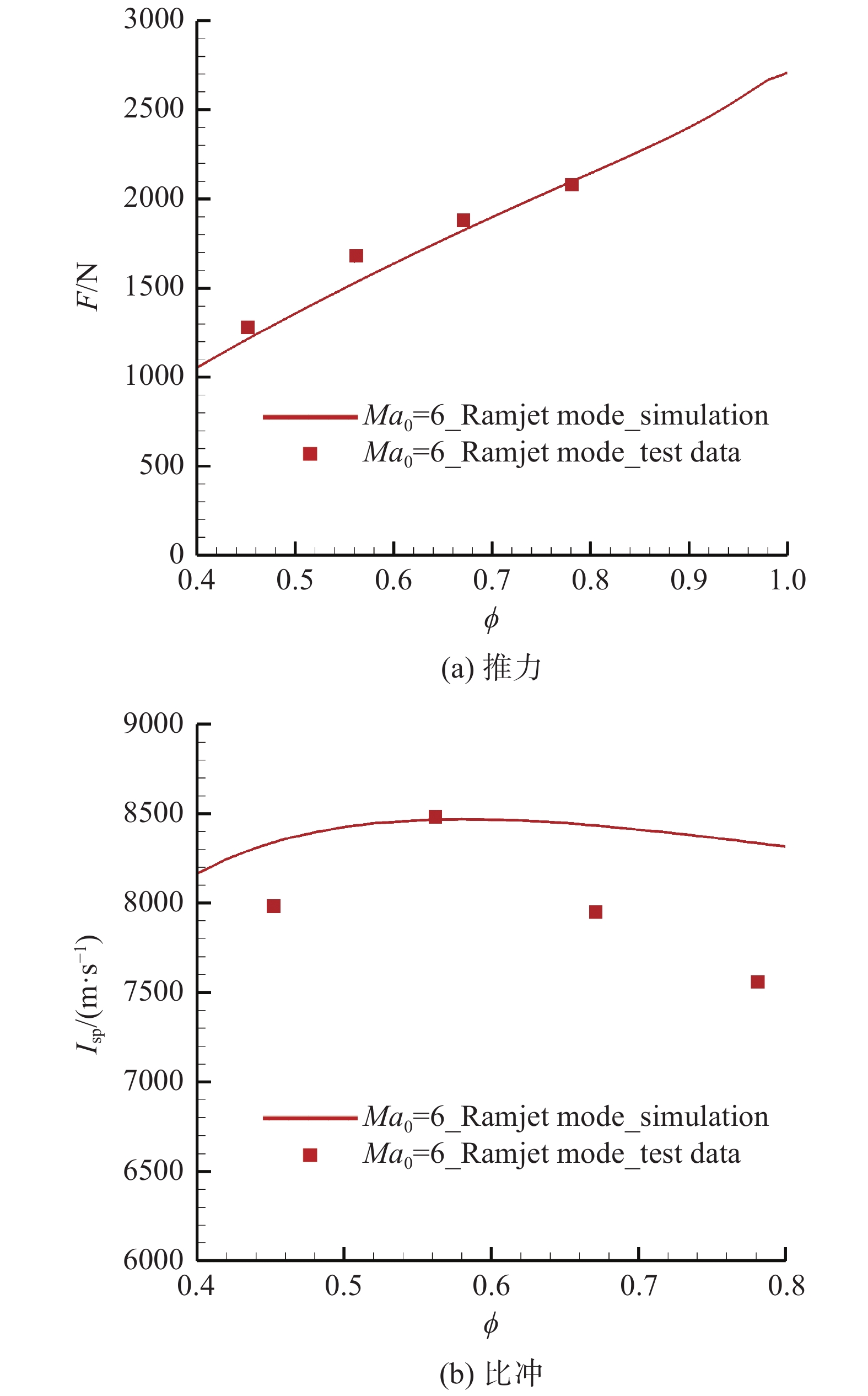
|
图 9 Ma0 |
为便于发动机结构描述及计算结果分析,定义发动机结构特征参数如下:
1)进气道收缩比Cr = A0/A2,即进气道捕获面积与进气道出口面积之比,Cr能够宏观反映进气道对来流空气的压缩程度。
2)燃烧室扩张比Dr = A4/A2,即燃烧室出口面积与燃烧室入口面积之比,Dr能够宏观反映燃烧室许用释热量及通流能力。
3)尾喷管扩张比Er = A6/A4,即尾喷管出口面积与尾喷管入口面积之比,Er能够宏观反映燃气加速膨胀程度。
4)发动机总面积比Ar = A6/A0,即尾喷管出口面积与进气道捕获面积之比,Ar能够宏观反映发动机可用性能水平。
针对图1给出的发动机构型,根据具体工作状态对进气道收缩比Cr、燃烧室扩张比Dr、尾喷管扩张比Er进行调节,使发动机达到给定状态下最高推力、比冲性能。
3 发动机特性分析发动机、火箭推力室燃料为煤油,火箭氧化剂为液氧。火箭额定流量10 kg/s、额定室压10 MPa、混合比3.4。进行了Ma0 = 0~8范围内火箭引射模态、冲压模态及火箭冲压模态的发动机速度-攻角、速度-节流、速度-高度、速度-火箭节流特性计算。
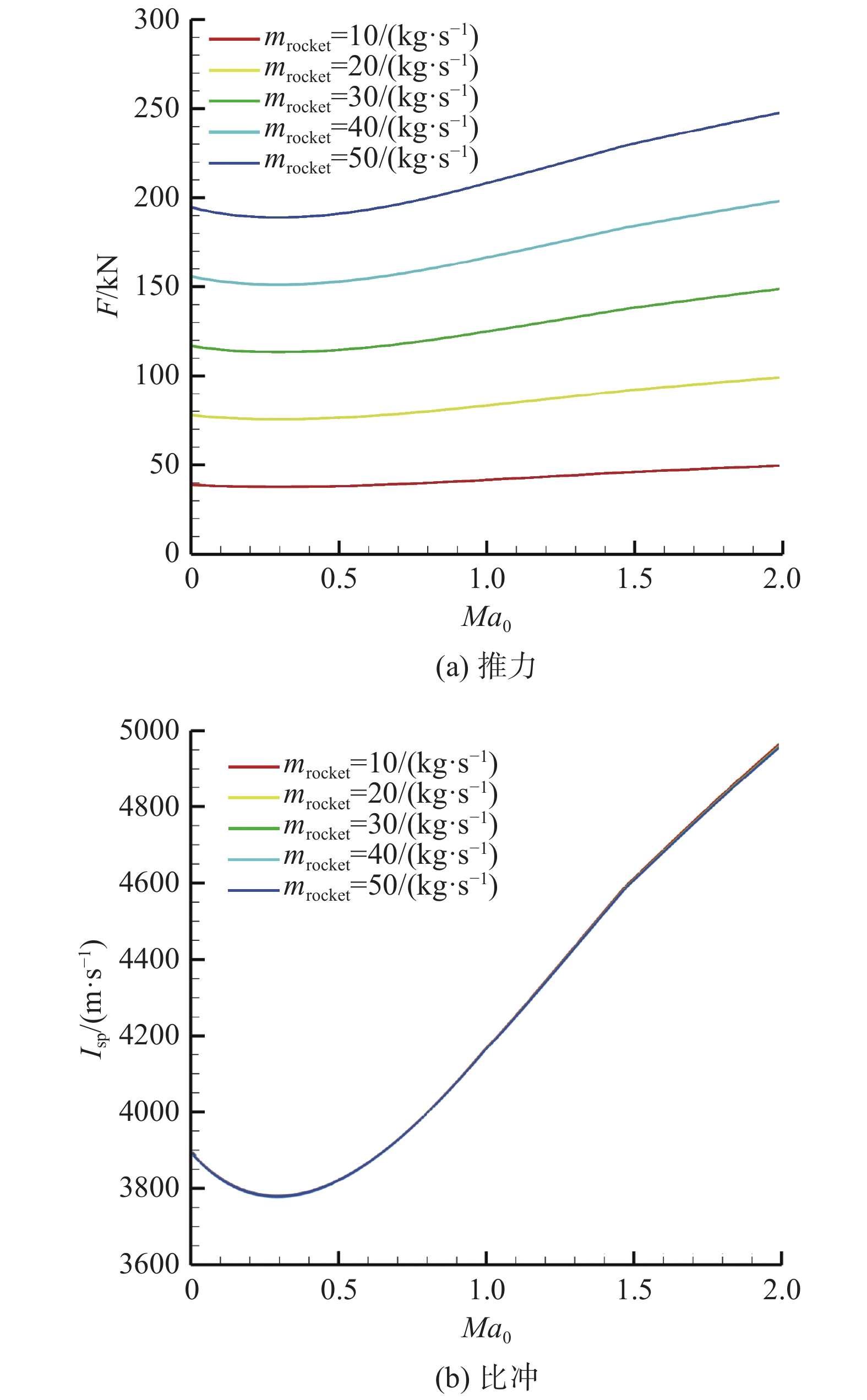
3.1 火箭引射模态工作特性假设发动机火箭引射模态从Ma0 = 0、H = 0 km弹道点开始工作,按照H = 6.27Ma0弹道爬升至Ma0 = 2、H = 12.54 km弹道点(动压Q = 50 kPa)。发动机不供油,保持飞行攻角α = 0°不变,完成不同火箭流量下发动机性能计算,获得发动机速度-火箭节流特性。图10给出了飞行马赫数Ma0 = 0~2、发动机火箭引射模态工作、火箭流量
|
图 10 火箭引射模态发动机速度-火箭节流特性 Fig.10 Velocity and rocket throttle characteristic at the ejector operation mode |
飞行马赫数给定时,火箭引射系数不变,被引射空气流量随着火箭流量的增加而增加,因此发动机推力随着火箭流量的增加而增加;当火箭流量增加时,由于发动机为完全可调结构,尾喷管出口气流均能够实现完全膨胀,因此尾喷管出口速度保持不变,进而发动机比冲保持不变。如图10所示,相同飞行马赫数下,随着火箭流量的增加,发动机推力线性增加,而发动机比冲保持不变。
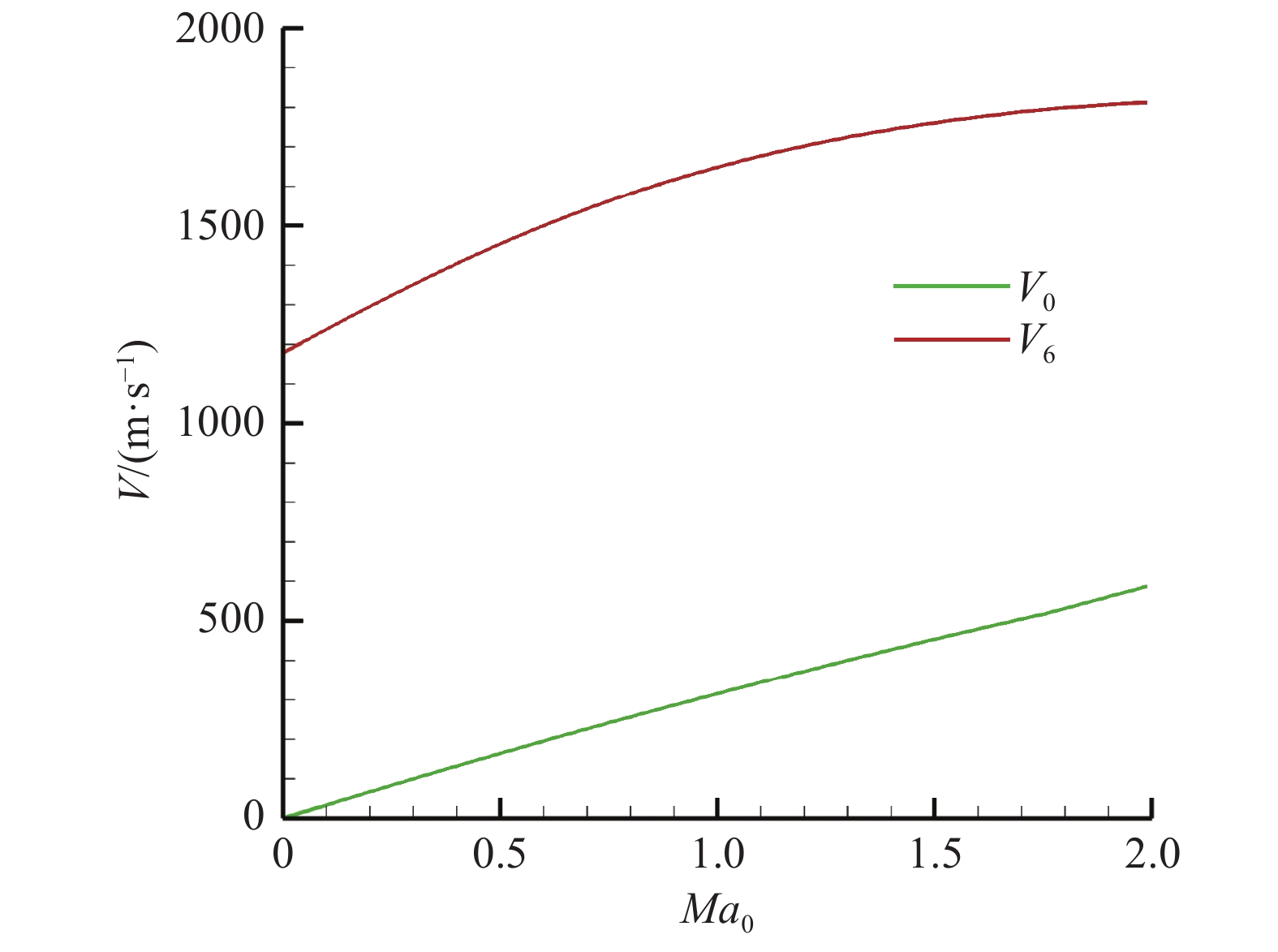
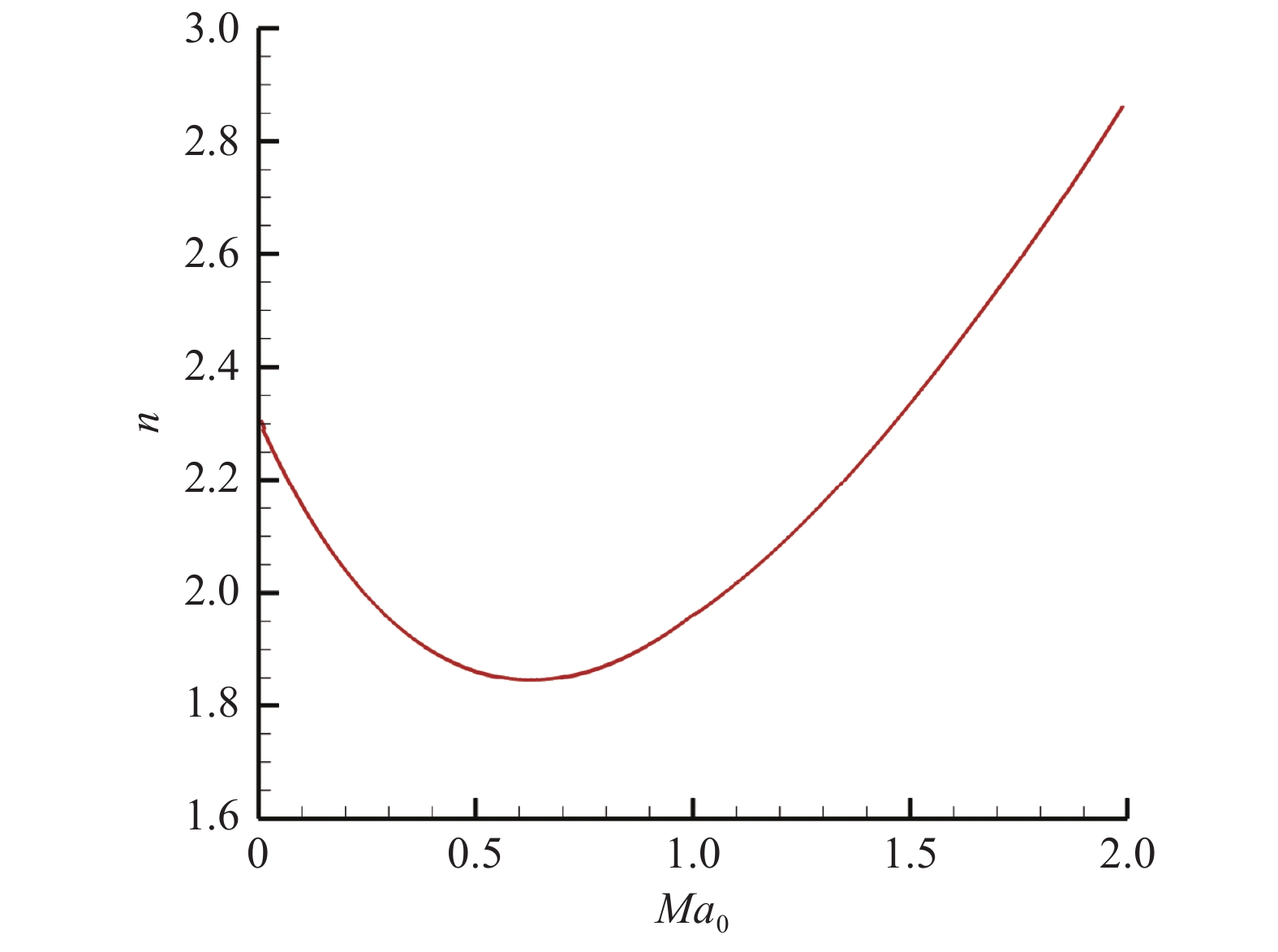
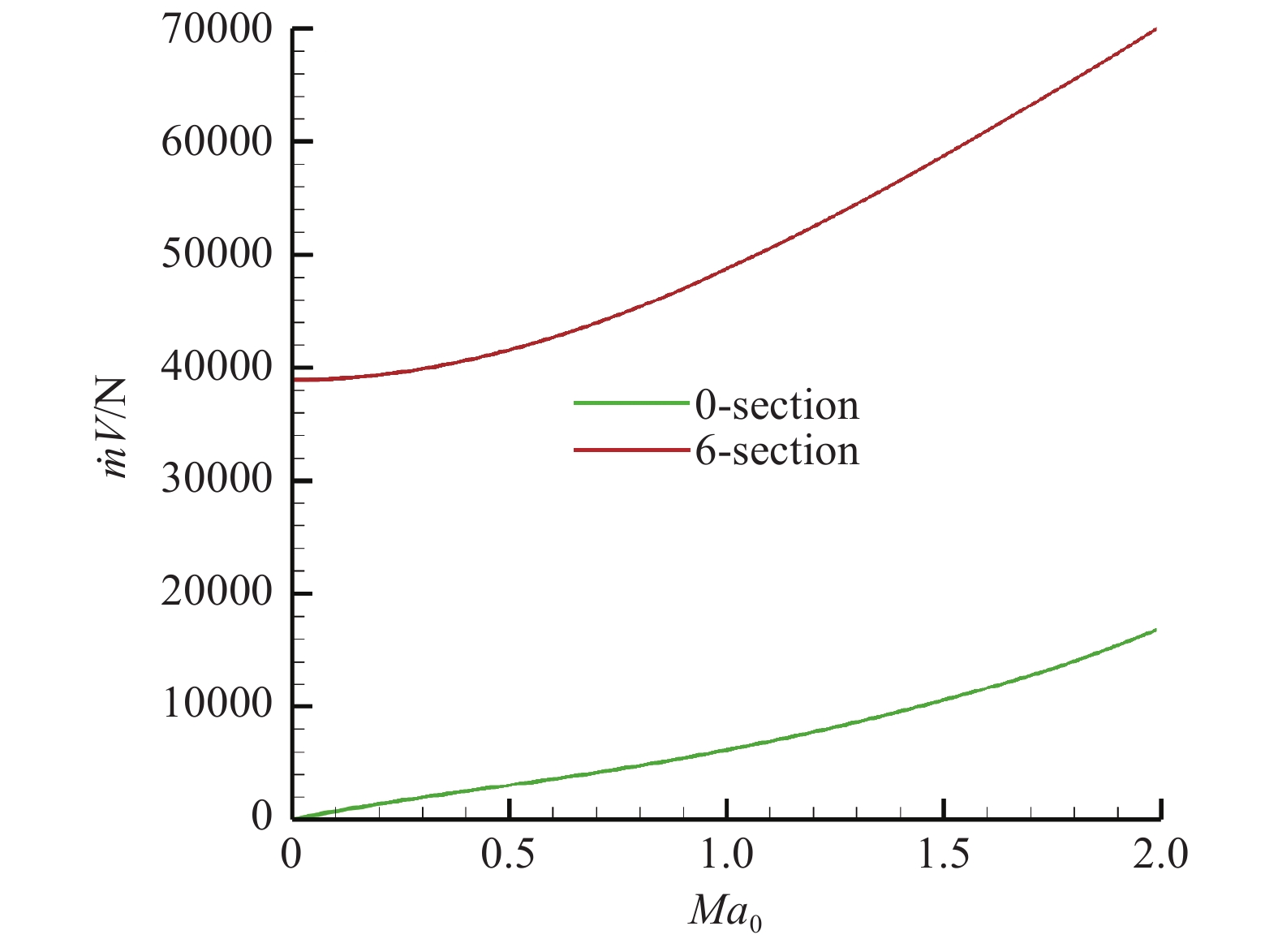
图11、图12、图13分别给出了火箭流量
|
图 11 发动机进出口速度随飞行马赫数变化 Fig.11 Variation of velocities at the engine inlet and outlet with the flight Mack number |
|
图 12 引射系数随飞行马赫数变化 Fig.12 Variation of the injection coefficient with the flight Mach number |
|
图 13 发动机进出口动量随飞行马赫数变化 Fig.13 Variation of momentum at the engine inlet and outlet with the flight Mach number |
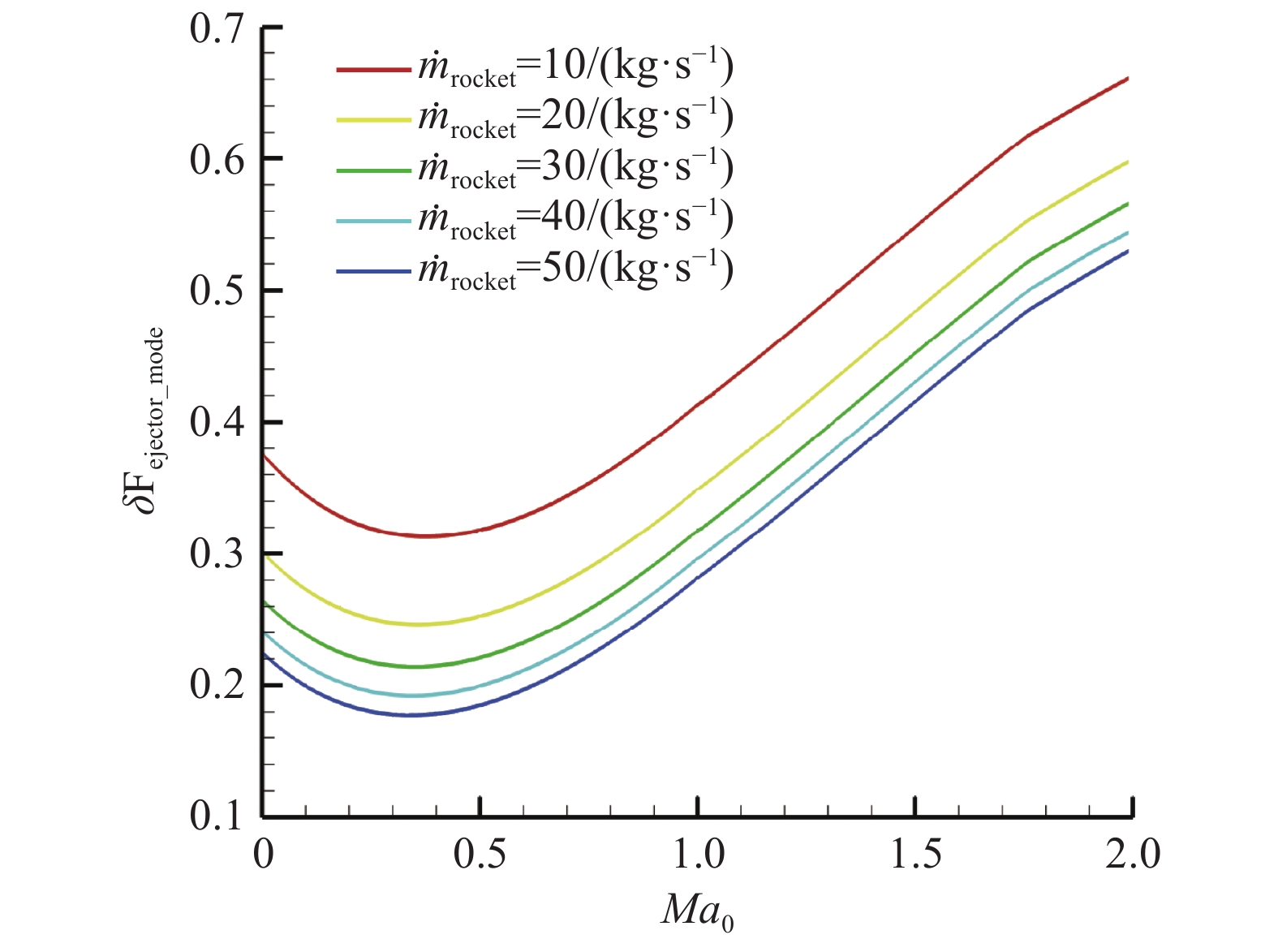
图14给出了火箭引射模态不同火箭流量下火箭推力增益ΔFejector_mode随飞行马赫数变化曲线。火箭引射模态火箭推力增益定义见式(17)。
| $ \Delta {F_{{\rm{ejetor\_mode}}}} = \frac{{F - {F_{{\rm{rocket}}}}}}{{{F_{{\rm{rocket}}}}}} $ | (17) |
式(17)中F为火箭引射模态发动机推力,Frocket为火箭燃气完全膨胀至对应飞行高度大气环境压力所产生的推力。Frocket计算中取火箭燃气总温Tt,rocket = 3 532.41K、比热比γrocket = 1.103、分子量Mrocket = 27.36 g/mol,并假设火箭推力室室压Pt,rocket子与火箭流量成正比例关系。
|
图 14 火箭引射模态火箭推力增益随飞行马赫数变化 Fig.14 Variation of the thrust gain with the flight Mach number at the ejector operation mode |
从图14中可以看出,保持火箭流量不变时,与发动机推力、比冲变化趋势相同,随着飞行马赫数的增加,火箭推力增益ΔFejector_mode先下降后增加;保持飞行马赫数不变时,随着火箭流量的增加,火箭推力增益ΔFejector_mode单调下降。
表1给出了火箭引射模态典型状态下的火箭推力增益,其中Mamin为给定火箭流量条件下火箭推力增益达到最小值时对应的飞行马赫数;ΔF/ΔMa为整个火箭引射模态工作范围(Ma0 = 0~2)内,ΔFejector_mode变化值与Ma0变化值的比值,其具体含义为飞行马赫数每增加1,火箭推力增益的变化量。从表1可以看出,火箭引射模态下,虽然火箭流量的变化对火箭推力增益影响较大,但整体而言,飞行马赫数每增加1,火箭推力增益增加约15%。
| 表 1 火箭引射模态典型点推力增益 Table 1 Thrust gain at typical conditions of the ejector operation mode |
|
|
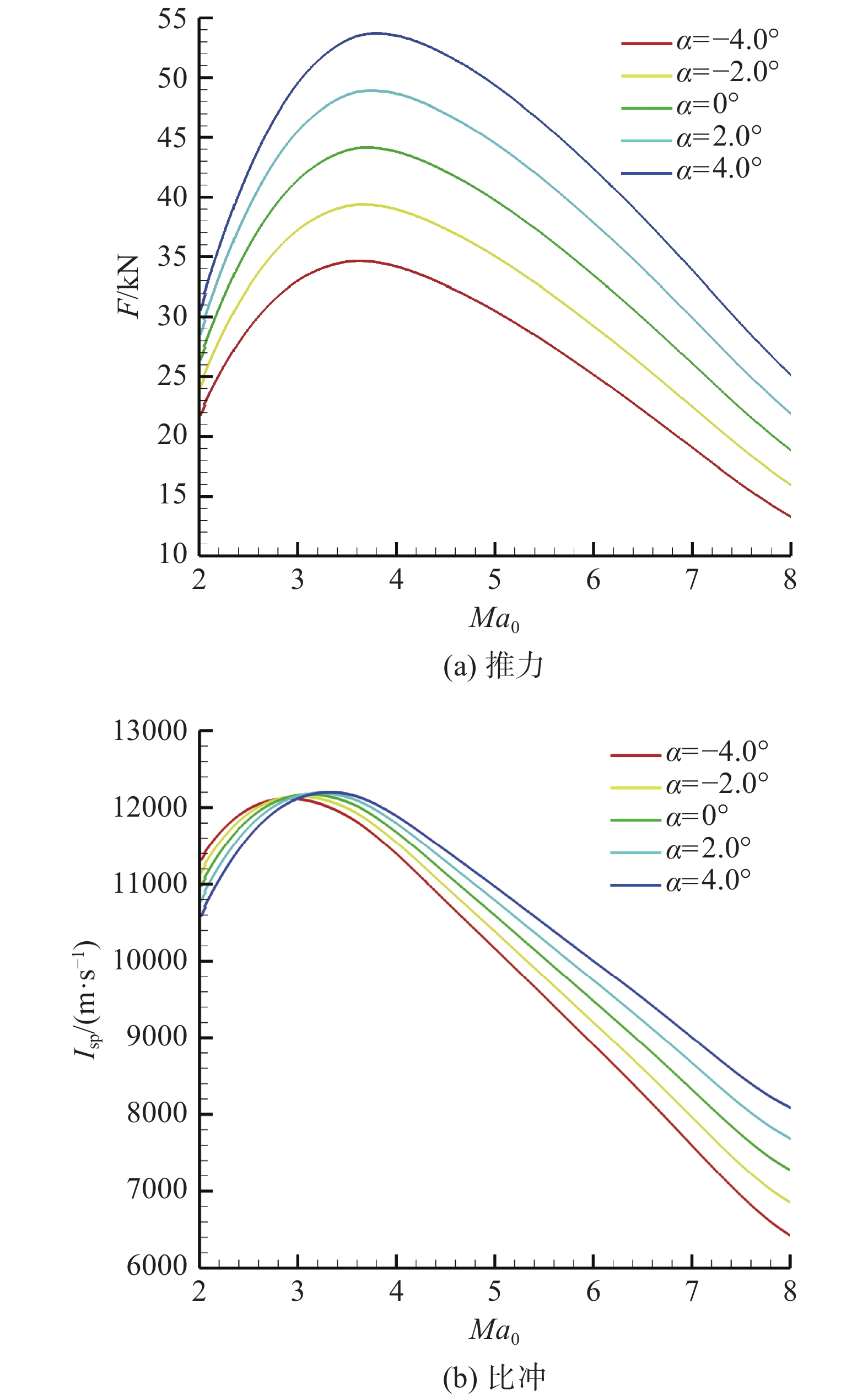
发动机等动压弹道工作,动压Q= 50 kPa。火箭推力室不工作,保持发动机当量比
|
图 15 冲压模态发动机速度-攻角特性 Fig.15 Velocity and attack angle characteristics of the engine at the ramjet operation mode |
随着飞行攻角的增加,进气道捕获空气流量增加;进气道对气流压缩程度有所提高,造成进气道总压损失增加,进气道总压恢复系数及出口马赫数减小;由于进气道出口马赫数的降低,降低了隔离段内激波串总压损失,最终表现为燃烧室总压恢复系数的提高。进气道捕获空气流量、燃烧室总压恢复系数的增加导致发动机推力的增加,而进气道总压恢复系数的减小导致发动机推力的减小。综合各种因素,如图15(a)所示,相同飞行马赫数下,随着飞行攻角的增加,发动机推力增加。
综上分析,飞行马赫数较低时,随着飞行攻角的增加,进气道总压恢复系数减小造成的发动机比冲损失,大于燃烧室总压恢复系数增加带来的发动机比冲增加;而飞行马赫数较高时,燃烧室内气流马赫数相应增加,燃烧室内气动、释热造成的流动损失对发动机性能的影响逐步趋为主导,此时随着飞行攻角的增加,燃烧室总压恢复系数增加带来的发动机比冲增加,大于进气道总压恢复系数减小造成的发动机比冲损失。综上分析,如图15(b)所示,Ma0<3时,相同飞行马赫数下,随着飞行攻角的增加,发动机比冲降低;Ma0>3时,相同飞行马赫数下,随着飞行攻角的增加,发动机比冲增加。
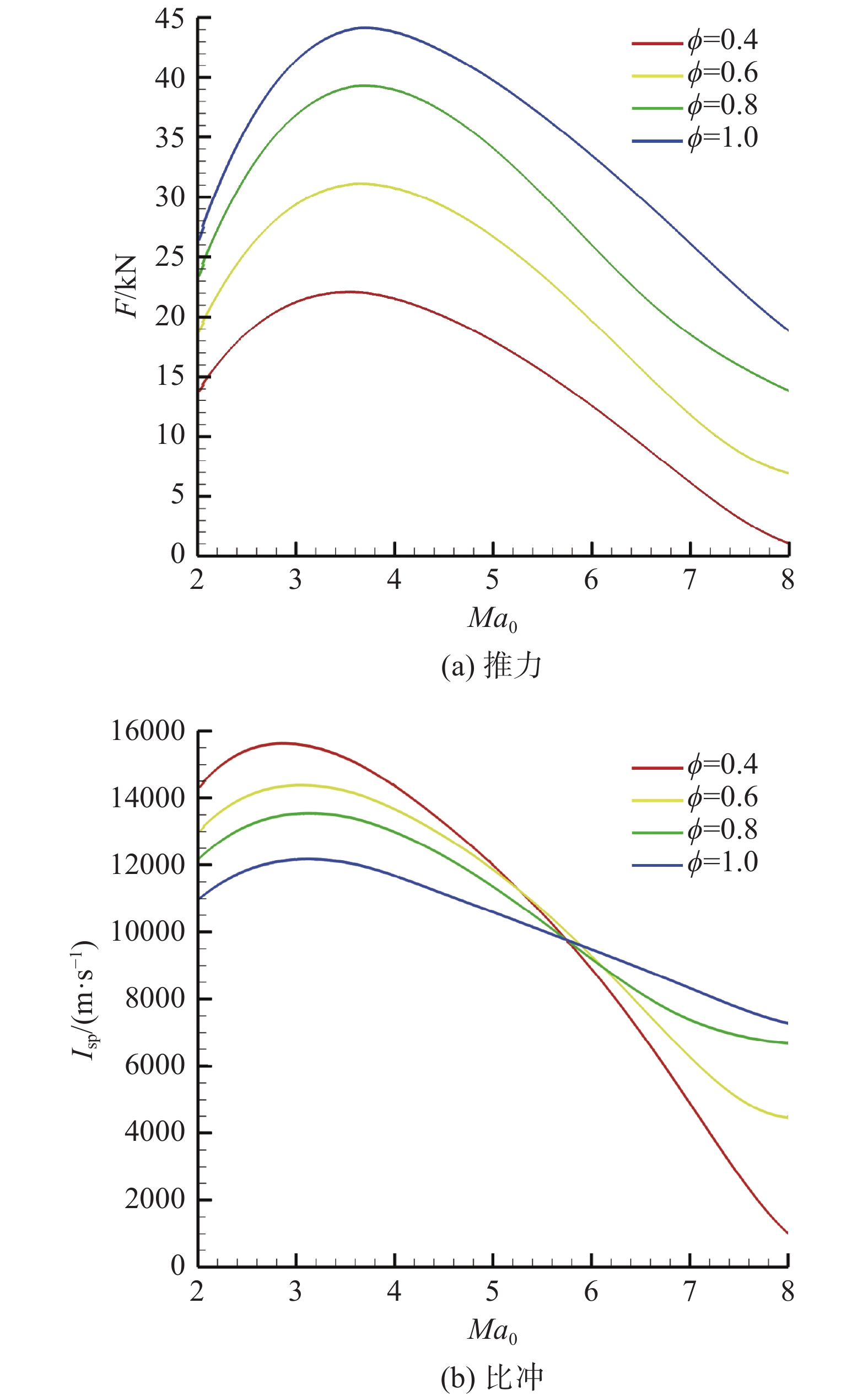
发动机等动压弹道工作,动压Q= 50 kPa。火箭推力室不工作,保持飞行攻角α = 0°不变,完成不同当量比下发动机性能计算,获得发动机速度-节流特性。图16给出了飞行Ma0 = 2~8、发动机冲压模态工作、当量比
|
图 16 冲压模态发动机速度-节流特性 Fig.16 Velocity and throttle characteristics of the engine at the ramjet operation mode |
随着当量比的增加,燃料流量及燃烧室内释热量提高,使得尾喷管出口燃气流量及速度均增加,发动机推力增加。如图16(a)所示,相同飞行马赫数下,随着当量比的增加,发动机推力增加。
保持其他参数不变,飞行马赫数增加时,来流速度及尾喷管出口燃气速度均增加。飞行马赫数较低时,来流空气总温较低,相同当量比下,燃气总温升高幅度较高,使得尾喷管出口燃气速度增幅高于来流速度增幅,发动机比冲呈现随飞行马赫数增加而增加趋势;而飞行马赫数较高时,来流空气总温较高,相同当量比下,燃气总温升高幅度低于低飞行马赫数条件下的总温升高幅度,使得尾喷管出口燃气速度增幅低于来流速度增幅,发动机比冲呈现随飞行马赫数增加而减小趋势。如图16(b)所示,相同当量比下,随着飞行马赫数增加,发动机比冲呈现先增加后减小趋势;相同飞行马赫数下,Ma0<5.7时,发动机比冲随着当量比的增加而降低,Ma0>5.7时,发动机比冲随着当量比的增加而增加。
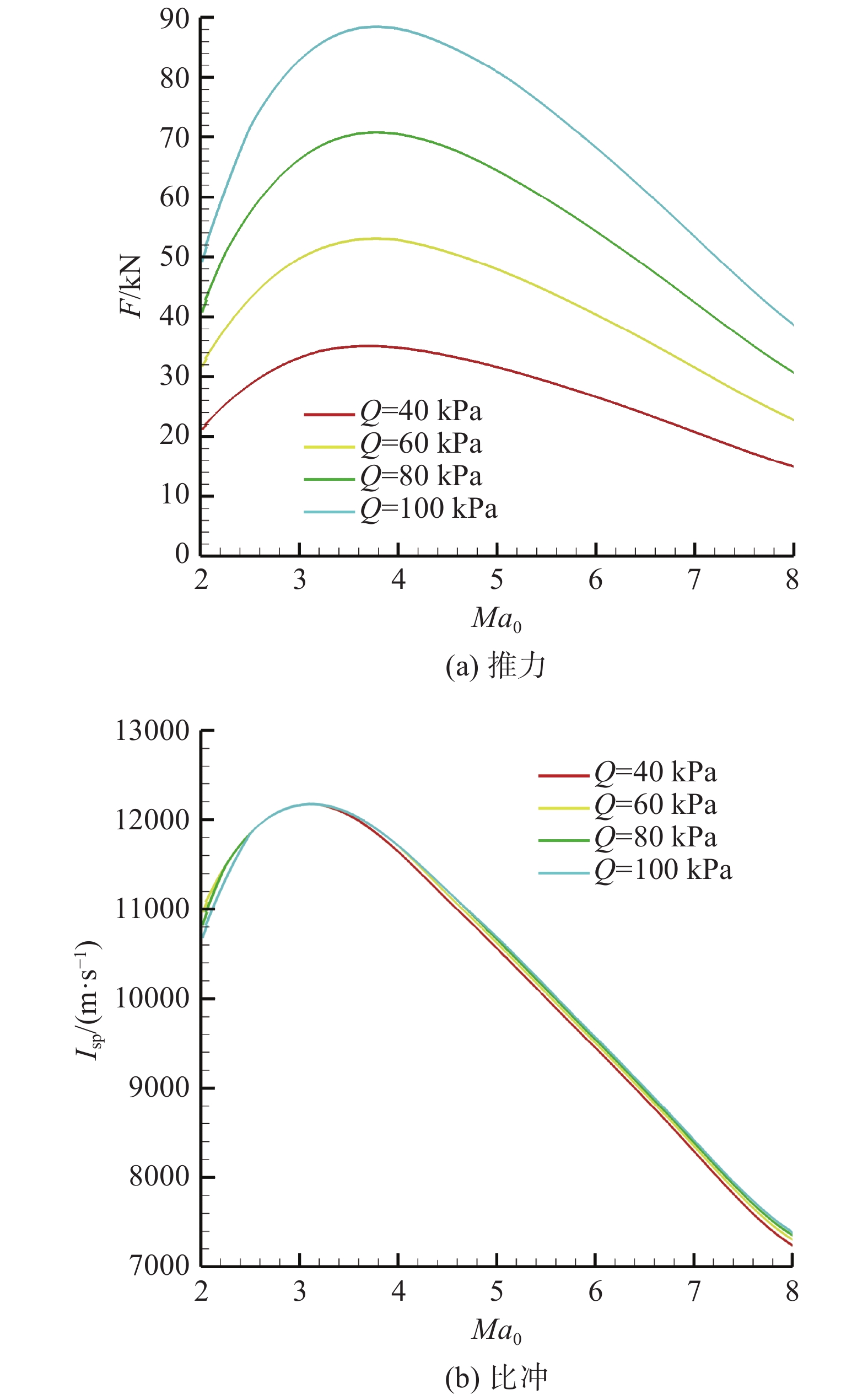
火箭推力室不工作,保持飞行攻角α = 0°、当量比
|
图 17 冲压模态发动机速度-高度特性 Fig.17 Velocity and altitude characteristics at the ramjet operation mode |
相同飞行马赫数条件下,飞行动压随着飞行高度的增加而降低,飞行动压越高,发动机捕获流量越大,发动机推力亦越大。如图17(a)所示,相同飞行马赫数下,随着飞行高度的增加(飞行动压降低),发动机推力减小;而发动机部件性能参数受飞行动压的影响较小,因此如图17(b)所示,发动机比冲基本不受飞行高度变化的影响。
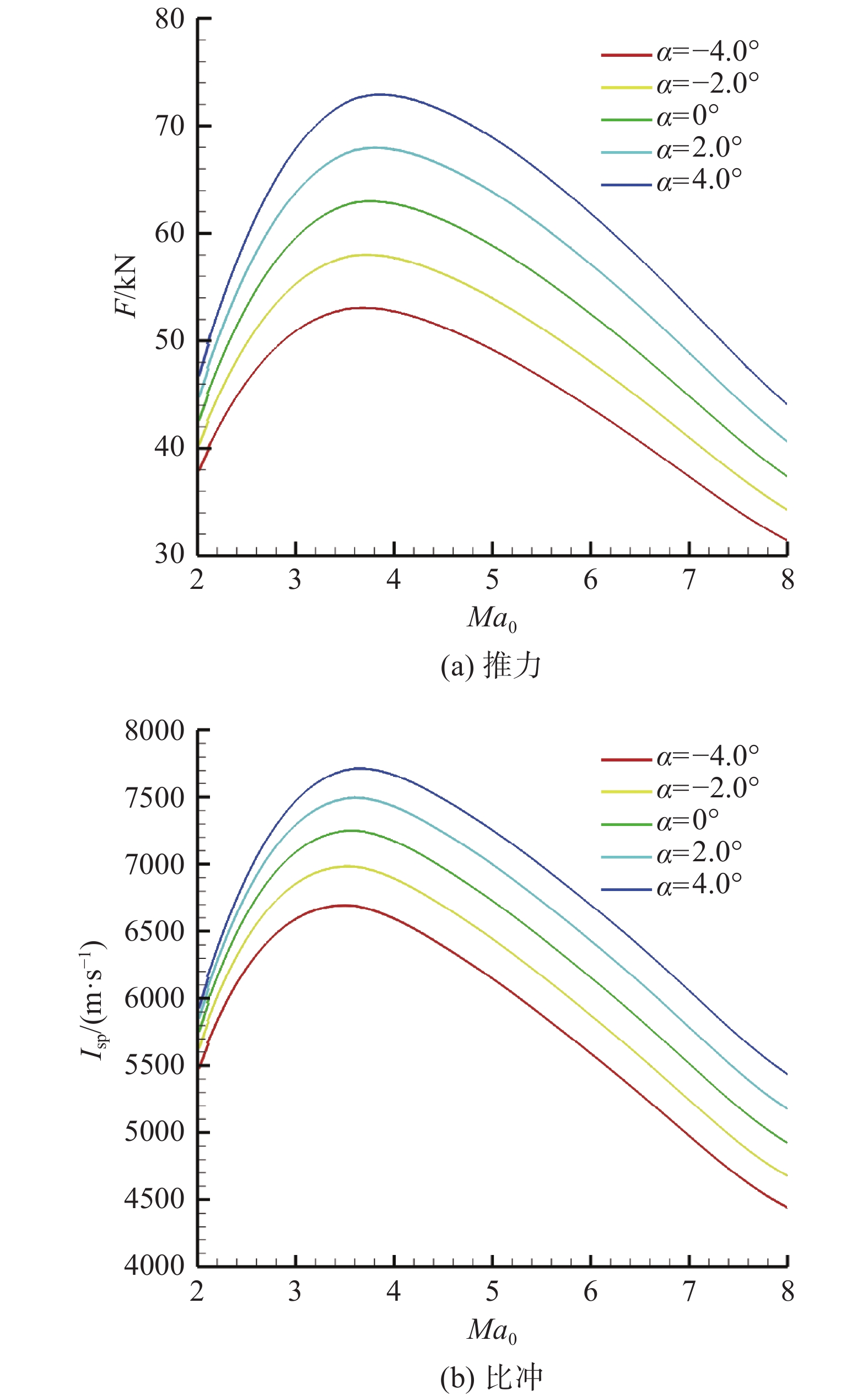
3.3 火箭冲压模态工作特性发动机等动压弹道工作,动压Q = 50 kPa。保持火箭流量
|
图 18 火箭冲压模态发动机速度-攻角特性 Fig.18 Velocity and attack angle characteristics at therocket & ramjet operation mode |
火箭冲压模态发动机推力-攻角特性与冲压模态一致,发动机推力随着飞行攻角的增加而增加。由于火箭流量的引入,发动机比冲-攻角特性与冲压模态存在差异,相同飞行马赫数下,攻角增加,发动机捕获空气流量增加,当量比保持不变条件下,火箭流量占总燃料消耗的比例下降,发动机比冲增加。综上分析,如图18所示,火箭冲压模态下,保持飞行马赫数不变,发动机推力、比冲均随着飞行攻角的增加而增加。
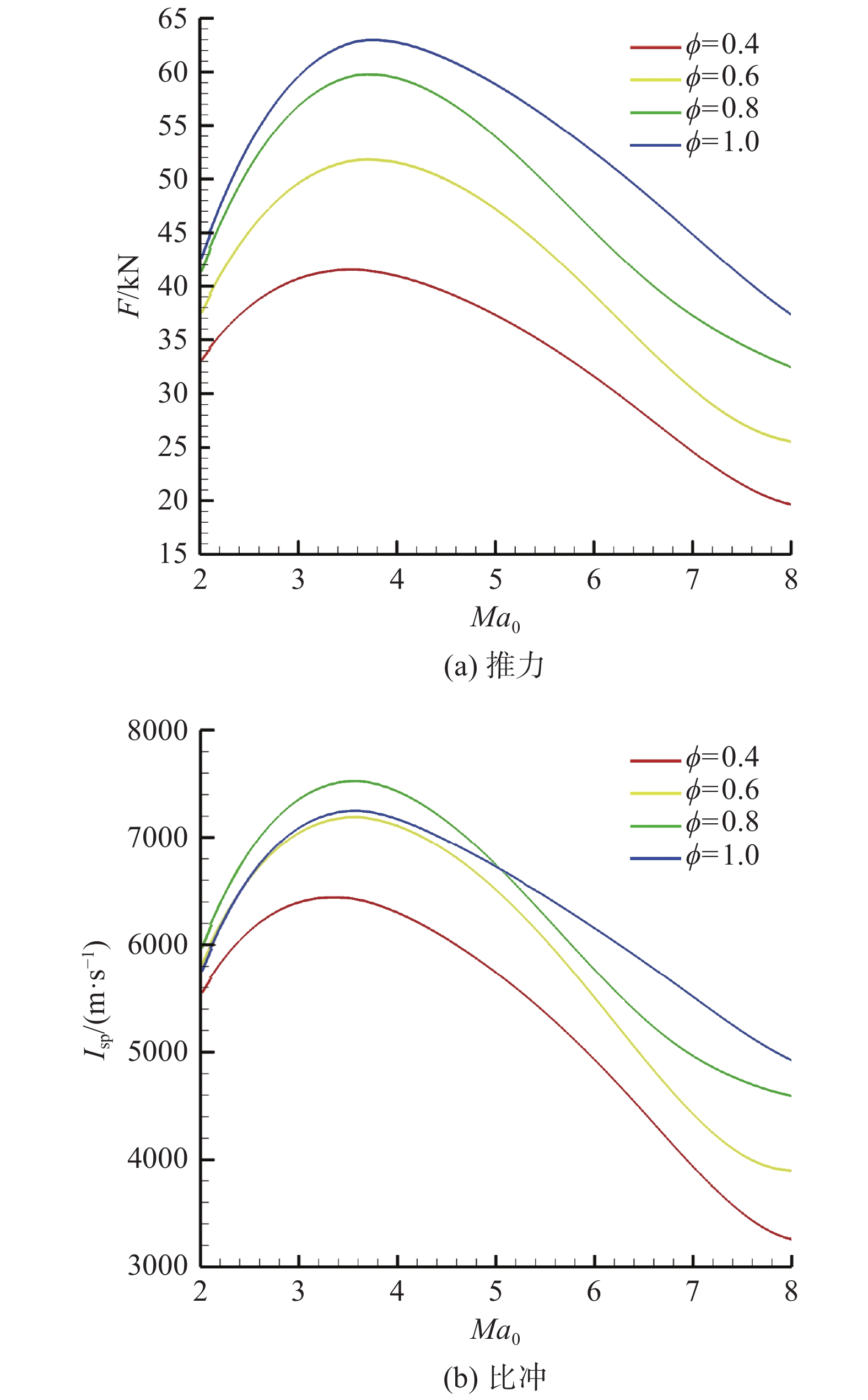
发动机等动压弹道工作,动压Q = 50 kPa。保持火箭流量
|
图 19 火箭冲压模态发动机速度-节流特性 Fig.19 Velocity and throttle characteristics at therocket & ramjet operation mode |
火箭冲压模态发动机推力-节流特性与冲压模态一致,发动机推力随着当量比的增加而增加。发动机比冲-节流特性则与冲压模态存在较大差异,一方面发动机所供应燃料产生的比冲与冲压模态有着相同的特性;另一方面,由于火箭流量的引入,随着当量比的增加,火箭流量占总燃料消耗的比例下降。在以上两方面因素的共同作用下,不同飞行马赫数区间发动机表现出不同的当量比-比冲特性(如图19所示)。火箭冲压模态下,Ma0<5.2时,发动机比冲随着当量比的增加先增加后降低,并且在当量比
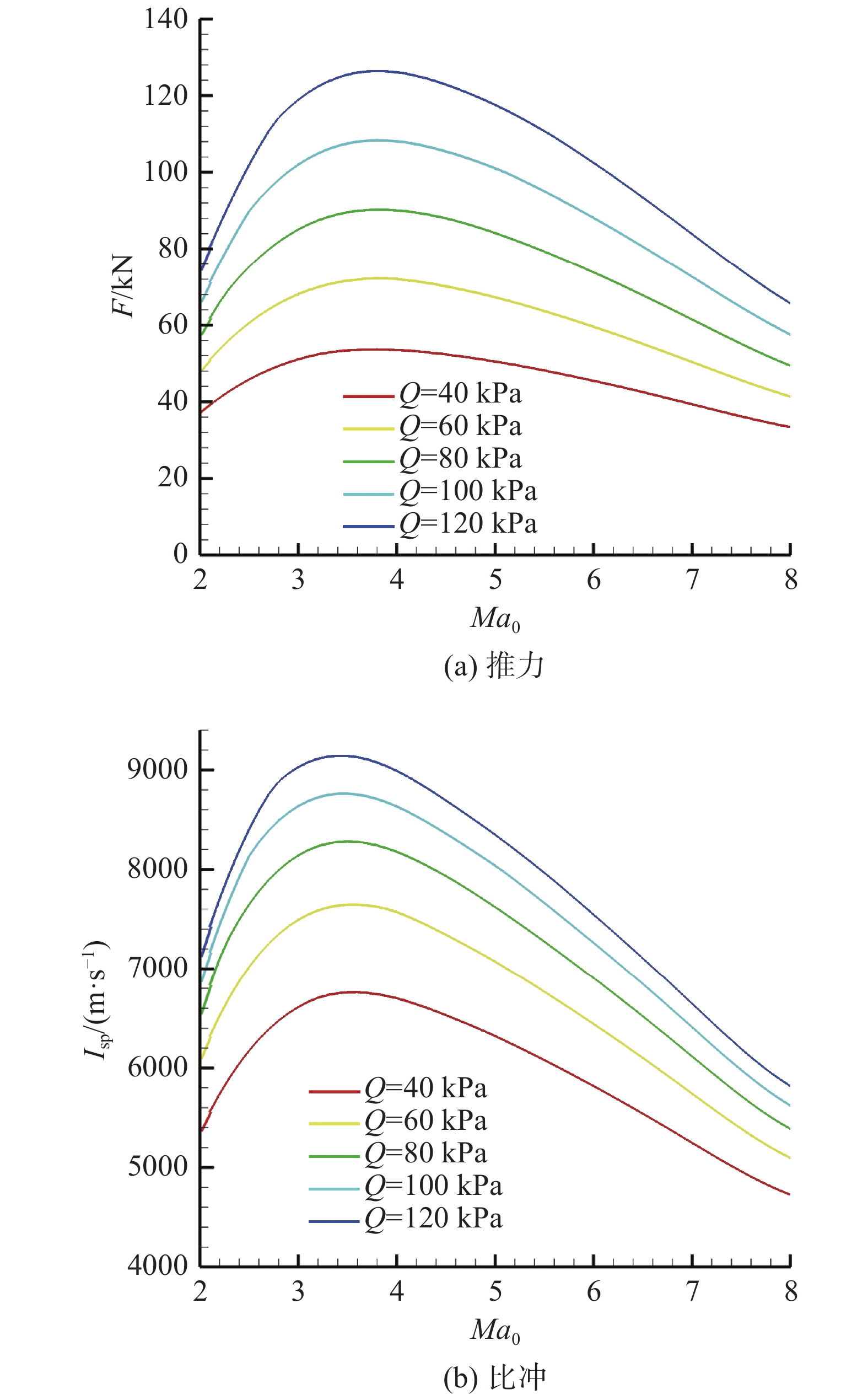
保持火箭流量
|
图 20 火箭冲压模态发动机速度-高度特性 Fig.20 Velocity and altitude characteristics at therocket & ramjet operation mode |
火箭冲压模态发动机推力-高度特性与冲压模态一致,相同飞行马赫数下,发动机推力随着飞行高度的增加(飞行动压降低)而降低。由于火箭流量的引入,发动机比冲-高度特性与冲压模态存在差异。相同飞行马赫数下,飞行高度增加(飞行动压降低),发动机捕获空气流量减小,当量比保持不变条件下,火箭流量占总燃料消耗的比例增加,发动机比冲下降。综上分析,如图20所示,火箭冲压模态下,保持飞行马赫数不变,发动机推力、比冲均随着飞行高度的增加而降低。
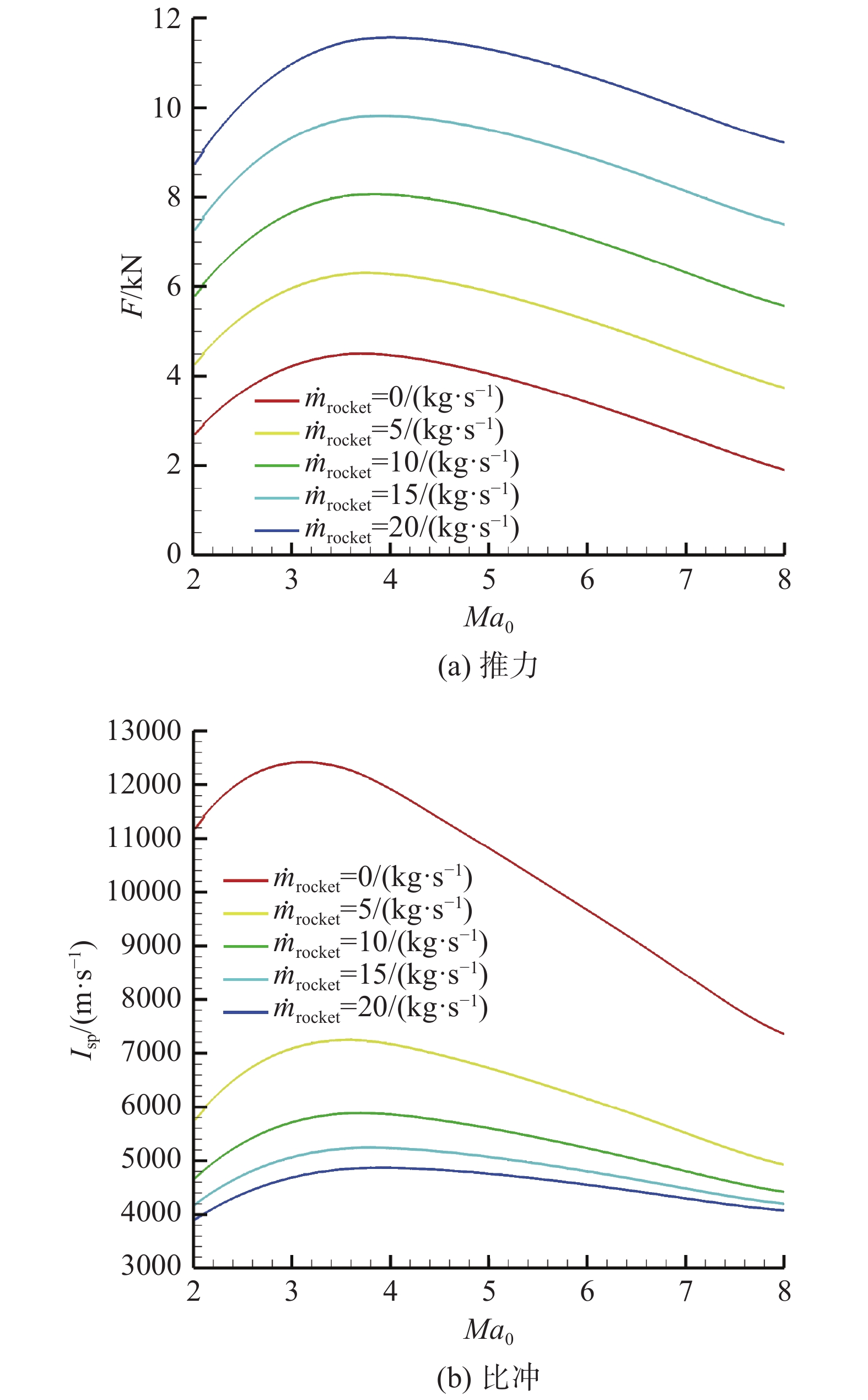
发动机等动压弹道工作,动压Q = 50 kPa。保持飞行攻角α = 0°、发动机当量比
|
图 21 火箭冲压模态发动机速度-火箭节流特性 Fig.21 Velocity and rocket throttle characteristics at the rocket & ramjet operation mode |
飞行马赫数保持不变,火箭流量增加,发动机出口燃气流量、速度均增加,发动机推力增加;而随着火箭流量的增加,火箭流量占发动机推进剂总消耗的比例升高,因此发动机比冲下降。综上分析,如图21所示,火箭冲压模态下,保持飞行马赫数不变,随着火箭流量的增加,发动机推力增加、比冲下降。
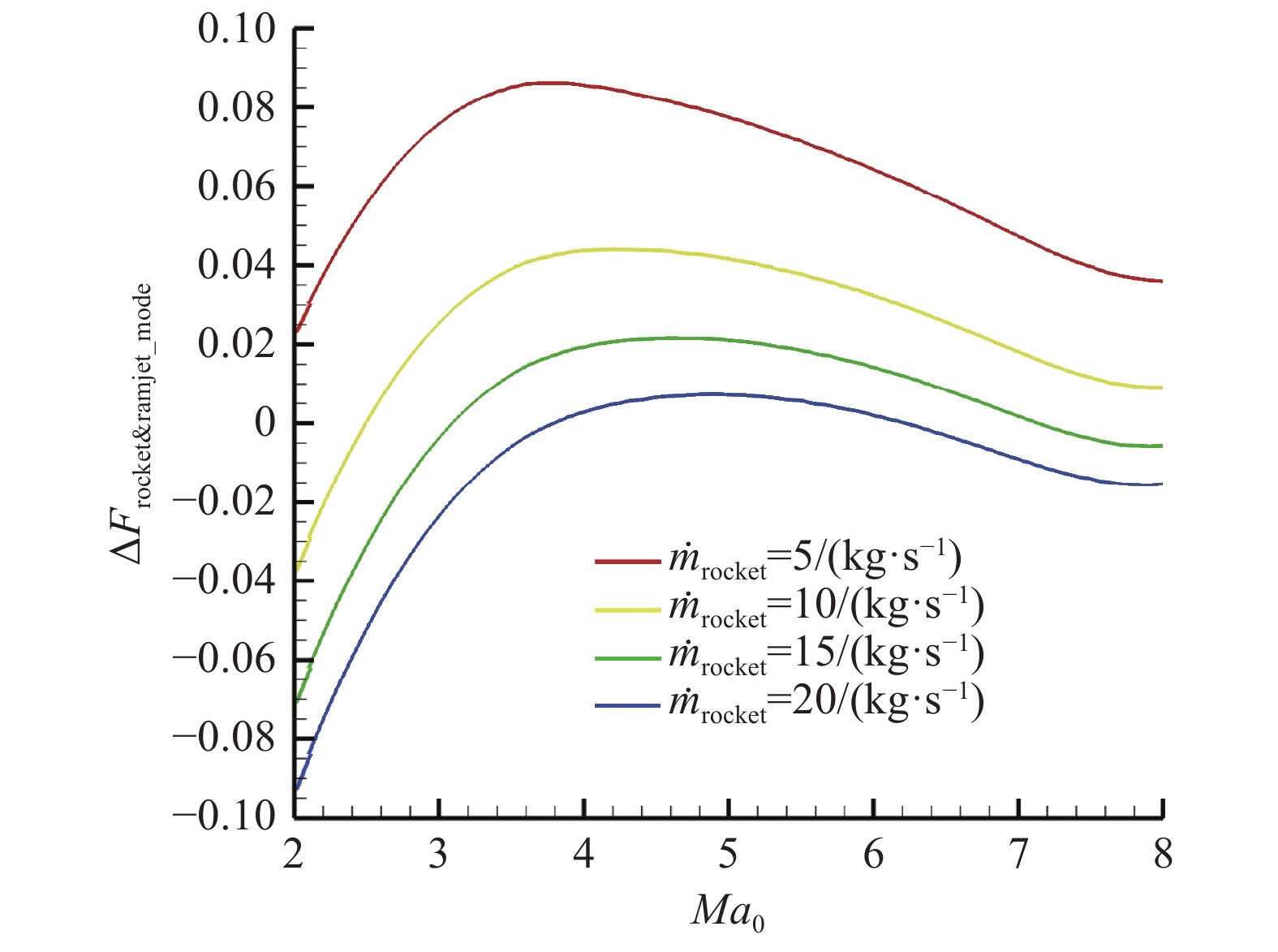
图22给出了火箭冲压模态不同火箭流量下火箭推力增益ΔFrocket&ramjet_mode随飞行马赫数变化曲线。火箭冲压模态火箭推力增益定义见式(18)。
| $ \Delta {F_{{\rm{rocket\& ramjet\_mode}}}} = \frac{{F - {F_{{\rm{ramjet}}}} - {F_{{\rm{rocket}}}}}}{{{F_{{\rm{rocket}}}}}} $ | (18) |
式(18)中F为火箭冲压模态发动机推力,Framjet为相同当量比下冲压模态发动机推力,Frocket为火箭燃气完全膨胀至对应飞行高度大气环境压力所产生的推力。Frocket计算方法与火箭引射模态相同。
从图22中可以看出,保持火箭流量不变时,与发动机推力、比冲变化趋势相同,随着飞行马赫数的增加,火箭推力增益ΔFrocket&ramjet_mode先下降后增加;保持飞行马赫数不变时,随着火箭流量的增加,火箭推力增益ΔFrocket&ramjet_mode下降。
表2给出了火箭冲压模态典型状态下火箭推力增益,其中Mamax为给定火箭流量条件下火箭推力增益达到最大值时对应的飞行马赫数。从表2可以看出,火箭冲压模态下,火箭流量的变化对火箭推力增益存在较大影响。
|
图 22 火箭冲压模态火箭推力增益随飞行马赫数变化 Fig.22 ΔFrocket&ramjet_mode - Ma0 relationship at the rocket & ramjet operation mode |
| 表 2 火箭冲压模态典型点推力增益 Table 2 Thrust gain at typical conditionsof the rocket & ramjet mode |
|
|
为研究发动机工作包线内的结构调节规律,采用如下模拟弹道:
1)Ma0 = 0~2,火箭引射模态工作,按照H = 6.27Ma0弹道从Ma0 = 0、H = 0 km爬升至Ma0 = 2、H = 12.54 km(Q = 50 kPa),火箭流量从Ma0 = 0时的30 kg/s线性减小至Ma0 = 2时的20 kg/s。
2)Ma0 = 2~8,火箭冲压模态工作,按照等动压弹道(Q = 50 kPa)从Ma0 = 2、H = 12.54 km爬升至Ma0 = 8、H = 30.48 km,保持当量比
3)Ma0 = 8,冲压模态工作,当量比
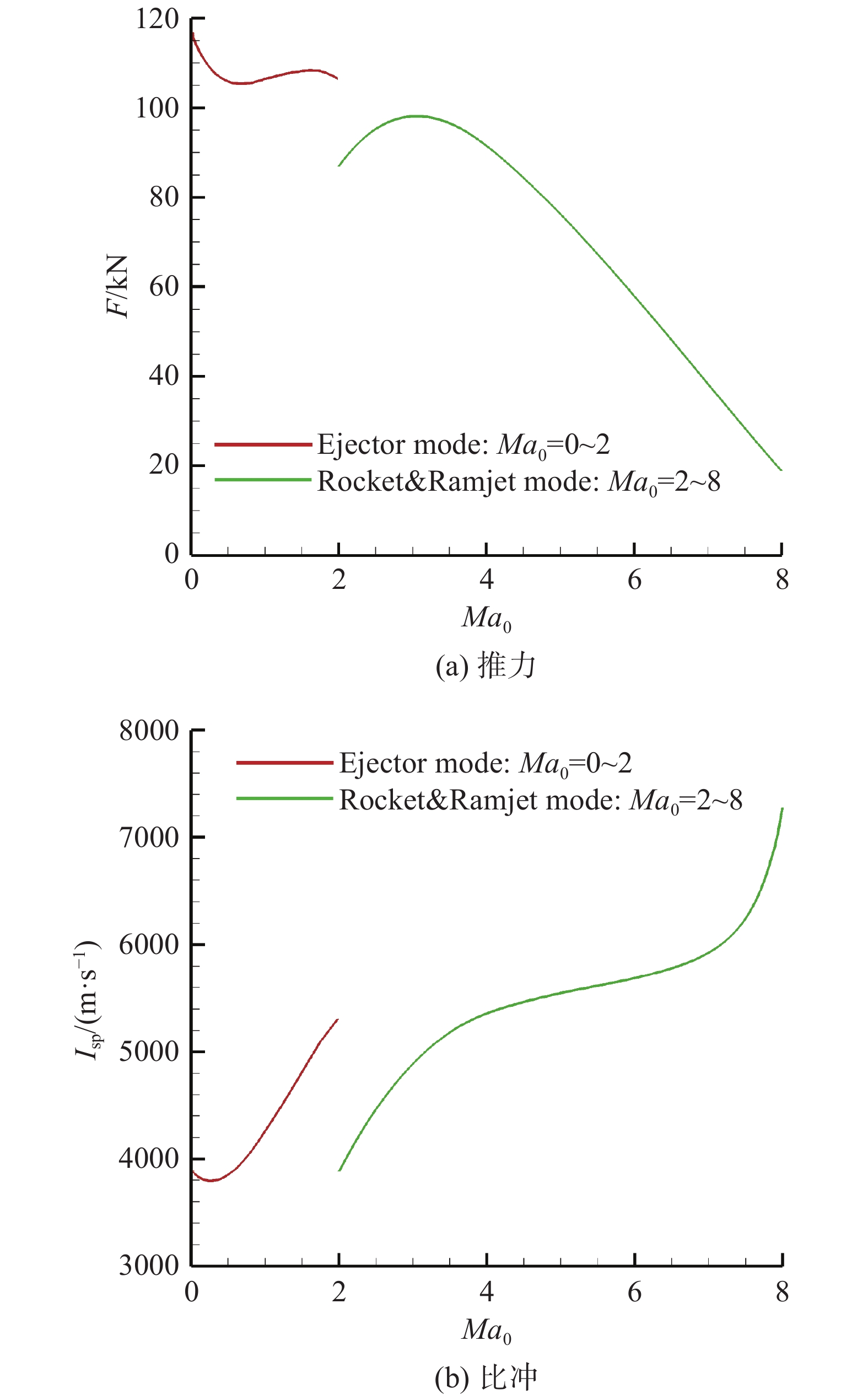
对上述模拟弹道,完成发动机特性计算。图23给出了发动机推力、比冲性能。Ma0 = 2为火箭引射模态转换至火箭冲压模态的转换点。由于在模态转换点进气道出口气流从亚声速开始转变为超声速,使得燃烧室内流态发生本质变化,造成推力、比冲出现间断。
|
图 23 模拟弹道下发动机性能 Fig.23 Engine performance along the simulated trajectory |
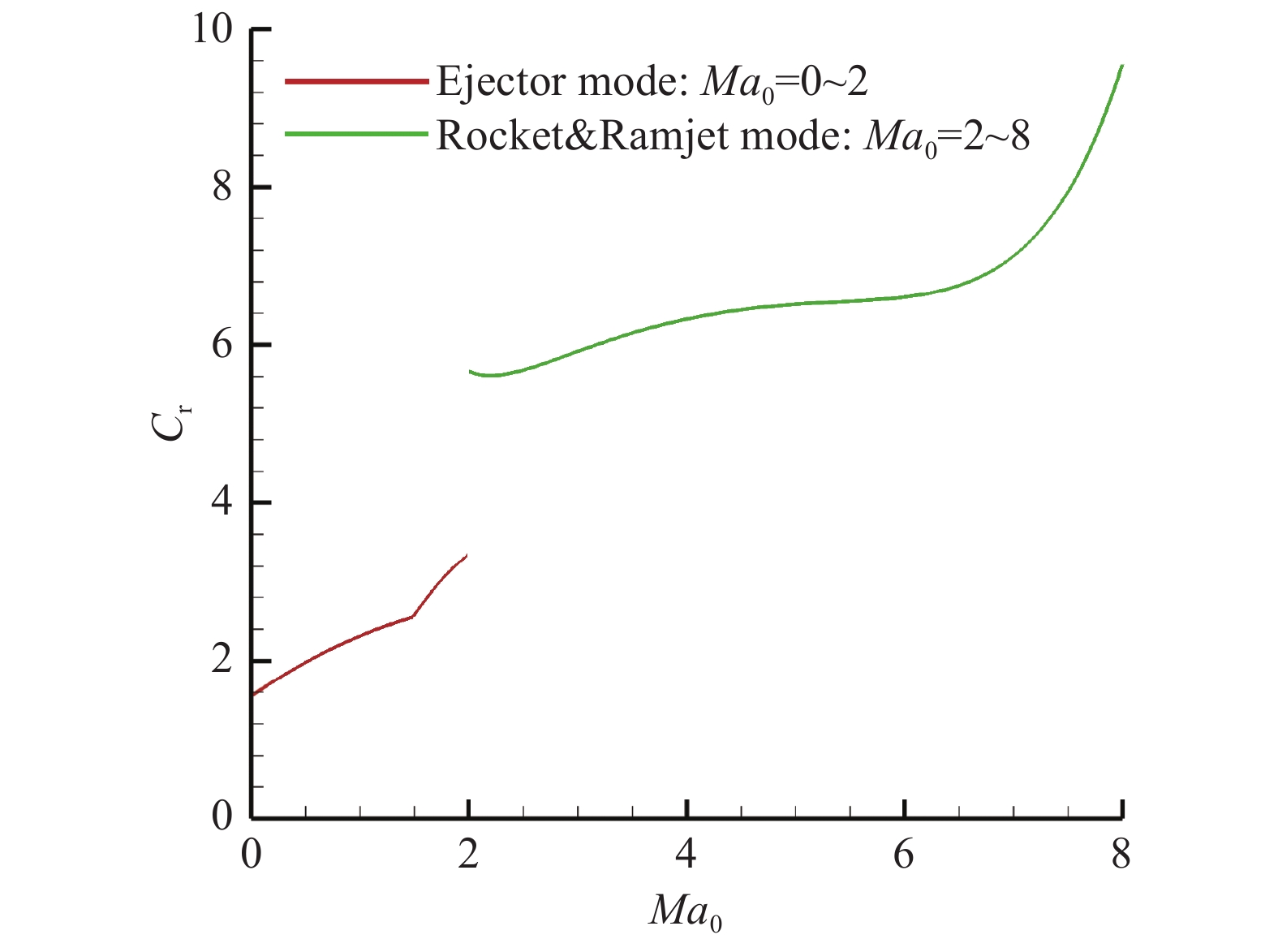
图24~图27分别给出了模拟弹道下进气道收缩比Cr、燃烧室扩张比Dr、尾喷管扩张比Er、发动机总面积比AR随飞行马赫数调节规律。从图中可以看出,进气道收缩比Cr及燃烧室扩张比Dr在Ma0 = 2模态转换点出现突变,而尾喷管扩张比Er及发动机总面积比AR整体随飞行马赫数保持连续变化。
|
图 24 模拟弹道下进气道收缩比随飞行马赫数变化 Fig.24 Variation of the air-inlet contraction ratio with the flight Mach number along the simulated trajectory |
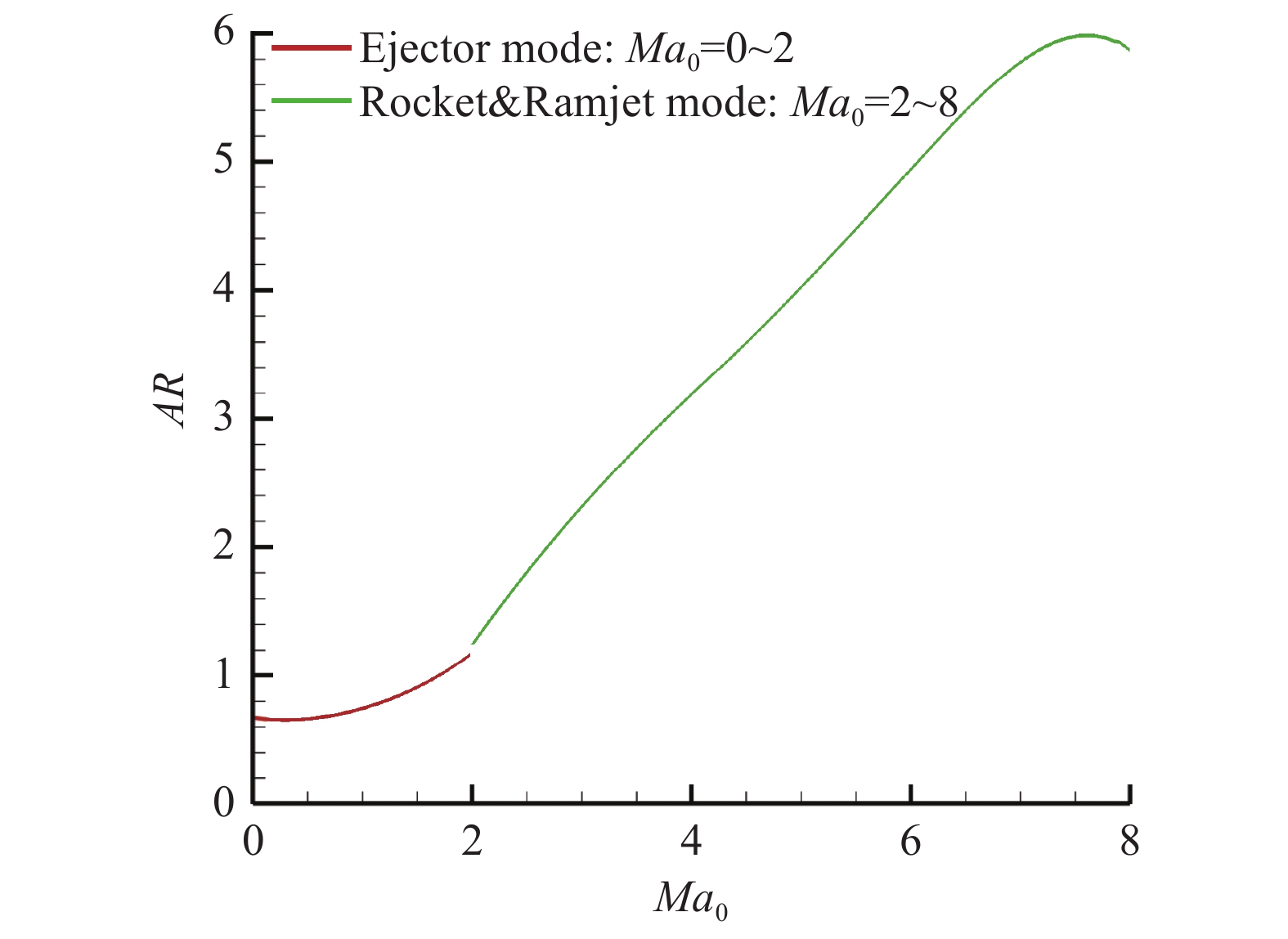
|
图 27 模拟弹道下发动机总面积比随飞行马赫数变化 Fig.27 Variation of the engine total area ratio with the flight Mach number along the simulated trajectory |
|
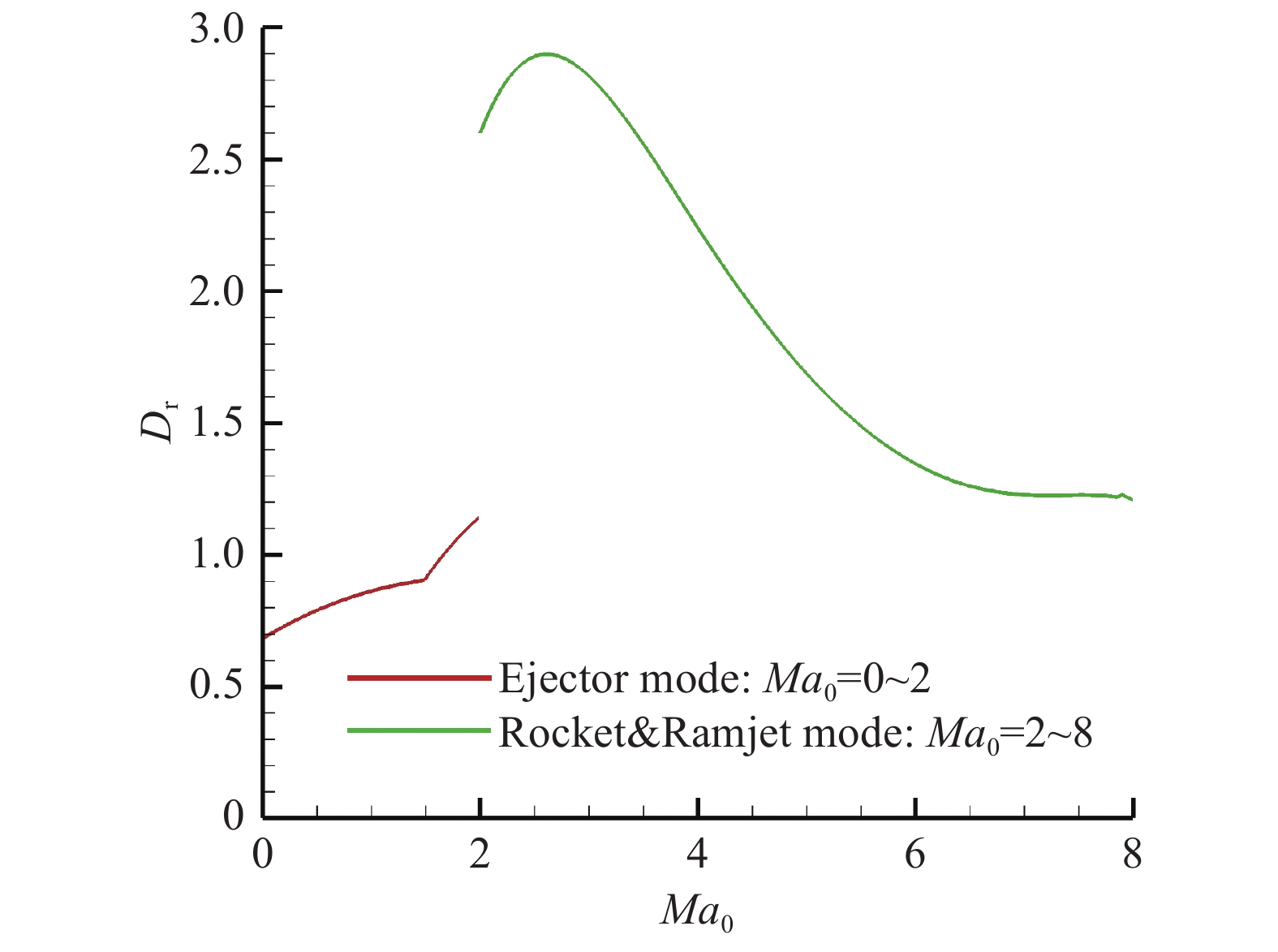
图 25 模拟弹道下燃烧室扩张比随飞行马赫数变化 Fig.25 Variation of the combustor expansion ratio with the flight Mach number along the simulated trajectory |
|
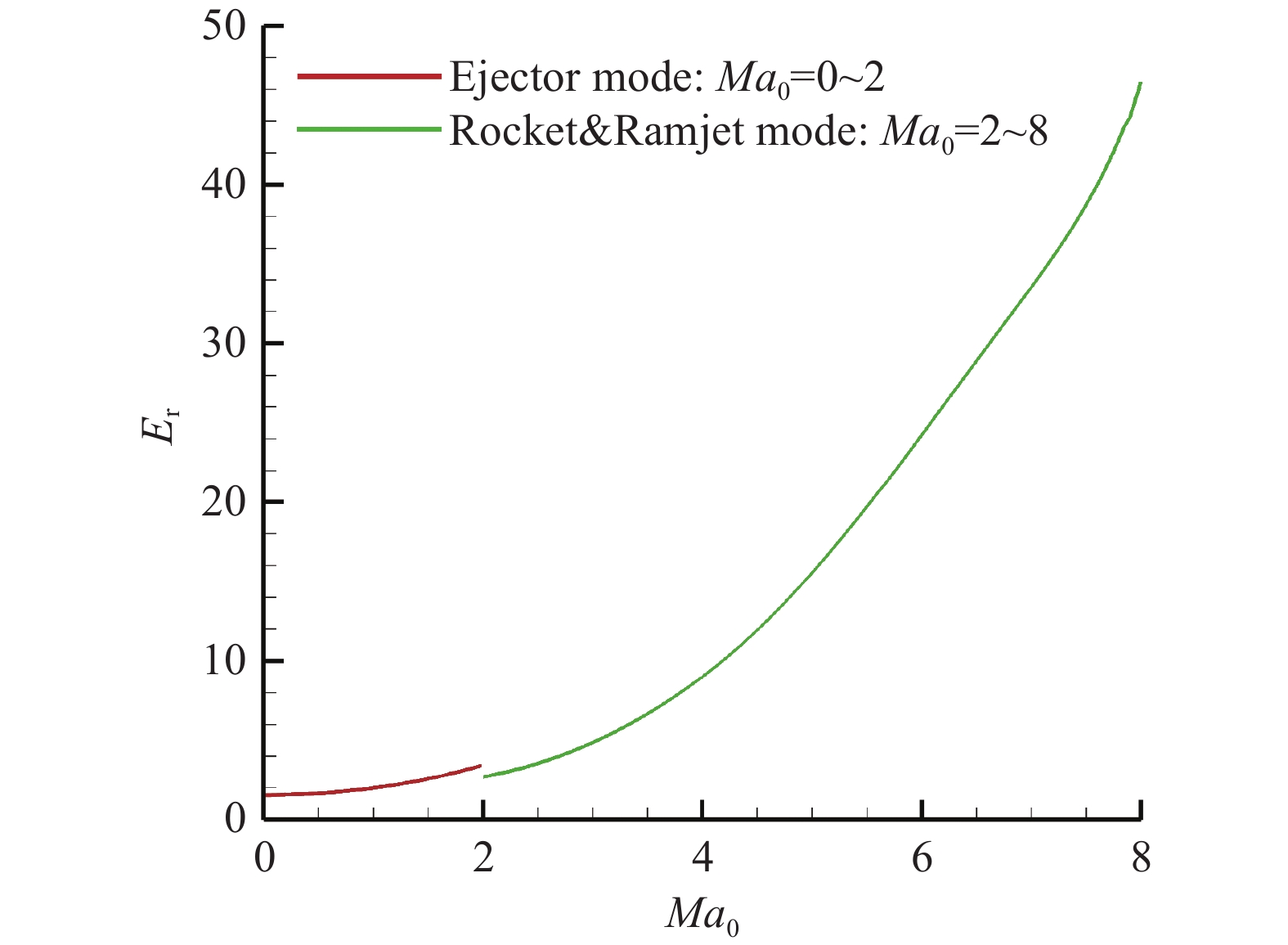
图 26 模拟弹道下尾喷管扩张比随飞行马赫数变化 Fig.26 Variation of the nozzel expansion ratio with the flight Mach number along the simulated trajectory |
进气道收缩比Cr随着飞行马赫数的增加而增加。火箭引射模态,从Ma0 = 0时1.55增加至Ma0 = 2时3.34;火箭冲压模态,从Ma0 = 2时5.67增加至Ma0 = 8时9.56。在Ma0 = 0~8范围内,Cr共变化6.17倍。
燃烧室扩张比Dr,火箭引射模态,随着飞行马赫数的增加而增加。从Ma0 = 0时的0.68增加至Ma0 = 2时的1.15;火箭冲压模态,随着飞行马赫数的增加先增加后下降,从Ma0 = 2时2.60增加至Ma0 = 2.6时最大值2.90,最后降至Ma0 = 8时1.21。在Ma0 = 0~8范围内,Dr共变化4.26倍。
尾喷管扩张比Er随着飞行马赫数的增加而增加,火箭引射模态,从Ma0 = 0时1.53增加至Ma0 = 2时4.46;火箭冲压模态,从Ma0 = 2时2.70增加至Ma0 = 8时46.48。在Ma0 = 0~8范围内,Er共变化30.38倍。
发动机进出口总面积比AR,火箭引射模态,随着飞行马赫数的增加而增加,从Ma0 = 0时的0.67增加至Ma0 = 2时的1.17;火箭冲压模态,随着飞行马赫数的增加先增加后下降,从Ma0 = 2时1.24增加至Ma0 = 7.6时最大值5.99,最后降至Ma0 = 8时5.87。在Ma0 = 0~8范围内,AR共变化8.94倍。
5 结 论基于RBCC发动机部件性能试验、自由射流试验数据,建立了发动机关键部件特性数学模型。采用控制体法,发展了考虑热完全气体效应、化学平衡流动效应、黏性损失及热损失的发动机特性分析模型。针对捕获面积A0 = 1 m2、采用中心火箭布局的二元变结构模型发动机,完成飞行马赫数Ma0 = 0~8范围内不同工作模态发动机速度特性、攻角特性、节流特性、高度特性、火箭节流特性仿真,并针对模拟弹道,给出了发动机结构调节规律。在本文给定的研究条件下,获得研究结论如下:
1)火箭引射模态,随着火箭流量的增加,推力线性增加,比冲保持不变。随着飞行马赫数的增加,推力、比冲及火箭推力增益均呈现先略微下降而后升高趋势。总体而言,飞行马赫数每增加1,发动机推力、比冲增加约18.2%,火箭推力增益增加约15%。
2)冲压模态,随着飞行攻角的增加,推力单调增加,Ma0<3时比冲降低,Ma0>3时比冲增加。随着飞行马赫数的增加,推力、比冲均呈现先增加后降低趋势,根据工作条件的不同,推力在Ma0 = 3.5~3.8区间达到最大值。比冲在Ma0 = 2.9~3.2区间达到最大值;随着当量比的增加,推力单调增加,Ma0<5.7时比冲降低,Ma0>5.7比冲增加。随着飞行高度的增加,推力减小,比冲基本保持不变。
3)火箭冲压模态,随着飞行攻角的增加,推力、比冲均增加。随着飞行马赫数的增加,推力、比冲均呈现先增加后降低趋势,根据工作条件的不同,推力在Ma0 = 3.3~4.0区间达到最大值,比冲在Ma0 = 3.2~3.8区间达到最大值。随着当量比的增加,推力单调增加,Ma0<5.2时比冲先增加后降低,Ma0>5.2时比冲增加。随着飞行高度的增加,推力、比冲均降低。随着火箭流量的增加,推力增加,比冲及火箭推力增益下降,并且火箭流量越大,获得正的火箭推力增益范围越窄。因此在发动机设计中要格外关注火箭/冲压工作及结构参数的匹配性问题。
4)火箭引射模态到火箭冲压模态转化过程中,不但发动机推力、比冲存在不连续现象,进气道收缩比、燃烧室扩张比也存在间断。在发动机具体设计实践中,如何通过发动机工作及结构参数的匹配设计,实现模态转化过程中发动机推力及结构的连续调节、匹配,将是限制宽范围RBCC发动机工程应用的瓶颈。
5)给定模拟弹道下,进气道收缩比、燃烧室扩张比、尾喷管扩张比、发动机总面积比分别变化6.17、4.26、30.38、8.94倍。一方面,如此大的结构调节比很难实现;另一方面,在飞行器总体空间布局约束下,发动机总面积比受限。因此在发动机具体设计实践中,首先应根据总体空间布局约束,确定发动机总面积比最大值,然后结合具体飞行剖面,开展发动机特性分析,确定发动机调节部位及调节比范围。
致谢:感谢南向军博士在进气道试验、尾喷管仿真方面提供的帮助。
| [1] |
ESCHER W, SCHNURSTEIN R. A retrospective on early cryogenic primary rocket subsystem designs as integrated into rocket-based combined-cycle (RBCC) engines[C]//29th Joint Propulsion Conference and Exhibit, Monterey, CA. Reston, Virginia: AIAA, 1993. AIAA-93-1944. doi:10.2514/6.1993-1944
|
| [2] |
CARL EHRLICH J. Early studies of RBCC applications and lessons learned for today[C]//36th AIAA/ASME/SAE/ASEE Joint Propulsion Conference and Exhibit, Las Vegas, NV. Reston, Virginia: AIAA, 2000. AIAA-2000-3105. doi:10.2514/6.2000-3105
|
| [3] |
CZYSZ P, LITTLE M. Rocket Based Combined Cycle engine (RBCC) - A propulsion system for the 21st century[C]//Proc of the 5th International Aerospace Planes and Hypersonics Technologies Conference, Munich, Germany. Reston, Virginia: AIAA, 1993. AIAA-93-5096. doi:10.2514/6.1993-5096
|
| [4] |
ESCHER W J D. A US history of airbreathing/rocket combined-cycle (RBCC) propulsion for powering future aerospace transports, with a look ahead to the year 2020[R]. ISABE-99-7028, 1999: 1-38. https://ntrs.nasa.gov/api/citations/19990062726/downloads/19990062726.pdf
|
| [5] |
MCDANIEL J C, CHELLIAH H, GOYNE C P, et al. US national center for hypersonic combined cycle propulsion-an overview[C]//16th AIAA/DLR/DGLR International Space Planes and Hypersonic Systems and Technologies Conference, HYTASP-17: Program Overview III, 2009. AIAA 2009-7280, 2009: 1-18. doi:10.2514/6.2009-7280
|
| [6] |
TANI K, TOMIOKA S, KATO K, et al. Current status of researches of the combined cycle engine at JAXA[R]. ISABE-2011-1334, 2011: 1-8.
|
| [7] |
ZHANG T T, WANG Z G, HUANG W, et al. The overall layout of rocket-based combined-cycle engines: a review[J]. Journal of Zhejiang University-SCIENCE A, 2019, 20(3): 163-183. DOI:10.1631/jzus.A1800684 |
| [8] |
张玫, 张蒙正, 刘昊. 火箭基组合循环动力研究进展[J]. 科技导报, 2020, 38(12): 54-68. ZHANG M, ZHANG M Z, LIU H. Progress and analysis of rocket based combined cycle(RBCC) propulsion system[J]. Science & Technology Review, 2020, 38(12): 54-68. DOI:10.3981/j.issn.1000-7857.2020.12.005 (in Chinese) |
| [9] |
ESCHER W, PRYOR D, HYDE E. Development of a 12-thrust chamber kerosene/oxygen primary rocket subsystem for an early (1964) air-augmented rocket ground test system[C]//9th International Space Planes and Hypersonic Systems and Technologies Conference, Norfolk, VA. Reston, Virginia: AIAA, 1999. AIAA 1999-4896. doi:10.2514/6.1999-4896
|
| [10] |
HYDE E, ESCHER W, RODDY J. Marquardt’s Mach 4.5 supercharged ejector ramjet high-performance aircraft engine project[C]//36th AIAA/ASME/SAE/ASEE Joint Propulsion Conference and Exhibit, Las Vegas, NV. Reston, Virginia: AIAA, 2000. AIAA 2000-3109. doi:10.2514/6.2000-3109
|
| [11] |
RATEKIN G, GOLDMAN A, ORTWERTH P, et al. Rocketdyne RBCC engine concept development[C]//14th International Symposium on Air Breathing Engines, 1999 . ISABE-99-7179.
|
| [12] |
BULMAN M, SIEBENHAAR A. The strutjet engine-Exploding the myths surrounding high speed airbreathing propulsion[C]//31st Joint Propulsion Conference and Exhibit, San Diego, CA. Reston, Virginia: AIAA, 1995. AIAA-95-2475. doi:10.2514/6.1995-2475
|
| [13] |
THOMAS S R, PALAC D T, TREFNY C J, et al. Performance evaluation of the NASA GTX RBCC flowpath[C]//5th International Symposium on Airbreathing Engines, 2001. ISABE-2001-1070. ISABE-2001-1070. https://ntrs.nasa.gov/api/citations/20010092480/downloads/20010092480.pdf?attachment=true
|
| [14] |
FOSTER R, ESCHER W, ROBINSON J. Studies of an extensively axisymmetric rocket based combined cycle (RBCC) engine powered single-stage-to-orbit (SSTO) vehicle[C]//25th Joint Propulsion Conference, Monterey, CA Reston, Virginia: AIAA, 1989. AIAA-89-2294. doi:10.2514/6.1989-2294
|
| [15] |
OLDS J, BRADFORD J, CHARANIA A, et al. Hyperion-An SSTO vision vehicle concept utilizing rocket-based combined cycle propulsion[C]//9th International Space Planes and Hypersonic Systems and Technologies Conference, Norfolk, VA. Reston, Virginia: AIAA, 1999. AIAA 1999-4944. doi:10.2514/6.1999-4944
|
| [16] |
STEMLER J N, BOGAR T J, FARRELL D J, et al. Assessment of RBCC-powered VTHL SSTO vehicles[C]//9th International Space Planes and Hypersonic Systems and Technologies Conference, Norfolk, VA, U. S. A., 1999. AIAA 99-4947. doi:10.2514/6.1999-4947
|
| [17] |
ROCHE J M, MCCURDY D R. Preliminary sizing of vertical take-off rocket-based combined-cycle powered launch vehicles[C]// Space Transportation and Safety: Combustion. Monterey, CA, 2000. NASA/TM-2001-21066. E-12503-1. NAS 1.15: 210668. https://ntrs.nasa.gov/api/citations/20010017162/downloads/20010017162.pdf
|
| [18] |
O’BRIEN T, LEWIS M. Transonic through hypersonic performance of an RBCC engine-airframe integrated vehicle[C]//10th AIAA/NAL-NASDA-ISAS International Space Planes and Hypersonic Systems and Technologies Conference, Kyoto, Japan. Reston, Virginia: AIAA, 2001. doi: 10.2514/6.2001-1919
|
| [19] |
CULVER G. Performance comparison of RBCC- and TBCC-based reusable launch vehicles with enhancing technologies[C]//39th AIAA/ASME/SAE/ASEE Joint Propulsion Conference and Exhibit, Huntsville, Alabama. Reston, Virginia: AIAA, 2003. AIAA-2003-5035. doi: 10.2514/6.2003-5035
|
| [20] |
KRIVANEK T M, ROCHE J M, RIEHL J P, et al. Affordable flight demonstration of the GTX air-breathing SSTO vehicle concept[R]. NASA/TM-2003-212315, 2003. https://ntrs.nasa.gov/api/citations/20030055618/downloads/20030055618.pdf
|
| [21] |
HANK J, FRANKE M, EKLUND D. TSTO reusable launch vehicles using airbreathing propulsion[C]//42nd AIAA/ASME/SAE/ASEE Joint Propulsion Conference & Exhibit, Sacramento, California. Reston, Virigina: AIAA, 2006: 1-19. AIAA-2006-4962. doi:10.2514/6.2006-4962
|
| [22] |
YOUNG D, KOKAN T, TANNER C, et al. Lazarus: A SSTO hypersonic vehicle concept utilizing RBCC and HEDM propulsion technologies[C]//14th AIAA/AHI Space Planes and Hypersonic Systems and Technologies Conference, Canberra, Australia. Reston, Virginia: AIAA, 2006. AIAA-2006-8099. doi:10.2514/6.2006-8099
|
| [23] |
STEELANT J, VARVILL R, WALTON C, et al. Achievements obtained for sustained hypersonic flight within the LAPCAT-II project[C]//20th AIAA International Space Planes and Hypersonic Systems and Technologies Conference, Glasgow, Scotland. Reston, Virginia: AIAA, 2015. AIAA-2008-2578. doi:10.2514/6.2015-3677
|
| [24] |
FALEMPIN F, BOUCHEZ M, PERRILLAT V. LAPCAT 2-Axisymmetric concept for a Mach 8 cruiser preliminary design and performance assessment[C]//16th AIAA/DLR/DGLR International Space Planes and Hypersonic Systems and Technologies Conference, Bremen, Germany. Reston, Virginia: AIAA, 2009. AIAA-2009-7437. doi:10.2514/6.2009-7437
|
| [25] |
KOTHARI A, LIVINGSTON J, TARPLEY C, et al. Rocket based combined cycle hypersonic vehicle design for orbital access[C]//17th AIAA International Space Planes and Hypersonic Systems and Technologies Conference, San Francisco, California. Reston, Virigina: AIAA, 2011: 1-26. AIAA-2011-2338. doi:10.2514/6.2011-2338
|
| [26] |
Quinn J E. ISTAR: Project status and ground test engine design[R]. AIAA-2003-5235, 2003: 1-12. https://ntrs.nasa.gov/api/citations/20030065949/downloads/20030065949.pdf
|
| [27] |
OLDS J, BRADFORD J. SCCREAM (simulated combined-cycle rocket engine analysis module): A conceptual RBCC engine design tool[C]//33rd Joint Propulsion Conference and Exhibit, Seattle, WA. Reston, Virginia: AIAA, 1997. AIAA-97-2760. http://www.ssdl.gatech.edu/sites/default/files/ssdl-files/papers/conferencePapers/AIAA-1997-2760.pdf doi:10.2514/6.1997-2760
|
| [28] |
BRADFORD J, OLDS J. Improvements and enhancements to SCCREAM, a conceptual RBCC engine analysis tool[C]//34th AIAA/ASME/SAE/ASEE Joint Propulsion Conference and Exhibit, Cleveland, OH. Reston, Virginia: AIAA, 1998. AIAA-98-3775. doi:10.2514/6.1998-3775
|
| [29] |
OLDS J R, BRADFORD J E. SCCREAM: A conceptual rocket-based combined-cycle engine performance analysis tool[J]. Journal of Propulsion and Power, 2001, 17(2): 333-339. DOI:10.2514/2.5746 |
| [30] |
OLDS J R. Launch vehicle systems analysis[R]. NASA-Marshall Grant NAG8-1302, 1999. https://ntrs.nasa.gov/api/citations/19990025901/downloads/19990025901.pdf
|
| [31] |
MCKAMEY R, LANDRUM D. A one-dimensional engineering model for the evaluation of rocket-based combined cycle engine performance[C]//37th Joint Propulsion Conference and Exhibit, Salt Lake City, UT. Reston, Virginia: AIAA, 2001. AIAA-2001-3462. doi:10.2514/6.2001-3462
|
| [32] |
黄生洪, 何洪庆, 何国强, 等. 火箭基组合循环(RBCC)推进系统概念设计模型[J]. 推进技术, 2003, 24(1): 1-5. HUANG S H, HE H Q, HE G Q, et al. Conceptual design model of rocket base combined cycle propulsion system[J]. Journal of Propulsion Technology, 2003, 24(1): 1-5. DOI:10.3321/j.issn:1001-4055.2003.01.001 (in Chinese) |
| [33] |
吕翔, 刘佩进, 何国强. RBCC发动机性能分析方法研究[J]. 固体火箭技术, 2007, 30(2): 120-123. LYU X, LIU P J, HE G Q. Study on RBCC motor performance analysis method[J]. Journal of Solid Rocket Technology, 2007, 30(2): 120-123. DOI:10.3969/j.issn.1006-2793.2007.02.009 (in Chinese) |
| [34] |
吕翔, 何国强, 刘佩进, 等. RBCC发动机性能分析模型改进方法研究[J]. 固体火箭技术, 2010, 33(4): 387-390. LYU X, HE G Q, LIU P J, et al. Improvements to RBCC engine performance analysis model[J]. Journal of Solid Rocket Technology, 2010, 33(4): 387-390. DOI:10.3969/j.issn.1006-2793.2010.04.006 (in Chinese) |
| [35] |
王洪信, 徐旭. 火箭基组合循环发动机性能迭代算法研究[J]. 火箭推进, 2015, 41(1): 56-62,89. WANG H X, XU X. Research on performance iterative algorithm of rocket based combined cycle engine[J]. Journal of Rocket Propulsion, 2015, 41(1): 56-62,89. DOI:10.3969/j.issn.1672-9374.2015.01.009 (in Chinese) |
| [36] |
安佳宁. RBCC(火箭基组合循环)引射模态研究[D]. 长沙: 国防科学技术大学, 2011. AN J N. Investigation of rocket-based combined cycle engine ejector mode[D]. Changsha: National University of Defense Technology, 2011. (in Chinese) |
| [37] |
叶中元. RBCC组合发动机的方案分析和工作模态[J]. 火箭推进, 2003, 29(1): 8-12. YE Z Y. Concept analyses and operation mode of RBCC engine[J]. Journal of Rocket Propulsion, 2003, 29(1): 8-12. DOI:10.3969/j.issn.1672-9374.2003.01.002 (in Chinese) |
| [38] |
黄伟, 罗世彬, 王振国. 火箭基组合循环(RBCC)发动机性能分析[J]. 火箭推进, 2007, 33(5): 6-10. HUANG W, LUO S B, WANG Z G. Performance analysis of RBCC engine[J]. Journal of Rocket Propulsion, 2007, 33(5): 6-10. DOI:10.3969/j.issn.1672-9374.2007.05.002 (in Chinese) |
| [39] |
张蒙正, 李斌, 王君, 等. 关于RBCC动力系统的思考[J]. 火箭推进, 2013, 39(1): 1-7. ZHANG M Z, LI B, WANG J, et al. Thinking about RBCC propulsion system[J]. Journal of Rocket Propulsion, 2013, 39(1): 1-7. DOI:10.3969/j.issn.1672-9374.2013.01.001 (in Chinese) |
| [40] |
张蒙正, 张玫, 严俊峰, 等. RBCC动力系统工作模态问题[J]. 火箭推进, 2015, 41(2): 1-6. ZHANG M Z, ZHANG M, YAN J F, et al. Discussion about work modal of RBCC power system[J]. Journal of Rocket Propulsion, 2015, 41(2): 1-6. DOI:10.3969/j.issn.1672-9374.2015.02.001 (in Chinese) |
| [41] |
路媛媛, 张蒙正, 严俊峰. 火箭推力室喷管内激波对RBCC性能影响分析[J]. 火箭推进, 2013, 39(5): 46-50,97. LU Y Y, ZHANG M Z, YAN J F. Influences of shock wave in rocket nozzle on RBCC performance[J]. Journal of Rocket Propulsion, 2013, 39(5): 46-50,97. DOI:10.3969/j.issn.1672-9374.2013.05.008 (in Chinese) |
| [42] |
刘昊, 王君. RBCC发动机火箭推力增益之探讨[J]. 火箭推进, 2017, 43(1): 18-23. LIU H, WANG J. Discussion of rocket thrust augmentation for RBCC engine[J]. Journal of Rocket Propulsion, 2017, 43(1): 18-23. DOI:10.3969/j.issn.1672-9374.2017.01.003 (in Chinese) |
| [43] |
刘慧玲. 自寻的炮射导弹弹道仿真及优化[D]. 太原: 中北大学, 2019. LIU H L. Trajectory simulation and optimization of self-seeking artillery missile[D]. Taiyuan: North University of China, 2019. (in Chinese) |
| [44] |
梁德旺, 李博, 容伟. 热完全气体的热力学特性及其N-S方程的求解[J]. 南京航空航天大学学报, 2003, 35(4): 424-429. LIANG D W, LI B, RONG W. Thermodynamic characteristics of thermally perfect gas and solution of N-S equations[J]. Journal of Nanjing University of Aeronautics & Astronautics, 2003, 35(4): 424-429. DOI:10.3969/j.issn.1005-2615.2003.04.018 (in Chinese) |
| [45] |
GORDON S, MCBRIDE B J. Computer program for calculation of complex chemical equilibrium compositions and applications. Part 1: Analysis [R]. NASA Reference Publication 1311, 1994. https://ntrs.nasa.gov/api/citations/19950013764/downloads/19950013764.pdf
|
 2022, Vol. 40
2022, Vol. 40

