2. 西北工业大学 翼型、叶栅空气动力学国家级重点实验室,西安 710072
2. National Key Laboratory of Science and Technology on Aerodynamic Design and Research, NWPU, Xi’an 710072, China
空天飞行器是以吸气式组合发动机为动力,能够水平起降,在稠密大气层、临近空间和近地轨道机动飞行的可重复使用高超声速飞行器[1]。其可利用普通机场快捷进入空间,经济高效,可大幅提升空间投送、空天攻防能力,具有军民两用价值,因此被当今世界各国竞相发展。
从20世纪80年代,美欧等国家就相继启动了相应的研究计划,如美国NASP计划开展了X-30单级入轨空天飞行器概念研究[2],德国提出了Sänger两级入轨空天飞行器方案[3],英国提出了HOTOL单级入轨空天飞行器方案[4],最后这些计划均因技术难度太大和经费需求过高等各种原因而最终下马。进入21世纪后,随着高超声速技术的不断突破,空天飞行器技术的研究也呈现加速发展态势。2014年,英国提出了Skylon云霄塔单级入轨空天飞行器新方案[5],“佩刀”发动机预冷器技术也取得了重大突破。2016年,美国提出了基于“佩刀”组合发动机的两级入轨空天飞行器概念方案[6]。近年来,国内外在吸气式组合发动机、气动设计等方面开展了相关探索研究,取得了一定进展。文献[7]阐述了空天组合动力面临的技术挑战,分析了飞行器跨声速飞行时存在推力陷阱问题,指出推阻矛盾突出。文献[8]对火箭动力助推上升滑翔再入和吸气组合动力水平起降天地往返空天飞行器的气动问题进行了综述,指出气动布局设计技术是空天飞行器设计中的一项关键研究内容。
空天飞行器历经亚/跨/超/高超声速飞行,不同速域的气动特性差异明显,全机气动焦点变化大,操稳匹配设计难度大。要实现水平起降,低马赫数飞行时要求高升力,高马赫数飞行时要求高升阻比,需求的矛盾进一步加大了宽速域飞行器设计难度,以往常规飞行器气动设计方法已不适用,需要探索新的气动设计方法。据公开文献报道,目前主要有两种宽速域气动设计方法:一种是采用变体气动布局,如机翼平面形状是变化的,变体飞行器根据需要改变气动外形来适应宽速域飞行要求,但是结构及控制系统复杂,尤其是高超声速下结构热防护实现难度更大,目前国外对变体飞行器的研究虽然已经有一定进展[9-10],但距离工程实用还有较大差距,仍有诸多关键技术尚待解决。另一种设计方法是采用固定构型气动布局,通过优化气动外形,来满足宽速域的设计要求,其优点是降低了结构热防设计的难度。文献[11]针对固定构型飞行器,提出了一种涡波效应宽速域气动布局的概念方案,认为通过合理设计定平面乘波体,可以兼顾低速和高超声速气动性能;但目前乘波体设计离工程化的应用还有较大差距,而且考虑飞行器容积、升重匹配等总体指标约束条件后,仅通过涡波效应,难以满足宽速域飞行器的工程设计要求。
众所周知,机翼是常规飞行器的主要升力部件,直接影响飞行器起飞着陆性能、操稳品质,因此机翼及翼型设计与优化是飞行器气动布局的重要研究内容[12]。应用新翼型,并通过气动外形的优化设计,来解决空天飞行器宽速域飞行的设计难题,是当前一种新的设计思路。
近年来,本文作者研究团队韩忠华等[13]提出了一种兼顾低速、超/高超声速气动特性的宽速域翼型(NPU-Hyper-04),该翼型具有一定弯度,上表面较平坦,下表面具有双“S”形特征,通过二维机翼数值模拟研究,证明宽速域翼型具有良好的气动特性,有望应用于空天飞行器。对于空天飞行器大后掠机翼,机翼的三维效应影响显著,需要开展三维流动下宽速域机翼及翼型的气动特性分析以及新机翼工程化应用研究。
本文针对固定构型的气动布局,首先围绕飞行环境的特点,分析低速高升力与高速高升阻比、宽速域升重匹配、翼前缘热防护等设计要求,给出空天飞行器对机翼/翼型的新需求;然后基于NPU-Hyper-04宽速域翼型,进行三维机翼几何参数化建模和三维流动条件下翼型和机翼平面形状一体化设计。最后开展新机翼的工程应用研究,对全机状态下机身/机翼/翼型进行优化设计,以获得满足空天飞行器总体设计要求的一种气动布局。
1 空天飞行器对机翼/翼型需求分析本节围绕空天飞行器飞行环境的特点,通过宽速域飞行对升力、升阻比、升重匹配、结构热防护等设计要求的分析,给出空天飞行器对机翼/翼型新的需求。
1.1 飞行环境的特点两级入轨空天飞行器,如德国Sänger,采用两级背负式水平起降方案,一级以涡轮冲压组合TBCC(Turbine Based Combined Cycle)发动机为动力,水平起降飞行时采用涡轮发动机,高速飞行时采用超燃冲压发动机,二级以火箭发动机为动力。
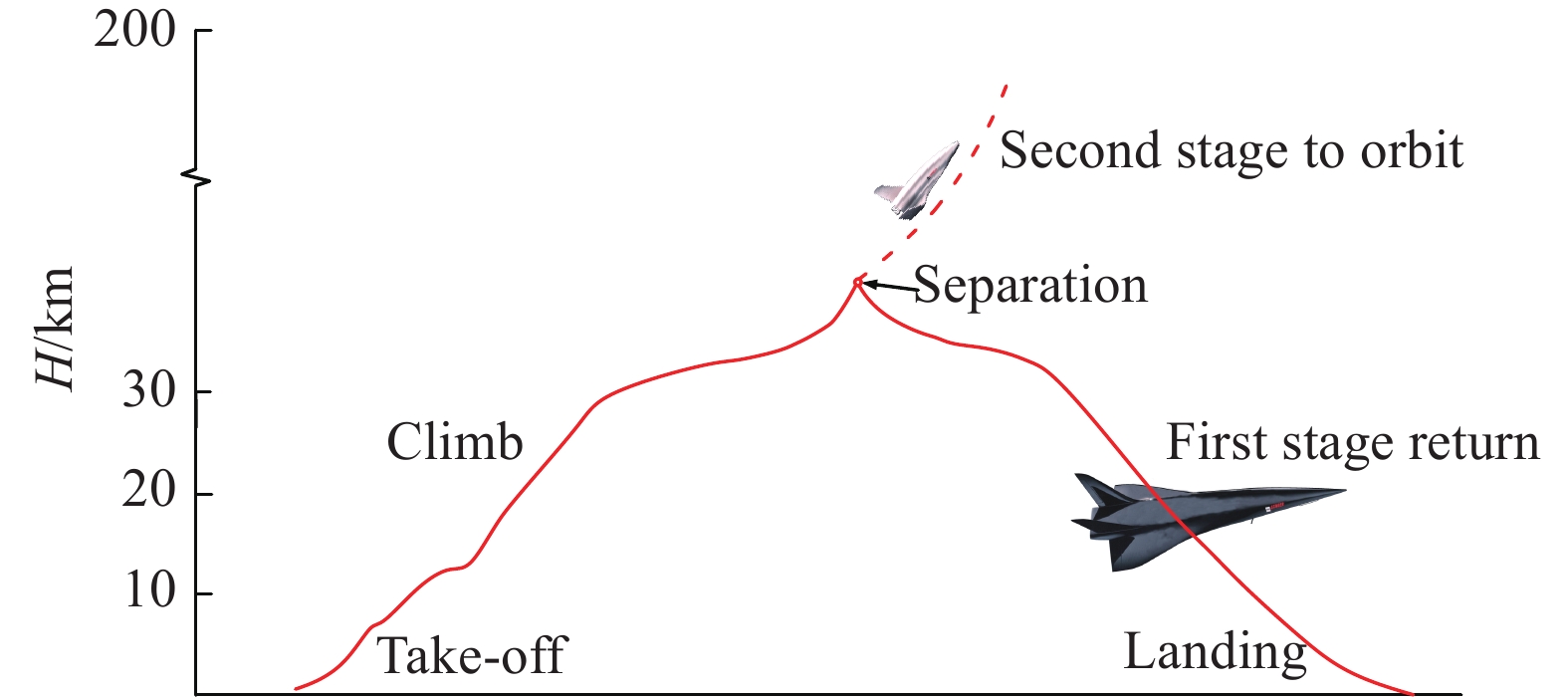
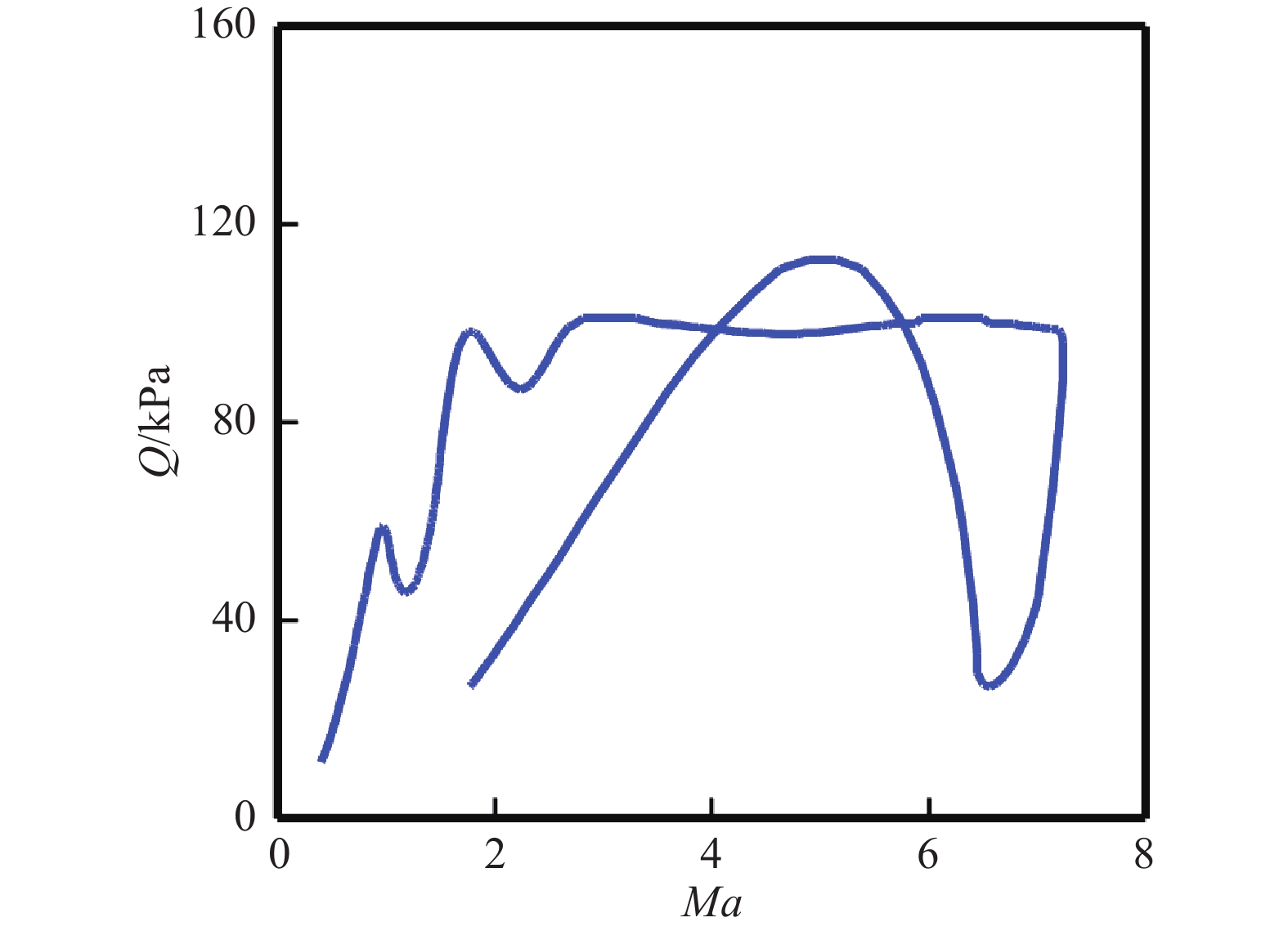
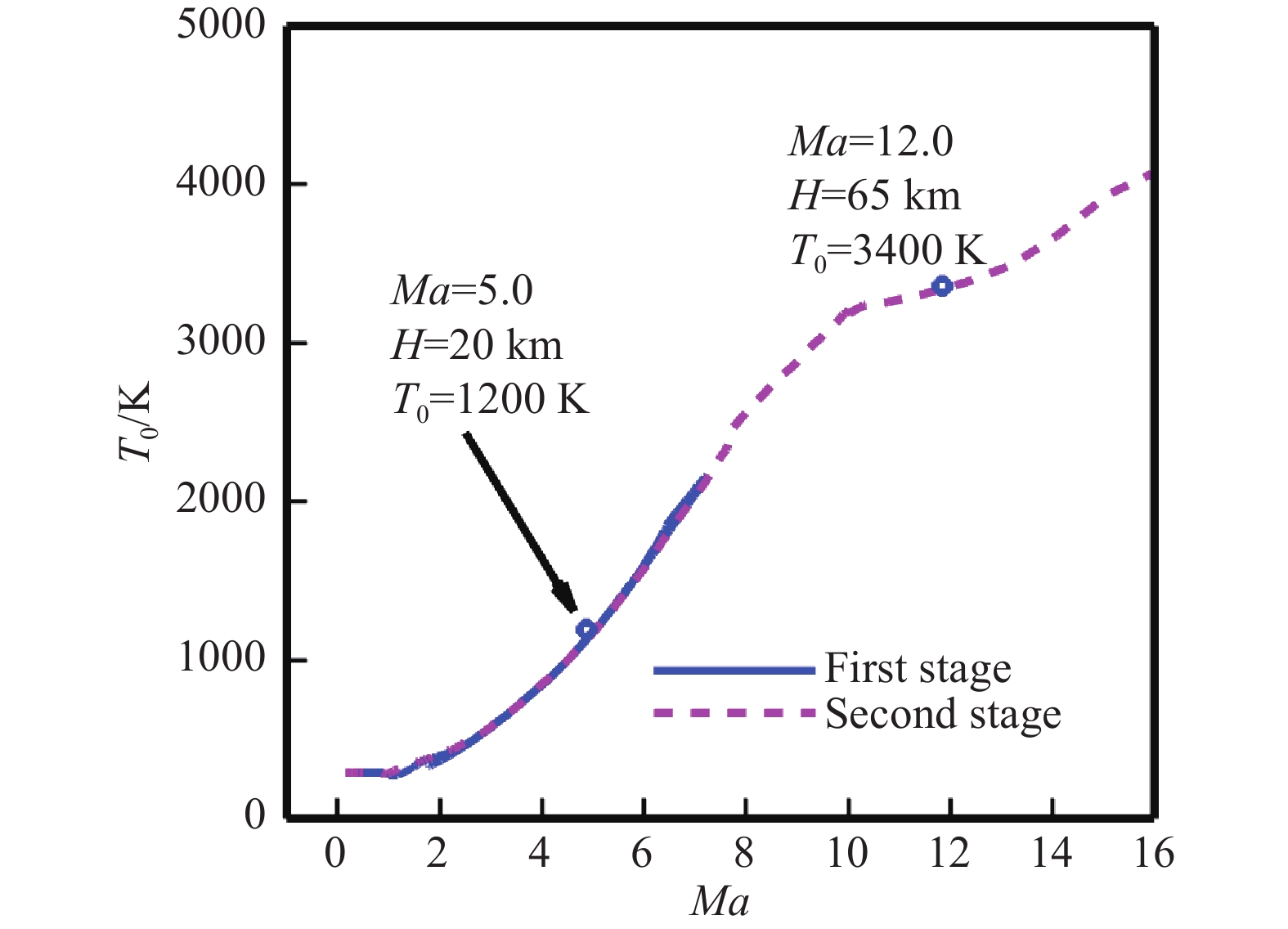
图1给出了空天飞行器典型飞行剖面示意图,一级飞行马赫数为Ma = 0~8,高度为H = 0~40 km,飞行环境复杂[14-16],宽广的空域和速域引起的动压变化大。图2给出了空天飞行器一级动压随马赫数的变化,由图可见,飞行过程中动压变化了一个数量级,高动压可达120 kPa,而低动压小于20 kPa。图3给出了空天飞行器来流总温随马赫数的变化,由图可见,当Ma = 5时来流总温为1200 K,当Ma = 12时二级飞行器来流总温为3400 K。由此可见,空天飞行器动压变化大,高超声速飞行时热环境严酷,对飞行器升力、升阻比及翼前缘热设计等提出了很高要求。
|
图 1 空天飞行器典型飞行剖面示意图 Fig.1 Sketch of flight trajectories of aerospace vehicles |
|
图 2 空天飞行器一级动压随马赫数的变化 Fig.2 Variation of the dynamic pressure as a function of Mach number of first stage aerospace vehicles |
|
图 3 空天飞行器来流总温随马赫数的变化 Fig.3 Variation of the freestream total temperature as a function of flight Mach number |
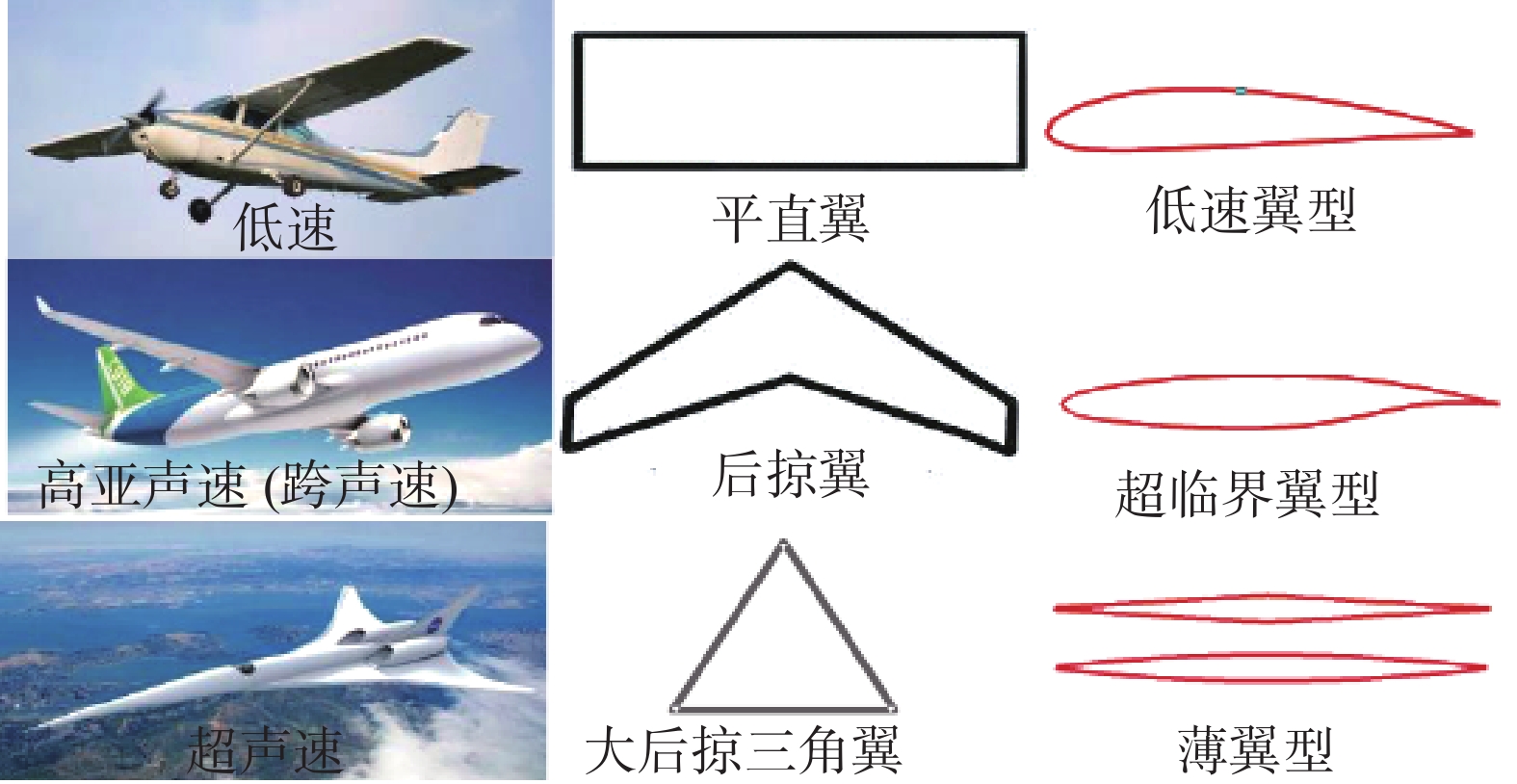
亚/跨/超声速飞行器气动设计经验表明:对于同一种构型,不同速域下增升减阻的流动机理不同,从而使得不同速域下最优机翼外形差别较大,对翼型的需求也显著不同。图4给出了不同速域下几种典型飞行器的机翼平面形状与翼型。由图可见,对于低速飞行器,机翼平面形状多采用大翼展平直翼,翼型相对厚度较大;对于超声速飞行器,机翼一般采用大后掠三角平面形状,翼型可采用相对厚度较薄的四边型、六边型或双弧型等翼型。由此可见,由于空天飞行器飞行空域大、速域宽,从而导致高低速域对机翼/翼型外形的需求存在矛盾。
|
图 4 不同速域下典型飞行器机翼平面形状及翼型 Fig.4 Wing and airfoil shapes of typical aircrafts with different speeds |
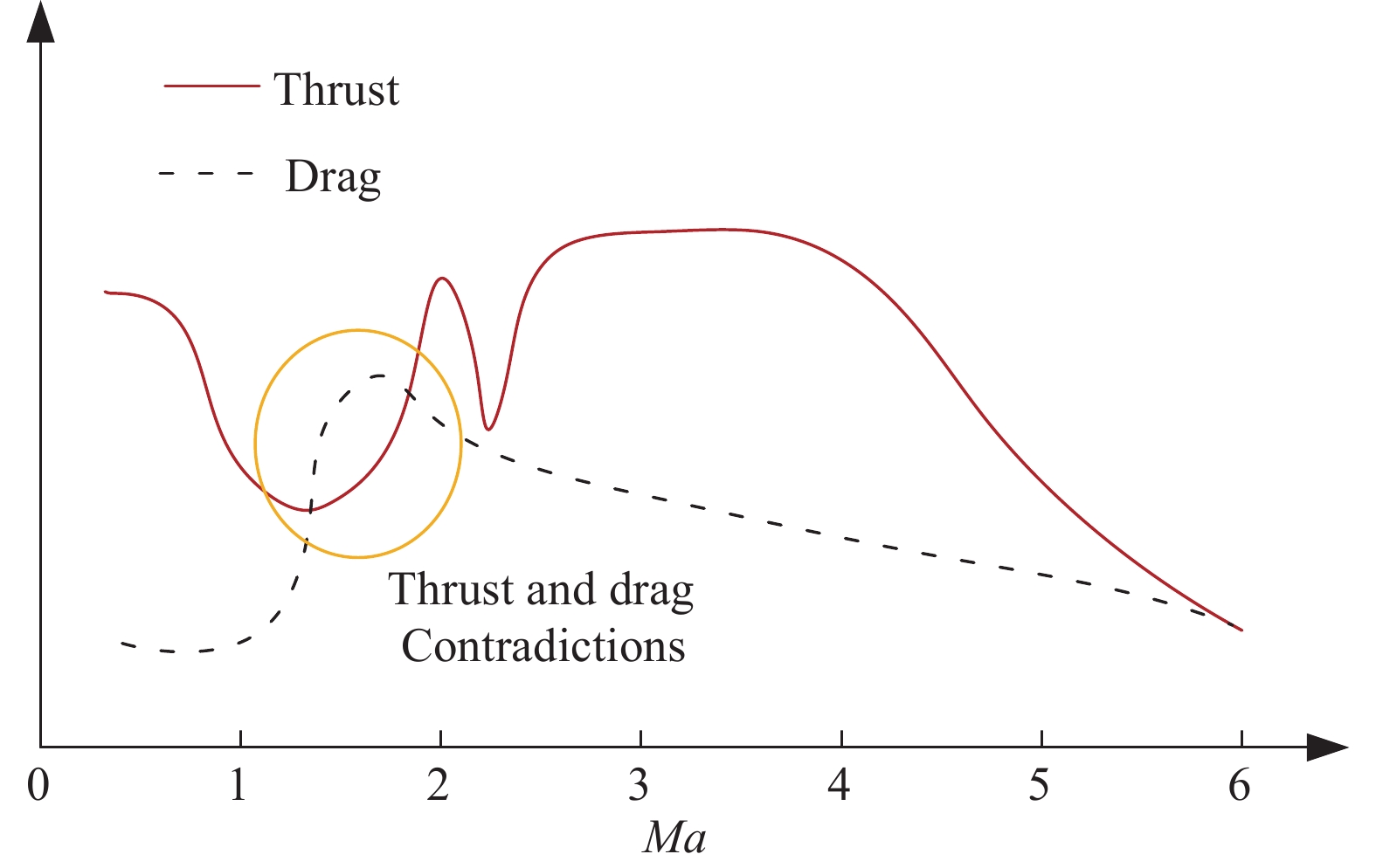
图5给出了空天飞行器推力与阻力随马赫数的变化[7]。由图可见,在低速起飞和降落阶段,发动机推力远大于阻力,推阻余量较大。起飞时,飞行器处于满油状态,重量最重,升重矛盾突出,这就要求机翼/翼型具有较高升力和升力线斜率,以满足起飞最大重力的需求。在高速飞行时,随着燃油的消耗,飞行器重量降低,升重矛盾逐步缓解。然而,在跨声速、低超声速和高超声速飞行时,发动机推力和阻力接近,推阻余量较小,推阻矛盾突出,这就要求机翼/翼型需要尽可能减小阻力,提高升阻比,以满足推阻匹配设计的要求。因此,对于空天飞行器一级,机翼/翼型需要同时满足低速高升力和高速高升阻比的设计要求。
|
图 5 空天飞行器推力与阻力随马赫数的变化 Fig.5 Variations of thrust and drag as a function of Mach number |
空天飞行器宽速域飞行动压变化范围大,导致飞行过程中升重匹配设计难度大。表1给出了空天飞行器一级在起飞和降落、爬升和巡航飞行时对升力系数的需求。由表1可见,不同飞行阶段对升力系数的需求差异较大。在以马赫数0.3~0.5起飞和降落阶段,飞行动压约为5~20 kPa,对升力系数的需求约为5~15;在以马赫数5~7爬升和巡航飞行阶段,飞行动压约为50~100 kPa,对升力系数的需求约为0.75~1.5。在升重平衡约束条件下,起飞时动压最低,满油状态下飞行器重量最重,升重匹配设计要求飞行器具有足够大的升力面。随着马赫数增加,飞行动压增大,燃油消耗使得飞行器重量逐渐减轻,升重匹配设计需要的升力面逐渐减小。由于要经历低速起降与高速飞行多种不同飞行阶段,将会出现起降时升力满足需求,但高速飞行时升力却过大的现象,从而导致升重平衡时使用升阻比偏离最大升阻比;或者高速巡航时升力合适,但是起降时却无法提供足够大的升力来平衡重力,从而导致起飞或着陆速度过大的问题。因此,空天飞行器机翼/翼型必须要满足宽速域升重匹配设计要求。
| 表 1 空天飞行器一级在不同飞行阶段对升力系数需求 Table 1 Requirements of lift coefficient for aerospace vehicles at the first stage |
|
|
空天飞行器在大气层中长时间以高超声速飞行时,翼前缘的热环境最为恶劣[17],且温度梯度也大,这会给结构与热防护设计带来困难。若翼前缘半径较小,则气动阻力小,但是热应力集中,使得机翼结构热防护存在破坏的风险;若翼前缘半径较大,虽然热环境会降低,但是阻力又会增大。因此,翼前缘降热与减阻的需求是矛盾的,需折中选取翼前缘半径。根据以往高速飞行器的设计经验,考虑结构热防护设计要求,翼型前缘半径可选取弦长的0.05%~0.2%。
此外,翼型通常具有一定厚度,以满足机翼的强度设计要求[18]。一般情况下,对于亚声速运输机,翼型最大相对厚度选择为12%~18%,可获得更大的升力系数。对于采用后掠机翼的超声速飞机,翼型最大相对厚度约为10%,以满足后掠机翼对结构强度设计的要求。对于常规超声速飞机,翼型最大相对厚度大多在2%~6%范围内。对于高超声速飞行器,为减小波阻,理论上来讲,翼型相对厚度应越薄越好,但是考虑结构热防护可实现性,建议宽速域翼型最大相对厚度可选取弦长的2%~6%。另外,考虑现有机械加工精度,建议翼型后缘厚度不小于弦长的0.8%。
2 宽速域翼型与机翼平面形状一体化设计针对空天飞行器对翼型设计的新需求,作者研究团队设计了一种宽速域翼型(NPU-Hyper-04)[13]。本节基于该翼型,考虑低速高升力、高速高升阻比以及宽速域升重匹配设计、结构热防护的设计要求,采用优化设计方法,进行三维流动下翼型与机翼平面形状一体化设计。
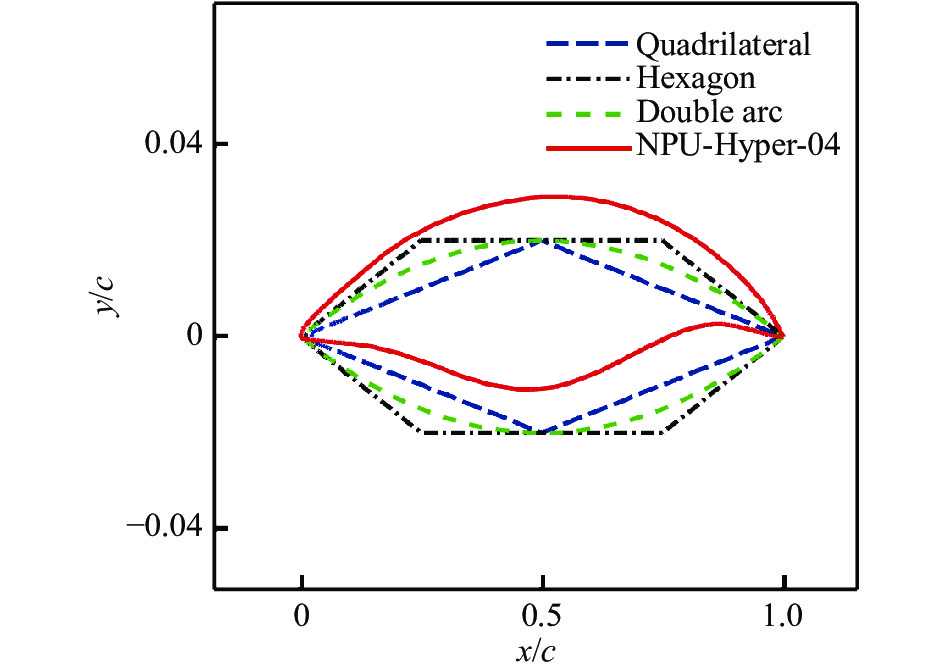
2.1 宽速域翼型的气动特性对于高亚声速飞行,一般可采用NACA翼型,翼型前缘半径较大,可减小大攻角下的负压峰值,且较为丰满的上表面头部型线可获得更好的升力特性和失速特性,翼型下表面前缘压缩较弱。对于超/高超声速飞行,一般采用菱形翼和六边形翼型,翼型前缘半径较小,可减小激波阻力,下表面前段具有较强的压缩激波以产生升力。根据翼型表面流动特点,低速时翼型上表面形状对升力影响大,而高速时翼型下表面形状对升力影响大。因此,为了能同时兼顾低速高升力和高速高升阻比的需求,设计了一种上表面类似弧形、下表面双“S”形的宽速域新翼型。考虑前缘结构热防护设计要求,当翼前缘半径取弦长的0.1%,最大相对厚度取弦长的4%时,图6给出了宽速域翼型(NPU-Hyper-04)与常规翼型形状的对比。由图可见,宽速域翼型的特点是:上表面采用较为丰满的头部型线,低速可获得更好的升力特性;下表面具有双“S”的外形特征,前缘反“S”形状在跨声速时形成前加载,可增加升力,而高超声速时形成等熵压缩波,可降低波阻,提高升阻比;后缘的“S”形,跨声速时形成后加载,可增加升力,而高超声速时,形成“二次高压”,有利于增加升力。另外,相对传统典型翼型,宽速域翼型下表面为双“S”的外形,曲面形状复杂,使得结构设计难度有所增大。因此,气动优化设计时,应尽量使得下表面外形曲率变化小,流线型较好,以降低结构热防护实现难度。
|
图 6 宽速域翼型与现有常规典型形状对比 Fig.6 Comparison of different airfoil geometries |
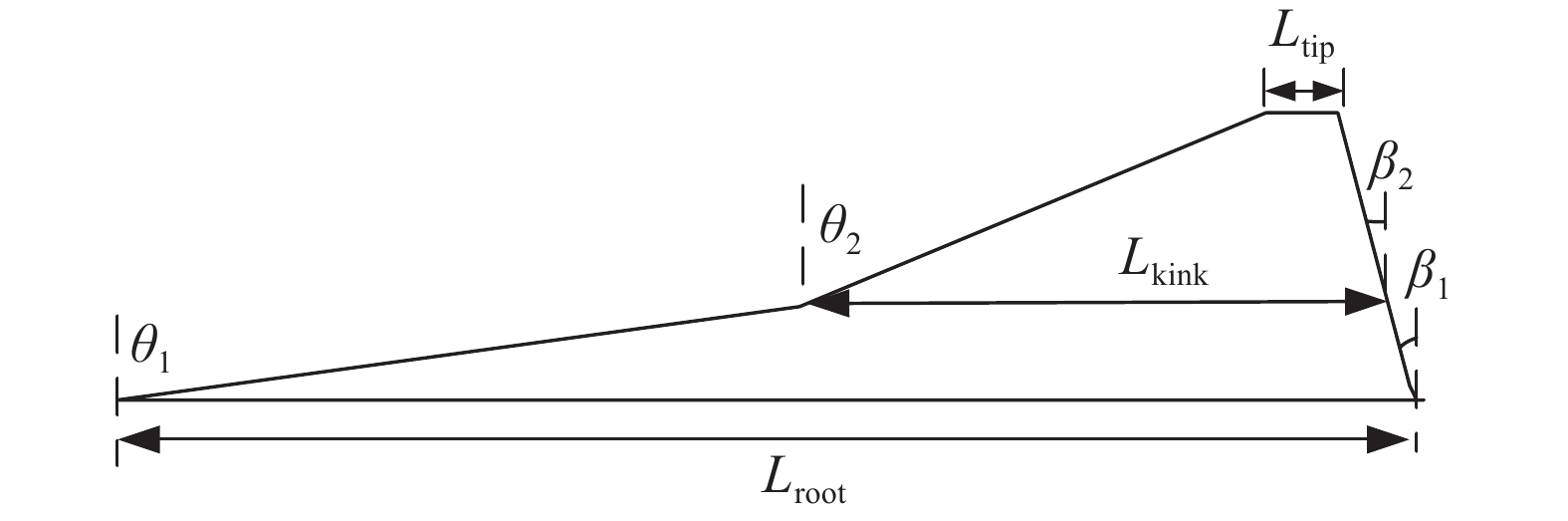
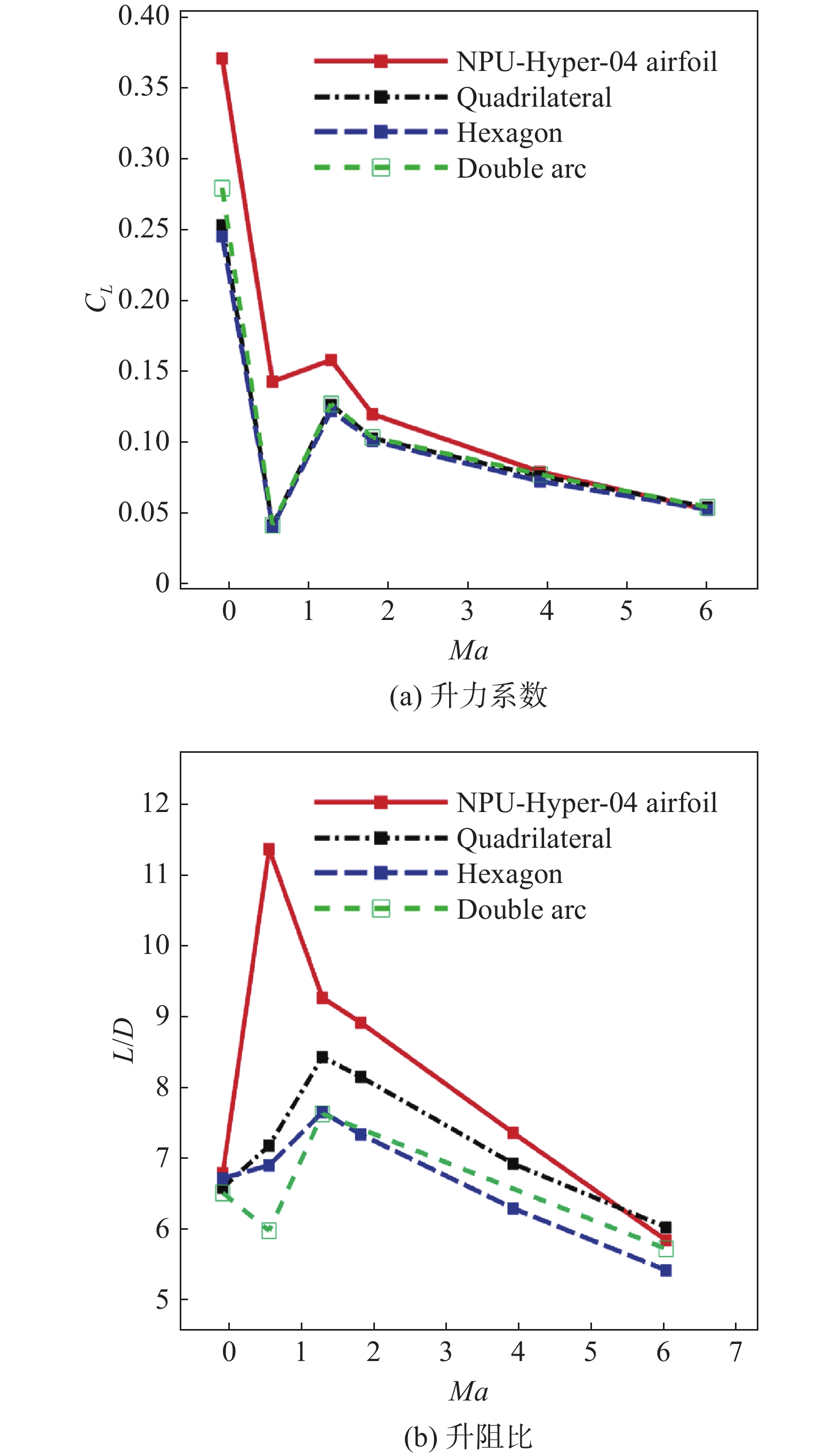
图7为双三角机翼平面形状。将NPU-Hyper-04宽速域翼型与四边形、六边形、双弧形翼型应用于双三角机翼,分别进行不同马赫数下的三维流场计算,获得了四种机翼的升力系数与升阻比随马赫数的变化,如图8所示。由图可见,相比于常规翼型,使用NPU-Hyper-04宽速域翼型的机翼在亚声速时的升力系数和亚/跨声速时的升阻比得到大幅度提升,如当Ma = 0.2时,宽速域翼型机翼的升力系数较四边形翼型的提升了45.9%,较六边形翼型的提升了50.5%,较双弧形翼型的提升了32.4%;当Ma = 0.8时,宽速域翼型机翼的升阻比较四边形翼型的提升了57.7%,较六边形翼型的提升了63.9%,较双弧形翼型的提升了89.1%;当Ma = 1.5时,宽速域翼型机翼的升阻比较四边形翼型的提升了9.8%,较六边形翼型的提升了28.3%,较双弧形翼型的提升了21.3%。而在高超声速时升阻比也有一定提高,当Ma = 6时,宽速域翼型机翼的升阻比较六边形翼型的提升了7.6%,较双弧形翼型的提升了1.8%,但稍微低于四边形翼型的,升阻比降低了3.1%。
|
图 7 双三角机翼平面形状 Fig.7 Sketch of double-triangle wing |
|
图 8 不同翼型的机翼升力系数与升阻比随马赫数变化的对比 Fig.8 Variations of CL and L/D as a function of Ma for wings with different airfoils |
综上,NPU-Hyper-04宽速域翼型在亚/跨/超/高超声速时均具有较高的升阻比,这与空天飞行器低速高升力与高速高升阻比的要求是一致的,具有较好的工程应用前景。然而,对于空天飞行器大后掠机翼,三维效应影响显著,需要开展三维流动优化设计,同时,还需要考虑升重匹配设计的约束条件。
2.2 三维机翼优化设计方法本节针对图7给出的双三角机翼,进行三维机翼几何参数化建模。三维机翼形状可采用机翼平面形状参数化与翼根、翼转折、翼尖三个站位处翼型参数化相结合的方法,来实现双三角翼外形三维参数化建模。
双三角翼平面外形可由内翼前缘后掠角(
控制翼型剖面采用一种基于型函数/类函数变换的CST方法进行参数化[19]。翼型上、下表面的表达式为:
| $ {y_{\text{u}}} = C\left( x \right) {S_{\text{u}}}\left( x \right) + x {y_{_{\text{TEu}}}} $ | (1) |
| $ {y_{\text{l}}} = C\left( x \right) {S_{\text{l}}}\left( x \right) + x {y_{_{\text{TEl}}}} $ | (2) |
其中,
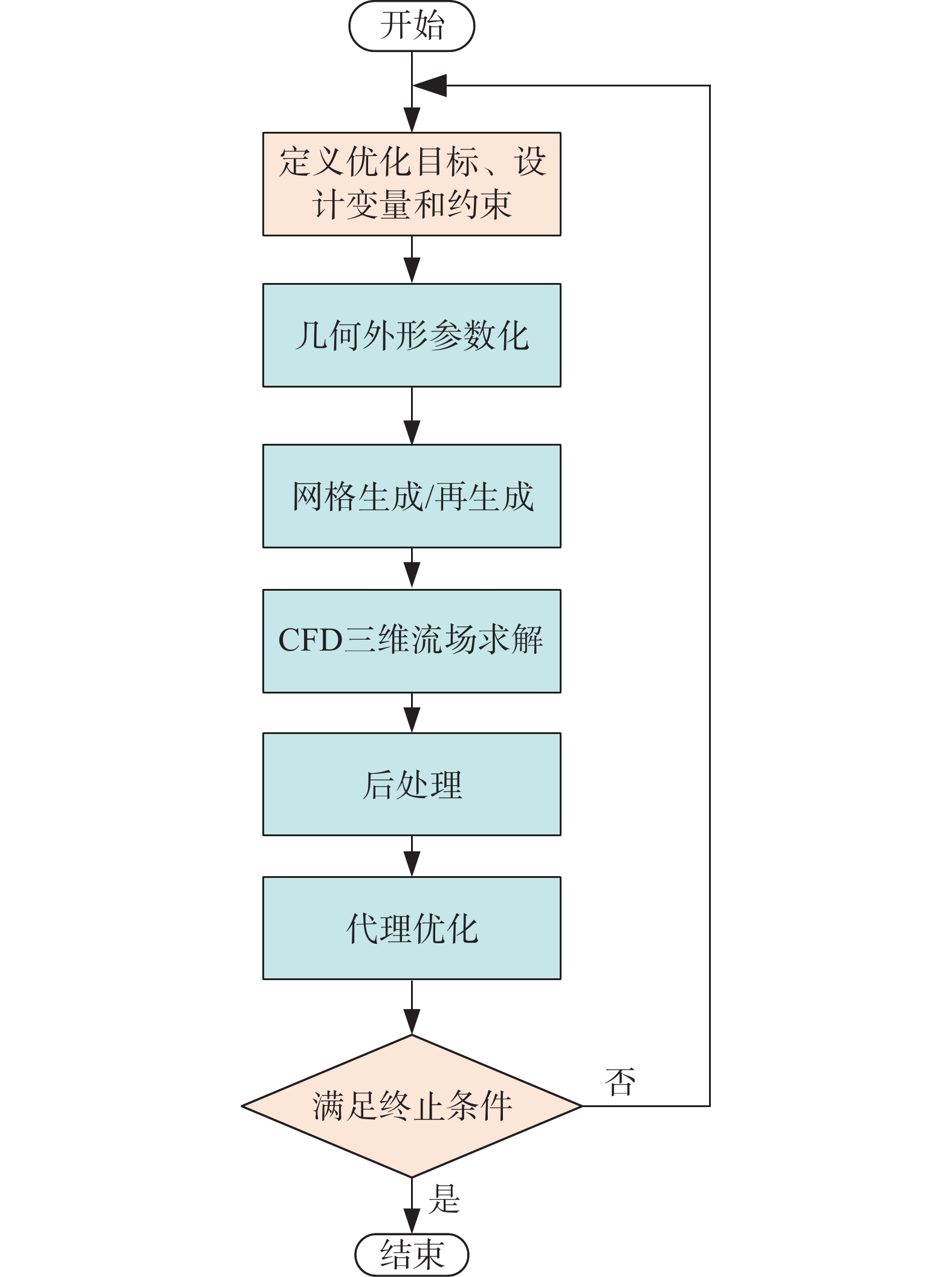
采用基于代理模型的多目标多约束优化软件“SurroOpt”[20]进行三维流动下的宽速域机翼优化设计,气动优化设计流程如图9所示。
|
图 9 气动优化设计流程 Fig.9 Process of aerodynamic design and optimization |
首先基于定义的优化目标、设计变量和约束条件,开展几何外形参数化建模,其次对参数化模型进行网格生成,并对其进行CFD三维流场计算,然后通过后处理,用所获得的样本数据集,建立真实目标函数的代理模型,逐步逼近最优解,最后经过综合评估,当满足一定的终止条件时,优化过程结束。
2.3 优化设计目标及约束条件优化设计目标是三维机翼在超声速和高超声速条件下阻力最小,以提高三维机翼在宽速域升重平衡时的升阻比。本节以超声速Ma = 2和高超声速Ma = 6为例进行优化设计,具体优化设计目标为:
| $ \min \; \; {\omega _1} \Bigg(\frac{{{D_{Ma \;=\; 2}}}}{{{D_{0,\;Ma \;=\; 2}}}}\Bigg) + {\omega _2} \Bigg(\frac{{{D_{Ma \;=\; 6}}}}{{{D_{0,\;Ma \;=\; 6}}}}\Bigg) $ | (3) |
其中,
三维机翼优化设计时,约束条件主要考虑两方面因素:一是宽速域升重匹配设计的约束条件;二是机翼结构热防护设计的约束条件。
飞行过程中随着燃料的消耗,飞行器重量发生变化,宽速域升重匹配设计的约束条件为:
| $ \begin{split} {\text{s.t.}}\;\;&{L_{Ma = 0.3}} \geqslant W \\& {L_{Ma = 2}} = 0.85W \\& {L_{Ma = 6}} = 0.7W \end{split} $ | (4) |
其中,
机翼/翼型优化时,结构热防护设计约束条件是通过约束翼型的前缘、后缘倒圆半径和最大厚度来实现的,约束条件为:
| $ \begin{split}{\text{s.t.}}\;\;&{t}_{\text{root}}\geqslant 0.99{t}_{0}{\text{,}}{t}_{\text{kink}}\geqslant 0.99{t}_{0}{\text{,}}{t}_{\text{tip}}\geqslant \text{0}\text{.99}{t}_{0}\\& {t}_{\text{10{\text{%}}root}}\geqslant 0.008{\text{,}}{t}_{\text{10{\text{%}}kink}}\geqslant 0.008{\text{,}}{t}_{\text{10{\text{%}}tip}}\geqslant 0.008\\& {t}_{\text{90{\text{%}}root}}\geqslant 0.008{\text{,}}{t}_{\text{90{\text{%}}kink}}\geqslant 0.008{\text{,}}{t}_{\text{90{\text{%}}tip}}\geqslant 0.008\end{split} $ | (5) |
其中,
基于NPU-Hyper-04宽速域翼型的双三角机翼,记为Case0基准状态,针对以下三种状态进行优化设计。第一种是采用NPU-Hyper-04宽速域翼型,沿机翼展向的翼型不变化,优化设计机翼平面形状,记为Case1优化状态;第二种是机翼平面形状不变,优化设计翼型,翼型沿机翼展向是变化的,记为Case2优化状态;第三种是沿机翼展向的翼型及机翼平面形状均可变化,即机翼/翼型一体化优化设计,记为Case3优化状态。
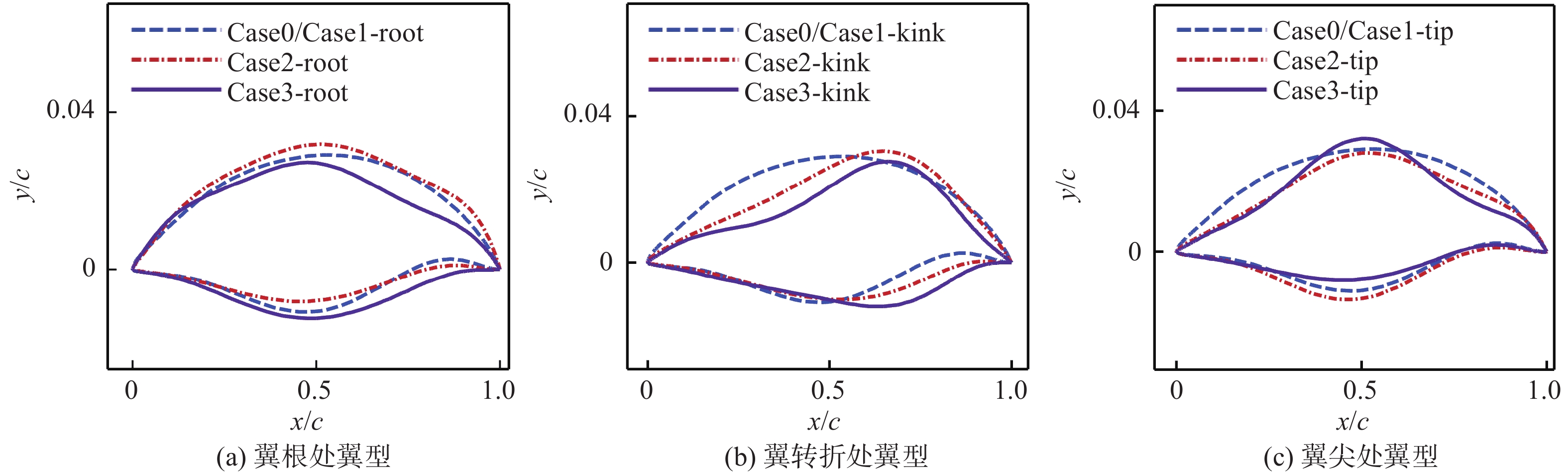
图10(a)~(c)分别给出了不同优化状态下获得的机翼在翼根、翼转折和翼尖处的翼型形状对比。由图中可见,在相同优化目标下,翼根、翼转折和翼尖处的翼型形状有较大差异,且Case2和Case3优化状态下获得的翼型沿机翼展向是变化的。
|
图 10 不同优化状态下机翼三个部位的翼型形状对比 Fig.10 Comparisons of airfoil geometries obtained by different optimization methods at three locations of a double-triangle wing |
对于Ma = 0.3、ɑ = 10°起飞状态,在相同升力约束条件下,进行不同优化状态下机翼三维流场数值计算。图11(a)~(d)分别给出了基准状态与三种优化状态下机翼表面压力系数及Cp = −1.2时的涡量图。由图可见,相对于基准状态,Case1和Case2优化状态的机翼面积均减小了37.2%,Case3优化状态的机翼面积减小了36.3%。三种优化状态下的机翼上表面均产生了较强旋涡流动,这有利于提高低速起飞状态的升力,即提高了机翼单位面积产生的升力。

|
图 11 Ma = 0.3时不同状态下机翼表面压力系数及Cp = −1.2涡量图 Fig.11 Comparisons of surface pressure and vorticity (Cp = −1.2) obtained by different optimization methods at Ma = 0.3 |
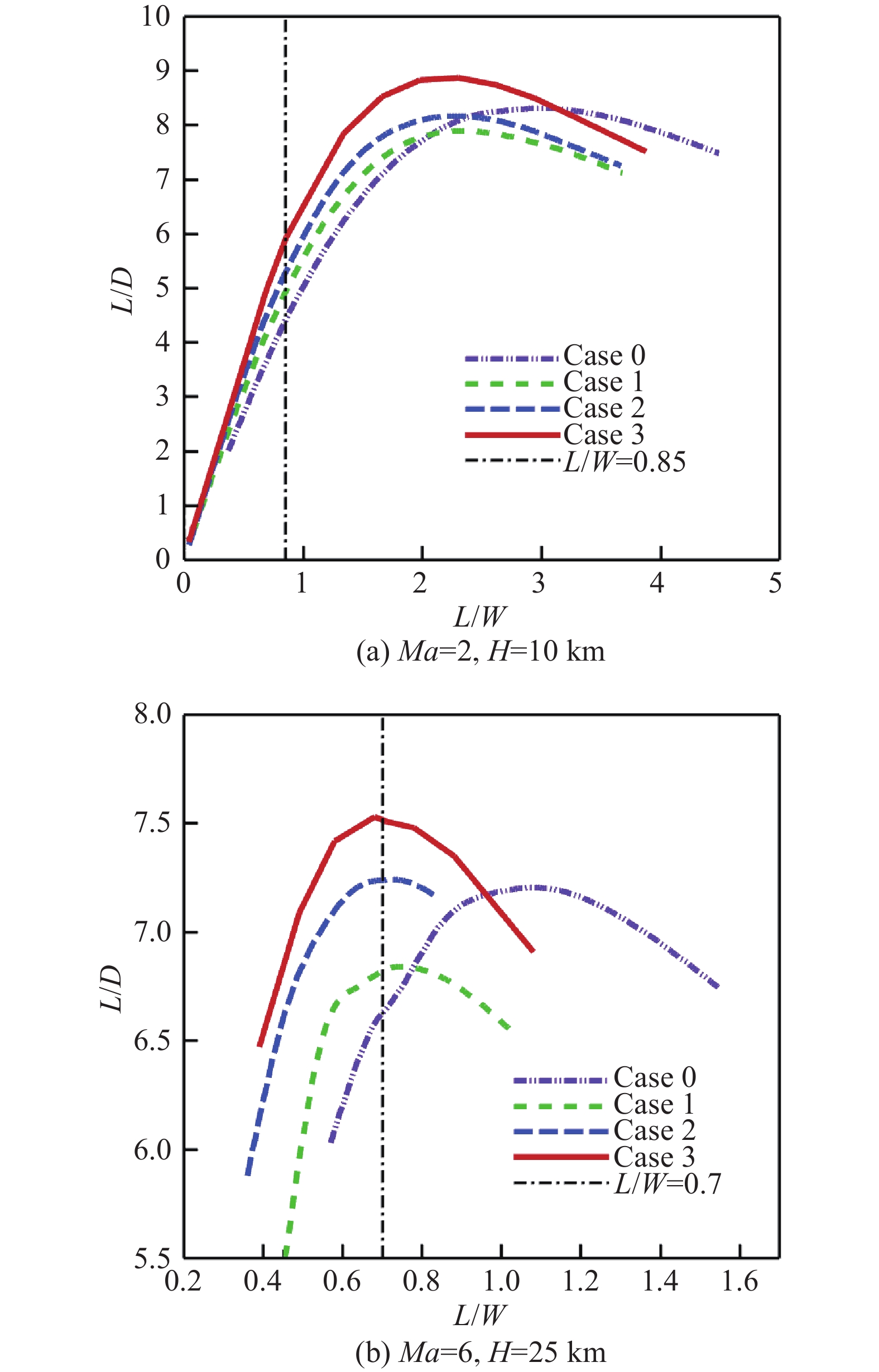
针对Ma = 2、H = 10 km与Ma = 6,H = 25 km飞行条件,考虑飞行器重力随飞行马赫数的变化,当Ma = 2时,飞行器重力变为起飞重力的0.85倍,当Ma = 6时,飞行器重力变为起飞重力的0.7倍,图12(a)~(b)分别给出了不同状态下超声速和高超声速飞行时升重平衡的升阻比,图中横坐标为升力与飞行器起飞重力的比值。结果表明:相对于基准状态Case0,三种优化状态下的超声速和高超声速升阻比均有所提高,Case1状态的升重平衡升阻比分别提高了11.9%和2.7%;Case2状态的升重平衡升阻比分别提高了19.5%和8.8%;Case3的优化结果效果最佳,升重平衡升阻比分别提高了33.5%和12.9%,特别是在高超声速飞行时,飞行攻角接近最大升阻比对应的攻角。
|
图 12 不同飞行条件下升重平衡的升阻比 Fig.12 Lift-weight-balance L/D at different fight status |
综上所述,对于Case1优化状态,采用定翼型、优化机翼平面形状,可实现兼顾不同速域对升力的需求。对于Case2优化状态,定机翼平面形状,优化机翼各剖面的翼型,可提升宽速域升阻比。对于Case3优化状态,同时优化机翼平面形状和机翼典型站位的翼型,能够获得宽速域综合性能更好的机翼,且机翼面积小,升力效率高,超/高超声速飞行时的升重平衡升阻比高。
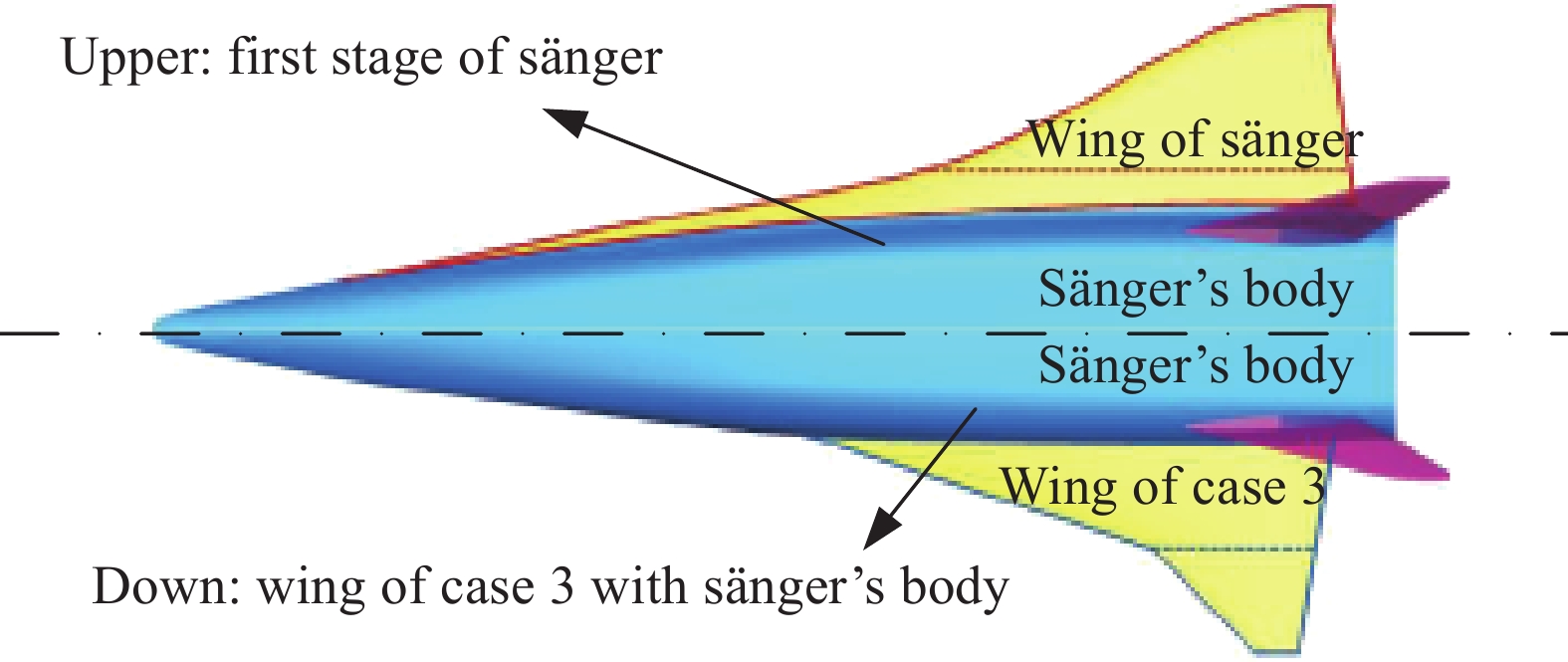
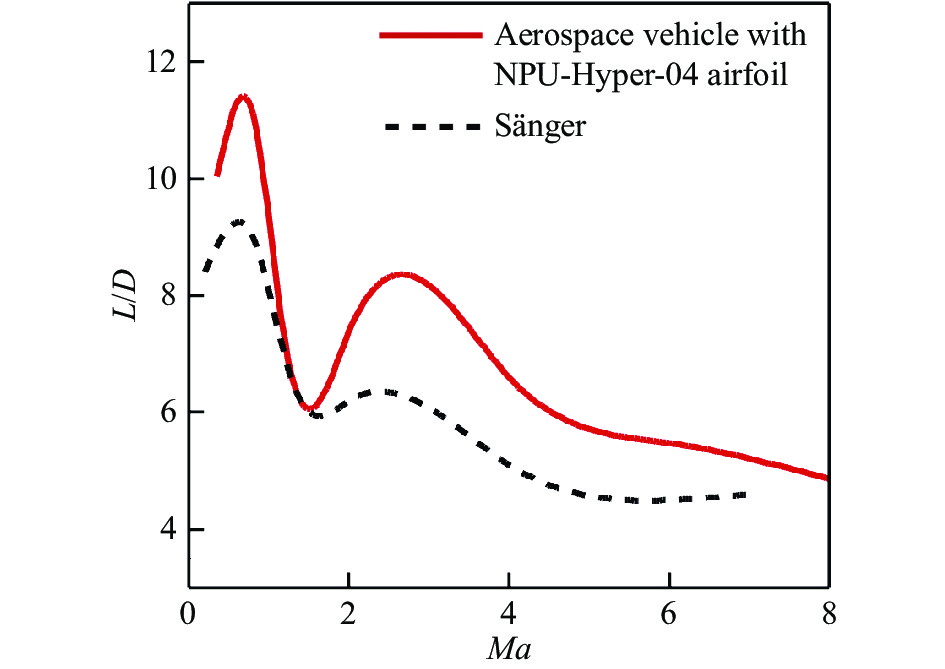
3 宽速域机翼/翼型的应用研究 3.1 宽速域机翼空天飞行器的升阻比文献[21]给出了德国两级入轨Sänger空天飞行器一级气动外形,机身长度为82.4 m,翼展宽度为45.2 m,机翼翼型未见报道。本文基于Sänger飞行器的机身,再采用2.4节中Case3优化状态下的机翼与翼型,进行空天飞行器一级外形设计。图13给出了两种机翼外形的空天飞行器示意图,图中上半部为Sänger一级飞行器半模外形,下半部为应用Case3优化状态下新机翼和Sänger飞行器机身的飞行器半模外形。采用数值模拟,获得全机气动特性,将全机的最大升阻比与Sänger一级飞行器进行对比,图14给出了不同机翼空天飞行器最大升阻比的对比。
|
图 13 两种机翼的空天飞行器外形示意图 Fig.13 Layouts of aerospace vehicles with different wings |
|
图 14 不同机翼空天飞行器最大升阻比的对比 Fig.14 Comparison of the maximum L/D for aerospace vehicles with different wings |
由图可见,将Case3状态的机翼和翼型应用于空天飞行器,在低速/高亚声速(Ma<1)和超/高超声速(Ma>2)条件下,对应的最大升阻比均大于Sänger飞行器,在跨声速附近(1<Ma<2)对应的最大升阻比与Sänger飞行器基本相同。原因是:宽速域机翼/翼型在低速时,翼型前缘低压吸力大,机翼产生较大涡升力,机翼升力效率高;高速时翼型波阻小,具有双“S”外形特征的下表面提升了升阻比。
综上所述,应用宽速域机翼/翼型的空天飞行器在低速、超声速和高超声速时具有较好的气动特性。但是在跨声速时,最大升阻比仍然较低。且从图12(a)可见,在超声速时升重平衡的升阻比偏离最大升阻比较多,特别是在1<Ma<2范围,正是发动机推阻矛盾最大的速域,还需优化升重平衡的使用升阻比。
对于Sänger空天飞行器一级,机身约占全机纵向投影面积的70%以上,机身的升力占比大。上述研究结果也表明,在机身外形不改变情况下,仅通过优化翼型与机翼平面形状,对提高全机宽速域的升阻比,特别是在跨声速状态下的升重平衡升阻比效果有限。因此,有必要在此基础上,进一步开展全机外形优化设计,降低阻力,提高跨声速时升重平衡的升阻比。
3.2 全机优化设计方法本节根据飞行器总体设计要求,基于配置Case3状态机翼的空天飞行器(记为Opt0基准构型),在进行翼型和机翼平面形状一体化设计时,同时考虑机身外形优化,开展全机状态下机身/机翼/翼型一体化优化设计,记为Opt1优化构型。
优化设计方法与三维机翼参数化建模方法均已在2.2节介绍,此处不再赘述。机身外形参数化建模采用自由变形(Free Form Deformation,FFD)参数化方法[22]。FFD方法具有变形能力强,不需要对初始外形进行拟合,并且可以保持初始几何外形的连续性、光滑性,且操作简单等优点,目前已作为一种常用几何外形参数化方法应用于飞行器气动外形设计[23]。完成参数化建模后,采用VBA语言对CATIA软件进行二次开发,对三维机翼与机身进行自动剪裁装配,最终实现全机复杂外形的参数化建模。
优化设计目标是全机在高亚声速/超声速/高超声速阻力最小,以提高全机宽速域升重平衡时的升阻比。设计中考虑宽速域升重匹配和结构热防护设计的约束条件。优化目标和约束条件的表达式与2.3节一致。
3.3 全机状态下机身/机翼/翼型优化结果分析对高亚声速(Ma = 0.8、H = 4 km)、超声速(Ma = 2、H = 10 km)与高超声速(Ma = 6、H = 25 km)飞行状态,在满足Ma = 0.3起飞时的升力条件下,图15(a)~(b)分别给出了基准构型Opt0和优化构型Opt1的全机升重平衡时的升阻比。当Ma = 0.8时,重力为起飞重力的0.9倍,当Ma = 2时,重力为起飞重力的0.85倍,当Ma = 6时重力为起飞重力的0.7倍。由图15可见,相对于基准构型Opt0,优化构型Opt1的宽速域升阻比全面提升。在满足低速起飞要求的前提下,高亚声速Ma = 0.8的升重平衡升阻比为12.2,提高了5.9%,超声速Ma = 2的升重平衡升阻比为4.6,提高了10.3%;高超声速Ma = 6的升重平衡升阻比为4.8,提高了0.7%。综上,通过全机优化设计,高亚声速至超声速时升重平衡升阻比明显提高,且此时飞行攻角接近最大升阻比对应的攻角。

|
图 15 亚/超/高超声速全机升重平衡时的升阻比 Fig.15 Comparisons of lift-weight-balance L/D |
本文围绕飞行环境特点、低速高升力与高速高升阻比、升重匹配和结构热防护等设计要求,给出了空天飞行器对机翼/翼型设计新需求。通过宽速域新翼型和机翼一体化设计,提高了机翼宽速域升重平衡时的使用升阻比。将宽速域新机翼应用于典型空天飞行器,通过全机状态下的机身/机翼/翼型外形优化设计,获得了一种宽速域气动布局。全机在低速、跨声速、超声速和高超声速时具有较好的气动特性。得到的主要结论如下:
1)通过宽速域翼型与机翼平面形状一体化优化设计,获得了气动特性良好的新机翼外形。相对优化前的机翼,低速时机翼产生的升力效率提高了36.3%,超声速和高超声速升重平衡升阻比分别提高了33.4%和12.9%,特别是在高超声速飞行时,飞行攻角接近最大升阻比对应攻角。
2)应用宽速域新机翼的空天飞行器,能够较好地兼顾低速、跨声速、超声速和高超声速气动设计要求,宽速域最大升阻比高于德国Sänger空天飞行器。
3)对固定构型空天飞行器,通过机身/机翼/翼型一体化的优化设计,获得了一种气动特性良好的宽速域空天飞行器气动布局。与优化前外形相比,提高了升重平衡时的升阻比,高亚声速时提高了5.9%,超声速时提高了10.3%,高超声速时提高了0.7%,基本满足宽速域飞行器的设计要求。
4)优化获得的新翼型下表面具有双“S”的外形特征,相对传统翼型,机翼下表面型面比较复杂,对结构热防护制备会带来一定难度。后续研究工作中,将进一步评估飞行器应用新机翼带来的热环境变化。
| [1] |
KUCZERA H, SACHER P W, 著. 可重复使用空间运输系统[M]. 魏毅寅, 张红文, 王长青, 译. 北京: 国防工业出版社, 2015. KUCZERA H, SACHER P W. Reusable space transportation systems[M]. WEI Y Y, ZHANG H W, WANG C Q, trans. Beijing: National Defense Industry Press, 2015. |
| [2] |
WALDMAN B, HARSHA P. NASP: focus on techology[C]//4th International Aerospace Planes Conference, Orlando, FL, 1992. AIAA-92-5001.
|
| [3] |
HOEGENAUER E, KOELLE D. Saenger-the German aerospace vehicle program[C]// National Aerospace Plane Conference, Dayton, OH, USA. Reston, Virigina: AIAA, 1989. doi: 10.2514/6.1989-5007
|
| [4] |
BURNS B R A. HOTOL, an economic space transport for Europe[J]. Interdisciplinary Science Reviews, 1988, 13(2): 171-179. DOI:10.1179/isr.1988.13.2.171 |
| [5] |
LONGSTAFF R, BOND A. The SKYLON project[C]//17th AIAA International Space Planes and Hypersonic Systems and Technologies Conference, San Francisco, California. Reston, Virigina: AIAA, 2011. AIAA 2011-2244. doi: 10.2514/6.2011-2244
|
| [6] |
黄志澄. “佩刀”为天地往返提供新动力[J]. 国际太空, 2015(7): 11-12. HUANG Z C. Sabre: new power for space shuttles[J]. Space International, 2015(7): 11-12. (in Chinese) |
| [7] |
凌文辉, 侯金丽, 韦宝禧, 等. 空天组合动力技术挑战及解决途径的思考[J]. 推进技术, 2018, 39(10): 2171-2176. LING W H, HOU J L, WEI B X, et al. Technical challenge and potential solution for aerospace combined cycle engine[J]. Journal of Propulsion Technology, 2018, 39(10): 2171-2176. (in Chinese) |
| [8] |
左光, 艾邦成. 先进空间运输系统气动设计综述[J]. 航空学报, 2021, 42(2): 624077. ZUO G, AI B C. Aerodynamic design of advanced space transportation system: Review[J]. Acta Aeronautica et Astronautica Sinica, 2021, 42(2): 624077. (in Chinese) |
| [9] |
乐挺, 王立新, 艾俊强. 变体飞机设计的主要关键技术[J]. 飞行力学, 2009, 27(5): 6-10. YUE T, WANG L X, AI J Q. Key technologies in morphing aircraft design[J]. Flight Dynamics, 2009, 27(5): 6-10. (in Chinese) |
| [10] |
孙杨, 昌敏, 白俊强. 变形机翼飞行器发展综述[J]. 无人系统技术, 2021, 4(3): 65-77. SUN Y, CHANG M, BAI J Q. Review of morphing wing aircraft[J]. Unmanned Systems Technology, 2021, 4(3): 65-77. (in Chinese) |
| [11] |
刘传振, 刘强, 白鹏, 等. 涡波效应宽速域气动外形设计[J]. 航空学报, 2018, 39(7): 121824. LIU C Z, LIU Q, BAI P, et al. Aerodynamic shape design integrating vortex and shock effects for width-velocity-range[J]. Acta Aeronautica et Astronautica Sinica, 2018, 39(7): 121824. (in Chinese) |
| [12] |
曹长强, 蔡晋生, 段焰辉. 超声速翼型气动优化设计[J]. 航空学报, 2015, 36(12): 3774-3784. CAO C Q, CAI J S, DUAN Y H. Aerodynamic design optimization of supersonic airfoils[J]. Acta Aeronautica et Astronautica Sinica, 2015, 36(12): 3774-3784. (in Chinese) |
| [13] |
孙祥程, 韩忠华, 柳斐, 等. 高超声速飞行器宽速域翼型/机翼设计与分析[J]. 航空学报, 2018, 39(6): 121737. SUN X C, HAN Z H, LIU F, et al. Design and analysis of hypersonic vehicle airfoil/wing at wide-range Mach numbers[J]. Acta Aeronautica et Astronautica Sinica, 2018, 39(6): 121737. (in Chinese) |
| [14] |
叶友达, 张涵信, 蒋勤学, 等. 近空间高超声速飞行器气动特性研究的若干关键问题[J]. 力学学报, 2018, 50(6): 1292-1310. YE Y D, ZHANG H X, JIANG Q X, et al. Some key problems in the study of aerodynamic characteristics of near-space hypersonic vehicles[J]. Chinese Journal of Theoretical and Applied Mechanics, 2018, 50(6): 1292-1310. DOI:10.6052/0459-1879-18-247 (in Chinese) |
| [15] |
希舍尔, 魏兰德. 高超声速飞行器气动热力学设计问题精选[M]. 唐志共, 等译. 北京: 国防工业出版社, 2013. HIRSCHEL E H, WEILAND C. Selected aerothermodynamic design problems of hypersonic flight vehicles[M]. TANG Z G, et al., trans. Beijing: National Defense Industry Press, 2013(in Chinese). |
| [16] |
王立宁. 空天飞行器气动技术研究[J]. 战术导弹技术, 2018(4): 32-37. WANG L N. Research on aerodynamic problem and technology of aerospace vehicles[J]. Tactical Missile Technology, 2018(4): 32-37. (in Chinese) |
| [17] |
罗金玲, 康宏琳, 操小龙, 等. 吸气式高超声速飞行器空气动力学[M]. 北京: 科学出版社, 2021. LUO J L, KANG H L, CAO X L, et al. Aerodynamics of airbreathing hypersonic vehicles[M]. Beijing: Science Press, 2021. |
| [18] |
吴子牛, 王兵, 周睿, 等. 空气动力学-下册[M]. 北京: 清华大学出版社, 2008.
|
| [19] |
张阳, 韩忠华, 柳斐, 等. 高超声速飞行器宽速域翼型多目标优化设计研究[J]. 气体物理, 2019, 4(4): 26-40. ZHANG Y, HAN Z H, LIU F, et al. Multi-objective aerodynamic shape optimization of wide-Mach-number-range airfoil[J]. Physics of Gases, 2019, 4(4): 26-40. (in Chinese) |
| [20] |
LIU F, HAN Z H, ZHANG Y, et al. Surrogate-based aerodynamic shape optimization of hypersonic flows considering transonic performance[J]. Aerospace Science and Technology, 2019, 93: 105345. DOI:10.1016/j.ast.2019.105345 |
| [21] |
WEILAND C, 著. 航天飞行器空气动力学数据集[M]. 唐志共, 陈喜兰, 译. 北京: 国防工业出版社, 2017. WEILAND CLAUS. Aerodynamic data of space vehicles[M]. TANG Z G, CHEN X L, trans. Beijing: Nationl Defense Industry Press, 2017. |
| [22] |
SEDERBERG T W, PARRY S R. Free-form deformation of solid geometric models[C]// 13th annual conference on Computer graphics and interactive techniques - SIGGRAPH '86. New York: ACM Press, 1986. doi: 10.1145/15922.15903
|
| [23] |
陈颂, 白俊强, 孙智伟, 等. 基于DFFD技术的翼型气动优化设计[J]. 航空学报, 2014, 35(3): 695-705. CHEN S, BAI J Q, SUN Z W, et al. Aerodynamic optimization design of airfoil using DFFD technique[J]. Acta Aeronautica et Astronautica Sinica, 2014, 35(3): 695-705. (in Chinese) |
 2021, Vol. 39
2021, Vol. 39

