2. 翼型、叶栅空气动力学国家级重点实验室,西安 710072
2. National Key Laboratory of Science and Technology on Aerodynamic Design and Research, Xi’an 710072, China
在航空领域,“翼型”一般定义为飞机机翼或其他升力面的截面形状(平行于对称面或垂直于某等百分比弦线)。随着航空飞行器的发展,翼型的概念也被推广应用到导弹翼面、直升机旋翼以及螺旋桨和风力机等旋转机械的叶片。翼型看似外形简单,却蕴含着层流、湍流、转捩、激波、分离和旋涡等复杂的空气动力学现象以及对气动力特性产生决定性影响的复杂流动机理。翼型的选择和设计是飞机设计中必须要进行的一项工作[1]。美国飞机设计专家D.P. Raymer曾指出[2],“从许多方面来说,翼型就是飞机的心脏”。这是因为翼型影响着飞机巡航速度、起飞和着陆性能、失速速度、操纵性能(特别是接近失速时)和所有飞行阶段的空气动力效率。翼型不仅是机翼气动外形设计的基本元素,也是影响飞机气动力与综合性能的核心因素之一。可以说,翼型是飞机气动力的“基因”和“灵魂”。正因如此,翼型成为发展航空飞行器的重要基础技术,先进翼型数据也被视作飞机设计的重要技术机密和飞机制造商保持商业竞争优势的重要筹码。
翼型是人类探索飞行奥秘的一项伟大发明。回顾航空科学技术发展史,翼型研究不仅直接促进了第一架飞机的诞生,而且在100多年发展历史中一直是飞机升级换代或性能显著提升的重要推动力。人类最早对翼型的研究可以追溯到19世纪末。1884年,被誉为“现代翼型鼻祖”的英国科学家H.F. Phillips 通过风洞试验发明了一系列有弯度和厚度的薄翼型[3]。莱特兄弟(W. Wright和O. Wright)测试了类似鸟类的薄翼型[4],并于1903年成功实现了人类历史上的第一次动力飞行。自第一架飞机诞生后的100多年来,为了探索飞行的奥秘,不断提升飞机性能,翼型研究逐渐得到了广泛重视。所谓“一代翼型/机翼,一代飞行器”,翼型研究的不断突破,极大促进了飞机性能的提升和更新换代;同时,飞机飞行速度的提高和性能要求的提升,反过来又对翼型提出了新的要求,从而牵引并促进了翼型的研究。
翼型研究的百年发展历程大致可以分为三个阶段。
第一阶段从20世纪初开始到20世纪50年代,主要为了探索飞机更高效飞行的奥秘,对翼型开展了系统性研究,形成了若干通用翼型族。英国、德国、美国、前苏联等航空强国,均开展了翼型基本理论、设计方法和测试技术的系统性研究,发展了RAE、DVL、NACA、TsAGI等著名的翼型族。受限于当时的技术水平,这段时期的翼型设计方法是半经验性的,很大程度上依赖风洞试验,所发展的通用翼型族一般不针对特定飞机,但飞机性能的提升很大程度上得益于选用这些新发展的翼型。
第二阶段大约从20世纪60年代开始到20世纪末,随着飞机飞行速度的不断提高和性能指标要求的不断提升,发展更先进翼型的需求日益迫切。同时,超临界翼型原理的发现使世界各航空强国开始重新重视翼型研究工作,并有针对性地发展了适用于不同类型飞机和直升机的各类现代翼型族。例如美国NASA发展了针对跨声速飞机的超临界翼型族,针对通用飞机、支线客机和高空无人机的先进层流翼型族,针对通用飞机的高升力翼型族;美国波音公司和欧洲空客公司等也分别发展了自己的大型客机翼型族。同时,直升机旋翼专用翼型族也在这一时期得到研究和发展。美国西科斯基公司和波音公司分别发展了专门针对直升机的SC和VR翼型族,法国宇航院(ONERA)和前苏联(俄罗斯)中央空气流体动力研究院(TsAGI)也分别发展了专门针对直升机的OA 2-5和TsAGI 2-5翼型族。随着计算机技术和计算流体力学的发展,这段时期的翼型研究(特别是20世纪70年代后)开始采用指定目标压力分布的反设计方法或直接对气动性能指标进行优化的多目标、多约束优化设计方法[5]。大约从20世纪80年代开始,由于意识到先进翼型对飞机性能提升的重要性,各国发展的新翼型数据很少公开。
第三个阶段大约从21世纪初开始到现在。为了满足战斗机、运输机、无人机、直升机更新换代的需求,先进数值模拟方法、优化设计技术、风洞试验和测试技术得到快速发展,牵引并促进了各类新翼型的研究,例如面向先进战斗机的薄翼型、面向飞翼布局飞机的力矩自平衡翼型、面向高空无人机的低雷诺数层流翼型、面向未来超高效率民机的高速层流翼型、面向高超声速飞行器的宽速域翼型、面向下一代直升机的旋翼翼型等。除了航空飞行器翼型外,面向螺旋桨和风力机等旋转机械叶片的专用翼型族也在这一时期得到快速发展。得益于这段时期的转捩预测与湍流数值模拟方法、高维全局气动优化设计技术和精细化试验测量技术的发展,翼型研究的手段和设计能力得到大幅提升,使得这一阶段可以在复杂工程约束下,设计出综合性能优良的翼型。
我国的翼型研究起步于20世纪80年代,以西北工业大学乔志德、张仲寅和原西安飞机设计研究所(现为航空工业第一飞机设计研究院)付大卫等为代表的空气动力学家在国内率先开展了翼型研究。为了打破国外封锁,支撑航空飞行器的自主研制,于1988年成立西北工业大学翼型研究中心,建成亚洲最大的低速翼型NF-3风洞。在低/高速翼型气动计算与设计、翼型风洞试验及翼型在机翼、直升机旋翼和螺旋桨设计中的应用等方面进行了开拓性研究,自主发展了一系列翼型,其中代表性翼型包括:国内第一个自然层流翼型、第一个低阻超临界翼型、第一个高升力螺旋桨翼型系列、第一个水下低噪声螺旋桨翼型系列和第一个通用直升机旋翼翼型系列,并成功应用于某无人机和干线飞机、支线飞机、巡航导弹和鱼雷螺旋桨方案设计。1995年,我国成立了翼型、叶栅空气动力学国家级重点实验室(创始人乔志德先生和周新海先生),2003年建成亚洲最大、国内唯一的增压降温连续式NF-6高速翼型风洞,形成了高、低速配套的完备分析、设计与验证体系,有力支撑了C919大型客机、Y-20大型军用运输机以及先进无人机和直升机的研制。经过20多年的研究与发展,于2020年建立国内第一个满足不同用途、不同飞行速度的新一代飞行器的先进翼型家族谱系(简称翼型谱系),标志着我国形成了支撑飞行器和相关装备发展的自主翼型研发体系。
进入21世纪以来,随着航空科学技术的进步和基于高可信度数值模拟的复杂外形多学科优化设计技术的快速发展与应用,各种新的设计理念、优化方法、设计技术和试验手段相继被提出,翼型研究被赋予了新的使命和内容。但同时,翼型研究的必要性也开始受到了一定的质疑,主要有三个方面的原因:(1)现代高速飞机采用小展弦比、大后掠机翼,流动三维效应显著。因此有学者认为此时研究二维翼型已经没有意义,甚至已经不再有“翼型”的概念。(2)随着一体化外形设计理念的提出和相关设计技术的发展,有学者认为翼剖面外形的研究应该与三维气动布局高度耦合,单独研究翼型的意义不大。(3)国外对新翼型的数据严格保密,相关研究很少公开,产生了国外不再研究翼型或不重视翼型的推论。
为了重新认识翼型研究对于飞行器和相关重要装备研究发展的作用,理清新时期翼型发展的思路和方向,本文梳理了100多年来国内外翼型研究与发展的历史,重点综述了本世纪以来翼型研究的最新进展和研究动态,给出了未来发展方向的建议,分析了翼型发展面临的挑战。需要说明的是,本文主要针对外流的单段翼型。当然多段翼型和发动机内流叶型/叶栅的研究对于飞行器发展也至关重要,但限于篇幅,不作为本文论述范畴。此外,限于作者的学识和水平,对于翼型研究的国内外进展可能存在不准确和不全面的地方,敬请读者批评指正。
1 翼型发展历程回顾 1.1 早期翼型早在1799年,G. Cayley就提出了固定翼飞机的概念,并在1804年设计和制造了第一架能够飞行的模型滑翔机,它拥有固定的机翼以及可以调整的水平和垂直尾翼[6]。在后续的研究与实践中,G. Cayley逐渐认识到机翼的升力是由上表面低压区域和下表面高压区域的压力差产生的,在运动方向上倾斜一定角度的平板可以产生升力,而弯曲的表面会产生更好的效果[7]。虽然平板并不是真正意义上的翼型,但G. Cayley的研究仍被认为是翼型设计思想的萌芽。
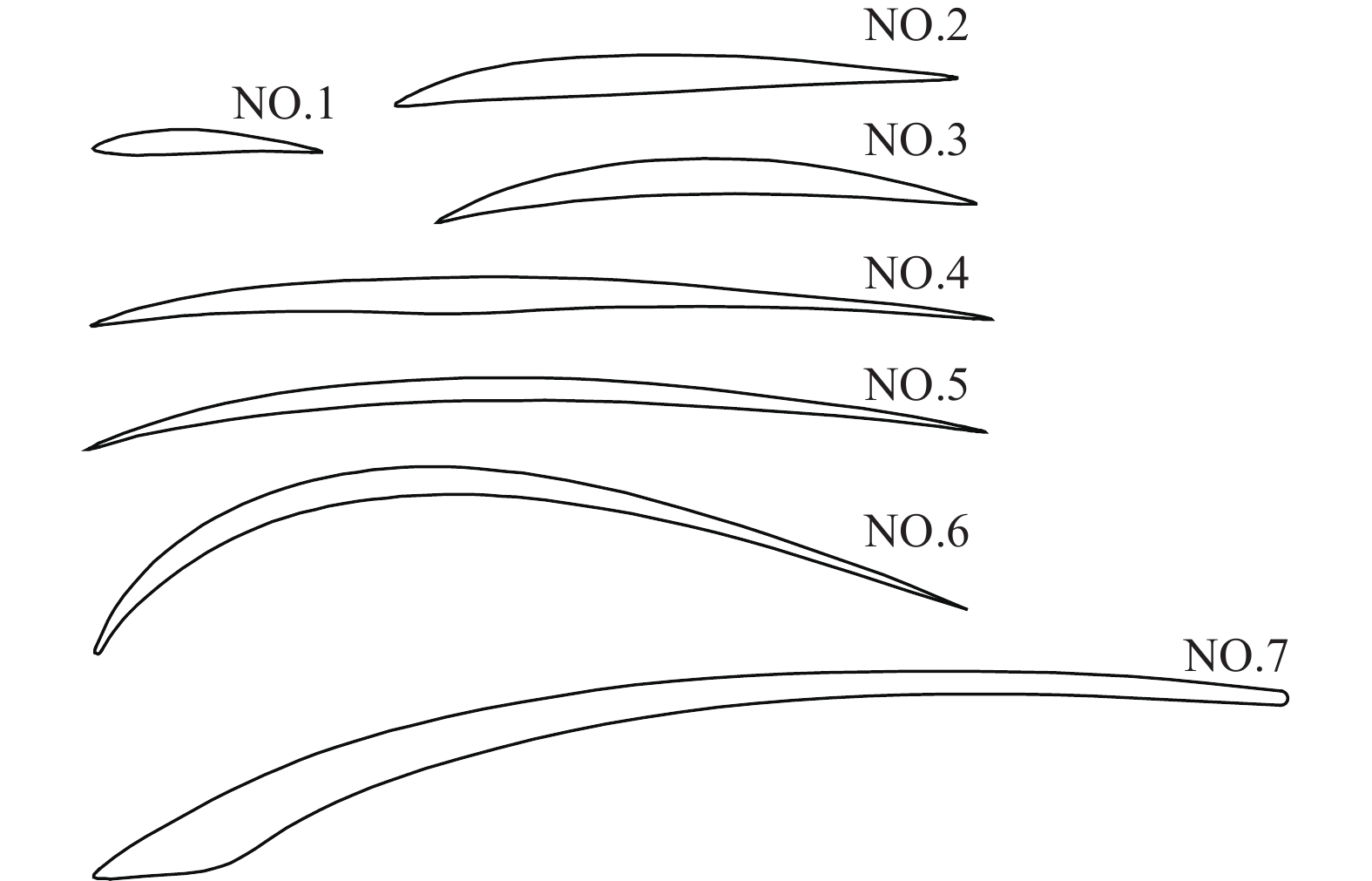
1884年,英国科学家H.F. Phillips通过风洞试验第一次发明了一系列具有实际意义(一定的厚度和弯度)的翼型[8],如图1所示。他的翼型研究成果对航空领域产生了重大影响,著名空气动力学家J.D. Anderson Jr在文献[3]中称其为“现代翼型鼻祖”。与此同时,德国工程师O. Lilienthal在观察并测量了鸟类翅膀的形状后,设计出了如图2所示的不同前缘半径和厚度的翼型,并认为翼型的弯度是成功飞行的关键[9]。
|
图 1 H.F. Phillips发明的翼型(上面6个在1884年发明,下面在1891年发明)[8] Fig.1 Double-surface airfoils proposed by H.F. Phillips (No.1 to No.6 were proposed in 1884, No.7 was proposed in 1891)[8] |
此后,莱特兄弟在自建的风洞中测试了200多种模仿鸟类翅膀形状设计的翼型(如图3),为1903年成功实现人类历史上第一次有动力飞行奠定了基础。虽然翼型的研究直接促进了第一架飞机的诞生,但从今天的视角来看,他们采用的翼型还是没有走出大弯度薄翼型的设计思想[10]。图4为法国航空先驱L. Bleriot设计的翼型[11],仍然具有厚度小和弯度大的特点。

|
图 3 莱特兄弟1902-1903年在风洞中测试的典型翼型[8] Fig.3 Typical airfoils tested by the Wright Brothersduring 1902-1903[8] |
早期的翼型研究是经验性的探索与尝试,缺乏理论支撑。直到1902年,德国数学家M.W. Kutta发现了速度环量的定解条件(Kutta条件),为翼型研究引入了理论依据。俄国空气动力学家N. Joukowsky也独立发现了该条件,并于1906年提出了著名的Joukowsky定理,也被称为Kutta-Joukowsky定理。1909年,N. Joukowsky利用复变函数的保角变换研究了翼型定常无黏流动,提出了著名的Joukowsky翼型理论。根据该理论,低速翼型应当是钝头且具有一定厚度的。基于上述理论和认识,他研究出了第一批理论翼型—— Joukowsky翼型[10]。Joukowsky翼型相比于早期的翼型,其相对厚度明显增大,相对弯度显著减小,如图5所示。N. Joukowsky的研究促进了翼型设计进入理论分析与风洞试验相结合的时代。
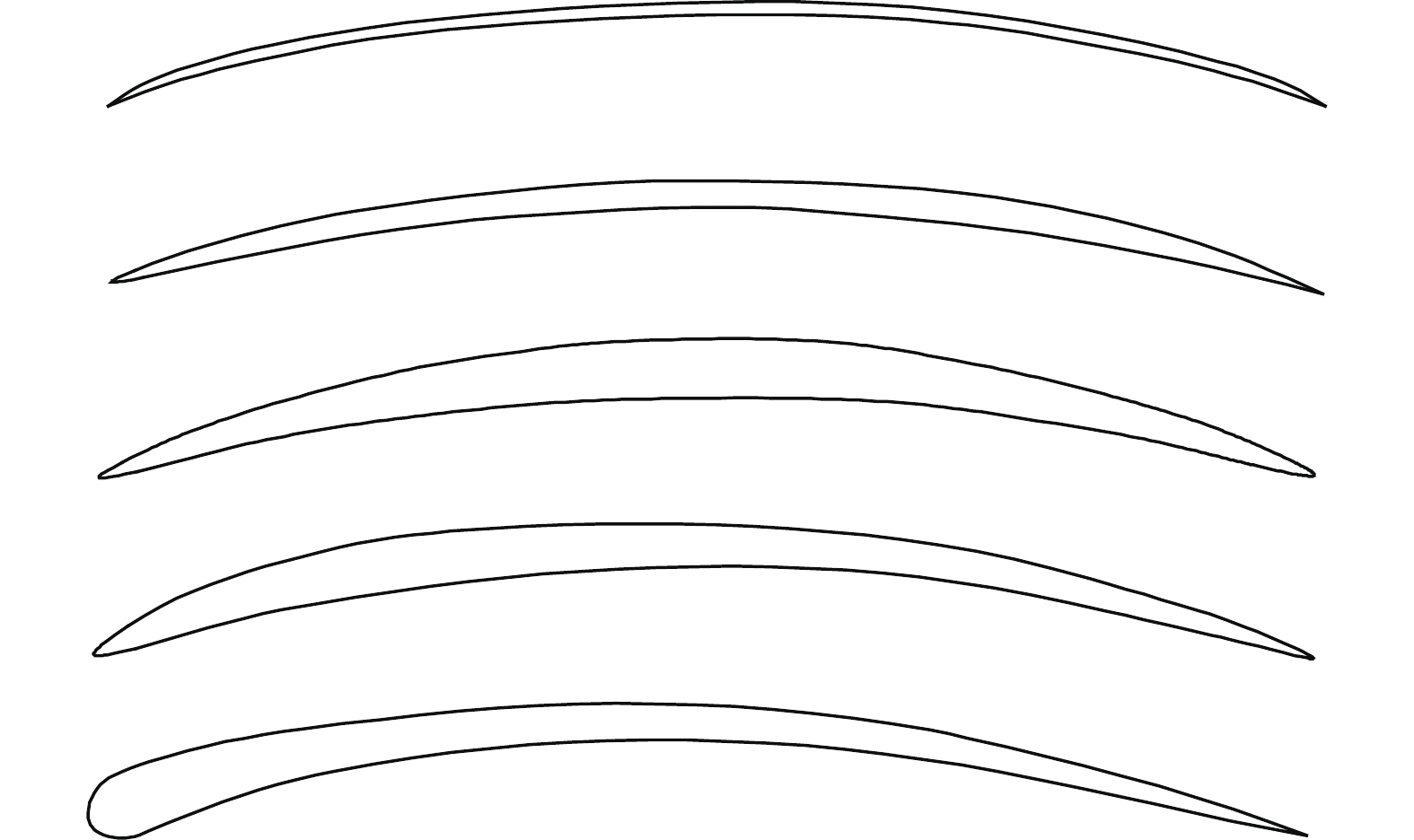
1912年,英国皇家飞机制造厂(Royal Aircraft Factory)开始对翼型进行研究与试验,发展了著名的RAF系列翼型(后改名为RAE翼型),其中具有代表性的RAF-6和RAF-15翼型如图6和图7所示[1]。
美国航空航天咨询委员会(NACA)自1915年成立以来就开始关注翼型研究,在首次年度报告中指出:“开展实际机翼盒段的高效率剖面研究,能够满足结构经济性要求的适当的尺寸,使压力中心移动范围适度,并能在较大迎角范围进行有效操纵”[12]。按此设计理念,发展了USA系列翼型,图8和图9分别为USA-6翼型和USA-27翼型的形状。
1917年,德国哥廷根大学建造了一个能够以实际速度进行全尺寸翼型试验的风洞,并通过大量试验证明了厚翼型相比于薄翼型的优势—较大的前缘半径允许翼型工作在更大的迎角,从而在失速前产生比薄翼型更大的升力;厚翼型阻力必然大于薄翼型的观点是错误的。在后续的研究中得到了著名的以哥根廷命名的系列翼型[8](如图10和图11的Göttingen 398翼型和Göttingen 387翼型)。1922年,V.E. Clark对Göttingen 398翼型尝试进行改造,得到了著名的Clark Y翼型(如图12),该翼型成为当时最流行的翼型。
上述翼型研究引起了美国政府的高度重视。NACA更是将翼型研究作为发展航空飞行器的重要基石。20世纪20年代,NACA兰利航空实验室最早进行了成系列的翼型研究,并进行了相关风洞试验,为后来设计NACA系列翼型积累了大量经验。NACA在1920年、1921年和1923年的年度报告上对当时世界上最先进的翼型进行了评估,并将翼型数据以统一的格式进行了公布[13]。
1924年在NACA工作的德国工程师M.M. Munk开始以薄翼理论为基础对翼型进行设计,得到了Munk系列翼型(图13为Munk M-6翼型)[14]。
综上,航空先驱们对早期翼型开展了开创性的研究,极大提升了人类对飞行奥秘的认识,直接促进了第一架飞机的诞生。表1列举了早期翼型及其特点(仅代表作者的有限认识)。随着人们对飞机升力和阻力特性认识的不断深入,从最初采用类似鸟类的大弯度薄翼型,演变成接近今天的头钝尾尖的小弯度厚翼型。这些早期翼型虽然在现代飞机设计中多数已不再使用,但毫无疑问的是它们对后续的翼型研究影响深远,意义重大。
| 表 1 早期翼型发展及特点 Table 1 The development and features of early airfoils |
|
|
20世纪30年代到40年代,NACA开始高度重视并系统地开展了翼型研究,发展了著名的NACA系列翼型,在气动领域奠定了美国航空强国的基础。值得一提的是,同一时期,前苏联的TsAGI也高度重视翼型研究,发展了著名的TsAGI翼型,形成了前苏联在航空领域能够与美国竞争的研究态势。
NACA兰利航空实验室的E.N. Jacobs等率先系统研究了翼型几何外形,并指出翼型的中弧线和厚度分布是影响翼型外形的最主要因素。然后,他首次使用了通过解析表达式来描述翼型的中弧线和厚度分布的几何方法,结合经验修形法,最终得到了NACA4位数和5位数系列翼型[15-17]。此外,E.N. Jacobs还开始了自然层流翼型的研究,他通过反演T. Theodorsen的翼型分析方法[18]来得到可以保持层流的压力分布所对应的翼型。在此基础上,发展了1~8系列等多个早期的层流翼型族。需要说明的是,本文中的“层流”均指代“自然层流”,即仅依靠翼型自身的表面外形维持层流流动。有关“层流控制”和“混合层流控制”的研究超出了本文范畴。
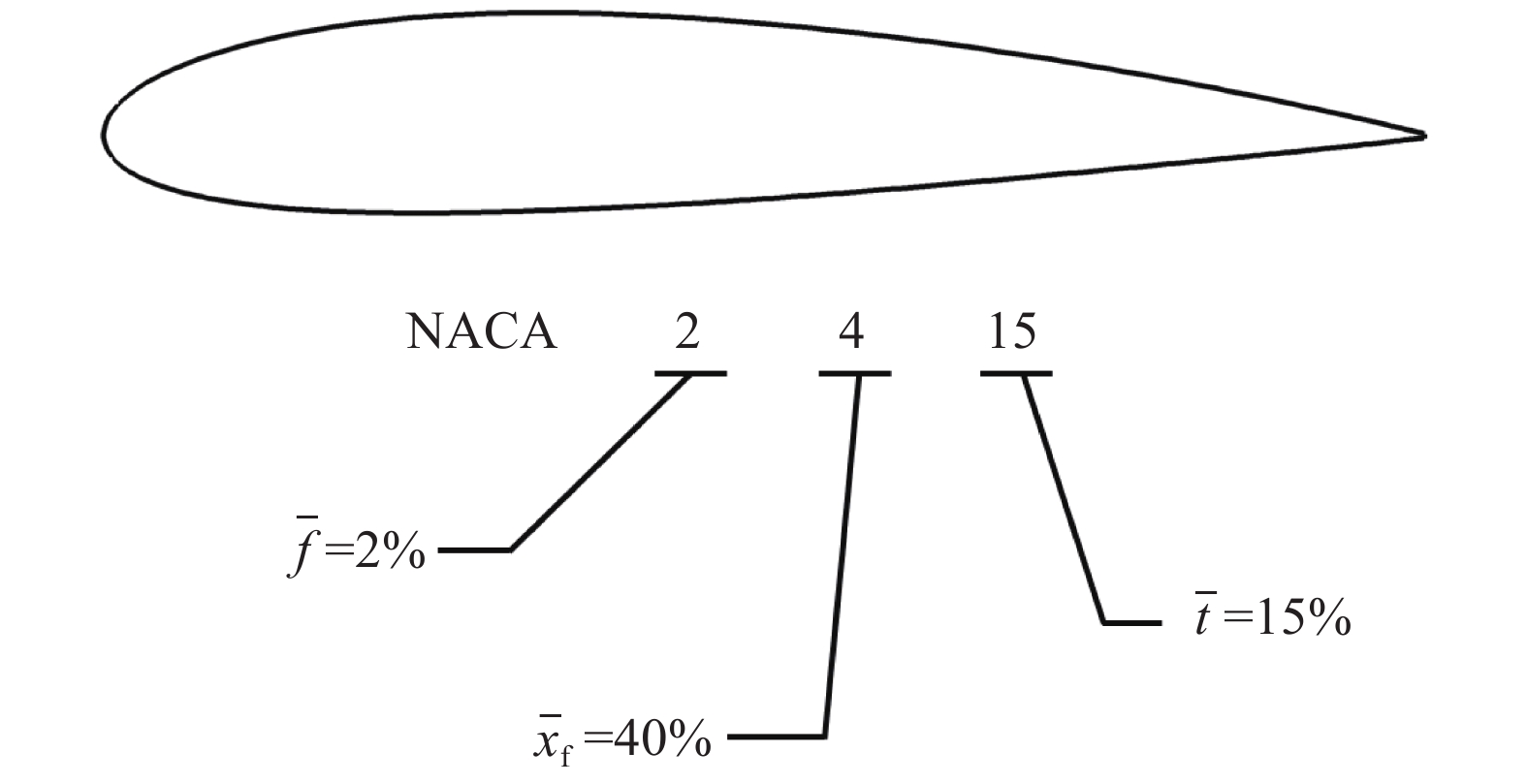
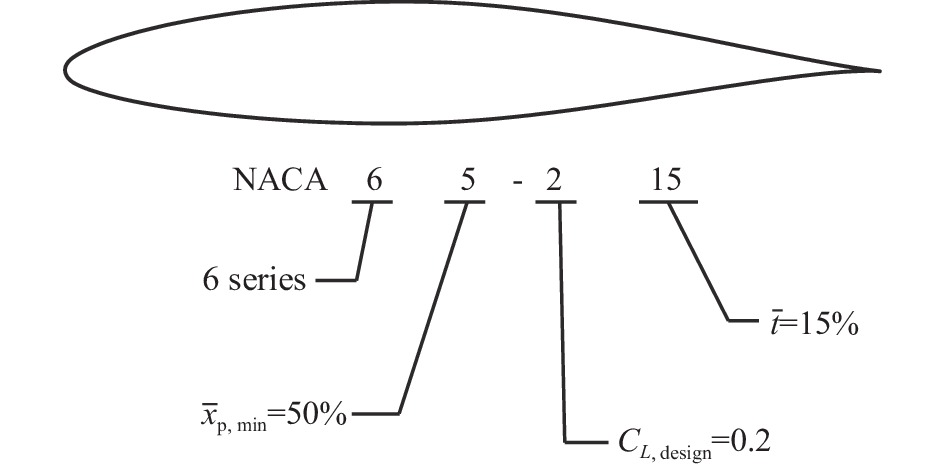
1.2.1 NACA4位数翼型NACA4位数系列是NACA第一批使用解析表达式设计生成的翼型族。该系列的命名规则如图14所示。以NACA2415翼型为例,“2”表示翼型的最大弯度为弦长的2%,“4”表示最大弯度位于弦长的40%处,“15”表示最大厚度为弦长的15%。将这些参数代入特定方程就可以获得翼型几何外形(生成方法参见文献[19]第一篇)。
NACA4位数翼型构造简单,在低速状态下具有较好的升阻和力矩特性,且该系列中的带弯度翼型具有较高的最大升力系数。因此,该系列翼型一经问世就受到低速飞机(如Cessna系列轻型飞机)的青睐。NACA2412、NACA4412等翼型在现代轻型飞机设计中仍然被选用。
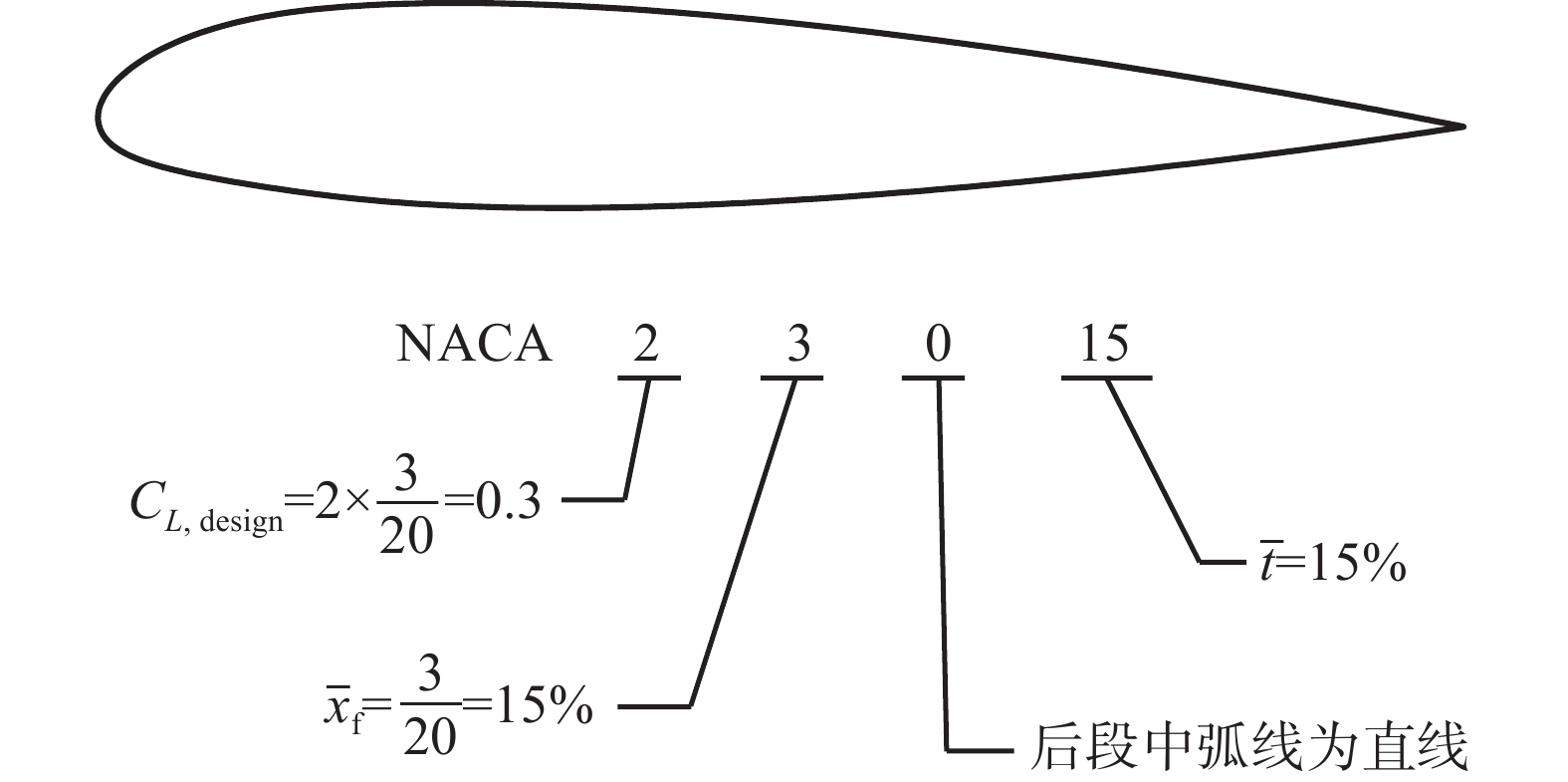
1.2.2 NACA5位数翼型NACA深入研究发现,翼型最大弯度位置的前移可以提高最大升力系数,降低最小阻力系数,但NACA4位数翼型的中弧线方程限制了这种前移,因此E.N. Jacobs等建立了新的中弧线方程,结合原有的厚度分布,形成了NACA5位数系列翼型。该系列翼型的5位数字表征了翼型的理论气动特性和几何特性。以NACA23015为例(如图15),“2”表示该翼型设计升力系数为0.3(即“2”×3/20),“3”表示最大弯度位于弦长的15%处(即“3”/20),“0”表示后段中弧线为直线(若为“1”则表示反弯度曲线),“15”表示最大厚度为弦长的15%。
NACA5位数翼型允许最大弯度位置更加靠前,从而可获得更加优越的气动性能。其中,NACA230系列(如NACA23015)是5位数翼型中最大升力系数最高的翼型,在以提升最大升力系数为主要气动设计目标的低速飞机(如Jurca MJ系列飞机)中得到了广泛使用。
1.2.3 NACA4位数、NACA5位数翼型的修改翼型在实际应用中,往往需要对选用的基础翼型进行一些修形,从而衍生出了NACA翼型的一系列修改翼型。NACA4、5位数翼型的修改翼型主要是针对前缘半径和最大厚度位置的修改,以NACA0012-34为例,基础翼型是NACA0012翼型,“3”表示翼型前缘半径修改为原有翼型前缘半径的1/4(如果取“0”则表示尖前缘,“6”表示前缘半径不变,“9”表示原有前缘半径的3倍),“4”表示最大厚度位置从原来的30%弦长处修改为40%弦长处。部分修改翼型还会对最大厚度进行修改,例如B-58轰炸机机翼翼根处选用的NACA0003.46-64.069翼型,其中,“3.46”表示将最大厚度修改为弦长的3.46%,“4.069”表示将NACA0003翼型的最大厚度位置修改为40.69%弦长处。值得一提的是,德国航空研究院(原名为DVL,即德国宇航院DLR的前身)研究了NACA4、5位数翼型的修改翼型,除了前缘半径和最大厚度位置修形外,还包括了对后缘角的修形,得到了DVL系列翼型。
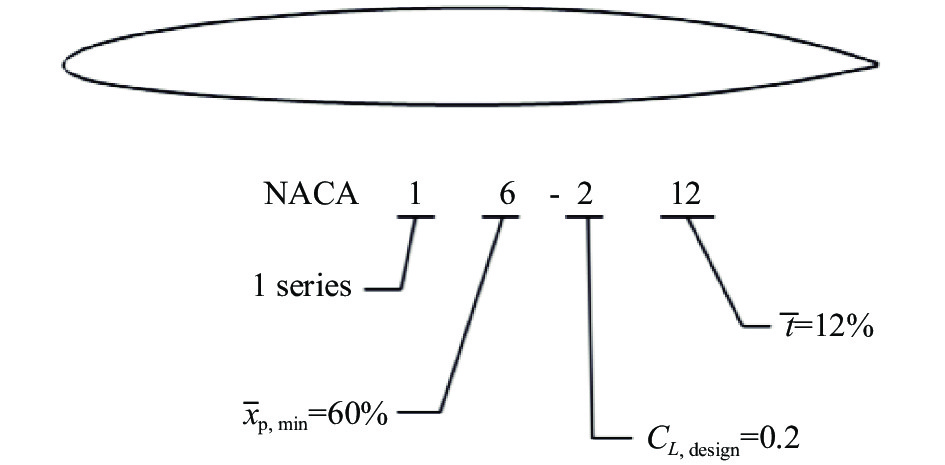
1.2.4 NACA1系列层流翼型随着翼型研究的不断深入,NACA在采用最初的几何方法来设计翼型基础上,开始尝试使用空气动力学理论方法来设计翼型。NACA1系列翼型是最早根据压力分布设计的翼型,因此该系列翼型几何外形没有解析表达式。NACA1系列翼型的命名由5位数字组成(如图16),第一位数字表征所属系列,第二位数字表征最小压力点位置,第三位数字表征设计升力系数,最后两位数字表征最大厚度。
NACA1系列翼型是最早的自然层流翼型,其设计目标是通过较宽的层流范围获得更低的阻力。但受当时翼型理论方法发展水平的限制,设计效果并不理想。事实上,该系列中只有NACA16系列翼型被ANT-31等飞机采用。在这之后,NACA又使用近似理论发展了2~5系列层流翼型,但都没有获得理想的压力分布。风洞和飞行试验均表明,这些早期的自然层流翼型在非设计状态下的气动特性不佳,且对翼面光滑程度要求较高,因此NACA2~5系列很快就被淘汰了。限于篇幅,此处不再赘述。
1.2.5 NACA6系列层流翼型NACA6系列是最受人们关注的NACA层流翼型[20-21]。该系列翼型在外形设计中使用了改进的理论方法,其厚度分布是由所要求的阻力系数、临界马赫数以及所需的最大升力系数推导求得的,中弧线由满足给定载荷分布的解析表达式确定。NACA6系列翼型的命名方式有很多种,图17给出了最常见的用5位数字表征该系列翼型几何外形和理论气动特性的命名方式。
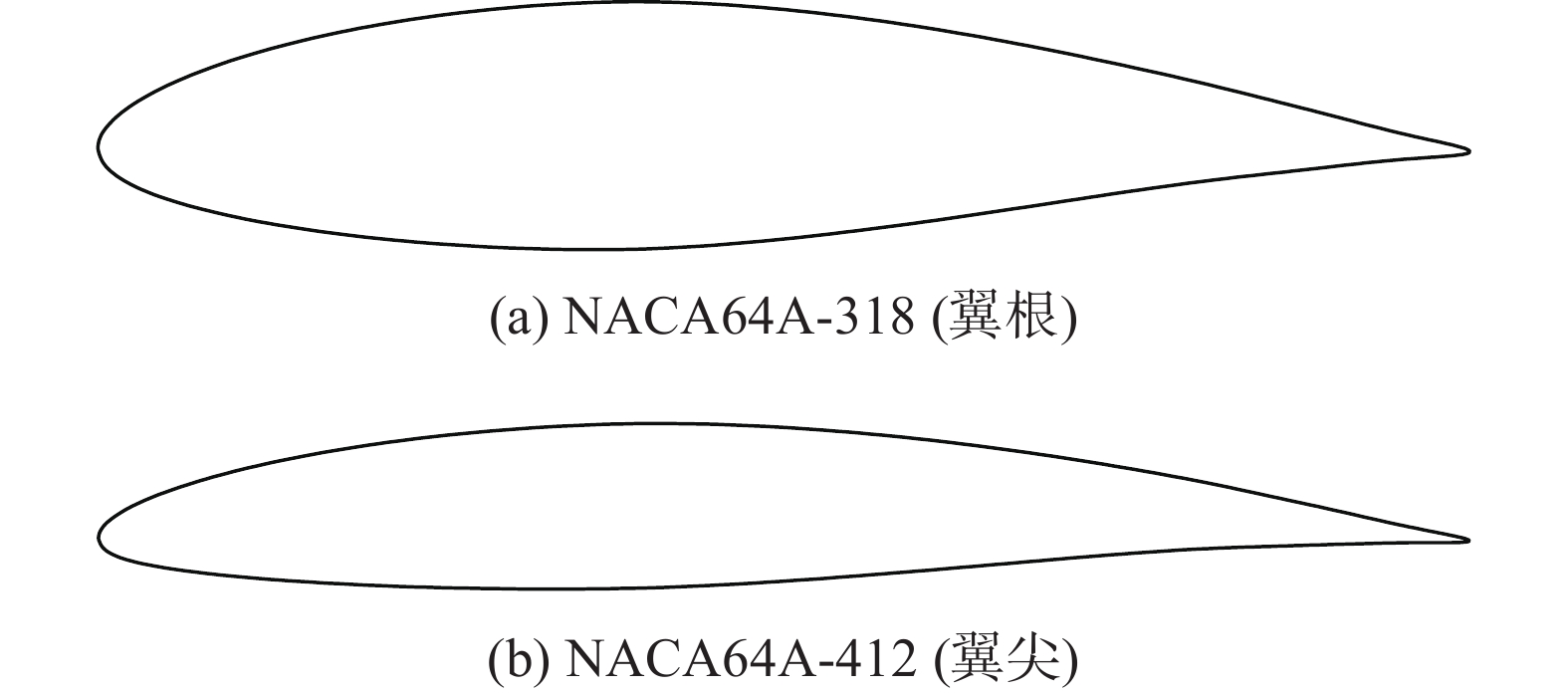
NACA6系列翼型的后缘较薄,在结构设计和制造上造成了很大困难。为了克服这一缺点,将翼型80%弦长处到后缘点的曲线修改为直线并修改后缘尖点为有限厚度,修改后的翼型被称为NACA6A系列翼型。NACA6A系列翼型在非设计状态下也保持了良好的气动特性,增加了其实用性,因而被广泛应用于现代高速战斗机和运输机的机翼设计。例如美国F-16战斗机的机翼采用了NACA64A-204翼型(如图18);C-130“大力神”运输机的翼根采用了NACA64A-318翼型,翼尖采用了NACA64A-412翼型(如图19)。
|
图 19 C-130运输机采用的NACA64A-318和NACA64A-412翼型[22] Fig.19 NACA64A-318 and NACA64A-412 airfoilsapplied to C-130 transport[22] |
NACA7、8系列是对层流翼型设计的进一步尝试。NACA7系列(图20)的特点是翼型下表面可以获得比上表面更大的层流范围,而NACA8系列可以使得翼型上下表面独立地获得尽可能大的层流范围。NACA7、8系列在某些方面已经具有了现代翼型设计的雏形,受到当时的翼型理论分析和设计技术的限制,这些翼型的气动特性并不理想,仅在BX-2、JT-5等飞机上被选用。
值得一提的是,20世纪50年代,NACA为了集中力量研究高速空气动力学,暂停了翼型研究[23],而德国逐渐取代美国成为了这个时期翼型研究的中心,F.X. Wortmann和R. Eppler等继续开展了层流翼型研究并取得了令人瞩目的研究成果[24-25]。
综上,NACA系列翼型毫无疑问是翼型发展史上最经典的翼型族之一,它的出现促进了战斗机、运输机的更新换代和性能的大幅提升,直至今天在飞机概念设计中仍然被广泛选用。NACA翼型的研究极大提升了人们对翼型研究重要性的认识,推动了翼型设计思想、设计理论和设计方法的发展,具有划时代的意义。虽然NACA翼型主要采用结合风洞试验的半经验方法,但NACA层流翼型系列已经开始采用根据压力分布进行反设计的现代设计方法,对现代翼型研究产生了深远影响。
1.3 现代翼型自20世纪60年代开始,由于超临界翼型原理的发现,翼型研究重新得到了高度重视。特别是70年代后,随着计算机技术的快速发展和计算流体力学(CFD)的兴起,翼型的设计不再主要依赖于风洞试验,而是可以通过数值模拟较为准确地预测翼型的气动特性,为现代翼型的研究和发展提供了重要的理论和技术基础。随着飞行器飞行速度的提高和性能要求的进一步提升,对翼型提出了新的要求。这个时期各种新的翼型设计思想不断涌现。以美国NASA为代表的研究机构发展了针对跨声速飞机的超临界翼型、针对高空无人机的先进自然层流翼型以及针对通用飞机的高升力翼型。这个阶段发展的翼型,主要采用现代数值分析和设计方法进行设计,称为现代翼型。
1.3.1 针对跨声速飞机的超临界翼型1958年NASA正式成立,取代了其前身NACA,并集中力量发展了在跨声速湍流流动中具有较高的阻力发散马赫数,同时在低速时具有较大的最大升力和良好的失速特性的实用翼型,这就是超临界翼型[26]。超临界翼型的概念是美国NASA兰利研究中心的R.T. Whitcomb于20世纪60年代后期研究提出的,直到1974年才第一次予以公开[27]。超临界翼型原理的发现,有力促进了飞机更新换代,也推动了翼型研究进入新的阶段。超临界翼型与后掠机翼是20世纪空气动力学的两项重大突破。
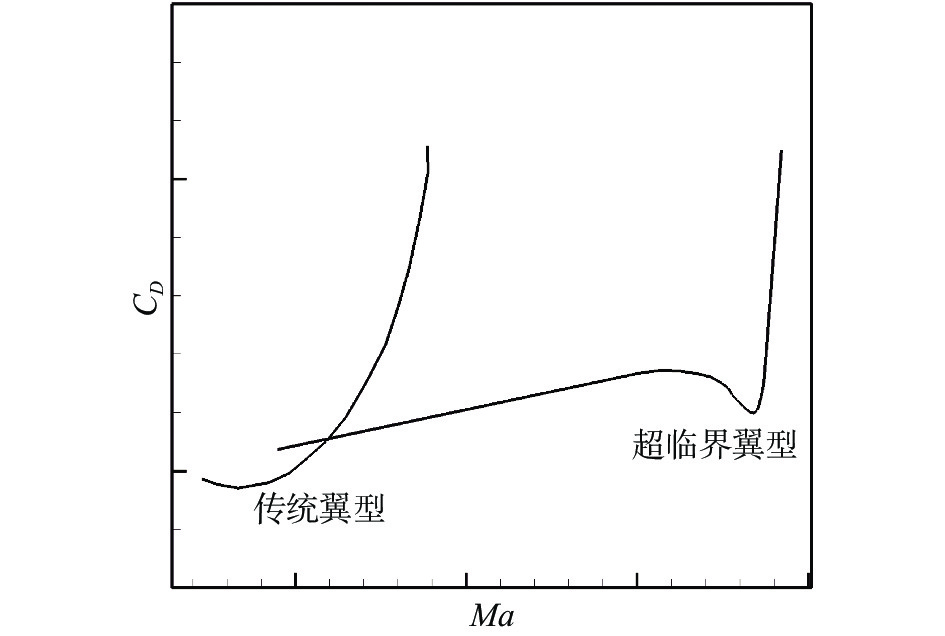
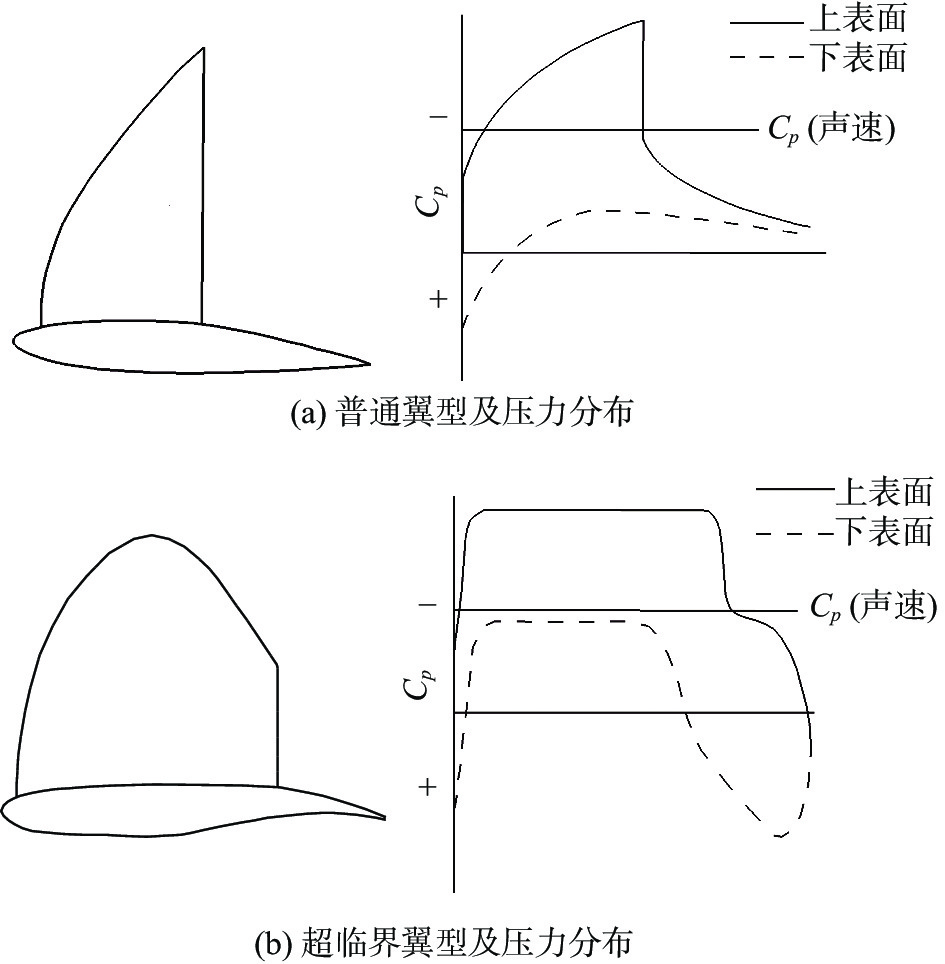
在相当长的一个时期内,人们普遍认为来流超过临界马赫数时,翼型绕流必然会出现激波。但是R.T. Whitcomb等[27]的研究突破了这一认识,证实了超临界情况下无激波或仅具有弱激波翼型的存在,从而发明了“超临界翼型”。这类翼型的特点是具有较大的前缘半径,在上表面中部区域有较小的曲率,同时在后缘附近具有较大的弯度。相比于传统的NACA翼型,超临界翼型极大提升了阻力发散马赫数(如图21)。图22给出了普通翼型和超临界翼型的表面压力分布对比。超临界翼型上表面大约5%弦向位置直到靠近后部的弱激波位置有均匀的超声速速度分布,超声速区以等熵或接近等熵压缩的方式恢复到亚声速区。激波强度的减弱主要是由于翼型上表面中部曲率的减少,激波后的压力平台可以推迟边界层分离,翼型后缘的后加载弥补了因翼型前部负弯度导致的升力不足的问题。
|
图 21 超临界翼型与传统翼型的阻力发散马赫数曲线对比 Fig.21 Comparison of the drag-divergence properties between traditional and supercritical airfoils |
|
图 22 超临界翼型与传统翼型外形和典型压力分布的比较 Fig.22 Comparison between ordinary and supercritical airfoils |
NASA对超临界翼型的研究分为三个阶段,分别发展了NASA SC(1)族、NASA SC(2)族和NASA SC(3)族超临界翼型[26]。翼型编号定义如下:如NASA SC(2)-0714翼型,SC(2)表示的是超临界(第二阶段),随后的两位数“07”是以十分数表示的翼型设计升力系数为0.7,最后两位数“14”表示的是翼型最大厚度为弦长的14%。
在发展第一阶段超临界翼型期间(大致从20世纪60年代后期到70年代初),NASA对超临界翼型进行了初步探索,通过大量的试验,分析了翼型最大厚度、后缘厚度和后部弯度等参数对其性能的影响,并给出了超临界翼型的一般设计准则[26],为下一阶段超临界翼型的发展奠定了理论基础。在发展第二阶段超临界翼型期间(大致从20世纪70年代初到70年代末),NASA设计了一系列超临界翼型(即NASA SC(2)族翼型),并建立了超临界翼型数据库[28-29]。虽然此阶段超临界翼型取得了巨大成功,但是还存在翼型的低头力矩过大以及翼型后缘没有足够结构空间等问题。NASA在第三阶段超临界发展期间(大致从20世纪70年代末到80年代初),针对第二阶段翼型的不足进行了改进,进而发展了NASA SC(3)族超临界翼型。在兰利研究中心0.3 m跨声速风洞,NASA SC(2)-0714和修形后的NASA SC(3)-0714翼型(如图23所示)的风洞试验结果表明:减小翼型后加载和修薄前部下表面可以有效减小低头力矩,同时不会显著降低设计点的翼型气动性能[26]。

|
图 23 14%厚度的第二阶段和第三阶段超临界翼型外形对比 Fig.23 Comparison of phase 2 and phase 3 supercritical airfoils of 14% thickness |
超临界翼型原理的发现,打破了人们对传统翼型的认知,是空气动力学技术的重大突破,极大提升了人们对翼型研究重要性的认识。超临界翼型不仅成为美军新型战略战术运输机C-17等飞机的核心技术之一,同时也被广泛应用于波音系列和空客系列现代民机,极大地提升了客机巡航效率和经济性。
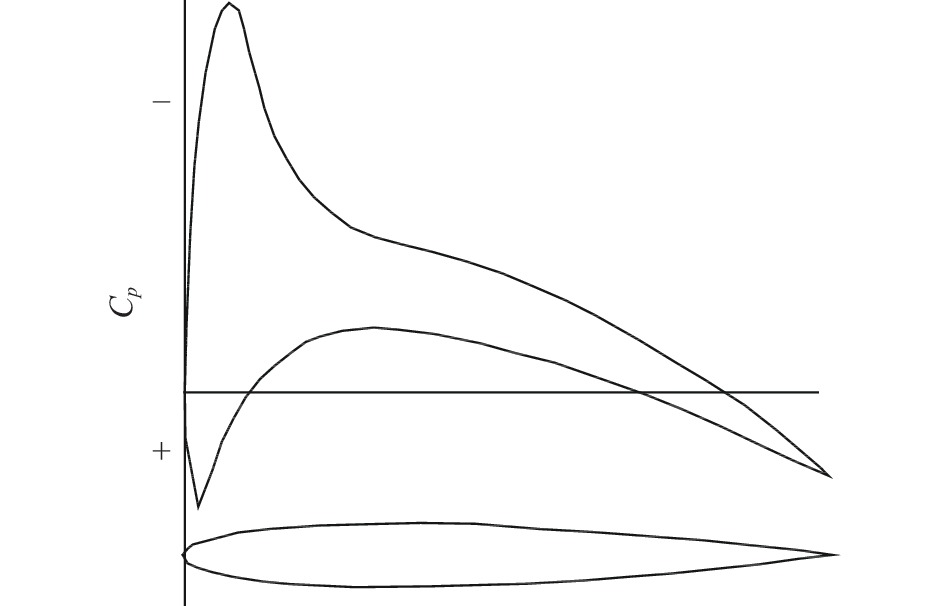
值得一提的是,在20世纪60年代,英国H.H. Pearcey[30]也发现了超临界下无激波翼型的存在,并发明了尖峰翼型,如图24所示。虽然Pearcey发明的尖峰翼型在A300B等高速客机上得到了实际应用,但是由于Whitcomb发明的超临界翼型在上表面有更大范围的超声速区,可以获得更大的升阻比,因而很快取代了尖峰翼型。
|
图 24 尖峰翼型及其压力分布 Fig.24 Peak airfoil and its pressure distribution |
我国学者自20世纪80年代开始对超临界翼型开展了大量研究,包括西工大张仲寅、乔志德、原西安飞机设计研究所付大卫等。同时,我国还在国内外进行了多期风洞试验,并采用K8教练机完成了超临界翼型及机翼的飞行验证。这些工作为我国C919大型客机[31]、Y-20大型军用运输机等型号采用超临界翼型打下了基础。
1.3.2 针对通用飞机、支线客机和高空无人机的先进自然层流翼型如前所述,NACA早在20世纪30年代就开始进行了层流翼型的研究[32],并因此诞生了著名的NACA6系列翼型,只不过受限于当时的材料、结构和工艺水平,在实际飞行器上并没有达到预期的减阻效果[33]。20世纪50年代NACA对层流翼型的研究基本停滞[23]。这一时期,德国的Wortmann和Eppler继续进行层流翼型设计,并开发了一类滑翔机专用翼型[24-25]。70年代以后,随着复合材料技术的出现及相应的加工制造技术的发展,使得自然层流翼型在实际飞行中也能够实现和在低湍流度风洞中同样的低阻力特性[34],因此针对自然层流翼型的研究又开始复苏[35]。值得一提的是,前苏联大约在1940年开始发展层流翼型,并在40年代后期用于飞机设计中,比如TsAGI C-5-18层流翼型就用在安-12和安-24飞机上。由于前苏联及俄罗斯的相关研究鲜有公开,下面主要针对美国NASA层流翼型展开介绍。
推动自然层流翼型发展的另一动力是设计方法的进步。早期的反设计方法,速度分布只能在一个迎角上指定,因而只能进行单点设计,所有其他的流动状态都需要作为所谓的非设计点来进行后验评估。1975年,NASA开始使用Eppler发展的翼型设计和分析程序,该程序集成了描述速度分布特征的保角变换方法以及边界层分析方法。保角变换方法的优势在于它允许在不同迎角下指定翼型不同位置的速度分布[36],从而可以实现多点设计。该程序可以用来预测任意速度分布下的层流和湍流边界层、转捩、分离以及层流分离泡的发生,其重要特点是能让设计者在翼型设计过程中直接对边界层特征进行控制[37],这也标志着NASA在层流翼型设计上取得了重要进步。以此为基础,NASA发展了新一代层流翼型[38-39]。
1.3.2.1 针对轻型通用飞机的低速自然层流翼型低速轻型通用飞机的发展推动了层流翼型的验证和实际应用,这一阶段层流翼型设计是在不可压假设下进行的。
1977年,NASA针对先进轻型单发通用飞机设计了NLF(1)-0416翼型[40](如图25)。在雷诺数400万下,该翼型在巡航升力系数(CL = 0.4)和爬升升力系数(CL = 0.5~1.0)下都具有较低的阻力系数。该翼型具有较钝的前缘和较明显的后加载,这两个特征保证了它具有较高的最大升力系数。风洞试验表明该翼型最大升力系数对粗糙度不敏感,压力梯度与设计目标吻合良好,理论预测的气动力也与试验值吻合良好。总体来说,NASA NLF(1)-0416翼型是中等雷诺数下层流翼型设计的一个成功案例。

|
图 25 NASA NLF(1)-0416翼型 Fig.25 NASA NLF(1)-0416 airfoil |
1979年,NASA针对高性能单发通用飞机[41](Bellanca Skyrocket Ⅱ)设计了具有更大层流范围的NASA NLF(1)-0215F翼型[40](如图26),在雷诺数900万下,该翼型在巡航状态和爬升状态下都具有较低的阻力系数。

|
图 26 Bellanca Skyrocket II 通用飞机与NASA NLF(1)-0215F翼型 Fig.26 Bellanca Skyrocket II general-aviation aircraft and NASA NLF(1)-0215F airfoil |
该翼型的一个显著特点是设计了一个25%弦长的简单襟翼,在上下表面各保持40%和60%弦长层流范围的前提下最大化升阻比。为了解决最大升力与力矩系数的矛盾,允许襟翼负偏,从而在保证较高最大升力系数的同时,在巡航升力系数附近可以保持较小的低头力矩[42]。
1987年,针对通用飞机低巡航阻力、高升力以及良好的失速特性要求,NASA又设计了NLF(1)-0414F翼型(如图27),并在Cessna 210飞机上进行了飞行试验[43]。测试结果表明,机翼上下表面都实现了70%的大范围层流,并且在非层流状态下升力特性也能得到保持,与风洞试验结果吻合。
1.3.2.2 针对支线客机的高速自然层流翼型为了解决更高马赫数(通常也意味着更高的雷诺数)问题,研究人员在设计过程中对速度和压力进行了压缩性修正[44],这种修正在亚声速范围内都适用。
1985年,针对30座支线客机,K.H. Horstmann等设计了NASA NLF(2)-0415翼型[45](如图28)。在巡航条件(Ma

|
图 27 NASA NLF(1)-0414F翼型 Fig.27 NASA NLF(1)-0414F airfoil |

|
图 28 NASA NLF(2)-0415翼型 Fig.28 NASA NLF(2)-0415 airfoil |
到20世纪末,美国NASA还设计了马赫数0.7的高速层流翼型HSNLF(1)-0213[46](如图29)。该翼型实际是由低速层流翼型NLF(1)-0414F改进而来。相对于传统超临界翼型,其前缘半径更小、前缘的负压值较低,使得在中弦长区域保持了一定的顺压梯度,可推迟流动转捩。同一时期,加拿大国家航空研究中心(NAE)也设计并试验了一系列超临界自然层流翼型,均显示出了较全湍流翼型更高的气动效率[47]。

|
图 29 NASA HSNLF(1)-0213高速层流翼型及压力分布[47] Fig.29 Geometry and pressure distribution of NASA HSNLF(1)-0213 high-speed NLF airfoil[47] |
高空长航时无人机设计的主要目标之一是获得尽可能长的续航时间,即高的“航时因子”(
20世纪80年代起,高空长航时无人机在军事应用方面受到了广泛关注。1986年,M.D. Maughmer等针对高空长航时飞行器设计了NASA NLF(1)-1015翼型[49](如图30)。在长续航状态(雷诺数70万,CL = 1.5)、巡航状态(雷诺数90万,CL = 1.0)和突击状态(雷诺数200万,CL = 0.4)下实现低阻力系数。由于该设计结合了高升力系数和低雷诺数,因此速度分布设计了“分离斜坡”和“曲线过渡斜坡”来实现较高的升力和抑制层流分离气泡的形成[50]。

|
图 30 NASA NLF(1)-1015翼型 Fig.30 NASA NLF(1)-1015 airfoil |
20世纪90年代,NASA针对诺斯罗普·格鲁曼公司的RQ-4“全球鹰”高空长航时无人机机翼设计了LRN-1015低雷诺数翼型[51](如图31)。全球鹰的飞行高度可达20 km,在马赫数0.2条件下雷诺数只有50万,设计状态下机翼上下表面的层流范围分别可达57%和88%弦长,具有较低的阻力和较高的升阻比。优异的翼型/机翼气动性能和推进系统使得“全球鹰”无人机至今仍然是高性能、高空长航时大型军用无人机平台中的佼佼者。

|
图 31 RQ-4全球鹰无人机与NASA LRN-1015翼型 Fig.31 RQ-4 Global Hawk UAV and NASA LRN-1015 airfoil |
20世纪60年代后期,理论方法和计算机技术的进步为新一代高升力翼型的研究和发展提供了先进的手段。美国于1972年启动了“先进技术轻型双发”飞机研制计划(ATLIT),其中关键技术之一就是研究厚度较大的先进高升力翼型。
ATLIT所采用的GAW-1翼型是首次通过计算流体力学方法设计的先进高升力翼型[52]。该翼型将爬升升阻比、最大升力作为主要设计指标,并且对零升力矩和巡航阻力进行了约束,其几何特点包括:(1)前缘半径较大,降低了大迎角下负压峰值并因此推迟了翼型失速;(2)翼型上表面比较平坦,从而使得在升力系数为0.4(对应0°迎角)时上表面载荷均匀分布;(3)下表面后缘有较大的弯度(后加载),并具有上、下表面斜率近似相等的钝后缘[1]。在成功设计出GAW-1翼型之后,NASA又设计了气动特性相近但厚度更小的GAW-2翼型。
在后续研究中,Tassel等将GAW-1翼型外形进行了分解得到了其厚度分布、弯度分布和上下表面坐标解析表达式,并通过扰动解析表达式生成了16个新的翼型,命名为GA(General Aviation)系列翼型[53],例如GAW-1翼型可表示为NASA GA-0417。此后NASA还发展了相对厚度从6%到22%、设计升力系数从0.4到1.0的一系列低速高升力翼型[1]。
除了美国NASA,德国Dornier公司于1975年也进行了先进高升力翼型的设计研究。针对NACA6系列翼型以及4位、5位数翼型在升力特性方面的缺陷,Dornier公司提出了两点改进措施:1)增大前缘半径和前缘弯度;2)增加翼型后部的弯度。同时考虑到制造工艺水平和螺旋桨滑流干扰等原因,未将保持层流作为设计条件。风洞试验结果表明,最终设计出的DO-5翼型,具备了先进高升力翼型的特征,并且低头力矩比GAW-1翼型有了大幅度减小。
以NASA发展的GAW-1和GAW-2为代表的高升力翼型得益于良好的升力特性和失速特性,被广泛应用于通用航空飞机。例如Oshkinis BRO-23KR Garnys、RANS S-16 Shekari和Piper PA-38 Tomahawk等通用航空飞机机翼翼根和翼尖翼型均采用了GAW-1翼型,如图32所示;Stoddard-Hamilton Glasair和OMF Aircraft OMF-160 Symphony等通用航空飞机翼根和翼尖翼型均采用GAW-2翼型。先进高升力翼型的提出,极大地促进了通用航空飞机的发展,也为后续建立通用飞机专用翼型族奠定了基础。

|
图 32 采用 NASA GAW-1翼型的Piper PA-38Tomahawk通用航空飞机 Fig.32 Piper PA-38 Tomahawk general aviation aircraft with NASA GW-1 airfoil |
20世纪80年代以后,国外针对各类飞机的高性能先进翼型数据已经很少公开,而国内的翼型研究也正是从这个时候起步。1984年,在我国自行设计支线飞机需求的带动下,西北工业大学乔志德率先开展了先进翼型的研究,设计了NPU-100翼型。1986年新支线飞机的论证和投标中,为了使飞机性能达到国外第二代支线飞机水平,大多数投标单位采用了该翼型。随后发展的一组系列化配套的高升力翼型,性能全面超过美国GAW-1翼型,并在Y-7飞机设计中得到成功应用,全机最大升力全面提升,稳定性范围和爬升升阻比均显著增加。
1986年,乔志德提出了基于弱激波形成顺压梯度的设计思想,通过压力分布反设计结合人工修形,设计了超临界层流翼型,并应用于中德合作MPC-75飞机方案,全机气动性能与德方水平相当。在随后的层流翼型研究中,乔志德将现代高速层流翼型分为了两类:第一类翼型在高低速均能够维持大范围的层流,具有比常规超临界翼型更小的前缘半径,代表性翼型NPU-L72513[54]如图33所示;第二类翼型仅在设计马赫数或更高的马赫数下能够维持大范围层流,前缘半径更大,外形与常规超临界翼型类似,代表性翼型NPU-S73613[54]如图34所示。其中NPU-L72513翼型是我国第一个经过跨声速风洞试验验证的超临界自然层流翼型。

|
图 33 NPU-L72513翼型(第一类跨声速层流翼型)[54] Fig.33 NPU-L72513 airfoil (the first category of high-speed NLF airfoils) [54] |

|
图 34 NPU-S73613翼型(第二类跨声速层流翼型)[54] Fig.34 NPU-S73613 airfoil (the second category of high-speed NLF airfoils)[54] |
同一时期,西北工业大学的华俊和张仲寅也发展了一种采用“正反迭代、余量修正”原理的跨声速层流翼型设计方法[55],并设计了NPU-NLF系列自然层流翼型[55-56],以及一系列超临界翼型,包括NPU7、NPUBS2和改进翼型NPUBS3等。
20世纪末,国内也开展了长航时无人机翼型研究。1999年,西北工业大学张仲寅等采用余量修正迭代及欧拉方程加黏性修正方法设计了供长航时飞机使用的低速高性能翼型NPU-ASN-1[57](如图35),该翼型的航时因子远高于著名的NASA GAW-1翼型,其最大厚度(19%)也远大于NASA GAW-1翼型(17%)。风洞试验结果证明该翼型的优良性能。2002年,北京航空航天大学孔繁美等设计了新型高升力及失速特性缓和的BUAA-K1/BUAA-K2翼型[58],风洞试验结果表明,BUAA-K1/BUAA-K2翼型不仅有较高的最大航时因子,并且实现了同时具有高升力和失速特性和缓的气动特性,该组翼型已成功应用于我国某大型长航时无人机。
综上,我国直到20世纪80年代才开始翼型的研究。当时,无论是在翼型设计的理论、方法、试验手段还是在工程应用方面都全面落后于美国、俄罗斯等世界航空强国。而我国飞行器研究又迫切需要自主研发先进翼型。在这种背景下,翼型、叶栅空气动力学国家级重点实验室在西北工业大学成立,并在先进翼型的设计理论、设计方法和试验验证技术方面开展了大量开创性的研究工作,设计出了一系列性能优异的层流翼型、超临界翼型、高升力翼型等,并成功应用于运输机、无人机、直升机和螺旋桨设计。但是,这段时期内国内针对翼型的研究不够全面和系统,没有形成针对各类飞行器的完整翼型谱系,能够在实际飞机型号得到应用的国产翼型也相对较少。随着我国在航空飞行器领域对国外追赶的步伐逐步加快,完善先进翼型谱系,并发展针对新一代飞行器的新概念翼型的研究也被提上日程。
2 21世纪翼型研究新进展21世纪以来,随着新一代飞行器的研究与发展,以及N-S方程高可信度数值模拟、边界层转捩预测、高维全局优化设计、多因素稳健设计和精细化试验测量等理论、方法与技术的不断进步,翼型研究被赋予新的使命和内容。21世纪以来的翼型研究全面地向着专用翼型和更强调综合性能的方向发展,因此本节主要按飞行器类别,综述了战斗机薄翼型、飞翼布局飞机翼型、高空长航时无人机翼型、跨声速与超声速运输机层流翼型以及高超声速飞行器宽速域翼型的最新研究进展。此外,也简要介绍了直升机旋翼翼型、螺旋桨翼型和风力机翼型等专用翼型的研究进展。需要说明的是,由于技术封锁和保密问题,有些研究无法查到公开文献,因此本文仅分析其发展动态。此外,为便于读者了解各类飞行器翼型完整的发展历程,部分内容也可能涉及到上个世纪的研究。
2.1 面向先进战斗机的薄翼型对于现代先进战斗机,一般采用大后掠角、小展弦比薄机翼,以减小超声速飞行时的阻力。这种机翼绕流具有较强的三维效应,三维机翼的压力分布相比二维翼型有所畸变。因此,针对战斗机机翼设计,传统方法主要考虑机翼平面形状以及弯扭和厚度分布的设计,而忽略对翼型的精细化气动设计。
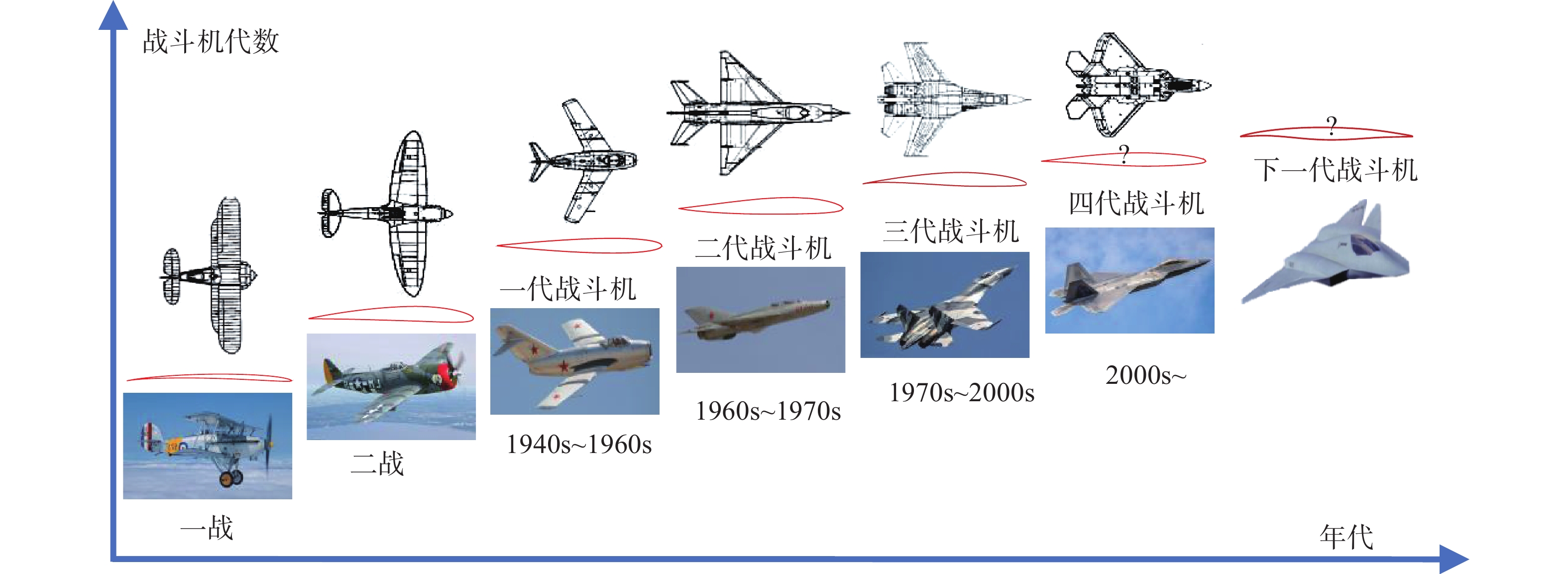
图36是不同代的战斗机及其所使用的典型翼型与发展趋势图(按照国内的“四代”战斗机划分标准[59])。早期战斗机的机翼剖面主要采用NACA标准翼型及其修改翼型。图37是第一、二、三代代表性战斗机F-86、F-4、F-16及其使用的翼型示意图。表2列出了美国典型第二、三代战斗机使用的翼型[1]。第二代战斗机主要强调超声速性能,因此减小超声速阻力非常重要,这一阶段的美国战斗机一般选用相对厚度较小的NACA对称翼型。第三代战斗机将跨声速大迎角机动性放在突出的位置,超声速性能处于相对次要的地位,因此机翼一般都采用小弯度薄翼型,以减小大迎角的阻力,同时又不会对超声速性能造成太大的损失,其基本翼型仍是NACA系列标准翼型或其修形。第二、三代战斗机的设计对翼型的精细化气动设计并不关注。
|
图 36 不同代的战斗机及其使用的典型翼型示意图 Fig.36 A sketch of different generations of fighters and airfoils |

|
图 37 第一、二、三代典型战斗机及其使用的翼型 Fig.37 Typical fighters and their airfoils |
| 表 2 美国第二、三代典型战斗机使用的翼型 Table 2 Airfoils used by the second- andthird-generation fighters |
|
|
从四代机研制开始,翼型又重新得到重视。虽然对于大后掠、小展弦比机翼,流动的三维效应显著,但是翼型对此类机翼设计仍然十分重要[60],具体表现在以下几点:(1)翼型的跨声速升阻特性直接影响飞机的航程,超声速阻力特性直接影响飞机的超声速巡航能力,翼型的弯度直接影响飞机的机动能力;(2)翼型的前缘形状可以影响三维分离涡面的生成、发展和涡的位置,从而影响飞机的大迎角升阻特性;(3)翼型的阻力发散边界和升力抖振边界仍然对机翼的性能有重要的影响。因此,即使对大后掠、小展弦比机翼,翼型的选用和设计仍然是飞机机翼设计的一项重要内容。
随着基于Navier-Stokes(N-S)方程的精细化数值模拟与优化设计技术的快速发展,设计者可以采用气动优化设计方法进行战斗机大后掠、小展弦比机翼构型甚至到全机构型的多剖面翼型优化设计,以充分考虑三维流动效应以及机身的干扰效应。针对大后掠小展弦比战斗机机翼翼型设计这一高维优化设计问题,西北工业大学高正红等[60-63]发展了曲线光顺方法、高维代理模型表示方法等,开展了三维流动环境下考虑工程约束的战斗机薄翼型精细化设计,设计翼型在亚、跨、超声速域内均保持良好的气动特性,有较高的工程实用价值。
研究表明,翼型精细化设计对于提升小展弦比机翼的气动性能仍是非常重要的[60]。随着未来战场环境愈发复杂,战斗机技战术指标的不断提高,第四代及未来战斗机的设计,将不再采用标准翼型,而是针对具体的飞行器,综合考虑气动、隐身、控制和结构等多个学科,为飞行器设计专用的翼型族。
2.2 面向飞翼布局飞机的翼型随着航空运输业的不断发展,飞机大型化趋势越来越明显,飞翼布局装载量和气动特性的优势使其广受青睐[64]。此外,未来的无人侦察机平台也向着“高速化、隐身化”的方向发展[65],在考虑隐身特性的需求时,通常也会采用飞翼布局。可见,在民用和军用领域,飞翼布局都代表了未来飞行器发展的一个重要方向。由于飞翼布局的自身特点,其翼型设计与常规布局相比存在较大差异[66-67]。
飞翼布局是一种将机翼与机身融为一体的非常规气动布局,其升阻比大,巡航气动效率高,有效装载空间大,可以有效满足超长航时、超高度、低可探测性等需求。由于去掉了水平尾翼和垂直尾翼等凸起气动部件,且机身与机翼高度融合,因此隐身性能得到大幅提高,全向雷达散射截面(RCS)有很大程度的降低。但同时也带来稳定性不足、操纵面难以布置等问题[68]。常规布局飞机的翼型设计主要考虑提高飞行器升阻性能,而飞翼布局飞机翼型设计则还需要考虑其对布局操稳的贡献,因而对翼型力矩特性有更加严苛的要求。此外,对于具有隐身需求的军用飞机而言,在翼型设计中还应充分考虑雷达隐身特性。因此,飞翼布局飞机的翼型设计需综合考虑气动、控制和隐身等多个学科的要求。
一般来说,飞翼布局飞机可以分为中央体区、中间区和翼尖区几个区域,如图38所示。不同分区的特性需求不一,其翼型设计要求也存在着较大差异。
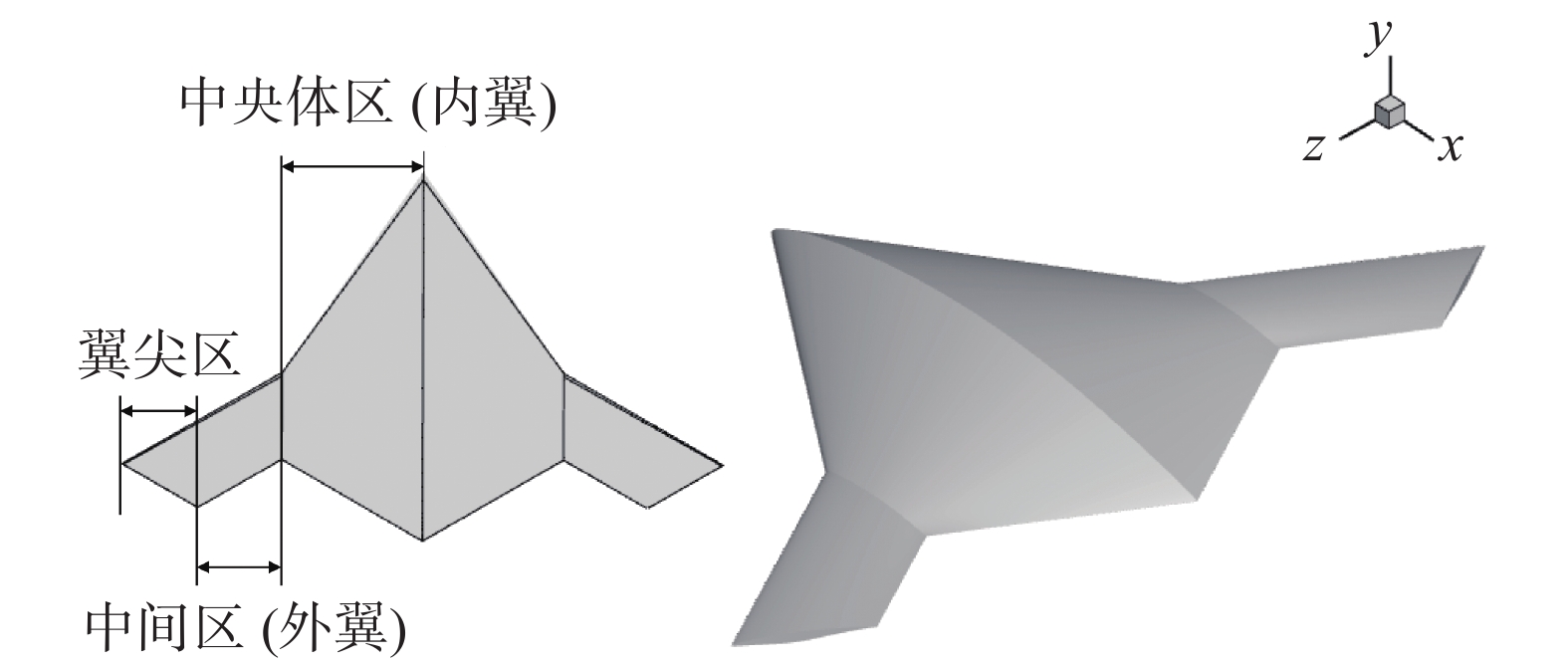
|
图 38 某飞翼布局飞行器外形示意图 Fig.38 Geometry of a flying wing configuration |
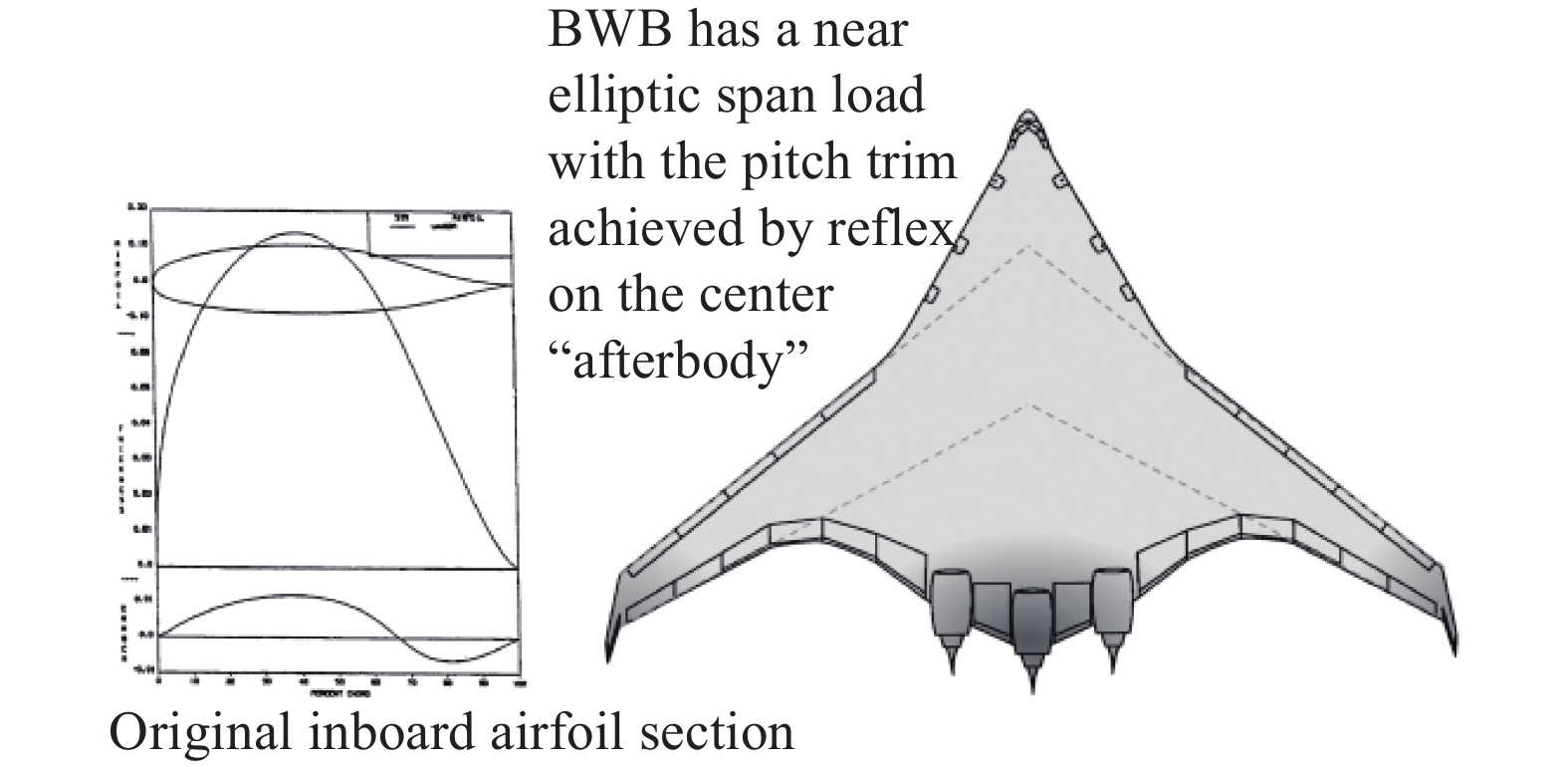
(1)中央体区(内翼)翼型设计。这一区域的翼型弦长较长,贡献了大部分的雷达散射面积,在满足人员与设备装载需求的同时,还需提供大部分升力,并且具备提供全机纵向稳定性和操纵的能力[69-70]。由于带有后掠角使得飞翼布局重心靠后,但焦点又因无平尾而前移。这种重心和焦点的矛盾,增加了飞翼布局对俯仰控制能力的要求[70]。因此,在设计中央体区的翼型时需要考虑:1)满足装载要求的翼型厚度约束;2)保证气动性能的升力或升阻比约束;3)满足纵向配平要求的俯仰力矩约束;4)满足军用飞机需要的雷达隐身性能约束。为了满足上述要求,一般采用大厚度的后卸载翼型(或反弯翼型)、前加载翼型和其他类翼型[71]。大厚度的后卸载翼型可有效提供抬头力矩,有利于实现力矩自平衡,但易导致气动效率下降且易产生激波[66,72]。BWB-450采用后缘反弯的LW109A翼型[66]作为其中央体区的基准翼型,如图39所示,以提供抬头力矩。但同时也会导致巡航性能的牺牲,且需要更大的控制面和舵面来控制飞机。
针对这一问题,可以采用前缘下表面“内凹”的前加载翼型,使压力中心前移,因此这种翼型组成的中央体外形可实现无平尾的纵向力矩自平衡;在巡航过程中燃油消耗引起的重心变化用增大矢量推力角来平衡,使静安定裕度保持为6%~9.5%,而采用后缘反弯翼型的BWB-450布局,该裕度只能达到5%。图40展示了SAX-29和SAX-40静音客机系列沿展向的翼型配置。从中可以看出,内翼段采用了升力系数较小的前加载翼型,升力主要集中于前缘部分,提供了抬头力矩,后缘附近升力系数基本为0。
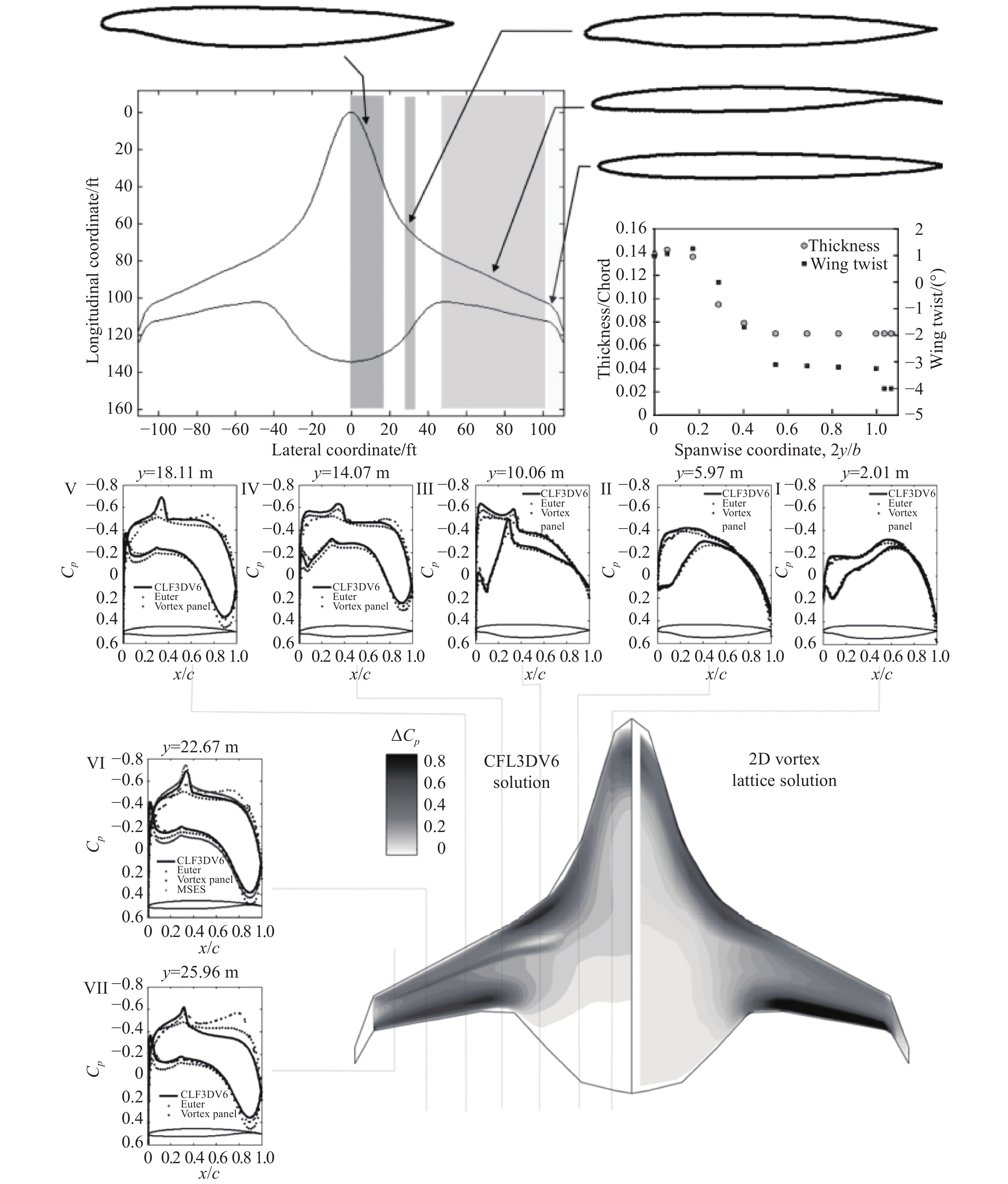
|
图 40 SAX系列静音客机翼型配置及压力分布(上:SAX-40;下:SAX-29)[67] Fig.40 The airfoil sections, planforms, and pressure distributions of SAX aircrafts (up: SAX-40; down: SAX-29)[67] |
如果考虑飞翼布局军用飞机的隐身特性,一般采用具有前加载特征的“鹰勾”前缘设计,可以有效避免由于俯仰入射而产生的镜面反射,从而进一步降低全机RCS[73],同时保持升阻特性与原构型一致。这样一来,飞翼布局的气动性能与隐身性能同时得到兼顾,如图41所示。从图中可以看到,通过对NACA65-013对称翼型进行气动/隐身综合优化设计后,最优翼型的前缘半径明显减小,下表面前段内凹(符合“鹰勾”前缘设计理念),散射电场强度被进一步减弱,且最大厚度位置后移,呈现出前加载与后卸载的特征。美国的B-2隐身轰炸机采用的就是前加载翼型,如图42所示。

|
图 41 飞翼布局内翼段翼型气动/隐身综合优化设计后翼型散射电场强度对比 Fig.41 Comparison of electric-field scattering around the optimal and baseline airfoils of a inner wing by aerodynamic/stealth integrated optimization design |

|
图 42 B-2轰炸机中央体外形 Fig.42 Central body of a B-2 boomer |
(2)中间区(外翼区)翼型设计。这一区域翼型设计与常规超临界翼型设计较为接近,须尽量避免强激波与流动分离,提高巡航升阻特性与阻力发散特性。同时,考虑飞翼布局无尾和后掠的特点,若直接采用超临界翼型会产生较大的低头力矩,增加飞翼布局的配平难度,因此进行外翼段翼型设计时,也需要将俯仰力矩控制在合理范围内[70]。
(3)翼尖区翼型设计。翼尖翼型设计需要尽可能降低巡航阻力,提高升阻比,以获得高的巡航效率,还要具备良好的低速升力特性和失速特性,推迟起降分离,为飞翼布局的起降阶段提供升力。此外,还需具备良好的隐身特性。
基于上述飞翼布局分区域翼型设计的理念,国内外学者开展了考虑气动/隐身特性的综合优化设计技术研究,包括:1)经典的二维飞翼翼型设计。它以实际飞翼飞行状态为基础,通过经验公式将三维设计状态映射为二维设计状态进行设计。Liebeck等[66]通过给出亚声速翼型的理想速度分布,然后进行了BWB-450内翼段翼型设计,得到了后缘反弯的LW109A的翼型;张彬乾等[69]进行了飞翼布局内翼段、外翼段翼型气动、隐身多学科设计,并分析了气动与隐身特性的关系;李权等[74-75]进行了融合式飞翼布局超临界翼型的设计研究;郑传宇等[76]利用PCA目标降维方法进行了飞翼翼型多学科优化设计。2)三维流动环境下的剖面翼型设计。该方法实际上是在三维的飞翼布局上直接进行沿展向不同站位处剖面翼型的设计。Pambagjo等[77]以NASA超临界翼型为基础,采用基于小扰动速势方程的余量修正法进行飞翼布局内翼段不同站位翼型剖面设计,设计翼型具有典型的超临界特征;Peigin等[78]利用基于代理模型全局优化方法,开展了三维环境下翼型剖面外形的单点和多点设计;Hileman等[79]结合内翼段和外翼段翼型的设计要求,利用MSES软件开展了静音客机翼型的反设计。在三维飞翼布局上进行二维剖面翼型的优化设计,可以更好地贴近真实的流动状态,获得针对需求的更优翼型,但同时也会造成计算成本过高的问题,尤其在涉及气动/隐身的多学科优化设计中,对计算资源需求更甚,更难在广阔的设计空间中实现高效的全局优化。Qin等[80]先进行了二维翼型的优化设计,再将得到的最优翼型配置到三维飞翼布局中进行剖面优化设计,实现了二维、三维条件结合的翼型设计,在一定程度上弥补了单纯二维翼型设计和三维环境剖面优化存在的问题。李杰等[81]针对飞翼类特殊布局无人机开展了翼型/机翼气动力设计研究,以提高升阻比为主要目的对飞翼翼型进行了设计,翼型后部采用适度反弯度技术以减小低头力矩,并将所设计的翼型配置到机翼上进行气动设计,并通过风洞试验验证了设计思路的有效性。高正红等[82-86]针对飞翼布局翼型精细化设计问题,发展了考虑大规模设计变量的分区代理模型技术,进行了三维流动环境下的翼型设计研究;针对飞翼布局气动隐身设计要求,发展了基于伴随方程的气动隐身协同设计方法,实现了飞翼翼型的高效精细化设计;此外,由于飞翼翼型对设计空间的需求与传统翼型迥异,通过有效样本的分析和研究,发展了自适应设计空间扩展技术。
综上所述,飞翼布局飞机的翼型设计是结合了气动、隐身、控制等学科的复杂多学科设计问题。这些设计要求很难同时兼顾,给优化设计带来巨大的困难。因此,需要发展更高效全局的气动/隐身综合优化设计理论与方法,对不同需求下的飞翼翼型及其三维气动布局外形进行设计。
2.3 面向高空长航时无人机的低雷诺数层流翼型高空长航时无人机作战半径大、留空时间长,具有较高精度的情报获取能力以及较高的生存能力,同时具有使用灵活、成本较低等特点,因此可以情报侦察应用领域中发挥重要作用,具有广阔的应用前景。
高空长航时无人机多采用大展弦比直机翼,机翼气动效率对全机的气动性能和飞行品质具有决定性影响,因此作为机翼剖面的翼型就显得尤为重要。由于飞行高度较高、空气密度小,高空无人机绕流呈现典型的低雷诺数流动特征。例如长航时太阳能无人机(如图43)飞行速度较低,雷诺数在10万量级;美国的“RQ-4全球鹰”(如图31)飞行速度达到马赫数0.6,雷诺数在50万~100万量级。低雷诺数下的层流分离效应是机翼气动特性恶化的主要原因[87]。

|
图 43 “太阳神”高空低速无人机 Fig.43 “Helios” high-altitude low speed UAV |
早在20世纪80年代末,美国麻省理工学院(MIT)的M. Drela就发展了XFOIL程序来设计低雷诺数翼型[88]。1995年至今,美国伊利诺伊大学研究发展了一系列的低速低雷诺数翼型(如图44),并通过试验给出了这些翼型在雷诺数为3万~50万时的气动特性[89]。近几十年来,包括美国、欧盟、俄罗斯、日本、韩国等国家和地区的多家研究机构在低雷诺数翼型气动性能和翼型气动设计方面开展了大量研究,有力支撑了高空无人机的研究与发展。
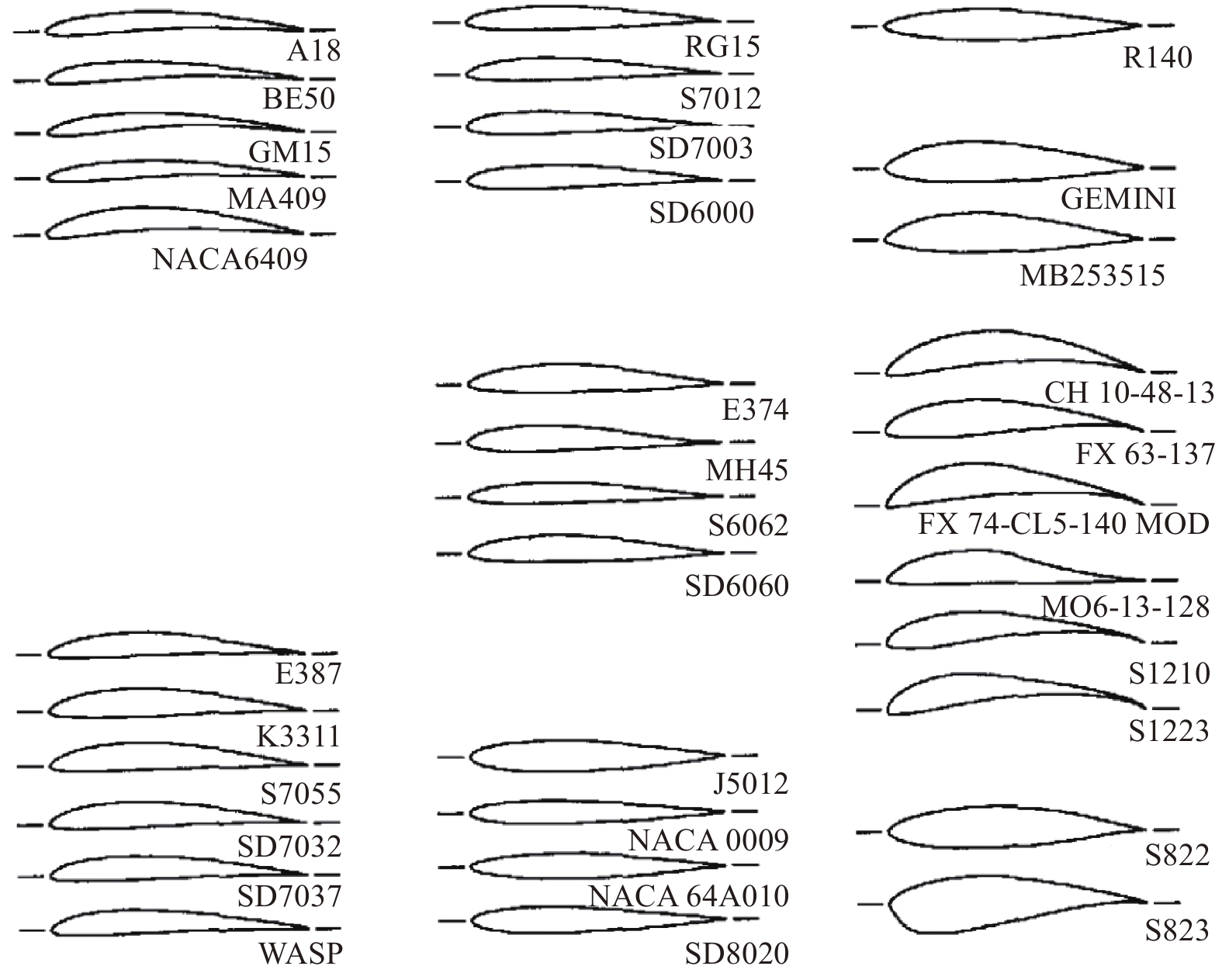
|
图 44 伊利诺伊大学测试的34个低速低雷诺数翼型[89] Fig.44 Low-speed and low-Reynolds-number airfoils tested at the UIUC[89] |
尽管现在发展了一系列的低雷诺数翼型,但大多数高空无人机并没有直接选用现有公开翼型,而是采用针对具体型号专门设计的翼型。例如“RQ-4全球鹰”,其配置的翼型为专门设计过的低雷诺数层流翼型LRN-1015,具有高的升阻比和良好的综合性能。
随着高空无人机的发展,国内针对低雷诺数翼型流动机理与优化设计开展了大量研究。王科雷等[90]针对所设计的某高空低速太阳能无人机的翼型,分析了不同雷诺数对翼型气动性能的影响机理,为低雷诺数翼型设计提供了理论参考;后来以NACA0012翼型为研究对象,认为上表面的边界层形态是影响翼型在低雷诺数条件下气动性能的关键,并根据该设计思想,开展了低雷诺数翼型优化设计。司江涛等[91]分析了低雷诺数流动的特点,结合理论分析和工程设计经验,从压力分布出发,重点放在边界层转捩点位置的控制上,提出了高亚声速低雷诺数翼型的设计思想,并以此为指导对C07翼型进行了初步设计。王皓田等[92]研究了S1223翼型在不同雷诺数、不同迎角下的流场变化情况,分析了翼型流动机理及翼型表面分离泡的演化规律。张亚锋等[93]采用遗传算法对低雷诺数翼型进行了优化设计,并且优化结果得到风洞试验验证。陈耀慧等[94]研究了翼型在极低雷诺数下施加电磁控制的效果,发现当电磁力与翼型表面流向一致时,翼型的流动分离被抑制,可以起到增升减阻的效果。陈学孔等[95-96]开展了单点和多点优化设计,提高了低雷诺数翼型在不同速度下的整体性能。李杰等[97]将遗传算法与反设计的余量修正方法有机结合,进行了低雷诺数高升力和大厚度的翼型设计。高正红等[98-101]在分析总结稳健性优化设计方法特点的基础上,以混沌多项式展开方法为基础,发展了高效不确定性分析方法,建立了考虑马赫数、雷诺数和升力系数等多参数不确定性的设计模型,开展了高升力自然层流翼型的稳健优化设计。
综上所述,针对高空无人机翼型的设计,早期主要采用基于风洞试验的半经验方法,后来更多采用数值模拟与优化设计技术,主要关注翼型在低雷诺数时边界层分离点和转捩点的控制。此外,低雷诺数条件下,转捩位置的准确预测对低雷诺数翼型设计具有重要影响,发展较精确的转捩预测方法至关重要。
2.4 面向跨声速与超声速运输机的高速层流翼型21世纪以来,随着全球变暖等环境问题日益严重,航空界对下一代民机提出了严格的节能减排目标。层流机翼技术作为一项革新性的空气动力学技术,由于其很大的减阻潜力,成为了下一代和未来民机设计关注的焦点技术之一。新一代民机一般在跨声速甚至超声速下飞行,这给层流机翼设计带来了新的挑战,主要包括:(1)如何在跨声速/超声速后掠机翼上推迟流动转捩,实现大范围层流;(2)如何兼顾机翼的层流特性与超临界/低声爆等特性。由于翼型是决定大展弦比机翼气动特性的最基本元素,因此高速层流翼型的研究对于解决上述问题具有重要意义。
为了在后掠机翼上实现大范围层流,首先要理解边界层转捩机理。根据稳定性理论,针对高空巡航状态的跨声速/超声速民机机翼,可能诱发边界层转捩的不稳定性包括[102]:(1)Tollmien-Schlichting(TS)不稳定性,源于边界层黏性剪切效应;(2)横流不稳定性,在机翼后掠和压力梯度共同作用下出现,源于边界层横流速度拐点;(3)前缘附着线不稳定性,主要作用于机翼前缘的驻点线附近,可通过控制机翼前缘曲率半径来抑制。
根据机翼边界层转捩中占主导的不稳定性类型,人们提出了一系列的高速层流机翼/翼型设计思想。
2.4.1 针对公务机和中短程窄体民机的高速层流翼型在无后掠或后掠角较小的情况下,边界层转捩主要由二维TS不稳定性诱导发生。因此,需要足够的顺压梯度控制TS波的增长。但区别于低速层流翼型,还需要避免因激波阻力增加而抵消层流减阻的收益,例如日本本田公司为“Honda Jet”公务机专门设计的高速层流翼型SHM-1[103](如图45)。该翼型上下表面的顺压梯度范围分别延伸至了42%和63%弦长处,同时具有较好的阻力发散特性。西北工业大学高正红和白俊强等也设计了用于公务机的高速层流翼型[104]。该翼型的压力恢复区经过特殊设计,使其在宽迎角范围内能够维持一定的顺压梯度。德国DLR针对前掠机翼采用2.75D反设计方法设计了跨声速层流翼型[105-106](如图46)。
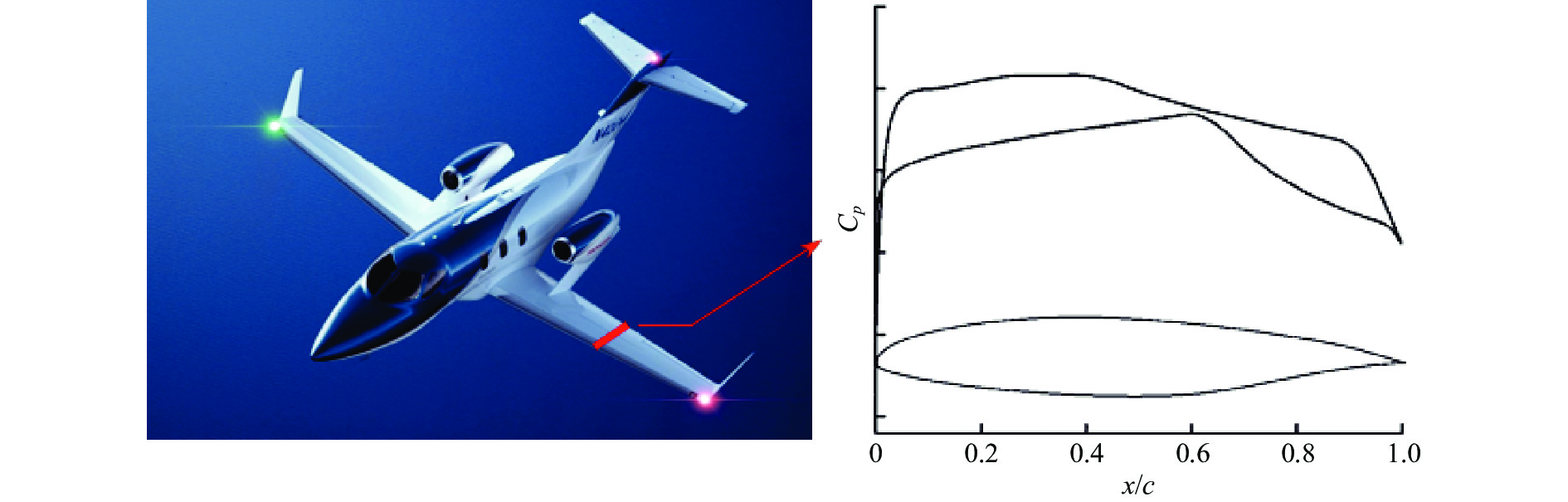
|
图 45 用于“Honda Jet”公务机的高速层流翼型SHM-1及典型压力分布[103] Fig.45 Geometry and pressure distribution of high-speed NLF airfoil SHM-1 used for Honda Jet[103] |
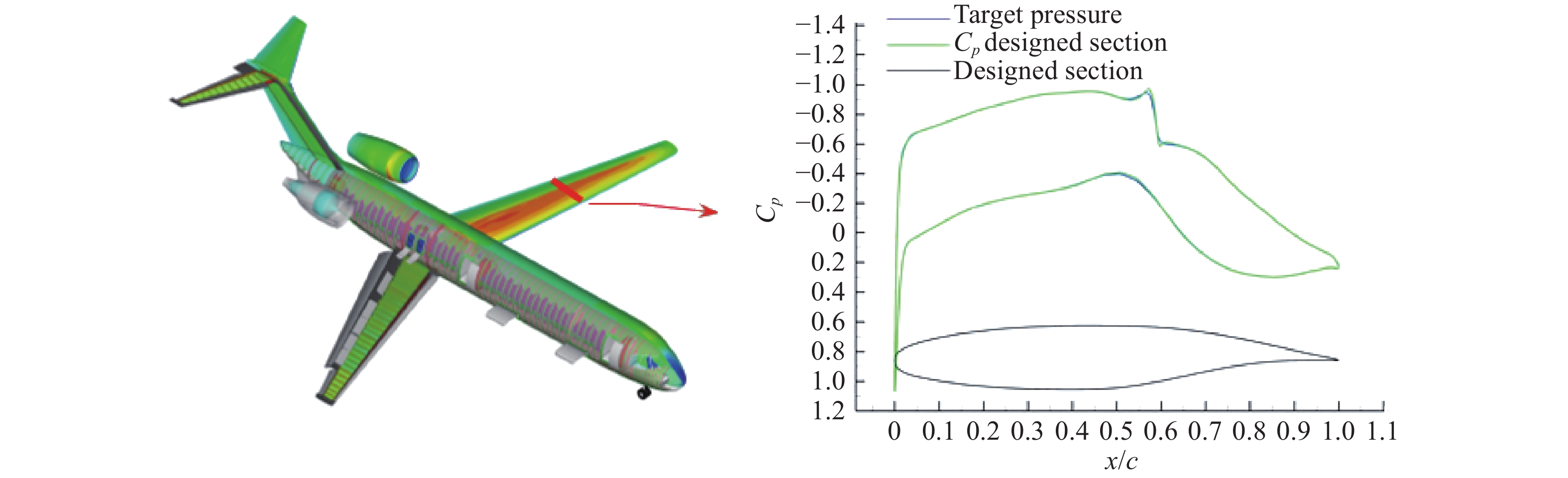
|
图 46 DLR LamAiR项目前掠翼布局及其跨声速层流翼型[105] Fig.46 Configuration of forward-swept-wing and its transonic NLF airfoil[105] |
为了解决波阻与摩阻权衡问题(即抑制TS波所需的顺压梯度与降低激波强度之间存在矛盾),数值优化算法被越来越多地应用到高速层流翼型的设计中。其中,梯度优化算法最先应用于该领域。2006年,Amoignon等[107]尝试将二维流场的扰动动能作为最小化目标,采用梯度优化算法降低了大部分扰动的累积放大因子,从而间接地推迟翼型表面层流到湍流的转捩过程。Zingg等[108-109]基于离散Adjoint方法和简化eN方法开展了层流翼型的多点优化设计。Lee和Jameson等[110]成功地采用连续Adjoint方法和eN-数据库转捩预测方法进行了层流翼型的减阻优化设计。马晓永等[111]采用序列二次规划算法对某民机层流机翼进行了多点优化设计,推迟了机翼上表面流动转捩的发生。除此之外,全局优化算法也逐渐被应用于该领域[112]。由于高速层流翼型,特别是跨声速层流翼型的设计很可能是一个多极值问题,理论上采用全局优化相比于梯度优化能够寻找到更好的全局最优解。2012年,西北工业大学韩忠华等[113-114]发展了高效的代理优化算法并用于超临界层流翼型的优化设计。韩忠华等[115-116]还提出了混合反设计/优化设计方法,可以将设计者对流动机理的物理认识与数值优化相结合,使得优化解更加符合工程实际的需要。清华大学的张宇飞等[117]则采用遗传算法开展了超临界自然层流翼型的优化设计,发现了其设计的关键在于顺压梯度与激波强度之间的权衡。此外,由于层流特性对来流扰动和表面粗糙度等因素都较为敏感,因此也十分有必要开展高速层流翼型稳健优化设计的研究[98-101]。
2.4.2 针对中远程宽体民机的高速层流翼型随着技术进步,空气动力学家们希望在更大掠角的机翼上实现层流(用于巡航马赫数更高的中远程宽体民机)。然而随着后掠角的增大,机翼边界层横流不稳定性显著增大,并可能使转捩提前发生。虽然横流不稳定性具有明显的三维特征,但其与压力分布和后掠角均密切相关[118-119]。因此,如果能在二维翼型的设计中就考虑对横流不稳定性的抑制,会对在大后掠机翼上维持层流打下良好的基础。早在1988年DLR的Redeker就研究了影响横流不稳定性增长的压力分布形态[120]。与仅考虑TS不稳定性的形态有所区别,这种压力分布上表面的前缘加速区更短、加速更快,并往往会连接一小段平台或弱逆压梯度从而抑制横流不稳定性的增长,中弦长区域依然保持合理的顺压梯度抑制TS波增长。近年来,美国NASA也提出了类似的压力分布形态(如图47),并应用于CRM构型机翼,取得了良好的效果[121-122]。西北工业大学的许朕铭和韩忠华提出了“无量纲横流压力梯度”,并通过这一新的物理量在翼型设计中考虑横流不稳定性[119,123],为相关研究提供了一种新的思路。目前,在翼型设计中考虑横流不稳定性的研究尚未成熟,仍然有待更多的风洞试验和飞行试验验证。
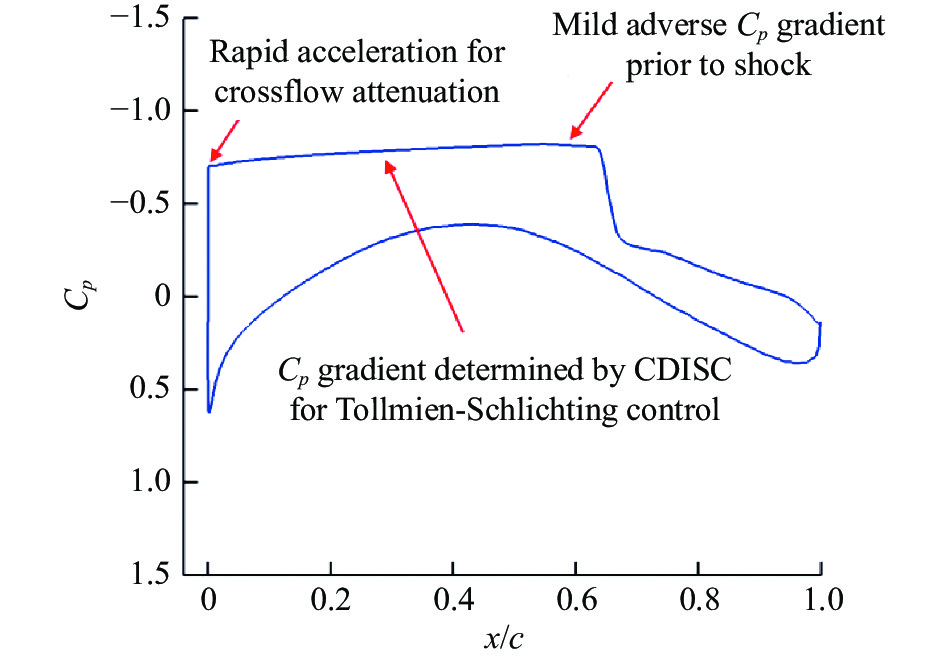
|
图 47 NASA提出用于大后掠机翼层流翼型的压力分布主要特征[122] Fig.47 Pressure distribution of the NLF wing withlarge sweep angles proposed by NASA[122] |
超声速民机机翼的后掠角进一步增大到了60°~70°左右。三维效应的显著增强和雷诺数的升高不仅使得边界层横流不稳定性变得更难抑制,而且还要考虑三维方向的TS斜波。这就要求对机翼多个展向站位处的剖面翼型进行设计。日本JAXA[124]和美国NASA[125]提出了让流动在前缘迅速加速,继而维持大范围弱压力梯度的设计思想(如图48)。类似于图47中的设计思想,这种流动一方面可以减少前缘的顺压梯度范围,避免横流不稳定性迅速增长并导致转捩在前缘发生,另一方面还可以通过维持弱压力梯度来抑制横流不稳定性的增长,尽可能增大层流范围。JAXA将该层流翼型设计思想应用于一系列超声速民机构型的层流机翼剖面翼型的设计[126]。根据风洞试验和数值模拟的结果,该设计实现了上表面40%的层流范围[124],可以使全机总阻力下降5%,减阻效果十分可观。
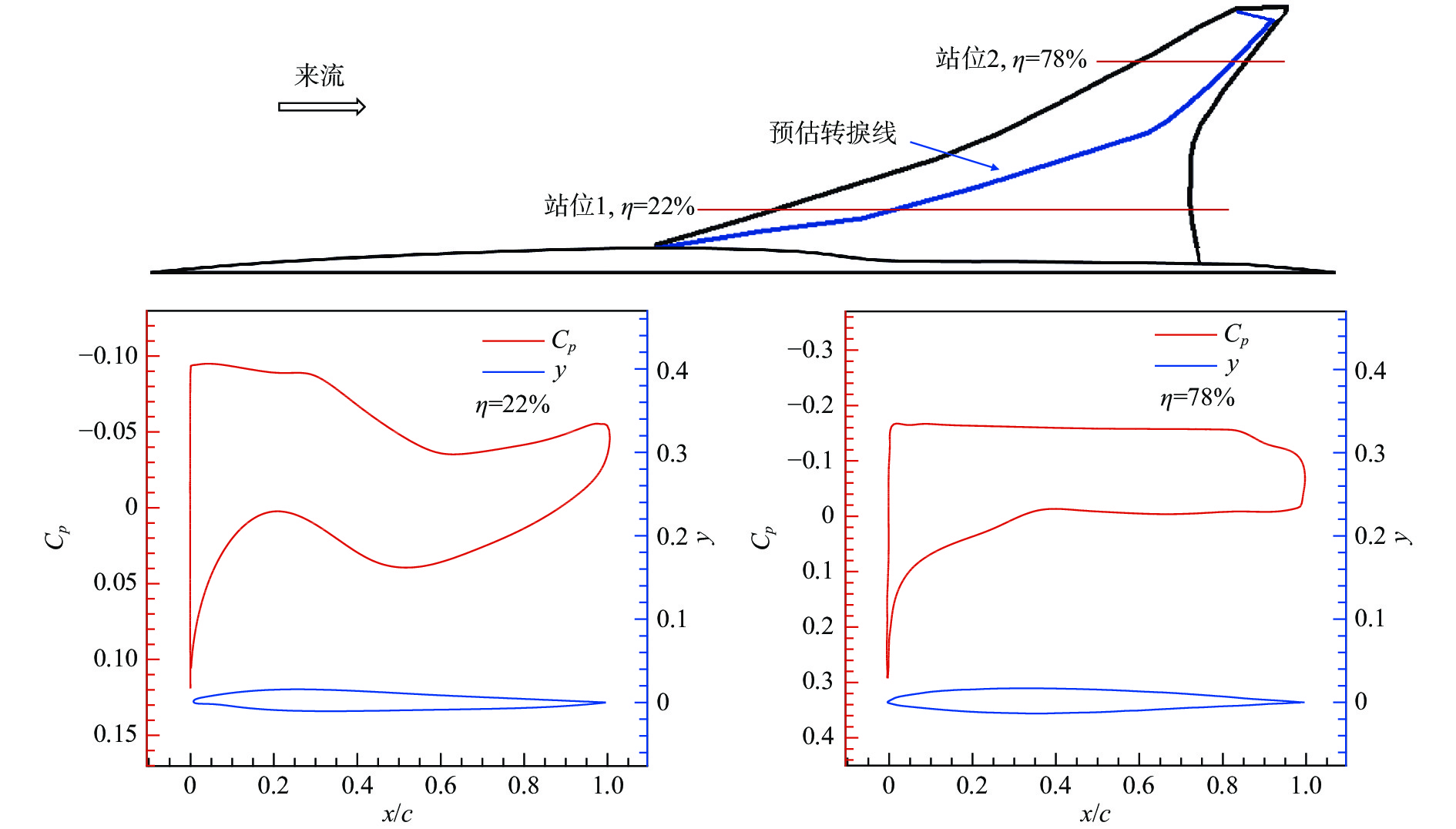
|
图 48 NASA设计的NJWB-NLF超声速层流民机构型的机翼剖面翼型压力分布和翼型[125] Fig.48 Cutplane pressure distribution and airfoil on the wing of NJWB-NLF supersonic laminar-flow transport concept designed by NASA[125] |
对于超声速层流翼型设计,还需要兼顾机翼层流特性和全机低声爆特性。初步研究表明,声爆与超声速民机的体积等效截面积和升力等效截面积相关,而这两种等效截面积与波阻和机翼升力分布密切相关,进而造成了声爆、波阻和层流范围之间的相互耦合关系。JAXA在初期设计超声速层流机翼剖面翼型时,采用反设计方法,获得了能够良好满足目标压力分布的外形[126-127];意大利宇航技术研发中心CIRA与法宇航ONERA[128-129]还采用了优化设计的方法,但由于设计变量多、设计问题复杂,其设计效果并不理想。此外,为了在层流机翼设计中考虑声爆特性,NASA联合JAXA针对翼身组合体NJWB[125,129],采用多轮次反设计方法,并且约束了对声爆水平存在较大影响的平面形状、翼载荷和机翼厚度等参数的情况下,不断对设计目标进行调整,设计后的外形在全机声爆水平基本不变的情况下,在机翼表面实现了表面约40%的层流。可见,在超声速层流机翼剖面翼型设计中主要采用的还是反设计方法,而在反设计中同时兼顾机翼层流和全机低声爆特性十分困难,极度依赖设计经验。
综上,针对公务机和中短程窄体民机的高速层流翼型发展相对更加成熟,并且已经开展了较多的风洞试验和飞行试验验证。而针对中远程宽体和超声速民机大后掠机翼的层流翼型目前仍处于设计思想与方法的探索阶段。可以预见,数值优化算法、稳健优化设计方法等将会更多地应用到高速层流翼型的设计中,用于解决多种设计需求之间的矛盾。
2.5 面向高超声速飞行器的宽速域翼型随着高超声速技术的快速发展与突破,高超声速飞机、空天飞机等新型飞行器由于其重要的商用及军用价值而备受关注。此类飞行器的飞行包线具有宽速域、大空域的特点,一次飞行中要经历亚、跨、超和高超声速多个速域(马赫数从0~6以上),并穿越0~30 km以上的空域,这要求飞行器在各个速域都具有良好的气动性能以满足飞行需求。然而,不同速域下最优气动外形存在很大差异,甚至相互矛盾,导致兼顾不同速域气动性能的宽速域气动设计面临极大挑战。
图49是Sanger号两级入轨空天飞机的第一级载机示意图。为了降低超/高超声速飞行状态下的阻力,高超声速飞行器的机翼通常具有大后掠角和小展弦比的特征。传统观点认为,对于大后掠角、小展弦比机翼,机翼的平面形状起着决定性的作用,而翼型重要性降低,因此现有方案通常采用前缘较尖的小弯度或对称的标准翼型。此类翼型具有较好的超声速/高超声速气动性能,但亚/跨声速性能欠佳,亟待发展具有更好宽速域气动性能的翼型。
由于宽速域综合性能对气动外形设计的苛刻要求,目前单一措施难以满足所有速域下的气动性能指标,为了进一步挖掘机翼的宽速域气动性能,宽速域新概念翼型受到关注。计算流体力学和气动优化设计技术的快速发展,为宽速域翼型设计提供了有力的工具,部分研究者开展了兼顾不同速域气动性能的高超声速飞行器宽速域翼型气动优化设计研究。
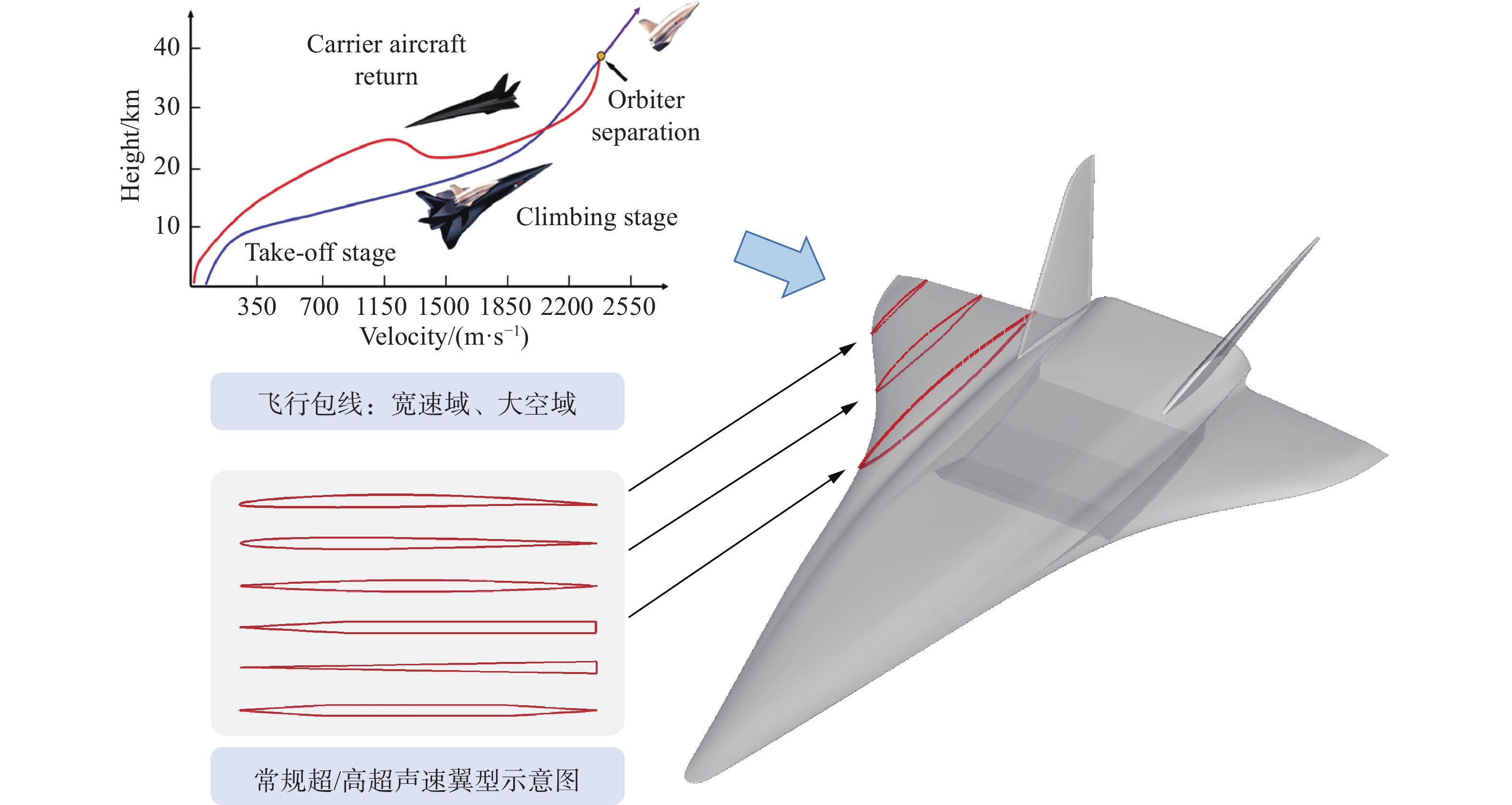
|
图 49 Sanger两级入轨空天飞机的载机示意图 Fig.49 Schematics of carrier of Sanger aircraft |
日本JAXA的研究人员采用梯度优化方法,针对其提出的两级入轨空天飞机方案开展了宽速域气动优化设计研究工作。其中,Ueno等[130]2008年开展了兼顾跨声速气动性能的高超声速运载机机翼剖面翼型的宽速域气动优化设计,并将优化翼型配置到了三维机翼上进行综合评估。结果表明,配置优化翼型后机翼的宽速域气动性能得到明显提升。2009年,Ueno等[131]又采用梯度优化方法开展了机翼的宽速域气动优化设计研究。文章指出,优化的二维翼型配置到机翼上可以明显改善机翼的宽速域气动性能,尽管对大后掠角、小展弦比的机翼而言,最终应该对剖面直接进行三维优化设计,但由宽速域翼型配置的机翼能提供一个更理想的初始外形,可以帮助设计人员更快地找到优化解。
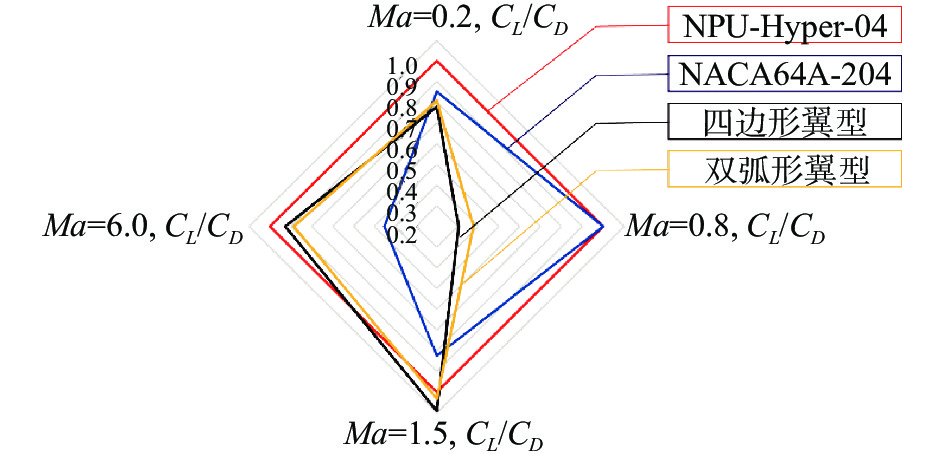
在国内,从2011年开始西北工业大学的韩忠华等开展了宽速域翼型分析与设计研究,并于2018年发明了一种能够兼顾高超声速和跨声速气动特性的新概念翼型[132](命名为NPU-Hyper-04)。该翼型几何外形如图50所示,是相对厚度4%、下表面具有“双S”形特征的小弯度翼型。机理研究表明:新翼型具有一定弯度,使其在保持良好超/高超声速气动性能前提下,亚/跨声速性能相比四边形和双弧形对称翼型有明显提升;高超声速状态下“双S”外形特征使得下表面压力分布具有多次压缩的特征,减小了头部激波阻力,也使升力在翼型上的分布更加均匀,改善了力矩特性;亚/跨声速下“双S”外形使翼型下表面形成前后加载,改善了升力特性。如图51所示,相比常规薄翼型,NPU-Hyper-04翼型关于不同速域性能的雷达图所围成的面积最大,说明具有最佳的宽速域气动性能。2019年,西北工业大学柳斐和韩忠华等[133]发展了基于代理模型的宽速域气动优化设计方法,并成功应用于宽速域翼型/机翼优化设计。2019年,西北工业大学张阳、韩忠华等[134]开展了高超声速飞行器宽速域翼型多目标优化设计研究,得到了优化翼型在不同速域下升阻比的Pareto前沿。2020年,张阳、韩忠华等[135]进一步开展了考虑升力匹配的双后掠机翼宽速域气动优化设计研究,结果表明剖面翼型优化设计对于提升机翼宽速域气动性能仍是十分重要的。
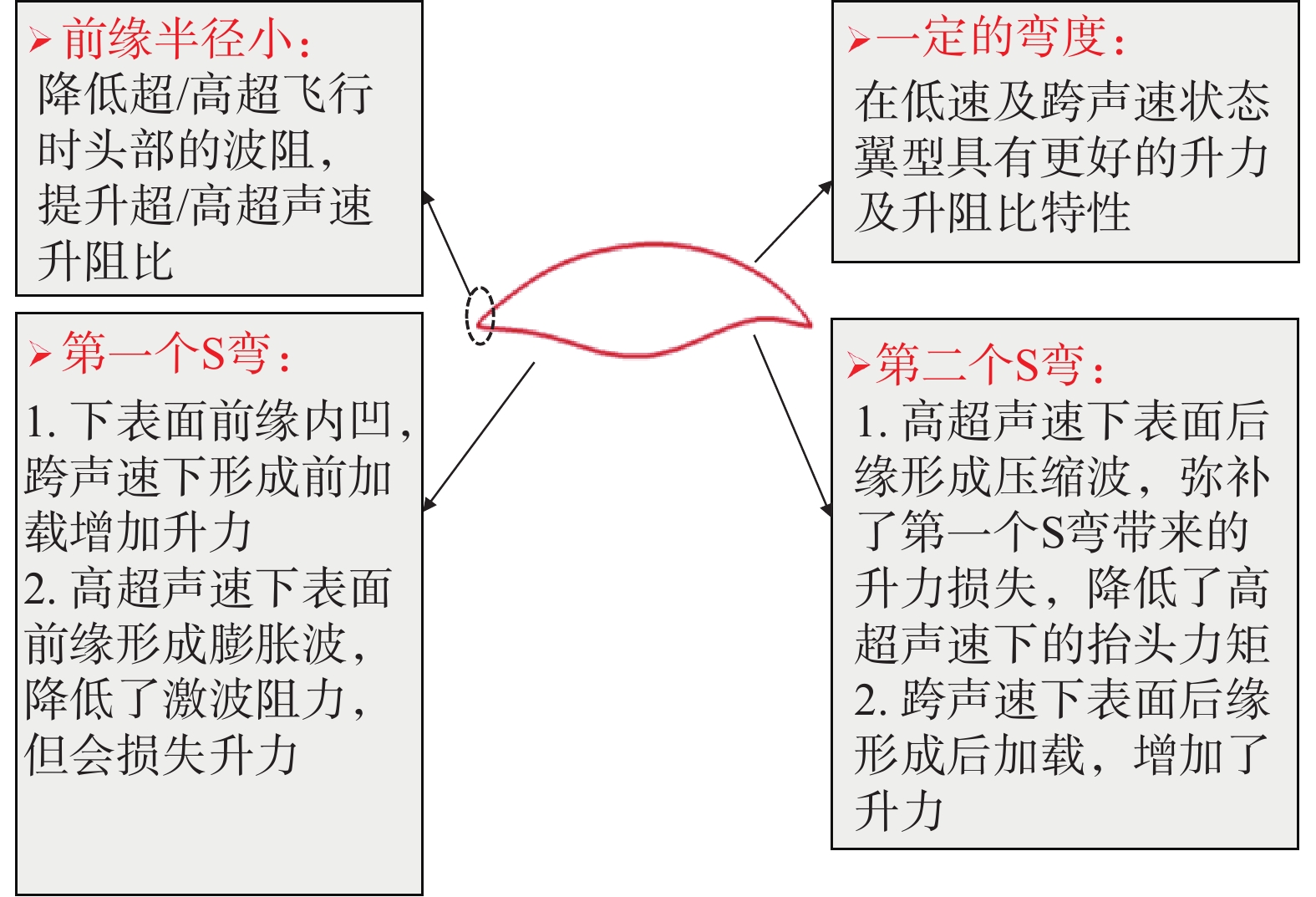
|
图 50 宽速域翼型NPU-Hyper-04翼型的几何外形与流动机理分析 Fig.50 Analysis of geometry and flow mechanism ofNPU-Hyper-04 airfoil |
|
图 51 新翼型与传统翼型的宽速域气动性能对比的雷达图(各速域的值关于NPU-Hyper-04翼型做归一化处理) Fig.51 Radar-chart comparison of aerodynamic performanceof different airfoils (values are normalized by the optimal airfoil at each point) |
目前,宽速域翼型/机翼的研究与设计尚处于起步阶段,主要关注的是气动性能。随着现代飞行器的技术指标越来越高,未来高超声速飞行器的宽速域翼型设计将更加关注气动热、隐身、控制和结构等多学科的综合性能,因此亟需发展相应的多学科多目标气动优化设计技术,以适应未来宽速域高超声速飞行器的发展需求。
2.6 面向下一代直升机的旋翼专用翼型旋翼翼型是直升机旋翼气动设计的基本要素(如图52),其气动特性优劣对旋翼性能有关键性影响,进而影响直升机悬停、前飞、机动、载重、升限高度、航程/航时、操纵性及噪声和振动水平等。
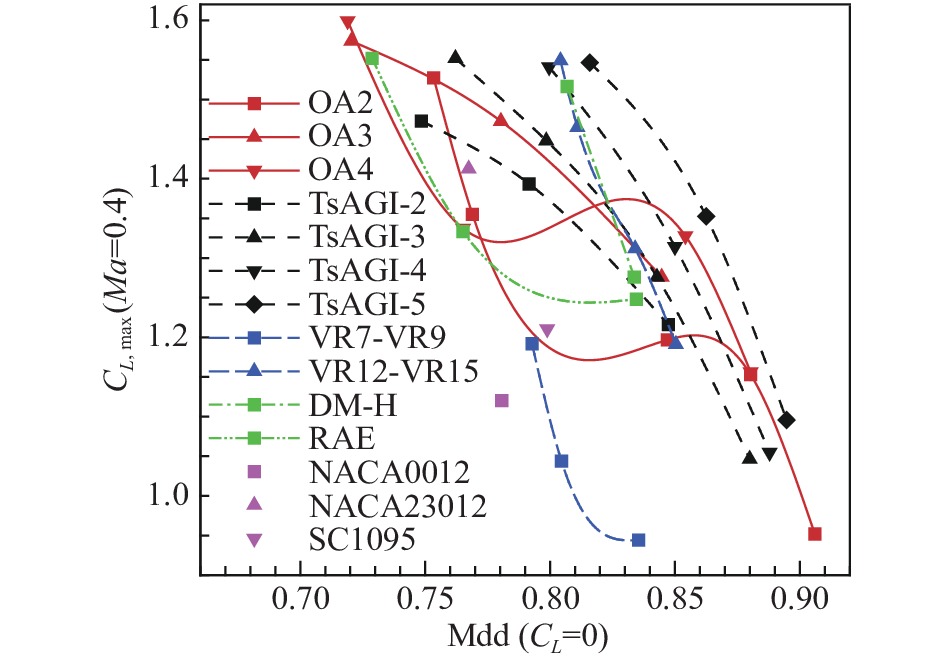
早期旋翼设计直接选用NACA0012等低力矩翼型。为了满足直升机更大载重、更高速度、更强机动性等需求,20世纪70年代起,旋翼专用翼型进入快速发展期,设计出了包括法国OA系列[136],前苏联(俄罗斯)TsAGI系列[137],美国VR、SC、HH系列,英国RAE系列,以及德国DM-H系列等。在此期间,通过引入自然层流和超临界等先进翼型设计理念,以及设计分析手段和风洞试验技术的进步,旋翼翼型的阻力发散马赫数和最大升力系数等关键性能稳步提升(如图53)。此外,还发展了针对高速直升机共轴刚性旋翼桨叶反流区的纺锤型(也称类椭圆)翼型[138]。

|
图 52 直升机旋翼及翼型 Fig.52 Helicopter rotor and airfoils |
|
图 53 典型旋翼翼型的阻力发散特性(Mdd)与最大升力特性(CL, max) Fig.53 Performance of drag divergence and maximum liftof typical airfoils for helicopter rotors |
国内较早开展直升机旋翼翼型研究的机构包括西北工业大学和南京航空航天大学。20世纪90年代初,西北工业大学乔志德教授提出了旋翼翼型关键气动特性与几何外形的关联特征,设计出了国内第一个旋翼专用翼型系列,其最大升力和阻力发散等关键性能优于法国OA2系列,与OA3系列相当,飞行试验表明直升机的升限、操纵性和稳定性等综合性能得到了显著提升。进入21世纪以来,高正红等[139]提出了局部修形控制俯仰力矩等新设计方法,开展了全工况条件下的高升力低力矩旋翼翼型设计研究(如图54),主要综合性能超过法国OA3系列[140-142];并针对旋翼翼型多目标设计要求,开展了基于PCA目标降维技术研究,通过SOM实现了高维目标可视化,实现旋翼翼型高效优化设计[143-144]。针对共轴刚性旋翼,韩少强等[145-147]设计的用于桨叶内侧的典型钝尾缘旋翼翼型,与国外主流翼型性能相当;所设计的桨尖翼型,阻力特性和阻力发散特性优于OA407翼型[148]。

|
图 54 全工况条件下的高升力低力矩旋翼翼型(西北工业大学) Fig.54 High-lift and low-moment rotor airfoils under all working conditions (NPU) |
中国空气动力研究与发展中心和南京航空航天大学等也开展了旋翼翼型的相关研究[149],开发了旋翼翼型气动设计与评估软件系统[150],发展了旋翼翼型多工况设计及非定常设计方法[151-152]等。
21世纪以来,各国对先进旋翼翼型设计的研究从未停止,针对直升机不同任务需求和工作环境的旋翼翼型必需进行定制化设计已成为共识。旋翼翼型研究的未来发展趋势是:悬停/前飞/机动多工况下的翼型多目标多约束优化设计[151,153-156],翼型/旋翼一体化设计[157-158],动态翼型非定常设计[159-163],基于流动控制的翼型设计[164-172],气动/结构/声学/隐身等多学科耦合设计和智能变形设计[173]等。
2.7 面向先进螺旋桨的专用翼型螺旋桨技术广泛应用于飞机、飞艇、鱼雷和登陆艇等。螺旋桨桨叶剖面翼型是决定螺旋桨气动性能的重要因素(如图55),它的选择与设计直接关系螺旋桨的推进效率、工况适应范围和气动噪声等。

|
图 55 螺旋桨桨叶及翼型系列示意图 Fig.55 Cross sections of a propeller blade |
著名的早期螺旋桨翼型有英国RAF-6E和美国Clark Y等,以及NACA16系列自然层流翼型。20世纪70年代后,英国和美国分别发展出了基于超临界设计思想的ARA-D系列和HS系列螺旋桨专用翼型。20世纪80年代起,美国、德国、英国等开始发展临近空间长航时无人机和飞艇等,该类飞行器的共同特点之一是都采用螺旋桨作为推进方式[174],因此以低雷诺数(30万以内)为主要特征的临近空间螺旋桨及其专用翼型得到了长足发展[175]。由于各国对螺旋桨技术封锁严密,关于先进螺旋桨专用翼型的公开报道极少。
国内最早开展螺旋桨翼型研究的是西北工业大学乔志德教授,其设计的NPU-PR、NPU-PLR等多个螺旋桨专用低雷诺数高升力翼型系列(如图56),以及提出的翼型-螺旋桨一体化设计方法和抗空化压力分布设计水下螺旋桨低噪声翼型的方法[176],成功应用于气垫登陆艇、高空飞艇和鱼雷等的螺旋桨设计,气动效率和噪声水平等指标均显著提升。进入21世纪以来,杨旭东等提出了针对更低雷诺数(10万以下)螺旋桨的仿生勺型NPU-SLR系列翼型[177-178];许建华等针对临近空间低雷诺数螺旋桨开展了高亚声速低雷诺数特殊流动机理研究[179](如图57),发展了考虑几何兼容的螺旋桨翼型系列设计方法[180]和低雷诺数翼型非定常设计方法[181]等研究,设计开发了适用于不同功率的临近空间螺旋桨系列翼型,形成了更加完备的临近空间螺旋桨专用翼型系列,基本满足我国临近空间飞艇和太阳能无人机螺旋桨的研制需求。北京航空航天大学刘沛清[182]概述了国内外螺旋桨翼型系列的发展情况,分析了三类国外低雷诺数翼型系列的气动特性,并归纳了低雷诺数螺旋桨翼型选择和设计的基本原则[183]。

|
图 56 临近空间低雷诺数螺旋桨高升力翼型系列NPU-PLR Fig.56 High-lift and low-Reynolds-number airfoils for propellers (NPU-PLR) |

|
图 57 高亚声速低雷诺数特殊条件下的复杂激波系-边界层干扰流动结构 Fig.57 Complex flow structures of shock waves-boundary layer interaction under high-subsonic and low Reynolds number |
随着飞行器对大空域/宽速域条件下的螺旋桨效率、螺旋桨与电机/发动机匹配以及低噪声等要求的不断提高,螺旋桨翼型设计将朝着翼型/桨叶一体化精细设计、宽高度-速度适应范围翼型设计、新概念流动控制翼型、气动/结构/声学等多学科耦合优化设计和智能变形翼型等方向发展。
2.8 面向先进风力机叶片设计的专用翼型实现“碳达峰”和“碳中和”是我国应对气候变化、保护地球家园、构建人类命运共同体的重大战略决策,因而发展绿色低碳的风力发电产业具有重要意义。风力机叶片设计技术是风力发电机组设计的一项核心技术,风力机叶片的性能决定了风力发电机的风能利用效率、载荷特性和噪声水平等。而作为叶片剖面的翼型是构成叶片外形的基本要素(如图58),是叶片设计的基础和核心技术,是决定叶片性能的最重要因素。因此,高性能风力机翼型设计,对于提高叶片风能捕获能力、降低叶片重量和系统载荷有着重要意义。

|
图 58 风力机翼型是风力机叶片设计的基本要素 Fig.58 Wind-turbine airfoils are the basic elements in the wind-turbine blade design |
早期风力机叶片设计直接采用传统航空翼型(如NACA翼型),但实践表明这些翼型并不能很好满足设计与使用要求。20世纪80年代起,欧美等风电发达国家开始研究和设计风力机专用翼型。文献[184]对全球的风力机叶片发展进行了综述。21世纪至今主要形成了美国可再生能源实验室的NREL S系列[185]、丹麦RISØ国家实验室的RISØ系列[186]、瑞典航空设计研究院的FFA-W系列[187]和荷兰代尔夫特理工大学的DU系列[188]等风力机翼型(族)。
我国在风力机叶片设计技术方面长期落后于欧美等风电强国。2007年以前,我国没有自己成系列的风力机专用翼型(族)。在时任中国风能专业委员会主任委员的贺德馨研究员(曾任中国空气动力研究与发展中心总师)和中科院热物理所徐建中院士的共同倡导下,西北工业大学乔志德教授撰写了发展具有我国自主知识产权的风力机专用翼型族的建议书,得到国家科技部高新技术中心的高度重视,被列入可再生能源领域“十一五”863计划目标导向类项目。在这以后,在科技部“十一五”、“十二五”863项目的支持下,国内开展了风力机专用翼型族的设计研究。西北工业大学自主设计了NPU-WA兆瓦级[189](如图59(a))和NPU-MWA多兆瓦级[184,190](如图59(b))风力机翼型(族)。经数值计算与风洞试验验证,其气动性能全面达到国外同类翼型性能水平,部分超过国外同类翼型性能水平,并成功应用于国产叶片设计与生产,中科院热物理所开发了CAS-W兆瓦级风力机翼型族[191]。此外,还有华北电力大学[192]、重庆大学[193]、汕头大学[194]和南京航空航天大学[195]等国内单位设计过风力机翼型或者提出了风力机翼型设计方法。

|
图 59 西北工业大学自主设计的NPU-WA兆瓦级和NPU-MWA多兆瓦级风力机翼型族 Fig.59 Geometries of the NPU-WA and NPU-MWA wind turbine airfoil family |
综上,我国已经发展了与国际同类风力机翼型性能相当的国产风力机翼型族,且在小范围内得到了成功应用。面对风力机超大型化和小型静音化的两个发展趋势,国产风力机翼型族仍需要进一步改进和优化。针对超大型风力机叶片设计需要的平底后缘翼型,由于存在流动分离问题,需要发展准确的高效数值模拟方法以及高精度风洞试验测试技术。针对小型静音化设计要求,需要发展新的耦合气动、噪声和结构的多学科优化设计方法。最终建立一套从方法到国产软件、从国产风力机翼型族到国产风力机叶片的国产化风电产业设计标准。
2.9 其他翼型除了以上介绍的翼型,还有其他类型的翼型值得关注。比如,模仿鸟翼羽毛分叉竖起减小流动分离的仿生翼型[196]、通过附加吹气增大层流区域的层流控制翼型[197]、通过吹吸气等主动流动控制技术达到增升减阻目的的环量控制翼型[198]和协同射流翼型[199],以及采用智能材料与结构设计结合飞控、传感器技术,在不同飞行状况下达到自适应气动构型目的的智能变体翼型[200]等。
3 翼型的未来发展与面临的挑战经过100多年的研究与发展,翼型的设计理念、气动特性、分析方法和优化设计技术均取得了长足进步,诞生了满足不同时期飞行器研制需要的通用与专用翼型族。翼型研究的未来发展呈现两大趋势:一方面,下一代和未来飞行器的苛刻性能指标需求,对翼型研究提出了新的挑战,翼型研究内涵、模式和手段都将发生改变;另一方面,湍流机理等基础研究的突破,大涡模拟(LES)和直接数值模拟(DNS)等方法的逐渐成熟和应用,大规模高性能并行计算的发展,以及多物理场、多学科分析与优化设计技术的进步与人工智能的引入,将为翼型研究提供新的思想、方法与手段。
针对下一代与未来飞行器的翼型研究,本文认为未来有四个方向值得重视,下面分别作简要介绍。
3.1 宽速域、大空域翼型宽速域、大空域是下一代飞行器发展的趋势之一。不同速域下飞行器的最优气动外形存在很大差异,机翼外形及剖面形状显著不同,流动机理也大相径庭(如图60),这使得实现良好宽速域气动设计面临极大挑战。2021年4月,中国宇航学会将 “大空域跨速域高超飞行器气动布局设计方法与技术”列为2021年宇航领域十大科学问题和技术难题之一,理由是:“大空域跨速域高超飞行器气动布局设计方法与技术需适应大范围的飞行空域及速域变化要求,是气动设计的关键和难点,也是跨速域高超飞行器所面临的重大共性基础问题。该技术的突破将大幅拓展高超飞行器的活动范围。”
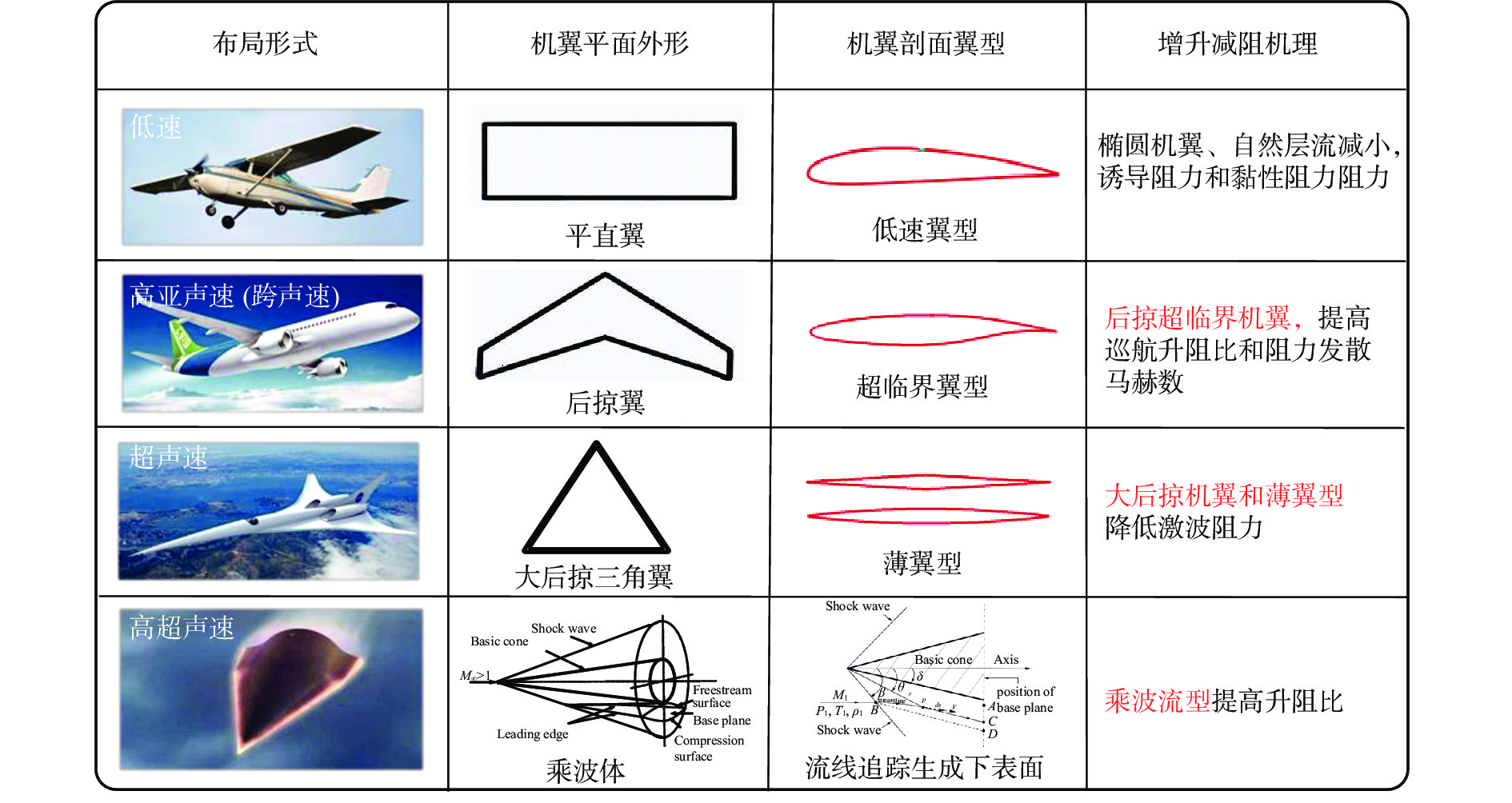
|
图 60 宽速域、大空域翼型/机翼气动设计面临的挑战 Fig.60 Aerodynamic design of airfoil/aircraft in different Mach-number regions |
除全机气动布局设计外,宽速域翼型/机翼也是提升飞行器宽速域气动性能的重要技术途径之一,亟待进一步开展深入研究,从而为未来宽速域高超声速飞行器的工程研制奠定技术基础。从目前宽速域翼型/机翼研究现状来看,尚面临如下几个方面的挑战:
(1)宽速域翼型/机翼复杂流动机理。对于高超声速飞行器小展弦比机翼,目前大多采用侧重超声速和高超声速性能的对称薄翼型,如四边形或双弧形翼型,其宽速域气动性能有很大提升空间。因此,亟需突破实现优良宽速域气动性能的翼型/机翼复杂流动机理,从而为宽速域飞行器设计提供理论指导。
(2)考虑复杂约束的宽速域翼型/机翼多目标优化设计技术。在优化设计的过程中除了升阻特性,还需要进一步考虑力矩、压心、焦点以及气动热等关键因素。这些性能参数决定了飞行器操稳特性和飞行品质,在飞行器设计中不可或缺。然而,不同速域下的力矩、压心和焦点等性能参数规律与特点迥异,使得优化问题的设计空间变得极为复杂,可行域将十分狭窄,亟需发展考虑复杂约束的宽速域翼型/机翼多目标优化设计技术。
(3)考虑升力匹配与操稳匹配的宽速域翼型/机翼优化设计技术。由于飞行马赫数和高度的巨大差异,宽速域高超声速飞行器起降和巡航状态飞行动压相差超过10倍以上。以相同重量飞行,所需的机翼面积相差也超过10倍,实现升力匹配设计面临极大困难。此外,随着马赫数的增加,宽速域飞行器的全机气动中心先后移、再前移,造成静稳定性的剧烈变化,从而使得实现操稳匹配设计面临极大挑战。因此在宽速域翼型设计中要考虑到升力匹配和操稳匹配问题的影响。
3.2 力/电磁/热多物理场翼型下一代飞行器概念研究如火如荼,其技术水平和性能指标要求将大幅超过现有型号。例如下一代战斗机大家公认应具备“5S”能力(超飞行能力、超隐身能力、超感知能力、超打击能力和超协同能力);而下一代大型民用飞机将向绿色环保与超声速方向发展,对低噪声、低声爆特性提出苛刻要求。在这种发展需求下,翼型作为构成飞行器翼面/舵面的基本元素,其设计过程需要关注的物理问题将大大拓展。翼型设计不仅需要进行空气流场以及相关联的气动力特性分析,还需要进行电磁、气动热和声学等多种物理场耦合分析(如图61所示)由此产生基础理论、分析方法和设计技术等方面的诸多挑战,具体包括:
(1)适用于翼型设计的高效、多物理场耦合数值模拟与分析方法。力/电磁/热/声等多物理场耦合模拟分析的难度高,计算量大。用于翼型设计特别是优化设计时,必须解决多物理场耦合模拟的效率问题,否则很难实现工程实用。
(2)翼型多学科设计方法与技术。传统翼型设计技术主要追求力学单一学科性能指标,设计工况范围较窄,难以满足考虑力/电磁/热/声等多种学科综合性能的新一代翼型设计需要,亟待发展以气动为核心的高效、考虑不稳定性的多学科稳健优化设计技术。
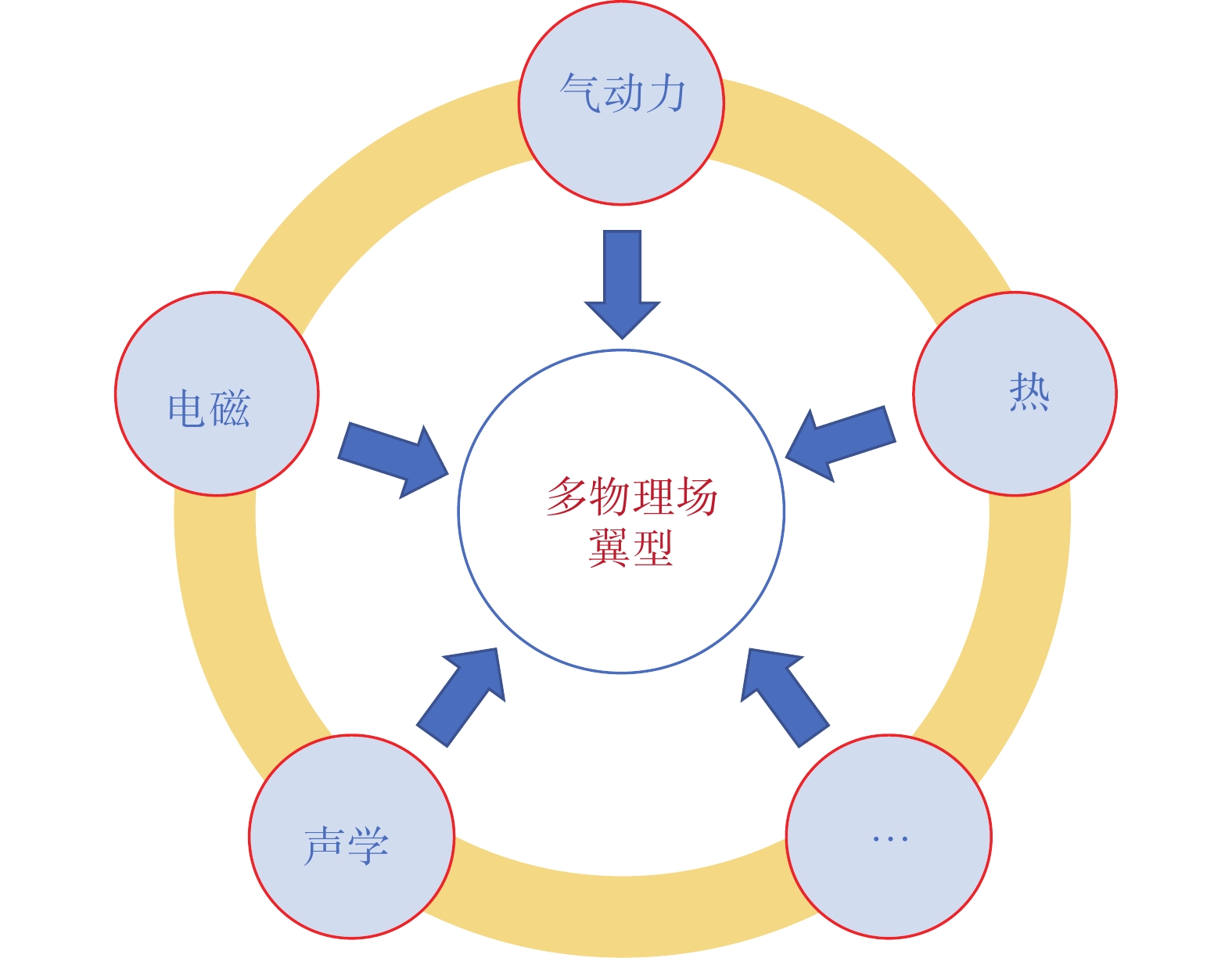
|
图 61 新一代翼型对多物理场分析的需求 Fig.61 Requirements of new-generation airfoils for multi-physics analysis |
机翼/机身的高度融合是下一代飞行器的重要发展趋势之一。通过翼身融合,大型民机可获得比传统飞机更高的升阻比,战斗机和轰炸机还能获得优秀的电磁隐身特性。对于此类构型,机翼/机身在外形和功能上不再存在明确界限。翼型设计的现有模式主要是考虑二维流动的2D设计模式,以及部分考虑三维流动效应的2.5D/2.75D模式,如图62所示。这些方法适用于机翼、机身、尾翼等部件外形界限明确、功能相对独立的飞行器传统布局,而难以胜任翼身高度融合的气动布局。从飞行器整体角度综合考虑,开展三维流动条件下的翼型设计以及翼型/飞行器一体化设计十分必要,而这种设计模式的主要难点和挑战包括:
(1)适用于一体化优化设计的复杂构型参数化与自动成形技术。现有的参数化方法中,剖面与平面的参数化基本是独立和解耦的,配套的成形方法单一,适用范围窄,无法满足翼型/飞行器一体化设计对复杂三维型面精细化处理以及拓扑优化的需要。而发展精细处理复杂型面与拓扑结构的参数化与成形新技术,需要飞机设计专业与几何学、计算机图形学等专业进行配合。
(2)二维翼型的气动与多学科性能同飞行器复杂三维构型性能的映射关系与影响机制。现有设计一般以性能良好的翼型构建飞行器基准机翼或全机构型,保证其具备较好的初始性能。而对于翼身高度融合的下一代飞行器,三维效应较现有飞机更加显著,二维剖面到三维构型的性能映射关系更加复杂,影响机制有待阐明。只有解决了这些问题,在翼型方面的丰富研究成果才能有效地利用起来,帮助和指导三维一体化设计。
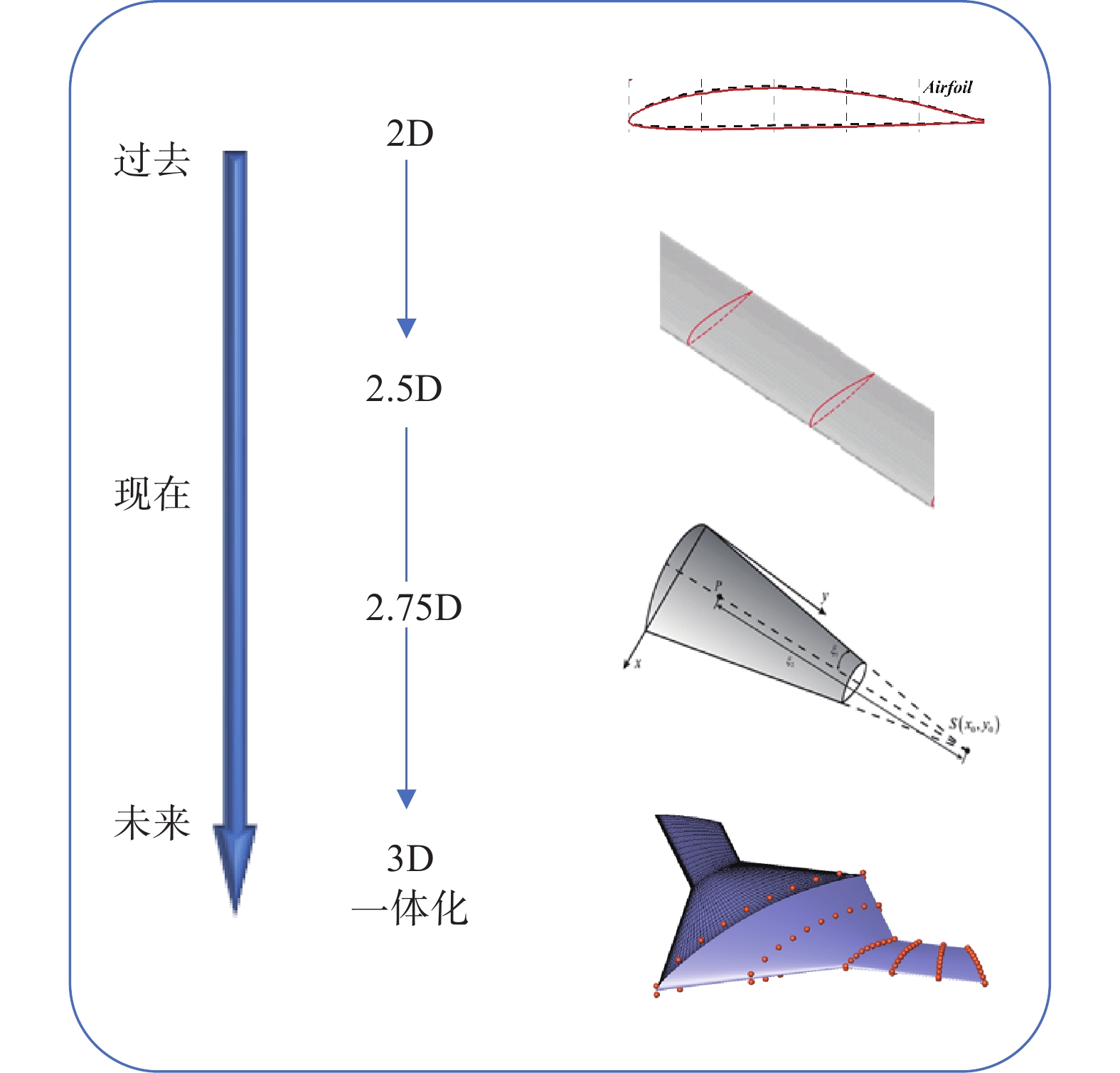
|
图 62 飞行器一体化设计与传统设计对比示意图 Fig.62 Evolution of airfoils' design patterns |
智能变体可能即将成为下一代飞行器研制的一项关键技术。智能变体是指通过自适应的主/被动变形,保证飞行器在不同飞行状态下实现最优飞行性能,并已成为各国关注与研究的焦点[201-205]。翼型对飞行器的重要性决定了智能变体的关键是实现翼型/机翼的变形(如图63),包括弦长、弯度、厚度、扭转和展长等。因此,翼型/智能变体一体化设计也是翼型未来发展的重要方向之一。近年来关于智能变体的研究主要集中于智能结构/材料[206]、飞行控制[207-208]和驱动机构[209]等,而翼型/智能变体一体化设计的研究相对较少[210]。
翼型/智能变体一体化设计面临的挑战主要有:
(1)翼型/智能变体总体布局技术。包括仿生柔性机翼、变后掠机翼和弯折机翼等各类变体布局及其原理,智能变体过程中的飞行力学、高效智能变形策略,以及变体动态快速气动分析方法等都需要进一步探索和研究。
(2)翼型/智能变体动态气动分析、设计与动态试验验证方法。传统方法无法解决翼型/智能变体一体化设计和试验验证问题,亟待研究翼型在智能变体过程中的流动新机理,以及高效高精度的非定常动态气动分析与设计新理论和新方法;智能变体过程的风洞试验模型设计和相似准则、气动力测量、流动显示等专用试验技术。
(3)翼型/智能变体控制技术。除了新概念变体气动布局技术和气动设计方法,实现翼型/智能变体一体化设计面临的挑战还表现为其涉及气动、结构、材料、飞行控制和驱动机构等多学科强耦合设计,其中气动是基础,智能结构和功能材料是关键,飞行控制和驱动机构是保障。
(4)仿生飞行和变形原理。仿生是翼型/智能变体一体化设计的一个重要研究方向和技术途径[211],而目前鸟类的飞行原理及其机体变形原理尚不完全清楚,实现其变形功能还有诸多材料、结构和可靠性等问题亟待解决。
4 总 结本文在回顾翼型百年发展历程基础上,重点综述了21世纪以来翼型研究的现状和发展动态,分析了未来发展方向和面临的挑战。一些结论或认识如下:
(1)实践证明,翼型是人类探索飞行奥秘的一项伟大发明。在过去100多年时间里,翼型研究对于航空飞行器的发展起到了至关重要的作用。美国和前苏联(俄罗斯)对先进翼型的研究,在气动领域奠定了其成为航空强国的基础。
(2)翼型是航空飞行器的一种重要基础技术,翼型研究与航空飞行器的发展相辅相成,相互促进。一方面,翼型研究的突破推动了航空飞行器升级换代或性能大幅提升;另一方面,飞行器性能要求的不断提升,牵引了翼型基本理论、设计理念和设计技术的创新。
(3)现代数值模拟方法、流动稳定性与转捩预测、优化设计技术、试验测试技术的进步,以及人工智能等新技术的引入,是翼型设计理念和设计方法创新的重要推动力。
(4)翼型绕流中包含了层流、湍流、转捩、激波和分离等复杂流动现象,翼型流动机理的研究是飞行器三维复杂流动机理研究的基础。
(5)对于高速飞行器小展弦比大后掠机翼,尽管三维流动效应显著,但翼型设计仍然具有意义。一方面,翼型设计可为三维机翼设计提供良好的基准剖面外形;另一方面,可以打破传统翼型设计模式,直接在三维流动环境下对翼型进行设计。
(6)根据线化理论,超声速情况应该采用对称薄翼型。然而,该理论并不能支持高超声速情况下也应该采用对称翼型的观点。实践证明,下表面具有“双S”形特征的小弯度薄翼型具有更好的高超声速升阻力特性和宽速域特性。
(7)为适应下一代和未来飞行器的发展需求,新一代翼型将在宽速域、大空域、多物理场及智能变体等复杂使用条件下具有优良的多学科综合性能。而翼型/飞行器多学科一体化设计和智能变体下的动态设计与控制是其中的难点和关键点。
致谢:感谢中国科学院院士、中国空气动力学会理事长唐志共研究员以及《空气动力学学报》编辑部的鼓励和支持。感谢翼型、叶栅空气动力学国家级重点实验室全体同仁的大力支持和无私帮助。感谢西北工业大学气动与多学科优化设计研究所宋科副教授、许建华副研究员、王跃副教授、许晨舟博士、韩少强博士、张阳博士、许朕铭博士、聂晗博士以及王雪鹤硕士、刘子侨硕士、刘明奇硕士、卢佐硕士、郭恒博硕士、陈晴硕士、昝博文硕士、杨跃波硕士、王迪博士等在撰写过程中的大力协助。谨以此文献给翼型研究的先辈们!
| [1] |
乔志德. 翼型的选择与设计[M]. 方宝瑞. 飞机气动布局设计. 北京: 航空工业出版社, 1997. QIAO Z D, Airfoil selection and design, in: FANG B R, Aircraft aerodynamic layout design[M]. Aviation industry press, 1997 (in Chinese). |
| [2] |
RAYMER D. Aircraft design: A conceptual approach[M]. 5th edition. Washington, DC: AIAA, Inc. , 2012. doi: 10.2514/4.869112
|
| [3] |
ANDERSON J D. Introduction to flight[M]. 8th edition. Boston: McGraw-Hill Book Company, 2008.
|
| [4] |
PADFIELD G D, LAWRENCE B. The birth of flight control: an engineering analysis of the wright brothers' 1902 glider[J]. Aeronautical Journal, 2003, 107(1078): 697-718. |
| [5] |
HICKS R M, HENNE P A. Wing design by numerical optimization[J]. Journal of Aircraft, 1978, 15(7): 407-412. DOI:10.2514/3.58379 |
| [6] |
ACKROYD J A D. Sir George Cayley: The invention of the aeroplane near Scarborough at the time of Trafalgar[J]. Journal of Aeronautical History, 2011, 6: 130-181.https://www.aerosociety.com/media/4862/sir-george-cayley-the-invention-of-the-aeroplane-near-scarborough-at-the-time-of-trafalgar.pdf
|
| [7] |
BART G C. On aerial navigation[J]. The Journal of the Royal Aeronautical Society, 1955, 59(530): 110-119. DOI:10.1017/s0368393100130202 |
| [8] |
小约翰·D·安德森, 著. 空气动力学基础[M]. 第5版, 双语教学译注版. 杨永, 宋文萍, 张正科, 等译. 航空工业出版社, 2014. ANDERSON D Jr. Fundamentals of aerodynamics[M]. 5th edition. Aviation Industry Press, 2014 (in Chinese). |
| [9] |
LILIENTHAL O. Bird flight as the basis of aviation : A Contribution Towards a System of Aviation[M]. Longmans, Green and Company Limited, 1911. https://s3-eu-west-1.amazonaws.com/bga-sg-archive/Books/BIRDFLIGHT%20AS%20THE%20BASIS%20OF%20AVIATION.pdf
|
| [10] |
李成智. 飞机机翼的发展[C]//中日机械技术史国际学术会议, 1998. LI C Z. The development of aeroplane wings[C]//China Academic Journal Electronic Publishing House, 1998 (in Chinese). |
| [11] |
ELLIOT B A. Herald of an age[M]. Arcadia Publishing, 2000.
|
| [12] |
AERONAUTICS N. Annual report of the national advisory committee for aeronautics (1st)[R]. Technical Report Archive & Image Library, 1916.
|
| [13] |
BOBBITT P J. Langley airfoil-research program[R]. NASA, N79-20032, 1979. https://ntrs.nasa.gov/api/citations/19790011861/downloads/19790011861.pdf
|
| [14] |
NICHELSON B J. Engineer in charge: a history of the langley aeronautical laboratory, 1917-1958. James R. Hansen[J]. Isis, 1988, 79(2): 319-320. DOI:10.1086/354738 |
| [15] |
JACOBS E N, WARD K E, PINKERTON R M. The characteristics of 78 related airfoil sections from tests in the variable-density wind tunnel[R]. NACA-TR-460, 1933. https://ntrs.nasa.gov/api/citations/19930091108/downloads/19930091108.pdf
|
| [16] |
JACOBS E N, PINKERTON R M. Tests in the variable-density wind tunnel of related airfoils having the maximum camber unusually far forward[R]. NACA-TR-537, 1936. https://ntrs.nasa.gov/api/citations/19930091610/downloads/19930091610.pdf
|
| [17] |
JACOBS E N, PINKERTON R M, GREENBERG H. Tests of related forward-camber airfoils in the variable-density wind tunnel[R]. NACA-TR-610, 1937. https://ntrs.nasa.gov/api/citations/19930091685/downloads/19930091685.pdf
|
| [18] |
THEODORSEN T. Theory of wing sections of arbitrary shape[R]. NACA-TR-411, 1931. https://ntrs.nasa.gov/api/citations/19930091485/downloads/19930091485.pdf
|
| [19] |
《飞机设计手册》总编委会, 编. 飞机设计手册, 第6册, 气动设计[M]. 北京: 航空工业出版社, 2002. Aircraft Design Manual editorial committee. Aircraft design manual, Volume 6, aerodynamic design[M]. Aviation Industry Press, 2002. |
| [20] |
JACOBS E N. Preliminary report on laminar-flow airfoils and new methods adopted for airfoil and boundary-layer investigations[R]. NACA-WR-L-345, 1939. https://ntrs.nasa.gov/api/citations/19930092782/downloads/19930092782.pdf
|
| [21] |
ABBOTT I H, VON DOENHOFF A E, STIVERS JR L S. Summary of airfoil data[R]. NACA-TR-824, NASA, 1945. https://ntrs.nasa.gov/api/citations/19930092747/downloads/19930092747.pdf
|
| [22] |
UIUC APPLIED AERODYNAMICS GROUP. UIUC Airfoil DataSite[EB/OL]. https://mselig.ae.illinois.edu/ads/coord_database.html
|
| [23] |
ABBOTT I H, VON DOENHOFF A E. Theory of wing sections: including a summary of airfoil data[M]. Dover Publications, 1959, 11.
|
| [24] |
TRUCKENBRODT E. A method of quadrature for calculation of the laminar and turbulent boundary layer in case of plane and rotationally symmetrical flow[R]. NACA-TM-1379, 1955. https://ntrs.nasa.gov/api/citations/19930093851/downloads/19930093851.pdf
|
| [25] |
WORTMANN F X. Progress in the design of low drag aerofoils[M]//Boundary Layer and Flow Control. Amsterdam: Elsevier, 1961: 748-770. doi: 10.1016/b978-1-4832-1323-1.50007-5
|
| [26] |
HARRIS C D. NASA supercritical airfoils: A matrix of family-related airfoils[R]. NASA-TP-2969, NASA, 1990. https://ntrs.nasa.gov/api/citations/19900007394/downloads/19900007394.pdf
|
| [27] |
WHICOMB R T. Review of NASA supercritical airfoils[C]//9th International Council of the Aeronautical Sciences Congress, 1974. ICAS PAPER 74-10.
|
| [28] |
HARRIS C D. Aerodynamic characteristics of 10 percent thick NASA supercritical airfoils with different aft camber[R]. NASA-TM-X-2977, NAS 1.15: X-72007, 1975. https://ntrs.nasa.gov/api/citations/19830002808/downloads/19830002808.pdf
|
| [29] |
HARRIS C D. Aerodynamic characteristics of a 14-percent-thick NASA supercritical airfoil designed for a normal-force coefficient of 0.7[R]. NASA-TM-X-72711, NAS 1.15: X-72712, 1975. https://ntrs.nasa.gov/api/citations/19830013896/downloads/19830013896.pdf
|
| [30] |
PEARCEY H H. The aerodynamic design of section shapes for swept wings[M]//Advances in Aeronautical Sciences. Amsterdam: Elsevier, 1962: 277-322. doi: 10.1016/b978-0-08-006550-2.50021-1
|
| [31] |
陈迎春, 张美红, 张淼, 等. 大型客机气动设计综述[J]. 航空学报, 2019, 40(1): 522759. CHEN Y C, ZHANG M H, ZHANG M, et al. Review of large civil aircraft aerodynamic design[J]. Acta Aeronautica et Astronautica Sinica, 2019, 40(1): 522759. (in Chinese) |
| [32] |
SOMERS D M. Subsonic natural-laminar-flow airfoils[M]// BARNWELL R W, HUSSAINI M Y, Eds. Natural laminar flow and laminar flow control. Springer New York, 1992: 143-176.
|
| [33] |
MCGHEE R J, BEASLEY W D, WHITCOMB R T. NASA low-and medium-speed airfoil development[R]. NASA-TM-78709, 1979. https://ntrs.nasa.gov/api/citations/19800012809/downloads/19800012809.pdf
|
| [34] |
NAEGELE H, EPPLER R. Plastic sailplane FS-24 phoenix[J]. Soaring, 1958, 22: 2-5. |
| [35] |
HANSON P W. Science and technology of low speed and motorless flight[R]. NASA-CP-2085-PT-2, NASA, 1979, 131-153. https://ntrs.nasa.gov/api/citations/19790015718/downloads/19790015718.pdf
|
| [36] |
EPPLER R, SOMERS D M. A computer program for the design and analysis of low-speed airfoils[R]. NASA-TM-80210, 1980. https://ntrs.nasa.gov/api/citations/19800020753/downloads/19800020753.pdf
|
| [37] |
EPPLER R. Airfoil data[M]//Airfoil Design and Data. Berlin, Heidelberg: Springer Berlin Heidelberg, 1990: 163-512. doi: 10.1007/978-3-662-02646-5_6
|
| [38] |
DOENHOFF A E V, ABBOTT F T. The Langley two-dimensional low-turbulence pressure tunnel[R]. NACA-TN-1283, 1947. https://ntrs.nasa.gov/api/citations/19930081899/downloads/19930081899.pdf
|
| [39] |
MCGHEE R J, BEASLEY W D, FOSTER J M. Recent modifications and calibration of the Langley low-turbulence pressure tunnel[R]. NASA-TP-2328, 1984. https://ntrs.nasa.gov/api/citations/20020043801/downloads/20020043801.pdf
|
| [40] |
SOMERS D M. Design and experimental results for a natural-laminar-flow airfoil for general aviation applications[R]. NASA-TP-1861, 1981. https://ntrs.nasa.gov/api/citations/19810015487/downloads/19810015487.pdf
|
| [41] |
PAYNE H E. Laminar flow rethink-using composite structure[R]. SAE Technical Paper 760473, 1976. doi: 10.4271/760473
|
| [42] |
PFENNINGER W. Investigations on reductions of friction on wings, in particular by means of boundary layer suction[M]. NACATM-1181, 1947. https://ufdc.ufl.edu/AA00009311/00001
|
| [43] |
BEFUS J, LATAS J, NELSON E, et al. In-flight measurements of lift, drag, and pitching moments on an advanced NLF wing on a Cessna Model T210[C]//NASA Symposium on NLF and LFC Research, 1987.
|
| [44] |
LABRUJERE T E, LOEVE W, SLOOFF J W. An approximate method for the determination of the pressure distribution on wings in the lower critical speed range[R]. NLR MP 68005 U, National Aerospace Laboratory NLR, 1968.
|
| [45] |
SOMERS D M, HORSTMANN K H. Design of a medium-speed natural-laminar-flow airfoil for commuter aircraft applications[J]. DFVLR IB, 1985, 129-85. |
| [46] |
VIKEN J K, WATSON-VIKEN S A, PFENNINGER W, et al. Design of the low-speed NLF(1)-0414F and the high-speed HSNLF(1)-0213 airfoils with high-lift systems[R]//Research in Natural Laminar Flow and Laminar-Flow Control, Part 3. N90-12540, 1987. https://ntrs.nasa.gov/api/citations/19900003224/downloads/19900003224.pdf
|
| [47] |
SEWALL W G, MCGHEE R J, HAHNE D E, et al. Wind tunnel results of the high-speed NLF(1)-0213 airfoil[R]//Research in Natural Laminar Flow and Laminar-Flow Control, Part 3. N90-12542, 1987. https://ntrs.nasa.gov/api/citations/19900003226/downloads/19900003226.pdf
|
| [48] |
KOSS D, STEINBUCH M, SHEPSHELOVICH M. . Design and experimental evaluation of a high-lift, mild-stall airfoil[C]//12th Applied Aerodynamics Conference, Colorado Springs, CO, USA. Reston, Virigina: AIAA, 1994. AIAA-1994-1867. doi: 10.2514/6.1994-1867
|
| [49] |
MAUGHMER M D, SOMERS D M. Design and experimental results for a high-altitude, long-endurance airfoil[J]. Journal of Aircraft, 1989, 26(2): 148-153. DOI:10.2514/3.45736 |
| [50] |
EPPLER R, SOMERS D M. Airfoil design for Reynolds numbers between 50, 000 and 500, 000[R]. NASA, 1985.
|
| [51] |
BANAL L F, UBANDO A T. Lift enhancement of the LRN 1015 airfoil using a gurney flap: a computational fluid dynamics investigation[J]. Journal of Computational Innovations and Engineering Applications, 2017, 2(1): 18-26. |
| [52] |
CRANE H L, MCGHEE R J, KOHLMAN D L. Applications of advanced aerodynamic technology to light aircraft[C]//SAE Technical Paper Series, 400 Commonwealth Drive, Warrendale, PA, United States: SAE International, 1973. doi: 10.4271/730318
|
| [53] |
VAN TASSEL D. Studies of a new family of general aviation airfoils[C]//12th Annual Meeting and Technical Display, Washington, DC, USA. Reston, Virigina: AIAA, 1976. AIAA-1976-0217. doi: 10.2514/6.1976-217
|
| [54] |
乔志德. 自然层流超临界翼型的设计研究[J]. 流体力学实验与测量, 1998, 12(4): 24-31. QIAO Z D. Design of supercritical airfoils with natural laminar flow[J]. Experiments and Measurements in Fluid Mechanics, 1998, 12(4): 24-31. (in Chinese) |
| [55] |
华俊, 张仲寅, 施宁光, 等. 现代自然层流翼型的设计方法[J]. 空气动力学学报, 1993, 11(1): 57-63. HUA J, ZHANG Z Y, SHI N G, et al. Numerical design method for modern NLF airfoils[J]. Acta Aerodynamica Sinica, 1993, 11(1): 57-63. (in Chinese) |
| [56] |
华俊, 张仲寅, G. Redeker, 等. NPU翼型的气动力分析和改进设计[J]. 航空学报, 1989, 10(4): 180-183. HUA J, ZHANG Z Y, G. REDEKER, et al. Aerodynamic analysis and modification design of npu airfoils[J]. Acta Aeronautica et Astronautica Sinica, 1989, 10(4): 180-183. DOI:10.3321/j.issn:1000-6893.1989.04.010 (in Chinese) |
| [57] |
张仲寅, 詹浩. 长航时飞机用的NPU-ASN-1翼型[J]. 西北工业大学学报, 1999, 17(B12): 36-38. ZHANG Z Y, ZHAN H. NPU-ASN-1 airfoil for long-endurance airplane[J]. Journal of Northwestern Polytechnical University, 1999, 17(B12): 36-38. (in Chinese) |
| [58] |
孔繁美, 华俊, 向锦武, 等. 高升力与失速特性缓和的翼型设计研究[J]. 北京航空航天大学学报, 2002, 28(2): 235-237. KONG F M, HUA J, XIANG J W, et al. Design and research of high-lift mild-stall airfoils[J]. Journal of Beijing University of Aeronautics and Astronautics, 2002, 28(2): 235-237. DOI:10.3969/j.issn.1001-5965.2002.02.029 (in Chinese) |
| [59] |
杨伟. 关于未来战斗机发展的若干讨论[J]. 航空学报, 2020, 41(6): 524377. YANG W. Development of future fighters[J]. Acta Aeronautica et Astronautica Sinica, 2020, 41(6): 524377. (in Chinese) |
| [60] |
王超, 高正红. 小展弦比薄机翼精细化气动优化设计研究[J]. 中国科学(技术科学), 2015, 45(6): 643-653. WANG C, GAO Z H. Refined aerodynamic design optimization of a wing with small aspect ratio[J]. SCIENTIA SINICA Technologica, 2015, 45(6): 643-653. DOI:10.1360/N092014-00156 (in Chinese) |
| [61] |
GAO Z H, WANG C, HUANG J T. HDMR-based surrogate model for high dimensional aerodynamic design problems[C]//16th AIAA/ISSMO Multidisciplinary Analysis and Optimization Conference, Dallas, TX. Reston, Virginia: AIAA, 2015. AIAA-2015-3094. doi: 10.2514/6.2015-3094
|
| [62] |
王超. 基于代理模型的高效气动优化与高维多目标问题研究[D]. 西安: 西北工业大学, 2018. WANG C. Research on surrogate-based efficient aerodynamic optimization and many-objective problems[D]. Xi'an: Northwestern Polytechnical University, 2018 (in Chinese). |
| [63] |
WANG C, GAO Z H, HUANG J T, et al. Smoothing methods based on coordinate transformation in a linear space and application in airfoil aerodynamic design optimization[J]. Science China Technological Sciences, 2015, 58(2): 297-306. DOI:10.1007/s11431-014-5745-4 |
| [64] |
李广义. 未来大型客机发展展望[J]. 国防科技工业, 2008(6): 24-29. |
| [65] |
蔡向阳, 董树军, 宋虹兴. 无人侦察机装备发展现状及趋势[J]. 飞航导弹, 2010(4): 33-36. |
| [66] |
LIEBECK R H. Design of the blended wing body subsonic transport[J]. Journal of Aircraft, 2004, 41(1): 10-25. DOI:10.2514/1.9084 |
| [67] |
MIALON B, FOL T, BONNAUD C. Aerodynamic optimization of subsonic flying wing configurations[C]//20th AIAA Applied Aerodynamics Conference, St. Louis, Missouri. Reston, Virigina: AIAA, 2002. AIAA-2002-2931. doi: 10.2514/6.2002-2931
|
| [68] |
王虎峰, 白俊强. 飞翼布局气动设计要点研究[J]. 科学技术与工程, 2009, 9(12): 3570-3573. WANG H F, BAI J Q. Design essentials research of the flying-wing configuration[J]. Science Technology and Engineering, 2009, 9(12): 3570-3573. DOI:10.3969/j.issn.1671-1815.2009.12.098 (in Chinese) |
| [69] |
张彬乾, 罗烈, 陈真利, 等. 飞翼布局隐身翼型优化设计[J]. 航空学报, 2014, 35(4): 957-967. ZHANG B Q, LUO L, CHEN Z L, et al. On stealth airfoil optimization design for flying wing configuration[J]. Acta Aeronautica et Astronautica Sinica, 2014, 35(4): 957-967. (in Chinese) |
| [70] |
夏露, 张欣, 杨梅花, 等. 飞翼布局翼型气动隐身综合设计[J]. 西北工业大学学报, 2017, 35(5): 821-826. XIA L, ZHANG X, YANG M H, et al. Airfoil aerodynamic stealth integrated design for a flying wing configuration[J]. Journal of Northwestern Polytechnical University, 2017, 35(5): 821-826. DOI:10.3969/j.issn.1000-2758.2017.05.012 (in Chinese) |
| [71] |
李沛峰, 张彬乾, 陶于金, 等. 翼身融合布局中央机体翼型设计研究[J]. 西北工业大学学报, 2018, 36(2): 203-210. LI P F, ZHANG B Q, TAO Y J, et al. Center body airfoil design for blended wing body configuration[J]. Journal of Northwestern Polytechnical University, 2018, 36(2): 203-210. DOI:10.3969/j.issn.1000-2758.2018.02.001 (in Chinese) |
| [72] |
ROMAN D, GILMORE R, WAKAYAMA S. Aerodynamics of high-subsonic blended-wing-body configurations[C]//41st Aerospace Sciences Meeting and Exhibit, Reno, Nevada. Reston, Virginia: AIAA, 2003. AIAA-2003-554 doi: 10.2514/6.2003-554
|
| [73] |
焦子涵, 张彬乾, 沈冬. 翼型几何参数对隐身特性的影响研究[J]. 机械科学与技术, 2012, 31(12): 1980-1987. JIAO Z H, ZHANG B Q, SHEN D. Investigation on the effects of geometric parameters on airfoils' stealth characteristics[J]. Mechanical Science and Technology for Aerospace Engineering, 2012, 31(12): 1980-1987. (in Chinese) |
| [74] |
陈曦, 白俊强, 李权. 某飞翼布局隐身飞行器的翼型优化[J]. 航空计算技术, 2013, 43(6): 46-49,53. CHEN X, BAI J Q, LI Q. Airfoil optimization of a stealth flying wind aerial vehicle[J]. Aeronautical Computing Technique, 2013, 43(6): 46-49,53. DOI:10.3969/j.issn.1671-654X.2013.06.012 (in Chinese) |
| [75] |
李权, 郭兆电, 雷武涛, 等. 融合体布局超临界翼型设计研究[J]. 空气动力学学报, 2017, 35(4): 579-586. LI Q, GUO Z D, LEI W T, et al. Study on supercritical airfoil of blended wing body[J]. Acta Aerodynamica Sinica, 2017, 35(4): 579-586. DOI:10.7638/kqdlxxb-2017.0073 (in Chinese) |
| [76] |
郑传宇, 黄江涛, 周铸, 等. 飞翼翼型高维目标空间多学科综合优化设计[J]. 空气动力学学报, 2017, 35(4): 587-597. ZHENG C Y, HUANG J T, ZHOU Z, et al. Multidisciplinary optimization design of high dimensional target space for flying wing airfoil[J]. Acta Aerodynamica Sinica, 2017, 35(4): 587-597. DOI:10.7638/kqdlxxb-2017.0079 (in Chinese) |
| [77] |
PAMBAGJO T, NAKAHASHI K, OBAYASHI S, et al. Aerodynamic design of a medium size blended-wing-body airplane[C]//39th Aerospace Sciences Meeting and Exhibit, Reno, NV, USA. Reston, Virigina: AIAA, 2001. AIAA-2001-0129. doi: 10.2514/6.2001-129
|
| [78] |
PEIGIN S, EPSTEIN B. Computational fluid dynamics driven optimization of blended wing body aircraft[J]. AIAA Journal, 2006, 44(11): 2736-2745. DOI:10.2514/1.19757 |
| [79] |
HILEMAN J I, SPAKOVSZKY Z S, DRELA M, et al. Airframe design for silent fuel-efficient aircraft[J]. Journal of Aircraft, 2010, 47(3): 956-969. DOI:10.2514/1.46545 |
| [80] |
QIN N, VAVALLE A, MOIGNE A L, et al. Aerodynamic studies for blended wing body aircraft[C]//9th AIAA/ISSMO Symposium on Multidisciplinary Analysis and Optimization, Atlanta, Georgia, 2002. AIAA-2002-5448. doi: 10.2514/6.2002-5448
|
| [81] |
王豪杰, 李杰, 周洲. 飞翼类特殊布局无人机气动力设计研究[J]. 西北工业大学学报, 2011, 29(5): 789-793. WANG H J, LI J, ZHOU Z. Airfoil and wing layout design for a certain flying wing UAV (unmanned air vehicle)[J]. Journal of Northwestern Polytechnical University, 2011, 29(5): 789-793. DOI:10.3969/j.issn.1000-2758.2011.05.024 (in Chinese) |
| [82] |
GAO Z H, ZHAO K, WANG C. Aerodynamic shape optimization of BWB aircraft based on multizone collaborative optimization design method[C]//33rd AIAA Applied Aerodynamics Conference, Dallas, TX. Reston, Virginia: AIAA, 201. AIAA-2015-2878. doi: 10.2514/6.2015-2878
|
| [83] |
ZHOU L, HUANG J T, GAO Z H, et al. Three-dimensional aerodynamic/stealth optimization based on adjoint sensitivity analysis for scattering problem[J]. AIAA Journal, 2020, 58(6): 2702-2715. DOI:10.2514/1.j059136 |
| [84] |
ZHANG W, GAO Z H, ZHOU L, et al. Research on multimodality in aerodynamic/stealth airfoil design optimization[C]//2021 12th International Conference on Mechanical and Aerospace Engineering (ICMAE), Athens, Greece. IEEE, 2021: 384-393. doi: 10.1109/ICMAE52228.2021.9522566
|
| [85] |
王超, 高正红, 张伟, 等. 自适应设计空间扩展的高效代理模型气动优化设计方法[J]. 航空学报, 2018, 39(7): 121745. WANG C, GAO Z H, ZHANG W, et al. Efficient surrogate-based aerodynamic design optimization method with adaptive design space expansion[J]. Acta Aeronautica et Astronautica Sinica, 2018, 39(7): 121745. (in Chinese) |
| [86] |
张伟, 高正红, 周琳, 等. 基于代理模型全局优化的自适应参数化方法[J]. 航空学报, 2020, 41(10): 123815. ZHANG W, GAO Z H, ZHOU L, et al. Adaptive parameterization method for surrogate-based global optimization[J]. Acta Aeronautica et Astronautica Sinica, 2020, 41(10): 123815. (in Chinese) |
| [87] |
王科雷, 祝小平, 周洲, 等. 基于转捩模型的低雷诺数翼型优化设计研究[J]. 西北工业大学学报, 2015, 33(4): 580-587. WANG K L, ZHU X P, ZHOU Z, et al. Studying optimization design of low Reynolds number airfoil using transition model[J]. Journal of Northwestern Polytechnical University, 2015, 33(4): 580-587. DOI:10.3969/j.issn.1000-2758.2015.04.011 (in Chinese) |
| [88] |
DRELA M. XFOIL: an analysis and design system for low Reynolds number airfoils[C]//Low Reynolds Number Aerodynamics, University of Notre Dame , 1989. https://www.researchgate.net/publication/235994182_XFOIL_An_Analysis_and_Design_System_for_Low_Reynolds_Number_Airfoils doi: 10.1007/978-3-642-84010-4_1
|
| [89] |
SELIG M S. Summary of Low-Speed Airfoil Data[R]. SoarTech Publications, 1995.
|
| [90] |
王科雷, 周洲, 甘文彪, 等. 太阳能无人机低雷诺数翼型气动特性研究[J]. 西北工业大学学报, 2014, 32(2): 163-168. WANG K L, ZHOU Z, GAN W B, et al. Studying aerodynamic performances of the low-Reynolds-number airfoil of solar energy UAV[J]. Journal of Northwestern Polytechnical University, 2014, 32(2): 163-168. DOI:10.3969/j.issn.1000-2758.2014.02.001 (in Chinese) |
| [91] |
司江涛, 赵克良, 韩先锂. 高亚音速低雷诺数翼型研究[J]. 飞机工程, 2003(2): 26-29. |
| [92] |
王皓田, 朱杨柱, 车学科, 等. S1223翼型低雷诺数下分离泡及气动特性[J]. 空气动力学学报, 2021, 39(3): 90-98. WANG H T, ZHU Y Z, CHE X K, et al. Separation bubble and aerodynamic characteristics of S1223 airfoil at low Reynolds numbers[J]. Acta Aerodynamica Sinica, 2021, 39(3): 90-98. DOI:10.7638/kqdlxxb-2020.0075 (in Chinese) |
| [93] |
张亚锋, 宋笔锋, 李占科. 高升力翼型的气动优化设计和实验研究[J]. 飞行力学, 2006, 24(4): 70-72. ZHANG Y F, SONG B F, LI Z K. Aerodynamic optimization design and experiment study for a high-lift airfoil[J]. Flight Dynamics, 2006, 24(4): 70-72. DOI:10.3969/j.issn.1002-0853.2006.04.018 (in Chinese) |
| [94] |
陈耀慧, 陈志华, 范宝春, 等. 低雷诺数翼型绕流的电磁控制[J]. 空气动力学学报, 2007, 25(z2): 91-96. CHEN Y H, CHEN Z H, FAN B C, et al. Electro-magnetic control of the flow past a foil at a low Reynolds number[J]. Acta Aerodynamica Sinica, 2007, 25(z2): 91-96. DOI:10.3969/j.issn.0258-1825.2007.z2.015 (in Chinese) |
| [95] |
陈学孔, 郭正, 易凡, 等. 低雷诺数翼型的气动外形优化设计[J]. 空气动力学学报, 2014, 32(3): 300-307. CHEN X K, GUO Z, YI F, et al. Aerodynamic shape optimization and design of airfoils with low Reynolds number[J]. Acta Aerodynamica Sinica, 2014, 32(3): 300-307. (in Chinese) |
| [96] |
陈学孔, 郭正, 易凡, 等. 低雷诺数翼型的单点与多点气动外形优化研究[C]//第14届中国系统仿真技术及其应用学术年会, 2012. CHEN X K, GUO Z, YI F, et al. Single and multi-point aerodynamic shape optimization of low Reynolds number airfoils[C]//14th Chinese Conference on System Simulation Technology and Application, 2012 (in Chinese). |
| [97] |
赵智明, 李杰. 遗传算法结合反设计的高升力翼型优化设计[J]. 弹箭与制导学报, 2008, 28(5): 183-187. ZHAO Z M, LI J. Optimal design of high-lift airfoil design based on genetic algorithm combined with inverse design method[J]. Journal of Projectiles, Rockets, Missiles and Guidance, 2008, 28(5): 183-187. DOI:10.3969/j.issn.1673-9728.2008.05.055 (in Chinese) |
| [98] |
ZHAO H, GAO Z H, XU F, et al. Review of robust aerodynamic design optimization for air vehicles[J]. Archives of Computational Methods in Engineering, 2019, 26(3): 685-732. DOI:10.1007/s11831-018-9259-2 |
| [99] |
ZHAO H, GAO Z H, XU F, et al. An efficient adaptive forward-backward selection method for sparse polynomial chaos expansion[J]. Computer Methods in Applied Mechanics and Engineering, 2019, 355: 456-491. DOI:10.1016/j.cma.2019.06.034 |
| [100] |
ZHAO H, GAO Z H, GAO Y, et al. Effective robust design of high lift NLF airfoil under multi-parameter uncertainty[J]. Aerospace Science and Technology, 2017, 68: 530-542. DOI:10.1016/j.ast.2017.06.009 |
| [101] |
ZHAO H, GAO Z H, WANG C, et al. Robust design of high speed natural-laminar-flow airfoil for high lift[C]//55th AIAA Aerospace Sciences Meeting, Grapevine, Texas. Reston, Virginia: AIAA, 2017. AIAA-2017-1414 doi: 10.2514/6.2017-1414
|
| [102] |
BALAKUMAR P, KING R. Receptivity and transition of supersonic boundary layers over swept wings[C]//48th AIAA Aerospace Sciences Meeting Including the New Horizons Forum and Aerospace Exposition, Orlando, Florida. Reston, Virginia: AIAA, 2010. AIAA-2010-1454. doi: 10.2514/6.2010-1454
|
| [103] |
FUJINO M, YOSHIZAKI Y, KAWAMURA Y. Natural-laminar-flow airfoil development for a lightweight business jet[J]. Journal of Aircraft, 2003, 40(4): 609-615. DOI:10.2514/2.3145 |
| [104] |
ZHU J, GAO Z H, ZHAN H, et al. A high-speed nature laminar flow airfoil and its experimental study in wind tunnel with nonintrusive measurement technique[J]. Chinese Journal of Aeronautics, 2009, 22(3): 225-229. DOI:10.1016/S1000-9361(08)60091-6 |
| [105] |
SEITZ A, KRUSE M, WUNDERLICH T, et al. The DLR project LamAiR: design of a NLF forward swept wing for short and medium range transport application[C]//29th AIAA Applied Aerodynamics Conference, Honolulu, Hawaii. Reston, Virginia: AIAA, 2011. AIAA-2011-3526. doi: 10.2514/6.2011-3526
|
| [106] |
STREIT T, WICHMANN G, VON KNOBLAUCH ZU HATZBACH F, et al. Implications of conical flow for laminar wing design and analysis[C]//29th AIAA Applied Aerodynamics Conference, Honolulu, Hawaii. Reston, Virginia: AIAA, 2011. AIAA-2011-3808. doi: 10.2514/6.2011-3808
|
| [107] |
AMOIGNON O, PRALITS J, HANIFI A, et al. Shape optimization for delay of laminar-turbulent transition[J]. AIAA Journal, 2006, 44(5): 1009-1024. DOI:10.2514/1.12431 |
| [108] |
DRIVER J, ZINGG D W. Numerical aerodynamic optimization incorporating laminar-turbulent transition prediction[J]. AIAA Journal, 2007, 45(8): 1810-1818. DOI:10.2514/1.23569 |
| [109] |
RASHAD R, ZINGG D W. Aerodynamic shape optimization for natural laminar flow using a discrete-adjoint approach[J]. AIAA Journal, 2016, 54(11): 3321-3337. DOI:10.2514/1.J054940 |
| [110] |
LEE J D, JAMESON A. NLF airfoil and wing design by adjoint method and automatic transition prediction[C]//27th AIAA Applied Aerodynamics Conference, San Antonio, Texas. Reston, Virginia: AIAA, 2009. AIAA-2009-3514. doi: 10.2514/6.2009-3514
|
| [111] |
马晓永, 张彦军, 段卓毅, 等. 自然层流机翼气动外形优化研究[J]. 空气动力学学报, 2015, 33(6): 812-817. MA X Y, ZHANG Y J, DUAN Z Y, et al. Study of aerodynamic shape optimization for natural laminar wing[J]. Acta Aerodynamica Sinica, 2015, 33(6): 812-817. (in Chinese) |
| [112] |
CAMERON L, EARLY J, MCROBERTS R. Metamodel assisted multi-objective global optimisation of natural laminar flow aerofoils[C]//29th AIAA Applied Aerodynamics Conference, Honolulu, Hawaii. Reston, Virginia: AIAA, 2011. AIAA-2011-3001. doi: 10.2514/6.2011-3001
|
| [113] |
HAN Z H, DENG J, LIU J, et al. Design of laminar supercritical airfoils based on Navier–Stokes equations[C]//28th International Congress of the Aeronautical Sciences, 2012. https://www.researchgate.net/publication/290032856_Design_of_laminar_supercritical_airfoils_based_on_Navier-Stokes_equations
|
| [114] |
HAN Z H, CHEN J, ZHANG K S, et al. Aerodynamic shape optimization of natural-laminar-flow wing using surrogate-based approach[J]. AIAA Journal, 2018, 56(7): 2579-2593. DOI:10.2514/1.J056661 |
| [115] |
陈静, 宋文萍, 朱震, 等. 跨声速层流翼型的混合反设计/优化设计方法[J]. 航空学报, 2018, 39(12): 122219. CHEN J, SONG W P, ZHU Z, et al. A hybrid inverse/direct optimization design method for transonic laminar flow airfoil[J]. Acta Aeronautica et Astronautica Sinica, 2018, 39(12): 122219. (in Chinese) |
| [116] |
CHI J B, HAN Z H, FAN T L, et al. Hybrid inverse/optimization design approach for transonic natural-laminar-flow airfoils[C]//AIAA Scitech 2019 Forum, San Diego, California. Reston, Virginia: AIAA, 2019. AIAA-2019-1475. doi: 10.2514/6.2019-1475
|
| [117] |
ZHANG Y F, FANG X M, CHEN H X, et al. Supercritical natural laminar flow airfoil optimization for regional aircraft wing design[J]. Aerospace Science and Technology, 2015, 43: 152-164. DOI:10.1016/j.ast.2015.02.024 |
| [118] |
SARIC W S, REED H L, WHITE E B. Stability and transition of three-dimensional boundary layers[J]. Annual Review of Fluid Mechanics, 2003, 35(1): 413-440. DOI:10.1146/annurev.fluid.35.101101.161045 |
| [119] |
XU Z M, HAN Z H, CHI J B, et al. Crossflow instability analysis for swept laminar flow wings using crossflow pressure gradient[J]. AIAA Journal, 2021, 59(8): 2878-2889. DOI:10.2514/1.J059971 |
| [120] |
REDEKER G, HORSTMANN K H, KOSTER H, et al. Investigations on high Reynolds number laminar flow airfoils[J]. Journal of Aircraft, 1988, 25(7): 583-590. DOI:10.2514/3.45627 |
| [121] |
LYNDE M N, CAMPBELL R L. Computational design and analysis of a transonic natural laminar flow wing for a wind tunnel model[C]//35th AIAA Applied Aerodynamics Conference, Denver, Colorado. Reston, Virginia: AIAA, 2017. AIAA-2017-3058. doi: 10.2514/6.2017-3058
|
| [122] |
LYNDE M N, CAMPBELL R L, VIKEN S A. Additional findings from the common research model natural laminar flow wind tunnel test[C]//AIAA Aviation 2019 Forum, Dallas, Texas. Reston, Virginia: AIAA, 2019. AIAA-2019-3292. doi: 10.2514/6.2019-3292
|
| [123] |
XU Z M, HAN Z H, SONG W P. Natural-laminar-flow airfoil design optimization considering crossflow instability when configured on a swept wing[C]// 32nd International Council of the Aeronuautical Sciencea, 2021. https://www.icas.org/ICAS_ARCHIVE/ICAS2020/data/papers/ICAS2020_0472_paper.pdf
|
| [124] |
YOSHIDA K. Supersonic drag reduction technology in the scaled supersonic experimental airplane project by JAXA[J]. Progress in Aerospace Sciences, 2009, 45(4-5): 124-146. DOI:10.1016/j.paerosci.2009.05.002 |
| [125] |
LYNDE M N, CAMPBELL R L. Expanding the natural laminar flow boundary for supersonic transports[C]//34th AIAA Applied Aerodynamics Conference, Washington, D. C. . Reston, Virginia: AIAA, 2016. AIAA-2016-4327. doi: 10.2514/6.2016-4327
|
| [126] |
UEDA Y, YOSHIDA K, MATSUSHIMA K, et al. Supersonic natural-laminar-flow wing-design concept at high-Reynolds-number conditions[J]. AIAA Journal, 2014, 52(6): 1294-1306. DOI:10.2514/1.J052555 |
| [127] |
VERMEERSCH O, YOSHIDA K, UEDA Y, et al. Natural laminar flow wing for supersonic conditions: Wind tunnel experiments, flight test and stability computations[J]. Progress in Aerospace Sciences, 2015, 79: 64-91. DOI:10.1016/j.paerosci.2015.07.003 |
| [128] |
IULIANO E, DIN I S E, DONELLI R, et al. Natural laminar flow design of a supersonic transport jet wing body[C]//47th AIAA Aerospace Sciences Meeting including The New Horizons Forum and Aerospace Exposition, Orlando, Florida. Reston, Virginia: AIAA, 2009. AIAA-2009-1279. doi: 10.2514/6.2009-1279
|
| [129] |
IULIANO E, QUAGLIARELLA D, DONELLI R S, et al. Design of a supersonic natural laminar flow wing-body[J]. Journal of Aircraft, 2011, 48(4): 1147-1162. DOI:10.2514/1.c031039 |
| [130] |
UENO A, SUZUKI K. CFD-based shape optimization of hypersonic vehicles considering transonic aerodynamic performance[C]//46th AIAA Aerospace Sciences Meeting and Exhibit, 2008: 288
|
| [131] |
UENO A, SUZUKI K. Two-dimensional shape optimization of hypersonic vehicles considering transonic aerodynamic performance[J]. Transactions of the Japan Society for Aeronautical and Space Sciences, 2009, 52(176): 65-73. DOI:10.2322/tjsass.52.65 |
| [132] |
孙祥程, 韩忠华, 柳斐, 等. 高超声速飞行器宽速域翼型/机翼设计与分析[J]. 航空学报, 2018, 39(6): 121737. SUN X C, HAN Z H, LIU F, et al. Design and analysis of hypersonic vehicle airfoil/wing at wide-range Mach numbers[J]. Acta Aeronautica et Astronautica Sinica, 2018, 39(6): 121737. (in Chinese) |
| [133] |
LIU F, HAN Z H, ZHANG Y, et al. Surrogate-based aerodynamic shape optimization of hypersonic flows considering transonic performance[J]. Aerospace Science and Technology, 2019, 93: 105345. DOI:10.1016/j.ast.2019.105345 |
| [134] |
张阳, 韩忠华, 柳斐, 等. 高超声速飞行器宽速域翼型多目标优化设计研究[J]. 气体物理, 2019, 4(4): 26-40. ZHANG Y, HAN Z H, LIU F, et al. Multi-objective aerodynamic shape optimization of wide-Mach-number-range airfoil[J]. Physics of Gases, 2019, 4(4): 26-40. (in Chinese) |
| [135] |
ZHANG Y, HAN Z H, LIU F, et al. Aerodynamic design optimization of hypersonic wing over wide Mach-number range considering lift matching[C]// 32nd International Council of the Aeronuautical Sciencea, 2021. https://www.icas.org/ICAS_ARCHIVE/ICAS2020/data/papers/ICAS2020_0476_paper.pdf
|
| [136] |
PHILIPPE J J. 30 Years of Rotorcraft Aeromechanics Research at ONERA[R]. ONERA TP 2007-33, 2007.
|
| [137] |
CHERNYSHEV S, GOLOVKIN M. Current state and progress in reseach of rotorcraft aerodynamics at TSAGI[C]//35th European Rotorcraft Forum, 2009. http://toc.proceedings.com/07271webtoc.pdf
|
| [138] |
PASSE B J, SRIDHARAN A, BAEDER J D. Computational investigation of coaxial rotor interactional aerodynamics in steady forward flight[C]//33rd AIAA Applied Aerodynamics Conference, Dallas, TX. Reston, Virginia: AIAA, 2015. AIAA-2015-2883. doi: 10.2514/6.2015-2883
|
| [139] |
高正红. 通过局部参数化修形控制旋翼翼型俯仰力矩等设计新方法: CN106777495A[P]. 2017-05-13.
|
| [140] |
杨旭东, 彭小康, 高正红, 等. 一种全工况条件下高升力低力矩特性12%厚度旋翼翼型: CN106741925A[P]. 2017-05-31.
|
| [141] |
宋文萍, 卜月鹏, 韩忠华, 等. 一种全工况条件下的高升阻比低力矩特性9%厚度旋翼翼型: CN106741924A[P]. 2017-05-31.
|
| [142] |
杨旭东, 彭小康, 高正红, 等. 一种全工况条件下高升力低力矩特性7%厚度旋翼翼型: CN106741923A[P]. 2017-05-31.
|
| [143] |
赵轲. 基于CFD的复杂气动优化与稳健设计方法研究[D]. 西安: 西北工业大学, 2015. ZHAO K. Complex aerodynamic optimization and robust design method based on computational fluid dynamics[D]. Xi'an: Northwestern Polytechnical University, 2015 (in Chinese). |
| [144] |
SUN W, GAO Z H, DU Y M, et al. Mechanism of unconventional aerodynamic characteristics of an elliptic airfoil[J]. Chinese Journal of Aeronautics, 2015, 28(3): 687-694. DOI:10.1016/j.cja.2015.03.009 |
| [145] |
HAN S Q, SONG W P, HAN Z H, et al. Hybrid inverse/optimization design method for rigid coaxial rotor airfoils considering reverse flow[J]. Aerospace Science and Technology, 2019, 95: 105488. DOI:10.1016/j.ast.2019.105488 |
| [146] |
赵佳祥, 宋文萍, 韩忠华, 等. 应用于高速直升机旋翼反流区的类椭圆翼型: CN109229364B[P]. 2019-06-11.
|
| [147] |
韩少强, 宋文萍, 韩忠华, 等. 用于高速直升机旋翼桨根的非对称双钝头翼型及设计方法: CN111717381B[P]. 2021-10-08.
|
| [148] |
高正红, 赵欢, 夏露. 一种具有低阻高发散马赫数的共轴双旋翼高速直升机桨尖翼型: CN112572787A[P]. 2021-03-30.
|
| [149] |
李萍, 庄开莲, 李静. 国外直升机旋翼翼型研究综述[J]. 直升机技术, 2007(3): 103-109. DOI:10.3969/j.issn.1673-1220.2007.03.025 |
| [150] |
孙俊峰, 卢风顺, 黄勇, 等. 旋翼翼型气动设计与评估软件HRADesign[J]. 空气动力学学报, 2021, 39(4): 59-68. SUN J F, LU F S, HUANG Y, et al. Rotor airfoil aerodynamic design and evaluation software HRADesign[J]. Acta Aerodynamica Sinica, 2021, 39(4): 59-68. DOI:10.7638/kqdlxxb-2019.0106 (in Chinese) |
| [151] |
王清, 招启军. 基于遗传算法的旋翼翼型综合气动优化设计[J]. 航空动力学报, 2016, 31(6): 1486-1495. WANG Q, ZHAO Q J. Synthetical optimization design of rotor airfoil by genetic algorithm[J]. Journal of Aerospace Power, 2016, 31(6): 1486-1495. (in Chinese) |
| [152] |
招启军, 王清, 赵国庆. 旋翼翼型定常-非定常特性综合优化设计新方法[J]. 南京航空航天大学学报, 2014, 46(3): 355-363. ZHAO Q J, WANG Q, ZHAO G Q. New optimization design method for rotor airfoil considering steady-unsteady characteristics[J]. Journal of Nanjing University of Aeronautics & Astronautics, 2014, 46(3): 355-363. DOI:10.3969/j.issn.1005-2615.2014.03.004 (in Chinese) |
| [153] |
钱瑞战, 乔志德, 陈迎春, 等. 基于N-S方程的旋翼翼型优化设计方法[J]. 飞行力学, 2004, 22(1): 26-29. QIAN R Z, QIAO Z D, CHEN Y C, et al. Rotor airfoil optimization design using Navier-Stokes equations[J]. Flight Dynamics, 2004, 22(1): 26-29. DOI:10.3969/j.issn.1002-0853.2004.01.007 (in Chinese) |
| [154] |
黄海生, 杨旭东. 基于控制理论的旋翼翼型优化设计[J]. 航空计算技术, 2010, 40(4): 22-26. HUANG H S, YANG X D. Optimum shape design of rotor airfoils via control theory[J]. Aeronautical Computing Technique, 2010, 40(4): 22-26. DOI:10.3969/j.issn.1671-654X.2010.04.007 (in Chinese) |
| [155] |
杨慧, 宋文萍, 韩忠华, 等. 旋翼翼型多目标多约束气动优化设计[J]. 航空学报, 2012, 33(7): 1218-1226. YANG H, SONG W P, HAN Z H, et al. Multi-objective and multi-constrained optimization design for a helicopter rotor airfoil[J]. Acta Aeronautica et Astronautica Sinica, 2012, 33(7): 1218-1226. (in Chinese) |
| [156] |
孙俊峰, 刘刚, 江雄, 等. 基于Kriging模型的旋翼翼型优化设计研究[J]. 空气动力学学报, 2013, 31(4): 437-441. SUN J F, LIU G, JIANG X, et al. Research of rotor airfoil design optimization based on the Kriging model[J]. Acta Aerodynamica Sinica, 2013, 31(4): 437-441. (in Chinese) |
| [157] |
VU N A, LEE J W, SHU J I. Aerodynamic design optimization of helicopter rotor blades including airfoil shape for hover performance[J]. Chinese Journal of Aeronautics, 2013, 26(1): 1-8. DOI:10.1016/j.cja.2012.12.008 |
| [158] |
尚克明, 招启军, 赵国庆, 等. 直升机旋翼翼型及桨叶气动外形反设计分析[J]. 南京航空航天大学学报, 2010, 42(5): 550-556. SHANG K M, ZHAO Q J, ZHAO G Q, et al. Inverse design analysis on helicopter rotor airfoils and aerodynamic shapes[J]. Journal of Nanjing University of Aeronautics & Astronautics, 2010, 42(5): 550-556. DOI:10.3969/j.issn.1005-2615.2010.05.003 (in Chinese) |
| [159] |
李生伟, 熊俊卿, 王鑫磊. 直升机新型旋翼翼型气动特性与布局分析[J]. 南京航空航天大学学报, 2020, 52(2): 318-333. LI S W, XIONG J Q, WANG X L. New helicopter rotor aerodynamic characteristics and layout analysis[J]. Journal of Nanjing University of Aeronautics & Astronautics, 2020, 52(2): 318-333. (in Chinese) |
| [160] |
MANI K, LOCKWOOD B A, MAVRIPLIS D J. Adjoint-based unsteady airfoil design optimization with application to dynamic stall[C]//American Helicopter Society 68th Annual Forum, 2012. http://scientific-sims.com/cfdlab/Dimitri_Mavriplis/HOME/assets/papers/AHS.2012.paper.pdf
|
| [161] |
WANG Q, ZHAO Q J. Rotor airfoil profile optimization for alleviating dynamic stall characteristics[J]. Aerospace Science and Technology, 2018, 72: 502-515. DOI:10.1016/j.ast.2017.11.033 |
| [162] |
喻伯平, 李高华, 谢亮, 等. 基于代理模型的旋翼翼型动态失速优化设计[J]. 浙江大学学报(工学版), 2020, 54(4): 833-842. YU B P, LI G H, XIE L, et al. Dynamic stall optimization design of rotor airfoil based on surrogate model[J]. Journal of Zhejiang University (Engineering Science), 2020, 54(4): 833-842. (in Chinese) |
| [163] |
孔卫红, 陈仁良, 孙振航. 旋翼翼型低速动态失速研究[J]. 南京航空航天大学学报, 2018, 50(2): 213-220. KONG W H, CHEN R L, SUN Z H. Numerical investigation of dynamic stall on rotor airfoil in low-speed flow[J]. Journal of Nanjing University of Aeronautics & Astronautics, 2018, 50(2): 213-220. (in Chinese) |
| [164] |
张顺磊, 杨旭东, 宋笔锋, 等. 应用协同射流原理的旋翼翼型增升减阻试验研究[J]. 航空工程进展, 2021, 12(4): 44-51,67. ZHANG S L, YANG X D, SONG B F, et al. Experimental investigation of lift enhancement and drag reduction of rotor airfoil using co-flow jet concept[J]. Advances in Aeronautical Science and Engineering, 2021, 12(4): 44-51,67. (in Chinese) |
| [165] |
MA Y Y, ZHAO Q J, ZHAO G Q. New combinational active control strategy for improving aerodynamic characteristics of airfoil and rotor[J]. Proceedings of the Institution of Mechanical Engineers, Part G:Journal of Aerospace Engineering, 2020, 234(4): 977-996. DOI:10.1177/0954410019893193 |
| [166] |
YANG X D, JIANG W R, ZHANG S L. Analysis of co-flow jet effect on dynamic stall characteristics applying to rotor airfoils[J]. IOP Conference Series:Materials Science and Engineering, 2019, 491: 012010. DOI:10.1088/1757-899x/491/1/012010 |
| [167] |
ZHAO Q J, MA Y Y, ZHAO G Q. Parametric analyses on dynamic stall control of rotor airfoil via synthetic jet[J]. Chinese Journal of Aeronautics, 2017, 30(6): 1818-1834. DOI:10.1016/j.cja.2017.08.011 |
| [168] |
ZHAO G Q, ZHAO Q J. Parametric analyses for synthetic jet control on separation and stall over rotor airfoil[J]. Chinese Journal of Aeronautics, 2014, 27(5): 1051-1061. DOI:10.1016/j.cja.2014.03.023 |
| [169] |
许和勇, 邢世龙, 叶正寅, 等. 基于充气前缘技术的旋翼翼型动态失速抑制[J]. 航空学报, 2017, 38(6): 120799. XU H Y, XING S L, YE Z Y, et al. Dynamic stall suppression for rotor airfoil based on inflatable leading edge technology[J]. Acta Aeronautica et Astronautica Sinica, 2017, 38(6): 120799. (in Chinese) |
| [170] |
赵国庆. 直升机旋翼非定常动态失速的CFD模拟及其主动流动控制研究[D]. 南京: 南京航空航天大学, 2015. ZHAO G Q. Investigations on CFD simulation and active flow control for unsteady dynamic stall of helicopter rotor[D]. Nanjing: Nanjing University of Aeronautics and Astronautics, 2015 (in Chinese). |
| [171] |
张威, 林永峰, 陈平剑. 基于零质量射流技术的旋翼翼型流场主动控制研究[J]. 直升机技术, 2010(1): 15-20. ZHANG W, LIN Y F, CHEN P J. The investigation of active control technology in airfoil flow field based on the synthetic jet[J]. Helicopter Technique, 2010(1): 15-20. DOI:10.3969/j.issn.1673-1220.2010.01.002 (in Chinese) |
| [172] |
韩忠华, 宋文萍, 乔志德. OA212翼型主动流动控制的数值模拟研究[J]. 空气动力学学报, 2009, 27(6): 639-644. HAN Z H, SONG W P, QIAO Z D. Numerical simulation of active dynamic stall control on an OA212 rotor airfoil[J]. Acta Aerodynamica Sinica, 2009, 27(6): 639-644. DOI:10.3969/j.issn.0258-1825.2009.06.003 (in Chinese) |
| [173] |
吴希明, 牟晓伟. 直升机关键技术及未来发展与设想[J]. 空气动力学学报, 2021, 39(3): 1-10. WU X M, MU X W. A perspective of the future development of key helicopter technologies[J]. Acta Aerodynamica Sinica, 2021, 39(3): 1-10. DOI:10.7638/kqdlxxb-2021.0042 (in Chinese) |
| [174] |
COLOZZA A. Initial feasibility assessment of a high altitude long endurance airship[R]. NASA/CR-212724, 2003. https://ntrs.nasa.gov/api/citations/20040021326/downloads/20040021326.pdf
|
| [175] |
COLOZZA A. APEX 3D propeller test preliminary design[R]. NASA/CR-2002-211866, 2002. https://ntrs.nasa.gov/api/citations/20020082943/downloads/20020082943.pdf
|
| [176] |
乔志德, 钟伯文, 吉州. 低噪声对转螺旋桨的翼型: 螺旋桨一体化设计方法[J]. 西北工业大学学报, 1997, 15(1): 37-42. QIAO Z D, ZHONG B W, JI Z. An integrated design method of low noise contrarotating propellers[J]. Journal of Northwestern Polytechnical University, 1997, 15(1): 37-42. (in Chinese) |
| [177] |
ZHANG S L, YANG X D, SONG B F, et al. Aerodynamic design of a novel low-Reynolds-number airfoil for near space propellers[J]. International Journal of Aerospace System Engineering, 2015, 2(1): 53-57. http://www.koreascience.kr/article/JAKO201508361186873.pdf
|
| [178] |
杨旭东, 张顺磊, 许建华, 等. 一种极低雷诺数高升阻比低速特殊勺型翼型: CN104118556A[P]. 2014-10-29.
|
| [179] |
XU J H, SONG W P, HAN Z H, et al. Effect of Mach number on high-subsonic and low-Reynolds-number flows around airfoils[J]. International Journal of Modern Physics B, 2020, 34(14n16): 2040112. DOI:10.1142/s0217979220401128 |
| [180] |
XU J H, LI H J, SONG W P, et al. An aerodynamic design method of propeller airfoils with geometric compatibility as constraints[C]//AIAA Aviation 2019 Forum, Dallas, Texas. Reston, Virginia: AIAA, 2019. AIAA-2019-3493. doi: 10.2514/6.2019-3493
|
| [181] |
XU J H, LI D, SONG W P, et al. Design optimization of airfoils at ultra-low Reynolds numbers[C]// 32nd International Council of the Aeronuautical Sciencea, 2021. https://www.icas.org/ICAS_ARCHIVE/ICAS2020/data/papers/ICAS2020_0839_paper.pdf
|
| [182] |
刘沛清. 空气螺旋桨理论及其应用[M]. 北京: 北京航空航天大学出版社, 2006.
|
| [183] |
马蓉, 刘沛清, 胡颖. 临近空间飞行器螺旋桨低雷诺数高升力翼型综述[C]//庆祝中国力学学会成立50周年暨中国力学学会学术大会, 北京, 2007.
|
| [184] |
韩忠华, 宋文萍, 高永卫. 大型风力机翼型族的设计与实验[J]. 应用数学和力学, 2013, 34(10): 1012-1027. HAN Z H, SONG W P, GAO Y W. Design and wind-tunnel verification of large-size wind turbine airfoils[J]. Applied Mathematics and Mechanics, 2013, 34(10): 1012-1027. DOI:10.3879/j.issn.1000-0887.2013.10.002 (in Chinese) |
| [185] |
TANGLER J L, SOMERS D M. NREL airfoil families for HAWTS[R]. National Renewable Energy Laboratory, 1995. NREL/TP-442-7109. https://www.nrel.gov/docs/legosti/old/7109.pdf DOI:10.2172/10106095
|
| [186] |
FUGLSANG P, BAK C. Development of the Risø wind turbine airfoils[J]. Wind Energy, 2004, 7(2): 145-162. DOI:10.1002/we.117 |
| [187] |
BJORK A. Coordinates and Calculations for the FFA-W1-XXX, FFA-W2-XXX, FFA-W3-XXX series of airfoils for HAWTs[R]. FFA TN 1990-15, Stockholm, Sweden, 1990. https://wind.nrel.gov/airfoils/Documents/FFA%20TN%201990-15%20v.1-2%20c.1.pdf
|
| [188] |
TIMMER W A, VAN ROOIJ R P J O M. Summary of the Delft university wind turbine dedicated airfoils[C]//41st Aerospace Sciences Meeting and Exhibit, Reno, Nevada. Reston, Virginia: AIAA, 2003. AIAA 2003-0352. https://odonata-research.com/references/wind-turbine/AIAA-2003-0352.pdf doi: 10.2514/6.2003-352
|
| [189] |
乔志德, 宋文萍, 高永卫. NPU-WA系列风力机翼型设计与风洞实验[J]. 空气动力学学报, 2012, 30(2): 260-265. QIAO Z D, SONG W P, GAO Y W. Design and experiment of the NPU-WA airfoil family for wind turbines[J]. Acta Aerodynamica Sinica, 2012, 30(2): 260-265. DOI:10.3969/j.issn.0258-1825.2012.02.023 (in Chinese) |
| [190] |
XU J H, HAN Z H, YAN X C, et al. Design optimization of a multi-megawatt wind turbine blade with the NPU-MWA airfoil family[J]. Energies, 2019, 12(17): 3330. DOI:10.3390/en12173330 |
| [191] |
白井艳, 杨科, 李宏利, 等. 水平轴风力机专用翼型族设计[J]. 工程热物理学报, 2010, 31(4): 589-592. BAI J Y, YANG K, LI H L, et al. Design of the horizontal axis wind turbine airfoil family[J]. Journal of Engineering Thermophysics, 2010, 31(4): 589-592. (in Chinese) |
| [192] |
陈飞虎. 风力机翼型优化设计研究[D]. 北京: 华北电力大学, 2013. CHEN F H. Research on optimum design of wind turbine airfoils[D]. Beijing: North China Electric Power University, 2013. (in Chinese) |
| [193] |
陈进, 张石强, 王旭东, 等. 基于粗糙度敏感性研究的风力机专用翼型设计[J]. 空气动力学学报, 2011, 29(2): 142-149. CHEN J, ZHANG S Q, WANG X D, et al. Dedicated wind turbine airfoil design based on the roughness sensitivity considerations[J]. Acta Aerodynamica Sinica, 2011, 29(2): 142-149. DOI:10.3969/j.issn.0258-1825.2011.02.003 (in Chinese) |
| [194] |
黄继雄. 风力机专用新翼型及其气动特性研究[D]. 汕头: 汕头大学, 2001. HUANG J X. Research on new wind turbine airfoils and their aerodynamic performances[D]. Shantou, China: Shantou University, 2001 (in Chinese). |
| [195] |
宋显成, 陈江, 杜刚, 等. 风力机翼型参数化方法[J]. 南京航空航天大学学报, 2012, 44(3): 301-306. SONG X C, CHEN J, DU G, et al. Parametric representation method for wind turbine airfoils[J]. Journal of Nanjing University of Aeronautics & Astronautics, 2012, 44(3): 301-306. DOI:10.3969/j.issn.1005-2615.2012.03.005 (in Chinese) |
| [196] |
HAO L S, GAO Y W, WEI B B, et al. Numerical simulation of flow over bionic airfoil[J]. International Journal of Aerospace Engineering, 2021, 2021: 1-17. DOI:10.1155/2021/5556463 |
| [197] |
杨一雄, 杨体浩, 白俊强, 等. HLFC后掠翼优化设计的若干问题[J]. 航空学报, 2018, 39(1): 121448. YANG Y X, YANG T H, BAI J Q, et al. Problems in optimization design of HLFC sweep wing[J]. Acta Aeronautica et Astronautica Sinica, 2018, 39(1): 121448. (in Chinese) |
| [198] |
XU H Y, QIAO C L, YANG H Q, et al. Active circulation control on the blunt trailing edge wind turbine airfoil[J]. AIAA Journal, 2018, 56(2): 554-570. DOI:10.2514/1.j056223 |
| [199] |
许建华, 李凯, 宋文萍, 等. 低雷诺数下协同射流关键参数对翼型气动性能的影响[J]. 航空学报, 2018, 39(8): 122018. XU J H, LI K, SONG W P, et al. Influence of co-flow jet key parameters on airfoil aerodynamic performance at low Reynolds number[J]. Acta Aeronautica et Astronautica Sinica, 2018, 39(8): 122018. (in Chinese) |
| [200] |
祝连庆, 孙广开, 李红, 等. 智能柔性变形机翼技术的应用与发展[J]. 机械工程学报, 2018, 54(14): 28-42. ZHU L Q, SUN G K, LI H, et al. Intelligent and flexible morphing wing technology: a review[J]. Journal of Mechanical Engineering, 2018, 54(14): 28-42. (in Chinese) |
| [201] |
白鹏, 陈钱, 徐国武, 等. 智能可变形飞行器关键技术发展现状及展望[J]. 空气动力学学报, 2019, 37(3): 426-443. BAI P, CHEN Q, XU G W, et al. Development status of key technologies and expectation about smart morphing aircraft[J]. Acta Aerodynamica Sinica, 2019, 37(3): 426-443. DOI:10.7638/kqdlxxb-2019.0030 (in Chinese) |
| [202] |
张尧, 张婉, 别大卫, 等. 智能变体飞行器研究综述与发展趋势分析[J]. 飞航导弹, 2021(6): 14-23. |
| [203] |
许云涛. 智能变形飞行器发展及关键技术研究[J]. 战术导弹技术, 2017(2): 26-33,46. XU Y T. Research on the development and key technology of smart morphing aircraft[J]. Tactical Missile Technology, 2017(2): 26-33,46. (in Chinese) |
| [204] |
NEAL D, GOOD M, JOHNSTON C, et al. Design and wind-tunnel analysis of a fully adaptive aircraft configuration[C]//45th AIAA/ASME/ASCE/AHS/ASC Structures, Structural Dynamics & Materials Conference, Palm Springs, California. Reston, Virigina: AIAA, 2004. AIAA-2004-1727. doi: 10.2514/6.2004-1727
|
| [205] |
ELZEY D M, SOFLA A Y N, WADLEY H N G. A bio-inspired high-authority actuator for shape morphing structures[C]//Smart Structures and Materials 2003: Active Materials: Behavior and Mechanics, San Diego, CA. SPIE, 2003. doi: 10.1117/12.484745
|
| [206] |
陈骐. Ag基IPMC柔性驱动器的制备及控制特性研究[D]. 南京: 南京航空航天大学, 2009. CHEN Q. Preparation and control performances of soft actuator IPMC based on silver electrode[D]. Nanjing: Nanjing University of Aeronautics and Astronautics, 2009 (in Chinese). |
| [207] |
殷明. 变体飞行器变形与飞行的协调控制问题研究[D]. 南京: 南京航空航天大学, 2016. YIN M. Coordinated control of deformation and flight for morphing aircraft[D]. Nanjing: Nanjing University of Aeronautics and Astronautics, 2016 (in Chinese). |
| [208] |
陆宇平, 何真. 变体飞行器控制系统综述[J]. 航空学报, 2009, 30(10): 1906-1911. LU Y P, HE Z. A survey of morphing aircraft control systems[J]. Acta Aeronautica et Astronautica Sinica, 2009, 30(10): 1906-1911. DOI:10.3321/j.issn:1000-6893.2009.10.019 (in Chinese) |
| [209] |
朱华, 刘卫东, 赵淳生. 变体飞行器及其变形驱动技术[J]. 机械制造与自动化, 2010, 39(2): 8-14,125. ZHU H, LIU W D, ZHAO C S. Morphing aircraft and its morph-driving techniques[J]. Machine Building & Automation, 2010, 39(2): 8-14,125. DOI:10.3969/j.issn.1671-5276.2010.02.002 (in Chinese) |
| [210] |
高彦峰, 刘志帆, 王晓宏. 可变形翼型超声速非定常气动力的研究[J]. 空气动力学学报, 2014, 32(1): 69-76. GAO Y F, LIU Z F, WANG X H. Study on the supersonic unsteady aerodynamic force for the morphing airfoil[J]. Acta Aerodynamica Sinica, 2014, 32(1): 69-76. DOI:10.7638/kqdlxxb-2012.0056 (in Chinese) |
| [211] |
崔尔杰, 白鹏, 杨基明. 智能变形飞行器的发展道路[J]. 航空制造技术, 2007, 50(8): 38-41. DOI:10.3969/j.issn.1671-833X.2007.08.002 |
 2021, Vol. 39
2021, Vol. 39