边界层从层流向湍流的转变过程被称为边界层的转捩。转捩问题实际是湍流的起源问题,是流体力学长期关注但尚未解决的重要研究领域之一[1]。研究清楚转捩过程的机理,对于提高转捩预测的准确性和理解湍流的产生至关重要。一般认为边界层的转捩是由流动不稳定性引起的,分析流动的失稳特性和研究扰动演化的过程,是流动稳定性分析的主要工作[2],也是理论以及工程上所关心的重要问题之一。
在高超声速边界层中,由于流动的压缩性,边界层局部会产生相对超声速区,由此产生的失稳模态被称作第二模态,它在较高来流马赫数时对流动失稳起着至关重要的作用。对于马赫数较高的情况(如Ma > 4),二维的第二模态的线性增长率最大,最不稳定,可能最先增长起来 [3]。但是只有二维流动是不能导致转捩的,因为湍流是三维流动的,这就说明中间过程会有三维流动的产生。Herbert的二次失稳理论是在这个过程中研究三维扰动产生原因的理论之一[3]。二次失稳的类型主要包括基频模态失稳和亚谐模态失稳[4-7],其中前者通常被称作为K型失稳而后者则被称作为H型失稳,表现为在转捩中不同的流场分布特征。早期的不可压缩边界层的相关研究通常认为K型失稳发生在较高的来流湍流度的情况下。
直到20世纪90年代之后,人们才将二次失稳的研究对象从低速问题转移到了高超声速问题。在1992年Ng 和 Erlebacher[8]采用二次失稳理论研究了
|
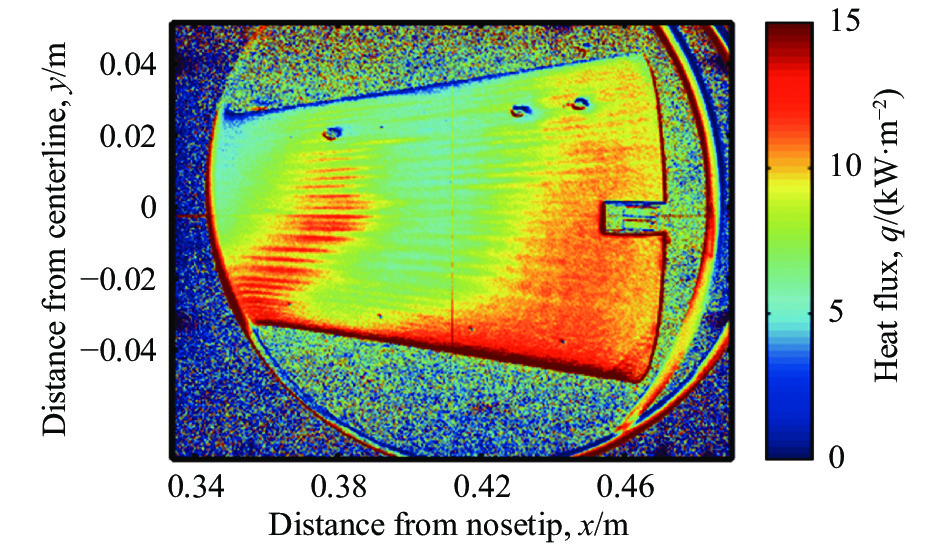
图 2 Purdue大学静风洞中观测到的条纹结构[10] Fig.2 Streaky structures observed in the quiet wind tunnel of Purdue University[10] |
很多研究都发现流场在变成湍流过程中都存在比较稳定的条纹结构。从条纹结构的生成来看,很多机制都会引起或者表现为流场内条纹结构的产生。除了前面提到的边界层内由Mack模态引起的基频二次失稳可以产生条纹结构以外,最典型的,条纹结构的生成可以和边界层内失稳扰动的非线性演化至饱和过程有关,例如横流涡、哥特涡等在流场中表现为条纹结构[15-17];三维边界层中由于边界层抬升效应也会产生典型的条纹结构,例如HiFiRE-5模型(椭圆锥)短轴处及粗糙元尾迹流动中出现的流向涡结构,可表现为流向条纹[18];此外,当外界湍流度较大时,也可以依靠感受性机制直接在边界层内激发出条纹结构[19-20]。
针对于以上如哥特涡、横流涡等机制引发的条纹结构,人们开展了相关的二次失稳研究,并将这些二次失稳机制与转捩过程相关联。研究结果说明湍流的突变(breakdown)过程可能和条纹结构的二次失稳有关,这说明条纹结构对转捩有很大的影响,对转捩的发生起着至关重要的作用。虽然针对于Mack模态的二次失稳机制引起边界层内条纹结构的产生问题开展了一些研究工作,但对由此产生的条纹结构的二次失稳研究则关注不够。基于此,本文以
本节介绍本文中用到的方程及求解所用的数值方法。
1.1 线性扰动方程设有可压缩气体流过平板,流动方向为x方向,y方向与z方向分别为法向和展向。考虑可压缩边界层,从有量纲的完全Navier-Stokes (N-S)方程出发,选取适当的特征量将其无量纲化,我们可以得到无量纲的N-S方程。将得到的无量纲N-S方程中的瞬时量设为基本流与扰动量的和:
| $ \varphi = {\varphi _0} + \varphi ' $ | (1) |
其中,
| $ \begin{split}& {V_{xx}}\frac{{{\partial ^2}\varphi '}}{{\partial {x^2}}}+ {V_{yy}}\frac{{{\partial ^2}\varphi '}}{{\partial {y^2}}}+ {V_{zz}}\frac{{{\partial ^2}\varphi '}}{{\partial {z^2}}} \\& + {V_{xy}}\frac{{{\partial ^2}\varphi '}}{{\partial x\partial y}} + {V_{xz}}\frac{{{\partial ^2}\varphi '}}{{\partial x\partial z}} + {V_{yz}}\frac{{{\partial ^2}\varphi '}}{{\partial y\partial z}} \\& +\left( {\varGamma \frac{{\partial \varphi '}}{{\partial t}} + A\frac{{\partial \varphi '}}{{\partial x}} + B\frac{{\partial \varphi '}}{{\partial y}} + C\frac{{\partial \varphi '}}{{\partial z}} + D\varphi '} \right) = 0 \end{split} $ | (2) |
其中,
首先对二维基本流进行线性稳定性分析(LST)。考虑到扰动的演化相对基本流主要发生在流向、展向和法向,可以假设扰动是时间、流向和展向的周期函数,则扰动可以写成下列形式:
| $ \varphi {'_{{\rm{LST}}}}(x,y,z,t) = \hat \varphi (y){{\rm{e}}^{{\rm{i}}(\alpha x + \beta z - \omega t)}} + {c.c.} $ | (3) |
式中,
将式(3)代入到线性的扰动方程(2)中,并忽略基本流的流向导数和法向速度,得到准平行性假设下的边界层的线性稳定性方程:
| $ {L_{{\rm{LST}}}}\hat \varphi = 0 $ | (4) |
其中,
| $ {\rm{|}}{L_{{\rm{LST}}}}{\rm{|}} = 0 $ | (5) |
式(5)描述了扰动的色散信息,即波数与频率的关系。通过求解式(5)得到色散关系后,可以从式(4)中求得形函数
经典的线性稳定性方程主要是针对二维基本流开展的稳定性研究,它所给出的失稳扰动信息又被称作首次失稳。然而,当二维基本流与首次失稳的扰动叠加时,又可以产生新的失稳现象,即二次失稳。本文采用经典的基于Floquet理论的二次失稳理论(SIT)进行二次失稳分析。根据二次失稳理论[8]可知,二次失稳分析的基本流由原基本流和有限幅值的首次失稳二维扰动组成,即:
| $ {\varphi}_{0\;{\rm{new}}}(x,y,z,t) = {\varphi _0}(y) + A({\hat \varphi _1}(y){{\rm{e}}^{{\rm{i}}(ax - \omega t)}} + c.c) $ | (6) |
其中,
| $ \tilde x = x - \frac{{{\omega _r}}}{{{\alpha _r}}}t = x - {c_r}t $ | (7) |
通过这样的变换,在首次失稳扰动的行进坐标系中,新构成的基本流就可以被看作为定常的。
为了研究二次失稳,在新构成的基本流即二次失稳的基本流上叠加二次失稳扰动,则瞬时流场可表示为:
| $ \tilde \varphi = {\tilde \varphi _{0\;{\rm{new}}}} + {\tilde \varphi _{\rm{2}}} $ | (8) |
上标“~”表示物理量在新坐标系下的值,
| $ {\tilde L_s}{\tilde \varphi _2} = 0 $ | (9) |
其中,
| $ {\tilde \varphi _2} = {{\rm{e}}^{\sigma t}}{{\rm{e}}^{{\rm{i}}{\beta _2}z}}{\hat \varphi _2}(\tilde x,y) + c.c. $ | (10) |
其中,
将式(10)代入到式(9)中,可以得到方程:
| $ \hat L{\hat \varphi _{\rm{2}}}{\rm{ = 0}} $ | (11) |
下面给出边界条件,在壁面
| $ \hat u = {\rm{0}},\hat v{\rm{ = }}0,\hat w = 0,\hat T = 0 $ | (12) |
在远场
| $ \hat \rho \to {\rm {0}}, \hat u \to {\rm{0}},\hat v \to 0,\hat w \to 0,\hat T \to 0 $ | (13) |
对于一个给定的展向波数
式(11)是一个大规模的特征值问题,我们在法向上采用四阶中心差分格式,流向采用傅里叶谱方法进行离散。特征值问题选用Arnoldi子空间迭代法进行求解,该方法是求解大规模稀疏矩阵局部特征值的迭代方法。ARPACK[22]是目前最流行的实现Arnoldi方法求解大型稀疏矩阵特征值的开源软件包。
1.4 程序验证为了验证本文所用程序的正确性,计算了Ng 和 Erlebacher 等[8]
|
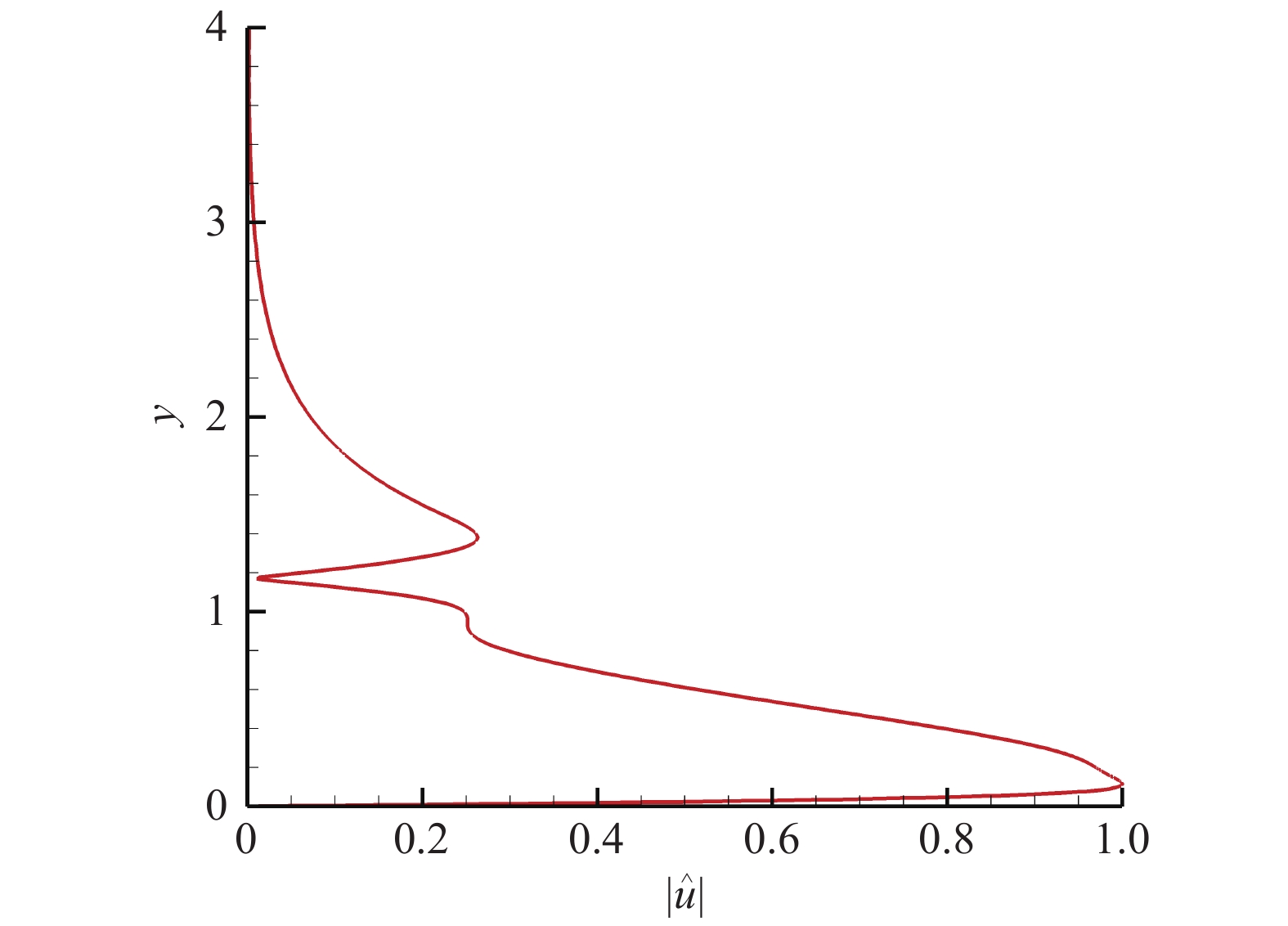
图 3 Mack模态的流向速度 |
|
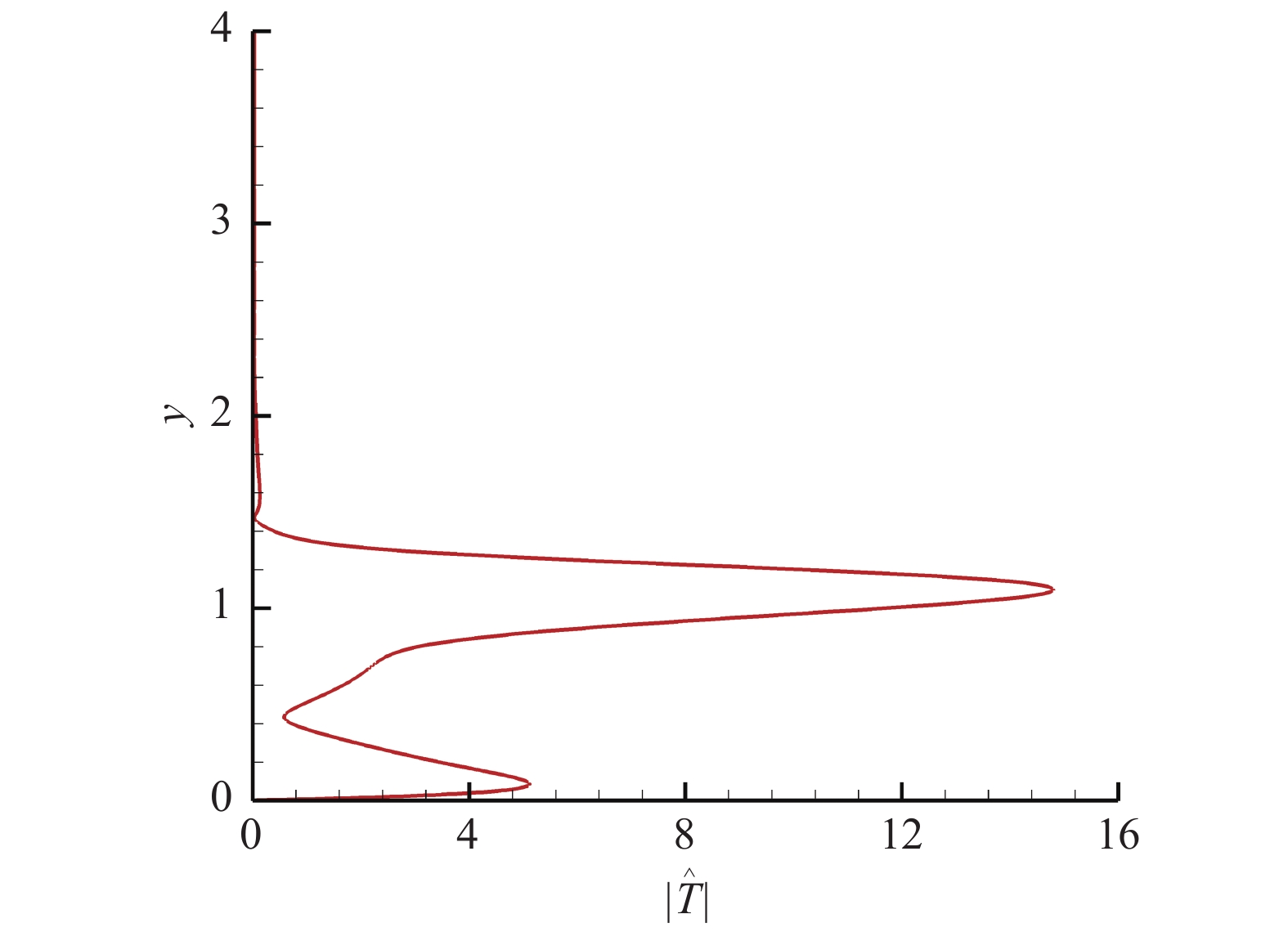
图 4 Mack模态的温度 |
从图中不难看出,Mack模态扰动的温度最大值明显大于速度最大值,因此以Mack模态的温度最大值来定义Mack模态扰动的幅值,即
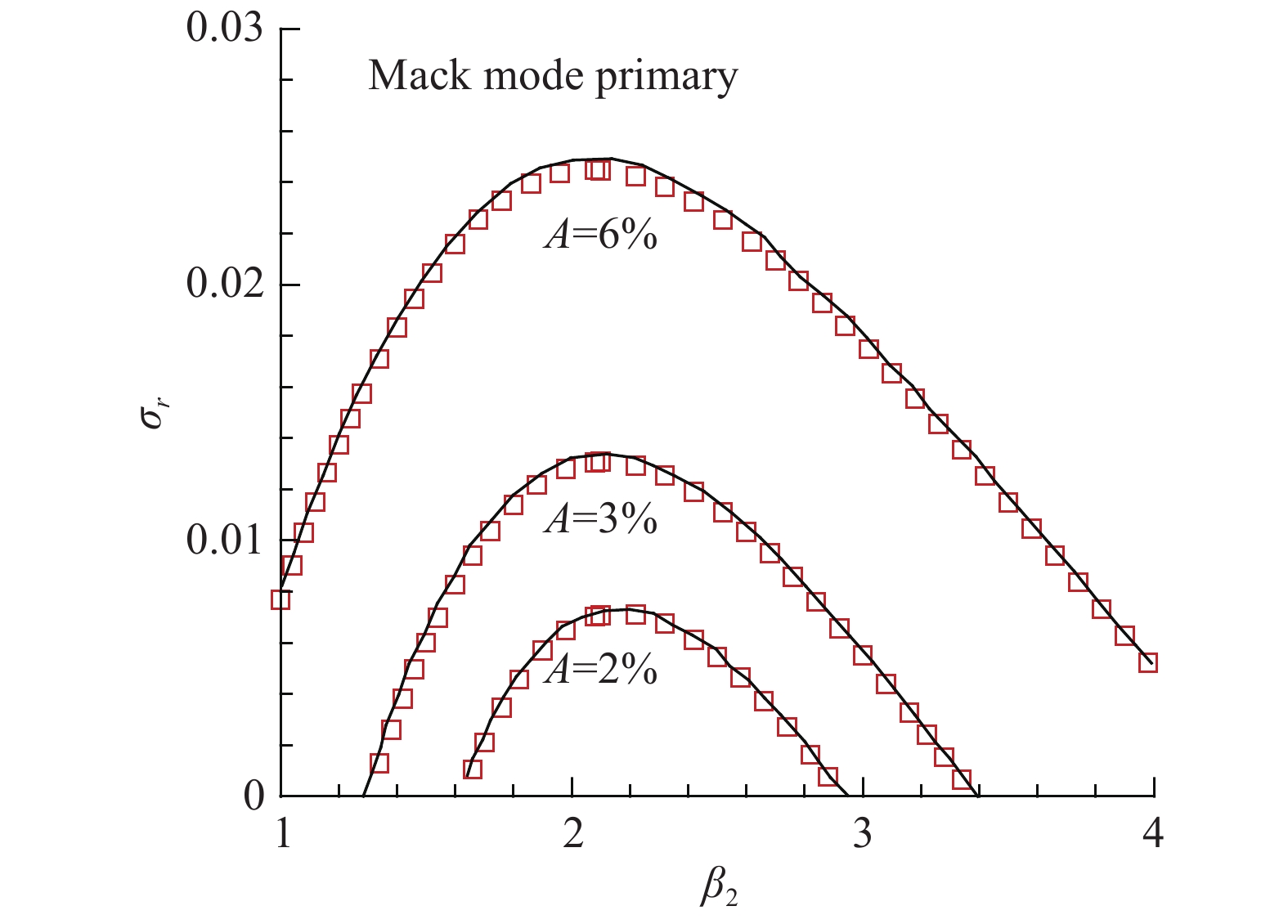
在二次失稳分析中,不考虑Mack模态的非线性作用,利用上述稳定性分析得到的Mack模态扰动乘以相应的幅值加上相似性解作为二次失稳分析的基本流,采用时间模式计算了三组不同幅值的工况。来流参数为:
|
图 5 二次失稳分析的结果与文献[8]的结果对比图(实线为文献中结果,方块为本文结果) Fig.5 Comparison between the secondary instability analysis results and those in Ref.[8](The solid lines are the results in literature, and the square symbols are the results in this study) |
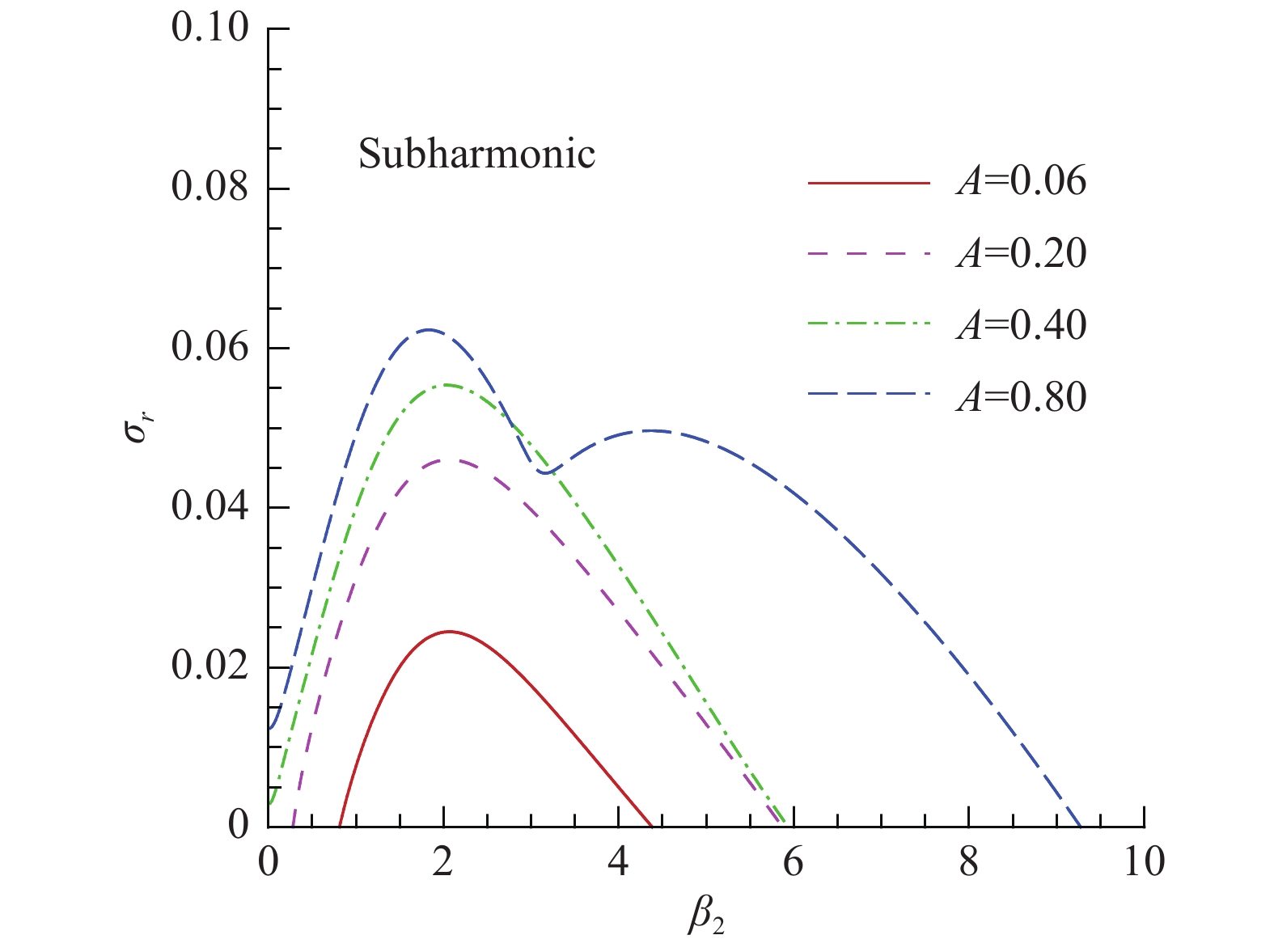
此前研究中都发现,首次失稳的扰动幅值对二次失稳的主导模态会产生较大的影响,为了研究这种影响,我们利用1.4节中通过线性稳定性方程求解器得到的Mack模态扰动作为首次失稳扰动,首次失稳扰动乘上相应的幅值A加上相似性解,作为二次失稳分析的基本流。研究了首次失稳扰动的幅值A从0.06增加到0.8时,亚谐模态和基频模态的增长率随展向波数
|
图 6 亚谐模态的增长率随展向波数变化的关系 Fig.6 Relationship between the growth rate of subharmonic modes and the spanwise wavenumber |
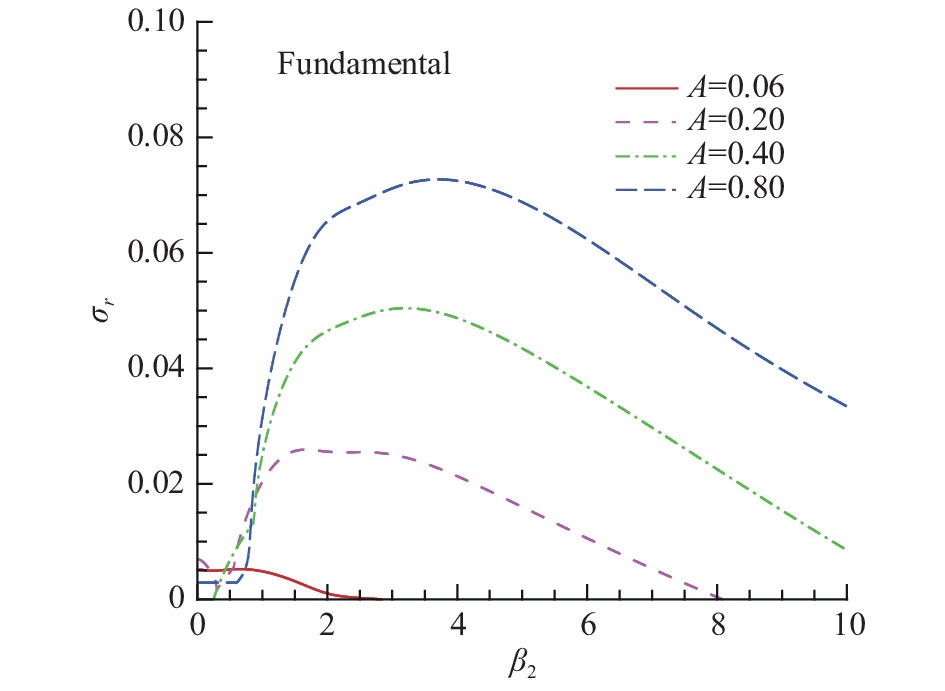
|
图 7 基频模态的增长率随展向波数变化的关系 Fig.7 Relationship between the growth rate of fundamental modes and the spanwise wavenumber |
结合两张图不难看出,相对于亚谐模态来讲,基频模态的增长率随着初始Mack模态幅值的增大而增长的更快,说明首次失稳扰动的幅值对基频模态扰动的影响更显著。进而说明在首次失稳扰动小幅值的情况下,亚谐模态在流场中占主导地位;反之基频模态占主导地位,这个结论与刘建新[14]等研究的结论是相符合的。这也解释了为什么在Ng和 Erlebacher 等[8]的论文中,只发现了亚谐模态的二次失稳,没有发现基频模态的二次失稳。因为文献中的首次失稳扰动幅值最大为6%,幅值等于6%属于小幅值的情况,此时流场中亚谐模态占主导地位,所以没有发现基频模态的二次失稳。
由于本文重点研究基频模态的失稳,所以围绕亚谐模态失稳的研究这里不再展开。图8给出了首次失稳扰动幅值

|
图 8 基频模态的流向速度特征函数沿法向的分布 Fig.8 Streamwise velocity eigenfunction of the fundamental mode along the normal direction |
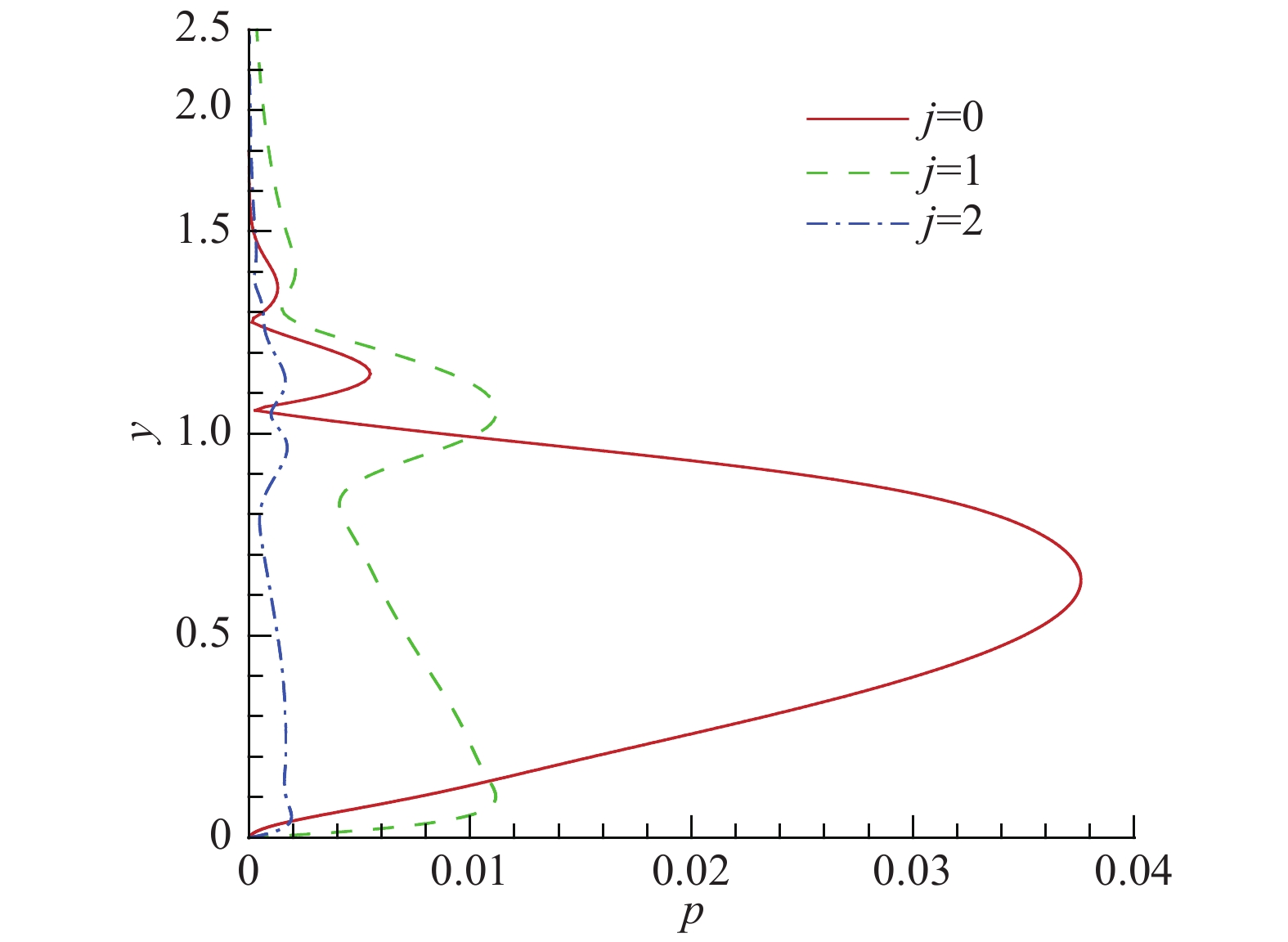
进一步的,我们可以对基频模态的特征函数进行傅里叶分析,即分析特征函数分量
|
图 9 基频模态特征函数的傅里叶分析 Fig.9 Fourier analysis of the fundamental mode eigenfunction |
通过对前人研究工作的调研,我们知道了在首次失稳扰动大幅值的情况下,基频模态在流场中占主导地位,而且随着流动向下游的发展,会产生条纹结构。为了研究条纹结构的失稳特性,我们首先要获得条纹结构。这里选择Blasius相似性解为原基本流,Mack模态作为首次失稳扰动,其幅值为0.6,基频模态扰动作为二次失稳扰动,根据一般计算的经典二次失稳结果,进行后处理,从而生成全部的流场和条纹结构的流场。这样,考虑到基频失稳扰动
| $ \begin{split} \tilde \varphi (\tilde x,y,z,t) =& {{\tilde \varphi }_0}(y) + A({{\hat \varphi }_1}(y){{\rm{e}}^{{\rm{i}}(\alpha x - \omega t)}}+ \\& c.c.) + B({{\hat \varphi }_{\rm{2}}}(y,\tilde x){{\rm{e}}^{{\rm{i}}{\beta _2}z}} + c.c.) \end{split} $ | (14) |
其中,
根据流场的性质,人们在研究中总是通过分析流动过程中涡结构的演化特点来研究扰动的发生、演化及其表现特征的。
图10给出了首次失稳扰动幅值
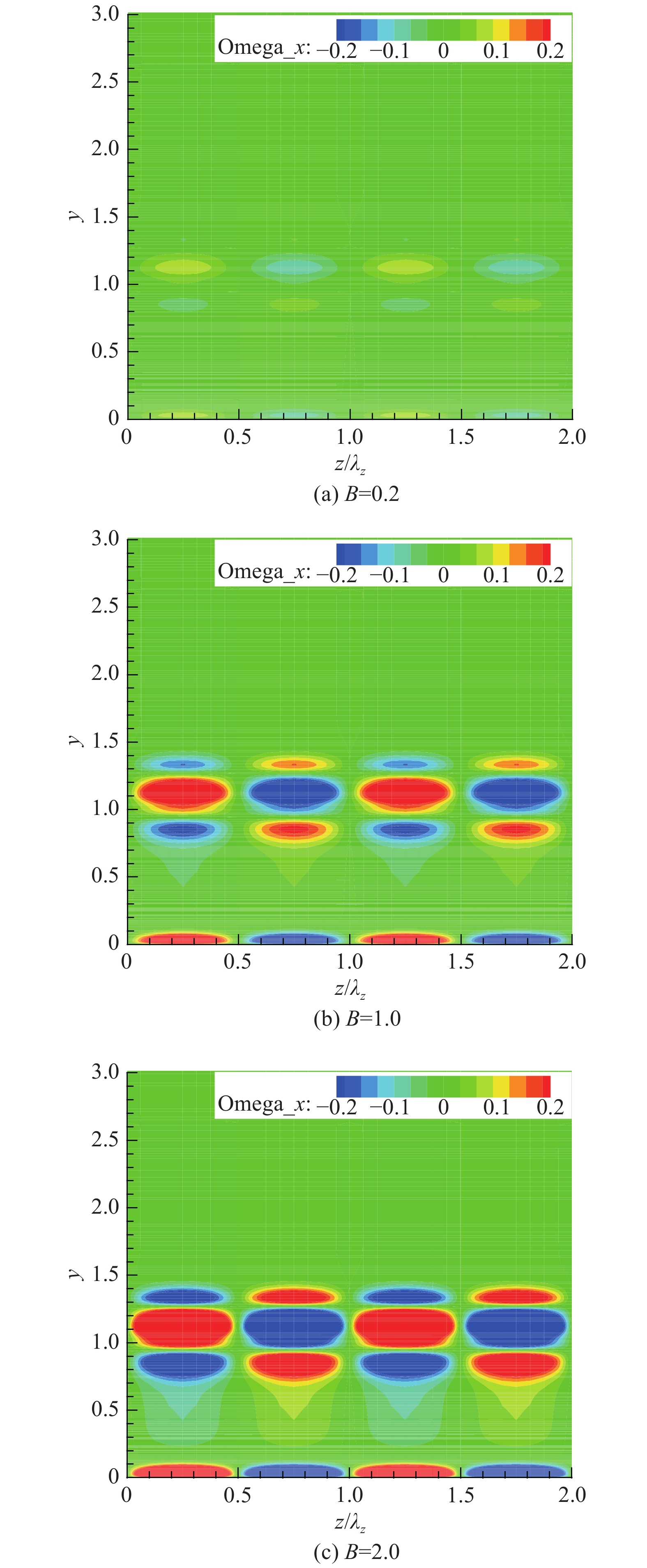
|
图 10 流向涡量云图 Fig.10 Streamwise vorticity contours |
图11给出了不同二次失稳扰动幅值下,全部流场的展向涡量云图,不难看出随着扰动的发展,
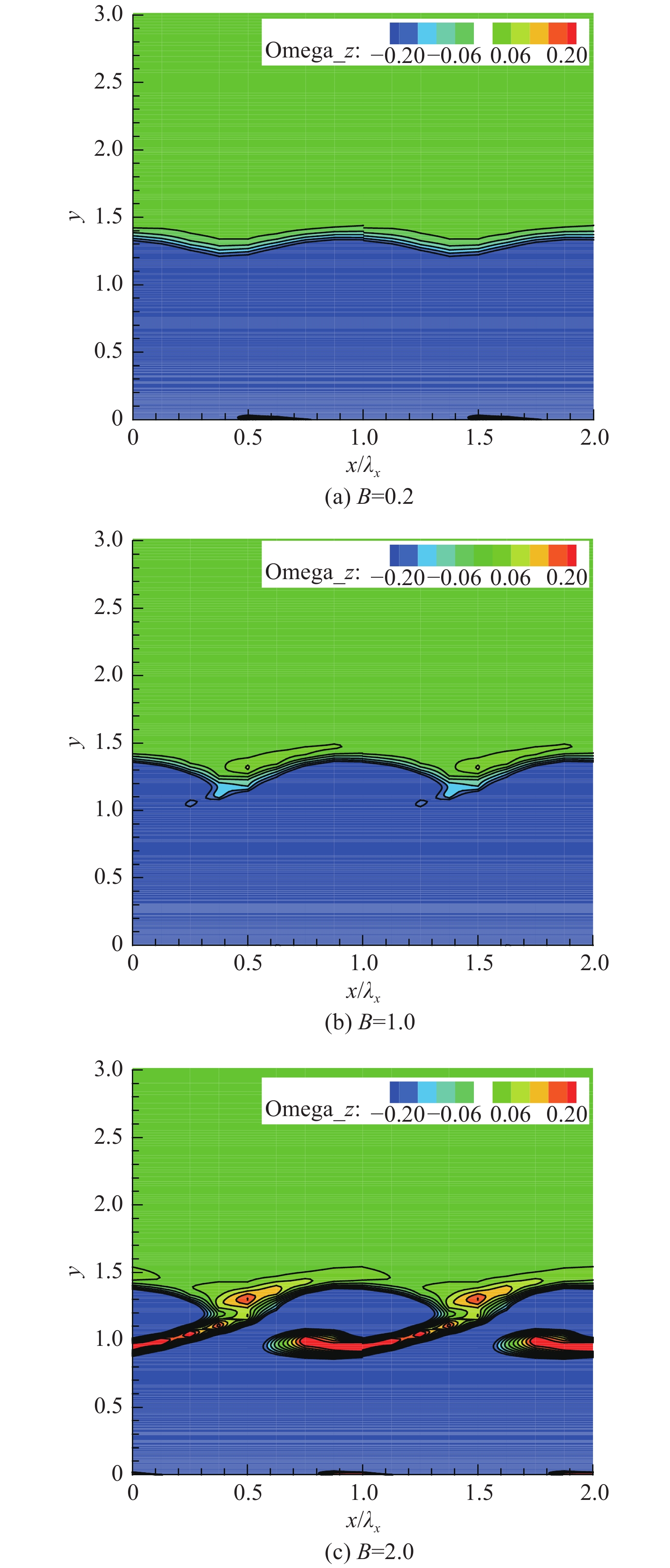
|
图 11 展向涡量云图 Fig.11 Spanwise vorticity contours |
对比图10和图11两组相同二次失稳扰动幅值下的流向涡量和展向涡量云图可以发现,流向涡量的强度要显著大于展向涡量的强度,说明在流场中流向涡量占主导地位,展向涡量次之。这意味着此时流场中的动力学结构应该主要受流向涡量的制约。因此,以下研究中我们主要关心流向涡量的条纹结构,而忽略掉展向结构的影响和特征,只研究某一个流向站位的流场结构。
根据前面的讨论,所谓流向涡量的条纹,其主要成分为基频模态的零阶扰动,因此,此时流向涡结构即基频失稳条纹可以写成如下形式:
| $ {\tilde \varphi _s}(y,z) = {\tilde \varphi _0}(y) + B({\hat \varphi _{{\rm{20}}}}(y){{\rm{e}}^{{\rm{i}}{\beta _2}z}} + c.c.) $ | (15) |
为了研究不同二次失稳扰动幅值对条纹结构基本流的影响,我们计算了四组不同的参数,二次失稳扰动幅值分别为0、0.2、1和2。
图12给出了两个周期内,不同二次失稳扰动幅值下的条纹结构流向速度云图。从图中不难看出,随着
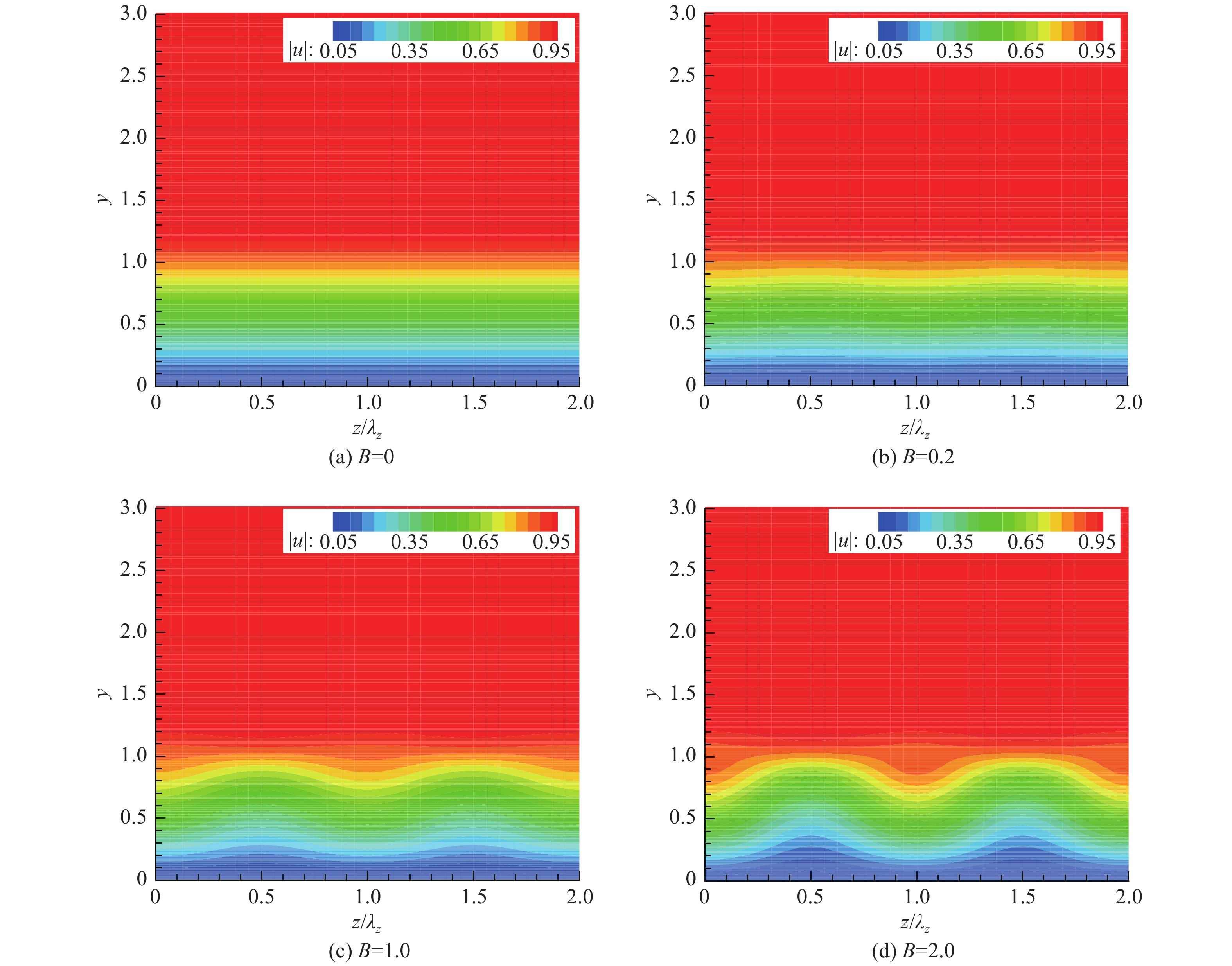
|
图 12 不同B值下的条纹结构(流向速度)沿法向的分布 Fig.12 Streamwise velocity contours of streaky structures under different B values along the normal direction |
得到条纹结构后,我们就可以进一步对该条文结构进行稳定性分析。这里我们使用无黏稳定性方程进行分析。因为根据通常的理论,条纹结构的稳定性主要是依赖于流场的局部剪切造成的,而黏性只起到阻尼作用,因此直接使用无黏稳定性分析就可以给出稳定性分布的本质与特征。无黏的控制方程可以写为:
| $ \begin{split}& [ - {\alpha ^2}(1 - {{\hat M}^2}) + {\nabla ^2}_{yz}]\hat p - \frac{\partial }{{\partial y}}[{\rm{ln}}({{\hat M}^2})]\frac{{\partial \hat p}}{{\partial y}} \\& \qquad -\frac{\partial }{{\partial z}}[{\rm{ln}}({{\hat M}^2})]\frac{{\partial \hat p}}{{\partial z}} = 0 \end{split} $ | (16) |
其中,
| $ \hat M = {M_\infty }\frac{{({U_b} - c)}}{{\sqrt {{T_b}} }} = M - \frac{c}{a} $ | (17) |
其中相速度
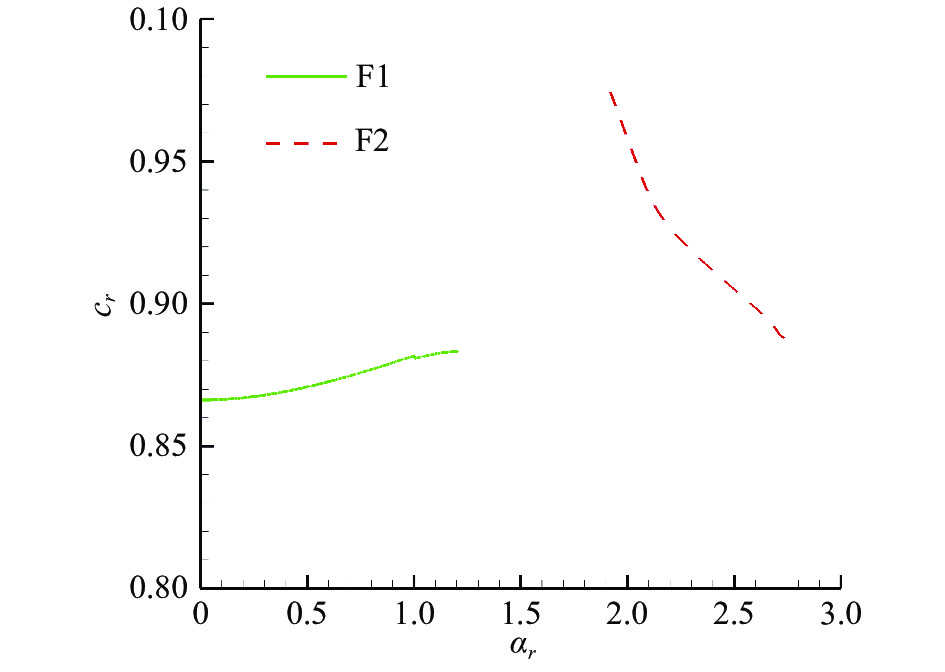
为了验证我们的分析,本文计算了两个二次失稳扰动幅值为0.2和2时的线性条带流场对应的无黏稳定性的工况。图13给出了二次失稳扰动幅值为0.2时最不稳定的两支扰动的增长率随波数的变化关系,对应图中的F1和F2曲线。两支解都是随着波数的增加,增长率呈先增大后减小的趋势。从图中不难看到,两支模态的增长率分布特征与二维Blassius边界层时的分布状态十分相似。这是由于此时条纹幅值较小,流场中保留了更多的二维性的特征。图14给出了与图13相对应的两支曲线的相速度随波数的对应关系。从图中不难看到,F1模态的相速度变化不大,其值约为0.865~0.88,该值基本对应于条纹边界层广义拐点位置的速度。因此F1模态主要对应于无黏剪切模态。相对于F1,F2模态的相速度范围变化较大,其中下支点相速度接近于1,上支点相速度接近于0.88,即广义拐点的值。这种相速度的分布特征与二维边界层中第二模态扰动的分布特征十分相近。
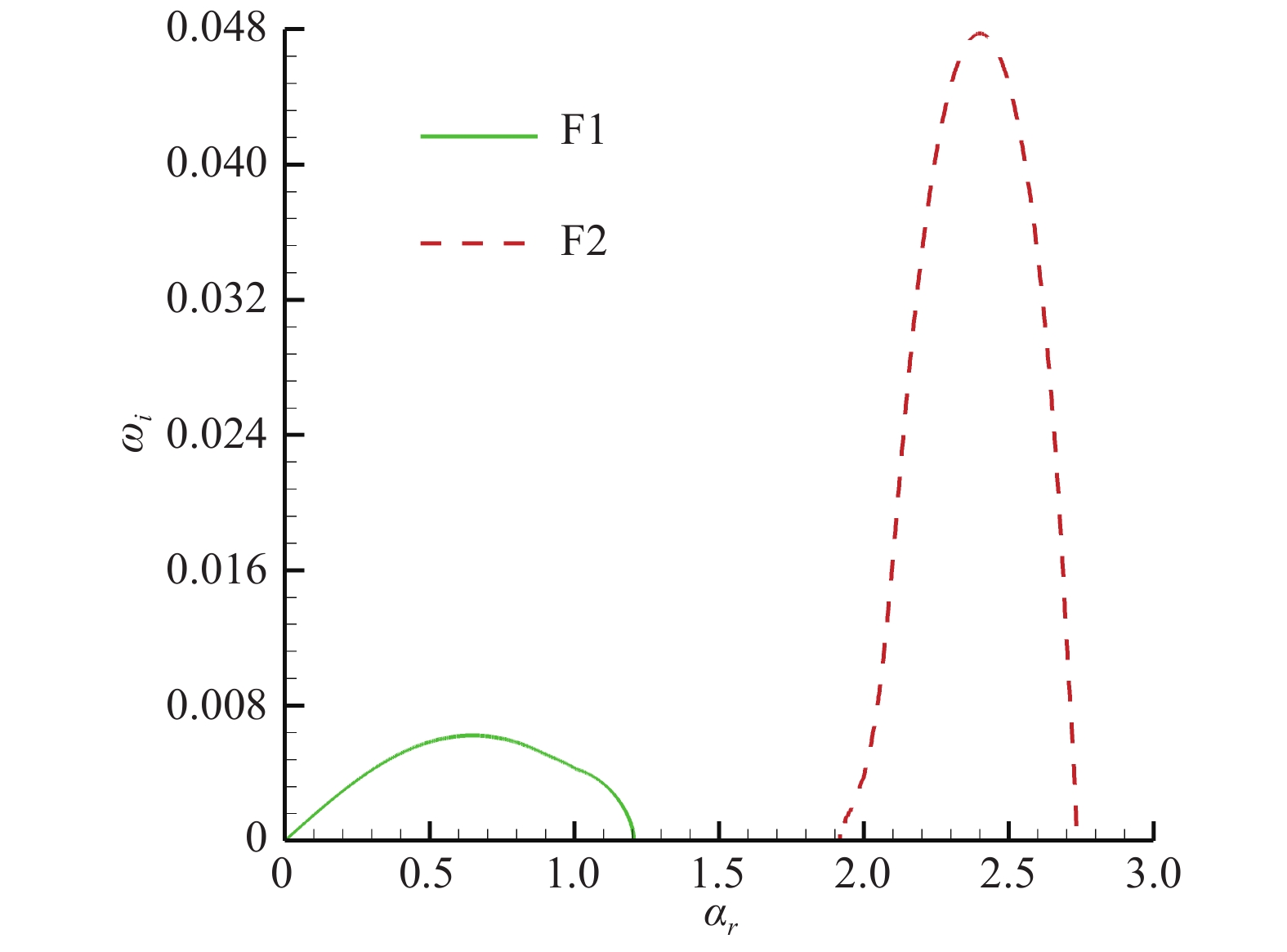
|
图 13 增长率随波数的变化关系 Fig.13 The relationship between the growth rate and the wavenumber |
|
图 14 相速度随波数的变化关系 Fig.14 The relationship between the phase velocity and the wavenumber |
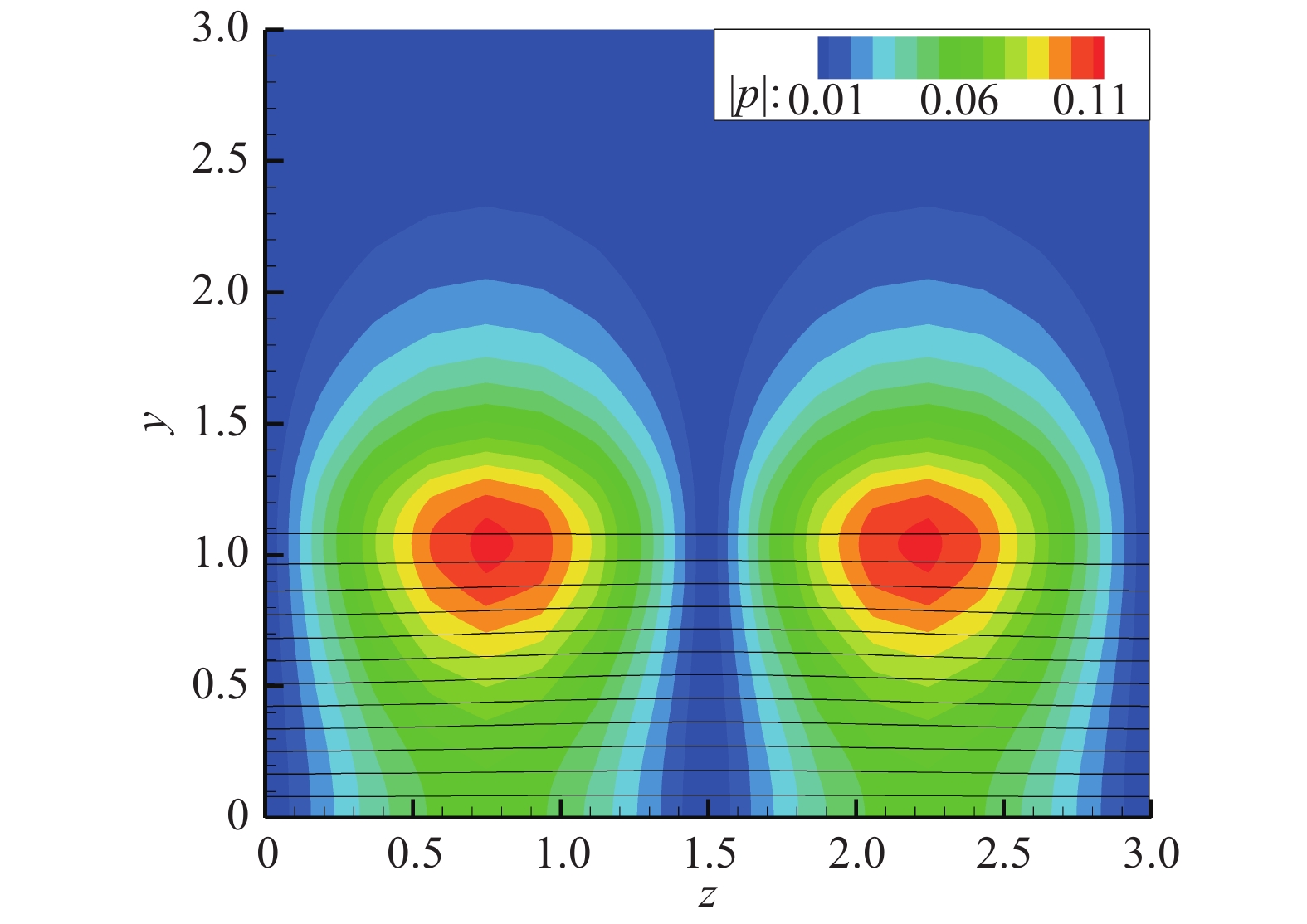
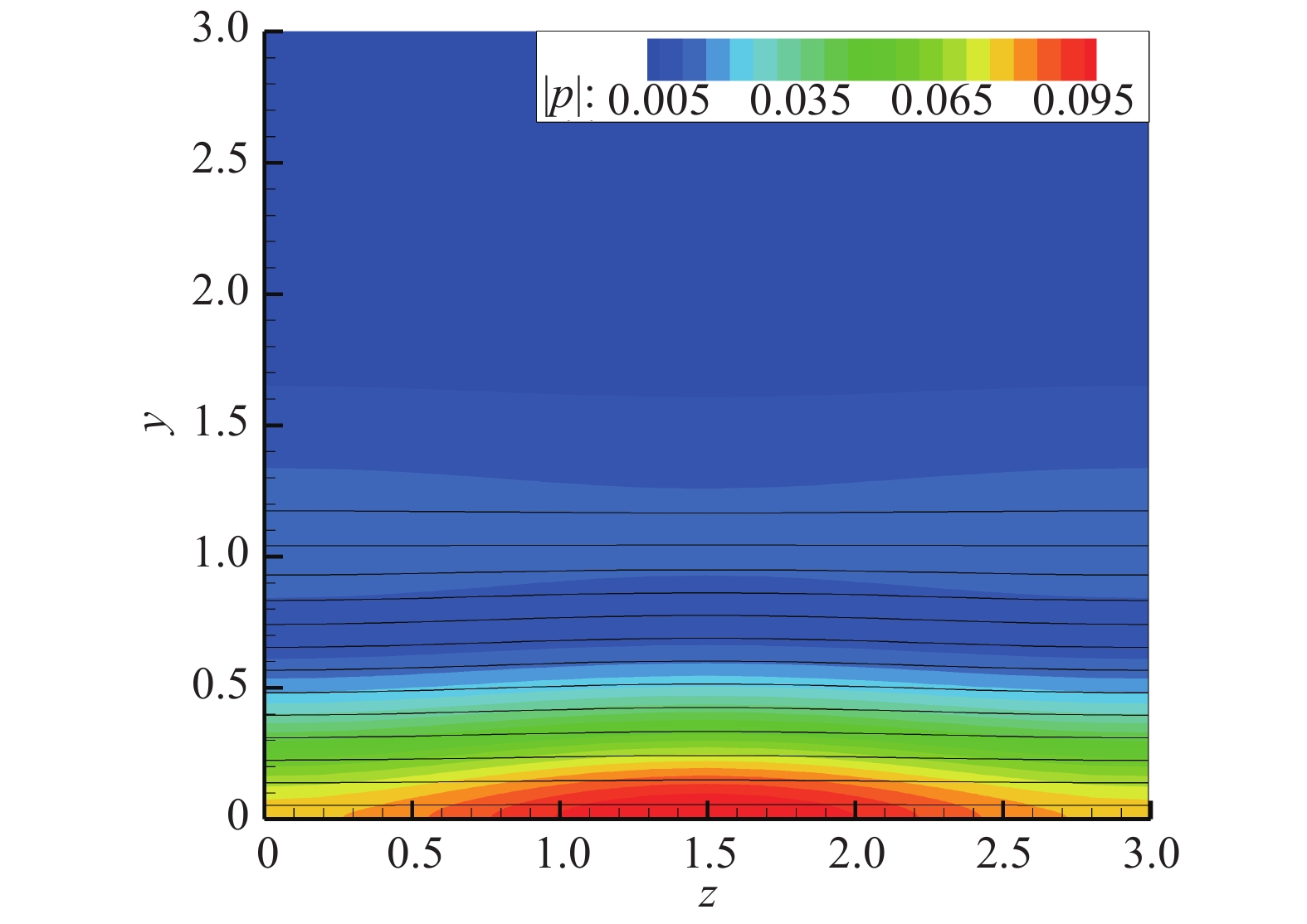
为了进一步研究两支解的性质,图15和图16分别给出了F1和F2两支曲线增长率最大时所对应的压力特征函数云图,分别为
|
图 15 |
由图15可以看到,对于F1模态,压力最大值主要集中
|
图 16 |
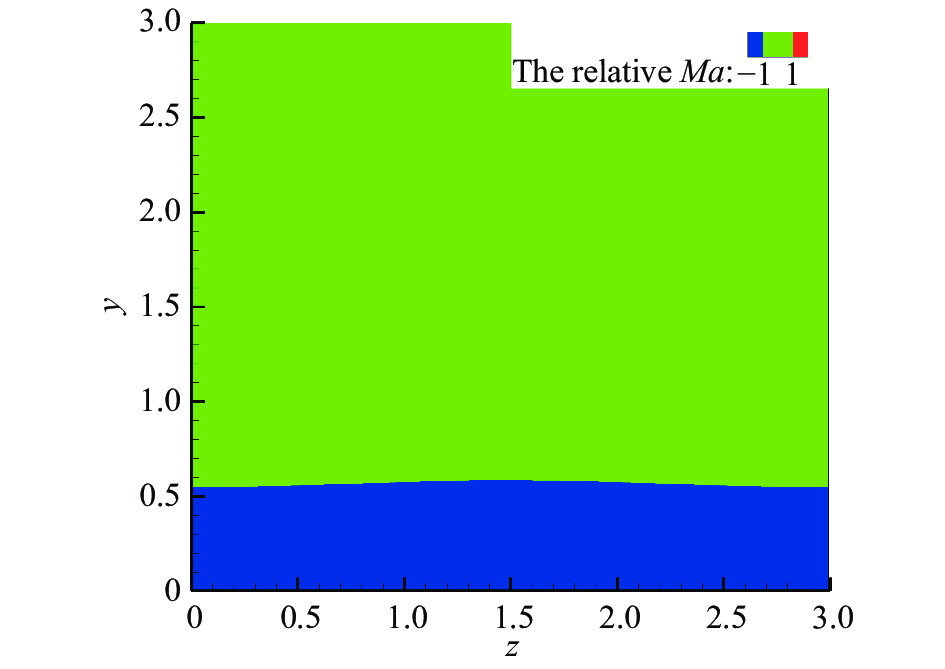
图17给出了F2模态所对应的相对马赫数分布。从图中不难看到近壁区域整体上相对马赫数都小于−1,因此扰动波在此处是超声速的,此时方程(16)在局部表现为波动方程特性,从而导致压力的波动解。该特征和结论与二维基本流情况时的Mack第二模态基本相同。比较F2和F1模态的特征我们不难得出,在高超条件下,由于微小条纹的存在,流场中可以存在此时在三维边界层中类似二维情况中第一模态和第二模态的解。因此,我们将F1类的扰动称之为条纹边界层的第一模态,将F2类似的扰动称之为条纹边界层的第二模态。其中,第一模态F1失稳频率较低,增长率较小,第二模态F2增长率较大,但频率较高。
|
图 17 |
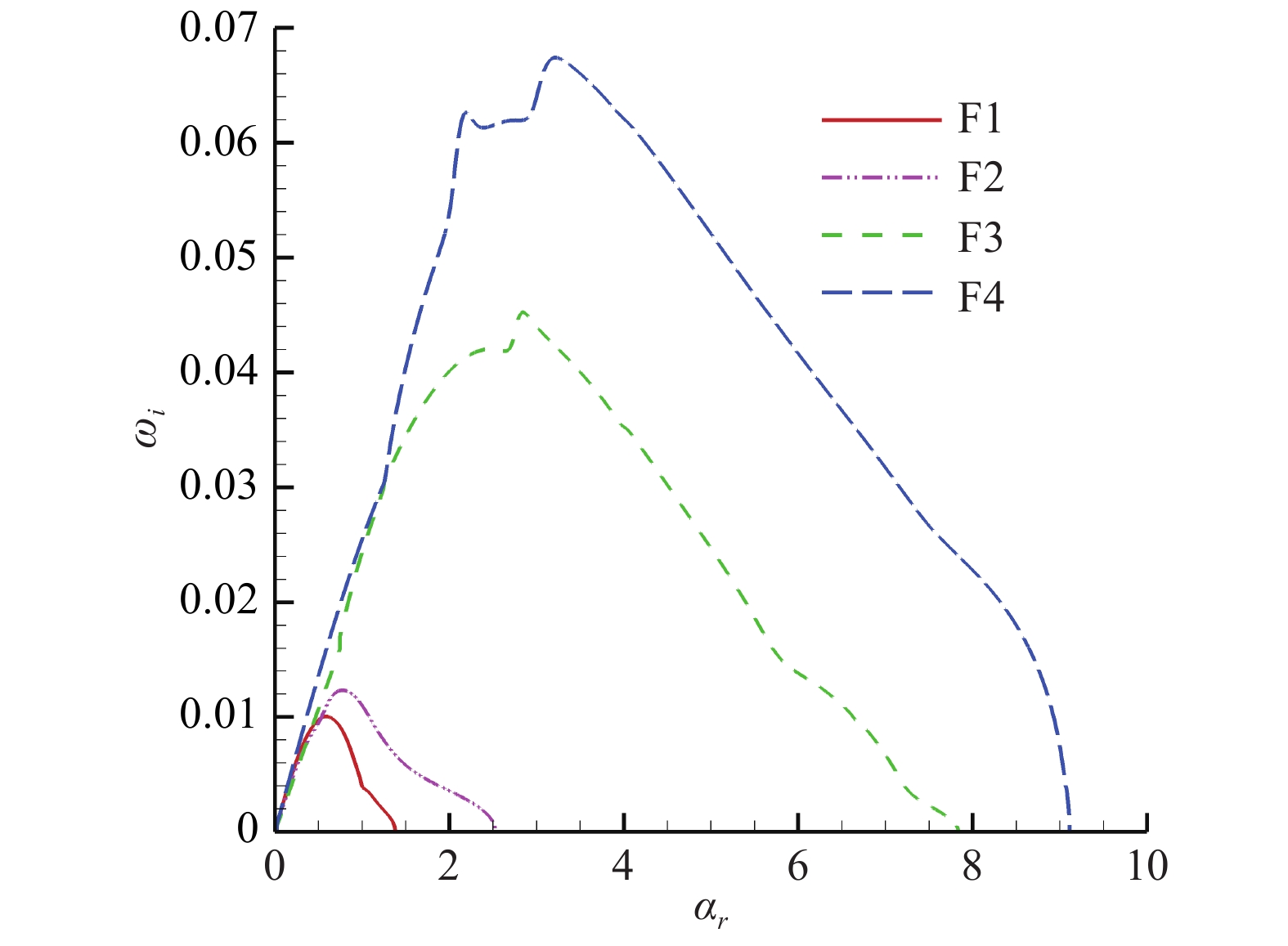
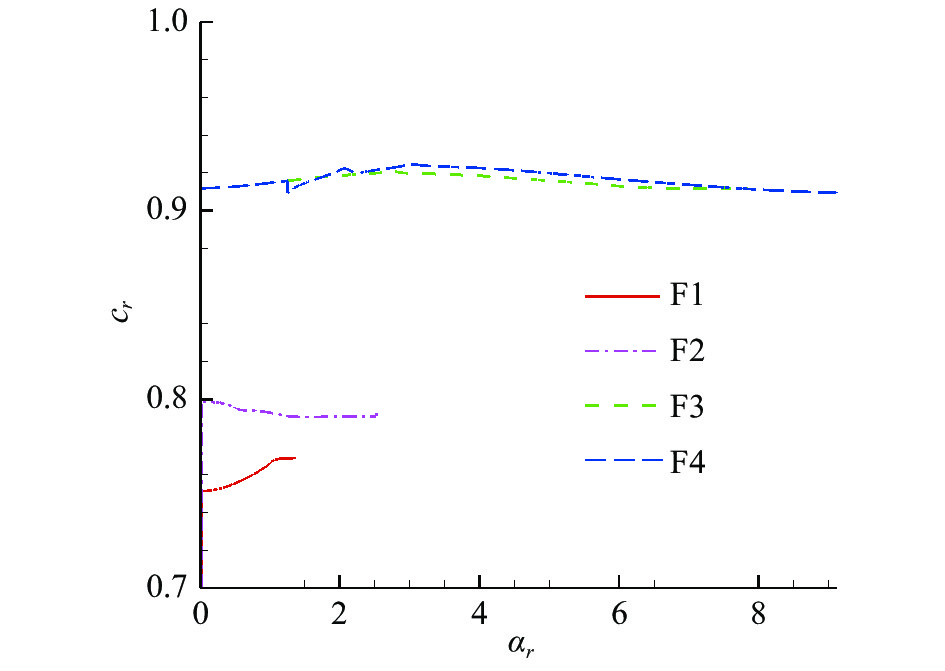
图18出了二次失稳扰动幅值B = 2时的增长率随波数变化的关系。可以看出,此时大幅值情况下,流场中主要存在四支解。图19为四支曲线对应的相速度分布。从图中不难看出,随着条纹幅值的增加,增长率有放大,其中第二模态的增长区域显著放大。同时,流场中失稳模态也较条纹幅值较低时更丰富。相速度分布行为随着条纹幅值的增加逐渐偏离二维边界层时的典型特征,但整体上第一模态的相速度较小,而第二模态的相速度较大。
|
图 18 增长率随波数的变化关系 Fig.18 The relationship between the growth rate and the wavenumber |
|
图 19 相速度随波数的变化关系 Fig.19 The relationship between the phase velocity and the wavenumber |
为了进一步说明问题,图20给出了F1、F3、F4最大增长率对应的压力云图,由于F1和F2曲线的压力云图类似,所以这里不再给出F2曲线对应的压力云图。图20(a)对应的是剪切解的情况,压力最大值在临界层附近。图20(b、c)对应的是压力最大值都集中在壁面附近。这与二次失稳扰动幅值为0.2时的结论类似,即第二模态类的解集中在壁面附近。其中第二模态类的解增长率较大,失稳频率范围和增长率随着条纹幅值增大而显著增大,而第一模态类的扰动相对变化范围要小。

|
图 20 不同波数下的压力特征函数云图 Fig.20 The eigenfunction of pressure for different wavenumbers |
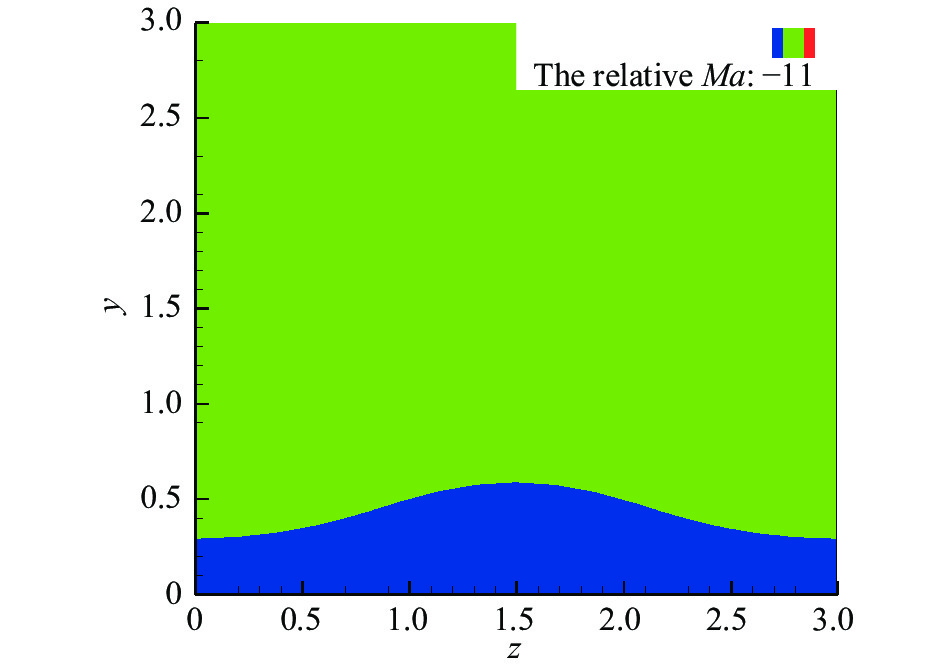
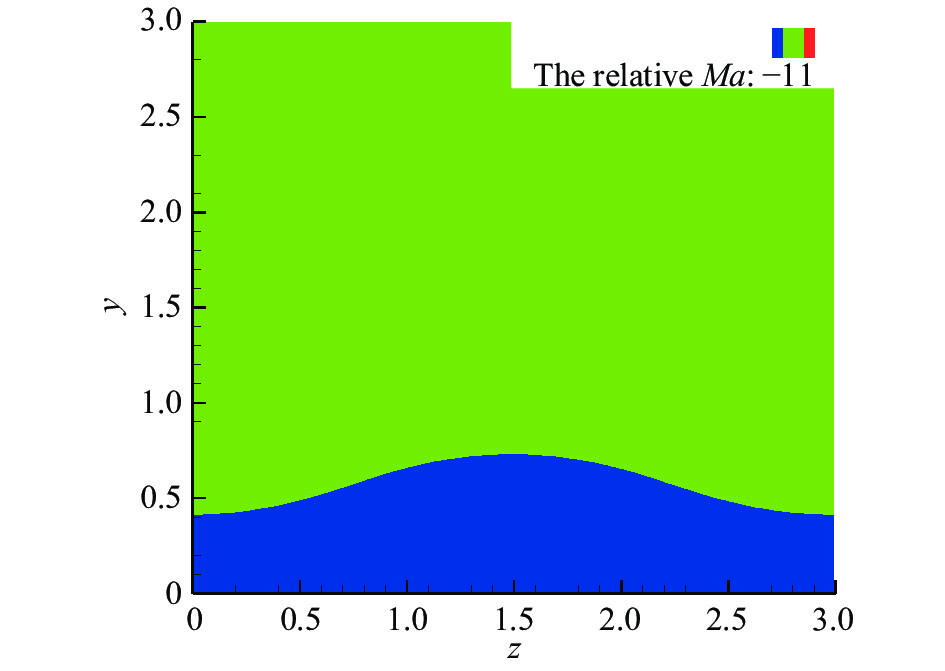
图21和图22给出了相速度为F3和F4模态最不稳定扰动对应的相对马赫数云图。从图中可以看到,依然满足于近壁区域相对马赫数小于−1的性质,这使得扰动在该区域呈现出波动的特征,从而导致了非平凡解的产生。
|
图 21 |
|
图 22 |
本文采用线性稳定性分析和二次稳定性分析的方法,以高超声速平板边界层为研究对象,围绕边界层基频二次失稳条纹结构的稳定性开展了研究,得到结论如下:
1)首次失稳扰动的幅值对二次失稳类型有影响。当首次失稳扰动幅值较小时,亚谐模态占主导;反之,基频模态占主导,其特征函数在边界层内有较大的值。
2)基频模态的主要成分为流向的条纹结构,表现为流向涡。二次失稳扰动的幅值对全流场的流向涡和展向涡结构分布和强度都有影响。在相同的扰动幅值的前提下,流向涡显著强于展向涡,这表明此时流场中的动力学特征主要受流向涡结构影响。同时,首次失稳扰动幅值相同的条件下,二次失稳基频模态扰动的幅值对条纹结构(流向涡)的产生直接相关。二次失稳扰动的幅值越大,条纹结构越明显,幅值越大。
3)通过对条纹结构的无黏稳定性分析,结果表明流场中存在多失稳模态特征,且失稳特征与多种物理机制相关。其中低频失稳扰动的增长率较小,对应于拐点无黏不稳定性,而高频扰动的增长率较大,对应于由于局部相对马赫数绝对值大于1导致的压缩性的解。从解的特征解来看,条纹边界层中的失稳模态可以看作为二维边界层流动中第一模态和第二模态在三维边界层中的扩展。
综上所述,本研究通过对边界层内条纹结构的产生和无黏稳定性特征进行了初步研究,基于线性模型构造条纹基本流,研究了条纹结构中的无黏模态分布以及其物理主导机制。这推进研究高超声速边界层转捩过程中的非线性稳定性机制以及转捩中的典型流动结构的物理机理的理论认识。
这里需要额外指出的是,在本文的研究中,条纹结构的产生主要是基于线性模型构造的,并未考虑条纹产生激发的初值效应以及饱和特征,后续需要对此进行更详细的分析和研究。此外,对条纹边界层的稳定性模态在转捩过程中的意义应进一步基于直接数值模拟开展研究工作。
| [1] |
罗纪生. 高超声速边界层的转捩及预测[J]. 航空学报, 2015, 36(1): 357-372. LUO J S. Transition and prediction for hypersonic boundary layers[J]. Acta Aeronautica et Astronautica Sinica, 2015, 36(1): 357-372. (in Chinese) |
| [2] |
刘建新. 不可压缩流体边界层条纹结构无粘稳定性的数值研究[D]. 天津: 天津大学, 2007. LIU J X. A numerical investigation on inviscid instability of streaky structures in incompressible boundary layer flow[D]. Tianjin: Tianjin University, 2007 (in Chinese). |
| [3] |
张存波. 与超声速边界层转捩有关的扰动非线性作用研究[D]. 天津: 天津大学, 2017. ZHANG C B. Research on nonlinear mode interactions relating to supersonic boundary layer transition[D]. Tianjin: Tianjin University, 2017(in Chinese). |
| [4] |
KLEBANOFF P S, TIDSTROM K D, SARGENT L M. The three-dimensional nature of boundary-layer transition[J]. Journal of Fluid Mechanics, 1962, 12(01): 1-34. DOI:10.1017/S0022112062000014 |
| [5] |
KACHANOV Y S, YA LEVCHENKO V. The resonant interaction of disturbances at laminar-turbulent transition in a boundary layer[J]. Journal of Fluid Mechanics, 1984, 138: 209-247. DOI:10.1017/S0022112084000100 |
| [6] |
HERBERT T. Analysis of the subharmonic route to transition in boundary layers[C]//22nd Aerospace Sciences Meeting, Reno, NV. Reston, Virginia: AIAA, 1984. doi: 10.2514/6.1984-9
|
| [7] |
HERBERT T. Secondary instability of boundary layers[J]. Annual Review of Fluid Mechanics, 1988, 20(1): 487-526. DOI:10.1146/annurev.fl.20.010188.002415 |
| [8] |
NG L L, ERLEBACHER G. Secondary instabilities in compressible boundary layers[J]. Physics of Fluids A: Fluid Dynamics, 1992, 4(4): 710-726. DOI:10.1063/1.858290 |
| [9] |
刘建新. 小攻角钝锥高超声速边界层的扰动演化[D]. 天津: 天津大学, 2010. LIU J X. Evolution of disturbance in hypersonic blunt cone boundary layer at small angle of attack[D]. Tianjin: Tianjin University, 2010 (in Chinese). |
| [10] |
CHOU A, WARD C, LETTERMAN L, et al. Transition research with temperature-sensitive paints in the boeing/AFOSR Mach-6 quiet tunnel[C]//41st AIAA Fluid Dynamics Conference and Exhibit, Honolulu, Hawaii. Reston, Virginia: AIAA, 2011. doi: 10.2514/6.2011-3872
|
| [11] |
YU M, LUO J S. Nonlinear interaction mechanisms of disturbances in supersonic flat-plate boundary layers[J]. Science China Physics, Mechanics & Astronomy, 2014, 57(11): 2141-2151. DOI:10.1007/s11433-014-5568-0 |
| [12] |
SIVASUBRAMANIAN J, FASEL H F. Direct numerical simulation of laminar-turbulent transition in a flared cone boundary layer at Mach 6[C]//54th AIAA Aerospace Sciences Meeting, San Diego, California, USA. Reston, Virginia: AIAA, 2016. doi: 10.2514/6.2016-0846
|
| [13] |
HADER C, LEINEMANN M, FASEL H F. Direct numerical simulations of hypersonic boundary-layer transition for a flared cone: fundamental breakdown[J]. Journal of Fluid Mechanics, 2019, 869: 341-384. DOI:10.1017/jfm.2019.202 |
| [14] |
LIU J X. The fundamental secondary instability of the primary mack mode in hypersonic boundary layers on flat plates[J]. Advances in Applied Mathematics and Mechanics, 2019, 11(3): 559-570. DOI:10.4208/aamm.2018.s01 |
| [15] |
于高通. 高超声速三维边界层e-N方法的应用及扰动演化的预测[D]. 天津: 天津大学, 2016. YU G T. Application of e-N method and prediction of disturbances propagation in three-dimensional hypersonic boundary layers[D]. Tianjin: Tianjin University, 2016 (in Chinese). |
| [16] |
WARD C, HENDERSON R, SCHNEIDER S P. Secondary instability of stationary crossflow vortices on an inclined cone at Mach 6[C]//45th AIAA Fluid Dynamics Conference, Dallas, TX. Reston, Virginia: AIAA, 2015. doi: 10.2514/6.2015-2773
|
| [17] |
LI F, CHOUDHARI M, CHANG C L, et al. Development and breakdown of Görtler vortices in high speed boundary layers[C]//48th AIAA Aerospace Sciences Meeting Including the New Horizons Forum and Aerospace Exposition, Orlando, Florida. Reston, Virginia: AIAA, 2010. doi: 10.2514/6.2010-705
|
| [18] |
PAREDES P, THEOFILIS V. Centerline instabilities on the hypersonic international flight research experimentation HIFiRE-5 elliptic cone model[J]. Journal of Fluids and Structures, 2015, 53: 36-49. DOI:10.1016/j.jfluidstructs.2014.11.002 |
| [19] |
任杰. 高超声速边界层Görtler涡二次失稳和转捩控制研究[D]. 北京: 清华大学, 2015. REN J. Secondary instabilities of Görtler vortices in high-speed boundary layers and control on flow transition[D]. Beijing: Tsinghua University, 2015 (in Chinese). |
| [20] |
LEIB S J, WUNDROW D W, GOLDSTEIN M E. Effect of free-stream turbulence and other vortical disturbances on a laminar boundary layer[J]. Journal of Fluid Mechanics, 1999, 380: 169-203. DOI:10.1017/S0022112098003504 |
| [21] |
周恒, 苏彩虹, 张永明. 超声速/高超声速边界层的转捩机理及预测[M]. 北京: 科学出版社, 2015. ZHOU H, SU C H, ZHANG Y M. Transition mechanism and prediction of supersonic/high supersonic boundary layer[M]. Beijing: Science Press, 2015 (in Chinese). |
| [22] |
LEHOUCQ R B, SORENSEN D C, YANG C. ARPACK users' guide: solution of large-scale eigenvalue problems with implicitly restarted Arnoldi methods[M]. DBLP, 1998.
|
 2021, Vol. 39
2021, Vol. 39