2. 同济大学 上海市地面交通工具空气动力学与热环境模拟重点试验室,上海 201804;
3. 北京民用飞机技术研究中心,北京 102211
2. Shanghai Key Lab of Vehicle Aerodynamics and Vehicle Thermal Management Systems, Tongji University, Shanghai 201804, China;
3. Beijing Aeronautical Science & Technology Research Institute, Beijing 102211, China
随着高速列车技术的快速发展,人们对高速列车的环保和乘坐舒适性提出了更高的要求[1]。实车测试表明[2-3]列车速度接近或超过300 km/h时,气动噪声将在列车噪声源中占主导地位。声学风洞研究[4]表明转向架区域是最大的气动噪声源。同时,运行工况下噪声传递路径分析技术发现[5],时速350~380 km列车通过气动噪声引起的空气声传递占车内噪声主要地位,转向架区域的空气声为车内噪声最主要贡献源。
Fremion等[6]对TGV铰接转向架区域在350 km/h时路试研究,近场麦克风结果指其噪声为具有多峰值的宽频噪声,其中196 Hz噪声在多个测点均存在,推断是铰接式转向架的车厢连接处空腔声模态导致,但路试结果是轮轨、结构振动和气动噪声的综合结果,不能确定是气动导致的噪声。
风洞是研究气动噪声的有力工具,避免了实车测试声源复杂的缺陷。高阳等[7]对1∶8缩比列车模型进行声学风洞实验,倍频程谱表明转向架区域远场噪声在中心频带315 Hz、400 Hz能量较高。德国DLR的Lauterbach等[8]对1∶25的高速列车缩比模型进行了风洞试验研究,结果表明,转向架区域的气动噪声存在两个驼峰,频率不随雷诺数增加,推测与空腔模态有关,但未观察到低阶和更高阶峰值。Igesias[9]、Yamazaki[10]在声学风洞进行1∶7缩比列车测试的结果指出,远场噪声1/3倍频程谱与转向架形式关联度较低,转向架舱腔体、车轮和车轴噪声占比为31%、16%,给出了工程性的结论,对于机理和声源特性有待深入。由于主要噪声源能量的频率范围较低,远场麦克风阵列无法准确定位声源位置[11],高精度可压缩数值计算对复杂结构的气动噪声仍存在挑战[12],近场噪声分离方法开始获得关注[13-14]。转向架区域作为气动噪声的源区,近场包含复杂的湍流流动,同时作为空气动力声源,向周围辐射声波,产生声压脉动。如何将近场的湍流和声学量区分,对理解噪声机理和降低气动噪声具有重要价值。
本文首先对我国高速列车和谐号、标准动车组的转向架舱尺寸进行统计,建立了高速列车转向架区域气动噪声研究模型。之后通过风洞实验的方法,对高速列车转向架区域模型进行风洞气动噪声实验研究。采用湍流和气动声学标度律分析的方法,来区分舱内近场湍流脉动和声压的主要频率范围,分析转向架区域气动噪声源、不同形式转向架气动噪声的特性,以及舱内压力分布。研究结果为理解转向架区域气动噪声源特性及降噪控制提供了理论和数据支撑。
1 转向架区域气动噪声研究模型 1.1 我国高速列车转向架舱几何尺寸统计分析高速列车转向架区域由转向架舱和转向架组成,转向架包含动力和拖车转向架两种形式。由于结构功能和气动减阻需要,我国高速列车转向架主体结构位于转向架舱所围成的空腔内,仅有轮对下缘和动力电机下缘局部处于车体底部高度下。因此,单个转向架区域可以看作包含复杂结构的近地空腔流动和气动噪声问题,其中近地空腔流动和气动噪声特性与空腔的长度(l)、宽度(w)、深度(d)、离地间隙(g)和来流条件有关。
对我国和谐号和复兴号高速列车的转向架舱几何尺寸进行统计分析。在统计方法上,由于车头流线型结构,我国高速列车头、尾车第一组转向架区域结构与其余转向架舱结构有差别,转向架舱空腔为非规则矩形,舱前部宽度略小于后部。在统计分析时,头车第一组转向架的宽度定义为舱后部宽度。头、尾车第二组转向架的舱结构尺寸和所有中间车转向架舱相同,在统计时均称为中间车转向架舱。离地间隙为转向架舱底部到无砟轨道地面的高度。CRH2、CRH3、CRH380A、CRH380B和标准动车组5种车型的转向架舱尺寸如表1、表2所示。
| 表 1 我国高速列车头、尾车第一组转向架舱几何尺寸统计表 Table 1 Geometry size statistics of the first bogie section of the head and tail cars of high-speed trains in China |
|
|
以上5种型号的高速列车转向架舱深度均在0.8 ~0.84 m,变化范围较小,因此以其作为无量纲化的基准,得到转向架舱的长深比(l/d)、宽深比(w/d)和离地间隙深度比(g/d)。由表1、表2可知,头、尾车第一组转向架舱的长深比为4.8~5.9,宽深比为3.3~4.1,离地间隙深度比为0.5。除头、尾车第一组转向架舱外,其他中间转向架舱的长深比为4.8~5.6,宽深比为3.4~4.1,离地间隙深度比为 0.5。综上,我国高速列车转向架舱为长∶宽∶深度比在5∶4∶1左右、离地间隙深度比为0.5的三维近地空腔。
| 表 2 我国高速列车中间车转向架舱几何尺寸统计表 Table 2 Geometry size statistics of the bogie section of the middle cars of high-speed trains in China |
|
|
本文研究相同来流条件下转向架区域舱内气动噪声特性。根据1.1节的统计结果,建立了1∶20的转向架区域气动噪声研究模型。模型总长度500 mm,总宽度160 mm,总高度60 mm,头部和尾部采用流线型以模拟高速列车周围的流场结构。转向架舱的长度、宽度、深度分别为200 mm、160 mm和40 mm,长宽深比(l∶w∶d)为5∶4∶1,转向架舱前缘距离模型头部鼻尖150 mm。模型底部与地面间的距离20 mm,离地间隙深度比(g/d)为0.5。两侧裙板为全覆盖形式,裙板厚度2 mm。
转向架为简化的动力和拖车转向架。动力转向架(MB)包含轮对、构架、齿轮箱、动力电机等主要结构,拖车转向架(TB)包含轮对、构架、轴箱、制动等主要结构,几何模型如图1所示。

|
图 1 转向架区域气动噪声研究模型 Fig.1 Models for the aerodynamics noise research of high-speed train bogie sections |
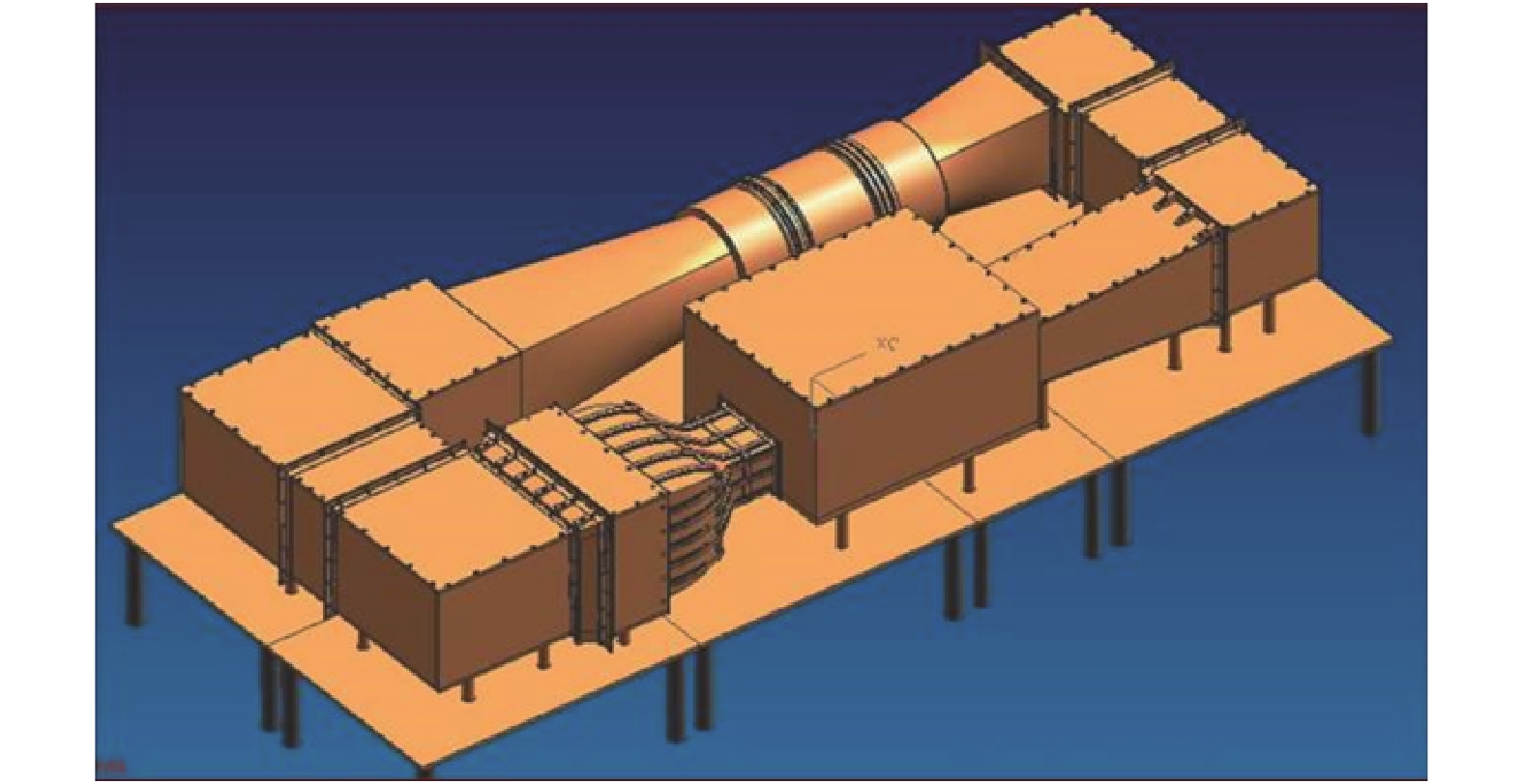
风洞实验在同济大学喷口面积为0.4 m×0.3 m的开口式回流风洞中进行。该开口式风洞包含风机、稳定段、收缩段、试验段、扩散段等组成,是一座空气动力学风洞,轮廓如图2所示。其中试验段尺寸长、宽和高为1.5 m×1.2 m×0.8 m,,喷口自由来流的湍流强度为0.38%,喷口最大风速可达45 m/s,轴向静压系数梯度小于0.005/m。
|
图 2 3/4开口式回流风洞 Fig.2 3/4 open jet wind tunnel |
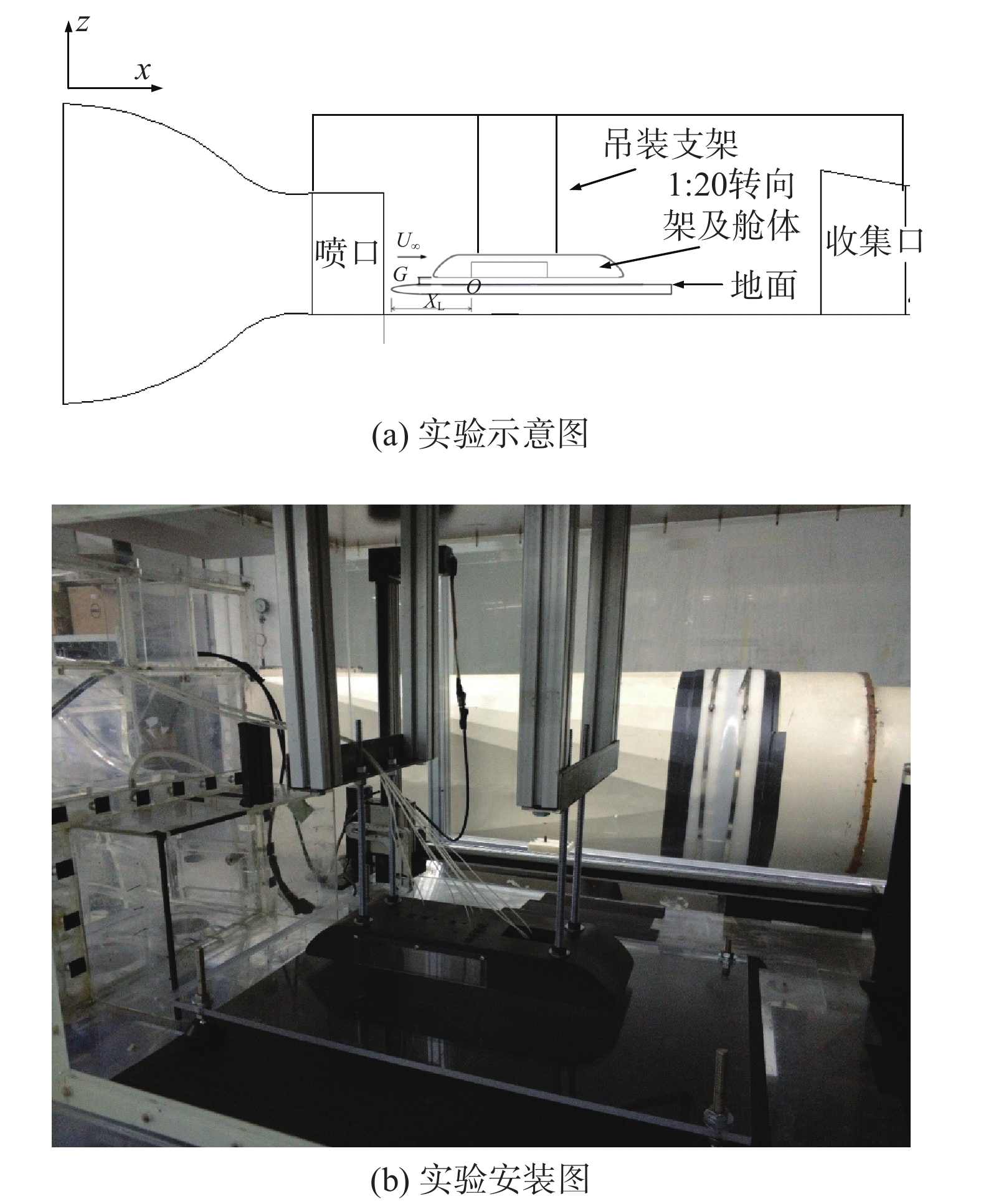
转向架舱体、动力和拖车转向架为ABS工程塑料加工而成。为了避免地面支撑对近转向架舱内流动和气动噪声的干扰,采用4根铝型材吊架和螺纹杆吊装在试验段顶部的支撑方式。为了减小模型受到的试验段底面边界层的影响,单独布置支撑地板,其前缘使用椭圆曲线进行平滑过渡,椭圆形曲线长轴与短轴比为8∶1,基本结构如图3(a)所示。转向架和转向架舱之间使用薄型铷铁硼磁铁进行连接,具有稳固、安装快捷不易脱落的特点。铝型吊架和地板支撑均位于喷口射流剪切层外,以减小气流与支撑之间的相互干扰,实物安装如图3(b)所示。
|
图 3 风洞实验布置示意及安装图 Fig.3 Wind tunnel test layout and setup |
实验模型的阻塞比为8%,满足开口式风洞试验阻塞比要求。在实验时,风洞喷口速度为:25 m/s、30 m/s、35 m/s、40 m/s,以转向架舱的长度l为参考长度,对应的雷诺数范围为3.6×105~5.3×105。
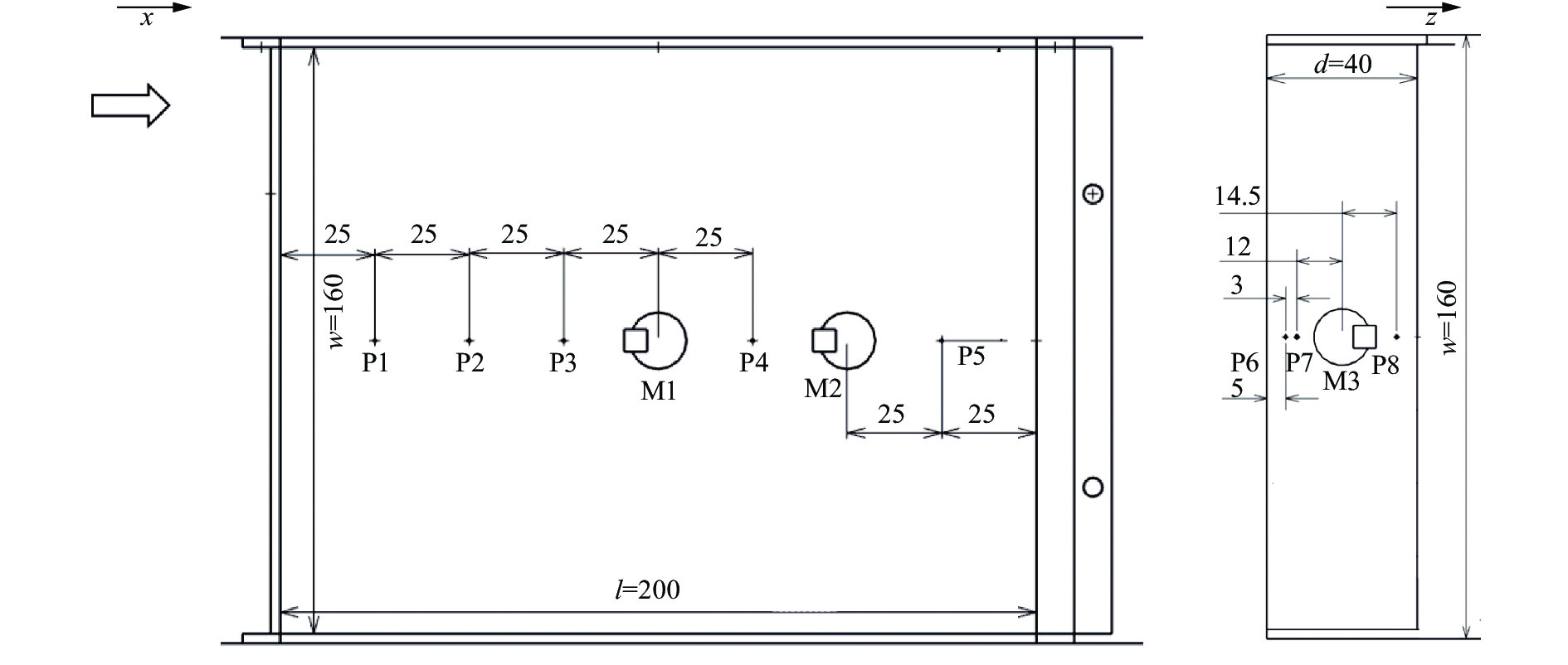
2.2 实验测量及数据处理为测量转向架舱内的近场气动噪声信号,在如图4所示的位置布置3个G.R.A.S.表面压力型传声器,预埋式安装,编号M1~M3,坐标原点位于转向架舱顶部前缘中心位置,其中M1、M2位于分别位于转向架舱顶板中心线流向位置x = 0.5l、0.75l位置,M3位于舱后壁垂向高度z = −0.5d位置。传声器频率响应范围为10 Hz~20 kHz,动态范围为30~136 dB。由于测点布置在舱内非定常流动影响区域,实验测量得到的信号包含声压脉动(真声)和湍流压力脉动(伪声),得到的近场噪声声压级比仅考虑声压脉动偏高。
|
图 4 压力和噪声测点位置(单位:mm) Fig.4 Locations of pressure and noise measurement points(unit: mm) |
实验时声学采样频率为48 kHz,采样时间10 s。使用Head Acoustic软件进行信号的采集处理,开口式风洞在50 Hz以下低频能量较大,对噪声信号均使用50 Hz的高通滤波,加汉宁窗函数,混叠率50%。对测量得到的时域信号进行快速傅里叶变换得到各频带和总声压级,如公式(1):
| $ {\text{SPL}} = 10\;{\text{l}}{{\text{g}}}\;\frac{{p{'^2}}}{{p_{{\text{ref}}}^2}} $ | (1) |
其中,pref = 2×10−5Pa为参考声压,数据处理时频率分辨率为1.46 Hz。
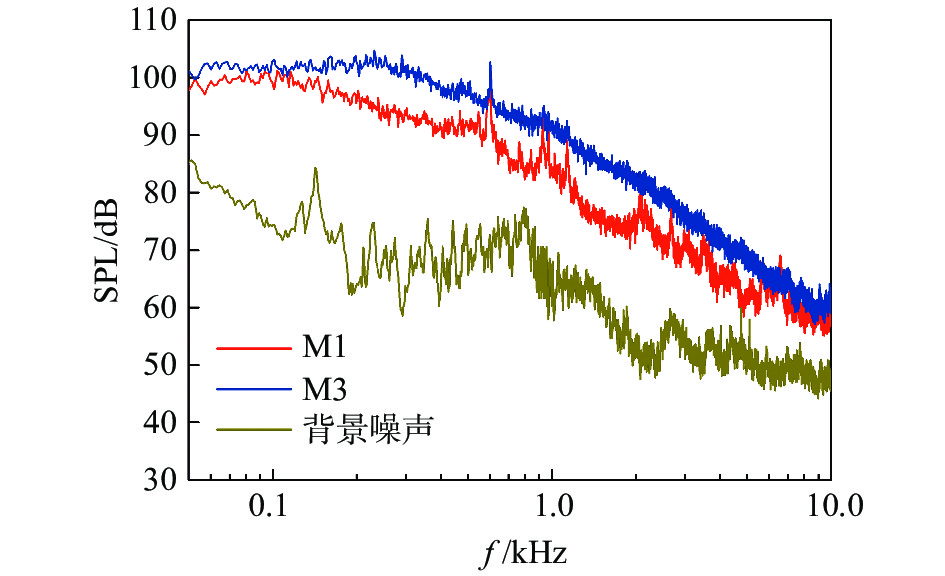
测量风洞试验段内背景噪声和带有动力转向架的模型舱内噪声总声压级和频谱,在喷口风速为从25 m/s、30 m/s、35 m/s和 40 m/s的工况下,背景噪声分别为91.4 dB、97.7 dB、104.7 dB和105 dB,M1测点的总声压级分别为108.0 dB、112.3 dB、116.0 dB和120.4 dB,各风速下差异在10 dB以上。测点M1、M3在风速40 m/s工况下的时频谱如图5所示,各个频段下舱内噪声与背景噪声差异均在6 dB以上。
|
图 5 背景噪声和舱内噪声频谱 Fig.5 Background and bogie section noise spectra |
为了测量转向架舱内的压力,沿转向架舱内顶板处中心线方向分布5个测压点P1~P5,转向架舱后壁中心线处分布3个测压点P6~P8,共计8个静压测点,分布具体位置如图4所示,使用Scanivalve 电子压力扫描阀MPS4264进行测量,采样频率850 Hz,采样时间10 s。将扫描得到的瞬态压力信号时均化处理得到平均静压数据,并计算压力系数和脉动压力级,计算公式如下:
| $ {C_p} = \frac{{p - {p_0}}}{{0.5\rho {v^2}}} $ | (2) |
| $ {\text{PFL}} = 10\;{\text{l}}{{\text{g}}}\;\frac{{p{'^2}}}{{p_{{\text{ref}}}^{\text{2}}}} $ | (3) |
其中,Cp为压力系数,p为测点平均静压,
转向架区域的非定常流动在近场产生两种脉动:1)湍流脉动压力,即伪声;2)声学压力脉动,即声波。对于低马赫数的气动声学问题,湍流压力和声学压力具有3个明显的差异:能量的差异、传播能力的差异和波数的差异。通常湍流脉动压力占流体的大部分能量,声学压力占极少部分。从传播能力的角度,前者以当地对流速度传播,后者以声速叠加对流速度向周围及远场传播。从波数的角度,声波在大部分频率范围与板件弯曲波的波数接近,而湍流压力的波数仅在低频区域和板件的弯曲波波数接近[15],对于列车车内噪声,近场声波具有更高的传递效率[16]。
近场测点包含湍流脉动压力和声学压力。根据伯努利方程和涡动力学理论,速度在空间的不均匀分布、分离旋涡中能量的耗散均会在引起压力在时间和空间的非均匀分布,形成压力脉动。湍流脉动压力级随速度的3~4次方增加,边界层、逆压梯度下的曲面、分离流动等不同流动结构,标度律存在差异[17]。湍流脉动的标度律由公式(4)计算得到:
| $ {\alpha _i} = \frac{{{\text{PF}}{{\text{L}}_i} - {\text{PF}}{{\text{L}}_0}}}{{10\;{\text{l}}{{\text{g}}}\;({{{v_i}} \mathord{\left/ {\vphantom {{{v_i}} {{v_0}}}} \right. } {{v_0}}})}} $ | (4) |
式中,基准风速v0=25 m/s,PFLi为更高风速下测点的湍流脉动压力级,PFL0为25 m/s时的湍流压力脉动级,
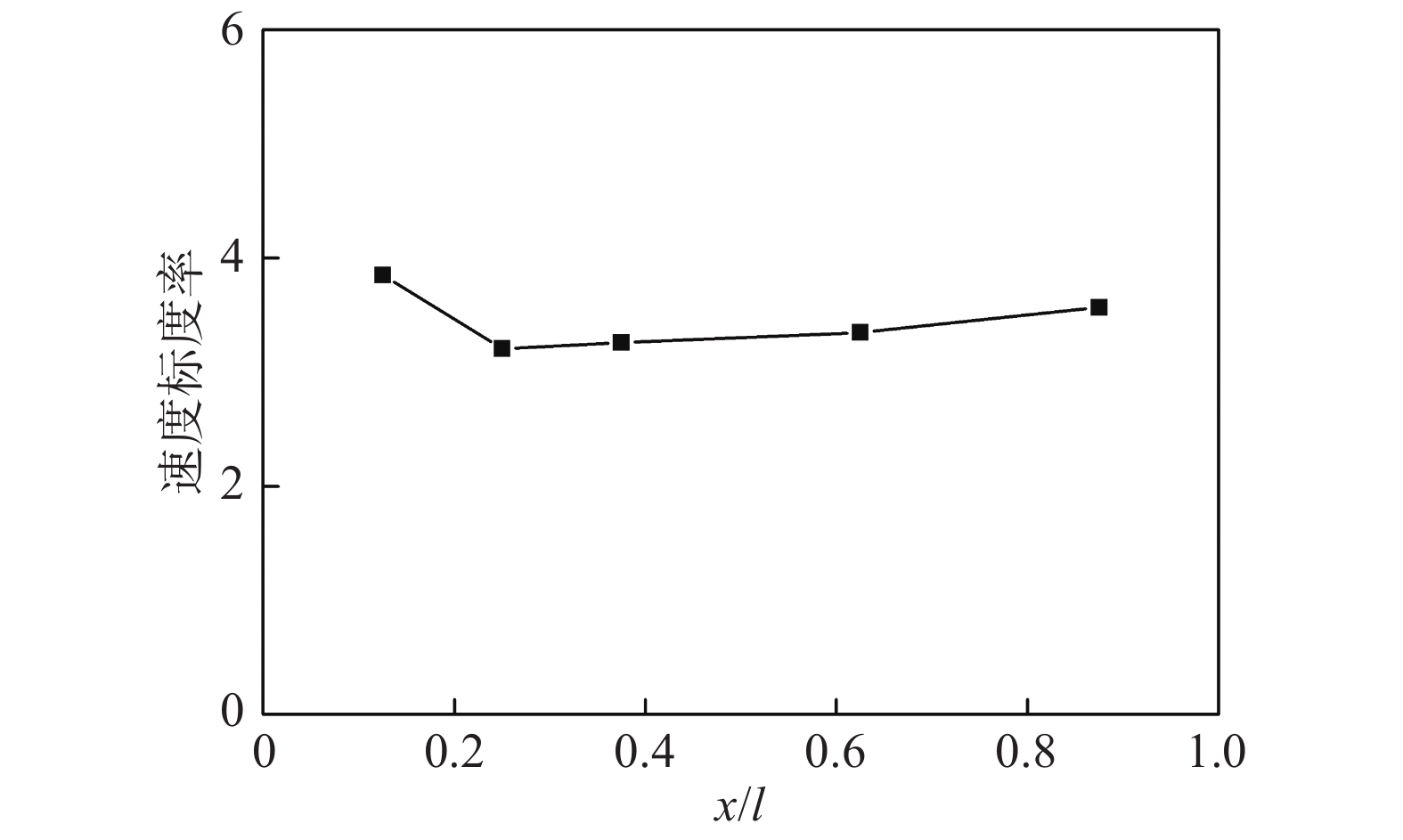
根据公式(4),计算得到v = 30 m/s、35 m/s和40 m/s工况下的标度律,后求其平均值得到该速度范围内的标度律。拖车转向架舱对舱顶部压力测点P1~P5的湍流脉动功率级进行速度标度律分析,可知其随速度的3.2~3.9次方增加,如图6所示。对于亚声速空腔流动,文献[18]采用动态压力传感器测量腔内压力脉动,能量近似随速度3.6次方增加,标度律结果与本文接近。根据Lighthill[19]和Curle[20]的气动声学声源类比理论,转向架区域的气动噪声,是气流与固体表面相互作用产生的脉动力偶极子声源和空间剪切应力的四极子声源,不包含脉动质量的单极子声源。偶极子声源和四极子声源的能量分别与速度的6次方和8次方成正比。
|
图 6 拖车转向架舱内湍流脉动压力功率级标度律 Fig.6 Scaling law of the turbulent pressure fluctuation level inside the trailer bogie cavity |
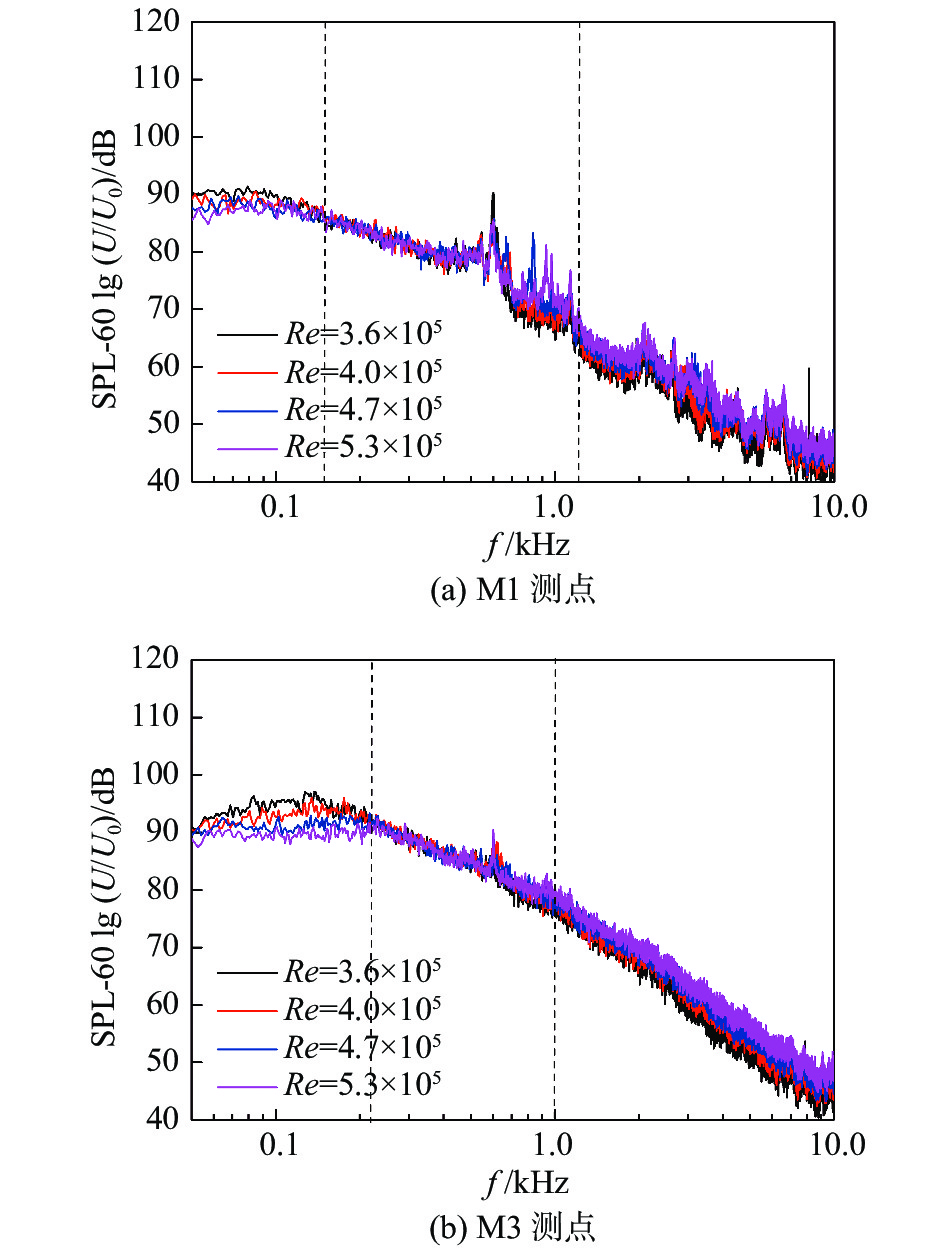
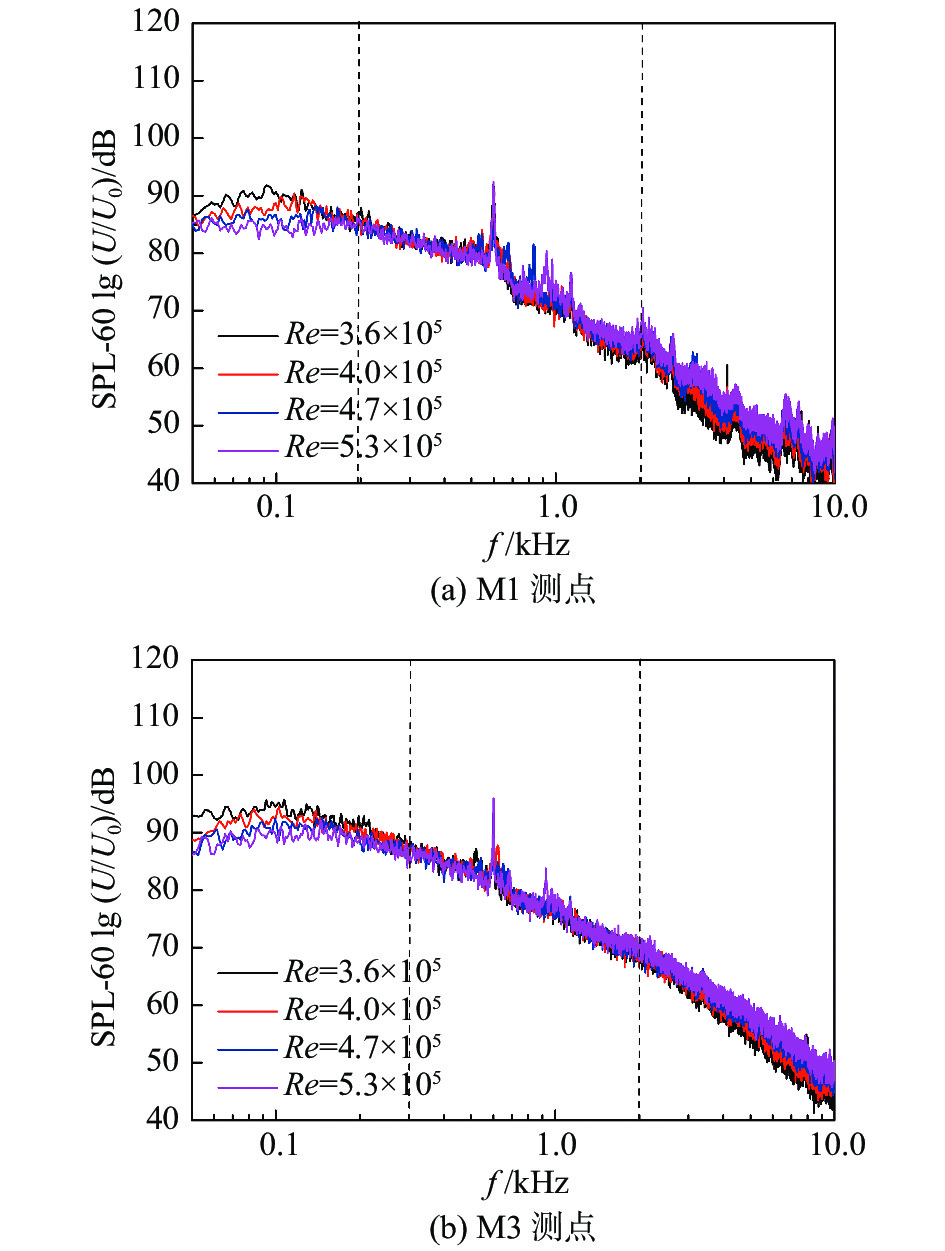
采用6次方率对不同雷诺数下转向架舱内M1、M3测点的噪声频谱进行标度律分析,归一化的动力、拖车转向架舱频谱分别如图7、图8所示,v0 = 25 m/s。可以看出,对于动力转向架舱M1测点,除轮对产生的噪声外,频谱在120~1200 Hz之间重合度较好,噪声能量近似随速度6次方增加,M3测点,在200~1000 Hz噪声能量近似随速度6次方增加。拖车转向架舱M1测点除轮对产生的噪声,频谱在200 ~2000 Hz之间重合度较好,噪声能量近似随速度6次方增加,M3测点,在300~2000 Hz噪声能量近似随速度6次方增加。
|
图 7 动力转向架舱内气动噪声标度律分析 Fig.7 Scaling law analysis of the aerodynamic noise inside the motor bogie cavity |
|
图 8 拖车转向架舱内噪声标度律分析 Fig.8 Scaling law analysis of the aerodynamic noise inside the trailer bogie cavity |
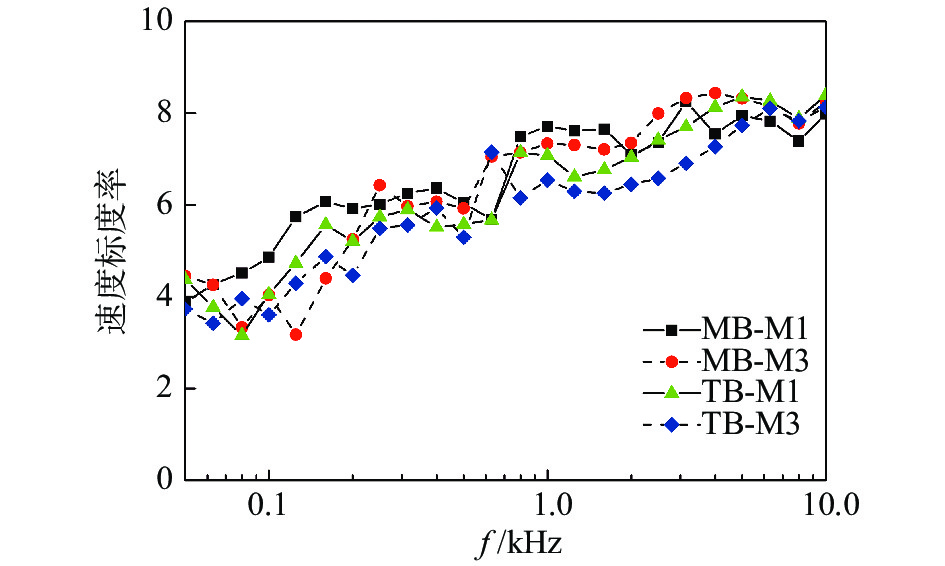
以雷诺数3.6×105的工况为基准,对动力和拖车转向架舱内M1、M3测点近场噪声的1/3倍频程谱进行速度标度律分析,如图9所示。对于舱顶部M1测点,在中心频率100 Hz以下时,近场噪声能量近似随速度的3~4次方增加,根据湍流脉动压力和声压的标度规律,可知其能量主要以湍流脉动压力为主。在中心频率125~800 Hz之间,近场噪声能量随速度的6次方增加,在1000 Hz以上随速度的7~8次方增加,能量均以声压为主。舱后壁M3测点,在中心频率200 Hz以下时,近场噪声能量近似随速度的3~4次方增加,能量以湍流脉动压力为主。在中心频率250~1600 Hz之间,近场噪声能量随速度的6次方增加,在2000 Hz以上随速度的7~8次方增加,能量均以声压为主。
|
图 9 舱内近场噪声1/3倍频程谱标度律分析 Fig.9 Scaling law analysis of the near-field 1/3 Octave band noise inside the bogie cavity |
以上分析表明,转向架舱内近场的气动噪声标度律分析可以区分湍流脉动压力和声压,其分界线频率,转向架舱后壁高于舱顶部。
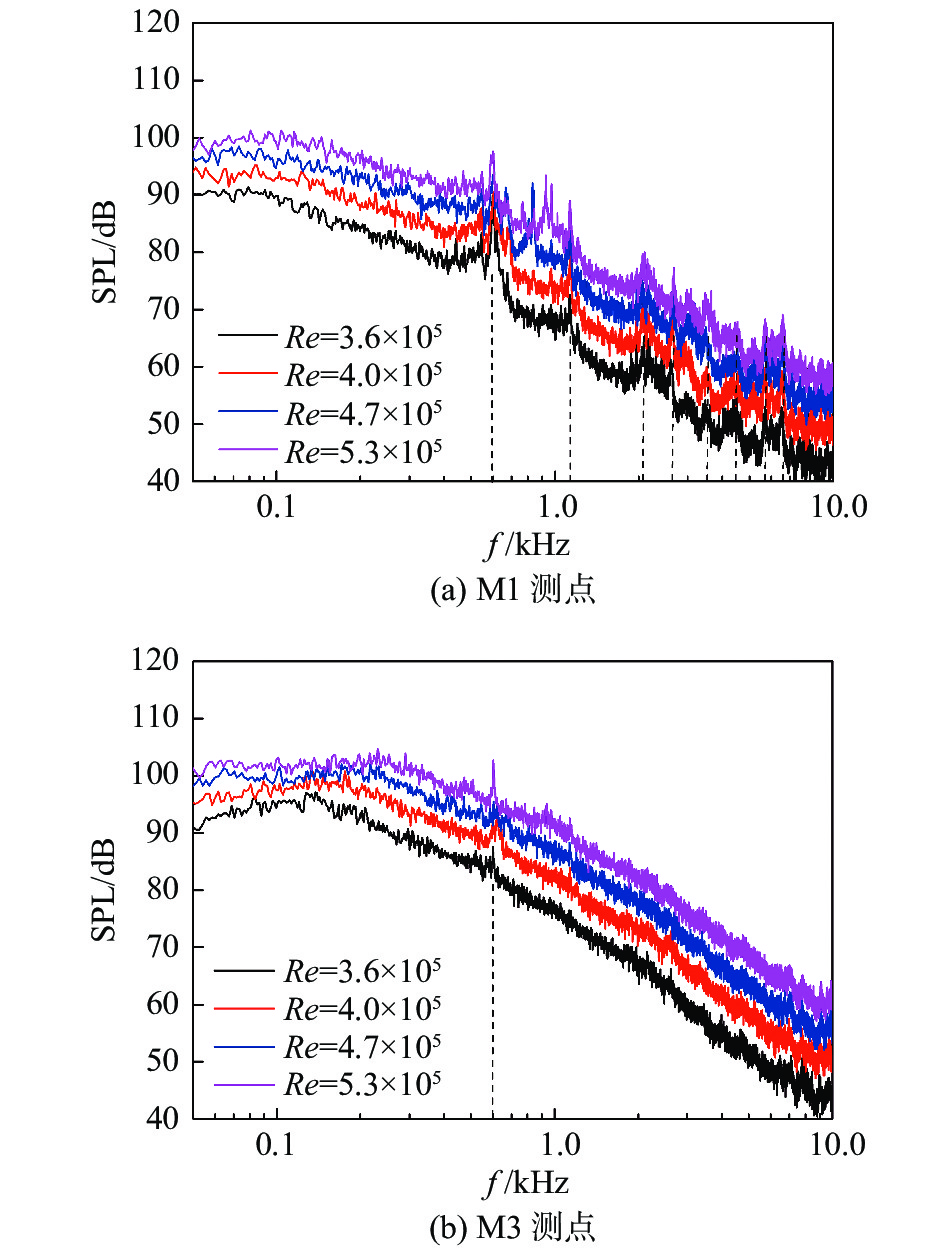
3.2 雷诺数效应及转向架形式对气动噪声影响图10给出了不同雷诺数下,动力转向架舱顶部的M1,舱后壁M3传声器的噪声频谱曲线图,频率范围50 Hz~10 kHz,本节讨论300 Hz以上的声学特性。转向架舱顶部M1的噪声频谱为具有多个峰值的宽频带噪声。其中f = 597 Hz、1136 Hz、2100 Hz、2684 Hz、3492 Hz、4523 Hz、6610 Hz附近的峰值,峰值频率不随雷诺数变化而变化,噪声能量随雷诺数增大而增加,如图10中标记线所示。在雷诺数为4.7×105、5.3×105的两个工况下,还分别出现f = 832 Hz、925 Hz两个峰值,该峰值表现为随雷诺数增加而增大。对于宽频带噪声,其能量随雷诺数增加而增大。转向架舱后壁M3的噪声频谱为具有f = 597 Hz单一峰值的宽频带噪声,该频率与M1测点的峰值频率相同,且幅值接近。转向架舱后壁受到舱底部气流的冲击,M3的宽频带噪声能量大于M1测点,对比M3和M1测点的噪声幅值,可知M3测点1000 Hz以上高频峰值被宽频噪声掩蔽。
|
图 10 动力转向架舱内气动噪声频谱 Fig.10 Noise spectra inside the motor bogie cavity |
转向架区域气动噪声为包含复杂结构的近地空腔流动噪声问题,转向架结构大部分位于转向架舱内,轮对下部受到底部气流的直接冲击。气流冲击轮对,会在轮对前缘两侧产生分离和强烈的脉动压力,进而辐射噪声,实验测量得到随雷诺数增加而增大的f = 823 Hz、925 Hz两个峰值,风速增加1.1倍,峰值频率增大1.1倍,与文献[21]数值计算得到单独轮对峰值频率与速度呈线性关系结论一致,推断该峰值噪声为气流冲击轮对下部导致。雷诺数3.6×105、4.0×105两个工况未看到明显峰值噪声,根据f = 823 Hz、925 Hz及其对应风速,得到无量纲频率(St = fD/v,D = 0.12 m为车轮直径、v为风速)St = 2.8,计算v = 25 m/s和30 m/s工况下其绝对频率分别为583 Hz和700 Hz,可知其在该频率被更高能量的峰值和宽频噪声所掩蔽。
转向架舱内气动噪声也是底部气流作为激励源,与复杂结构近地腔体系统共同作用的结果。参考空腔流动流声耦合反馈的Rossiter模型,绝对峰值频率随风速的增加而增大[22],不符合本次实验观测得到的规律。转向架舱区域作为一个复杂的声学系统,随雷诺数增加声学系统噪声的峰值频率固定,推断这些峰值频率噪声是激励该声学系统的声共振导致。
由于空腔的长宽比为5∶4,剪切层展向的宽度与流向长度为相同量级,剪切层会产生宽频的剪切层噪声源,在向后部发展过程中,由于剪切层的厚度增加,同时离地间隙较小,剪切层会与地面发生相互作用,最终撞击舱后缘产生近场宽频噪声。
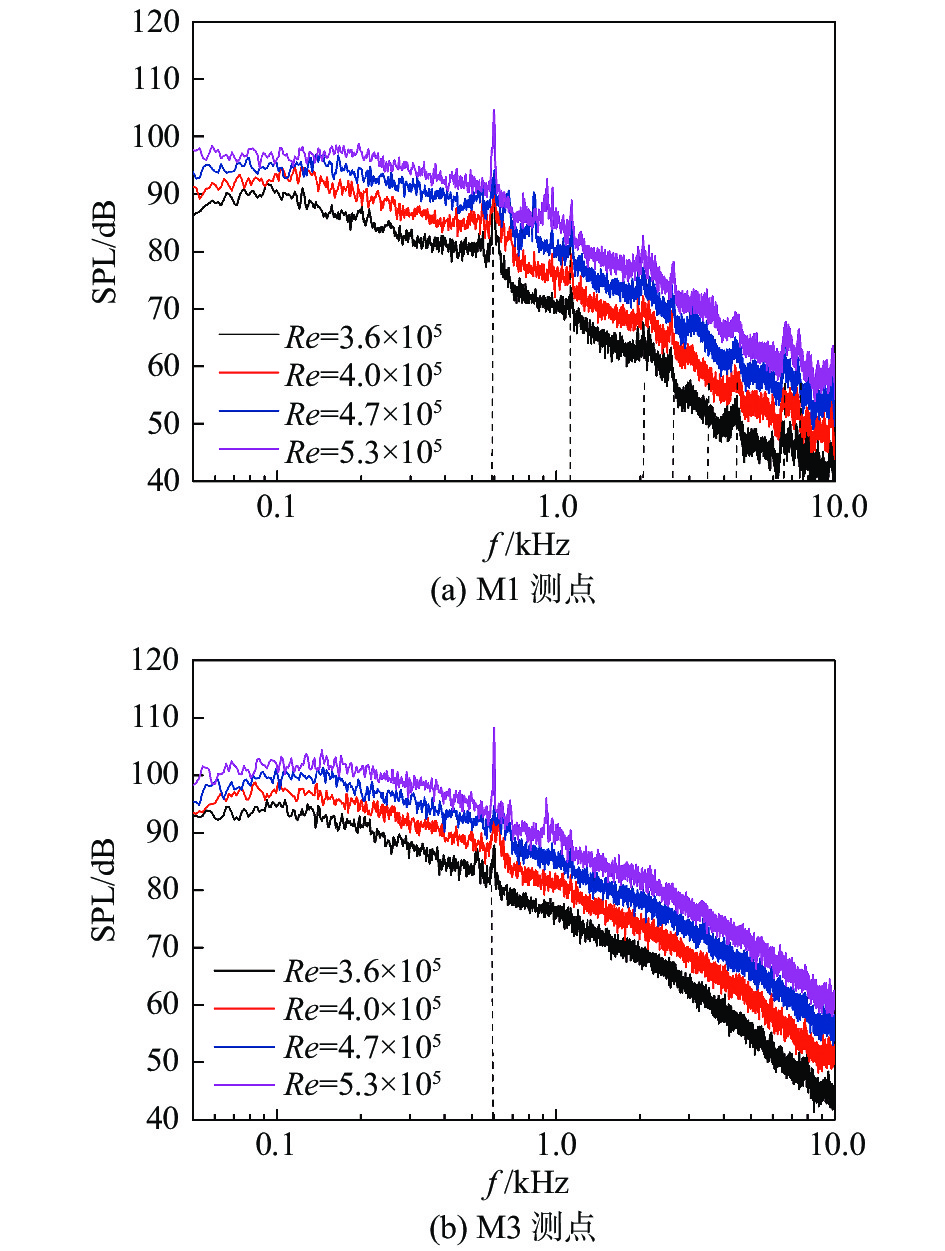
图11给出不同雷诺数下,拖车转向架舱顶部的M1,舱后壁M3传声器的噪声频谱曲线图。可知,拖车转向架M1的舱内噪声频谱为具有多个峰值的宽频带噪声,M3测点的噪声频谱为具有单一峰值的宽频带噪声,频谱特征与动力转向架一致。
|
图 11 拖车转向架舱内气动噪声频谱 Fig.11 Noise spectra inside the trailer bogie cavity |
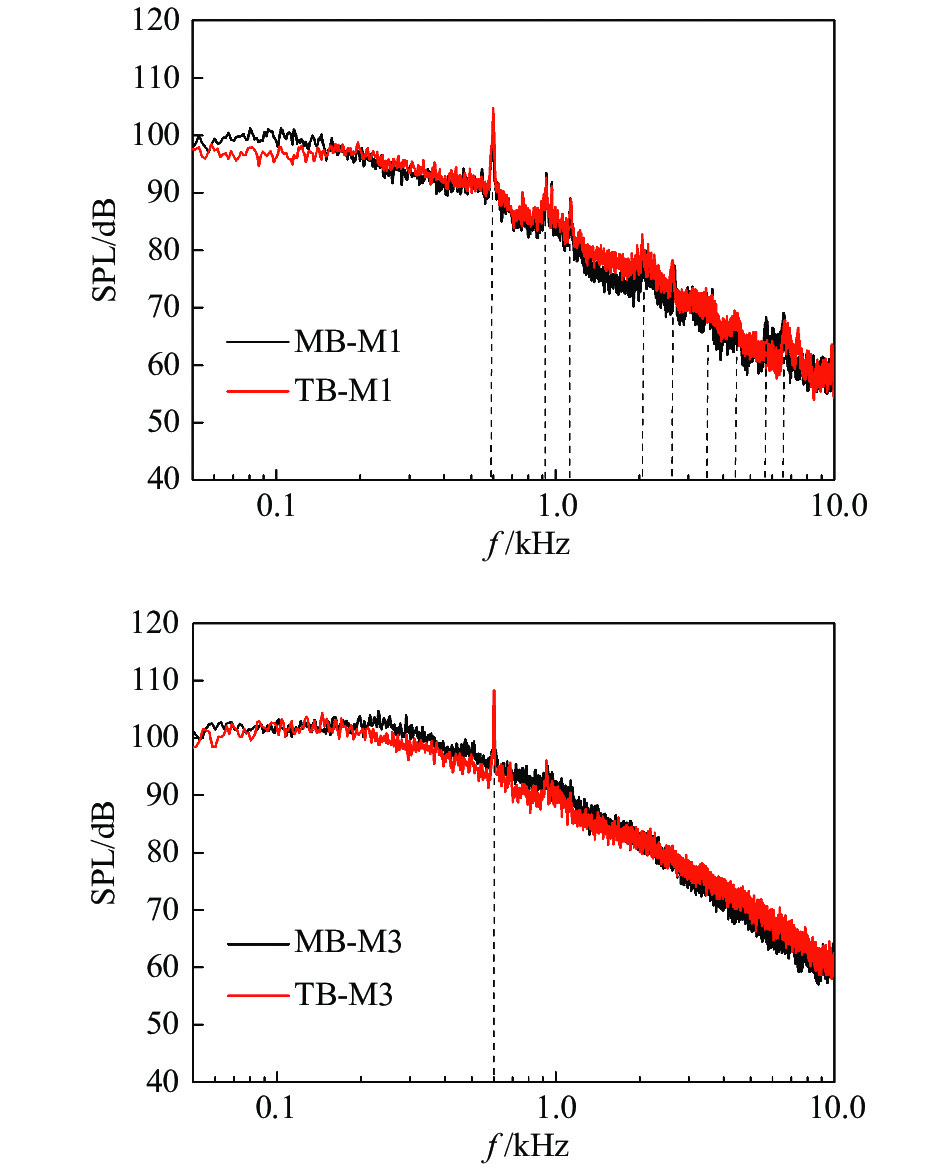
图12给出两种形式转向架的舱内M1、M3噪声在雷诺数5.3×105时的频谱对比。可知,转向架舱几何尺寸和来流条件相同时,动力和拖车转向架的舱内M1、M3测点噪声峰值频率相同。由转向架舱内噪声随雷诺数变化的分析可知,f = 925 Hz峰值为轮对产生。以上峰值噪声的频率与转向架舱尺寸、轮对尺寸有关,不受转向架形式的影响。由图12还可以看出,在M1测点,动力转向架1200~2500 Hz的宽频噪声能量小于拖车转向架,在M3测点,动力转向架宽频带噪声在300 ~1000 Hz大于拖车转向架,在4000~8000 Hz大于拖车转向架,表明宽频带噪声幅值受转向架形式影响。
|
图 12 Re= 5.3×105不同形式转向架舱内气动噪声频谱 Fig.12 Noise spectra inside different bogie cavities at Re= 5.3×105 |
不同雷诺数下动力转向架舱顶部和后壁静压分布如图13所示。在舱顶部上游区域(0 < x/l < 0.6),舱顶部静压小于来流静压,静压系数均位于−0.05~−0.06,说明该区域流场压力梯度较小,在舱顶下游区域 x/l > 0.6时,静压系数逐步升高。底部气流冲击舱后壁,可知舱后壁明显增高,顶部静压系数为0.05,舱下部静压系数为0.2,舱后壁静压增大并使得舱顶下游区域静压系数显著升高。随雷诺数的增加,动力转向架舱顶和后壁压力系数不发生变化。

|
图 13 动力转向架舱内静压系数分布 Fig.13 Static pressure coefficient inside the motor bogie cavity |
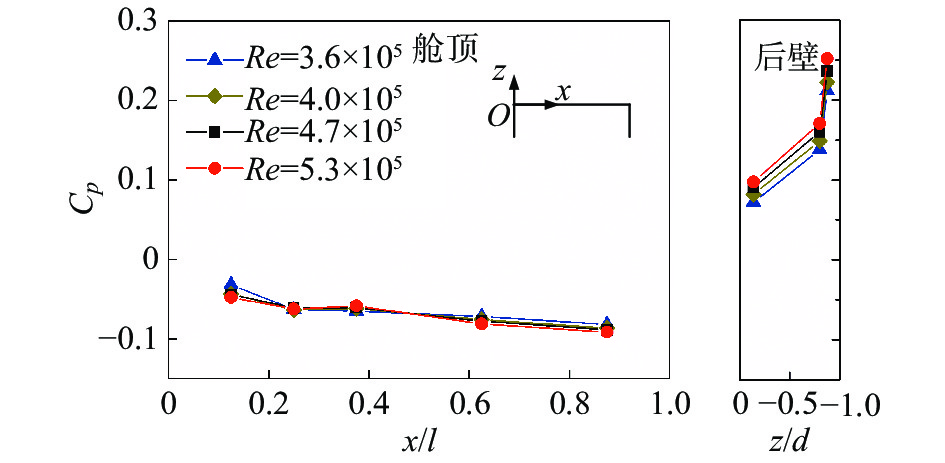
拖车转向架舱内的静压系数分布如图14所示。舱顶前部静压系数为−0.04,拖车与动力转向架舱前部静压系数接近,之后沿主流方向不断降低,在x/l = 0.875位置降到−0.09,不随雷诺数变化。舱后壁顶部静压系数为0.09左右,可知在拖车转向架舱后部(x/l > 0.875)有着更大的压力梯度,流场结构复杂。后壁下部静压系数随雷诺数增加略有增大,在雷诺数5.3×10 5时为0.25,高于动力转向架舱后壁底部的0.20,是动力电机下部处于底部气流直接冲击下,降低了气流速度进而减小来流动压。
|
图 14 拖车转向架舱内静压系数分布 Fig.14 Static pressure coefficient inside the trailer bogie cavity |
对我国高速列车和谐号、标准动车组的转向架舱尺寸进行统计,结果表明我头、尾车和中间车转向架区域特征为:长∶宽∶深度比为5∶4∶1左右、离地间隙深度比为0.5的含复杂结构三维近地空腔,并据此建立了高速列车转向架区域气动噪声研究模型。采用风洞实验方法,对动力、拖车转向架区域气动噪声和舱内压力分布特性进行研究。通过分析可以发现:
1)通过转向架舱内近场的气动噪声测试及标度律分析,可以区分湍流脉动压力和声压。标度律分析表明,舱内的湍流脉动压力能量随速度的3.2~3.9次方增加,声压级随速度的6~8次方增加,湍流压力与声压的频率分界线,转向架舱后壁高于舱顶部。由于声波在大部分频率范围与板件弯曲波的波数接近,空气声传递对车内噪声具有更高的效率,在车内降噪控制时需要引起注意。
2)高速列车转向架区域的气动噪声为具有多个峰值的宽频带噪声。峰值频率不随雷诺数变化的597 Hz、1136 Hz、2100 Hz、2684 Hz、3492 Hz、4523 Hz、6610 Hz峰值噪声,是声共振导致,1个峰值频率随雷诺数增加而频率增大的噪声信号,为气流冲击轮对下部导致;动力和拖车转向架区域的峰值噪声频率与舱、轮对尺寸有关,转向架形式影响舱内宽频带噪声的幅值。
3)动力转向架和拖车转向架舱顶部的压力系数不随雷诺数变化,拖车转向架舱后部(x/l > 0.875)较动力转向架舱有更大的压力梯度,该区域流场结构复杂。
综上,高速列车转向架区域气动噪声控制,可以从声共振峰值噪声和宽频带噪声两个方向深入开展;针对大尺寸模型,进一步给出其舱内湍流压力与声压的频率分界线,对于指导实车的车内噪声控制、车体隔声降噪设计有重要意义。
| [1] |
丁叁叁, 陈大伟, 刘加利. 中国高速列车研发与展望[J]. 力学学报, 2021, 53(1): 35-50. DING S S, CHEN D W, LIU J L. Research, development and prospect of China high-speed train[J]. Chinese Journal of Theoretical and Applied Mechanics, 2021, 53(1): 35-50. (in Chinese) |
| [2] |
HE B, XIAO X B, ZHOU Q, et al. Investigation into external noise of a high-speed train at different speeds[J]. Journal of Zhejiang University SCIENCE A (Applied Physics & Engineering), 2014, 15(12): 1019-1033. DOI:10.1631/jzus.A1400307 |
| [3] |
SHENG X, CHENG G, THOMPSON D. Modelling wheel/rail rolling noise for a high-speed train running along an infinitely long periodic slab track[J]. The Journal of the Acoustical Society of America, 2020, 148(1): 174. DOI:10.1121/10.0001566 |
| [4] |
YAMAZAKI N, KITAGAWA T, UDA T, et al. Evaluation method for aerodynamic noise generated from the lower part of cars in consideration of the characteristics of under-floor flows on shinkansen trains[J]. Quarterly Report of RTRI, 2016, 57(1): 61-68. DOI:10.2219/rtriqr.57.1_61 |
| [5] |
袁旻忞, Anne Shen, 鲁帆, 等. 高速列车运行工况下噪声传递路径及声源贡献量分析[J]. 振动与冲击, 2013, 32(21): 189-196. YUAN M M, SHEN A, LU F, et al. Operational transfer path analysis and noise sources contribution for China railway high-speed(CRH)[J]. Journal of Vibration and Shock, 2013, 32(21): 189-196. (in Chinese) |
| [6] |
FRÉMION N, VINCENT N, JACOB M, et al. Aerodynamic noise radiated by the intercoach spacing and the bogie of a high-speed train[J]. Journal of Sound and Vibration, 2000, 231(3): 577-593. DOI:10.1006/jsvi.1999.2546 |
| [7] |
高阳, 王毅刚, 王金田, 等. 声学风洞中的高速列车模型气动噪声试验研究[J]. 声学技术, 2013, 32(6): 506-510. GAO Y, WANG Y G, WANG J T, et al. Testing study of aerodynamic noise for high speed train model in aero-acoustic wind tunnel[J]. Technical Acoustics, 2013, 32(6): 506-510. (in Chinese) |
| [8] |
LAUTERBACH A, EHRENFRIED K, LOOSE S, et al. Microphone array wind tunnel measurements of Reynolds number effects in high-speed train aeroacoustics[J]. International Journal of Aeroacoustics, 2012, 11(3-4): 411-446. DOI:10.1260/1475-472x.11.3-4.411 |
| [9] |
LATORRE IGLESIAS E, THOMPSON D J, SMITH M, et al. Anechoic wind tunnel tests on high-speed train bogie aerodynamic noise[J]. International Journal of Rail Transportation, 2017, 5(2): 87-109. DOI:10.1080/23248378.2016.1274685 |
| [10] |
YAMAZAKI N, UDA T, KITAGAWA T, et al. Influence of bogie components on aerodynamic bogie noise generated from shinkansen trains[J]. Quarterly Report of RTRI, 2019, 60(3): 202-207. DOI:10.2219/rtriqr.60.3_202 |
| [11] |
MUELLER T J, PRASAD M G. Aeroacoustic measurements[J]. Applied Mechanics Reviews, 2003, 56(5): B66-B67. DOI:10.1115/1.1584413 |
| [12] |
MINELLI G, YAO H D, ANDERSSON N, et al. An aeroacoustic study of the flow surrounding the front of a simplified ICE3 high-speed train model[J]. Applied Acoustics, 2020, 160: 107125. DOI:10.1016/j.apacoust.2019.107125 |
| [13] |
YUAN H D, YANG Z G, WANG Y G, et al. Experimental analysis of hydrodynamic and acoustic pressure on automotive front side window[J]. Journal of Sound and Vibration, 2020, 476: 115296. DOI:10.1016/j.jsv.2020.115296 |
| [14] |
HE Y Z, WAN R X, LIU Y M, et al. Transmission characteristics and mechanism study of hydrodynamic and acoustic pressure through a side window of DrivAer model based on modal analytical approach[J]. Journal of Sound and Vibration, 2021, 501: 116058. DOI:10.1016/j.jsv.2021.116058 |
| [15] |
LECOQ D, PÉZERAT C, THOMAS J H, et al. Extraction of the acoustic component of a turbulent flow exciting a plate by inverting the vibration problem[J]. Journal of Sound and Vibration, 2014, 333(12): 2505-2519. DOI:10.1016/j.jsv.2014.02.003 |
| [16] |
ZHANG J, XIAO X B, SHENG X Z, et al. Sound source localisation for a high-speed train and its transfer path to interior noise[J]. Chinese Journal of Mechanical Engineering, 2019, 32(1): 1-16. DOI:10.1186/s10033-019-0375-1 |
| [17] |
BLAKE W K. Mechanics of flow-induced sound and vibration: complex flow-structure interactions[EB/OL]. 2017
|
| [18] |
朱幼君. 管道空腔流声耦合振荡及压电振子流动控制技术的研究[D]. 上海: 上海交通大学, 2010. ZHU Y J. Research on acoustic oscillation over the duct cavity and suppression with piezoelectric vibrator[D]. Shanghai: Shanghai Jiaotong University, 2010. (in Chinese) |
| [19] |
LIGHTHILL M J. On sound generated aerodynamically I. General theory[J]. Proceedings of the Royal Society of London Series A Mathematical and Physical Sciences, 1952, 211(1107): 564-587. DOI:10.1098/rspa.1952.0060 |
| [20] |
CURLE N. The influence of solid boundaries upon aerodynamic sound[J]. Proceedings of the Royal Society of London Series A Mathematical and Physical Sciences, 1955, 231(1187): 505-514. DOI:10.1098/rspa.1955.0191 |
| [21] |
ZHU J Y, HU Z W, THOMPSON D J. Flow simulation and aerodynamic noise prediction for a high-speed train wheelset[J]. International Journal of Aeroacoustics, 2014, 13(7-8): 533-552. DOI:10.1260/1475-472x.13.7-8.533 |
| [22] |
ROSSITER J E. Wind tunnel experiments on the flow over rectangular cavities at subsonic and transonic speeds[R]. Aeronautical Research Council, R&M3438, 1964.
|
 2021, Vol. 39
2021, Vol. 39

