0 引　言

数值模拟技术可以替代部分风洞试验建立相应流场的数学模型，在降低实验成本的基础上更便捷地预测流场结果，相应的对数值模型的可信度也有一定的要求。

数值模型中涉及了一系列参数，有的由观测仪器间接计算或直接获得，有的无法测量只能通过经验推导估计。为了提高数学模型可信度使其能正确再现流场变化，有必要结合流场实测数据对参数进行辨识，目前工程上普遍采用优化算法。

优化算法通过建立目标函数表示数值模型的输出与实测数据之间的距离，查找目标函数极小时数值模型中的参数组合，实现参数辨识。水文预报领域中陆续引入了遗传算法^[1-3]、下坡单纯形法^[4]、粒子群算法^[5-6]；气动力领域中广泛应用了最大似然法^[7]。由于最大似然法依赖目标函数梯度以及参数初值的选取，有一定的局限性，张天姣等^[8]也将粒子群算法引入到气动力领域中求解参数辨识问题。优化算法在求解过程中需要对目标函数或目标函数梯度进行大量迭代计算，而目标函数中又包含了流场复杂的数值模型，因此参数辨识过程十分耗时。

随着深度学习的发展，数值模拟与神经网络技术的结合逐渐成为一项研究热点，尤其是在气动力建模领域之中。Miyanawala等^[9]通过卷积神经网络（Convolutional Neural Networks，CNN）对气动载荷实现准确预测。陈海等^[10]利用CNN和翼型图像建立气动模型。王超等^[11]基于参数辨识数据利用人工神经网络建立气动模型。这些研究都表明深度学习应用在气动建模中的潜力。

鉴于上述研究背景，本文考虑用深度学习实现参数辨识，克服传统方法计算量大耗时长这一缺陷。提出利用CNN从数值模拟结果中提取状态时间序列和模型参数之间的映射关系，建立参数辨识模型，这种参数辨识模型可在实际应用中直接通过一段时间的实测数据对一系列数值模型参数进行快速估计。

1 Lorenz63混沌系统 1.1 数值模型

本文使用Lorenz63对提出的参数辨识方案进行具体的实验和讨论。Lorenz63是Lorenz于1963年建立的一个简单的大气对流数学模型^[12]，是混沌系统最早的数值表示。混沌系统是指确定性系统中存在看似随机的不规则运动。混沌的特征在于不确定性，不可重复性和不可预测性。其模式控制方程由非线性系统给出，具体如下：

$\begin{array}{l} \dfrac{{{\rm{d}}x}}{{{\rm{d}}t}} = - \sigma x + \sigma y \\ \dfrac{{{\rm{d}}y}}{{{\rm{d}}t}} = \gamma x - y - xz \\ \dfrac{{{\rm{d}}z}}{{{\rm{d}}t}} = xy - \beta z \end{array} $

(1)

其中， $\sigma $ 、 $\gamma $ 分别表示Prandtl数和Rayleigh数， $\;\beta $ 表示与对流尺度相联系的参数。

实验中采用龙格-库塔数值积分方法求解方程的解 $(x,y,z)$ 。 $x$ 、 $y$ 、 $z$ 在这里就是我们所说的数值模型计算的状态变量。通常使用一个状态矢量来表示当前系统的全部状态变量，即 $x(x,y,z)$ 。

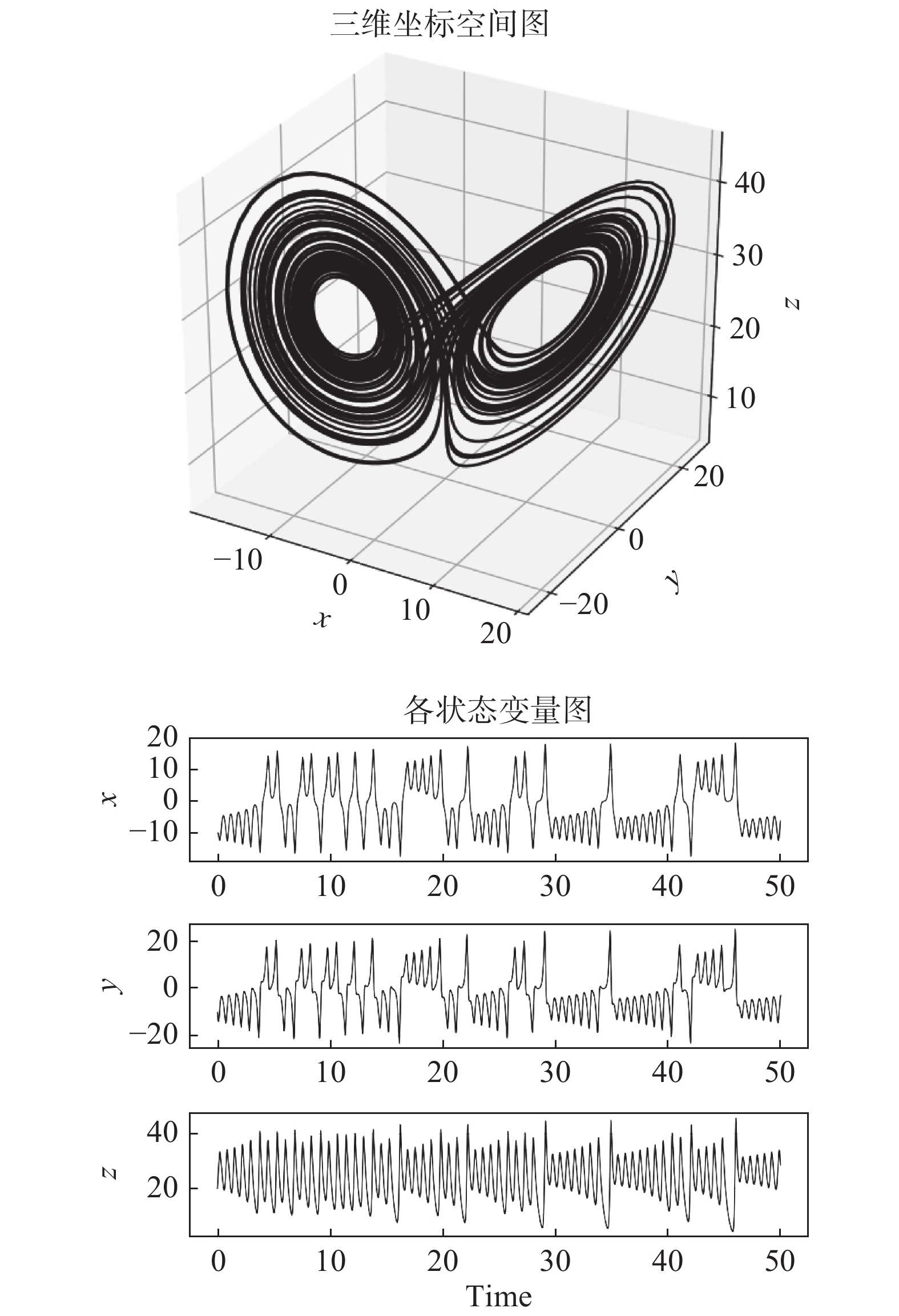
我们使用三维空间表示Lorenz63系统的状态变化，每个维度对应每个状态变量的值，见图1。图1是Lorenz63在参数 $\sigma = 10.0$ 、 $\gamma = 28.0$ 、 $\;\beta = 8/3$ 下的积分结果，积分步长为0.01。参照Lorenz给的原始数据，该系统会在这种参数设置下表现为混沌现象，并且其在其他参数下还会呈现不同的运动状态。

1.2 参数分析

本文讨论的是混沌模式下的Lorenz63系统，根据前人的总结，首先参数 $\gamma $ 要符合条件 $24.0 \leqslant \gamma \leqslant 28.0$ ，且以 $\sigma = 10.0$ 、 $\;\beta = 8/3$ 固定不变为前提。如果改变这两个控制参数，结果不必然。由于本文要实现的是多参数估计，这对于实际工程更有意义，因此只变化一个参数将无法实现任务目标，需要对 $\sigma $ 和 $\;\beta $ 参数的取值范围也进行讨论。

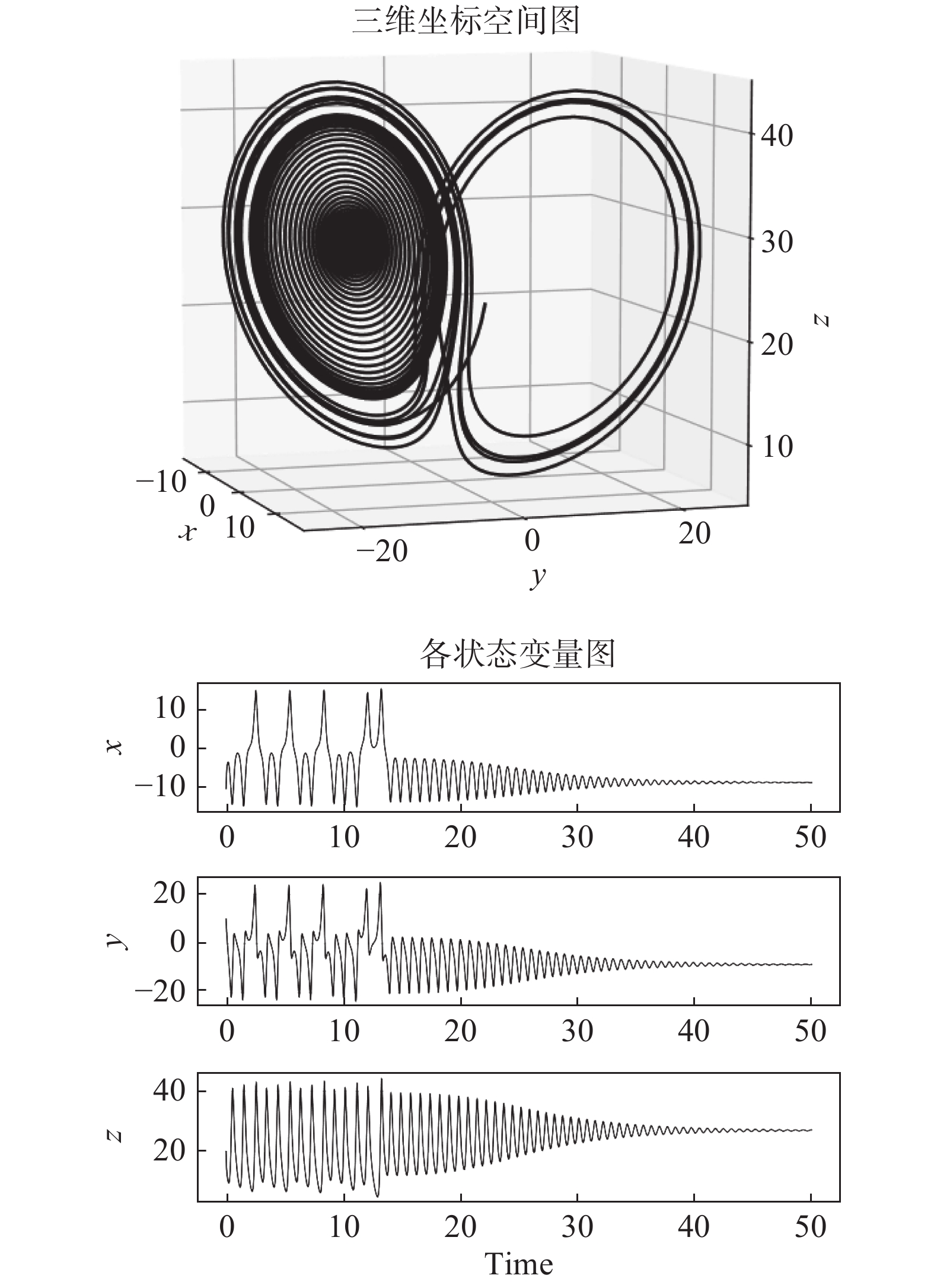
我们可以看Lorenz63在 $\sigma = 4.8$ 、 $\;\beta = 8/3$ 、 $\gamma = 28.0$ 时的结果，见图2。

在该状态的Lorenz63系统状态变量会在刚开始的时间区间中不断震荡然后不断某个点趋近，最后稳定在不动点上。从左图中可以看到系统状态只会在最外圈呈现出蝴蝶吸引子，之后不断收缩到右边的不动点上。这样的物理状态一是和我们需要的混沌模式不一致，二是不符合训练数据的基本要求。我们需要的数据是一小段连续时间步的状态变量，用于输入到CNN中提取运动特征，如果我们输入上述结果的[60,61]之间的状态矢量，那么输入的数据在时间序列上实际是定值，对于神经网络来说，虽然输入的原始特征是一个二维矩阵，但其实只有三个特征值，要单从这三个特征中学习到隐藏的运动特征，并预测三个参数，十分困难，再加上状态变量 $x$ 和 $y$ 很接近，则等于要用神经网络从二个特征值中提取到三个特征。因此，我们需要排除掉会导致这样结果的参数，设置好参数的取值范围。

通过手动实验，我们基本可以确定好三个参数的范围：

$\begin{array}{l} 5.0 \leqslant \sigma \leqslant 15.0 \\ 1.1 \leqslant \beta \leqslant 8/3 \\ 24.0 \leqslant \gamma \leqslant 28.0 \end{array} $

(2)

在上述取值范围下，不同的参数组合还是会导致产生不动点的可能，因此我们对各种参数组合分别进行了Lorenz63数值实验，实验结果见表1，其中区间的选取是手动尝试结果。

2 参数辨识模型

本文的参数辨识模型可以依据多个连续时间步的实测系统状态逆推出流场数值模型的参数。因此，模型的输入数据是状态时间序列，输出数据是参数估计结果。我们用神经网络提取输入数据中的隐藏特征，构建参数和状态时间序列的映射关系。

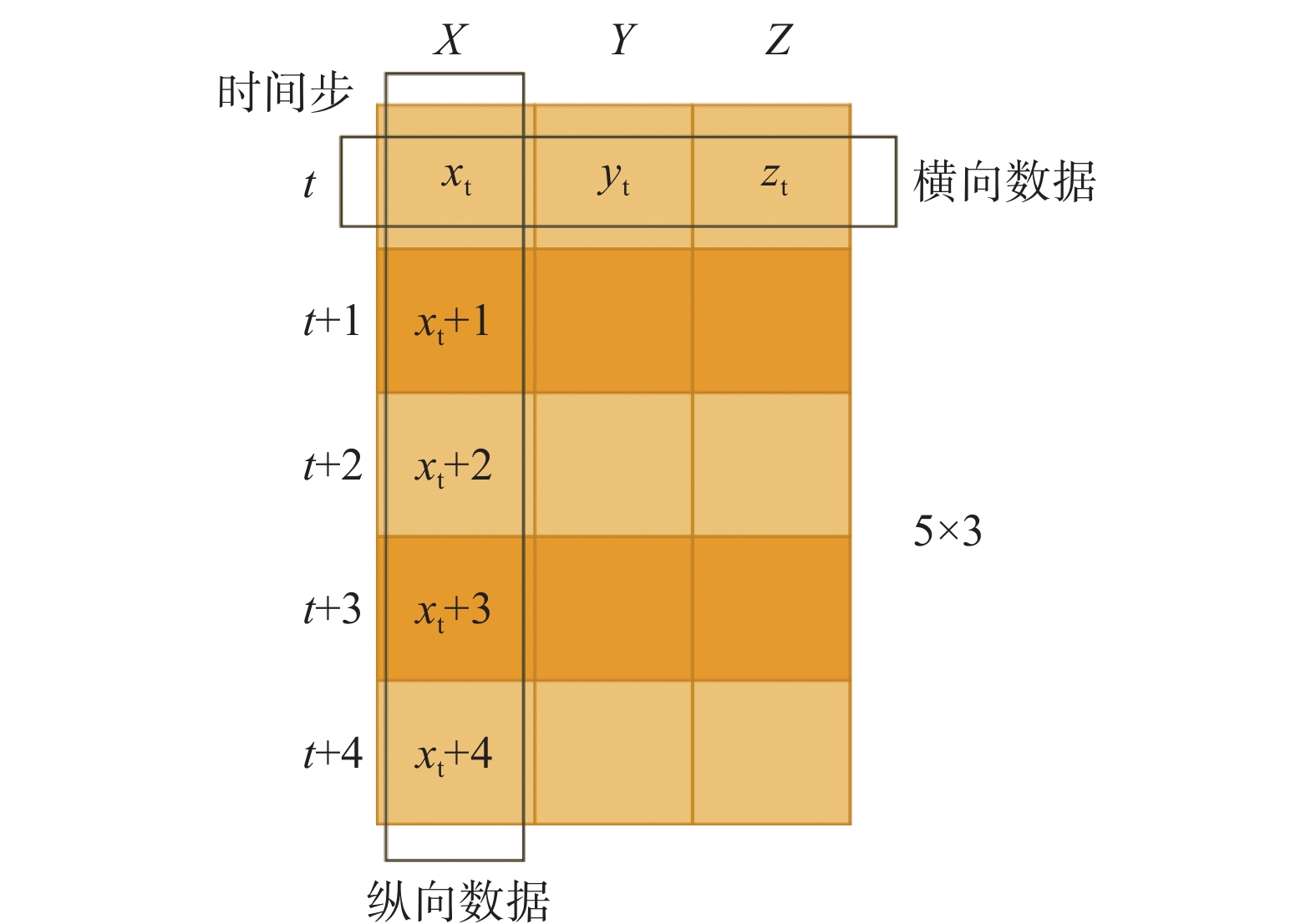
2.1 状态时间序列输入

首先向神经网络输入多个时间步的状态矢量，每个状态矢量含有多个状态变量，以Lorenz63系统的3个状态变量为例，假设输入5个时间步的数据，后文相同，因此有如下的数据格式，见图3。

输入数据是一个二维矩阵，类似一张单通道图像。矩阵上的行向量表示一个时刻的状态矢量，列向量表示特定状态变量的多个连续时刻的数值。我们将行向量和列向量上的数据分别称作横向数据和纵向数据。

从每条纵向数据上看，一条数据表示对应状态变量在该5个时间步下的数值。我们将数据输入到CNN中希望网络能够根据变量变化的趋势提取系统的运动特征。然而状态变量在不同时间区间上会在不同数值范围上变化，在不同初始场的驱动下也会有不一样的结果，因此纵向数据需要弱化数值对神经网络提取特征的影响，使其更关注仅仅在5个时间步下的数值变化趋势的特征。我们选择基于原始数据均值以及标准差的标准差标准化方法，对每个输入数据的每条纵向数据进行单独标准化，以X列数据为例，将原始值 ${x_i}$ 标准化到 ${x_i}'$ ，

$\begin{array}{l} {x_i}' = \dfrac{{{x_i} - \overline x + \delta }}{{s + \delta }} \\ \overline x = \dfrac{1}{5}\displaystyle\sum\limits_{i = t}^{t + 4} {{x_i}} \\ s = \sqrt {\dfrac{1}{5}\displaystyle\sum\limits_{i = t}^{t + 4} {({x_i} - } \overline x {)^2}} \end{array} $

(3)

其中， $\delta $ 为一个非常小的常数，是为了防止标准差为0而做的平滑操作，称作平滑指数。

纵向数据的标准化处理将每列状态变量进行单独处理，在数值上仅由单列数据决定。因此，从单条横向数据上看，每个位置上的状态变量在数值上有不同的取值范围，大小不相同。这些状态变量在神经网络中也被称为特征。这些特征如果不处理直接使用原始数据输入模型中，那么不同特征对模型训练过程将会产生不同程度的影响，梯度下降过程会更受某些数值大的特征的引导，忽略那些数值小的特征。因此我们需要使不同的特征具有相同的尺度，这样在训练神经网络的时候，不同特征对参数的影响程度就可达成一致。我们通过数据标准化以实现这个目的。同样采用标准差标准化方法，对横向数据进行由 ${x_i}'$ 到 ${x_i}''$ 变换：

$\begin{array}{l} {x_i}'' = \dfrac{{{x_i}' - \overline x + \delta }}{{s + \delta }} \\ \overline x = \dfrac{1}{3}({x_i}' + {y_i}' + {z_i}') \\ s = \sqrt {\dfrac{1}{3}[{{({x_i}' - \overline x )}^2} + {{({y_i}' - \overline y )}^2} + {{({z_i}' - \overline z )}^2}]} \end{array} $

(4)

最后将纵向和横向的结果相加，作为我们双向数据标准化的最终结果，输入到神经网络中去。

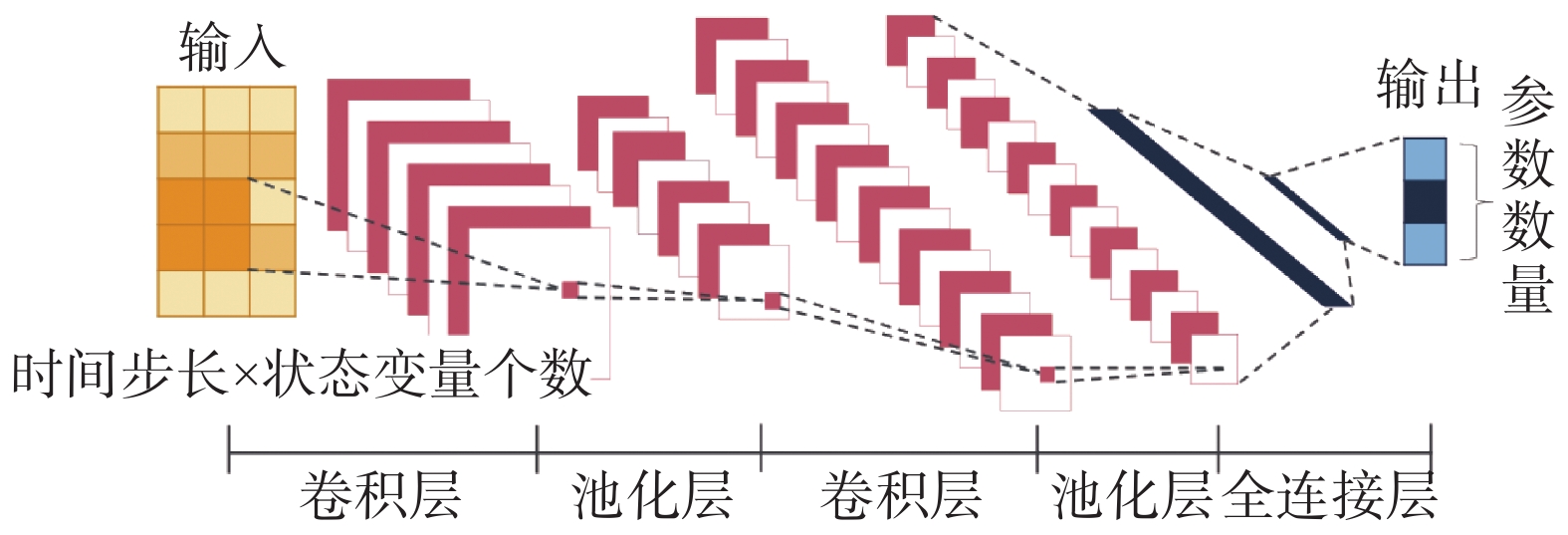
2.2 CNN结构

我们的参数辨识模型输入的是经过上述双向标准化后的时间序列数据，数据格式见图3，输出的是参数估计的结果，格式为一维向量。由于输入数据格式类似于单通道图像，每个单元位置可以看作图像中的像素点，因此选择常被用作图像特征提取的CNN^[13-14]。典型的CNN在输入层后由多个交替执行的卷积层、池化层和全连接层构成。故针对本文任务的模型图如图4所示。

1）卷积层

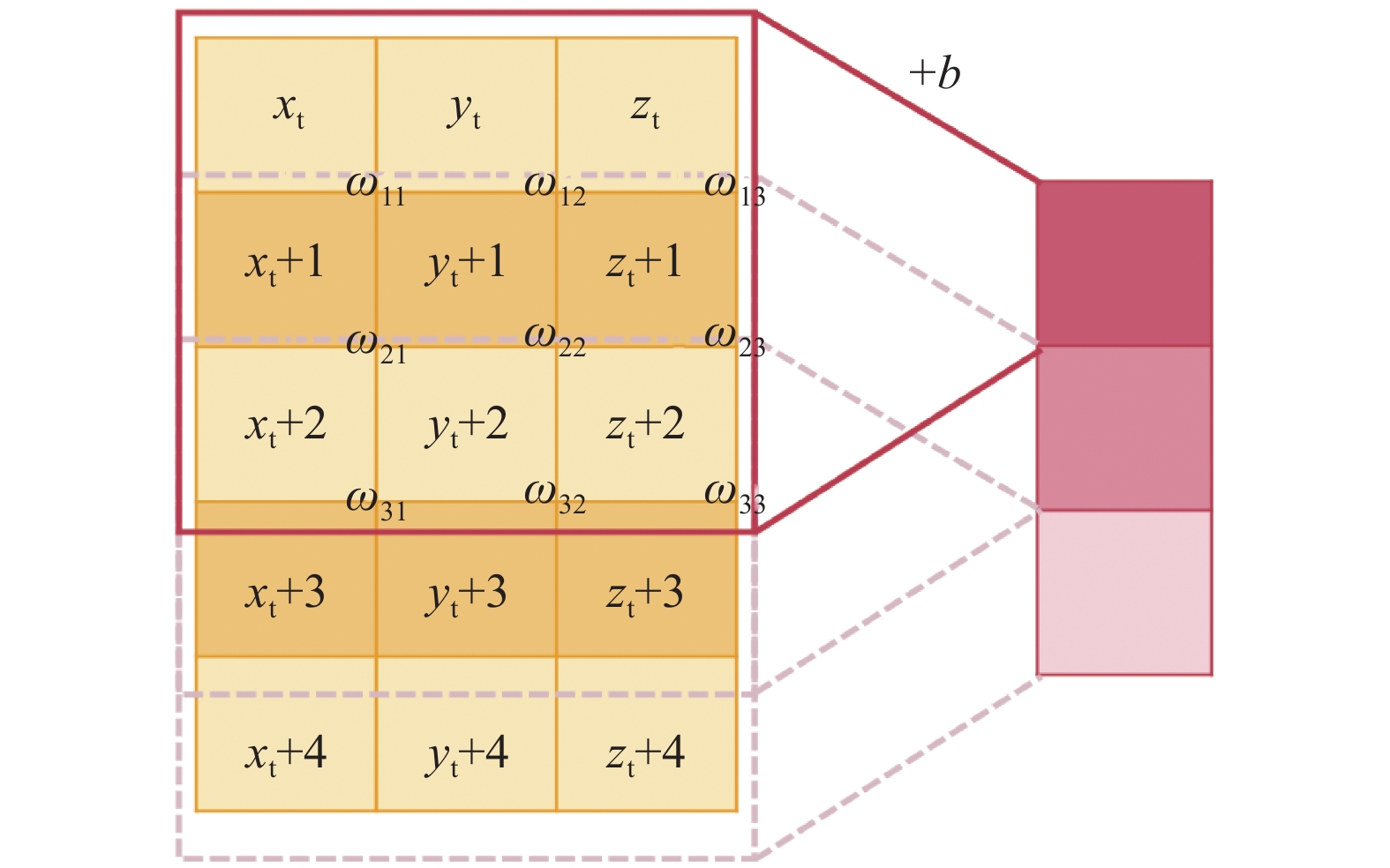
使用多个卷积层从原始特征中提取隐藏特征。由于系统状态变量之间不像图像像素，不单单是相近的像素点之间彼此有联系，头尾状态变量之间也由于物理模型的控制方程而存在着相互影响的制约关系，因此进行卷积运算时需要将对应横向数据上的所有状态变量包含在内。我们使用“一维卷积”（卷积完后的数据呈一维）进行卷积操作，沿着时间步移动来提取系统在当前时间区内的运动特征，见图5。

“一维卷积核”设置的维度大小和数据横向上的大小相同。其中，输入特征中圈出来的区域为局部感受野。因此“一维卷积”只需要在原始输入的多通道特征中垂直移动，提取更深层次的特征。

以第一个卷积层为例，输入特征只有一个通道，因此使用大小为3的卷积核执行卷积运算，通过垂直滑动获得3×1的特征图，第一个位置的特征值为：

$\left(\sum\nolimits_{j = 1}^3 {\sum\nolimits_{i = 1}^3 {{\omega _{ij}}{x_{p + i,j}}} } \right) + b$

(5)

其中， $p$ 为当前局部感受野的位置， $b$ 为当前卷积层的偏置， ${\omega _{ij}}$ 为卷积核 $(i,j)$ 位置上的权值。当前卷积层有多个卷积核，每个卷积核的权值不共享，但偏置是共享的，即多个卷积核分别进行卷积运算后都加上当前卷积层的偏置，从而生成多个特征图，输入到下一层中。每个特征图在下一层中表示图的一个通道，在进行卷积运算时，需要将每个通道上的结果相加，最后加上共同的偏差 $b$ 。

2）池化层

池化层通过最大池化或平均池化等来减小输出维的大小，其主要目的是通过压缩卷积层的输出来简化网络的计算复杂性。每个卷积层之后可以跟随一个池化层，根据数据特征的维数大小适度添加。

3）全连接层

我们的任务是估计参数，即要输出一维向量，向量中每个数表示对应参数的值。因此我们需要将卷积操作输出的二维或三维数据展平，该操作由全连接层进行。直观来说，就是讲原本的三维矩阵展平重新排列变成一个全连接层的各个神经元。

4）输出层

在多个全连接层的映射之后输出参数预测结果。由于数值模型的每个参数有不同的物理意义和单位，由真实物理环境决定。因此，为了使得目标输出数据（也可称为标签）符合正态分布，在训练神经网络时，我们不仅要对输入数据进行双向标准化，标签也要进行标准化，采用同样的标准差标准化方式。假设为了得到这个参数辨识模型，生成了 $a$ 组参数对应的数值模型解，数值模型解用于构造输入数据，参数值用于构造标签，以Lorenz63为例对参数 $\sigma $ 进行如下标准化操作：

$\begin{array}{l} {\sigma _i}' = \dfrac{{{\sigma _i} - \overline \sigma }}{s} \\ \overline \sigma = \dfrac{1}{a}\displaystyle\sum\limits_{i = 1}^a {{\sigma _i}} \\ s = \sqrt {\dfrac{1}{a}\displaystyle\sum\limits_{i = 1}^a {({\sigma _i} - } \overline \sigma {)^2}} \end{array} $

(6)

$\gamma $ ， $\beta $ 操作相同。

使用标准化后的数据作为标签训练网络，因此输出层的预测结果 ${\sigma ^o}$ 需要进行还原，使用公式（6）中的均值 $\overline \sigma $ 和标准差 $s$ ，即：

${\sigma ^o} = {\sigma ^o} \times s + \overline \sigma $

(7)

构建好网络结构后采用反向传播方式对网络进行训练。

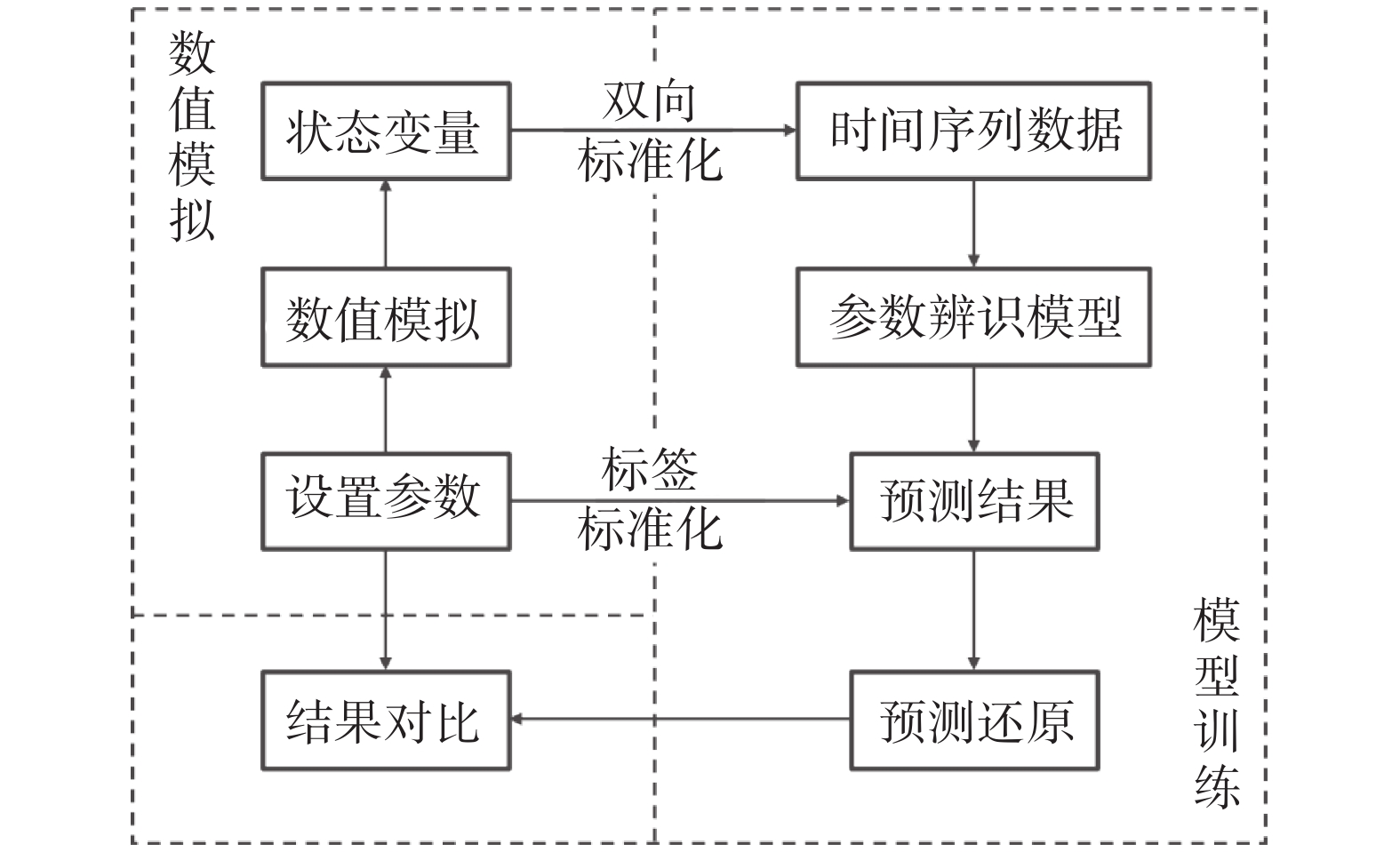
3 方法验证 3.1 CNN模型训练

Lorenz63的CNN参数辨识模型训练过程由图6给出。

在进行数值实验时，多组实验的初始状态矢量均为 $({\rm{ - }}10,10,20)$ ，积分步长取0.01。每组实验中的参数是在设置好取值范围的前提下随机选择的。从参数分析可以得到参数组合的取值范围实际分为两组，如表2所示。我们在第一组取值范围下分别对三个参数进行随机取值，生成1000组参数组合，并在第二组取值范围下同样随机取值了500个参数组合，每组实验积分区间为[0，100]。因此一共生成了15000000条状态矢量数据。

将数值实验生成的数据处理成模型需要的格式。比如一次实验中，设定初始特征图的维度为5×3，采用长度为5的滑动窗口将每次窗口内的5个时间步的状态变量合成一个二维矩阵，滑动步长为1。格式处理好后进行标准化操作，即准备好了模型训练需要的样本数据，进行网络的训练。

实验是在Nvidia Tesla P100 GPU上进行的，使用Keras框架搭建神经网络。本文的CNN模型包含三个卷积层，每个卷积层分别设置了大小为3的一维卷积核，padding方式选择了‘valid’（不在外圈补0）；由于Lorenz63系统简单，维数不高，因此当输入时间步较少时可不添加池化层进行降维操作，如果输入时间步较大（如100,1000···），则适当添加池化层；之后，跟随着3个全连接层，神经元的激活函数选择了‘Relu’^[15]，

$f(x) = \max (0,x) = \left\{ {\begin{array}{*{20}{c}} {0,x \leqslant 0} \\ {x,x > 0} \end{array}} \right.$

(8)

损失函数为平均绝对误差（Mean Absolute Error，MAE），

${\rm{MAE}}({{\boldsymbol{P}}^o},{{\boldsymbol{P}}^{ta}}) = \frac{1}{3}\sum\limits_{i = 1}^3 {\left| {p_{_i}^o - p_{_i}^{ta}} \right|} $

(9)

其中， ${{\boldsymbol{P}}^o}$ 、 ${{\boldsymbol{P}}^{ta}}$ 分别表示神经网络输出结果和目标结果， $p_i^o$ 、 $p_i^{ta}$ 的下标 $i$ 为1、2、3时表示参数 $\sigma $ 、 $\gamma $ 、 $\;\beta $ 。优化器选择了‘Adam’^[16]，学习率为0.001。

我们将样本数据随机打乱，以避免时间序列的影响。取80%的数据作为训练集，余下的20%为测试集；batch的大小为512，表示每次取512条数据来计算损失函数的平均值，进行梯度下降的训练；epoch为100，表示最多进行100次重复训练，其中当损失函数降到最低时停止训练。

3.2 实验分析

使用神经网络对系统参数进行估计的主要目的是减少参数辨识的计算量，缩短计算时间，但前提是要保证参数预测结果的准确度，必须在验证这种辨识方法的准确可行之后才能进一步讨论其对于效率的提升。

因此，实验结果主要关注准确度和时间两个方面。同时，为了更好的讨论本文方法的优劣，在进行上述实验的同时，还分别做了一些比较实验。

1）输入不同数量时间步的结果

在实验中我们尝试改变输入的时间序列数据的长度，查看了向CNN输入不同数量特征的结果，见表3。训练的超参数均与上一节实验设计的描述相同。

表中 $\overline {{\rm{MAE}}}$ 直观地表示了在测试集上模型预测结果与目标结果的整体的平均绝对误差，我们可以看到这个误差在0.2之内，且在输入100、200、500个时间步时仅为0.04。

首先从输入时间步为10、50、100的结果来看，可以得到一个初步结论：当输入时间步数量越多时，模型精度越高。这是由于向模型输入更多时间步的数据，等于使模型能得到更多原始特征，因此我们能认为这种结果是自然现象。

然而当输入时间步大于100之后，平均误差并没有如预期继续降低，保持在0.04不变。由此我们可以认为神经网络能从100个时间步的状态变量中提取到Lorenz63系统的运动特征，再向其输入更多的状态变量是没有必要的。

同时还需要注意一点，由于系统所处的物理场景经常是瞬息万变的，我们需要参数逆推模型能根据当前的系统状态变化来估计参数，如果输入过长时间区间的系统状态，则会导致参数估计不准确。因此不认为输入过多时间步的数量是好的选择。

结合以上，基于CNN-时间序列的参数辨识方法，在针对具体任务时需要综合考量以确定输入数据格式。针对Lorenz63实验，输入100时间步是较好的选择。

2）实验预测结果

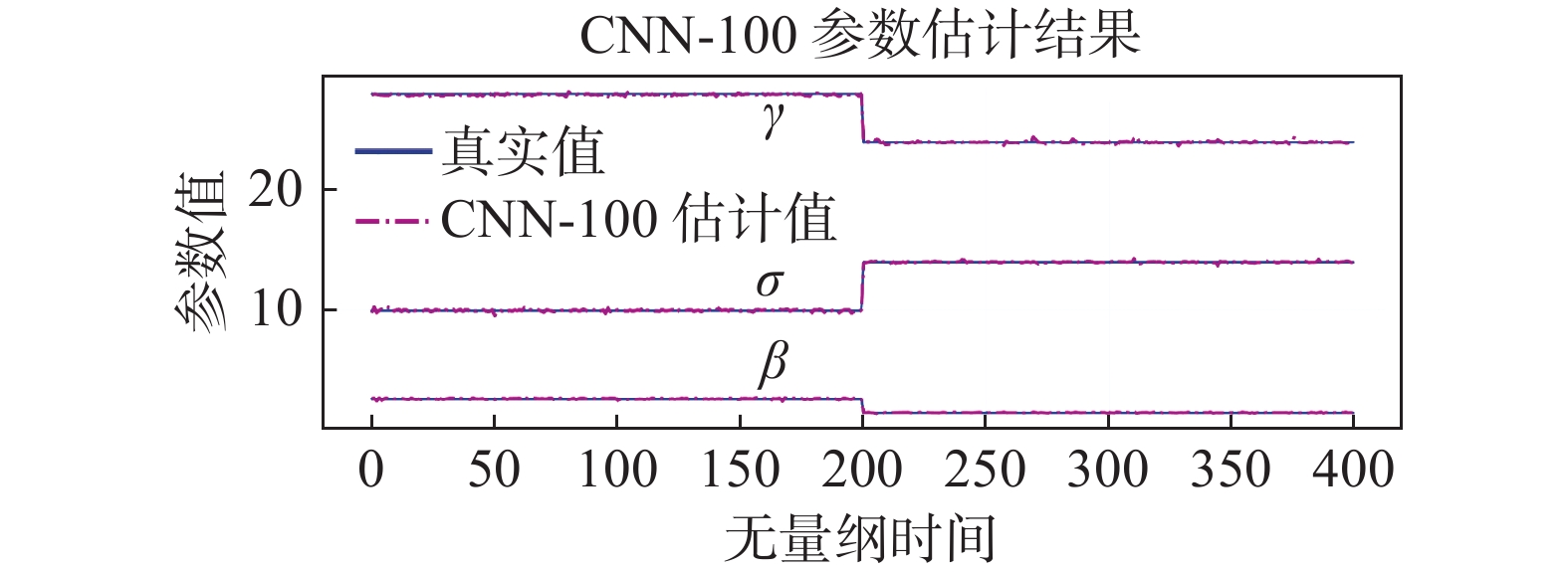
用图7抽样展示实验结果，更直观的体现模型预测的准确度。图中[0,200]区间的参数为 $\sigma = 10.0$ ， $\gamma = 28.0$ ， $\;\beta = 8/3$ ，[200,400]的参数为 $\sigma = 14.0$ ， $\gamma = 24.0$ ， $\;\beta = 1.5$ 。在这两组参数下另外进行Lorenz63实验得到了两段状态变量时间序列，均未参与模型的训练，选择的是[0,200]区间的数据输入到模型进行参数估计，估计结果为图7中虚线。我们可以看到这个结果近似真实值。其中用到的模型为输入时间步为100的模型（称为CNN-100）。

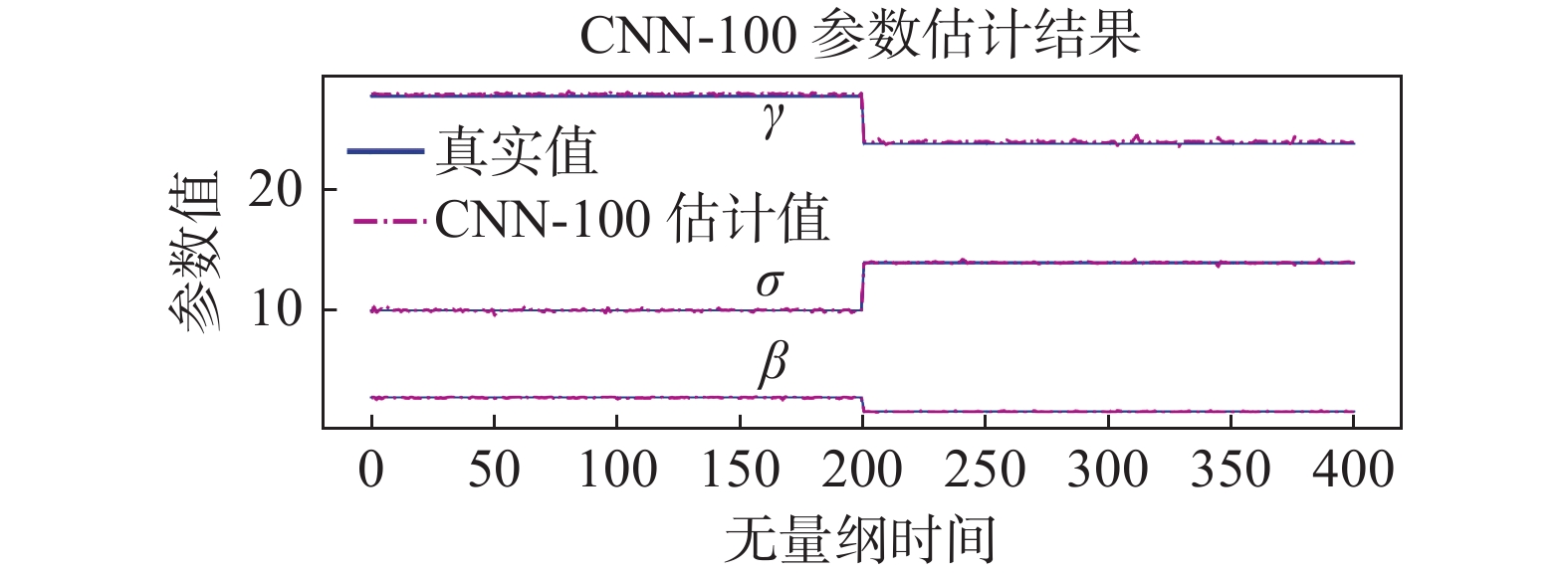
由于实际问题中观测中存在噪声，因此向这两段状态变量数据添加标准差为对应量值的1%的噪声扰动，再次查看结果，见图8。结果表明，模型依旧能近似估计真实参数。

3）同类实验比较

有研究工作者也在进行通过神经网络估计Lorenz63模型参数的实验（ https://github.com/Yajing-Zhao/Lorenz_MLP）。

本课题进行了同类实验的对比分析。

该实验使用到的神经网络为多层感知机（Multi-layer Perceptron，MLP），输入数据为展平成一维向量的状态时间序列。本文对MLP的实验方案和模型进行了改进：采用我们CNN实验相同的数据，输入50/100个时间步的状态变量，输入层的神经元数量为150/300，添加了三个隐藏层，神经元数量分别为128/256、64/128、16/64，激活函数选择‘Relu’。结果见表4。

表中 $\overline {{\rm{MAE}}}$ 为模型在测试集上的统计结果，而参数估计结果为向MLP和CNN分别输入一段相同的状态变量时间序列（含1%噪声扰动）得到的。可看出，不论是50或者100时间步，CNN模型的预测精度都比MLP好，CNN的估计结果比MLP更接近真实值，且模型参数较少。因此，通过CNN提取状态变量时间序列上的运动特征的模型更加高效。

4）与PSO参数辨识方法的时间比较

本文选用粒子群算法^[17]也进行了实验，展示了基于神经网络的参数辨识在时间上带来的优势。

我们设置了粒子群法的惯性权值因子为0.8，学习因子c1、c2为2，群体大小为40，在合适范围内随机初始化，最后输入上一时间步的系统状态变量（数值模型输出）以及当前的实测值（添加了1%噪声扰动的状态变量），对目标函数进行全局最优化，最大迭代次数为200，并同时计算了10个结果取平均。

选用CNN-100与粒子群算法的结果进行比较，两个程序均运行在Inter(R) Core(TM) i5-6200U CPU上，结果见表5。

从准确度上看，两种方法都能估计出系统参数的近似解，传统的粒子群算法并没有更胜一筹。

从时间上看，我们的模型在通过逆推参数实现参数辨识的过程中只耗费了0.09 s（包括了对输入数据进行双向标准化并对输出数据进行还原的时间），比粒子群算法2.23 s少了96%。从该点上看，使用神经网络的参数辨识方法能够大大的缩短参数辨识过程的时间，从而使参数辨识工作能够更快的完成。

另外，神经网络模型在进行参数辨识之前需要耗费一定时间进行数据生成和网络学习，不过这些工作并不发生在参数辨识阶段，不会耽误原本工程的开展；且一旦构建好模型，便可以反复使用，无需在每次参数辨识时都进行神经网络训练。因此从整体上看，本文方法耗费的时间依旧较少。

4 结　论

本文基于卷积神经网络对数值模拟的参数进行估计，结合双向数据标准化的方式提取系统变量在时间上的运动特征。通过Lorenz63混沌系统的验证，本文的参数辨识模型在具有高精度的同时，比粒子群参数辨识法的计算时间降低了96%。

总的来说，本文的研究可以节省参数辨识过程耗费的大量计算时间，实现快速估计参数的目标。