2. 空气动力学国家重点实验室,绵阳 621000;
3. 陆军工程大学 爆炸冲击防灾减灾国家重点实验室,南京 210007
2. State Key Laboratory of Aerodynamics, Mianyang 621000, China;
3. State Key Laboratory for Explosion Shock Prevention and Mitigation, Army Engineering University, Nanjing 210007, China
随着临近空间无人机及微小型飞行器的应用与经济价值不断提升,各国均展开了不同程度的探索。临近空间无人机及微小型飞行器工作时,其周围流场均为低雷诺数流场。
低雷诺数下(Re = 6×104~2×105),翼型空气动力学性能受到层流分离泡的不利影响,认识层流分离泡现象是深入了解低雷诺数下流体动力学特性的重要内容。当翼型表面层流受到剧烈的逆向压力梯度时,会导致层流边界层分离,分离边界层通过二维Kelvin-Helmholtz不稳定性过渡为湍流,高能湍流剪切层会重新附着到机翼表面,形成层流分离泡。Jones[1]和Gault[2]最先发现层流分离泡现象。Gaster[3]对不同压力梯度条件下一系列雷诺数的层流分离泡现象进行了详细研究,发现分离泡的尺寸以及变化(生成和破裂)取决于分离剪切层的雷诺数和压力梯度。Wong等[4]观察发现在高雷诺数(Re = 4×106)下,分离泡的尺寸随攻角的上升而减小,而在低雷诺数条件下(Re = 1.3×105)情况相反。
研究低雷诺数下翼型气动特性,是减轻甚至解决低雷诺数下气动特性恶化的基础。国内外学者对各种翼型低雷诺数下的气动特性进行了大量的研究。Koca等[5]运用烟线法、热线法以及应变片测力法对NACA4412翼型展开了研究,发现雷诺数变化会引起上翼面层流分离泡形态的明显改变,另外层流分离泡会随着攻角的增大前移。Shen等[6]发现低雷诺数翼型E387表面曲率梯度不连续导致了较大的层流分离泡,且随着攻角增加,分离泡朝前缘快速移动,破裂后引发失速。王庶等[7]在水洞中研究了来流湍流度对NACA0012在超低雷诺数下气动性能的影响,研究表明湍流度较低时,由于转捩发生较迟,上表面出现流动分离,导致升力系数较低,随着湍流度的升高,转捩加快,发生流动再附。吴鋆[8]运用氢气泡流动显示和PIV技术,研究了NACA0012翼型在雷诺数为8200时的流动特性,发现分离点和分离剪切层的位置随攻角增大向前移动,且回流区尺寸随攻角的增大而增大。朱志斌等[9]运用大涡模拟法对SD7003翼型层流分离现象展开数值研究,表明翼型低雷诺数层流分离流动中存在分离、转捩及再附等多尺度复杂流动结构,并具有强烈的非定常运动特征。白鹏等[10-13]采用非定常数值模拟和水洞PIV实验方法,以SD8020翼型为对象,研究了低雷诺数小攻角时,时均化及非定常的层流分离流动结构和压力系数分布,以及升力系数非线性的动力学特性和演化规律,提出小攻角范围内存在不同于长层流分离泡的后缘层流分离泡理论。孟宣市等[14-15]在研究低雷诺数下等离子体流动控制技术时发现,低雷诺数下由于分离泡尺寸随攻角的变化导致气动外形随攻角不断变化,从而造成了升力随攻角的非线性变化。
临界攻角附近发生的非定常分离流动是典型的流动状态。众多研究表明,当雷诺数大约为1 × 105、攻角处于临近失速范围时,会出现薄翼型失速的低频振荡现象,其判定依据主要是斯特劳哈尔数St,有别于St在0.2左右的钝体脱落现象,这一现象的St数量级更低,约为10−2~10−3[16-18]。Zaman等[19]通过对雷诺数为0.15×105~3×105下二维翼型的实验及仿真研究,最先观察到明显的低频振荡现象,该现象有别于钝体脱落、腔体上的流动以及超声速喷射等流动现象,发现了可能发生低频振荡的机翼类型,即出现后缘失速或薄型机翼失速的机翼。Bragg[20]测试了雷诺数0.3×106~1.25×106、攻角为14.4°和16.6°的LRN-007翼型,发现升力系数存在明显的低频振荡现象,这一现象的St是钝体脱落现象的十分之一,且随着攻角的上升,St增大。Broeren等[21]展开了另外的实验,在雷诺数为3×105、攻角为15°条件下,同样针对LRN-007翼型,实验结果表明,相位平均下,随着相位增加,上翼面同时出现前缘分离泡的生长以及尾缘失速,随后二者合并,引发完全的边界层分离和失速现象。Rinoie和Takemura[22]开展了相似实验,翼型选用 NACA0012,雷诺数为1.3×105,攻角为10°和11°,对低频振荡的背后机制进行了研究。在攻角为11.5°时,通过平均速度得到的时均化流场,发现存在长度为35%弦长的长泡,此时流动出现规则的低频振荡现象,该现象表现为10%弦长的前缘短泡与完全分离之间的转换。相位平均下,在0相位时,形成短泡,随后相位在45°和90°,后缘分别形成30%和50%弦长的流动分离。在相位90°到270°之间,流动完全分离没有再附发生。
目前翼型表面分离泡的形态、位置、演化规律等仍无法准确预测,分离泡对不同翼型的气动特性的影响尚无统一定论,需要进一步研究低雷诺数下翼型气动特性、层流分离泡演化规律。
Selig[23]设计的S1223翼型是一种高升力低雷诺数薄翼型,被广泛运用在平流层飞艇螺旋桨[24-25]、微小型飞行器机翼[26]、扑翼[27]、扩压涡轮叶片[28]等研究当中,是一种重要的低雷诺数翼型。目前关于S1223翼型的低雷诺数下气动特性研究较为有限。
本文采用表面测压法,对S1223翼型不同雷诺数、不同攻角下流动特性展开研究,旨在为低雷诺数翼型气动特性研究提供参考。
1 研究方法采用翼型表面测压研究翼型低雷诺数下非定常流动气动特性。将压力数据进行时均化处理及瞬态分析,获得翼型在稳态及瞬态下的气动特性及流场结构,分析低雷诺数翼型非定常气动特性机理。
1.1 风洞及翼型实验在航天工程大学直流开口低湍流度风洞中进行(图1)。风洞实验段尺寸1 m×0.8 m×4 m,收缩比16∶9,最低湍流度小于0.03%。风速范围3~70 m/s。翼型攻角α范围−20°~30°,调节精度为 ± 0.01°。
实验模型为S1223翼型,弦长c为200 mm,展长为790 mm,最大厚度处为距前缘19.8%处,最大厚度为弦长的12.1%,翼型表面允差0.03 mm。翼型表面中线处,斜向布有32个测压孔,上、下翼面各16个对称分布,测压孔通过测压管与压力扫描阀连接。测压孔内径为0.5 mm,测控位置精度小于等于0.5 mm。翼型表面测压孔弦向分布如图1(b)所示,数字为测压管弦向位置与弦长的比值,即x/c。
1.2 实验仪器及实验工况翼面压力测量采用192通道DSY-32型电子压力扫描阀测量,系统精度为0.05% FS,采集频率为100 Hz,每个攻角工况下采集2 000组数据。
离散傅里叶变换要求,所处理的信号的采样频率大于振动频率分量的两倍[29-30],翼型尾缘的钝体脱落现象的频率通常为50 Hz左右[19],同时由于压力采集过程中频率也存在波动,因此这一高频震荡信号可能会被过滤。但本研究主要针对临界攻角附近出现的升力系数低频振荡现象,其频率在10 Hz以下,满足进行频谱分析的要求,可以通过压力采集分析本研究中的非定常现象。
实验工况如表1所示,选取三个雷诺数6.0×104、1.0×105、2.0×105,分别对应于翼型低雷诺数工作环境范围的起始、中间、末尾。在相同来流速度下进行了攻角逐渐增大和攻角逐渐减小两组实验,攻角变化间隔为1°。

|
图 1 试验装置 Fig.1 Experimental equipment |
| 表 1 实验工况 Table 1 Experimental conditions |
|
|
通过对压力数据瞬态及时均化处理,获得瞬态和时均化的压力系数和升力系数,计算公式如下。
翼面的压力系数为:
| $ {C}_{p}=\frac{p-{p}_{\infty }}{{q}_{\infty }} $ | (1) |
其中,
升力系数为:
| $ {C}_{N}=\dfrac{{\displaystyle\int }_{0}^{c}\left({p}_{\mathrm{d}\mathrm{o}\mathrm{w}\mathrm{n}}-{p}_{\mathrm{u}\mathrm{p}}\right)\mathrm{d}x}{\dfrac{1}{2}\rho {V}_{\infty }^{2}c} $ | (2) |
| $ {C}_{A}=\dfrac{{\displaystyle\int }_{{y}_{\mathrm{d}\mathrm{o}\mathrm{w}\mathrm{n},\mathrm{m}\mathrm{a}\mathrm{x}}}^{{y}_{\mathrm{u}\mathrm{p},\mathrm{m}\mathrm{a}x}}\left({p}_{\mathrm{f}\mathrm{o}\mathrm{r}\mathrm{w}\mathrm{a}\mathrm{r}\mathrm{d}}-{p}_{\mathrm{b}\mathrm{a}\mathrm{c}\mathrm{k}\mathrm{w}\mathrm{a}\mathrm{r}\mathrm{d}}\right)\mathrm{d}y}{\dfrac{1}{2}\rho {V}_{\infty }^{2}c} $ | (3) |
| $ {C_L} = {C_N}{\rm{cos}}\alpha - {C_A}{\rm{sin}}\alpha $ | (4) |
其中,
斯特劳哈尔数计算式见式(5),其中f为频率。
| $ St=fc \mathrm{s}\mathrm{i}\mathrm{n}\mathrm{\alpha }/{V}_{\infty } $ | (5) |
对N = f (x,y,z,···),不确定度的合成公式为:
| $ {U}_{N}=\sqrt{{\left(\frac{\partial N}{\partial x}\right)}^{2} {U}_{x}^{2}+{\left(\frac{\partial N}{\partial y}\right)}^{2} {U}_{y}^{2}+{\left(\frac{\partial N}{\partial z}\right)}^{2} {U}_{z}^{2}+\cdots \cdots } $ | (6) |
其中U代表不确定度,下标代表所对应的分量。
升力系数的不确定度主要来源于翼面压力、来流速度以及大气密度。所测压力范围内最大仪器误差为 ± 0.3 Pa,密度通过大气压计及温度计测得,其不确定度分别为150 Pa以及0.5 ℃,其间接不确定度为 ± 0.0025 kg/m3,速度通过风洞收缩段压力差值计算,其间接不确定度为 ± 0.023 m/s。
由CL的计算公式以及间接不确定度计算公式可得,CL不确定度计算式如下:
| $ \begin{split}& {U}_{{C}_{N}}= \sqrt{\Bigg({\frac{\partial {C}_{N}}{\partial {p}_{\mathrm{d}\mathrm{o}\mathrm{w}\mathrm{n}}}\Bigg)}^{2}{U}_{{p}_{\mathrm{d}\mathrm{o}\mathrm{w}\mathrm{n}}}^{2}+\Bigg({\frac{\partial {C}_{N}}{\partial {p}_{\mathrm{u}\mathrm{p}}}\Bigg)}^{2}{U}_{{p}_{\mathrm{u}\mathrm{p}}}^{2}+\Bigg({\frac{\partial {C}_{N}}{\partial {V}_{\infty }}\Bigg)}^{2}{U}_{{V}_{\infty }}^{2}+\Bigg({\frac{\partial {C}_{N}}{\partial \rho }\Bigg)}^{2}{U}_{\rho }^{2}} \end{split}$ | (7) |
| $ {U}_{{C}_{A}}=\sqrt{\Bigg({\frac{\partial {C}_{N}}{\partial {p}_{\mathrm{f}\mathrm{o}\mathrm{r}\mathrm{w}\mathrm{a}\mathrm{r}\mathrm{d}}}\Bigg)}^{2}{U}_{{p}_{\mathrm{f}\mathrm{o}\mathrm{r}\mathrm{w}\mathrm{a}\mathrm{r}\mathrm{d}}}^{2}+\Bigg({\frac{\partial {C}_{N}}{\partial {p}_{\mathrm{b}\mathrm{a}\mathrm{c}\mathrm{k}\mathrm{w}\mathrm{a}\mathrm{r}\mathrm{d}}}\Bigg)}^{2}{U}_{{p}_{\mathrm{b}\mathrm{a}\mathrm{c}\mathrm{k}\mathrm{w}\mathrm{a}\mathrm{r}\mathrm{d}}}^{2}+\Bigg({\frac{\partial {C}_{N}}{\partial {V}_{\infty }}\Bigg)}^{2}{U}_{{V}_{\infty }}^{2}+\Bigg({\frac{\partial {C}_{N}}{\partial \rho }\Bigg)}^{2}{U}_{\rho }^{2}} $ | (8) |
| $ {U}_{{C}_{L}}=\sqrt{{\mathrm{c}\mathrm{o}\mathrm{s}}^{2}\alpha {U}_{{C}_{N}}^{2}+{\mathrm{s}\mathrm{i}\mathrm{n}}^{2}\alpha {U}_{{C}_{A}}^{2}} $ | (9) |
由于S1223翼型是一种高升力低雷诺数薄翼型,尤其是翼型尾部极薄无法布置测压孔,因此造成后缘驻点附近压力点的缺失,针对这一问题,结合Selig[23]翼型设计压力分布以及本实验所测得的压力分布区间,S1223翼型尾缘处上下翼面压差产生的升力仅占总体升力的6%,会造成计算得到的升力系数小于真实升力系数值,但影响很小,同时由于S1223翼型本就属于上下尾流无法合流翼型,因此尾流处总是存在小范围分离,此处压力较为恒定,并不会引起升力系数剧烈波动,因此非定常流动特性的研究可以忽略这一问题带来的影响。
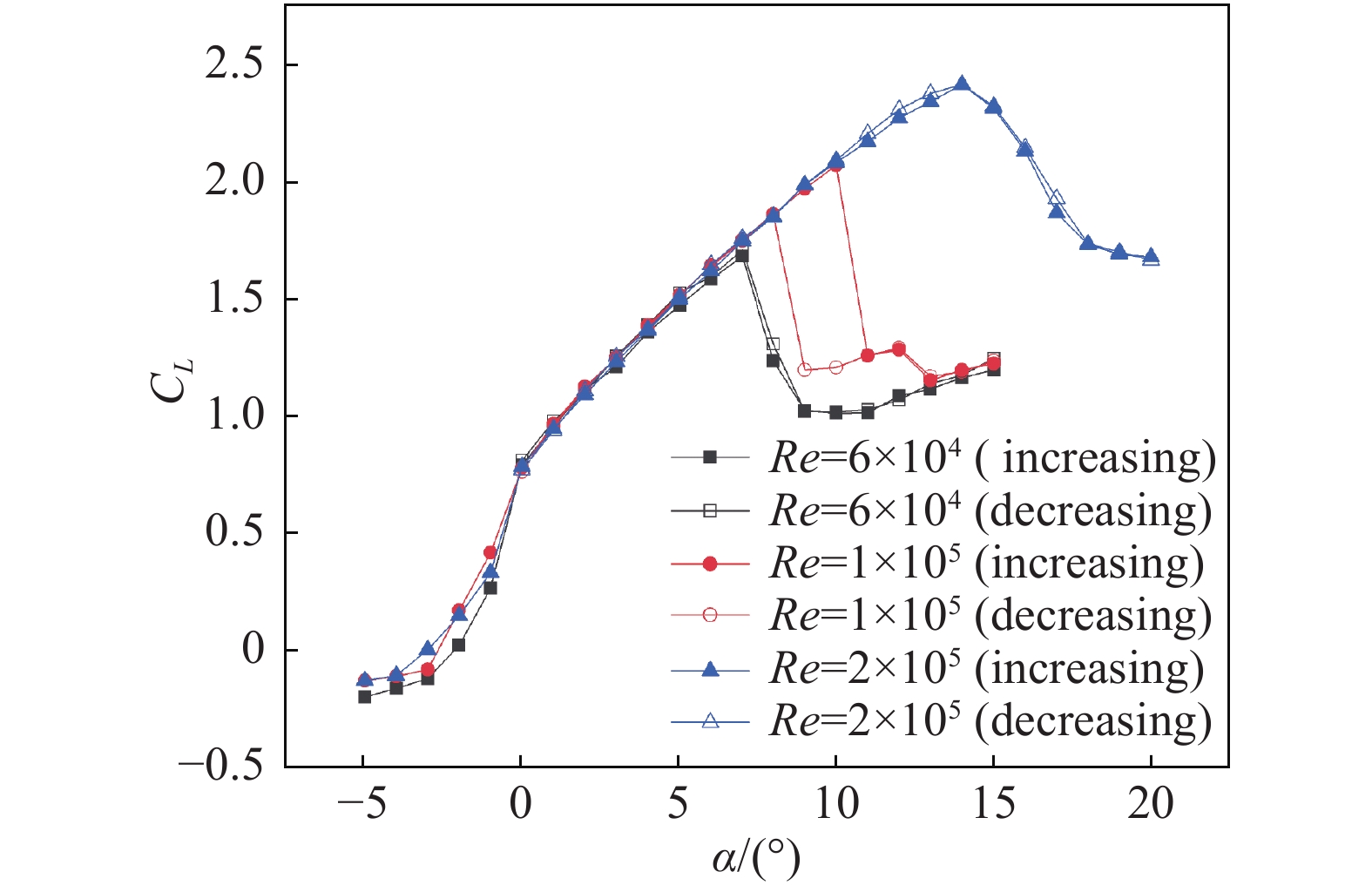
2 低雷诺数下时均化气动特性 2.1 时均化升力特性图2为不同雷诺数下S1223翼型的升力系数,图中increasing代表实验过程中攻角由小增大变化过程,decreasing代表实验过程中攻角由大减小变化过程。
|
图 2 S1223翼型升力特性 Fig.2 Lift characteristics of S1223 airfoil |
分析图2,发现S1223翼型升力特性具有以下特点:以Re = 6.0×104为例,α = −5°~0°之间时,升力线斜率(升力线斜率 = 升力系数增量/攻角增量)分别为0.0371、0.0421、0.142、0.244、0.527,可以看到升力线斜率随攻角增大而增大。三种雷诺数下,α < 0°时,升力系数均表现出非线性,随着攻角的增大,斜率增大。
Re = 6.0×104、1.0×105时,攻角大于临界攻角后,升力系数发生突降;Re = 2.0×105时,攻角大于临界攻角后,升力系数下降缓慢。推测S1223翼型在不同雷诺数下,失速流场存在不同。
Re = 6.0×104、2.0×105时,攻角增加和减小过程中,升力系数曲线基本保持相同。但是Re = 1.0×105时,在翼型由大攻角失速状态逐渐减小攻角的过程中,其临界攻角为8°,最大升力系数为1.86,小于攻角逐渐增加过程,存在明显的“静态滞回”效应。
2.2 非线性升力现象分析图3所示为Re = 6.0×104、α < 0°时的表面压力系数曲线。图中实心点线为上翼面压力系数曲线,空心点线为下翼面压力系数。针对 图2中负攻角时出现的升力系数非线性现象,下面通过翼型表面压力系数随攻角的变化进一步分析原因。

|
图 3 不同攻角下压力分布(Re = 6×104) Fig.3 Pressure distribution at different anglesof attack (Re = 6×104) |
首先观察上翼面压力系数随攻角变化规律。攻角由−5°变为−3°时,上翼面压力系数变化不明显,整体略微减小,压力系数变化平均值为−0.05;当攻角由−3°变为−1°时,上翼面压力系数大幅减小,压力系数变化平均值为−0.31;当攻角由−1°变为0°时,攻角变化仅1°,上翼面压力系数明显减小,各测点压力系数变化平均值约为−0.17。
其次观察下翼面压力随攻角变化规律。攻角为−5°和−3°时,压力系数曲线基本保持水平,因此下翼面呈完全流动分离状态;攻角为-1°时,分离减弱,0.05 < x/c < 0.2875区域压力系数曲线仍为水平状态,而后压力系数增大,下翼面前缘处存在明显的层流分离泡现象;当攻角进一步增大到0°时,0.05 < x/c < 0.15区域压力系数曲线为水平,相较于攻角为−1°时,层流分离泡明显缩小。
通过以上分析可知,攻角为负时,升力呈现非线性,主要是由两方面因素导致:一方面上翼面压力减小幅度随攻角增大而增大;另一方面,随着攻角的增加,下翼面由完全流动分离状态转为出现层流分离泡状态,且分离泡尺寸随攻角的增大而减小,由于分离泡尺寸随攻角的变化导致气动外形随攻角不断变化,从而造成了升力随攻角的非线性变化,这与孟宣市等[20-21]的升力非线性研究结论一致。
2.3 临界攻角附近流场时均化结构图4为文献[22]中长层流分离泡与短层流分离泡压力分布图,图中Separation和Reattachment分别代表分离泡边界的分离及再附区域。短泡通常出现在翼型前缘,引起前缘附近的负压峰被破坏,另一重要特征为其分离及再附区域压力分布相对陡峭。长泡有别于完全分离,分离的气流会重新附着在尾缘附近的位置形成长泡[31],长泡的压力分布相对平坦,长度较长,同时分离及再附区域压力分布相对平缓。
由图2可知雷诺数为1.0×105时,临界攻角为10°,继续增大攻角,升力系数剧烈下降,发生流动失速现象。图5为Re = 1.0×105时,失速现象附近各攻角下的压力系数曲线。α ≤ 10°时,翼型上表面出现短层流分离泡结构,短泡长度约为0.18c。α > 10°后,上翼面压力系数在短暂上升后随即保持近似水平,上翼面压力系数整体明显增大,此时上翼面发生大范围流动分离现象,从而导致升力系数迅速降低。正是由于流场结构随攻角发生上述变化,导致攻角大于临界攻角后,升力系数迅速下降。

|
图 5 失速附近压力系数分布(Re= 1.0×105) Fig.5 Pressure coefficient distribution nearstall (Re= 1.0×105) |
Re = 6.0×104时,翼型表面压力分布随攻角变化规律同Re = 1.0×105类似,这里不再赘述。
图6为Re = 2.0×105时,失速现象附近各个攻角下的压力系数曲线,其临界攻角为14°。可以看出,临界攻角附近,压力分布变化规律与另外两种雷诺数下明显不同。
当α ≤ 14°时,上翼面并未出现层流分离泡结构。当α = 15°,即刚刚超过临界攻角时,翼型表面并没有出现大规模分离结构,其压力分布与α = 14°时相似,仅仅是整体上负压系数相对下降。当攻角进一步增大到16°时,可以看到上翼面出现明显的长泡压力分布,该长泡的长度约为0.4c。当α = 17°时,长泡破裂,发生大范围流动分离。

|
图 6 失速附近压力系数分布(Re= 2.0×105) Fig.6 Pressure coefficient distributionnear stall (Re= 2.0×105) |
通过以上分析可做如下总结,不同雷诺数下S1223翼型时均化流场的失速演化规律不同。图7所示为雷诺数相对较低(Re = 6.0×104、1.0×105)时,上翼面流场结构变化的示意图。当攻角小于等于临界攻角,即未发生失速现象时,上翼面就存在短泡结构,其大致位于翼型中间偏前缘处;当攻角超过临界攻角后,即发生失速现象后,上翼面瞬间发生完全流动分离。

|
图 7 失速前后流场结构的概念图(Re = 6.0×104、1.0×105) Fig.7 Schematics of the flow structure before and after stall (Re = 6.0×104, 1.0×105) |
图8所示为雷诺数相对较高(Re = 2.0×105,仍属低雷诺数范畴)时,上翼面时均流场结构变化的示意图。当攻角小于等于临界攻角,未发生失速时,上翼面并未出现层流分离泡现象;当攻角超过临界攻角后,起初上翼面负压降低,但气流仍保持附着状态,升力略微下降;攻角进一步增大后,失速初期,上翼面存在长度约为0.4c的长层流分离泡,升力下降仍较为缓慢;随着攻角进一步增大,长泡发生破裂,导致上翼面发生大规模流动分离现象,升力下降增速。总的来说,随着攻角的增加,上翼面负压先略微下降,后出现长层流分离泡结构,最后分离泡破裂引发完全分离,因此升力随攻角增大,下降速率逐渐增大。

|
图 8 失速前后流场结构的示意图(Re = 2.0×105) Fig.8 Schematics of the flow structure beforeand after stall (Re = 2.0×105) |
S1223翼型升力系数随时间变化规律如图9所示。三条曲线雷诺数分别为2.0×105、1.0×105、6.0×104,攻角均为临界攻角 + 2°。通过不确定度计算公式得,图中Re = 2.0×105、1.0×105、6.0×104三种工况的不确定度分别为0.007、0.013、0.031。

|
图 9 瞬时升力系数 Fig.9 Instantaneous lift coefficient |
观察图9可以发现,当 Re = 6.0×104、1.0×105时,升力系数波动无明显规律;而Re = 2.0×105时,升力系数振动幅度很大,且随时间呈明显准周期性变化。前文分析已知攻角略微大于临界攻角后,当Re = 6.0×104、1.0×105时,时均流场迅速发生大范围失速,升力系数快速下降,并导致其瞬时升力系数呈无规则波动;而Re = 2.0×105、α = 16°时,上翼面出现40%弦长的长泡结构,升力系数缓慢下降。因此推测,升力系数呈周期性波动与层流分离泡变化有关。
图10是将图9数据通过快速傅里叶变换得到的频率-振幅图。从图中可以清晰地看到相较于Re = 6.0×104、1.0×105,当Re = 2.0×105时,存在一个明显的低频峰值,计算得此时St为0.004,符合发生低频振荡现象时的St范围[16-18],因此判断此时翼型上表面发生了低频振荡现象。

|
图 10 三种雷诺数的频率-振幅图 Fig.10 Frequency-amplitude diagram atthree Reynolds numbers |
图11为Re = 2.0×105、α=16°时一个波动周期中,连续的56个时间间隔的压力分布图。由于数量较多,图中未使用图例来区分每一时刻的压力分布曲线,仅用于展示压力振荡现象。从图中可以看出,在一个周期内,上翼面有两个区域存在明显的压力波动,一个区域为位于前缘的短泡区,另一个区域为位于尾缘的分离区。

|
图 11 一个波动周期内压力分布变化图 Fig.11 Change graph of pressure distribution over a fluctuation period |
采用相位平均法,得到图12所示的前半周期不同相位时翼型表面压力分布曲线图。相位0°时,前缘附近的负压峰被破坏,存在明显的逆压梯度,因此存在前缘短泡,同时后缘存在大范围流动分离引起的压力不连续现象,压力系数存在上下波动,此时升力系数最小。随着相位的增加,前缘分离泡逐渐减弱,直到相位38°时,逆压梯度消失,前缘不再存在层流分离泡,同时后缘分离也随相位增加而减弱。相位38°后,随着相位增加,前缘压力峰逐渐升高,上翼面整体负压增加,升力系数进一步增加,直到相位160°时,升力系数达到最大值。

|
图 12 前半周期不同相位时翼型表面压力系数曲线 Fig.12 Surface pressure coefficient curves on the airfoil atdifferent phases during the first half period |
图13为后半周期不同相位翼型表面压力曲线分布图。由相位160°开始,随着相位的增加,起初上翼面负压缓慢下降,直到相位257°时,前缘出现逆压梯度,短泡出现;随后相位继续增加,短泡引起的逆压梯度加剧,同时尾缘处出现明显的流动分离现象。通过以上分析可以得出结论,由于短泡的周期性生成引起升力系数周期性波动,造成了S1223翼型在特定低雷诺数、特定攻角下,发生低频震荡现象。
图14为Re = 2.0×105时不同攻角下升力系数瞬时变化曲线。当α = 14°时,此时并未发生失速现象,升力系数相对恒定。当α = 15°时,升力系数出现准周期性波动,即低频振荡现象,但振荡幅度较小。当α = 16°时,升力系数振荡幅度增大,频率增大,低频振荡现象更加明显。当α = 17°时,升力系数呈现无规则波动,此时翼型表面出现大范围流动分离现象。
通过以上分析可以总结,S1223翼型在某些低雷诺数下,当攻角略微大于临界攻角时,存在升力系数准周期性变化现象,这一现象主要是由S1223翼型上翼面出现的层流分离泡导致的,此时S1223翼型会周期性生成前缘短泡,从而引发低频振荡现象,导致其时均流场呈现长泡状态,这一变化同文献[22]结论类似。同时该现象的振幅及频率均随攻角的增加而增大,即振荡随攻角的增加而剧烈,当攻角超过一定值时,低频振荡消失,翼型表面发生大范围流动分离。

|
图 13 后半周期不同相位时翼型表面压力系数曲线 Fig.13 Surface pressure coefficient curves on the airfoil at different phases during the second half period |

|
图 14 不同攻角下瞬时升力系数(Re = 2×105) Fig.14 Instantaneous lift coefficients at different angles of attack (Re = 2×105) |
本文针对S1223翼型在不同雷诺数下时均流场的对比分析,探究3种雷诺数下(Re = 6.0×104、1.0×105、2.0×105)翼型临界攻角附近流场变化规律的差异,发现S1223翼型在特定雷诺数下临界攻角附近出现低频振荡现象。结合非定常结果,进一步解释了时均流场不同的原因,分析了翼型表面层流分离泡的变化规律。研究得出以下结论:
1)S1223翼型时均化升力特性总体上有以下特点。负攻角时,升力系数存在非线性现象,该现象与雷诺数无关;Re = 1.0×105时,升力系数曲线存在 “静态滞回”;当攻角由临界攻角逐渐增大时,不同雷诺数下升力系数变化规律不同,Re = 6.0×104、1.0×105时,升力系数迅速下降,而Re = 2.0×105时,升力系数缓慢下降。
2)下翼面层流分离泡的变化,是造成负攻角条件下升力系数非线性现象的主要原因。攻角由负逐渐增大至0°的过程中,下翼面起初呈现大范围流动分离状态,后随着攻角增大出现层流分离泡,分离泡随攻角增大逐渐减小并消失,升力曲线斜率逐渐增大;另外上翼面负压增强随攻角增大而增大,也是造成这一现象的部分原因。
3)低雷诺数下,雷诺数变化会引起失速流场的变化规律出现本质的不同。在攻角由临界攻角逐渐增大过程中,雷诺数较低时(Re = 6.0×104、1.0×105),攻角刚超过临界攻角后,流场迅速发生大范围流动分离现象,升力系数迅速减小;雷诺数较高但仍属于低雷诺数时(Re = 2.0×105),攻角刚刚超过临界攻角时,流场并没有迅速发生大范围流动分离,上翼面周期性生成前缘短泡,引发低频振荡现象,导致瞬时升力系数呈现准周期性振荡,时均化升力系数随攻角缓慢下降,时均化流场呈长泡结构。
本研究目前采用表面测压法,描绘了低雷诺数下翼型表面流场结构特点及准周期性变化的定性规律,但无法准确测量层流分离泡的分离及再附点,以及失速分离的分离点。因此针对低雷诺数下流场结构及变化规律的定量研究将是下一步的工作重点。
| [1] |
JONES B M. An experimental study of stalling of the wings[J]. The Aeronautical Journal, 1934, 38(285): 753-770. |
| [2] |
GAULT D E. Boundary-layer and stalling characteristics of the NACA 63-009 airfoil section[R]. NACA TN-1894.
|
| [3] |
GASTER M. The structure and behaviour of laminar separation bubbles[R]. R&M 1966-3595.
|
| [4] |
WONG C W, KURITA S, RINOIE K. Bubble burst control for stall suppression on a NACA 631-012 airfoil[C]//47th AIAA Aerospace Sciences Meeting including The New Horizons Forum and Aerospace Exposition, Orlando, Florida. Reston, Virginia: AIAA, 2009. doi: 10.2514/6.2009-1111.
|
| [5] |
KOCA K, GENÇ M S, AÇıKEL H H, et al. Identification of flow phenomena over NACA 4412 wind turbine airfoil at low Reynolds numbers and role of laminar separation bubble on flow evolution[J]. Energy, 2018, 144: 750-764. DOI:10.1016/j.energy.2017.12.045 |
| [6] |
SHEN X, AVITAL E, PAUL G, et al. Experimental study of surface curvature effects on aerodynamic performance of a low Reynolds number airfoil for use in small wind turbines[J]. Journal of Renewable and Sustainable Energy, 2016, 8(5): 053303. DOI:10.1063/1.4963236 |
| [7] |
王庶, 米建春. 大湍流度对超低雷诺数下翼型受力及绕流的影响[J]. 航空学报, 2011, 32(1): 41-48. WANG S, MI J C. Effect of large turbulence intensity on airfoil load and flow[J]. Acta Aeronautica et Astronautica Sinica, 2011, 32(1): 41-48. (in Chinese) |
| [8] |
吴鋆, 王晋军, 李天. NACA0012 翼型低雷诺数绕流的实验研究[J]. 实验流体力学, 2013, 27(6): 32-38. WU J, WANG J J, LI T. Experimental investigation on low Reynolds number behavior of NACA0012 airfoi[J]. Journal of Experiments in Fluid Mechanics, 2013, 27(6): 32-38. DOI:10.3969/j.issn.1672-9897.2013.06.006 (in Chinese) |
| [9] |
朱志斌, 刘强, 白鹏. 低雷诺数翼型层流分离现象大涡模拟方法[J]. 空气动力学学报, 2019, 37(06): 915-923. ZHU Z B, LIU Q, BAI P. Large eddy simulation method for the laminar separation phenomenon on low Reynolds number airfoils[J]. Acta Aerodynamica Sinica, 2019, 37(06): 915-923. DOI:10.7638/kqdlxxb-2018.0025 (in Chinese) |
| [10] |
白鹏, 崔尔杰, 李锋, 等. 对称翼型低雷诺数小攻角升力系数非线性现象研究[J]. 力学学报, 2006, 38(1): 1-8. BAI P, CUI E J, LI F, et al. Study of the nonlinear lift coefficient of the symmetrical airfoil at low Reynolds number near the 0° angle of attack[J]. Chinese Journal of Theoretical and Applied Mechanics, 2006, 38(1): 1-8. DOI:10.3321/j.issn:0459-1879.2006.01.001 (in Chinese) |
| [11] |
白鹏, 崔尔杰, 周伟江, 等. 隐式格式求解拟压缩性非定常不可压Navier-Stokes方程[J]. 计算物理, 2005, 22(5): 386-392. BAI P, CUI E J, ZHOU W J, et al. An implicit method for the pseudo-compressibility incompressible navier-stokes equation[J]. Chinese Journal of Computational Physics, 2005, 22(5): 386-392. DOI:10.3969/j.issn.1001-246X.2005.05.002 (in Chinese) |
| [12] |
白鹏, 崔尔杰, 周伟江, 等. 翼型低雷诺数层流分离泡数值研究[J]. 空气动力学学报, 2006, 24(4): 416-424. BAI P, CUI E J, ZHOU W J, et al. Numerical simulation of laminar separation bubble over 2D airfoil at low Reynolds number[J]. Acta Aerodynamica Sinica, 2006, 24(4): 416-424. DOI:10.3969/j.issn.0258-1825.2006.04.004 (in Chinese) |
| [13] |
白鹏, 李锋, 詹慧玲, 等. 翼型低Re数小攻角非线性非定常层流分离现象研究[J]. 中国科学: 物理学 力学 天文学, 2015, 45(2): 46-57. BAI P, LI F, ZHAN H L, et al. Study about the non-linear and unsteady laminar separation phenomena around the airfoil at low Reynolds number with low incidence[J]. Scientia Sinica (Physica, Mechanica & Astronomica), 2015, 45(2): 46-57. (in Chinese) |
| [14] |
孟宣市, 杨泽人, 陈琦, 等. 低雷诺数下层流分离的等离子体控制[J]. 航空学报, 2016, 37(7): 2112-2122. MENG X S, YANG Z R, CHEN Q, et al. Laminar separation control at low Reynolds numbers using plasma actuation[J]. Acta Aeronautica et Astronautica Sinica, 2016, 37(7): 2112-2122. DOI:10.7527/S1000-6893.2015.0244 (in Chinese) |
| [15] |
MENG X S, HU H Y, YAN X, et al. Lift improvements using duty-cycled plasma actuation at low Reynolds numbers[J]. Aerospace Science and Technology, 2018, 72: 123-133. DOI:10.1016/j.ast.2017.10.038 |
| [16] |
ALMUTAIRI J H, JONES L E, SANDHAM N D. Intermittent bursting of a laminar separation bubble on an airfoil[J]. AIAA Journal, 2010, 48(2): 414-426. DOI:10.2514/1.44298 |
| [17] |
ALMUTAIRI J, ALQADII, ELJACK E. Large eddy simulation of a NACA-0012 airfoil near stall[R]//Direct and Large-Eddy Simulaton IX, ERCOFTAC Series 20, 2015. doi: 10.1007/978-3-319-14448-1_49.
|
| [18] |
ALMUTAIRI J, ELJACK E, ALQADI I. Dynamics of laminar separation bubble over NACA-0012 airfoil near stall conditions[J]. Aerospace Science and Technology, 2017, 68: 193-203. DOI:10.1016/j.ast.2017.05.015 |
| [19] |
ZAMAN K B M Q, MCKINZIE D J, RUMSEY C L. A natural low-frequency oscillation of the flow over an airfoil near stalling conditions[J]. Journal of Fluid Mechanics, 1989, 202: 403-442. DOI:10.1017/s0022112089001230 |
| [20] |
BRAGG M B, HEINRICH D C, BALOW F A, et al. Flow oscillation over an airfoil near stall[J]. AIAA Journal, 1996, 34(1): 199-201. DOI:10.2514/3.13045 |
| [21] |
BROEREN A P, BRAGG M B. Flowfield measurements over an airfoil during natural low-frequency oscillations near stall[J]. AIAA Journal, 1999, 37(1): 130-132. DOI:10.2514/2.678 |
| [22] |
RINOIE K, TAKEMURA N. Oscillating behaviour of laminar separation bubble formed on an aerofoil near stall[J]. The Aeronautical Journal, 2004, 108(1081): 153-163. DOI:10.1017/s0001924000000063 |
| [23] |
SELIG M S, GUGLIELMO J J. High-lift low Reynolds number airfoil design[J]. Journal of Aircraft, 1997, 34(1): 72-79. DOI:10.2514/2.2137 |
| [24] |
LIU P Q, TANG Z H, CHEN Y X, et al. Experimental feasibility assessment of counter-rotating propellers for stratospheric airships[C]//53rd AIAA Aerospace Sciences Meeting, Kissimmee, Florida. Reston, Virginia: AIAA, 2015. doi: 10.2514/6.2015-1029.
|
| [25] |
陈庆亚, 田希晖, 车学科, 等. 平流层螺旋桨等离子体流动控制地面实验方法[J]. 实验流体力学, 2015(5): 90-96. CHEN Q Y, TIAN X H, CHE X K, et al. Ground experimental method for stratospheric propeller plasma flow control[J]. Journal of Experiments in Fluid Mechanics, 2015(5): 90-96. DOI:10.11729/syltlx20140140 (in Chinese) |
| [26] |
SUDHAKAR S, VENKATAKRISHNAN L, RAMESH O N. The influence of leading-edge tubercles on airfoil performance at low Reynolds numbers[C]//Proc of the AIAA Scitech 2020 Forum, Orlando, FL. Reston, Virginia: AIAA, 2020. doi: 10.2514/6.2020-2219.
|
| [27] |
GUERRERO J E. Aerodynamic performance of cambered heaving airfoils[J]. AIAA Journal, 2010, 48(11): 2694-2698. DOI:10.2514/1.J050036 |
| [28] |
ARANAKE A C, LAKSHMINARAYAN V K, DURAISAMY K. Computational analysis of shrouded wind turbine configurations using a 3-dimensional RANS solver[J]. Renewable Energy, 2015, 75: 818-832. DOI:10.1016/j.renene.2014.10.049 |
| [29] |
高建强, 姜华伟, 夏豹, 等. 鼓泡流化床风帽压力信号的频谱分析[J]. 动力工程学报, 2011, 31(5): 336-341. GAO J Q, JIANG H W, XIA B, et al. Frequency spectrum analysis on pressure signals of wind caps in a bubbling fluidized bed[J]. Chinese Journal of Power Engineering, 2011, 31(5): 336-341. (in Chinese) |
| [30] |
张伏生, 耿中行, 葛耀中. 电力系统谐波分析的高精度FFT算法[J]. 中国电机工程学报, 1999(3): 63-66. ZHANG F S, GENG Z X, GE Y Z. Fft algorithm with high accuracy for harmonic analysis in power system[J]. Proceedings of the Chinese Society for Electrical Engineering, 1999(3): 63-66. DOI:10.3321/j.issn:0258-8013.1999.03.015 (in Chinese) |
| [31] |
TANI I. Low-speed flows involving bubble separations[J]. Progress in Aerospace Sciences, 1964, 5: 70-103. DOI:10.1016/0376-0421(64)90004-1 |




