2. 中国石油大学(北京) 重质油国家重点实验室,北京 102249;
3. 中国科学院 绿色过程制造创新研究院,北京 100190;
4. 中国科学院大学 化学工程学院 北京 100049
2. State Key Laboratory of Heavy Oil Processing, China University of Petroleum (Beijing), Beijing 102249, China;
3. Innovation Academy for Green Manufacture, Chinese Academy of Sciences, Beijing 100190, China;
4. School of Chemical Engineering, University of Chinese Academy of Sciences, Beijing 100049, China
圆球绕流曳力系数(drag coefficient,CD)是流体力学研究的重要基础问题,其可作为量化指标广泛应用于航空航天、医药加工、石油化工及能源工业等领域中。
在通常的不可压缩连续流体中,圆球绕流曳力系数CD被认为是雷诺数(Reynolds number,Re)的函数,一百多年来的国内外学者也对此进行了详尽研究。而在飞行器涉及的高速高空环境中,往往伴有高马赫数的可压缩性以及高努森数条件下的稀薄效应,CD不仅与Re相关,还与马赫数(Mach number,Ma)或者努森数(Knudsen number,Kn)相关。
高马赫数条件下圆球绕流曳力系数CD的研究主要有地面实验[1-13]和数值模拟[14-19]等方法。实验方法又可分为直接测量和间接计算两种方式。直接测量是指在风洞实验中通过测量细线悬挂球体偏转角度或金属支撑球体受力计算球体的CD[1, 2, 4, 8-11, 13]。1961年Peter等[10]在干燥的空气中用细线悬挂球体,测量偏转角度来计算圆球受流体作用力,获得了3.8 < Ma < 4.3,50 < Re < 1000范围内圆球绕流的 CD值。1962年Aroesty[9]采用相似的方法在伯克利低密度风洞中测量得到了2 < Ma < 6,10 < Re < 10000范围内的 CD。间接计算是指通过弹道的形式发射物体,获得位置与时间的关系,从而求解获得CD[3, 5-7, 12]。1967年Short等[7]通过弹道实验测量获得了0.4×106 < Re < 1.6×10 6,0.4 < Ma < 14.5范围内圆球绕流的 CD。1968年Crowe等[5]通过弹道实验获得了0.01 < Re < 5.1,0.036 < Ma < 1.77范围内圆球绕流的 CD。1972年Bailey[3]发射泡沫塑料球至干燥空气中,记录不同时刻球的位置,计算得到球体的CD。
风洞及弹道实验获得的CD结果较为可信,但其成本高昂,测量过程易受其他因素影响,误差较大且难以获得流场的细节特征。随着计算机技术和流体力学计算方法的发展,数值模拟作为一种可信的方法被用来研究圆球绕流。
Tao等[14]用格子玻尔兹曼方法(lattice Boltzmann method, LBM)模拟研究了0.1 < Re < 3.5和0.1 < Kn < 1.1条件下的圆球绕流。Nagata等 [15]采用计算流体力学(computational fluid dynamics,CFD)方法,模拟研究圆柱区域中50 < Re < 300和0.3 < Ma < 2条件下的圆球绕流,并获得了丰富的绕流尾迹特征。Dogra等 [19]使用直接数值模拟蒙特卡洛方法(direct simulation Monte Carlo, DSMC)研究了Re > 100和 Kn < 0.1条件下的圆球绕流。
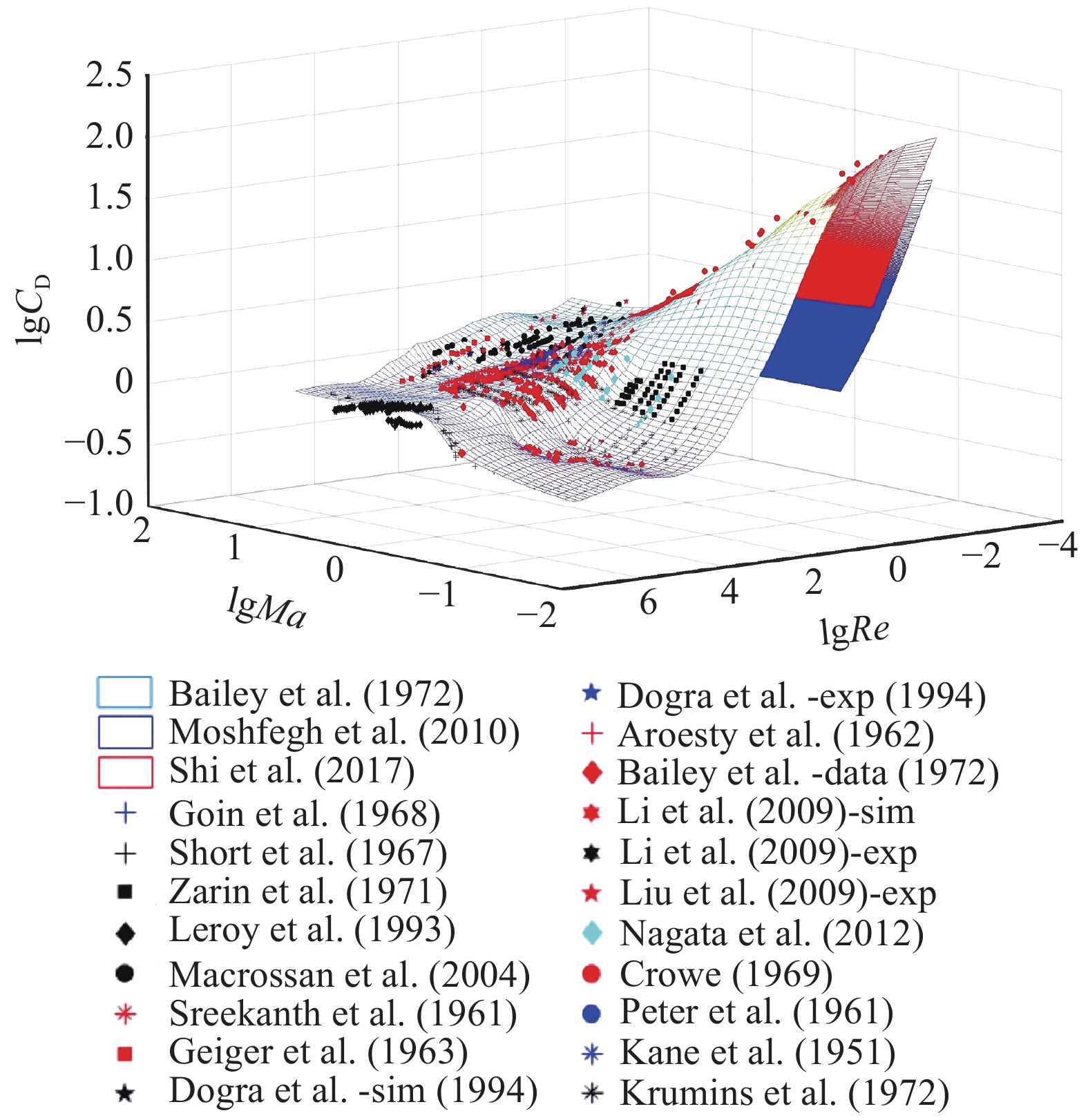
我们整理了文献中不同Re和Ma下的CD数据,绘制于图1中。可以发现,文献中CD数据较为分散,不同文献中的变化规律有时还有所差异;另外,在1≤Re≤20和0.1≤Ma≤3这一趋势变化剧烈的范围内,特别在1≤Re≤10和0.5≤Ma≤3高马赫数低雷诺数区间内,文献中CD数据不全,难以准确揭示该范围内的CD与马赫数的变化规律。
|
图 1 圆球绕流曳力系数 Fig.1 A compilation of drag coefficients of flows past a sphere |
在高马赫数低雷诺数条件下,努森数Kn较大,气体流动为过渡流(0.1≤Kn≤10)或者分子流(Kn≥10)。该状态下实验测量困难,而基于连续流体的CFD方法难以适用,LBM方法的玻尔兹曼方程适合描述Kn≥10的流体,分子动力学(molecular dynamics, MD)方法计算精确但计算需求极大。
葛蔚等[20-21]提出的拟颗粒模型(pseudo-particle model,PPM)将软球模型的时驱算法结合到硬球模型(hard sphere,HS)中,具有MD计算精确和DSMC计算高效的优点,同时PPM采用时间驱动,提高了计算可扩展性。在PPM中,两个拟颗粒在接触碰撞时距离会稍小于粒子直径,将碰撞时距离的统计平均作为粒子有效直径,此时拟颗粒性质就能与硬球颗粒等效,即拟颗粒模型可以视作一种可变径硬球模型。沈国飞和葛蔚[22]将HS与 PPM 耦合建立了硬球-拟颗粒方法(HS-PPM):在各子区域内部采用HS模拟流场,而用PPM模拟边界区域,在保证碰撞精确性的同时解决了传统HS不易扩展的问题,便于大规模并行计算。HS-PPM为高马赫数低雷诺数条件下的圆球绕流研究提供了合适的模拟计算方法。
本文计划应用HS-PPM方法模拟1≤Re≤20和0.1≤Ma≤3条件下圆球绕流过程,获得的曳力系数数据用于初步分析CD(Re, Ma)。
1 圆球绕流HS-PPM模拟HS-PPM耦合方法模拟圆球绕流示意于图2中,其中U表示来流气速,L为模拟区域长度,H为高度,W为宽度,L1为圆球离入口距离。

|
图 2 圆球绕流模拟示意 Fig.2 A sketch of the numerical simulation of a flow past a sphere |
本文分别将气体粒子的质量、直径作为质量、长度单位,拟颗粒更新时间步长为1个时间单位。
1.1 HS-PPM方法在HS-PPM耦合方法中,HS用于精确计算粒子碰撞,而PPM有效扩展计算规模。两个粒子是否发生碰撞的判据表述为两粒子间距离|r1–r2|小于它们的半径之和以及r1–r2与v1–v2的点积为负值,则它们将以光滑硬球方式碰撞。
| $ {{v}}_{1}'={{v}}_{1}-\frac{(1+e){m}_{2}}{{m}_{1}+{m}_{2}}\frac{({{v}}_{1}-{{v}}_{2})\cdot ({{r}}_{1}-{{r}}_{2})}{{|{{r}}_{1}-{{r}}_{2}|}^{2}}({{r}}_{1}-{{r}}_{2}) $ | (1) |
| $ {{v}}_{2}'={{v}}_{2}+\frac{(1+e){m}_{1}}{{m}_{1}+{m}_{2}}\frac{({{v}}_{1}-{{v}}_{2})\cdot ({{r}}_{1}-{{r}}_{2})}{{|{{r}}_{1}-{{r}}_{2}|}^{2}}({{r}}_{1}-{{r}}_{2}) $ | (2) |
其中
根据模拟需要将区域划分为Nx×Ny×Nz个子区域,每个子区域内部采用HS,边界区采用PPM连接各HS模拟区域,示意于图2中。每个进程负责一个子区域内计算,相邻进程间构建一层虚拟缓冲区由消息传递接口(message passing interface,MPI)协议实现信息交换。
1.2 气体-圆球作用运动的气体粒子与圆球发生接触时其路径会发生变化,涉及的气体-圆球间作用通常采用反弹或漫反射方式处理。反弹模型中入射粒子速度法向分量沿法线反转,切向分量保持。漫反射模型中出射粒子速度遵循给定温度下的偏麦克斯韦分布,与入射速度无关,具有完全热适应能力。在高马赫数流动中,实际气体粒子与圆球的作用同时结合了上述两种方式,引入热适应系数α(0≤α≤1)来描述[23],即粒子的出射速度中α部分来自于偏麦克斯韦分布的漫反射,(1–α)部分采用反弹模型。
| $ {v}'=\alpha {v}_{\mathrm{d}\mathrm{i}\mathrm{f}\mathrm{f}\mathrm{u}\mathrm{s}\mathrm{e}}+\left(1-\alpha \right){v}_{\mathrm{s}\mathrm{p}\mathrm{e}\mathrm{c}\mathrm{u}\mathrm{l}\mathrm{a}\mathrm{r}}{} $ | (3) |
如图2所示,气体从左边以速度U均匀流入模拟区域,从右边出去的气体粒子将在左边控制区内应用速度重新标定控温法[20-21]被赋予初速U重新生成,而上下和前后方向采用周期性边界条件,保证气体粒子数守恒。控制区厚度为1,沿y方向和z方向被分割成4Ny×4Nz个子区。这样处理后,气体的流动长时间演化达到稳态状态。
1.4 曳力系数的计算气体粒子与圆球之间的每次碰撞均会对圆球产生一个冲量,则在一定时间段内统计这些冲量得到圆球受到气体的平均作用力FD为:
| $ {F}_{\mathrm{D}}=\frac{{P}_{2}-{P}_{1}}{{T}_{2}-{T}_{1}}{} $ | (4) |
其中P2–P1表示T2–T1时间内动量改变量的累加值。圆球绕流的曳力系数CD计算公式为:
| $ {C}_{{\rm{D}}}=\frac{{F}_{\mathrm{D}}}{A\rho {U}^{2}/2}=\frac{8{F}_{\mathrm{D}}}{{\rho U}^{2}{\text{π}} {D}^{2}}{} $ | (5) |
其中D为圆球直径。
在本文涉及的条件下,体系运行1×106时间后流动达到稳定,随后开始统计计算曳力系数,统计持续时间为4×106(Re<15)或1×106(Re≥15)。
2 结果与讨论圆球绕流HS-PPM模拟得到的CD不仅与Re和Ma相关,还受到模拟设置的影响,主要包括模拟区域设置和热适应系数α。因此本部分首先考察模拟区域设置和热适应系数等模拟设置对CD的影响规律,从而获得合理的模拟设置用于1≤Re≤20和0.1≤Ma≤3条件下圆球绕流CD数据的补充和分析。
2.1 曳力系数模拟计算以Re = 19.4和Ma = 1.195条件下的圆球绕流模拟为例,说明曳力系数的计算过程和误差分析。在L×W×H = 276.8×276.8×276.8区域内用3.24×106气体粒子,模拟了Re = 19.4和Ma = 1.195条件下的圆球绕流过程,记录不同时间段内的气体粒子与圆球间碰撞信息,用于曳力系数计算,结果如图3所示。从图3中可以看到,模拟计算的曳力系数在1×106时间后趋于定值,

|
图 3 Re = 19.4和Ma = 1.195,随时间变化的曳力系数和累积碰撞数 Fig.3 Temporal evolutions of the drag coefficient and accumulative collision number at Re = 19.4 and Ma = 1.195 |
圆球绕流曳力系数的计算精度还与流场是否充分发展相关,因此比较了三个不同条件下的圆球绕流流场模拟结果,见图4。从中可以发现:随着Re增大,尾流在圆球后部逐渐分离,形成对涡(图4(b));当Ma > 1时,在圆球前面形成激波,此时需要更宽的模拟区域用于激波面往两侧发展( 图4(c))。这些发现与文献[22,24]中的结果较为相符。

|
图 4 |

|
图 4 中间截面上的密度云图和流线示意 Fig.4 Density contours and streamlines in the middle plane |
圆球绕流HS-PPM模拟在一个有限空间内进行,获得的结果通常会与无限大流场内圆球绕流有差异,因此有必要讨论如何设置模拟区域使偏差在合理范围内。
在一定的Re和Ma条件下,分别改变模拟区域长度、宽度(高度)以及圆球位置,作了一系列圆球绕流HS-PPM模拟,其中长度或宽度范围为5D~40D,圆球位置为长度的0.25处、0.38处和0.5处。
图5表示Re = 19.4和Ma = 1.195条件下,CD模拟结果随长度或宽度的变化趋势。从图中可以看到,随着长度或宽度的增大,CD逐渐趋于稳定值CD∞,且在20D后CD与CD∞偏差较小。图5还显示了该条件下CD实验值处于热适应系数α = 0及α = 1下的两个CD∞之间,从另一个角度论证了HS-PPM模拟获得圆球绕流CD的合理性。

|
图 5 |

|
图 5 Re= 19.4和Ma = 1.195,不同长度和宽度的CD Fig.5 The variation of drag coefficient with the lengths and widths of the simulation domain at Re = 19.4 and Ma = 1.195 |
进一步模拟研究发现:Ma < 1和 Re < 10时,CD与模拟区域的相关性较小;Ma < 1和 Re > 10时,随着 Re的增大,圆球绕流逐渐不稳定,需要适当增大区域长度满足尾迹的发展;Ma > 1和 Re < 10时,圆球前方流体出现激波面,此时需要增大区域宽度(高度)用于激波面的发展;Ma > 1和 Re>10时,模拟区域长度和宽度(高度)均需要增大。基于上述认识,我们给出了不同条件下模拟区域的建议设置,列于表1中。并按照建议的区域设置模拟了不同Re和Ma下的圆球绕流,得到的CD结果与CD∞偏差在2%以内(见表2),表明有限区域的模拟结果可以近似表达无限区域内圆球绕流。
| 表 1 合适的模拟区域 Table 1 Appropriate simulation domains under different conditions |
|
|
| 表 2 不同条件下CD模拟结果 Table 2 Drag coefficients at different Re and Ma |
|
|
在高马赫数下稀薄效应明显,气体-圆球间通常介于无滑移条件和完全滑移条件之间,HS-PPM模拟圆球绕流引入热适应系数α来表达气体-圆球间作用中漫反射成分:α = 0时,镜面反弹滑移;α = 1时,完全漫反射。而α的不同取值会对CD结果造成影响,佐证于图5中。赵琪和马琳博等[23-24]已对此进行了初步分析,发现圆球绕流CD模拟值与热适应系数α正相关。
基于上述发现,将不同α下的CD与实验结果进行比较,获得两者偏差最小的热适应系数合理值αr。图6表示Re = 5.1和Ma = 0.4条件下不同α模拟得到不同CD,可以发现CD与α的关系呈显著的线性关系,CD=1.78α+4.16(R2 = 0.998),进而得到CD与实验值相符的αr = 0.643。类似地,完成了Re = 19.4和Ma = 1.195、Re = 30.2和Ma = 1.896条件下的CD与α的关系研究,获得对应的αr,结果列于表3中。采用αr作了验证性模拟,获得的CD与实验值偏差在1%以内。

|
图 6 Re = 5.1和Ma = 0.4,CD与α的关系 Fig.6 The variation of drag coefficient with α atRe = 5.1 and Ma = 0.4 |
| 表 3 不同条件下的热适应系数合理值αr Table 3 Reasonable accommodation coefficients αrat different Re and Ma |
|
|
不同Re和Ma条件下的αr存在一定的差异,表3也表明αr约在0.65-0.75之间,将αr统一设置为0.7可以平衡精度和严格验证所需的大批量模拟需求。我们采用αr = 0.7模拟计算得到其他条件下的CD,并与相应的实验值比较,结果列于表4中。可以发现,αr = 0.7时的模拟值与实验值偏差均较小(5%以内),故后续模拟均采用αr = 0.7。
2.4 1≤Re≤20和0.1≤Ma≤3的曳力系数CD在得到合适的区域设置条件和热适应系数后。应用HS-PPM模拟圆球绕流获得了1≤Re≤20,0.1≤Ma≤3范围内的曳力系数CD,结果绘制于图7中。详细的模拟参数和结果列于附录A的表格中。
| 表 4 α = 0.7, 不同条件下CD模拟结果 Table 4 Drag coefficients at α = 0.7 |
|
|

|
图 7 1≤Re≤20时,CD与Ma的关系 Fig.7 The variation of the drag coefficient with Ma at 1≤Re≤20 |
图7中的实心点表示HS-PPM模拟计算得到的CD,空心点表示Ma→0条件下标准阻力系数CD (Re)。从图7中可以看出,在1≤Re≤20范围内,CD随着Ma的增加而逐渐下降;Re越大,CD下降趋势趋缓。
马赫数Ma对CD(Re)的修正可以表达为下面形式,
| $ {C}_{{\rm{D}}}\left(Re,Ma\right)={C}_{{\rm{D}}}\left(Re\right)[a{e}^{-bMa}+(1-a\left)\right] $ | (6) |
其中[ae–bMa + (1–a)]为曳力系数修正项,系数a和b与Re相关。
按照公式(6)拟合CD数据得到了不同Re下的系数a和b(列于表5中),并将系数a和b分别拟合成Re的函数(如图8)。
| 表 5 不同Re下的参数a和b Table 5 Parameters a and b at different Re |
|
|

|
图 8 参数a,b与Re的关系 Fig.8 The variations of the parameters a and b with Re |
| $ a\left(Re\right)=-0.0238Re+0.845 $ | (7) |
| $ b\left(Re\right)=0.203+6.19/\left(Re+1.18\right){} $ | (8) |
本文应用HS-PPM方法模拟了1≤Re≤20和0.1≤Ma≤3条件下的圆球绕流过程。在讨论确认合理的模拟区域设置和热适应系数αr = 0.7后,获得不同Re和Ma下的圆球绕流曳力系数CD数据,并基于此建立高马赫数低雷诺数条件下马赫数Ma对CD(Re)的修正模型,
| $ {C}_{{\rm{D}}}\left(Re,Ma\right)={C}_{{\rm{D}}}\left(Re\right)[a\left(Re\right){e}^{-b\left(Re\right)Ma}+(1-a\left(Re\right)\left)\right]{} $ |
其中,
| $\begin{split}& a\left(Re\right)=-0.0238Re+0.845\\& b\left(Re\right)=0.203+6.19/ \left(Re+1.18\right) \end{split}{\text{。}}$ |
高马赫数下圆球绕流流动形态复杂,本文仅对1≤Re≤20和0.1≤Ma≤3范围内的圆球绕流曳力系数作了定量分析,而其他范围内的曳力系数变化趋势仍难以用统一的方式进行描述。此外,高马赫数特别是Ma > 3条件下,激波的存在和发展对圆球绕流流动形态影响巨大,而且会发生强烈的高速热效应,这些都会对曳力系数的计算产生重要影响,需要进一步深入研究。
| [1] |
SPEARMAN M L, BRASWELL D O. Aerodynamics of a sphere and an oblate spheroid for Mach numbers from 0.6 to 10.5 including some effects of test conditions[R]. National Aeronautics and Space Administration, Langley. NASA TM-109016.
|
| [2] |
KRUMINS M V. A review of sphere drag coefficients applicable to atmospheric density sensing[R]. NASA CR-126742, NOLTR 72-34, 1972.
|
| [3] |
BAILEY A B, HIATT J. Sphere drag coefficients for a broad range of Mach and Reynolds numbers[J]. AIAA Journal, 1972, 10(11): 1436-1440. DOI:10.2514/3.50387 |
| [4] |
ZARIN N A, ARTHUR NICHOLLS J. Sphere drag in solid rockets—non-continuum and turbulence effects[J]. Combustion Science and Technology, 1971, 3(6): 273-285. DOI:10.1080/00102207108952295 |
| [5] |
CROWE C T, BABCOCK W R, WILLOUGHBY P G, et al. Measurement of particle drag coefficients in flow regimes encountered by particles in a rocket nozzle[R]. Defense Technical Information Center, AD0850098, 1968. doi: 10.21236/ad0850098.
|
| [6] |
GOIN K L, LAWRENCE W R. Subsonic drag of spheres at Reynolds numbers from 200 to 10, 000[J]. AIAA Journal, 1968, 6(5): 961-962. DOI:10.2514/3.4648 |
| [7] |
SHORT B J. Dynamic flight behavior of a ballasted sphere at Mach numbers from 0.4 to 14.5[R]. National Aeronautics and Space Administration, NASA TN D-4198, 1967.
|
| [8] |
GEIGER R E. Some sphere drag measurements in low density shock tunnel flows[R]. Defense Technical Information Center, AD0409517, 1963. doi:10.21236/ad0409517.
|
| [9] |
AROESTY J. Sphere drag in a low density supersonic flow[M]//Rarefied gas dynamics, Volume 2: Proceedings of the third international symposium. LAURMANN J A, edited. New York: Academic Press, 1963: 261-277.
|
| [10] |
WEGENER P P, ASHKENAS H. Wind tunnel measurements of sphere drag at supersonic speeds and low Reynolds numbers[J]. Journal of Fluid Mechanics, 1961, 10(4): 550-560. DOI:10.1017/s0022112061000354 |
| [11] |
SREEKANTH A K. Drag measurements on circular cylinders and spheres in the transition regime at a Mach number of 2[R]. Ontario: University of Toronto, UTIA Report, No. 74, ARL-53, 1961. doi:10.1007/978-3-642-02890-8_821.
|
| [12] |
MAY A. Supersonic drag of spheres at low Reynolds numbers in free flight[J]. Journal of Applied Physics, 1957, 28(8): 910-912. DOI:10.1063/1.1722886 |
| [13] |
KANE E D. Sphere drag data at supersonic speeds and low Reynolds numbers[J]. Journal of the Aeronautical Sciences, 1951, 18(4): 259-270. DOI:10.2514/8.1924 |
| [14] |
TAO S, ZHANG H L, GUO Z L. Drag correlation for micro spherical particles at finite Reynolds and Knudsen numbers by lattice Boltzmann simulations[J]. Journal of Aerosol Science, 2017, 103: 105-116. DOI:10.1016/j.jaerosci.2016.10.006 |
| [15] |
NAGATA T, NONOMURA T, TAKAHASHI S, et al. Investigation on subsonic to supersonic flow around a sphere at low Reynolds number of between 50 and 300 by direct numerical simulation[J]. Physics of Fluids, 2016, 28(5): 056101. DOI:10.1063/1.4947244 |
| [16] |
MOSHFEGH A, SHAMS M, AHMADI G, et al. A new expression for spherical aerosol drag in slip flow regime[J]. Journal of Aerosol Science, 2010, 41(4): 384-400. DOI:10.1016/j.jaerosci.2010.01.010 |
| [17] |
LI Z H, ZHANG H X. Gas-kinetic numerical studies of three-dimensional complex flows on spacecraft re-entry[J]. Journal of Computational Physics, 2009, 228(4): 1116-1138. DOI:10.1016/j.jcp.2008.10.013 |
| [18] |
CUI Z X, LIU Y, SO R M C. Lattice Boltzmann simulation of flow past a sphere up to Reynolds number of 300[M]//Computational Mechanics. Tsinghua University Press and Springer-Verlag, 2004: 327-332.
|
| [19] |
DOGRA V K, MOSS J N, WILMOTH R G, et al. Hypersonic rarefied flow past spheres including wake structure[J]. Journal of Spacecraft and Rockets, 1994, 31(5): 713-718. DOI:10.2514/3.26503 |
| [20] |
GE W, LI J H. Macro-scale phenomena reproduced in microscopic systems—pseudo-particle modeling of fluidization[J]. Chemical Engineering Science, 2003, 58(8): 1565-1585. DOI:10.1016/S0009-2509(02)00673-5 |
| [21] |
GE W, ZHANG J Y, LI T H, et al. Pseudo-particle simulation of multi-scale heterogeneity in fluidization[J]. Chinese Science Bulletin, 2003, 48(7): 634-636. DOI:10.1007/BF03325644 |
| [22] |
张成龙, 沈国飞, 葛蔚. 硬球-拟颗粒耦合模拟超声速流动[J]. 计算机与应用化学, 2016, 33(11): 1135-1144. ZHANG C L, SHEN G F, GE W. Simulation of supersonic flow with hard-sphere/pseudo-particle modeling(HS-PPM)[J]. Computers and Applied Chemistry, 2016, 33(11): 1135-1144. DOI:10.16866/j.com.app.chem201611001 (in Chinese) |
| [23] |
赵祺, 赵明璨, 马琳博, 等. 硬球-拟颗粒模拟高超声速稀薄气体流动[J]. 过程工程学报, 2019, 19(6): 1093-1100. ZHAO Q, ZHAO M C, MA L B, et al. Hard-sphere/pseudo-particle modeling(HS-PPM) for hypersonic rarefied gas flow[J]. The Chinese Journal of Process Engineering, 2019, 19(6): 1093-1100. DOI:10.12034/j.issn.1009-606X.219120 (in Chinese) |
| [24] |
马琳博, 赵明璨, 赵祺, 等. 低马赫数下圆球绕流的硬球-拟颗粒模拟[J]. 计算机与应用化学, 2019, 36(5): 439-444. MA L B, ZHAO M C, ZHAO Q, et al. Simulation of flow around a single sphere at low Mach numbers by hard sphere/pseudo particle modeling(HS-PPM)[J]. Computers and Applied Chemistry, 2019, 36(5): 439-444. DOI:10.16866/j.com.app.chem201905001 (in Chinese) |



