2. 北京大学 应用物理与技术研究中心和高能量密度物理数值模拟教育部重点实验室,北京 100871;
3. 北京理工大学 爆炸科学与技术国家重点实验室,北京 100081;
4. 南京理工大学 瞬态物理国家重点实验室,南京 210094;
5. 北京理工大学 宇航学院,北京 100081
2. Center for Applied Physics and Technology, MOE Key Center for High Energy Density Physics Simulations, Peking University, Beijing 100871, China;
3. State Key Laboratory of Explosion Science and Technology, Beijing Institute of Technology, Beijing 100081, China;
4. Key Laboratory of Transient Physics, Nanjing University of Science and Technology, Nanjing 210094, China;
5. School of Aerospace Engineering, Beijing Institute of Technology, Beijing 100081, China
在自然界和工程技术领域存在着大量形式各异的多相复杂流动,例如超新星爆发、岩土矿石开采中的多孔介质流动、石油开采中原油在运输管道中的运输、航空发动机中的气液燃烧、武器物理、惯性约束核聚变,等等。多相复杂流动研究具有重要的基础与现实意义。
多相复杂流动系统研究,需要不同层次、不同视角的方法和认识。目前,在微观、介观和宏观层面都有相应的描述方法。在微观层面,主要建模和模拟方法是分子动力学(Molecular Dynamics, MD)[1-8],其中分子间作用势的构建是模型构建的关键,分子间作用势有效半径的选取是模拟过程中的关键。有效半径的选取,以满足需求且最小为最佳原则,一般通过模拟结果拟合已知的关键物性参数,根据模拟结果的合理性来判断。MD的优点是提供的信息完备,但缺点是能够模拟的时间和空间尺度有限,目前主要用于一些分子、原子层次的机理研究[9]。宏观模型主要是指基于纳维-斯托克斯(Navier-Stokes,NS)方程的各类多相流模型,模拟方法以传统计算流体力学方法为主[10- 11],近年来,光滑粒子方法、格子玻尔兹曼方法(Lattice Boltzmann Method, LBM)等得到了快速发展和广泛应用[12-13]。多相流系统的介观模型,一般是指基于非平衡统计物理学中动理学理论构建的动理学模型。
经过30年左右的迅猛发展,LBM已经快速成长为计算流体力学领域中的重要组成部分[14-26]。LBM方法与应用方面的研究论文,其作者的学习、研究背景涵盖领域极广,因而同一个词汇在不同的文献里承载的内涵也许并不相同。文献中的很多LBM是以恢复或者求解流体力学方程为目的和功能的。但作为一种全新的数值解法,一大批非流体方程例如Benjamin方程、Korteweg-de Vries (KdV)-Burgers方程、Ginzburg-Landau方程、波动方程、Poisson方程、Laplace方程、Lorenz方程、Fisher方程、Kuramoto-Sivashinsky方程、Richards方程、Schrödinger方程等的LBM解法也引起了广泛的兴趣,获得了广泛研究。因为恢复或者求解的方程并不是一般意义下的流体力学方程(组),所以这部分LBM所用的“玻尔兹曼方程”、“矩关系”也并不是非平衡统计物理学意义下的玻尔兹曼方程、矩关系。这部分LBM是纯计算数学意义下的偏微分方程(Partial Differential Equation, PDE)数值解法。即便是恢复或者求解流体力学方程(组)的LBM中,有些LBM使用的“玻尔兹曼方程”和“矩关系”是与非平衡统计物理学理论一致的,有些则不一致或者部分不一致。这些具体处理方法的不同,展现的是LBM方法内涵的多样性;只要处理得当,LBM便可满足相应的需求。
在复杂流体数值研究中,物理模型构建和方程解法设计是不可或缺的两个重要环节。在传统计算流体力学中,物理建模和算法设计的界限是清晰的,后者为数值求解前者所获方程(方程组)提供离散格式和步骤。近几十年来,元胞自动机-格子气-格子玻尔兹曼系列方法的出现,让二者在某些情形的界限变得模糊。因为从不同的视角看,这些方法便具有不同的功能。或者说,这些方法本身就可以朝着不同的方向发展。一方面,从物理学视角,长期以来,元胞自动机-格子气模型就是一大类复杂系统研究的理想化模型,统计物理与复杂系统的很多研究就是基于这类理想化模型的。另一方面,近30年来,格子气-格子玻尔兹曼又被作为一种全新的方程解法,在计算数学的规范下获得了广泛的研究。因为目标不同,决定了构建规则不可能完全相同,所以朝着不同目标发展的这两个方向成为这类方法研究的重要内容。在目前的绝大多数文献中,LBM的功能是恢复或者求解相应的偏微分方程,因而LBM在很大程度上成为“偏微分方程数值解法LBM”的简称。
在物理建模方面,又可粗略地分为两种情形:A.传统模型存在、合理、物理功能足够且方便有效的情形;B.传统模型不存在(以前未涉猎的新领域)、不再合理或物理功能不足的情形。元胞自动机-格子气-格子玻尔兹曼系列方法在情形A和情形B均适用。在情形A,这些方法又可视为求解传统模型方程或方程组的一种全新方法(其求解思路与传统解法完全不同)。因为数值解法研究和物理建模研究目标不同,所以需要遵循的规则不会完全相同;即使是从同一起点出发,即使有重叠,二者的发展轨迹也不会完全相同;二者时而近时而远,在相互启发中发展。
在本文中,基于或借鉴动理学理论的方法粗略地划分为两类:方程解法设计和物理模型构建方法,重点讨论流体系统的物理建模,重点关注传统模型描述不了或描述不好而MD又由于适用尺度受限无能为力的“介尺度”、两难情形。这类“介尺度”物理问题的研究需求是离散玻尔兹曼方法(Discrete Boltzmann Method, DBM)产生的背景和驱动力。在不产生歧义的情形,DBM又可视为离散玻尔兹曼模型(Discrete Boltzmann Model)、离散玻尔兹曼建模方法(Discrete Boltzmann Modeling method)的简称。
原则上,广义地讲,将玻尔兹曼方程在某些方面做些离散而做进一步研究的方法,甚至基于玻尔兹曼方程发展起来的离散方法都可以顾名思义地称为离散玻尔兹曼方法(DBM)。这些DBM方法可以是理论物理中的建模方法,也可以是计算数学中的方程解法。由于可以根据理论或模拟研究需要,分别将时间、空间和粒子速度这三个自变量之一、之二或之三进行离散,所以DBM的含义可以很广。有些DBM是包含离散速度图像的(例如LBM),也有些并不包含(例如,计算流体力学中的有些动理学方法充分借助麦克斯韦分布函数动理学矩的解析解,并不使用离散速度图像,其中的离散指的可以是时间和空间的离散)。为方便描述,在本文中,如果没有特殊说明,则DBM特指针对上述“介尺度”、“两难”情形而构建的一类相对具体的理论模型或方法,其中的离散指的是粒子速度空间的离散。
具体来说,本文要重点介绍的离散玻尔兹曼建模,是非平衡统计物理学粗粒化建模方法在流体力学领域的具体应用,是理论物理范畴下的模型构建方法。它根据研究需求,抓主要矛盾,选取一个视角,研究系统的一组动理学性质,因而它要求描述这组性质的动理学矩其计算结果不能因为模型简化而改变。除了分布函数的守恒矩(质量、动量和能量),DBM同时关注部分关系最密切的非守恒矩的时空演化,从一个更宽的视角来考察和描述系统。除了为实现模拟而进行的抓主要矛盾和粗粒化建模,DBM同时关注模拟之后的复杂物理场分析(复杂物理场分析,也需要通过建模来提取更多有价值的信息),它本身自带一套复杂物理场分析方法或技术[27-28]。
广义的DBM包含LBM,LBM是其中使用离散速度的一类。本文要重点介绍的这类具体的DBM也可以视为广义的LBM系列中物理建模这一类的进一步发展[29]。文献[29]指出,在模型构建与非平衡统计物理学理论一致的情形,可以借助
本文结构如下:第1节,介绍流体系统的微观、介观和宏观三种建模方法;第2节,介绍从格子气模型到离散玻尔兹曼方法的发展历程;第3节,给出离散玻尔兹曼方法的理论框架,然后分别介绍含外场力情形、含分子间作用势情形、含化学反应情形和等离子体情形的DBM建模;第4节,介绍基于DBM模拟的多相流机理研究,包括在流体不稳定性研究、相分离研究、化学反应流研究等方面的进展。第5节,给出本文的小结与说明。
1 流体系统的微观、介观与宏观建模物质世界是无限可分的,微观、介观、宏观的界定是相对的。对于流体系统来说,微观描述一般是指基于MD的描述。在MD中,分子间相互作用势的建立是模型构建的关键,有效作用半径的截取是模拟计算的关键。宏观描述一般是指基于欧拉(Euler)方程、NS方程等连续介质力学建模的描述。在这个层面上,人们关注的系统行为通过密度、流速、温度、压强、应力、热流等物理量表征,其控制方程是代表质量、动量和能量守恒的流体演化方程组。其本构关系往往是根据经验或唯象给出的。因为非平衡统计物理学可以联系微观和宏观连续描述,所以经常称为介观描述。其中,使用比较多的是基于玻尔兹曼方程的描述。在这类描述中,描述的起点是理想气体模型,恩斯柯格方程可以看作是玻尔兹曼方程的推广,可以根据具体系统引入合适的分子间作用力或势。
对于多相流等复杂流体系统来说,系统本身可能是宏观尺度的,但其内部存在大量的中间尺度的空间结构和动理学模式,这些结构和模式的存在和演化极大地影响着系统的物理性能和功能。多相复杂流体系统内部往往具有大量的界面,包括物质界面和力学界面,系统内部的受力和响应过程非常复杂。对于这些复杂系统的研究,NS方程等宏观流体模型只能对系统中大尺度的和缓变的行为进行较好的描述,而对于一些锐利的界面(例如冲击波和爆轰波等)和快变模式的描述,则不能满足要求,这至少体现在两个方面:(1)只考虑线性响应(一阶非平衡效应)的NS方程给出的应力和热流幅度可能偏大或偏小[32-33];甚至在某些情形,NS方程给出的应力、热流、速度连方向都是错误的[34];(2)从动理学理论视角,锐利界面的精细物理结构描述不仅需要(分布函数的)守恒矩,还需要部分关系最密切的非守恒矩,而NS方程描述的只是守恒矩及其演化[27]。同时,发展相对成熟、大家相对熟悉的MD和直接模拟蒙特卡罗(Direct Simulation Monte Carlo, DSMC)方法,理论上相对完备,但由于运算量极大,对计算机内存的要求极高,所以在绝大多数情况下,它们能够模拟的系统大小和时间尺度都远远不能满足需求。
到这里,我们面对的状况是,当系统的克努森(Knudsen, Kn)数①很小时,连续介质假设合理程度很高,传统流体力学模型可以很好地描述;当Kn很大时,系统的离散性很高,在关注的尺度内粒子数较少;少到一定程度,就可以使用MD或DSMC来进行模拟。而当Kn介于这两种情形之间(介尺度情形)时,传统连续模型不再合理,而MD和DSMC又由于适用的时空尺度受限而无能为力。同时,随着进入低压稀疏、微介观或者快变模式情形,Kn逐渐升高,系统偏离平衡程度增加,系统行为的复杂度急剧上升,因而使用分布函数非守恒矩对系统行为进行描述的必要性在逐渐增加。DBM就是在这个背景下,应这些物理问题的研究需求而产生的理论模型[28]。因为这些以前知之甚少的非平衡行为蕴含着大量尚待开发的物理功能,所以随着时间的推进,使用分布函数非守恒矩描述系统行为的收益正在增加,这在后面介绍DBM应用时将会看到。
2 粗粒化建模:从格子气模型到离散玻尔兹曼元胞自动机又称为格子气(元胞)自动机(Lattice Gas(Cellular)Automata, LG(C)A)或格子气模型(Lattice Gas Model,LGM)。LGM的使用在统计物理学的研究中有着悠久的历史。1952年,李政道和杨振宁发表在《物理评论》的《Statistical Theory of Equations of State and Phase Transitions. II. Lattice Gas and Ising Model》[35]就是一个关于LGM的工作。
从20世纪60年代开始,人们设想使用一种称之为“格子气”或“元胞自动机”的简单离散模型来作为连续流体系统的理想化模型。这类模型通常由一个背景网格、分布在网格结点上的一群“虚拟粒子”和一套简单作用规则这三个部分构成。其中,背景网格提供空间粗粒化坐标。分布在网格结点上的“虚拟粒子”具有相同的质量,并且只具有少数和网格点的连接方式绑定的运动方向和速度大小。常用的简单规则为—在一个时间步长内,粒子只能从当前格点沿格点的连线方向运动到相邻格点上,这个过程称为“传播”。当来自不同方向的粒子在某个网格点相遇时,它们则发生“碰撞”。碰撞的设计要使得碰撞前后系统局域的质量守恒、动量守恒以及能量守恒。为了能够模拟连续的流体系统,特别是让在微观层次上破缺的对称性在宏观上得到恢复,格子气模型的构建必须满足对称性约束条件。到20世纪80年代后期,LGM开始得到快速发展[36-37]。其中,以Frisch-Hasslacher-Pomeau(FHP)模型为典型代表[38]。
物理图像简单、直观、易于编程等优点,使得LGM在粗略模拟流体行为(特别是复杂流体行为)方面发挥着重要作用。NS等偏微分方程的数值解法和非平衡复杂流动的粗粒化物理建模是LGM的两个发展方向。这两类LGM目标不同,所以构建规则不同,使用的判据也不同。
LBM是在LGM的基础上经过几个主要的演变发展而来的。LGM的简单离散规则使得它和以Euler、NS方程为代表的连续模型描述的流体行为之间出现差异。由于连续模型在其适用的范围内的可靠性是经过大量的实践检验的,为了减小模拟的误差,人们对LGM的合理构造展开了广泛的研究。经过引入局域平衡态分布函数、线性碰撞算符、单弛豫时间模型等,LGM逐渐发展成了现在文献中普遍使用的LBM。后来人们发现,LBM可以看作是单弛豫时间线性化玻尔兹曼方程在时间、空间和粒子速度空间的一种巧妙的离散化形式。随后,多弛豫时间模型也得到了广泛的研究。根据对玻尔兹曼方程输运项所采用的不同的计算方式,LBM可以分为有限差分LBM、有限体积LBM、有限元LBM等等。相应的,由LGM发展而来的、继承了“传播+碰撞”这一简单演化规则的LBM通常称为标准LBM[29]。不同研究背景和知识结构的研究人员都结合自己的研究兴趣和需求,对LBM进行了广泛的推广和发展。总体来讲,LBM也有着两个不同的发展方向:一是NS等偏微分方程的全新的数值解法,二是非平衡复杂流动的动理学建模方法。
在现有文献中,多数LBM的功能是从一个全新的角度求解流体方程或其他偏微分方程。“LBM”已经被普遍接受为一种全新的偏微分方程的数值解法,并且往往是标准LBM的代称。作为流体力学偏微分方程数值解法的LBM,模拟结果在数值误差范围内要与需要求解的流体方程相符。LBM数值解法并不局限于流体力学方程,只要能找到一个模拟中的可控量与Kn相对应,再将分布函数和动理学矩的概念根据需要求解的方程作合理的延伸(例如,使所有离散“分布函数”之和等于某个需要求解的量),就可以通过在格子“玻尔兹曼方程”中添加合适的修正项来求解一些其他的偏微分方程。但是,概念延伸后的“分布函数”和“动理学矩”可能已经不再具有统计力学中分布函数和动理学矩的物理含义,概念延伸后的“玻尔兹曼方程”也可能不再是非平衡统计力学中用于描述非平衡行为的玻尔兹曼方程。它们只是形式上的“分布函数”、“动理学矩”、“玻尔兹曼方程”,因而只是一种叫法上的延续。相对于作为非平衡复杂流动的动理学建模方法而言,作为偏微分方程数值解法的格子玻尔兹曼,在算法的设计上可以不拘泥于严格的物理对应,具有更大的灵活性。
相对于数值解法这一方向来说,LBM在微介观与非平衡效应和建模方面并没有得到同样快速的发展。在作为非平衡复杂流动动理学建模方法时,根据关注点不同,LBM又可以分为两类。一类主要关注质量、动量和能量三个守恒动理学矩及其演化;另一类则兼顾三个守恒矩和部分与之密切相关的非守恒矩,其中非平衡状态的描述和非平衡行为的研究是核心(例如,通过非守恒矩与其相应的平衡态值的差异研究熵增等不可逆机制,研究当前非平衡状态对下一步流动行为的影响等)。
为了与作为偏微分方程数值解法的LBM相区别,同时由于第二类作为非平衡流动动理学建模方法的模型一般不再使用来自格子气方法的“虚拟粒子”、“传播+碰撞”图像(在一个时间步内,虚拟粒子由当前格点,沿着网格线方向移动到相邻的格点上去,来自相邻格点的虚拟粒子在当前格点发生碰撞),“格子”称谓已经失去了原有的与格子气方法对应的含义,但因仍然使用离散的玻尔兹曼方程,所以在近期的文献中逐渐改称为离散玻尔兹曼模型或建模方法(Discrete Boltzmann Model/Modeling method),简称DBM。这里,对空间导数的离散格式和控制方程的时间积分方法不做特别约束,可以根据具体情况合理选取,“离散玻尔兹曼”中的“离散”指的是分子速度空间的离散[27-28]。
3 离散玻尔兹曼理论框架 3.1 玻尔兹曼方程简介在统计物理中,对于
假设系统宏观量为
| $B\left( {{{x}},t} \right) = \int {{\rm{d}}{{p}}{\rm{d}}{{q}}b\left( {{{q}},{{p}};{{x}},t} \right)F} \left( {{{q}},{{p}}} \right)$ | (1) |
其中,
对于保守力学体系,哈密顿量等于系统总能量,等于常数,即:
| $ H=E={\text{常数}}$ | (2) |
若使用统计力学的“薛定谔图像”,即系统的力学函数(
| $ \frac{{{\rm{d}}F\left( {{{q}},{{p}};t} \right)}}{{{\rm{d}}t}} = \frac{{\partial F}}{{\partial t}} + \sum\limits_{i = 1}^N {\left( {\frac{{\partial F}}{{\partial {{{q}}_i}}}\frac{{\partial {{{q}}_i}}}{{\partial t}} + \frac{{\partial F}}{{\partial {{{p}}_i}}}\frac{{\partial {{{p}}_i}}}{{\partial t}}} \right)} = 0 $ | (3) |
由哈密顿正则方程:
| $ \frac{{\partial {{{q}}_i}}}{{\partial t}} = \frac{{\partial H\left( {{{q}},{{p}}} \right)}}{{\partial {{{p}}_i}}}, \frac{{\partial {{{p}}_i}}}{{\partial t}} = - \frac{{\partial H\left( {{{q}},{{p}}} \right)}}{{\partial {{{q}}_i}}} $ | (4) |
即可得到非平衡统计力学的基本方程—刘维(Liouville)方程:
| $ \frac{{\partial F}}{{\partial t}} = {\left[ {H,F} \right]_P} $ | (5) |
上式又经常写为:
| $\frac{{\partial F}}{{\partial t}} = LF\left( t \right)$ | (6) |
线性算法
| $ LF\left( t \right) = {\left[ {H,F} \right]_P} $ | (7) |
其中
| $ {\left[ {b,c} \right]_p} =\sum\limits_{i= 1}^N {\left( {\frac{{\partial b}}{{\partial {{{q}}_i}}}\frac{{\partial c}}{{\partial {{{p}}_i}}} - \frac{{\partial b}}{{\partial {{{p}}_i}}}\frac{{\partial c}}{{\partial {{{q}}_i}}}} \right)} $ | (8) |
为便于描述,引入简记:
| $ {{{x}}_i} \equiv \left( {{{{q}}_i},{{{p}}_i}} \right) $ | (9) |
引入
| $ {f_s} = \frac{{N!}}{{\left( {N - s} \right)!}}\int {{\rm{d}}{{{x}}_{s + 1}} \cdots {\rm{d}}{{{x}}_N}F\left( {{{{x}}_1}, \cdots ,{{{x}}_s},{{{x}}_{s + 1}}, \cdots ,{{{x}}_N}} \right)} $ | (10) |
其中
| ${H_N} = \sum\limits_{j = 1}^N {\left( {H_j^0 + H_j^F} \right)} + \sum\limits_{j < n} {H_{jn}'} $ | (11) |
其中
| $ H_j^0 = \frac{{{{\left( {{{{p}}_j}} \right)}^2}}}{{2m}},H_j^F = V\left( {{{{q}}_j}} \right),H_{jn}' = {U_{jn}}\left( {{{{q}}_j},{{{q}}_n}} \right) $ | (12) |
刘维量和哈密顿量成线性关系,所以刘维算法可作类似的分解:
| $L = \sum\limits_{j = 1}^N {\left( {L_j^0 + L_j^F} \right)} + \sum\limits_{j < n} {L_{jn}'} $ | (13) |
刘维方程可写为:
| ${\partial _t}F = \sum\limits_{j = 1}^N {\left( {L_j^0 + L_j^F} \right)} F + \sum\limits_{j < n} {L_{jn}'} F$ | (14) |
根据系统内粒子数守恒和粒子在分布函数中的对称性,得:
| $ \begin{split}& {\partial _t}{f_s}\left( {{{{x}}_1},{{{x}}_2}, \cdots ,{{{x}}_s};t} \right) =\\&\qquad \left[ {\sum\limits_{j = 1}^s {\left( {L_j^0 + L_j^F} \right)} + \sum\limits_{j < n}^s {{L_{jn}'}} } \right] {f_s}\left( {{{{x}}_1},{{{x}}_2}, \cdots ,{{{x}}_s};t} \right) +\\&\qquad \left( {N - s} \right) \sum\limits_{j = 1}^s {\int {{\rm{d}}{{{x}}_{s + 1}}{L_{j(s + 1) }'}{f_{s + 1}}\left( {{{{x}}_1},{{{x}}_2}, \cdots ,{{{x}}_{s + 1}};t} \right)} } \end{split} $ | (15) |
上式可进一步写为:
| $ \begin{split}& {\partial _t}{f_s}\left( {{{{x}}_1},{{{x}}_2}, \cdots ,{{{x}}_s};t} \right) =\\&\quad \left[ {\sum\limits_{j = 1}^s {\left( {L_j^0 + L_j^F} \right)} + \sum\limits_{j < n}^s {{L_{jn}'}} } \right] {f_s}\left( {{{{x}}_1},{{{x}}_2}, \cdots ,{{{x}}_s};t} \right) +\\&\quad \left( {N - s} \right) \sum\limits_{j = 1}^s {\int {{\rm{d}}{{{x}}_{s + 1}}\frac{{\partial {U_{j({s + 1})}}}}{{\partial {{{q}}_j}}}\frac{\partial }{{\partial {{{p}}_j}}}{f_{s + 1}}\left( {{{{x}}_1},{{{x}}_2}, \cdots ,{{{x}}_{s + 1}};t} \right)} } \end{split} $ | (16) |
或
| $ \begin{split}& {\partial _t}{f_s}\left( {{{{x}}_1},{{{x}}_2}, \cdots ,{{{x}}_s};t} \right) =\\&\quad {\left[ {{H_s},{f_s}} \right]_P} + \\&\quad\left( {N - s} \right) \sum\limits_{j = 1}^s {\int {{\rm{d}}{{{x}}_{s + 1}}\frac{{\partial {U_{j({s + 1})}}}}{{\partial {{{q}}_j}}}\frac{\partial }{{\partial {{{p}}_j}}}{f_{s + 1}}\left( {{{{x}}_1},{{{x}}_2}, \cdots ,{{{x}}_{s + 1}};t} \right)} } \end{split} $ | (17) |
这是一个确定约化分布函数的方程链(或谱系),因其作者的名字(Bogoliubov-Born-Green-Kirkwood-Yvon)而称为BBGKY谱系。由于在引入过程中没有作任何的近似,所以BBGKY谱系与刘维方程完全等价。
BBGKY方程链的第一、第二两个方程为:
| $ {\partial _t}{f_1} = {\left[ {{H_1},{f_1}} \right]_P} + \left( {N - 1} \right)\int {{\rm{d}}{{{p}}_2}{\rm{d}}{{{q}}_2}\frac{{\partial {U_{12}}}}{{\partial {{{q}}_1}}}\frac{{\partial {f_2}}}{{\partial {{{p}}_1}}}} $ | (18) |
| $ \;{\partial _t}{f_2} = {\left[ {{H_2},{f_2}} \right]_P} \!+\! \left( {N - 2} \right)\int {{\rm{d}}{{{p}}_3}{\rm{d}}{{{q}}_3}\left( {\frac{{\partial {U_{13}}}}{{\partial {{{q}}_1}}}\frac{{\partial {f_3}}}{{\partial {{{p}}_1}}} + \frac{{\partial {U_{23}}}}{{\partial {{{q}}_2}}}\frac{{\partial {f_3}}}{{\partial {{{p}}_2}}}} \right)} $ | (19) |
其中
| $ {\left[ {{H_1},{f_1}} \right]_P} = \frac{{\partial V\left( {{{{q}}_1}} \right)}}{{\partial {{{q}}_1}}}\frac{{\partial {f_1}}}{{\partial {{{p}}_1}}} -\frac{{{{{p}}_1}}}{m}\frac{{\partial {f_1}}}{{\partial {{{q}}_1}}} $ | (20) |
| $ \begin{split} {\left[ {{H_2},{f_2}} \right]_P} = & \frac{{\partial \left[ {V\left( {{{{q}}_1}} \right) + {U_{12}}} \right]}}{{\partial {{{q}}_1}}}\frac{{\partial {f_2}}}{{\partial {{{p}}_1}}} - \frac{{{{{p}}_1}}}{m}\frac{{\partial {f_2}}}{{\partial {{{q}}_1}}} + \\& \frac{{\partial \left[ {V\left( {{{{q}}_2}} \right) + {U_{12}}} \right]}}{{\partial {{{q}}_2}}}\frac{{\partial {f_2}}}{{\partial {{{p}}_2}}}- \frac{{{{{p}}_2}}}{m}\frac{{\partial {f_2}}}{{\partial {{{q}}_2}}} \end{split} $ | (21) |
如果我们引入五个假设对研究系统进行约束:
假设一:当
| $ {\partial _t}{f_2} = {\left[ {{H_2},{f_2}} \right]_P}$ | (22) |
假设二:三个及以上粒子间的相互作用可以忽略,两个粒子间的相互作用只与它们之间的距离有关,即:
| $ {U_{jn}}\left( {{{{q}}_j},{{{q}}_n}} \right) = U\left( {\left| {{{{q}}_j} - {{{q}}_n}} \right|} \right) $ | (23) |
假设三:外场保守假设,即粒子的加速度:
| $ {{a}}\left( {q} \right) = - \frac{1}{m}\frac{{\partial V\left( {q} \right)}}{{\partial {q}}} $ | (24) |
假设四:分子混沌假设,即在同一时刻在
| $ {f_2}\left( {{{x}_1},{{x}_2};t} \right) = {f_1}\left( {{{x}_1},t} \right){f_1}\left( {{{x}_2},t} \right) $ | (25) |
假设五:刚球模型和弹性碰撞假设,即分子之间的碰撞用刚球之间的弹性碰撞近似。
由式(18)、式(19),再根据角动量守恒,碰撞前后粒子“瞄准距离”相等,可推导得到:
| $ \begin{split}& \left[ {\frac{\partial }{{\partial t}} + \frac{{p}}{m}\frac{\partial }{{\partial {q}}} + m{a}\left( {q} \right)\frac{\partial }{{\partial {p}}}} \right]{f_1}\left( {{{q}},{{p}};t} \right) =\\&\qquad N\int {\left[ {{f_1}\left( {{{q}},{{p}}'} \right)} \right.} \left. {{f_1}\left( {{{q}},{{{{p}}'}_1}} \right) - {f_1}\left( {{{q}},{{p}}} \right){f_1}\left( {{{q}},{{{p}}_1}} \right)} \right]\\&\qquad \left| {{{{p}}_1} - {{p}}} \right|{b}{\rm{d}}{b}{\rm{d}}\chi {\rm{d}}{{{p}}_1} \end{split} $ | (26) |
其中,
从BBGKY方程链出发,经过一系列假设,我们得到了玻尔兹曼方程。下面,我们从物理图像的角度对玻尔兹曼方程进行比较直观的解释。
分子动理学提出,物质是由大量粒子组成的,物质在宏观上的性质是由粒子的种类和粒子运动决定的。对于气体来说,气体的宏观性质主要受到分子与分子之间以及分子和壁面之间的碰撞的影响。分子间发生三体碰撞的概率远低于分子间发生二体碰撞的概率,所以我们暂且只考虑三体碰撞概率或效应小到可以忽略的稀薄情形,这时只需考虑分子间的二体碰撞。
分子二体碰撞中,最简单的碰撞为弹性碰撞,即分子间的碰撞没有发生平动能和内能之间的能量交换,碰撞过程中机械能守恒。分子对碰撞前后的速度的大小可由动量守恒和能量守恒来确定,而要确定分子对碰撞后速度的方向,则需要根据引入的不同的分子间作用势模型来确定分子对的瞄准距离
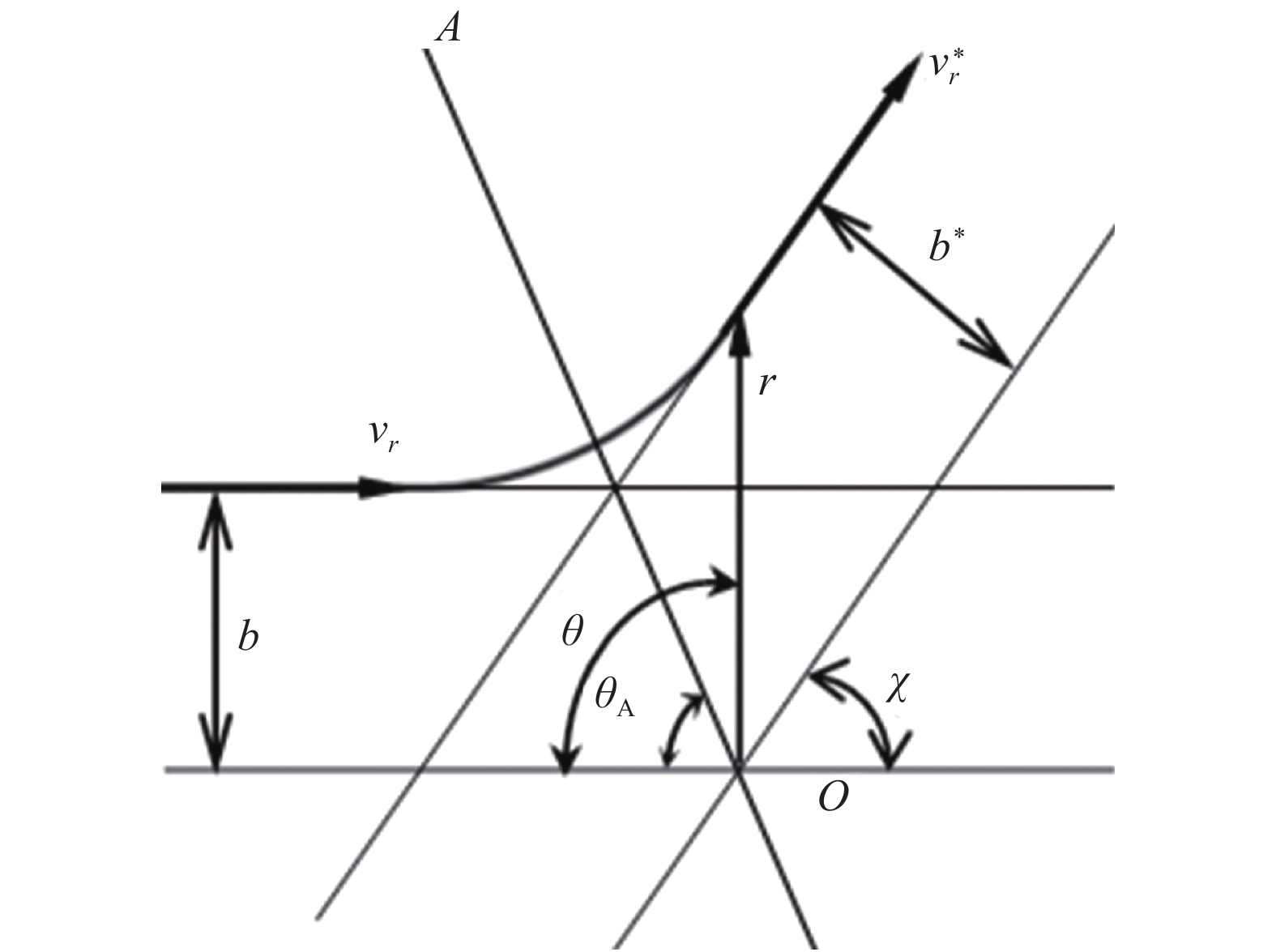
瞄准距离
图1所示为质心坐标中二体碰撞的分子运动轨迹示意图。其中,
|
图 1 质心坐标系中二体碰撞的分子运动轨迹 Fig.1 The molecular trajectory of two-body collision in the centroid coordinate system. |
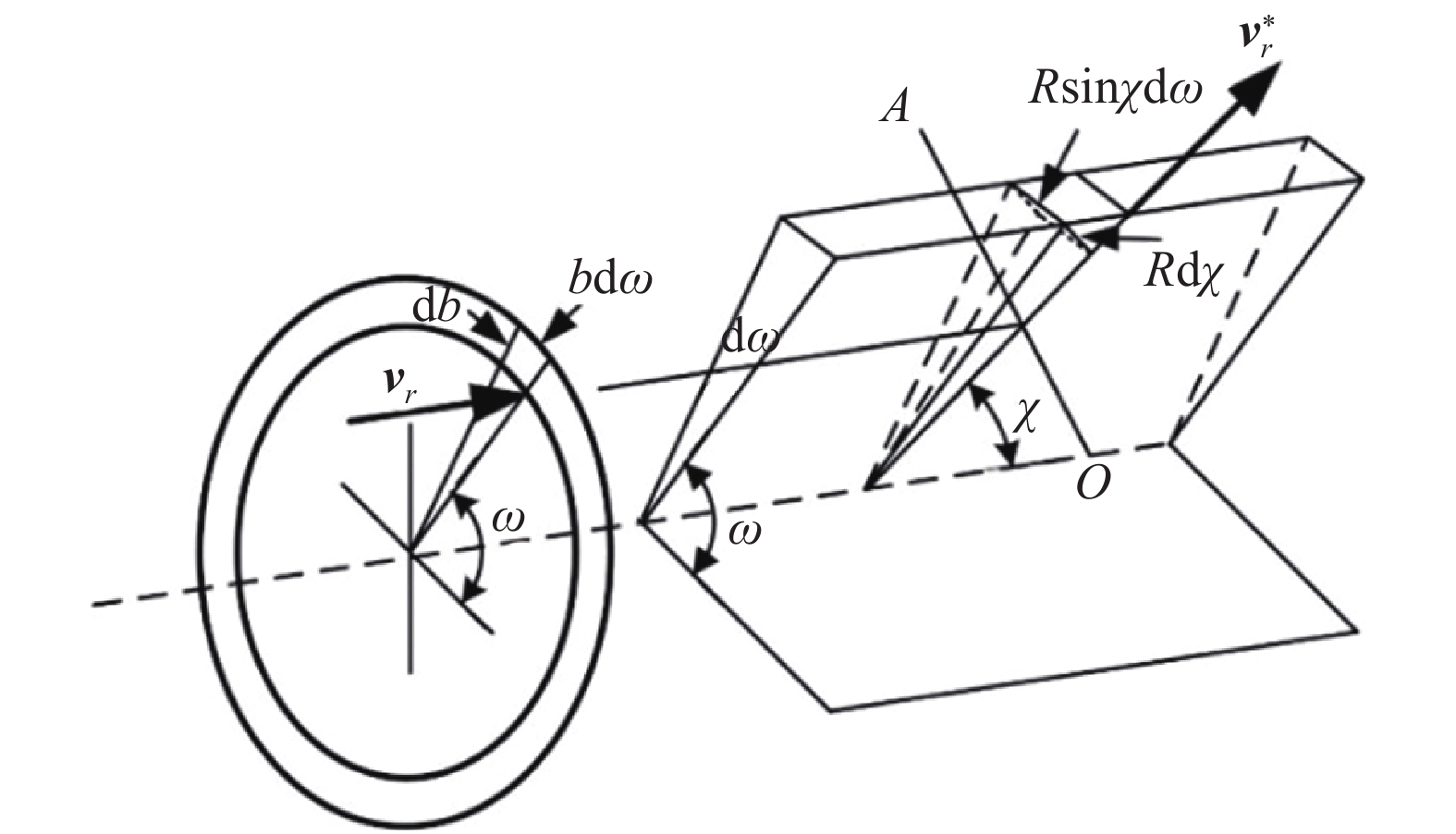
通过引入不同的分子间作用势,可以得到不同的分子碰撞的散射特征。图2为三维情形下分子碰撞和散射示意图。
|
图 2 三维分子碰撞截面和散射示意图 Fig.2 Schematic of 3D molecular collision cross section and scattering |
假设两个分子的相对速度为
| $ {\rm{d}}\varOmega = \frac{{R\sin {\chi} {\rm{d}}{\omega} R{\rm{d}}\chi }}{{{R^2}}} = \sin \chi {\rm{d}}{\chi} {\rm{d}}{\omega} $ | (27) |
设
| $ \sigma {\rm{d}}\varOmega = b{\rm{d}}b{\rm{d}}{\omega} $ | (28) |
可得:
| $ \sigma = \frac{{b{\rm{d}}b{\rm{d}}{\omega} }}{{{\rm{d}}\varOmega }} = \frac{b}{{\sin \chi }}\frac{{{\rm{d}}b}}{{{\rm{d}}\chi }} $ | (29) |
由式(28)和式(29)可得总的碰撞截面
| ${\sigma _T} = \int\nolimits_0^{4{\text{π}} } \sigma {\rm{d}}\varOmega = 2{\text{π}} \int\nolimits_0^{\text{π}} \sigma \sin \chi {\rm{d}}\chi {\rm{ = }}2{\text{π}} \int {b{\rm{d}}b} $ | (30) |
其中,偏转角
对于三维空间中的气体系统,约化的分布函数
| $n = \int {f\left( {{{r}},{{v}},t} \right){\rm{d}}{{v}}} $ | (31) |
分布函数在速度空间的一阶矩和二阶缩并矩则分别表示
| $n{{u}} = \int {f\left( {{{r}},{{v}},t} \right){{v}}{\rm{d}}{{v}}} $ | (32) |
| $\frac{3}{2}nkT = \int {\frac{m}{2}f\left( {{{r}},{{v}},t} \right){{\left( {{{v}} - {{u}}} \right)}^2}{\rm{d}}{{v}}} $ | (33) |
其中
| $f\left( {{{r}} + {\rm{d}}{{r}},{{v}} + {{a}}{\rm{d}}t,t + {\rm{d}}t} \right){\rm{d}}{{r}}{\rm{d}}{{v}} = f\left( {{{r}},{{v}},t} \right){\rm{d}}{{r}}{\rm{d}}{{v}}$ | (34) |
对等式(34)的左端进行泰勒展开可以得到:
| $\frac{{\partial f}}{{\partial t}} + {{v}} \cdot \frac{{\partial f}}{{\partial {{r}}}} + {{a}} \cdot \frac{{\partial f}}{{\partial {{v}}}} = 0$ | (35) |
其中
| $\frac{{\partial f}}{{\partial t}} + {{v}} \cdot \frac{{\partial f}}{{\partial {{r}}}} + {{a}} \cdot \frac{{\partial f}}{{\partial {{v}}}} = {\left( {\frac{{\partial f}}{{\partial t}}} \right)_c}$ | (36) |
等式右端的碰撞项表示由于分子间的碰撞导致的分布函数的变化。对于碰撞项的具体形式,我们做如下分析。假设在空间体积
类似地,如果碰撞前分子速度分别为
所以,在时间
| $ {\left( {\frac{{\partial f}}{{\partial t}}} \right)_c}{\rm{d}}{{v}}{\rm{d}}{{r}}{\rm{d}}t = \left[ {\int_{ - \infty }^{ + \infty } {\int_0^{4{\text{π}} } {\left( {{f^ * }f_1^ * - f{f_1}} \right){v_r}\sigma {\rm{d}}\varOmega {\rm{d}}{{{v}}_1}} } } \right]{\rm{d}}{{v}}{\rm{d}}{{r}}{\rm{d}}t $ | (37) |
将碰撞项代入式(36),可以得到完整形式的玻尔兹曼方程:
| $\frac{{\partial f}}{{\partial t}} + {{v}} \cdot \frac{{\partial f}}{{\partial {{r}}}} + {{a}} \cdot \frac{{\partial f}}{{\partial {{v}}}} = \int_{ - \infty }^{ + \infty } {\int_0^{4{\text{π}} } {\left( {{f^ * }f_1^ * - f{f_1}} \right){v_r}\sigma {\rm{d}}\varOmega {\rm{d}}{{{v}}_1}} } $ | (38) |
Chapman-Enskog多尺度分析是Chapman和Enskog在1910年至1920年提出的一种多尺度分析技术[24]。从数学角度看,Chapman-Enskog多尺度分析实际上就是将分布函数
我们以一维情形为例来说明。在
| $f = {f^{\left( 0 \right)}} + {Kn} {f^{\left( 1 \right)}} + {{Kn} ^2}{f^{\left( 2 \right)}} + \cdots $ | (39) |
| $\frac{\partial }{{\partial t}} = {Kn} \frac{\partial }{{\partial {t_1}}} + {{Kn} ^2}\frac{\partial }{{\partial {t_2}}} + \cdots $ | (40) |
| $\frac{\partial }{{\partial x}} = {Kn} \frac{\partial }{{\partial {x_1}}} + {{Kn} ^2}\frac{\partial }{{\partial {x_2}}} + \cdots $ | (41) |
其中,
| ${f^{\left( 0 \right)}} \equiv {\left. f \right|_{{Kn} = 0}} = {f^{\left( {eq} \right)}}$ | (42) |
为麦克斯韦分布,
| ${\left. {\frac{\partial }{{\partial t}}} \right|_{{Kn} = 0}} \equiv \frac{\partial }{{\partial {t_0}}}$ | (43) |
| ${\left. {\frac{\partial }{{\partial x}}} \right|_{{Kn} = 0}} \equiv \frac{\partial }{{\partial {x_0}}}$ | (44) |
| ${f^{\left( l \right)}} \equiv {\left. {\frac{1}{{l!}}\frac{{{\partial ^l}f}}{{\partial {{Kn} ^l}}}} \right|_{{Kn} = 0}},l \geqslant 1$ | (45) |
| $\frac{\partial }{{\partial {t_n}}} \equiv {\left[ {\frac{1}{{n!}}\frac{{{\partial ^n}}}{{\partial {{Kn} ^n}}}\frac{\partial }{{\partial t}}} \right]_{{Kn} = 0}},n \geqslant 1$ | (46) |
| $ \frac{\partial }{{\partial {x_m}}} \equiv {\left[ {\frac{1}{{m!}}\frac{{{\partial ^m}}}{{\partial {{Kn} ^m}}}\frac{\partial }{{\partial x}}} \right]_{{Kn} = 0}},m \geqslant 1 $ | (47) |
将展开式(39)~(41)代入分布函数
下面,对时间、空间变化率的多尺度展开方法蕴含的测量逐步细化的思路做些理解性分析。首先,由式(46)可以看到,
从扰动论角度看,在Chapman-Enskog多尺度分析中,
非平衡统计力学是联系微观与宏观的桥梁。玻尔兹曼方程使用单体分布函数描述系统动理学行为随时间的演化。尽管相对于刘维方程来说,玻尔兹曼方程已经是个高度粗粒化的模型,但其碰撞项仍然非常复杂,以至于在绝大多数情形下仍然不方便求解。为了进行有效使用,不得不根据具体情形,继续对其进行简化(抓住主要矛盾,有所保,有所丢)。
与动理学宏观建模(从动理学理论出发推导宏观模型方程组)不同,DBM是一种根据系统性质研究需求直接建模的方法。在这种建模方式中,只是根据系统性质研究需求,借助某种方式(例如Chapman-Enskog多尺度分析的物理图像、经过验证的唯象理论等)快速确定建模过程中要保持不变的底层动理学矩关系,原则上无需经过繁琐的理论推导获得最终的宏观流体动力学方程组。DBM模型对应的宏观流体动力学方程组可以是后知的结果,而不必是DBM建模与模拟的前提。同时,DBM自动提供部分关系最密切的非守恒动理学矩及其演化,自动弥补宏观流体动力学方程组在非平衡行为和效应描述方面的功能不足。在借助Chapman-Enskog多尺度分析物理图像的情形,Chapman-Enskog多尺度分析理论是这类建模思路合理的理论依据。
从玻尔兹曼方程到目前版本DBM的建立,包括三个步骤:(1)碰撞算符的简约化;(2)分子速度空间的离散化;(3)非平衡状态描述与非平衡信息的提取。其中,前两步是针对待研系统的粗粒化物理建模;第三步是针对复杂物理场的描述与粗粒化信息提取,是DBM建模方法的目的和核心。
由于玻尔兹曼方程的碰撞项非常复杂,在绝大多数情况下,不得不对其进行简化。简化的方法之一就是引入一个形式上的局域目标分布函数
DBM借助离散速度,将原本连续、积分形式的动理学矩转化为求和进行计算。由于任何一个分子都可以朝向任何一个方向运动,且其范围都是
| $\int {f\varPsi '\left( {{v}} \right)} {\rm{d}}{{v}} = \sum\limits_i {{f_i}} \varPsi '\left( {{{{v}}_i}} \right)$ | (48) |
其中
密度
动量
能量
其中
由Chapman-Enskog多尺度分析,
| $ \int {{f^ {eq} }\varPsi ''\left( {{v}} \right)} {\rm{d}}{{v}} = \sum\limits_i {f_i^ {eq} } \varPsi ''\left( {{{{v}}_i}} \right) $ | (49) |
离散速度的具体取法取决于要保的不变量、基本的守恒性和必要的对称性。可见,DBM给出的是对离散速度的物理约束,并不包含具体的离散格式。
非平衡信息的提取和分析技术是DBM的目的和核心。在宏观流体模型中,克努森数、黏性、热传导、密度、温度、压强等宏观量的梯度等都是常用的非平衡程度表征量,都从各自的角度来描述系统的非平衡程度。但它们都是将相关信息高度浓缩的、平均化、粗粒化描述,很多物理上感兴趣的具体的非平衡信息(例如:不同自由度上的内能,黏性应力,热流或更高阶动理学矩)通常它们是看不到且无法直接研究的。DBM借助
用
| $ {{{\varDelta}} _n} = {{{M}}_n}\left( {{f_i}} \right) - {{{M}}_n}\left( {f_i^{eq}} \right) $ | (50) |
描述的就是相应视角下流体系统偏离热力学平衡态的具体信息。动理学矩
| $ {\varDelta} _n^ * = {{M}}_n^ * \left( {{f_i}} \right) - {{M}}_n^ * \left( {f_i^{eq}} \right) $ | (51) |
其中
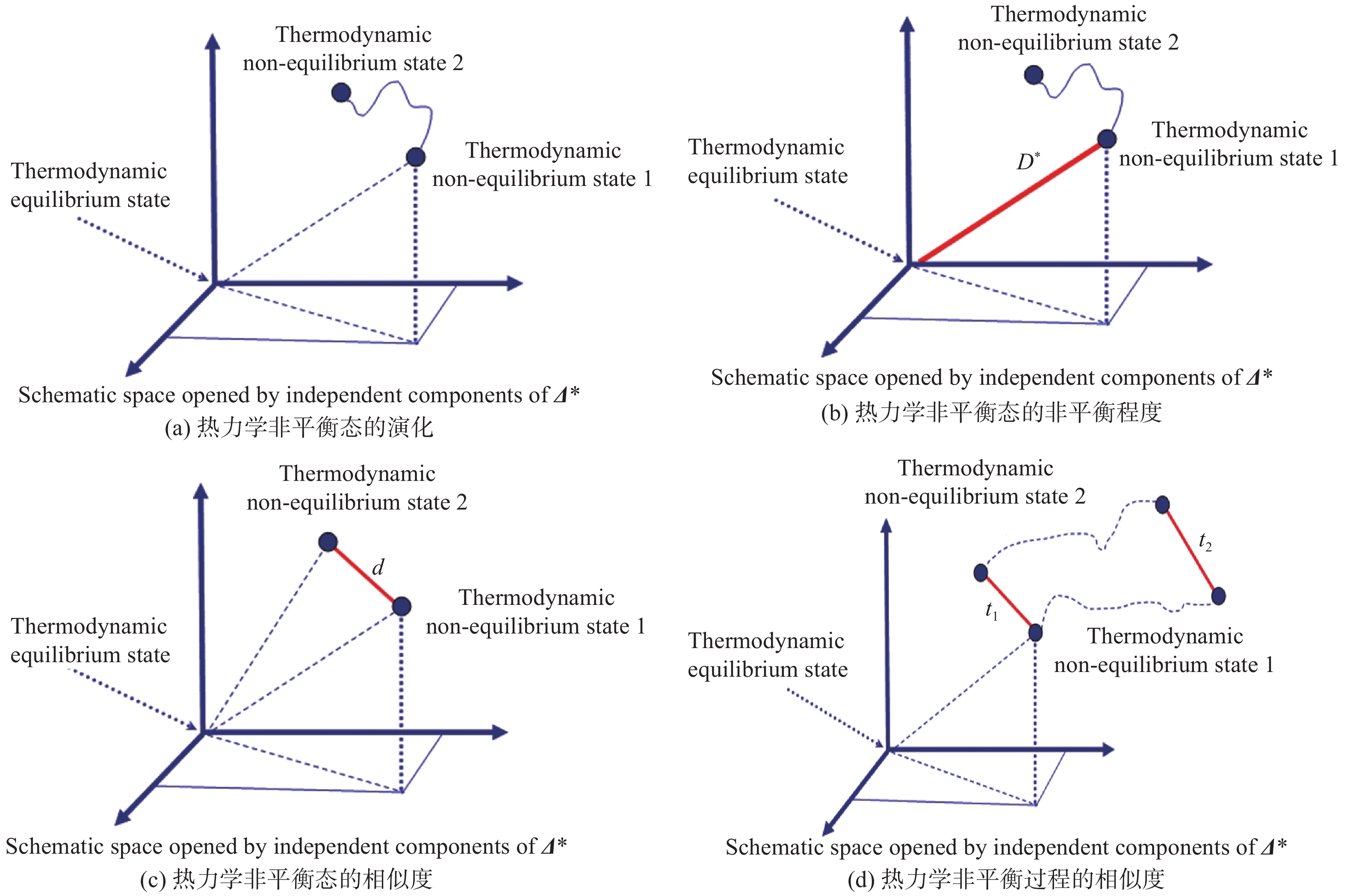
这些非守恒矩(或非平衡特征量)张量皆由若干分量构成,其中只有部分分量是独立的。这些张量构成一个集合,其中的独立分量也构成一个集合。这里可以使用非平衡特征量集合
通过这些非平衡特征量,我们可以研究系统的熵增,进而通过熵增研究物质混合,研究系统内不同非平衡行为特征之间的空间关联、时间关联、时空关联、竞争与协作[44]。在非平衡特征量张开的相空间中,某点到原点的距离可以定义为该状态的非平衡程度或强度。在图3(b)中,线段
|
图 3 非平衡特征量张开的非平衡相空间 Fig.3 Phase space opened by non-equilibrium characteristic quantities |
当流场中的外场力不可忽略时(例如重力场存在下的瑞利-泰勒不稳定性(Rayleigh-Taylor instability, RTI)问题,电场力、磁场力存在下的等离子体输运问题等),需要考虑外场力对流体介质的作用。包含外场力的玻尔兹曼方程具有如下形式:
| $\frac{{\partial f}}{{\partial t}} + {{v}} \cdot \frac{{\partial f}}{{\partial {{r}}}} + {{a}} \cdot \frac{{\partial f}}{{\partial {{v}}}} = {\left( {\frac{{\partial f}}{{\partial t}}} \right)_c}$ | (52) |
引入BGK近似后成为:
| $ \frac{{\partial {f}}}{{\partial t}} + {{{v}}} \cdot \frac{{\partial {f}}}{{\partial {{r}}}} + {{a}} \cdot \frac{{\partial {f}}}{{\partial {{{v}}}}} = - \frac{1}{\tau }\left( {{f} - f^{eq}} \right) $ | (53) |
如果分布函数偏离平衡部分即
| $\frac{{\partial {f_i}}}{{\partial t}} + {{{v}}_i} \cdot \frac{{\partial {f_i}}}{{\partial {{r}}}} - \frac{{{{a}} \cdot \left( {{{{v}}_i} - {{u}}} \right)}}{T}f_i^{eq} = - \frac{1}{\tau }\left( {{f_i} - f_i^{eq}} \right)$ | (54) |
其中,
作为一个粗粒化模型和诸多问题的研究起点,玻尔兹曼方程描述的是理想气体系统。对于理想气体系统,在确定的温度和压强下,只能有一个密度,系统基态永远是单一态,是不可能发生相变的。因此,在涉及相变的多相流问题研究中,一个关键的问题就是分子间作用力的引入。
从微观分子相互作用势角度来看,分子间的相互作用可以通过成对的势
| $ \phi \left( r \right) = 4{\varepsilon} \left[ {{{\left( {\frac{\sigma }{r}} \right)}^{12}} - {{\left( {\frac{\sigma }{r}} \right)}^6}} \right] $ | (55) |
| $ H = \frac{1}{{2m}}{\sum\limits_i {\left| {{{{p}}_i}} \right|} ^2} + \sum\limits_{\left\langle {i,j} \right\rangle } {\phi \left( {{r_{ij}}} \right)} $ | (56) |
其中
| $ \begin{split} {Z_N} = &\frac{1}{{N!{{\left( {2{\text{π}} \hbar } \right)}^{DN}}}}\int {\int {\exp \left( { - \beta H} \right){\rm{d}}{{{p}}_1} \cdots {\rm{d}}{{{p}}_N}{\rm{d}}{{{r}}_1} \cdots {\rm{d}}} } {{{r}}_N} \\= & \frac{1}{{N!{{\left( {{\lambda _{th}}} \right)}^{DN}}}}\int {\exp \left[ { - \beta \sum\limits_{\left\langle {i,j} \right\rangle } {\phi \left( {{r_{ij}}} \right)} } \right]{\rm{d}}{{{r}}_1} \cdots {\rm{d}}} {{{r}}_N} \\[-17pt] \end{split} $ | (57) |
其中
| ${\lambda _{th}} = \hbar \sqrt {\frac{{2{\text{π}} }}{{mkT}}} $ | (58) |
由配分函数,可得自由能
| $F = - \frac{1}{\beta }\ln {Z_N}$ | (59) |
以及压强
| $P = - {\left( {\frac{{\partial F}}{{\partial V}}} \right)_{TN}}$ | (60) |
| $e = {\left( {\frac{{\partial \beta F}}{{\partial \beta }}} \right)_{VN}}$ | (61) |
| $s = - \dfrac{{{{\left( {\dfrac{{\partial F}}{{\partial T}}} \right)}_{VN}}}}{N}$ | (62) |
其中下标表示求导时的不变量。
范德瓦尔斯(Van Der Waals,VDW)理论提出对式(55)中的Lenard-Jone势进行简化,简化后的
| $ {Z_N} = \frac{1}{{N!{{\left( {{\lambda _{th}}} \right)}^{DN}}}}{\left( {V - {v_0}N} \right)^N}\exp \left( \frac{{\beta \varepsilon{v_0}{N^2}}}{V} \right) $ | (63) |
其中
| $ F = NkT\left[ {\ln \left( {\lambda _{th}^3} \right) - 1} \right] + NkT\ln \left( {\frac{n}{{1 - {v_0}n}}} \right) - \varepsilon {v_0}nN $ | (64) |
其中
| $\ln \left( {N!} \right) = N\ln \left( N \right) - N$ | (65) |
再由式(60)可得VDW气体状态方程:
| $ P = \frac{{kTn}}{{1 - {v_0}n}} - {\varepsilon} {v_0}{n^2} $ | (66) |
或者写为:
| $P = \frac{{kT}}{{v - b}} - \frac{a}{{{v^2}}}$ | (67) |
其中
将VDW气体状态方程和表面张力引入DBM,可以得到如下形式的离散分布函数演化方程[46]:
| $\frac{{\partial {f_i}}}{{\partial t}} + {{{v}}_i} \cdot \nabla {f_i} = - \frac{1}{\tau }\left( {{f_i} - f_i^{eq}} \right) + {I_i}$ | (68) |
其中
| ${I_i} = - \left[ {A + {{B}} \cdot {{{c}}_i} + \left( {C + {C_q}} \right)c_i^2} \right]f_i^{eq}$ | (69) |
A、B、C和
为了更准确地描述硬球间的相互作用,Carnhan和Starling在VDW状态方程的基础上,对斥力项进行了修正,提出Carnhan-Starling(C-S)状态方程[48]:
| ${P^{CS}} = \rho T\left( {1 + \eta + {\eta ^2} - {\eta ^3}} \right){\left( {1 - \eta } \right)^{ - 3}} - a{\rho ^2}$ | (70) |
其中
基于C-S状态方程的DBM同样具有式(68)和式(69)所示的形式,但是与基于VDW状态方程的DBM不同,基于C-S状态方程的DBM中
| $A = - 2\left( {C + {C_q}} \right)T$ | (71) |
| ${{B}} = \frac{1}{{\rho T}}\left[ {\nabla \left( {{P^{cs}} - \rho T} \right) + \nabla \cdot {{\varLambda }} - \nabla \left( {\zeta \nabla \cdot {{u}}} \right)} \right]$ | (72) |
| $\begin{split} C =& \frac{1}{{2\rho {T^2}}}\left\{ {\left( {{P^{CS}} - \rho T} \right)\nabla \cdot {{u}} + {{\varLambda }}:\nabla {{u}} - \zeta {{\left( {\nabla \cdot {{u}}} \right)}^2} + a{\rho ^2}\nabla \cdot {{u}}} +\right. \\& \left. { K\left[ { - \frac{1}{2}\left( {\nabla \rho \cdot \nabla \rho } \right)\nabla \cdot {{u}} - \rho \nabla \rho \cdot \nabla \left( {\nabla \cdot {{u}}} \right) - \nabla \rho \cdot \nabla {{u}} \cdot \nabla \rho } \right]} \right\} \end{split} $ | (73) |
| $ {C_q} = \frac{1}{{\rho {T^2}}}\nabla \cdot \left( {q\rho T\nabla T} \right) $ | (74) |
| ${{\varLambda }} = K\nabla \rho \nabla \rho - K\left( {\rho {\nabla ^2}\rho + {{{{\left| {\nabla \rho } \right|}^2}} / 2}} \right){{I}} - \left[ {\rho T\nabla \rho \cdot \nabla \left( {{K / T}} \right)} \right]{{I}}$ | (75) |
系统总的能量密度为:
| $ {e_T} = \rho T - a{\rho ^2} + \frac{K}{2}{\left| {\nabla \rho } \right|^2} + \frac{1}{2}\rho {u^2} $ | (76) |
在对玻尔兹曼方程进行介绍时提到,玻尔兹曼方程的碰撞项是基于理想气体假设的,是忽略分子体积效应的。在处理稠密气体或液体时,这个假设并不合理。随着分子数密度的增加,相对于平均分子间距,分子大小不再可以忽略。考虑分子的体积效应,对玻尔兹曼碰撞算符进行修正,可以得到恩斯柯格(Enskog)碰撞算符:
| $\begin{split} {\left( {\frac{{\partial f}}{{\partial t}}} \right)_E} =& \int_{ - \infty }^{ + \infty } {\int_0^{4{\text{π}} } {\left[ {\chi \left( {{{r}} + \frac{{{d_0}}}{2}{{{\hat{ e}}}_r}} \right){f^ * }\left( {{r}} \right)f_1^ * \left( {{{r}} + {d_0}{{{\hat{ e}}}_r}} \right)} \right.} } - \\& \left. { \chi \left( {{{r}} - \frac{{{d_0}}}{2}{{{\hat{ e}}}_r}} \right)f\left( {{r}} \right){f_1}\left( {{{r}} - {d_0}{{{\hat{ e}}}_r}} \right)} \right]{v_r}\sigma {\rm{d}}\varOmega {\rm{d}}{{{v}}_1} \end{split}$ | (77) |
其中
| $ \begin{split} {\left( {\frac{{\partial f}}{{\partial t}}} \right)_E} = &{\chi} \int_{ - \infty }^{ + \infty } {\int_0^{4{\text{π}} } {\left( {{f^ * }f_1^ * - f{f_1}} \right){v_r}\sigma {\rm{d}}\varOmega {\rm{d}}{{{v}}_1}} } + \\& {d_0}{\chi} \int_{ - \infty }^{ + \infty } {\int_0^{4{\text{π}} } {\left( {{f^ * }\nabla f_1^ * + f\nabla {f_1}} \right) \cdot {{{\hat{ e}}}_r}{v_r}\sigma {\rm{d}}\varOmega {\rm{d}}{{{v}}_1}} } + \\& \frac{1}{2}{d_0}\int_{ - \infty }^{ + \infty } {\int_0^{4{\text{π}} } {\nabla\chi \cdot {{{\hat{ e}}}_r}\left( {{f^ * }f_1^ * - f{f_1}} \right){v_r}\sigma {\rm{d}}\varOmega {\rm{d}}{{{v}}_1}} } \end{split} $ | (78) |
其中
| ${f^{eq}} = \rho \frac{1}{{{{\left( {2{\text{π}} RT} \right)}^{\tfrac{3} {2}}}}}\exp \left[ { - \frac{{{{\left( {{{v}} - {{u}}} \right)}^2}}}{{2RT}}} \right]$ | (79) |
则恩斯柯格碰撞算符可写为:
| $ \begin{split} {\left( {\frac{{\partial f}}{{\partial t}}} \right)_E} =& {\chi} \int_{ - \infty }^{ + \infty } {\int_0^{4{\text{π}} } {\left( {{f^ * }f_1^ * - f{f_1}} \right){v_r}\sigma {\rm{d}}\varOmega {\rm{d}}{{{v}}_1}} }- \\& {f^{eq}}b\rho \chi \left\{ {\left( {{{v}} - {{u}}} \right) \cdot \left\{ {\frac{2}{\rho }\nabla \rho + \frac{3}{{5T}}\nabla T\left[ {\frac{{{\left( {{{v}} - {{u}}} \right)}^2}}{{2RT}} - \frac{5}{{2}}} \right]} \right\}} \right.+ \\& \left. { \frac{3}{{5RT}}\left( {{{v}} - {{u}}} \right)\left( {{{v}} - {{u}}} \right):\nabla {{u}} + \frac{3}{{5}}\left[ { \frac{{{{\left( {{{v}} - {{u}}} \right)}^2}}}{{2RT}}- \frac{5}{{2}}} \right]\nabla \cdot {{u}}} \right\} - \\& {f^{eq}}b\rho \left( {{{v}} - {{u}}} \right)\cdot \nabla \chi \end{split} $ | (80) |
其中
| $ \begin{split} {\left( {\frac{{\partial f}}{{\partial t}}} \right)_E} =& {\chi} {\int}_{ - {\infty} }^{ + {\infty} } {{\int}_0^{4{\text{π}} } {\left( {{f^ * }f_1^ * - f{f_1}} \right){v_r}{\sigma} {\rm{d}}{\varOmega} {\rm{d}}{{{v}}_1}} } - \\& {f^{eq}}b{\rho} {\chi} \left( {{{v}} - {{u}}} \right) \cdot \frac{2}{\rho }{\nabla} {\rho} - {f^{eq}}b{\rho} \left( {{{v}} - {{u}}} \right) \cdot{\nabla} {\chi} \end{split} $ | (81) |
使用BGK模型对上式右端第一项进行简化,可得:
| $ {\left( {\frac{{\partial f}}{{\partial t}}} \right)_E} = - \frac{1}{\tau }\left( {f - {f^{eq}}} \right) - {f^{eq}}b\rho \chi \left( {{{v}} - {{u}}} \right) \cdot \nabla \ln \left( {{\rho ^2}\chi } \right) $ | (82) |
由式(82)则可以得到近似不可压、等温系统的简化恩斯柯格方程:
| $ \begin{split}& \frac{{\partial f}}{{\partial t}} + {{v}} \cdot \nabla f + {{a}} \cdot {\nabla _{{v}}}f =\\&\qquad - \frac{1}{\tau }\left( {f - {f^{eq}}} \right) - {f^{eq}}b\rho \chi \left( {{{v}} - {{u}}} \right) \cdot \nabla \ln \left( {{\rho ^2}\chi } \right) \end{split} $ | (83) |
如果将外力项中的分布函数
| $ {{a}} \cdot {\nabla _{{v}}}f \approx {{a}} \cdot {\nabla _{{v}}}{f^{eq}} = - \frac{{F \cdot \left( {{{v}} - {{u}}} \right)}}{{\rho RT}}{f^{eq}} $ | (84) |
则可以将简化的恩斯柯格方程写为:
| $\begin{split}& \frac{{\partial f}}{{\partial t}} + {{v}} \cdot \nabla f - \frac{{{{F}} \cdot \left( {{{v}} - {{u}}} \right)}}{{\rho RT}}{f^{eq}} = \\&\qquad - \frac{1}{\tau }\left( {f - {f^{eq}}} \right) - \frac{{\left( {{{v}} - {{u}}} \right) \cdot \nabla \left( {b{\rho ^2}RT\chi } \right)}}{{\rho RT}}{f^{eq}} \end{split}$ | (85) |
右端最后一项代表分子间斥力的作用,即为分子的体积效应。
恩斯柯格方程引入了分子间斥力作用。如果在恩斯柯格方程中引入分子间的引力,就可以得到基于恩斯柯格方程的多相流模型。由平均场理论,分子间的相互吸引可用平均力势[17],
| $\varPhi \left( {{{{r}}_{{1}}}} \right) = \int_{{r_{12}} > {d_0}} {{\phi _{{\rm{attr}}}}\left( {{r_{12}}} \right)} \rho \left( {{{{r}}_2}} \right){\rm{d}}{{{r}}_2}$ | (86) |
来描述,其中
| $\varPhi \left( {{{{r}}_{{1}}}} \right) = - 2a\rho - K{\nabla ^2}\rho $ | (87) |
其中第一项通过
| ${{F}} = - \rho \nabla \varPhi = \nabla \left( {a{\rho ^2}} \right) + \rho \nabla \left( {K{\nabla ^2}\rho } \right)$ | (88) |
将
| $\frac{{\partial f}}{{\partial t}} + {{v}} \cdot \nabla f - \frac{{{{F'}} \cdot \left( {{{v}} - {{u}}} \right)}}{{\rho RT}}{f^{eq}} = - \frac{1}{\tau }\left( {f - {f^{eq}}} \right)$ | (89) |
其中,
| ${{F'}} = \left[ { - \nabla \psi + \rho \nabla \left( {K{\nabla ^2}\rho } \right)} \right]$ | (90) |
| $\psi = b{\rho ^2}RT\chi - a{\rho ^2}$ | (91) |
由式(89)则可以得到相应的DBM演化方程为:
| $ \frac{{\partial {f_{i}}}}{{\partial t}} + {{{v}}_{i}} \cdot \nabla {f_{i}} - \frac{{{{F'}} \cdot \left( {{{{v}}_{i}} - {{u}}} \right)}}{{\rho RT}}f_{i}^{eq} = - \frac{1}{\tau }\left( {{f_{i}} - f_{i}^{eq}} \right) $ | (92) |
在模拟含化学反应的系统时,通过引入化学反应项考虑化学反应对系统的影响。以BGK模型为例,考虑化学反应的玻尔兹曼-BGK方程具有如下形式:
| $\frac{{\partial f}}{{\partial t}} + {{v}} \cdot \nabla f = - \frac{1}{\tau }\left( {f - {f^{eq}}} \right) + C$ | (93) |
其中:
通常情况下,系统化学反应的时间尺度
| $ C = -\frac{1}{\tau }\left( {{f^{eq}} - {f^{ * eq}}} \right) $ | (94) |
其中,
若化学反应不可逆,则反应进程可由下面的反应率方程来描述:
| $\frac{{{\rm{d}}\lambda }}{{{\rm{d}}t}} = F\left( \lambda \right)$ | (95) |
其中
| ${T^ * } = T + \tau QF\left( \lambda \right)$ | (96) |
其中
由于单弛豫时间模型是多弛豫时间模型的特例,所以模拟燃烧系统的DBM演化方程可统一由下式描述[27]:
| $ \frac{{\partial {f_i}}}{{\partial t}} + {v_{i\alpha }}\frac{{\partial {f_i}}}{{\partial {r_{\alpha} }}} = - M_{il}^{ - 1}\left[ {{{\hat R}_{lk}}\left( {{{\hat f}_k} - \hat f_k^{eq}} \right) + {{\hat A}_l}} \right] + {C_i} $ | (97) |
其中,
| $\left\{ \begin{array}{l} {R_1} = {R_2} = \cdots = {R_N} = {1 / \tau } \\ {{\hat A}_l} = 0 \\ {C_i} = \dfrac{1}{\tau }\left( {f_i^{ * eq} - f_i^{eq}} \right) \\ {f^{ * eq}} = {f^{ * eq}}\left( {\rho ,{{u}},T + \tau QF\left( \lambda \right)} \right) \\ {f^{eq}} = {f^{eq}}\left( {\rho ,{{u}},T} \right) \end{array} \right.$ | (98) |
对于多弛豫时间模型,Chapman-Enskog多尺度分析按如下方式展开:
| $\left\{ \begin{array}{l} {f_i} = f_i^{\left( 0 \right)} + {Kn} f_i^{\left( 1 \right)} + {{Kn} ^2}f_i^{\left( 2 \right)} + \cdots \\ {A_i} = {Kn} {A_{1i}} \\ {C_i} = {Kn} {C_{1i}} \\ \dfrac{\partial }{{\partial t}} = {Kn} \dfrac{\partial }{{\partial {t_1}}} + {{Kn} ^2}\dfrac{\partial }{{\partial {t_2}}} + \cdots \\ \dfrac{\partial }{{\partial {r_{\alpha} }}} = {Kn} \dfrac{\partial }{{\partial {r_{1\alpha }}}} \end{array} \right.$ | (99) |
与宏观二流体、多流体模型相对应,DBM也有二流体、多流体模型。
对于多介质流体系统,引入速度空间和动理学矩相空间的离散分布函数
| ${\rho ^\sigma } = {m^\sigma }{n^\sigma } = {m^\sigma }\sum\limits_i {f_i^\sigma } $ | (100) |
| $J_{\alpha} ^\sigma = {\rho ^\sigma }u_{\alpha} ^\sigma = {m^\sigma }\sum\limits_i {f_i^\sigma v_{i\alpha }^\sigma } $ | (101) |
其中
| $\rho = \sum\limits_\sigma {{\rho ^\sigma }} $ | (102) |
| $n = \sum\limits_\sigma {{n^\sigma }} $ | (103) |
| ${J_{\alpha} } = \rho {u_{\alpha} } = \sum\limits_\sigma {J_{\alpha} ^\sigma } $ | (104) |
介质
| ${E^\sigma } = \frac{1}{2}{m^\sigma }\sum\limits_i {f_i^\sigma \left[ {{{\left( {v_i^\sigma } \right)}^2} + {{\left( {\eta _i^\sigma } \right)}^2}} \right]} $ | (105) |
| $E = \sum\limits_\sigma {{E^\sigma }} $ | (106) |
其中,
比单介质情形复杂的是,内能(温度)的定义依赖于作为参考的流速,而在多介质情形,既有介质
| ${T^{\sigma * }} = \frac{{2{E^\sigma } - {\rho ^\sigma }{u^2}}}{{\left( {D + {I^\sigma }} \right){n^\sigma }}}$ | (107) |
| $ T = \frac{{2{E } - {\rho }{u^2}}}{{\displaystyle\sum\limits_\sigma {\left( {D + {I^\sigma }} \right){n^\sigma }} }} $ | (108) |
| ${T^\sigma } = \frac{{2{E^\sigma } - {\rho ^\sigma }{{\left( {{u^\sigma }} \right)}^2}}}{{\left( {D + {I^\sigma }} \right){n^\sigma }}}$ | (109) |
至此,引入了三种温度。温度和压强之间由状态方程相联系。有几种温度,就有几种压强。鉴于问题的复杂性,在本节讨论中暂且忽略分子间作用力,使用理想气体状态方程,给出一种建模思路。对于理想气体情形,首先定义介质
| ${P^{\sigma * }} = {n^\sigma }{T^{\sigma * }}$ | (110) |
则混合物的压强:
| $P = \sum\limits_\sigma {{P^{\sigma * }}} $ | (111) |
同时,定义介质
| ${P^\sigma } = {n^\sigma }{T^\sigma }$ | (112) |
可见,如果将混合物(平均)流速作为参考,则混合物的总压强等于各介质的分压强之和。
平衡态分布函数依赖于粒子数密度、流速和温度,温度的定义依赖于流速,而我们有两种流速—介质
| $f_i^{\sigma ,eq} = f_i^{\sigma ,eq}\left( {{n^\sigma },u_{\alpha} ^\sigma ,T^\sigma } \right)$ | (113) |
| $ f_i^{\sigma ,eq * } = f_i^{\sigma ,eq}\left( {{n^\sigma },u_{\alpha} ,T^{\sigma * }} \right) $ | (114) |
| $ f_i^{\sigma ,meq} = f_i^{\sigma ,eq}\left( {{n^\sigma },u_{\alpha} ,T} \right) $ | (115) |
与此对应,动理学矩空间的分布函数也有三种:
| $\hat f _i^{\sigma ,eq} = \hat f _i^{\sigma ,eq}\left( {{n^\sigma },u_{\alpha} ^\sigma ,T^\sigma } \right)$ | (116) |
| $ \hat f _i^{\sigma ,eq * } = \hat f _i^{\sigma ,eq}\left( {{n^\sigma },u_{\alpha} ,T^{\sigma * }} \right) $ | (117) |
| $ \hat f _i^{\sigma ,meq} = \hat f _i^{\sigma ,eq}\left( {{n^\sigma },u_{\alpha} ,T} \right) $ | (118) |
在多介质流动中,分子碰撞的最终结果是使得
| ${\partial _t}f_i^\sigma + v_{i\alpha }^\sigma {\partial _{\alpha} }f_i^\sigma = - \frac{1}{{{\tau ^\sigma }}}\left( {f_i^\sigma - f_i^{\sigma ,meq}} \right)$ | (119) |
二步(弛豫)碰撞模型的思路是:介质内先平衡,介质间再平衡。演化方程可写为:
| $\begin{split}& {\partial _t}f_i^\sigma + v_{i\alpha }^\sigma {\partial _{\alpha} }f_i^\sigma = - \frac{1}{{\tau _1^\sigma }}\left( {f_i^\sigma - f_i^{\sigma ,seq}} \right) - \\&\qquad {\rm{ }} \frac{1}{{\tau _2^\sigma }}\left( {f_i^{\sigma ,seq} - f_i^{\sigma ,meq}} \right) \end{split} $ | (120) |
当
在单流体模型中,只有一套流体力学量
在含示踪粒子的系统中,我们可以使用斯托克斯数(Stokes number, St)来描述该粒子的动力学状态:
| ${St} = \frac{{{u_0} {\tau _P}}}{{{l_0}}}$ | (121) |
其中
我们往往需要引入一批示踪粒子。沿着每一个示踪粒子的轨迹,都可以给出拉格朗日视角的基于示踪粒子的描述。对于第
| $\frac{{d{{{r}}_k}}}{{dt}} = {{{u}}_P}\left( {{{{r}}_k}} \right)$ | (122) |
其中,
示踪粒子往往需要尽可能的小。假设其体积与质量极小,在流场中用一个点来表示,其与流体之间的动量交换在瞬间完成,那么示踪粒子的速度就直接由局域的流动速度决定:
| $ {{{u}}_P}\left( {{{{r}}_k}} \right) = \int_D {{{u}}\left( {{r}} \right)} \cdot \vartheta\left( {\left| {{{r}} - {{{r}}_k}} \right|} \right){\rm{d}}a $ | (123) |
其中
因为示踪粒子在运动过程中,很难刚好落在网格点上,所以,其速度需要根据它附近的流体网格点的速度确定。具体而言,就是将附近的网格点上的速度根据网格点位置与示踪粒子位置的距离远近而作加权平均,在数学上通过使用离散的Dirac函数(
| ${{{u}}^t}\left( {{{{r}}_k}} \right) = \sum\limits_{i,j} {{{u}}_{i,j}^t} \psi \left( {{{{r}}_{i,j}},{{{r}}_k}} \right)$ | (124) |
| $\psi \left( {{{{r}}_{i,j}},{{{r}}_k}} \right) = \psi \left( {\left| {{{{r}}_{i,j}} - {{{r}}_k}} \right|} \right) = \varphi \left( {\varDelta {r_x}} \right) \cdot \varphi \left( {\varDelta {r_y}} \right)$ | (125) |
其中,
| $\varphi \left( {\varDelta {r_x}} \right) = \left\{ \begin{array}{l} \left\{ {1 + \cos \left[ {\left( {{{\varDelta {r_x}} / {\varDelta x}}} \right) \cdot {{\text{π}} / 2}} \right]} \right\},\varDelta {r_x} \leqslant 2\varDelta x \\ 0,\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\varDelta {r_x} > 2\varDelta x \end{array} \right.$ | (126) |
据此,示踪粒子从流场中获得了自己的运动速度。
3.9 离散玻尔兹曼建模:等离子体情形等离子体是由大量处于非束缚态的带电粒子组成的具有宏观时间和空间尺度的体系。在等离子体中,时空尺度以及密度、温度等宏观状态量可以跨越10个数量级及以上的范围,这使得:(1)相关的特征时间和空间尺度极其丰富,例如研究中常用到的空间尺度有德拜半径、拉莫尔半径等,常用到的时间尺度有朗缪尔振荡周期等;(2)研究中使用的物理模型和方法从宏观到微观种类繁多,如磁流体力学、弗拉索夫动理学方程、粒子模拟方法(如质点网格法,Particle in Cell,PIC)等。
受控热核聚变是解决人类能源问题的关键,其中等离子体的运动处于高温高密高压的极端环境,同时涉及到多时空尺度的多场耦合及带电粒子间的碰撞输运过程,是人们关注的重点。
在等离子体介观动理学模拟中,一般采用德拜半径作为特征空间尺度将等离子体间的相互作用划分为自洽电磁场(长程外力项部分)和碰撞(短程输运部分),描述方程如式(127)所示:
| $\begin{split}&\frac{{\partial {f^{\alpha} }}}{{\partial t}} + {{v}} \cdot \frac{{\partial {f^{\alpha} }}}{{\partial {{r}}}} + \frac{{{{{F}}^{\alpha} }}}{{{m^{\alpha} }}} \cdot \frac{{\partial {f^{\alpha} }}}{{\partial {{v}}}} + \\&\qquad \frac{{{q^{\alpha} }}}{{{m^{\alpha} }}}\left( {{{E}} + {{v}} \times {{B}}} \right) \cdot \frac{{\partial {f^{\alpha} }}}{{\partial {{v}}}} = \sum\limits_{\beta = e,i} {{{\left( {\frac{{\partial {f^{\alpha} }}}{{\partial t}}} \right)}_\beta }} \end{split}$ | (127) |
其中
由于作用的时空尺度不同,人们往往在长程作用及碰撞输运作用中选其一进行研究,这种取舍一方面是基于部分物理现实问题的尺度分离(具有合理性),另一方面也是由于不同尺度耦合问题的复杂性和处理方法的不足甚至是缺乏(具有无奈性)。但是,对于有些问题如静电激波阵面结构、惯性约束聚变中的流体不稳定性问题等,两种作用的时空尺度接近,无法将其中之一作为微扰,因而两种作用需要同时加以考虑。
等离子体中自洽电磁场同等离子体运动相耦合,采用有限差分的Maxwell方程组解法主要有时域有限差分(Finite difference time domain, FDTD或Yee格式)、交替方向隐式迭代时域有限差分(Alternating direction implicit-FDTD, ADI-FDTD)及分裂算子时域有限差分(Splitting operator-FDTD, S-FDTD)等。
等离子体中粒子间多体碰撞可以看作发生在德拜半径以内,根据适用的碰撞算子的复杂性可以分为Boltzmann算子、Fokker-Planck算子、Landau算子以及BGK算子,其中BGK算子由于较为简单适用性最为广泛。和多介质DBM类似,等离子体DBM也可以分为单步(弛豫)建模及多步(弛豫)建模。
忽略中间动理学过程,采用由Andries[52]等发展的AAP单步弛豫模型的等离子体动理学模型为:
| $\frac{{\partial {f^{\alpha} }}}{{\partial t}} + {{v}} \cdot \frac{{\partial {f^{\alpha} }}}{{\partial {{r}}}} + {{{{{a}}^{\alpha} }}} \cdot \frac{{\partial {f^{\alpha} }}}{{\partial {{v}}}}= - \frac{{{f^{\alpha} } - {f^{\alpha ,{\rm{AAP}}}}}}{{{\tau ^{\alpha} }}}$ | (128) |
其中
| ${f^{\alpha ,{\rm{AAP}}}} = {n^{\alpha} }{\left( {\frac{{{m^{\alpha} }}}{{2{\text{π}} k{{\bar T}^{\alpha} }}}} \right)^{\tfrac{3}{2}}}\exp \left( { - \frac{{{m^{\alpha} }{{\left| {{{v}} - {{{\bar{ u}}}^{\alpha} }} \right|}^2}}}{{2k{{\bar T}^{\alpha} }}}} \right)$ | (129) |
若考虑不同种粒子间的碰撞弛豫(中间动理学过程),采用由Haack[53]等发展的等离子体动理学模型为:
| $\left\{ \begin{array}{l} \dfrac{{\partial {f^{\alpha} }}}{{\partial t}} + {{v}} \cdot \dfrac{{\partial {f^{\alpha} }}}{{\partial {{r}}}} + {{{{{a}}^{\alpha} }}} \cdot \dfrac{{\partial {f^{\alpha} }}}{{\partial {{v}}}} = \displaystyle\sum {{\nu ^{\alpha \beta }}({{c}})({{M}^{\alpha \beta }} - {f^{\alpha} })} \\ {{M}^{\alpha \beta }}({{c}}) = {n^{\alpha} }{\left( {\dfrac{{{m^{\alpha} }}}{{2{\text{π}} k{T^{\alpha \beta }}}}} \right)^{{\tfrac{3}{2}}}}\exp \left( { - \dfrac{{{m^{\alpha} }{{\left| {{{v}} - {{{u}}^{\alpha \beta }}} \right|}^2}}}{{2k{T^{\alpha \beta }}}}} \right) \end{array} \right.$ | (130) |
其中
| $\left\{ \begin{array}{l} {{{u}}^{\alpha \beta }} = \dfrac{{{{{u}}^{\alpha} } + {{{u}}^\beta }}}{2} \\ {T^{\alpha \beta }} = \dfrac{{{m^{\alpha} }{T^\beta } + {m^\beta }{T^{\alpha} }}}{{{m^{\alpha} } + {m^\beta }}} + \dfrac{{{m^{\alpha} }{m^\beta }}}{{6({m^{\alpha} } + {m^\beta })}}{({{{u}}^{\alpha} } - {{{u}}^\beta })^2} \end{array} \right.$ | (131) |
| $\left\{ \begin{array}{l} {{{u}}^{\alpha \beta }} = \dfrac{{{m^{\alpha} }{{{u}}^{\alpha} } + {m^\beta }{{{u}}^\beta }}}{{{m^{\alpha} } + {m^\beta }}} \\ {T^{\alpha \beta }} = \dfrac{{{T^{\alpha} } + {T^\beta }}}{2} + \dfrac{{{m^{\alpha} }{m^\beta }}}{{6({m^{\alpha} } + {m^\beta })}}{({{{u}}^{\alpha} } - {{{u}}^\beta })^2} \end{array} \right.$ | (132) |
式(131)和式(132)分别为满足动量弛豫约束的BGK-EM模型和满足能量弛豫约束的BGK-ET模型。目前,基于式(130)及有限差分的Maxwell方程组解法正用于等离子体静电激波及相关问题的研究。
如前面所述,将离子和电子分别作为不同的流体介质,可以使用双流体玻尔兹曼模型。当然,还存在其他不同粗粒化程度的物理建模形式,如采用分布函数描述离子的行为特征,而假设电子始终处于局域热力学平衡态或对电子采用流体描述方法。
在等离子体系统的动理学描述中,系统行为由相应的分布函数
DBM主要针对的是非平衡效应较强,以至于传统流体建模失效,同时粒子之间碰撞效应又不能忽略的情形。目前,等离子体系统的DBM建模与模拟研究尚处于起步阶段,后期我们将开展进一步研究。
4 多相流机理研究:基于DBM作为系统行为粗粒化描述的一种物理模型构建方法,DBM本身并不包含具体的数值离散格式。获得了DBM模型,跟获得了NS模型一样,在数值模拟中还需根据问题特点选取合适的数值方法。从物理问题研究的角度,可以选用满足当次物理问题研究需求的任何一种离散格式。在下面物理结果的原始文献中使用的离散格式只是满足当次研究需求的多种离散格式之一。
4.1 流体不稳定性方面流体界面不稳定性(经常简称流体不稳定性)与物质混合现象广泛存在于自然界、惯性约束核聚变和武器物理等领域。惯性约束核聚变和武器物理等领域重点关注的流体不稳定性主要有三种:RM不稳定性(Richtmyer-Meshkov instability, RMI)、RT不稳定性(Rayleigh-Taylor instability, RTI)和KH不稳定性(Kelvin-Helmholtz instability, KHI)。
流体不稳定性系统通常具有以下特点:系统的本身可能是宏观尺度的,但其内部存在大量的中间尺度的空间结构和动理学模式;这些结构和模式的存在与演化极大地影响着系统的物理性能和功能。系统内部往往具有大量的界面,包括物质界面和力学界面,系统内部的受力和响应过程非常复杂。对于这些系统的研究,NS方程只能描述大尺度缓变行为,而对于一些锐利的边界,流体的平均分子间距相对于界面尺度已经不再是可以忽略的小量,基于连续介质假设的NS方程受到挑战。在一些快变流动模式描述方面,流体系统趋于热力学平衡的弛豫时间相对于该流动的特征时间来讲,不再是可以忽略的小量,热力学非平衡效应较强,只考虑一阶热力学非平衡效应的NS描述不再能满足需求。
对于流体不稳定性问题,DBM可以根据需要研究的非平衡程度和选定研究的具体非平衡行为特征构建满足需求的物理模型。在只考虑一阶热力学非平衡效应的情况,除了NS可以描述的流体行为,借助所定义的各种非平衡特征量,DBM可以给出NS所遗漏的一系列非平衡行为的描述。
2016年,利用单弛豫时间DBM,赖惠林等重点研究了流体界面不稳定性演化过程中的热力学非平衡效应[54-55]。研究发现,可压性对RT界面演化呈现出“先抑制、减速,后促进、加速”的阶段性,这一阶段性可从能量转换角度获得很好的解释。在每个时刻,所有非平衡动理学模式均随可压性增强而增强;随可压性增强,可观测的非平衡效应越来越丰富,后期高阶非平衡动理学模式慢慢凸显出来;在不同阶段,非平衡模式之间相对强弱会发生改变;某些非平衡动理学模式的强度始终较小。
陈锋等使用多弛豫时间(Multiple Relaxation Time, MRT)DBM从宏观行为和非平衡特征两个角度研究Rayleigh-Taylor不稳定性问题,尤其探讨了以下两方面问题:(1)系统内密度、流速、温度、压强等宏观量的不均匀度与各种不同形式的非平衡行为之间的关联度;(2)黏性、热传导、Prandtl数对界面扰动增长过程、对上述各类关联的影响[56]。
2019年,借助DBM,甘延标等研究了KH不稳定性系统的流变和形态特征[57]。重点研究了传统流体建模所忽略、而MD模拟因适用时空尺度受限而无法直接研究的热力学非平衡行为和效应。同时,为解决KH不稳定性演化过程中各类复杂物理场的分析问题,他们提出了通过追踪非平衡行为特征和形态分析技术相结合[58-60],进行特征结构或模式的物理甄别与追踪技术设计,定量表征KH混合层宽度和发展速率的新途径。借助双介质DBM,林传栋等人更加细致地研究了RT不稳定性系统的非平衡行为特性[61]。
陈锋等人的研究[62]表明,在RM不稳定性或RT不稳定性演化过程中,系统内的温度不均匀度和无组织能量流(Non-Organized Energy Flux, NOEF)之间、密度不均匀度和TNE强度之间的相关度较高,接近1;速度不均匀度和无组织动量流(Non-Organized Momentum Flux,NOMF)强度之间相关度也相对较高(见图4);热传导是影响相关度的重要因素(见图5)。
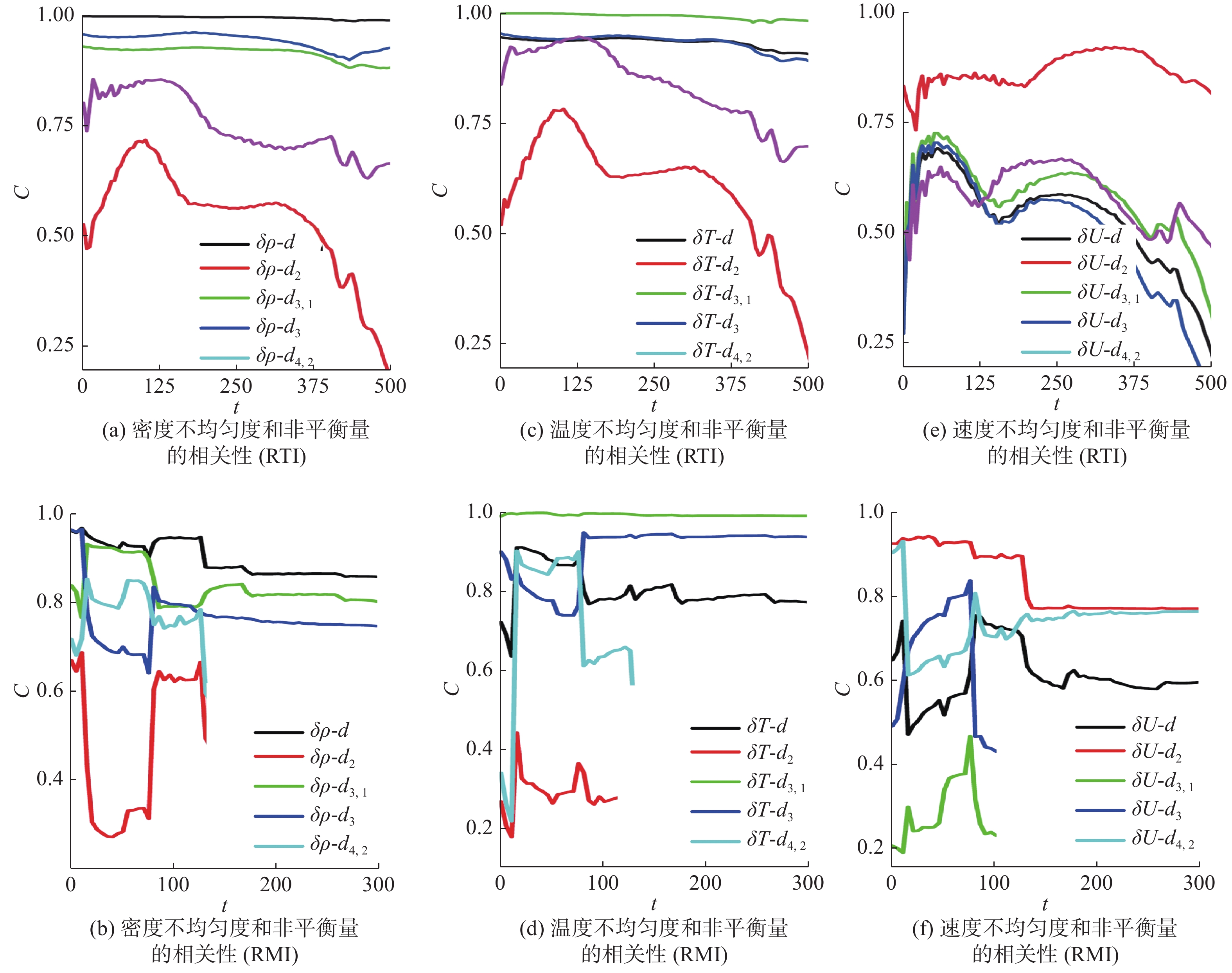
|
图 4 RT与RM不稳定性演化过程中系统内不同类型的非平衡强度与密度、温度、流速不均匀度之间关联程度的对比[56, 62](更多细节参见文献[62]) Fig.4 Comparison of the correlation degree between different types of non-equilibrium strength and density, temperature and flow rate unevenness in the evolution of RT and RM instability[56, 62] (see Ref. [62] for more details) |
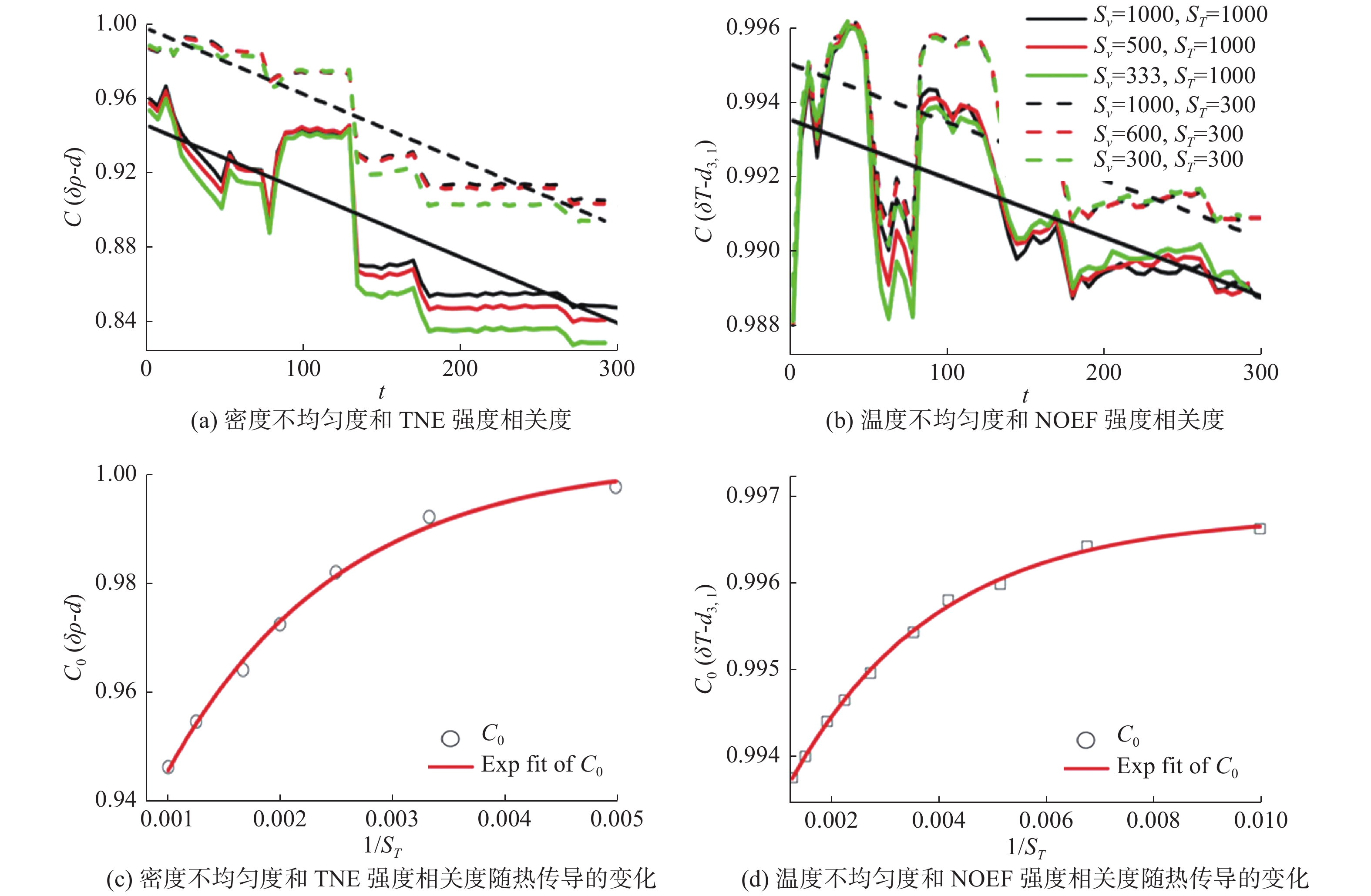
|
图 5 RM不稳定性演化过程中热传导对相关度的影响[62](更多细节参见文献[62]) Fig.5 Effect of heat conduction on the degree of correlation in the evolution of RM instability[62] (see Ref. [62] for more details) |
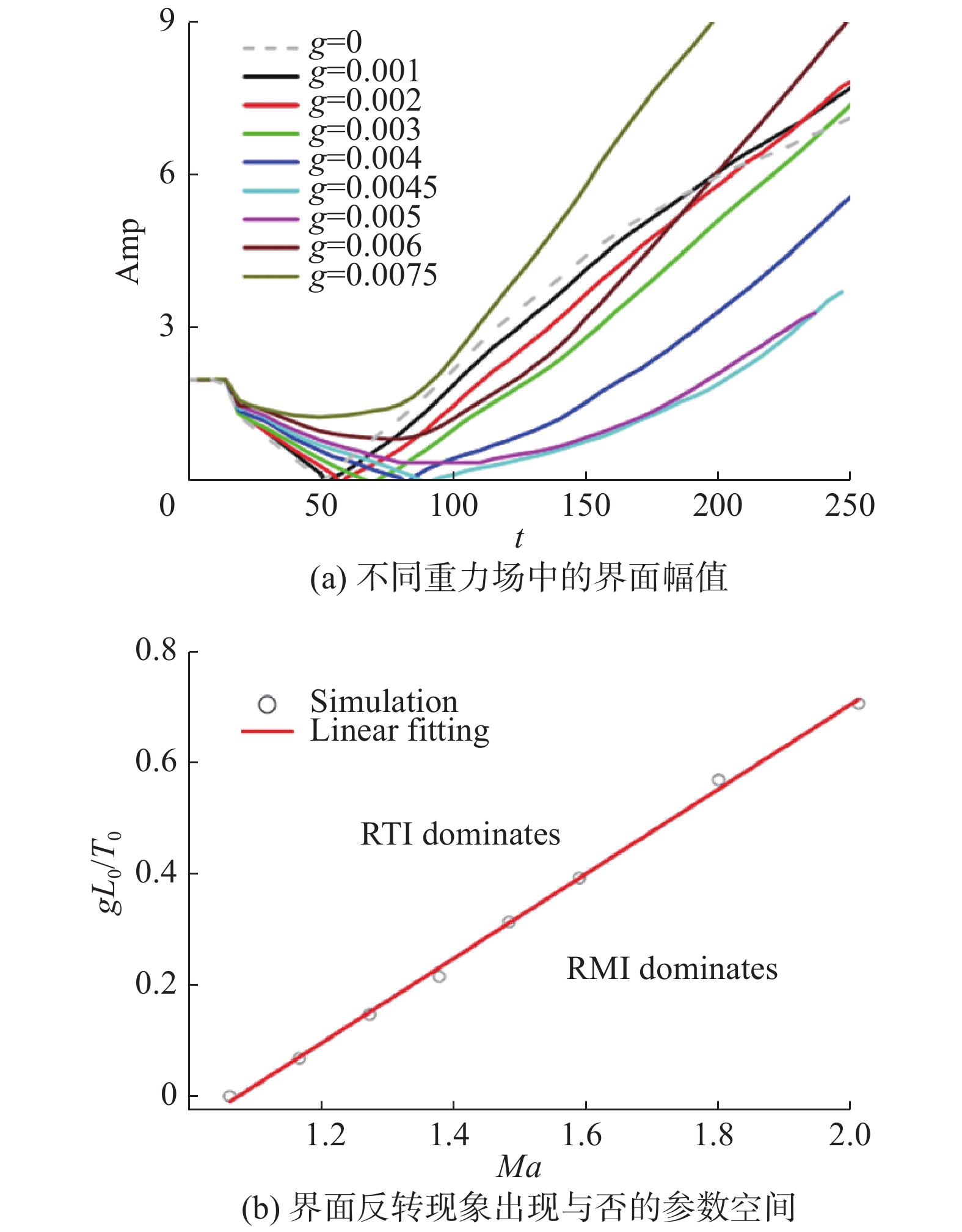
相比于RT不稳定性系统,在RM不稳定性系统中,冲击波的透射和反射使得相关度演化曲线出现“跳变”(见图4)。在RT不稳定性与RM不稳定性共存的系统中,重力加速度和冲击波强度之间合作、竞争,共同主导着界面演化与物质和能量混合过程。在RM不稳定性主导的情形初始扰动界面会出现反转(见图6-图7,更多细节参见文献[62])。
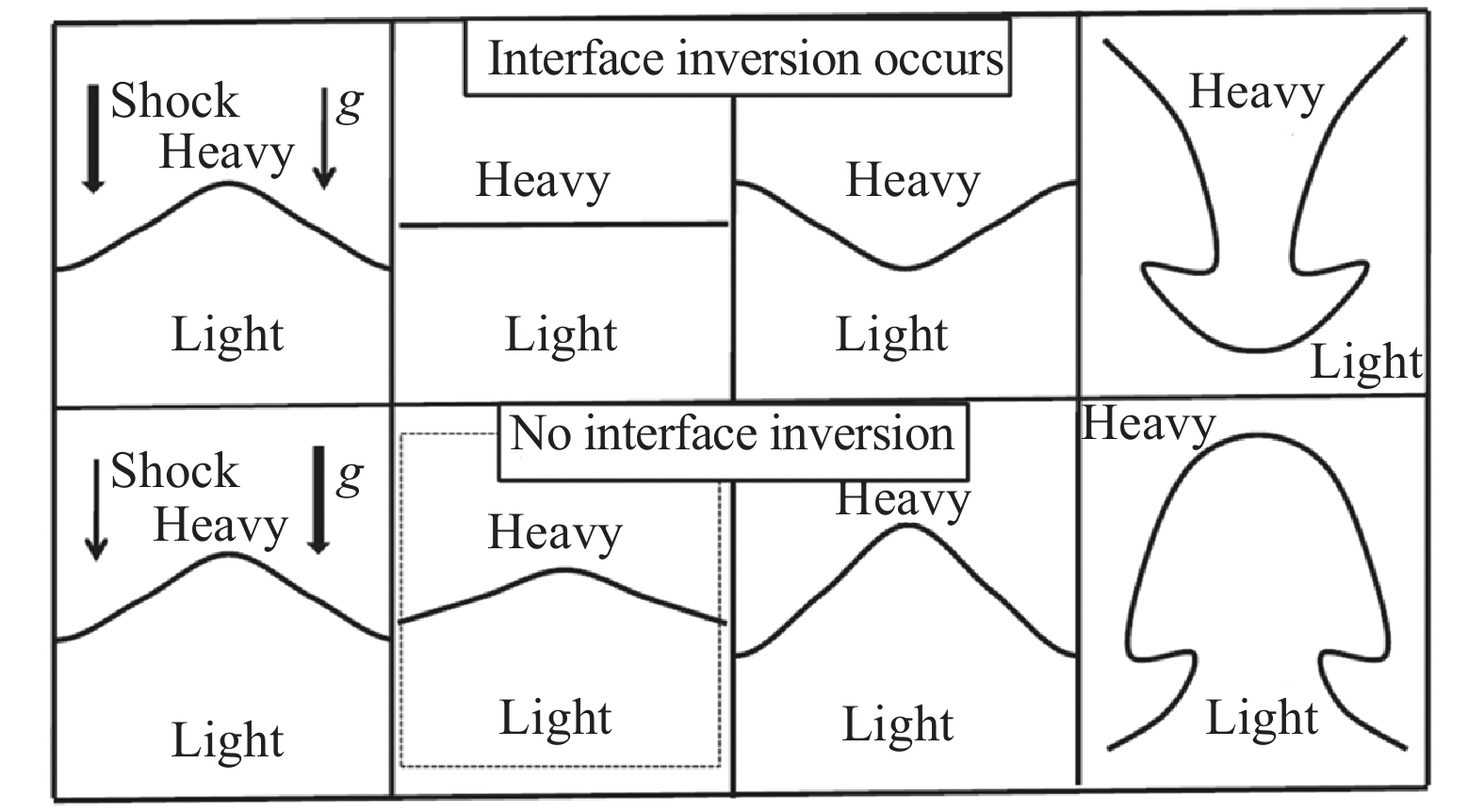
|
图 6 RTI与RMI共存系统界面反转现象出现机制的示意图[62] Fig.6 The schematic diagram of the collaboration and competition relations between RM and RT instability[62] |
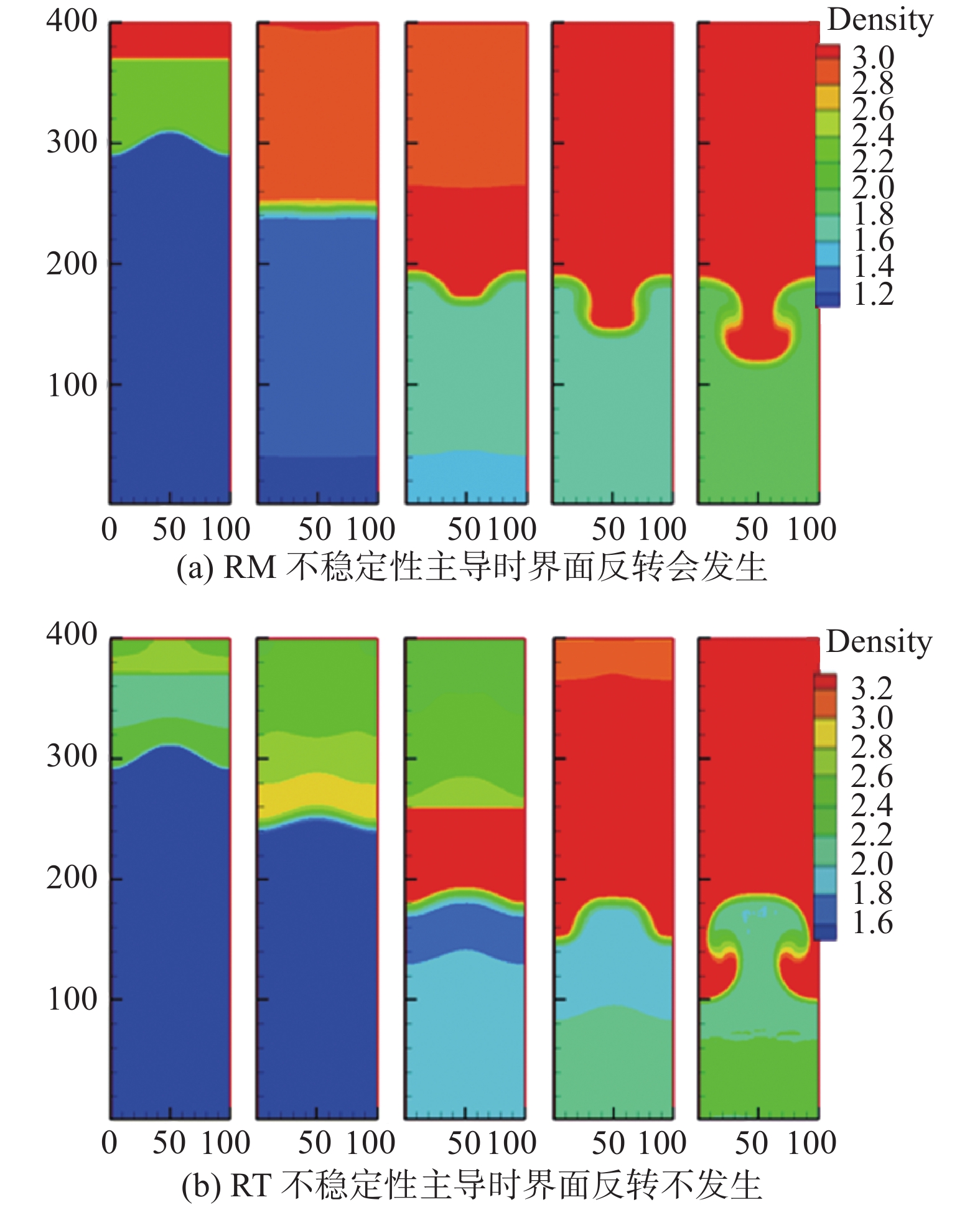
|
图 7 RTI与RMI共存系统界面反转现象出现与否的数值模拟密度云图[62] Fig.7 Numerical simulation density nephogram of interface inversion in RTI and RMI coexistence system[62] |
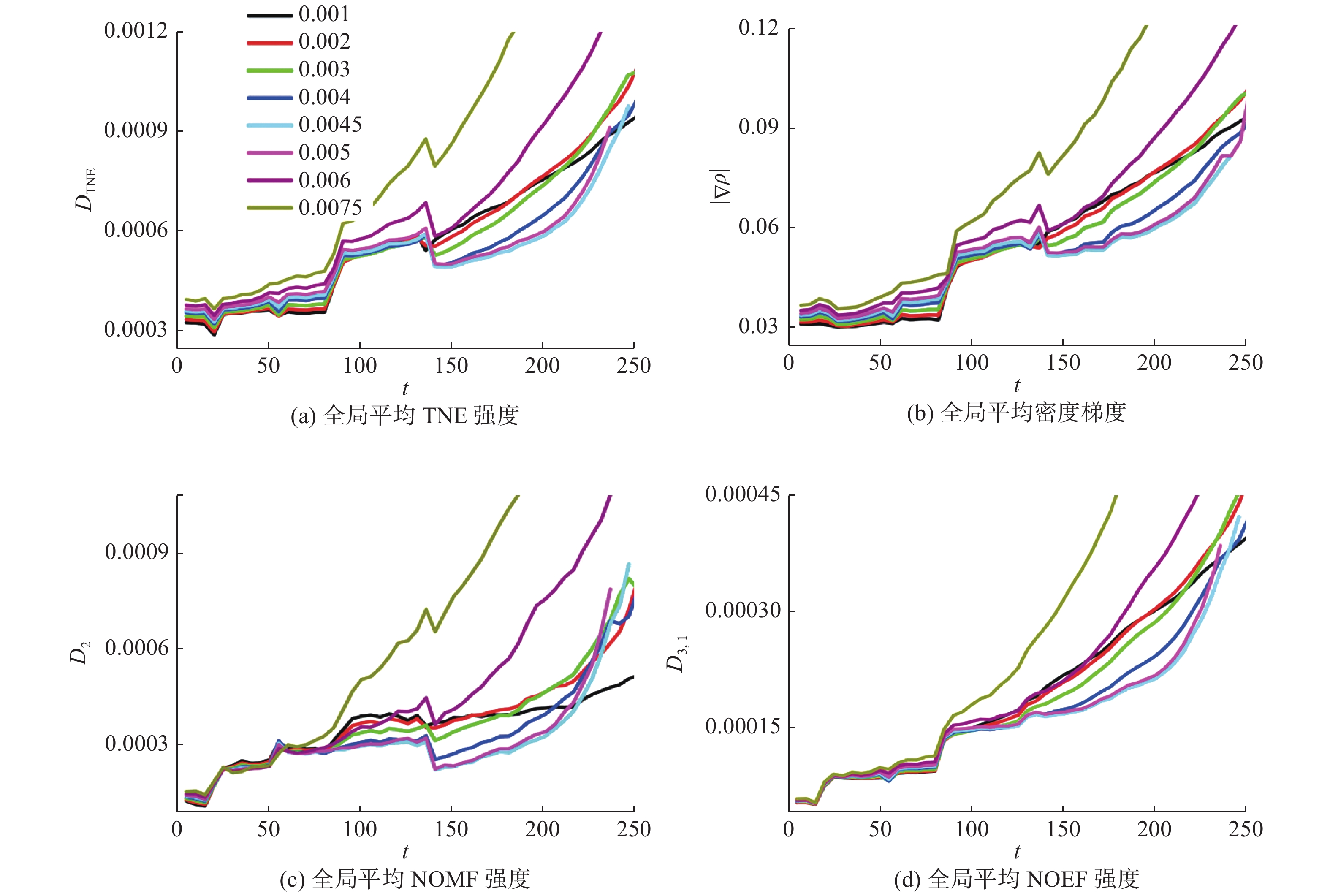
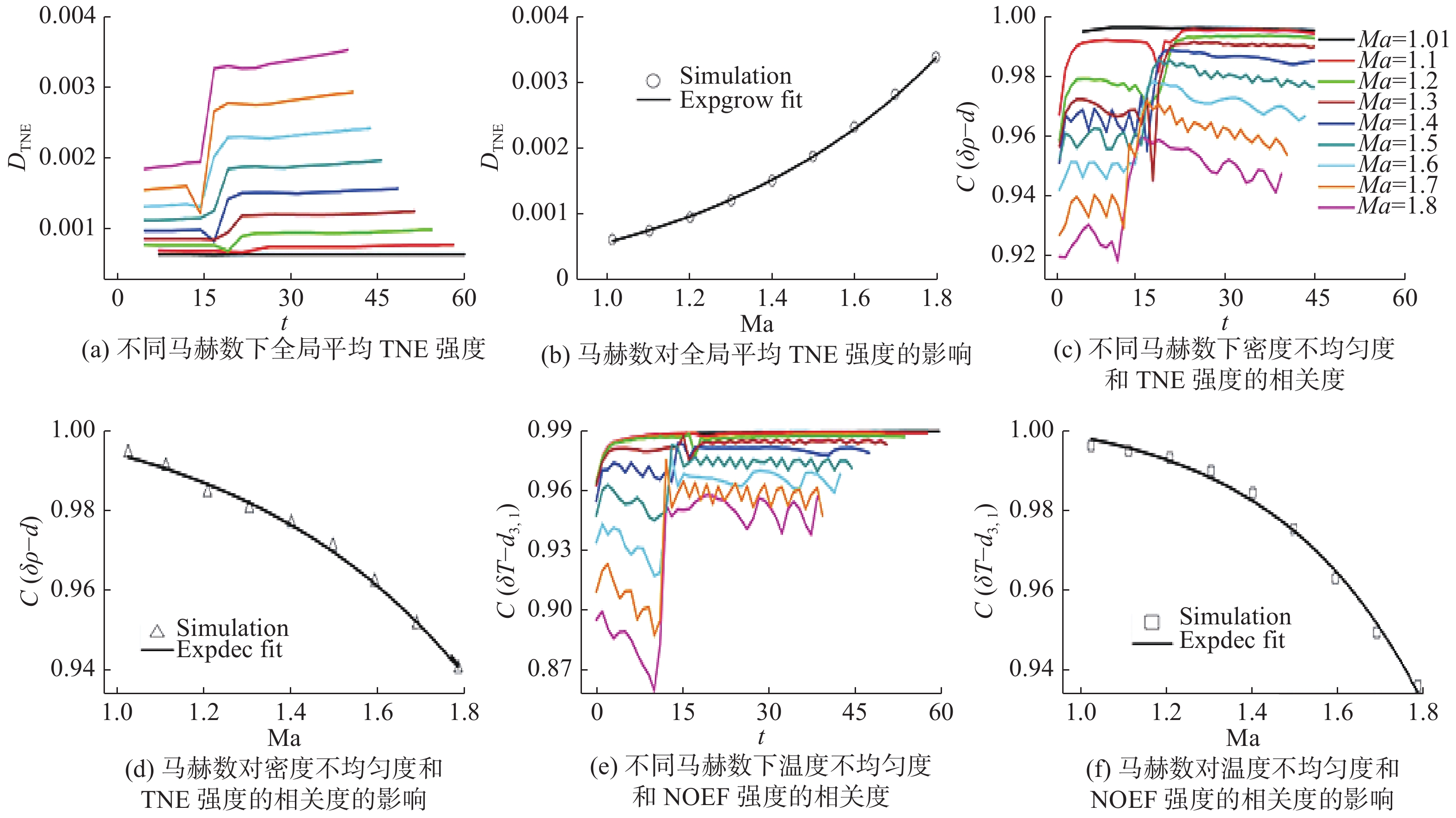
RT不稳定性和RM不稳定性分别主导的参数区间如图8所示。图9展示了全局平均TNE强度、全局平均密度梯度、全局平均NOMF强度以及全局平均NOEF强度随时间的演化;重力加速度对非平衡行为特征的影响表现出阶段性(见图9);随着马赫数的增加,系统的整体非平衡强度指数增加,而温度不均匀度与NOEF的相关度指数衰减(见图10)。图8~图10为数值模拟结果,更多细节参见文献[62]。
|
图 9 不同重力场下RTI与RMI共存系统的非平衡行为特征[62] Fig.9 Non-equilibrium characteristics of RTI and RMI coexistence system under different gravity fields[62] |
|
图 10 马赫数对RTI与RMI共存系统TNE强度、宏观量梯度与非平衡特征相关度的影响[62] Fig.10 Influence of Mach number on thermodynamic non-equilibrium strength, macroscopic gradient and non-equilibrium characteristic correlation of RTI and RMI coexistence system[62] |
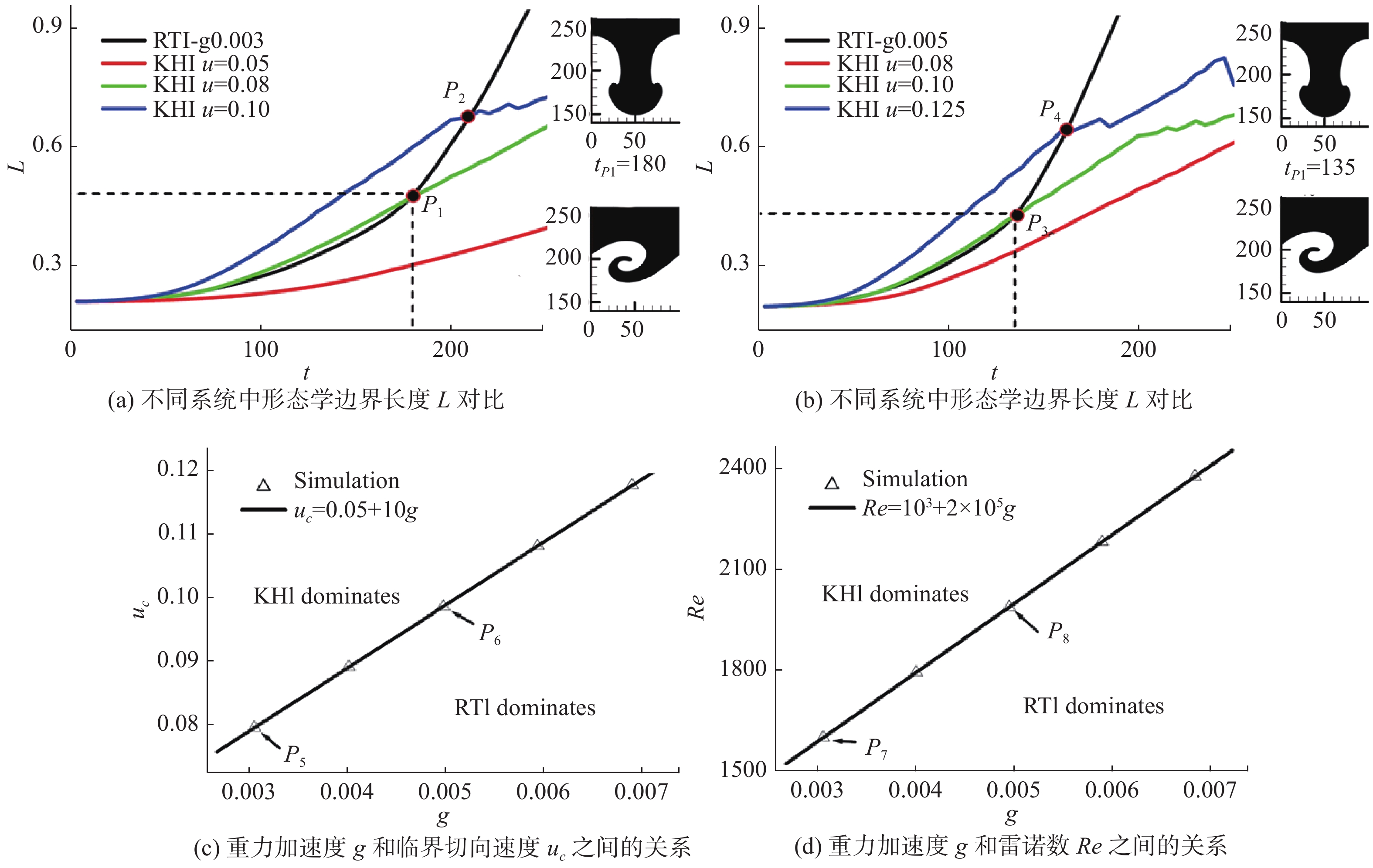
2020年,基于多弛豫时间DBM,结合形态学分析、时空关联等方法,陈锋等进一步对耦合瑞利-泰勒-开尔文-亥姆霍兹不稳定性(RTKHI)系统进行了研究[63]。研究发现:温度场图灵斑图的总边界长度L和平均热通量强度
图11为重力加速度
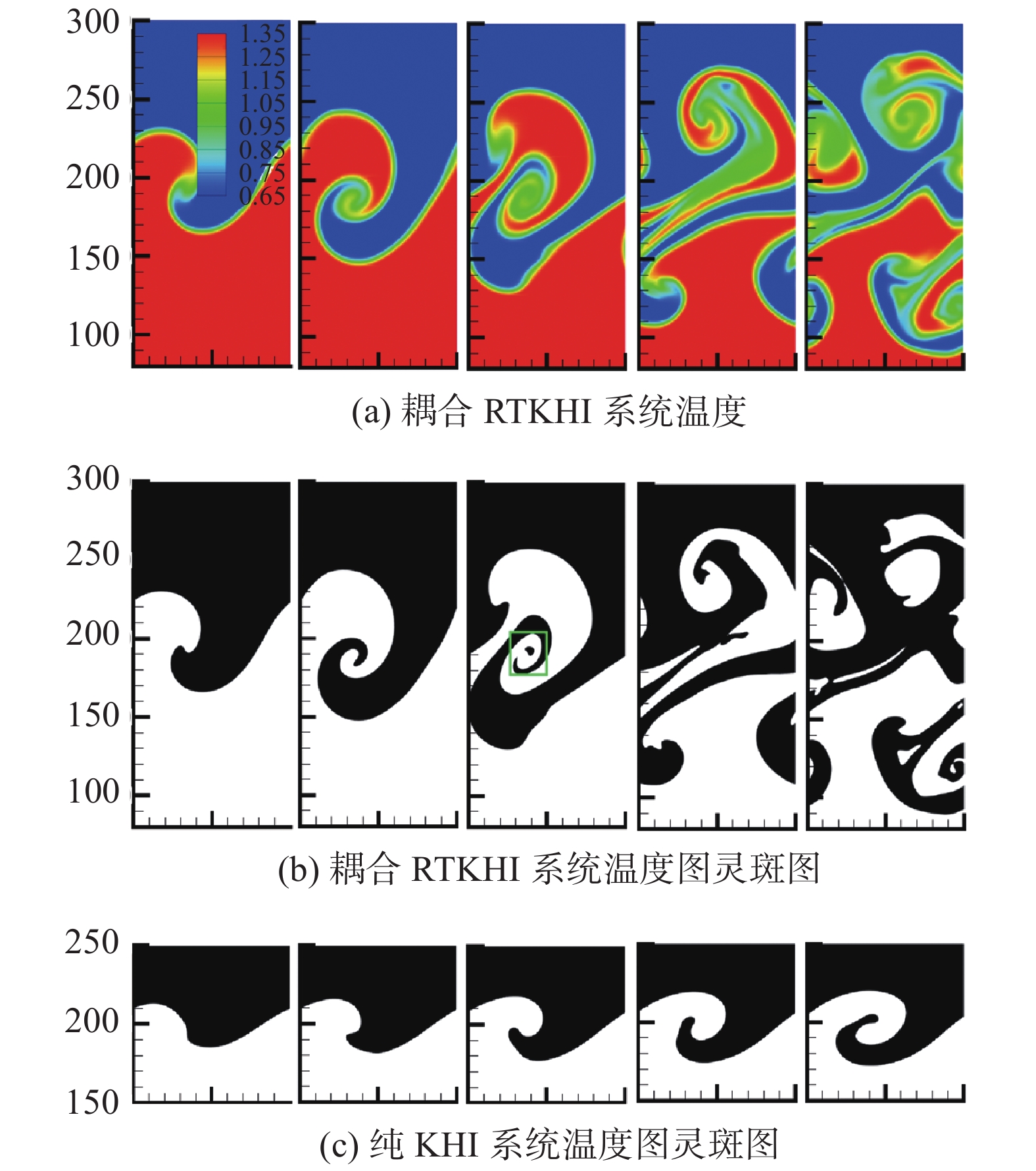
|
图 11 耦合RTKHI系统( |
图12展示了扰动幅值A、扰动幅值的增长率
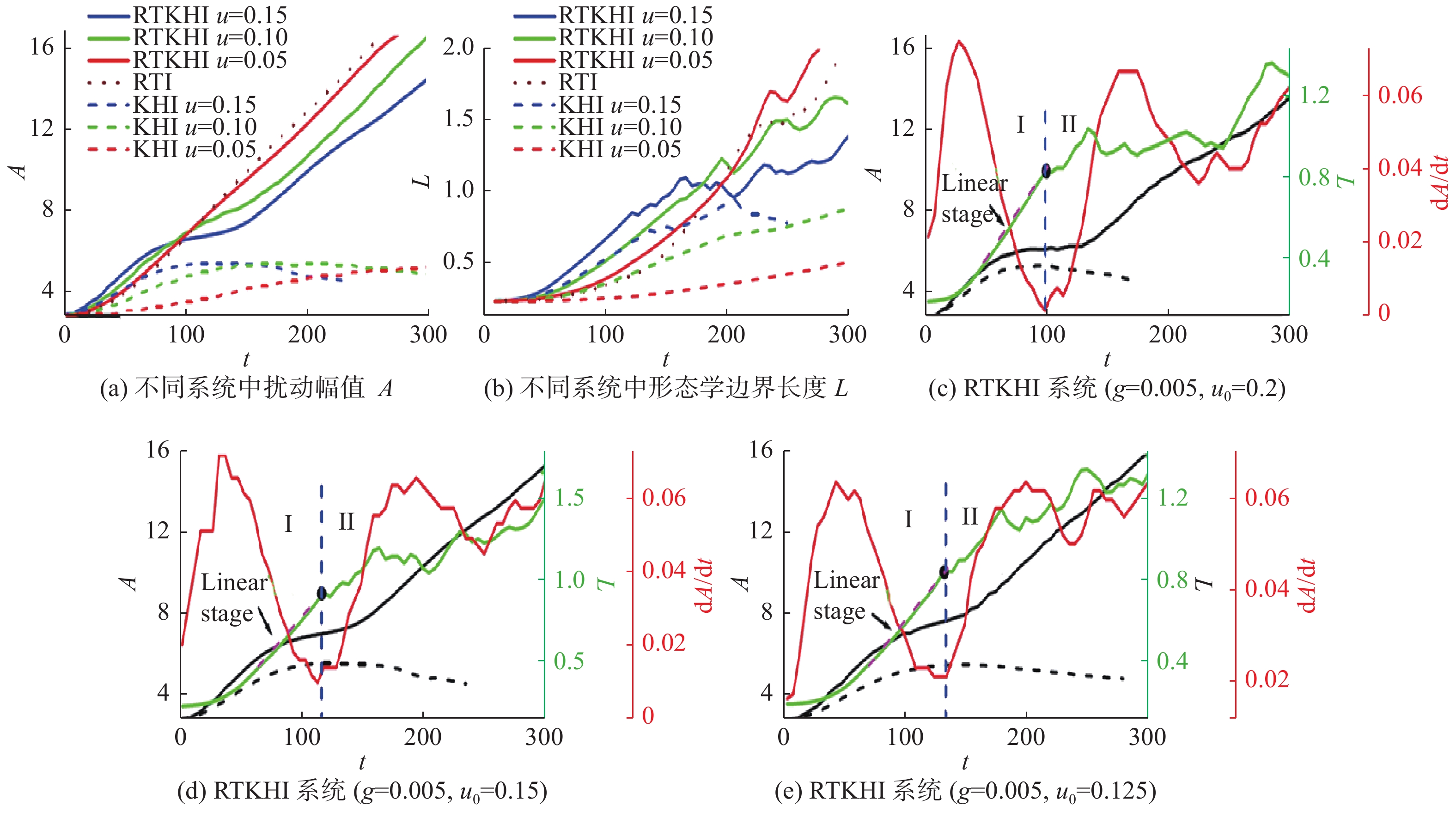
|
图 12 振幅 A、振幅增长率 |
图13为耦合RTKHI系统早期主要机制的形态分析曲线。对不稳定性发展程度和材料混合程度,形态学总边界长度的值是一个很有用和有效的指标。更进一步,温度场图灵斑图的边界长度L可以用来测量浮力和剪切强度的比值,因此,它可以用来定量地判断RTKHI系统早期阶段的主要作用机理。特别的,当KHI(RTI)主导时,LKHI>LRTI (LKHI < LRTI);当KHI和RTI相互平衡时,LRTI = LKHI。
|
图 13 根据温度场的形态分析早期主要机制[63] Fig.13 Morphological analysis of the main mechanism in the early stage[63] |
图14展示了
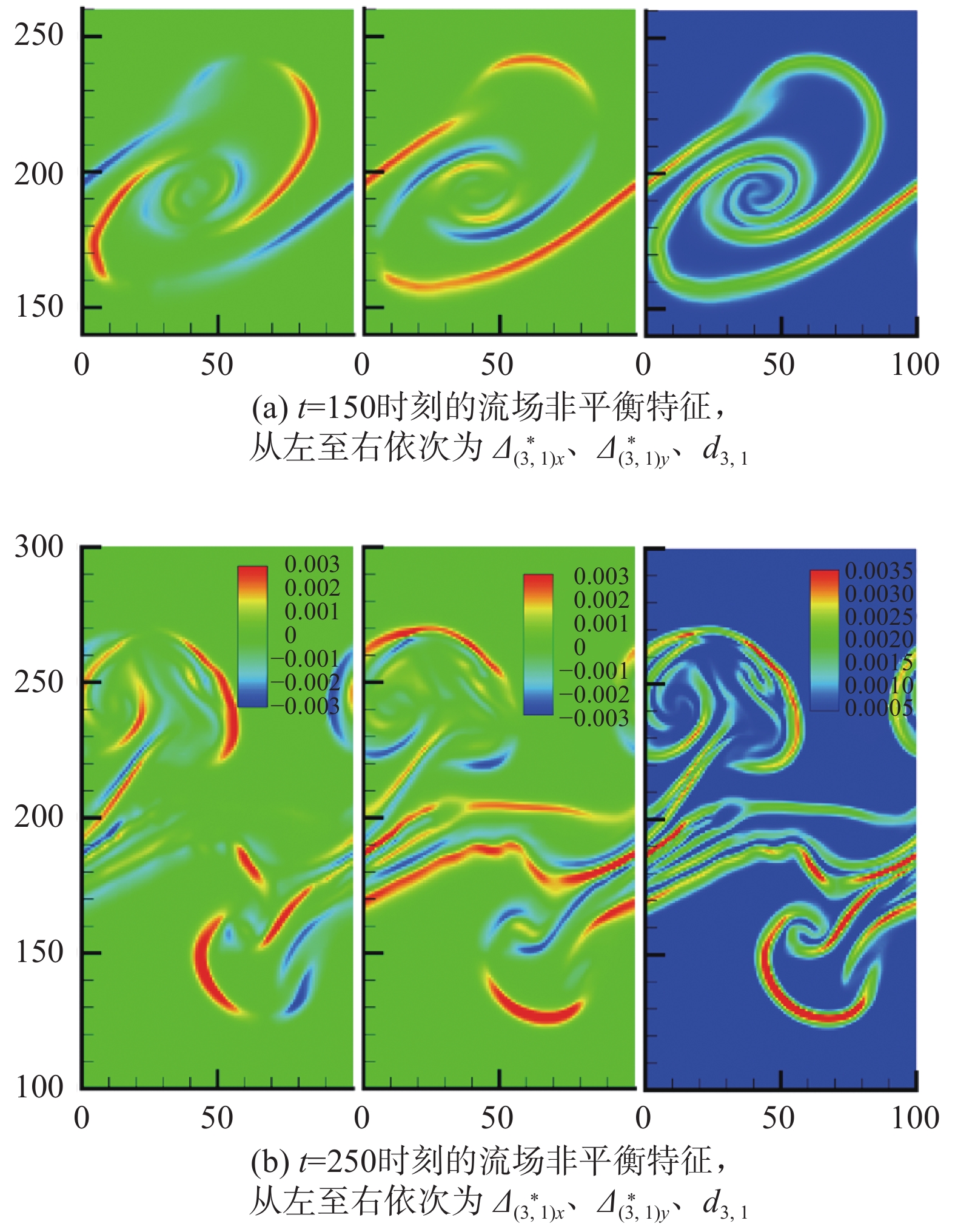
|
图 14 RTKHI系统( |
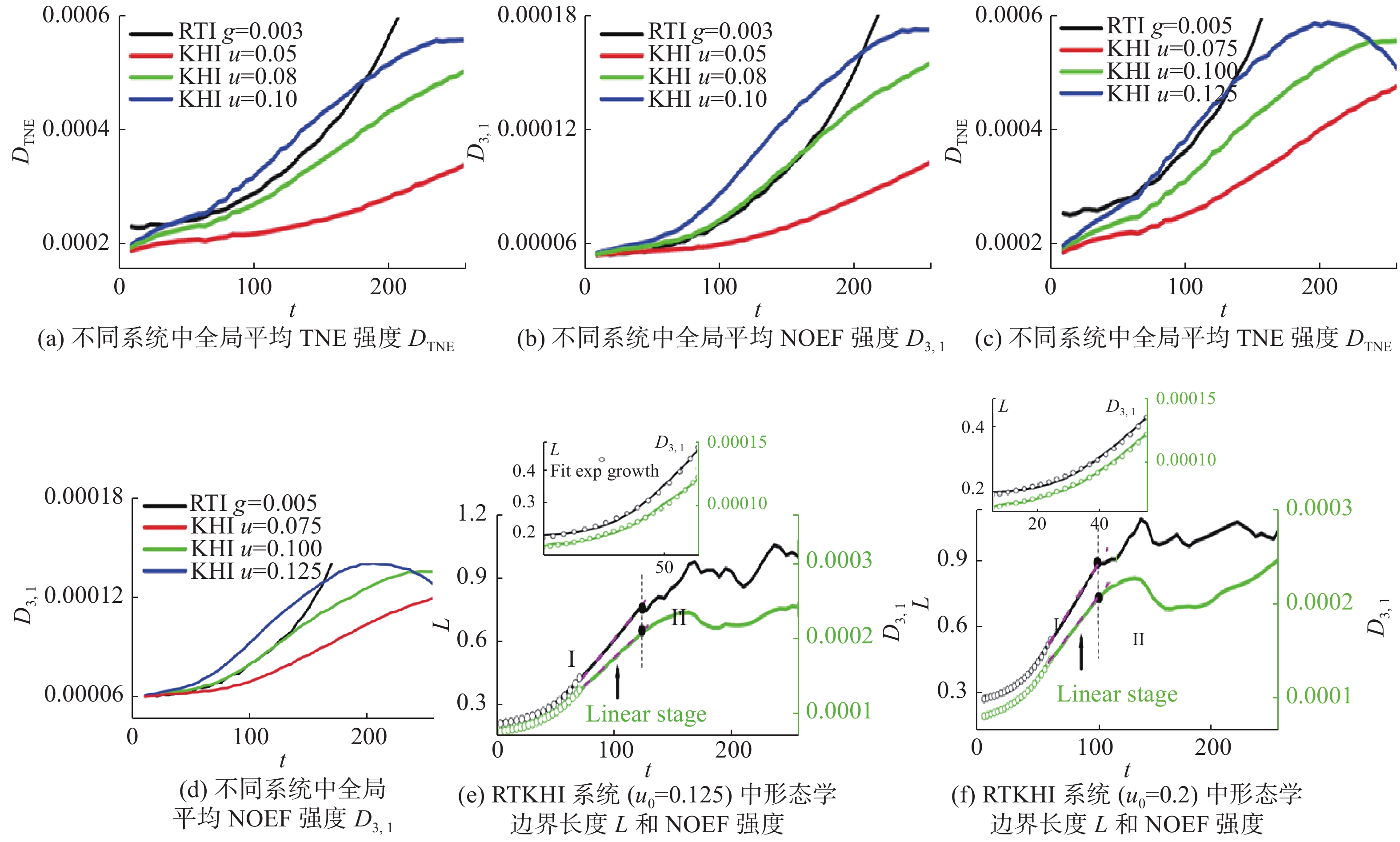
图15(a)~15(d)展示了非平衡特征在早期主要机理判断中的应用。和全局平均TNE强度
|
图 15 耦合RTKHI系统的非平衡特征在早期主要机理判断和过渡点捕获中的应用[63] Fig.15 The applications of non-equilibrium characteristics in the early main mechanism judgment and transition point capture[63] |
由于流体界面不稳定性系统的DBM建模与模拟尚处于起步阶段,所以以上研究均是基于理想气体模型的。表面张力、材料强度等对流体不稳定性演化过程的影响,以及更加实际系统中流体不稳定性的DBM建模与模拟有待进一步研究。
4.2 相分离方面当介质由高温均匀态突然降温到两相共存区域时,原均匀态会因自由能太高而失稳,从而发生相变和两相的分离,这个过程通常称为淬火。在这个过程中,流体系统经历两个动力学阶段—前期的亚稳相分解或旋节线分解(spinodal decomposition, SD)阶段和后期的相畴增长(domain growth, DG)阶段。两个阶段分别对应于单相区域的形成和相区的融合增长。
在早期相分离研究中,怎样准确地划分亚稳相分解和相畴增长两个阶段一直是个开放的问题。一种方法是,两个阶段的临界时间可以通过特征尺度的增长特征来大致给出,即将标度率开始的时刻作为两个阶段的临界点,但这样区分两个阶段是非常粗略的。
2012年,甘延标等发现:密度场图灵斑图的边界总长度L是描述相分离进程的有效特征量—边界总长度L首先随着时间逐渐增长,后期则随着时间逐渐减小;结合相分离两个阶段的其他物理特征,提出使用边界总长度 L极大值点作为划分亚稳相分解和相畴增长两个阶段的几何判据;基于该判据,对亚稳相分解的统计特征给出一些新的认识[64]。但总体来说,亚稳相分解阶段的热力学非平衡行为特征还远远没有获得充分的理解。近期的研究[44, 65]表明,热力学非平衡强度和熵增率均在亚稳相分解阶段随时间逐渐增大,在相畴增长阶段随时间减小,所以热力学非平衡强度和熵增率极大值点均可作为划分这两个阶段的物理判据。根据时间先后,分别称之为第一和第二物理判据。2016年之前的相关研究综述可参见文献[66]。
受篇幅限制,这里只简单介绍一下2019年张玉东等发表在Soft Matter上的一项工作[44]。研究表明,部分非平衡特征和熵产生速率之间存在较为紧密的关系。相分离过程中的熵产生主要有两种机制,分别来源于NOMF和NOEF。图16所示为等温与非等温相分离过程熵产生速率演化特征的对比。由图16可以看出,熵产生速率在相分离的第一阶段(亚稳相分解阶段)随时间增加,而在第二阶段(相畴增长阶段)随时间降低,因此熵产生速率的极大值点可以作为划分相分离两个阶段的一个物理判据。
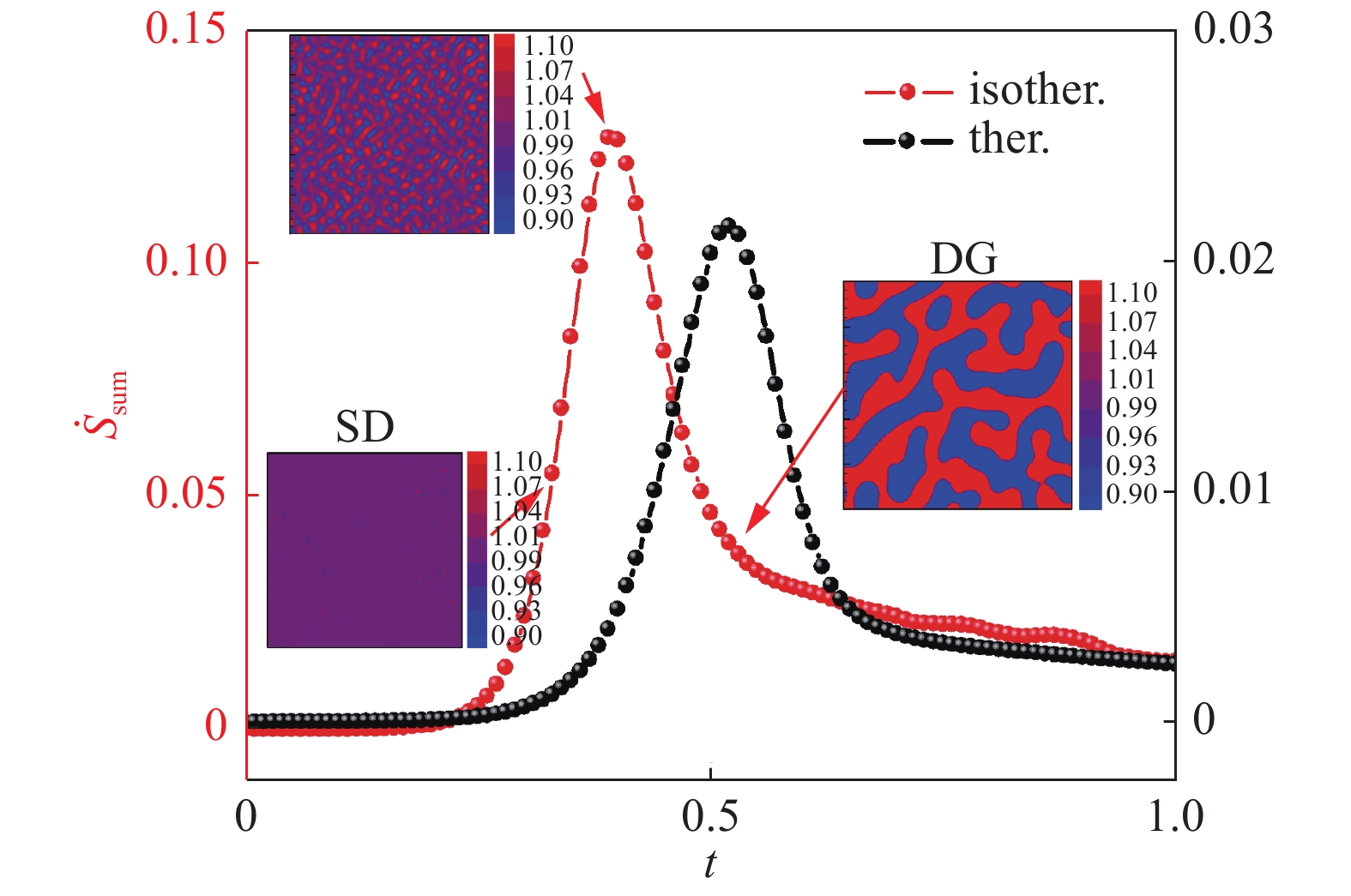
|
图 16 等温与非等温相分离过程熵产生速率演化特征的对比[44] Fig.16 Comparison of entropy generation rate evolution characteristics between isothermal and non-isothermal phase separation processes[44] |
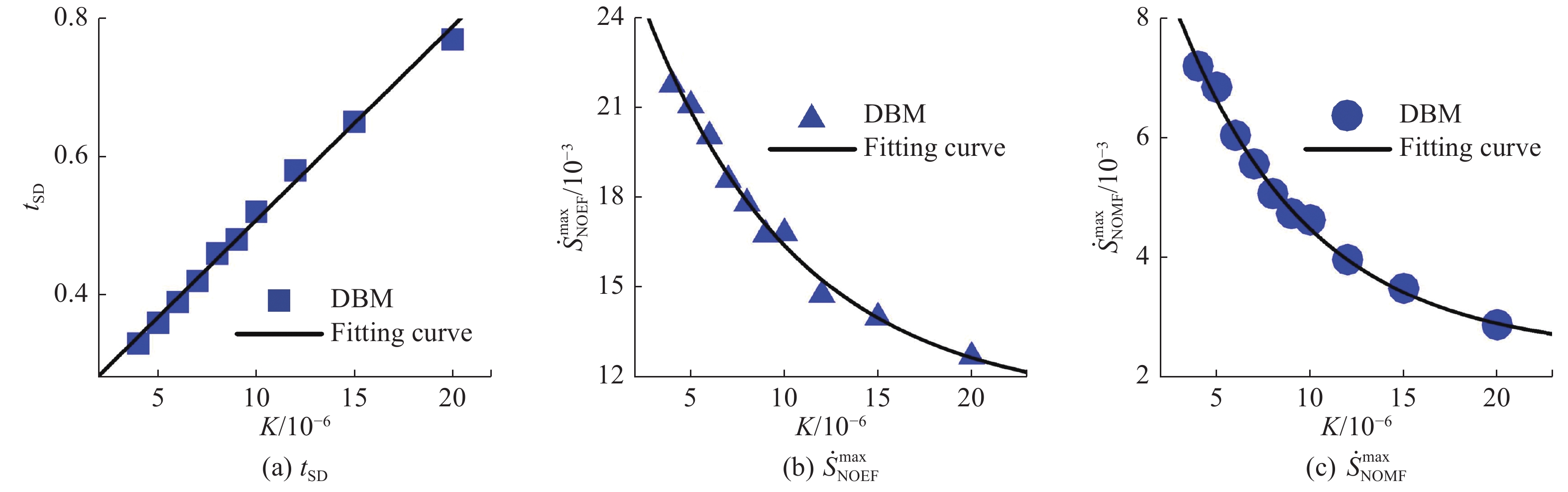
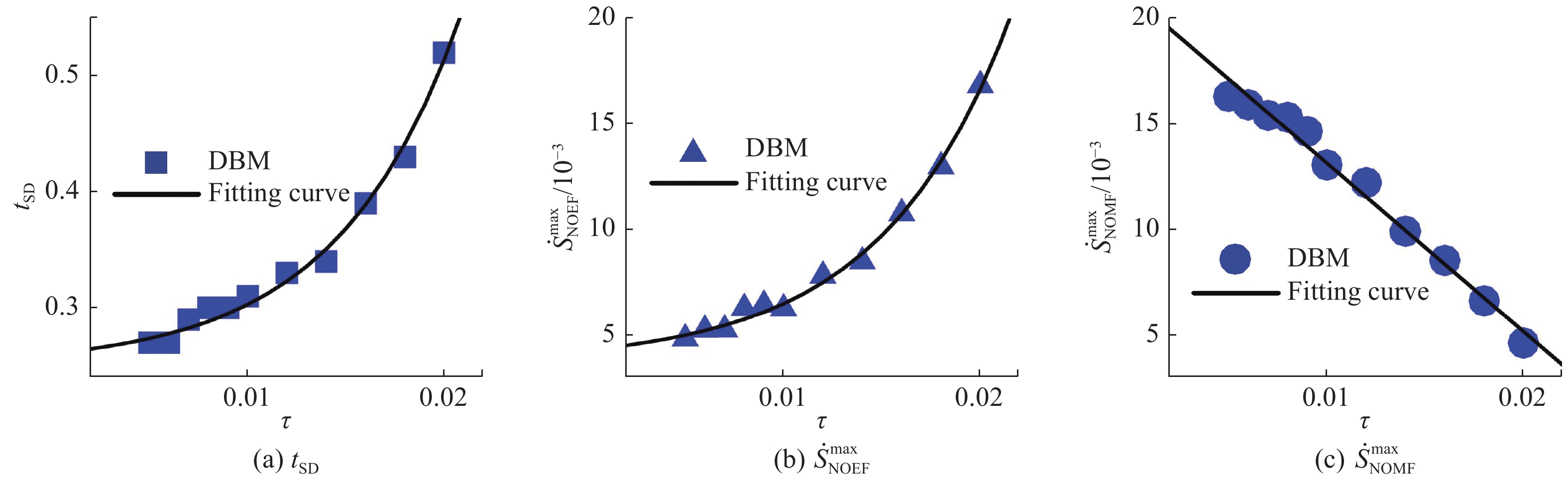
图17至图19所示为相分离过程中热流、黏性和表面张力对相分离SD阶段的持续时间和熵产生特性的影响。如图17至图19所示,热流的作用是加快相分离的SD阶段,黏性和表面张力的作用是延缓SD阶段,并且热流和黏性对SD持续时间的影响是(近似)指数形式的,而表面张力的影响是线性的。热流对NOEF部分的熵产生速率起抑制作用,对NOMF部分的熵产生速率起促进作用;黏性对NOEF部分的熵产生速率起促进作用,对NOMF部分的熵产生速率起抑制作用;表面张力对NOEF和NOMF的熵产生速率都起抑制作用。其物理原因可以从流场中温度梯度和速度梯度的变化来获得解释,更多细节参见文献[44]。
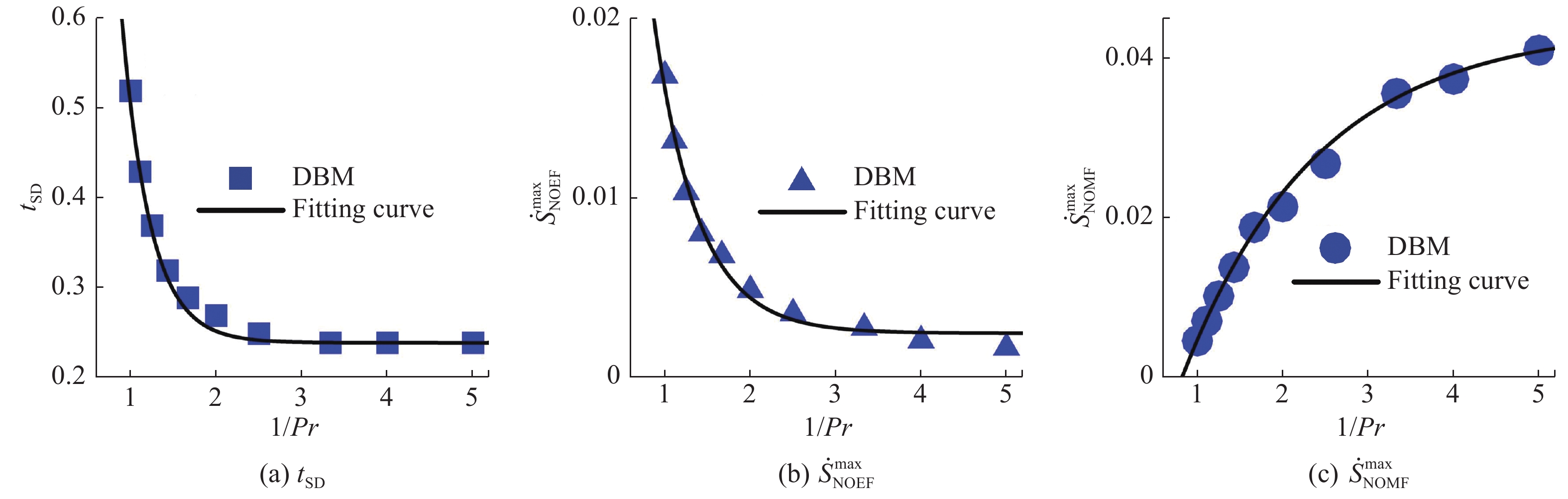
|
图 17 热流对热相分离过程中SD阶段持续时间和熵产生速率的影响[44] Fig.17 Effect of heat flow on duration of SD stage and entropy generation rate in thermal phase separation[44] |
|
图 19 表面张力对热相分离过程中SD阶段持续时间和熵产生速率的影响[44] Fig.19 Effect of surface tension on duration of SD stage and entropy generation rate in thermal phase separation process[44] |
|
图 18 黏性对热相分离过程中SD阶段持续时间和熵产生速率的影响[44] Fig.18 Effect of viscosity on duration of SD stage and entropy generation rate in thermal phase separation[44] |
图20给出了不同热流、黏性和表面张力情形下,两种熵产生机制之间的竞争与协作关系。发现,在热流和黏性的作用下,两种熵产生机制之间存在竞争关系;在表面张力作用下,两种熵产生机制之间存在协作关系。
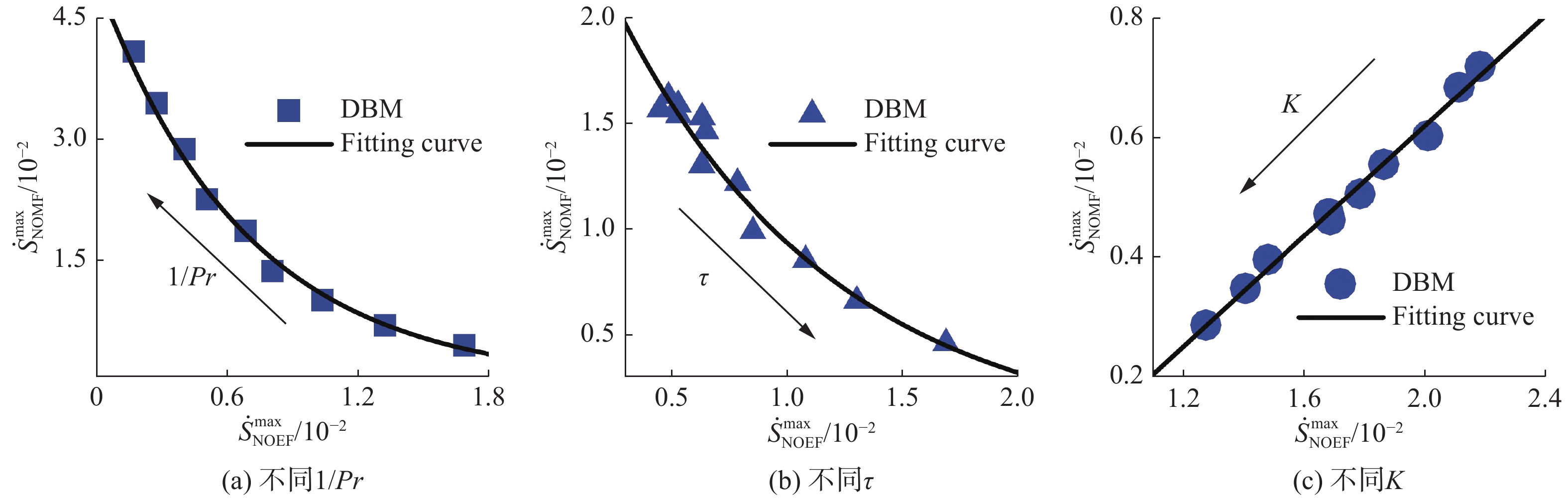
|
图 20 两种熵产生速率幅值之间的关系曲线,图中箭头指向热传导系数(1/Pr)、黏性系数( |
近年来,DBM在燃烧领域的应用取得了一系列的进展。
2013年,闫铂等提出了一个模拟燃烧和爆轰现象的二维DBM模型,研究了爆轰波的精细物理结构和附近的非平衡效应[67]。这是2012年许爱国等提出“借助
上述燃烧DBM均是单流体模型。2016年,林传栋等提出一个二维双流体DBM[69]。使用两个分布函数,分别描述反应物和产物,其演化方程是两个相耦合的离散玻尔兹曼方程。该模型可用于亚声速和超声速燃烧现象的模拟,比热比可调。原文中证明,宏观流体模型(例如带有化学反应的NS方程、Fick第一和第二定律、Stefan-Maxwell扩散定律等)所描述的行为均包含在DBM描述范围之内。除此之外,通过DBM还可以很方便地观测、研究各种热力学非平衡效应。
下面介绍2016年张玉东等在带有爆轰的反应流动理学建模与模拟方面的一项工作[70]。首先从理论上推导了一套新的流体力学方程组,如式(133)所示:
| $ \left\{ \begin{array}{l} \dfrac{{\partial \rho }}{{\partial t}} + \nabla \cdot \left( {\rho {{u}}} \right) = 0\\ \dfrac{{\partial \rho {{u}}}}{{\partial t}} + \nabla \cdot \left( {\rho {{uu}} + P{{I}} + {{\varDelta}} _2^*} \right) = 0\\ \dfrac{{\partial \rho \left( {e + \dfrac{{{{\bf{u}}^2}}}{2}} \right)}}{{\partial t}} + \nabla \cdot \left( {\rho {{u}}\left( {e + T + \dfrac{{{{{u}}^2}}}{2}} \right) + {{\varDelta}} _2^* \cdot {{u}} + {{\varDelta}} _{3,1}^*} \right) = 0 \end{array} \right. $ | (133) |
对比(133)和NS方程组可以看出,NS方程中的黏性应力和热流分别用文中定义的两个非平衡量
为了从理论上研究各种可能的反应率温度依赖关系对燃烧、爆轰等过程的影响,选取式(133)所示的反应率模型。反应速率系数按式(134)所示的函数形式构造。
| $\frac{{{\rm{d}}\lambda }}{{{\rm{d}}t}} = \left\{ \begin{array}{l} k\left( {1 - \lambda } \right)\lambda ,\;\;T \geqslant {T_{th}}{\rm{\; and\; 0}} \leqslant \lambda \leqslant {\rm{1}} \\ 0,\;\;\;\;\;\;\;\;{\rm{else}} \end{array} \right.$ | (134) |
| $k = a + b\int_0^T {\left( {t - {T_1}} \right)\left( {t - {T_2}} \right){\rm{d}}t} $ | (135) |
式中
| $ a = - \frac{{ - {h_2}T_1^3 + 3{h_2}T_1^2{T_2} - 3{h_1}{T_1}T_2^2 + {h_1}T_2^3}}{{{{\left( {{T_1} - {T_2}} \right)}^3}}} $ | (136) |
| $b = - \frac{{6\left( {{h_1} - {h_2}} \right)}}{{{{\left( {{T_1} - {T_2}} \right)}^3}}}$ | (137) |
通过选取如图21所示的四种反应速率系数,研究了四种情况下起爆过程中的非平衡效应(包括熵产生特性),具体研究结果如下。
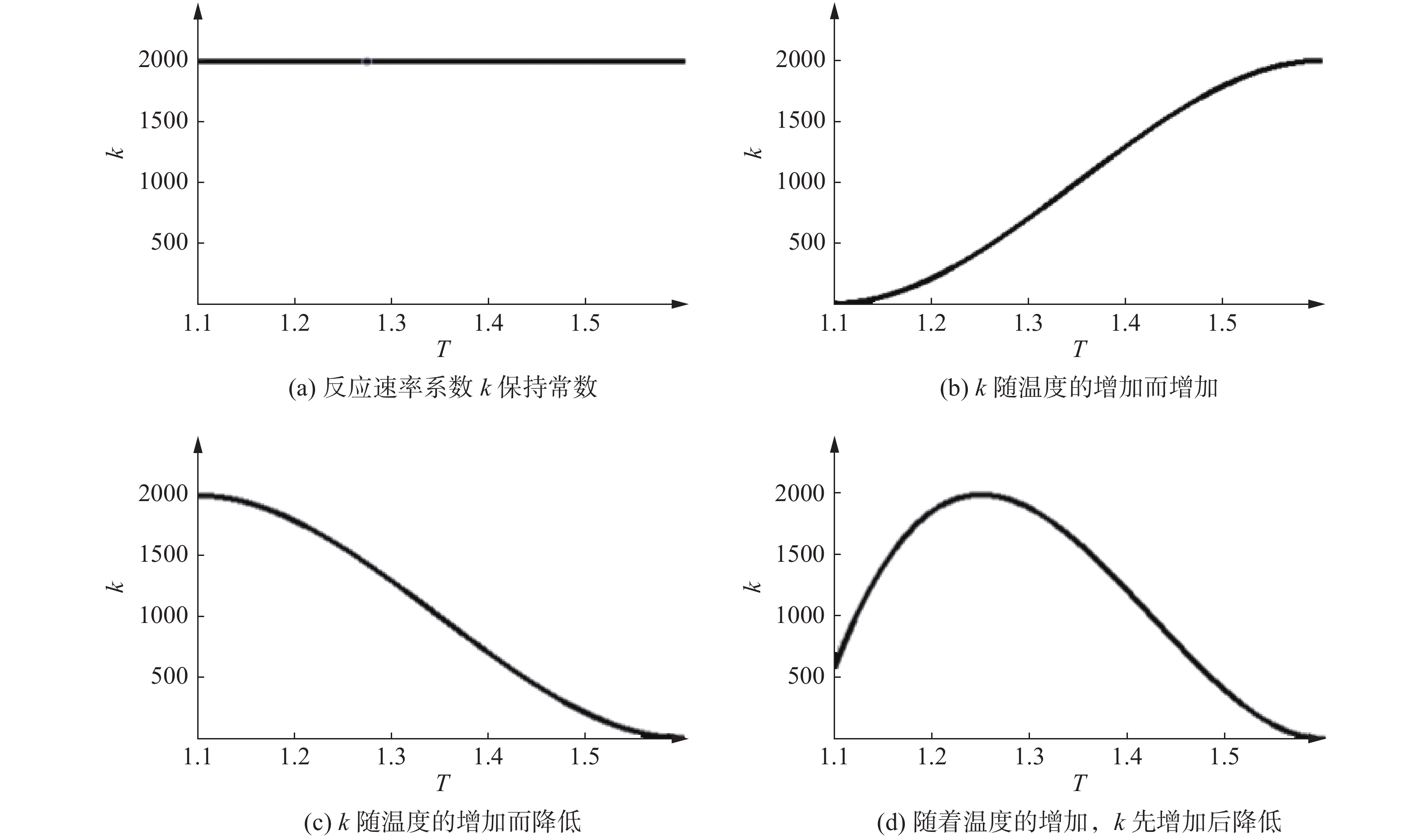
|
图 21 四种反应速率系数随温度变化特征图[70] Fig.21 Profiles of k in function of temperature for four different cases[70] |
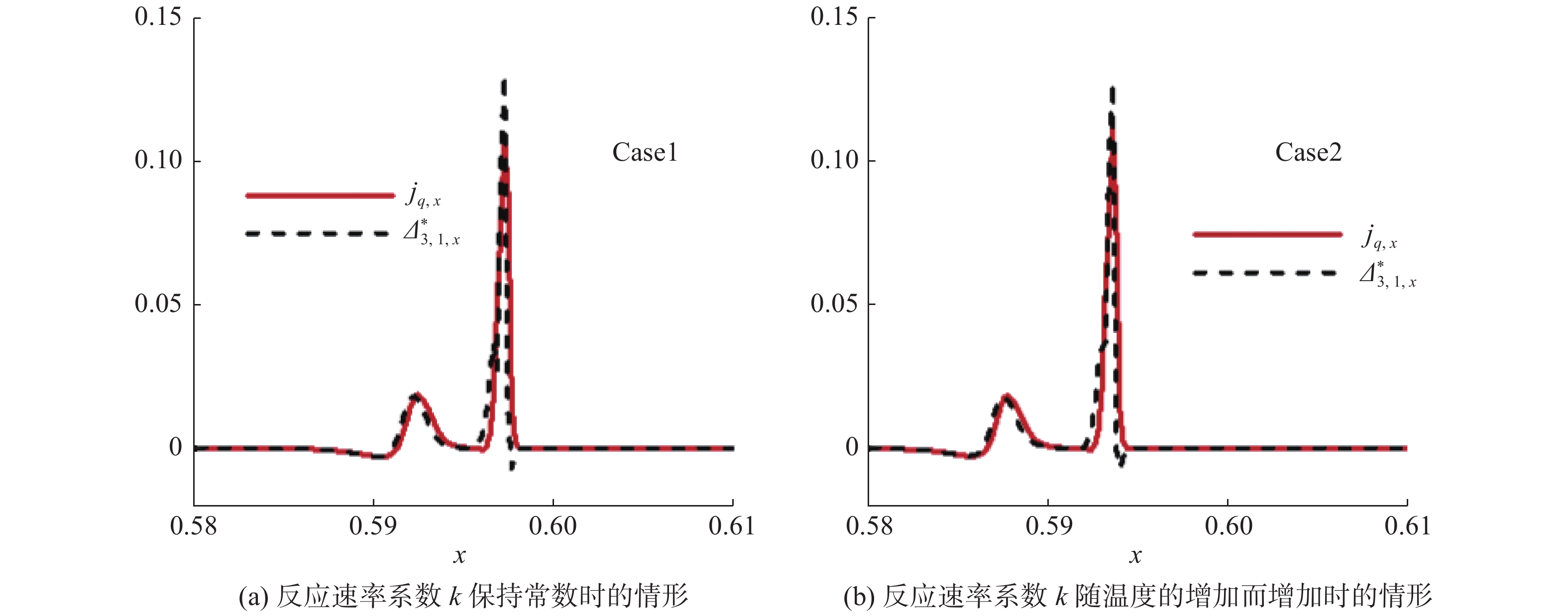
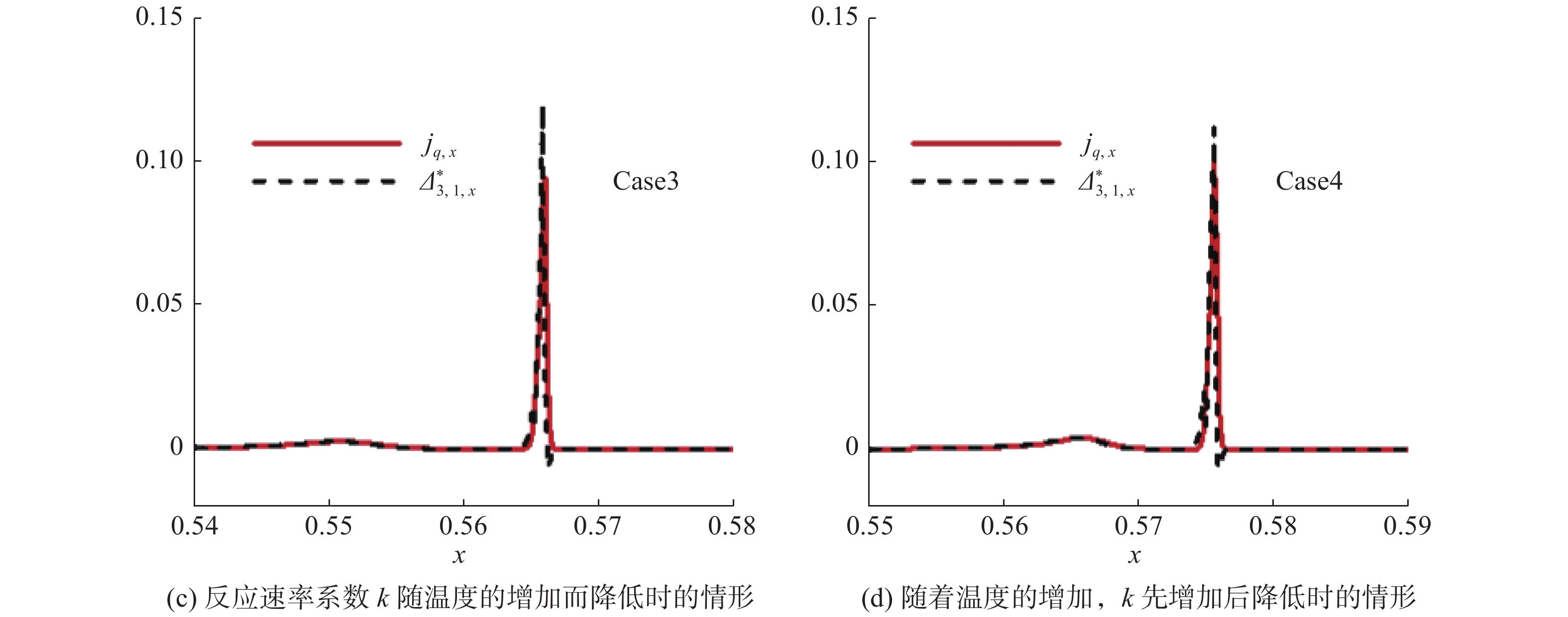
图22和图23分别反映了四种反应率情形下爆轰波过程中NS黏性应力和
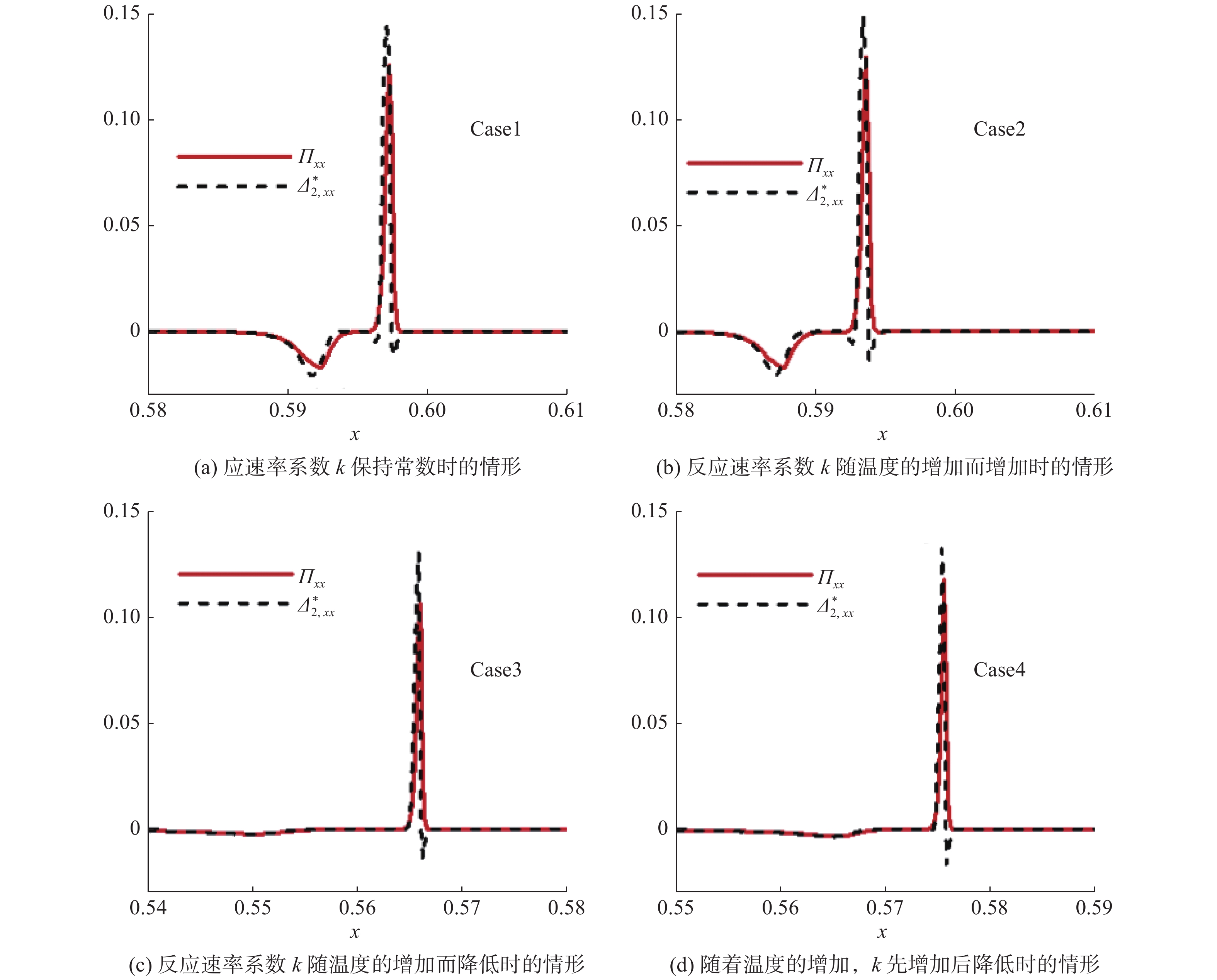
|
图 22 非平衡量 |
|
图 23 |
|
图 23 非平衡量 |
两个非平衡特征量和熵产生率之间的关系如式(138 )所示:
| $ \frac{{\partial S}}{{\partial t}} = - \nabla \cdot {J_S} + \sigma $ | (138) |
其中
| $ \left\{ \begin{array}{l} {{{J}}_S} = S{{u}} + \dfrac{1}{T}{{\varDelta}}_{3,1}^*\\ \sigma = {{\varDelta}} _{3,1}^* \cdot \nabla \dfrac{1}{T} - \dfrac{1}{T}{{\varDelta}} _2^*:\nabla {{u}} + \rho \dfrac{Q}{T}F(\lambda ) \end{array} \right. $ | (139) |
式(139)中
图 24和图 25为四种情形下三种局域熵产生率的分布图。可以看出,熵产生主要出现在两个区域:在波前附近,熵产生主要由NOEF和NOMF构成,后者贡献大于前者;在反应区,NOMF的贡献大于NOEF,但两者的量级均远小于化学反应贡献的熵产生。图 26给出了四种情形下的全局熵产生率
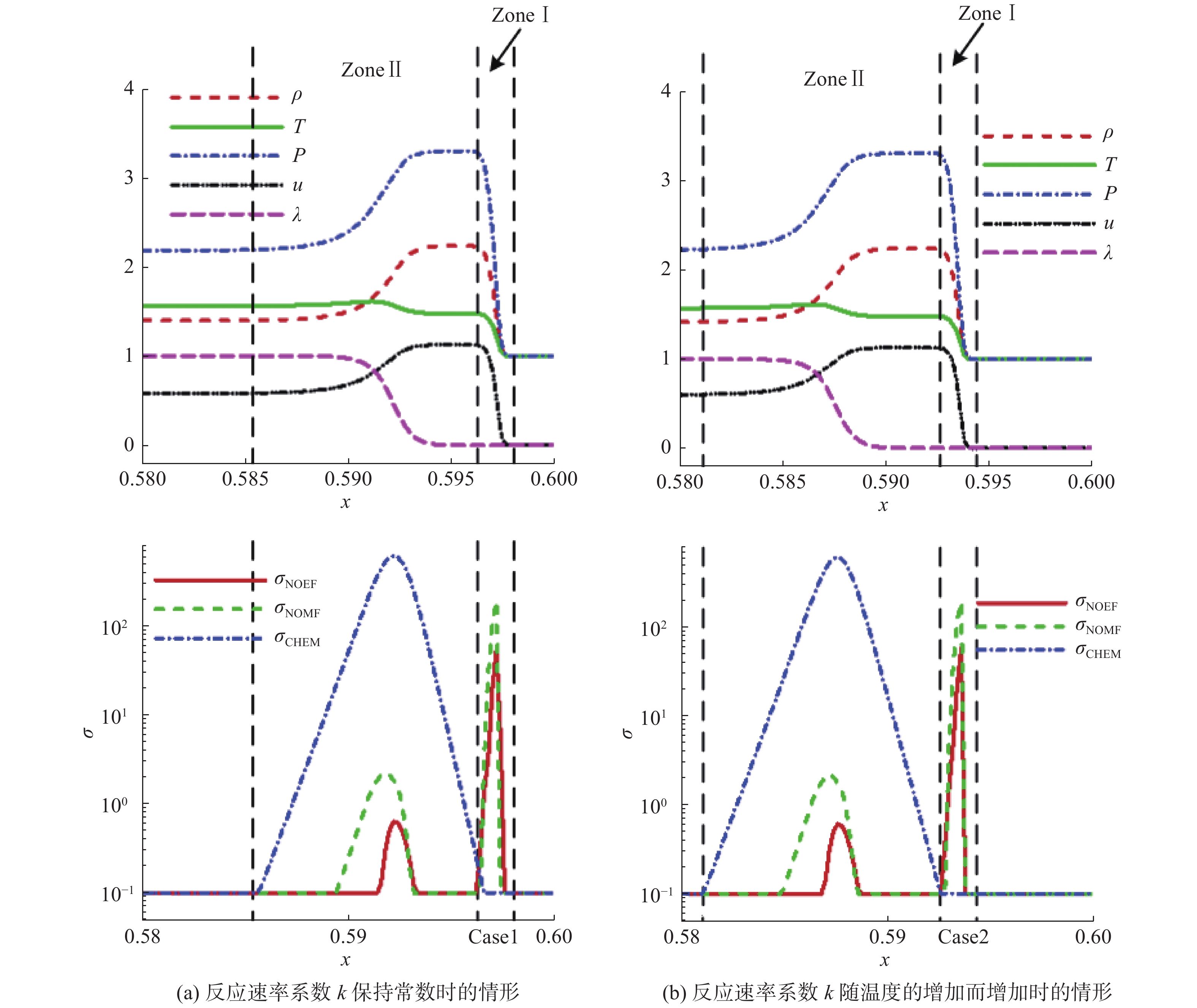
|
图 24 情形1与情形2下的三种局域熵产生率分布[70] Fig.24 Three kinds of profiles of entropy productions for case1 and case2[70] |
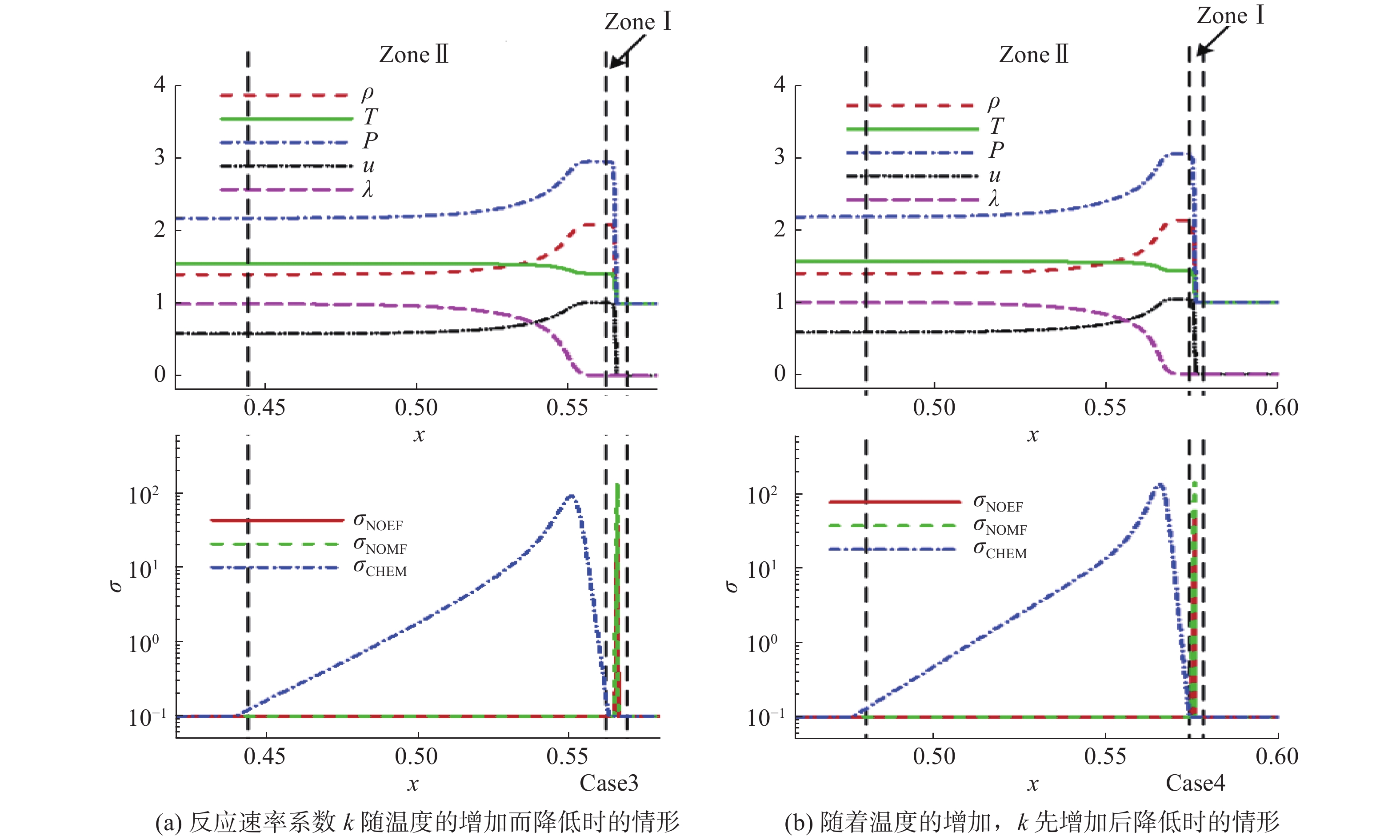
|
图 25 情形3与情形4下的三种局域熵产生率分布[70] Fig.25 Three kinds of profiles of entropy productions for case3 and case4[70] |
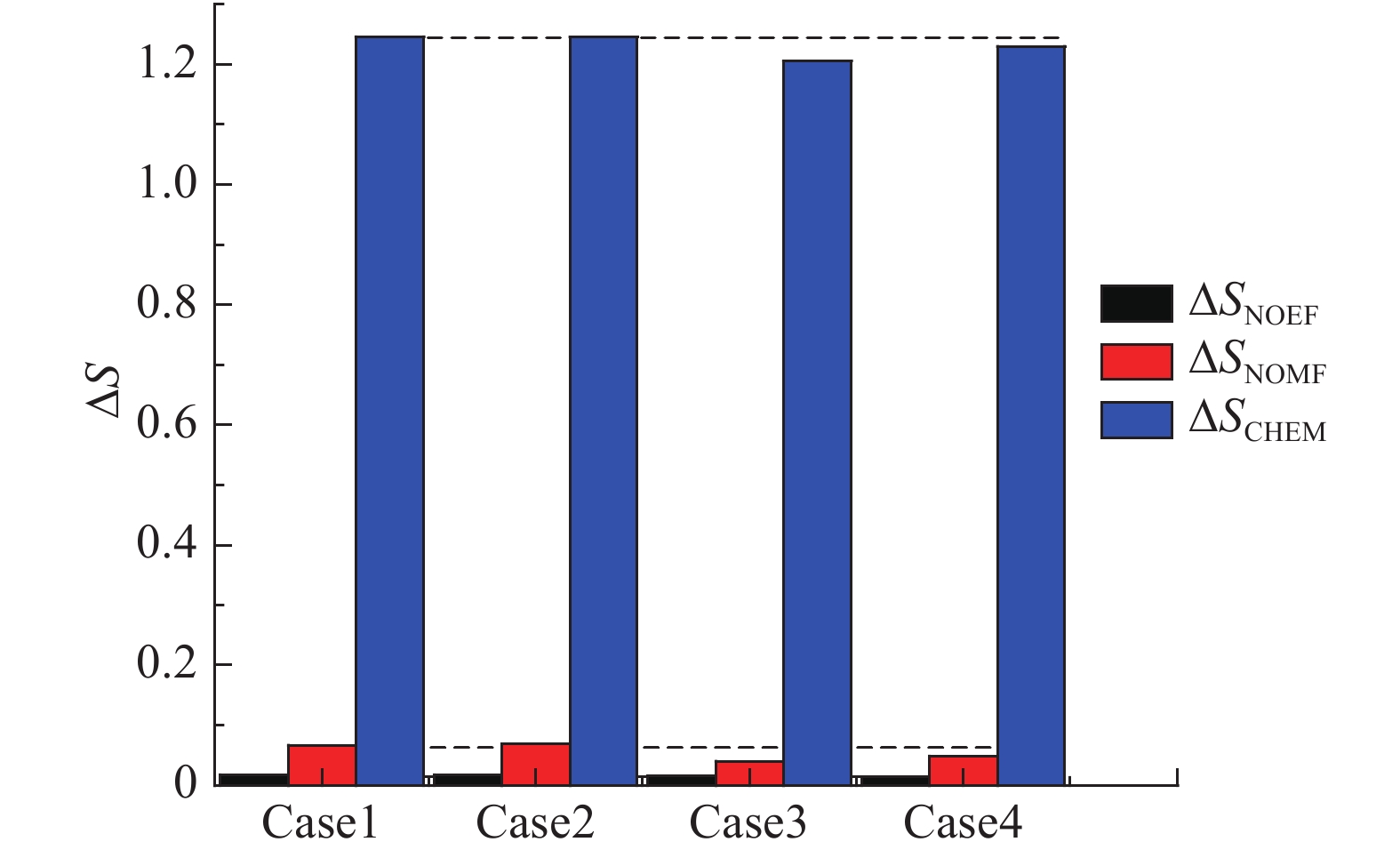
|
图 26 四种反应速率情形下的全局熵产生率[70] Fig.26 Three kinds of profiles of global entropy productions for four cases[70] |
林传栋后期与清华大学合作导师罗开红教授等人一起,将复杂多相流动的DBM建模研究进一步推向深入。2017年发表了一个可用于预混、非预混或部分预混的非平衡反应流的多组分DBM[71],模型适用于亚声速和超声速流动,可用于化学反应流或不带化学反应的流动,可模拟外力项存在或不存在的情况。2018年发表一个用于可压缩放热反应流的多松弛时间DBM,模型具有可调的比热比和普朗特数[72];使用DBM研究了爆轰波面附近的动力学和热力学非平衡(HTNE)效应[73],考察了化学反应物和化学产物的全局和当地HTNE特征,并分析了它们分布函数的主要特征。
2019年,张玉东等提出了一个用于模拟爆轰的一维DBM[74]。基于新模型,对反应速率负温度系数对爆轰的影响进行了进一步研究,发现了在负温度系数条件下,会发生周期性出现两个波面的反常爆轰现象。2020年,林传栋等研究了初始扰动幅值和波长以及化学反应放热对具有非平衡效应的非稳定爆轰演化的影响[75]。
5 小结与说明对于多相复杂流体系统的研究,宏观、微观和介观都有相应的模型和描述方法。微观方法由于时间和空间尺度的限制,目前主要用于从原子(或分子)层次进行一些机理性的研究[76-78]。而只考虑一阶离散效应和非平衡效应的NS方程组只能对系统中大尺度和缓变行为进行较好的描述,对于流体系统中存在的一些锐利界面和快变模式的描述则不能满足要求。从物理描述能力角度,DBM描述的动理学性质比玻尔兹曼方程要少(研究视角相对较窄),但比NS等宏观流体力学方程组要多(研究视角相对较宽);要保的动理学性质可以根据离散或非平衡程度的研究需求来选取。所以,DBM为多相复杂流体系统中各种空间尺度和时间尺度上的各类非平衡行为的建模与模拟提供了一条简洁有效的思路和方法。
在复杂物理场分析方面,DBM在
系统内不同非平衡行为特征之间的空间关联、时间关联、时空关联、竞争与协作等是多相复杂流动过程中特征、机制与规律研究的重要内容。这些以前知之甚少的“介尺度”非平衡行为特征,蕴含着大量有待开发的物理功能。随着研究逐步深入,DBM将在连续介质建模失效或物理功能不足、而微观MD方法因适用尺度受限而无能为力的各类复杂流动研究中发挥更加重要的作用。
最后需要说明的是,与NS模型一样,DBM模型是粗粒化描述系统行为的一种理论模型,它对系统动理学性质描述的广度与深度根据具体问题研究需求而调整。获得了DBM模型,跟获得了NS模型一样,还需要选择合适的数值计算方法,才能进行数值实验研究。从物理问题研究需求的角度,可以选用满足物理问题研究需求的且当前硬软件环境允许的任何一种数值计算方法。对数值计算方法感兴趣的读者可参阅更专业的文献著作。希望这篇理论物理视角的多相流研究综述能与探讨多相流实验、多相流计算方法的研究论文和综述论文形成互补与借鉴。
致谢:感谢甘延标、陈锋、林传栋、张玉东、赖惠林、李华、应阳君、谢侃、陶建军、马天宇、刘枝朋、张戈、张德佳、单奕铭、孙光兰、陈铖、李晗蔚等在研究过程中不同形式的有益讨论。
分子的平均自由程λ与平均分子间距l成正相关,所以克努森数Kn可视为重新标度的平均分子间距,描述的是系统的离散程度,其倒数描述的是系统的连续程度。对于非平衡流动,Kn又可视为两个分子发生碰撞的平均时间间隔与以分子平均速度通过关注的宏观特征尺度所需时间之比,因而可视为重新标度的分子碰撞平均时间间隔。因其与热力学弛豫时间成正相关,所以可进一步视为重新标度的热力学弛豫时间。从这个意义上,Kn描述的是系统偏离热力学平衡的程度。
| [1] |
ALDER B J, WAINWRIGHT T E. Phase transition for a hard sphere system[J]. Journal of Chemical Physics, 1957, 27(5): 1208-1209. DOI:10.1063/1.1743957 |
| [2] |
ALDER B J, WAINWRIGHT T E. Studies in molecular dynamics. I. General method[J]. The Journal of Chemical Physics, 1959, 31(2): 459-466. DOI:10.1063/1.1730376 |
| [3] |
RAHMAN A. Correlations in the motion of atoms in liquid argon[J]. Physical Review, 1964, 136(2A): A405-A411. DOI:10.1103/PhysRev.136.A405 |
| [4] |
RYCKAERT J P, CICCOTTI G, BERENDSEN H J C. Numerical integration of the cartesian equations of motion of a system with constraints: molecular dynamics of n-alkanes
[J]. Journal of Computational. Physics, 1977, 23(3): 327-341. DOI:10.1016/0021-9991(77)90098-5 |
| [5] |
ANDERSEN H C. Molecular dynamics simulations at constant pressure and/or temperature[J]. The Journal of Chemical Physics, 1980, 72(4): 2384-2393. DOI:10.1063/1.439486 |
| [6] |
PARRINELLO M, RAHMAN A. Crystal structure and pair potentials: A molecular-dynamics study[J]. Physical Review Letters, 1980, 45(14): 1196-1199. DOI:10.1103/PhysRevLett.45.1196 |
| [7] |
CAR R, PARRINELLO M. Unified approach for molecular dynamics and density-functional theory[J]. Physical Review Letters, 1985, 55(22): 2471. DOI:10.1103/PhysRevLett.55.2471 |
| [8] |
CAGIN T, PETTITT B M. Grand molecular dynamics: A method for open systems[J]. Molecular Simulation, 1991, 6(1-3): 5-26. DOI:10.1080/08927029108022137 |
| [9] |
KARBALAEI A, KUMAR R, CHO H J. Thermocapillarity in microfluidics—A review[J]. Micromachines, 2016, 7(1): 13. DOI:10.3390/mi7010013 |
| [10] |
CRISTINI V, TAN Y C. Theory and numerical simulation of droplet dynamics in complex flows--A review[J]. Lab on A Chip, 2004, 4(4): 257-264. DOI:10.1039/B403226H |
| [11] |
TEZDUYAR T E. Interface-tracking and interface-capturing techniques for finite element computation of moving boundaries and interfaces[J]. Computer Methods in Applied Mechanics and Engineering, 2006, 195(23/24): 2983-3000. |
| [12] |
SZEWC K, POZORSKI J, MINIER J P. Simulations of single bubbles rising through viscous liquids using smoothed particle hydrodynamics[J]. International Journal of Multiphase Flow, 2013, 50(Complete): 98-105. |
| [13] |
JACQMIN D. Calculation of two-phase Navier–Stokes flows using phase-field modeling[J]. Journal of Computational Physics, 1999, 155(1): 96-127. DOI:10.1006/jcph.1999.6332 |
| [14] |
GUNSTENSEN A K, ROTHMAN D H, ZALESKI S, et al. Lattice Boltzmann model of immiscible fluids[J]. Physical Review A, 1991, 43(8): 4320-4327. DOI:10.1103/PhysRevA.43.4320 |
| [15] |
SHAN X W, CHEN H D. Lattice Boltzmann model for simulating flows with multiple phases and components[J]. Physical Review E, 1993, 47(3): 1815-1819. DOI:10.1103/PhysRevE.47.1815 |
| [16] |
SWIFT M R, OSBORN W R, YEOMANS J M. Lattice Boltzmann simulation of non-ideal fluids[J]. Physical Review Letters, 1995, 75(5): 830-833. DOI:10.1103/PhysRevLett.75.830 |
| [17] |
HE X Y, CHEN S Y, ZHANG R Y. A lattice Boltzmann scheme for incompressible multiphase flow and its application in simulation of Rayleigh-Taylor Instability[J]. Journal of Computational Physics, 1999, 152(2): 642-663. DOI:10.1006/jcph.1999.6257 |
| [18] |
GONNELLA G, LAMURA A, SOFONEA V. Lattice Boltzmann simulation of thermal nonideal fluids[J]. Physical Review E, 2007, 76(3): 036703. DOI:10.1103/PhysRevE.76.036703 |
| [19] |
LI Q, LUO K H, KANG Q J, et al. Lattice Boltzmann methods for multiphase flow and phase-change heat transfer[J]. Progress in Energy and Combustion Science, 2016, 52: 62-105. DOI:10.1016/j.pecs.2015.10.001 |
| [20] |
LI Q, LUO K H, GAO Y J, et al. Additional interfacial force in lattice Boltzmann models for incompressible multiphase flows[J]. Physical Review E, 2012, 85(2): 026704. DOI:10.1103/PhysRevE.85.026704 |
| [21] |
SUN D K, ZHU M F, WANG J, et al. Lattice Boltzmann modeling of bubble formation and dendritic growth in solidification of binary alloys[J]. International Journal of Heat and Mass Transfer, 2016, 94(MAR.): 474-487. |
| [22] |
MILLER W, SUCCI S, MANSUTTI D. Lattice Boltzmann model for anisotropic liquid-solid phase transition[J]. Physical Review Letters, 2001, 86(16): 3578. DOI:10.1103/PhysRevLett.86.3578 |
| [23] |
SUCCI S. The lattice Boltzmann equation for fluid dynamics and beyond[M]. Oxford: Oxford univeristy press, 2001.
|
| [24] |
何雅玲, 王勇, 李庆. 格子Boltzmann方法的理论及应用[M]. 北京: 科学出版社, 2009. HE Y L, WANG Y, LI Q. Lattice Boltzmann method: Theory and applications[M]. Beijing: Science Press, 2009(in Chinese). |
| [25] |
郭照立, 郑楚光. 格子Boltzmann方法的原理及应用[M]. 北京: 科学出版社, 2009. GUO Z L, ZHENG C G. Theory and applications of lattice Boltzmann method[M]. Beijing: Science Press, 2009(in Chinese). |
| [26] |
HUANG H B, SUKOP M C, LU X Y. Multiphase lattice Boltzmann methods: Theory and application[M], John Wiley & Sons, Ltd, 2015.
|
| [27] |
许爱国, 张广财, 应阳君. 燃烧系统的离散Boltzmann建模与模拟研究进展[J]. 物理学报, 2015, 64(18): 35-60. XU A G, ZHANG G C, YING Y J. Progress of discrete Boltzmann modeling and simulation of combustion system[J]. Acta Physica Sinica, 2015, 64(18): 35-60. (in Chinese) |
| [28] |
XU A G, ZHANG G C, ZHANG Y D. Discrete Boltzmann modeling of compressible flows, Chapter 2[M]//KYZAS G Z, MITROPOULOS A C, edited. Kinetic Theory. Croatia: InTech, 2018.
|
| [29] |
XU A G, ZHANG G C, GAN Y B, et al. Lattice Boltzmann modeling and simulation of compressible flows[J]. Frontiers of Physics, 2012, 7(5): 582-600. DOI:10.1007/s11467-012-0269-5 |
| [30] |
XU A G, LIN C D, ZHANG G C, et al. Multiple-relaxation-time lattice Boltzmann kinetic model for combustion[J]. Physical Review E, 2015, 91(4): 043306. DOI:10.1103/PhysRevE.91.043306 |
| [31] |
XU A G, ZHANG G C, YING Y J, et al. Complex fields in heterogeneous materials under shock: modeling, simulation and analysis[J]. Science China Physics, 2016, 59(5): 650501. DOI:10.1007/s11433-016-5801-0 |
| [32] |
LIN C D, LUO K H. Discrete Boltzmann modeling of unsteady reactive flows with nonequilibrium effects[J]. Physical Review E, 2019, 99(1): 012142. DOI:10.1103/PhysRevE.99.012142 |
| [33] |
GAN Y B, XU A G, ZHANG G C, et al. Discrete Boltzmann trans-scale modeling of high-speed compressible flows[J]. Physical Review E, 2018, 97(5): 053312. DOI:10.1103/PhysRevE.97.053312 |
| [34] |
ZHANG Y D, XU A G, ZHANG G C, et al. Discrete Boltzmann method for non-equilibrium flows: Based on Shakhov model[J]. Computer Physics Communications, 2019, 238: 50-65. DOI:10.1016/j.cpc.2018.12.018 |
| [35] |
LEE T D, YANG C N. Statistical theory of equations of state and phase transitions. II. Lattice gas and ising model[J]. Physical Review, 1952, 87(3): 410-419. DOI:10.1103/PhysRev.87.410 |
| [36] |
聂小波. 模拟可压缩流体的二维格子气模型[D]. 北京: 应用物理与计算数学研究所, 1988. NIE X B. A two-dimensional lattice gas model for compressible fluid simulation[D]. Bei Jing: Institute of Applied Physics and Computational Mathematics, 1988(in Chinese). |
| [37] |
CHOPARD B, DROZ M. Cellular automata modeling of physical systems[M]. Cambridge: Cambridge University Press, 1998.
|
| [38] |
FRISCH U, HASSLACHER B, POMEAU Y. Lattice-gas automata for the Navier-Stokes equation[J]. Physical Review Letters, 1986, 56(14): 1505-1508. DOI:10.1103/PhysRevLett.56.1505 |
| [39] |
BHATNAGAR P L, GROSS E P, KROOK M. A Model for Collision Processes in Gases. I. Small Amplitude Processes in Charged and Neutral One-Component Systems[J]. Physical Review, 1954, 94(3): 511-525. DOI:10.1103/PhysRev.94.511 |
| [40] |
HOLWAY, L H. New Statistical Models for Kinetic Theory: Methods of Construction[J]. Physics of Fluids, 1966, 9(9): 1658-1673. DOI:10.1063/1.1761920 |
| [41] |
SHAKHOV E M. Generalization of the Krook kinetic relaxation equation[J]. Fluid Dynamics, 1968, 3(5): 142-145. DOI:10.1007/BF01029546 |
| [42] |
LARINA I N, RYKOV V A. Kinetic model of the Boltzmann equation for a diatomic gas with rotational degrees of freedom[J]. Computational Mathematics and Mathematical Physics, 2010, 50(12): 2118-2130. DOI:10.1134/S0965542510120134 |
| [43] |
LIU G J. A method for constructing a model form for the Boltzmann equation[J]. Physics of Fluids A, 1990, 2(2): 277-280. DOI:10.1063/1.857777 |
| [44] |
ZHANG Y D, XU A G, ZHANG G C, et al. Entropy production in thermal phase separation: a kinetic-theory approach[J]. Soft Matter, 2019, 15(10): 2245-2259. DOI:10.1039/C8SM02637H |
| [45] |
ONUKI A. Phase transition dynamics[M]. Cambridge: Cambridge University Press, 2002.
|
| [46] |
张玉东. 非平衡流与多相流的建模与研究—基于离散Boltzmann方法[D]. 南京: 南京理工大学, 2019.
|
| [47] |
KLIMONTOVICH Y L. Kinetic theory of nonideal gases & nonideal plasmas[M]. Oxford: Pergamon, 1982.
|
| [48] |
CARNAHAN N F, STARLING K E. Equation of state of non attracting rigid spheres[J]. The Journal of Chemical Physics, 1969, 51(2): 635-636. DOI:10.1063/1.1672048 |
| [49] |
许爱国, 张广财, 李英骏, 等. 非平衡与多相复杂系统模拟研究—Lattice Boltzmann动理学理论与应用[J]. 物理学进展, 2014, 34(03): 136-167. XU A G, ZHANG G C, LI Y J, et al. Modeling and simulation of nonequilibrium and multiphase complex systems -lattice Boltzmann kinetic theory and application[J]. Progress in Physics, 2014, 34(03): 136-167. (in Chinese) |
| [50] |
ZHANG D J, XU A G, ZHANG Y D, et al. Two-fluid discrete Boltzmann model for compressible flows: Based on ellipsoidal statistical Bhatnagar–Gross–Krook[J]. Physics of Fluids, 2020, 32(12): 126110. DOI:10.1063/5.0017673 |
| [51] |
ZHANG G, XU A G, LI Y J, et al. Particle tracking manifestation of compressible flow and mixing induced by Rayleigh-Taylor instability. arXiv: 1912.13181.
|
| [52] |
ANDRIES P, AOKI K, PERTHAME B. A consistent BGK-type model for gas mixtures[J]. Journal of Statistical Physics, 2002, 106(5-6): 993-1018. DOI:10.1023/A%3A1014033703134 |
| [53] |
HAACK J R, HAUCK C D, MURILLO M S. A conservative, entropic multispecies BGK model[J]. Journal of Statistical Physics, 2017, 168(9): 1-31. DOI:10.1007/s10955-017-1824-9 |
| [54] |
LAI H L, XU A G, ZHANG G C, et al. Non-equilibrium thermo-hydrodynamic effects on the Rayleigh-Taylor instability in compressible flows[J]. Physical Review E, 2016, 94(2): 023106. DOI:10.1103/PhysRevE.94.023106 |
| [55] |
李德梅, 赖惠林, 许爱国, 等. 可压流体Rayleigh-Taylor不稳定性的离散Boltzmann模拟[J]. 物理学报, 2018, 67(8): 080501. LI D M, LAI H L, XU A G, et al. Discrete Boltzmann simulation of Rayleigh-Taylor instability in compressible flows[J]. Acta Physica Sinica, 2018, 67(8): 080501. DOI:10.7498/aps.67.20171952 (in Chinese) |
| [56] |
CHEN F, XU A G, ZHANG G C. Viscosity, heat conductivity, and Prandtl number effects in the Rayleigh-Taylor Instability[J]. Frontiers of Physics, 2016, 11(6): 114703. DOI:10.1007/s11467-016-0603-4 |
| [57] |
GAN Y B, XU A G, ZHANG G C, et al. Nonequilibrium and morphological characterizations of Kelvin-Helmholtz instability in compressible flows[J]. Frontiers of Physics, 2019, 4(14): 83-99. |
| [58] |
XU A G, ZHANG G C, PAN X F, et al. Morphological characterization of shocked porous material[J]. Journal of Physics D Applied Physics, 2009, 42(7): 075409. DOI:10.1088/0022-3727/42/7/075409 |
| [59] |
GAN Y B, XU A G, ZHANG G C, et al. Phase separation in thermal systems: A lattice Boltzmann study and morphological characterization[J]. Physical Review E, 2011, 84(4): 046715. DOI:10.1103/PhysRevE.84.046715 |
| [60] |
GAN Y B, XU A G, ZHANG G C, et al. Lattice Boltzmann study on Kelvin-Helmholtz instability: the roles of velocity and density gradients[J]. Physical Review E, 2010, 83(2): 056704. |
| [61] |
LIN C D, XU A G, ZHANG G C, et al. Discrete Boltzmann modeling of Rayleigh-Taylor instability in two-component compressible flows[J]. Physical Review E, 2017, 96(5): 053305. DOI:10.1103/PhysRevE.96.053305 |
| [62] |
CHEN F, XU A G, ZHANG G C. Collaboration and competition between Richtmyer-Meshkov instability and Rayleigh-Taylor instability[J]. Physics of Fluids, 2018, 30(10): 102105. DOI:10.1063/1.5049869 |
| [63] |
CHEN F, XU A G, ZHANG Y D, et al. Morphological and non-equilibrium analysis of coupled Rayleigh–Taylor–Kelvin–Helmholtz instability[J]. Physics of Fluids, 2020, 32(10): 104111. DOI:10.1063/5.0023364 |
| [64] |
GAN Y B, XU A G, ZHANG G C, et al. Lattice Boltzmann study of thermal phase separation: Effects of heat conduction, viscosity and Prandtl number[J]. EPL, 2012, 97(4): 44002. DOI:10.1209/0295-5075/97/44002 |
| [65] |
GAN Y B, XU A G, ZHANG G C, et al. Discrete Boltzmann modeling of multiphase flows: hydrodynamic and thermodynamic non-equilibrium effects[J]. Soft Matter, 2015, 11: 5336-5345. DOI:10.1039/C5SM01125F |
| [66] |
许爱国 张广财, 甘延标. 相分离过程的离散Boltzmann方法研究进展[J]. 力学与实践, 2016, 38(4): 361-374. XU A G, ZHANG G C, GAN Y B. Progress in studies on discrete Boltzmann modeling of phase separation process[J]. Mechanics in engineering, 2016, 38(4): 361-374. DOI:10.6052/1000-0879-16-006 (in Chinese) |
| [67] |
YAN B, XU A G, ZHANG G C, et al. Lattice Boltzmann model for combustion and detonation[J]. Frontiers of Physics, 2013, 8(1): 94-110. DOI:10.1007/s11467-013-0286-z |
| [68] |
LIN C D, XU A G, ZHANG G C, et al. Polar coordinate lattice Boltzmann kinetic modeling of detonation phenomena[J]. Communications in Theoretical Physics, 2014, 62(5): 737-748. DOI:10.1088/0253-6102/62/5/18 |
| [69] |
LIN C D, XU A G, ZHANG G C, et al. Double-distribution-function discrete Boltzmann model for combustion[J]. Combustion and Flame, 2016, 164: 137-151. DOI:10.1016/j.combustflame.2015.11.010 |
| [70] |
ZHANG Y D, XU A G, ZHANG G C, et al. Kinetic modeling of detonation and effects of negative temperature coefficient[J]. Combustion and Flame, 2016, 173: 483-492. DOI:10.1016/j.combustflame.2016.04.003 |
| [71] |
LIN C D, LUO K H, FEI L, et al. A multi-component discrete Boltzmann model for nonequilibrium reactive flows[J]. Scientific Reports, 2017, 7(1): 14580. DOI:10.1038/s41598-017-14824-9 |
| [72] |
LIN C D, LUO K H. MRT discrete Boltzmann method for compressible exothermic reactive flows[J]. Computers and Fluids, 2018, 166: 176-183. DOI:10.1016/j.compfluid.2018.02.012 |
| [73] |
LIN C D, LUO K H. Mesoscopic simulation of nonequilibrium detonation with discrete Boltzmann method[J]. Combustion and Flame, 2018, 198: 356-362. DOI:10.1016/j.combustflame.2018.09.027 |
| [74] |
ZHANG Y D, XU A G, ZHANG G C, et al. A one-dimensional discrete Boltzmann model for detonation and an abnormal detonation phenomenon[J]. Communications in Theoretical Physics, 2019, 71: 117-126. DOI:10.1088/0253-6102/71/1/117 |
| [75] |
LIN C D, LUO K H. Kinetic simulation of unsteady detonation with thermodynamic nonequilibrium effects[J]. Combustion Explosion and Shock Waves, 2020, 56(4): 435-443. DOI:10.1134/S0010508220040073 |
| [76] |
LIU H, KANG W, ZHANG Q, et al. Molecular dynamics simulations of microscopic structure of ultra strong shock waves in dense helium[J]. Frontiers of Physics, 2016, 11(6): 1-11. DOI:10.1007/s11467-016-0590-5 |
| [77] |
LIU H, ZHANG Y, KANG W, et al. Molecular dynamics simulation of strong shock waves propagating in dense deuterium, taking into consideration effects of excited electrons[J]. Physical Review E, 2017, 95(2-1): 023201. DOI:10.1103/PhysRevE.95.023201 |
| [78] |
刘浩, 康炜, 段慧玲, 等. 流体中强冲击波的微观结构数值模拟研究进展[J]. 中国科学: 物理学 力学 天文学, 2017, 47(7): 19-27. LIU H, KANG W, DUAN H L, et al. Recent progresses on numerical investigations of microscopic structure of strong shock waves in fluid[J]. Scientia Sinica (Physica,Mechanica & Astronomica), 2017, 47(7): 19-27. (in Chinese) |