2. 中国空气动力研究与发展中心 低速空气动力研究所,绵阳 621000
2. Low Speed Aerodynamics Institute of China Aerodynamics Research and Development Center, Mianyang 621000, China
2019年12月以来,我国湖北省武汉市发现多起肺炎病例[1],2020年1月8日初步确认病原体为新型冠状病毒。截止2020年12月24日,国内外累积有78964495个确诊病例,累积死亡病例1733050[2]。这种惊人的增长速度是病毒快速、隐蔽传播方式所造成的。
新型冠状病毒有3种传播方式:呼吸飞沫、空气气溶胶和直接接触。呼吸飞沫是病毒最主要的传播载体,通过病人说话、咳嗽、喷嚏传播。较大粒径的飞沫会在重力作用下逐步沉降到地面[3],较小粒径的飞沫则会较长时间悬浮在空气中。呼吸飞沫还会蒸发转变成飞沫核,转为气溶胶[4-5]。因此,呼吸飞沫是最主要的传播途径。早在20世纪30年代就有实验验证[6]了飞沫是最主要的传播途径,也诞生了空气传染病毒的传播理论[7]。2020年新冠疫情的爆发,关于呼吸飞沫在空气中流动传播的文章大量出现,给相关的研究提供了很好的指导[8-11]。BHAGAT等[8]研究了建筑物通风对呼吸飞沫传播路径的影响,进一步证明病毒在空气中传播的风险。MITTAL等[9]更是警示飞沫在空气中的扩散和沉积是传播的关键因素,同时还总结了面罩、洗手、室内通风等背后的科学意义和机理。AGRAWAL等[10]通过研究表明,咳嗽产生的飞沫云团会大量污染空气,而飞沫云团具有自相似的性质,可以帮助人们设计更好的封闭空间通风系统。VERMA等[11]利用流动显示技术研究了医用口罩在降低呼吸飞沫速度和传播距离的作用,同时也发现口罩边缘会存在一些小的泄漏,为医护人员和口罩制造商提供了有效的评估。
喷嚏产生呼吸飞沫的喷射速度通常是20~50 m/s[4, 12],最快可达100 m/s[13],在不到1 s的时间,单个喷嚏可喷射出约75400个粒径0.5~12 µm的飞沫[14-15]。相对而言,咳嗽产生呼吸飞沫的喷射速度要低得多,通常10 m/s左右[16],单次咳嗽可产生几千个粒径1~5 µm的飞沫[17]。说话产生的飞沫则比前两者要少得多,速度不超过5 m/s[18]。
喷嚏分3个阶段:启动阶段、爆发阶段、衰减阶段[19]。启动阶段、衰减阶段的飞沫含量较低,爆发阶段的飞沫含量较高,出现峰值。喷嚏的时间历程类似伽马函数或正弦函数[20],经历了从零到峰值、然后从峰值下降至零的过程。呼吸飞沫的呼出具有一定的喷射角度[19-22],通常,下喷射角较大,上喷射角较小。呼出的飞沫粒径分布非常复杂,既有双峰结构,也有单峰结构[23]。
防呼吸飞沫的最好办法是通过戴口罩的方法物理隔绝鼻口,防止吸入飞沫。防飞沫面罩是一种防止飞沫喷射到脸部的透明遮挡物(图1),结构简单、方便实用,遮挡面积大,防疫医护人员将其作为辅助防护用具。防飞沫面罩能否代替防护口罩?计算流体力学方法是研究呼吸飞沫运动的有效手段,研究人员对呼吸飞沫运动和传播[24-33]进行了很多有价值工作。基于这些基础,本文针对日常生活中病人与戴防飞沫面罩的健康人之间呼吸飞沫传播和防护进行研究,重点研究了防飞沫面罩是否能阻止呼吸飞沫传播的问题,期望对日常的新型肺炎疫情防护提供参考。
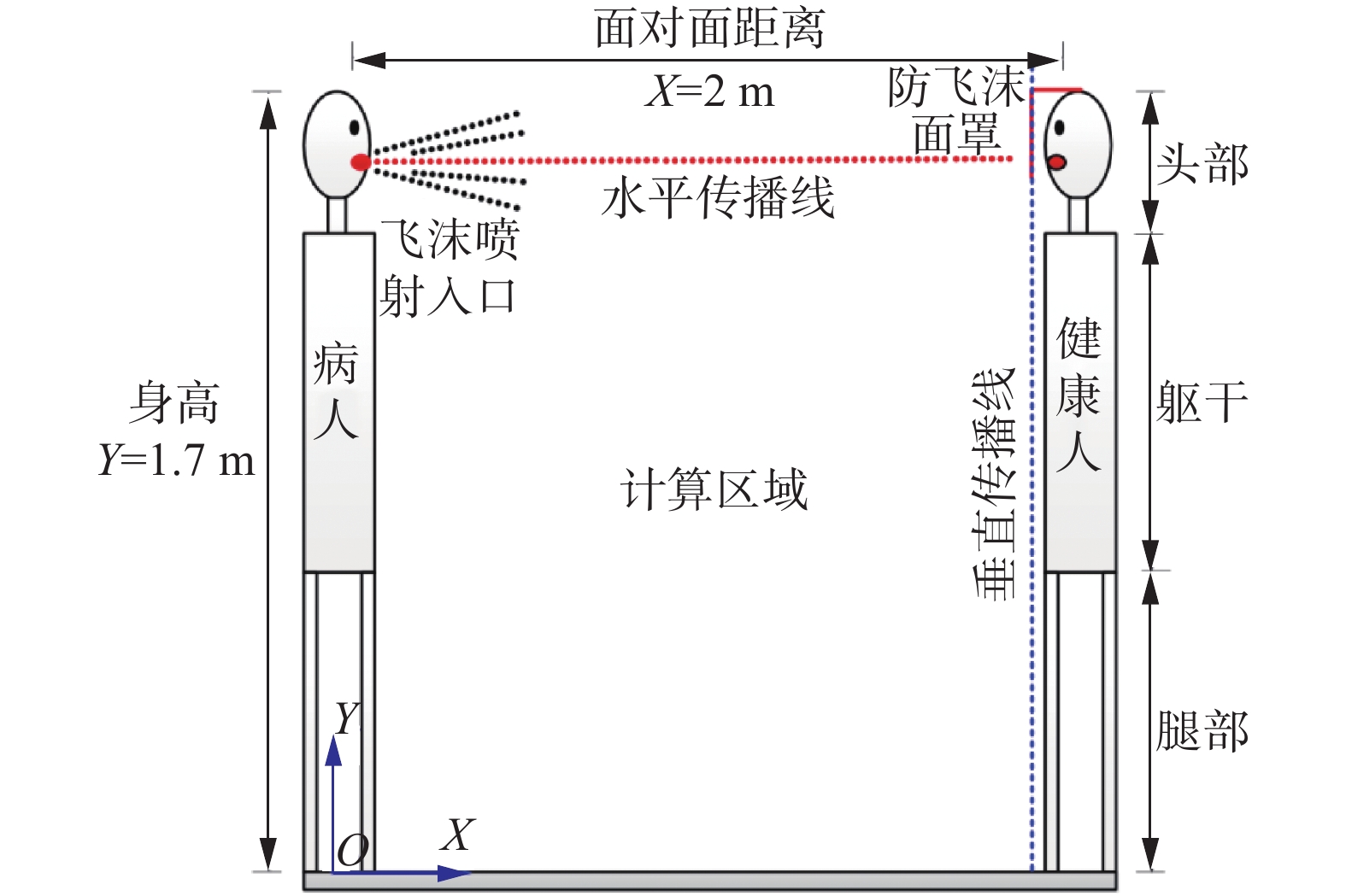
1 研究方法本文以病人和戴防飞沫面罩的健康人之间的传播区域作为研究对象。计算域的大小为2 m×2.8 m,病人与健康人面对面站立,距离为2 m,两者身高均为1.7 m。病人喷嚏、咳嗽时,嘴巴宽度为0.02 m,处于1.5 m高度位置。健康人呼吸时嘴巴宽度、高度位置与病人的相同。健康人戴防飞沫面罩,面罩长度0.2 m,处于1.7 m高度位置,覆盖鼻口位置。以病人脚底为原点O,病人脚底沿地面水平指向健康人脚底设为横坐标X,病人脚底沿身体垂直指向头顶设为纵坐标Y (图2)。
|
图 2 病人和健康人面对面呼吸飞沫传播示意图 Fig.2 Sketch of respiratory droplets transmission between patient and healthy person face to face |
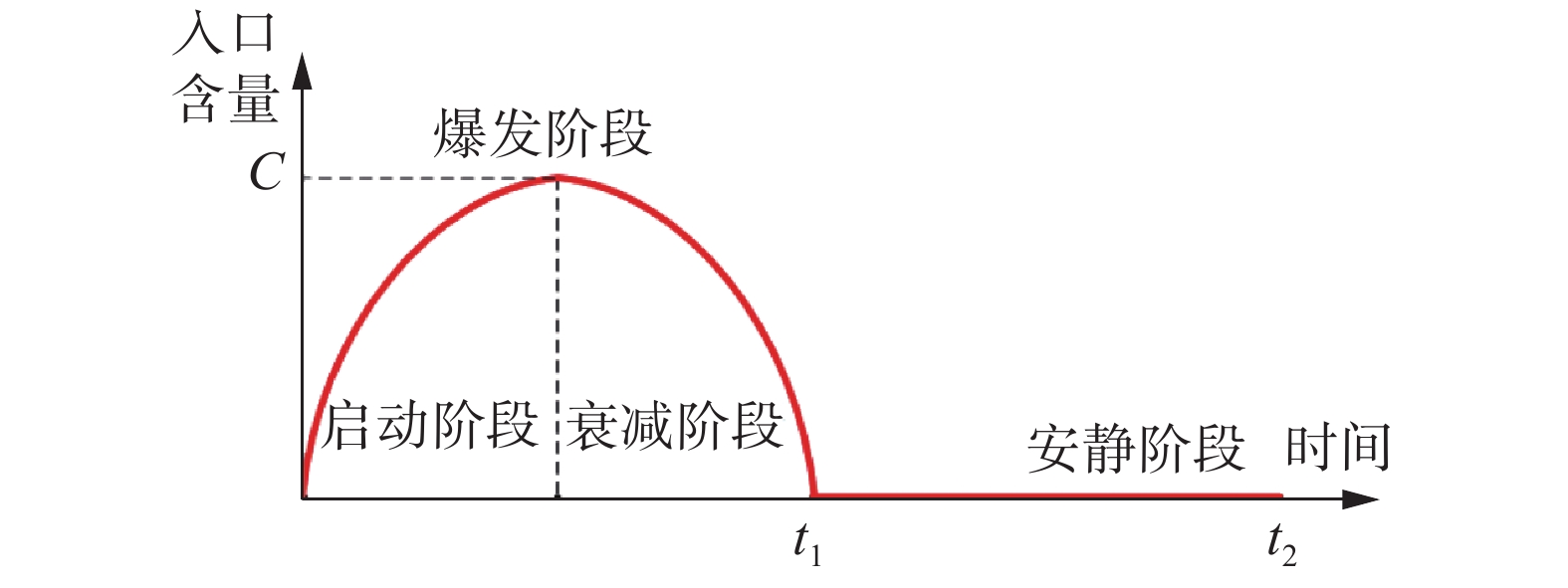
采用正弦函数来描述喷嚏、咳嗽、说话产生飞沫的喷射浓度变化[21],单个喷嚏、咳嗽、说话周期t2为1 s,启动、爆发、衰减阶段共占0.5 s (图3),浓度分别为100 、10、1 、0.1 mg/m3,覆盖喷嚏、咳嗽、说话喷射的飞沫浓度。采用上喷射角θ1 = 30°,下喷射角θ2 = −30°。本文假定飞沫颗粒为球形,只研究粒径影响,不研究粒径分布影响,采用均匀分布的粒径1 、5、10、20 μm,采用50 、30 、10 、2 m/s的喷射速度,以覆盖喷嚏、咳嗽、说话喷射的飞沫速度和粒径[5, 15-16]。
|
图 3 喷嚏、咳嗽、说话产生飞沫的喷射浓度随时间变化 Fig.3 Time evolution of spraying concentration of droplets from sneezing, coughing and talking |
采用计算流体力学方法对非稳态不可压缩雷诺平均N-S方程进行求解[22],获得了病人和健康人面对面呼吸飞沫传播区域的流场。采用有限体积方法离散控制方程组,采用二阶迎风格式离散动量方程、湍动能和湍流耗散速率项,压力方程采用二阶中心格式离散,速度和压力的耦合采用相耦合的SIMPLE方法[34]。采用多相流的欧拉模型[34-37]描述呼吸飞沫跟随空气的两相流动。空气和飞沫的连续性方程采用公式(1)表示:
| $ \frac{{\partial \left( {{\alpha _k}{\rho _k}} \right)}}{{\partial t}} + \nabla \cdot \left( {{\alpha _k}{\rho _k}{{{U}}_k}} \right) = 0 $ | (1) |
其中,α为体积分数;U为速度矢量,m/s;下标k代表某相,空气相用下标a表示,飞沫相用下标d表示;ρ为密度,kg/m3,空气和飞沫的密度和黏性均保持常数。
空气的动量方程采用公式(2)表示:
| $\begin{split}& \frac{{\partial \left( {{\alpha _{\rm{a}}}{\rho _{\rm{a}}}{U_{\rm{a}}}} \right)}}{{\partial t}} + \nabla \cdot \left( {{\alpha _{\rm{a}}}{\rho _{\rm{a}}}{U_{\rm{a}}}{U_{\rm{a}}}} \right) = \\& - {\alpha _{\rm{a}}}\nabla p + \nabla \cdot {{{\tau}} _{\rm{a}}} + {\alpha _{\rm{a}}}{\rho _{\rm{a}}}g + K\left( {{U_{\rm{d}}} - {U_{\rm{a}}}} \right) \end{split} $ | (2) |
飞沫的动量方程采用公式(3)表示:
| $\begin{split}& \frac{{\partial \left( {{\alpha _{\rm{d}}}{\rho _{\rm{d}}}{U_{\rm{d}}}} \right)}}{{\partial t}} + \nabla \cdot \left( {{\alpha _{\rm{d}}}{\rho _{\rm{d}}}{U_{\rm{d}}}{U_{\rm{d}}}} \right) = \\& - {\alpha _{\rm{d}}}\nabla p + \nabla \cdot {{{\tau}} _{\rm{d}}} + {\alpha _{\rm{d}}}{\rho _{\rm{d}}}g + K\left( {{U_{\rm{a}}} - {U_{\rm{d}}}} \right) \end{split} $ | (3) |
其中,p为流场压力,Pa; τ为应力张量; g为重力加速度,m/s2; K是空气相和飞沫相之间的动量交换系数。
RNG k-ε湍流模型具有广泛的适应性,不仅可以模拟高雷诺数流动,而且湍流模型中还有低雷诺数流动的黏性解析式,文献[36]表明,该湍流模型在模拟室内气流组织具有较好的效果。因此,本文采用RNG k-ε湍流模型描述湍流流动[36],采用壁面函数法将近壁面的物理量与湍流核心区域的未知量进行联系,最靠近壁面的节点与壁面间的无量纲距离满足30≤y+≤300[36-37]。采用如下形式来描述湍流模型方程:
| $\frac{{\partial \left( {{\rm{\rho}} {\phi _k}} \right)}}{{\partial t}} + \nabla \cdot \left( {{\rm{\rho}} {U_k}{\phi _k} - {{{\varGamma}} _{{\phi _k}}}{\rm{grad}}{\phi _k}} \right) = {{{S}}_{{\phi _k}}}\;,\quad k = 1,...,N$ | (4) |
其中,
采用结构网格技术和H型网格的拓扑结构对计算区域进行划分,全场采用直角网格,保证近壁网格的正交性以及计算结果的精度。
飞沫入口采用给定的速度入口条件,不仅给定喷射速度,而且给定湍流参数,包括湍流强度和湍流黏性比,采用如下公式描述[35-37]:
| $u = V\cos \theta $ | (5) |
| $v = V\sin \theta $ | (6) |
| ${C_{\rm{d}}} = {C}\sin \left( {2{\text{π}} t} \right)$ | (7) |
| $I = \frac{{{u'}}}{V} = 3\% $ | (8) |
| $\sigma = \frac{{{\mu _t}}}{\mu } = 10$ | (9) |
其中,V是入口的飞沫喷射速度,u、v分别是X、Y向速度分量,m/s;θ是飞沫的喷射角度,°;C是入口的飞沫浓度峰值;Cd是流场中的飞沫浓度,mg/m3;t是流动时间,s;u'是速度脉动的均方根,m/s;I是湍流强度;σ是湍流黏性比;湍流强度、湍流黏性比分别按照3%、10来给定,采用中等的湍流强度值。
出口边界采用流动变量的法向梯度为零的条件。同时,出口的湍流强度、湍流黏性比等参数均采用了入口边界的给定值。
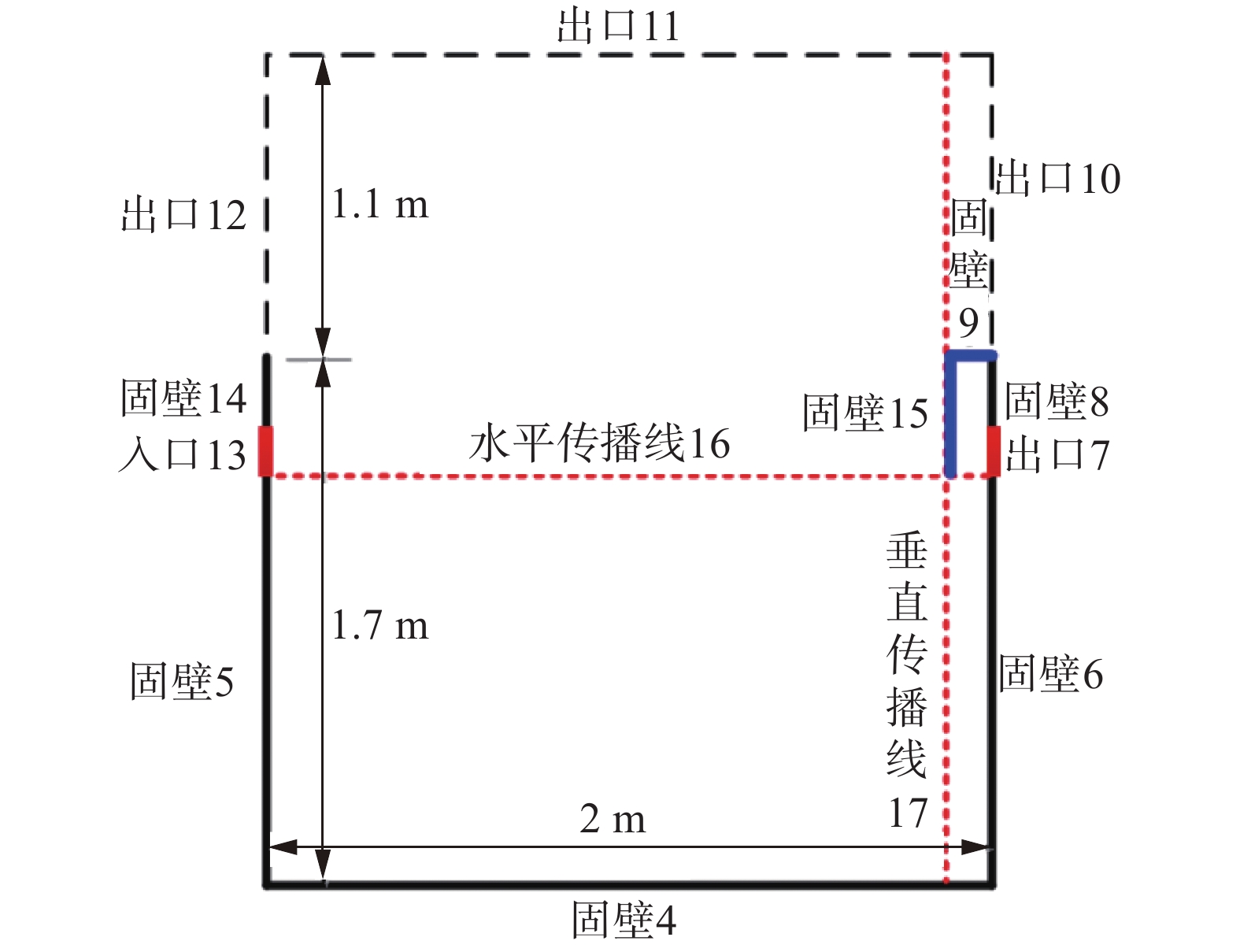
边界条件设置如图4所示,由于本文研究的是开放空间中面对面的飞沫流动和传播,因此将出口设置在健康人、病人的头部上方(图4中的出口10、出口12)和整个计算区域的顶部(图4中的出口11)。如果计算区域是电梯内的狭窄空间,则计算区域的顶部应该设置为固壁(也就是出口11改为固壁11),而健康人和病人的头部上方仍然设置为出口(出口10、出口12)。
|
图 4 计算区域的边界条件和传播线示意图 Fig.4 Sketch of boundary condition and transmission line in computation domain |
病人、健康人、防飞沫面罩、地面均采用固壁边界条件(图4),防飞沫面罩分内、外表面以及顶部,固壁边界采用速度无滑移条件。初始条件采用静止的流动参数值,也即初场各流动参数均为零。
入口飞沫的喷射浓度峰值与飞沫数量之间的关系采用如下公式[23]表示:
| ${M} = {C}\Bigg/\left( {{\rm{\rho }}\frac{1}{6}{\rm{{\text{π}} }}{{d}^3}} \right)$ | (10) |
其中,C是入口的飞沫浓度峰值,mg/m3;M是入口单位体积内飞沫的数量,1/m3;ρ是飞沫的密度,kg/m3;d是飞沫的直径,m。
入口的飞沫浓度峰值与体积分数的关系[23]如下:
| ${\alpha _{\rm{d}}} = \frac{{C}}{{\rm{\rho}} }$ | (11) |
其中,αd为飞沫体积分数,表示单位体积内飞沫所占的体积比; 下标d表示飞沫。
本文重点对水平传播线(0≤X≤2 m,Y = 1.5 m)、垂直传播线(X = 1.95 m,0≤Y≤2.8 m)和健康人鼻口(X = 2 m,1.5 m≤Y≤1.52 m)的飞沫浓度进行分析。本文忽略了呼吸飞沫的相变问题。
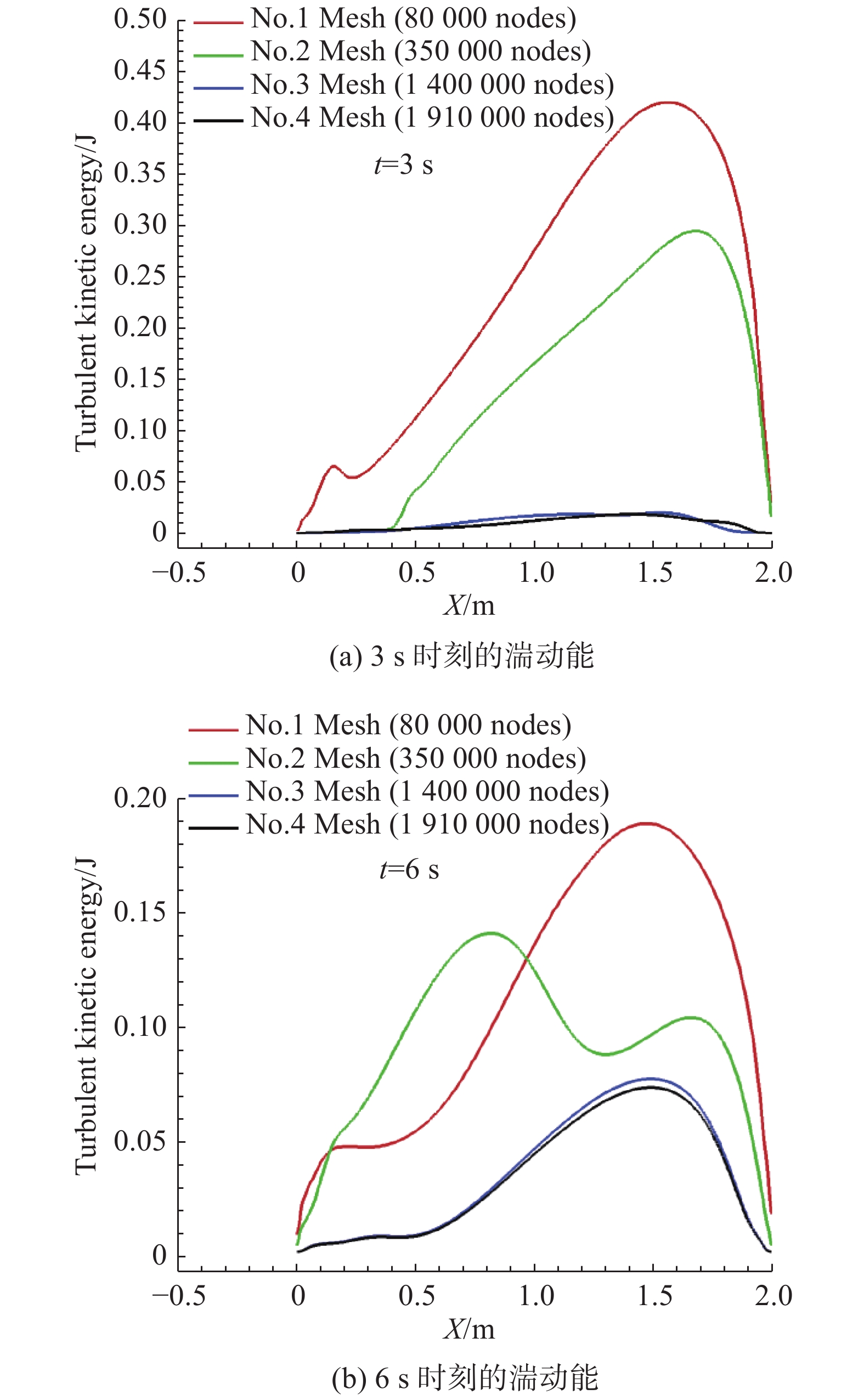
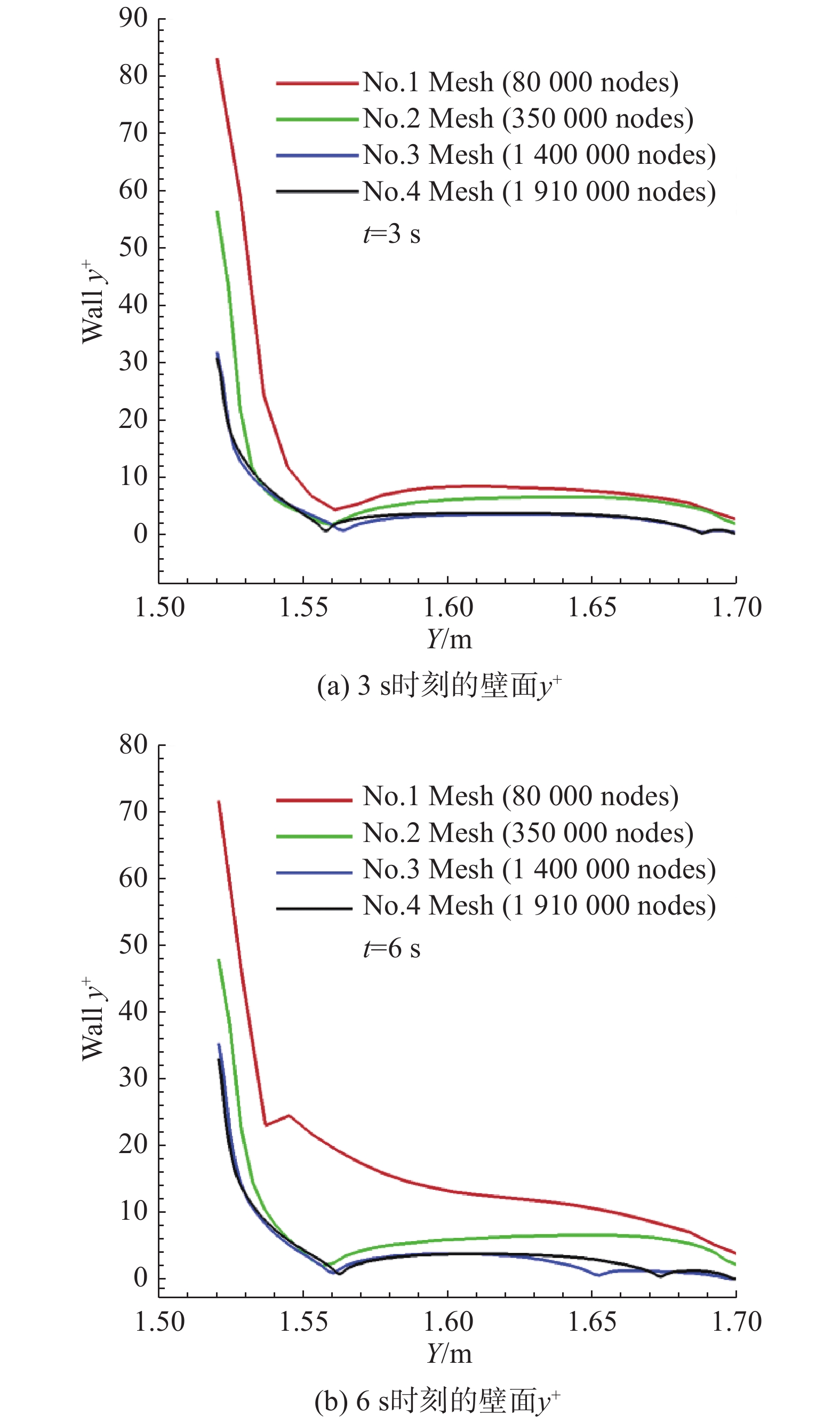
对于网格无关性,本文分别对80 000、350000、1400000、1910000节点数的四套网格进行了数值模拟,获得了不同时刻病人和健康人之间固壁4的湍动能分布曲线(图5),以及健康人面部固壁8的壁面y+分布(图6),可以发现,在3 s和6 s时刻,第三套网格(1400000节点数)和第四套网格(1910000节点数)不仅固壁4的湍动能分布(图5)非常接近,而且固壁8的壁面y+分布(图6)也相差很小,这就说明第三套网格和第四套网格的计算精度非常接近,因此本文采用第三套网格的尺寸,计算网格为1001×1401,也就是1400000节点数的网格。
|
图 5 不同网格下固壁4的湍动能分布 Fig.5 Turbulent kinetic energy distribution along wall 4 for different mesh grids |
|
图 6 不同网格下固壁8的壁面y+分布 Fig.6 y+ distribution along wall 8 for different mesh grids |
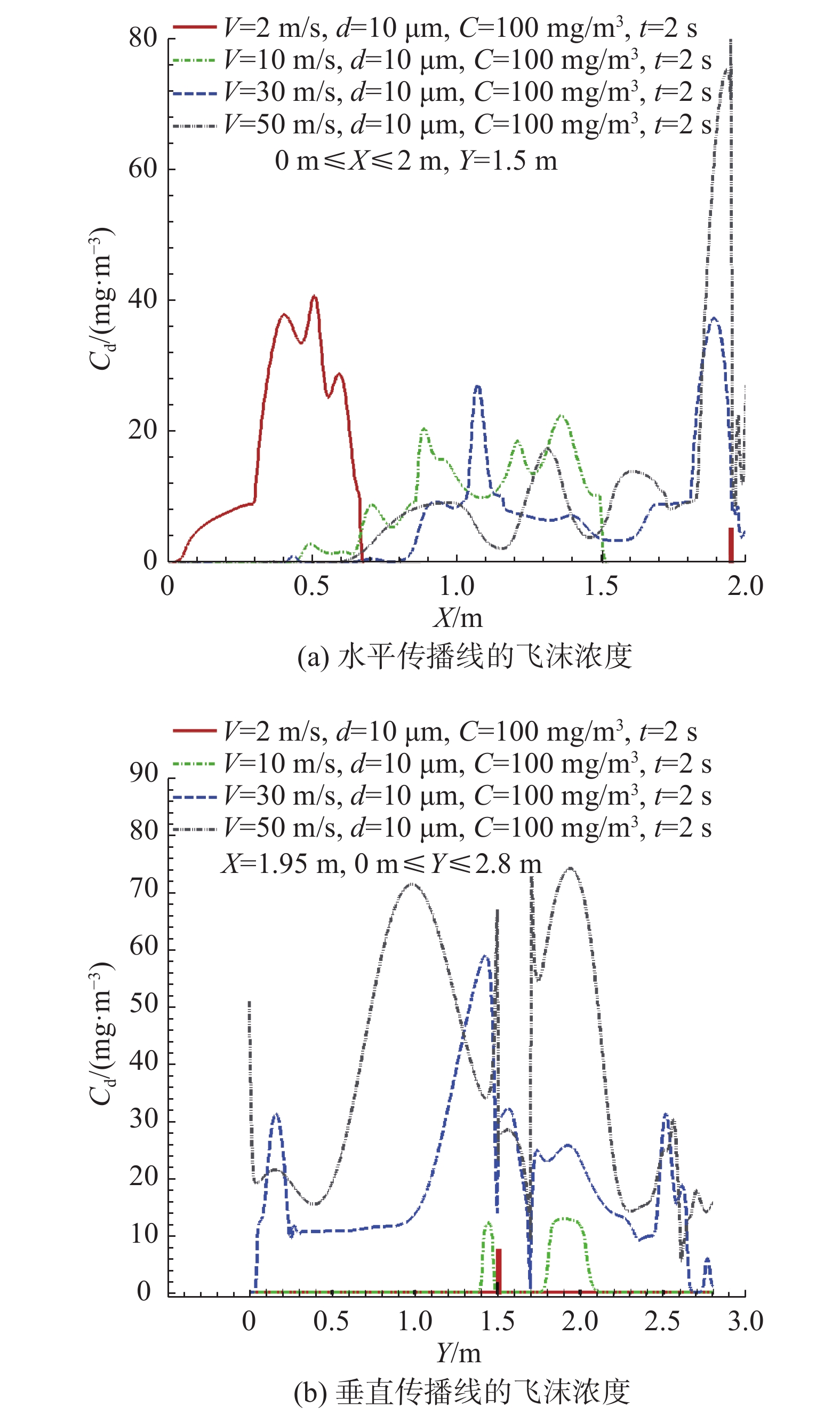
图7给出了不同喷射速度下水平传播线和垂直传播线的飞沫浓度分布(V = 2、10、30、50 m/s, d = 10 μm, C = 100 mg/m3)。喷射速度为2 m/s时,飞沫跟随空气的流动传播很慢,在2 s时刻沿着水平传播线才传播到水平距离X = 0.68 m处。喷射速度为10 m/s时,飞沫在2 s时刻传播到水平距离X = 1.5 m处。而喷射速度为30、50 m/s时,飞沫在相同时刻已经完全传播到防飞沫面罩内和健康人鼻口。每种状态对应的水平传播线都会出现浓度极大值,有的甚至出现多个极大值,喷射速度越大出现的浓度极大值越多,这是周期性呼出飞沫所产生的现象。因为防飞沫面罩的存在,垂直传播线的1.5 m≤Y≤1.7 m范围内飞沫浓度远低于旁边的值,喷射速度2 m/s时,4.2 s时刻飞沫还未到达防飞沫面罩,喷射速度10 m/s时,4.2 s时刻防飞沫面罩上、下附近出现了飞沫浓度,喷射速度30、50 m/s时,4.2 s时刻防飞沫面罩内部已经出现了较大的飞沫浓度,飞沫已经完全侵入了防飞沫面罩。喷射速度在飞沫流动传播中起到了关键作用,喷射速度的增大将导致飞沫流动传播速度的相应增加,其周期性的呼出特征使得飞沫的水平传播和垂直传播均存在多个浓度峰值。
|
图 7 不同喷射速度下水平传播线和垂直传播线的飞沫浓度分布(V= 2、10、30、50 m/s, d= 10 μm, C= 100 mg/m3) Fig.7 Concentration distribution of droplets along horizontal and vertical transmission line for different spraying speed (V= 2、10、30、50 m/s, d= 10 μm, C= 100 mg/m3) |
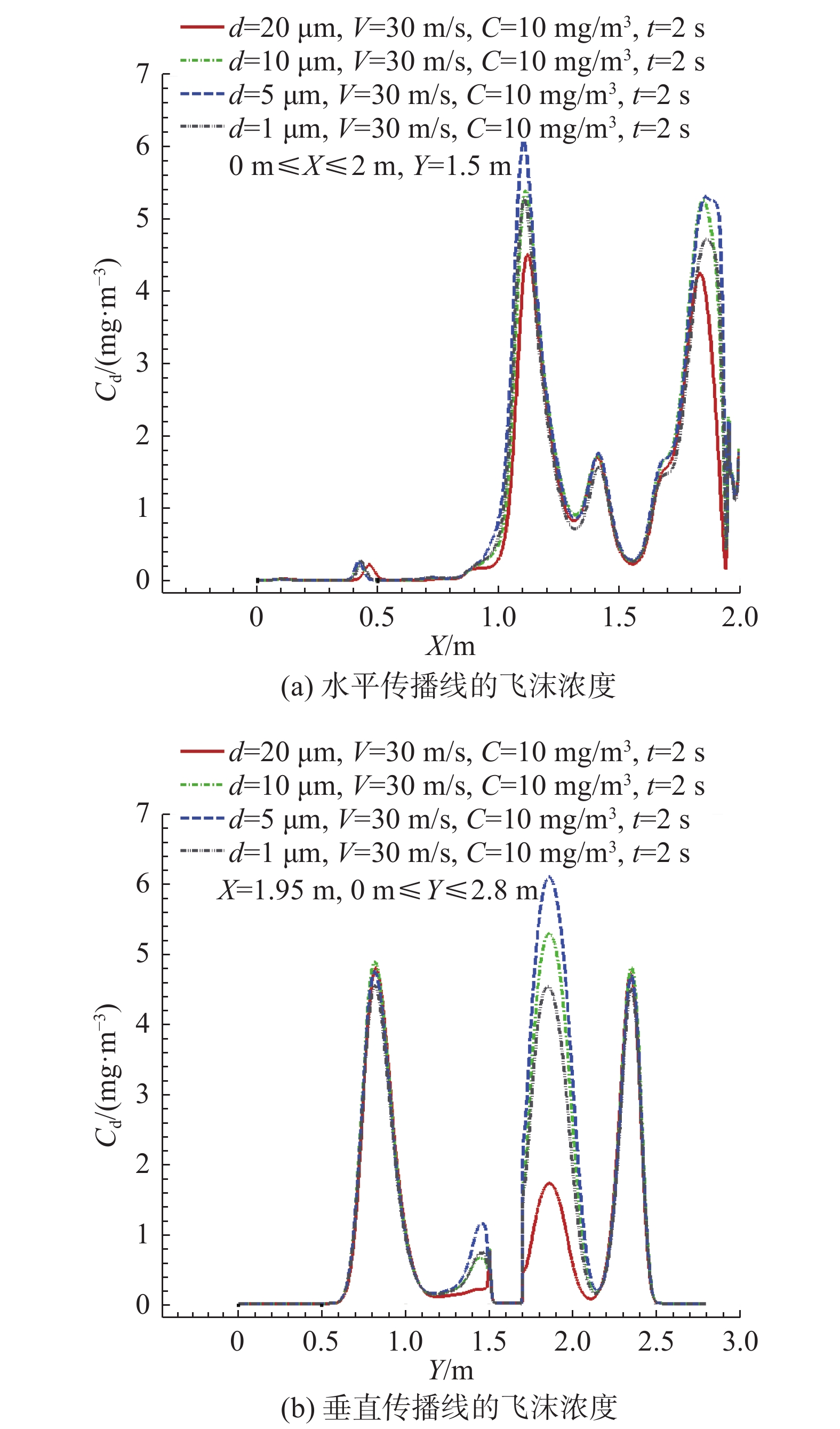
图8给出了不同粒径下水平传播线和垂直传播线的飞沫浓度分布(d = 20、10、5、1 μm, V = 30 m/s, C = 10 mg/m3)。2 s时刻,飞沫在水平传播线的X = 1.1 m、1.4 m和1.8 m位置出现了两大、一小的浓度峰值。相似的,2 s时刻飞沫在垂直传播线的Y = 0.8 m、1.45 m、1.85 m和2.35 m位置出现了三大、一小的浓度峰值。不同粒径下,各个位置的浓度峰值存在差异,其它位置的飞沫浓度相差很小。因此,粒径对飞沫的影响主要体现在浓度峰值的差异。相同位置,小粒径飞沫的浓度峰值比大粒径的略微高一些。对于水平传播线,粒径对飞沫的峰值浓度影响更加明显,特别是第三个浓度峰值,即1.8 m≤Y≤1.9 m位置的飞沫浓度。该位置靠近防飞沫面罩,粒径20 μm的飞沫浓度明显低于其它粒径的。但是,粒径1 μm是特殊情况,浓度峰值反而比粒径10 μm的还略低。粒径对飞沫水平传播和垂直传播的主要影响是体现在浓度峰值,对其它位置的浓度分布影响不大。考虑呼吸飞沫的相变,实际上是考虑飞沫颗粒在流动过程中的能量和质量传递,质量传递将导致飞沫粒径的改变,飞沫蒸发较多会导致飞沫粒径变小,蒸发较少则飞沫粒径的变化不大。从飞沫粒径的影响曲线可以发现,不同粒径的飞沫,在水平传播线和垂直传播线的分布相差不大,差异是在出现峰值的地方,主要是峰值大小的差异。因此,相变问题和粒径的影响联系很紧密,文章考虑的粒径影响,实际上也反映了相变的影响。
|
图 8 不同粒径下水平传播线和垂直传播线的飞沫浓度分布(d = 20、10、5、1 μm, V = 30 m/s, C = 10 mg/m3) Fig.8 Concentration distribution of droplets along horizontal and vertical transmission line for different droplet diameter (d = 20、10、5、1 μm, V = 30 m/s, C = 10 mg/m3) |
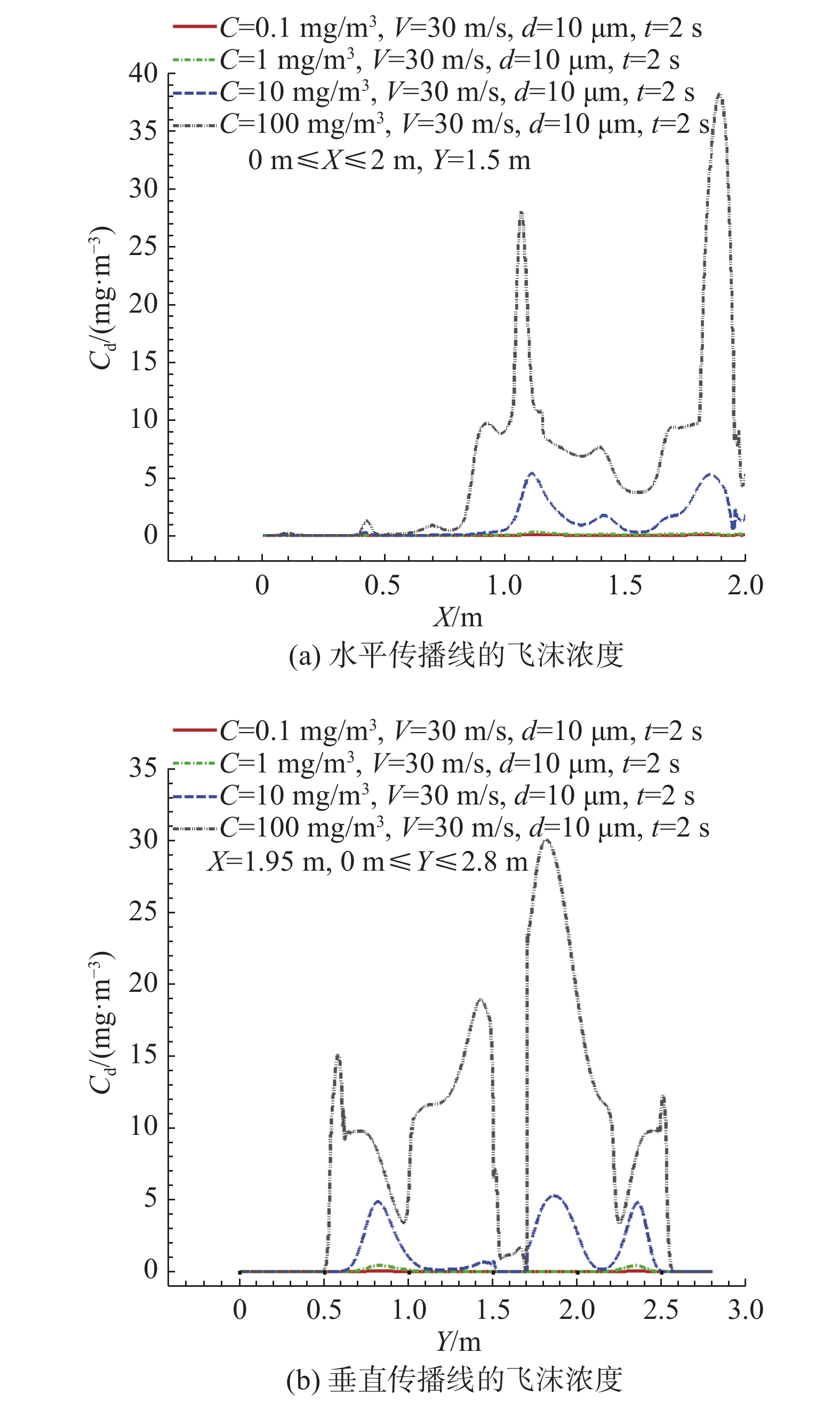
图9给出了不同入口含量下水平传播线和垂直传播线的飞沫浓度分布(C = 0.1、1、10、100 mg/m3, V = 30 m/s, d = 10 μm)。2 s时刻,水平传播线X = 1.2 m、1.9 m位置出现两个较大的浓度峰值,出现的位置非常一致。同一时刻,垂直传播线出现了更多个飞沫浓度峰值,但是出现的位置相差较大,飞沫入口含量不同使得垂直方向的扩散速度差异较大。不管是水平传播线还是垂直传播线,不同入口含量下的浓度分布相差很大,C = 100 mg/m3的浓度峰值是C = 10 mg/m3的6倍左右。这就说明入口含量对飞沫水平传播和垂直传播的影响很大,这种影响不仅体现在浓度的峰值,还体现在浓度分布。入口含量和飞沫流动传播的浓度分布存在正相关性,入口含量越大,飞沫在垂直传播和垂直传播方向的浓度分布就越大,入口含量对靠近防飞沫面罩附近区域的浓度分布影响特别大。
|
图 9 不同入口含量下水平传播线和垂直传播线的飞沫浓度分布(C = 0.1、1、10、100 mg/m3, V = 30 m/s, d = 10 μm) Fig.9 Concentration distribution of droplets for different inlet condition (C = 0.1、1、10、100 mg/m3, V = 30 m/s, d = 10 μm) |
图10是不同时刻的飞沫浓度云图(V = 30 m/s, C = 100 mg/m3, d = 10 μm)。喷射速度V = 30 m/s属于喷嚏的速度范围,飞沫云团在1.2 s时刻已传播到防飞沫面罩内和健康人鼻口。

|
图 10 不同时刻的飞沫浓度云图 (V = 30 m/s, C = 100 mg/m3, d = 10 μm) Fig.10 Concentration contour of droplet for different time (V = 30 m/s, C = 100 mg/m3, d = 10 μm) |
呼吸飞沫在传播过程中,先是以水平的对流传播为主,同时往上和往下进行扩散传播。飞沫云团接近健康人时,转为以扩散传播为主,同时发生往下顺时针、往上逆时针的回卷流动,形成“猫眼”状飞沫云团。与此同时,在飞沫云团出现的位置也相应出现了两个相反的大旋涡。因此,空气旋涡对于飞沫云团的产生具有重要作用,对流和扩散在不同时刻呼吸飞沫的流动传播中发挥了不同的作用。
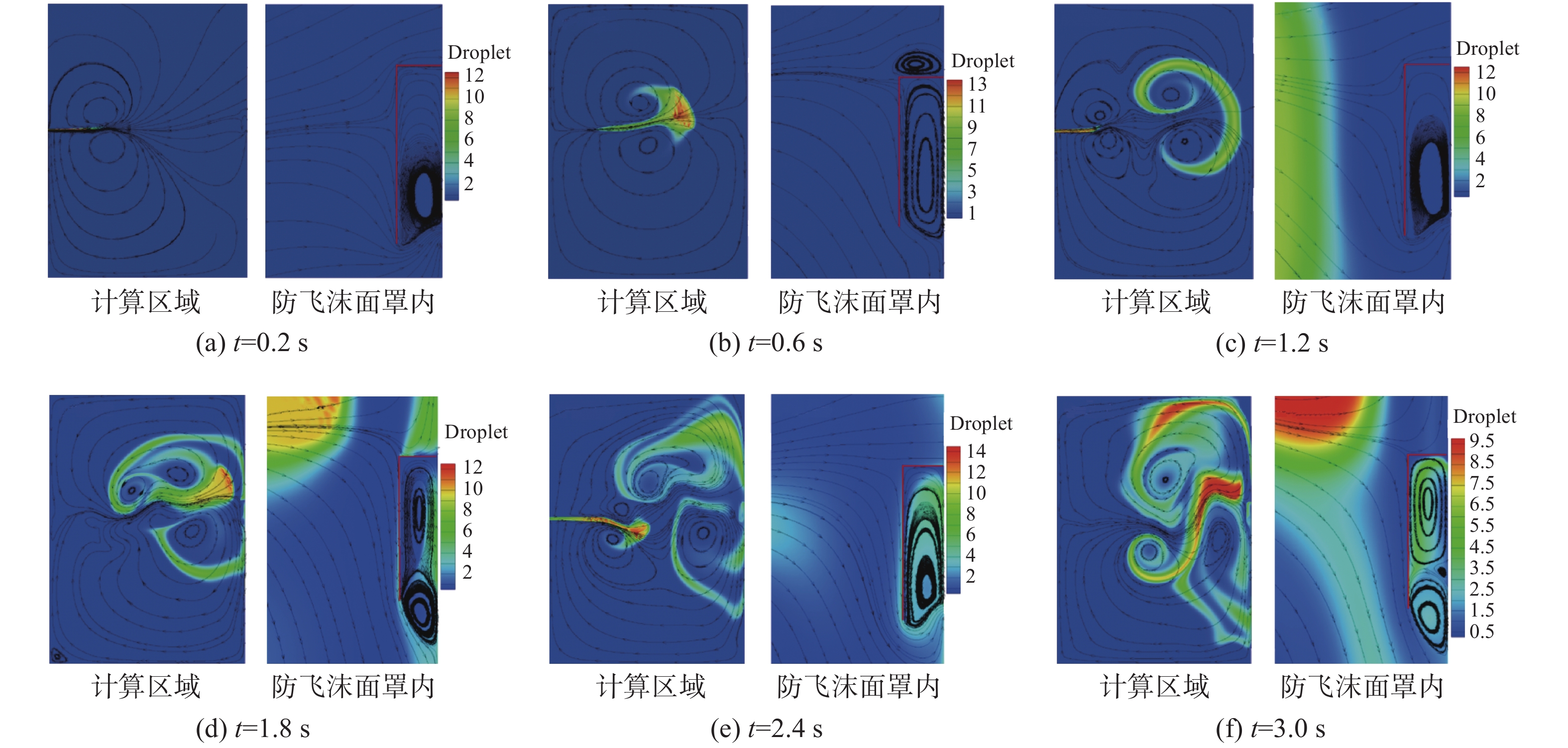
图11是不同时刻的计算区域和防飞沫面罩内部飞沫浓度云图和流线图。与图10类似的,在计算区域中出现的飞沫云团附近空气流线分成往上和往下两股,分别往逆时针和顺时针方向形成两个旋涡,这是产生“猫眼”状云团的关键,也是呼吸飞沫流动传播的增强方式。对于防飞沫面罩内部,在飞沫喷射的最初阶段(0.2 s),只有一个较小的空气旋涡出现在防飞沫面罩内部的中下部;随着飞沫云团的开始形成(0.6 s),防飞沫面罩内部出现了一个很大的空气旋涡,占据了整个面罩内部空间,同时,在面罩顶部也出现了一个较小旋涡;而随着飞沫云团的继续扩大(1.2 s),防飞沫面罩内部中下部又只出现一个较小的空气旋涡;当飞沫云团撞击防飞沫面罩并发生反向流动和扩散时(1.8 s),面罩内部出现了两个较大的空气旋涡,一个占据了面罩中上部,另一个占据面罩下部的入口;当飞沫云团撞到人体并出现往四周的扩散后(2.4 s),面罩内部又恢复到一个较大的空气旋涡;当飞沫云团出现较严重的四周扩散时(3.0 s),面罩内部出现了两个较大的旋涡,分别占据面罩内部的中央和下部入口,另外还出现一个很小的旋涡夹杂在两个大旋涡中间。由于咳嗽或喷嚏的周期性特征,防飞沫面罩内部也出现了单个空气旋涡和两个空气旋涡形成的周期性变化,在空气旋涡的带动下,健康人鼻口出现上方飞沫浓度大、下方浓度小的现象,这就使得防飞沫面罩内部特别是靠近头部和脸部附近的飞沫浓度较大。空气旋涡在呼吸飞沫侵入防飞沫面罩过程中起到非常关键作用。
|
图 11 不同时刻的计算区域和防飞沫面罩内部飞沫浓度云图和流线图(V = 30 m/s, C = 10 mg/m3, d = 10 μm) Fig.11 Concentration contour and streamline of droplets in computational domain and anti-droplets face shield for different time instant(V = 30 m/s, C = 10 mg/m3, d = 10 μm) |
采用计算流体力学方法对病人和戴防飞沫面罩的健康人之间的飞沫传播和防护进行了计算研究,得出如下特定的结论:
1)喷嚏形成的呼吸飞沫流动传播最强,1 s左右即可传播2 m距离,飞沫跟随空气流动开始以对流传播为主,然后以扩散传播为主,扩散传播过程会形成“猫眼”状飞沫云团。
2)喷射速度、入口含量和飞沫流动传播速度、浓度是正相关性的,而粒径对呼吸飞沫流动传播的影响主要体现在对浓度峰值的影响。
3)呼吸飞沫跟随空气的流动会在防飞沫面罩内形成旋涡,增加飞沫被吸入的可能性,仅凭防飞沫面罩是无法防止飞沫的传播和吸入。
三维模型将给出更多的流动细节,特别是空气-飞沫云团在撞击身体表面之后,会往身体两侧进行流动传播,侧向的流动结构会很丰富,可以为分析飞沫的流动传播机理提供更多的支撑。相变问题,实际上是考虑飞沫颗粒在流动过程中的能量和质量传递,质量传递将导致飞沫粒径的改变,飞沫蒸发较多会导致飞沫粒径变小,蒸发较少则飞沫粒径的变化不大。从飞沫粒径的影响曲线可以发现,不同粒径的飞沫,在水平传播线和垂直传播线的分布相差不大,差异是在出现峰值的地方,主要是峰值大小的差异。因此,相变问题和粒径的影响联系很紧密,文章考虑的粒径影响,实际上也反映了相变的影响。
文章主要研究面对面喷射方向的飞沫流动传播问题,因此,二维模型可以反映呼吸飞沫在喷射方向的流动特点,而相变对不同粒径的飞沫在水平传播线和垂直传播线分布影响不是很大。下一步将进行三维模型和相变问题的影响研究。
| [1] |
武汉不明原因肺炎不能断定是SARS, 7例病情危重[EB/OL]. 2019-12-31. https://ah.people.com.cn/n2/2019/1231/c358314-33679094.html
|
| [2] | |
| [3] |
病毒气溶胶飞沫在室内环境中传播扩散机制的研究进展[J]. 军事医学, 2011, 35(8): 631-633, 638. DU Q, WEN Z B, LI J S. Mechanism of viral aerosol and its droplet transmission and distribution in the indoor environment: a research progress[J]. Bulletin of the Academy of Military Medical Sciences, 2011, 35(8): 631-633, 638. DOI:10.3969/j.issn.1674-9960.2011.08.018 (in Chinese) |
| [4] |
飞沫气溶胶污染源特性研究现状[J]. 暖通空调, 2018, 48(7): 22-30. FENG G H, CAI Y L, ZHANG Y X, et al. Research situation of characteristics of aerosol droplet pollution sources[J]. Heating Ventilating & Air Conditioning, 2018, 48(7): 22-30. (in Chinese) |
| [5] |
呼吸道传染病气溶胶传染致病机理及预测方法[J]. 科学通报, 2018, 63(10): 931-939. QIAN H, ZHANG C Y, ZHENG X H. The function of aerosols in transmitting and infecting of respiratory infectious diseases and its risk prediction[J]. Chinese Science Bulletin, 2018, 63(10): 931-939. DOI:10.1360/N972017-01070 (in Chinese) |
| [6] |
WELLS W F. On airborne infection studyⅡ: droplets and droplet nuclei[J]. American Journal of Hygiene, 1934, 20(3): 619-627. |
| [7] |
RATCLIFFE H L, WELLS W F. Tuberculosis of rabbits induced by droplet nuclei infection; initial response to infection[J]. The Journal of Experimental Medicine, 1948, 87(6): 575-584. DOI:10.1084/jem.87.6.575 |
| [8] |
BHAGAT R K, DAVIES WYKES M S, DALZIEL S B, et al. Effects of ventilation on the indoor spread of COVID-19[J]. Journal of Fluid Mechanics, 2020, 903: F1-18. DOI:10.1017/jfm.2020.720 |
| [9] |
MITTAL R, NI R, SEO J H. The flow physics of COVID-19[J]. Journal of Fluid Mechanics, 2020, 894: F2-14. DOI:10.1017/jfm.2020.330 |
| [10] |
AGRAWAL A, BHARDWAJ R. Reducing chances of COVID-19 infection by a cough cloud in a closed space[J]. Physics of Fluids, 2020, 32(10): 101704. DOI:10.1063/5.0029186 |
| [11] |
VERMA S, DHANAK M, FRANKENFIELD J. Visualizing the effectiveness of face masks in obstructing respiratory jets[J]. Physics of Fluids (Woodbury, N Y, 2020, 32(6): 061708. DOI:10.1063/5.0016018 |
| [12] |
JENNISON M W, EDGERTON H E. Droplet infection of air: hih-speed photoraphy of droplet production by sneezing[J]. Experimental Biology and Medicine, 1940, 43(3): 455-458. DOI:10.3181/00379727-43-11230p |
| [13] |
DUTRA F R. Airborne contagion and air hygiene: an ecological study of droplet infections[J]. American Journal of Clinical Pathology, 1955, 25(11): 1301. DOI:10.1093/ajcp/25.11.1301 |
| [14] |
LINDSLEY W G, PEARCE T A, HUDNALL J B, et al. Quantity and size distribution of cough-generated aerosol particles produced by influenza patients during and after illness[J]. Journal of Occupational and Environmental Hygiene, 2012, 9(7): 443-449. DOI:10.1080/15459624.2012.684582 |
| [15] |
DUGUID J P. The size and the duration of air-carriage of respiratory droplets and droplet-nuclei[J]. The Journal of Hygiene, 1946, 44(6): 471-479. DOI:10.1017/s0022172400019288 |
| [16] |
ZHU S W, KATO S, YANG J H. Study on transport characteristics of saliva droplets produced by coughing in a calm indoor environment[J]. Building and Environment, 2006, 41(12): 1691-1702. DOI:10.1016/j.buildenv.2005.06.024 |
| [17] |
HERSEN G, MOULARAT S, ROBINE E, et al. Impact of health on particle size of exhaled respiratory aerosols: case-control study[J]. Clean: Soil, Air, Water, 2008, 36(7): 572-577. DOI:10.1002/clen.200700189 |
| [18] |
CHAO C Y H, WAN M P, MORAWSKA L, et al. Characterization of expiration air jets and droplet size distributions immediately at the mouth opening[J]. Journal of Aerosol Science, 2009, 40(2): 122-133. DOI:10.1016/j.jaerosci.2008.10.003 |
| [19] |
KWON S B, PARK J, JANG J, et al. Study on the initial velocity distribution of exhaled air from coughing and speaking[J]. Chemosphere, 2012, 87(11): 1260-1264. DOI:10.1016/j.chemosphere.2012.01.032 |
| [20] |
GUPTA J K, LIN C H, CHEN Q. Flow dynamics and characterization of a cough[J]. Indoor Air, 2009, 19(6): 517-525. DOI:10.1111/j.1600-0668.2009.00619.x |
| [21] |
GUPTA J K, LIN C H, CHEN Q. Characterizing exhaled airflow from breathing and talking[J]. Indoor Air, 2010, 20(1): 31-39. DOI:10.1111/j.1600-0668.2009.00623.x |
| [22] |
XU C, NIELSEN P V, LIU L, et al. Human exhalation characterization with the aid of schlieren imaging technique[J]. Building and Environment, 2017, 112: 190-199. DOI:10.1016/j.buildenv.2016.11.032 |
| [23] |
刘鹏. 病房飞沫污染物的浓度变化特征及污染控制[D]. 重庆: 重庆大学, 2016. LIU P. Variation characteristics and pollution control of droplet contaminant concentration in wards[D]. Chongqing: Chongqing University, 2016. (in Chinese) |
| [24] |
MURAKAMI S, KATO S, NAGANO S, et al. Diffusion characteristics of airborne particles with gravitational settling in a convection-dominant door flow field[J]. ASHRAE Transactions, 1992, 98: 82-97. |
| [25] |
HOLMBERG S, LI Y G. Modelling of the indoor environment - particle dispersion and deposition[J]. Indoor Air, 1998, 8(2): 113-122. DOI:10.1111/j.1600-0668.1998.t01-2-00006.x |
| [26] |
非典型肺炎病毒在空气中传播过程的初步数值模拟[J]. 西安交通大学学报, 2003, 37(7): 764-766. LI G X, TAO W Q, SUN X J. Primary numerical investigation of SARS virus spreading in air[J]. Journal of Xi'an Jiaotong University, 2003, 37(7): 764-766. DOI:10.3321/j.issn:0253-987X.2003.07.026 (in Chinese) |
| [27] |
ZHAO B, LI X T, YAN Q S. A simplified system for indoor airflow simulation[J]. Building and Environment, 2003, 38(4): 543-552. DOI:10.1016/S0360-1323(02)00182-8 |
| [28] |
XIE X J, LI Y G, ZHANG T, et al. Bacterial survival in evaporating deposited droplets on a teflon-coated surface[J]. Applied Microbiology and Biotechnology, 2006, 73(3): 703-712. DOI:10.1007/s00253-006-0492-5 |
| [29] |
WANG M, LIN C H, CHEN Q Y. Advanced turbulence models for predicting particle transport in enclosed environments[J]. Building and Environment, 2012, 47: 40-49. DOI:10.1016/j.buildenv.2011.05.018 |
| [30] |
GAO N P, NIU J L, MORAWSKA L. Distribution of respiratory droplets in enclosed environments under different air distribution methods[J]. Building Simulation, 2008, 1(4): 326-335. DOI:10.1007/s12273-008-8328-0 |
| [31] |
LI X P, NIU J L, GAO N P. Spatial distribution of human respiratory droplet residuals and exposure risk for the co-occupant under different ventilation methods[J]. HVAC& R Research, 2011, 17(4): 432-445. DOI:10.1080/10789669.2011.578699 |
| [32] |
ZHANG L, LI Y G. Dispersion of coughed droplets in a fully-occupied high-speed rail cabin[J]. Building and Environment, 2012, 47: 58-66. DOI:10.1016/j.buildenv.2011.03.015 |
| [33] |
VILLAFRUELA J M, OLMEDO I, RUIZ DE ADANA M, et al. CFD analysis of the human exhalation flow using different boundary conditions and ventilation strategies[J]. Building and Environment, 2013, 62: 191-200. DOI:10.1016/j.buildenv.2013.01.022 |
| [34] |
刘树森. 口腔散发微生物气溶胶在室内传播和运动规律的研究[D]. 天津: 天津大学, 2007. LIU S S. Study on transport mechanisms of bio-aerosol produced by mouth in the indoor environment[D]. Tianjin: Tianjin University, 2007 (in Chinese). |
| [35] |
任春勇. 基于欧拉模型的风沙流运动模拟[D]. 兰州: 兰州大学, 2011. REN C Y. Numerical simulation of wind-blown sand movements based on eulerian model[D]. Lanzhou: Lanzhou University, 2011. (in Chinese) |
| [36] |
WANG J L, CHOW T T. Numerical investigation of influence of human walking on dispersion and deposition of expiratory droplets in airborne infection isolation room[J]. Building and Environment, 2011, 46(10): 1993-2002. DOI:10.1016/j.buildenv.2011.04.008 |
| [37] |
LAI A C K, CHENG Y C. Study of expiratory droplet dispersion and transport using a new Eulerian modeling approach[J]. Atmospheric Environment, 2007, 41(35): 7473-7484. DOI:10.1016/j.atmosenv.2007.05.045 |
 2021, Vol. 39
2021, Vol. 39


