2. 北京大学 应用物理与技术研究中心, 北京 100871
2. Center for Applied Physics and Technology, Peking University, Beijing 100871, China
可压缩多介质流动问题,是指流场涉及多种物质,且物质之间存在相互耦合作用的流动现象。它广泛存在于各种自然现象、工程应用中。如超新星爆发、超燃冲压发动机中的燃料混合、惯性约束聚变和武器物理等[1],有着非常重要的科学研究意义和工程应用价值。
在这种流动问题中,由于移动且可变形界面的存在,界面处流体性质不连续给物理建模与数值方法带来了极大的困难。目前,文献中存在多种具有不同复杂度和适用范围的物理模型及数值计算方法。从界面处理方式来看,它们可以分为两类[2]:第一类将界面处理为清晰的间断,即清晰界面模型/方法;第二类将将界面处理为多物质相互扩散而成的混合区,即扩散界面模型/方法。
在扩散界面模型中,界面被处理为多物质相互扩散而成的混合区,就像数值捕获空气动力学中的接触间断一样[2]。虽然这类扩散界面是一种人为做成的数值混合,但这类模型最重要的优点就是可以在固定网格上,所有计算单元都采用相同的数值方案来求解,而不用考虑流场中存在什么样类型的波(冲击波、稀疏波,界面等)以及它们之间的相互作用。这类模型/方法可进一步分为两小类:基于欧拉/Navier-Stokes方程的扩散界面模型和基于多相流方程的扩散界面模型。
1) 基于单流体欧拉/Navier-Stokes方程的扩散界面模型。这类模型是由传统的欧拉/Navier-Stokes方程,附加每种物质的(质量)浓度方程构成,每个计算网格即使含有多种流体组分仍具有相同的运动速度。这类方法虽然形式上简单,但却存在一些问题:①过界面非物理振荡。Abgrall通过数值实验表明[3],对于两种理想气体的多介质问题,直接采用这类模型会在界面处产生压力振荡。为了消除这个问题,他提出了非守恒的四方程模型(拟守恒方法)[3]及等效四方程模型[4],在恰当数值离散的基础上,可以使用同种有限体积/差分算法来处理由界面分开的可压缩多介质流动问题[5]。但是这样的操作最终导致方程组丧失守恒性。②等温等压假设限制此模型的应用范围。这类模型通过两种组分的状态方程构造混合物的状态方程。压强均衡会导致两相的声速必须耦合,而且显然无法满足某些真实物理情况。
2) 基于多相流方程的扩散界面模型。多介质流动是一类含有可区分大尺度物质界面的多相流问题,因此很多学者也直接将多介质流动称为多相流动。多相流方程的扩散界面模型是指将所有相视为连续介质,利用各种平均方法(时间平均、空间平均、系综平均)对各相的场方程进行平均后得到的一类忽略了流动的一些微观细节的宏观均质或平均混合模型[6]。由于使用平均方法,最终的模型会出现非守恒项(即最终的模型无法写成散度形式)和较多的附加项(物质之间的质量、动量和能量传递等过程的宏观模化)。对这些附加项建立不同的唯象模式,就形成了不同的模型(对于两种介质的流动,又称双流体模型或七方程模型),如Baer-Nunziato模型(BN模型)[7]、Saurel-Abgrall模型(SA模型)[8]。这类模型具体如下一些特点:①不同相之间是完全非平衡的,即每个相流体都有自己的密度、压力、速度、温度等,因此一维情况下共有7个方程。由于这类模型包含的方程个数多、波系复杂、存在非守恒项[10],有时候并不能满足严格双曲特性,给数值求解带来了很大挑战。②双流体多相流模型一般只适用于稠密多相流情形,即可以离散可近似看做一种连续的流体(如大量颗粒、液滴等)。对于颗粒相稀疏或者处于稀疏到稠密过渡情形,双流体多相流模型的适应性还存在问题(为克服这一困难,最近我们提出了一种适用于稀疏到稠密跨流态可压缩两相流的模拟方法(CMP-PIC)[9])。③对于一些特殊情况,这类模型还可以退化为一系列简化模型[1]。
在实际的工程应用中,我们会根据具体问题的特殊性,针对性选择一些简化模型来开展相应的数值模拟工作。但不管选择何种类型的模型,为建立一套高效的高精度数值模拟算法,我们遇到的问题都是基本类似的。因此,本文内容不局限于某种特殊模型,而将从数值框架的选择、非守恒方程相容离散、高精度有界格式构造、界面压缩、界面-单介质分区计算方法等5个维度出发,综述近几年我们在可压缩多介质流动问题高精度数值模拟工作中的一些进展。
1 高精度数值模拟方法 1.1 基本要求为了准确模拟可压缩多介质流动问题,尤其是其中涉及的界面大变形运动,需要探索和建立一套高效的高精度数值算法。同面向其他可压缩流动问题的数值算法一样,这套算法同样需要满足一定的要求,如守恒性、高分辨率、健壮性等。但可压缩多介质流动问题又有其特殊性,因此有一些额外的特殊要求,其中包括:1) 过界面不产生各种非物理的数值振荡;2) 在长时间计算过程中,保持界面的锐利结构。界面不能随着计算时间的增加而不断弥散变宽,最终影响流场其他结构;3) 保界性。可压缩多介质流动的物理模型中往往会涉及其他类型的物理量,如质量分数、体积分数。这类物理量有着明确的上界和下界。因此,在对可压缩多介质流动问题进行模拟时,不仅仅需要考虑热力学量的保正问题,还得同时考虑如质量分数这类物理量的保界问题。从而保证程序的稳定运行和界面混合封闭模式的精准执行。
为了实现构建满足上述约束条件的数值方法,我们做了一系列探索和研究工作。下面详细介绍研究的进展以及一些具体工作。
1.2 数值框架的选择流体力学数值方法通常可以分为拉格朗日方法和欧拉方法两种类型。拉格朗日方法,计算网格随流体一起运动,适宜计算一些变形不大的多介质界面问题。欧拉方法,网格固定不动,能够模拟界面大变形问题。本文主要关注欧拉数值方法。目前欧拉数值离散方法大致分为有限差分方法、有限体积方法、有限元方法三种基本框架。这些数值框架能否适用于可压缩多介质流动问题,需要做适应性分析。而对这类框架开展适用性分析的指导思想是Abgrall提出的界面无振荡分析方法[3]——过界面速度-压力需要保持为常数。
1.2.1 过界面非物理振荡现象考虑如下经典的满足气体状态方程的界面运动问题(见图 1)。左边是一种气体,如空气,其比热比为γL=1.4。右边是另一种气体,如氦气,其比热比为γL=1.667。跨过界面时,两种介质的压力和速度均相同。

|
图 1 界面运动问题 Fig.1 The interface advection problem |
对于这个问题,采用如下模型(一维形式)[3]:
| $ \left\{\begin{array}{l} \frac{\partial \rho}{\partial t}+\frac{\partial \rho}{\partial x}=0 \\ \frac{\partial \rho u}{\partial t}+\frac{\partial\left(\rho u^{2}+p\right)}{\partial x}=0 \\ \frac{\partial \rho E}{\partial t}+\frac{\partial(\rho E+p) u}{\partial x}=0 \\ \frac{\partial \rho Y_{L}}{\partial t}+\frac{\partial \rho Y_{L} u}{\partial x}=0 \end{array}\right. $ | (1) |
其中,ρ、u、E、p、YL分别为密度、速度、总能、压力和左边物质的质量分数。其中质量分数满足:
| $ \rho e=\frac{1}{\gamma-1} p=\left(\frac{\frac{Y_{L}}{\gamma_{L}-1} \frac{1}{W_{L}}+\frac{Y_{R}}{\gamma_{R}-1} \frac{1}{W_{R}}}{\frac{Y_{L}}{W_{L}}+\frac{Y_{R}}{W_{R}}}\right) p $ | (2) |
其中WL和WR分别是作用物质的摩尔质量。对于这个模型,可以采用经典的有限体积方法或有限差分方法进行数值离散。但是大量数值结果表明,过界面的压力和速度无法继续保持常数。此即所谓的界面压力振荡现象。
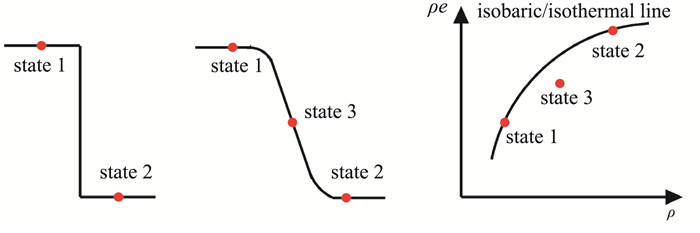
目前,此现象的数值机理已经很明确。即,传统的数值方法具有数值黏性,会产生界面处的数值扩散,导致界面处的不同介质进行了伪混合。在这种伪混合区域,数值方法计算出的压力和温度是不准确的。此过程可以用图 2更清晰地进行阐述。如图 2所示,初始状态1和状态2在等压线上,但是由于数值黏性的存在,界面处会产生新的混合状态3,而这个新状态如果不在等压线上,那么一定会出现压力振荡现象。
|
图 2 数值混合的不兼容性示意图 Fig.2 A diagram of incompatibility of numerical mixing |
在文献[11]中,作者证明,当介质具有p=Aρe+B(其中A和B是常数)这样类型的状态方程时,采用传统的高精度差分方法是可以实现单介质接触间断处压力无振荡属性。但是当介质具有非线性状态方程,或者多介质混合问题(两种气体的混合造成混合物的状态方程呈现非线性特点),接触间断/界面处一定会出现压力振荡现象。
1.2.2 数值方案引起的非物理振荡机制分析除了上述根本原因外,不同的数值方案会额外导致过界面非物理振荡。为此,我们以有限差分方法为例[12],开展了数值方案引起的非物理数值振荡的分析工作。
基于通量分裂的高精度差分方法[13],由于算法简单,容易实现高精度计算,因此得到了大量应用。我们在文献[11-12, 15]中详细分析了此套方案应用于多介质流动问题时引起的非物理振荡现象的数值机制。
考虑Abgrall提出的拟守恒方法[3]:
| $ \left\{\begin{array}{l} \frac{\partial \rho}{\partial t}+\frac{\partial \rho}{\partial x}=0 \\ \frac{\partial \rho u}{\partial t}+\frac{\partial\left(\rho u^{2}+p\right)}{\partial x}=0 \\ \frac{\partial \rho E}{\partial t}+\frac{\partial(\rho E+p) u}{\partial x}=0 \\ \frac{\partial}{\partial t}\left(\frac{1}{\gamma-1}\right)+u \frac{\partial}{\partial x}\left(\frac{1}{\gamma-1}\right)=0 \end{array}\right. $ | (3) |
通过求解最后一个非守恒方程,避免了使用混合封闭模式(2)。此方法的本质在于将原有的等温假设修正为等压假设。这种修正对多介质界面运动问题是合理的。对于拟守恒方法的控制方程,我们可以将其写为:
| $ \frac{\partial \boldsymbol{u}}{\partial t}+\frac{\partial \boldsymbol{f}}{\partial t}+\boldsymbol{h} \frac{\partial \boldsymbol{u}}{\partial x}=0 $ | (4) |
其中,
| $ \begin{array}{c} \boldsymbol{u}=(\rho, \rho u, \rho E, 1 /(\gamma-1))^{\mathrm{T}} \\ \boldsymbol{f}=\left(\rho u, \rho u^{2}+p, \rho E u+p u, 0\right)^{\mathrm{T}} \\ \boldsymbol{h}=\operatorname{diag}(0,0,0, u) \end{array} $ | (5) |
采用传统的基于通量分裂的高精度差分方法[13],可以得到如下的半离散形式:
| $ \frac{\mathrm{d} \boldsymbol{u}_{i}}{\mathrm{~d} t}=-\frac{\hat{\boldsymbol{f}}_{i+\frac{1}{2}}-\hat{\boldsymbol{f}}_{i-\frac{1}{2}}}{\Delta x}-\boldsymbol{m}_{i} $ | (6) |
其中,ui是一套网格间距为Δx的N点网格上i点处的值,
逐方程有限差分方法包括两步。第一步,采用某种通量分裂方法,将通量f分裂为正通量f+和负通量f-两部分。第二步,使用某种守恒型差分格式
| $ \hat{\boldsymbol{f}}_{i \pm \frac{1}{2}}=D_{i+\frac{1}{2}}^{+}\left[\boldsymbol{f}^{+}\right]+D_{i+\frac{1}{2}}^{-}\left[\boldsymbol{f}^{-}\right] $ | (7) |
对于逐特征场有限差分方法,需要在通量分裂后,通过局部特征分解后在每个特征场上应用差分格式获得相应的特征场数值通量,进而通过变换最终获得物理空间的数值通量。
在文献[12],我们系统分析了逐方程有限差分方法在求解多介质界面问题时存在的问题。
首先,假定采用的差分格式为线性格式,通过推导发现,传统的Steger-Warming通量分裂方法[14]无法保持界面处压力不振荡。只有Lax-Friedrichs类型通量分裂方法可以满足质量-动量-能量方程的分裂得到的正通量之间/负通量之间保持相容性,其中global Lax-Friedrichs通量分裂方法[13]是最简单有效的方法。具体推导参见文献[12]。
其次,在固定使用global Lax-Friedrichs通量分裂方法的情况下,有限差分方法需要采用非线性WENO差分格式[13]来计算各个方程的数值通量。但是,由于每个方程的通量的量级大小不同,每个方程所计算出的WENO格式的非线性权系数不同,进而导致质量-动量-能量方程所获得的数值通量之间不满足相容性,进而造成界面处的压力振荡现象。具体推导参见文献[12]。
进一步,为了使方程之间的非线性WENO离散具有兼容性,我们提出了一套“公共权”方案。即质量-动量-能量方程分别计算得到的WENO格式的非线性权修正为所有方程采用一套WENO权系数,这样就可以保证质量-动量-能量方程所获得的数值通量之间的兼容性。在文献[12]中,我们给出了一种具体的设计方法。但是更为鲁棒的公共权方法需要进一步研究。
最后,根据界面输运问题中速度和压力要保持常数这一原则,推导出了非守恒方程相容离散形式为:
| $ \begin{aligned} \frac{\mathrm{d} \phi_{i}}{\mathrm{~d} t}=& 0-\frac{u_{i}+\alpha}{2} \frac{D_{i+\frac{1}{2}}^{+}[\phi]-D_{i-\frac{1}{2}}^{+}[\phi]}{\Delta x}-\\ & \frac{u_{i}-\alpha}{2} \frac{D_{i+\frac{1}{2}}^{-}[\phi]-D_{i-\frac{1}{2}}^{-}[\phi]}{\Delta x} \end{aligned} $ | (8) |
其中,ϕ=1/(γ-1),α为global Lax-Friedrichs通量分裂方法中所取的全局常数。
对于双曲系统,逐特征场的有限差分方法更加匹配双曲系统。当使用局部特征分解时,我们发现[11, 15]:上述的WENO公共权方案的约束条件可以得到部分放松;质量-动量-能量方程之间的相容性会得到更好的保持。在文献[11]中,详细证明了只要非线性特征场和描述界面演化的线性场采用公共权技术,就可以实现过界面压力无振荡属性。但是设计满足这种条件的公共权技术仍然是一个悬而未决的问题。
基于前期的工作,我们在文献[15]中最终给出了避免界面压力振荡的有限差分方法的一般性的处理方案[15]。具体如下:
首先,将拟守恒方程写成“守恒+源项”的如下具体形式:
| $ \frac{\partial \boldsymbol{u}}{\partial t}+\frac{\partial \boldsymbol{f}}{\partial t}=s $ | (9) |
其中,
| $ \begin{array}{c} \boldsymbol{u}=\left(\rho, \rho u, \rho E, \frac{1}{\gamma-1}\right)^{\mathrm{T}} \\ \boldsymbol{f}=\left(\rho u, \rho u^{2}+p, \rho E u+p u, \frac{1}{\gamma-1} u\right)^{\mathrm{T}} \\ \boldsymbol{s}=\left(0,0,0, \frac{1}{\gamma-1} \frac{\partial u}{\partial x}\right)^{\mathrm{T}} \end{array} $ | (10) |
其次,在计算
| $ \boldsymbol{f}_{i}=\left(\begin{array}{c} (\rho u)_{i} \\ \left(\rho u^{2}+p\right)_{i} \\ (\rho E u+p u)_{i} \\ \left(\frac{1}{\gamma-1}\right) \hat{u}_{i+\frac{1}{2}} \end{array}\right) $ | (11) |
采用上述的方法结合局部特征分解技术可以保证界面输运问题压力-速度保持常数的属性,具体证明见文献[15]。
再其次,提出一个新的准则[15]“单介质保持准则”——多介质算法应能自动保持单介质流动属性。利用这个性质,推导出了源项的兼容离散形式为:
| $ \boldsymbol{s}_{i}=\left(\begin{array}{c} 0 \\ 0 \\ 0 \\ \left.\left(\frac{1}{\gamma-1}\right)_{i} \frac{\hat{u}_{i+\frac{1}{2}}-\hat{u}_{i-\frac{1}{2}}}{\Delta x}\right) \end{array}\right) $ | (12) |
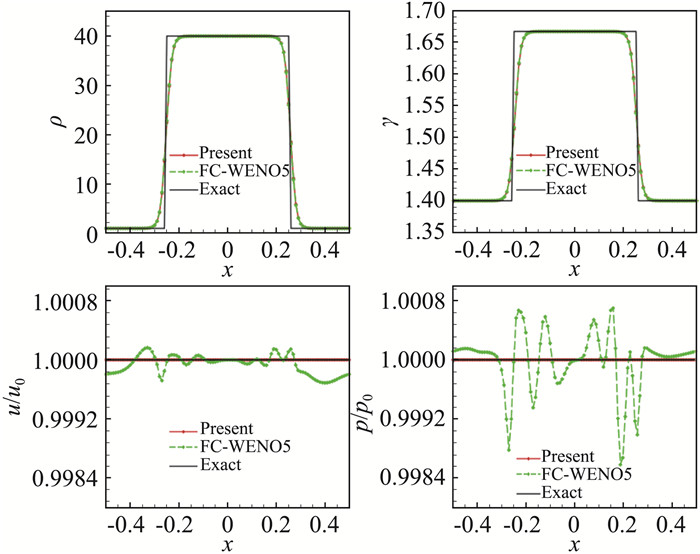
至此,就完成了新算法的推导过程。此推导过程清楚地表明, 新算法不需要对非保守项进行任何特殊处理。它成功地避免了设计WENO格式的公共权重技术。此外,它可以直接应用于任何差分格式,而不局限于WENO格式。更详细的内容请参考文献[15]。这里以如下的界面输运问题为例给出具体效果。此问题的初始条件为:
| $ (\rho ,u,p,\gamma ) = \left\{ {\begin{array}{*{20}{l}} {(40,1,1/1.4,1.667),}\\ {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} - 0.25 < x < 0.25}\\ {(1,1,1/1.4,1.4),{\rm{ }}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\rm{other }}} \end{array}} \right. $ |
此问题的具体设置见文献[15]。
从图 3中可以看出,采用五阶精度的WENO格式[13]的差分方法直接求解守恒型多组分方程时,速度和压力都会产生非物理数值振荡。相反,当使用新提出的算法求解拟守恒方法时,获得了与精确解的吻合较好的数值结果。
相比于只能采用通量分裂形式的有限差分方法,有限体积框架则具有更多的灵活性。如在重构过程中,可以采用原始变量、守恒变量、特征量变等。在计算通量的过程中,可以采用各种黎曼求解器、矢通量分裂方法等[16]。Abgrall在最初的文章中就使用了基于原始变量重构的有限体积方法。Johnsen[17]进一步确认了采用原始变量重构的有限体积方法可以有效避免数值框架带来的非物理数值振荡。
这里需要特别指出,Deng等提出的基于半点值的紧致型有限差分方法[18-19],由于可以借助有限体积中的重构和通量计算策略,因此也比较容易拓展应用于可压缩多介质流动问题的数值模拟中。对此问题,Nonomura等做了相关分析[20]。
1.3 非守恒方程相容离散在可压缩多介质流动问题中,我们会遇到一些额外类型的方程。典型的如上节里提到的对流方程。这类方程与传统的双曲守恒方程不同,它们无法写成守恒形式。从上一节的分析还可以看出:这类方法如果不恰当离散,同样会导致过界面的非物理振荡。因此对于一个包含守恒方程和非守恒方程的可压缩多介质流动问题的控制方程,需要进一步解决的问题是:当守恒方程采用确定的双曲守恒离散方法(如有限差分方法、有限体积方法)后,这些非守恒方程如何进行相容离散。
其实,在上一节数值框架的分析过程中,已经给出了一种有限差分方法框架下的离散方案。此外,对于有限体积方法,不同研究者也已经提出了一些不同方法[15, 17, 21]。最近,我们进一步拓展了此工作,给出了一套统一的离散方案。新方案自动兼容我们提出的有限差分离散方法[15]及其他部分研究者提出的有限体积离散方法[21]。此外,新方案还可以进一步导出一些黎曼求解器对应的新离散方案。关于这部分工作,详见文献[22]。
这里需要指出的是,针对一般性非守恒系统,Dal Maso、LeFloch和Murat的提出了DLM理论[49],其中跨间断的非守恒乘积项被定义为连接左右状态的沿路径积分。基于上述理论发展了所谓的路径守恒离散方案[50-51]。但是,这类方法在路径的选择、收敛性等方面还没有确切结论[52],仍需进一步发展。
1.4 高精度有界数值格式构造不同于单介质欧拉方程和N-S方程,可压缩多介质流动的物理模型中会涉及其他类型的物理量,如质量分数、体积分数。这类物理量有着明确的上界和下界,直接影响界面混合封闭模式的精准执行。因此,在对可压缩多介质流动问题进行模拟时,我们不仅需要考虑热力学量的保正问题,还得同时考虑如质量分数这类物理量的保界问题。因此,除了要求具备高精度、基本无振荡属性等基本性质外,如何实现物理量的保界/保正要求是我们选择和构造可压缩多介质流动问题的高精度数值格式的额外指导原则。
目前,经数值实验验证比较成功的高精度数值格式为WENO类型格式[13]。这类格式在实现高精度计算的同时,也实现了对各种间断结构的基本无振荡捕捉。但是WENO格式同样存在一些缺点:如WENO-JS格式耗散偏大,导致对一些多尺度问题(如激波-湍流边界层干扰问题、声学问题)的计算效率过低。为此,相关研究者进行了大量的探索。提出了诸如WENO-M[23]、WENO-Z[24]、TENO[25]、杂交方法[26-27]等各种方法。
除了上述经典方法外,其实还有其他一些类型格式。如:高精度保单调格式(monotonicty-preserving, MP)[28]。这种格式的基本思想为:首先采用任意类型高精度格式预估一个初始结果;其次通过构造局地的上界和下界,形成一个局地的区间;最终通过探测初始结果是否落入此区间内,决定是否对预估的初始结果进行进一步处理。这类格式继承了TVD类型格式的保界思想,并进一步拓展至高精度计算[29-30]。
因为WENO格式不具备保界性,Balsara在2000年提出了MPWENO格式[31]。其基本思想是用WENO格式预估初始结果,然后用MP格式构造的局地上界和下界来对初始结果进行进一步限制,从而实现保界性。
在2016年,我们发现[32],MP格式的局地上界和下界的设计方法会导致形成的区间过大,无法抑制一些数值振荡。这些数值振荡会持续传播,最终导致MP格式的稳定性较差。上述发现也得到了进一步工作的证实[33]:“It was recently found that this limiting procedure is no longer accurate for long - term integrations. As indicated by He et al., the major problem arises mostly due to the use of considerable amounts of room for the MP constraint, resulting in either problem-dependent solutions or abundant room for the growth of spurious oscillations”。结合TVD有界理论,我们给出了一种改进版本的MP格式[32],即MP-R格式。数值实验表明改进的局地保界方案可以较为显著地提高最终方案的健壮性。
由于保界/保正要求对于模拟多介质问题至关重要,我们自然希望计算法自动实现这个要求。因此,上述基于保界思想构造的MP格式是一类比较适用于可压缩多介质流动问题的方法。但是,对于非线性问题而言,这种先验性的保界/保正算法不具备普适性。因此,为了进一步提升算法的保界性和保正性,可以进一步采用最新发展的保界/保正处理方法,如Postivity-Preserving方法[34]、Multi-dimensional Optimal Order Detection(MOOD)方法[35]。
1.5 界面压缩扩散界面方法是将界面视为数值扩散的狭窄区域,比如气体动力学中的数值模拟所捕捉的接触间断。因此造成的结果是——数值界面会一直弥散变宽。并且随着计算时间的增加,这种弥散变宽现象会越来越严重,最终可能会导致影响流动的其他物理结构[36]。因此,如何避免或抑制界面的持续弥散变宽问题,一直是可压缩多介质流动问题界面捕捉算法的一个研究重点。
一个自然的想法是发展高精度间断捕捉数值格式。在同样的网格上,高精度间断捕捉格式可实现高阶精度计算,对间断的分辨能力也显著提高。但是文献[37]中发现,采用高精度间断捕捉格式,虽然可以在一定程度上提高间断/界面的分辨能力,但依旧无法抑制长时计算情况下的界面弥散变宽问题。此外,由于高精度间断捕捉格式引入的数值耗散较小,因此结果具有更多的数值振荡。为了抑制这些数值振荡,虽然可以采用局部特征分解方法来获得基本无振荡结果,但如果物质由非常复杂的状态方程(EOS)所描述,如何构造一个稳定且与物理模型兼容的局部特征分解方法仍需要进一步探索[37]。
总之,采用高精度格式依旧无法抑制长时计算情况下的界面弥散变宽问题。此外,还会带来可能的数值振荡[37]。
因此,即使采用了高精度间断捕捉格式来进行计算,界面压缩算法也是必须的[37]。目前,相关研究者提出了各种界面压缩/反耗散算法[36-39, 53]。这些方法可以大致分为四类:(1) 限制型下游格式方法[53]。这种方法的基本思想是在满足TVD稳定性理论的基础上尽可能使用下游格式。目前仅适用于Lagrange-Remap方案。(2) 反扩散方法[54]。这类方法的基本思想是直接求解反扩散方程从而实现界面压缩。(3) 基于修改重构过程的代数型VOF方法,如基于双曲正切函数发展的界面捕捉算法(THINC)[38-39]。(4) 界面重整化(又叫扩散-锐利化)方法[36]。这类方法的基本思想是添加恰当的扩散项和锐利化项,从而保证界面的数值解是收敛的(宽度不随计算时间增加而变宽)。目前这几类方法推广应用到可压缩多介质问题时,均会遇到一个共同且依旧没有彻底解决的问题——当描述界面演化的方程(如体积分数方程)采用上述界面压缩方法后,其他方程(质量-动量-能量方程)如何进行相容的压缩。前三类方法为了实现相容压缩,目前已有的方案仅有一阶精度,我们的数值实验证实过低的精度可能会抑制界面的大变形运动。第四类方法的相容压缩方法已经从理论上得到解决(针对五方程模型[43]),但是目前这类方法添加的扩散项和锐利化项均来源于level set方法[55]或相场方法[56],如何设计和离散这些项(稳定且保界)目前还没有得到彻底解决[57]。
为了易于实现高精度计算且避免如何设计扩散项和锐利化项的问题,在文献[37]中,针对五方程模型[40-41],我们提出了一种基于界面压缩方案(第三类和第四类方法的杂交方案)。
考虑如下两种物质的五方程模型[40]:
| $ \begin{array}{c} \frac{\partial \rho_{1} \alpha_{1}}{\partial t}+\nabla \cdot\left(\rho_{1} \alpha_{1} \boldsymbol{u}\right)=0 \\ \frac{\partial \rho_{2} \alpha_{2}}{\partial t}+\nabla \cdot\left(\rho_{2} \alpha_{2} \boldsymbol{u}\right)=0 \\ \frac{\partial \rho \boldsymbol{u}}{\partial t}+\nabla \cdot(\rho \boldsymbol{u} \boldsymbol{u})+\nabla p=0 \\ \frac{\partial \rho E}{\partial t}+\nabla \cdot((\rho E+p)\boldsymbol{u})=0 \\ \frac{\partial \alpha_{1}}{\partial t}+\boldsymbol{u} \cdot \nabla \alpha_{1}=0 \end{array} $ | (13) |
其中,ρ、u、E、p分别为混合物密度、速度、总能和压力,ρk、αk分为是第k种物质的相密度和体积分数。其中体积分数满足α1+α2=1。上述方程可以写成(以一维情况为例):
| $ \begin{array}{l} \frac{\partial \boldsymbol{V}}{\partial t}+\frac{\partial \boldsymbol{f}(\boldsymbol{V})}{\partial x}=0 \\ \frac{\partial \alpha_{1}}{\partial t}+\boldsymbol{u} \frac{\partial \alpha_{1}}{\partial x}=0 \end{array} $ | (14) |
其中V=(ρ1α1, ρ2α2, ρu, ρE)T。
采用标准的有限体积方案,上述方程可以离散为:
| $ \begin{array}{c} \frac{\partial \overline{\boldsymbol{V}}_{i}}{\partial t} &=-\frac{\hat{\boldsymbol{f}}_{i+\frac{1}{2}}-\hat{\boldsymbol{f}}_{i-\frac{1}{2}}}{\Delta x} \\ \frac{\partial \bar{\alpha}_{1, i}}{\partial t} &=-\frac{\hat{\alpha}_{1, i+\frac{1}{2}}-\hat{\alpha}_{1, i-\frac{1}{2}}}{\Delta x} \end{array} $ | (15) |
其中,Vi、α1, i是物理量V、α1在计算单元Ii上的单元平均值。采用恰当的重构方法(如上述WENO方法、MP方法等),可获得单元边界的左右重构状态,进一步采用各种黎曼求解器来计算出单元边界的数值通量。从而完成空间离散过程。
提出的界面压缩方案主要包括两部分[37]:
1) 界面压缩物理量的选择。针对五方程模型,采用了如下的原始变量进行(相密度、速度、压力、体积分数)重构[37](可进一步投影至特征空间进行重构),来获得单元边界的左右重构状态:
| $ \begin{array}{l} \breve{\boldsymbol{W}}_{i+\frac{1}{2}}^{\mathrm{L}}=\left(\rho_{1, i+\frac{1}{2}}^{L}, \rho_{2, i+\frac{1}{2}}^{L}, u_{i+\frac{1}{2}}^{L}, p_{i+\frac{1}{2}}^{L}, \alpha_{1, i+\frac{1}{2}}^{L}\right)^{\mathrm{T}} \\ \breve{\boldsymbol{W}}_{i+\frac{1}{2}}^{R}=\left(\rho_{1, i+\frac{1}{2}}^{R}, \rho_{2, i+\frac{1}{2}}^{R}, u_{i+\frac{1}{2}}^{R}, p_{i+\frac{1}{2}}^{R}, \alpha_{1, i+\frac{1}{2}}^{R}\right)^{\mathrm{T}} \end{array} $ | (16) |
对于这些物理量,可采用上述的各种高精度数值格式进行计算。具体内容详见文献[37]。
上述方案不具备界面压缩效应。为了引入界面的压缩效应(即采用THINC格式进行计算),需要对上述的标准方案进行改进。对何种物理量采用界面压缩是需要考虑的首要问题。在文献[37]中提出了如下方案:只对体积分数采用THINC格式进行计算,从而获得的单元边界的左右重构状态。
| $ \begin{aligned} \breve{\boldsymbol{W}}_{i+\frac{1}{2}}^{L} &=\left(\rho_{1, i+\frac{1}{2}}^{L}, \rho_{2, i+\frac{1}{2}}^{L}, u_{i+\frac{1}{2}}^{L}, p_{i+\frac{1}{2}}^{L}, \breve{\alpha}_{1, i+\frac{1}{2}}^{L}\right)^{\mathrm{T}} \\ \breve{\boldsymbol{W}}_{i+\frac{1}{2}}^{R} &=\left(\rho_{1, i+\frac{1}{2}}^{R}, \rho_{2, i+\frac{1}{2}}^{R}, u_{i+\frac{1}{2}}^{R}, p_{i+\frac{1}{2}}^{R}, \breve{\alpha}_{1, i+\frac{1}{2}}^{R}\right)^{\mathrm{T}} \end{aligned} $ | (17) |
可以看到,在这里获得的单元边界的左右重构状态时,除了体积分数采用了其他类型界面压缩方法来计算,其他物理量均采用原高精度数值格式方案来进行计算。
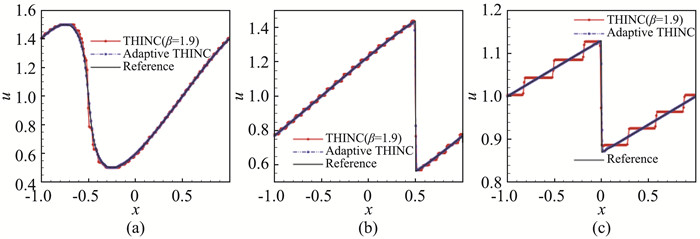
提出上述方案的基本思想主要基于两点考虑:①我们知道,物质界面/接触间断是一类非常特殊的流动结构。各种物理量过界面的表现性质不一样。我们可以把这些物理量分为快变量和慢变量。其中慢变量定义为过界面连续的物理量。与之相反,快变量定义为过界面存在间断的变化剧烈的物理量。从这个分类可以看出,上述五方程模型中,相密度、速度、压力均是慢变量,而只有体积分数是快变量。②仅对快变量做界面压缩方法。这个观点是基于如下事实:我们发现,界面压缩方法,尤其是THINC类型的具有反耗散性质的方法,存在一个问题:这类方法可以使光滑的物理结构被反物理地压缩成锯齿状间断结构[42]。如图 4所示,当采用THINC格式对Burgers方程进行计算时,反耗散方法对间断结构的分辨率非常高。但如果在光滑区也采用THINC方法,光滑的物理结构亦被非物理地压缩为间断结构。关于这个问题的讨论,详见最新的文献[42]。基于这样的实际情况,可以得出如下结论:界面压缩只能应用于快变量。正是基于上述观点,我们提出了仅对体积分数进行压缩处理的界面压缩方案。
|
图 4 采用THINC格式计算Burgers方程[42] Fig.4 Solutions of the non-linear Burgers equation obtained by the THINC scheme[42] |
2) 相容性。大量数值实验表明:上述方案在工程计算中可以取得较好的计算结果,这种方案也可以应用于其他模型。我们所需要做的仅仅是:①选择重构的原始变量;②对这些原始变量进行区分:快变量还是慢变量;③对快变量进行界面压缩处理。表 1给出了四方程模型和五方程模型的一些典型快变量和慢变量。
| 表 1 四方程模型和五方程模型的一些典型快变量和慢变量 Table 1 Some fast and slow variables of four- and five-equation models |
|
|
虽然工程应用上大致可行,但上述方案不能从理论上证明所有方程之间是否严格相容,从而能保持界面/接触间断处的特殊性质(这类间断属于线性场,速度、压力等物理量过界面保持不变)。针对五方程模型,Tiwari[43]从理论上严格证明,质量方程、动量方程、能量方程、体积分数方程之间存在定量的相容关系。当体积分数方程存在界面压缩项时,其他所有方程必需要添加相容的一些界面压缩项。因此,为了实现方程之间的严格相容,我们[37]进一步提出了将上述两种方案的差做为体积分数的源项Si*=σiSi,这里:
| $ \begin{array}{c} \sigma_{i}=\left\{\begin{array}{l} 1-\frac{\left|\bar{\alpha}_{1, i+1}-2 \bar{\alpha}_{1, i}-\bar{\alpha}_{1, i-1}\right|^{q}+\zeta}{\left(\left|\bar{\alpha}_{1, i+1}-\bar{\alpha}_{1, i}\right|+\left|\bar{\alpha}_{1, i}-\bar{\alpha}_{1, i-1}\right|\right)^{q}+\zeta} \\ \ \ \ \ \ \ \ \ \ \ \ \ , \text { if }\ \varepsilon \leqslant \bar{\alpha}_{1, i} \leqslant 1-\varepsilon\\ 0\ \ \ \ \ \ \ \ \ \ ,\text {otherwise} \end{array}\right. \\ \begin{array}{c} S_{i}=\left[-\frac{\hat{\alpha}_{1, i+\frac{1}{2}}\left(\breve{\boldsymbol{W}}_{i+\frac{1}{2}}^{L}, \breve{\boldsymbol{W}}_{i+\frac{1}{2}}^{R}\right)-\hat{\alpha}_{1, i-\frac{1}{2}}\left(\breve{\boldsymbol{W}}_{i-\frac{1}{2}}^{L}, \breve{\boldsymbol{W}}_{i-\frac{1}{2}}^{R}\right)}{\Delta x}\right]+ \\ {\left[\frac{\hat{\alpha}_{1, i+\frac{1}{2}}\left(\boldsymbol{W}_{i+\frac{1}{2}}^{L}, \boldsymbol{W}_{i+\frac{1}{2}}^{R}\right)-\hat{\alpha}_{1, i-\frac{1}{2}}\left(W_{i-\frac{1}{2}}^{L}, W_{i-\frac{1}{2}}^{R}\right)}{\varDelta x}\right]} \end{array} \end{array} $ | (19) |
其中,q是一个人为设定参数,ζ是一个避免分母为0的小量。ε≤α1, i≤1-ε是用于判定界面位置的常用方法,从而保证压缩操作仅在界面处的狭窄区域。
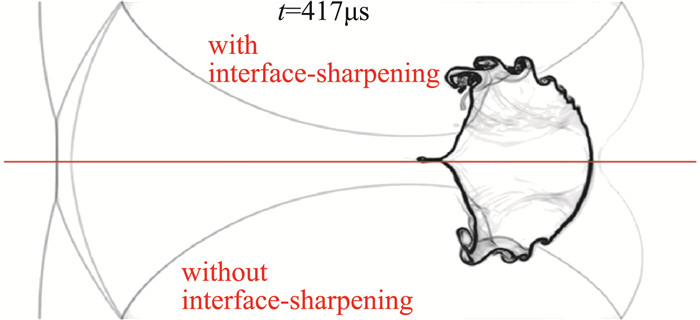
有了上述的体积分数方程的源项,就可以直接利用Tiwari的理论结果:在质量方程、动量方程、能量方程上加入能严格保证相容的源项。具体表达式详见文献[37]。图 5给出了激波-气泡干扰问题(具体设置参见文献[37])的模拟结果(有/无界面压缩情况)。
从图 5中可以看到,采用了界面压缩方法后,界面的分辨率得到显著提高。此外,数值结果亦表明界面的宽度基本不随时间增加而变宽[37]。
但是,上述方法也存在一定的缺陷——最终的方案不是严格守恒[43]。此外,文献[37]中指出,在实际应用中,不同近似黎曼求解器带来的数值耗散不一样。而由这部分因素带来的数值耗散不能仅通过修改重构方法而彻底回避。因此,如何构造守恒且相容的界面压缩方法仍值得进一步深入研究。
1.6 界面-单介质分区计算方案开展可压缩多介质流动问题数值模拟时,由于我们采用的模型为扩散界面模型。其本质假设是每一空间点上同时存在多种介质,介质之间满足一定的关系(如压力平衡-温度非平衡假设)。因此为了避免模型的退化,必须在纯流体中添加一个小的体积分数[37]。
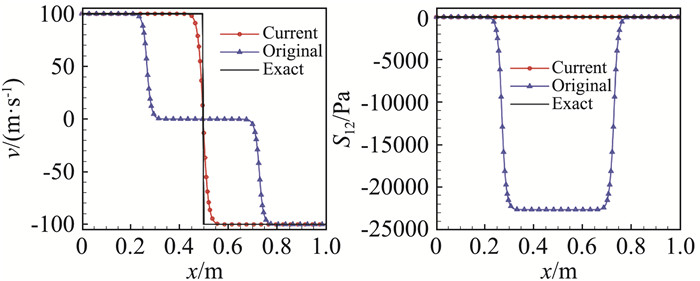
在文献[44-45]中我们发现,这种人为处理方法会给计算带来非物理的波。这种现象在考虑弹塑性-流体相互作用的问题时尤为明显:①在流体中添加小部分固体,会让流体产生抵抗剪切的能力;②固体和流体的声速差异很大,即使是一小部分的固体,也会影响纯流体的声速。在此发现基础上,我们提出了一个改进的压力平衡-温度非平衡扩散界面模型,该模型在等压缩假设的基础上,导出了和体积分数无关的相密度方程。采用该模型,即使体积分数为0,也不会导致方程退化,避免了非物理波的产生。图 6给出了新模型和旧模型模拟纯剪切问题的对比,新模型可以保持住剪切间断,不产生额外的剪应力。而采用原模型,必须在方程中添加小的体积分数,导致虚假剪切应力的产生,以及剪切波向两侧扩散。但上述方案是否能推广到实际工程应用中,还需进一步探索。
另一种解决方案是采用区域分解这类典型的多尺度问题计算方案。即将计算区域分解为纯物质区和界面区,不同区域采用不同的方案进行计算。其实,在上一节构造界面压缩算法过程中,已经人为地区分了界面区域和纯物质区域。相关数值实验亦证实了此方案的可行性。但界面区域与纯物质区域的边界处是否会人为引入一些非物理波,这一问题还需要更深入的研究。
2 应用通过上述多个维度的工作,建立了一套适用于可压缩多介质流动问题的低耗散、基本无数值振荡的高精度欧拉方法。相关数值方法成果已集成至工程问题数值模拟软件,为相关工程任务提供了重要技术支撑。在具体应用方面,不同的问题往往具有自身的特殊性,需要有针对性地选择不同的具体离散方案进行应用。本小节给出几个具体应用算例。
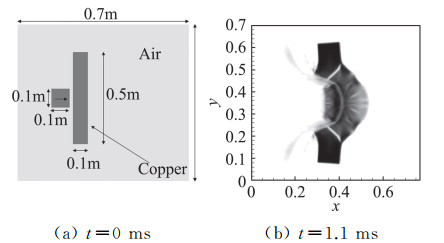
第一个算例是弹塑性介质的高速冲击问题。金属等固体材料在受到高速冲击后,会发生弹性到塑性的转变,甚至产生断裂、破碎等复杂的物理现象,对数值模拟提出了极大的挑战。我们基于上述五方程模型,采用有限差分方法、高精度(MP)WENO格式、非守恒离散方法以及结合界面压缩技术,并进一步对弹塑性效应进行了建模和数值离散,成功地实现了对此类问题的模拟。图 7给出了如下问题的数值模拟结果:铜块以800 m/s的初始速度冲击一个静止的铜靶,铜靶先后经历弹性变形、塑性变形,最终发生断裂和射流现象。相关结果和已有的文献结果一致。
|
图 7 铜块冲击铜靶问题 Fig.7 The impact of a copper projectile on a copper plate |
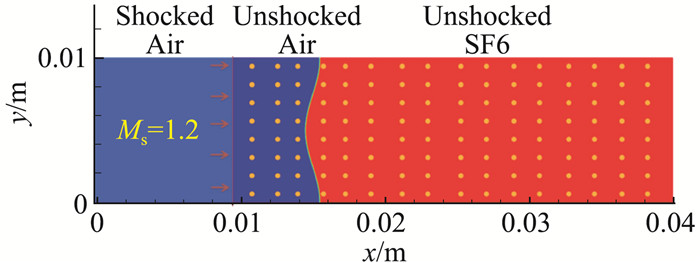
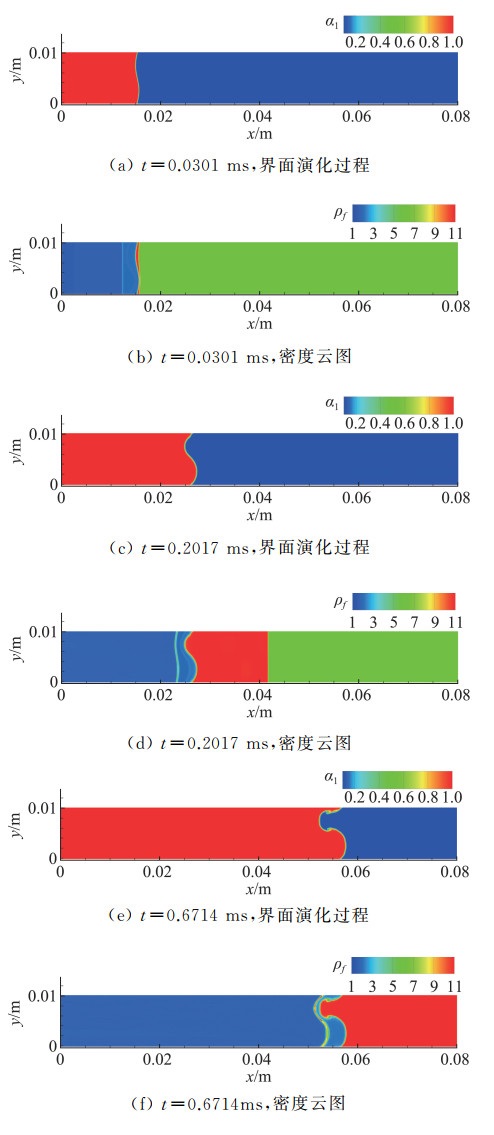
第二个算例是含颗粒Richtmyer-Meshkov(RM)不稳定性问题[9]。激波驱动的多相流动(如气固多相流)中经常伴随着多相流RM不稳定性的的发生。在气固两相流动体系中,颗粒相在流动体系中显著影响了界面的动力学行为。我们基于上述五方程模型,采用有限体积方法、高精度(MP)WENO格式、非守恒离散方法,并进一步对跨流态颗粒运动进行了数值建模(CMP-PIC方法[9]),成功实现了对此类问题的数值模拟。图 8具体给出了模拟的含空气/SF6的多相RM问题(其中颗粒均匀分布于空间)问题的具体情况:空气以及SF6界面存在单模扰动,入射激波由空气进入到SF6区域。颗粒均匀布置于计算域,其分布区域为:0.01 m < x < 0.04 m。初始时界面形状受扰动。颗粒密度为50 kg/m3,颗粒的尺度设置为1 μm。由此计算得到的颗粒响应时间为1×10-7s,流体特征时间τc≈10-5,Stoke数约为0.01,颗粒跟随性良好。不同时刻界面演化形态如图 9所示。
|
图 8 计算域示意图 Fig.8 The computational domain visualized by the density |
|
图 9 不同时刻RMI流场演化 Fig.9 The temporal evolution of the RMI |
图 10进一步给出了颗粒不同体积分数下混合区宽度随时间衍化结果。详细的数据在表 2中给出。其中,αp, ini是初始的颗粒相体积分数,αp0+是激波波后的颗粒相体积分数。由于激波的压实作用,αp0+略大于αp, ini。需要说明的是,Case A属于颗粒稀疏的气固流动,Case B-F属于颗粒稠密的气固流动。ADm+是Atwood数模型,其由激波波后的参量所决定。dh/dt为混合区的线性增长速率,由理论计算式所得到。dhCFD/dt为数值计算结果。我们选择了0.12~0.22 ms的数据用于数值计算结果的拟合分析。不论是颗粒稀疏或者稠密的情况,数值计算结果与理论计算结果呈现很好的一致性。随着颗粒体积分数增加,扰动增长速率下降,也就是说,颗粒的存在抑制了RM的发展。

|
图 10 不同颗粒体积分数下混合区宽度随时间演化 Fig.10 The temporal evolution of the mixing zone widths for cases with different volume fractions of particles |
| 表 2 不同体积分数下混合区宽度数值及理论预测比较 Table 2 Comparison between the numerical results and theoretical predictions of the mixing zone width |
|
|
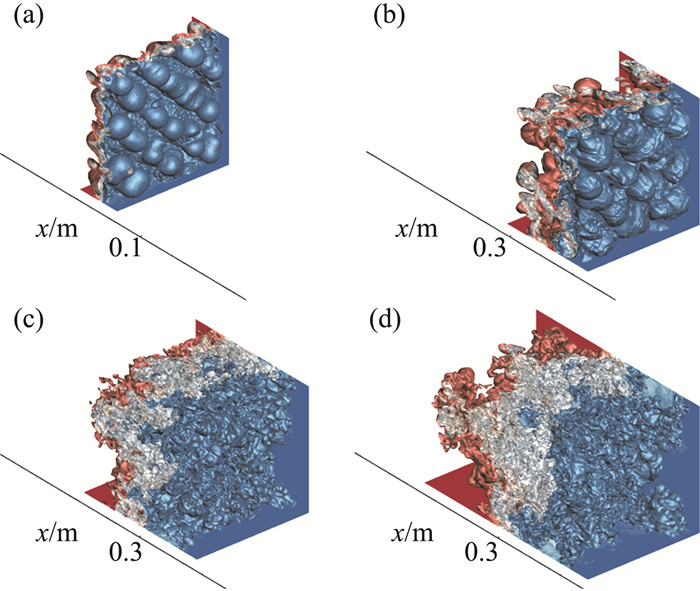
第三个算例为含激波二次冲击的RM湍流混合问题[46]。含激波冲击的湍流混合问题是工程应用及自然现象中的基本物理过程,其典型特点是波系与混合区的多次作用。针对该问题,开展了直接数值模拟研究,采用了四方程模型,并且由于考虑物理黏性,所以没有使用界面压缩技术。并且采用的网格规模达到11亿。初始激波从轻流体向重流体传播,透射激波在下游壁面反弹后二次作用于混合区,混合区快速湍流化(如图 11所示),随后混合区依次被稀疏波和压缩波加速。稀疏波和压缩波作用期间,混合区内形成了明显的平均速度梯度,混合区被拉伸或者压缩。采用混合宽度无量纲化的平均组分剖面在二次激波作用后基本保持不变。借助高精度直接数值模拟结果,对多介质湍流的生成、衰减过程进行了收支平衡分析。结果表明,在稀疏波和压缩波作用阶段,速度梯度生成项和压力梯度生成项是主导项。压力梯度生成项和速度梯度生成项的贡献相反,前者的幅值更大。因此,稀疏波导致湍动能增强而压缩波导致湍动能减弱。进一步统计了含能结构的尺度变化。结果表明,混合宽度的增长伴随着大尺度结构的形成,稀疏波阶段,结构被纵向拉伸,而压缩波作用阶段,结构被纵向压缩。
|
图 11 三维质量组分等值面的时间演化[46]. (a) t=0.0005 s和(b) t=0.0002 s为二次激波作用前;(c) t=0.003 s和(d) t =0.0045 s为二次激波作用后 Fig.11 The temporal evolution of the three-dimensional iso-surfaces of mass fraction[46] of air (a) before reshock at t=0.0005 s, (b) t=0.0002 s, (c) after reshock at t=0.003 s, and (d) t=0.0045 s. Orange, light pink, silver, and blue correspond to mass fractions of the air being 0.9, 0.6, 0.4, and 0.1 |
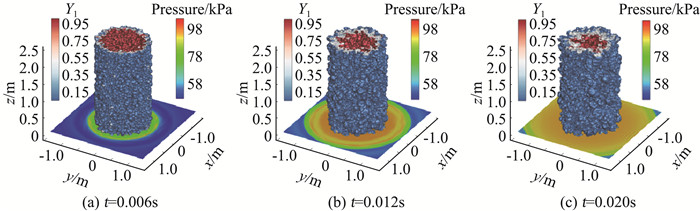
最后一个算例是汇聚几何不稳定及湍流混合问题。在实际工程应用中,RM湍流混合往往发生在不断向中心汇聚(如柱面、球面等)的物质界面上。相比于平面界面上的RM湍流混合,汇聚界面上的RM湍流混合区在演化过程中会伴随有其周向长度的改变,而这种改变将会深刻影响混合区的后续发展。针对该问题,基于集成上述方案所开发的模拟程序(具体方案同上一个算例),对圆柱界面上的RM不稳定性开展了数值模拟研究。初始激波由外部的重流体向内部的轻流体传播,并在随后往复运动于几何中心和混合区之间,使得激波多次作用于混合区,混合区快速湍流化(如图 12所示)。对于混合区宽度,其演化被分解为混合区整体的拉伸压缩和两种流体组分相互穿插两部分的贡献。通过与平面算例进行对比,我们发现向内汇聚的物质界面将整体拉伸混合区,并在同时促进两种流体的相互穿插。在激波第三次冲击混合区之后,轻重流体穿插效应所贡献的混合宽度W满足W∝(t-t0)θ,这与平面工况中混合宽度的自相似增长相类似。对于混合区内部的平均组分剖面,经过混合区宽度归一化的曲线近似重合。通过统计混合区前沿位置的分布,本文计算了气泡和尖钉结构各自的直径演化。数值结果表明,气泡和尖钉的直径与其对应的混合区高度之比在演化后期趋近于常数。
|
图 12 三维质量组分等值面的时间演化. (a) t=0.006 s为二次激波冲击后,三次激波冲击前和(b) t=0.012 s为三次激波作用后;(c) t=0.020 s为激波强度衰减至可以忽略后 Fig.12 The temporal evolution of the three-dimensional iso-surfaces of mass fraction of air (a) between the second and the third reshock at t=0.006 s, (b) after the third reshock at t=0.012 s, and (c) when the strength of the shock wave is negligible at t=0.020 s |
从以上的算例可以发现,实际工程问题往往都是耦合多种物理因素和过程的多尺度多物理复杂流动问题。因此为了更好地模拟实际工程问题,我们需要进一步考虑黏性[58-59]、热传导[60-61]等耦合物理效应(更多物理效应见Saurel的系列工作及其综述[62]),以及弹塑性[63-64]、辐射扩散[65]等多物理耦合过程。即需进一步研究上述可压缩多介质数值方法在这类多物理效应/过程情况下的适用性问题。但是到目前为止,这一方面的研究还远不够成熟,我们的研究工作也正在进一步开展。
3 结论建立一套高效的可压缩多介质流动问题的高精度数值模拟方案是一个系统工程,其中涉及的因素较多,主要有:数值框架选择、非守恒方程相容离散、高精度有界格式构造、界面压缩、界面-单介质分区计算方法等。本文从上述维度出发,综述了本研究方向以及课题组的一些工作。主要结论有:
1) 不同数值方案可能导致过界面出现非物理振荡现象。因此,不管选用何种类型的数值方案,必需对此方案在可压缩多介质流动问题中的适用性先进行分析。为此,我们针对有限差分方法在此类问题中的适用性进行了分析。
2) 非守恒类型方程必需现相容离散。当守恒方程采用确定的双曲守恒离散方法(如有限差分方法、有限体积方法)后,非守恒方程如何进行相容离散。这类方法如果离散不恰当,同样会导致过界面的非物理振荡。针对此问题,我们提出了一套相对普适的离散方案。
3) 保界/保正是构造适用于可压缩多介质流动问题的高精度格式的重要要求。因为在对可压缩多介质流动问题进行模拟时,不仅需要考虑热力学量的保正问题,还得同时考虑如质量分数这类物理量的保界问题。为此,我们改进了经典的保单调限制器,进一步提升了此算法的保界性能。
4) 在扩散界面模型框架下,界面会一直数值弥散变宽,并且随着计算时间的增加,这种弥散变宽现象会越来越严重。为了避免或抑制界面的持续弥散变宽现象,我们提出了一种界面压缩方法。
5) 界面-单介质分区计算方案。为了避免模型的退化,必须在纯流体中添加一个小的体积分数。我们发现,文献上常用的这种方法会带来非物理的波。因此,我们建议采用区域分解的这种多尺度计算方法,开展界面-单介质的分区计算。但如何保证边界处不产生非物理振荡需要进一步研究。
通过上述多个维度的工作,我们建立了一套适用于可压缩多介质流动的低耗散、基本无数值振荡的高精度欧拉方法,相关数值方法成果已集成至工程问题数值模拟软件,为相关工程任务提供了重要技术支撑。
由于实际工程问题往往都是耦合其他效应和过程的多尺度多物理问题。因此,为了进一步提高模拟的置信度,需要进一步研究的工作有:
1) 多物理效应和多物理过程的建模与计算方案。即需进一步研究“在上述多尺度多物理问题情况下的多介质数值方法的适用性”问题。比如当存在物理黏性时,界面压缩能否与物理黏性自洽识别、可溶与不可溶界面的能否自动区分等问题。典型的进展如最近Xiao等最近提出了Boundary Variation Diminishing (BVD)算法[66],在此方面做了较为成功的尝试。
2) 极端条件下的数值算法研究。相比单介质问题,多介质问题往往更容易遇到各种极端条件(如复杂状态方程、非牛顿流体、固体的弹塑性效应与超低马赫数效应、物性差异巨大等),目前的计算流体数值方法能否适用于这些极端情况、以及如何优化改进现有算法值得进一步研究。
3) 高效的大规模计算软件研发。可压缩多介质问题中流场每一空间点可能为单介质或多介质,如何构造一种高效表征多介质流动问题的数据结构,以及大规模并行计算情况的下的如何荷载平衡等问题,均对软件研发提出了挑战。此外,多介质问题的各类模型并没有经过大量大规模并行计算的测试与检验,进一步对研发高效的大规模计算软件提出了需求。
| [1] |
LUND H. A hierarchy of relaxation models for two-phase flow[J]. SIAM Journal on Applied Mathematics, 2012(72): 1713-1741. |
| [2] |
SAUREL R, PETITPAS F, BERRY. A simple and efficient relaxation methods for interfaces separating compressible fluids, cavitating flows and shocks in multiphase mixtures[J]. Journal of Computational Physics, 2009, 228: 1678-1712. DOI:10.1016/j.jcp.2008.11.002 |
| [3] |
ABGRALL R. How to prevent pressure oscillations in multicomponent flow calculations: A quasi conservative approach[J]. Journal of Computational Physics, 1996, 125: 150-160. DOI:10.1006/jcph.1996.0085 |
| [4] |
SAUREL R, ABGRALL R. A simple method for compressible multifluid flows[J]. SIAM Journal on Scientific Computing, 1999, 21: 1115-1145. DOI:10.1137/S1064827597323749 |
| [5] |
SHYUE K. An effcient shock-capturing algorithm for compressible multicomponent problems[J]. Journal of Computational Physics, 1998, 142: 208-242. DOI:10.1006/jcph.1998.5930 |
| [6] |
DREW D. Mathematical modeling of two-phase flow[J]. Annual Review of Fluid Mechanics, 1983, 15: 261-291. DOI:10.1146/annurev.fl.15.010183.001401 |
| [7] |
BAER M, NUNZIATO J. A two-phase mixture theory for the deflagration-to-detonation transition (DDT) in reactive granular materials[J]. International Journal of Multiphase Flows, 1986, 12: 861-889. DOI:10.1016/0301-9322(86)90033-9 |
| [8] |
SAUREL R, ABGRALL R. A multiphase Godunov method for compressible multifluid and multiphase flows[J]. Journal of Computational Physics, 1999, 150: 425-467. DOI:10.1006/jcph.1999.6187 |
| [9] |
TIAN B, ZENG J, MENG B, et al. Compressible multiphase particle-in-cell method (CMP-PIC) for full pattern flows of gas-particle system[J]. Journal of Computational Physics, 2020, 418: 109602. DOI:10.1016/j.jcp.2020.109602 |
| [10] |
ANDRIANOV N, WARNECKE G. The Riemann problem for the Baer-Nunziato two-phase flow model[J]. Journal of Computational Physics, 2004, 195: 434-464. DOI:10.1016/j.jcp.2003.10.006 |
| [11] |
HE Z, ZHANG Y, LI X, et al. Preventing numerical oscillations in the flux-split based finite difference method for compressible flows with discontinuities, Ⅱ[J]. International Journal for Numerical Methods in Fluids, 2016, 80: 306-316. DOI:10.1002/fld.4080 |
| [12] |
HE Z, ZHANG Y, LI X, et al. Preventing numerical oscillations in the flux-split based finite difference method for compressible flows with discontinuities[J]. Journal of Computational Physics, 2015, 300: 269-287. DOI:10.1016/j.jcp.2015.07.049 |
| [13] |
JIANG G, SHU C W. Efficient implementation of weighted ENO schemes[J]. Journal of Computational Physics, 1996, 126: 202-228. DOI:10.1006/jcph.1996.0130 |
| [14] |
STEGER J L, WARMING R F. Flux vector splitting of the inviscid gas dynamic equations with applications to finite difference methods[J]. Journal of Computational Physics, 1981, 40: 263-293. DOI:10.1016/0021-9991(81)90210-2 |
| [15] |
HE Z, LI L, ZHANG Y, et al. Consistent implementation of characteristic flux-split based finite difference method for compressible multi-material gas flows[J]. Computers and Fluids, 2018, 168: 190-200. DOI:10.1016/j.compfluid.2018.04.007 |
| [16] |
TORO E. Riemann solvers and numerical methods for fluid dynamics[M]. Springer, Berlin, 1999
|
| [17] |
JOHNSEN E. Implementation of WENO schemes in compressible multicomponent flow problems[J]. Journal of Computational Physics, 2006, 219: 715-732. DOI:10.1016/j.jcp.2006.04.018 |
| [18] |
DENG X, ZHANG H. Developing high-order weighted compact nonlinear schemes[J]. Journal of Computational Physics, 2000, 165: 22-44. DOI:10.1006/jcph.2000.6594 |
| [19] |
HE Z, GAO F, TIAN B, LI J. Implementation of finite difference weighted compact nonlinear schemes with the two-stage fourth-order accurate temporal discretization[J]. Communications in Computational Physics, 2020, 27: 1470-1484. DOI:10.4208/cicp.OA-2019-0029 |
| [20] |
NONOMURA T, MORIZAWA S, TERASHIMA H, et al. Numerical (error) issues on compressible multicomponent flows using a high-order differencing scheme: weighted compact nonlinear scheme[J]. Journal of Computational Physics, 2012, 231: 3181-3210. DOI:10.1016/j.jcp.2011.12.035 |
| [21] |
MURRONE A, GUILLARD H. A five equation reduced model for compressible two phase flow problems[J]. Journal of Computational Physics, 2005, 202: 664-698. DOI:10.1016/j.jcp.2004.07.019 |
| [22] |
HE Z, LI L, TIAN B. A numerical framework of non-conservative product. (In preparation)
|
| [23] |
HENRICK A, ASLAM T, POWERS J. Mapped weighted-essentially-non-oscillatory schemes: achieving optimal order near critical points[J]. Journal of Computational Physics, 2005, 207: 542-567. DOI:10.1016/j.jcp.2005.01.023 |
| [24] |
BORGES R, CARMONA M, COSTA B, et al. An improved weighted essentially non-oscillatory scheme for hyperbolic conservation laws[J]. Journal of Computational Physics, 2008, 227: 3191-3211. DOI:10.1016/j.jcp.2007.11.038 |
| [25] |
FU L, HU X, ADAM N. A family of high-order targeted ENO schemes for compressible-fluid simulations[J]. Journal of Computational Physics, 2016, 305: 333-359. DOI:10.1016/j.jcp.2015.10.037 |
| [26] |
REN Y, LIU M, ZHANG H. A characteristic-wise hybrid compact-WENO scheme for solving hyperbolic conservation laws[J]. Journal of Computational Physics, 2003, 192: 365-386. DOI:10.1016/j.jcp.2003.07.006 |
| [27] |
HE Z, LI X, LIANG X. Nonlinear spectral-like schemes for hybrid schemes[J]. Science China Physics, Mechanics and Astronomy, 2014, 57: 753-763. DOI:10.1007/s11433-013-5234-y |
| [28] |
SURESH A, HUYNH H. Accurate monotonicity-preserving schemes with Runge-Kutta time stepping[J]. Journal of Computational Physics, 1997, 136: 83-99. DOI:10.1006/jcph.1997.5745 |
| [29] |
DARU V, TENAUD C. High order one-step monotonicity-preserving schemes for unsteady compressible flow calculations[J]. Journal of Computational Physics, 2004, 193: 563-594. DOI:10.1016/j.jcp.2003.08.023 |
| [30] |
HE Z, LI X, FU D, MA Y. A 5th order monotonicity-preserving upwind compact difference scheme[J]. Science China Physics, Mechanics and Astronomy, 2011, 54: 511-522. DOI:10.1007/s11433-010-4220-x |
| [31] |
BALSARA D, SHU C W. Monotonicity preserving WENO schemes with increasingly high-order of accuracy[J]. Journal of Computational Physics, 2000, 160: 405-452. DOI:10.1006/jcph.2000.6443 |
| [32] |
HE Z, ZHANG Y, GAO F, et al. An improved accurate monotonicity-preserving scheme for the Euler equations[J]. Computers and Fluids, 2016, 140: 1-10. DOI:10.1016/j.compfluid.2016.09.002 |
| [33] |
HA C, LEE J. A modified monotonicity-preserving high-order scheme with application to computation of multi-phase flows[J]. Computers and Fluids, 2020, 197: 104345. DOI:10.1016/j.compfluid.2019.104345 |
| [34] |
ZHANG X, SHU C W. Maximum-principle-satisfying and positivity-preserving high-order schemes for conservation laws: survey and new developments[J]. Proc Roy Soc A, 2011, 467: 2752-76. DOI:10.1098/rspa.2011.0153 |
| [35] |
CLAIN S, DIOT S, LOUBERE R. A high-order finite volume method for systems of conservation laws-multi-dimensional optimal order detection(MOOD)[J]. Journal of Computational Physics, 2011, 230: 4028-4050. DOI:10.1016/j.jcp.2011.02.026 |
| [36] |
SHUKLA R. Nonlinear preconditioning for efficient and accurate interface capturing in simulation of multicomponent compressible flows[J]. Journal of Computational Physics, 2014, 276: 508-540. DOI:10.1016/j.jcp.2014.07.034 |
| [37] |
HE Z, TIAN B, ZHANG Y, et al. Characteristic-based and interface-sharpening algorithm for high-order simulations of immiscible compressible multi-material flows[J]. Journal of Computational Physics, 2017, 333: 247-268. DOI:10.1016/j.jcp.2016.12.035 |
| [38] |
SHYUE K, XIAO F. An Eulerian interface sharpening algorithm for compressible two-phase flow: the algebraic THINC approach[J]. Journal of Computational Physics, 2014, 268: 326-354. DOI:10.1016/j.jcp.2014.03.010 |
| [39] |
XIAO F, Ⅱ S, CHEN C. Revisit to the THINC scheme: a simple algebraic VOF algorithm[J]. Journal of Computational Physics, 2011, 230: 7086-7092. DOI:10.1016/j.jcp.2011.06.012 |
| [40] |
ALLAIRE G, CLERC S, KOKN S. A five-equation model for the simulation of interfaces between compressible fluids[J]. Journal of Computational Physics, 2002, 181: 577-616. DOI:10.1006/jcph.2002.7143 |
| [41] |
KAPILA A, MENIKOFF R, BDZIL J, et al. Two-phase modeling of deflagration-to-detonation transition in granular materials: reduced equations[J]. Physics of Fluids, 2001, 13: 3002-3024. DOI:10.1063/1.1398042 |
| [42] |
HE Z, RUAN Y, YU Y, et al. Self-adjusting steepness based schemes that preserve discontinuous structures in compressible flows[J]. Journal of Computational Physics, 2021. (submitted)
|
| [43] |
TIWARI A, FREUND J, PANTANO C. A diffuse interface model with immiscibility preservation[J]. Journal of Computational Physics, 2013, 252: 2900-309. |
| [44] |
LI L, CHEN Q, TIAN B. Transport diffuse interface model for simulation of solid-fluid interaction[J]. Applied Mathematics and Mechanics-English Edition, 2019, 40: 321-330. DOI:10.1007/s10483-019-2443-9 |
| [45] |
LI L, CHEN Q, HE Z, et al. An improved pressure-equilibrium diffuse interface model for solid-fluid interaction[J]. Communications in Computational Physics, 2020, 27: 546-568. DOI:10.4208/cicp.OA-2018-0261 |
| [46] |
LI H, HE Z, ZHANG Y, et al. On the role of rarefaction/compression waves in Richtmyer-Meshkov instability with reshock[J]. Physics of Fluids, 2019, 31: 054102. DOI:10.1063/1.5083796 |
| [47] |
HU Z, ZHANG Y, TIAN B. Evolution of Rayleigh-Taylor instability under interface discontinuous acceleration induced by radiation[J]. Physical Review E, 2020, 101: 043115. DOI:10.1103/PhysRevE.101.043115 |
| [48] |
GAO F, ZHANG Y, HE Z, et al. Formula for growth of mixing width applied to Richtmyer-Meshkov instability[J]. Physics of Fluids, 2016, 28: 114101. DOI:10.1063/1.4966226 |
| [49] |
DAL MASO G, LEFLOCH P, MURAT F. Definition and weak stability ofnoncon-servative product[J]. Journal de Mathématiques Pures et Appliqués, 1995, 74: 483-548. |
| [50] |
PARES C. Numerical methods fornonconservative hyperbolic systems: A theoretical framework[J]. SIAM Journal on Numerical Analysis, 2006, 44: 300-321. DOI:10.1137/050628052 |
| [51] |
DUMBSER M, HIDALGO A, CASTRO M, et al. FORCE schemes on unstructured meshes Ⅱ: Non-conservative hyperbolic systems[J]. Computer Methods in Applied Mechanics and Engineering, 2010, 199: 625-647. DOI:10.1016/j.cma.2009.10.016 |
| [52] |
ABGRALL R, KARNI S. A comment on the computation of non-conservative products[J]. Journal of Computational Physics, 2010, 229: 2759-2763. DOI:10.1016/j.jcp.2009.12.015 |
| [53] |
KOKH S, LAGOUTIERE F. An anti-diffusive numerical scheme for the simulation of interfaces between compressible fluids by means of a five-equation model[J]. Journal of Computational Physics, 2010, 229: 2773-2809. DOI:10.1016/j.jcp.2009.12.003 |
| [54] |
SO K, HU X, ADAMS N. Anti-diffusion interface sharpening technique for two-phase compressible flow simulations[J]. Journal of Computational Physics, 2012, 231: 4304-4323. DOI:10.1016/j.jcp.2012.02.013 |
| [55] |
OLSSON E, KREISS G, ZAHEDI S. A conservative level set method for two phase flow, Ⅱ[J]. Journal of Computational Physics, 2007, 225: 785-807. DOI:10.1016/j.jcp.2006.12.027 |
| [56] |
CHIU P, LIN Y. A conservative phase field method for solving incompressible two-phase flows[J]. Journal of Computational Physics, 2011, 230: 185-204. DOI:10.1016/j.jcp.2010.09.021 |
| [57] |
JAIN S, MANI A, MOIN P. A conservative diffuse-interface method for compressible two-phase flows[J]. Journal of Computational Physics, 2020, 418: 109606. DOI:10.1016/j.jcp.2020.109606 |
| [58] |
PERIGAUD G, SAUREL R. A compressible flow model with capillary effects[J]. Journal of Computational Physics, 2005, 209: 139-178. DOI:10.1016/j.jcp.2005.03.018 |
| [59] |
CARALIC V, COLONIUS T. Finite-volume WENO scheme for viscous compressible multicomponent flows[J]. Journal of Computational Physics, 2014, 274: 95-121. DOI:10.1016/j.jcp.2014.06.003 |
| [60] |
THORNBER B, GROOM M, YOUNGS D. A five-equation model for the simulation of miscible and viscous compressible fluids[J]. Journal of Computational Physics, 2018, 372: 256-280. DOI:10.1016/j.jcp.2018.06.028 |
| [61] |
JOHNSEN E, HAM F. Preventing numerical errors generated by interface-capturing schemes in compressible multi-material flows[J]. Journal of Computational Physics, 2012, 231: 5705-5717. DOI:10.1016/j.jcp.2012.04.048 |
| [62] |
SAUREL R, PANTANO C. Diffuse-interface capturing methods for compressible two-phase flows[J]. Annual Review of Fluid Mechanics, 2018, 50: 105-30. DOI:10.1146/annurev-fluid-122316-050109 |
| [63] |
FAVRIE N, GAVRILYUK S. Diffuse interface model for compressible fluid-compressible elastic-plastic solid interaction[J]. Journal of Computational Physics, 2012, 231: 2695-2723. DOI:10.1016/j.jcp.2011.11.027 |
| [64] |
NDANOU S, FAVRIE N, GAVRILYUK S. Multi-solid and multi-fluid diffuse interface model: Applications to dynamic fracture and fragmentation[J]. Journal of Computational Physics, 2015, 295: 523-555. DOI:10.1016/j.jcp.2015.04.024 |
| [65] |
HOWELL L, GREENOUGH J. Radiation diffusion for multi-fluid Eulerian hydrodynamics with adaptive mesh refinement[J]. Journal of Computational Physics, 2003, 184: 53-78. DOI:10.1016/S0021-9991(02)00015-3 |
| [66] |
DENG X, SHIMIZU Y, XIAO F. A fifth-order shock capturing scheme with two-stage boundary variation diminishing algorithm[J]. Journal of Computational Physics, 2019, 386: 323-349. DOI:10.1016/j.jcp.2019.02.024 |
| [67] |
DENG X, JIANG Z, XIAO F, et al. Implicit large eddy simulation of compressible turbulence flow with PnTm-BVD scheme[J]. Applied Mathematical Modelling, 2020, 77: 17-31. DOI:10.1016/j.apm.2019.07.022 |
 2021, Vol. 39
2021, Vol. 39