The current design tools in aerospace engineering are mostly based on the Reynolds averaged Navier-Stokes (RANS) approach because of its low cost, and reasonable accuracy for attached flow. In an assessment of the state-of-the-art CFD tools, NASA's CFD Vision 2030 Study[1] states.
"The use of CFD in the aerospace design process is severely limited by the inability to accurately and reliably predict turbulent flows with significant regions of separation. Advances in Reynolds-averaged Navier-Stokes (RANS) modeling alone are unlikely to overcome this deficiency, while the use of large-eddy simulation (LES) methods will remain impractical for various important applications for the foreseeable future, barring any radical advances in algorithmic technology. Hybrid RANS-LES and wall-modeled LES offer the best prospects…"
The vision study explicitly calls for scale-resolving large eddy simulation (LES) to be further developed for vortex-dominated separated flow, either with or without a wall-model or in the context of hybrid RANS-LES approaches. The concept of LES was developed over half a century ago[2] and has been applied over many decades to low Reynolds number problems to study fundamental turbulent flow physics. The major obstacle in its wider application is the computational cost especially for high-Reynolds number flows. Relative to wall-resolved LES (WRLES), wall-modeled LES (WMLES) is much less expensive because the small turbulence scales near solid walls are not fully resolved on a computational mesh. For WMLES, Chapman[3] estimated that the number of degrees of freedom (nDOF) scales with the Reynolds number according to Re2/5, which is considered too optimistic. Choi & Moin[4] provided the following estimate: nDOF~Re. Taking into account of the cost for time integration, Slotnick et al[1] offered the following cost estimate C~Re4/3. In addition, an estimate of computational time was also provided for an explicit, 2nd order numerical method.
The resolution of a computational simulation depends not only on nDOF, but also the order of accuracy of the numerical method. For example, a spectral method and a 2nd-order finite volume (FV) method with the same nDOF have dramatically different resolution power for turbulence scales.
Because of the disparate length and time scales in a turbulent flow, spectral methods[5] was the method of choice for earlier direct numerical simulation (DNS) investigations involving relatively simple geometries, such as fully developed channel flow[6]. Such studies have been invaluable in understanding fundamental turbulent physics, and in developing turbulence models for RANS approaches.
Although spectral methods possess the high accuracy, and have achieved considerable success in DNS, their potential for industrial applications are limited due to the difficulty in handling complex geometries. The present design tools in industry are almost always based on unstructured meshes. The cost to maintain a separate tool handling structured meshes far out-weighs the efficiency benefit in memory and speed. Therefore, it is a common practice to handle structured meshes as if they are unstructured with the associated benefits in modularity, maintainability and load-balance in a parallel implementation.
In an effort to reduce the cost of scale-resolving simulations, the international CFD community has invested significantly in high-order methods, which are at least 3rd order accurate, in the last two decades. This effort has spurred the further development of many high-order methods. Interested readers can refer to many review articles[7-14]. Five International Workshops on High-order CFD Methods have been organized in both the US and Europe to provide a forum to evaluate the status of high-order methods and identify pacing items. One conclusion from these workshops is that high-order methods are indeed much more efficient/accurate than 2nd order methods for scale resolving simulations. To achieve the same accuracy, high-order methods are orders of magnitude faster.
Since the publication of the review article of the first high-order CFD workshop (HOCFDW)[10], significant progress has been made in many pacing items. The progress has enabled applications of LES based on high-order methods by many research groups in academia, industry and government research labs[15-24]. To narrow the scope of the present paper, we review major advancements in the development of high-order methods for scale-resolving simulation in the last decade. We start our review by examining the pacing items listed in[10]:
·High-order mesh generation
·Solution-based hp-adaptations
·Scalable, low memory efficient time integrators for RANS and hybrid RANS/LES approaches
·Robust, accuracy-preserving, and parameter-free shock capturing.
Note that in[10], the emphasis was on the development of high-order CFD methods for both RANS and LES applications. In the present one, we focus only on LES to limit the scope of the present paper. Therefore, in the following sections, we will review the challenges in using high-order methods for LES, progress in high-order mesh generation, space discretization, time integration, hp-adaptation. The paper will conclude with an outlook for further development in the near future.
1 Challenges in using high-order methods for LESThe benefits of high-order methods for LES and DNS were well-known since some of the earliest DNS studies used spectral methods[6]. Spectral methods represent the ultimate high-order methods in term of accuracy. However, the global nature of the methods limited the application to simple geometries, and to flow problems without discontinuities. High-order methods for structured meshes have achieved far more success for more complex geometries than spectral methods[9]. However, high-order methods capable of handling unstructured meshes are preferred for industrial LES because the cost for mesh generation is significantly reduced, and the parallel implementation is more straightforward.
Although high-order methods can be orders of magnitude faster than 2nd order methods for LES to achieve the same accuracy, many challenges still remain. Some are related to intrinsic challenges for LES, and some others are unique for high-order methods. In the following paragraphs, we briefly describe some of the challenges.
1.1 Flow at high Reynolds numbersThis is an intrinsic challenge for LES. At a high Reynolds number, such as 10 million or above, the range of scales that must be captured increases, and the cost becomes prohibitively high. The smallest scales near a solid wall make WRLES very expensive. To reduce cost, wall models have been developed for such simulations. In particular, non-equilibrium wall models capable of handling flow separations are needed. Progress made in developing robust and accurate non-equilibrium wall models will impact the range of Reynolds numbers that can be tackled. Meanwhile, fast implicit methods which can be implemented on GPU clusters will further increase the range of Reynolds numbers that can be tackled.
1.2 High-order mesh generationThis is a challenge unique to adaptive high-order methods. The need for high-order meshes has been demonstrated by many researchers with the DG and related methods. Because of the high accuracy of such methods, the nDOFs to achieve an engineering level of accuracy is dramatically reduced. Many studies have shown that even a 3rd order scheme can save over an order of magnitude in nDOFs comparing with a 2nd order scheme[25]. Since DG and related methods add internal DOFs, the computational meshes are therefore much coarser than those used in a FV method. For example, let's assume that a 2nd order FV method needs a billion hexahedral cells to achieve an acceptable level of accuracy. For a FR/CPR code running at 3rd order accuracy at solution polynomial degree of 2 (or p2), the number of DOFs to achieve a similar accuracy is about 1 billion/16, which is 62.5 million DOFs/equation. Since each element has 33=27 DOFs, the mesh needs only 2.3 million elements! This is a very coarse mesh comparing with one having 1 billion elements. At such a coarse resolution, the wall boundaries must be represented with at least degree 2 polynomial patches. Otherwise, the error near a linear wall-representation will destroy the high-order accuracy.
1.3 Robustness of high-order LESHigh-order methods have much less dissipation and dispersion errors than 2nd order methods. For under-resolved LES, scales that cannot be resolved on a given mesh alias into high-wave number/high frequency modes. Energy from these modes can often accumulate because of a lack of dissipation from the numerical scheme or the sub-grid scale stress model. At high Reynolds numbers, the physical dissipation is too low to damp these aliased modes, which can drive under-resolved LES divergent.
Many remedies have been developed to improve the robustness of under-resolved LES:
◇Filtering to remove high-frequency modes;
◇Over-integration to reduce the impact of aliasing errors;
◇Approaches to preserve the discrete kinetic energy and/or entropy;
◇Entropy-stable formulations;
◇Limiters to redistribute the solution when a blow-up is about to occur.
1.4 Efficiency, accuracy and memory requirement of time integration approachesLarge eddy simulations are time-accurate 3D computations with a time step small enough to capture the dominant turbulent dynamics. The efficiency and accuracy of the time marching scheme is therefore a very important factor in determining the simulation cost. Both explicit and implicit schemes of various order of accuracy have been used successfully for LES. The time step used in explicit schemes is determined by the smallest element size usually located near solid walls and the speed of the fastest acoustic wave. This time step is often orders of magnitude smaller than the dominant turbulent time scale, making explicit schemes inefficient. On the other hand, implicit schemes do allow time steps many orders larger. However, the cost per time step is often many times of that of explicit schemes. In addition, implicit schemes often need to store the Jacobian matrices, whose size increases dramatically with the order of accuracy as p6. Much research is still needed to develop efficient low memory time integration schemes.
2 High-order mesh generationResearch into high-order mesh generation started at least as early as 2000[26]. There is a reason why high-order mesh generation was the top pacing item identified in the first HOCFDW. By that time, it was well-known that high-order accuracy could not be achieved with linear meshes. In addition, linear meshes can cause stability problems and possibly induce flow separations. However, the capability to generate high-order meshes was not available in commercial mesh generators simply because no commercial CFD software can handle high-order meshes, and only research codes in the small high-order CFD community needed such meshes. As a result, each research group had their own ad-hoc solutions to produce high-order meshes. In fact, there was not even a standard format for high-order meshes.
At the time of the first HOCFDW, the most well-known high-order mesh generator was gmsh[27], which also established the first public-domain high-order mesh format. Because of that, the high-order meshes supplied by the first HOCFDW used the gmsh format. There was no alternative. Unfortunately, gmsh was a research code geared towards mesh generation researchers, not necessarily high-order CFD practitioners. Ultimately, in order for industry to used high-order LES solvers, it is necessary to convince commercial mesh generators to produce production-level high-order mesh generators. As a precondition for that to become a reality, there must be a standard mesh format for both mesh generators and flow solvers.
Soon after the first HOCFDW ended, there was an effort to standardize a high-order mesh format. Although gmsh was very popular in the high-order CFD community, it was not an international standard. The international standard for CFD meshes is the CGNS format[28], widely used in the CFD community, not only for meshes, but also for flow solvers and flow visualization packages. It appears the only possible route to standardize a high-order mesh format is to extend CGNS to high-order meshes. A graduate student from the University of Kansas (KU) (M. Yu) wrote the proposals to formally extend the CGSN standard to handle cubic and quartic meshes. The quadratic mesh format was already part of CGNS. The proposals were quickly approved by the CGNS committee, and these formats were later implemented.
After the 1st HOCFDW, there was a lot of interest in developing high-order meshing tools which made high-order CFD simulations feasible. Gmsh continued to develop its high-order meshing capability. Many university groups also took part in producing tools converting linear meshes into high-order ones because producing high-order meshing tools directly for CAD geometries was beyond the capability of academic research groups, and it was completely unnecessary. At University of Stuttgart, Prof. Munz's group produced a tool called HOPR[29], which can translate linear meshes into high-order ones, and also convert structured meshes into high-order unstructured meshes. Under the support of NASA, University of Kansas produced a meshing tool called meshCurve[30] to convert unstructured linear meshes into high-order meshes in the CGNS format. In meshCurve, it was assumed that the mesh is generated by an external mesh generator, and the access to the geometry is not possible. Therefore, the geometry is reconstructed from scratch only using the surface meshes. To make the process user-friendly, a graphical user interface was developed, which allows the user to select wall surfaces, detect important geometric features such as sharp edges and critical points. These features are then preserved in the geometry-reconstruction phase. After that, high-order surface meshes are generated, followed by high-order volume meshes. Finally, the entire mesh is examined for possible negative Jacobians, which are removed through smoothing iterations. A sample reconstructed high-order mesh from a linear mesh is shown in Fig. 1. Note the blue sharp edges have also been upgraded to high-order curves. After meshCurve was announced in 2016, it has been downloaded by more than 220 unique users from all over the world.

|
Fig.1 A sample reconstructed high-order mesh by meshCurve with feature preservation 图 1 带有特征保留由meshCurve重构的样本高阶网格 |
In the past few years, research on high-order mesh generation has been supported all over the world, see references[31-36]. The main breakthrough came when Pointwise[32] and GridPro announced the capability for high-order mesh generation. Pointwise can generate mixed high-order meshes including tetrahedral, prismatic, hexahedral and pyramidic elements, while GridPro is capable of producing unstructured hexahedral meshes. Both mesh generators first generate linear meshes, which are then elevated to high-order ones. Both support the CGNS high-order mesh format. An example high-order mesh for the NASA Common Research Model high-lift configuration is displayed in Fig. 2. Ultimately the availability of high-order commercial mesh generators is a sure sign that the CFD community now embraces high-order CFD, and industrial high-order LES is becoming a reality[24].

|
Fig.2 Sample high-order meshes for the NASA common research model high-lift configuration generated by pointwise (image courtesy of Steve Karman) 图 2 Pointwise生成的NASA通用研究模型高升力配置的高阶网格样本(图片由Steve Karman提供) |
As described by many review papers, there has been considerable research interest on high-order methods in the past two decades. Many methods have seen implementation and application in production-level LES solvers. We divide methods capable of handling unstructured meshes into the following main categories:
·High-order finite volume (FV) or WENO methods[37-38];
·Continuous finite element methods such asstreamline upwind Petrov-Galerkin (SUPG)[39];
·Discontinuous finite element and related methods such as discontinuous Galerkin (DG)[40], spectral difference (SD)[41] and flux reconstruction (FR)[42-43];
·Hybrid FV/DG type or PnPm methods[44-45].
As reviewed in[14], most modern super-computers are mixed CPU/GPU/vector-processor clusters. On a GPU card, the motto is "communication is everything" because the GPU performance hinges on the cost of communication. Computations with continuous local data and coalesced memory access are orders of magnitude faster than computations with remote data and non-coalesced memory access. This property immediately makes discontinuous finite element methods such as the DG, SD and FR methods stand out for maximum potential efficiency.
Let's illustrate this point in a FV and FR context. We assume inviscid flow for simplicity. In a FV method, one time-marching step consists of the following major operations:
1) Reconstruct solution distributions from cell-averaged state variables;
2) Compute the Riemann fluxes at face quadrature points;
3) March one time step.
Linear reconstructions need at least face-neighbor solution data, as shown in Fig. 3, and high-order reconstructions usually need data from neighbor's neighbors. For the reconstruction step, the higher the polynomial order, the more the communication penalty. This operation incurs a significant penalty on a GPU because the data required by the reconstruction is scattered all over the place in the data array. Since the mesh is unstructured, the solution data is stored in the memory without any fixed patterns to exploit. Furthermore, to compute the Riemann flux on the face quadrature point, more data communication is needed to obtain the solution from the neighboring element. Any communication carries a penalty to performance. Note that once the residual is obtained, explicit time marching does not involve data communication.
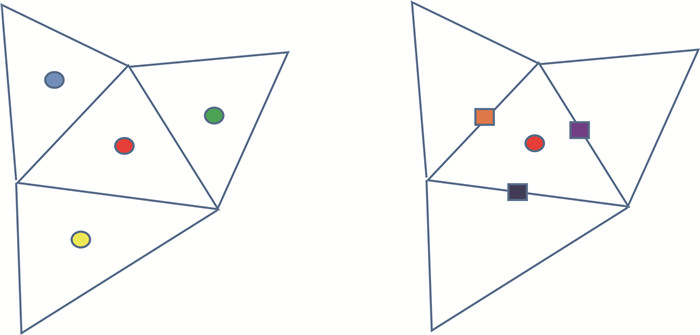
|
Fig.3 Reconstruction stencil and flux point locations in a finite volume scheme. Different colors indicate discontinuous data in the solution array. The flux always needs data from neighboring elements 图 3 在有限体积方法中重建模具和通量点的位置(不同的颜色表示数值解在数组中不连续, 通量始终需要来自相邻单元的解) |
In a DG or FR method, on the other hand, the solution data is stored in an element-wise manner. The state variables on an element are stored continuously in the data array, as illustrated in Fig. 4. One time-marching step consists of the following major operations:
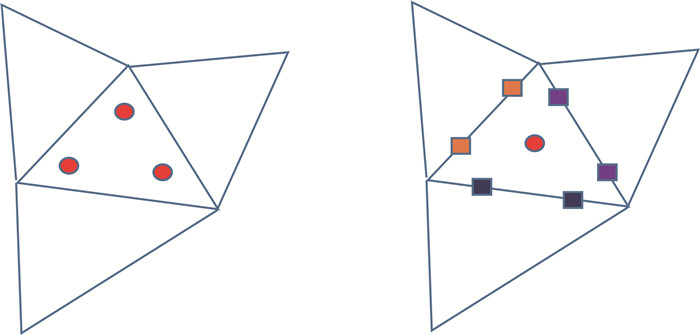
|
Fig.4 Reconstruction stencil and flux point locations in a DG/FR method. Same color indicates continuous data in the solution array. The flux always needs data from neighboring elements 图 4 DG / FR方法中的重建模具和通量点位置(相同的颜色表示数据在数组中是连续的, 通量始终需要来自相邻单元的解) |
1) Evaluate the flux diverge based on the local solution data on each element;
2) Compute the Riemann fluxes at the flux points and correct the local flux divergence;
3) March one time step.
The 1st step uses completely local data on the element. It involves computing the solution gradients at the solution points, and the solutions at the face flux points. The higher the polynomial degree is, the higher the computational intensity. Communication is only needed when the Riemann flux is evaluated at the face flux points. Only immediate neighbors are included in the stencil no matter how high the polynomial degree is. Once the Riemann flux is computed, the correction operation is again local. This communication pattern gives the discontinuous high-order FE method the best chance in maximizing performance on GPUs. Depending on how data is stored in SUPG, the reconstruction operator may need to access remote data. Therefore, we expect the GPU performance of SUPG and PnPm methods to be between the FV and DG/FR methods.
Indeed, recently the FR/CPR solver, hpMusic[24, 46], was successfully ported to one of the fastest supercomputers in the world, Summit. On a single NVIDIA V100 card, the speedups of one GPU card over a single Intel Xeon CPU E5-2620 processor for different polynomial degrees and element types are shown in Fig. 5. The speedup ranges from 400 to over 1 600. Note the clear trend of increasing GPU performance with increasing p orders. This is because of the higher local computational intensity with increasing p orders. In addition, the performance reaches the highest on tetrahedral elements because stride-one local memory access is achieved on the local solution array for tetrahedral elements. An astonishing speedup of 1 600 was achieved at p=5 on tetrahedral elements[47].
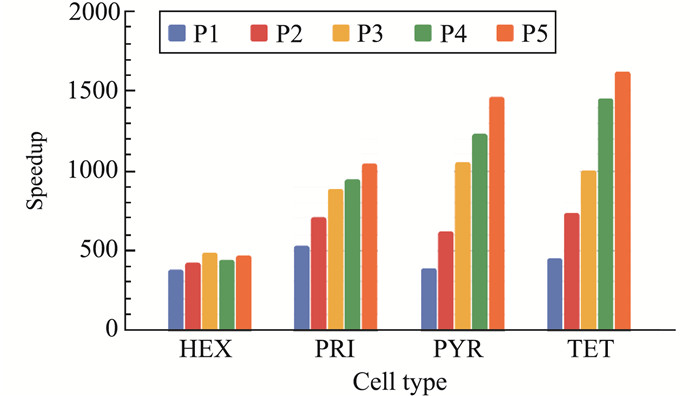
|
Fig.5 Speedups of a single NVIDIA V100 card over an Intel Xeon CPU E5-2620 processor for the FR/CPR method running different p orders on four types of elements, in double precision 图 5 FR/CPR方法在单张NVIDIA V100卡相对Intel Xeon CPU E5-2620处理器的加速,FR / CPR方式在四种不同网格上双精度运行不同的高阶格式 |
To deal with shock-waves, the most popular approaches include artificial viscosity[48-50] or with solution limiters[51-53]. Shock-fitting has also seen a new life in the moving discontinuous Galerkin context[54] with promising results for 3D unsteady flow problems. Although progress has been made in shock-capturing, we have not witnessed a major breakthrough. For example, user-specified parameters are still needed in artificial viscosity. Limiters continue to hinder convergence to steady state and can degrade solution accuracy. The vision of robust, parameter free and accuracy-preserving and convergent shock computing has not been realized yet. However, enough progress has been made that high-order LES from transonic to hypersonic speeds has been successfully performed regularly.
Shock-capturing is first order accurate since the position within an element is undecided. For a stationary shock wave, the characteristic wave originating from the shock always carries a first-order error. Based on this argument, strict accuracy-preserving shock-capturing is difficult or impossible to realize. Perhaps shock-fitting is necessary to strictly preserve accuracy away from the shock-wave. Nevertheless, much higher resolution has been obtained with high-order methods than with 2nd order ones using shock-capturing when shock-waves are present.
4 Time integrationScale-resolving simulations are expensive because time accurate computations must be performed with a time-step small enough to capture the dominant turbulent dynamics. Such computations need to be sufficient long so that the flow reaches a statistically steady state. To complicate things even further, some turbulent flows appear to oscillate between different states. In this case, the problem may have multiple statistically "steady" states. Finding a time-invariant mean solution is even more challenging in such a situation.
Both explicit and implicit approaches have been used in high-order LES. The advantage of explicit schemes is the ease to implement on parallel computers and its usually excellent parallel efficiency[55-56]. The major disadvantage is that the global time step is limited by the smallest element size due to the CFL condition. This problem is particularly severe for unstructured meshes generated for complex geometries, which often have a few bad elements with diminishing cell volumes. Such bad cells can make explicit schemes prohibitively expensive.
To remedy this problem, time-accurate local time-stepping approaches were developed to overcome the time step limit[57-58, 17]. Each element advances in time based on its own time step, and only synchronizes with other elements for post-processing purposes. Orders of magnitude in speedup were demonstrated comparing with a global time stepping approach. The challenge in implementing the time-accurate local time-marching approach is how to maintain load balance in an extreme-scale parallel environment.
The most-often used approach to improve time-marching efficiency is to adopt an implicit approach. There are two major components in an implicit approach which affect the accuracy and efficiency: the time discretization scheme and the numerical algorithm to solve the resulting time-discretized system. The order of accuracy is determined by the time discretization scheme, while the efficiency is mostly dictated by the nonlinear equation solver (or just solver when there is no ambiguity), and the convergence tolerance of the unsteady residual. To illustrate the point, let's consider the semi-discretized system written as
| $ \frac{{\partial U}}{{\partial t}} = Res (U) $ | (1) |
where U is the global DOFs, and Res(U) is the residual after space discretization. Various time-marching schemes have been developed for high-order spatial discretizations in the past decade. Popular choices include backward difference formulas (BDF)[59], implicit Runge-Kutta (IRK)[60-62], diagonally implicit Runge-Kutta (DIRK)[63], and its variant, explicit singly diagonally implicit Runge-Kutta (ESDIRK) and implicit-explicit Runge-Kutta[64-66], linearly implicit Rosenbrock-type method[67-68], and high-order space-time method[69]. Recently an IRK scheme called Radau IIA was studied by several researchers because of its high-accuracy, being L-stable, and having fewer stages than other DIRK schemes. However, a fully coupled system of all the stages needs to be inverted. The BDF schemes need to solve one non-linear system per time step, but not L-stable for higher than 2nd order accuracy. All other schemes need to solve multiple non-linear systems, or a fully coupled nonlinear system at each time step.
Several popular schemes are compared in[70-72] for efficiency and accuracy. To illustrate the two main components, we consider the 2nd-order backward difference formula
| $ \frac{{3{U^{n + 1}} - 4{U^n} + {U^{n - 1}}}}{{2\Delta t}} = Res\left( {{U^{n + 1}}} \right) $ | (2) |
In solving (2), we often define the unsteady residual as
| $ Res{{\rm{ }}^*}\left( {{U^{n + 1}}} \right) = Res \left( {{U^{n + 1}}} \right) - \frac{{3{U^{n + 1}} - 4{U^n} + {U^{n - 1}}}}{{2\Delta t}} $ | (3) |
Eq. (3) is sometimes solved with a dual-time approach with a pseudo-time τ[44] defined in
| $ \frac{{\partial U}}{{\partial \tau }} = Res{ ^*}(U) $ | (4) |
Any iterative solvers for steady-state problems can be used to decrease the unsteady residual by the convergence tolerance εN (N meaning the non-linear residual), including explicit local time-marching (in pseudo-time), hp-multigrid solvers or implicit Newton-like solvers. Let the initial guess for Un+1 be the solution at the previous time step, Un. The unsteady residual is considered converged if
| $ \frac{{\left\| {Res{ ^*}({U^{n + 1}})} \right\|}}{{\left\| {Res{ ^*}({U^n})} \right\|}} \le {\varepsilon _N} $ | (5) |
This convergence tolerance does indeed influence efficiency and accuracy. Through a comparative study in[72], it was shown a two-order convergence (εN=0.01) is sufficient in capturing both the mean flow quantities such as mean pressure and skin-friction and the power spectral density, which highlights turbulence dynamics.
The well-known Newton's method can be used to solve (3), i.e.,
| $ \frac{{\partial Re{s^*}}}{{\partial {U^n}}}\Delta U = - Re{s^*}({U^{(k)}}) $ | (6) |
where k is the iteration index, and ΔU=U(k+1)-U(k). Normally multiple Newton steps are necessary to satisfy (5). This Newton loop is sometimes called the outer loop. The linear equation (6) is a large sparse system, which is again solved using an iterative solver such as Gauss-Seidel, or the Jacobian-free Newton-Krylov (JFNK) method[73] with various preconditioners, e.g., ILU(n), element Jacobi, line[74], p-multigrid, or no preconditioner. The iterative loop for this linear equation is called the inner loop with a convergence tolerance of εL. The inner loop usually does not need to converge very far (with εL~0.1) as long as the outer loop satisfies the convergence tolerance.
The inclusion of the unsteady term with a small time-step to capture the turbulence makes the non-linear system less stiff than the corresponding steady system. As an alternative to this dual loop approach, the non-linear LU-SGS approach[75-76] avoids the dual loop by directly updating and converging the unsteady residual in a single loop. Let the update equation for element i be
| $ {D_i}\Delta {U_i} = - Res _i^*({U^{(*)}}) $ | (7) |
where Di is the element Jacobian matrix, U(*) represents the latest global solution. Symmetric forward and backward Gauss-Seidel loops over the elements are then used to solve (7) until the unsteady residual satisfies (5). The requirement to store the element Jacobian matrix makes the LU-SGS approach unattractive for higher p>3, as the size of this matrix goes up according to p6. In addition, LU-SGS is not a very strong implicit solver, and the time step size is often smaller than the one dictated by flow physics.
For steady flow computations, a JFNK approach needs a good preconditioner to converge. The most used preconditioners are usually based on the Jacobian matrix, for example, the incomplete LU decomposition with various levels of fill-in, ILU(n), or the element Jacobi preconditioner. Unfortunately, for DG-type methods at higher p orders >3, matrix-based preconditioners are out of the questions. Other preconditioners such as p-multigrid have been developed, and demonstrated various levels of success[77-79]. Fortunately, weaker-preconditioners which do not need to store the large Jacobian matrix such as p-multigrid have a chance to perform well. The search for low-memory and efficient time integration is still ongoing.
5 Solution-based hp-adaptationsVarious adaptation criteria have been used for mesh adaptations in CFD[80-81]. There are four main types of error indicators in the literature[82].
1) Feature based indicators. Such indicators use the gradient, curvature or smoothness of certain flow variables. They can be directional to enable anisotropic mesh adaptations.
2) Solution error or discretization error based indicators. To apply this indicator, the solution error needs to be estimated. Since it is the discretization error that we wish to reduce with mesh adaptation, on the surface it might appear the discretization error would serve as an appropriate driver for the adaption process. Reference[82] showed discretization error is not an appropriate mesh adaption criterion.
3) Truncation error or residual based indicators. For complex non-linear equations, the truncation error is not easy to compute. Instead, the numerical solutions or residuals on coarse and fine meshes or with different polynomial orders are used to approximate the truncation error. Furthermore, the transport of the discretization error is driven by the local truncation error[83].
4) Output adjoint based indicators[84]. Adjoint-based error indicators relate a specific functional output directly to the local residuals by the adjoint solution, which can be used to construct a very effective error indicator to drive an adaptive procedure towards any engineering output. Such indicators can target elements which contribute the most to the output, such as the lift or drag forces.
For steady RANS flow computations, output adjoint based mesh adaptation approaches appear to be the most efficient[85] in obtaining mesh-independent lift, drag and moment coefficients. In addition, they can also provide a reasonable error estimate, which can further increase the accuracy. Comparisons with fixed grid approaches indicate that orders of magnitude in CPU time can be saved to achieve the same accuracy[85-86].
For unsteady flow problems, however, a similar output-adjoint approach is very expensive because an extra dimension in time needs to be traversed. For example, if the drag at a final time needs to be predicted, an unsteady output adjoint problem needs to be solved in reverse time. In addition, the mesh needs to be adapted at different times to produce the most accurate output[87]. Furthermore, for turbulent flow problems the instantaneous quantities are usually very irregular and chaotic[88]. Design engineers are interested in mean quantities, such as the mean lift, drag and moment coefficients. The mean quantities can take many time steps to achieve convergence in time averaging. All these challenges make output adjoint-based adaptation impractical for LES.
Instead, physics-based adaptation criteria have been developed for LES[89-92], e.g., solution features (steep gradients or curvature), smoothness of the numerical solution either within an element or cross element boundaries, truncation errors, the smallest resolved scales. Instead of mesh adaptations, several papers used p-adaptation to increase the resolution[89, 93-95] and achieved significant cost-savings.
In particular, an adaptation criterion based on the smallest resolved scales in any coordinate direction is developed in Ref.[96]. The criterion allows a directional indicator in any direction to enable anisotropic mesh adaptations for mixed unstructured meshes. Further-more, by equalizing error distributions in all coordinate directions, an "optimal" computational mesh can be obtained, which is capable of producing a LES solution of a given resolution with minimum cost. Promising results have been demonstrated for hexahedral meshes. The basic idea of the approach is reviewed here.
Let the LES solution at element i be Ui. An implicit low pass test filter
| $ {U_i} = \left( {I - \frac{{{\mathit{\Delta }^2}}}{4}\frac{{{\partial ^2}}}{{\partial {x^2}}}} \right){\hat U_i} $ | (8) |
where Δ is the test filter size, which can be the same as the element size. The implicit filter can be approximated by the following explicit filter
| $ {\hat U_i} = \left( {I + \frac{{{\mathit{\Delta }^2}}}{4}\frac{{{\partial ^2}}}{{\partial {x^2}}}} \right){U_i} $ | (9) |
After that, the smallest resolved scales are extracted as
| $ U_i^* = {U_i} - {{\hat U}_i} = - \frac{{{\mathit{\Delta }^2}}}{4}\frac{{{\partial ^2}{U_i}}}{{\partial {x^2}}} $ | (10) |
This idea can be generalized to compute the smallest resolved scales in any direction of unit vector n
| $ \begin{array}{c} U_{i}^{*,(\boldsymbol{n})}=U_{i}-\hat{U}_{i}^{(n)} \\ =-\frac{\varDelta_{n}^{2}}{4} \frac{\partial^{2} U_{i}}{\partial n^{2}}=-\frac{\Delta_{n}^{2}}{4} \boldsymbol{n}^{\mathrm{T}}\left(\nabla \nabla^{\mathrm{T}} U_{i}\right) \boldsymbol{n} \end{array} $ | (11) |
Finally the anisotropic error indicator in direction n is defined as
| $ A(\mathit{\boldsymbol{n}}) = \sqrt {\left\langle {(U_i^{*,(n)},U_i^{*,(n)})} \right\rangle } $ | (12) |
where (·, ·) denotes an inner product, while 〈·〉 indicates time or phase averaging. With this adaptation criterion, nearly "optimal" LES meshes have been obtained for well-known benchmark test cases[96]. Figure 6 shows an "optimal" mesh for the backward facing problem.
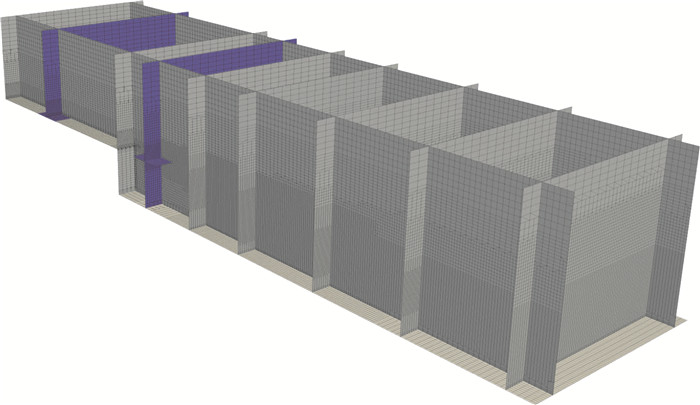
|
Fig.6 "Optimal" LES mesh obtained for flow over a backward facing step by Toosi and Larsson[96] (image courtesy of Johan Larsson) 图 6 Toosi和Larsson[96]获得的“最佳”LES网格,用于后台阶流动(图片由Johan Larsson提供) |
Significant progress has been made in the past decade in advancing LES as a simulation tool for mission critical applications in industry. In fact, a team in France just accomplished an important milestone: simulating an entire jet engine operation using LES[97] with 20 billion grid points. At present, such computations can only be accomplished on some of the biggest computers owned by government agencies, and the cost is prohibitive for industrial use. However, at least in turbomachinery, the progress has dramatically increased the use of LES as an analysis tool. Scale-resolving simulations which took months to compute on a small cluster only 5 years ago can now be completed in just a few days.
In the next decade, I believe overnight turnaround time can be achieved on small GPU clusters (~100 GPU cards) for problems of moderate Reynolds numbers (a few million) encountered in turbomachinery. It is expected that mixed CPU, GPU and vector accelerators will continue to be the main computer architecture in the not too distant future. Further progress in the following pacing items will have the highest payoffs:
1) Low memory efficient time integration approaches for higher p orders. P-multigrid, JFNY approaches with dual time stepping are strong candidates. Perhaps new ideas will emerge which will significantly improve the current state-of-the-art.
2) Efficient implementation on mixed CPU/GPU/accelerator clusters[23, 98]. Such architectures (such as GPU cards) have limited amount of memory, and cannot store even the element Jacobi matrices from high-order finite elements methods. Progress made in 1 can significantly influence the performance of large scale simulations.
3) The development of non-equilibrium wall models for high Reynolds number flows. Wall-resolved simulations at such Reynolds numbers are still prohibitively expensive. New ideas in wall-modeling including machine-learning may spur significant progress, especially for highly separated flow. In the past few years, many equilibrium wall-models have been developed and demonstrated[99-101]. These need to be extended to the non-equilibrium flow regime.
4) Improvement in the robustness of high-order methods, which include shock-capturing and improved non-linear stability for under-resolved flow features. Ideas such as entropy stability, kinetic energy and entropy preserving schemes[21, 102-103] have already shown promise, and will continue to play an important role.
5) Multi-physics and multi-disciplinary LES. The resolved scales embedded in a LES solution can significantly affect other physical phenomenon such as combustion and fluid structure interactions since fluids mechanics, chemical reaction and structural mechanics are all tightly coupled. Flow simulations with moving boundaries will also mature for industrial applications. It is only natural that more and more physics will be considered in high-fidelity LES with high-order methods.
Acknowledgements: The author gratefully acknowledges the support from AFOSR under grant FA9550-20-1-0315 with Dr. Fariba Fahroo being the Program Manager.
| [1] |
SLOTNICK J, KHODADOUST A, ALONSO J, et al. CFD Vision 2030 Study: A path to revolutionary computational aerosciences[R]. NASA/CR-2014-218178.
|
| [2] |
SMAGORINSKY J. General circulation experiments with the primitive equations. I. The basic experiment[J]. Mon. Weather Rev, 1963, 91(3): 99-164. DOI:10.1175/1520-0493(1963)091<0099:GCEWTP>2.3.CO;2 |
| [3] |
CHAPMAN D R. Computational aerodynamics development and outlook[J]. AIAA J, 1979, 17(12): 1293-1313. DOI:10.2514/3.61311 |
| [4] |
CHOI H, MOIN P. Grid-point requirements for large eddy simulation: Chapman's estimates revisited[J]. Physics of Fluids, 2012, 24: 011702. DOI:10.1063/1.3676783 |
| [5] |
GOTTLIEB D, ORSZAG S A. Numerical analysis of spectral method: theory and applications[J]. Philadelphia: SIAM, 1977. |
| [6] |
KIM J, MOIN P, MOSER R. Turbulence statistics in fully developed channel flow at low Reynolds number[J]. J Fluid Mechanics, 1987, 177: 133-166. DOI:10.1017/S0022112087000892 |
| [7] |
EKATERINARIS J. High-order accurate, low numerical diffusion methods for aerodynamics[J]. Progress in Aerospace Sciences, 2005, 41: 192-300. DOI:10.1016/j.paerosci.2005.03.003 |
| [8] |
WANG Z J. High-order methods on unstructured grids for Navier-Stokes equations[J]. Journal of Progress in Aerospace Sciences, 2007, 43(1): 1-41. |
| [9] |
DENG X, MAO M, TU G, et al. High-order and high accurate CFD methods and their applications for complex grid problems. Commun[J]. Comput Phys, 2012, 11: 1081-1102. DOI:10.4208/cicp.100510.150511s |
| [10] |
WANG Z J, FIDKOWSKI K J, ABGRALL R, et al. High-order CFD methods: current status and perspective[J]. International Journal for Numerical Methods in Fluids, 2013, 72(8): 811-45. DOI:10.1002/fld.3767 |
| [11] |
HUYNH H T, WANG Z J, VINCENT P E. High-order methods for computational fluid dynamics: A brief review of compact differential formulations on unstructured grids[J]. Computers & Fluids, 2014, 98: 209-220. |
| [12] |
WANG Z J. High-order computational fluid dynamics tools for aircraft design[J]. Philos Trans A Math Phys Eng Sci, 2014, 13, 372(2022): 20130318. |
| [13] |
WANG Z J. A perspective on high-order methods in computational fluid dynamics[J]. Science China Physics Mechanics & Astronomy, 2016, 59(1): 1-6. |
| [14] |
WITHERDEN F D, JAMESON A. Future directions in computational fluid dynamics[R]. AIAA 2017-3791. https://doi.org/10.2514/6.2017-3791
|
| [15] |
BECK A D, BOLEMANN T, FLAD D, et al. High-order discontinuous Galerkin spectral element methods for transitional and turbulent flow simulations[J]. Int J Numer. Methods Fluids, 2014, 76(8): 522-548. DOI:10.1002/fld.3943 |
| [16] |
CHAPELIER J B, DE LA LLAVE PLATA M, RENAC F, et al. Evaluation of a high-order discontinuous Galerkin method for the DNS of turbulent flows[J]. Computers & Fluids, 2014, 95(22): 210-226. DOI:10.1016/j.compfluid.2014.02.015 |
| [17] |
LU Y, LIU K, DAWES W N. Flow simulation system based on high order space-time extension of flux reconstruction method[C]//53rd AIAA Aerospace Sciences Meeting. AIAA SciTech Forum, (AIAA 2015-0833).
|
| [18] |
CARTON DE WIART C, HILLEWAERT K, BRICTEUX L, et al. Implicit LES of free and wall-bounded turbulent flows based on the discontinuous Galerkin/symmetric interior penalty method[J]. International J for Numerical Methods in Fluids, 2015(6). DOI:10.1002/fld.4021 |
| [19] |
FLAD D, BECK A, MUNZ C D. Simulation of under-resolved turbulent flows by adaptive filtering using the high order discontinuous Galerkin spectral element method[J]. Journal of Computational Physics, 2016, 313(15): 1-12. DOI:10.1016/j.jcp.2015.11.064 |
| [20] |
FERRER E. An interior penalty stabilized incompressible discontinuous Galerkin-Fourier solver for implicit large eddy simulations[J]. Journal of Computational Physics, 2017, 348(1): 754-775. DOI:10.1016/j.jcp.2017.07.049 |
| [21] |
LV Y, MA P, IHME M. On under-resolved simulations of compressible turbulence using an entropy-bounded DG method: Solution stabilization, scheme optimization, and benchmark against a finite-volume solver[J]. Computers & Fluids, 2016, 161(15): 89-106. |
| [22] |
VERMEIRE B C, NADARAJAH S, TUCKER P G. Implicit large eddy simulation using the high-order correction procedure via reconstruction scheme[J]. J Numer Meth Fluids, 2016, 82: 231-260. DOI:10.1002/fld.4214 |
| [23] |
VERMEIRE B C, WITHERDEN F D, VINCENT P E. On the utility of GPU accelerated high-order methods for unsteady flow simulations: A comparison with industry-standard tools[J]. Journal of Computational Physics, 2017, 334(1): 497-521. DOI:10.1016/j.jcp.2016.12.049 |
| [24] |
WANG Z J, LI Y, JIA F, et al. Towards industrial large eddy simulation using the FR/CPR method[J]. Computers and Fluids, 2017, 156(12): 579-589. |
| [25] |
JIA F, IMS J, WANG Z J, et al. Evaluation of second- and high-order solvers in wall-resolved large-eddy simulation[J]. AIAA Journal, 2019, 57(4). |
| [26] |
SHERWIN S J, PEIRO J. Mesh generation in curvilinear domains using high-order elements[J]. International Journal for Numerical Methods in Engineering, 2000, 53(1): 207-23. |
| [27] |
GEUZAINE C, REMACLE J F. Gmsh: a three-dimensional finite element mesh generator with built-in pre- and post-processing facilities[J]. International Journal for Numerical Methods in Engineering, 2009, 47(11): 1309-1331. |
| [28] |
CFD General Notation System, https://cgns.github.io/
|
| [29] |
HOPR, High-order preprocessor, https://www.hopr-project.org
|
| [30] |
IMS J, WANG Z J. Automated low-order to high-order mesh conversion[J]. Engineering with Computers, 2019, 35(1). DOI:10.1007/s00366-018-0602-x |
| [31] |
FORTUNATO M, PERSSON P O. High-order unstructured curved mesh generation using the Winslow equations[J]. Journal of Computational Physics, 2016, 307: 1-14. DOI:10.1016/j.jcp.2015.11.020 |
| [32] |
KARMAN S L, ERWIN J T, GLASBY R S, et al. High-order mesh curving using WCN mesh optimization[C]//46th AIAA Fluid Dynamics Conference, AIAA 2016-3178.
|
| [33] |
MARCON J, TURNER M, PEIRO J, et al. High-order curvilinear hybrid mesh generation for CFD simulations[R]. AIAA-2018-1403.
|
| [34] |
TURNER M, PEIRO J, MOXEY D. A variational framework for high-order mesh generation[J]. Procedia Engineering, 2016, 163: 340-352. DOI:10.1016/j.proeng.2016.11.069 |
| [35] |
YANG H Q, ZHOU X A, HARRIS R E, et al. An open source geometry kernel-based high-order element mesh generation tool[R]. AIAA-2019-1719.
|
| [36] |
ZHONG Z, MING L, LEI H, et al. High-order curvilinear mesh generation technique based on an improved RBF approach[J]. International Journal for Numerical Methods in Fluids, 2019, 91(3): 97-111. DOI:10.1002/fld.4741 |
| [37] |
BARTH T J, FREDERICKSON P O. High-order solution of the Euler equations on unstructured grids using quadratic reconstruction[R]. AIAA Paper No. 90-0013, 1990.
|
| [38] |
WANG Q, REN Y X, PAN J, et al. Compact high order finite volume method on unstructured grids Ⅲ: Variational reconstruction[J]. Journal of Computational Physics, 337: 1-26. |
| [39] |
BROOKS A N, HUGHES T J. Streamline upwind/Petrov-Galerkin formulations for convection dominated flows with particular emphasis on the incompressible Navier-Stokes equations[J]. Computer Methods in Applied Mechanics and Engineering, 1982, 32(1-3): 199-259. DOI:10.1016/0045-7825(82)90071-8 |
| [40] |
COCKBURN B, KARNIADAKIS GE, SHU C W. Discontinuous Galerkin methods. Theory, computation and applications[M]. Berlin: Lecture Notes in Computational Science and Engineering, Springer-Verlag, 2000.
|
| [41] |
LIU Y, VINOKUR M, WANG Z J. Discontinuous spectral difference method for conservation laws on unstructured grids[J]. Journal of Computational Physics, 2006, 216: 780-801. DOI:10.1016/j.jcp.2006.01.024 |
| [42] |
HUYNH H T. A flux reconstruction approach to high-order schemes including discontinuous Galerkin methods[R]. AIAA Paper 4079, 2007.
|
| [43] |
WANG Z J, GAO H. A unifying lifting collocation penalty formulation including the discontinuous Galerkin, spectral volume/difference methods for conservation laws on mixed grids[J]. Journal of Computational Physics, 2009, 228(21): 8161-8186. DOI:10.1016/j.jcp.2009.07.036 |
| [44] |
DUMBSER M, KAISER M, TORO E F. An arbitrary high-order discontinuous Galerkin method for elastic waves on unstructured meshes V[J]. Local time stepping and p-adaptivity. Geophysical Journal International, 2007, 171(23): 695-717. |
| [45] |
ZHANG L, LIU W, HE L, et al. A class of hybrid DG/FV methods for conservation laws Ⅱ: Two-dimensional cases[J]. Journal of Computational Physics, 2012, 231(4): 1104-1120. DOI:10.1016/j.jcp.2011.03.032 |
| [46] |
HAGA T, GAO H, WANG Z J. A high-order unifying discontinuous formulation for the Navier-Stokes equations on 3D mixed grids[J]. Math Model Nat Phenom, 2011, 6(3): 28-56. DOI:10.1051/mmnp/20116302 |
| [47] |
JOURDAN E, WANG Z J. Efficient Implementation of the FR/CPR Method on GPU Clusters for Industrial Large Eddy Simulation[R]. AIAA-2020-3031.
|
| [48] |
PERSSON P O, PERAIRE J. Sub-cell shock capturing for discontinuous Galerkin methods[R]. AIAA-2006-112.
|
| [49] |
BARTER G E, DARMOFAL D L. Shock capturing with PDE-based artificial viscosity for DGFEM: Part I.Formulation[J]. J Comput Phys, 2010, 229: 1810-1827. DOI:10.1016/j.jcp.2009.11.010 |
| [50] |
YU M L, GIRALDO F X, PENG M, et al. Localized artificial viscosity stabilization of discontinuous Galerkin methods for nonhydrostatic mesoscale atmospheric modeling[J]. Monthly Weather Review, 2015, 143(12): 4823-4845. DOI:10.1175/MWR-D-15-0134.1 |
| [51] |
LILIA KRIVODONOVA, JIANGUO XIN, JEAN-FRANÇOIS REMACLE, et al. Shockd detection and limiting with discontinuous Galerkin methods for hyperbolic conservation laws[J]. Applied Numerical Mathematics, Elsevier, 2004, 48(3-4): 323-338. DOI:10.1016/j.apnum.2003.11.002 |
| [52] |
PARK J S, KIM C. Higher-order multi-dimensional limiting strategy for discontinuous Galerkin methods in compressible inviscid and viscous flows[J]. Computers & Fluids, 2014, 96(13): 377-396. |
| [53] |
LI Y, WANG Z J. Recent progress in developing a convergent and accuracy preserving limiter for the FR/CPR method[C]//55th AIAA Aerospace Sciences Meeting AIAA SciTech Forum, (AIAA 2017-0756).
|
| [54] |
CORRIGAN A, KERCHER A D, KESSLER D A. A moving discontinuous Galerkin finite element method for flows with interfaces[J]. International J. for Numerical Methods in Fluids, 2019, 89(9): 362-406. DOI:10.1002/fld.4697 |
| [55] |
ALTMANN C, BECK A D, HINDENLANG F, et al. An efficient high performance parallelization of a discontinuous Galerkin spectral element method. In: Keller R., Kramer D., Weiss JP. (eds) Facing the Multicore-Challenge Ⅲ. Lecture Notes in Computer Science, vol 7686[M]. Springer, Berlin, Heidelberg, 2013. https://doi.org/10.1007/978-3-642-35893-7_4
|
| [56] |
GOTTLIEB S, SHU C W. Total variation diminishing Runge-Kutta schemes[J]. Math Comput, 1998, 67(221): 73-85. DOI:10.1090/S0025-5718-98-00913-2 |
| [57] |
DUMBSER M. Arbitrary high order PNPM schemes on unstructured meshes for the compressible Navier-Stokes equations[J]. Computers & Fluids, 2010, 39(1): 60-76. |
| [58] |
GASSNER G, DUMNSER M, HINDENLANG F, et al. Explicit one-step time discretization for discontinuous Galerkin and finite volume schemes based on local predictors[J]. Journal of Computational Physics, 2011, 230: 4232, 4247. |
| [59] |
VATSA V N, CARPENTER M H, LOCKARD D P. Re-evaluation of an Optimized Second Order Backward Difference (BDF2OPT) scheme for unsteady flow applications[R]. AIAA-2010-0122.
|
| [60] |
BUTCHER J C. Numerical methods for ordinary differential equations[M]. Chichester: Wiley, 2002.
|
| [61] |
JAMESON A. Evaluation of fully implicit Runge Kutta schemes for unsteady flow calculations[J]. J Sci Comput, 2017, 73: 819-852. DOI:10.1007/s10915-017-0476-x |
| [62] |
PAZNER W, PERSSON P O. Stage-parallel fully implicit Runge-Kutta solvers for discontinuous Galerkin fluid simulations[J]. Journal of Computational Physics, 2017, 335: 700-717. DOI:10.1016/j.jcp.2017.01.050 |
| [63] |
KENNEDY C A, CARPENTER M H. Diagonally implicit Runge-Kutta methods for ordinary differential equations. A Review[R]. NASA/TM-2016-219173, March, 2016.
|
| [64] |
PARESCHI L, RUSSO G. Implicit-explicit Runge-Kutta schemes and applications to hyperbolic systems with relaxation[J]. Journal of Scientific Computing, 2005, 25: 129-155. |
| [65] |
PERSSON P O. High-order LES simulations using implicit-explicit Runge-Kutta schemes, in: Proceedings of the 49th AIAA Aerospace Sciences Meet-ing and Exhibit[R]. AIAA-2011-684.
|
| [66] |
VERMEIRE B C, NADARAJAH S. Adaptive IMEX schemes for high-order unstructured methods[J]. Journal of Computational Physics, 2015, 280(1): 261-286. DOI:10.1016/j.jcp.2014.09.016 |
| [67] |
BASSI F, BOTTI L, COLOMBO A, et al. Linearly implicit Rosenbrock-type Runge Kutta schemes applied to the Discontinuous Galerkin solution of compressible and incompressible unsteady flows[J]. Computers & Fluids, 2015, 118: 305-320. |
| [68] |
LIU X, XIA Y, LUO H, et al. A comparative study of rosenbrock-type and implicit Runge-Kutta time integration for discontinuous Galerkin method for unsteady 3D compressible Navier-Stokes equations[J]. Communications in Computational Physics, 2016, 20(4): 1016-1044. DOI:10.4208/cicp.300715.140316a |
| [69] |
DIOSADY L T, MURMAN S M. Tensor-product preconditioners for higher-order space-time discontinuous Galerkin methods[J]. Journal of Computational Physics, 2017, 330: 296-318. DOI:10.1016/j.jcp.2016.11.022 |
| [70] |
MARTINELLI L, LOHRY M W. Implicit time integration of discontinuous Galerkin approximations to the Navier-Stokes equations[R]. AIAA-2020-0774.
|
| [71] |
WANG L, YU M L. Comparison of ROW, ESDIRK, and BDF2 for unsteady flows with the high-order flux reconstruction formulation[J]. Journal of Scientific Computing, 2020, 83(39). |
| [72] |
JIA F, WANG Z J, BHASKARAN R, et al. Accuracy, efficiency and scalability of explicit and implicit FR/CPR schemes in large eddy simulation[J]. Computers and Fluids, 2019, 195: 104316. DOI:10.1016/j.compfluid.2019.104316 |
| [73] |
KNOLL D, KEYESD. Jacobian-free Newton-Krylov methods: a survey of approaches and applications[J]. Journal of Computational Physics, 2004, 193(2): 357-397. DOI:10.1016/j.jcp.2003.08.010 |
| [74] |
PERSSON P O. A sparse and high-order accurate line-based discontinuous Galerkin method for unstructured meshes[J]. Journal of Computational Physics, 2013, 233: 414-429. DOI:10.1016/j.jcp.2012.09.008 |
| [75] |
YOON S, JAMESON A. Lower-upper symmetric-Gauss-Seidel method for the Euler and Navier-Stokes equations[J]. AIAA J, 1988, 26(9): 1025-1026. DOI:10.2514/3.10007 |
| [76] |
CHEN R F, WANG Z J. Fast, block lower-upper symmetric Gauss-Seidel scheme for arbitrary grids[J]. AIAA J, 2000, 38(12): 2238-2245. DOI:10.2514/2.914 |
| [77] |
JOURDAN E, WANG Z J. A Study of p-multigrid approach for the high order FR/CPR method[R]. AIAA-2019-3711.
|
| [78] |
LOPPI N A, WITHERDEN F D, JAMESON A, et al. A high-order cross-platform incompressible Navier-Stokes solver via artificial compressibility with application to a turbulent jet[J]. Computer Physics Communications, 2018, 233: 193-205. DOI:10.1016/j.cpc.2018.06.016 |
| [79] |
WANG L, YU M L. A p-multigrid flux reconstruction method for the steady Navier-Stokes equations[R]. AIAA 2019-3061.
|
| [80] |
FREY P J, ALAUZET F. Anisotropic mesh adaptation for CFD computations[J]. Comput Methods Appl Mech Engrg, 2005, 194: 5068-5082. DOI:10.1016/j.cma.2004.11.025 |
| [81] |
HABASHI W G, DOMPIERRE J, BOURGAULT Y, et al. Anisotropic mesh adaptation: towards user-independent, mesh-independent and solver-independent CFD. Part I: general principles.
|
| [82] |
ROY C J. Strategies for driving mesh adaptation in CFD[R]. AIAA-2009-1302.
|
| [83] |
SHIH T, QIN Y. A method for estimating grid-induced errors in finite-difference and finite-volume methods[R]. AIAA-2003-845.
|
| [84] |
FIDKOWSKI K J. Review of output-based error estimation and mesh adaptation in computational fluid dynamics[J]. AIAA Journal, 2011, 49(4): 673-694. DOI:10.2514/1.J050073 |
| [85] |
YANO M, DARMOFAL D L. An optimization-based framework for anisotropic simplex mesh adaptation[J]. Journal of Computational Physics, 2012, 231(22): 7626-7649. DOI:10.1016/j.jcp.2012.06.040 |
| [86] |
ZHOU C, SHI L, WANG Z J. Adaptive high-order discretization of the Reynolds-averaged Navier-Stokes equations[J]. Computers and Fluids, 2017, 159: 137-155. DOI:10.1016/j.compfluid.2017.09.009 |
| [87] |
FIDKOWSKI K J. Output-based space-time mesh optimization for unsteady flows using continuous-in-time adjoints[J]. Journal of Computational Physics, 2017, 341(15): 258-277. |
| [88] |
WANG Q, HU R, BLONIGAN P. Least squares shadowing sensitivity analysis of chaotic limit cycle oscillations[J]. Journal of Computational Physics, 2014, 267(15): 210-224. |
| [89] |
ABBÀ A, RECANATI A, TUGNOLI M, et al. Dynamical p-adaptivity for LES of compressible flows in a high order DG framework[J]. Journal of Computational Physics, 2020, 420: 109720. DOI:10.1016/j.jcp.2020.109720 |
| [90] |
ANTEPARA O, LEHMKUHL O, BORRELL R, et al. Parallel adaptive mesh refinement for Large-Eddy Simulations of turbulent flows[J]. Comput Fluids, 2015, 110: 48-61. DOI:10.1016/j.compfluid.2014.09.050 |
| [91] |
BENARD P, BALARAC G, MOUREAU V, et al. Mesh adaptation for large-eddy simulations in complex geometries[J]. International Journal for Numerical Methods in Fluids, 2016, 81(12): 719-740. DOI:10.1002/fld.4204.hal-01339519 |
| [92] |
PARK M A, KLEB B, ANDERSON W K, et al. Exploring unstructured mesh adaptation for hybrid Reynolds-averaged Navier-Stokes/large eddy simulation[R]. AIAA-2020-1139.
|
| [93] |
TUGNOLI M, ABBÀ A, BONAVENTURA L, et al. A locally p-adaptive approach for large eddy simulation of compressible flows in a DG framework[J]. J Comput Phys, 2047, 349: 33-58. https://arxiv.org/abs/1610.03319
|
| [94] |
NADDEI F, DE LA LLAVE PLATA M, COUAILLIER V, et al. A comparison of refinement indicators for p-adaptive simulations of steady and unsteady flows using discontinuous Galerkin methods[J]. Journal of Computational Physics, 2019, 376: 508-533. DOI:10.1016/j.jcp.2018.09.045 |
| [95] |
WANG L, MATTHIAS GOBBERT, YU M L. A dynamically load-balanced parallel p-adaptive implicit high-order flux reconstruction method for under-resolved turbulence simulation[J]. Journal of Computational Physics, 2020, 417: 109581. DOI:10.1016/j.jcp.2020.109581 |
| [96] |
TOOSI S, LARSSON J. Anisotropic grid adaptation in large eddy simulations[J]. Comput Fluids, 2017, 156: 146-61. DOI:10.1016/j.compfluid.2017.07.006 |
| [97] |
ARROYO C P, DOMBARD J, DUCHAINE F, et al. Large-eddy simulation of an integrated high-pressure compressor and combustion chamber of a typical turbine engine architecture[R]. ASME Turbo Expo GT2020-16288, May 2020.
|
| [98] |
VINCENT P, WITHERDEN F, VERMEIRE B, et al. Towards green aviation with python at petascale[C]//High Performance Computing, Networking, Storage and Analysis, SC16: International Conference for, IEEE, 2016: 1-11.
|
| [99] |
FRÈRE, CARTON DE WIART C, HILLEWAERT K, et al. Application of wall-models to discontinuous Galerkin LES[J]. Physics of Fluids, 2017, 29: 085111. DOI:10.1063/1.4998977 |
| [100] |
LODATO G, CASTONGUAY P, JAMESON A. Structural wall-modeled LES using a high-order spectral difference scheme for unstructured meshes[J]. Flow, Turbulence and Combustion, 2014, 92(1-2): 579-606. DOI:10.1007/s10494-013-9523-3 |
| [101] |
SHI J, YAN H, WANG Z J. Flux reconstruction implementation of an algebraic wall model for large-eddy simulation[J]. AIAA Journal, 2020, 58(7): 3051-3062. DOI:10.2514/1.J058957 |
| [102] |
CHAN J, DEL REY FERNÁNDEZ D C, CARPENTER M H. Efficient entropy stable Gauss collocation methods[J]. SIAM J Sci Comput, 2019, 41(5): A2938-A2966. DOI:10.1137/18M1209234 |
| [103] |
MANZANERO J, RUBIO G, FERRER E, et al. Insights on aliasing driven instabilities for advection equations with application to Gauss-Lobatto discontinuous Galerkin methods[J]. Journal of Scientific Computing, 2018, 75: 1262-1281. DOI:10.1007/s10915-017-0585-6 |
 2021, Vol. 39
2021, Vol. 39

