爆轰是由激波诱导的、以稳定方式传播的燃烧。由于该燃烧的化学反应比较激烈,故具有极高的火焰传播速度,其产物也具有极高的温度和压力。因此,爆轰是一种具有更高热效率的燃烧方式,将其应用到推进系统,具有广泛的应用前景,比如脉冲爆轰发动机、驻定爆轰发动机和旋转爆轰发动机等。另一方面,爆轰波后的高温高压环境具有较强的破坏能力,会引发各种工业灾害,比如煤矿瓦斯爆炸、各种粉尘爆炸等事故。因此,为了对爆轰有更好的控制,需要对爆轰波的特性有更深入的了解[1-2]。
与爆轰密切相关的两个现象是爆轰波的生成和传播。爆轰波的生成主要有两类——直接起爆和间接起爆[3]。直接起爆需要较高的能量[4],因此,普通工业生产和生活中遇到更多的是间接起爆。其中由弱点火先形成层流燃烧,再逐渐发展成爆轰的方式称为爆燃转爆轰(DDT),这种方式需要较小的点火能量,因而受到广泛的关注和研究。在DDT过程中,层流燃烧依靠分子输运来维持火焰面的传播,是以亚声速传播的膨胀波,属于输运预混火焰;而爆轰依靠激波诱导来实现火焰面的传播,是以超声速传播的激波,属于对流预混火焰,这是两种不同的火焰传播模式,要实现它们之间的转换,湍流起到至关重要的作用[5]。目前为止,在一定的初始条件和边界条件下,很难精确地预测爆燃转爆轰是否能发生以及何时何地发生。定性上来说,相关的机理已经研究得较透彻,但仍无法精确预测的主要难点在于其中的湍流燃烧。与爆轰密切相关的另一个现象是爆轰波的传播,对于活化能较大的高度不稳定可燃气体,激波阵面脉动很大,波系之间的作用使反应区呈现湍流状态,湍流脉动会影响波阵面处的燃烧,进而影响爆轰波的传播[3]。此外,由于反应诱导区较宽,可燃物在波阵面不能完全燃烧,会在其下游形成燃烧产物包围的未燃气团,该未燃气团的消耗需借助于湍流扩散来完成燃烧,释放的能量有可能会影响爆轰波阵面[6]。
气相爆轰波的传播速度在马赫数5左右,具有高马赫数、高雷诺数和高温高压的特性,其中涉及到燃烧、高强度湍流、波系(包括激波、膨胀波等)之间的相互作用。在理论研究方面,采用Navier-Stokes方程来描述爆轰波的结构及其传播特性,这是一组偏微分方程,在高雷诺数下方程会失稳。此外,方程还具有奇异性(超声速流中的声速点),导致流场出现壅塞,这些因素使得理论求解上述偏微分方程组没有可能,只得借助于实验测试和数值模拟。随着实验测试技术的发展,很多光学测试手段已经较好地应用在了爆轰波的研究中,比如纹影、阴影、全息干涉、激光诱导荧光等,这些测试得到的图像反映的是光强和位相的信息,经过适当的转换,就可得到流场的参数分布。然而,实验得到的参数有限,且多为定性分析,难以进行定量研究。由于气相爆轰波的三个特点,数值模拟也面临着较大的困难。在普通的低速湍流燃烧中,压力可以近似为常数,进而引入反应标量概念,使得研究得到简化。但这种简化在与爆轰相关的湍流燃烧中是不适用的,较高的马赫数使与爆轰有关的湍流燃烧面临高可压缩性,尤其是流场中存在强间断。爆轰波的高速使得波阵面和波后等相关流场具有较高的雷诺数,故流场中的最小流动尺度Kolmogorov尺度具有较小的值,而直接数值模拟采用的网格需小于该尺度,因而会面临较大的困难。而基于RANS方程的湍流模型得到的是流场参数的平均量,其值无法反映真实的流场状况。因此,从精度和计算量的综合考虑,大涡模拟更适合研究与爆轰有关的湍流燃烧,但其面临的难点是湍流的亚网格模型的封闭和燃烧模型的封闭。此外,高速流动使得滤波后的能量方程(或平均能量方程)中出现高速源项,该项体现了压缩波与膨胀波对流场的影响,是无法求解的,也需要采用一定的模型进行封闭。高温高压的环境使得真实化学反应更加复杂,现有的湍流燃烧模型针对的大多是简化反应机理,而对于反映真实燃烧情况的基元反应则面临较大的困难,这是基元反应中差别悬殊的反应速率引起的刚性问题造成的。本文对爆燃转爆轰和爆轰波结构中涉及的湍流燃烧的研究现状进行了分析和评述,并对未来的研究进行了展望。
1 爆燃转爆轰中的湍流燃烧 1.1 爆燃转爆轰的典型过程利用较小的点火能量,生成层流火焰,在适当的条件下,火焰持续加速,形成激波,甚至可发展为爆轰。这种以弱点火生成爆轰的现象称为爆燃转爆轰。影响爆燃转爆轰的因素很多,点火方式、边界条件和变换机制等皆可以影响其转换过程[7]。因此,爆燃转爆轰的过程也不具有唯一性。
一端封闭的管,于封闭端点火,只要足够长,燃烧便可转换为爆轰,该转换过程可反映爆燃转爆轰的主要环节,常被视作爆燃转爆轰的典型过程。图 1是利用火焰自发光拍摄的,爆燃转爆轰的狭缝扫描照片[3]。可燃气为C2H2+O2。在封闭端,用热射流点火,点3为点火点,曲线4表示层流火焰加速轨迹,曲线5处的发光区域逐渐变宽,表示湍流火焰加速轨迹,点6表示突然转变为爆轰,随后,形成过驱爆轰7,逐渐衰减为CJ爆轰。同时,出现回传爆轰,即曲线9,在曲线7与9之间的区域内,周期出现光亮的弯曲横线8,此为壁面反射的横向激波对燃烧产物气体进行压缩的结果。从点火点3到爆轰突发点6之间的距离称为转换距离,它不仅决定于燃料特性,还决定于点火方式和边界条件。

|
图 1 燃烧产物射流形成爆轰的狭缝扫描照片 Fig.1 Typical streak photography of the abrupt transition to detonation via a jet of hot combustion products |
图 2为爆燃转爆轰过程的高速分幅纹影照片[8]。可燃气为H2+O2,封闭端点火,在边界作用下,失稳加速,形成湍流火焰,表面呈现精细的胞格状结构。湍流火焰使燃烧进一步增强,燃烧产物膨胀,压缩火焰前的未燃气体,形成系列压缩波,压缩波的追赶最终形成激波。在壁面附近的湍流火焰内,出现局部爆炸,形成爆轰波,最终发展成强爆轰,同时出现回爆。

|
图 2 燃烧转爆轰的分幅纹影照片 Fig.2 Sequence of schlieren photographs in DDT process |
因此,爆燃转爆轰的典型过程大致可以分为三个阶段[5]:
1) 燃烧。弱点火后,生成层流火焰,在边界作用下失稳加速。加速火焰与壁面具有正反馈作用,使火焰持续加速,乃致猝发湍流,形成湍流火焰,导致燃烧速度进一步增强。
2) 爆燃。燃烧产物的膨胀对火焰阵面前的介质有压缩作用,形成系列压缩波,最终发展成激波,该诱导激波随火焰的持续加速而不断增强。在此阶段,诱导激波与火焰面形成一复合波,且激波传播速度大于火焰传播速度,燃烧是通过分子扩散进行的。诱导激波强度决定于火焰燃烧速度,而燃烧速度决定于边界条件。
3) 爆轰。加速火焰形成的诱导激波足够强时,激波预压区可能出现局部爆炸,形成爆轰泡,使燃烧突然转变为强爆轰。强爆轰不稳定,逐步衰减为稳定传播的CJ爆轰。此时,激波与火焰耦合,形成激波-火焰耦合波。激波强度决定了火焰速度,两者的传播速度相等。
在爆燃转爆轰过程中,第一阶段的火焰加速和第二阶段诱导激波的增强均与湍流燃烧密切相关,国内外大量的实验已证实了这一点[6-15]。
1.2 湍流对火焰加速的影响火焰在直管中传播时,燃烧产物的膨胀导致波前质点的流动,该流动称为背景流场。由于黏性,背景流场在壁面附近形成黏性边界层,即出现速度梯度场。此时,火焰传播时,阵面不同部分传播的环境不同,因而具有不同的传播速度,从而使得火焰变形。火焰变形导致燃烧面积增大,燃烧速率增加。加速火焰容易失稳,燃烧速率会进一步增加。背景流场的速度随着的燃烧速率的增加而增加,这又导致流场雷诺数的增加。当雷诺数大于临界值时,背景流场出现湍流,如图 3所示[9],湍流边界层使燃烧速率急剧增加,火焰传播速度也愈大。背景流场的雷诺数愈大,湍流愈强,燃烧速度愈快,使火焰持续加速,在火焰前面形成激波,如图 4所示[10-11],当出现热点时,出现局部爆炸,形成爆轰。

|
图 3 加速火焰前方边界层的阴影照片 Fig.3 Sequence of shadow photographs showing boundary layers ahead of accelerated flame |
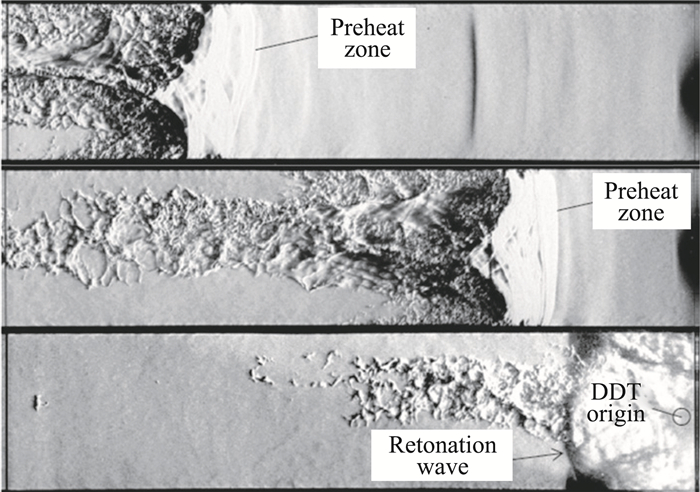
|
图 4 乙烯-氧气混合物的DDT过程的阴影照片 Fig.4 Sequence of shadow photographs during DDT in ethylene-oxygen mixture, P0=0.12 bar |
如在火焰的传播路径上设置障碍物,将会加剧火焰的失稳,其间涉及不同的火焰失稳机制,如Taylor不稳定,Richtmyer-Meshkov不稳定,Helmholtz不稳定和Landau-Darrieus不稳定等。当火焰失稳达到一定程度时,过度的变形必然猝发湍流。湍流使火焰变形更为严重,并大大增强输运能力,使已燃流团与未燃流团充分掺混,从而大幅增加燃烧速度。
图 5为障碍物作用下,火焰失稳并诱发湍流的实验照片。其中图 5(a)为薄片障碍物[3],图 5(b)为方块障碍物[12]。管道中的障碍物减少了通道中的流动面积,导致背景流场的流动加速。因此,受背景流场的影响,火焰在抵达障碍物之前已经变形,上部的传播速度明显大于下部,流场的这种特性会导致火焰失稳(主要为Taylor不稳定)。对于薄片状障碍物(图 5a),火焰跨越障碍物后,头部出现湍流燃烧,湍流刷明显可见。当障碍物具有一定厚度时(图 5b),障碍物与上壁面形成了狭长通道,火焰穿越时,变形火焰的头部依然保持流向传播,但底部为横向传播(向壁面逼近)。由于火焰的压缩作用,横向传播的火焰在狭长通道中形成了来回振荡的压缩波,从而导致横向火焰失稳,形成湍流燃烧,使燃烧充满狭长通道,见图 5(b)的最后一幅照片。背景流场中的气体,在狭长通道中加速后,以射流形式离开障碍物,在障碍物背部形成带涡环的绕流(Helmholtz不稳定),于是,湍流火焰也具有涡环结构,带有绕流特性[5]。

|
图 5 障碍物作用下火焰的传播 Fig.5 Propagation of a flame past an obstacle in a channel |
障碍物诱导的湍流火焰,一般是不能自持的,一旦撤销诱发湍流的外部因素,火焰将减速。如果重复设置障碍物,由于障碍物对流动的影响与火焰加速之间存在的正反馈的机制,火焰可持续加速(如图 6所示[7]),达到一定程度,会诱发爆轰的形成。

|
图 6 阻塞比为0.6时,氢气-空气混合物中火焰传播的阴影照片 Fig.6 Sequence of shadow photographs of flame propagation in 10% H2-Air mixture with BR=0.6 |
爆燃转爆轰是个比较复杂的物理化学过程,包含湍流燃烧、压缩波反射、激波边界层以及热点自爆炸等现象,该过程不但具有强烈的非线性,还存在范围宽广的时空特征尺度。实验得到的数据有限,如需对该过程进行更深入的了解,需要借助数值计算。采用数值计算时,不但需要合适的湍流燃烧模型、高分辨率的捕捉激波格式以及尺度极小的网格等,还需处理方程刚性等问题,因此面临诸多挑战。但是因为爆燃转爆轰的研究具有特殊的理论和实用价值,而数值计算是研究该过程的有效手段,所以尽管面临很多困难,人们还是进行了大量的工作。
Ivanov对长方形管道中氢气-氧气混合物的DDT过程采用了三维直接数值模拟[16],化学反应模型采用详细基元化学反应模型,网格尺寸为25 μm。图 7代表了火焰在边界层的作用下失稳加速、诱导激波的过程,图 7(a)是火焰面和激波的三维流场结构,图 7(b)是相应的x-y截面云图和流线图。初始的不规则扰动诱发了火焰刷,火焰加速产生的压缩波不断追赶,逐渐在火焰前方合并成激波,波后流动引起的边界层使得火焰面发生皱褶。值得关注的是,火焰和其前方的流动一直是层流,直到形成爆轰。图 8(a)和图 8(b)是根据图 7的流场绘制的火焰加速的计算阴影图,从图上看,似乎形成了“湍流火焰刷”,与图 8(c)的实验阴影图[17]定性上是一致的,然而,根据图 7的三维数值结果,无论是火焰还是流动,均是层流,图 8(a)和8(b)中的“湍流”效果是光束通过胞格层流火焰折射形成的,这意味着三维的层流火焰经过二维的投影后,可以得到湍流效果,这可能造成对该类现象研究的误导。

|
图 7 火焰在方管加速过程中,火焰结构和压缩波(激波)的作用 Fig.7 Images of the flame structure and compression (shock) wave in square-cross channel |

|
图 8 火焰面附近流场的计算阴影图 Fig.8 Shadow graphy of the flow pattern in the vicinity of the flame front |
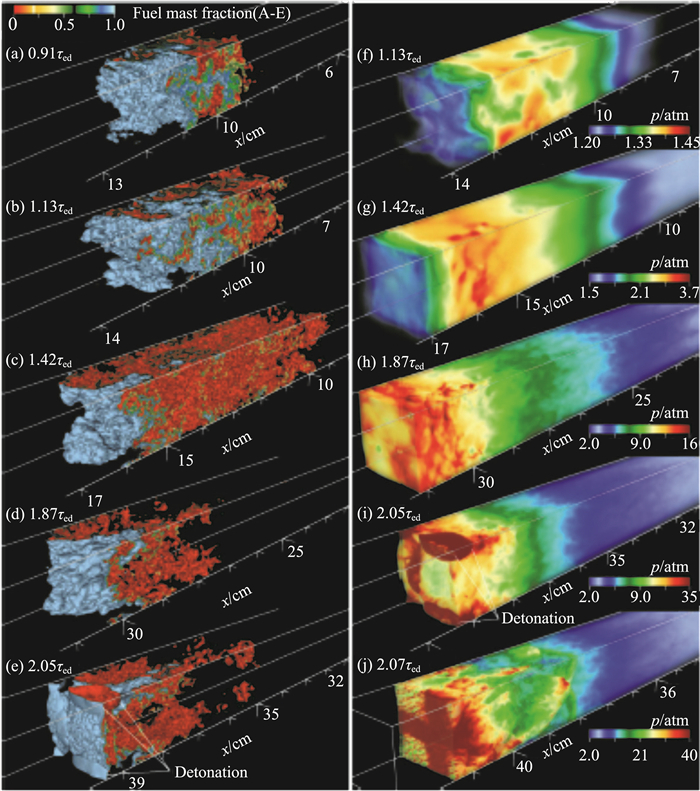
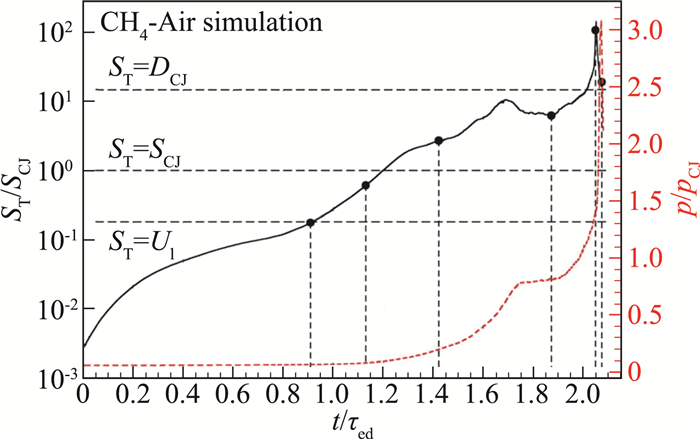
Poludnenko采用更细的网格对非受限空间内的DDT过程进行了直接数值模拟[18-19],网格尺寸为δL, 0/16,其中δL, 0为层流火焰厚度,可燃气采用甲烷-空气混合物,化学反应模型采用单步化学反应。图 9为湍流火焰发展和DDT过程,其中左图为燃料质量分数的等值面,右图是压力场。火焰加速引起的背景流场产生的高强度湍流与火焰相互作用形成的正反馈过程使得火焰不断加速,当湍流火焰速度超过CJ爆燃速度时,火焰非常不稳定,极易形成爆轰。湍流火焰速度与最大压力的发展历程如图 10所示,图中黑实线代表湍流速度的发展变化,红虚线代表最大压力的发展变化。从理论上来说,CJ爆燃速度是满足守恒方程的最大爆燃速度。而湍流火焰速度依赖于湍流强度和湍流火焰结构,因此可以超过CJ爆燃速度。根据反应流守恒方程,当燃烧速度超过CJ爆燃速度时,无法形成稳定的爆燃波,流动需要发展,产生激波,达到满足守恒方程的一种新的稳定状态。最终,出现两种状态,一种是火焰呈现脉冲不稳定,火焰速度在CJ爆燃速度上下周期性的振荡,另一种是形成CJ爆轰。
|
图 9 在等当量比的甲烷-空气混合物中,湍流火焰和转变成爆轰的演变 Fig.9 Evolution of a turbulent flame and transition to a detonation in a stoichiometric methane-air mixture |
|
图 10 实验和数值模拟中,压力和湍流火焰速度的变化曲线 Fig.10 Pressure and turbulent flame speeds observed in experiments and simulation for chemical and thermonuclear flames |
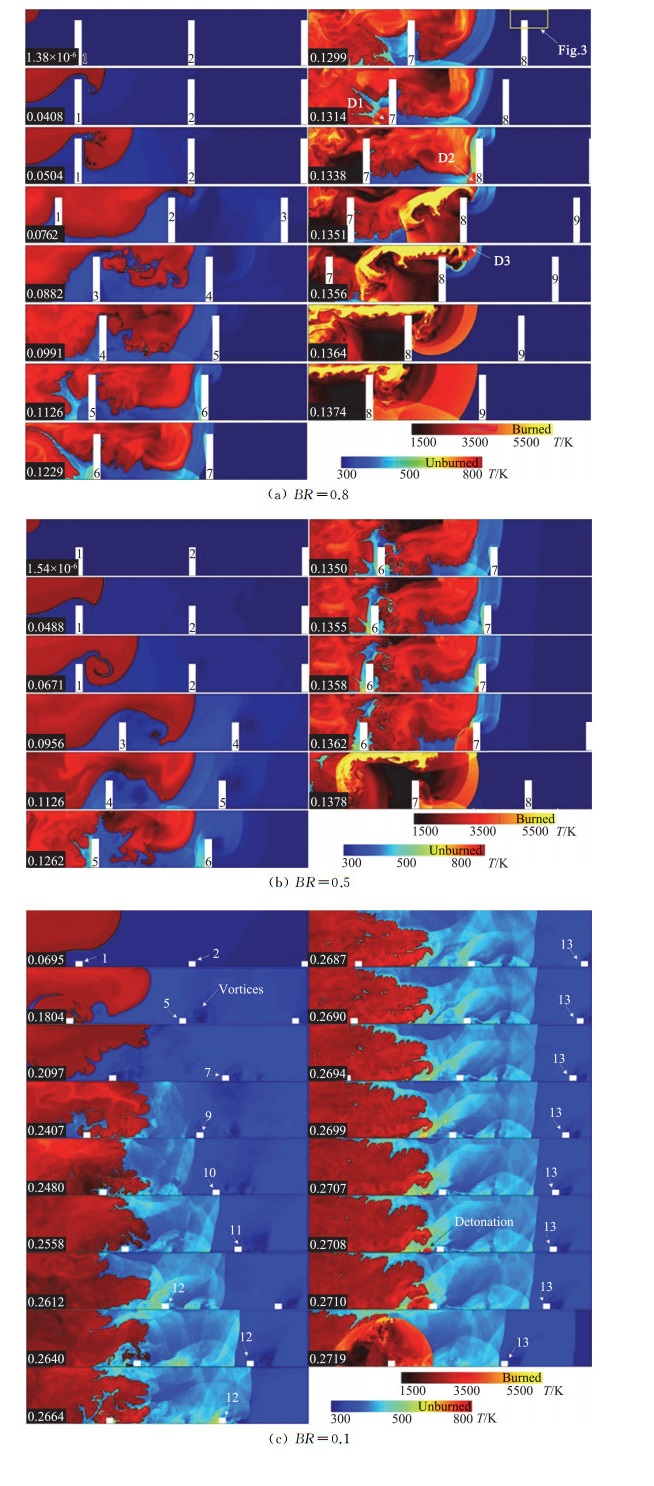
Gamezo采用二维N-S方程对有障碍物的管道中的DDT过程进行了数值研究[20],并讨论了障碍物间距对DDT过程的影响,可燃气体采用氢气-空气混合物,化学反应模型采用单步化学反应,最小网格尺寸为1/512 cm。图 11为火焰通过有障碍物的管道时加速及DDT形成过程的温度等值云图。障碍物的作用使得火焰卷曲变形,燃烧面积增加,火焰加速,伴随着火焰的不稳定,如激波与火焰作用的Richtmyer-Meshkov不稳定。燃烧产物以热射流形式穿过障碍物上方的狭窄通道,由于Helmholtz不稳定,形成剪切层和涡环结构,火焰进一步加速。障碍物的持续作用,使得爆轰最终形成。然而,此计算始终基于层流模型。变形层流火焰与湍流燃烧一样,也可使火焰持续加速,进而诱导激波。因此,层流燃烧计算也能使燃烧转为爆轰,但计算结果描述的物理过程与实验并不吻合。这是由于火焰严重变形时,已发展成湍流燃烧,不再是层流燃烧,若采用直接模拟,网格尺度应为Kolmogorov微尺度,远小于该文章的网格尺寸。

|
图 11 有障碍物的管道中,火焰加速和DDT过程 Fig.11 Flame acceleration and DDT in channel with obstacles |
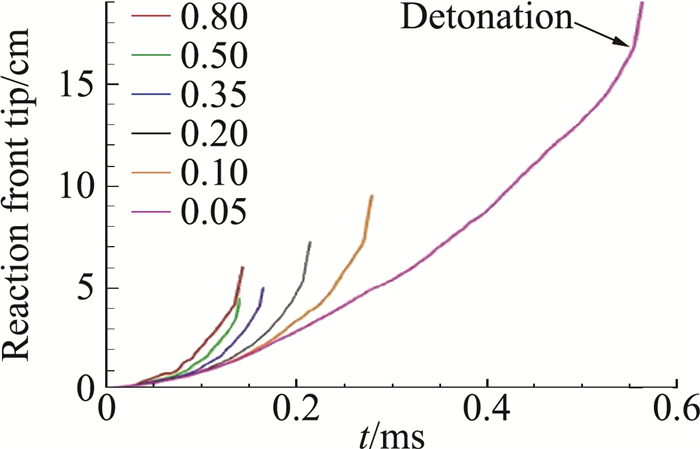
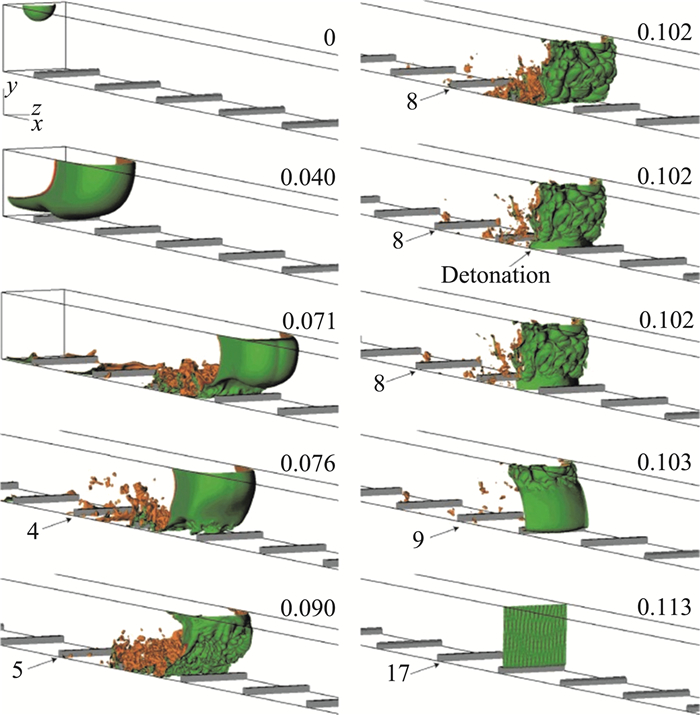
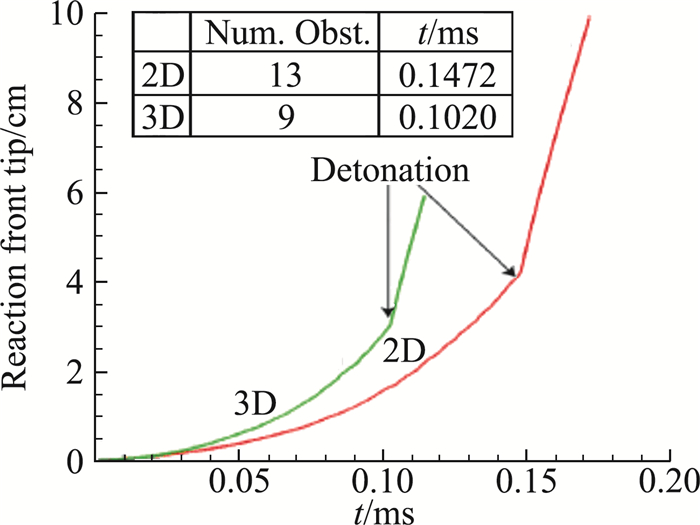
Goodwin通过数值模拟对障碍物阻塞比对管道内DDT的影响进行了二维和三维研究[21-22]。二维数值模拟采用的最小网格是3.3 μm,最大网格是53.3 μm,三维数值模拟采用的最小网格是6.67 μm,最大网格是53.3 μm,可燃气体采用氢气-空气混合物,化学反应模型采用一步反应模型。图 12为不同阻塞比的管道中,火焰加速和DDT形成的二维温度等值云图。随着阻塞比的降低,可观察到两种不同的DDT机理。对于阻塞比为0.5时,在障碍物处形成马赫反射,马赫干后形成热点,诱发爆轰; 阻塞比为0.1时,激波在边界层处多次反射,形成能量聚焦,诱发爆轰; 对于高阻塞比0.8,爆轰的诱发同时具有上述两种机理。图 13为不同阻塞比下,火焰前锋随时间的变化。障碍物的阻塞比越大,对火焰的扰动越厉害,越容易诱发湍流,进而更容易形成爆轰。图 14为阻塞比为0.1时,火焰加速和DDT形成的三维反应物质量分数等值面图。层流火焰通过障碍物时开始加速,在t=0.071 ms时,经过第三个障碍物,此时,在管道的下侧壁面附近开始形成湍流火焰结构,经过第六个障碍物时,形成充分发展的湍流火焰,t=0.102 ms时,在下壁面开始起爆。与二维数值模拟的结果相比,火焰加速和DDT形成的过程是相似的。但是,在三维的数值计算结果中,湍流使得火焰加速更快,也就越早形成爆轰。图 15表示阻塞比为0.1时,二维和三维数值计算的火焰锋面位置随时间的变化曲线。对于二维数值计算的DDT过程,经过13个障碍物,大约t=0.1472 ms,开始形成爆轰波,而三维数值计算的DDT过程,只需经过9个障碍物,用时0.102 ms就可以形成爆轰波。这也表明,不考虑湍流效应的DDT过程,其计算结果无法用来对DDT进行定量预测,比如DDT距离。
|
图 12 不同阻塞比的二维管道中,火焰加速和爆轰形成过程 Fig.12 Accelerating flame and detonation in 2D quarter-channel with different blockage ratios |
|
图 13 不同阻塞比下,火焰面前端随时间变化 Fig.13 Reaction front tip as a function of time for all blockage ratio in this series of simulations |
|
图 14 阻塞比为0.1的三维管道中,以反应物质量分数的等值面表示火焰加速和爆轰形成过程 Fig.14 Isosurface of reactant mass fractions, y=0.2, 0.5, 0.8 show flame acceleration and detonation in 3D channel with BR=0.1 |
|
图 15 阻塞比为0.1、高度为0.16 cm的管道中,二维和三维数值模拟的火焰面前端随时间变化 Fig.15 Reaction front tip position vs. time for 2D and 3D simulations with a channel height of 0.16 cm and BR=0.1 |
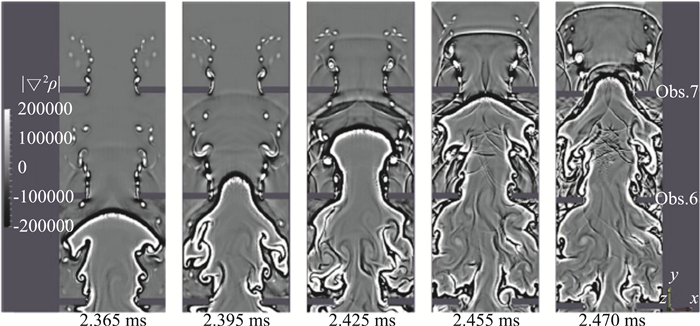
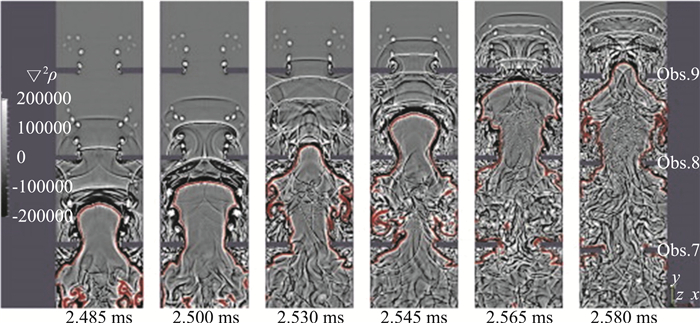
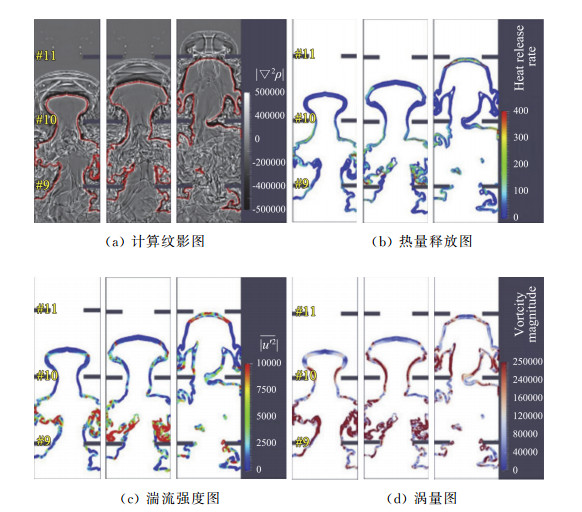
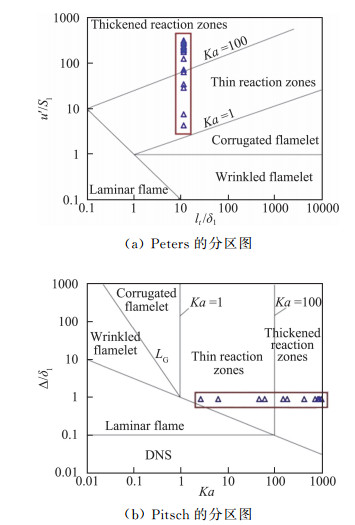
尽管之前的直接数值模拟研究采用了较细的网格,但是湍流中的最小尺寸Kolmogorov尺寸却没有提及。Emami采用大涡模拟对氢气-空气的DDT过程进行了数值模拟[23],亚网格的湍动能采用输运方程描述[24],燃烧模型采用ATF(Artificial Thickened Flame)方法,化学反应采用9组分27步详细反应机理模型,采用ISAT(In Situ Adaptive Tabulation)方法,以减小详细化学反应带来的计算消耗。图 16和图 17为火焰在障碍物之间传播时的计算阴影图,燃烧产物的膨胀在火焰的前方形成压缩波,该波在与障碍物和壁面的反射中不断加强,形成激波,激波随后与障碍物附近的涡相关作用,已有的研究表明,激波-涡和激波-湍流的相互作用可以增加湍动能和涡量,同时减小流动的长度尺度[25],因此障碍物附近的湍流得到增强,进一步使火焰加速(图 16)。随着激波与涡的作用,激波及其反射激波在壁面和障碍物上反射,火焰面的前方出现复杂的湍流区域(图 17中的2.5 ms)。当火焰传播速度达到压缩过的未燃混合物的声速时,远处障碍物的下游流动没有得到加强,反而逐渐衰减。因此,障碍物前方没有形成较强的涡量场,该现象在图 18中可以观察到,图 18中依次为计算纹影图、热量释放图、湍流强度图和涡量图,时间依次为2.64、2.65、2.67 ms。在2.64 ms时刻,火焰前锋通过第十个障碍物,此时,火焰没有与壁面的反射激波作用,火焰锋面的热量释放率和湍流强度较低。当火焰速度达到未燃物的声速时,远处障碍物的流动减弱,湍流强度降低,因此,障碍物与火焰的强作用没有发生。在2.65 ms时刻,壁面反射的激波开始与火焰面作用,导致能量释放、湍流强度和涡量均急剧增加。在2.67 ms时刻,火焰前锋到达第11个障碍物,火焰与更强的反射激波作用,使得能量释放进一步增加,这与Ciccarelli提出的快速火焰传播机理[26]是一致的。基于大涡模拟计算的数据,火焰通过障碍物加速时,涉及的湍流燃烧处于不同的湍流燃烧区域,如图 19所示,其中19(a)表示Peters提出的湍流燃烧分区[27],19(b)表示Pitsch提出的针对大涡模拟的修正的湍流燃烧分区[28]。在这两幅分区图中可以观察到,传播的火焰位于“薄火焰区”(Ka>1)和“厚火焰区”(Ka>100)。随着火焰的传播,湍流燃烧进入“厚火焰区”,此时,燃烧速率由化学反应控制,而不是由混合控制,这表明计算采用的ATF模型是合适的。
|
图 16 火焰在障碍物5和7之间传播的计算阴影图 Fig.16 Time sequence of shadowgraph pictures of flame propagation between obstacle No.5 and No.7 |
|
图 17 火焰在障碍物7和9之间传播的计算阴影图 Fig.17 Time sequence of shadowgraph pictures of flame propagation between obstacle No.7 and No.9 |
|
图 18 |
|
图 19 在预混湍流燃烧分区图中,火焰在有障碍物的管道中传播时的位置 Fig.19 Estimated flame position during the propagating past over the obstacles in premixed turbulent combustion regime diagram |
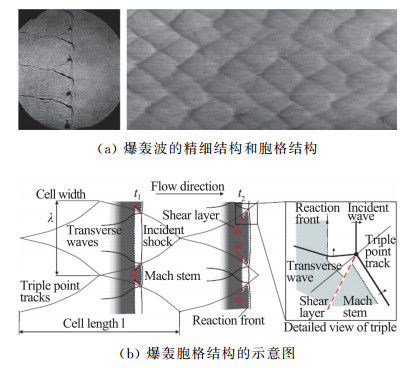
爆轰波在管道中传播时,在管壁会留下鱼鳞状的胞格结构[37]。这些胞格结构与爆轰波阵面上激波的相关作用有关,如图 20(a)所示,其中横波对爆轰波的传播起到关键的作用。每次横波相碰时,其距离大约等于爆轰波结构中反应区宽度的100倍左右,该距离称为爆轰胞格宽度,如图 20(b)所示,它是可燃系统的本征值,是爆轰的动力学参数[38],反映了系统气体动力学和化学反应动力学之间的非线性关系。
|
图 20 爆轰波的结构 Fig.20 Structure of detonation wave |
爆轰在本质上是不稳定的,胞格结构较规则的可燃系统称为“弱不稳定”胞格结构不规则的可燃系统称为“强不稳定”[39],如图 21所示。稳定性强弱与可燃系统的活化能密切相关。NG提出了一个稳定参数来区分爆轰波的稳定性[40],该参数可表示为:
| $ \chi=\varepsilon_{1} \frac{\Delta_{1}}{\Delta_{R}} $ | (1) |

|
图 21 初压为20 kPa下的爆轰胞格 Fig.21 Cell structure of detonation, P0=20 kPa |
其中,
对于弱不稳定爆轰的可燃系统来说,混合物具有较低的活化能,比如H2+O2、C2H2+O2或者氩稀释的燃料-氧气混合物。低活化能使激波后的未燃气体有较短的点火延迟,能量可在较短的时间释放,爆轰波阵面处的燃烧呈现层流燃烧。此时,弱不稳定爆轰的传播仅由激波压缩来驱动,其结构可以较好地通过波后气体的点火延迟历程来预测,而输运效应可以忽略[41]。
对于强不稳定爆轰的可燃系统来说,混合物的活化能较高,反应诱导区较宽,三波点附近的剪切层及各种不稳定使得波阵面处的燃烧呈现湍流燃烧[42-46]。此时,爆轰波的传播由激波压缩和湍流输运共同维持,这类混合物主要是碳氢燃料和氧气或其他氧化剂组成,形成的胞格尺寸有较宽广的范围。
2.2 强不稳定的爆轰波结构中的湍流燃烧已有的实验表明,对于强不稳定的爆轰波,激波阵面脉动较大。马赫干较强,波后的可燃气体在较短的时间内完全燃烧,而入射激波的强度较弱,波后的诱导区较长,反射横波分为两部分,一部分在入射激波压缩后的未燃气体中传播,使其燃烧,另一部分在燃烧产物中传播。同时,横波与入射激波后的火焰面作用,产生Richtmyer-Meshkov(RM)不稳定,加强了局部燃烧速率。在反射横波与马赫干后的燃烧产物具有不同的速度,因此在这两道波间出现一剪切层,该层是由Kelvin-Helmholtz(KH)不稳定引起的,如图 22所示,其中图 22(a)是实验纹影图,图 22(b)是流场简图。入射激波后的火焰面为湍流燃烧,剪切层是一道接触间断,也呈湍流状态,是湍流剪切层[43]。
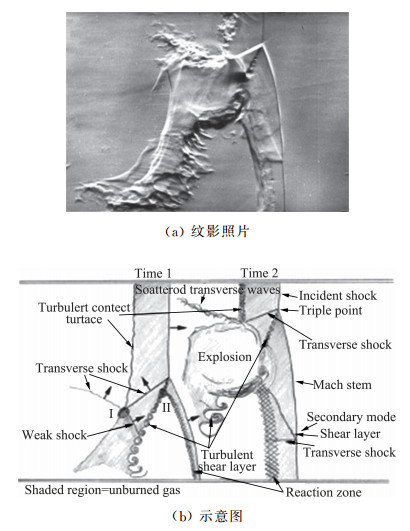
|
图 22 甲烷与氧气混合物在初压3.4 kPa下的爆轰波的精细结构 Fig.22 Detailed structure of detonation wave in a CH4+2O2 mixture at 3.4 kPa initial pressure |
此外,由于入射激波较弱,可燃气体不能完全燃烧,在波阵面的后部形成被燃烧产物包围的未燃气团,如图 23所示,未燃气团清晰可见。该气团被燃烧产物包围,其大小和距离波阵面的位置随活化能的增加而增加。实验表明,这些未燃气团的燃烧速度非常快,其数量级明显快于定常激波的点火时间。因此,ZND模型不能预测前导激波后的流场特性。这意味着波后的未燃气团与周围的燃烧产物以湍流混合的方式进行燃烧,而不仅仅是激波压缩引起的燃烧。这些未燃气团仍然在爆轰波的流体力学结构中,即激波阵面与平均声速面之间,因而压力脉冲可以影响爆轰波阵面[6]。而且,三波点对未燃气团的燃烧动力过程起到关键的作用,这是由于三波点不仅能提供高温高压的环境,而且能加强湍流混合。
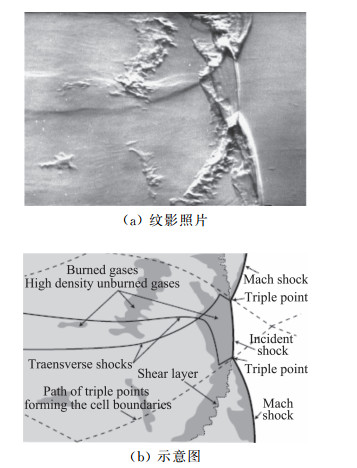
|
图 23 甲烷与氧气混合物在初压3.4 kPa下的爆轰波的精细结构 Fig.23 Detailed structure of detonation wave in a CH4+2O2 mixture at 3.4 kPa initial pressure |
目前为止,数值研究表明,在精度足够的条件下,中等活化能的不规则爆轰波结构可以较好地通过数值求解Euler方程得到[47-48]。然而,更多的数值研究表明,采用同样的方法求解带有较高活化能的不规则混合物时,取得的成功有限[6]。尽管这种努力使人们对理解激波压缩或湍流运动对爆轰波传播的影响有限,得到的解也受限于精度的影响,不能收敛于唯一解。但是,这种研究证实,波阵面存在较长的诱导时间,其数量级是实验中观察到的100倍左右,未燃气团通过数值算法的精度误差引起的扩散迅速地燃烧。一些研究者试图通过直接数值求解Navier-Stokes(N-S)方程,得到流场涉及到的完整谱尺度,包括分子扩散效应。不幸的是,这些研究表明,对二维问题涉及的全谱尺度的求解,得到的数值解不足以正确地反映未燃气团的燃烧速率[49]。因此,全尺度的直接数值模拟只能针对单个的事件,比如三波点的碰撞[50]。此外,湍流本质上是三维的,湍流的运动满足能量串级,其耗散取决于第三个方向的拉伸[51]。
Radulescu分析了高活化能的不稳定爆轰波的流场中的Kolmogorov尺度,认为Kolmogorov尺度是爆轰波ZND模型诱导区长度的1×10-4倍,意味着诱导区内至少有1×104个网格,网格尺度只有达到精度,才能准确模拟爆轰波结构中的湍流扩散过程,目前的计算能力还无法完成这种计算[6]。因此,目前数值模拟无法通过直接模拟来求解爆轰波中的湍流燃烧,而大涡模拟(LES)兼顾求解精度和计算能力的平衡,其中大尺度的运动通过直接数值求解N-S方程,无法求解的小尺度湍流采用建模的方法[52-58]。
虽然二维流动只能描述大尺度的流体运动,Radulescu采用二维Euler方程对高度不稳定爆轰波结构整体特性进行了数值研究,如图 24所示。在爆轰波阵面后方也出现了未燃气团,横波与未燃气团作用,不会明显改变气团的形状,这与实验中观察到是一致的。但是,该未燃气团的燃烧是通过数值扩散进行,速度较慢,无法维持激波的自持传播[43]。
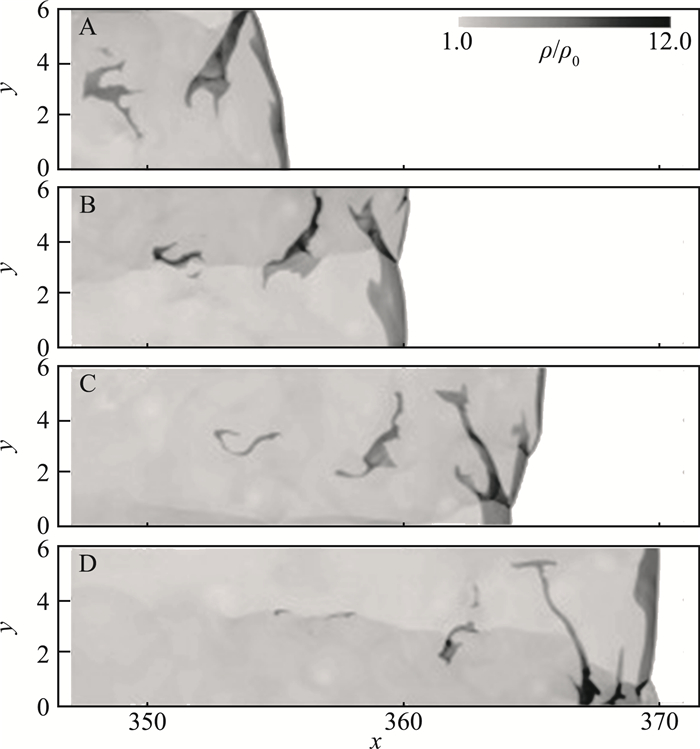
|
图 24 数值实验中的密度等值云图 Fig.24 Density profiles in a consecutive frames of numerical experiments |
Mahmoudi对不稳定爆轰波的结构分别采用Euler方程、Navier-Stokes方程和大涡模拟进行了数值模拟[49]。大涡模拟中亚网格模型采用的是Smagorinsky涡黏模型,化学反应模型采用滤波后的Arrhenius定律,即假定湍流的亚网格时间小于所有的化学反应时间。图 25是密度等值云图,图 25(a) ~25(c)分别为Euler方程、N-S方程和大涡模拟计算的结果,Euler方程和N-S方程计算的结果定性是一致的,但是N-S方程的结果中KH不稳定引起的小尺度涡被分子扩散所抑制。采用大涡模拟计算的结果,由于湍流扩散的存在,KH不稳定引起涡的尺度更加小,并且与射流有关的长舌状未燃气体几乎消失,这使得该射流与激波作用形成的第二三波点B也不存在,结构更加规则些。图 26是相应的压力等值云图,由于湍流使未燃气体的快速消耗,横波未与未燃气体作用,因此局部最高压力比Euler方程和N-S方程计算的均低,且横波直接在壁面上反射。通过与Kiyanda的实验[59]对比(图 27),大涡模拟计算的结果吻合的更好。

|
图 25 热力学参数:Ea/RT0=20, Q/RT0=50, γ=1.2,精度为半个反应区600网格时,爆轰波结构的密度等值线云图 Fig.25 Contour of the density of the detonation structure in a mixture with Ea/RT0=20, Q/RT0=50, γ=1.2, and resolution of 600 cells per HRL |
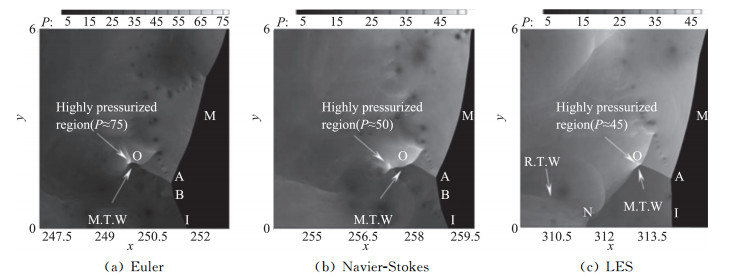
|
图 26 热力学参数:Ea/RT0=20, Q/RT0=50, γ=1.2,精度为半个反应区600网格时,爆轰波结构的压力等值线云图 Fig.26 Pressure contour of the detonation structure in a mixture with Ea/RT=20, Q/RT0=50, γ=1.2, and resolution of 600 cells per HRL |
|
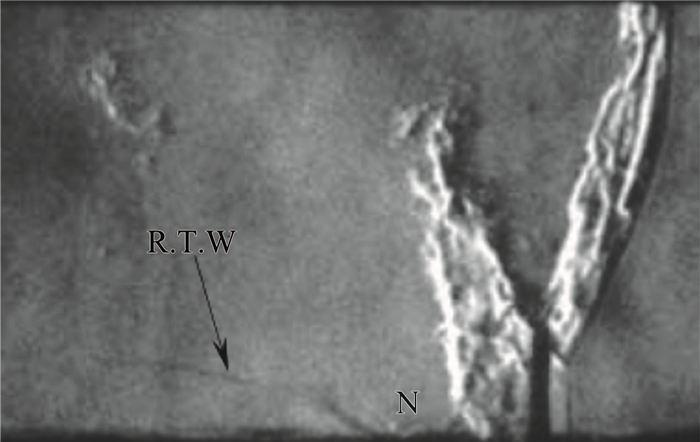
图 27 爆轰波的反应区结构的纹影图 Fig.27 Schlieren of the reaction zone structure of the detonation |
Mahmoudi的研究虽然对爆轰波的结构进行了较好的模拟,但其对反应封闭问题的处理采用了一定的假设,爆轰波后面的燃料的反应速率的求解精度还是有问题的,该研究工作是将湍流混合与燃烧速率分开单独求解。随后,Maxwell采用CLEM-LES方法对爆轰波结构进行了数值模拟[56-58],其中N-S方程采用LES,组元守恒方程采用线性涡模型[60-64](Linear Eddy Model, LEM)。计算时,需要采用两套网格,LES在大尺度主网格中进行,基于LEM的组元守恒方程在小尺度亚网格中进行,湍流扩散用随机翻转模型处理, 该方法的主要优点是可以同时处理化学反应与同一尺度的流动,不需要对反应速率进行假设。图 28是爆轰波结构的数值计算结果与实验结果,其中图 28(a)为Maxwell数值计算结果,图 28(b)为Kiyanda的实验自发光图片[65]。爆轰波后部出现明显的未燃气团,该气团的湍流火焰速度可通过数值结果计算得到。对于气团,局部湍流火焰速度可以采用下式计算:
| $ S_{t, \text { local }}=\frac{\dot{m}}{\rho_{u} A_{c}} $ | (2) |
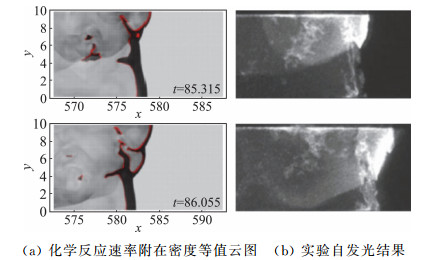
|
图 28 爆轰波的精细结构 Fig.28 Detailed structure of the detonation wave |
其中,
| $ {{S}_{t}}=\sum\limits_{1}^{n}{{{S}_{t, \text { local }}}}/n $ | (3) |
为了得到局部湍流混合速率对湍流火焰速度的影响,图 29表示平均湍流火焰速度St/SL随湍流强度u′/SL的变化曲线,对于每一湍流强度,火焰速度采用u′/SL±0.5之间的平均值。结果表明,平均湍流火焰速度随着湍流强度呈线性增长,这与Abdel-Gayed的实验结果[66]是一致的。
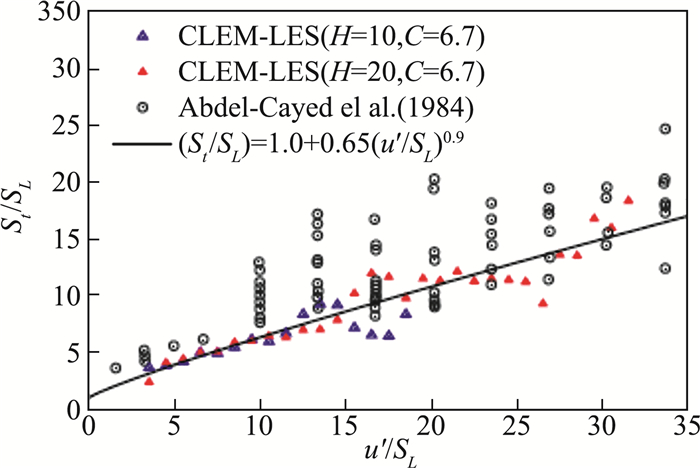
|
图 29 根据数值计算结果与Abdel-Gayed的实验结果,湍流火焰速度随湍流强度的变化 Fig.29 Average turbulent flame speed (St/SL) versus turbulent intensities (u′/SL), obtained from simulation and compared to experiments of Abdel-Gayed |
爆轰的生成和传播是爆轰的两个重要现象,其中的爆燃转爆轰(DDT)和强不稳定的爆轰波结构是关注的重点,目前主要采用实验观测和数值模拟研究。在DDT的研究中,燃烧产物的膨胀导致燃烧波前质点的流动,形成背景流场,无论是管道中的边界层还是障碍物均对背景流场施加影响,使火焰面变形加速,燃烧速率增加,而背景流场的速度随着的燃烧速率的增加而增加,这又导致流场雷诺数的增加。当雷诺数大于临界值时,背景流场出现湍流,形成湍流燃烧,当燃烧速率超过CJ爆燃速率时,流场极不稳定,或出现热点形成局部爆炸中心,或出现强激波诱发燃烧,最终形成爆轰。在强不稳定的爆轰波结构研究中,较高的活化能使得反应诱导区较宽,三波点附近的火焰面和剪切层出现了湍流,加强了燃烧速率和产物之间的混合速率。此外波后的未燃气团也出现了湍流燃烧,燃烧释放的压力脉冲有可能会影响爆轰波的结构,这取决于未燃气团的位置。无论是DDT中火焰的加速,还是强不稳定的爆轰波结构中激波与火焰的耦合,湍流在其中都起了关键的作用,因此,在爆轰的未来研究中需要结合其自身特点开展研究。
爆轰是一种超声速燃烧,具有高马赫数、高雷诺数和高温高压的特点。对该物理现象的描述可以采用反应流N-S方程(包括质量方程、动量方程和能量方程)处理,这是一组偏微分方程,具有不适定性(方程不稳定导致的湍流燃烧)和奇异性(跨声速中的声速点),至今没有解析解,这属于数学层面的难题,在未来相当长的时间可能也无法得到解析解,而爆轰的重要特性显然与方程的这种不适定性和奇异性密切相关。关于爆轰现象的实验测试,目前主要还是主要采用光学测试技术,这是一种非接触式测量技术,它对流场的干扰小,有着高精度、高灵敏度、快速和实时测量的特点,能对爆轰波流场进行清晰的测试,其结果多用于爆轰现象的定性讨论和少量的定量测试,比如实验测量的爆速,一直是判断爆轰是否形成的标准参数。对于爆轰现象的定量分析还得更多借助于数值模拟,模拟方法可以分为直接数值模拟、基于RANS的湍流模型和大涡模拟。直接数值模拟具有流场分辨率最高、信息量最大等优点,其缺点也很明显,比如需占用较大的计算资源,因此,该方法主要用于小尺度的基础研究。基于RANS的湍流模型得到的流场数据不是流场的真实信息,而是流场参数的平均值,可以反映流场的整体结构,因此,该方法可以用于爆轰的工程应用,比如各种爆轰推进系统。大涡模拟是介于直接数值模拟和基于RANS的湍流模型之间的湍流数值方法,无论是基础研究还是工程应用,该方法都具有较大的潜力,其面临的难题是各种模型的封闭问题,比如湍流的亚格子应力模型、燃烧模型、高速流动源项的封闭模型等。由于组分守恒方程中含有温度的指数项,故燃烧模型的封闭是其关键难题。线性涡模型(LEM)已被用来处理爆轰中的燃烧问题,并取得了较好的效果。此外,Flamelet模型、TPDF(Transported Probability Density Function)模型和ODT(One Dimensional Turbulence)模型已用于高速湍流燃烧,并取得了一定成果,未来也可用于爆轰的模拟中,这些值得进一步研究。
| [1] |
WOLAŃSKI P. Detonative propulsion[J]. Proceedings of the Combustion Institute, 2013, 34(1): 125-158. DOI:10.1016/j.proci.2012.10.005 |
| [2] |
LU F K. Progress and challenges in the development of detonation engines for propulsion and power production[J]. Applied Mechanics and Materials, 2016, 819: 3-10. DOI:10.4028/www.scientific.net/amm.819.3 |
| [3] |
LEE J H S. The detonation phenomena[M]. Cambridge University Press, 2008. ISBN-13: 978-0521897235 ISBN-10: 0521897238
|
| [4] |
HE L T, CLAVIN P. On the direct initiation of gaseous detonations by an energy source[J]. Journal of Fluid Mechanics, 1994, 277: 227-248. DOI:10.1017/s0022112094002740 |
| [5] |
范宝春. 极度燃烧[M]. 北京: 国防工业出版社, 2018. FAN B C. Extremecombustion[M]. Beijing: National Defense Industry Press, 2018. (in Chinese) |
| [6] |
RADULESCU M I, SHARPE G J, LAW C K, et al. The hydrodynamic structure of unstable cellular detonations[J]. Journal of Fluid Mechanics, 2007, 580: 31-81. DOI:10.1017/s0022112007005046 |
| [7] |
CICCARELLI G, DOROFEEV S. Flame acceleration and transition to detonation inducts[J]. Progress in Energy and Combustion Science, 2008, 34(4): 499-550. DOI:10.1016/j.pecs.2007.11.002 |
| [8] |
Urtiew P A, Oppenheim A K. Experimental observations of the transition to detonation in an explosive gas[J]. Proceedings of the Royal Society of London Series A, 1966, 295: 13-28. DOI:10.1098/rspa.1966.0223 |
| [9] |
KUZNETSOV M, ALEKSEEV V, MATSUKOV I, et al. DDT in a smooth tube filled with a hydrogen-oxygen mixture[J]. Shock Waves, 2005, 14(3): 205-215. DOI:10.1007/s00193-005-0265-6 |
| [10] |
LIBERMAN M A, KUZNETSOV M, IVANOV A, et al. Formation of the preheated zone ahead of a propagating flame and the mechanism underlying the deflagration-to-detonation transition[J]. Physics Letters A, 2009, 373(5): 501-510. DOI:10.1016/j.physleta.2008.12.008 |
| [11] |
LIBERMAN M A, IVANOV M F, KIVERIN A D, et al. Deflagration-to-detonation transition in highly reactive combustible mixtures[J]. Acta Astronautica, 2010, 67(7/8): 688-701. DOI:10.1016/j.actaastro.2010.05.024 |
| [12] |
FAN B C, YING Z F, CHEN Z H, et al. Observations of flame behavior during flame-obstacleinteraction[J]. Process Safety Progress, 2008, 27(1): 66-71. DOI:10.1002/prs.10223 |
| [13] |
CICCARELLI G, JOHANSEN C, HICKEY M C. Flame acceleration enhancement by distributed ignitionpoints[J]. Journal of Propulsion and Power, 2005, 21(6): 1029-1034. DOI:10.2514/1.14425 |
| [14] |
GOODWIN G B, HOUIM R W, ORAN E S. Shock transition to detonation in channels with obstacles[J]. Proceedings of the Combustion Institute, 2017, 36(2): 2717-2724. DOI:10.1016/j.proci.2016.06.160 |
| [15] |
ZIPF R K, GAMEZO V N, MOHAMED K M, et al. Deflagration-to-detonation transition in natural gas-air mixtures[J]. Combustion and Flame, 2014, 161(8): 2165-2176. DOI:10.1016/j.combustflame.2014.02.002 |
| [16] |
IVANOV M F, KIVERIN A D, YAKOVENKO I S, et al. Hydrogen-oxygen flame acceleration and deflagration-to-detonation transition in three-dimensional rectangular channels with no-slip walls[J]. International Journal of Hydrogen Energy, 2013, 38(36): 16427-16440. DOI:10.1016/j.ijhydene.2013.08.124 |
| [17] |
KUZNETSOV M, LIBERMAN M, MATSUKOV I. Experimental study of the preheat zone formation and deflagration to detonationtransition[J]. Combustion Science and Technology, 2010, 182(11/12): 1628-1644. DOI:10.1080/00102202.2010.497327 |
| [18] |
POLUDNENKO A Y, GARDINER T A, ORAN E S. Spontaneous transition of turbulent flames to detonations in unconfined media[J]. Physical Review Letters, 2011, 107(5): 054501. DOI:10.1103/physrevlett.107.054501 |
| [19] |
POLUDNENKO A Y, CHAMBERS J, AHMED K, et al. A unified mechanism for unconfined deflagration-to-detonation transition in terrestrial chemical syste ms and type Ia supernovae[J]. Science, 2019, 366(6465): eaau7365. DOI:10.1126/science.aau7365 |
| [20] |
GAMEZO V N, OGAWA T, ORAN E S. Flame acceleration and DDT in channels with obstacles:Effect of obstacle spacing[J]. Combustion and Flame, 2008, 155(1/2): 302-315. DOI:10.1016/j.combustflame.2008.06.004 |
| [21] |
GOODWIN G B, HOUIM R W, ORAN E S. Effect of decreasing blockage ratio on DDT in small channels with obstacles[J]. Combustion and Flame, 2016, 173: 16-26. DOI:10.1016/j.combustflame.2016.07.029 |
| [22] |
GOODWIN G B, ORAN E S. Premixed flame stability and transition to detonation in a supersonic combustor[J]. Combustion and Flame, 2018, 197: 145-160. DOI:10.1016/j.combustflame.2018.07.008 |
| [23] |
EMAMI S, MAZAHERI K, SHAMOONI A, et al. LES of flame acceleration and DDT in hydrogen-air mixture using artificially thickened flame approach and detailed chemical kinetics[J]. International Journal of Hydrogen Energy, 2015, 40(23): 7395-7408. DOI:10.1016/j.ijhydene.2015.03.165 |
| [24] |
VAAGSAETHER K, KNUDSEN V, BJERKETVEDT D. Simulation of flame acceleration and DDT in H2-air mixture with a flux limiter centered method[J]. International Journal of Hydrogen Energy, 2007, 32(13): 2186-2191. DOI:10.1016/j.ijhydene.2007.04.006 |
| [25] |
ELLZEY J L, HENNEKE M R, PICONE J M, et al. The interaction of a shock with a vortex:Shock distortion and the production of acoustic waves[J]. Physics of Fluids, 1995, 7(1): 172-184. DOI:10.1063/1.868738 |
| [26] |
CICCARELLI G, JOHANSEN C T, PARRAVANI M. The role of shock-flame interactions on flame acceleration in an obstacle laden channel[J]. Combustion and Flame, 2010, 157(11): 2125-2136. DOI:10.1016/j.combustflame.2010.05.003 |
| [27] |
Peters N. Turbulent combustion[M]//Cambridge Monographs on Mechanics. Cambridge University Press, 2001. ISBN-13: 978-0521660822 ISBN-10: 0521660823
|
| [28] |
PITSCH H, de LAGENESTE L D. Large-eddy simulation of premixed turbulent combustion using a level-set approach[J]. Proceedings of the Combustion Institute, 2002, 29(2): 2001-2008. DOI:10.1016/S1540-7489(02)80244-9 |
| [29] |
BANG B H, AHN C S, KIM Y T, et al. Deflagration-to-detonation transition in pipes:The analytical theory[J]. Applied Mathematical Modelling, 2019, 66: 332-343. DOI:10.1016/j.apm.2018.09.023 |
| [30] |
HAN W H, GAO Y, LAW C K. Flame acceleration and deflagration-to-detonation transition in micro- and macro-channels:an integrated mechanistic study[J]. Combustion and Flame, 2017, 176: 285-298. DOI:10.1016/j.combustflame.2016.10.010 |
| [31] |
COATES A M, MATHIAS D L, CANTWELL B J. Numerical investigation of the effect of obstacle shape on deflagration to detonation transition in a hydrogen-air mixture[J]. Combustion and Flame, 2019, 209: 278-290. DOI:10.1016/j.combustflame.2019.07.044 |
| [32] |
OGAWA T, GAMEZO V N, ORAN E S. Flame acceleration and transition to detonation in an array of square obstacles[J]. Journal of Loss Prevention in the Process Industries, 2013, 26(2): 355-362. DOI:10.1016/j.jlp.2011.12.009 |
| [33] |
VALIEV D, BYCHKOV V, AKKERMAN V, et al. Flame acceleration in channels with obstacles in the deflagration-to-detonationtransition[J]. Combustion and Flame, 2010, 157(5): 1012-1021. DOI:10.1016/j.combustflame.2009.12.021 |
| [34] |
BYCHKOV V, AKKERMAN V, FRU G, et al. Flame acceleration in the early stages of burning intubes[J]. Combustion and Flame, 2007, 150(4): 263-276. DOI:10.1016/j.combustflame.2007.01.004 |
| [35] |
SAIF M, WANG W T, PEKALSKI A, et al. Chapman-Jouguet deflagrations and their transition to detonation[J]. Proceedings of the Combustion Institute, 2017, 36(2): 2771-2779. DOI:10.1016/j.proci.2016.07.122 |
| [36] |
KESSLER D A, GAMEZO V N, ORAN E S. Simulations of flame acceleration and deflagration-to-detonation transitions in methane-air syste ms[J]. Combustion and Flame, 2010, 157(11): 2063-2077. DOI:10.1016/j.combustflame.2010.04.011 |
| [37] |
FICKETT W, DAVIS W C. Detonation: theory and experiment[M]. New York: Dover Publication, 2000. ISBN-10: 0486414566 ISBN-13: 978-0486414560
|
| [38] |
LEE JH S. Dynamic parameters of gaseous detonations[J]. Annual Review of Fluid Mechanics, 1984, 16: 311-336. DOI:10.1146/annurev.fl.16.010184.001523 |
| [39] |
AUSTIN J M. The role of instability in gaseous detonation[D]. Caliofornia: California Institute of Technology, 2003.
|
| [40] |
NG H D. The effect of chemical reaction kinetics on the structure of gaseous detonations[D]. Montreal: McGill University, 2005.
|
| [41] |
JACKSON S I, SHORT M. The influence of the cellular instability on lead shock evolution in weakly unstable detonation[J]. Combustion and Flame, 2013, 160(10): 2260-2274. DOI:10.1016/j.combustflame.2013.04.028 |
| [42] |
SHEPHERD J E. Detonation in gases[J]. Proceedings of the Combustion Institute, 2009, 32(1): 83-98. DOI:10.1016/j.proci.2008.08.006 |
| [43] |
RADULESCU M I, SHARPE G J, LEE J H S, et al. The ignition mechanism in irregular structure gaseous detonations[J]. Proceedings of the Combustion Institute, 2005, 30(2): 1859-1867. DOI:10.1016/j.proci.2004.08.047 |
| [44] |
MASSA L, AUSTIN J M, JACKSON T L. Triple-point shear layers in gaseous detonationwaves[J]. Journal of Fluid Mechanics, 2007, 586: 205-248. DOI:10.1017/s0022112007007008 |
| [45] |
RADULESCU M I, LEE J H S. The failure mechanism of gaseous detonations:experiments in porous wall tubes[J]. Combustion and Flame, 2002, 131(1/2): 29-46. DOI:10.1016/s0010-2180(02)00390-5 |
| [46] |
MAZAHERI K, MAHMOUDI Y, SABZPOOSHANI M, et al. Experimental and numerical investigation of propagation mechanism of gaseous detonations in channels with porous walls[J]. Combustion and Flame, 2015, 162(6): 2638-2659. DOI:10.1016/j.combustflame.2015.03.015 |
| [47] |
RADULESCU M I. A detonation paradox:Why inviscid detonation simulations predict the incorrect trend for the role of instability in gaseous cellular detonations?[J]. Combustion and Flame, 2018, 195: 151-162. DOI:10.1016/j.combustflame.2018.05.002 |
| [48] |
MAZAHERI K, MAHMOUDI Y, RADULESCU M I. Diffusion and hydrodynamic instabilities in gaseous detonations[J]. Combustion and Flame, 2012, 159(6): 2138-2154. DOI:10.1016/j.combustflame.2012.01.024 |
| [49] |
MAHMOUDI Y, KARIMI N, DEITERDING R, et al. Hydrodynamic instabilities in gaseous detonations:comparison of Euler, Navier-Stokes, and Large-Eddy simulation[J]. Journal of Propulsion and Power, 2014, 30(2): 384-396. DOI:10.2514/1.b34986 |
| [50] |
BHATTACHARJEE RR, LAU-CHAPDELAINE S S M, MAINES G, et al. Detonation re-initiation mechanism following the Mach reflection of a quenched detonation[J]. Proceedings of the Combustion Institute, 2013, 34(2): 1893-1901. DOI:10.1016/j.proci.2012.07.063 |
| [51] |
KUO KK, ACHARYA R. Fundamentals of turbulent and multiphase combustion[M]. Hoboken, NJ, USA: John Wiley & Sons, Inc., 2012. https://doi.org/10.1002/9781118107683
|
| [52] |
GONZALEZ-JUEZ E D, KERSTEIN A R, RANJAN R, et al. Advances and challenges in modeling high-speed turbulent combustion in propulsion syste ms[J]. Progress in Energy and Combustion Science, 2017, 60: 26-67. DOI:10.1016/j.pecs.2016.12.003 |
| [53] |
ZBIKOWSKI M, MAKAROV D, MOLKOV V. LES model of large scale hydrogen-air planar detonations:Verification by the ZND theory[J]. International Journal of Hydrogen Energy, 2008, 33(18): 4884-4892. DOI:10.1016/j.ijhydene.2008.05.071 |
| [54] |
ZBIKOWSKI M, MAKAROV D, MOLKOV V. Numerical simulations of large-scale detonation tests in the RUT facility by the LESmodel[J]. Journal of Hazardous Materials, 2010, 181(1/2/3): 949-956. DOI:10.1016/j.jhazmat.2010.05.105 |
| [55] |
RIKANATI A, SADOT O, BEN-DOR G, et al. Shock-wave Mach-reflection slip-stream instability:a secondary small-scale turbulent mixingphenomenon[J]. Physical Review Letters, 2006, 96(17): 174503. DOI:10.1103/physrevlett.96.174503 |
| [56] |
MAXWELL B M, FALLE S A E G, SHARPE G, et al. A compressible-LEM turbulent combustion subgrid model for assessing gaseous explosion hazards[J]. Journal of Loss Prevention in the Process Industries, 2015, 36: 460-470. DOI:10.1016/j.jlp.2015.01.014 |
| [57] |
MAXWELL B M, BHATTACHARJEE R R, LAU-CHAPDELAINE S S M, et al. Influence of turbulent fluctuations on detonation propagation[J]. Journal of Fluid Mechanics, 2017, 818: 646-696. DOI:10.1017/jfm.2017.145 |
| [58] |
MAXWELL B, PEKALSKI A, RADULESCU M. Modelling of the transition of a turbulent shock-flame complex to detonation using the linear eddy model[J]. Combustion and Flame, 2018, 192: 340-357. DOI:10.1016/j.combustflame.2018.02.013 |
| [59] |
KIYANDA C B. Photographic study of the structure of irregular detonation waves[D]. Montreal: McGill University, 2005.
|
| [60] |
KERSTEIN A R. Linear-eddy modeling of turbulent transport. Ⅱ:Application to shear layer mixing[J]. Combustion and Flame, 1989, 75(3/4): 397-413. DOI:10.1016/0010-2180(89)90051-5 |
| [61] |
CHAKRAVARTHY V K, MENON S. Subgrid Modeling of Turbulent Premixed Flames in the Flamelet Regime[J]. Flow, Turbulence and Combustion, 2000, 65: 133-161. DOI:10.1023/A:1011456218761 |
| [62] |
CHAKRAVARTHY V K, MENON S. Linear eddysimulations of Reynolds number and Schmidt number effects on turbulent scalar mixing[J]. Physics of Fluids, 2001, 13(2): 488-499. DOI:10.1063/1.1335540 |
| [63] |
SANKARAN V, MENON S. LES of scalar mixing in supersonic mixinglayers[J]. Proceedings of the Combustion Institute, 2005, 30(2): 2835-2842. DOI:10.1016/j.proci.2004.08.027 |
| [64] |
WOOSLEY S E, KERSTEIN A R, SANKARAN V, et al. Type Ia Supernovae:calculations of turbulent flames using the linear eddy model[J]. The Astrophysical Journal, 2009, 704(1): 255-273. DOI:10.1088/0004-637x/704/1/255 |
| [65] |
KIYANDA C B, HIGGINS A J. Photographic investigation into the mechanism of combustion in irregular detonationwaves[J]. Shock Waves, 2013, 23(2): 115-130. DOI:10.1007/s00193-012-0413-8 |
| [66] |
ABDEL-GAYED R G, AL-KHISHALI K J, BRADLEY D. Turbulent burning velocities and flame straining in explosions[J]. Proceedings of the Royal Society A, 1984, 391: 393-414. DOI:10.1098/rspa.1984.0019 |
 2019, Vol. 38
2019, Vol. 38

