2. 上海市动力工程多相流动与传热重点实验室, 上海 200093
2. Key Laboratory of Multiphase Flow and Heat Transfer in Shanghai Power Engineering, Shanghai 200093, China
涡是湍流边界层拟序结构的核心,影响条带、猝发、上升流、下扫流等其它拟序结构的发展和演化[1],著名空气动力学家Küchemann曾说,“旋涡是流体运动的肌腱”[2],这句话深刻概括了涡的重要性。自从1952年Theodorsen[3]提出马蹄涡(又称发卡涡)模型以来,无数科研工作者致力于研究涡的相关机理。精确可靠的实验测量是诸多机理研究的前提与保障。目前,国内外已发展了多种实验测量和流场可视化方法,如氢气泡法、烟流法、染料法等。Kline等人[4]采用氢气泡法发现了湍流边界层近壁流场中的快慢斑和长带条结构,利用染料发现了猝发现象。Brodkey等人[5]使用示踪粒子和立体摄影发现了上升流和呈手指状的下扫流,并认为下扫流是产生雷诺应力的主要来源。Lian[6]利用氢气泡法对不同单个流向涡进行了研究,结果显示流向涡的旋转运动会导致下扫流和上升流的产生,流向涡结构沿流向拉伸后会从周围吸收能量,导致旋转速度增大。虽然这些可视化方法是基于定性研究的,但因其经济且易于实现,所以成为了观察大尺度湍流结构很好的实验方法[7],为人们认识和理解湍流边界层中拟序结构的宏观特性提供了很大的帮助。
随着光学技术及计算机技术的快速发展,粒子图像测速(particle image velocimetry, PIV)和粒子追踪测速(particle tracking velocimetry, PTV)等得到了广泛应用。Adrain等人[8-10]利用PIV测量到了边界层外区存在着沿流向排列且具有相同速度的发卡涡,它们组成了大尺度发卡涡包结构。近年来,三维(3D)测量技术得到了迅速发展。3D PIV或PTV测量的基本原理是结合多个2D PIV或PTV,采用多个相机进行同步测量,再利用算法重构得到3D速度场。如Kinzel等人[11]利用两个具有不同空间分辨率的PTV开展3D测量,低空间分辨率的PTV测量速度场及大尺度流动特征,高空间分辨率的PTV测量与大尺度流动特征相关的涡量和应力等小尺度物理量。Hutchins等人[12]使用两个成一定角度布置的相机开展体视PIV研究,测量与流向成45°和135°平面中的涡结构,其中在135°平面中测量到了一对反向旋转的涡结构,两涡中间发生上喷现象,这与发卡涡的涡腿特征一致。将PIV与高速相机和高能连续激光或高频脉冲激光结合,形成了时间分辨PIV(time-resolved PIV, TRPIV),可以测量流场随时间的连续变化过程[13-14]。层析PIV技术可以得到瞬时三维三分量(3D3C)速度场,已经被应用于测量湍流边界层和深入分析拟序结构机理[15-17]。如Schroder等人[15]使用六个CMOS相机,采用层析TRPIV测量了与负雷诺应力事件(Q2和Q4)相关的拟序结构及其在湍流边界层对数律层中的时间演化过程,研究了高雷诺数湍流边界层中发夹涡的初始发展机理。Katz等人[18]详细介绍了数字全息3D流场测量的原理和应用。上述测量方法在定量测量3D流场以及研究湍流机理方面发挥了巨大作用,不过测量系统非常复杂,且存在测量分辨率和测量区域大小的矛盾,难以测量涡随时空的动态演变过程。对此,蔡小舒等人[19]提出了运动单帧长曝光(moving single-frame and long-exposure, MSFLE)图像法,测量系统简单方便,可以得到直观的低雷诺数湍流边界层中涡随时空的演变过程。
除实验测量外,测量结果中的涡提取手段也是湍流研究的重要议题。Epps[20]对涡识别方法进行了全面总结,其中基于欧拉体系的方法有λ2[21]、Q[22]、λci[10]、Ω[23]等,基于拉格朗日体系的方法有有限时间Lyapunov指数法[24]、MZ[25]等。上述涡识别方法大都需要人为设定阈值,不同的阈值可能会得到不同的涡结构,而且不能提供涡的准确定义。近几年,刘超群团队基于涡的数学定义提出了一种新的涡识别方法Liutex[26-30],相比于其它涡识别方法,Liutex向量可以准确表征流体旋转强度及当地旋转轴方向。
综上所述,本文结合MSFLE图像测量法和Liutex涡识别方法对湍流边界层涡结构的时空演变过程开展了实验研究,得到了直观的涡结构特征及其演化过程,并对涡合并现象进行了量化分析。
1 实验方法及装置 1.1 MSFLE图像测量方法MSFLE图像测量方法是从单帧长曝光(single-frame and long-exposure, SFLE)图像法[31]发展而来。在SFLE测量方法中,流场中布撒跟随性良好的示踪粒子,激光器连续照明流场,通过设置相机较长的合适的曝光时间,可以将粒子的运动轨迹清晰地记录在单帧图像中。
图像中运动轨迹的长度代表了曝光时间内示踪粒子的运动距离,进而可以得到流体运动速度,通过前后两帧图像可得到流体运动方向。示踪粒子的运动速度可以由下式得到:
| $v=\frac{s}{m \Delta t} $ | (1) |
式中:v为示踪粒子的运动速度,s表示图像中示踪粒子运动轨迹长度,m为相机镜头的放大倍率,Δt是相机曝光时间。
相比于PIV和PTV采用两次曝光和两帧图像来获得粒子运动的始末位置,SFLE法采用一次长曝光可以在单帧图像中非常直观地显示粒子运动轨迹。而且SFLE法对实验条件要求较低,仅需较小功率的连续激光器和工业相机,测量装置简单,实验成本低。
通常的流场测量方法是通过欧拉视角研究流场,如PIV等。在这些方法中,测量系统固定在某个位置,只能得到在该固定位置的流场信息,无法测量湍流边界层中涡结构随时空演变过程。另外图像法测量中相机视场和图像分辨率是一对矛盾,采用高分辨率的相机镜头测量涡精细结构时,因图像视场较小,无法捕捉快速运动的涡结构。针对上述问题,本文在SFLE的基础上,采用MSFLE图像测量方法,通过拉格朗日视角研究湍流边界层中涡结构特征及其演化过程。
MSFLE图像测量方法具有运动和长曝光两大特点。一方面,实验中相机测量系统匀速运动以跟踪捕捉到与其速度相同或相近的涡结构;另一方面,采用较长曝光时间将示踪粒子运动轨迹记录在单帧图像中,得到的连续测量图像可以清晰反映涡结构及周围流场的发展变化过程。
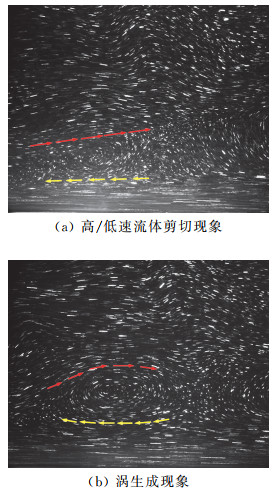
MSFLE是一种拉格朗日型测量方法,可得到涡结构随时空运动演变过程的直观图像,但得到的流体速度是相对于相机运动速度的相对速度。在该方法中高于相机移动速度的流体在图像中向下游方向运动,低于相机移动速度的流体向上游方向运动,与相机基本相同移动速度的流体结构则在图像中位置基本不变。这样可以清晰地显示出高低速流体之间的剪切作用。如图 1所示,连续拍摄的图像清晰地显示出相对相机运动速度的高/低速流动间的剪切现象及涡是如何“搓”出来的。图 1(a)为低速流体(黄色)与高速流体(红色)发生剪切的现象,剪切导致顺时针旋转涡的产生如图 1(b)所示。图 1直观地显示了涡与上下高/低速流体的联系,即涡是由高/低速流体的剪切作用产生的,这正如著名流体力学家陆士嘉提出的观点,“流体的本质就是涡,因为流体经不住搓,一搓就搓出了涡”,“搓”就是高/低速流体之间的剪切。
|
图 1 MSFLE测量到的涡生成现象 Fig.1 Vortex generation measured by MSFLE |
实验测量系统如图 2所示。实验中片光位于矩形管道展向中间位置,平行于来流并垂直矩形管道入射,以尽可能避免测量区受到管道两侧壁面边界层的影响。实验测量了矩形管道底部湍流边界层流向-法向二维平面内的涡结构演变过程。图 2中x轴为流向方向,y轴为法向方向,z轴为展向方向。实验系统由恒位水箱、回水箱、水泵、流量计、流量调节阀、实验管道、相机镜头、激光器和电动导轨等构成。水泵将回水箱中的水输送至恒位水箱以保证管道入口处压力恒定,从而确保实验段来流的稳定,水流过实验管道之后经流量调节阀和流量计回到水箱,形成循环。

|
图 2 实验测量系统示意图 Fig.2 Schematic diagram of the experimental measurement system |
有机玻璃实验管道长2200 mm,管道横截面为80 mm×80 mm的正方形。长1500 mm、宽78 mm、厚4 mm有机玻璃平板水平放置在实验管道底部,故流体流通横截面为80 mm×76mm的矩形,平板前缘距管道入口处700 mm,正对来流方向的平板前缘设计为半椭圆形,长短轴比例为4:1,以减少平板前缘对流动的干扰。将直径为4 mm的拌线布置于距平板前缘50 mm处以加速边界层的转捩。示踪粒子选用平均直径5 μm、比重1.04和折射率为1.584的聚酰胺树脂颗粒(polyamide resin particle, PSP)。图像测量系统由分辨率1280 pixel×1024 pixel、像元大小4.8 μm的XIMEA相机,放大倍率为0.14倍的远心镜头和输出1 mm厚片光、450 nm波长、4 W功率的连续半导体激光器组成。图像视场范围为44 mm×35 mm,空间分辨率为34 μm。相机曝光时间为100 ms,帧率9.995 fps,帧间间隔50 μs,基本实现连续测量。
图像测量系统安装在沿流向平行布置的导轨上,伺服电机控制图像测量系统匀速运动以捕捉矩形管道底部边界层中与此运动速度相近的涡结构。当流量为1.6 m3/h时,采用SFLE图像法由公式(1)计算得到来流速度约为U∞=100 mm/s。令Uc表示图像测量系统运动速度,U*=Uc/U∞。通过大量实验发现,当U*∈ 0.8, 0.9时测量到的边界层内涡结构现象最为丰富,这表明涡大都以这个速度运动,故图像测量系统速度在此区间内选取。令x表示距平板前缘的流向位置,实验测量范围从x=400 mm到x=1300 mm,两个位置对应的边界层厚度分别为10 mm和20 mm,动量厚度θ分别为0.97 mm和1.94 mm,基于动量损失厚度的雷诺数分别为Reθ=θU∞/ν=97和194,其中ν为流体运动黏性系数。
需要指出的是本研究中得到的是3D涡结构在流向-法向2D截面的涡特性,反映的是涡在该截面的时空演变过程。该2D时空演变过程与3D涡结构时空演变过程密切相关。
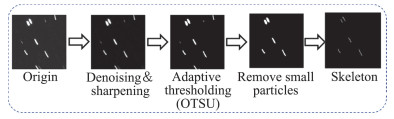
2 基于骨架提取的图像处理方法从图像获取流场速度信息的图像处理方法主要包括粒子轨迹识别和速度计算两部分[32]。粒子轨迹识别图像处理流程如图 3所示,由去噪锐化、自适应阈值分割(OTSU)、去除小颗粒和骨架提取四部分组成。自适应阈值分割算法是一种多阈值自动分割方法,通过分析像素周围局部范围的灰度特性来决定该像素点的阈值,不需要人为设定阈值,这样能够使阈值分割后的图片保留更多信息。对图像进行骨架提取后粒子轨迹是单像素宽度的轨迹,即像素精度的迹线。可以更准确计算轨迹长度,且对于弯曲的轨迹也能区分各像素点处速度方向的细微区别,同时保持图像的形态学特征。
|
图 3 轨迹识别处理流程图 Fig.3 Process flow chart of trajectory identification |
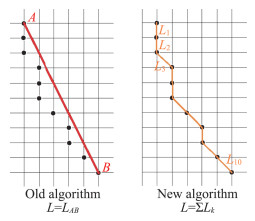
获得像素精度的迹线后,通过连通区域分割函数识别出每条轨迹上的所有像素点,传统算法采用迹线起点与终点之间的距离作为长度,在处理弯曲轨迹时会产生较大误差。本文采用求线积分的长度计算算法[32],先求出每两个像素点之间的距离,然后迭加得到总的轨迹长度,两种算法的对比如图 4所示。得到轨迹长度后由公式(1)计算流场速度,速度方向由连续的两帧图像得到。
3 Liutex涡识别方法通过骨架提取算法计算得到速度场后,要进行涡结构的识别。由于涡量在近壁强剪切区域值很大,而在涡旋转区域较小,但不能够表征流体旋转,本文采用Liutex理论[26-30]进行涡的识别和表征。Liutex理论可以系统地描述当地流体的转动强度大小及旋转轴方向,其基本思想为:如果速度梯度张量▽V存在一对复特征值λcr±λci和一个实特征值λr,那么当地流体旋转轴方向即为▽V的实特征向量的方向,即Liutex的矢量方向。Liutex的大小与方向分别以R和r表示:
| $\nabla \boldsymbol{V} \cdot \boldsymbol{r}=\lambda_{r} \boldsymbol{r} $ | (2) |
R的显示计算公式如下:
| $R=\boldsymbol{\omega} \cdot \boldsymbol{r}-\sqrt{(\boldsymbol{\omega} \cdot \boldsymbol{r})^{2}-4 \lambda_{c i}^{2}} $ | (3) |
因此,Liutex向量R被定义为R=Rr。
综上,本文所采用的涡识别与表征方法是通过骨架提取图像处理方法得到速度场,进一步使用三角剖分法进行插值,插值大小为图像像素数,之后插入第三维数据,令z=1,w=0,再计算速度梯度张量,最终通过公式(3)计算得到Liutex以实现涡强度的表征。
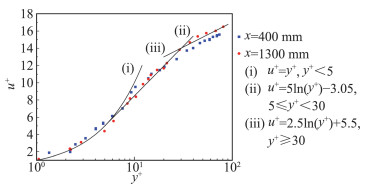
4 MSFLE测量结果与分析 4.1 湍流边界层实验验证为验证矩形管道底部边界层为湍流边界层,利用SFLE方法分别测量了x=400 mm与x=1300 mm处边界层沿法向平均速度分布。测量时片光位于展向中心处,垂直矩形管道平行来流方向布置,相机垂直片光进行测量。对测得的瞬时速度场进行统计分析,再根据公式y+=yuτ/v,u+=u/uτ将平均速度u和法向高度y用摩擦速度uτ无量纲化。摩擦速度uτ通过壁面切应力τw获得。τw根据黏性底层的速度梯度获得。
| $u_{\tau}=\sqrt{\frac{\tau_{\omega}}{\rho}}, \quad \tau_{\omega}=\mu \frac{\partial u}{\partial y} $ | (4) |
式中ρ为流体密度,μ为动力黏性系数。最终计算得到x=400 mm处uτ=6 mm/s,x=1300 mm处uτ=5.48 mm/s。两处边界层法向平均速度分布结果见图 5,该无量纲速度分布与湍流边界层内层[33]速度分布公式吻合,且两个流向位置的平均速度分布呈现自相似,表明在矩形管道底部的实验测量区域内为湍流边界层。
|
图 5 x=400 mm与1300 mm处边界层法向平均速度分布 Fig.5 Dimensionless velocity profile of experimental results at x=400 mm and x=1300 mm |
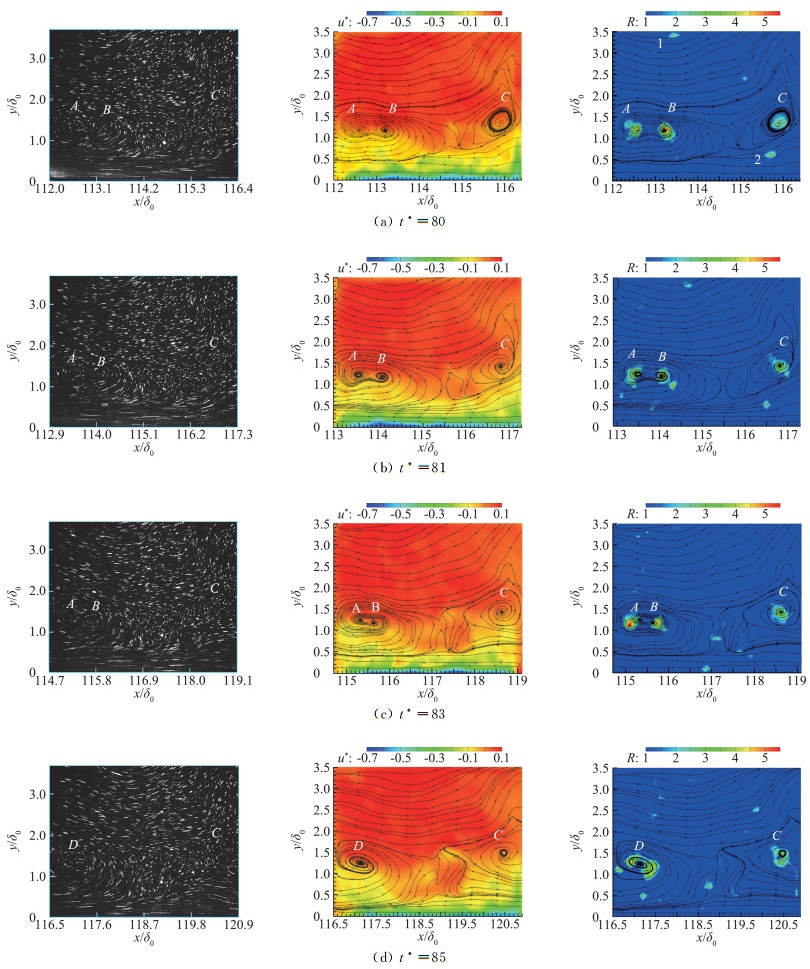
采用MSFLE测量,获得了在矩形管道底部湍流边界层内涡结构合并的整个过程。图 6给出了其中获得的两对涡合并过程中的部分时刻的图像,以及计算处理结果。其中左图为原始图像,中图为图像处理后得到的u*云图及流线图(u*=u/U∞,u为相对流向速度),右图为计算得到的R云图及流线图。图中横坐标和纵坐标均用δ0无量纲化,δ0为实验初始位置(即x=400 mm)处的边界层厚度10 mm,图像下边缘对应矩形管道底层上表面,白色轨迹线是示踪粒子在曝光时间下的运动轨迹。流体从图像左侧流向图像右侧,由于测量系统以速度Uc匀速运动,当在连续测量的图像中示踪粒子轨迹向右侧运动表示该处流体流动速度大于相机运动速度Uc,如u*云图中上部区域流线所示;当流体速度小于Uc时,示踪粒子轨迹向左侧移动,如u*云图中下部区域流线所示。定义相对于Uc运动快慢的流体分别为高速流体和低速流体。当示踪粒子轨迹在图像中仅为亮点时,则表明该粒子为稳定匀速运动状态,速度大小为Uc。
|
图 6 U*=0.9时涡合并过程图像及处理结果 Fig.6 Experimental images and processing results of vortex merging when U*=0.9 |
图 6为流向位置接近实验终止位置、U*=0.9时测量到的位于边界层内的涡合并过程中的4帧典型实验图像及处理结果。图 6的u*云图和R云图显示的涡结构的法向高度y/δ0在1~1.5之间,这里采用的δ0=10 mm,实验终止位置处的边界层厚度为20 mm。该系列图像捕捉到了三个顺时针旋转的A涡、B涡和C涡。A涡和B涡在流动过程中发生合并形成尺寸更大的D涡,而C涡在此期间位置及形状基本保持不变,表明运动速度与Uc基本一致。
令t*=tU∞/δ0, t为测量时刻。图 6(a)为t*=80时,两个尺寸基本相同的A涡和B涡开始发生合并,从u*云图及流线图可知此时A涡和B涡涡心之间的距离约为0.65。t*=81时,如图 6(b)所示,两涡涡心之间的距离减小到0.55。从测量可知B涡运动速度逐渐变慢,A涡运动速度基本不变,逐渐追上B涡,两涡水平靠近。到图 6(c)t*=83时,A涡和B涡开始接触且互相绕对方沿顺时针方向发生了旋转,此时两涡不仅具有流向方向的速度差,也具有法向方向的速度差。当t*=85时,如图 6(d)所示,新的顺时针旋转的D涡形成。
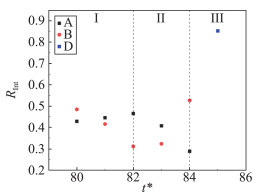
因为R可以表征涡区域和涡强度,所以利用R分析图 6中A涡和B涡合并过程中涡强度随时间的变化。涡强度由对涡区域每一点处R的积分值RInt=
|
图 7 A涡和B涡合并过程中RInt随时间的变化 Fig.7 Temporal distributions of RInt during the merging process of A vortex and B vortex |
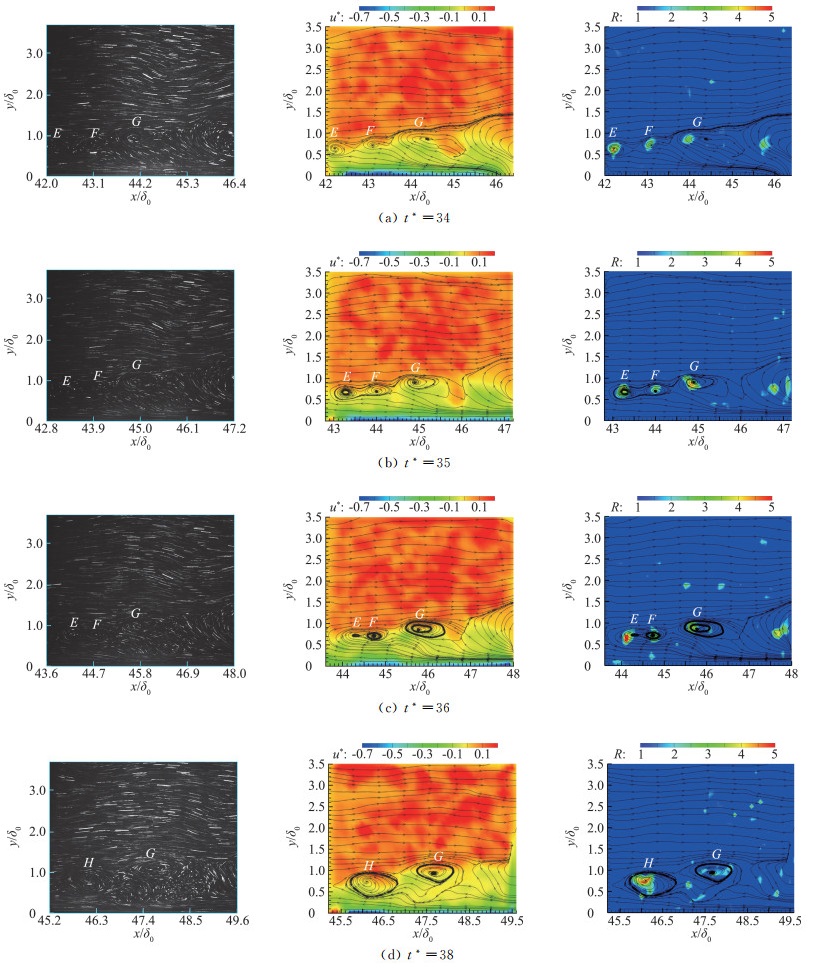
图 8为U*=0.8时测量到的另一组涡合并过程中的4帧典型的实验图像及处理结果。t*=34时,由图 8(a)R云图得到三个涡的ΔS分别为0.075、0.08和0.12,E涡和F涡开始发生合并,但F涡没有同G涡合并。分析认为由于F涡和E涡的尺寸更加接近,而F涡尺寸小于G涡,且G涡诱使下方流体向上运动到了F涡和G涡之间,阻碍了F涡和G涡的接触。t*=34时由图 8(a)u*云图可知E涡和F涡两涡心之间的距离为0.9,t*=35时涡心距离减小到了0.7,由连续两张u*云图可知E涡运动速度变快,F涡速度基本不变,两个涡在流向方向具有速度差,因此E涡逐渐平移靠近F涡。到t*=36时,由图 8(c)可知E涡和F涡发生接触互相绕对方沿顺时针方向发生旋转,表明两涡此时也具有了法向方向的速度差。当t*=38时,如图 8(d)所示,新的顺时针旋转的G涡生成,其ΔS为0.18,即新生成的G涡尺寸约为合并初始时E涡和F涡尺寸之和。
|
图 8 U*=0.8时涡合并图像及处理结果 Fig.8 Experimental images and processing results of vortex merging when U*=0.8 |
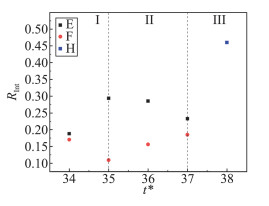
E涡和F涡在合并过程中RInt随时间的变化如图 9所示。合并过程可以分为三个阶段。第一个阶段为从t*=34到t*=35,由于流向速度差,在两个涡水平靠近过程中E涡不断吸收F涡能量,从而E涡RInt逐渐增大,F涡RInt则逐渐减小,此阶段称为平移靠近阶段。从t*=35到t*=37为第二阶段,两涡相互接触并在水平和法向方向速度差共同作用下绕对方沿顺时针旋转,在旋转过程中两个涡的能量发生扩散,能量高的E涡会将能量传输给F涡,因此E涡RInt逐渐降低,F涡RInt逐渐上升,此阶段称为相互旋转阶段。从t*=37到t*=38为第三阶段,RInt值为0.42的H涡生成,初始合并时E涡和F涡的RInt值分别为0.22和0.18,可见H涡强度基本为初始合并时两涡强度之和,此阶段为最终合并阶段。
|
图 9 E涡和F涡合并过程中RInt随时间的变化 Fig.9 Temporal distributions of RInt during the merging process of E vortex and F vortex |
综合分析以上两组涡合并现象,发生合并的一对涡为相邻且尺寸、强度基本一致的同向旋转涡,且涡之间没有流体流动隔离,合并过程可以分为平移靠近、相互旋转和最终合并三个阶段。合并过程中两涡的Liutex强度R呈反向变化,新生成的涡尺寸和强度基本为初始合并时两个涡之和,且旋转方向与两个涡同向。
由于Liutex可以灵敏地捕捉到流体的转动,在图 6和图 8R云图中也有一些R不等于零的局部小区域,如图 6(a)R云图中的1、2区域。从流线图可以观察到在这些局部小区域中流体没有形成涡,但存在弯曲,即存在转动。
5 结论采用具有拉格朗日性质的MSFLE图像测量方法和Liutex理论对矩形管道底部湍流边界层涡结构开展了实验研究。实验测量了湍流边界层流向-法向平面内涡结构随时空演变过程,并基于骨架提取算法及Liutex理论对涡合并现象进行了分析,得到如下结论:
1) MSFLE图像测量方法具有测量装置简单,对实验条件要求低的特点,通过拉格朗日视角可以更加直观地测量湍流边界层涡结构特征及周围流场的时空演变过程。
2) Liutex涡识别算法能准确表征涡区域及涡旋转强度,MSFLE测量方法结合Liutex涡识别算法可以很好地应用于湍流边界层中涡结构时空演变过程的可视化与量化研究。
3) 矩形管道湍流边界层中涡合并的条件是两个涡相邻、尺寸和强度基本相同且为同向旋转涡,涡之间没有流体流动隔离。涡合并过程分为平移靠近、相互旋转和最终合并三个阶段。合并中两个涡的Liutex强度R呈反向变化,最终生成的新涡强度和尺寸基本为初始合并时两个涡之和,且旋转方向与两个涡同向。
| [1] |
连祺祥. 湍流边界层拟序结构的实验研究[J]. 力学进展, 2006, 36(3): 373-388. LIAN Q X. Experimental studies on coherent structures in turbulent boundary layers[J]. Advances in Mechanics, 2006, 36(3): 373-388. DOI:10.3321/j.issn:1000-0992.2006.03.005 (in Chinese) |
| [2] |
KÜCHEMANN D. Report on the I. U. T. A. M. symposium on concentrated vortex motions in fluids[J]. Journal of Fluid Mechanics, 1965, 21(1): 1. |
| [3] |
THEODORSEN T. Mechanism of turbulence[C]//Proceedings of the Second Midwestern Conference on Fluid Mechanics. Columbus, Ohio, USA, 1952.
|
| [4] |
KLINE S J, REYNOLDS W C, SCHRAUB F A, et al. The structure of turbulent boundary layers[J]. Journal of Fluid Mechanics, 1967, 30(4): 741-773. DOI:10.1017/S0022112067001740 |
| [5] |
PRATURI A K, BRODKEY R S. A stereoscopic visual study of coherent structures in turbulent shear flow[J]. Journal of Fluid Mechanics, 1978, 89(2): 251-272. DOI:10.1017/S0022112078002608 |
| [6] |
LIAN Q X. A visual study of the coherent structure of the turbulent boundary layer in flow with adverse pressure gradient[J]. Journal of Fluid Mechanics, 1990, 215: 101. DOI:10.1017/S0022112090002579 |
| [7] |
张兆顺, 崔桂香, 许春晓. 走进湍流[J]. 力学与实践, 2002, 24(1): 1-8. ZHANG Z S, CUI G X, XU C X. Approach to turbulence[J]. Mechanics in Engineering, 2002, 24(1): 1-8. DOI:10.3969/j.issn.1000-0879.2002.01.001 (in Chinese) |
| [8] |
ADRIAN R J, MEINHART C D, TOMKINS C D. Vortex organization in the outer region of the turbulent boundary layer[J]. Journal of Fluid Mechanics, 2000, 422: 1-54. DOI:10.1017/S0022112000001580 |
| [9] |
ADRIAN R J. Hairpin vortex organization in wall turbulence[J]. Physics of Fluids, 2007, 19(4): 041301. DOI:10.1063/1.2717527 |
| [10] |
ZHOU J, ADRIAN R J, BALACHANDAR S, et al. Mechanisms for generating coherent packets of hairpin vortices in channel flow[J]. Journal of Fluid Mechanics, 1999, 387: 353-396. DOI:10.1017/S002211209900467X |
| [11] |
KINZEL M, WOLF M, HOLZNER M, et al. Simultaneous two-scale 3D-PTV measurements in turbulence under the influence of system rotation[J]. Experiments in Fluids, 2011, 51(1): 75-82. DOI:10.1007/s00348-010-1026-6 |
| [12] |
HUTCHINS N, HAMBLETON W T, MARUSIC I. Inclined cross-stream stereo particle image velocimetry measurements in turbulent boundary layers[J]. Journal of Fluid Mechanics, 2005, 541: 21. DOI:10.1017/S0022112005005872 |
| [13] |
WANG W, GUAN X L, JIANG N. TRPIV investigation of space-time correlation in turbulent flows over flat and wavy walls[J]. Acta Mechanica Sinica, 2014, 30(4): 468-479. DOI:10.1007/s10409-014-0060-7 |
| [14] |
姜楠, 于培宁, 管新蕾. 湍流边界层相干结构空间拓扑形态的层析TRPIV测量[J]. 航空动力学报, 2012, 27(5): 1113-1121. JIANG N, YU P N, GUAN X L. Tomo-TRPIV measurement of coherent structure spatial topology in turbulent boundary layer[J]. Journal of Aerospace Power, 2012, 27(5): 1113-1121. (in Chinese) |
| [15] |
SCHRÖDER A, GEISLER R, STAACK K, et al. Eulerian and Lagrangian views of a turbulent boundary layer flow using time-resolved tomographic PIV[J]. Experiments in Fluids, 2011, 50(4): 1071-1091. DOI:10.1007/s00348-010-1014-x |
| [16] |
王洪平, 高琪, 王晋军. 基于层析PIV的湍流边界层涡结构统计研究[J]. 中国科学:物理学力学天文学, 2015, 45(12): 73-86. WANG H P, GAO Q, WANG J J. The statistical study of vortex structure in turbulent boundary layer flow based on Tomographic PIV[J]. Scientia Sinica(Physica, Mechanica & Astronomica), 2015, 45(12): 73-86. (in Chinese) |
| [17] |
高琪, 王洪平. 层析PIV技术及其合成射流测量[J]. 中国科学:技术科学, 2013, 43(7): 828-835. |
| [18] |
KATZ J, SHENG J. Applications of holography in fluid mechanics and particle dynamics[J]. Annual Review of Fluid Mechanics, 2010, 42(1): 531-555. DOI:10.1146/annurev-fluid-121108-145508 |
| [19] |
曲宁宁, 蔡小舒, 周骛, 等. 运动单帧图像法湍流边界层相干结构的实验测量[J]. 化工学报, 2017, 68(11): 4088-4094. QU N N, CAI X S, ZHOU W, et al. Experimental measurement of coherent structures of turbulent boundary layer by motion single frame imaging method[J]. CIESC Journal, 2017, 68(11): 4088-4094. DOI:10.11949/j.issn.0438-1157.20170469 (in Chinese) |
| [20] |
EPPS B. Review of vortex identification methods[C]//55th AIAA Aerospace Sciences Meeting, Grapevine, Texas. Reston, Virginia: AIAA. AIAA 2017-0989. https://doi.org/10.2514/6.2017-0989
|
| [21] |
JEONG J, HUSSAIN F. On the identification of a vortex[J]. Journal of Fluid Mechanics, 1995, 285: 69-94. DOI:10.1017/S0022112095000462 |
| [22] |
HUNT J C R, WRAY A A, MOIN P. Eddies, streams, and convergence zones in turbulent flows[C]//Proceedings of the Summer Program in Center for Turbulence Research. Stanford University, USA, 1988: 193-208.
|
| [23] |
LIU C Q, WANG Y Q, YANG Y, et al. New omega vortex identification method[J]. Science China Physics, Mechanics & Astronomy, 2016, 59(8): 684711. |
| [24] |
潘翀, 王晋军, 张草. 湍流边界层Lagrangian拟序结构的辨识[J]. 中国科学(G辑), 2009(4): 627-636. DOI:10.1360/2009-39-4-627 |
| [25] |
HALLER G. An objective definition of a vortex[J]. Journal of Fluid Mechanics, 2005, 525: 1-26. DOI:10.1017/S0022112004002526 |
| [26] |
GAO Y S, LIU C Q. Rortex and comparison with eigenvalue-based vortex identification criteria[J]. Physics of Fluids, 2018, 30(8): 085107. DOI:10.1063/1.5040112 |
| [27] |
LIU C Q, GAO Y S, TIAN S L, et al. Rortex:a new vortex vector definition and vorticity tensor and vector decompositions[J]. Physics of Fluids, 2018, 30(3): 035103. DOI:10.1063/1.5023001 |
| [28] |
GAO Y S, LIU C Q. Rortex based velocity gradient tensor decomposition[J]. Physics of Fluids, 2019, 31(1): 011704. DOI:10.1063/1.5084739 |
| [29] |
DONG X R, GAO Y S, LIU C Q. New normalized Rortex/vortex identification method[J]. Physics of Fluids, 2019, 31(1): 011701. DOI:10.1063/1.5066016 |
| [30] |
WANG Y Q, GAO Y S, LIU J M, et al. Explicit formula for the Liutex vector and physical meaning of vorticity based on the Liutex-Shear decomposition[J]. Journal of Hydrodynamics, 2019, 31(3): 464-474. DOI:10.1007/s42241-019-0032-2 |
| [31] |
周雷, 周骛, 郭延昂, 等. 射流卷吸边界层内相干结构的实验研究[J]. 化工学报, 2019, 70(7): 2520-2527. ZHOU L, ZHOU W, GUO Y A, et al. Experimental studies on coherent structures in jet entrainment boundary layers[J]. CIESC Journal, 2019, 70(7): 2520-2527. DOI:10.11949/0438-1157.20190048 (in Chinese) |
| [32] |
吴凡, 周骛, 蔡小舒. 粒子运动轨迹的图像处理及流场重构算法研究[J]. 实验流体力学, 2019, 33(4): 100-107. WU F, ZHOU W, CAI X S. Image processing algorithm for particle trajectory image and reconstruction study on flow field[J]. Journal of Experiments in Fluid Mechanics, 2019, 33(4): 100-107. (in Chinese) |
| [33] |
范宝春, 董刚, 张辉. 湍流控制原理[M]. 北京: 国防工业出版社, 2011. FAN B C, DONG G, ZHANG H. Principles of turbulence control[M]. Beijing: National Defense Industry Press, 2011. (in Chinese) |
 2020, Vol. 38
2020, Vol. 38