自然界中涡无处不在,小到原子中的电子运动,大到银河系星云,都属于涡。肉眼可见的涡更是比比皆是,龙卷风、飓风、台风,这些典型的集中涡具有极强的破坏力。更为重要的是湍流中存在着大量各种尺度不一和强度各异的涡结构,并且这些涡在湍流生成和维持过程中发挥着关键性的作用。然而长期以来涡并没有一个为大家普遍接受的定义[1-2]。直观上讲,涡代表流体的旋转运动,也就是说,有流体转动的地方就有涡,反过来,有涡就有流体转动。但这只是物理概念,我们需要给涡一个定量的数学定义。显然,涡是一个流体转动的物理现象,而速度的旋度或者涡量是一个数学定义,二者并没有天然的必然联系,但长期以来很多教科书,都将涡(Vortex)和涡量管(Vorticity Tube)混淆,认为涡的强度(Vortex Strength)就是涡量(Vorticity),这就是所谓的“涡涡不分”或者“涡就是涡”(Vortex is Vorticity)。追根究底,“涡就是涡”的概念来源于Helmholtz。1858年Helmholtz[3]提出涡量丝、涡量线和涡量管的概念以及Helmholtz三定律,文中Helmholtz就直接就用涡量(Vorticity)表示涡丝(Vortex Filament)。当然,如果考虑流体黏性,经典涡动力学的Helmholtz三大定律并不成立。这里,我们把基于涡量来显示和识别涡结构的方法称为第一代涡识别方法。尽管Helmholtz涡定义出现在几乎所有流体力学教科书中,但科学研究表明涡量和涡是两个截然不同的概念。二者都是矢量,但方向和大小各不相同,完全不能画等号。Robinson[4]在1991年就发现高涡量区域和实际流体旋转之间的关联性非常低。Wang和Liu等人[5]在直接数值模拟结果中发现不仅涡量和涡的方向完全分道扬镖,而且存在旋转强但涡量反而小的区域,其周围不旋转的地方涡量反而很大。也就是说,如果将涡看成一个有大小和方向的物理量,那么其大小和方向与涡量都大相径庭。因此,不能用涡量来表示涡,也就是不能“涡涡不分”。“涡涡”的区别必须研究清楚。为了应对第一代涡识别方法存在的问题,自20世纪80年代以来,人们陆续提出了以Q、λ2、Δ和λci等方法[6-9]为代表的第二代涡识别方法,在涡识别方面取得了很大进展。这些方法都从某种程度上认识到不能用涡量来度量涡的强度,由于涡量是由Cauchy-Stokes速度梯度张量分解得到的反对称张量而来,人们认识到不能单纯用反对称张量或者涡量来显示涡,而应整体考虑速度梯度张量,首先就是它的特征值。速度梯度张量的特征值和特征值的任何组合都是伽利略不变量,不随坐标平移或者匀速转动而改变,所以第二代涡识别方法可以归纳为以特征值为基础的涡识别方法(Eigenvalue-Based)。但第二代涡识别方法存在先天性的缺陷:1) Q、λ2、Δ和λci都模糊地代表涡的强度,但本身物理意义并不清晰,其等值面在多大程度上能代表涡结构存在争议;2)涡是流体绕轴线的旋转,具有方向性,而第二代涡识别方法都是标量,无法给出方向的信息;3)在使用中存在随意选择阈值的问题,不具有唯一性;4)第二代涡识别方法基本上都是基于Cauchy-Stokes分解和速度梯度张量▽V的特征值,而忽略了特征向量所提供的信息;5)识别结果存在不同程度的剪切污染,将剪切和拉伸压缩都错误地当作流体旋转的一部分或者涡强度的一部分;6)无法同时识别强涡和弱涡,阈值太大则弱涡消失,阈值太小则强弱涡混在一起,一团模糊。
针对第一代和第二代涡识别方法存在的问题,德州大学阿灵顿分校Chaoqun Liu教授及其团队从2014年开始,开展了一系列工作,先后提出了Ω涡识别方法[10]、Liutex向量[11-13]、Liutex-Ω涡显示方法[14-15]、客观性Ω涡识别方法[16]、客观性Liutex向量[17]、基于Liutex的涡量分解和速度梯度张量分解[18]、Liutex涡核线[19-20]、Liutex相似律[21]。自2018年以来团队已经在Physics of Fluids上发表14篇、Journal of Hydrodynamics上发表14篇相关论文。这里将这一系列工作归纳为第三代涡识别方法,并在下面进行详细介绍。
2016年,Liu等人[10]提出了Ω涡识别方法。与其他第二代涡识别方法相比,Ω方法具有物理意义清晰、易于实现、归一化(取值范围0~1)、能够同时捕捉强涡和弱涡,并且无需大幅度调节阈值的优点。Liu等人在2014年[1]就指出,涡量不能代表当地流体的刚性旋转,而应该将涡量进一步分解为旋转部分和非旋转部分。基于这一概念,2017年12月在上海理工大学举办的“首届涡和湍流若干关键问题研究进展和再认识研讨会”上,Liu第一次提出从流体运动中提取刚性转动部分,并命名为Rortex向量[11],随后在2018年底更名为Liutex向量。基于Liutex向量R的定义,涡量ω可以进一步分解为刚性转动R和反对称剪切ω-R。同样,速度梯度张量▽v也可以分解为刚性旋转的部分(对应R)和非旋转(NR)部分。这一分解与传统的Cauchy-Stokes分解将▽v分解为对称部分和反对称部分不同,真正找到了当地流动中刚性旋转部分。时至今日,已经形成一个较为完整的理论系统[11-13]。
自然界的涡有六大要素:1)涡的绝对强度;2)涡的相对强度;3)涡的当地旋转轴;4)涡整体转轴位置;5)涡核大小;6)涡边界定义。第一代涡识别方法无法给出这些要素,而第二代仅能在特定阈值条件下提供涡的大致边界。以Liutex向量为基础的第三代涡识别方法能够完整回答以上涡的六大要素问题。
本文第一部分简单介绍基于涡量的第一代和基于特征值的第二代涡识别方法,包括Ω方法及其优越性;第二部分介绍涡科学的数学基础;第三部分介绍Liutex定义,和基于Liutex的涡量分解及速度梯度张量分解;第四部分介绍基于Liutex的涡识别方法,包括Liutex向量、Liutex等值面、Liutex-Ω等值面、Liutex涡核线等;第五部分介绍涡的六大要素和三代涡方法比较;第六部分介绍湍流边界层中的Liutex相似律。最后对未来第三代涡识别方法进一步发展做出展望。
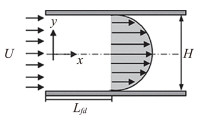
1 第一代和第二代涡定义和识别方法简单回顾 1.1 第一代涡定义和识别方法涡虽然无处不在,但却难以给出严格定义。1858年,Helmholtz[3]提出涡丝(Vortex Filament)的概念,至今仍有很多教科书把涡(Vortex)定义为涡量管(Vorticity Tube),把涡量大小定义为涡的强度,或者旋转强度,这里将之称为第一代涡定义。一般将涡量线(Vorticity Line)定义为处处与涡量向量相切的曲线,将涡量管(Vorticity Tube)定义为涡区的一条封闭曲线(非涡量线)上各点的所有涡量线所组成的管状曲面,将涡量丝(Vorticity Filament)定义为截面趋近于无穷小时的涡管。事实上,Helmholtz在他的论文中把涡量线称为涡线(Vortex Line),把涡量管称为涡管(Vortex Tube),把涡量丝称为涡丝(Vortex Filament),可见在Helmholtz的定义中就已把流体旋转的自然现象即旋涡(Vortex)和涡量(Vorticity)等价起来,并且这种混淆随着涡线、涡管和涡丝这些术语的沿用延续到现在。基于以上涡量线、涡量管和涡量丝的概念,Helmholtz提出著名的涡动力学三大定律:1)在同一瞬间,沿涡管(或涡丝)的强度不变;2)涡管(或涡丝)不能在流体中中断,而只能结束于流场边界处或者形成闭合的曲线;3)如果流体初始无旋,并且体积力有势,那么流体将保持无旋。很明显,虽然Helmholtz在定律中用的术语都是旋涡(Vortex),但实际上讲的全是涡量(Vorticity),也就是把自然界的旋涡和数学上的涡量完全等价起来,即“涡涡不分”“涡就是涡”。Helmholtz涡定义和Helmholtz三大定律是近代涡动力学基础,至今仍作为经典理论出现在流体力学教科书中。但随着研究的进展和人们认识的加深,应该进一步强调Helmholtz的定义和三大定律是针对涡量而言,而非涡,“涡涡不分”的问题仍是困扰涡科学发展的阻力之一。为了进一步说明涡不是涡量,涡量管不能代表涡, 请看如图 1所示的平面Poiseuille流动,其精确解具有形式:U=y(H-y), V=0(省去由压力梯度和黏性系数决定的常数),因此涡量ωz=
|
图 1 二维渠道层流 Fig.1 2D laminar channel flow with no fluid rotation, or vortex (涡量大但没有旋涡或者流体转动) |
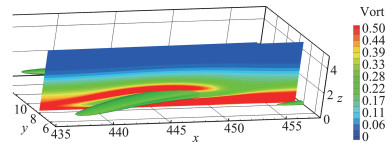
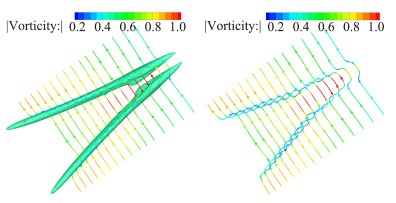
具体到湍流流动中,Robinson[4]在1991年就报道湍流边界层中,尤其是在壁面附近,涡量与涡的相关性相当微弱。Wang和Liu[5]也在边界层转捩的DNS计算中发现,Λ涡在涡核处涡量较小,在涡核外反而涡量较大(见图 2)。另外,图 3给出穿过Λ涡的涡量线和涡结构分布,可以看到无论是方向还是大小, 二者都分道扬镳。根据以上分析和例证,还有无数工程技术研究人员的报告,都表明不能用涡量(Vorticity)来代表涡或者捕捉涡结构。当然他们加了一些限制条件比如理想正压体积力有势等,但涡动力学主要用来研究湍流,理想流体还有什么湍流?结果学生基本上一致误认为Vortex就是Vorticity。显然基于涡量的第一代涡识别方法来代表或者捕捉涡结构是不合适的。
1.2 第二代涡识别方法
事实上,正是由于基于涡量的第一代涡识别方法无法准确地捕捉和识别流场的涡结构,在20世纪80和90年代,人们陆续提出很多新的涡识别方法,比较著名和具有代表性的包括Q、λ2、Δ和λci等方法。尽管它们理论基础各不相同,但基本都是由当地速度梯度▽v的特征值唯一确定,可以将它们归纳为基于速度梯度张量特征值的第二代涡识别方法。速度梯度张量▽v是:
| $ \nabla \mathit{\boldsymbol{v}} = \left[ {\begin{array}{*{20}{l}} {\frac{{\partial {\kern 1pt} u}}{{\partial {\kern 1pt} x}}}&{\frac{{\partial {\kern 1pt} u}}{{\partial {\kern 1pt} y}}}&{\frac{{\partial {\kern 1pt} u}}{{\partial {\kern 1pt} z}}}\\ {\frac{{\partial {\kern 1pt} v}}{{\partial {\kern 1pt} x}}}&{\frac{{\partial {\kern 1pt} v}}{{\partial {\kern 1pt} y}}}&{\frac{{\partial {\kern 1pt} v}}{{\partial {\kern 1pt} z}}}\\ {\frac{{\partial {\kern 1pt} w}}{{\partial {\kern 1pt} x}}}&{\frac{{\partial {\kern 1pt} w}}{{\partial {\kern 1pt} y}}}&{\frac{{\partial {\kern 1pt} w}}{{\partial {\kern 1pt} z}}} \end{array}} \right] $ | (1) |
它的的特征方程为:
| $ \left| {{\kern 1pt} \nabla \mathit{\boldsymbol{v}} - \lambda \mathit{\boldsymbol{I}}{\kern 1pt} } \right| = \left[ {\begin{array}{*{20}{c}} {\frac{{\partial {\kern 1pt} u}}{{\partial {\kern 1pt} x}} - \lambda }&{\frac{{\partial {\kern 1pt} u}}{{\partial {\kern 1pt} y}}}&{\frac{{\partial {\kern 1pt} u}}{{\partial {\kern 1pt} z}}}\\ {\frac{{\partial {\kern 1pt} v}}{{\partial {\kern 1pt} x}}}&{\frac{{\partial {\kern 1pt} v}}{{\partial {\kern 1pt} y}} - \lambda }&{\frac{{\partial {\kern 1pt} v}}{{\partial {\kern 1pt} z}}}\\ {\frac{{\partial {\kern 1pt} w}}{{\partial {\kern 1pt} x}}}&{\frac{{\partial {\kern 1pt} w}}{{\partial {\kern 1pt} y}} - \lambda }&{\frac{{\partial {\kern 1pt} x}}{{\partial {\kern 1pt} z}}} \end{array}} \right] = 0 $ | (2) |
可以写为:
| $ {\lambda ^3} + P{\lambda ^2} + Q\lambda + R = 0 $ | (3) |
用λ1、λ2和λ3代表式的三个特征值,则有
| $ P = - ({\lambda _1} + {\lambda _2} + {\lambda _3}) = - {\rm{tr}} (\nabla \mathit{\boldsymbol{V}}) $ | (4) |
| $ Q = {\lambda _1}{\lambda _2} + {\lambda _2}{\lambda _3} + {\lambda _3}{\lambda _1} = - \frac{1}{2}[ {\rm{tr}} (\nabla {\mathit{\boldsymbol{V}}^2}) + {\rm{tr}} {(\nabla \mathit{\boldsymbol{V}})^2}] $ | (5) |
| $ R = - {\lambda _1}{\lambda _2}{\lambda _3} = - {\rm{det}} (\nabla \mathit{\boldsymbol{V}}) $ | (6) |
其中,tr代表矩阵的迹,det代表矩阵的行列式。P、Q和R是速度梯度张量▽v的三个伽利略不变量,并且对于不可压缩流动,根据连续方程有P=∂u/∂x+∂v/∂y+∂w/∂z=0。
1.2.1 Q-判据在第二代涡识别方法中,Q准则是应用最为广泛的一种涡识别方法。Hunt[6]等人(1988)建议使用速度梯度张量▽v的第二个伽利略不变量Q>0代表涡结构。根据Cauchy-Stokes分解,
| $ \nabla \mathit{\boldsymbol{v}} = \mathit{\boldsymbol{A}} + \mathit{\boldsymbol{B}} $ | (7) |
| $ \mathit{\boldsymbol{A}} = \left( {\begin{array}{*{20}{c}} {\frac{{\partial u}}{{\partial x}}}&{\frac{1}{2}(\frac{{\partial u}}{{\partial y}} + \frac{{\partial v}}{{\partial x}})}&{\frac{1}{2}(\frac{{\partial w}}{{\partial x}} + \frac{{\partial u}}{{\partial z}})}\\ {\frac{1}{2}(\frac{{\partial u}}{{\partial y}} + \frac{{\partial v}}{{\partial x}})}&{\frac{{\partial v}}{{\partial y}}}&{\frac{1}{2}(\frac{{\partial v}}{{\partial z}} + \frac{{\partial w}}{{\partial y}})}\\ {\frac{1}{2}(\frac{{\partial w}}{{\partial x}} + \frac{{\partial u}}{{\partial z}})}&{\frac{1}{2}(\frac{{\partial v}}{{\partial z}} + \frac{{\partial w}}{{\partial y}})}&{\frac{{\partial w}}{{\partial z}}} \end{array}} \right) $ |
| $ \begin{array}{l} \mathit{\boldsymbol{B}} = \\ \left. {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \left( {\begin{array}{*{20}{c}} 0&{ - \frac{1}{2}(\frac{{\partial v}}{{\partial x}} - \frac{{\partial u}}{{\partial y}})}&{\frac{1}{2}(\frac{{\partial u}}{{\partial z}} - \frac{{\partial w}}{{\partial x}})}\\ {\frac{1}{2}(\frac{{\partial v}}{{\partial x}} - \frac{{\partial u}}{{\partial y}})}&0&{ - \frac{1}{2}(\frac{{\partial w}}{{\partial y}} - \frac{{\partial v}}{{\partial z}})}\\ { - \frac{1}{2}(\frac{{\partial u}}{{\partial z}} - \frac{{\partial w}}{{\partial x}})}&{\frac{1}{2}(\frac{{\partial w}}{{\partial y}} - \frac{{\partial v}}{{\partial z}})}&0 \end{array}} \right.} \right) \end{array} $ |
Q表达式可以写为:
| $ Q = \frac{1}{2}(\left\| \mathit{\boldsymbol{B}} \right\|_F^2 - \left\| \mathit{\boldsymbol{A}} \right\|_F^2) $ | (8) |
式中,‖ ‖F代表矩阵的Frobenius范数。根据上文的讨论,对称张量A有抵消反对称张量B旋转的效果,因此Q的物理意义在于涡结构中不仅要求存在涡量(反对称张量B),更进一步要求反对称张量B要能克服对称张量A所代表的变形效果。
| $ \begin{array}{l} \begin{array}{*{20}{l}} {\mathit{\boldsymbol{a}} = \left\| \mathit{\boldsymbol{A}} \right\|_F^2 = {{\left( {\frac{{\partial u}}{{\partial x}}} \right)}^2} + {{\left( {\frac{{\partial v}}{{\partial y}}} \right)}^2} + {{\left( {\frac{{\partial x}}{{\partial z}}} \right)}^2} + }\\ {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \frac{1}{2}{{\left( {\frac{{\partial u}}{{\partial y}} + \frac{{\partial v}}{{\partial x}}} \right)}^2} + \frac{1}{2}{{\left( {\frac{{\partial u}}{{\partial z}} + \frac{{\partial w}}{{\partial x}}} \right)}^2} + }\\ {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \frac{1}{2}{{\left( {\frac{{\partial v}}{{\partial z}} + \frac{{\partial w}}{{\partial y}}} \right)}^2}} \end{array}\\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \begin{array}{*{20}{l}} { = {{\left( {\frac{{\partial u}}{{\partial x}}} \right)}^2} + {{\left( {\frac{{\partial v}}{{\partial y}}} \right)}^2} + {{\left( {\frac{{\partial w}}{{\partial z}}} \right)}^2} + \frac{1}{2}{{\left( {\frac{{\partial u}}{{\partial y}}} \right)}^2} + }\\ {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \frac{1}{2}{{\left( {\frac{{\partial u}}{{\partial z}}} \right)}^2} + \frac{1}{2}{{\left( {\frac{{\partial v}}{{\partial x}}} \right)}^2} + \frac{1}{2}{{\left( {\frac{{\partial v}}{{\partial z}}} \right)}^2} + \frac{1}{2}{{\left( {\frac{{\partial w}}{{\partial x}}} \right)}^2} + }\\ {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \frac{1}{2}{{\left( {\frac{{\partial w}}{{\partial y}}} \right)}^2} + \frac{{\partial u}}{{\partial y}}\frac{{\partial v}}{{\partial x}} + \frac{{\partial u}}{{\partial z}}\frac{{\partial w}}{{\partial x}} + \frac{{\partial v}}{{\partial z}}\frac{{\partial w}}{{\partial y}}} \end{array} \end{array} $ | (9) |
| $ \begin{array}{l} \mathit{\boldsymbol{b}} = \left\| \mathit{\boldsymbol{B}} \right\|_F^2 = \frac{1}{2}{\left( {\frac{{\partial u}}{{\partial y}} - \frac{{\partial v}}{{\partial x}}} \right)^2} + \frac{1}{2}{\left( {\frac{{\partial u}}{{\partial z}} - \frac{{\partial w}}{{\partial x}}} \right)^2} + \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \frac{1}{2}{\left( {\frac{{\partial v}}{{\partial z}} - \frac{{\partial w}}{{\partial y}}} \right)^2}\\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \begin{array}{*{20}{l}} { = \frac{1}{2}{{\left( {\frac{{\partial u}}{{\partial y}}} \right)}^2} + \frac{1}{2}{{\left( {\frac{{\partial u}}{{\partial z}}} \right)}^2} + \frac{1}{2}{{\left( {\frac{{\partial v}}{{\partial x}}} \right)}^2} + \frac{1}{2}{{\left( {\frac{{\partial v}}{{\partial z}}} \right)}^2} + }\\ {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \frac{1}{2}{{\left( {\frac{{\partial w}}{{\partial x}}} \right)}^2} + \frac{1}{2}{{\left( {\frac{{\partial w}}{{\partial y}}} \right)}^2} - \frac{{\partial u}}{{\partial y}}\frac{{\partial v}}{{\partial x}} - \frac{{\partial u}}{{\partial z}}\frac{{\partial w}}{{\partial x}} - \frac{{\partial v}}{{\partial z}}\frac{{\partial w}}{{\partial y}}} \end{array} \end{array} $ | (10) |
| $ \begin{array}{l} \begin{array}{*{20}{l}} {\left\| \mathit{\boldsymbol{A}} \right\|_F^2 = \left\| \mathit{\boldsymbol{B}} \right\|_F^2 + {{\left( {\frac{{\partial {\kern 1pt} u}}{{\partial {\kern 1pt} x}}} \right)}^2} + {{\left( {\frac{{\partial {\kern 1pt} v}}{{\partial {\kern 1pt} y}}} \right)}^2} + {{\left( {\frac{{\partial {\kern 1pt} w}}{{\partial {\kern 1pt} z}}} \right)}^2} + }\\ {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} 2\frac{{\partial {\kern 1pt} u}}{{\partial {\kern 1pt} y}}\frac{{\partial {\kern 1pt} v}}{{\partial {\kern 1pt} x}} + 2\frac{{\partial {\kern 1pt} u}}{{\partial {\kern 1pt} z}}\frac{{\partial {\kern 1pt} w}}{{\partial {\kern 1pt} x}} + 2\frac{{\partial {\kern 1pt} v}}{{\partial {\kern 1pt} z}}\frac{{\partial {\kern 1pt} x}}{{\partial {\kern 1pt} y}}} \end{array}\\ \begin{array}{*{20}{l}} {Q = \frac{1}{2}(\left\| \mathit{\boldsymbol{B}} \right\|_F^2 - \left\| \mathit{\boldsymbol{A}} \right\|_F^2)}\\ {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} = - \frac{1}{2}[{{\left( {\frac{{\partial {\kern 1pt} u}}{{\partial {\kern 1pt} x}}} \right)}^2} + {{\left( {\frac{{\partial {\kern 1pt} v}}{{\partial {\kern 1pt} y}}} \right)}^2} + {{\left( {\frac{{\partial {\kern 1pt} w}}{{\partial {\kern 1pt} z}}} \right)}^2} + 2\frac{{\partial {\kern 1pt} u}}{{\partial {\kern 1pt} y}}\frac{{\partial {\kern 1pt} v}}{{\partial {\kern 1pt} x}} + }\\ {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} 2\frac{{\partial {\kern 1pt} u}}{{\partial {\kern 1pt} z}}\frac{{\partial {\kern 1pt} w}}{{\partial {\kern 1pt} x}} + 2\frac{{\partial {\kern 1pt} v}}{{\partial {\kern 1pt} z}}\frac{{\partial {\kern 1pt} w}}{{\partial {\kern 1pt} y}}]} \end{array} \end{array} $ | (11) |
从式(11)可见,右端前三项是拉伸压缩,都成为Q的一部分,也就是误认为拉伸压缩为流体旋转一部分,而且无论拉伸(
Jeong和Hussain[7]在忽略不可压缩Navier-Stokes方程中的非定常和黏性项的条件下,同样将速度梯度张量分解为对称部分A和反对称部分B,经过推导得到A2+B2=-▽(▽p)/ρ, 其中p代表压强,ρ代表密度。当对称张量A2+B2存在两个负的特征值时,压强在由这两个负特征值对应特征向量组成的平面内为极小值。如果将特征值按λ1>λ2>λ3排列,A2+B2存在两个负特征值,等价于λ2 < 0,因此该方法称为λ2方法。在λ2方法中,将涡定义为λ2 < 0的区域。但λ2方法假定流体不可压,又忽略了非定常项和黏性项,当流场存在较强的非定常和黏性效应时,不可能准确找到涡结构。同样λ2也是标量,并且为拉压剪切所污染。
1.2.3 Δ-判据对于3×3的矩阵而言,其特征值大致存在两种情况:(1)三个实特征值,(2)一个实特征值和一对复共轭特征值。这完全取决于Δ。如果Δ≤0,则▽v的三个特征值均为实数,而如果Δ>0,则▽v有一个实特征值和一对复共轭特征值。这里,
| $ \Delta = {(\tilde Q/3)^2} + {(\tilde R/2)^2} $ | (12) |
其中,
λci方法是对Δ方法的进一步发展,当▽v有一对共轭实特征值时(即Δ>0),设其特征值为λ1=λr, λ2, 3=λcr±iλci,对应的特征向量分别为v1=vr, v2, 3=vcr±ivci,则▽v可以分解为:
| $ \nabla \mathit{\boldsymbol{v}} = \left[ {\begin{array}{*{20}{l}} {{\mathit{\boldsymbol{v}}_r}}&{{\mathit{\boldsymbol{v}}_{cr}}}&{{\mathit{\boldsymbol{v}}_{ci}}} \end{array}} \right]{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \left[ {\begin{array}{*{20}{c}} {{\lambda_r}}&0&0\\ 0&{{\lambda_{cr}}}&{{\lambda_{ci}}}\\ 0&{ - {\lambda_{ci}}}&{{\lambda_{cr}}} \end{array}} \right]{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\left[ {\begin{array}{*{20}{l}} {{\mathit{\boldsymbol{v}}_r}}&{{\mathit{\boldsymbol{v}}_{cr}}}&{{\mathit{\boldsymbol{v}}_{ci}}} \end{array}} \right]^{ - 1}} $ | (13) |
在由(vr, vcr, vci)张成的当地曲面坐标系(c1, c2, c3)下,λci-判据把涡的强度用λci表示。问题是方程(13)是相似变换不是正交变换,变换后得到的是非正交坐标系。非正交坐标系中反对角线项一般不能代表流体旋转强度。根据我们的正交变换(见下面第2节):(R+ε)R=λci2,R代表刚性转动,ε是反对称剪切,显然λci含有剪切,为剪切所污染,不能用来表达涡的旋转强度。
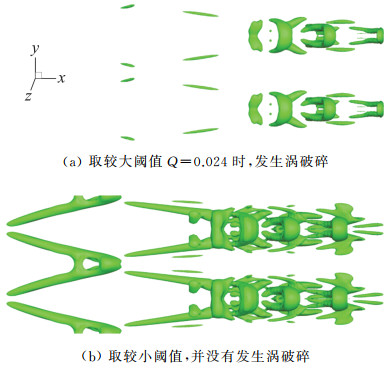
1.3 第二代涡显示方法的问题涡是一个流体做旋转运动的自然现象,应该有方向有大小,是一个矢量。但所有的第二代涡识别方法都是标量,标量有大小无方向,原则上讲标量不能用来代表矢量,也就是第二代涡识别方法不可能给出涡的完整信息。由于是标量,在使用第二代涡识别方法时需要一个人为给定的阈值,而这个阈值对于涡结构的显示具有重要影响。Q>QThreshold实际上是Q>0的一个子集,显然取不同的QThreshold代表不同的子集,它们各不相同。换句话说不同的阈值会得到不同的涡结构。例如,将Q方法应用到边界层转捩直接数值模拟结果时,使用较大阈值Q=0.024会导致涡结构相互分离,或者习惯叫涡破碎,如图 4(a)所示;而使用较小阈值Q=0.002得到的涡结构是连续的,即未发生涡破碎,如图 4(b)所示。这一阈值问题在Q、λ2、Δ和λci方法中均存在,并且在实际应用中阈值的选择需要根据问题的不同进行调节,甚至同一问题不同时间也要进行调节。由于第二代涡识别准则是标量,工程中只有用等值面来代表涡的结构,这就需要取一个合适的阈值,但阈值的选取具有随意性,所得到的结果也不尽相同,进而可能得到不同的物理结论。
|
图 4 Q方法采用不同阈值时的识别结果[11] Fig.4 Different vortex structures identified by the Q criterion with different thresholds[11] |
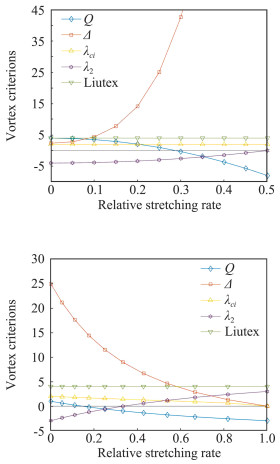
如上所述,Q把拉伸压缩、变形剪切都当作涡强度的一部分,λci把剪切当成涡强度一部分,其他第二代方法也受到不同程度的拉压剪切污染,加之是标量不是向量,都存在阈值问题。当我们改变拉伸压缩,Q、Δ和λ2值都会改变,但Liutex和λci不变。如果我们改变剪切,Q、Δ、λ2、λci都会改变,但Liutex不变。第二代方法不能定量表示涡,所以第二代涡识别方法不可能准确地识别涡的结构(见图 5a和图 5b)。
|
图 5 第二代涡识别法把流体剪切当成涡强度一部分(Pushpa, CNSM Report, 2019) Fig.5 Mistreatment of shearing as vortex strength by the second-generation methods |
为了克服第二代涡识别方法存在的问题,从2013年开始,UTA团队开始探索新一代涡识别方法。2016年Liu等人[10]提出了Ω涡识别方法,首次提出了将涡量进一步分解为旋转部分和非旋转部分的概念,并克服了第二代涡识别方法需要人为调节阈值的问题。
1.4.1 Ω涡识别方法很明显,涡量ω不能代表流体的旋转运动。因此应将涡量ω进一步分解为旋转部分和非旋转部分,即:
| $ \mathit{\boldsymbol{\omega }} = \mathit{\boldsymbol{R}} + \mathit{\boldsymbol{S}} $ | (14) |
其中R代表旋转部分涡量,S代表非旋转部分涡量,即纯剪切。通常而言,R和ω的方向不同。这里引入一个参数Ω,代表旋转部分涡量大小占总涡量大小的比例,计算公式为[10]:
| $ \varOmega = \frac{{\left\| \mathit{\boldsymbol{B}} \right\|_F^2}}{{\left\| \mathit{\boldsymbol{A}} \right\|_F^2 + \left\| \mathit{\boldsymbol{B}} \right\|_F^2}} $ | (15) |
在实际使用中,为了防止分母为极小数时误差极大问题,在上式的分母项加上一个小的正数ε,这样Ω的表达式变为:
| $ \varOmega = \frac{{\left\| \mathit{\boldsymbol{B}} \right\|_F^2}}{{\left\| \mathit{\boldsymbol{A}} \right\|_F^2 + \left\| \mathit{\boldsymbol{B}} \right\|_F^2 + \varepsilon }} $ | (16) |
显然Ω的取值范围为0≤Ω≤1,可以将其理解为涡量的浓度,更具体而言,Ω代表流体运动的刚性,当Ω=1时,代表流体做刚体旋转。当Ω>0.5代表反对称张量B较对称张量A占优,因此可以采用Ω略大于0.5来作为涡识别的判据。Liu提出用Ω=0.52来判断涡的边界。董等[22]提出ε=0.002Qmax=0.001(‖B‖F2-‖A‖F2)max作为这个小参数的近似表达式。大量算例表明,ε还是需要根据不同算例进行调节,不能完全依赖董的近似公式,但目标是共同的,即消除分母为极小数时造成的巨大误差。Teusdell[23-24]有类似思想但方法不同。
1.4.2 Ω涡识别方法的优势因为Ω是一个正则化的标量,它有几个非常明显的优点:1)简单易行; 2)物理意义清晰(涡量大于变形); 3)无量纲; 4)对阈值不敏感(调节阈值Ω=0.52~0.65,涡结构变化不大); 5)能同时捕捉到强涡与弱涡。最后一点非常重要,比如Q方法,对强涡和弱涡共存的算例,如果阈值太大,弱涡一扫而空;如果阈值太小,弱涡能发现,但涡结构变得模糊不清。Ω方法对阈值不敏感。
1.4.3 Ω涡识别方法和Q方法的关系很明显,Ω涡识别方法仍然用对称张量反对称张量,应当说它还是属于第二代涡识别方法,只是它对阈值不敏感,能同时捕捉到强涡和弱涡,从这个意义上讲,Ω涡识别方法是第二代涡识别方法中最好的方法,这一个方法可以替代所有其他的第二代涡识别方法。它的一个特例就是Q方法:
| $ \begin{array}{*{20}{l}} {{\rm{令}}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \varOmega = \frac{{\left\| \mathit{\boldsymbol{B}} \right\|_F^2}}{{\left\| \mathit{\boldsymbol{B}} \right\|_F^2 + \left\| \mathit{\boldsymbol{A}} \right\|_F^2 + \varepsilon }}}\\ {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} = \frac{{\left\| \mathit{\boldsymbol{B}} \right\|_F^2}}{{\left\| \mathit{\boldsymbol{B}} \right\|_F^2 + \left\| \mathit{\boldsymbol{A}} \right\|_F^2 + 2{Q_{{\rm{ Threshold }}}}}} \ge 0.5} \end{array} $ | (17) |
可以得到:Q=0.5(‖B‖F2-‖A‖F2)≥QTheshold。
可见这时二者完全等价。当然,我们不会取Ω=0.5,也不会取ε=QTheshold,这儿只是想说明Ω涡识别方法可以代替Q方法,但Q方法不能代替Ω涡识别方法。比如:
| $ \varOmega = \frac{{\left\| \mathit{\boldsymbol{B}} \right\|_F^2}}{{\left\| \mathit{\boldsymbol{B}} \right\|_F^2 + \left\| \mathit{\boldsymbol{A}} \right\|_F^2 + \varepsilon }} = 0.6 $ | (18) |
| $ \begin{array}{*{20}{l}} {Q = 0.5(\left\| \mathit{\boldsymbol{B}} \right\|_F^2 - \left\| \mathit{\boldsymbol{A}} \right\|_F^2)}\\ {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} = 0.1(\left\| \mathit{\boldsymbol{B}} \right\|_F^2 + \left\| \mathit{\boldsymbol{A}} \right\|_F^2) + 0.6\varepsilon } \end{array} $ | (19) |
不能写成Q≥QTheshold,因为右端项是变量,但QTheshold是人为给定的一个常数。
2 流场中的主坐标系 2.1 速度梯度张量和Cauchy-Stokes分解非均匀流场中任意一点在特定坐标系(x, y, z)下可生成一个速度梯度张量,也就是一个3×3矩阵,根据Cauchy-Stokes分解,这个矩阵可以分解为一个对称张量和一个反对称张量:
| $ \nabla \mathit{\boldsymbol{v}} = \left[ {\begin{array}{*{20}{l}} {\frac{{\partial {\kern 1pt} u}}{{\partial {\kern 1pt} x}}}&{\frac{{\partial {\kern 1pt} u}}{{\partial {\kern 1pt} y}}}&{\frac{{\partial {\kern 1pt} u}}{{\partial {\kern 1pt} z}}}\\ {\frac{{\partial {\kern 1pt} v}}{{\partial {\kern 1pt} x}}}&{\frac{{\partial {\kern 1pt} v}}{{\partial {\kern 1pt} y}}}&{\frac{{\partial {\kern 1pt} v}}{{\partial {\kern 1pt} z}}}\\ {\frac{{\partial {\kern 1pt} x}}{{\partial {\kern 1pt} x}}}&{\frac{{\partial {\kern 1pt} x}}{{\partial {\kern 1pt} y}}}&{\frac{{\partial {\kern 1pt} x}}{{\partial {\kern 1pt} z}}} \end{array}} \right] = \mathit{\boldsymbol{A}} + \mathit{\boldsymbol{B}} $ | (20) |
| $ \begin{array}{l} \mathit{\boldsymbol{A}} = \frac{1}{2}(\nabla \mathit{\boldsymbol{v}} + \nabla {\mathit{\boldsymbol{v}}^{\rm{T}}})\\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} = \left[ {\begin{array}{*{20}{c}} {\frac{{\partial u}}{{\partial x}}}&{\frac{1}{2}\left( {\frac{{\partial u}}{{\partial y}} + \frac{{\partial v}}{{\partial x}}} \right)}&{\frac{1}{2}\left( {\frac{{\partial u}}{{\partial z}} + \frac{{\partial w}}{{\partial x}}} \right)}\\ {\frac{1}{2}(\frac{{\partial v}}{{\partial x}} + \frac{{\partial u}}{{\partial y}})}&{\frac{{\partial v}}{{\partial y}}}&{\frac{1}{2}\left( {\frac{{\partial v}}{{\partial z}} + \frac{{\partial w}}{{\partial y}}} \right)}\\ {\frac{1}{2}\left( {\frac{{\partial w}}{{\partial x}} + \frac{{\partial u}}{{\partial z}}} \right)}&{\frac{1}{2}\left( {\frac{{\partial w}}{{\partial y}} + \frac{{\partial v}}{{\partial z}}} \right)}&{\frac{{\partial w}}{{\partial z}}} \end{array}} \right] \end{array} $ | (21) |
| $ \begin{array}{l} \mathit{\boldsymbol{B}} = \frac{1}{2}(\nabla \mathit{\boldsymbol{v}} - \nabla {\mathit{\boldsymbol{v}}^{\rm{T}}})\\ \ \ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\rm{ = }}\left[ {\left. {\begin{array}{*{20}{c}} 0&{\frac{1}{2}(\frac{{\partial u}}{{\partial y}} - \frac{{\partial v}}{{\partial x}})}&{\frac{1}{2}(\frac{{\partial u}}{{\partial z}} - \frac{{\partial w}}{{\partial x}})}\\ { - \frac{1}{2}(\frac{{\partial u}}{{\partial y}} - \frac{{\partial v}}{{\partial x}})}&0&{\frac{1}{2}(\frac{{\partial v}}{{\partial z}} - \frac{{\partial w}}{{\partial y}})}\\ { - \frac{1}{2}(\frac{{\partial u}}{{\partial z}} - \frac{{\partial w}}{{\partial x}})}&{ - \frac{1}{2}(\frac{{\partial v}}{{\partial z}} - \frac{{\partial w}}{{\partial y}})}&0 \end{array}} \right]} \right. \end{array} $ | (22) |
根据涡量或者速度向量的旋度定义,ω=▽×v,反对称张量可进一步写成:
| $ \begin{array}{l} \mathit{\boldsymbol{B}} = \frac{1}{2}(\nabla \mathit{\boldsymbol{v}} - \nabla {\mathit{\boldsymbol{v}}^{\rm{T}}})\\ \left. {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} = \left[ {\begin{array}{*{20}{c}} 0&{ - \frac{1}{2}{\omega _{{\kern 1pt} {\kern 1pt} z}}}&{\frac{1}{2}{\omega _{{\kern 1pt} {\kern 1pt} y}}}\\ {\frac{1}{2}{\omega _{{\kern 1pt} {\kern 1pt} {\kern 1pt} z}}}&0&{ - \frac{1}{2}{\omega _{{\kern 1pt} {\kern 1pt} x}}}\\ { - \frac{1}{2}\omega {{\kern 1pt} _{{\kern 1pt} y}}}&{\frac{1}{2}{\omega _{{\kern 1pt} {\kern 1pt} x}}}&0 \end{array}} \right.} \right] \end{array} $ | (23) |
而对称张量可写成:
| $ \begin{array}{l} \mathit{\boldsymbol{A}} = \left[ {\begin{array}{*{20}{c}} {\frac{{\partial {\kern 1pt} u}}{{\partial {\kern 1pt} x}}}&0&0\\ 0&{\frac{{\partial {\kern 1pt} v}}{{\partial {\kern 1pt} y}}}&0\\ 0&0&{\frac{{\partial {\kern 1pt} w}}{{\partial {\kern 1pt} z}}} \end{array}} \right] + \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \left[ {\begin{array}{*{20}{c}} 0&{\frac{1}{2}\left( {\frac{{\partial u}}{{\partial y}} + \frac{{\partial v}}{{\partial x}}} \right)}&{\frac{1}{2}\left( {\frac{{\partial u}}{{\partial z}} + \frac{{\partial w}}{{\partial x}}} \right)}\\ {\frac{1}{2}\left( {\frac{{\partial v}}{{\partial x}} + \frac{{\partial u}}{{\partial y}}} \right)}&0&{\frac{1}{2}\left( {\frac{{\partial v}}{{\partial z}} + \frac{{\partial w}}{{\partial y}}} \right)}\\ {\frac{1}{2}\left( {\frac{{\partial w}}{{\partial x}} + \frac{{\partial u}}{{\partial z}}} \right)}&{\frac{1}{2}\left( {\frac{{\partial w}}{{\partial y}} + \frac{{\partial v}}{{\partial z}}} \right)}&0 \end{array}} \right] \end{array} $ | (24) |
传统的流体力学认为涡量就代表流体旋转,所以流体微团运动可以分解为平移、变形和旋转。对称张量代表变形,包括拉伸、压缩、对称形变,反对称张量代表旋转。或者Helmholtz速度分解等价于Cauchy-Stokes张量分解。这个概念依然出现在几乎所有流体力学教科书上,成为经典流体运动学的基础。仔细分析就会发现它的致命缺陷:1) Cauchy-Stokes张量分解显然与坐标有关,也就是不同的(x, y, z)坐标会得到完全不同的A和B; 2)尽管ω=▽×v是伽利略不变量,不同的坐标(ωx, ωy,ωz)完全不同; 3)没有任何证据显示涡量ω代表流体旋转(对于刚体是对的,对流体不对)。进一步分析,A是对称张量,有三个实特征值λ1、λ2、λ3,与此对应的三个正交的实特征向量(r1, r2,r3),如果用这三个特征向量作为坐标,可以构成一个正交矩阵Q=(r1, r2,r3),在旧坐标系(x, y, z)下,▽v=A+B,
在新坐标系(r1, r2,r3)或者(X, Y, Z)下,这个速度梯度张量变成▽V=QT▽vQ,它可以得到一个新的Cauchy-Stokes分解:
| $ \begin{array}{l} \begin{array}{*{20}{l}} {\nabla \mathit{\boldsymbol{V}} = {\mathit{\boldsymbol{Q}}^{\rm{T}}}\nabla \mathit{\boldsymbol{vQ}}}\\ {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} = {\mathit{\boldsymbol{Q}}^{\rm{T}}}(\mathit{\boldsymbol{A}} + \mathit{\boldsymbol{B}})\mathit{\boldsymbol{Q}}}\\ {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} = {\mathit{\boldsymbol{Q}}^{\rm{T}}}\mathit{\boldsymbol{AQ}} + {\mathit{\boldsymbol{Q}}^{\rm{T}}}\mathit{\boldsymbol{BQ}}} \end{array}\\ \ \ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\rm{ = }}\left[ {\begin{array}{*{20}{c}} {{\lambda _1}}&0&0\\ 0&{{\lambda _2}}&0\\ 0&0&{{\lambda _3}} \end{array}} \right] + \left[ {\begin{array}{*{20}{c}} 0&{ - \frac{1}{2}{\omega _Z}}&{\frac{1}{2}{\omega _Y}}\\ {\frac{1}{2}{\omega _Z}}&0&{ - \frac{1}{2}{\omega _X}}\\ { - \frac{1}{2}{\omega _Y}}&{\frac{1}{2}{\omega _X}}&0 \end{array}} \right] \end{array} $ | (25) |
很明显在这个坐标系下,对称张量只有拉伸压缩,没有变形。但是显然对称张量必然含有变形, 反对称张量必然含有剪切。否则剪切和变形哪里去了?反对称张量能代表转动吗?这给我们一个严肃的启示,我们必须找到一个唯一的坐标系,本文称之为主坐标系,在这个主坐标系下进行张量分解才有意义,才唯一,才能代表流体运动的分解。Cauchy-Stokes分解显然依赖坐标系,不唯一,不是伽利略不变量。
2.2 伽利略不变性我们要找到一个变量显示涡,必须要求它具备伽利略不变,就是在新的平移、匀速运动或者匀速转动坐标(惯性坐标系)下,这个变量方向和大小不变。很明显速度不是伽利略不变量,因为在不同惯性坐标系下速度的大小和方向都会变,所以不是伽利略不变量,而是伽利略变量,其附带生成的流线和迹线都不是伽利略不变量,不能用来表示涡。涡量是一个伽利略不变量,在不同惯性系中大小和方向不变。这主要归功于dv=▽v·dl是伽利略不变量,因为在新旧坐标系有以下关系dL=QT·dl, ▽V=QT▽vQ, dV=▽V·dL=QT▽vQ·QT·dl=QT▽v·dl=QTdv。但如上文所述涡量并不代表流体旋转。
2.3 转动张量和坐标旋转 2.3.1 二维旋转矩阵如果点的坐标在原始坐标系中是
| $ \left[ {\begin{array}{*{20}{l}} X\\ Y \end{array}} \right] = P\left[ {\begin{array}{*{20}{l}} x\\ y \end{array}} \right] $ |
这里
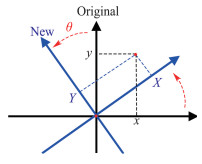
|
图 6 二维旋转矩阵 Fig.6 2-dimensional rotation matrix |
三维旋转矩阵比较复杂,但我们的主坐标系第一步就是把z轴转到▽v的实特征向量方向:
| $ \left[ {\begin{array}{*{20}{l}} X\\ Y\\ Z \end{array}} \right] = Q\left[ {\begin{array}{*{20}{l}} x\\ y\\ z \end{array}} \right] $ | (26) |
这里Q=Qx(α)Qy(β)Qz(γ),QQT=I。
| $ {{Q_x}(\alpha ) = \left[ {\begin{array}{*{20}{c}} 1&0&0\\ 0&{{\rm{cos}}\alpha }&{ - {\rm{sin}}\alpha }\\ 0&{{\rm{sin}}\alpha }&{{\rm{cos}}\alpha } \end{array}} \right]} $ |
| $ {{Q_y}(\beta ) = \left[ {\begin{array}{*{20}{c}} {{\rm{cos}}\beta }&0&{{\rm{sin}}\beta }\\ 0&1&0\\ { - {\rm{sin}}\beta }&0&{{\rm{cos}}\beta } \end{array}} \right]} $ |
| $ {{Q_z}(\gamma ) = \left[ {\begin{array}{*{20}{c}} {{\rm{cos}}\gamma }&{ - {\rm{sin}}\gamma }&0\\ {{\rm{sin}}\gamma }&{{\rm{cos}}\gamma }&0\\ 0&0&1 \end{array}} \right]} $ |
其中Z轴就是▽v的实特征向量,▽vr3=λ3r3, Z轴与r3平行。
2.3.3 ▽v的特征值和特征向量▽v作为一个3×3矩阵,其特征值方程|▽v-λI|=0可求出三个特征值。由于特征值方程是三次多项式,只有两个可能,一个是三个实特征值λ1、λ2、λ3,另一个是一个实特征值、两个共轭复特征值,可以写成:λcr+iλci, λcr-iλci, λr。无论如何,至少有一个实特征值λr,对应有一个实特征向量r。三个实特征值情况,都可用坐标旋转正交变换变成下三角阵,按照Liu[12]的定理一个零一个方向不转,两个零两个方向不转,三个零三个方向不转,就不存在流体转动,或者无涡区,不在我们考虑范围内。
| $ \nabla \mathit{\boldsymbol{V}} = {Q^{\rm{T}}}\nabla \mathit{\boldsymbol{v}}Q = \left[ {\begin{array}{*{20}{c}} {{\lambda _1}}&0&0\\ {\frac{{\partial V}}{{\partial X}}}&{{\lambda _2}}&0\\ {\frac{{\partial W}}{{\partial X}}}&{\frac{{\partial W}}{{\partial Y}}}&{{\lambda _3}} \end{array}} \right] $ | (27) |
一个零一根轴不转,比如
由于本文只是研究涡,在这里只考虑涡区,也就是只考虑一个实特征值、两个共轭复特征值的情况。对于主坐标系,首先把原坐标通过三维旋转,使新坐标系的Z轴与实特征向量r平行:
| $ \nabla \mathit{\boldsymbol{V}} = {Q^{\rm{T}}}\nabla \mathit{\boldsymbol{v}}Q = \left[ {\begin{array}{*{20}{c}} {\frac{{\partial U}}{{\partial X}}}&{\frac{{\partial U}}{{\partial Y}}}&0\\ {\frac{{\partial V}}{{\partial X}}}&{\frac{{\partial V}}{{\partial Y}}}&0\\ {\frac{{\partial W}}{{\partial X}}}&{\frac{{\partial W}}{{\partial Y}}}&{\frac{{\partial W}}{{\partial Z}}} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} {\frac{{\partial U}}{{\partial X}}}&{\frac{{\partial U}}{{\partial Y}}}&0\\ {\frac{{\partial V}}{{\partial X}}}&{\frac{{\partial V}}{{\partial Y}}}&0\\ {\frac{{\partial W}}{{\partial X}}}&{\frac{{\partial W}}{{\partial Y}}}&{{\lambda _r}} \end{array}} \right] $ | (28) |
这里及下文所提到的特征向量都是指单位向量,并且人为约定ω·r>0。
2.3.4 二维坐标系下的旋转新坐标系的Z轴已经唯一确定,就是▽v的实特征向量r,但是在与Z轴垂直的X-Y平面,坐标轴需要唯一确定,这就需要在二维平面X-Y中的P旋转:
| $ \begin{array}{*{20}{l}} {\nabla {\mathit{\boldsymbol{V}}_\theta } = {P^{\rm{T}}}\nabla \mathit{\boldsymbol{V}}P}\\ {P = \left[ {\begin{array}{*{20}{c}} {{\rm{cos}}\theta }&{ - {\rm{sin}}\theta }&0\\ {{\rm{sin}}\theta }&{{\rm{cos}}\theta }&0\\ 0&0&1 \end{array}} \right]} \end{array} $ | (29) |
我们要将
| $ \nabla {\mathit{\boldsymbol{V}}_\theta } = \left[ {\begin{array}{*{20}{c}} {\lambda {{\kern 1pt} _{cr}}}&{\frac{{\partial {U_\theta }}}{{\partial {Y_\theta }}}}&0\\ {\frac{{\partial {V_\theta }}}{{\partial {X_\theta }}}}&{\lambda {{\kern 1pt} _{cr}}}&0\\ {\frac{{\partial W}}{{\partial X}}}&{\frac{{\partial W}}{{\partial Y}}}&{\lambda {{\kern 1pt} _r}} \end{array}} \right] $ | (30) |
这是由于Q和P旋转都是正交变换,特征值不变,▽Vθ和▽v特征值相同。也就是λr、λcr+iλci、λcr-iλci或者λ1、λ2、λ3在(x, y, z)、(X, Y, Z)、(Xθ, Yθ, Z)不同惯性坐标系中,值都一样。
2.3.5 三维转动的判别在Q旋转和P旋转以后,我们已得到主坐标系下的速度张量:
| $ \nabla {\mathit{\boldsymbol{V}}_\theta } = \left[ {\begin{array}{*{20}{c}} {\frac{{\partial {U_\theta }}}{{\partial {X_\theta }}}}&{\frac{{\partial {U_\theta }}}{{\partial {Y_\theta }}}}&0\\ {\frac{{\partial {V_\theta }}}{{\partial {X_\theta }}}}&{\frac{{\partial {V_\theta }}}{{\partial {Y_\theta }}}}&0\\ {\frac{{\partial W}}{{\partial X}}}&{\frac{{\partial W}}{{\partial Y}}}&{\lambda {{\kern 1pt} _r}} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} {\lambda {{\kern 1pt} _{cr}}}&{\frac{{\partial {U_\theta }}}{{\partial {Y_\theta }}}}&0\\ {\frac{{\partial {V_\theta }}}{{\partial {X_\theta }}}}&{\lambda {{\kern 1pt} _{cr}}}&0\\ {\frac{{\partial W}}{{\partial X}}}&{\frac{{\partial W}}{{\partial Y}}}&{\lambda {{\kern 1pt} _r}} \end{array}} \right] $ |
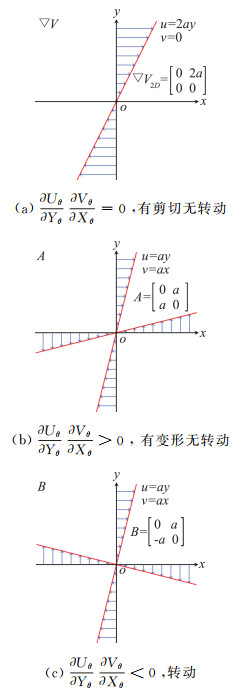
物理上的转动完全由左上角二维矩阵非对角元素决定(图 7),对角元素只代表拉伸或者压缩,
| $ \left[ {\begin{array}{*{20}{c}} {\lambda {{\kern 1pt} _{cr}}}&{\frac{{\partial {U_\theta }}}{{\partial {Y_\theta }}}}\\ {\frac{{\partial {V_\theta }}}{{\partial {X_\theta }}}}&{\lambda {{\kern 1pt} _{cr}}} \end{array}} \right] $ | (31) |
| $ {(\lambda - \lambda {{\kern 1pt} _{cr}})^2} = \frac{{\partial {U_\theta }}}{{\partial {Y_\theta }}}\frac{{\partial {V_\theta }}}{{\partial {X_\theta }}} $ | (32) |
如果
如果
其实
| $ \left| {\frac{{\partial {U_\theta }}}{{\partial {Y_\theta }}}} \right| < \left| {\frac{{\partial {V_\theta }}}{{\partial {X_\theta }}}} \right|,\frac{{\partial {U_\theta }}}{{\partial {Y_\theta }}} < 0, $ |
令
| $ \frac{{\partial V{{\kern 1pt} _\theta }}}{{\partial X{{\kern 1pt} _\theta }}} = \frac{R}{2} + \varepsilon ,R > 0。$ |
主坐标系中的速度梯度张量变为:
| $ \nabla {\mathit{\boldsymbol{V}}_\theta } = \left[ {\begin{array}{*{20}{c}} {\lambda {{\kern 1pt} _{cr}}}&{\frac{{\partial {U_\theta }}}{{\partial {Y_\theta }}}}&0\\ {\frac{{\partial {V_\theta }}}{{\partial {X_\theta }}}}&{\lambda {{\kern 1pt} _{cr}}}&0\\ {\frac{{\partial W}}{{\partial X}}}&{\frac{{\partial W}}{{\partial Y}}}&{\lambda {{\kern 1pt} _r}} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} {\lambda {{\kern 1pt} _{cr}}}&{ - \frac{R}{2}}&0\\ {\frac{R}{2} + \varepsilon }&{\lambda {{\kern 1pt} _{cr}}}&0\\ \xi &\eta &{\lambda {{\kern 1pt} _r}} \end{array}} \right] $ | (33) |
这里
两个未知量可以由两个方程求解:
| $ \begin{array}{*{20}{l}} {(R/2 + \varepsilon ) - ( - R/2) = \mathit{\boldsymbol{\omega }} \cdot \mathit{\boldsymbol{Z}} = \omega {{\kern 1pt} _Z}}\\ {(R/2 + \varepsilon )R/2 = \lambda _{ci}^2} \end{array} $ | (34) |
注意到涡量ω和特征值λr、λci都是惯性系下的伽利略不变量,已经在原坐标系(x, y, z)下求出。求解这两个方程,很容易得到,
| $ R = \omega {{\kern 1pt} _Z} - \sqrt {\omega {\kern 1pt} _Z^2 - 4\lambda {\kern 1pt} _{ci}^2} , $ |
这里ωZ=▽×v·r。
| $ \varepsilon = \lambda {\kern 1pt} _{ci}^2/(R/2) - R/2 $ | (35) |
写到这里大家会觉得有些麻烦,又是Q旋转又是P旋转。其实R由涡量ωZ和λci唯一确定,ωZ和λci都是惯性系下的不变量,由原始坐标(x, y, z)唯一确定,我们并不需要Q旋转和P旋转。这样我们已经得到在主坐标下的速度梯度张量:
| $ \nabla \mathit{\boldsymbol{V}}{{\kern 1pt} _\theta } = \left[ {\begin{array}{*{20}{c}} {\lambda {{\kern 1pt} _{cr}}}&{ - R/2}&0\\ {R/2 + \varepsilon }&{\lambda {{\kern 1pt} _{cr}}}&0\\ \xi &\eta &{\lambda {{\kern 1pt} _r}} \end{array}} \right] $ | (36) |
它是唯一的,只有根据它来进行张量分解和速度分解才是唯一的。传统的经典的Cauchy-Stokes张量分解都是与坐标有关,不是伽利略不变量,是不唯一也不合理的。
3 Liutex定义和主坐标系下的速度梯度张量和涡量分解 3.1 速度梯度张量分解| $ \begin{array}{l} \nabla \mathit{\boldsymbol{V}}{{\kern 1pt} _\theta } = \left[ {\begin{array}{*{20}{c}} {\lambda {{\kern 1pt} _{cr}}}&{ - R/2}&0\\ {R/2 + \varepsilon }&{\lambda {{\kern 1pt} _{cr}}}&0\\ \xi &\eta &{\lambda {{\kern 1pt} _r}} \end{array}} \right]\\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} = \left[ {\begin{array}{*{20}{c}} 0&{ - R/2}&0\\ {R/2}&0&0\\ 0&0&0 \end{array}} \right] + \left[ {\begin{array}{*{20}{c}} {\lambda {{\kern 1pt} _{cr}}}&0&0\\ \varepsilon &{\lambda {{\kern 1pt} _{cr}}}&0\\ \xi &\eta &{\lambda {{\kern 1pt} _r}} \end{array}} \right]\\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} = R + NR \end{array} $ | (37) |
右端第一项代表刚性旋转张量,第二项有三个实特征值代表不转张量。不转张量部分可以进一步分解:
| $ \begin{array}{l} NR = \left[ {\begin{array}{*{20}{c}} {\lambda {{\kern 1pt} _{cr}}}&0&0\\ \varepsilon &{\lambda {{\kern 1pt} _{cr}}}&0\\ \xi &\eta &{\lambda {{\kern 1pt} _r}} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} {\lambda {{\kern 1pt} _{cr}}}&0&0\\ 0&{\lambda {{\kern 1pt} _{cr}}}&0\\ 0&0&{\lambda {{\kern 1pt} _r}} \end{array}} \right] + \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \left[ {\begin{array}{*{20}{c}} 0&{\frac{1}{2}\varepsilon }&{\frac{1}{2}\xi }\\ {\frac{1}{2}\varepsilon }&0&{\frac{1}{2}\eta }\\ {\frac{1}{2}\xi }&{\frac{1}{2}\eta }&0 \end{array}} \right] + \left[ {\begin{array}{*{20}{c}} 0&{ - \frac{1}{2}\varepsilon }&{ - \frac{1}{2}\xi }\\ {\frac{1}{2}\varepsilon }&0&{ - \frac{1}{2}\eta }\\ {\frac{1}{2}\xi }&{\frac{1}{2}\eta }&0 \end{array}} \right]\\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} = C + D + S \end{array} $ |
不转张量可进一步分解为拉伸压缩C、对称变形D和反对称剪切S。这个分解是在主坐标系下的分解,主坐标轴是唯一的,所以这个分解是由原始速度梯度张量▽v唯一确定,是伽利略不变量,但是所有其他分解,包括Cauchy-Stokes分解显然与坐标轴选择有关,是不可靠和没有道理的。
3.2 Liutex定义由主坐标系下速度梯度张量分解可见,一个刚性旋转部分可以从速度梯度张量中分解出来,这也代表流体运动可以分解为一个刚性转动部分和完全不转部分(拉伸压缩、变形和剪切)。2017年Chaoqun Liu首次系统性地提出了如何从流体运动中提取刚体旋转运动部分,并将涡量的旋转部分命名为Rortex向量,2018年12月Rortex向量更名为Liutex向量,其严格推导过程及定义可以参见文献[12-13]。本世纪有关速度梯度张量进一步分解的思想有不少人研究,有人有类似思想[26]。
定义:Liutex定义为流场中当地流体运动的刚性转动部分,其方向是速度梯度张量的实特征向量,代表当地转轴,其大小是刚性转动的角速度,其显式公式为:R =Rr。这里,
| $ R = (\mathit{\boldsymbol{\omega }} \cdot \mathit{\boldsymbol{r}}) - \sqrt {{{(\mathit{\boldsymbol{\omega }} \cdot \mathit{\boldsymbol{r}})}^2} - {4^2}\lambda {{\kern 1pt} _{ci}}} $ | (38) |
r是▽v的实特征向量:▽v·r=λrr, ω=▽×v。由于特征向量r有两个方向,我们定义ω·r>0。这个显式公式首先由Wang等人给出[25]。Liutex方向为当地转轴也是很明显的,如果Z是转轴,沿Z只有
| $ {\rm{d}}\mathit{\boldsymbol{V}} = \nabla \mathit{\boldsymbol{V}} \cdot \mathit{\boldsymbol{Z}} = \left[ {\begin{array}{*{20}{c}} {\frac{{\partial U}}{{\partial Z}}}\\ {\frac{{\partial V}}{{\partial Z}}}\\ {\frac{{\partial W}}{{\partial Z}}} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} 0\\ 0\\ {\frac{{\partial W}}{{\partial Z}}} \end{array}} \right] = \frac{{\partial W}}{{\partial Z}}\left[ {\begin{array}{*{20}{l}} 0\\ 0\\ 1 \end{array}} \right] = \frac{{\partial W}}{{\partial Z}}\mathit{\boldsymbol{Z}} $ |
这是因为Z是转轴,流体绕着它转,它本身不能转,也就是要求
这个物理量Liutex,它是一个向量,有方向,有大小,代表流体刚性转动,方向就是当地转轴,大小就是流体转动强度,Liutex和涡(Vortex)形成了一一对应关系。Liutex是一个数学定义,Vortex是一个自然现象,我们终于找到一个物理量Liutex代表流体旋转,或者旋涡。这就好像冷热是自然现象,但温度是一个物理量,温度高低可以代表热和冷一样,Liutex能代表流体转动快和慢。由于涡原先没有定义,所谓Vortex Dynamics,其实是Vorticity Dynamics,但“涡”(Vorticity)不是“涡”(Vortex)。湍流由无数涡组成,但描述涡需要有一个物理量,它就是Liutex。
3.3 Liutex存在性、唯一性、稳定性和伽利略不变性 3.3.1 Liutex的存在性根据以上定义,Liutex定义为:
| $\boldsymbol{R}=R \boldsymbol{r} $ |
Liutex方向的存在性来自实特征向量的存在性:如果3×3矩阵存在1个实特征值和2个共轭复特征值,实特征向量存在且对应实特征值。Liutex的存在性由定义确定(见公式(38))。
3.3.2 Liutex的唯一性Liutex方向的唯一性来自实特征向量的唯一性:如果3×3矩阵存在1个实特征值和2个共轭复特征值,表明矩阵具有3个不同的特征值,因此单位特征向量加上ω·r>0的要求,其方向是唯一的。Liutex的唯一性来自刚性转动(P旋转最小值)的唯一性。存在性和唯一性也可以由矩阵的Real Schur Decomposition[12]证明。根据Schur Decomposition,任何3×3矩阵都可以通过Unitary(实空间是正交)变换成唯一的Hessenberg矩阵, 也就是:
| $ \nabla {\mathit{\boldsymbol{V}}_\theta } = \left[ {\begin{array}{*{20}{c}} {\lambda {{\kern 1pt} _{cr}}}&{ - R/2}&0\\ {R/2 + \varepsilon }&{\lambda {{\kern 1pt} _{cr}}}&0\\ \xi &\eta &{\lambda {{\kern 1pt} _r}} \end{array}} \right]{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\rm{是唯一的}}。$ |
根据我们主坐标系定义,任何涡点速度梯度张量矩阵(一个实特征值、两个共轭复特征值)可写为:
| $ \begin{array}{l} \nabla \mathit{\boldsymbol{V}}{{\kern 1pt} _\theta } = \left[ {\begin{array}{*{20}{c}} {\lambda {{\kern 1pt} _{cr}}}&{ - R/2}&0\\ {R/2 + \varepsilon }&{\lambda {{\kern 1pt} _{cr}}}&0\\ \xi &\eta &{\lambda {{\kern 1pt} _r}} \end{array}} \right]\\ \ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} = \left[ {\begin{array}{*{20}{c}} 0&{ - R/2}&0\\ {R/2}&0&0\\ 0&0&0 \end{array}} \right] + \left[ {\begin{array}{*{20}{c}} {\lambda {{\kern 1pt} _{cr}}}&0&0\\ \varepsilon &{\lambda {{\kern 1pt} _{cr}}}&0\\ \xi &\eta &{\lambda {{\kern 1pt} _r}} \end{array}} \right]\\ \ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} = \mathit{\boldsymbol{R}} + \mathit{\boldsymbol{NR}} \end{array} $ | (39) |
我们先考虑二维问题,三维是类似的。如果我们任意加一个2D扰动,
| $ \begin{array}{l} E = \left[ {\begin{array}{*{20}{c}} 0&0&0\\ { \pm {E_{21}}}&0&0\\ 0&0&0 \end{array}} \right],\quad 0 < {E_{21}} \ll R\\ \nabla {\mathit{\boldsymbol{V}}_\theta } + E = \left[ {\begin{array}{*{20}{c}} 0&{ - R/2}&0\\ {R/2}&0&0\\ 0&0&0 \end{array}} \right] + \left[ {\begin{array}{*{20}{c}} {\lambda {{\kern 1pt} _{cr}}}&0&0\\ {\varepsilon \pm {E_{21}}}&{\lambda {{\kern 1pt} _{cr}}}&0\\ \xi &\eta &{\lambda {{\kern 1pt} _r}} \end{array}} \right]\\ \ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} = \mathit{\boldsymbol{R}} + \mathit{\boldsymbol{NR}} \end{array} $ | (40) |
该点仍然是涡点,而且转动强度未变。如果
| $ \begin{array}{l} E = \left[ {\begin{array}{*{20}{c}} 0&{{E_{12}}}&0\\ 0&0&0\\ 0&0&0 \end{array}} \right]\\ \nabla \mathit{\boldsymbol{V}}{{\kern 1pt} _\theta } + E = \left[ {\begin{array}{*{20}{c}} 0&{ - R/2 + {E_{12}}}&0\\ {R/2 - {E_{21}}}&0&0\\ 0&0&0 \end{array}} \right] + \\ \ \ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \left[ {\begin{array}{*{20}{c}} {\lambda {{\kern 1pt} _{cr}}}&0&0\\ {\varepsilon + {E_{12}}}&{\lambda {{\kern 1pt} _{cr}}}&0\\ \xi &\eta &{\lambda {{\kern 1pt} _r}} \end{array}} \right]\\ \ \ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} = \mathit{\boldsymbol{R}} + \mathit{\boldsymbol{NR}} \end{array} $ | (41) |
由于是扰动,E21≪R/2, 该点还是涡点, 不过转动强度略有减弱。要让该点不转,不是涡点,必须E21≥R/2,那就不是小扰动了。如果取其他扰动,比如E11、E22,不改变旋转强度。总之只要|Eij|≪R/2, 该点还是涡点, 换句话说,Liutex或者流体转动是十分稳定的,不受外界小扰动影响。外界的小扰动不能让涡点(转动点)变为非涡点。
3.3.4 Liutex的伽利略不变性伽利略不变性很重要,我们必须保证涡定义在所有惯性坐标系保持不变,比如涡量、Q、λci, 都是伽利略不变量,但速度不是,所以依赖于速度的流线或者迹线不能用来直接描述涡,因为不同坐标系下看流线或者迹线完全不一样。伽利略变换包括匀速平移或者转动,也就是:
| $ \left[ {\begin{array}{*{20}{l}} {{x^\prime }}\\ {{y^\prime }}\\ {{z^\prime }} \end{array}} \right] = {\mathit{\boldsymbol{Q}}_c}\left[ {\begin{array}{*{20}{l}} x\\ y\\ z \end{array}} \right] + {\mathit{\boldsymbol{c}}_1}{\kern 1pt} t + {\mathit{\boldsymbol{c}}_2} $ | (42) |
这里,
| $ \left[ {\begin{array}{*{20}{c}} {{u^\prime }}\\ {{v^\prime }}\\ {{w^\prime }} \end{array}} \right] = \mathit{\boldsymbol{Q}}{{\kern 1pt} _c}\left[ {\begin{array}{*{20}{c}} u\\ v\\ w \end{array}} \right] + {\mathit{\boldsymbol{c}}_1} $ |
在新的坐标系下:
| $ \begin{array}{l} \nabla {\mathit{\boldsymbol{v}}^\prime } = \left[ {\begin{array}{*{20}{c}} {\frac{{\partial {\kern 1pt} {u^\prime }}}{{\partial {\kern 1pt} {x^\prime }}}}&{\frac{{\partial {\kern 1pt} {u^\prime }}}{{\partial {\kern 1pt} {y^\prime }}}}&{\frac{{\partial {\kern 1pt} {u^\prime }}}{{\partial {\kern 1pt} {z^\prime }}}}\\ {\frac{{\partial {\kern 1pt} {v^\prime }}}{{\partial {\kern 1pt} {x^\prime }}}}&{\frac{{\partial {\kern 1pt} {v^\prime }}}{{\partial {\kern 1pt} {y^\prime }}}}&{\frac{{\partial {\kern 1pt} {v^\prime }}}{{\partial {\kern 1pt} {z^\prime }}}}\\ {\frac{{\partial {\kern 1pt} {w^\prime }}}{{\partial {\kern 1pt} {x^\prime }}}}&{\frac{{\partial {\kern 1pt} {w^\prime }}}{{\partial {\kern 1pt} {y^\prime }}}}&{\frac{{\partial {\kern 1pt} {w^\prime }}}{{\partial {\kern 1pt} {z^\prime }}}} \end{array}} \right]\\ \begin{array}{*{20}{l}} {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} = {\mathit{\boldsymbol{Q}}_c}{\kern 1pt} \nabla \mathit{\boldsymbol{vQ}}_c^{\rm{T}}}\\ {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} = {\mathit{\boldsymbol{Q}}_c}\left[ {\begin{array}{*{20}{l}} {\frac{{\partial {\kern 1pt} u}}{{\partial {\kern 1pt} x}}}&{\frac{{\partial {\kern 1pt} u}}{{\partial {\kern 1pt} y}}}&{\frac{{\partial {\kern 1pt} u}}{{\partial {\kern 1pt} z}}}\\ {\frac{{\partial {\kern 1pt} v}}{{\partial {\kern 1pt} x}}}&{\frac{{\partial {\kern 1pt} v}}{{\partial {\kern 1pt} y}}}&{\frac{{\partial {\kern 1pt} v}}{{\partial {\kern 1pt} z}}}\\ {\frac{{\partial {\kern 1pt} w}}{{\partial {\kern 1pt} x}}}&{\frac{{\partial {\kern 1pt} w}}{{\partial {\kern 1pt} y}}}&{\frac{{\partial {\kern 1pt} w}}{{\partial {\kern 1pt} z}}} \end{array}} \right]\mathit{\boldsymbol{Q}}_c^{\rm{T}}} \end{array} \end{array} $ | (43) |
如果▽v的实特征向量是r,在新坐标下必定是r′=Qcr。
| $ \begin{array}{l} \nabla {\mathit{\boldsymbol{v}}^\prime }{\mathit{\boldsymbol{r}}^\prime } = \left[ {\begin{array}{*{20}{l}} {\frac{{\partial {\kern 1pt} {u^\prime }}}{{\partial {\kern 1pt} {x^\prime }}}}&{\frac{{\partial {\kern 1pt} {u^\prime }}}{{\partial {\kern 1pt} {y^\prime }}}}&{\frac{{\partial {\kern 1pt} {u^\prime }}}{{\partial {\kern 1pt} {z^\prime }}}}\\ {\frac{{\partial {\kern 1pt} {v^\prime }}}{{\partial {\kern 1pt} {x^\prime }}}}&{\frac{{\partial {\kern 1pt} {v^\prime }}}{{\partial {\kern 1pt} {y^\prime }}}}&{\frac{{\partial {\kern 1pt} {v^\prime }}}{{\partial {\kern 1pt} {z^\prime }}}}\\ {\frac{{\partial {\kern 1pt} {w^\prime }}}{{\partial {\kern 1pt} {x^\prime }}}}&{\frac{{\partial {\kern 1pt} {w^\prime }}}{{\partial {\kern 1pt} {y^\prime }}}}&{\frac{{\partial {\kern 1pt} {w^\prime }}}{{\partial {\kern 1pt} {z^\prime }}}} \end{array}} \right]\mathit{\boldsymbol{Q}}{{\kern 1pt} _c}\mathit{\boldsymbol{r}}\\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \begin{array}{*{20}{l}} { = {\mathit{\boldsymbol{Q}}_{{\kern 1pt} c}}{\kern 1pt} \nabla {\kern 1pt} \mathit{\boldsymbol{vQ}}_c^{\rm{T}}{\mathit{\boldsymbol{Q}}_c}\mathit{\boldsymbol{r}}}\\ { = {\lambda _{{\kern 1pt} r}}{\mathit{\boldsymbol{Q}}_c}\mathit{\boldsymbol{r}}}\\ { = \lambda {{\kern 1pt} _r}{\mathit{\boldsymbol{r}}^\prime }} \end{array} \end{array} $ | (44) |
根据Liutex定义,其方向是▽v′的实特征向量,所以Liutex方向没变。其大小由下述公式确定:
| $ R = (\mathit{\boldsymbol{\omega }}{\kern 1pt} {\kern 1pt} .{\kern 1pt} {\kern 1pt} \mathit{\boldsymbol{r}}) - \sqrt {{{(\mathit{\boldsymbol{\omega }} \cdot \mathit{\boldsymbol{r}})}^2} - {4^2}\lambda {{\kern 1pt} _{ci}}} $ |
由于涡量和λci都是伽利略不变量,所以Liutex强度也是伽利略不变量[27]。其实Omega也是伽利略不变量[28]。
3.3.5 原始坐标下的张量分解和涡量的RS分解我们前面已提到得到Liutex定义和主坐标下的速度梯度张量分解并不需要Q旋转和P旋转,因为涡量、Liutex、特征值都是伽利略不变量,从而我们可以直接从原始坐标下速度梯度张量
| $ \mathit{\boldsymbol{R}} = \left[ {\begin{array}{*{20}{c}} 0&{ - \frac{1}{2}r{{\kern 1pt} _z}}&{\frac{1}{2}r{{\kern 1pt} _y}}\\ {\frac{1}{2}r{{\kern 1pt} _z}}&0&{ - \frac{1}{2}r{{\kern 1pt} _x}}\\ { - \frac{1}{2}r{{\kern 1pt} _y}}&{\frac{1}{2}r{{\kern 1pt} _x}}&0 \end{array}} \right] $ | (45) |
| $ \begin{array}{l} \nabla \mathit{\boldsymbol{v}} = \left[ {\begin{array}{*{20}{c}} {\frac{{\partial {\kern 1pt} u}}{{\partial {\kern 1pt} x}}}&{\frac{{\partial {\kern 1pt} u}}{{\partial {\kern 1pt} y}}}&{\frac{{\partial {\kern 1pt} u}}{{\partial {\kern 1pt} z}}}\\ {\frac{{\partial {\kern 1pt} v}}{{\partial {\kern 1pt} x}}}&{\frac{{\partial {\kern 1pt} v}}{{\partial {\kern 1pt} y}}}&{\frac{{\partial {\kern 1pt} v}}{{\partial {\kern 1pt} z}}}\\ {\frac{{\partial {\kern 1pt} x}}{{\partial {\kern 1pt} x}}}&{\frac{{\partial {\kern 1pt} x}}{{\partial {\kern 1pt} y}}}&{\frac{{\partial {\kern 1pt} w}}{{\partial {\kern 1pt} z}}} \end{array}} \right]\\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} = \left[ {\begin{array}{*{20}{c}} 0&{\frac{1}{2}r{{\kern 1pt} _z}}&{\frac{1}{2}r{{\kern 1pt} _y}}\\ {\frac{1}{2}r{{\kern 1pt} _z}}&0&{ - \frac{1}{2}r{{\kern 1pt} _x}}\\ { - \frac{1}{2}r{{\kern 1pt} _y}}&{\frac{1}{2}r{{\kern 1pt} _x}}&0 \end{array}} \right] + \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \left. {\left[ {\begin{array}{*{20}{c}} {\frac{{\partial {\kern 1pt} u}}{{\partial {\kern 1pt} x}}}&{\frac{{\partial {\kern 1pt} u}}{{\partial {\kern 1pt} y}} + \frac{1}{2}r{{\kern 1pt} _z}}&{\frac{{\partial {\kern 1pt} u}}{{\partial {\kern 1pt} z}} - \frac{1}{2}r{{\kern 1pt} _y}}\\ {\frac{{\partial {\kern 1pt} v}}{{\partial {\kern 1pt} x}} - \frac{1}{2}r{{\kern 1pt} _z}}&{\frac{{\partial {\kern 1pt} v}}{{\partial {\kern 1pt} y}}}&{\frac{{\partial {\kern 1pt} v}}{{\partial {\kern 1pt} z}} + \frac{1}{2}r{{\kern 1pt} _x}}\\ {\frac{{\partial {\kern 1pt} w}}{{\partial {\kern 1pt} x}} + \frac{1}{2}r{{\kern 1pt} _y}}&{\frac{{\partial {\kern 1pt} w}}{{\partial {\kern 1pt} y}} - \frac{1}{2}r{{\kern 1pt} _x}}&{\frac{{\partial {\kern 1pt} w}}{{\partial {\kern 1pt} z}}} \end{array}} \right.} \right]\\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} = \mathit{\boldsymbol{R}} + \mathit{\boldsymbol{NR}} \end{array} $ | (46) |
这个在原始坐标下的张量分解是唯一的。同样我们可以对涡量进行唯一的转动和剪切分解,或者涡量的RS分解:
| $ \begin{array}{l} \mathit{\boldsymbol{B}} = \frac{1}{2}(\nabla \mathit{\boldsymbol{v}} - \nabla {\mathit{\boldsymbol{v}}^{\rm{T}}})\\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} = \left[ {\begin{array}{*{20}{c}} 0&{\frac{1}{2}(\frac{{\partial u}}{{\partial y}} - \frac{{\partial v}}{{\partial x}})}&{\frac{1}{2}(\frac{{\partial u}}{{\partial z}} - \frac{{\partial w}}{{\partial x}})}\\ { - \frac{1}{2}(\frac{{\partial u}}{{\partial y}} - \frac{{\partial v}}{{\partial x}})}&0&{\frac{1}{2}(\frac{{\partial v}}{{\partial z}} - \frac{{\partial w}}{{\partial y}})}\\ { - \frac{1}{2}(\frac{{\partial u}}{{\partial z}} - \frac{{\partial w}}{{\partial x}})}&{ - \frac{1}{2}(\frac{{\partial v}}{{\partial z}} - \frac{{\partial w}}{{\partial y}})}&0 \end{array}} \right]\\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} = \left[ {\begin{array}{*{20}{c}} 0&{ - \frac{1}{2}\omega {{\kern 1pt} _z}}&{\frac{1}{2}\omega {{\kern 1pt} _y}}\\ {\frac{1}{2}\omega {{\kern 1pt} _z}}&0&{ - \frac{1}{2}\omega {{\kern 1pt} _x}}\\ { - \frac{1}{2}\omega {{\kern 1pt} _y}}&{\frac{1}{2}\omega {{\kern 1pt} _x}}&0 \end{array}} \right]\\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} = \left[ {\begin{array}{*{20}{c}} 0&{ - \frac{1}{2}r{{\kern 1pt} _z}}&{\frac{1}{2}r{{\kern 1pt} _y}}\\ {\frac{1}{2}r{{\kern 1pt} _z}}&0&{ - \frac{1}{2}r{{\kern 1pt} _x}}\\ { - \frac{1}{2}r{{\kern 1pt} _y}}&{\frac{1}{2}r{{\kern 1pt} _x}}&0 \end{array}} \right] + \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \left[ {\begin{array}{*{20}{c}} 0&{ - \frac{1}{2}({\omega _z} - {r_z})}&{\frac{1}{2}({\omega _y} - {r_y})}\\ {\frac{1}{2}({\omega _z} - {r_z})}&0&{ - \frac{1}{2}({\omega _X} - {r_X})}\\ { - \frac{1}{2}({\omega _y} - {r_y})}&{\frac{1}{2}({\omega _x} - {r_x})}&0 \end{array}} \right]\\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} = \mathit{\boldsymbol{R}} + \mathit{\boldsymbol{S}} \end{array} $ | (47) |
| $ \begin{array}{*{20}{l}} {\mathit{\boldsymbol{B}} \cdot {\rm{d}}\mathit{\boldsymbol{l}} = \mathit{\boldsymbol{\omega }} \times {\rm{d}}\mathit{\boldsymbol{l}} = \mathit{\boldsymbol{R}} \times {\rm{d}}\mathit{\boldsymbol{l}} + \mathit{\boldsymbol{S}} \times {\rm{d}}\mathit{\boldsymbol{l}}}\\ {\mathit{\boldsymbol{\omega }} = \mathit{\boldsymbol{R}} + \mathit{\boldsymbol{S}}} \end{array} $ | (48) |
这就是Liu[10, 18]提出的Vorticity的Liutex和剪切分解(图 8)。从上式明显可见,我们不能用Vorticity去代表流体旋转,只能用张量R代表旋转,S代表不转的反对称剪切。在大多数情况下S是ω的主要组成部分,R(流体旋转)远远不是涡量ω。
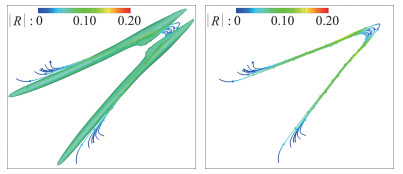
4 Liutex为基础的几个涡识别方法 4.1 Liutex向量线由于Liutex是一个向量,首先可以考虑用向量线来表示涡结构(图 9~图 10),这一点是Q、λci等第二代方法无可比拟的。因为第二代方法都是标量,它们没有对应的向量,只有用等值面来显示涡结构,这样涡结构完全由阈值决定,也就是一个阈值会给出一个涡结构,不同阈值给出不同涡结构。而如何判断阈值合适不合适,没有标准,只有以经验为准,谁也解释不了它们是合适还是不合适的阈值。如同流线用来描述流场一样,Liutex线可以用来描述Liutex场,或者涡场。显然这些Liutex线可以用来描述流场中的涡结构。
|
图 9 层流转捩Λ涡与Liutex线[11] Fig.9 Λ vortex and Liutex lines in a laminar-turbulent boundary layer transition[11] |
|
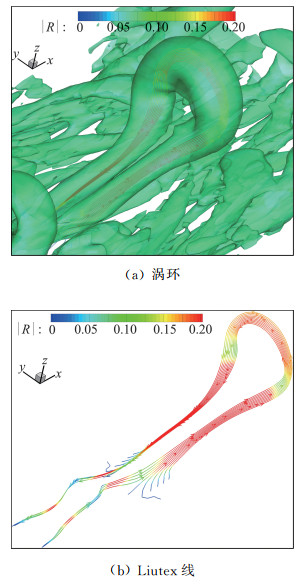
图 10 层流转捩涡环与Liutex线[11] Fig.10 Vortex rings and Liutex lines in a laminar-turbulent boundary layer transition[11] |
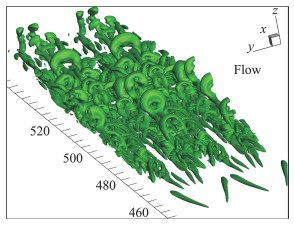
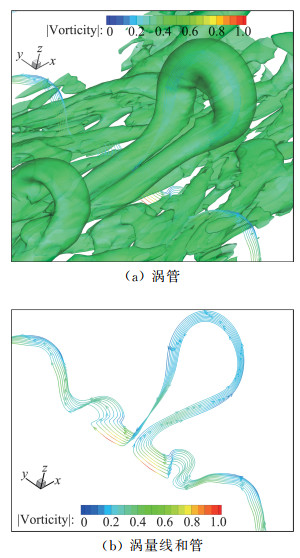
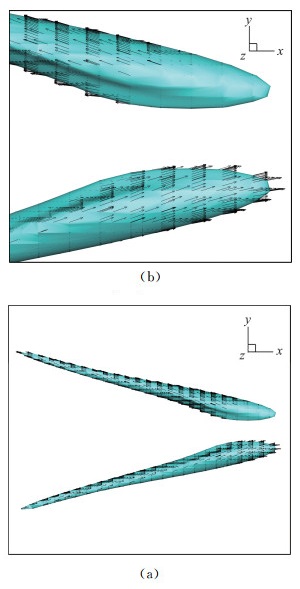
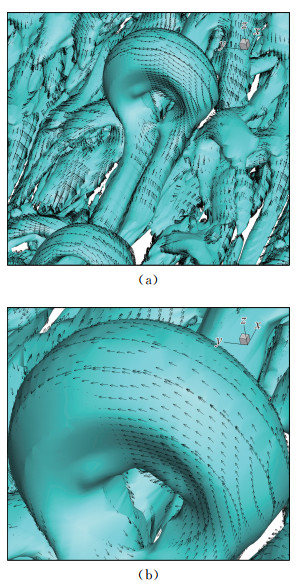
和Q一样,Liutex大小R也是一个标量,可以用Liutex等值面来表示涡结构(图 11)。这就又要用到阈值,但与第二代不同之处是R代表刚性旋转,不会被拉压和剪切所污染,R本身就是一个物理量,是当地流体旋转角速度的两倍,或者流体旋转的强度,下面三个图是用Liutex等值面画的早期层流流动转捩。其图与Q法画出的涡结构类似,但注意到Liutex等值面和Liutex向量线大致平行,换句话说,Liutex等值面上的Liutex向量方向和等值面方向一致(图 12和图 13)。Q无法对比,因为它是标量。涡量线和涡量管与Liutex等值面(涡面)也完全不同(图 14)。
|
图 12 流动自然转捩早期Λ涡腿的Liutex等值面(R=0.06)[12] Fig.12 Liutex iso-surfaces and Liutex vectors on the leg part of Λ vortex (R=0.06)[12] |
|
图 13 流动自然转捩早期Λ涡涡环的Liutex等值面(R=0.06)[12] Fig.13 Liutex iso-surfaces and Liutex vectors on vortex rings (R=0.06)[12] |
4.3 Liutex-Omega涡识别方法
前面我们已经介绍了Omega方法的若干优点,但是它还是基于Cauchy-Stokes分解的对称、反对称速度梯度张量分解,属于第二代涡识别方法,但比其他第二代涡识别方法更好,最主要是可代表涡的相对强度,对阈值不敏感,并可以同时捕捉到强涡和弱涡。这一点特别重要,尤其是在强涡、弱涡共存的情况下,如何能捕捉到弱涡就显得特别重要。很自然地会想到如何把Liutex方法和Omega方法的思想结合起来,这就产生了Liutex-Omega[14-15]涡识别方法。简单推导如下。根据主轴下的张量:
| $ \begin{array}{l} \nabla \mathit{\boldsymbol{V}}{{\kern 1pt} _{\theta {\rm{min}}}} = \left[ {\begin{array}{*{20}{c}} {\lambda {{\kern 1pt} _{cr}}}&{ - (\beta - \alpha )}&0\\ {\beta + \alpha }&{\lambda {{\kern 1pt} _{cr}}}&0\\ \xi &\eta &{\lambda {{\kern 1pt} _r}} \end{array}} \right]\\ \ \ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} = \left[ {\begin{array}{*{20}{c}} {\lambda {{\kern 1pt} _{cr}}}&\alpha &{\frac{1}{2}\xi }\\ \alpha &{\lambda {{\kern 1pt} _{cr}}}&{\frac{1}{2}\eta }\\ {\frac{1}{2}\xi }&{\frac{1}{2}\eta }&{\lambda {{\kern 1pt} _r}} \end{array}} \right] + \left[ {\begin{array}{*{20}{c}} 0&{ - \beta }&{ - \frac{1}{2}\xi }\\ \beta &0&{ - \frac{1}{2}\eta }\\ {\frac{1}{2}\xi }&{\frac{1}{2}\eta }&0 \end{array}} \right]\\ \ \ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} = \mathit{\boldsymbol{A}} + \mathit{\boldsymbol{B}} \end{array} $ | (49) |
和原始Ω的定义:
| $ {\varOmega _{3D}} = \frac{{{\beta ^2} + \frac{1}{4}({\xi ^2} + {\eta ^2})}}{{{\beta ^2} + \frac{1}{2}({\xi ^2} + {\eta ^2}) + {\alpha ^2} + \lambda {\kern 1pt} _{cr}^2 + \frac{1}{2}\lambda {\kern 1pt} _{cr}^2 + \varepsilon }} $ | (50) |
但是正如前面已经介绍的,(ξ2+η2)代表剪切,不应当用来度量流体转动或者涡强度,从而新的相对涡强度应当不含有剪切,这就得到了新的Liutex-Omega涡识别方法:
| $ {\tilde \varOmega _R} = \frac{{{\beta ^2}}}{{{\beta ^2} + {\alpha ^2} + \lambda {\kern 1pt} _{cr}^2 + \frac{1}{2}\lambda {\kern 1pt} _r^2 + \varepsilon }} $ | (51) |
这里,R=ω·r-
| $ \begin{array}{*{20}{l}} {\beta = \frac{1}{2}\mathit{\boldsymbol{\omega }} \cdot \mathit{\boldsymbol{r}}}\\ {\alpha = \frac{1}{2}\sqrt {{{(\mathit{\boldsymbol{\omega }} \cdot \mathit{\boldsymbol{r}})}^2} - 4\lambda {\kern 1pt} _{ci}^2} } \end{array} $ |
这里取ε=b0(β2-α2)max, b0是小值正数0.001~0.002,
或者用另一种表达式:
| $ {\tilde \varOmega _R} = \frac{{{{(\mathit{\boldsymbol{\omega }} \cdot \mathit{\boldsymbol{r}})}^2}}}{{2[{{(\mathit{\boldsymbol{\omega }} \cdot \mathit{\boldsymbol{r}})}^2} - 2\lambda {\kern 1pt} _{ci}^2 + 2\lambda {\kern 1pt} _{cr}^2 + \lambda {\kern 1pt} _r^2] + \varepsilon }} $ | (52) |
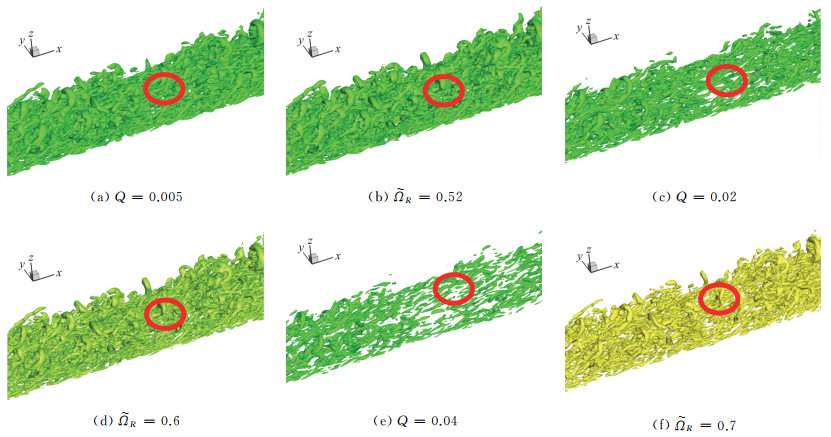
图 15显示用这种方法显示涡相对强度效果很好,涡结构用Q显示对阈值极为敏感,但
|
图 15 Q对阈值十分敏感,但Liutex-Omega对阈值不敏感[15] Fig.15 Comparison of sensitivity to thresholds between Q criterion and the Liutex-Omega method[15] |
以上各种涡显示方法都有一个致命缺点,就是不唯一,与阈值有关,即使Liutex-Omega方法也没有完全摆脱阈值。同时物理上的旋涡是有旋转轴的,前人尝试找涡核转轴均未获得成功。许多人尝试找到涡量极值,但那不是涡心。找Q极值,但一调大Q阈值,所有弱涡涡心一扫而空。当提出Liutex向量后,使得寻找涡心变为可能。Liu等[19-20]在2019年提出涡的转动核心定义,它是一条特殊的Liutex线,满足:
| $ \nabla R \times \mathit{\boldsymbol{r}} = 0,{\rm{ 并且}}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} R > 0 $ | (53) |
即,当▽R和r平行时,这根Liutex线就是涡的转轴。因为在R的等值面上:
| $ {\rm{d}}R = \nabla R \cdot {\rm{d}}\mathit{\boldsymbol{l}} = 0 $ |
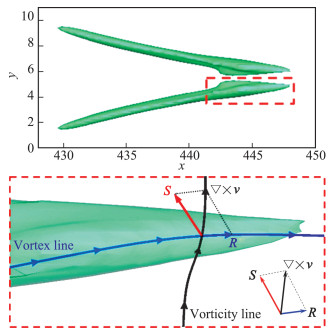
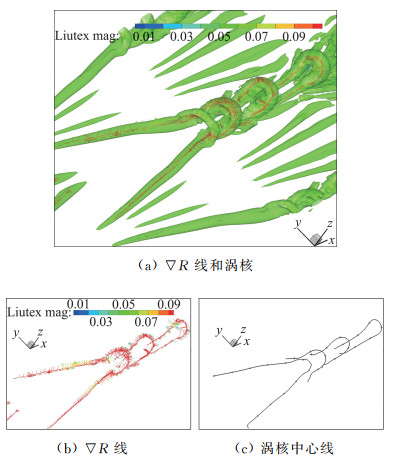
因为R的等值面上R不变,dR=0, 这就导致▽R和等值面垂直,到处一样,但是在涡心处,等值面退化为一根线,等值面不再存在,▽R· r≠0,二者平行。其实▽R是一个向量,直指R极值或者涡心,不论从哪儿起始,▽R线总是向涡心跑,直到涡心与r平行,这根Liutex线就是涡核中心或者转轴,它是唯一的,与阈值毫无关系。图 16显示各处▽R线都向涡核中心跑,涡核中心就是涡的转轴。
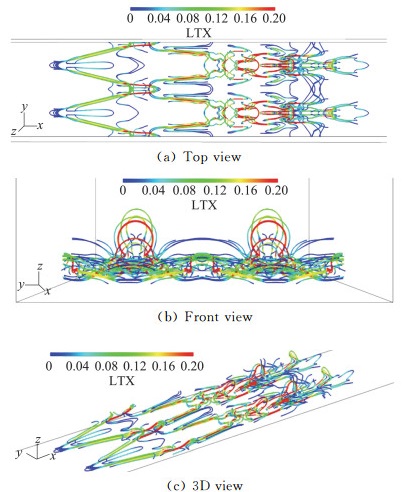
根据Liutex的涡核中心定义,高[19]等用手动方法找到流动早期转捩的涡核中心结构(图 17)。徐[20]等进一步根据Liutex的涡心定义,通过找到许多种子点,用计算机自动画出流动转捩的涡核结构(图 18)。
5 涡的六大要素和Liutex为代表的第三代涡识别方法
自然界的涡有六大要素:1)涡的绝对强度; 2)涡的相对强度; 3)当地旋转轴; 4)涡核中心位置; 5)涡核大小; 6)涡边界。第一代涡识别方法用涡量来描述涡结构。第二代涡识别方法当阈值接近零的时候能给出涡的大致边界,但因为它们都是标量,但涡有轴,是矢量,标量怎么能显示矢量?更为严重的是,它们都把拉压剪切当作流动旋转强度的一部分,或者被剪切严重污染。涡量大的地方流体转动强的结论不对。Q大的地方转动强,对复杂涡结构常常也不正确。而Ω涡识别方法和基于Liutex涡定义的第三代涡识别方法基本上回答了这六大要素的问题。
1) 涡的绝对强度即为Liutex的大小R,代表当地流体刚性旋转运动部分旋转角速度的二倍。根据以上讨论,Liutex的大小能够度量当地流体刚性旋转运动部分的绝对强度的物理量[13]。
2) 相对强度可以用Liutex-Omega衡量,它类似流体中Liutex的浓度或者流体的刚度。实际上,相对强度往往比绝对强度的更加重要,就像相对误差往往比绝对误差更重要一样。在复杂流场中,有可能存在转速为1000 rps的强涡和10 rps的弱涡,这时使用100 rps作为阈值,就会导致10 rps的弱涡被完全忽略。而使用相对强度,即Liutex-Omega可以同时捕捉到强涡和弱涡,对阈值不敏感。
3) 当地旋转轴就是Liutex向量的方向r,也就是速度梯度张量▽v的实特征向量。涡的一个重要信息旋转轴在第二代涡识别方法中被忽略掉了,而第一代涡量也是向量,但一般不是当地流体的转轴,涡量和涡两个矢量往往有两个完全不同的方向,而Liutex永远和涡有完全相同的方向。Liutex向量唯一地提供了当地旋转轴信息。
4) 涡核中心是一根特殊的Liutex线,满足▽R×r=0并且R>0的条件。可以先找到满足上述条件的点,再通过该点作Liutex线,涡核中心就可以找到。一般来说,为了寻找代表涡核中心的Liutex线,要求Liutex的大小在垂直于涡核线的平面上取极值,即要求Liutex大小的梯度方向与Liutex向量的方向相同。它们是唯一的,没有人为的阈值要求。
5) 涡核的大小可以按照从涡核处相对强度减少至涡核处的95%来确定,这是经验值,不能作为精确定义。由于流场中,存在强度不同的涡结构,使用Liutex-Omega方法可以同时显示强涡和弱涡,并利用其相对强度由涡核处减小至95%来定义涡核的尺寸。这样强涡和弱涡可以同时显示。
6) 涡的边界由旋转区域和非旋转区域的交界面来定义,一般要选取一个阈值,比如Ω=0.52, Q>QThreshold,等等。这一点所有涡识别方法在阈值很小的时候,都能给出涡的大致边界,这是因为根据Chong-Perry[8] (1990),涡内点必须满足速度梯度张量有一实两虚特征值。
回顾历代涡识别方法,第一代涡识别方法不能回答涡的六个要素问题。涡和涡量是两个不同的概念,使用涡量没有办法正确地识别涡结构,更不可能给出正确的涡核和涡边界。第二代涡识别方法通过针对具体问题选择合适的阈值,Q、λ2、Δ和λci等能够给出近似的涡边界,但作为标量,无法给出当地旋转轴信息,涡结构完全依赖于阈值选择,其大小被拉压和剪切污染,也不能准确代表涡强度。表 1给出了三代涡识别方法所能够提供的信息对比,可以看到只有第三代涡识别方法给出了涡六大要素的全部信息。
| 表 1 三代涡识别方法对比 Table 1 Comparison of three generation of vortex identification method |
|
|
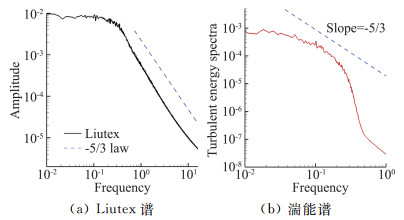
1941年前苏联数学家Kolmogorov给出了著名的三大假说两大相似律,提出大雷诺数条件下湍流局部均匀各向同性假定,并建立了被视为现代湍流研究开端的K41理论。作为K41理论王冠上最闪耀的一颗明珠,Kolmogorov预言的湍动能谱-5/3幂次律在大约十年后被许多实验所证实,被认为是湍流研究历史上最大的成功,也是唯一被学者广泛接受的湍流理论。然而,湍能谱的-5/3幂次律是在不可压缩、均匀、各向同性和惯性子区无黏的假定下得到。在实际流动中,尤其是在中低雷诺数条件下的边界层,所谓惯性子区不可能无黏,Kolmogorov这些假定往往不能满足。DNS和实验都广泛报道结果与Kolmogorov的-5/3定律相差甚远。团队[21]用高精度DNS研究层流边界层转捩和低雷诺数湍流时(Reθ≈1000)时发现,Liutex向量大小的能谱与-5/3幂次律吻合较好,相反湍能谱只有在很小的波数(频率)范围内才微弱满足-5/3幂次律,如图 19所示。
|
图 19 湍流边界层中Liutex谱和湍能谱与-5/3幂次律的对比[21] Fig.19 Liutex spectrum and turbulent energy spectrum in a turbulent boundary layer[21] |
Liutex的-5/3幂次律之所以具有更普遍的适用范围, 是因为Liutex向量代表流动中的刚性旋转部分,而刚性旋转部分的速度梯度无剪切、无黏性耗散,因而不受黏性的影响,从而独立于雷诺数。因此Liutex在中低雷诺数下的湍流小尺度结构仍然符合相似律。但如果对Vorticity和Q等第二代涡识别方法做频谱分析,它们都不具备相似律,与-5/3幂次律相距甚远。这一发现不仅增进了人们对湍流物理的认识,同时对建立更普适的亚格子模型具有重要的意义。
7 结论和展望涡是一个自然现象,更是湍流的组分和肌腱,但长久以来没有明确定义,这也是涡科学和湍流研究长期进展缓慢的重要原因之一。
第一代涡识别方法用涡量来代表涡,尽管为几乎所有教科书采用,但无数工程计算和实验都证明,不能用涡量、涡线、涡面、涡管来显示涡结构。
以Q方法为代表的第二代涡显示方法取得一些成功。但涡是向量,有方向,有大小,有转轴,但第二代全是标量,标量无法代表向量,第二代只有取阈值、用等值面来显示涡结构,从而涡结构依赖于阈值,导致涡结构随意化和不唯一。在复杂涡结构流场中由于阈值选取不当,弱涡常常被抹去。如果减小阈值,弱涡可能找回,但全流场涡结构变得模糊。更为严重的是第二代往往把拉伸、压缩和剪切当作涡强的一部分,也就是被拉压、剪切污染,不能用来度量流体旋转强度。因而从科学研究角度讲,第二代涡识别方法也不能用来显示涡结构。
经过长期努力,UTA团队找到物理量Liutex代表涡,它是一个向量,能够用来描述流体转动,也就是涡的方向和强弱。它的方向就是当地流体转动的方向,其实就是当地速度梯度张量的特征向量,它的大小就是当地流体刚性旋转的角速度的两倍。以Liutex为代表的涡定义和第三代涡识别方法,能够正确地代表、显示和度量涡。涡有六大基本要素,以Liutex为基础的涡定义和第三代涡识别方法,包括Liutex向量、Liutex向量线/面/管、Liutex等值面、Liutex-Omega等值面、Liutex-Core Lines能够全面地正确地回答涡的六大要素。
更为重要的是Liutex代表流体转动,涡量不能代表流体转动,这就要改变对流体运动认识近两百年的误解。传统的流体运动学中对Helmholtz速度分解和Cauchy-Stokes张量分解而言,涡量就是流体转动强度,反对称张量代表流体旋转,这些传统概论都必须要重新审视。由于主坐标系概念的引入,基于Liutex的涡量RS分解,基于Liutex的流体转动拉压剪切变形的张量分解,都是与坐标无关的,它们给出了唯一的伽利略不变的张量分解。希望Liutex这个新物理量的引入,能对流体动力学发展产生影响,使湍流理论从定性研究逐步向定量研究发展。
需要第三代涡识别方法程序,可以访问https://www.uta.edu/math/cnsm/public_html/cnsm/cnsm.html免费下载。
致谢:感谢UTA数学系长期的支持。感谢美国德克萨斯州先进计算中心(TACC)长期提供DNS计算机时。感谢UTA团队的王义乾、高宜胜、刘剑明、董祥瑞、许文倩,以及合作者徐弘一、蔡小舒、阎永华、杨勇、杨光、闫盼盼等人。此外,还要感谢Journal of Hydrodynamics周连第执行主编的多次讨论,并提出涡的六大要素。
| [1] |
LIU C Q, YAN Y H, LU P. Physics of turbulence generation and sustenance in a boundary layer[J]. Computers & Fluids, 2014, 102: 353-384. |
| [2] |
Green S I. Fluid Vortices[M]. Dordrecht: Kluwer Academic Publishers, 1995.
|
| [3] |
HELMHOLTZ H. Über Integrale der hydrodynamischen Gleichungen, welche den Wirbelbewegungen entsprechen[J]. Journal Für Die Reine Und Angewandte Mathematik, 1858, 1858(55): 25-55. DOI:10.1515/crll.1858.55.25 |
| [4] |
ROBINSON S K. Coherent motions in the turbulent boundary layer[J]. Annual Review of Fluid Mechanics, 1991, 23(1): 601-639. DOI:10.1146/annurev.fl.23.010191.003125 |
| [5] |
WANG Y Q, YANG Y, YANG G, et al. DNS study on vortex and vorticity in late boundary layer transition[J]. Communications in Computational Physics, 2017, 22(2): 441-459. DOI:10.4208/cicp.OA-2016-0183 |
| [6] |
HUNT J, WRAY A, MOIN P. Eddies, streams, and convergence zones in turbulent flows[R]. Center for Turbulence Research Proceedings of the Summer Program, 1988: 193.
|
| [7] |
JEONG J, HUSSAIN F. On the identification of a vortex[J]. Journal of Fluid Mechanics, 1995, 285: 69. DOI:10.1017/S0022112095000462 |
| [8] |
CHONG M S, PERRY A E, CANTWELL B J. A general classification of three-dimensional flow fields[J]. Physics of Fluids A:Fluid Dynamics, 1990, 2(5): 765-777. DOI:10.1063/1.857730 |
| [9] |
ZHOU J, ADRIAN R J, BALACHANDAR S, et al. Mechanisms for generating coherent packets of hairpin vortices in channel flow[J]. Journal of Fluid Mechanics, 1999, 387: 353-396. DOI:10.1017/S002211209900467X |
| [10] |
LIU C Q, WANG Y Q, YANG Y, et al. New omega vortex identification method[J]. Science China Physics, Mechanics & Astronomy, 2016, 59(8): 684711. |
| [11] |
LIU C Q, GAO Y S, DONG X R, et al. Third generation of vortex identification methods:Omega and Liutex/Rortex based systems[J]. Journal of Hydrodynamics, 2019, 31(2): 205-223. DOI:10.1007/s42241-019-0022-4 |
| [12] |
LIU C Q, GAO Y S, TIAN S L, et al. Rortex:a new vortex vector definition and vorticity tensor and vector decompositions[J]. Physics of Fluids, 2018, 30(3): 035103. DOI:10.1063/1.5023001 |
| [13] |
GAO Y S, LIU C Q. Rortex and comparison with eigenvalue-based vortex identification criteria[J]. Physics of Fluids, 2018, 30(8): 085107. DOI:10.1063/1.5040112 |
| [14] |
DONG X, GAO Y, LIU C. New normalized rortex/vortex identification method[J]. Physics of Fluids, 2019, 31: 011701. DOI:10.1063/1.5066016 |
| [15] |
LIU J M, LIU C Q. Modified normalized rortex/vortex identification method[J]. Physics of Fluids, 2019, 31(6): 061704. DOI:10.1063/1.5109437 |
| [16] |
LIU J M, GAO Y S, WANG Y Q, et al. Objective Omega vortex identification method[J]. Journal of Hydrodynamics, 2019, 31(3): 455-463. DOI:10.1007/s42241-019-0028-y |
| [17] |
LIU C Q. An objective version of the Rortex vector for vortex identification[J]. Physics of Fluids, 2019, 31(6): 065112. DOI:10.1063/1.5095624 |
| [18] |
GAO Y, LIU C. Letter:rortex based velocity gradient tensor decomposition[J]. Physics of Fluids, 2019, 31: 011704. DOI:10.1063/1.5084739 |
| [19] |
GAO Y S, LIU J M, YU Y F, et al. A Liutex based definition and identification of vortex core center lines[J]. Journal of Hydrodynamics, 2019, 31(3): 445-454. DOI:10.1007/s42241-019-0048-7 |
| [20] |
XU H Y, CAI X S, LIU C Q. Liutex (vortex) core definition and automatic identification for turbulence vortex structures[J]. Journal of Hydrodynamics, 2019, 31(5): 857-863. DOI:10.1007/s42241-019-0066-5 |
| [21] |
XU W, WANG Y, GAO Y, et al. Liutex similarity in turbulent boundary layer[J]. Journal of Hydrodynamics, 2019, 31: 1259-1262. DOI:10.1007/s42241-019-0094-1 |
| [22] |
DONG X R, WANG Y Q, CHEN X P, et al. Determination of epsilon for Omega vortex identification method[J]. Journal of Hydrodynamics, 2018, 30(4): 541-548. DOI:10.1007/s42241-018-0066-x |
| [23] |
TEUESDELL C. Two measure of vorticity[J]. J Rational Mech Anal, 1953, 2: 173-217. |
| [24] |
TUEESDELL C. The kinematics of vorticity[M]. Indiana University Press, 1954: 106-112.
|
| [25] |
WANG Y Q, GAO Y S, LIU J M, et al. Explicit formula for the Liutex vector and physical meaning of vorticity based on the Liutex-Shear decomposition[J]. Journal of Hydrodynamics, 2019, 31(3): 464-474. DOI:10.1007/s42241-019-0032-2 |
| [26] |
BOULANGER, PH HAYES M. On shearing, stretching and spin[J]. Theoretical and Computational Fluids, 2002, 15: 199-229. DOI:10.1007/s001620100050 |
| [27] |
LIU C Q. Letter:Galilean invariance of rortex[J]. Physics of Fluids, 2018, 30(11): 111701. DOI:10.1063/1.5058939 |
| [28] |
LIU J M, WANG Y Q, GAO Y S, et al. Galilean invariance of Omega vortex identification method[J]. Journal of Hydrodynamics, 2019, 31(2): 249-255. DOI:10.1007/s42241-019-0024-2 |
 2020, Vol. 38
2020, Vol. 38