2. State Key Laboratory of Aerodynamics, China Aerodynamics Research and Development Center, Mianyang 621000, China
2. 中国空气动力动力与发展中心 空气动力学国家重点实验室, 绵阳 621000
The design of silent turbofan jet engine is an important issue on civilian aircraft, which usually comprises a low-speed cold bypass flow and the heated high-speed core stream. The coaxial jet is capable of raising the fuel efficiency and reducing the turbulent mixing noise[1]. In recent decades, much attention has been paid to the experiments and numerical simulations of flow developments and noise emission in turbulent coaxial jets[2-5]. Moreover, from the perspective of hydrodynamic stability, the evolutions of flow perturbations in coaxial jets with different operating conditions (e.g. different bypass ratios and temperature ratios) have also been analyzed based on local linear stability theory (LST)[1, 6-7]. Near the nozzle exit, two kinds of instability modes, namely, the 'inner mode' and 'outer mode', corresponding to the primary and secondary shear layer, can be obtained by LST, both of which have a great influence on the initial flow development, especially the evolution of large-scale flow structures.
Since the pioneer study of Crow and Champagne[8], large-scale coherent structures in turbulent flows have been studied extensively. Recently, great efforts have been made to construct wavepacket models for far-field noise prediction in order to mimic the noise radiated by large-scale coherent structures in turbulent single-stream jets[9-11] and coaxial jets[12-14]. Considering the slow-varying and non-parallel effects of mean flow, a wavepacket model based on Parabolized Stability Equations (PSE)[15] has been proven to be relatively effective before the end of the potential core in turbulent jets[16-20]and also in subsonic coaxial jets[21-23].
However, the limitations of wavepackets based on linear-PSE model are also significant, which cause underestimation of far-field sound pressure levels (SPL) greatly in subsonic jets compared to the predictions of large-eddy simulation (LES)[24-26]. As stated by Tissot et al.[27], the nonlinearity might be the most important missing factor and should be considered in the modeling framework. The effects of nonlinearity on wavepackets and sound generation have gained more and more attentions in recent years[27-30]. Semeraro et al.[14] discussed that the nature of nonlinearity might come from nonlinear wave-wave interactions, or stochastic turbulence interactions. The simplest weakly nonlinear model considering the nonlinear interaction effect of two instability modes was proposed by Sandham and Salgado[31], which was tested numerically in the subsonic transitional jet[26]. It was found that the nonlinear interactions could raise the acoustic efficiency to a certain extent at low polar angles in the downstream region, but such model is still far from the real situation. Up to now, the nonlinear effects on sound generation in subsonic jets are still ambiguous, which are far more complicated in turbulent jets under realistic operating conditions, since the 'real' nonlinearity is originated from full Navier-Stokes equations. In a word, this subject is worthy of further and deeper investigation.
The present work is inspired by the work of Tissot et al.[27], where an 'external' harmonic forcing term interpreted as the effect of nonlinearity is added to the linear model in the subsonic single-stream turbulent jet. The largest sensitivity of wavepackets and flow responses to this forcing are found to be located in the vicinity of the critical layer, where the phase speed equals to the mean-flow velocity at each streamwise location. However, in the coaxial jets, where two distinct shear layers accompanied by two critical layers exist, we here mainly concern about the differences in sensitivity and response of flow disturbances between the coaxial jet and single-stream jet, and whether interplay between two instability modes exists.
The rest of paper is organized as follows. In Sec.1, the mean flow fields of coaxial jets with different velocity ratios are obtained by solving Reynolds-averaged Navier-Stokes (RANS) equations, and the numerical methods of PSE and adjoint PSE are introduced. The results and discussions of the local linear stability analysis, linear wavepacket model based on PSE and the sensitivity of wavepackets with respect to external forcing are presented in Sec.2 and Sec.3. Finally, the summary of results is presented in Sec.4.
1 Problem formulation 1.1 Flowconfiguration In this study, we obtain the turbulent mean flow fields of subsonic coaxial jets with different velocity ratios by solving the RANS equations together with the SST (Menter's Shear Stress Transport) turbulence model. A co-planar coaxial nozzle similar to Ref. [32] is inserted into the computational domain (see Fig. 1), where the primary nozzle diameter is Dp=0.1 m and the secondary nozzle diameter is D=0.2 m. The RANS computational domain is a cylinder with [-2.7D, 30D] in the streamwise direction and 0, 12D in the radial direction, where the center of coaxial nozzle exit is located at z=0 and r=0. An O-grid based structured mesh with about 5 million nodes is adopted, with mesh refinement near the jet exit z=0 and around the two shear layers at r=0.25D and r=0.5D. The detailed conditions of two coaxial jets are listed in Table 1, where U is the velocity, T is the temperature, Ma is the Mach number and a is the sound speed. The subscripts 'p' and 's' refer to the exit conditions at primary and secondary nozzle, respectively. The Reynolds number corresponding to the primary nozzle diameter ReDp=ρpUpDp/μp is 2×106. The velocity decay along the jet centerline has been validated by investigating the mean flow field of a heated coaxial jet compared with Bogey et al. (2009)[4]. Details can be found in the Appendix.
|
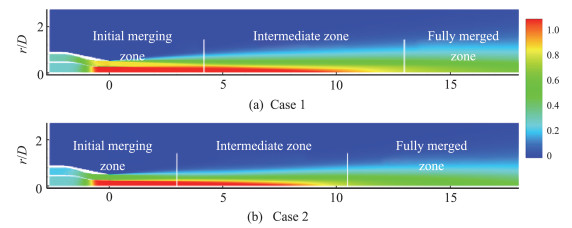
Fig.1 Mean axial velocity fields Uz/Up in subsonic coaxial jets 图 1 亚声速同轴射流基本流流向速度场 |
Figure 1 shows the mean axial velocity fields of two coaxial jets considered. In general, three stages of jet development can be identified, referred to as the initial merging zone, intermediate zone and fully merged zone, marked in Fig. 1, which are qualitatively similar to previous work[13]. As illustrated in Fig. 1(a), the initial merging zone starts from the nozzle exit and ends near the end of outer potential core at about z=4D where the two shear layers begin to merge. The intermediate zone, where most of jet mixing takes place, starts from the end of outer potential core and extends to the point where the outer shear layer reaches the jet axis at about z=13D. The fully merged zone is located just downstream of the intermediate zone, where the flow field becomes similar to the single-stream jet. We also find that both the inner and outer potential core lengths become shorter when the velocity ratio decreases, in consistence with the results of Gloor et al.[15].
| Table 1 Parameters of two subsonic coaxial jets with different velocity ratios for the mean flow computations 表 1 具有不同速度比的亚声速同轴射流基本流计算参数列表 |
|
|
The flow variables Q in cylindrical coordinates can be decomposed into mean and disturbance parts,
| $ \mathit{\boldsymbol{Q}} = \mathit{\boldsymbol{\bar q}} + {\mathit{\boldsymbol{q}}^\prime } $ | (1) |
where the mean flow
| $ \begin{array}{l} \boldsymbol{q}^{\prime}(z, r, \theta, t)= \\ \boldsymbol{q}(z, r) \exp \left[\mathrm{i}\left(\int_{z_{0}}^{z} \alpha(\xi) \mathrm{d} \xi+m \theta-\omega t\right)\right] \end{array} $ | (2) |
where α is the complex local streamwise wavenumber, m is the azimuthal wavenumber, and Ω is the angular frequency. By substituting the Eq.(1) and Eq.(2) into compressible Euler equations, and neglecting the viscous terms and high-order nonlinear components, the disturbance equations could be written in compact matrix forms as:
| $ \mathcal{L} \boldsymbol{q}=0, \mathcal{L}=i \alpha \boldsymbol{M}+\boldsymbol{M} \frac{\partial}{\partial z}+\boldsymbol{N} \frac{\partial}{\partial r}+\boldsymbol{A} $ | (3) |
where M, Nand A are linear operators associated with mean flow variables q. The detailed expression of M, N and A can be found in the appendix of our previous work[33]. An additional constraint must be imposed to keep the equations well-posed and ensure that q(z, r) varies slowly in the axial direction[15]:
| $ \int_{0}^{R} \boldsymbol{q}^{H} \frac{\partial \boldsymbol{q}}{\partial z} r \mathrm{d} r=0 $ | (4) |
where the superscript H denotes transpose conjugate, and R is the maximum of the radial computational domain. A downstream marching algorithm is employed to solve the PSE iteratively. Following Andersson et al.[34], a modified formulation of linear-PSE is utilized to treat numerical instabilities[15] :
| $ \boldsymbol{M}^{\prime} \frac{\partial \boldsymbol{q}}{\partial z}+\left(\mathrm{i} \alpha \boldsymbol{M}+\boldsymbol{N} \frac{\partial}{\partial r}+\boldsymbol{A}\right) \boldsymbol{q}=0 $ | (5) |
where
| $ \left\{\begin{array}{l} s=s_{0}, \quad \text { if } \quad \mathrm{d} z>\frac{1}{\left|\alpha_{r}\right|}-2 s_{0} \\ s=\left(\frac{1}{\left|\alpha_{r}\right|}-\mathrm{d} z\right) / 2+0.01, \quad \text { otherwise } \end{array}\right. $ | (6) |
where dz=0.1D, s0=0.1.
The boundary conditions of PSE in radial direction are given as
| $ \left\{\begin{aligned} |m|=0: u_{r}=u_{\theta} &=0 \\ \mathrm{d} \rho / \mathrm{d} r &=\mathrm{d} u_{z} / \mathrm{d} r=\mathrm{d} T / \mathrm{d} r=0 \\ |m|=1: u_{z}=\rho &=T=0 \\ \mathrm{d} u_{r} / \mathrm{d} r &=\mathrm{d} u_{\theta} / \mathrm{d} r=0 \end{aligned}\right. $ | (7) |
In this work, we investigate the influence of the external harmonic forcing on the spatial development of instability waves, so a spatial integration form of flow disturbance is used in the objective function in the adjoint procedures. Similar to Ref.[34], the generalized total disturbance energy is defined as the objective function and the external forcing
As a prerequisite, the innerproducts in the radial direction and in the whole domain are defined as follows:
| $ \begin{aligned} \langle\boldsymbol{a}, \boldsymbol{b}\rangle_{r} &=\int_{0}^{R} \boldsymbol{a}^{H} \boldsymbol{b} r \mathrm{d} r \\ \langle\boldsymbol{a}, \boldsymbol{b}\rangle_{\Omega} &=\int_{z_{0}}^{z_{f}} \int_{0}^{R} \boldsymbol{a}^{H} \boldsymbol{b} r \mathrm{d} r \mathrm{d} z \end{aligned} $ | (8) |
where Ω=[z0, zf]×[0, R] is the computational domain of PSE and APSE. The streamwise axis starts from z0 and ends by zf.
The local disturbance energy Ez is defined as follows:
| $ E_{z}(z)=\int_{0}^{R}\left(\chi_{\boldsymbol{q}}(z, r)\right)^{H} \chi_{\boldsymbol{q}}(z, r) r \mathrm{d} r $ | (9) |
and we further define the cost function J as
| $ J=\int_{z_{0}}^{z_{f}} E_{z}(z) \mathrm{d} z $ | (10) |
and the exponential function χ as
| $ \chi(z)=\exp \left[\mathrm{i} \int_{z_{0}}^{z} \alpha(\xi) \mathrm{d} \xi\right] $ | (11) |
An unconstrained Lagrangian function L, which accounts for linear-PSE, the normalized condition and the cost function, is introduced
| $ L=\mathcal{R}\left\{J-\left\langle\hat{\boldsymbol{q}}^{*}, \chi \mathcal{L} \boldsymbol{q}-\hat{\boldsymbol{f}}\right\rangle_{\Omega}-\int_{z_{0}}^{z_{f}} n^{H} \int_{0}^{R} \boldsymbol{q}^{H} \frac{\partial \boldsymbol{q}}{\partial z} r \mathrm{d} r \mathrm{d} z\right\} $ | (12) |
where
| $ \hat{\boldsymbol{q}}^{*}=\chi^{*} \boldsymbol{q}^{*} $ | (13) |
where
| $ \mathcal{L}^{*} \boldsymbol{q}^{*}=\operatorname{RHS}(n, \boldsymbol{q}) $ | (14) |
where
| $ \begin{array}{*{20}{c}} {{{\cal L}^*} = - \frac{1}{r}{\boldsymbol{N}^H} + \left( {{\boldsymbol{A}^H} - {\rm{i}}\alpha {\boldsymbol{M}^H}} \right) - \frac{{\partial {\boldsymbol{M}^H}}}{{\partial {\bf{z}}}} - }\\ {\frac{{\partial {\boldsymbol{N}^H}}}{{\partial r}} - {\boldsymbol{M}^H}\frac{\partial }{{\partial {\bf{z}}}} - {\boldsymbol{N}^H}\frac{\partial }{{\partial r}}} \end{array} $ | (15) |
| $ \mathrm{RHS}=\frac{1}{\chi_{f}^{H}}\left[\left(n-n^{H}\right) \frac{\partial \boldsymbol{q}}{\partial \boldsymbol{z}}+\left(\frac{\partial n}{\partial \boldsymbol{z}}+\chi \chi^{H}\right) \boldsymbol{q}\right] $ | (16) |
Then, the adjoint normalized condition becomes
| $ \mathcal{R}\left\{\frac{E_{z}}{E_{0}}+\chi_{f} \int_{0}^{R} \frac{\partial\left(\boldsymbol{q}^{* H} \boldsymbol{M} \boldsymbol{q}\right)}{\partial z} r \mathrm{d} r\right\}=0 $ | (17) |
where E0=Ez(z=z0).
Finally, the sensitivity S with respect to k-th component of the external forcing f is
| $ \hat{S}_{f k}=\nabla \hat{L}_{f k}=\mathcal{R}\left(\hat{q}_{k}^{*}\right) $ | (18) |
The sub-domain Ω inside the RANS computational domain is used to solve the PSE and APSE, where z0 is 0.5D slightly downstream of the nozzle exit to remove the influence of nozzle, zf is 20D downstream of the nozzle exit, and R is 10D away from the jet axis. The equations are discretized by the first-order backward difference scheme in z-direction with 196 grid points and uniform grid spacing dz=0.1D, and the sixth-order compact difference scheme[35] in r-direction with 300 stretched grid points, clustering near the nozzle-lip.
The radial boundary conditions of APSE can be also derived together with the APSE,
| $ \mathcal{R}\left\{\left.\chi_{f} \int_{z_{0}}^{z_{f}}\left[\boldsymbol{q}^{* H} \boldsymbol{N} \delta \boldsymbol{q} r\right]\right|_{r=0} ^{r=R} \mathrm{d} z\right\}=0 $ | (19) |
An upstream marching algorithm is applied in solving APSE iteratively, contrary to PSE, while the streamwise terminal condition at z=zf is
| $ \boldsymbol{q}^{*}\left(z_{f}, r\right)=0, \quad n\left(z_{f}\right)=0 $ | (20) |
More details including discretization and the validation of PSE and APSE codes can be found in our previous work[36].
2 Hydrodynamic stability and instability wavesIn order to characterize the behaviors of large-scale coherent structures in the hydrodynamic region of coaxial jets, the PSE-based linear instability wave model is constructed, similar to Sinha et al.[23]. The local stability analysis is firstly carried out near the nozzle exit in purpose of obtaining the instability characteristics of both inner and outer modes in coaxial jets. Then, the two kinds of instability modes, normalized by the disturbance energy in Eq. (9) at the position z=z0, are used as the initial conditions for solving the PSE to obtain the spatial development of instability waves.
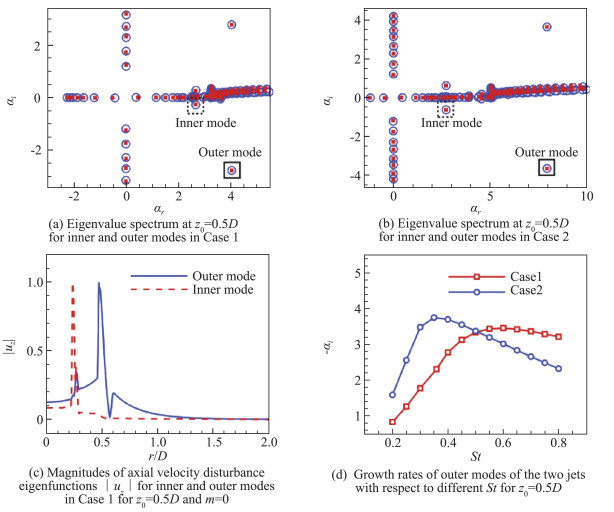
2.1 Locallyparallel analysis Firstly, the local stability analysis is carried out for different Strouhal numbers St=fDs/Up at z=z0 near the nozzle exit where f=Ω/2π represents the frequency. Two meshes with 280 and 300 r-grid points are adopted to show the convergence of eigenvalues. Generally, the low-frequency and low-azimuthal-wavenumber components of wavepackets are recognized to be associated with the major sound sources of turbulent jet noise, thus in the following the axisymmetric mode m=0 is investigated. Gloor et al.[5] have reported a representative frequency of St=0.4 in the sound pressure spectrum at low polar angle in their isothermal coaxial jet. Thus, we also take the axisymmetric mode m=0 and St=0.4 as an example. From the eigenvalue spectrum shown in Fig. 2, two distinct unstable modes can be identified. The two different modes are corresponding to the hydrodynamic Kelvin-Helmholtz (K-H) modes of the two mixing layers, where the definition of 'inner mode' refers to the K-H mode at the primary mixing region, and the 'outer mode' refers to the K-H mode at the secondary mixing region. At St=0.4, the local growth rate of the outer mode is much higher than its counterpart of inner mode, indicating that the outer mode dominates the local instability near the nozzle exit, which is consistence with the conclusion of Kwan and Ko[12], Léon and Brazier[22]. The imaginary part of the eigenvalues obtained by LST representing the local growth rate with respect to the Strouhal number is presented in Fig. 2(d). It is seen that the peak frequency of growth rate is reduced when the velocity ratio decreases. For St=0.4 and m=0, the growth rates in the two cases are relatively high, so this frequency component is appropriate for comparison between the two cases.
|
Fig.2 Results of locally parallel stability analysis in coaxial jets at z0=0.5D 图 2 同轴射流z0=0.5D站位当地平行流稳定性分析结果 |
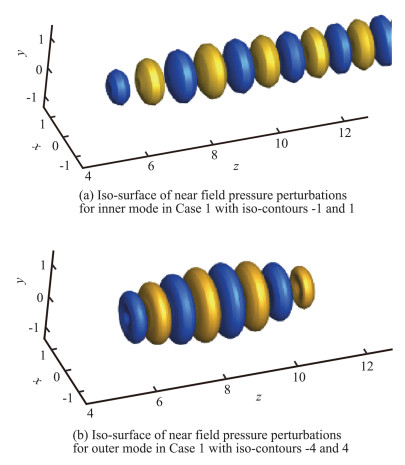
analysis In this section, we consider the slowly diverging base flows obtained by RANS simulations and carry out non-parallel analysis based on PSE. Starting from the solutions of locally parallel analysis, the spatial evolutions of instability waves for both inner and outer modes in the whole domain are obtained by solving the PSE with non-parallel effect. The near-field pressure structures for inner and outer modes in Case 1 for St=0.4 and m=0, characterized by the iso-contours of pressure disturbance, are shown in Fig. 3 (a) and Fig. 3 (b), respectively. It shows that our present linear-PSE model could capture the key characteristics of coherent wavepackets for both inner and outer modes. The pressure disturbance magnitudes increase at first, then come to saturation and finally decay. Moreover, the peak of pressure disturbance for outer mode occurs earlier upstream with a larger amplitude compared with the inner mode, suggesting that the outer mode plays a dominant role in the upstream of the end of potential core of secondary nozzle, also in agreement with locally parallel analysis. However, it is worth mentioning that the outer mode decays more rapidly after saturation, because the two shear layers in the coaxial jet flow begin to merge in the downstream of the outer potential core. These results are also in reasonable agreement with that of Sinha et al.[23].
|
Fig.3 Near field pressure wavepackets in coaxial jets (St=0.4, m=0) 图 3 同轴射流近场压力波包(St=0.4, m=0) |
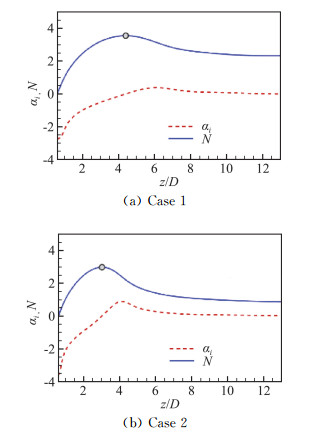
Figure 4 compares the imaginary part of local streamwise wavenumber αi and the 'N-factor', defined as imaginary part of -χ in Eq.(11), representing the spatial growth rate between the two cases for outer modes. It shows that the rapid growth of instability wave mainly occurs before 3D~4D to nozzle exit inside the potential core in both cases. Moreover, as the velocity ratio decreases, the peak of N-factor corresponding to the neutrally stable axial location moves upstream to the nozzle exit, due to a shorter length of the outer potential core in Case 2. The change of neutrally stable axial location will affect the spatial distribution of sensitivity and flow response.
|
Fig.4 Streamwise evolution of spatial growth rate of wavepackets in coaxial jets (St=0.4 and m=0, The circle denotes the peak position of N-factor) 图 4 同轴射流波包空间增长率的流向演化(St=04,m=0, 圆圈表示N因子的峰值位置) |
analysis to external forcing In this section, in order to determine the effects of nonlinearities on wavepackets in present subsonic coaxial jets, the sensitivity of disturbance energy with respect to the external forcing is obtained by the solution of adjoint PSE. Here, we firstly focus on the sensitivity around the homogenous situation (f=0), in which the infinitesimal forcing is defined as δf obtained by the definition of sensitivity
| $ \delta \boldsymbol{f}=\beta \frac{\partial J}{\partial \boldsymbol{f}} $ | (21) |
The relaxation coefficient β is set to 10-6. The jet flow mainly evolves along the streamwise direction, therefore we investigate the infinitesimal forcing, namely the sensitivity forcing fs with the vector form of fs=δf=(0, 0, 0, fs, 0)T, added to the right-hand side of linear-PSE as Eq. (22). Here, fs is the axial momentum component of the external forcing,
| $ \mathcal{L} \boldsymbol{q}=\boldsymbol{f}_{s} $ | (22) |
It is worth mentioning that fs is real-valued according to the definition of sensitivity in Eq. (18).
The corresponding flow response can be defined in a similar way. For instance, q0 is the solution of homogeneous linear-PSE, and qf is the solution of inhomogeneous forced-PSE defined by Eq. (22). Then, the flow response can be defined as the difference of the above two states, i.e. δq=qf-q0. Note that these two equations are solved starting from the same inflow conditions. The axial velocity disturbance component of δq is utilized correspondingly to show the flow response.
The sensitivity results of forcing fs and flow response δq are presented in Fig. 5 and Fig. 6 for St=0.4 and m=0 in both jets. In the theory of shear-flow stability, critical layers arise as a singularity of the linearized Euler equations in frequency-wavenumber space, where the phase velocity of instability wave is equal to the local fluid velocity. Since a local streamwise wavenumber of the flow perturbations is defined by PSE, we can determine the critical-layer position at each streamwise location. In present coaxial flows, there are two distinct K-H modes, which means there are two critical layers as well. In Fig. 5 and Fig. 6, we plot the outer and inner critical layers as solid and dashed lines on the z-r map, respectively. It is found that there are some similarities in the sensitivity results between our present coaxial jets and the results of Tissot et al.[27] in their single-stream jet. The most striking feature is that the peak values of both forcing and flow response of inner or outer mode are mainly distributed around its own critical layer. This is related to the inherent nature of critical layer. According to the inviscid stability theory, from Rayleigh's stability equation and its adjoint formulation, the adjoint solution could reach infinity around the critical layer, giving rise to such a region with high sensitivity, as discussed by Tissot et al.[27]. In addition, for both inner and outer modes, the spatial distributions of forcing and flow response show tilted structures of perturbations characterized by the shear in the downstream region, which is related to the Orr mechanisms[29]. The details about the wavepackets in connection with Orr mechanisms can also refer to the recent work of Schmidt et al.[37].
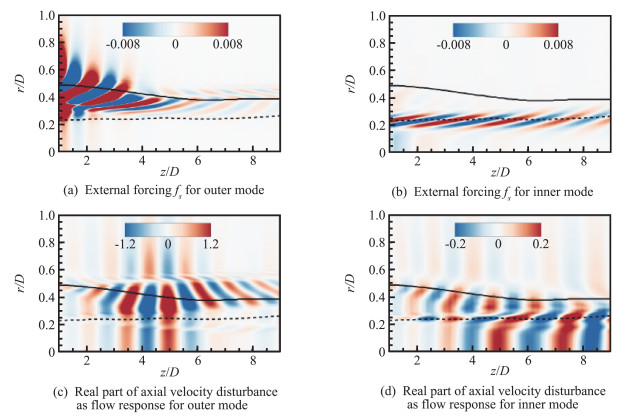
|
Fig.5 Spatial distribution of sensitivity forcing and flow response for inner and outer modes in Case 1 (St=0.4, m=0, Solid line: outer critical layer; dashed line: inner critical layer) 图 5 算例1中内外模态敏感性激励和流动响应的空间分布对比(St=0.4, m=0.实线:外临界层;虚线:内临界层) |
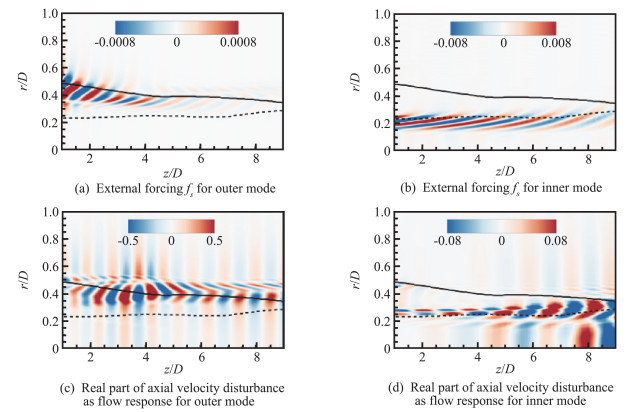
|
Fig.6 Spatial distribution of sensitivity forcing and flow response for inner and outer modes in Case 2 (St=0.4, m=0, Solid line: outer critical layer; dashed line: inner critical layer) 图 6 算例2中内外模态敏感性激励和流动响应的空间分布对比(St=0.4, m=0.实线:外临界层;虚线:内临界层) |
One aim of present work is to study the mutual influence of the inner and outer shear layers based on the forcing and flow response, which is the major difference between the coaxial jet and single-stream jet. Based on the sensitivity results, it is shown that the forcing fs of inner/outer mode is mainly located in the vicinity of its own critical layer, which has little effect in the region near the other critical layer, as seen in Figs. 5(a, b). Along the critical layers, the highest values of sensitivity are mainly located near the nozzle exit which decay in the downstream region, due to the fact that the growth rates of instability waves are higher in the upstream near the nozzle as illustrated in Fig. 4.
However, from the flow response δq, some mutual influences of the inner and outer shear layers can be clearly identified. As shown in Figs. 5(c, d), it is seen that both the forcing of inner or outer mode has some influence on flow responses near the critical layer of the other mode. For the outer mode, we find that the flow response reaches its peak near the neutral stability axial position. Moreover, the peak location of flow response in the radial direction in general matches with the critical layer location before the neutral stability axial position. However, after this axial location, it is clearly found that the forcing of inner mode has a certain influence on the flow response with a secondary peak around the outer critical layer, as shown in Fig. 5 (d). In order to show the effects of forcing more clearly, we present the radial distribution of real part of axial velocity forcing and flow response for inner and outer modes of Case 1 at three different positions z=2D, 3D and 5D in Fig. 7 and Fig. 8, respectively. From Fig. 7(a), at z=2D, for the outer mode, there is a secondary peak close to the inner critical layer which is almost identical to that of the primary peak around the outer critical layer. At z=3D and 5D, the secondary peak is relatively weak compared to the primary peak when the axial position moves downstream, as shown in Fig. 7(b, c). On the other hand, from Fig. 8, for the inner mode, the absolute value of flow response near the outer critical layer is even greater than that near the inner critical layer before the end of the outer potential core (e.g. z=2D or z=3D), implying that nonlinearities near the inner critical layer in this region can contribute considerably to instabilities near the outer shear layer. Moreover, it is interestingly found that in downstream region where the two shear layers begin to merge, the flow response magnitudes of inner mode near the jet axis increase rapidly, as illustrated in Fig. 5 (d) and Fig. 6 (d). In other words, in the downstream core region close to the jet axis, the inner mode plays an increasingly important role. It is worth mentioning that such a kind of response pattern is to some extent similar to that of the single-stream jet[27].
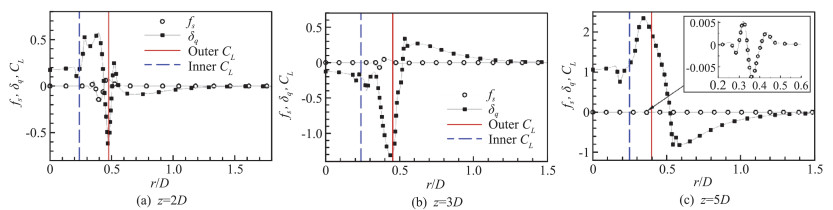
|
Fig.7 Comparison of sensitivity forcing and flow response at different streamwise locations for outer mode in Case 1(St=0.4, m=0. Solid line represents the axial position of outer critical layer and dashed line for inner critical layer) 图 7 算例1外模态不同流向站位处敏感性激励和流动响应对比(St=0.4, m=0.实线代表外临界层的流向位置,虚线代表内临界层的流向位置) |
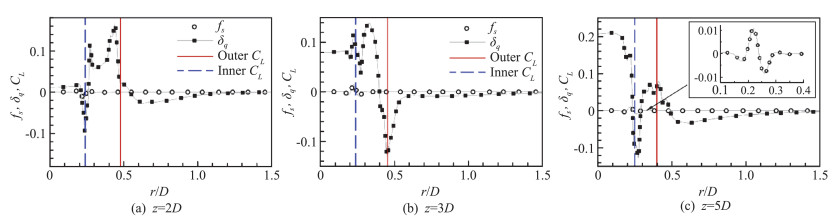
|
Fig.8 Comparison of sensitivity forcing and flow response at different streamwise locations for inner mode in Case 1 (St=0.4, m=0. Solid line represents the axial position of outer critical layer and dashed line for inner critical layer) 图 8 算例1内模态不同流向站位处敏感性激励和流动响应对比(St=0.4, m=0.实线代表外临界层的流向位置,虚线代表内临界层的流向位置) |
In addition, comparing Fig. 5 and Fig. 6, we find that the axial location of maximum flow response moves upstream when the velocity ratio is smaller, which seems to be consistent with the PSE results for the change of neutral stability axial position shown in Fig. 4. Accordingly, the effect of forcing of outer mode becomes weaker in Case 2 because of its lower velocity and shorter length of potential core to the secondary nozzle. More importantly, in both cases, the outer modes have larger amplitudes of flow response than the inner modes, indicating that the outer modes are not only dominant in the evolution of instability waves but also more sensitive to the external forcing. In a word, the nonlinearity plays a more significant role around the inner and outer critical layers, especially for the outer mode inside the outer potential core near the nozzle exit.
3.2 Optimalforcing In this section, we are committed to searching optimal volumetric forcing with a specific amplitude using an APSE-based optimization algorithm, in order to achieve wavepackets with higher disturbance kinetic energy with the same relaxation parameter β in building the nonlinear wavepacket model. In practice, the stochastic forcing magnitudes in real turbulent jets are relatively small. From the perspective of the formulation of Eq. (22), the nonlinear terms in PSE are in fact some form of higher-order flow disturbances acting as Reynolds stresses. The entire magnitude of such external forcing must be restricted in order to prevent the fast growth of disturbance energy, otherwise it may cause the excessive magnitudes of flow disturbances, or even invalid solutions. Following Ref.[36], the integral of k-th component of external forcing in the whole domain (k=1, 2, ..., 5) is
| $ \varepsilon_{k}=\int_{\mathit {\Omega}} f_{k} \mathrm{d} \mathit {\Omega} $ | (23) |
Therefore, in convenience, we keep the value of εk constant as a constraint for optimization procedures. The target of optimization is to achieve the maximum of disturbance energy over the full computational domain, i.e. to obtain the most energetic wavepacket in the hydrodynamic region.
Firstly, the direct and adjoint PSE are solved iteratively until convergence with the same εk as the sensitivity analysis. The optimal forcing is computed as following procedures
| $ \boldsymbol{f}^{(n+1)}=\boldsymbol{f}^{(n)}+\beta^{(n)}\left(\frac{\partial J}{\partial \boldsymbol{f}}\right)^{(n)} $ | (24) |
Since the downstream evolution of wavepackets is dominated by outer mode, we only build the wavepacket model for outer modes including optimal forcing. Similarly, the axial momentum component of optimal forcing is adopted, then the optimal forcing fopt is added to the right-hand side of linear PSE for obtaining the nonlinear wavepackets.
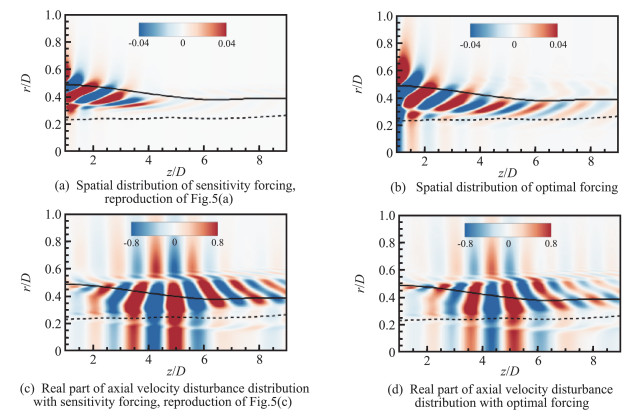
Next, we take the component of St=0.4 and m=0 in Case 1 as an example. Fig. 9 shows the spatial distribution of optimal volumetric forcing and axial velocity disturbance as the flow response compared with the results of sensitivity analysis. The outer and inner critical layers are also shown. It is clear that the shape of optimal forcing is quite similar to that of sensitivity results. The region of maximum forcing magnitude is also located in vicinity of the outer critical layer. However, there are some differences that the optimal forcing is more widely distributed, especially at z>4D downstream of the outer potential core. Additionally, Figs. 9 (c, d) show the axial velocity disturbances as the flow responses. We find the results of flow response remain qualitatively the same, except the minor difference occurring downstream of the outer potential core. In short, the optimization procedures mainly change the distribution of forcing and flow response in the downstream region to some extent.
|
Fig.9 Comparison of sensitivity forcing and optimal forcing and their flow response for outer mode in Case 1 (St=0.4, m=0, Solid line: outer critical layer; dashed line: inner critical layer) 图 9 算例1外模态敏感性激励和最优激励及其流动响应对比(St=0.4, m=0, 实线:外临界层;虚线:内临界层) |
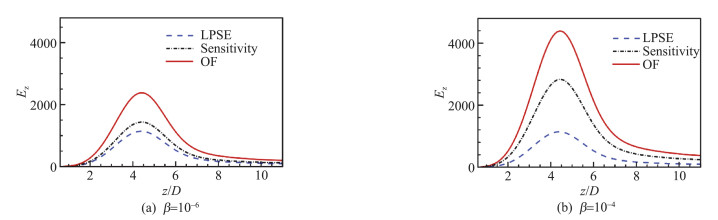
Furthermore, the influence of the nonlinear intensity on wavepackets is investigated by increasing the value of β to 10-4. The corresponding objective function of disturbance energy compared with the linear-PSE model is presented in Fig. 10 for different β. The amplification of local disturbance energy increases greatly when adding the optimal forcing to the linear-PSE model, while their peak axial locations remain the same. The peak value of Ez can reach twice the results of linear model as β=10-6, and the local disturbance energy is amplified more as forcing magnitude increases. In a word, these results indicate that the intensity and spatial distribution of f, interpreted as nonlinearity, play a vital role in shaping wavepackets.
|
Fig.10 Comparison of streamwise evolution of local disturbance energy with different wavepacket models (St=0.4, m=0, 'OF'means wavepacket model with optimal forcing, 'sensitivity' represents wavepacket model with sensitivity forcing and 'LPSE' represents the linear PSE model without any external forcing) 图 10 不同波包模型得到的当地扰动能量的流向演化对比(St=0.4, m=0, “OF”代表包含最优激励的波包模型,“sensitivity”代表包含敏感性激励的波包模型,“LPSE”代表不包含任何外部激励的线性PSE模型) |
To summarize, we have attempted to investigate the sensitivity and flow response to the small external forcing added to the linear-PSE model in subsonic coaxial jets. Nonlinearity is considered based on the linear modeling framework, using adjoint PSE algorithm. The effects of nonlinearity on modelling wavepackets are analyzed systematically in subsonic coaxial jets with different velocity ratios.
In coaxial jets, two kinds of distinct shear layer modes exist and affect the near-field wavepackets, which leads to differences in sensitivity and flow response between coaxial and single-stream jets. The sensitivity and flow response for outer or inner modes reach their maximum around their own critical layers, which are extremely sensitive to external forcing, similar to prior results of single-stream jets. The mutual influences between two instability modes are mainly identified in the downstream region from flow responses. It is found that the outer modes dominate the evolution of instability waves until the end of the outer potential core, which is more important for building wavepacket model for coaxial jets.
In addition, the forced-PSE wavepacket models based on optimal forcing for the outer mode is also obtained using an APSE-based optimization algorithm. In general, the spatial distribution of optimal forcing shows some similar trends to sensitivity results, while the major differences appear in the downstream region. In purpose of building nonlinear wavepacket model, to apply forcing f based on APSE-based optimization methodology in the linear-PSE framework seems to be a promising and efficient way, at a negligible computational cost.
In a nutshell, from a reduced-order-modeling perspective, such a modelling framework might have some insight in building wavepacket acoustic models based on the database obtained by numerical simulations, with an appropriate consideration of nonlinearity.
| [1] |
GLOOR M R. Numerical investigation on hydrodynamic stability and noise radiation of coaxial jet flows[D]. Ph. D. thesis, ETH Zurich, 2014.
|
| [2] |
DAHL M D, MORRIS P J. Noise from supersonic coaxial jets, part 2:normal velocity profile[J]. Journal of Sound and Vibration, 1997, 200(5): 665-699. DOI:10.1006/jsvi.1996.0724 |
| [3] |
TINNEY C E, JORDAN P. The near pressure field of co-axial subsonic jets[J]. Journal of Fluid Mechanics, 2008, 611: 175-204. DOI:10.1017/S0022112008001833 |
| [4] |
BOGEY C, BARRÉ S, JUVÉ D, et al. Simulation of a hot coaxial jet:Direct noise prediction and flow-acoustics correlations[J]. Physics of Fluids, 2009, 21(3): 035105. |
| [5] |
GLOOR M, BVHLER S, KLEISER L. Transition to turbulence and noise radiation in heated coaxial jet flows[J]. Physics of Fluids, 2016, 28(4): 044103. DOI:10.1063/1.4944753 |
| [6] |
PERRAULT-JONCAS D, MASLOWE S A. Linear stability of a compressible coaxial jet with continuous velocity and temperature profiles[J]. Physics of Fluids, 2008, 20(7): 074102. DOI:10.1063/1.2946443 |
| [7] |
GLOOR M, OBRIST D, KLEISER L. Linear stability and acoustic characteristics of compressible, viscous, subsonic coaxial jet flow[J]. Physics of Fluids, 2013, 25(8): 084102. DOI:10.1063/1.4816368 |
| [8] |
CROW S C, CHAMPAGNE F H. Orderly structure in jet turbulence[J]. Journal of Fluid Mechanics, 1971, 48(3): 547-591. |
| [9] |
SUZUKI T, COLONIUS T. Instability waves in a subsonic round jet detected using a near-field phased microphone array[J]. Journal of Fluid Mechanics, 2006, 565: 197. DOI:10.1017/S0022112006001613 |
| [10] |
TAM C K W, VISWANATHAN K, AHUJA K K, et al. The sources of jet noise:experimental evidence[J]. Journal of Fluid Mechanics, 2008, 615: 253-292. DOI:10.1017/S0022112008003704 |
| [11] |
JORDAN P, COLONIUS T. Wave packets and turbulent jet noise[J]. Annual Review of Fluid Mechanics, 2013, 45(1): 173-195. |
| [12] |
KWAN A S H, KO N W M. Coherent structures in subsonic coaxial jets[J]. Journal of Sound and Vibration, 1976, 48(2): 203-219. DOI:10.1016/0022-460X(76)90460-0 |
| [13] |
SEGALINI A, TALAMELLI A. Experimental analysis of dominant instabilities in coaxial jets[J]. Physics of Fluids, 2011, 23(2): 024103. |
| [14] |
SEMERARO O, LUSSEYRAN F, PASTUR L, et al. Qualitative dynamics of wave packets in turbulent jets[J]. Physical Review Fluids, 2017, 2(9): 094605. DOI:10.1103/PhysRevFluids.2.094605 |
| [15] |
HERBERT T. Parabolized Stability Equations[J]. Annual Review of Fluid Mechanics, 1997, 29: 245-283. |
| [16] |
CHEUNG L C. Aeroacoustic noise prediction and the dynamics of shear layers and jets using the nonlinear parabolized stability equations[D]. Ph. D. thesis, Stanford University, 2007.
|
| [17] |
GUDMUNDSSON K, COLONIUS T. Instability wave models for the near-field fluctuations of turbulent jets[J]. Journal of Fluid Mechanics, 2011, 689: 97-128. DOI:10.1017/jfm.2011.401 |
| [18] |
CAVALIERI A V G, RODRÍGUEZ D, JORDAN P, et al. Wavepackets in the velocity field of turbulent jets[J]. Journal of Fluid Mechanics, 2013, 730: 559-592. DOI:10.1017/jfm.2013.346 |
| [19] |
SINHA A, RODRÍGUEZ D, BRōS G A, et al. Wavepacket models for supersonic jet noise[J]. Journal of Fluid Mechanics, 2014, 742: 71-95. DOI:10.1017/jfm.2013.660 |
| [20] |
RYU J, LELE S K. Instability waves in high-speed jets:near-and far-field DNS/LES data analysis[J]. International Journal of Aeroacoustics, 2015, 14(3/4): 643-673. |
| [21] |
LÉON O, BRAZIER J P. Application of the linear parabolized stability equations to a subsonic coaxial jet[C]//17th AIAA/CEAS Aeroacoustics Conference, 2011: 2839.
|
| [22] |
LÉON O, BRAZIER J P. Investigation of the near and far pressure fields of dual-stream jets using an Euler-based PSE model[C]//19th AIAA/CEAS Aeroacoustics Conference, Berlin, Germany. Reston, Virginia: AIAA 2013-2280.
|
| [23] |
SINHA A, GAITONDE D V, SOHONI N. Parabolized stability analysis of dual-stream jets[C]//22nd AIAA/CEAS Aeroacoustics Conference, Lyon, France. Reston, Virginia: AIAA, 2016: 3057.
|
| [24] |
BREAKEY D E, JORDAN P, CAVALIERI A, et al. Near-field wavepackets and the far-field sound of a subsonic jet[C]//19th AIAA/CEAS Aeroacoustics Conference, Berlin, Germany. Reston, Virginia: AIAA 2013-2083.
|
| [25] |
JORDAN P, COLONIUS T, BRES G A, et al. Modeling intermittent wavepackets and their radiated sound in a turbulent jet[C]//Proceedings of the Summer Program, Center for Turbulence Research, Stanford University, 2014.
|
| [26] |
WAN Z H, YANG HH, ZHANG X C, et al. Instability waves and aerodynamic noise in a subsonic transitional turbulent jet[J]. European Journal of Mechanics-B, 2016, 57: 192-203. DOI:10.1016/j.euromechflu.2016.01.002 |
| [27] |
TISSOT G, ZHANG M Q, LAJÚS F C Jr, et al. Sensitivity of wavepackets in jets to nonlinear effects:the role of the critical layer[J]. Journal of Fluid Mechanics, 2017, 811: 95-137. DOI:10.1017/jfm.2016.735 |
| [28] |
TOWNE A, COLONIUS T, JORDAN P, et al. Stochastic and nonlinear forcing of wavepackets in a Mach 0.9 jet[C]//21st AIAA/CEAS Aeroacoustics Conference, Dallas, TX. Reston, Virginia: AIAA 2015-2217.
|
| [29] |
TISSOT G, LAJÚS F C, CAVALIERI A V G, et al. Wave packets and Orr mechanism in turbulent jets[J]. Physical Review Fluids, 2017, 2(9): 093901. DOI:10.1103/PhysRevFluids.2.093901 |
| [30] |
QADRI U A, SCHMID P J. Effect of nonlinearities on the frequency response of a round jet[J]. Physical Review Fluids, 2017, 2(4): 043902. |
| [31] |
SANDHAM N D, SALGADO A M. Nonlinear interaction model of subsonic jet noise[J]. Philosophical Transactions of the Royal Society A:Mathematical, Physical and Engineering Sciences, 2008, 366(1876): 2745-2760. DOI:10.1098/rsta.2008.0049 |
| [32] |
VUILLOT F, LUPOGLAZOFF N, RAHIER G. Double-stream nozzles flow and noise computations and comparisons to experiments[C]//46th AIAA Aerospace Sciences Meeting and Exhibit, Reno, Nevada. doi: 10.2514/6.2008.9.
|
| [33] |
ZHANG X C, RAN L K, SUN D J, et al. Optimal 'quiet' inlet perturbation using adjoint-based PSE in supersonic jets[J]. Fluid Dynamics Research, 2018, 50(4): 045504. DOI:10.1088/1873-7005/aac554 |
| [34] |
ANDERSSON P, HENNINGSON D, HANIFI A. On a stabilization procedure for the parabolic stability equations[J]. Journal of Engineering Mathematics, 1998, 33(3): 311-332. |
| [35] |
LELE S K. Compact finite difference schemes with spectral-like resolution[J]. Journal of Computational Physics, 1992, 103(1): 16-42. |
| [36] |
AIRIAU C, ANSALDI T. Sensitivity analysis for subsonic jet using adjoint of non local stability equations[C]//21st AIAA/CEAS Aeroacoustics Conference. Reston: AIAA 2015-2019.
|
| [37] |
SCHMIDTO T, TOWNE A, RIGAS G, et al. Spectral analysis of jet turbulence[J]. Journal of Fluid Mechanics, 2018, 855: 953-982. DOI:10.1017/jfm.2018.675 |
 2020, Vol. 38
2020, Vol. 38


