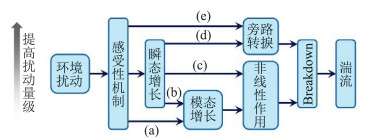
层流向湍流的转捩会使壁面热流和摩阻提高最多一个量级,因此对转捩位置的准确预测对于高速飞行器设计具有重要意义。但是转捩现象是极其复杂的,一个重要表征是转捩过程强烈地依赖于边界条件和外部环境。Morkovin等[1]根据来流环境扰动量级的不同,给出了如图 1所示的五条不同转捩路径,其中环境扰动最小的路径被称为自然转捩,适用于背景湍流度较低的高空大气环境。对于自然转捩,外部扰动经过感受性机制在边界层内形成扰动波,而后扰动首先经历线性模态增长,再由于非线性引发模态间相互作用,最终经过更复杂的非线性过程发展为湍流。由于高超声速边界层流动转捩问题的重要性和复杂性,相关研究是近期空气动力学的热点之一,文献[2]和文献[3]对此进行了综述。
|
图 1 不同来流扰动幅值下转捩路径示意图[1] Fig.1 Paths to boundary layer transition with different freestream disturbance amplitudes[1] |
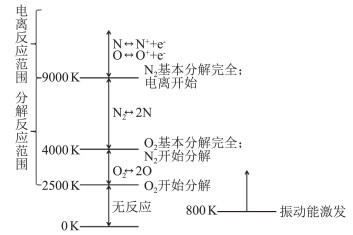
高超声速流动的另一个重要特点是随着马赫数升高而快速上升的流场温度。量热完全气体下高马赫时正激波后温度近似与马赫数平方成正比,极高的温度会激发空气分子的振动能和引起空气的化学分解甚至电离,导致量热完全气体假设的失效,这就是所谓的高温(真实)气体效应[4]。图 2给出了标准大气压下空气发生不同热化学过程的温度范围。基于统计热力学,研究者们建立了对热化学平衡态的描述方法,并通过系列拟合式实现了对热化学平衡流场的求解[5-6]。
|
图 2 标准大气压下空气发生振动能激发和化学反应的温度范围[4] Fig.2 Temperature ranges of air for vibrational and chemical processes under normal atmosphere [4] |
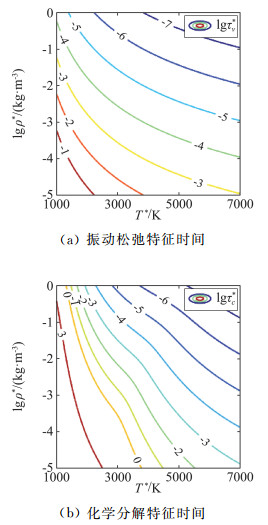
然而研究者们很快发现热化学过程的时间尺度在高超声速高焓流动下常与流动时间尺度相当,例如图 3给出了不同温度和密度下氧气热化学过程的特征时间,而高超声速流动的速度恰在km/s量级,因此流场内的热化学过程并不能处处达到平衡态,需要额外考虑振动能、电子能与组分质量的守恒方程,来建立对热化学非平衡流场的模拟[7]。热化学过程对层流场的主要影响可定性描述为:通过能量松弛和化学反应降低流场温度,使得流场密度升高、激波层变薄;在相同马赫数下,来流温度和密度越高,则热化学过程的时间尺度越小,流场越趋向于平衡态。但是热化学过程对稳定性和转捩的影响难以系统回答,这一方面是由于热化学过程所涉及的尺度和参数众多,与扰动场有复杂的相互作用,另一方面是由于较恶劣的气动环境导致相关实验较为缺乏,因而高温流场模型的可靠性还有待进一步验证。
|
图 3 不同温度和密度下氧气振动松弛和化学分解特征时间 Fig.3 Characteristic time of oxygen versus temperature and density for thermal and chemical processes |
1991年,Malik等[8]率先分析了“真实气体效应”对平板边界层稳定性的影响,他们比较了热化学平衡气体与量热完全气体的第二模态增长率,发现真实气体效应会使第二模态更不稳定,这与他们预期的“真实气体效应对不稳定模态的影响类似冷壁效果”一致,但是最不稳定波的频率却与预期相反地下降了。Stuckert等[9]则发现平衡流假设下“热”壁面也会出现量热完全气体冷壁时才有的“超声速模态”。天津大学的樊宇[10]、万兵兵[11]等也对平衡流假设下马赫数、高度、输运模型等对稳定性和转捩的影响进行了研究。除此之外,研究者们进一步分析了热化学非平衡流动下边界层的稳定性特征,发现与平衡流时有显著不同[9, 12],从而更加关注时间尺度在流动发展和扰动传播中的作用。同时,研究者们发现热化学非平衡效应对边界层稳定性的影响并不单一,而是与气体模型、黏性模型、边界条件等多种因素密切相关[13-15],例如热化学过程引起的流场温度降低和边界层变薄有使得第二模态增长率增加的趋势,但能量松弛引起的胀压黏性又会降低扰动增长率(尤其是对CO2等极性气体)。另一方面,从稳定性方程数学求解的角度,Federov等[16]提出的高速边界层稳定性分析新框架为研究模态演化与相互作用提供了新思路。在此基础上,Bitter等[17]详细分析了振动非平衡效应对马赫数5左右极冷壁平板边界层的影响,发现振动非平衡效应有助于在极冷壁条件下形成超声速不稳定模态。除了线性稳定性分析之外,相关直接数值模拟[18-20]、抛物化扰动方程[21-22]等研究也正在开展。同时,T5[23]、LENS[24]、HIEST[25]、VKI-Longshot[26]等高焓风洞也进行了针对考虑高温气体效应的流动稳定性和转捩的验证与分析工作。
综合来看,热化学非平衡效应对高超声速边界层的稳定性和转捩过程有重要影响,但相关研究依然是有限和不充分的。本文旨在利用线性稳定性框架,分析热化学非平衡平板边界层离散谱模态的演化特性,并尝试探究不同热化学过程如何对不稳定模态的增长率和频率产生影响。
1 物理模型和数值方法 1.1 热化学非平衡N-S方程本文的计算工质为空气,不考虑电离取经典5组分模型(N2、O2、NO、N和O)。增加振动能守恒和组分质量守恒方程,得到描述热化学非平衡流动的N-S方程如式(1)所示,其中引入了Park[27]的双温度模型,即使用热力学平动/转动温度T和振动温度Tv这两个温度来描述流场。
| $ \frac{\partial \boldsymbol{U}}{\partial t}+\frac{\partial \boldsymbol{F}_{j}}{\partial x_{j}}=\frac{\partial \boldsymbol{F}_{v, j}}{\partial x_{j}}+\boldsymbol{S} $ | (1) |
式(1)中U表示守恒变量,F和Fv分别表示无黏和黏性通量,S表示源项。各项具体写为:
| $ \begin{array}{l} \mathit{\boldsymbol{U}} = \left[ {\begin{array}{*{20}{c}} \rho \\ {\rho {u_i}}\\ {\rho E}\\ {{\rho _s}}\\ {\rho {e_v}} \end{array}} \right],{\mathit{\boldsymbol{F}}_{v,j}} = \left[ {\begin{array}{*{20}{c}} 0\\ {{\tau _{ij}}}\\ {{u_k}{\tau _{jk}} - {q_j} - {q_{v,j}} - {h_m}{d_{mj}}}\\ { - {d_{sj}}}\\ { - {q_{v,j}} - {e_{v,m}}{d_{mj}}} \end{array}} \right],\\ \\ {\mathit{\boldsymbol{F}}_j} = \left[ {\begin{array}{*{20}{c}} {\rho {u_j}}\\ {\rho {u_i}{u_j} + p{\delta _{ij}}}\\ {\rho {u_j}H}\\ {{\rho _s}{u_j}}\\ {\rho {u_j}{e_v}} \end{array}} \right],\;\;\;{\kern 1pt} \mathit{\boldsymbol{S}} = \left[ {\begin{array}{*{20}{c}} 0\\ 0\\ 0\\ {{{\dot \omega }_s}}\\ {{Q_{t - v}} + {e_{v,m}}{{\dot \omega }_m}} \end{array}} \right] \end{array} $ |
其中:i是空间维数指标,s∈[2, ns]是组分指标,j和m分别表示对空间维数和组分的Einstein求和。ρs是组分密度,ev是混合物的比振动能;τij是黏性应力张量,qj和qv, j是温度和振动温度的扩散项,dsj是组分s的质量扩散项;Qt-v是振动松弛源项,
| $ h_{s}=c_{\mathrm{ptr}, s} T+e_{v, s}+\Delta h_{f, s}^{\circ} $ | (2) |
黏性应力采用牛顿流体本构和Stokes假设,能量扩散采用Fourier导热定律,质量扩散采用Fick定律。混合物的黏性相关系数使用Wilke规则[28]对各组分进行加权,其中组分黏性系数由Blottner[29]给出,组分热扩散系数采用Eucken关系[30],组分质量扩散系数假设恒定的Schmidt数Sc=0.5。
振动能的非平衡松弛过程引入Landau-Teller方程来描述:
| $ \begin{array}{l} Q_{t-v}=\sum\limits_{s=1}^{n v} \rho_{s} \frac{e_{v \cdot s}(T)-e_{v \cdot s}\left(T_{v}\right)}{\tau_{s}} \\ e_{v, s}\left(T_{v}\right)=\frac{\theta_{v \cdot s} R_{s}}{\exp \left(\theta_{v, s} / T_{v}\right)-1} \end{array} $ |
其中松弛特征时间τs基于Millikan和White[31]的半经验拟合。
化学反应过程采用有限速率化学反应模型。所用5组分5反应模型写为:
R1: N2+M ↔ 2N+M
R2: O2+M ↔ 2O+M
R3: NO+M ↔ N+O+M
R4: N2+O ↔ NO+N
R5: NO+O ↔ O2+N
其中R1~R3是分解反应,R4和R5是交换反应,M表示催化剂,可取5组分中任意一个。化学反应平衡常数由Gibbs自由能得到,其中自由能拟合式由文献[32]给出,反应速率常数使用Arrhenius公式,其中拟合系数采用Park模型[33]。
振动温度的边界条件与温度边界相一致,取为绝热或等温。组分边界取决于壁面的催化条件,本文使用无催化壁。
将N-S方程(1)写为算子形式以便后续分析:
| $ \begin{array}{l} {\cal L}(\mathit{\boldsymbol{q}}) = \mathit{\boldsymbol{S}}(\mathit{\boldsymbol{q}})\\ \mathit{\boldsymbol{q}} = \left[ {\rho ,u,v,w,T,{Y_s},{T_v}} \right],\;\;\;{\kern 1pt} s \in [2,5] \end{array} $ | (3) |
其中算子
稳定性分析需要高精度边界层基本流,这可以通过求解上节N-S方程得到。但N-S方程的求解时间一般较长,为此尝试求解边界层方程以提高求解效率。对来流0°迎角的平板几何,在没有流动分离的情况下,借鉴量热完全气体的Lees-Dorodnitsyn相似性变换来求解边界层方程:
| $ \left\{\begin{array}{l} \mathrm{d} \xi=\rho_{e} U_{e} \mu_{e} \mathrm{d} x \\ \mathrm{d} \eta=U_{e} \sqrt{\frac{R e_{L}}{\xi}} \rho \mathrm{d} y \end{array}\right. $ |
利用连续性方程消去法向速度后,得到变换后的ϕ=[U, T, Ys, Tv]满足下列形式的方程:
| $ C\frac{{{\partial ^2}\phi }}{{\partial {\eta ^2}}} + \left( {\frac{{\partial C}}{{\partial \eta }} + \frac{\mathit{\Pi} }{2}} \right)\frac{{\partial \phi }}{{\partial \eta }} = \xi \left( {\phi \frac{{\partial \phi }}{{\partial \xi }} - \frac{{\partial \mathit{\Pi} }}{{\partial \xi }}\frac{{\partial \phi }}{{\partial \eta }} + S} \right) $ |
上式中非平衡源项S的存在使得即使对平板也不存在相似性解。针对于此,本文采用流向推进解[34],在η和ξ方向分别用Chebyshev配置点法和三阶差分进行离散,然后利用牛顿法进行隐式迭代。此方法求解效率很高,在每个流向位置所需迭代一般不超过6次。
1.3 模态稳定性计算以下推导热化学非平衡流场的小扰动控制方程。将流场基本变量q分为平均量q和对应扰动量
| $ \boldsymbol{q}(x, y, z, t)=\overline{\boldsymbol{q}}(x, y)+\tilde{\boldsymbol{q}}(x, y, z, t) $ |
| $ \left\{\begin{array}{l} \overline{\boldsymbol{q}}=\left[\bar{\rho}, \bar{U}, \bar{V}, \bar{W}, \bar{T}, \bar{Y}_{s}, \bar{T}_{v}\right] \\ \tilde{\boldsymbol{q}}=\left[\tilde{\rho}, \tilde{u}, \tilde{v}, \tilde{w}, \widetilde{\theta}, \widetilde{y}_{s}, \widetilde{\theta}_{v}\right] \end{array}, \quad s \in[2,5]\right. $ |
代入式(3)后得到扰动方程:
| $ \mathcal{L}(\overline{\boldsymbol{q}}+\widetilde{\boldsymbol{q}})-\mathcal{L}(\overline{\boldsymbol{q}})=\boldsymbol{S}(\overline{\boldsymbol{q}}+\widetilde{\boldsymbol{q}})-\boldsymbol{S}(\overline{\boldsymbol{q}}) $ | (4) |
上式可整理为矩阵形式:
| $ \begin{array}{c} \boldsymbol{F} \frac{\partial \tilde{\boldsymbol{q}}}{\partial t}+\boldsymbol{A} \frac{\partial {\tilde{\boldsymbol{q}}}}{\partial x}+\boldsymbol{B} \frac{\partial {\tilde{\boldsymbol{q}}}}{\partial y}+\boldsymbol{C} \frac{\partial \widetilde{\tilde{\boldsymbol{q}}}}{\partial z}+\boldsymbol{D} {\tilde{\boldsymbol{q}}}= \\ \boldsymbol{H}_{x x} \frac{\partial^{2} \tilde{\boldsymbol{q}}}{\partial x^{2}}+\boldsymbol{H}_{y y} \frac{\partial^{2} \tilde{\boldsymbol{q}}}{\partial y^{2}}+\boldsymbol{H}_{z z} \frac{\partial^{2} \tilde{\boldsymbol{q}}}{\partial z^{2}}+ \\ \boldsymbol{H}_{x y} \frac{\partial^{2} \tilde{\boldsymbol{q}}}{\partial x \partial y}+\boldsymbol{H}_{x z} \frac{\partial^{2} {\tilde{\boldsymbol{q}}}}{\partial x \partial z}+\boldsymbol{H}_{y z} \frac{\partial^{2} \tilde{\boldsymbol{q}}}{\partial y \partial z}+\boldsymbol{N} \end{array} $ |
其中F、A、B、C、D和H为均为10×10的矩阵,且只与基本流有关;N为非线性项,在线性分析时被忽略。引入当地平行流假设与行波解假设:
| $ \boldsymbol{q}=\overline{\boldsymbol{q}}(y)+\hat{\boldsymbol{q}}(y) \exp [\mathrm{i}(\alpha x+\beta z-\omega t)] $ |
其中
| $ \frac{\omega}{R e_{\delta}}=F=2 \pi f^{*<H z>} \frac{\nu_{\infty}^{*}}{U_{\infty}^{* 2}} $ |
模态扰动求解是一个特征值问题,矩阵规模为(19Ny)2,其中Ny是法向网格点数。本文的法向导数离散采用Chebyshev配置点法。
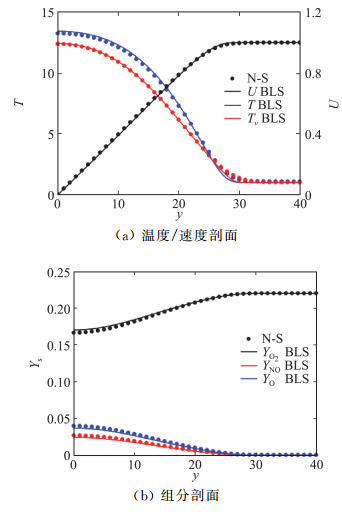
2 结果与分析 2.1 计算结果验证首先验证基本流。选取马赫10热化学非平衡绝热平板算例,来流参数与Malik[8]相同:静温350 K单位雷诺数6.6×106/m,N2占比78%。将边界层方程解(BLS)与N-S方程解进行比较,其中N-S解所用的组分数目、非平衡模型和计算参数均与BLS相同。比较两者在x=0.6 m处的剖面如图 4所示。可以看出,两者的速度和振动温度剖面重合得很好,而温度和组分剖面有2%左右的偏差,这主要是由于边界层方程解忽略了流向压力梯度。总体来看,使用上述流向推进法求解边界层方程有很高的计算效率和精度,适用于稳定性分析计算。
|
图 4 马赫数10热化学非平衡绝热平板边界层解与N-S方程解比较 Fig.4 Comparison between BLS and N-S solvers for Mach 10 non-equilibrium adiabatic flat-plate |
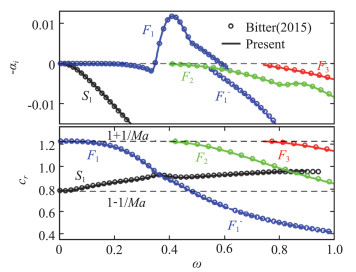
再验证稳定性计算结果。首先选取Bitter[17]的热非平衡、化学冻结的极冷壁平板算例,来流条件为马赫数4.5、静温1500 K,静压10 kPa,壁温为300 K。比较流向位置Reδ=2000处的模态演化过程如图 5所示。由于冷壁效果,此时F模态成为了不稳定模态,且在ω>0.48后成为超声速模态, 引起了增长率曲线的拐折。
|
图 5 马赫数4.5热非平衡极冷壁平板的增长率和相速度验证 Fig.5 Verification of growth rate and phase velocity for Mach 4.5 thermal non-equilibrium flat-plate with highly cooled wall |
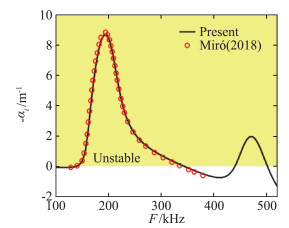
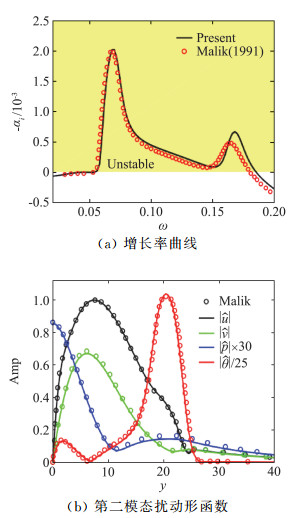
最后验证高马赫数下引起较充分化学反应的算例。选取马赫数10绝热平板,单位雷诺数6.6×106/m、流向位置0.6 m。分别与Miró[35](来流静温600 K)的化学非平衡结果,和Malik[8](来流静温350 K)的热化学平衡结果进行比较。与Miró比较增长率曲线如图 6所示,与Malik比较增长率曲线和第二模态扰动形函数如图 7所示。可以看出,本文稳定性计算结果同样能与文献较好地符合。平衡气体算例的增长率在高频时与文献稍有偏离,这可能是由于黏性模型的不一致引起。
|
图 6 马赫数10化学非平衡绝热平板增长率验证 Fig.6 Verification of growth rate for Mach 10 chemical non-equilibrium adiabatic flat-plate |
|
图 7 马赫数10热化学平衡绝热平板增长率和形函数验证 Fig.7 Verification of growth rate and shape function for Mach 10 equilibrium adiabatic flat-plate |
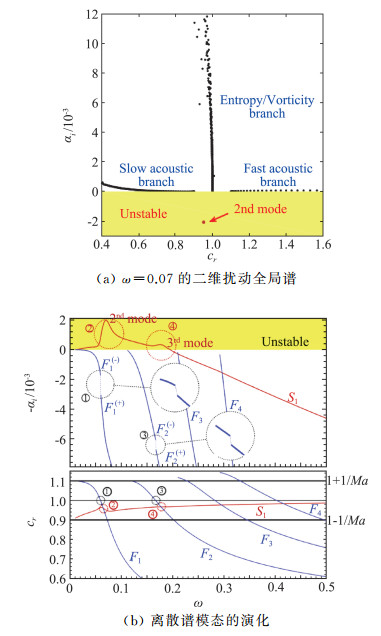
关于离散谱的演化过程,Federov等[16]已针对量热完全气体进行了详细叙述,以下检验热化学非平衡边界层是否存在相似演化过程。图 8(a)给出了马赫数10非平衡绝热平板边界层(计算参数与“基本流验证”处相同)的二维扰动全局谱。该全局谱是由离散模态和由离散点近似的连续谱共同组成。以相速度cr为分类依据,图中连续谱出现了快声波、慢声波和熵/涡波等四个分支,这与非平衡N-S方程无黏通量线化矩阵的特征值分布相一致。除了连续谱,图中还存在从连续谱中脱落的单个离散谱模态,典型之一是此时位于不稳定区的传统意义上的第二模态,以红色箭头在图中标出。
|
图 8 马赫数10热化学非平衡绝热平板的全局谱和模态演化 Fig.8 Spectrum and mode evolution for Mach 10 non-equilibrium adiabatic flat-plate |
图 8(b)给出了不同离散模态的增长率和相速度随频率ω的变化曲线。随着频率从0开始逐渐升高,连续谱中会有一系列模态发生“cut-in”,即从连续谱中脱落成为离散谱。从快声波分支中脱落的离散模态按照脱落顺序依次称为F1、F2、F3、…模态等。慢声波中也会脱落一个离散模态,称为S模态。以下重点关注同步过程,“同步”指的是两个模态的相速度相互接近时发生的过程,这会导致模态增长率的间断或突增/降。具体来说,本算例中,F和S模态首先分别与快慢声波发生同步,即相速度分别达到1±1/Ma。随着F1模态相速度逐渐降低,其在ω=0.06附近与熵/涡波同步、导致F1模态增长率间断(如图中①处虚线圈部分所示),随后在ω=0.07附近与S模态同步,导致S模态相速度曲线的扭曲和增长率的突增(如图中②处虚线圈部分所示),这样产生的不稳定S模态即是所谓第二模态。F2及更高模态也经历了类似过程,但同步强度已小于F1。在冷壁条件下,F与S模态的同步过程会出现分叉,即F模态也可能发展为不稳定模态,正如图 5所示。由上述分析,热化学非平衡平板边界层存在与量热完全气体类似的模态演化和同步过程。
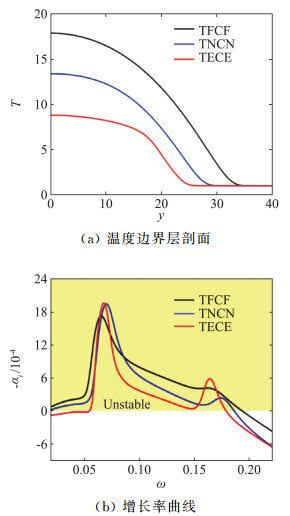
2.3 热化学过程对不稳定模态的影响以下比较热化学冻结气体(相当于量热完全气体)、非平衡气体和平衡气体的稳定性特征,仍选用马赫数10绝热平板算例,比较温度剖面和增长率曲线如图 9所示(其中T和C分别表示热和化学过程,F、N和E分别表示冻结、非平衡和平衡态)。
|
图 9 马赫数10绝热平板在热化学冻结、非平衡和平衡假设下边界层剖面和增长率曲线比较 Fig.9 Comparison of profiles and growth rates for Mach 10 adiabatic flat-plate with frozen, non-equilibrium and equilibrium flow |
随着热化学过程由冻结到非平衡再到平衡,边界层温度和厚度逐渐降低,使得非平衡和平衡态气体的第二模态增长率和对应频率相比量热完全气体都有增加,这与量热完全气体降低壁温时的效果类似。但从非平衡态向平衡态的过渡却出现相反趋势:平衡态的第二模态增长率峰值没有继续增加、与非平衡态相当,而且对应频率反而小于非平衡态。这说明热化学过程除了降低流场温度外,还有其他影响稳定性的途径。
以下从方程出发进行探究。描述热化学非平衡流场需要增加振动能和组分质量方程,而将额外方程耦合进流场的正是非平衡源项Qt-v和
| $ \text { 基本流方程 }: \quad \mathcal{L}(\overline{\boldsymbol{q}})=\boldsymbol{S}(\overline{\boldsymbol{q}}) $ | (5a) |
| $ \text { 扰动方程 }: \quad \frac{\partial \mathcal{L}}{\partial \boldsymbol{q}} \tilde{\boldsymbol{q}}=\frac{\partial \boldsymbol{S}}{\partial \boldsymbol{q}} \tilde{\boldsymbol{q}} $ | (5b) |
可见非平衡效应影响边界层稳定性的路径有两条:第一是源项S加入了基本流方程、改变了基本流剖面,从而间接影响稳定性;第二是源项的扰动(∂S/∂q)
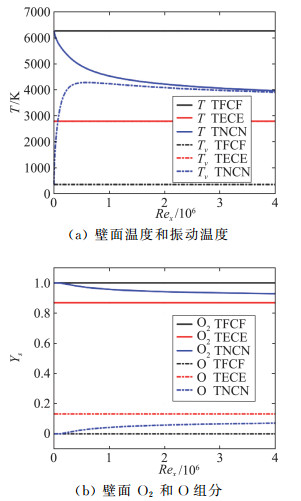
给出热化学冻结、非平衡和平衡假设下基本流的壁面处温度T、振动温度Tv和组分质量分数Ys随流向的变化如图 10所示。作为非平衡流动的参照,图中以黑线表示的量热完全气体的振动能未被激发、化学反应也未发生,而以红线表示的平衡流的壁温和壁面组分沿流向也不变化。以蓝线表示的非平衡流在x=0处为冻结状态,而后向下游逐渐趋向平衡态。
|
图 10 马赫数10绝热平板在热化学冻结、非平衡和平衡假设下壁面物理量随流向变化曲线 Fig.10 Streamwise distribution of wall quantities for Mach 10 non-equilibrium adiabatic flat-plate with different disturbance assumptions |
引入无量纲数Damköhler数来描述不同过程时间尺度的相对关系:
| $ D a_{v / c}^{\mathrm{baxc}}=\frac{\tau_{v / c}^{*}}{\tau_{f}^{*}}=\frac{U \tau_{v / c}}{R e_{x}} \propto \frac{1}{R e_{x}} $ | (6) |
若Dav/cbase越大,则热化学过程对基本流的影响越小。当x=0时Dav/cbase→∞,而后沿流向以雷诺数分之一的量级减小。
2.3.2 非平衡源项的扰动的影响Mack[36]详细分析了量热完全气体的模态稳定性,指出第二及更高模态主要源于无黏框架。由于高马赫数时第二模态成为主导模态,因此对热化学非平衡的无黏扰动方程进行分析,给出方程如式(7)所示。由于Mack模态在二维时增长率最大,因此展向波数β取为0。
| $ \left\{ {\begin{array}{*{20}{l}} {\frac{{\hat p}}{{\bar p}} = \frac{{\hat \rho }}{{\bar \rho }} + \frac{{\hat \theta }}{{\bar T}} + \frac{{{R_m}{{\hat y}_m}}}{R}}\\ {{\rm{i}}\alpha (\bar U - c)\hat \rho + \left( {{D_y}\bar \rho } \right)\hat v + \bar \rho \left( {{\rm{i}}\alpha \hat u + {D_y}\hat v} \right) = 0}\\ {\bar \rho \left[ {{\rm{i}}\alpha (\bar U - c)\hat u + \left( {{D_y}\bar U} \right)\hat v} \right] + {\rm{i}}\alpha \left( {\frac{{\hat p}}{{{\gamma _f}M{a^2}}}} \right) = 0}\\ {\bar \rho {\rm{i}}\alpha (\bar U - c)\hat v + {D_y}\left( {\frac{{\hat p}}{{{\gamma _f}M{a^2}}}} \right) = 0}\\ {{\rm{i}}\alpha (\bar U - c)\hat w = 0}\\ {\bar \rho {{\bar c}_{v,{\rm{tr}}}}\left[ {{\rm{i}}\alpha (\bar U - c)\hat \theta + \left( {{D_y}\bar T} \right)\hat v} \right] + \frac{{{\gamma _f} - 1}}{{{\gamma _f}}}\left( {{\rm{i}}\alpha \hat u + {D_y}\hat v} \right)\bar p}\\ { = - \left( {{{\bar e}_m}{{\hat S}_m} + {{\hat S}_q}} \right)}\\ {\bar \rho \left[ {{\rm{i}}\alpha (\bar U - c){{\hat y}_s} + \left( {{D_y}{{\bar Y}_s}} \right)\hat v} \right] = {{\hat S}_s}}\\ {\bar \rho {{\bar c}_{{\rm{vib}}}}\left[ {{\rm{i}}\alpha (\bar U - c){{\hat \theta }_v} + \left( {{D_y}{{\bar T}_v}} \right)\hat v} \right] = {{\hat S}_q}} \end{array}} \right. $ | (7) |
式中Dy=d/dy表示法向导数,γf是冻结流比热比,
| $ \frac{D^{2}}{\alpha^{2}}\left(\frac{\hat{p}}{\gamma_{f} M a_{r}^{2}}\right)=\left(1-M a_{r}^{2}\right) \frac{\widehat{p}}{\gamma_{f} M a_{r}^{2}}+\mathrm{i} F_{s}\left(\widehat{S}_{q}, \widehat{S}_{s}\right) $ |
其中Mar=(U-c)/af是扰动传播的相对马赫数,af是冻结声速。上式除了新增的非平衡源项扰动函数Fs外,与Mack给出的量热完全气体结果相同,所以声速同样是非平衡流动的Mack模态的重要参数。
由于氧气相比氮气在更低的温度时激发振动能和发生化学分解,因此对空气考虑相同温度下热化学过程最显著的情况YO2, ∞=1,由式(7)解出振动能和组分质量的扰动形函数:
以
| $ D a_{v}^{\mathrm{dist}}=\left(\frac{\bar{U}}{c_{r}}-1\right) F \bar{\tau}_{v}=\left(\frac{\bar{U}}{c_{r}}-1\right) 2 \pi f^{*<H z>} \tau_{v}^{*} $ | (8) |
对大气来流的高超声速边界层,典型第二模态失稳频率的量级为0.1 MHz~1 MHz,而τv*的量级可以图 3为参考,所以对边界层内大多数区域,有Fτv < < 1。虽然在临界层附近U≈cr,但临界层一般靠近边界层外缘,温度较低且黏性效应较强,所以Davdist < < 1总体上满足。再考虑到温度和振动温度的量级关系,若分母远大于1则有:
| $ \hat{\theta}_{v} \approx \frac{-\frac{\bar{\tau}_{v}}{R e}\left(D_{y} \bar{T}_{v}\right) \hat{v}}{\mathrm{i}(\bar{U} / c-1) F \bar{\tau}_{v}}=\frac{\mathrm{i}\left(D_{y} \bar{T}_{v}\right) \hat{v}}{(\bar{U} / c-1) \omega} $ | (9) |
对组分扰动
作为验证,在完整黏性框架下分别计算包括和忽略非平衡源项扰动的稳定性方程,即分别求解:
| $ \frac{\partial \mathcal{L}}{\partial \boldsymbol{q}} \widetilde{\boldsymbol{q}}=\frac{\partial \boldsymbol{S}}{\partial \boldsymbol{q}} \widetilde{\boldsymbol{q}} \text { 和 } \frac{\partial \mathcal{L}}{\partial \boldsymbol{q}} \widetilde{\boldsymbol{q}}=0 $ | (10) |
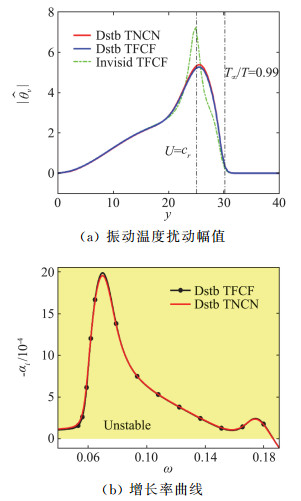
其中基本流同为热化学非平衡基本流。求得的两者的振动温度扰动形函数对比如图 11(a)所示,同时画出式(9)如绿线所示作为参照。由图可见,虽然忽略了非平衡源项的扰动(∂S/∂q)
|
图 11 包括和忽略非平衡源项的扰动对马赫数10热化学非平衡绝热平板的振动温度扰动和增长率的影响 Fig.11 Comparison of shape function and growth rate between those with and without the disturbance of source term for Mach 10 non-equilibrium adiabatic flat-plate |
文献[37]将式(8)中第二模态不稳定波的频率与边界层厚度进行了关联,得到以下结果:
| $ D a_{v}^{\mathrm{dist}}=\left(\frac{\bar{U}}{c_{r}}-1\right) \frac{\pi C}{K} \frac{\bar{\tau}_{v}}{\sqrt{R e_{x}}} \propto \frac{1}{\sqrt{R e_{x}}} $ | (11) |
对比式(6),可见Dadist相比Dabase沿流向衰减更慢,所以扰动引起的非平衡效应的影响域相比基本流更靠下游,或者说扰动相比基本流更趋向于热化学冻结态,因此有些论文中假设“基本流为非平衡态、扰动为平衡态”是不符合物理过程的。
综上所述,在大气来流条件和空气5组分模型下,对由第二模态主导的高超声速二维边界层,扰动方程中新增的非平衡源项的扰动对稳定性的影响很小,非平衡效应主要是通过改变边界层剖面来间接影响稳定性的。
2.3.3 声速的影响由上述分析,声速是影响Mack模态的重要参数,但不同气体模型假设的声速计算式是不同的。由于非平衡源项的扰动对稳定性影响较小,因此只需比较热化学冻结态、热平衡化学冻结态和热化学平衡态这三种模型。声速表示压力小扰动在等熵条件下的传播速度,定义式为:
| $ a=\sqrt{\left(\frac{\partial p}{\partial \rho}\right)_{s}} $ | (12) |
对热化学冻结态(即量热完全气体),声速只与温度有关:
| $ a_{\mathrm{TFCF}}^{2}=\gamma_{f} \bar{R} \bar{T}, \quad \gamma_{f}=\frac{\bar{c}_{p, \mathrm{tr}}}{\bar{c}_{v, \mathrm{tr}}} $ | (13) |
对热平衡和化学平衡态,等熵过程同步引起了振动温度和组分的变化,推导出热平衡化学冻结和热化学平衡态这两种假设下的声速表达式如下所示:
| $ \left\{ {\begin{array}{*{20}{l}} {{{\hat \theta }_v} = \frac{{ - \frac{{{{\bar \tau }_v}}}{{R{e_\delta }}}\left( {{D_y}{{\bar T}_v}} \right)\hat v + \frac{{{{\bar c}_{{\rm{vib}}}}(\bar T)}}{{{{\bar c}_{{\rm{vib}}}}\left( {{{\bar T}_v}} \right)}}\hat \theta }}{{1 + {\rm{i}}(\bar U/c - 1)F{{\bar \tau }_v}}}}\\ {{{\hat y}_s}\frac{{ - \frac{{{{\bar \tau }_c}}}{{R{e_\delta }}}\left( {{D_y}{{\bar Y}_s}} \right)\hat v + {{\hat y}_{s,{\rm{eq}}}}}}{{1 + {\rm{i}}(\bar U/c - 1)F{{\bar \tau }_c}}}} \end{array}} \right. $ |
| $ \begin{array}{*{20}{l}} {a_{{\rm{TECF}}}^2 = \gamma \bar R\bar T,\;\;\;{\kern 1pt} \gamma = \frac{{{{\bar c}_p}}}{{{{\bar c}_v}}} = \frac{{{{\bar c}_{p,{\rm{tr}}}} + {{\bar c}_{{\rm{vib}}}}}}{{{{\overline c }_{v,{\rm{tr}}}} + {{\overline c }_{{\rm{vib}}}}}} < {\gamma _f},}\\ {a_{{\rm{TECE}}}^2 = a_{{\rm{TECF}}}^2\left[ {1 + \left( {{{\bar h}_m} - \gamma {{\overline e}_m} } \right)\frac{{\frac{{{{\bar \rho }^2}{{\overline c }_p}}}{{\gamma - 1}}\frac{{\partial {{\bar Y}_m}}}{{\partial \bar \rho }} + \frac{{\partial {{\bar Y}_m}}}{{\partial \bar T}}}}{{{{\overline c }_p} + \gamma {{\bar e}_m}\frac{{\partial {{\bar Y}_m}}}{{\partial \bar T}}}}} \right]} \end{array} $ |
其中hs和es是如式(2)所示的基本流的组分比焓和组分比内能。
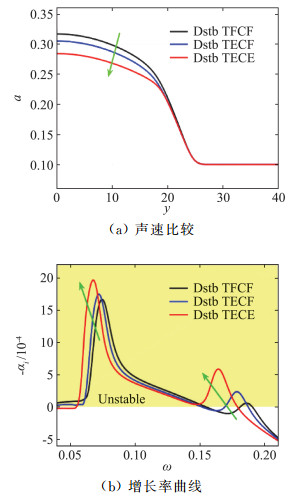
以下进行数值结果分析。为控制变量,在同样的基本流(只能是热化学平衡态基本流)上传播上述三种不同假设的小扰动,比较三种声速和对应的模态增长率曲线如图 12所示。如绿色箭头所示,本算例下热化学冻结扰动的声速最大,热化学平衡扰动的声速最小。与此相对应,声速越小则第二和第三模态的最大增长率越大,最不稳定波对应的频率越小。
|
图 12 马赫数10热化学平衡绝热平板在不同扰动假设下的声速和增长率比较 Fig.12 Comparison of the speeds of sound and growth rates for Mach 10 equilibrium adiabatic flat-plate with different disturbance assumptions |
由此,图 9中平衡气体第二模态的增长率和频率的反转趋势可以被解释:相比于非平衡态,虽然平衡态气体的流场温度和边界层厚度进一步降低,引起第二模态最大增长率和对应频率增加,但同时平衡态假设下等熵传播的扰动还引起了振动能和组分的变化,使得声速降低,从而引起第二模态最大增长率的升高和对应频率降低。由于这两个作用的增长率峰值对应的频率不同,因此相互叠加后造成平衡气体第二模态的最大增长率与非平衡气体持平、对应的频率相比非平衡气体出现降低。
3 结论本文利用空气5组分(N2、O2、NO、N和O)模型,开展了考虑热化学非平衡效应的高超声速平板边界层的线性稳定性研究。针对非平衡边界层基本流不存在相似性解的问题,本文实现和验证了求解边界层非相似性解的流向推进方法,相比直接求解N-S方程有很高效率。同时,针对热化学冻结、非平衡和平衡等不同气体模型,本文验证了所发展的线性稳定性计算程序的可靠性。
以此为基础,本文重点研究了热化学过程对模态稳定性的影响,并探究了离散谱模态的同步和演化过程。计算结果表明,热化学非平衡边界层中存在与量热完全气体类似的离散谱演化和模态同步过程。对于由第二模态主导的高超声速二维边界层,本文的计算和分析表明:第一,扰动所引起的非平衡效应的影响域相比基本流更靠近下游,即扰动相比基本流更趋向于热化学冻结态;第二,扰动方程中新出现的非平衡源项的扰动项对稳定性影响很小,非平衡过程主要是通过改变基本流剖面来间接影响稳定性;第三,对考虑热化学过程的边界层,声速同样是影响第二及更高模态(Mack模态)的重要参数,热化学平衡态假设引起的声速计算式的变化能够解释边界层温度和厚度降低时第二模态频率反而降低的非常规趋势。
| [1] |
MORKOVIN M V, RESHOTKO E, HERBERT T. Transition in open flow systems-a reassessment[J]. Bulletin of the APS, 1994, 39(9): 1-31. |
| [2] |
陈坚强, 涂国华, 张毅锋, 等. 高超声速边界层转捩研究现状与发展趋势[J]. 空气动力学学报, 2017, 35(3): 311-337. CHEN J Q, TU G H, ZHANG Y F, et al. Hypersnonic boundary layer transition:what we know, where shall we go[J]. Acta Aerodynamica Sinica, 2017, 35(3): 311-337. (in Chinese) |
| [3] |
杨武兵, 沈清, 朱德华, 等. 高超声速边界层转捩研究现状与趋势[J]. 空气动力学学报, 2018, 36(2): 183-195. YANG W B, SHEN Q, ZHU D H, et al. Tendency and current status of hypersonic boundary layer transition[J]. Acta Aerodynamica Sinica, 2018, 36(2): 183-195. (in Chinese) |
| [4] |
ANDERSON J D. Hypersonic and high-temperature gas dynamics, second edition[M]. Reston, VA: AIAA, 2006.
|
| [5] |
TANNEHILL J C, MUGGE P H. Improved curve fits for the thermodynamic properties of equilibrium air suitable for numerical computation using time-dependent or shock capturing methods[R]. Iowa State University, 1974.
|
| [6] |
SRINIVASAN S, TANNEHILL J C, WEILMUENSTER K J. Simplified curve fits for the transport properties of equilibrium air: NASA CR-180422[R]. NASA contractor report, 1986.
|
| [7] |
GNOFFO P A, GUPTA R N, SHINN J. Conservation equations and physical models for hypersonic air flows in thermal and chemical nonequilibrium: NASA-TP-2867[R]. Hampton, VANTRS: NASA Langley Research Center, 1989.
|
| [8] |
MALIK M R, ANDERSON E C. Real gas effects on hypersonic boundary-layer stability[J]. Physics of Fluids A:Fluid Dynamics, 1991, 3(5): 803-821. DOI:10.1063/1.858012 |
| [9] |
STUCKERT G, REED H L. Linear disturbances in hypersonic, chemically reacting shock layers[J]. AIAA Journal, 1994, 32(7): 1384-1393. DOI:10.2514/3.12206 |
| [10] |
樊宇, 万兵兵, 韩宇峰, 等. 平衡空气模型的流动稳定性及转捩预测[J]. 航空动力学报, 2016, 31(7): 1658-1668. FAN Y, WAN B B, HAN Y F, et al. Hydrodynamic stability and transition prediction with the chemical equilibrium gas model[J]. Journal of Aerospace Power, 2016, 31(7): 1658-1668. (in Chinese) |
| [11] |
万兵兵, 韩宇峰, 樊宇, 等. 高温空气传输特性对边界层稳定性及转捩预测的影响[J]. 航空动力学报, 2017, 32(1): 188-195. WAN B B, HAN Y F, FAN Y, et al. Effect of transport properties of high-temperature air on boundary layer stability and transition prediction[J]. Journal of Aerospace Power, 2017, 32(1): 188-195. (in Chinese) |
| [12] |
HUDSON M L, CHOKANI N, CANDLER G V. Linear stability of hypersonic flow in thermochemical nonequilibrium[J]. AIAA Journal, 1997, 35: 958-964. DOI:10.2514/2.204 |
| [13] |
JOHNSON H, SEIPP T, CANDLER G, et al. Numerical study of hypersonic reacting boundary layer transition on cones[C]//32nd Thermophysics Conference, Atlanta, GA, USA. Reston, Virigina: AIAA, 1997.
|
| [14] |
BERTOLOTTI F P. The influence of rotational and vibrational energy relaxation on boundary-layer stability[J]. Journal of Fluid Mechanics, 1998, 372: 93-118. DOI:10.1017/S0022112098002353 |
| [15] |
MALIK M R. Hypersonic flight transition data analysis using parabolized stability equations with chemistry effects[J]. Journal of Spacecraft and Rockets, 2003, 40(3): 332-344. DOI:10.2514/2.3968 |
| [16] |
FEDOROV A, TUMIN A. High-speed boundary-layer instability:old terminology and a new framework[J]. AIAA Journal, 2011, 49(8): 1647-1657. DOI:10.2514/1.J050835 |
| [17] |
BITTER N P, SHEPHERD J E. Stability of highly cooled hypervelocity boundary layers[J]. Journal of Fluid Mechanics, 2015, 778: 586-620. DOI:10.1017/jfm.2015.358 |
| [18] |
STEMMER C. Hypersonic transition investigations in a flat-plate boundary-layer flow at M=20[C]//35th AIAA Fluid Dynamics Conference and Exhibit, Toronto, Ontario, Canada. Reston, Virigina: AIAA, 2005.
|
| [19] |
MARXEN O, IACCARINO G, MAGIN T E. Direct numerical simulations of hypersonic boundary-layer transition with finite-rate chemistry[J]. Journal of Fluid Mechanics, 2014, 755: 35-49. DOI:10.1017/jfm.2014.344 |
| [20] |
MORTENSEN C H, ZHONG X L. Real-gas and surface-ablation effects on hypersonic boundary-layer instability over a blunt cone[J]. AIAA Journal, 2016, 54(3): 980-998. DOI:10.2514/1.J054404 |
| [21] |
CHANG C L, VINH H, MALIK M, et al. Hypersonic boundary-layer stability with chemical reactions using PSE[C]//28th Fluid Dynamics Conference, Snowmass Village, CO, USA. Reston, Virigina: AIAA, 1997.
|
| [22] |
ZANUS L, MIRÓ MIRÓ F, PINNA F. Nonlinear parabolized stability analysis of hypersonic flows in presence of curvature effects[C]//2018 AIAA Aerospace Sciences Meeting, Kissimmee, Florida. Reston, Virginia: AIAA, 2018.
|
| [23] |
ADAM P H, HORNUNG H G. Enthalpy effects on hypervelocity boundary-layer transition:ground test and flight data[J]. Journal of Spacecraft and Rockets, 1997, 34(5): 614-619. DOI:10.2514/2.3278 |
| [24] |
WADHAMS T, MACLEAN M, HOLDEN M, et al. A review of transition studies on full-scale flight vehicles at duplicated flight conditions in the LENS tunnels and comparisons with prediction methods and flight measurement[C]//48th AIAA Aerospace Sciences Meeting Including the New Horizons Forum and Aerospace Exposition, Orlando, Florida. Reston, Virigina: AIAA, 2010.
|
| [25] |
GRONVALL J E, JOHNSON H B, CANDLER G V. Boundary-layer stability analysis of the high enthalpy shock tunnel transition experiments[J]. Journal of Spacecraft and Rockets, 2014, 51(2): 455-467. DOI:10.2514/1.A32577 |
| [26] |
GROSSIR G, PINNA F, BONUCCI G, et al. Hypersonic boundary layer transition on a 7 degree half-angle cone at Mach 10[C]//7th AIAA Theoretical Fluid Mechanics Conference, Atlanta, GA. Reston, Virginia: AIAA, 2014.
|
| [27] |
PARK C. Assessment of two-temperature kinetic model for ionizing air[J]. Journal of Thermophysics and Heat Transfer, 1987, 3(3): 233-244. |
| [28] |
WILKE C R. A viscosity equation for gas mixtures[J]. The Journal of Chemical Physics, 1950, 18(4): 517-519. |
| [29] |
BLOTTNER F G, JOHNSON M, ELLIS M. Chemically reacting viscous flow program for multi-component gas mixtures[R]. Office of Scientific and Technical Information (OSTI), 1971. doi: 10.2172/4658539
|
| [30] |
VINCENTI W G, KRUGER C H. Introduction to Physical Gas Dynamics[M]. John Wiley and Sons, 1967.
|
| [31] |
MILLIKAN R C, WHITE D R. Systematics of vibrational relaxation[J]. The Journal of Chemical Physics, 1963, 39(12): 3209-3213. DOI:10.1063/1.1734182 |
| [32] |
MCBRIDE B J, HEIMEL S, EHLERS J, et al. Thermodynamic properties to 6000 K for 210 substances involving the first 18 elements. NASA SP-3001[R]. NASA Lewis Research Center, 1963.
|
| [33] |
PARK C, JAFFE R L, PARTRIDGE H. Chemical-kinetic parameters of hyperbolic earth entry[J]. Journal of Thermophysics and Heat Transfer, 2001, 15(1): 76-90. |
| [34] |
BLOTTNER F G. Chemical nonequilibrium boundary layer[J]. Journal of Spacecraft and Rockets, 2003, 40(5): 810-818. DOI:10.2514/2.6907 |
| [35] |
MIRÓ MIRÓ F, PINNA F, BEYAK E S, et al. Diffusion and chemical non-equilibrium effects on hypersonic boundary-layer stability[C]//2018 AIAA Aerospace Sciences Meeting, Kissimmee, Florida. Reston, Virginia: AIAA, 2018.
|
| [36] |
MACK L M. Boundary-layer linear stability theory[R]. AGARD Report No. 709, 1984.
|
| [37] |
BITTER N P. Stability of hypervelocity boundary layers[D]. California Institute of Technology, 2015.
|
 2020, Vol. 38
2020, Vol. 38


