从层流到湍流的转捩问题是航空航天工程中所关注的重要基础问题[1-2]。一般来说,层流边界层表面的摩擦阻力明显小于湍流边界层,因而,若能通过有效的设计手段推迟转捩的发生,则有利于减少燃料的消耗或在携带有限燃料的前提下使飞行器飞得更远。在航空领域,美国的波音公司[3]、欧洲的空客公司[4]以及我国的商飞公司等都投入了大量的人力与物力,致力于发展可靠、有效的层流控制方法。在航天领域,人们在关注如何推迟转捩的同时,还通过大量的实验和计算研究高速飞行器表面由材料编织、烧蚀等引起的粗糙度对转捩的影响。另一方面,考虑在逆压梯度下,湍流边界层的分离区明显小于层流边界层,因而,在有些情况下,人们希望采取措施促进转捩的发生。一个典型的例子就是在高超声速吸气式飞行器的前体进气道布置有限尺寸的三维粗糙元[5-8]。此外,对于航天飞行器,转捩区域往往伴随着高热流的出现,对转捩的准确预测也是热防护设计的前题。
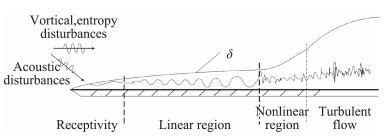
当环境扰动的强度较低时,边界层转捩由模态扰动的失稳导致,这一过程包括如图 1所示的四个阶段[9]。(a)在感受性(receptivity)阶段,自由流中的声波、涡波和熵波进入边界层并激发边界层中的不稳定模态;(b)激发出的不稳定模态在线性稳定性机制下呈指数规律增长;(c)当扰动累积到有限幅值以后,扰动与扰动、扰动与平均流之间的非线性作用导致层流的breakdown;(d)最后流动进入湍流状态,表现为脉动强度达到平稳状态,而边界层的厚度迅速增长。
由于不稳定模态的线性增长占据了层流阶段的绝大部分区域,因而很自然的想法就是基于由线性稳定性理论给出的扰动增长率来预测转捩。根据图 1所给出的转捩途径,这一预测方法需要考虑三个子问题:确定扰动的初始幅值、描述扰动的线性演化以及确定转捩的判据。这一思想早在20世纪50年代就被提出,Smith[10]基于不可压缩边界层中的Tollmien-Schlichting(T-S)波(其是Orr-Sommerfeld或O-S方程的特征解)的增长率,给出了早期的转捩预测准则,即当T-S波被线性放大eeN倍时转捩发生。因而,该方法也被简称为eN法。实际上,该方法只是较准确地考虑了上述三个子问题中的第二个,而把达到转捩的门限幅值与感受性阶段的初始幅值的比值的对数刻画为人为参数N。由于感受性过程较复杂,对扰动初始幅值的确定往往需要通过经验。而eN方法中的人为参数只有一个,因而,该方法广受欢迎。其后,一直到20世纪70年代,通过对一系列低速流实验数据的拟合,人们发现不管是T-S波失稳[11]、横流失稳[12],还是由离心力引起的Gortler失稳[13],转捩因子N的取值一般都在10左右。但是,转捩不仅仅由平均流剖面决定,它同时还受自由流扰动强度的影响;上述实验展示的转捩因子N相近的现象只是巧合。Mack[14]通过理论预测与实验数据的对比,发现随着来流湍流度的增强,N因子迅速下降。因而,现阶段在工程上预测转捩时,N的选取要借助由实验数据拟合得到的经验关系来确定。另外,横流和Gortler失稳模态自身的累积并不能直接导致转捩,故不考虑二次失稳的转捩预测模型从本质上来看是存在问题的。
超声速或高超声速边界层中的转捩问题更加复杂。首先,自由流中除了存在涡扰动(湍流脉动)外,还存在压力脉动主导的声扰动和温度脉动主导的熵扰动。由于不同风洞的背景噪声强度大不相同,因而它们所对应的转捩因子N也大相径庭。更重要的是,高空中的环境扰动类型可能与风洞中不同,这样,从风洞实验中拟合出的N因子不能直接推广到真实飞行情况。其次,超声速与高超声速边界层存在多个失稳模态(可压缩O-S方程的特征解)[15]。在二维层流条件下,除了展向波数较大的第一模态是亚声速黏性T-S波的延伸[16]以外,其它模态都是无黏的,被称为Mack模态。Mack模态在边界层前缘附近的感受性机制与黏性T-S波的机制[17]完全不同。Fedorov和Khokhlov[18-19]指出,在自然状态下(无局部突变引起的感受性机制),Mack模态通过与自由流中扰动的同步而被激发。这种同步包括三类:(a)在前缘附近,慢声波与慢模态(第一模态)同步;(b)在下游某处,涡波、熵波与快模态同步;(c)在第二模态下支界附近,快慢模态同步。这一现象其后被一系列直接数值模拟验证[20-22]。Fedorov[23]进一步应用该理论,计算了高超声速平板边界层对自由流中三维声波的感受性问题,结果与Maslov[24]的实验在波角(θ=tan-1(β/α),其中α与β分别为扰动的流向和展向波数)小于50°时吻合很好。更大波角所对应的不稳定模态应属于黏性T-S波,其感受性应该由三层结构理论描述[25]。由于同步的机制比黏性T-S波的前缘感受性效率高得多,一般在超声速或高超声速风洞中,转捩因子N明显小于低速流的值。
eN法的优点是应用起来简单方便,因为只需要在平行流假设下对基本流剖面求解局部增长率再做积分即可。但是,人们发现,即使对于光滑壁情况,在增长率不太大的时侯,由线性稳定性理论预测的局部增长率不够准确,这样就影响了整体积分的精度。一个更加准确的方法是抛物化稳定性方程(PSE)[26-30]。该方法只忽略了原始Navier-Stokes(N-S)方程黏性项中扰动对流向的二阶导数项,这样,原来椭圆型的方程系统就变成了抛物型的。该方法的优点是:(a)平均流的非平行性与扰动对流项的一阶导数被考虑进来,这样,在大部分情况下其计算精度是可以与直接数值模拟相当的;(b)另外,扰动与扰动、扰动与平均流的弱非线性作用也可以被考虑进来(非线性PSE或NPSE)。因而,对于光滑壁面的边界层流动,如果确定了模态扰动的初始幅值,NPSE可以一直被应用到层流breakdown的起始阶段[31]。值得说明的是,在使用线性PSE做转捩预测时,同样需要设置转捩判据,即达到转捩的时候不稳定模态要线性放大多少倍;但在使用NPSE预测时,只需要设置模态扰动的初始幅值,转捩发生在计算发散或壁面摩擦系数曲线抬升时[31]。
以上基于O-S方程特征解的eN法与考虑部分非平行性效应的PSE方法都是针对光滑壁面的边界层流动的。如果壁面上存在流向尺度与不稳定模态波长相当的局部突变,如粗糙元、吹吸、台阶、缝隙等,则系统表现为强椭圆型。这样,平行流假设或对系统进行抛物化从数学上来讲是错误的。实际上,壁面绝对光滑的边界层问题在工程上并不常见,而出现更多的是存在壁面缺陷或突变的边界层问题,如第一段介绍的层流控制与壁面编织、烧蚀引起的粗糙度等。这样,就需要发展一套适用于此类问题的转捩预测理论框架。
从原理上来看,局部突变对边界层自然转捩的影响主要有两种机制。一种是局部感受性机制,即自由流中的扰动与由局部突变引起的快速畸变的平均流之间相互作用而直接激发不稳定模态。由于由前缘感受性机制[17]激发出的不稳定模态需要经历长距离的衰减过程,因而,这种局部感受性机制的效率更高。这样,如果在飞行器表面较上游的位置存在局部突变,则在转捩预测中这一局部感受性机制必须考虑。另一种机制被称为线性模态的局部散射机制。当局部突变出现在较下游的位置时,其上游传播过来的不稳定模态会与快变的平均流作用而迅速改变前者在下游的渐近幅值(把下游扰动的幅值依照线性稳定性理论拓展到局部突变处)。渐近幅值的增大或减小会促使下游转捩的提前或推迟,新的转捩预测理论必须考虑这一定量的变化。当然,如果局部突变的尺寸足够大,以至于其引起的平均流修正使流动失稳的性质发生改变,则流动可以逾越过不稳定模态的线性放大过程,而通过旁路(bypass)转捩途径到达湍流。但本文主要关注的还是自然转捩过程,假设壁面的局部突变尺寸较小。
本文的结构设计如下:首先在1.1节介绍考虑局部突变影响的转捩预测方法的基本思想,引出局部感受性系数与透射系数的概念;在1.2节中介绍局部散射理论的基本原理;由于二维层流边界层中的失稳特性包括黏性和无黏两种,1.3节将重点讨论它们的区别与数学描述方法。在第2节中,本文重点介绍黏性T-S波的局部感受性过程,包括T-S波的局部散射、T-S波的局部感受性以及抽吸与台阶对T-S波的影响。在第3节中,介绍了无黏Mack模态的局部感受性与局部散射问题。最后在第4节对本文做总结与展望。
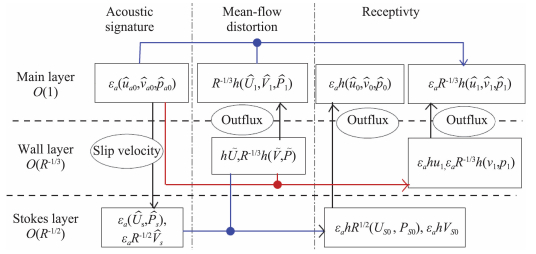
1 局部散射理论的基本框架 1.1 考虑局部突变影响的转捩预测模型传统的eN转捩预测方法的核心思想是认为当边界层中最危险的扰动(或称为主导扰动)在线性的机制下放大eN倍时转捩发生。如果边界层中存在局部突变,则扰动的感受性和线性演化阶段会受到影响,这将表现为转捩位置的推迟或提前。最简单的构建新的转捩模型的方法是把这些影响定量地刻画,然后用它们来修正转捩的判据N值。如引言所述,局部突变对转捩的影响主要通过局部感受性机制与线性模态的局部散射机制来实现,而这两种机制可以由Wu和Dong[32]提出的一套通用的理论框架——局部散射理论——来定量刻画。在实际问题的应用中,这两种机制可能只有一个重要,也可能同时重要,这是由具体的条件(包括来流条件、主导扰动的频率以及局部突变的位置等)决定的。本节主要介绍在两种机制下如何修正转捩判据N值。
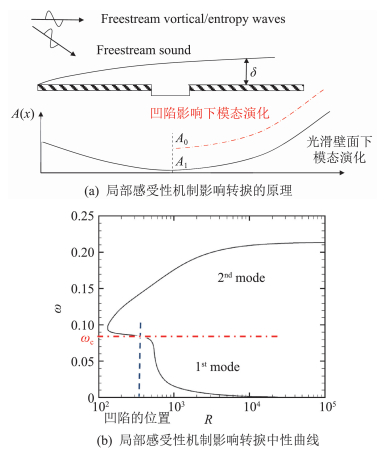
在局部感受性机制下,不稳定模态的初始幅值将发生改变。图 2展示了局部感受性机制影响转捩的原理,其中局部突变以小尺寸凹槽为例。
|
图 2 局部感受性机制影响转捩的原理与中性曲线 Fig.2 Mechanism of the impact of local receptivity on transition and the neutral curve |
如果壁面是光滑的,则边界层中某一频率下的模态扰动将经历如图 2(a)中黑实线所示的先衰减后增长的过程。这是因为模态失稳是受雷诺数R影响的,而后者随着流向坐标x的增大而增大。当某一流向位置的剖面所对应的扰动是中性的时,幅值演化曲线就会在这里经历由衰减到增长的变化。图 2(b)给出了在给定工况下(这里马赫数Ma=5.92,壁面为无滑移、绝热边界条件)反映扰动既不增长又不衰减扰动的频率ω与雷诺数R的关系的中性曲线。由于来流是高超声速的,不稳定模态出现了两族,分别是第一模态与第二模态[15]。这里两个模态合并在一起,出现了同步现象[33]。令凹槽处所对应的雷诺数超过临界雷诺数(本工况约为130),其对应的中性曲线下支界的频率为ωc。一般,在该频率附近的模态扰动的局部感受性最强。受凹槽引起的局部感受性影响,新的模态扰动被激发,这样扰动的演化规律变成图 2(a)中的红色实线。定义局部感受性系数K为激发出的模态扰动的渐近初始幅值A0与自由流中的扰动幅值Af之比。转捩预测则要考虑由前缘感受性和局部感受性两种机制所激发的模态扰动的叠加。若该频率下的扰动是触发转捩的主导模态,且在前缘感受性机制下得到该位置处的幅值为A1,则eN法中的转捩因子N将会减小,其改变量为
| $ \Delta N = - {\rm{ln}}\left| {1 + \frac{{{A_0}}}{{{A_1}}}} \right| = - {\rm{ln}}\left| {1 + \frac{{K{A_f}}}{{{A_1}}}} \right| $ | (1) |
其中A0与A1都是带相位的复数。若凹槽相对较深,使得|A0|≫|A1|,则转捩的预测可只考虑由局部感受性机制引起的模态扰动的演化,而此时使用NPSE方法预测转捩更加合适。但如果主导模态的频率不在ωc附近,则局部感受性对转捩的影响较弱。
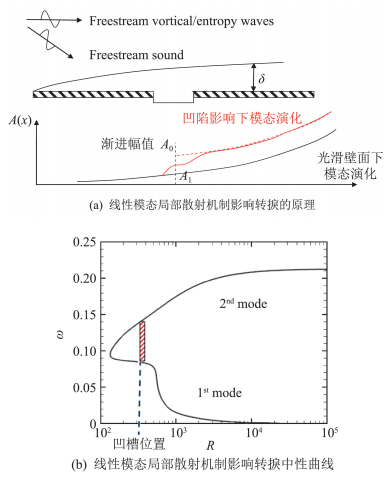
在线性模态的局部散射机制下,不稳定模态的增长可能会被促进或抑制,进而影响转捩位置。图 3给出了线性模态局部散射机制影响转捩的原理。如图 3(b)所示,现在我们关注的是所有不稳定频率下的扰动(如图中红色阴影区域)。在光滑边界层内,不稳定扰动如图 3(a)中黑色实线所示呈指数增长。当凹槽存在于壁面上时,局部快变的平均流会与上游不稳定模态相作用,表现为如红色实线所示的局部“跳跃”。在下游,扰动的增长规律再次恢复到光滑壁面的情况。如果把上下游的远场扰动做渐近延拓,则可以在凹槽处看到由A1到A0的跳跃。在新的转捩预测方法中,定义透射系数T=A0/A1,则转捩因子N的变化为
|
图 3 线性模态局部散射机制影响转捩的原理与中性曲线 Fig.3 Mechanism of the impact of linear-mode local scattering on transition and the neutral curve |
| $ ~\Delta N=-\text{ln}\left| \frac{{{A}_{0}}}{{{A}_{1}}} \right|=-\text{ln}T $ | (2) |
注意在线性模态的局部散射机制中,A0和A1的定义与局部感受性机制不同。当|T|>1时,不稳定模态被促进,则转捩提前,ΔN < 0;反之不稳定模态被抑制,ΔN>0。若壁面上存在一系列局部突变,则总的ΔN为所有ΔN之和。
新的转捩预测模型就是在传统的eN方法的基础上,根据公式(1)与公式(2)确定新的转捩判据N+ΔN。接下来的问题就是如何定量地刻画局部感受性系数K和局部透射系数T,这就是局部散射理论框架的任务。
1.2 局部散射理论的基本思想局部感受性和线性模态的局部散射问题都可由图 4的示意图表示。本质上,局部散射问题就是通过来流扰动和由局部突变引起的快变平均流的非线性作用而激发不稳定模态的过程。这里对于局部感受性问题,来流扰动表现为自由流中的声波、涡波或熵波;而对于线性模态的局部散射问题,来流扰动表现为上游的不稳定模态。对于后者,激发出的模态扰动与来流扰动形式相同,透射系数表现为二者幅值的叠加与来流扰动幅值之比。

|
图 4 局部散射问题的本质 Fig.4 Intrinsic mechanism of the local scattering problem |
如果来流扰动和快变平均流的强度都很小,该系统可以转化成一个线性问题。首先把瞬时流场写成
| $ \phi ={{\phi }_{B}}+\bar{\varepsilon }\bar{\phi }+\hat{\varepsilon }\hat{\phi }{{\text{e}}^{-\text{i}\omega t}}+\bar{\varepsilon }\hat{\varepsilon }\tilde{\phi }{{\text{e}}^{-\text{i}\omega t}}+c.c. $ | (3) |
其中:ϕ=(ρ, u, v, w, T, p)分别表示密度、流向、法向和展向的速度、温度与压力;ϕB表示光滑壁面情况下的平均流;ϕ为由局部突变引起的强度为ε≪1平均流修正;
| $ L(\mathit{\boldsymbol{k}}, \omega ){\tilde \phi _{\rm{F}}} = \int {{{\tilde \phi }_{\rm{F}}}} ({\mathit{\boldsymbol{k}}_1}){\hat \phi _{\rm{F}}}(\mathit{\boldsymbol{k}}{\rm{ - }}{\mathit{\boldsymbol{k}}_1}, \omega ){\rm{d}}{\mathit{\boldsymbol{k}}_1} $ | (4) |
其中,k为波数矢量,ω为频率,下标F表示谱空间的扰动,等式左边的L为线性算子,等式右端的卷积表示平均流修正与来流扰动的非线性作用。对于空间增长的扰动,ω为给定实数,波数矢量至少在一个方向上(不妨设流向波数kx)是复数,其虚部表示增长率的相反数。对于流线型固壁,非平行效应的流向尺度远大于局部突变的流向尺度,因而对基本流ϕB做平行流假设是合适的,从而,线性算子L可化简为O-S算子。当k与ω满足一定特征关系(色散关系)时,方程

|
图 5 在复kx平面内的环路积分路径 Fig.5 Integral path in the complex kx plane |
但如果局部突变对平均流修正的强度较大,即ε≪1不成立,则基本流
当壁面突变(如粗糙元)的流向尺度与不稳定模态的波长相当的时候,局部散射问题表现为一个局部的椭圆型系统,表现为在粗糙元附近的扰动不但受上游信息影响,还受下游信息影响。因而,只关注局部剖面的O-S方程或把系统抛物化的PSE方法都是不适用的。虽然人们可以同样通过实验或直接数值模拟对特定工况下的感受性系数K与透射系数T进行测量,但要想系统地研究K与T对整个参数空间的依赖,并总结规律性结论,则需要构建定量的理论框架。本文讨论的局部散射理论框架包括大雷诺数渐近理论和有限雷诺数理论两部分,前者能够清晰地展示尺度之间的作用机理,而后者在定量上更加准确。
1.3 黏性与无黏不稳定机制以最简单的二维层流边界层为例,失稳模态包括黏性和无黏两类。这两类模态扰动受局部突变影响而产生的局部散射现象的机理是不同的,但这种不同只能通过渐近理论的分析得到。为清晰地展示两种模态的区别,本节采用渐近理论分别介绍两类模态的特征尺度。
黏性模态主要包括不可压缩与亚声速边界层中的T-S波以及超声速边界层中波角
| $ ~\theta =\text{ta}{{\text{n}}^{-1}}\left( \beta /\alpha \right)>\text{ta}{{\text{n}}^{-1}}(\sqrt{M{{a}^{2}}-1}) $ | (5) |
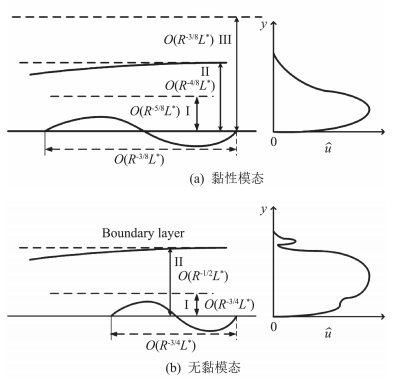
的第一模态不稳定波,其渐近尺度(不包括中性曲线上支界附近)如图 6(a)所示,其中α与β分别为不稳定模态的流向与展向波数。
|
图 6 黏性与无黏模态的渐近尺度 Fig.6 Asymptotic scalings of the viscous and inviscid modes |
Lin[38]和Smith[39-40]通过渐近分析指出,在不可压缩或亚声速边界层中,T-S波的下支界中性频率是O(R1/4U∞/L*)的量级,而波长是O(R-3/8L*)的量级,其中R=U∞L*/ν∞是以当地到前缘的距离L*为特征长度、分别以来流速度U∞和黏性系数ν∞为特征速度和黏性系数的雷诺数。这里要强调的是,T-S波的波长比当地边界层的厚度O(R-1/2L*)长,这两个尺度的差别是O(R-1/8)的量级。但是,有限雷诺数的实验或直接数值模拟往往给人们一个错误的印象——T-S波的波长和边界层厚度相当。因为即使在R=106时,这两个尺度的差别R-1/8也只有0.178。而只有当尺度的估计是正确时,后面的数学分析才有意义。Lin[38]和Smith[39-40]的尺度分析告诉我们,T-S波的相速度c≡ω/α=O(R-1/8U∞)≪U∞。因而,T-S波的特征函数集中在非常靠近壁面的薄层y~R-5/8L*内。这一尺度恰好与三层结构理论[41-43]的尺度相同,后者被应用于描述如平板尾缘、粗糙元等对平板边界层的修正。更巧合的是,低速流中的声波也在壁面附近O(R-5/8L*)的区域内激发非定常的Stokes层。因而,Ruban[34]和Goldstein[35]基于对黏性底层的分析,最早描述了T-S波被声波与粗糙元作用而激发的物理过程。另外,在中性曲线上支界附近的T-S波不满足图 6(a)的渐近尺度,它在法向表现为如Bodonyi和Smith[44]给出的五层结构尺度。在这一分析中,边界层内出现相速度与基本流速度相同的临界层,非平行性效应也要被考虑进来。但是不稳定模态在通过中性曲线上支界后进入线性衰减区,转捩受其影响很小,故本文不详细讨论中性曲线上支界的稳定性问题。
当来流变成超声速时,三层结构公式体系的上层的控制方程由椭圆型的拉普拉斯方程变成了双曲型的亥姆霍兹方程,这样,只有条件(5)被满足时才能得到黏性机制下的不稳定模态解[16]。而这种解恰好对应于超声速边界层中的三维第一模态,因而,三维性较强(波角tan-1(β/α)较大)的超声速第一模态扰动也可以被称为黏性T-S波。
在超声速边界层中,O-S方程存在多族不稳定模态解,Mack[15]对该问题的数值研究进行了详细的综述。研究发现,大部分第一模态以及所有高阶模态都属于无黏失稳,这是因为边界层剖面存在广义拐点,即满足
| $ \frac{\text{d}}{\text{d}y}\left( {{\rho }_{B}}\frac{\text{d}{{U}_{B}}}{\text{d}y} \right)=0 $ | (6) |
的点。这些无黏模态的渐近尺度如图 6(b)所示。无黏模态的频率和波长分别为O(R1/2U∞/L*)和O(R-1/2L*)的量级,故其相速度c=O(U∞)。这样,无黏模态的特征函数出现在边界层的主层,一般可以用线性欧拉方程或Rayleigh方程描述。但是,注意到无黏方程的解并不满足无滑移边界条件,因而必须在非常靠近壁面的O(R-3/4L*)的区域内引入一个Stokes层,其作用是使得主层无黏解的滑移速度在这一薄层内迅速衰减到壁面的零值。
不管是黏性还是无黏模态,基本流非平行性的影响都是O(R-1)的量级,因而它在首阶上是可以忽略的。本文在采用大雷诺数渐近理论描述局部散射理论框架时,区分不稳定模态的黏性属性,能清晰地展示局部散射过程的本质。
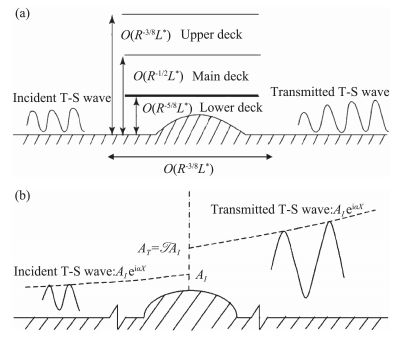
2 黏性机制下的局部散射理论 2.1 粗糙元对亚声速T-S波的局部散射如1.3节所述,黏性模态在大雷诺数渐近理论框架下可由三层结构理论描述,而由局部突变引起的平均流修正也在这一尺度范围内,因而,Wu和Dong[32]采用三层结构理论,系统地研究了亚声速平板边界层中二维T-S波被局部粗糙元散射的问题。其尺度作用如图 7(a)所示。在该工作中,粗糙元的高度被假设为O(R-5/8L*)的量级,由其引起的平均流修正在底层满足非线性边界层方程。虽然底层(Lower deck)的控制方程是抛物型的,但是由于压力梯度也是解的一部分,该方程组不封闭。对该系统的求解需要叠加上层(Upper deck)的信息,即自激发的压力梯度与边界层的排移效应之间的线性关系。后者可化成一个椭圆型的希尔伯特积分,因而整个系统表现为下游影响上游的椭圆型特性。
|
图 7 三层结构尺度(a)与T-S波的局部散射(b)示意图 Fig.7 Sketches of triple-deck structure (a) and local scattering of the T-S wave (b) |
平均流修正只局限在粗糙元附近O(R-3/8L*)的流向范围内,因而,在距离粗糙元较远的上游与下游,平均流趋近于未受扰动的Blasius解,脉动场也趋近于由Blasius剖面的稳定性决定的T-S波
| $ A\tilde{\phi }=TB\tilde{\phi } $ | (7) |
其中A与B是系数矩阵,其具体表达形式见文献[32],透射系数T就是系统的特征值。对于一个特定的工况,图 8展示了粗糙元附近脉动场
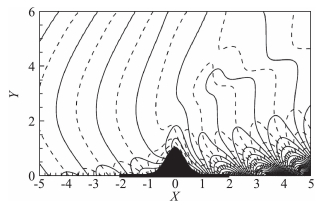
|
图 8 脉动场的速度特征函数实部的等值线[32](其中实线表示正值,虚线表示负值) Fig.8 Contours of the real part of the velocity eigenfunction of the perturbation field, where the solid and dashed lines represent positive and negative values (from Ref.[32]) |
采用三层结构理论的另一个好处是,系统参数的个数大大减少了。本质上,透射系数T受来流马赫数、雷诺数、壁面温度、来流温度(影响Sutherland黏性律)、上游T-S波频率和粗糙元形状的影响,在大雷诺数三层结构体系下,T只受T-S波的频率和粗糙元形状的影响。通过系统的参数研究,发现凸起和凹陷都会促进T-S波的增长,但凸起的效果更明显;随着T-S波频率和粗糙元高度的增加,散射效应增强;当粗糙元的宽度与T-S波的波长相当时,散射效应出现峰值。该理论框架也被应用于由抽吸、台阶引起的局部散射问题[45-46]。
2.2 粗糙元与声波作用而激发T-S波的局部感受性Ruban[34]和Goldstein[35]最早采用三层结构理论,描述了亚声速和不可压缩边界层中T-S波的局部感受性。声波在底层激发了黏性非定常Stokes层,其流向、法向速度和压力在首阶上可表示为
| $ ({{U}_{S}}, {{V}_{S}}, {{P}_{S}})\sim {{(1-{{\text{e}}^{-(-\text{i}\omega }})}^{1/{{2}_{Y}}}}, 0, 1){{\text{e}}^{-\text{i}\omega t}}+c.c. $ | (8) |
其中
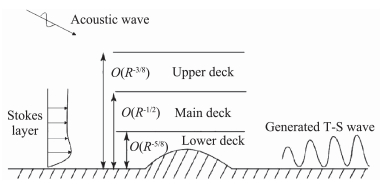
|
图 9 T-S波的局部感受性机制示意图[45](略作改动) Fig.9 Sketch of the local receptivity regime (From Ref.[45] with small modification) |
由于粗糙元上下游扰动的形式不同,整个系统可以化成一个线性代数方程组
| $ {\mathit{\boldsymbol{A}}_1}{\tilde \phi _1} = \mathit{\boldsymbol{b}} $ | (9) |
其中,未知向量
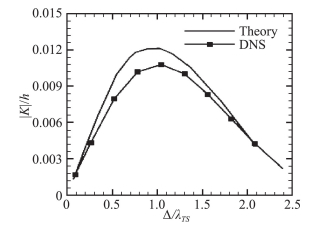
|
图 10 感受性系数对粗糙元宽度的依赖 Fig.10 Dependence of receptivity coefficient on the roughness width |
本节应用局部散射理论讨论一个有趣的设计。在航空工程中,常会遇到两块材料拼接的情况,而拼接处难免出现缝隙与台阶。在实际操作中,常用填充物把缝隙堵上,但这会给维护工作增加困难,并且当填充物在连续荷载作用下发生变形时,转捩也会受到影响。Zahn和Rist[48]通过DNS发现,虽然缝隙本身会促进T-S波的增长,但当它被安置在前台阶之前或后台阶之后时,它有可能抑制台阶对T-S波的促进作用。而如果在缝隙处引入抽吸,补偿效果就更明显了,甚至有些时候T-S波会被缝隙与台阶的组合所抑制。更重要的是,由于在前台阶前缘和后台阶后缘有自激发的压力梯度,这样,在缝隙内不需要引入额外的能量就可以使部分流体在压力梯度下产生自然的抽吸效果[49]。这在实际操作中更容易实现。
本节所考虑的物理问题如图 11所示,考虑一个带台阶的平板放在一个亚声速来流中。图 11(a)展示的是一个前台阶,在其前缘安置一个抽吸元;图 11(b)展示的是在后缘安置抽吸元的后台阶。假设台阶处在T-S波的不稳定区域,则上游传播过来的T-S波可以与台阶发生局部散射作用。考虑台阶的高度远低于边界层厚度,为O(R-5/8L*)的量级,则它们之间的作用仍然可以被大雷诺数三层结构描述,具体过程与2.1节中的介绍完全相同。
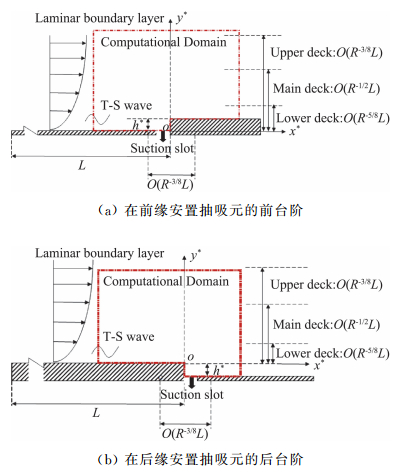
|
图 11 用抽吸补偿台阶对T-S波的促进作用 Fig.11 Compensation of the enhancement effect of steps on T-S waves by suction |
计算发现,若抽吸的流量为0,则前、后台阶都会对T-S波有促进作用(T>1),而且相同尺寸的后台阶对T-S波的促进作用更强。透射系数随着来流频率与台阶高度的增加而增加[46]。而如果从壁面引入体积流量为O(R-3/4L*U∞)的抽吸时,台阶对T-S波的促进作用则可被补偿,甚至得到较好的抑制转捩的效果。
为验证渐近理论的定量结果的精度,我们还发展了有限雷诺数版本的局部散射理论。这一方法与文献[50-53]中的线性化N-S方法相同,其原理是把随时间简谐振动的脉动场带入N-S方程并做线性化,这样,在给定入口条件下,该系统化成一个高维线性代数方程组。这被称为Harmonic Linearized Navier-Stokes(HLNS)方法。通过两个方法计算结果的对比,发现渐近理论在抽吸流量较小时与HLNS的结果吻合较好,但随着抽吸流量的增大,二者存在一定差别。这是可以理解的,因为渐近理论只考虑首阶近似。但在渐近理论下,不同马赫数、雷诺数的计算结果可通过合适的归一化而合并到一起,这对理解局部散射问题的本质有重要意义。该工作尚未发表,正在审稿中。
3 无黏机制下的局部散射理论 3.1 超声速无黏模态的局部感受性本节讨论的问题是超声速边界层中的无黏Mack模态被自由流中声波和壁面粗糙元作用而激发的问题,如图 12所示。
由于无黏模态的渐近尺度与黏性T-S波不同,其感受性过程也大不一样。从大雷诺数渐近理论来看,频率为O(U∞/δ)的声波在边界层中的响应可分两层,分别是O(δ)的边界层主层和O(Rδ-1/2δ)的Stokes层,其中
无黏感受性机制可由图 13所示的作用机制表示,其中箭头表示不同渐近分层之间的相互作用。如果入射声波的幅值为εa≪1,则边界层对声波的响应是无黏、线性的,它可以用可压缩Rayleigh方程对应于声波分支的连续谱来描述。在边界层的主层,速度与压力脉动都是O(εa)。但是,由于壁面上没有强制的无滑移条件,需要在壁面附近引入O(Rδ-1/2)的Stokes层。在该层内,流向速度脉动与压力的幅值仍然是O(εa),但法向速度脉动为O(Rδ-1/2εa)。后者会在主层引起声波扰动的二阶修正。以上只是光滑平板对声波的响应,如果壁面存在O(h)粗糙元,则流向脉动速度在Stokes薄层内的的量级可达到O(εahRδ1/3),这正是首阶感受性的量级。与此同时,在主层声波响应与平均流的非线性作用决定二阶感受性的量级为O(εah)。
采用渐近理论对每一阶的感受性系数的求解都要用到如1.2节中介绍留数定理,只是式(4)左端的线性算子改成无黏Rayleigh算子。在首阶上,式(4)右端的非线性作用项为0,非齐次强迫来自壁面边界条件;在二阶上,非齐次强迫既包括右端的非线性作用项,又包括从底层贡献的法向非定常出流。另外,还可以用类似的概念构建有限雷诺数理论,只是此时粗糙元的高度必须假设为h≪Rδ-1/3δ。在该理论中,式(4)左端的线性算子为O-S算子,右端非线性作用项和壁面边界条件同时存在。
图 14展示的是来流马赫数为5.92的绝热壁平板边界层中局部感受性系数随雷诺数的变化规律。通过对该基本流的稳定性分析,可得到表征模态既不增长也不衰减的中性曲线,如图 2(b)或图 3(b)所示。计算中,选择了三个典型频率,分别为ω=0.108、0.110和0.120。这三个频率都对应于第二模态不稳定波,且ω=0.108接近第一模态与第二模态的同步点。图 14(a)中的符号表示DNS结果,实线表示基于留数定理的有限雷诺数理论的计算结果。因为增大雷诺数后DNS的计算量太大,所以这里DNS计算的最大雷诺数为15 600。对于所计算的雷诺数范围,DNS结果与有限雷诺数理论几乎重合。而当雷诺数继续增大时,有限雷诺数理论的计算结果趋近于大雷诺数渐近理论的结果(虚线所示)。这说明了本节发展的两套理论都是可靠的。但是,我们还发现,对于一个中等的雷诺数,渐近理论的预测精度显然不够。其原因主要是来自Rayleigh算子和O-S算子的差别。考虑到Rayleigh方程的最大简化是忽略了底层对主层的影响,我们引入一个修正方法,即把无穿透的壁面边界条件改为考虑Stokes层贡献的边界条件,具体形式见文献[54]。这样,可以计算出修正渐近理论的结果,如图 14(b)中的虚线所示。与有限雷诺数结果(实线)对比,渐近理论的精度大大提高了,其结果可以精确到雷诺数是几千的情况。
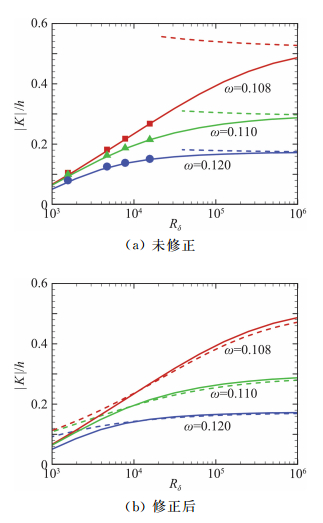
|
图 14 感受性系数随雷诺数的变化(选自文献[54]) Fig.14 Dependence of receptivity coefficient on Reynolds number (from Ref.[54]) |
渐近理论给我们的另一个启示是,对于粗糙元+声波引起的局部感受性问题,在首阶上,激发的扰动场由Rayleigh方程加上非定常壁面吹吸的边界条件控制。这很容易让人联想到一个更加基本的感受性问题,即模态扰动被非定常壁面吹吸所激发。后者不需要在自由流中引入任何扰动;且在小幅值吹吸下,平均流修正为0。尽管两个感受性问题的物理本质不同,但在数学描述上完全一样,这一比拟有助于对局部感受性问题本质的理解。
3.2 超声速无黏模态的线性局部散射为了描述有限高度(h~δ)的粗糙元对无黏模态的散射作用,本节采用另一套有限雷诺数理论——HLNS[53]。该理论与2.3节中介绍的有限雷诺数理论相同。研究的物理问题与图 7相同,只是在高超声速边界层中,二维不稳定模态是无黏Mack模态,而不是黏性T-S波。
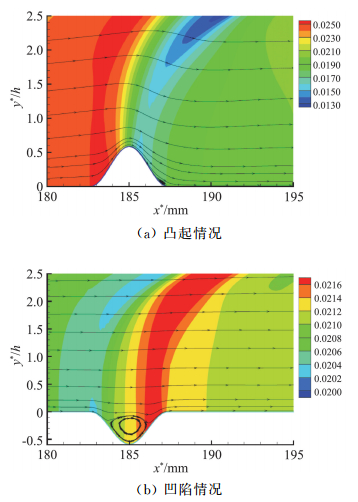
选取的计算工况仍然是马赫数为5.92的绝热平板边界层,其中性曲线与图 2(b)或图 3(b)相同。首先通过直接数值模拟,求得被有限高度的凸起及凹陷修正的平均流,图 15展示了平均压力云图及流线。在粗糙元处的边界层名义厚度为2.36 mm。可以看到在凸起的尾端和凹陷的内部存在回流区。
Duan等[55]和Fong等[56-57]通过直接数值模拟,研究了来流马赫数为5.92的边界层中Mack模态被粗糙元局部散射的问题。他们发现,粗糙元对频率高于同步频率的Mack模态有抑制作用,而对频率低于同步频率的模态有促进作用。但直接数值模拟只能针对个别工况做定量研究,无法在整个参数空间内总结规律性结论,而这一任务可以被HLNS[53]完成。
图 16展示了透射系数随来流Mack模态频率的变化。图中展示了五个工况(Case 1.1~Case 1.5),分别表示五个不同高度的凸起型粗糙元(h/δ99=0.05、0.10、0.15、0.20和0.25,其中δ99为边界层名义厚度),它们的宽度都是2δ99。对于本节所研究的基本流,有量纲的同步频率约为128 kHz。在图中,同步频率相当于一条区分促进与抑制作用的分界线,粗糙元只对频率高于同步频率的Mack模态有抑制作用。而且,可以明显看出,粗糙元越高,散射效应越强。另外,局部凹陷对Mack模态的散射作用与凸起相同,只是相同高度的凹陷的散射作用更弱。
值得说明的是,以上有限雷诺数理论仍然无法解释为什么同步频率表现为区分粗糙元促进与抑制作用的分界线,而这需要采用渐近理论做进一步分析。只是该工作尚未完成,故本文暂不做综述。
4 结束语为适应工程上对非光滑壁面飞行器转捩预测的需求,需要发展考虑局部突变影响的边界层转捩预测方法。本文建议了一个新的转捩预测模型,即在传统的eN方法基础上,依据公式(1)和公式(2)修正转捩判据。这里最重要的环节就是如何量化局部突变对转捩的影响,即计算局部感受性系数与透射系数。本文综述了定量刻画以上两个系数的局部散射理论在近年来的研究进展。
对于二维层流边界层,不稳定波包括黏性T-S模态和无黏Mack模态两类,它们的渐近尺度以及与局部突变的作用机制是不同的。局部散射理论框架把大雷诺数渐近理论与有限雷诺数理论相结合,得到了物理机制清晰、定量上准确的刻画两个特征参数的方法。本文展示了局部散射理论在一系列具体物理问题中的应用。
作为一套通用的理论框架,局部散射理论保留了局部散射系统的椭圆性,从数学上来讲是严格的。另一方面,通过理性的简化处理,该理论使系统地研究描述局部散射系统的特征参数对全参数空间的依赖关系成为可能。更重要的是,该理论所描述的特征参数可与传统转捩预测方法无缝对接,以获得适用于非光滑壁面的边界层转捩预测的方法。
关于局部散射理论的后续研究工作包括两方面。首先,在更丰富的壁面突变情况下描述局部感受性系数与透射系数,比如折角、多孔壁、波纹壁等,特别是在高超声速边界层中的应用。值得说明的是,本文介绍的局部散射理论可以推广到如波纹壁等的分布式突变的情况。在求解感受性(透射)系数时,需要用格林函数法把局部感受性(透射)系数沿流向积分,这里要注意的是流向的非平行性要考虑进来,如Choudhari[58]。另一方面,需要把发展的考虑局部突变影响的转捩预测方法应用于求解航空航天工程的实际问题中,用实验或直接数值模拟数据验证新的转捩预测模型。
致谢: 本文图 6为刘银辉博士生制作,在此表示感谢。
| [1] |
周恒, 张涵信. 空气动力学的新问题[J]. 中国科学:物理学力学天文学, 2015, 45(10): 109-113. ZHOU H, ZHANG H X. New problems of aerodynamics[J]. Scientia Sinica (Physica, Mechanica & Astronomica), 2015, 45(10): 104709. (in Chinese) |
| [2] |
周恒, 张涵信. 有关近空间高超声速飞行器边界层转捩和湍流的两个问题[J]. 空气动力学学报, 2017, 35(2): 151-155. ZHOU H, ZHANG H X. Two problems in the transition and turbulence for near space hypersonic flying vehicles[J]. Acta Aerodynamica Sinica, 2017, 35(2): 151-155. (in Chinese) |
| [3] |
CROUCH J. Predicting laminar-turbulent transition influenced by surface-induced flow distortions[R]. IUTAM-2019, 2019: London.
|
| [4] |
PERRAUD J, ARNAL D, KUEHN W. Laminar-turbulent transition prediction in the presence of surface imperfections[J]. International Journal of Engineering Systems Modelling and Simulation, 2014, 6(3/4): 162. |
| [5] |
SCHNEIDER S P. Effects of roughness on hypersonic boundary-layer transition[J]. Journal of Spacecraft and Rockets, 2008, 45(2): 193-209. |
| [6] |
WHEATON B M, SCHNEIDER S P. Roughness-induced instability in a laminar boundary layer at Mach 6[C]//48th AIAA Aerospace Sciences Meeting Including the New Horizons Forum and Aerospace Exposition. 2010. AIAA 2010-1574.
|
| [7] |
DUAN Z W, XIAO Z X, FU S. Simulation of transition triggered by isolated roughness in hypersonic boundary layer[C]//42nd AIAA Fluid Dynamics Conference and Exhibit, New Orleans, Louisiana. Reston, Virigina: AIAA, 2012. AIAA 2012-3076.
|
| [8] |
董明. 高超声速边界层中由粗糙元引起强制转捩的机理[J]. 气体物理, 2016, 1(5): 25-38. DONG M. Mechanism of roughness-induced transition in hypersonic boundary layers[J]. Physics of Gases, 2016, 1(5): 25-38. (in Chinese) |
| [9] |
KACHANOV Y S. Physical mechanisms of laminar-boundary-layer transition[J]. Annual Review of Fluid Mechanics, 1994, 26(1): 411-482. |
| [10] |
SMITH A M O. Transition, pressure gradient and stability theory[C]//IX International Congress for Applied Mechanics, 1956: Brussels.
|
| [11] |
JAFFE N A, OKAMURA T T, SMITH A M O. Determination of spatial amplification factors and their application to predicting transition[J]. AIAA Journal, 1970, 8(2): 301-308. |
| [12] |
SROKOWSKI A J, ORSZAG S A. Mass flow requirements for LFC wing design: AIAA-77-1222[R]. Reston: AIAA, 1977.
|
| [13] |
SMITH A M O. On the growth of Taylor-Görtler vortices along highly concave walls[J]. Quarterly of Applied Mathematics, 1955, 13(3): 233-262. |
| [14] |
MACK L M. Transition prediction and linear stability theory[R]. AGARD CP-224.1977.
|
| [15] |
MACK L M. Review of linear compressible stability theory[M]. New York, N Y: Springer New York, 1987: 164-187.
|
| [16] |
SMITH F T. On the first-mode instability in subsonic, supersonic or hypersonic boundary layers[J]. Journal of Fluid Mechanics, 1989, 198: 127. |
| [17] |
Goldstein M E. The evolution of Tollmien-Schlichting waves near a leading edge[J]. J Fluid Mech, 1983, 127: 59-81. |
| [18] |
FEDOROV A V, KHOKHLOV A P. Excitation of unstable modes in a supersonic boundary layer by acoustic waves[J]. Fluid Dynamics, 1991, 26(4): 531-537. |
| [19] |
FEDOROV A V, KHOKHLOV A P. Prehistory of instability in a hypersonic boundary layer[J]. Theoretical and Computational Fluid Dynamics, 2001, 14(6): 359-375. |
| [20] |
MA Y B, ZHONG X L. Receptivity of a supersonic boundary layer over a flat plate. Part 1. Wave structures and interactions[J]. Journal of Fluid Mechanics, 2003, 488: 31-78. |
| [21] |
MA Y B, ZHONG X L. Receptivity of a supersonic boundary layer over a flat plate. Part 2. Receptivity to free-stream sound[J]. Journal of Fluid Mechanics, 2003, 488: 79-121. |
| [22] |
MA Y B, ZHONG X L. Receptivity of a supersonic boundary layer over a flat plate. Part 3. Effects of different types of free-stream disturbances[J]. Journal of Fluid Mechanics, 2005, 532: 63-109. |
| [23] |
FEDOROV A V. Receptivity of a high-speed boundary layer to acoustic disturbances[J]. Journal of Fluid Mechanics, 2003, 491: 101-129. |
| [24] |
MASLOV A A, SHIPLYUK A N, SIDORENKO A A, et al. Leading-edge receptivity of a hypersonic boundary layer on a flat plate[J]. Journal of Fluid Mechanics, 2001, 426: 73-94. |
| [25] |
GOLDSTEIN M E, RICCO P. Non-localized boundary layer instabilities resulting from leading edge receptivity at moderate supersonic Mach numbers[J]. Journal of Fluid Mechanics, 2018, 838: 435-477. |
| [26] |
BERTOLOTTI F P, HERBERT T, SPALART P R. Linear and nonlinear stability of the Blasius boundary layer[J]. Journal of Fluid Mechanics, 1992, 242: 441-474. |
| [27] |
HERBERT T. Parabolized stability equations[J]. Annual Review of Fluid Mechanics, 1997, 29(1): 245-283. |
| [28] |
CHANG C L, MALIK M, ERLEBACHER G, et al. Compressible stability of growing boundary layers using parabolized stability equations[C]//22nd Fluid Dynamics, Plasma Dynamics and Lasers Conference, Honolulu, HI, USA. Reston, Virigina: AIAA, 1991. AIAA-91-1636.
|
| [29] |
MALIK M R, LI F, CHANG C L. Crossflow disturbances in three-dimensional boundary layers:nonlinear development, wave interaction and secondary instability[J]. Journal of Fluid Mechanics, 1994, 268: 1-36. |
| [30] |
CHOUDHARI M, CHANG C L, STREETT C, et al. Integrated transition prediction: a case study in supersonic laminar flow control[C]//41st Aerospace Sciences Meeting and Exhibit, Reno, Nevada. Reston, Virigina: AIAA, 2003.
|
| [31] |
DONG M, ZHANG Y M, ZHOU H. A new method for computing laminar-turbulent transition and turbulence in compressible boundary layers:PSE+DNS[J]. Applied Mathematics and Mechanics, 2008, 29(12): 1527-1534. |
| [32] |
WU X S, DONG M. A local scattering theory for the effects of isolated roughness on boundary-layer instability and transition:transmission coefficient as an eigenvalue[J]. Journal of Fluid Mechanics, 2016, 794: 68-108. |
| [33] |
FEDOROV A. Transition and stability of high-speed boundary layers[J]. Annual Review of Fluid Mechanics, 2011, 43(1): 79-95. |
| [34] |
RUBAN A I. On Tollmien-Schlichting wave generation by sound[M]. Berlin, Heidelberg: Springer Berlin Heidelberg, 1985: 313-320.
|
| [35] |
GOLDSTEIN M E. Sound generation and upstream influence due to instability waves interacting with non-uniform mean flows[J]. Journal of Fluid Mechanics, 1984, 149: 161. |
| [36] |
CHOUDHARI M, STREETT C L. A finite Reynolds-number approach for the prediction of boundary-layer receptivity in localized regions[J]. Physics of Fluids A:Fluid Dynamics, 1992, 4(11): 2495-2514. |
| [37] |
CROUCH J D. Localized receptivity of boundary layers[J]. Physics of Fluids A:Fluid Dynamics, 1992, 4(7): 1408-1414. |
| [38] |
LIN C C. On the stability of two-dimensional parallel flows. III. Stability in a viscous fluid[J]. Quarterly of Applied Mathematics, 1946, 3(4): 277-301. |
| [39] |
SMITH F T. Nonlinear stability of boundary layers for disturbances of various sizes[J]. Proceedings of the Royal Society A:Mathematical Physical and Engineering Sciences, 1979, 368(1735): 573-589. |
| [40] |
SMITH F T. On the non-parallel flow stability of the Blasius boundary layer[J]. Proceedings of the Royal Society A:Mathematical Physical and Engineering Sciences, 1979, 366(1724): 91-109. |
| [41] |
STEWARTSON K, WILLIAMS P G. Self-induced separation[J]. Proceedings of the Royal Society A:Mathematical, Physical and Engineering Sciences, 1969, 312(1509): 181-206. |
| [42] |
SMITH F T. Laminar flow over a small hump on a flat plate[J]. Journal of Fluid Mechanics, 1973, 57(4): 803-824. |
| [43] |
董明, 赵慧勇. 超声速边界层中壁面抽吸对流动分离的抑制作用[J]. 气体物理, 2019, 4(2): 17-29. DONG M, ZHAO H Y. Suppression of flow separation by wall suction in supersonic boundary layers[J]. Physics of Gases, 2019, 4(2): 17-29. (in Chinese) |
| [44] |
BODONYI R J, SMITH F T. The upper branch stability of the Blasius boundary layer, including non-parallel flow effects[J]. Proceedings of the Royal Society A:Mathematical, Physical and Engineering Sciences, 1981, 375(1760): 65-92. |
| [45] |
DONG M, WU X S. Local scattering theory and the role of an abrupt change on boundary-layer instability and acoustic radiation[C]//46th AIAA Fluid Dynamics Conference, Washington, D C. Reston, Virginia: AIAA, 2016. AIAA 2016-3194.
|
| [46] |
DONG M, ZHANG A Y. Scattering of Tollmien-Schlichting waves as they pass over forward-/backward-facing steps[J]. Applied Mathematics and Mechanics, 2018, 39(10): 1411-1424. |
| [47] |
DONG M, WU X S. Generation of convective instability modes in the near-wake flow of the trailing edge of a flat plate[C]//8th AIAA Theoretical Fluid Mechanics Conference, Denver, Colorado. Reston, Virginia: AIAA, 2017. AIAA 2017-4022.
|
| [48] |
ZAHN J, RIST U. Impact of deep gaps on laminar-turbulent transition in compressible boundary-layer flow[J]. AIAA Journal, 2016, 54(1): 66-76. |
| [49] |
ZAHN J, RIST U. Active and natural suction at forward-facing steps for delaying laminar-turbulent transition[J]. AIAA Journal, 2017, 55(4): 1343-1354. |
| [50] |
THOMAS C, MUGHAL S, ASHWORTH R. Development of Tollmien-Schlichting disturbances in the presence of laminar separation bubbles on an unswept infinite wavy wing[J]. Physical[WX)] [WX(4.5mm, 75.5mm] Review Fluids, 2017, 2(4): 043903. |
| [51] |
RAPOSO H, MUGHAL S, ASHWORTH R. Acoustic receptivity and transition modeling of Tollmien-Schlichting disturbances induced by distributed surface roughness[J]. Physics of Fluids, 2018, 30(4): 044105. |
| [52] |
FRANCO SUMARIVA J A, HEIN S J. Adaptive Harmonic Linearized Navier-Stokes equations used for boundary layer instability analysis in the presence of large streamwise gradients[C]//2018 AIAA Aerospace Sciences Meeting, Kissimmee, Florida. Reston, Virginia: AIAA, 2018. AIAA 2018-1548.
|
| [53] |
ZHAO L, DONG M, YANG Y. Harmonic linearized Navier-Stokes equation on describing the effect of surface roughness on hypersonic boundary-layer transition[J]. Physics of Fluids, 2019, 31(3): 034108. |
| [54] |
DONG M, LIU Y, WU X. Receptivity of inviscid modes in supersonic boundary layers due to scattering of freestream sound by wall roughness[J]. J Fluid Mech. Under review.. |
| [55] |
DUAN L, WANG X W, ZHONG X L. Stabilization of a Mach 5.92 boundary layer by two-dimensional finite-height roughness[J]. AIAA Journal, 2013, 51(1): 266-270. |
| [56] |
FONG K D, WANG X W, ZHONG X L. Numerical simulation of roughness effect on the stability of a hypersonic boundary layer[J]. Computers & Fluids, 2014, 96: 350-367. |
| [57] |
FONG K D, WANG X W, ZHONG X L. Parametric study on stabilization of hypersonic boundary layer waves using 2-D surface roughness[C]//53rd AIAA Aerospace Sciences Meeting, Kissimmee, Florida. Reston, Virginia: AIAA, 2015. AIAA 2015-0837.
|
| [58] |
CHOUDHARI M. Distributed acoustic receptivity in laminar flow control configurations[J]. Physics of Fluids, 1994, 6(2): 489-506. |
 2020, Vol. 38
2020, Vol. 38