2. 中国空气动力研究与发展中心 计算空气动力研究所, 四川 绵阳 621000
2. Computational Aerodynamics Institute, China Aerodynamics Research and Development Center, Mianyang 621000, China
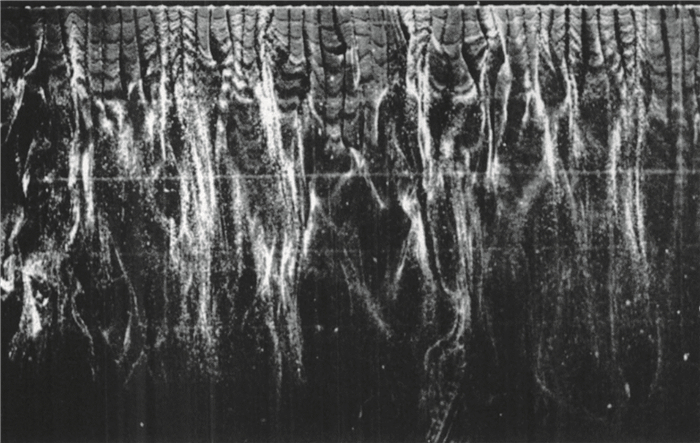
壁湍流广泛地存在于自然界中,早在500多年前,意大利画家达芬奇便在他的画作中记录了这一复杂的流动现象。长期以来人们认为壁湍流是杂乱无序的,直到1967年,斯坦福大学Kline等[1]采用氢气泡示踪法证实了壁湍流中存在近似规则的低速条带结构(Streaks),如图 1。这些条带结构在往下游演化的过程中会发生摆动,然后急骤破碎,进而伴随大量雷诺应力的产生[2]。Kline等将这一过程命名为“猝发”(Bursting)。
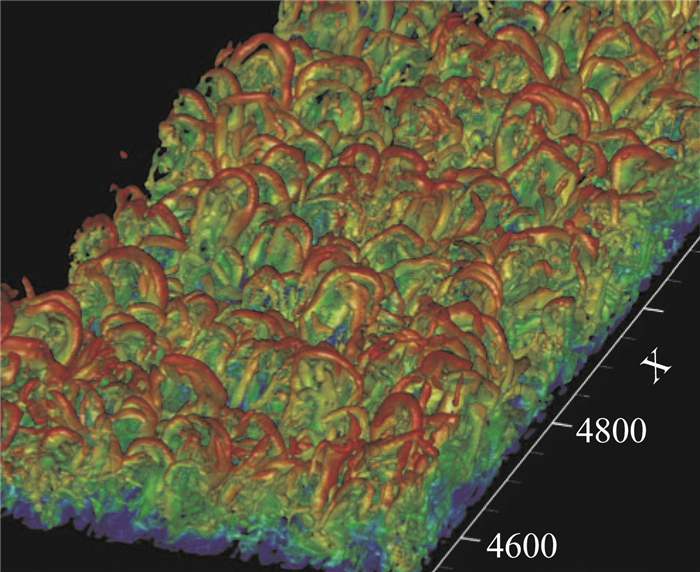
到1981年,Head和Bandyopadhyay[3]采用烟线示踪方法发现了壁湍流边界层中的流向涡结构。它们依形态分有发卡涡、马蹄涡、Ω涡等,分别对应于湍流演化的不同阶段和不同区域[4]。这其中最常见的就是发卡涡结构(如图 2),它由正向和反向旋转的两条涡腿及头部组成,实际壁湍流中以不对称的形态为主,即通常无头部且只出现一条涡腿。同时发卡涡也可以抱团形成更大的涡包[5]。
Robinson[4]定义湍流中的相干结构为:“三维区域内的至少一个流动变量与它本身或与另一个变量在一定的时间和空间尺度上保持较强的相关性,并且这个尺度比当地最小的流动尺度要大很多。”根据这个定义可见湍流中的相干结构是很多的,但本文的关注点仅限于前面提及的低速条带和流向涡两类相干结构。具体而言,低速条带体现的是湍流流向速度脉动量的相关性,而流向涡则体现的是湍流法向速度和展向速度间的相关性,后面我们将着重讨论这两类基本相干结构在湍流中的核心作用。这里我们考虑四类典型的壁湍流情形,即平板泊肃叶流动、平板库特叶流动、圆管泊肃叶流动和零压力平板边界层流动,其中前三种内流文献数据丰富是主要讨论对象。本文中x、y和z分别代表流向、法向和展向。外区参考尺度δ分别取泊肃叶流动和库特叶流动的半槽道高度h、圆管流动的圆管半径R和边界层位移厚度δ*;黏性尺度无量纲化后用上标+表示,即y+=yuτ/ν,t+=tuτ2/ν,其中ν为流体的运动黏性系数,uτ为摩擦速度。雷诺数定义为Re= δU/ν,其中参考速度U分别取泊肃叶流动中相同流量层流时的中心线速度Uc、库特叶流动中壁面运动速度Uw和边界层流动中的自由来流速度U∞;摩擦雷诺数定义为Reτ= δuτ/ν。
1 湍流结构的自相似过去一个世纪的壁湍流研究中最大的发现之一是壁定律[7-8],即湍流边界层包含黏性子区(y+ < 5);缓冲区(5 < y+ < 30);对数区(y+>30,y/δ < 0.3)。这个分区主要是从流向平均速度剖面的标度来界定的;如果从流动的特征尺度来分,壁湍流边界层亦可分为内区(y/δ < 0.1)、外区(y+>50)和介于二者之间的对数区。不同的区域存在不同的特征长度:内区的特征长度为黏性尺度ν/uτ,外区的特征长度为δ,而对数区的特征长度为壁面距离y。由上面的定义可以看到,对数区的下界是由黏性尺度决定的,而上界是由外区尺度决定的,当上下界有一个量级的差别,大约在Reτ=O(103)时,内区尺度和外区尺度开始出现明显的分离,对数区才变得清晰起来。因此对数区的存在是高雷诺数壁湍流特有的现象。然而长期以来,受限于实验测量条件和计算机运行速度,20世纪研究的绝大部分充分发展壁湍流均在Reτ=O(102)量级,比如Kim等[9]在1987年开展的首个壁湍流的直接数值模拟(DNS)雷诺数为Reτ≈180,并成为了充分发展壁湍流的标准数据库被广泛应用。由于过去研究的雷诺数不够高,对数区不够明显,以致关于卡门常数κ究竟是不是常数成为争论的热点[10-11]。
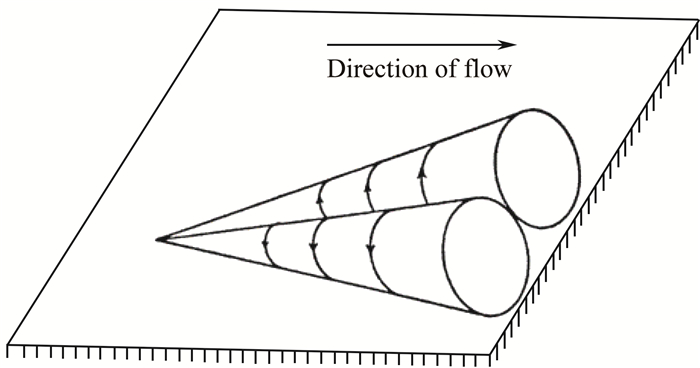
Townsend[12-13]较早意识到壁湍流的对数律暗示着壁湍流中存在一系列大小与其中心离壁面距离成正比的附面涡结构,并给出了壁湍流中最早的统计模型(双锥模型,如图 3)。通过假设湍流边界层中具有一系列不同大小的附面涡且它们具有相似的速度分布,Townsend成功地导出了无穷大雷诺数下流向平均速度的对数律,同时他还预测在无穷大雷诺数下壁湍流的流向和展向速度脉动也存在对数律,而法向速度和雷诺应力为常数。这一预测结果后来得到了实验[14-15]和DNS[16-17]的证实。Townsend的附面涡模型(AEM)后来得到进一步发展[18-20],Marusic & Monty[21]最近对这方面的工作进行了综述。需要指出的是Townsend的附面涡只是统计意义上抽象的湍流相干结构模型,它可以包含实际观察到的条带和流向涡结构。
|
图 3 Townsend提出的壁湍流中的双锥模型[13] Fig.3 Double-cone model for wall-bounded turbulence proposed by Townsend[13] |
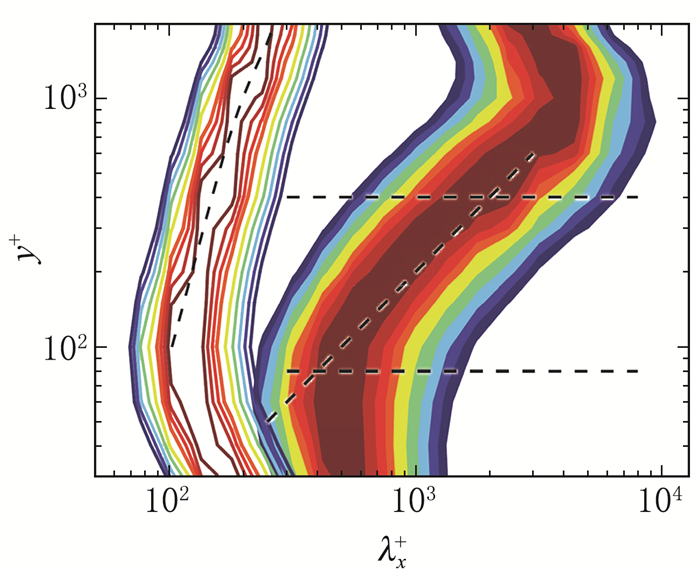
Townsend的附面涡模型与Richardson[22]的能量级串具有一定的相似性。能量由最大含能涡进入系统,然后经过惯性子区尺度间能量的逐级传递,最终至Kolmogorov尺度完成能量耗散[23]。对于壁湍流,这种能量级串的过程发生在不同的壁面高度。由于壁面的约束,使得不同的壁面高度处的含能尺度和耗散尺度随高度发生变化。Jiménez[24]分析了高雷诺数壁湍流中的湍动能谱和耗散能谱,发现含能尺度和Kolmogorov耗散尺度随着高度增大而增大,而且两个尺度间的分离也随高度增加而增加,表明在更高的壁面位置需要经历更长的能量级串历程(如图 4)。大部分能量在其生成高度完成耗散,但由于不同壁面高度处相干结构间的相互作用,能量也沿壁面高度发生传递。Townsend的附面涡模型反映了这一含能尺度的分布规律,同时,由于附面涡尺度随壁面距离发生变化,同一附面涡在较低高度是含能尺度,但在较高高度却可能也是惯性区尺度。
|
图 4 壁湍流中沿壁面高度的能量生成与耗散能谱[24] Fig.4 Energy production and dissipation spectra along wall- normal distance in wall-bounded turbulence[24] |
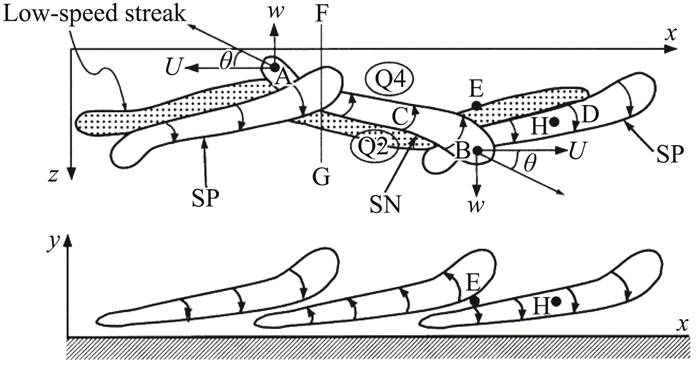
长期以来,壁湍流的实验和计算研究都局限于低雷诺数情形,因此对近壁区湍流相干结构的认识也最为充分。这一区域是由黏性主导的,其核心的相干结构是近壁条带和流向涡[4]。Kim等[9]首先尝试了用DNS的方法模拟湍流中的所有含能结构,给出了槽道湍流三维全流场数据和一系列湍流统计量,与以前的实验测量很好地吻合,证实了DNS是湍流研究的一种有效手段。DNS提供了湍流相干结构的全方位视角,实现了壁湍流的研究从方法驱动转变为数据驱动,大大促进了壁湍流的研究。为了显示三维计算流场中的相干结构,大量涡判据被提出,其中最为著名的是Jeong等[25]提出的基于速度梯度张量特征值的λ2判据。Jeong等[26]采用λ2判据对槽道近壁湍流中的流向涡结构进行条件平均后,发现流向涡结构沿流向呈9°倾斜角,正向旋转流向涡在展向呈4°偏斜角,反向旋转流向涡在展向呈-4°偏斜角。正、反向旋转流向涡首尾相接形成交错的涡串,位于其下的为条带结构(如图 5)。这是对条带和流向涡的相对空间分布的首次完整描述。近壁条带的长度为λx+≈1000,流向涡的长度为λx+≈300,二者组成的相干结构的展向间距为λz+≈100[27-28],它们以c+≈10的速度向下游传播[29]。
|
图 5 壁湍流中条带和流向涡结构示意图[26] Fig.5 Schematics of streaks and streamwise vortices in wall-bounded turbulence[26] |
Willmarth等[30-32]对壁湍流中的雷诺应力-u′v′进行了象限分析,依(u′, v′)的符号将雷诺应力分为Q1、Q2、Q3和Q4事件。旋转的流向涡在一侧将近壁的低速流体带到远壁区,形成上抛(Ejection),对应Q2事件;而在另一侧将远壁面的高速流体带到近壁区,形成下扫(Sweep),对应Q4事件。Q2和Q4事件是壁湍流雷诺应力的主要贡献者,且靠近壁面区(y+ < 12)由Q4事件主导,而远离壁面区由Q2事件主导[9]。这两个事件直接造成流向速度的法向梯度增加,形成壁面的高摩阻区域[33]。图 5给出的条带和流向涡相干结构的分布能够很好地解释壁湍流中包括上抛和下扫在内的诸多实验观测到的现象。
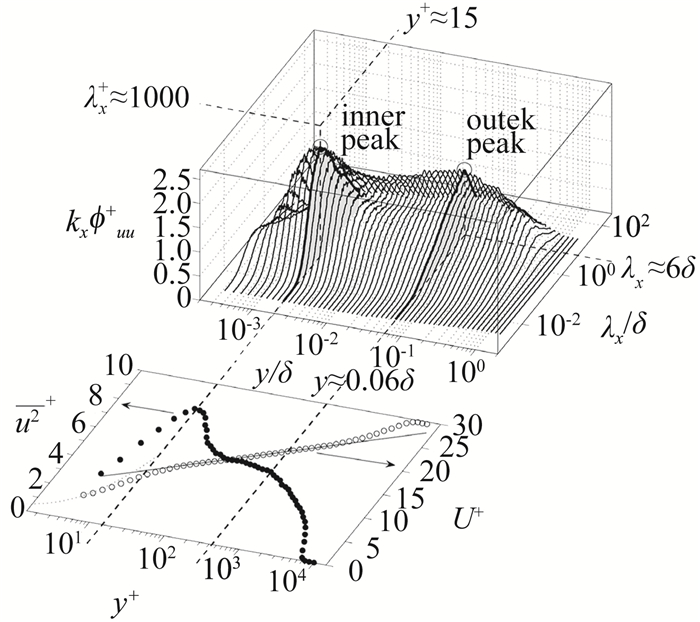
1.2 远壁区随着实验和计算技术的不断进步,壁湍流研究的雷诺数也在不断提高,如直接数值模拟的最高雷诺数已从Reτ=180上升到Reτ=8000[9, 16-17, 27, 34-36],实验雷诺数目前最高已达到Reτ=O(106)量级[15, 37]。从湍流统计量来看,高雷诺数湍流中最直观的反映是:湍流脉动量和能谱分布中除了内区峰值外,在外区也出现了一个新的峰值,且外区峰值能量随雷诺数增加逐渐升高(如图 6)[38]。这一现象预示着高雷诺数湍流中外区相干结构的作用不容忽视,因此自上世纪末它们成为壁湍流研究新的热点。
|
图 6 流向速度脉动的一维预乘谱和统计平均量[39] Fig.6 One-dimensional pre-multiplied spectra and statistical mean of streamwise velocity fluctuations[39] |
实验中很早就观察到在边界层的外缘存在大尺度的湍流结构,它们将边界层的湍流区和层流区沿法向分开,其大小为O(δ)量级[40]。Meinhart[41]通过PIV测量发现湍流边界层远壁区存在均匀的流向速度动量区,与近壁区的条带结构类似,但流向尺度为2δ~3δ,展向尺度为1δ~1.5δ,这一结构被命名为大尺度结构(LSM)。接着,Kim & Adrian[42]在Reτ=3175圆管流动测量中发现远壁区除了长度为2δ~3δ的大尺度结构外,还存在长度为14δ的超大尺度的湍流结构(VLSM)。Hutchins & Marusic[38]分析Reτ=O(106)大气边界层数据,也发现远壁区存在20δ的超大尺度结构,并将其称为超结构(Superstructures)。del lamo & Jiménez[43]对Reτ=550泊肃叶流动的DNS数据库分析发现其中存在长度大于5δ的超大尺度结构,且在更高雷诺数下变得更为清晰(如图 7)[44]。Monty等[45]对平板边界层流动、槽道流动和圆管流动中的大尺度/超大尺度结构进行了综合比较,发现大尺度/超大尺度结构广泛地存在于这些典型流动的对数区和外区(远壁区)。
远壁区的这些大尺度/超大尺度结构在统计意义上存在自相似性[46-52],与Townsend的附面涡模型描述情形一致。关于远壁区大尺度/超大尺度结构的形成,Adrian等[53]结合实验观测结果给出了解释:大量的流向涡聚集在一起会形成更大的涡团(如图 7),涡团的上抛和下扫形成了大尺度的均匀动量区,而多个均匀的动量区又会进一步聚集形成更长的均匀动量区,即所谓的“Bottom-up”效应。但最新数值实验表明,外区的大尺度结构可以不依赖近壁的小尺度结构而单独存在[54-55],因此“Bottom-up”可能并非远壁区大尺度/超大尺度结构生成的机制,后面将继续论述这一点。
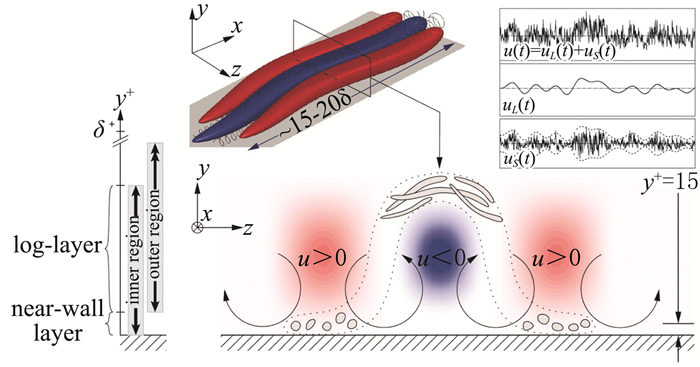
高雷诺数下,远壁区的这些大尺度/超大尺度结构对近壁区的动力学和统计学行为有着重要影响,主要表现为“叠加”(Superposition)和“调制”(Modulation)两种作用[39, 56-57],即所谓的“Top-down”效应。由于大尺度/超大尺度结构的存在,近壁区的湍流速度脉动的峰值即便在黏性尺度下也不是固定不变,而是随着雷诺数升高不断增加[58-59]。这些大尺度/超大尺度结构对壁面摩阻有着重要贡献,在Reτ≈2000时贡献率已达20%~30%[60]。远壁区的大尺度结构对近壁区的小尺度结构的幅值、频率、相位、对流速度等均有影响[39, 59, 61-65],且高速大尺度结构和低速大尺度结构对近壁区小尺度结构产生的影响是不同的[66-68]。据此,Marusic等[69-71]提出了一种近壁流动参数的预测模型,仅通过测量远壁区流动量便可预测出近壁区的流动参数(如图 8)。然而,Toh & Itano[72]认为近壁区的小尺度结构与远壁区的大尺度结构间的作用不是单方面的,而是相互依存影响的,即所谓的“Co-supporting”机制。目前,内外区不同尺度间的相互干扰仍是一个尚无共识的领域,有待进一步探索。
|
图 8 内区和外区湍流结构相互作用[69] Fig.8 Interaction between turbulence structures in the inner and outer regions[69] |
高雷诺数壁湍流是一个刚刚兴起的研究热点,里面有许多新的物理现象和开放性问题[73],感兴趣的读者可以参考最近的综述文章[5, 24, 37, 74-76]。
2 湍流结构的自维持湍流结构的自维持(SSP)是壁湍流中的又一个核心研究问题。Jiménez & Moin[77]考虑了小槽道内的湍流相干结构演化过程,发现存在一个最小流动单元(MFU),即Lx+≈300, Lz+≈100,当计算域大于这个流动单元时湍流能够持续存在,小于这个流动单元时湍流逐渐转变为层流。MFU的湍流结构表现出周期性的猝发,得到的近壁区的湍流统计量仍具有较高的精度。Jiménez & Pinelli[78]在MFU里采用衰减函数的方法人为地移除外区的湍流结构,发现近壁区的湍流仍能持续存在,且近壁区的湍流统计量与全尺度槽道情形吻合较好。这一数值实验证明了湍流近壁区相干结构的自维持过程可以独立于外区存在。Flore & Jiménez[79]进一步提出了对数区MFU,发现对于计算域受限的高雷诺数湍流,在某一高度yc下的湍流能谱和统计量可以模拟得较为准确,但在yc以上的湍流能谱和统计量误差较大,并且yc与对数区MFU的宽度成线性关系,而与其长度关系不大。这是由于计算域的宽度直接决定了能够模拟的“健康”湍流相干结构的大小,间接验证了Townsend的附面涡模型。对数区的湍流结构表现出与近壁区一样的猝发现象,但对数区的猝发周期并非常数,而是与湍流结构的大小成线性关系。
Mizuno & Jiménez[80]研究槽道湍流时人为地将壁面移除,在对数区施加约束条件,发现近壁区的湍流结构消失了,但对数区和外区的湍流结构和统计量几乎没有受到影响。这一结果说明,壁面的存在仅仅是提供湍流生成所需的平均速度剪切,且对数区的相干结构可以不依赖于近壁区相干结构独立存在。Hwang & Cossu[81]对此作了进一步证实。他们在对数区MFU中人为提高大涡模拟的Smagorinsky涡黏系数CS以抹去近壁区的湍流结构,发现对数区的湍流结构仍然能够自维持。Hwang & Cossu[54]在大槽道中采用同样的方法将近壁区和对数区的湍流结构都人为抹去,发现外区的大尺度湍流结构仍能自维持。由此说明壁湍流结构在各个壁面高度都能独立存在——壁湍流的自维持现象。
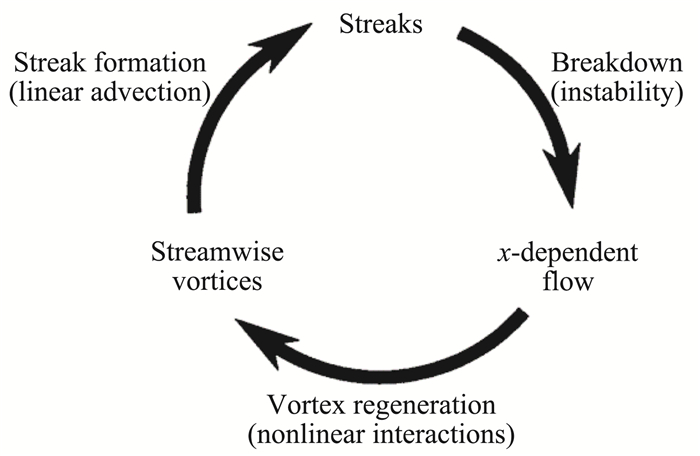
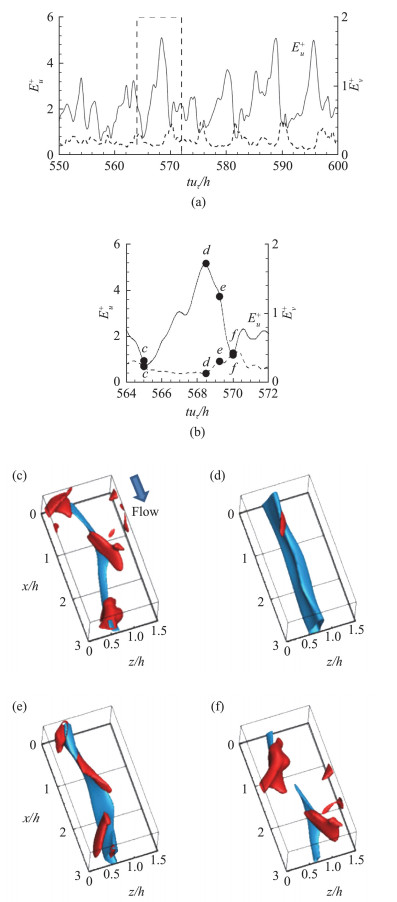
为了探寻壁湍流自维持的机理,Hamilton等[82]基于库特叶流动的MFU率先对缓冲区进行了研究,提出了壁湍流自维持的闭环(如图 9)。这个过程描述如下:1.由于“Lift-up”效应,流向涡激发出流向均匀的条带结构(线性过程);2.流向均匀的条带由于瞬态增长或二次失稳变得蜿蜒最终破碎;3.具有流向梯度的流场在非线性作用下生成流向涡(非线性过程)。湍流的自维持将前面实验和计算中所观察到的条带和流向涡紧紧地联系在了一起,两者互相依存,缺一不可。最近发现,缓冲区的自维持过程同样也适用于对数区和外区湍流相干结构[55, 83], 破坏三个环节中的任何一环都会造成流动的层流化。图 10展示了对数区MFU中的一个典型的自维持过程。最近,Yang等[84]发现自维持过程也可以在Kolmogorov尺度上发生,但是此过程的能量生成量相对于能量级串过程的能量传递量是很小的。
|
图 10 对数区的自维持过程[83]: (a, b)流向和法向速度脉动能量随时间的演化;(c-f)典型时刻的条带和流向涡结构 Fig.10 SSP in the logarithmic region[83]: (a, b) time evolution of streamwise and wall-normal velocity fluctuation energy; (c-f) streaks and streamwise vortices at typical instances |
伴随湍流的自维持过程的是湍流的猝发现象,它对应着条带的破碎和流向涡的生成[24],这也正是Kline等[1]在实验中观察到的氢气泡线的突然上升破碎过程。猝发过程需要区别于流向涡的上抛和下扫,也要区别于由于湍流结构对流引起固定测点的信号变化[85-87]。统计意义上,湍流结构在近壁缓冲区的猝发周期为Tb+≈200~300[79],对数区为Tb≈2λz/uτ[79, 83],外区为Tb≈3δ/uτ[83]。从能量的角度看,它是高能的条带将能量传递给流向涡的过程[88-89];从动力系统的角度看,它对应着流动从湍流的平衡态沿其不稳定包络逃逸的过程[90]。
基于Townsend的附面涡模型,最近Hwang[50]提出了一个适用于内区、对数区和外区的湍流相干结构的统一框架:在给定壁面高度y,存在尺度为λx ≈10λz,λz ≈10y的条带(流向速度脉动量)和尺度为λx ≈2~3λz,λz ≈1~2y的流向涡结构(法向和展向速度脉动量);对于近壁区,y=10ν/uτ;对于外区,y=δ。每个壁面高度的条带和流向涡形成自维持的闭环。实验和计算中观察到的LSM和VLSM可以分别看作是外区的流向涡和条带结构。
2.1 条带的生成继Kline等[1]后,条带作为壁湍流的基本结构受到广泛重视。实验测量[28]和DNS[9]均发现近壁区这些条带的展向间距为λz+≈100,流向长度为λx+≈1000。远离壁面,条带的尺度逐渐变大,直至在外区形成长度为O(10δ)、宽度为O(δ)的超条带(Superstreaks)。关于条带的形成机制和条带的尺度选择机理成为一个重要的研究点。
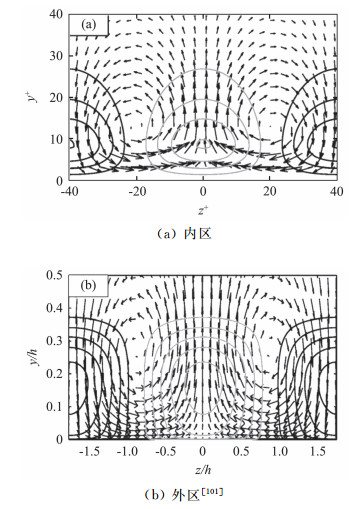
对泊肃叶流动和边界层流动,经典的线性稳定性理论预示的最不稳定模态是二维的;而对于库特叶流动和圆管流动更是不存在不稳定的模态。因此,基于小扰动线化N-S方程的特征值分析无法解释条带的尺度选择问题。由于线化N-S方程具有非正则性,其特征模态并非正交,这样即便对于线性稳定的系统(无穷长时间后任何初始小扰动都会衰减为零),也会存在扰动能量的瞬态增长(代数增长)过程,而且最优瞬态增长可以达到2~3个数量级,足以触发流动的非线性机制造成流动失稳[91-96]。最优瞬态增长中主要存在两种初始扰动放大机制:一种是初始扰动涡结构由逆着来流向顺着来流转换,以从平均流中提取能量(“Orr”机制)[93];另一种是流向均匀的低能流向涡激发流向均匀的高能条带的过程(“Lift-up”机制)[97-98]。二维扰动主要通过“Orr”机制实现能量瞬态增长,而三维扰动则主要通过“Lift-up”机制实现能量瞬态增长[93]。Butler & Farrell[97]采用Reynolds-Tiederman速度型来近似Reτ=180全湍流的平均流,通过选取合适的优化时间长度,发现通过“Lift-up”机制激发的最优条带的展向间距为λz+≈100。del lamo & Jiménez[99]考虑了高雷诺数泊肃叶流动(Reτ=2×104)中的最优瞬态增长,并在线化的N-S方程中通过可变黏性系数加入了雷诺应力贡献,分析发现存在两个最优的能量放大区:一个是λz+≈100(对应近壁区的条带),另一个是λz≈4δ(对应外区的超条带)[100-101]。图 11展示了内、外区的最优扰动放大结构,在两者之间还存在一系列连续过渡的最优扰动尺度,对应于对数区的条带。内区峰值大小在内尺度标度下几乎不变,而外区峰值的大小在外尺度标度下随雷诺数增加线性升高[100-101]。Hwang & Cossu[102]通过线化N-S方程对随机力和谐振力的瞬态响应分析获得了同样的结果。
|
图 11 最优扰动放大结构 Fig.11 The most amplified structures |
虽然线性瞬态增长较成功地解释了条带的展向间距选择,但是最优增长条带在流向是均匀的,并无条带流向尺度的选择。Rabin等[103]考虑了非线性框架下的最优瞬态增长,发现最优放大条带具有三维局域性,在流向也有尺度的选择。Waleffe[104]从非线性N-S方程不变解的鞍-结点分叉的角度研究了条带的尺度选择,发现鞍-节点处λx+≈273.7,λz+≈105.5,与近壁流向涡尺度相当。
2.2 流向涡的生成流向涡的生成主要有两类解释[105]:一种是“Parent-offspring”机制;另一种是条带不稳定性(“Streak-instability”)机制。“Parent-offspring”机制更具有唯象性,需要预先有流向涡存在;而条带不稳定性机制是基于稳定性理论,不需要预先有流向涡存在,但需要有条带存在。
Brooke & Hanratty[106]通过观察展向和法向二维涡截面,发现流场中的流向涡通过下扫在壁面生成流向涡量进而演化成新的流向涡,类似于偶极子涡在壁面的反弹过程[107]。然而现在的研究更多地发现壁面的存在并不是壁湍流自维持所必需的[80],说明基于壁面的涡生成机制不是主要的。Zhou等[108]通过直接数值模拟观测到当流向涡超过一定的强度后,会在边部生成新的二次流向涡,然后二次流向涡又会生成新的三次流向涡。
从湍流自维持的角度,条带不稳定性机制更被接受。饱和的条带具有不同的失稳模态:反对称模态的失稳对应着交错排列的流向涡结构;对称模态的失稳对应着发夹涡结构,其中反对称模态失稳更为常见[109-110],也更为危险[111]。Schoppa & Hussain[112]详细讨论了基于当地稳定性理论的饱和条带失稳形成流向涡的过程。Schoppa & Hussain[86]发现湍流中实际满足失稳条件的条带所占比例很小,大部分条带是通过瞬态增长途径实现失稳的,称为条带的瞬态增长(STG)机制。图 12展示了通过STG生成的流向交错排列的流向涡,与DNS结果十分类似(见图 5)。
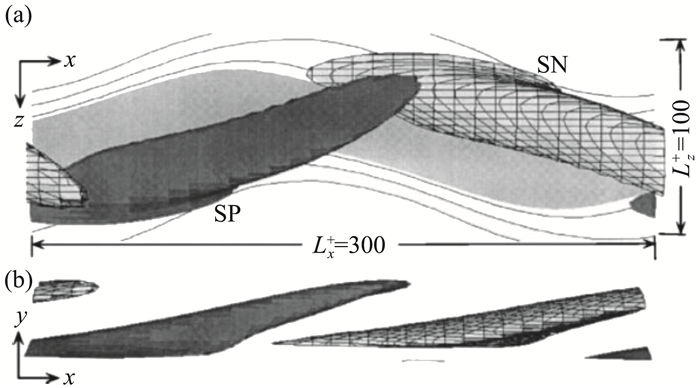
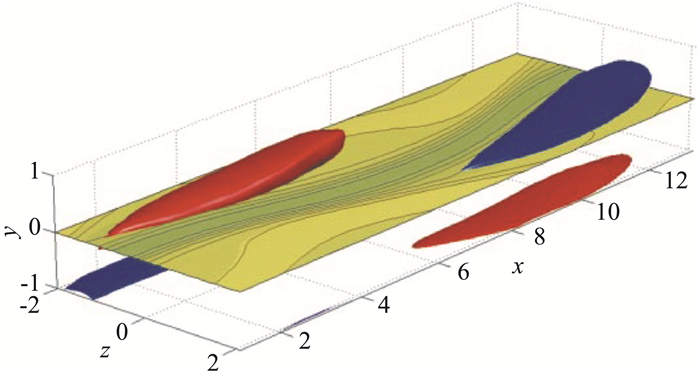
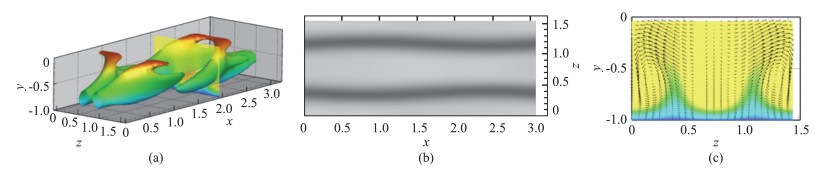
3 精确相干态意识到湍流中的自维持后,Waleffe[110, 113]尝试获得一个简化的数学模型来描述这一过程。他将滑移壁面条件下的N-S方程分解成流向速度部分(条带)和法向、展向速度部分(流向涡)。由于流向均匀的条带无法失稳形成流向涡,因此引入一个人为的体积力以维持流向涡。然后,Waleffe[113]逐渐降低体积力的大小至零,发现由于非线性的作用系统中出现了两个自维持的状态。Waleffe[114]进一步将这两个自维持态延拓到无滑移壁面条件下,获得了泊肃叶流动中的首个N-S方程的非线性解(又称不变解,见图 13)。这一非线性解具有蜿蜒的流向条带和伴随两侧的流向涡结构,以一固定的相速度向下游传播(行波解),在相对坐标系下解的结构不发生变化,与Jeong等[26]从DNS湍流场提取的湍流相干结构(见图 5)极为相似,因此这个非线性解被普遍认为是对湍流的自维持过程的精确描述[75]。鉴于此,Waleffe率先将这个非线性解命名为精确相干态(ECS,又称精确相干结构)[114]。从动力系统的角度看,ECS的种类有很多,包括湍流的平衡态、行波解、周期轨道及其包络等,湍流即是在这些ECS间穿梭[115-116]。Jiménez等[87]将ECS和MFU及全尺度湍流近壁区的统计量和猝发特征进行了比较,发现ECS可以作为一个简化的系统进行湍流研究。
将ECS沿雷诺数进行延拓就可以获得一条分叉曲线,转折点为鞍-结点,是下支的鞍点与上支的结点汇聚的地方。在给定雷诺数下,上支ECS摩阻比下支ECS高很多,流向涡强度更大、条带更蜿蜒[114]。从动力系统角度看上支ECS是湍流区的平衡态/准平衡态,湍流运动轨迹在它附近停留一段时间后再沿其不稳定包络转移到另一个平衡态/准平衡态。下支ECS位于湍流与层流的分界面(Edge of Chaos),至少有一个不稳定的特征方向,从一侧施加扰动可以快速地到达湍流区,而从另一侧施加扰动可以快速地到达层流态(如图 14)。如果下支ECS有且只有一个不稳定的特征方向,它也被称为边界态(Edge State)[117]。可见,ECS不仅是充分发展湍流里的基本相干结构,它也是转捩过程中的基本相干结构。需要指出的是,真正意义上的首个ECS是Nagata[118]分析库特叶流动的亚临界失稳时通过对泰勒-库特叶流动进行同伦变换获得的,随后Clever & Busse[119]在研究热对流问题时也通过同伦变换获得了相同的解,它与Waleffe[114]从自维持角度发现的泊肃叶流动中的ECS是同一族解,统称为NBCW解。同样采用人为体积力的方法[113],Faisst & Eckhardt[120]和Wedin & Kerswell[121]获得了圆管流动中的NBCW解。这样,ECS就将各种剪切流动中的充分发展湍流与转捩过程统一在了同一分析框架中。由于ECS通常是不稳定的,实际流动中很难观测到,但最终Hof等[122]通过精细的实验首次在圆管中拍到了ECS,证实了精确相干态的真实性。
ECS是从湍流自维持的角度考虑N-S方程的非线性解,而实际中这样含有流向涡与条带的三维相干结构在其它的理论中也有发现。比如,Hall & Smith[124]研究无穷大雷诺数下T-S波与流向涡的非线性作用时,发展了一套涡波干扰(VWI)理论。通过VWI理论获得的解其实是ECS在无穷大雷诺数下的渐近态[125]。McKeon & Sharma[126]将N-S方程的非线性作用视为一个随机力效应,发展了湍流的Resolvent分析方法,可以较好地反映壁湍动中一系列的相干结构[76]。最近,他们发现只需要几个Resolvent模态就可以构造出ECS[127-128]。
3.1 全湍流区Kawahara & Kida[129]获得了库特叶流动中的首个周期轨道,完整地再现了湍流自维持中条带的生成破碎和流向涡的生长衰减过程(如图 15)。从相空间看,湍流在这个周期轨道上停留了大量的时间,因此仅此单个轨道周期内的统计量(平均速度和速度脉动均分根)就与湍流统计量十分吻合。Jiménez & Simens[130]在MFU中通过衰减函数移除外区某一高度Δ+以上的湍流结构后获得了近壁区的低维度相干结构,与ECS十分相似:当Δ+>50时,此相干结构为一行波解;当Δ+>60,此相干结构为含有两个频率的周期轨道。Toh & Itano[131]采用打靶法发现了泊肃叶流动中的一个周期轨道。这个周期轨道是一个边界态,由两个典型的状态构成:一个状态只含有一个条带;另一个状态含有两个条带,两个状态的转换对应了猝发过程。Kreilos等[132]在渐近吸气边界层中也发现了类似的非定常边界态,并作了更细致的研究。低雷诺数壁湍流中像这样的ECS已有大量报道[133-135]。
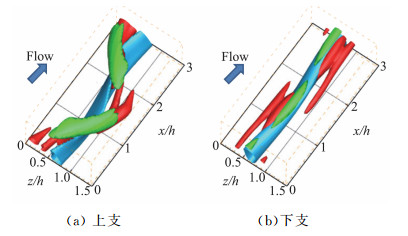
由于外区的湍流结构存在自维持[54],Hwang等[136]尝试寻找外区的ECS。他们在Reτ≈1000泊肃叶流动中采用过度提高Smagorinsky涡黏系数CS的方法分离出外区的大尺度结构,并以此作为二分法的初始流场,进而获得了外区湍流的ECS。同样地,上支解相比于下支解对应的条带更蜿蜒,且流向涡强度更高(图 16)。
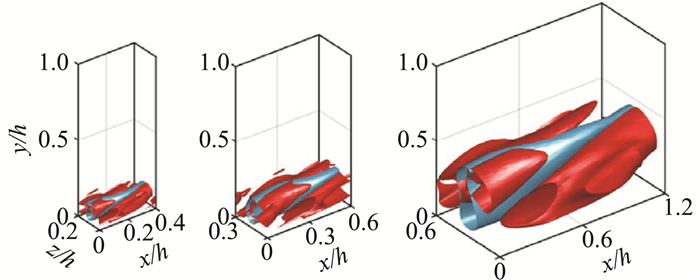
最近,Yang等[137]发现Hwang等[136]获得的ECS与NBCW解其实是同一族解不同的分支。Rawat等[138]将NBCW解延拓到更高雷诺数后,发现在固定槽道大小下,即Lx+≈250,Lz+≈100,这些解的速度脉动均分根峰值在黏性尺度标度下并不是固定不变的,而是不断地向外区移动。由此说明NBCW解其实是对应于外区的湍流结构。Yang等[137]从大涡模拟计算的高雷诺数湍流中直接提取了法向局域化的边界态,然后通过延拓获得了N-S方程对应的法向局域化的ECS(图 17)。在高雷诺数下,这族解在鞍-结点处对应的计算域宽度维持在Lz+≈50,相速度为c+≈11,而且黏性尺度标度下近壁区统计量在高雷诺数时趋于固定,与近壁区湍流相干结构的特性一致。最近,Doohan等[139]为描述库特叶流动近壁区在高雷诺数下的渐近行为,发展了一个剪切模型,获得了与VWI理论相当的近壁湍流ECS预测结果。据此,Yang等[137]提出了与“Bottom-up”机制相反的湍流相干结构生成顺序:当雷诺数高于某一临界值时,首先是尺度为δ的外区相干结构开始出现(在黏性尺度下λz+≈50);随着雷诺数的进一步升高,新的λz+≈50的相干结构开始出现,而这些新的相干结构更靠近壁面。这族ECS与Townsend的附面涡模型具有很好的相似性。类似的具有自相似特征的ECS也出现在了库特叶流动中[140-141],甚至是任意剪切湍流中[142-144]。这一方面说明了ECS的普遍性;另一方面也说明壁湍流中壁面的主要作用确实只是提供速度的平均剪切。
ECS可以具有不同的对称性。NBCW解满足平移-翻转对称性,对应于条带的反对称不稳定模态,因而获得的ECS含有沿流向交错排列的流向涡结构。Gibson等[135]通过在泊肃叶流动中引入不同的对称性,获得了一系列新的ECS。Itano & Generalis[145]和Deguchi & Nagata[146]获得了库特叶流动中具有展向镜像对称性的ECS,与发卡涡类似。Nagata & Deguchi[147]和Shekar & Graham[148]在泊肃叶流动中引入了展向镜像对称,也获得了发卡涡形式的ECS。图 18展示了发卡涡形式的ECS[149]。
当然,N-S方程描述的是一个高维的动力系统,其中存在的ECS非常多,所幸的是典型ECS的不稳定包络的个数并不太多,如果能够找到所有的这些典型的ECS构成的湍流的骨架,那么湍流的动力学行为就能很好地得以描述了[115]。Kawahara等[150]对湍流中ECS的重要性作了全面的综述。
3.2 转捩区从ECS的角度看,转捩区湍流与充分发展湍流是相关联的,二者统一于非线性的N-S方程,这区别于传统的基于线化N-S方程的转捩研究。对于典型的壁湍流,库特叶流动和圆管流动是线性稳定的[151-152],泊肃叶流动的临界雷诺数是Rec=5772[153-154]。然而,通常实验中在Re≈1000就会发生转捩[155]。不可压边界层流动的临界雷诺数为Rec=520[156-157],当来流噪声较高时实验中也能观察到较低雷诺数的转捩。由于这些典型流动的转捩雷诺数要低于线性稳定性预测的失稳雷诺数,因此称为亚临界转捩;另外,由于这种转捩过程没有二维T-S波的增长过程,而是直接出现沿展向变化的条带结构,因此也称为Bypass转捩[158]。这种转捩途径给传统的基于小扰动的线性稳定性分析带来了挑战[159]。
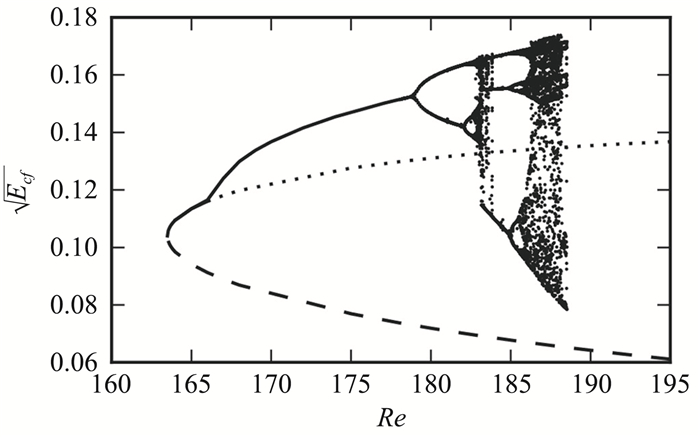
从动力系统的角度看,流动可以看作由层流态经过一系列的Hopf分叉形成新的平衡态/准平衡态直至成为湍流,这也是早期Landau的观点[160]。然而,研究发现亚临界转捩并不是源自层流态连续的Hopf分叉,而是源于前面叙述的NBCW解的鞍-结点分叉[161-162]。图 19显示了库特叶流动经过一系列的分叉(包括鞍-结点分叉、Hopf分叉、倍周期分叉和危机分叉)从NBCW解发展为湍流的过程。对于泊肃叶流动,存在二次平衡态[163-165],其失稳雷诺数为Rec=2900[166-167]。Ehrenstein & Koch[168]基于此二次平衡态失稳获得了三次平衡态,进而得到了更低的临界雷诺数Rec≈1000,然而,这个三次平衡态的存在有可能是由于他们计算中过度的截断误差引起的虚假解[147]。进一步地,对于线性稳定的库特叶流动和圆管流动,流动无法通过首次失稳获得二次平衡态。为此,Cherhabili & Ehrenstein[169]将泊肃叶流动中的二次平衡态延拓到库特叶流动中,发现其为展向均匀而流向局域化的孤立波形态;并基于此二次平衡态的失稳获得了三次平衡态,同样具有流向局域化特征,是不同于NBCW解的一族新的解。因此,从目前的认识来看,对于亚临界转捩,相对于层流态的直接失稳,湍流态更易源自鞍-结点分叉形成的ECS,也即Nagata所谓的无穷远处的分叉。考虑鞍-结点分叉后,对于泊肃叶流动、库特叶流动和圆管流动,其临界雷诺数分别降低到Rec=977[170], Rec=125[104, 118],Rec=1250[120],均与实验观测到的临界雷诺数比较接近。
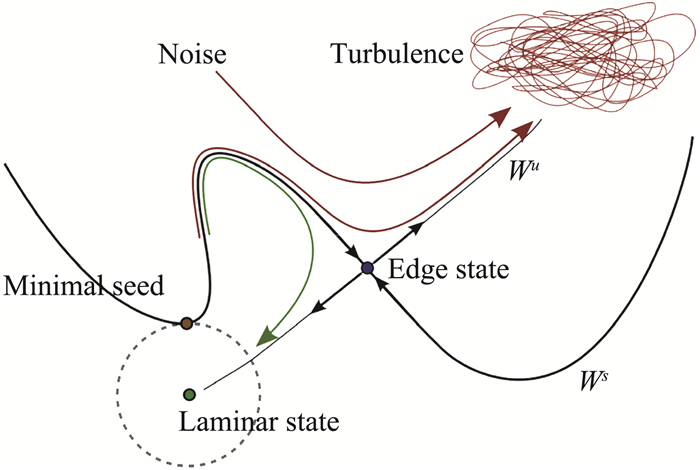
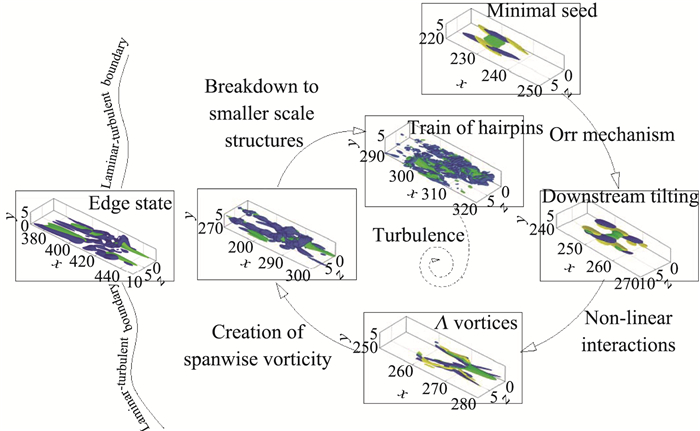
鞍-结点分叉曲线下支的ECS(尤其是边界态)与亚临界转捩最为相关,其条带和流向涡的幅值与雷诺数分别满足Re0和Re-1的标度率[125, 172-173],因此在高雷诺数下,来流中只需要很小的扰动就可以激发出自维持的ECS,进而使流动沿着ECS的不稳定包络进入湍流。由此生成的湍流的生命周期随雷诺数呈指数增长[174-176]。由于ECS广泛地存在于各种剪切流动中[141-144, 177],这种转捩途径具有普适性,据此Cherubini等[178]提出了一条完全非线性的转捩途径(图 20)。实际流动中,非线性最优扰动是触发湍流的最小能量种子(Minimum Seeds)[103, 179-185],它也是由条带和流向涡构成,与边界态非常接近。从动力系统的角度看触发湍流的最小能量种子实际上是位于湍流与层流的边界靠近湍流态的一侧,在相空间里距离湍流态最近(图 20);相对而言,线性最优扰动位于湍流与层流的边界靠近层流态一侧,因此其对湍流的激发效率要低于最小能量种子[103]。
与最小能量种子形态一致,实际亚临界转捩过程中出现的扰动形态通常是局域化的,如湍斑[186-188]、湍带[189-192]等,它们将流动分成湍流与层流相间的状态。与之对应的是位于层流/湍流边界上的局域化的、不依赖于计算域大小的边界态,如泊肃叶流动[193-195]、库特叶流动[196-200],圆管流动[201-204]、边界层流动[123, 205-206]、渐近吸气边界层流动[207-208]等。图 21展示了圆管流动中一个典型的局域化的边界态(又称Puff)。对这些局域化的边界态的分析有助于深入理解转捩的动力学行为:比如,Reetz等[200]发现库特叶流动中倾斜的湍带其实是源自于NBCW解。圆管流动中的亚临界转捩过程也由于Puff的发现变得更为明晰:在低雷诺数下Puff是不随时间发展的平衡态,但随着雷诺数的升高,Puff在流向开始扩展,最终充斥整个圆管形成充分发展湍流[209-213]。
4 总结与展望壁湍流是一个复杂的多尺度系统,湍流相干结构的发现及研究极大地提升了我们对壁湍流的认识。经过一个多世纪的研究,近壁区的湍流行为被认识得已较为透彻。当前,高雷诺数壁湍流成为新的研究热点,一些新的流动现象,尤其是壁湍流中含能尺度的多样性问题更为凸显。基于目前对壁湍流相干结构的认识,其最核心的特征是不同壁面高度相干结构的自相似和给定壁面高度下相干结构的自维持。为此,关于近壁区湍流相干结构的一些性质、规律可以为对数区和外区的湍流相干结构的研究提供很好的借鉴。从湍流相干结构出发,Townsend的附面涡模型已经在壁湍流的数值模拟方面展现出了一定的生机。但与此同时,我们也应该看到,尺度分离/尺度干扰将是不可压高雷诺数壁湍流研究中不可规避的重要问题。
长期以来,湍流与转捩作为流体力学两个独立的分支分别开展着各自的研究,ECS的发现让非线性动力系统理论架起了统一研究二者的桥梁。亚临界转捩(乃至一般转捩的后期)湍斑/湍带中的相干结构与充分发展湍流中的相干结构是十分类似的,它们所对应的ECS也是一致的,均是由条带和流向涡构成的自维持单元。认识这些基本的ECS的性质有望后续精确地进行转捩路径和湍流运动轨迹的预测。Barkley[213]已经对圆管流动的亚临界转捩展开了卓有成效地模型预测。目前也有学者开始针对ECS开展湍流/转捩相关的控制研究,并获得了一定的效果[214-216]。但是我们也必须认识到湍流的高维特性,从动力系统角度实现湍流的预测仍然需要大量的工作。
最后,壁湍流相干结构的认识目前主要集中在不可压流动中,而可压流动中涉及到马赫数效应、温度效应等,其相干结构尤其是ECS可能出现不同于不可压情形的动力学行为,值得未来研究。
| [1] |
KLINE B S J, REYNOLDS W C, SCHRAUBT F A, et al. The structure of turbulent boundary layers[J]. Journal of Fluid Mechanics, 1967, 30: 741-773. |
| [2] |
WALLACE J M. Highlights from 50 years of turbulent boundary layer research[J]. Journal of Turbulence, 2012, 13: 1-70. |
| [3] |
HEAD M R, BANDYOPADHYAY P. New aspects of turbulent boundary-layer structure[J]. Journal of Fluid Mechanics, 1981, 107: 297-338. |
| [4] |
ROBINSON S. Coherent motions in the turbulent boundary Layer[J]. Annual Review of Fluid Mechanics, 1991, 23: 601-639. |
| [5] |
ADRIAN R J. Hairpin vortex organization in wall turbulence[J]. Physics of Fluids, 2007, 19(4): 041301. |
| [6] |
WU X, MOIN P. Direct numerical simulation of turbulence in a nominally zero-pressure-gradient flat-plate boundary layer[J]. Journal of Fluid Mechanics, 2009, 630: 5-41. |
| [7] |
POPE S B. Turbulent flows[M]. Cambridge University Press, 2000.
|
| [8] |
MILLIKAN C B. A critical discussion of turbulent flows in channels and circular tubes[C]//Proceedings of the fifth International Congress for Applied Mechanics, 1938.
|
| [9] |
KIM J, MOIN P, MOSER R. Turbulence statistics in fully developed channel flow at low Reynolds number[J]. Journal of Fluid Mechanics, 1987, 177: 133-166. |
| [10] |
DEGRAAFF D B, EATON J K. Reynolds-number scaling of the flat-plate turbulent boundary layer[J]. Journal of Fluid Mechanics, 2000, 422: 319-346. |
| [11] |
SHE Z S, CHEN X, HUSSAIN F. Quantifying wall turbulence via a symmetry approach:A Lie group theory[J]. Journal of Fluid Mechanics, 2017, 827: 322-356. |
| [12] |
TOWNSEND A A. The structure of turbulent shear flow[M]. 1st edn. Cambridge University Press, 1956.
|
| [13] |
TOWNSEND A A. The structure of turbulent shear flow[M]. 2nd edn. Cambridge University Press, 1976.
|
| [14] |
NICKELS T B, MARUSIC I, HAFEZ S, et al. Evidence of the k1-1 law in a high-Reynolds-number turbulent boundary layer[J]. Physical Review Letters, 2005, 95(7): 074501. |
| [15] |
MARUSIC I, MONTY J P, HULTMARK M, et al. On the logarithmic region in wall turbulence[J]. Journal of Fluid Mechanics, 2013, 716: R3. |
| [16] |
BERNARDINI M, PIROZZOLI S, ORLANDI P. Velocity statistics in turbulent channel flow up to Reτ=4000[J]. Journal of Fluid Mechanics, 2014, 742: 171-191. |
| [17] |
LEE M, MOSER R D. Direct numerical simulation of turbulent channel flow up to Reτ≈5200[J]. Journal of Fluid Mechanics, 2015, 774: 395-415. |
| [18] |
PERRY A E, CHONG M S. On the mechanism of wall turbulence[J]. Journal of Fluid Mechanics, 1982, 119: 173-217. |
| [19] |
PERRY A E, MARUSIC I. A wall-wake model for the turbulence structure of boundary layers. Part 1. Extension of the attached eddy hypothesis[J]. Journal of Fluid Mechanics, 1995, 298: 361-388. |
| [20] |
WOODCOCK J D, MARUSIC I. The statistical behaviour of attached eddies[J]. Physics of Fluids, 2015, 27(1): 015104. |
| [21] |
MARUSIC I, MONTY J P. Attached eddy model of wall turbulence[J]. Annual Review of Fluid Mechanics, 2019, 51: 49-74. |
| [22] |
RICHARDSON L F. Weather prediction by numerical process[M]. 2nd edn. Cambridge University Press, 1922.
|
| [23] |
KOLMOGOROV A N. The local structure of turbulence in incompressible viscous fluid for very large Reynolds numbers[J]. Proceedings of the Royal Society A, 1991, 434(1890): 9-13. |
| [24] |
JIMÉNEZ J. Cascades in wall-bounded turbulence[J]. Annual Review of Fluid Mechanics, 2012, 44: 27-45. |
| [25] |
JEONG J, HUSSAIN F. On the identification of a vortex[J]. Journal of Fluid Mechanics, 1995, 285: 69-94. |
| [26] |
JEONG J, HUSSAIN F, SCHOPPA W, et al. Coherent structures near the wall in a turbulent channel flow[J]. Journal of Fluid Mechanics, 1997, 332: 185-214. |
| [27] |
HOYAS S, JIMENEZ J. Scaling of the velocity fluctuations in turbulent channels up to Reτ=2003[J]. Physics of Fluids, 2006, 18(1): 011702. |
| [28] |
SMITH C R, METZLER S P. The characteristics of low-speed streaks in the near-wall region of a turbulent boundary layer[J]. Journal of Fluid Mechanics, 1983, 129: 27-54. |
| [29] |
KIM J, HUSSAIN F. Propagation velocity of perturbations in turbulent channel flow[J]. Physics of Fluids A, 1992, 5(3): 695-706. |
| [30] |
WILLMARTH W W, LU S S. Structure of the Reynolds stress near the wall[J]. Journal of Fluid Mechanics, 1972, 55(1): 65-92. |
| [31] |
LU S S, WILLMARTH W W. Measurements of the structure of the Reynolds stress in a turbulent boundary layer[J]. Journal of Fluid Mechanics, 1973, 60: 481-511. |
| [32] |
WALLACE J M. Quadrant analysis in turbulence research:History and evolution[J]. Annual Review of Fluid Mechanics, 2016, 48: 131-158. |
| [33] |
KRAVCHENKO A G, CHOI H, MOIN P. On the relation of near-wall streamwise vortices to wall skin friction in turbulent boundary layers[J]. Physics of Fluids A, 1993, 5(12): 3307-3309. |
| [34] |
MOSER R D, KIM J, MANSOUR N N. Direct numerical simulation of turbulent channel flow up to Reτ=590[J]. Physics of Fluids, 1999, 11(4): 943-945. |
| [35] |
LOZANO-DURÁN A, JIMÉNEZ J. Effect of the computational domain on direct simulations of turbulent channels up to Reτ=4200[J]. Physics of Fluids, 2014, 26(1): 011702. |
| [36] |
YAMAMOTO Y, TSUJI Y. Numerical evidence of logarithmic regions in channel flow at Reτ=8000[J]. Physical Review Fluids, 2018, 3(1): 012602. |
| [37] |
MARUSIC I, MCKEON B J, MONKEWITZ P A, et al. Wall-bounded turbulent flows at high Reynolds numbers:Recent advances and key issues[J]. Physics of Fluids, 2010, 22(6): 065103. |
| [38] |
HUTCHINS N, MARUSIC I. Evidence of very long meandering features in the logarithmic region of turbulent boundary layers[J]. Journal of Fluid Mechanics, 2007, 579: 1-28. |
| [39] |
HUTCHINS N, MARUSIC I. Large-scale influences in near-wall turbulence[J]. Philosophical Transactions of the Royal Society A, 2007, 365(1852): 647-664. |
| [40] |
KOVASZNAY L S G, KIBENS V, BLACKWELDER R F. Large-scale motion in the intermittent region of a turbulent boundary layer[J]. Journal of Fluid Mechanics, 1970, 41: 283-325. |
| [41] |
MEINHART C D, ADRIAN R J. On the existence of uniform momentum zones in a turbulent boundary layer[J]. Physics of Fluids, 1995, 7(4): 694-696. |
| [42] |
KIM K C, ADRIAN R J. Very large-scale motion in the outer layer[J]. Physics of Fluids, 1999, 11(2): 417-422. |
| [43] |
DEL ÁLAMO J C, JIMÉNEZ J. Spectra of the very large anisotropic scales in turbulent channels[J]. Physics of Fluids, 2003, 15(6): L41. |
| [44] |
LOZANO-DURÁN A, JIMÉNEZ J. Time-resolved evolution of coherent structures in turbulent channels:Characterization of eddies and cascades[J]. Journal of Fluid Mechanics, 2014, 759: 432-471. |
| [45] |
MONTY J P, HUTCHINS N, NG H C H, et al. A comparison of turbulent pipe, channel and boundary layer flows[J]. Journal of Fluid Mechanics, 2009, 632: 431-442. |
| [46] |
DEL ÁLAMO J C, JIMÉNEZ J, ZANDONADE P, et al. Self-similar vortex clusters in the turbulent logarithmic region[J]. Journal of Fluid Mechanics, 2006, 561: 329-358. |
| [47] |
LOZANO-DURÁN A, FLORES O, JIMÉNEZ J. The three-dimensional structure of momentum transfer in turbulent channels[J]. Journal of Fluid Mechanics, 2012, 694: 100-130. |
| [48] |
DENNIS D J C, NICKELS T B. Experimental measurement of large-scale three-dimensional structures in a turbulent boundary layer. Part 1. Vortex packets[J]. Journal of Fluid Mechanics, 2011, 673: 180-217. |
| [49] |
DENNIS D J C, NICKELS T B. Experimental measurement of large-scale three-dimensional structures in a turbulent boundary layer. Part 2. Long structures[J]. Journal of Fluid Mechanics, 2011, 673: 218-244. |
| [50] |
HWANG Y. Statistical structure of self-sustaining attached eddies in turbulent channel flow[J]. Journal of Fluid Mechanics, 2015, 767: 254-289. |
| [51] |
HELLSTRÖM L H O, MARUSIC I, SMITS A J. Self-similarity of the large-scale motions in turbulent pipe flow[J]. Journal of Fluid Mechanics, 2016, 792: R1. |
| [52] |
BAARS W J, HUTCHINS N, MARUSIC I. Self-similarity of wall-attached turbulence in boundary layers[J]. Journal of Fluid Mechanics, 2017, 823: R2. |
| [53] |
ADRIAN R J, MEINHART C D, TOMKINS C D. Vortex organization in the outer region of the turbulent boundary layer[J]. Journal of Fluid Mechanics, 2000, 422: 1-54. |
| [54] |
HWANG Y, COSSU C. Self-sustained process at large scales in turbulent channel flow[J]. Physical Review Letters, 2010, 105(4): 044505. |
| [55] |
DE GIOVANETTI M, SUNG H J, HWANG Y. Streak instability in turbulent channel flow:The seeding mechanism of large-scale motions[J]. Journal of Fluid Mechanics, 2017, 832: 483-513. |
| [56] |
BANDYOPADHYAY P R, HUSSAIN A K M F. The coupling between scales in shear flows[J]. Physics of Fluids, 1984, 27(9): 2221-2228. |
| [57] |
ABE H, KAWAMURA H, CHOI H. Very large-scale structures and their effects on the wall shear-stress fluctuations in a turbulent channel flow up to Reτ=640[J]. Journal of Fluids Engineering, 2004, 126(5): 835-843. |
| [58] |
MARUSIC I, MATHIS R, HUTCHINS N. High Reynolds number effects in wall turbulence[J]. International Journal of Heat and Fluid Flow, 2010, 31(3): 418-428. |
| [59] |
AGOSTINI L, LESCHZINER M A. On the influence of outer large-scale structures on near-wall turbulence in channel flow[J]. Physics of Fluids, 2014, 26(7): 075107. |
| [60] |
DE GIOVANETTI M, HWANG Y, CHOI H. Skin-friction generation by attached eddies in turbulent channel flow[J]. Journal of Fluid Mechanics, 2016, 808: 511-538. |
| [61] |
MATHIS R, HUTCHINS N, MARUSIC I. Large-scale amplitude modulation of the small-scale structures in turbulent boundary layers[J]. Journal of Fluid Mechanics, 2009, 628: 311-337. DOI:10.1017/S0022112009006946 |
| [62] |
GANAPATHISUBRAMANI B, HUTCHINS N, MONTY J P, et al. Amplitude and frequency modulation in wall turbulence[J]. Journal of Fluid Mechanics, 2012, 712: 61-91. DOI:10.1017/jfm.2012.398 |
| [63] |
JACOBI I, MCKEON B J. Phase relationships between large and small scales in the turbulent boundary layer[J]. Experiments in Fluids, 2013, 54(3): 1481. DOI:10.1007/s00348-013-1481-y |
| [64] |
TALLURU K M, BAIDYA R, HUTCHINS N, et al. Amplitude modulation of all three velocity components in turbulent boundary layers[J]. Journal of Fluid Mechanics, 2014, 746: R1. DOI:10.1017/jfm.2014.132 |
| [65] |
BAARS W J, TALLURU K M, HUTCHINS N, et al. Wavelet analysis of wall turbulence to study large-scale modulation of small scales[J]. Experiments in Fluids, 2015, 56(10): 188. DOI:10.1007/s00348-015-2058-8 |
| [66] |
AGOSTINI L, LESCHZINER M, GAITONDE D. Skewness-induced asymmetric modulation of small-scale turbulence by large-scale structures[J]. Physics of Fluids, 2016, 28(1): 015110. |
| [67] |
AGOSTINI L, LESCHZINER M. On the validity of the quasi-steady-turbulence hypothesis in representing the effects of large scales on small scales in boundary layers[J]. Physics of Fluids, 2016, 28(4): 045102. DOI:10.1063/1.4944735 |
| [68] |
ZHANG C, CHERNYSHENKO S I. Quasisteady quasihomogeneous description of the scale interactions in near-wall turbulence[J]. Physical Review Fluids, 2016, 1(1): 014401. DOI:10.1103/PhysRevFluids.1.014401 |
| [69] |
MARUSIC I, MATHIS R, HUTCHINS N. Predictive model for wall-bounded turbulent flow[J]. Science, 2010, 329(5988): 193-196. DOI:10.1126/science.1188765 |
| [70] |
MATHIS R, HUTCHINS N, MARUSIC I. A predictive inner-outer model for streamwise turbulence statistics in wall-bounded flows[J]. Journal of Fluid Mechanics, 2011, 681: 537-566. DOI:10.1017/jfm.2011.216 |
| [71] |
MATHIS R, MARUSIC I, CHERNYSHENKO S I, et al. Estimating wall-shear-stress fluctuations given an outer region input[J]. Journal of Fluid Mechanics, 2013, 715: 163-180. DOI:10.1017/jfm.2012.508 |
| [72] |
TOH S, ITANO T. Interaction between a large-scale structure and near-wall structures in channel flow[J]. Journal of Fluid Mechanics, 2005, 524: 249-262. DOI:10.1017/S002211200400237X |
| [73] |
MCKEON B J, SREENIVASAN K R. Introduction:Scaling and structure in high Reynolds number wall-bounded flows[J]. Philosophical Transactions of the Royal Society A, 2007, 365(1852): 635-646. DOI:10.1098/rsta.2006.1952 |
| [74] |
SMITS A J, MCKEON B J, MARUSIC I. High-Reynolds number wall turbulence[J]. Annual Review of Fluid Mechanics, 2011, 43: 353-375. DOI:10.1146/annurev-fluid-122109-160753 |
| [75] |
JIMÉNEZ J. Coherent structures in wall-bounded turbulence[J]. Journal of Fluid Mechanics, 2018, 842: P1. DOI:10.1017/jfm.2018.144 |
| [76] |
MCKEON B J. The engine behind (wall) turbulence:Perspectives on scale interactions[J]. Journal of Fluid Mechanics, 2017, 817: P1. DOI:10.1017/jfm.2017.115 |
| [77] |
JIMÉNEZ J, MOIN P. The minimal flow unit in near-wall turbulence[J]. Journal of Fluid Mechanics, 1990, 225: 213-240. |
| [78] |
JIMÉNEZ J, PINELLI A. The autonomous cycle of near-wall turbulence[J]. Journal of Fluid Mechanics, 1999, 389: 335-359. DOI:10.1017/S0022112099005066 |
| [79] |
FLORES O, JIMÉNEZ J. Hierarchy of minimal flow units in the logarithmic layer[J]. Physics of Fluids, 2010, 22(7): 071704. DOI:10.1063/1.3464157 |
| [80] |
MIZUNO Y, JIMÉNEZ J. Wall turbulence without walls[J]. Journal of Fluid Mechanics, 2013, 723: 429-455. DOI:10.1017/jfm.2013.137 |
| [81] |
HWANG Y, COSSU C. Self-sustained processes in the logarithmic layer of turbulent channel flows[J]. Physics of Fluids, 2011, 23(6): 061702. DOI:10.1063/1.3599157 |
| [82] |
HAMILTON J M, KIM J, WALEFFE F. Regeneration mechanisms of near-wall turbulence structures[J]. Journal of Fluid Mechanics, 1995, 287: 317-348. DOI:10.1017/S0022112095000978 |
| [83] |
HWANG Y, BENGANA Y. Self-sustaining process of minimal attached eddies in turbulent channel flow[J]. Journal of Fluid Mechanics, 2016, 795: 708-738. DOI:10.1017/jfm.2016.226 |
| [84] |
YANG Q, WILLIS A P, HWANG Y. Energy production and self-sustained turbulence at the Kolmogorov scale in Couette flow[J]. Journal of Fluid Mechanics, 2018, 834: 531-554. DOI:10.1017/jfm.2017.704 |
| [85] |
KIM J, SPALART P R. Scaling of the bursting frequency in turbulent boundary layers[J]. Physics of Fluids, 1987, 30(11): 3326-3328. DOI:10.1063/1.866464 |
| [86] |
SCHOPPA W, HUSSAIN F. Coherent structure generation in near-wall turbulence[J]. Journal of Fluid Mechanics, 2002, 453: 57-108. DOI:10.1017/S002211200100667X |
| [87] |
JIMÉNEZ J, KAWAHARA G, SIMENS M P, et al. Characterization of near-wall turbulence in terms of equilibrium and "bursting" solutions[J]. Physics of Fluids, 2005, 17(1): 015105. DOI:10.1063/1.1825451 |
| [88] |
CHERUBINI S, DE PALMA P. Nonlinear optimal perturbations in a Couette flow:Bursting and transition[J]. Journal of Fluid Mechanics, 2013, 716: 251-279. DOI:10.1017/jfm.2012.544 |
| [89] |
FARANO M, CHERUBINI S, ROBINET J C, et al. Optimal bursts in turbulent channel flow[J]. Journal of Fluid Mechanics, 2017, 817: 35-60. DOI:10.1017/jfm.2017.107 |
| [90] |
ITANO T, TOH S. The dynamics of bursting process in wall turbulence[J]. Journal of the Physical Society of Japan, 2001, 70(3): 703-716. DOI:10.1143/JPSJ.70.703 |
| [91] |
ELLINGSEN T, PALM E. Stability of linear flow[J]. Physics of Fluids, 1975, 18(4): 487-488. |
| [92] |
LANDAHL M T. A note on an algebraic instability of inviscid parallel shear flows[J]. Journal of Fluid Mechanics, 1980, 98: 243-251. DOI:10.1017/S0022112080000122 |
| [93] |
BUTLER K M, FARRELL B F. Three-dimensional optimal perturbations in viscous shear flow[J]. Physics of Fluids A, 1992, 4(8): 1637-1650. DOI:10.1063/1.858386 |
| [94] |
TREFETHEN L N, TREFETHEN A E, REDDY S C, et al. Hydrodynamic stability without eigenvalues[J]. Science, 1993, 261(5121): 578-584. DOI:10.1126/science.261.5121.578 |
| [95] |
REDDY S C, HENNINGSON D S. Energy growth in viscous channel flows[J]. Journal of Fluid Mechanics, 1993, 252: 209-238. DOI:10.1017/S0022112093003738 |
| [96] |
RESHOTKO E. Transient growth:A factor in bypass transition[J]. Physics of Fluids, 2001, 13(5): 1067-1075. DOI:10.1063/1.1358308 |
| [97] |
BUTLER K M, FARRELL B F. Optimal perturbations and streak spacing in wall-bounded turbulent shear flow[J]. Physics of Fluids A, 1992, 5(3): 774-777. |
| [98] |
BRANDT L. The lift-up effect:The linear mechanism behind transition and turbulence in shear flows[J]. European Journal of Mechanics, B/Fluids, 2014, 47: 80-96. DOI:10.1016/j.euromechflu.2014.03.005 |
| [99] |
DEL ÁLAMO J C, JIMÉNEZ J. Linear energy amplification in turbulent channels[J]. Journal of Fluid Mechanics, 2006, 559: 205-213. DOI:10.1017/S0022112006000607 |
| [100] |
PUJALS G, GARCíA-VILLALBA M, COSSU C, et al. A note on optimal transient growth in turbulent channel flows[J]. Physics of Fluids, 2009, 21(1): 015109. DOI:10.1063/1.3068760 |
| [101] |
COSSU C, PUJALS G, DEPARDON S. Optimal transient growth and very large-scale structures in turbulent boundary layers[J]. Journal of Fluid Mechanics, 2009, 619: 79-94. DOI:10.1017/S0022112008004370 |
| [102] |
HWANG Y, COSSU C. Linear non-normal energy amplification of harmonic and stochastic forcing in the turbulent channel flow[J]. Journal of Fluid Mechanics, 2010, 664: 51-73. DOI:10.1017/S0022112010003629 |
| [103] |
RABIN S M E, CAULFIELD C P, KERSWELL R R. Triggering turbulence efficiently in plane Couette flow[J]. Journal of Fluid Mechanics, 2012, 712: 244-272. DOI:10.1017/jfm.2012.417 |
| [104] |
WALEFFE F. Homotopy of exact coherent structures in plane shear flows[J]. Physics of Fluids, 2003, 15(6): 1517-1534. DOI:10.1063/1.1566753 |
| [105] |
PANTON R L. Overview of the self-sustaining mechanisms of wall turbulence[J]. Progress in Aerospace Sciences, 2001, 37(4): 341-383. DOI:10.1016/S0376-0421(01)00009-4 |
| [106] |
BROOKE J W, HANRATTY T J. Origin of turbulence-producing eddies in a channel flow[J]. Physics of Fluids A, 1992, 5(4): 1011-1022. |
| [107] |
ORLANDI P. Vortex dipole rebound from a wall[J]. Physics of Fluids, 1990, 2(8): 1429-1436. DOI:10.1063/1.857591 |
| [108] |
ZHOU J, ADRIAN R J, BALACHANDAR S, et al. Mechanisms for generating coherent packets of hairpin vortices in channel flow[J]. Journal of Fluid Mechanics, 1999, 387: 353-396. DOI:10.1017/S002211209900467X |
| [109] |
WALEFFE F. Hydrodynamic stability and turbulence:Beyond transients to a self-sustaining process[J]. Studies in Applied Mathematics, 1995, 95(3): 319-343. DOI:10.1002/sapm1995953319 |
| [110] |
WALEFFE F. On a self-sustaining process in shear flows[J]. Physics of Fluids, 1997, 9(4): 883-900. DOI:10.1063/1.869185 |
| [111] |
ANDERSSON P, BRANDT L, BOTTARO A, et al. On the breakdown of boundary layer streaks[J]. Journal of Fluid Mechanics, 2001, 428: 29-60. DOI:10.1017/S0022112000002421 |
| [112] |
SCHOPPA W, HUSSAIN F. Coherent structure dynamics in near-wall turbulence[J]. Fluid Dynamics Research, 2000, 26(2): 119-139. DOI:10.1016/S0169-5983(99)00018-0 |
| [113] |
WALEFFE F. Three-dimensional coherent states in plane shear flows[J]. Physical Review Letters, 1998, 81(19): 4140-4143. DOI:10.1103/PhysRevLett.81.4140 |
| [114] |
WALEFFE F. Exact coherent structures in channel flow[J]. Journal of Fluid Mechanics, 2001, 435: 93-102. DOI:10.1017/S0022112001004189 |
| [115] |
GIBSON J F, HALCROW J, CVITANOVIC' P. Visualizing the geometry of state space in plane Couette flow[J]. Journal of Fluid Mechanics, 2008, 611: 107-130. DOI:10.1017/S002211200800267X |
| [116] |
SURI B, TITHOF J, GRIGORIEV R O, SCHATZ M F. Forecasting fluid flows using the geometry of turbulence[J]. Physical Review Letters, 2017, 118(11): 114501. DOI:10.1103/PhysRevLett.118.114501 |
| [117] |
SKUFCA J D, YORKE J A, ECKHARDT B. Edge of chaos in a parallel shear flow[J]. Physical Review Letters, 2006, 96(17): 174101. DOI:10.1103/PhysRevLett.96.174101 |
| [118] |
NAGATA M. Three-dimensional finite-amplitude solutions in plane Couette flow:Bifurcation from infinity[J]. Journal of Fluid Mechanics, 1990, 217: 519-527. DOI:10.1017/S0022112090000829 |
| [119] |
CLEVER R M, BUSSE F H. Three-dimensional convection in a horizontal fluid layer subjected to a constant shear[J]. Journal of Fluid Mechanics, 1992, 234: 511-527. DOI:10.1017/S0022112092000892 |
| [120] |
FAISST H, ECKHARDT B. Traveling waves in pipe flow[J]. Physical Review Letters, 2003, 91(22): 224502. DOI:10.1103/PhysRevLett.91.224502 |
| [121] |
WEDIN H, KERSWELL R R. Exact coherent structures in pipe flow:Travelling wave solutions[J]. Journal of Fluid Mechanics, 2004, 508: 333-371. DOI:10.1017/S0022112004009346 |
| [122] |
HOF B, VAN DOORNE C W H, WESTERWEEL J, et al. Experimental observation of nonlinear travelling waves in turbulent pipe flow[J]. Science, 2004, 305: 1594-1598. DOI:10.1126/science.1100393 |
| [123] |
KHAPKO T, KREILOS T, SCHLATTER P, et al. Edge states as mediators of bypass transition in boundary-layer flows[J]. Journal of Fluid Mechanics, 2016, 801: R2. DOI:10.1017/jfm.2016.434 |
| [124] |
HALL P, SMITH F T. On strongly nonlinear vortex/wave interactions in boundary-layer transition[J]. Journal of Fluid Mechanics, 1991, 227: 641-666. DOI:10.1017/S0022112091000289 |
| [125] |
HALL P, SHERWIN S. Streamwise vortices in shear flows:Harbingers of transition and the skeleton of coherent structures[J]. Journal of Fluid Mechanics, 2010, 661: 178-205. DOI:10.1017/S0022112010002892 |
| [126] |
MCKEON B J, SHARMA A S. A critical-layer framework for turbulent pipe flow[J]. Journal of Fluid Mechanics, 2010, 658: 336-382. DOI:10.1017/S002211201000176X |
| [127] |
SHARMA A S, MOARREF R, MCKEON B J, et al. Low-dimensional representations of exact coherent states of the Navier-Stokes equations from the resolvent model of wall turbulence[J]. Physical Review E, 2016, 93(2): 021102. DOI:10.1103/PhysRevE.93.021102 |
| [128] |
ROSENBERG K, MCKEON B J. Efficient representation of exact coherent states of the Navier-Stokes equations using resolvent analysis[J]. Fluid Dynamics Research, 2019, 51(1): 011401. DOI:10.1088/1873-7005/aab1ab |
| [129] |
KAWAHARA G, KIDA S. Periodic motion embedded in plane Couette turbulence:Regeneration cycle and burst[J]. Journal of Fluid Mechanics, 2001, 449: 291-300. DOI:10.1017/S0022112001006243 |
| [130] |
JIMÉNEZ J, SIMENS M P. Low-dimensional dynamics of a turbulent wall flow[J]. Journal of Fluid Mechanics, 2001, 435: 81-91. DOI:10.1017/S0022112001004050 |
| [131] |
TOH S, ITANO T. A periodic-like solution in channel flow[J]. Journal of Fluid Mechanics, 2003, 481: 67-76. DOI:10.1017/S0022112003003768 |
| [132] |
KREILOS T, VEBLE G, SCHNEIDER T M, et al. Edge states for the turbulence transition in the asymptotic suction boundary layer[J]. Journal of Fluid Mechanics, 2013, 726: 100-122. DOI:10.1017/jfm.2013.212 |
| [133] |
VISWANATH D. Recurrent motions within plane Couette turbulence[J]. Journal of Fluid Mechanics, 2007, 580: 339-358. DOI:10.1017/S0022112007005459 |
| [134] |
HALCROW J, GIBSON J F, CVITANOVIĆ P, Viswanath D. Heteroclinic connections in plane Couette flow[J]. Journal of Fluid Mechanics, 2009, 621: 365-376. DOI:10.1017/S0022112008005065 |
| [135] |
GIBSON J F, HALCROW J, CVITANOVI P. Equilibrium and travelling-wave solutions of plane Couette flow[J]. Journal of Fluid Mechanics, 2009, 638: 243-266. DOI:10.1017/S0022112009990863 |
| [136] |
HWANG Y, WILLIS A P, COSSU C. Invariant solutions of minimal large-scale structures in turbulent channel flow for Reτ up to 1000[J]. Journal of Fluid Mechanics, 2016, 802: R1. DOI:10.1017/jfm.2016.470 |
| [137] |
YANG Q, WILLIS A P, HWANG Y. Exact coherent states of attached eddies in channel flow[J]. Journal of Fluid Mechanics, 2019, 862: 1029-1059. DOI:10.1017/jfm.2018.1017 |
| [138] |
RAWAT S, COSSU C, HWANG Y, et al. On the self-sustained nature of large-scale motions in turbulent Couette flow[J]. Journal of Fluid Mechanics, 2015, 782: 515-540. DOI:10.1017/jfm.2015.550 |
| [139] |
DOOHAN P, WILLIS A P, HWANG Y. Shear stress-driven flow:The state space of near-wall turbulence as Reτ→∞[J]. Journal of Fluid Mechanics, 2019, 874: 606-638. DOI:10.1017/jfm.2019.472 |
| [140] |
DEGUCHI K, HALL P. Free-stream coherent structures in growing boundary layers:A link to near-wall streaks[J]. Journal of Fluid Mechanics, 2015, 778: 451-484. DOI:10.1017/jfm.2015.314 |
| [141] |
ECKHARDT B, ZAMMERT S. Small scale exact coherent structures at large Reynolds numbers in plane Couette flow[J]. Nonlinearity, 2018, 31(2): R66-R77. DOI:10.1088/1361-6544/aa9462 |
| [142] |
BLACKBURN H M, HALL P, SHERWIN S J. Lower branch equilibria in Couette flow:The emergence of canonical states for arbitrary shear flows[J]. Journal of Fluid Mechanics, 2013, 726: R2. DOI:10.1017/jfm.2013.254 |
| [143] |
SEKIMOTO A, JIMÉNEZ J. Vertically localised equilibrium solutions in large-eddy simulations of homogeneous shear flow[J]. Journal of Fluid Mechanics, 2017, 827: 225-249. DOI:10.1017/jfm.2017.450 |
| [144] |
HALL P. Vortex-wave interaction arrays:A sustaining mechanism for the log layer?[J]. Journal of Fluid Mechanics, 2018, 850: 46-82. DOI:10.1017/jfm.2018.425 |
| [145] |
ITANO T, GENERALIS S C. Hairpin vortex solution in planar Couette flow:A tapestry of knotted vortices[J]. Physical Review Letters, 2009, 102(11): 114501. DOI:10.1103/PhysRevLett.102.114501 |
| [146] |
DEGUCHI K, NAGATA M. Traveling hairpin-shaped fluid vortices in plane Couette flow[J]. Physical Review E, 2010, 82(5): 056325. DOI:10.1103/PhysRevE.82.056325 |
| [147] |
NAGATA M, DEGUCHI K. Mirror-symmetric exact coherent states in plane Poiseuille flow[J]. Journal of Fluid Mechanics, 2013, 735: R4. DOI:10.1017/jfm.2013.515 |
| [148] |
SHEKAR A, GRAHAM M D. Exact coherent states with hairpin-like vortex structure in channel flow[J]. Journal of Fluid Mechanics, 2018, 849: 76-89. DOI:10.1017/jfm.2018.409 |
| [149] |
PARK J S, SHEKAR A, GRAHAM M D. Bursting and critical layer frequencies in minimal turbulent dynamics and connections to exact coherent states[J]. Physical Review Fluids, 2018, 3(1): 014611. DOI:10.1103/PhysRevFluids.3.014611 |
| [150] |
KAWAHARA G, UHLMANN M, VAN VEEN L. The significance of simple invariant solutions in turbulent flows[J]. Annual Review of Fluid Mechanics, 2012, 44: 203-225. DOI:10.1146/annurev-fluid-120710-101228 |
| [151] |
ROMANOV V A. Stability of plane-parallel Couette flow[J]. Functional Analysis and Its Applications, 1973, 7(2): 137-146. DOI:10.1007/BF01078886 |
| [152] |
LESSEN M, SADLER S G, LIU T Y. Stability of pipe Poiseuille flow[J]. Physics of Fluids, 1968, 11(7): 1404-1409. DOI:10.1063/1.1692122 |
| [153] |
THOMAS L H. The stability of plane poiseuille flow[J]. Physical Review, 1953, 91(4): 780-783. DOI:10.1103/PhysRev.91.780 |
| [154] |
ORSZAG S A. Accurate solution of the Orr-Sommerfeld stability equation[J]. Journal of Fluid Mechanics, 1971, 50: 689-703. DOI:10.1017/S0022112071002842 |
| [155] |
NISHIOKA M, ASAI M. Some observations of the subcritical transition in plane Poiseuille flow[J]. Journal of Fluid Mechanics, 1985, 150: 441-450. DOI:10.1017/S0022112085000210 |
| [156] |
JORDINSON R. The flat plate boundary layer. Part 1. Numerical integration of the Orr-Sommerfeld equation[J]. Journal of Fluid Mechanics, 1970, 43: 801-811. DOI:10.1017/S0022112070002756 |
| [157] |
SCHMID P J, HENNINGSON D S. Stability and transition in shear flows[M]. Springer-Verlag, 2001.
|
| [158] |
KLEBANOFF P S, TIDSTROM K D, SARGENT L M. The three-dimensional nature of boundary-layer instability[J]. Journal of Fluid Mechanics, 1962, 12: 1-34. DOI:10.1017/S0022112062000014 |
| [159] |
ECKERT M. The troublesome birth of hydrodynamic stability theory:Sommerfeld and the turbulence problem[J]. European Physical Journal H, 2010, 35(1): 29-51. DOI:10.1140/epjh/e2010-00003-3 |
| [160] |
LANDAU L D, LIFSHITZ E M. Fluid mechanics[M]. Pergamon Press, 1959.
|
| [161] |
ECKHARDT B, FAISST H, SCHMIEGEL A, et al. Dynamical systems and the transition to turbulence in linearly stable shear flows[J]. Philosophical Transactions of the Royal Society A, 2008, 366(1868): 1297-1315. DOI:10.1098/rsta.2007.2132 |
| [162] |
MANNEVILLE P. Transition to turbulence in wall-bounded flows:Where do we stand?[J]. Mechanical Engineering Reviews, 2016, 3(2): 15-00684. |
| [163] |
CHEN T S, JOSEPH D D. Subcritical bifurcation of plane Poiseuille flow[J]. Journal of Fluid Mechanics, 1973, 58: 337-351. DOI:10.1017/S0022112073002624 |
| [164] |
ORSZAG S A, KELLS L C. Transition to turbulence in plane Poiseuille and plane Couette flow[J]. Journal of Fluid Mechanics, 1980, 96: 159-205. DOI:10.1017/S0022112080002066 |
| [165] |
ORSZAG S A, PATERA A T. Secondary instability of wall-bounded shear flows[J]. Journal of Fluid Mechanics, 1983, 128: 347-385. DOI:10.1017/S0022112083000518 |
| [166] |
ZAHN J P, TOOMRE J, SPIEGEL E A, et al. Nonlinear cellular motions in Poiseuille channel flow[J]. Journal of Fluid Mechanics, 1974, 64: 319-346. DOI:10.1017/S0022112074002424 |
| [167] |
SOIBELMAN I, MEIRON D I. Finite-amplitude bifurcations in plane Poiseuille flow:Two-dimensional Hopf bifurcation[J]. Journal of Fluid Mechanics, 1991, 229: 389-416. DOI:10.1017/S0022112091003075 |
| [168] |
EHRENSTEIN U, KOCH W. Three-dimensional wavelike equilibrium states in plane Poiseuille flow[J]. Journal of Fluid Mechanics, 1991, 228: 111-148. |
| [169] |
CHERHABILI A, EHRENSTEIN U. Finite-amplitude equilibrium states in plane Couette flow[J]. Journal of Fluid Mechanics, 1997, 342: 159-177. DOI:10.1017/S0022112097005661 |
| [170] |
PARK J S, GRAHAM M D. Exact coherent states and connections to turbulent dynamics in minimal channel flow[J]. Journal of Fluid Mechanics, 2015, 782: 430-454. DOI:10.1017/jfm.2015.554 |
| [171] |
KREILOS T, ECKHARDT B. Periodic orbits near onset of chaos in plane Couette flow[J]. Chaos, 2012, 22(4): 047505. DOI:10.1063/1.4757227 |
| [172] |
WANG J, GIBSON J, WALEFFE F. Lower branch coherent states in shear flows:Transition and control[J]. Physical Review Letters, 2007, 98(20): 6-8. |
| [173] |
VISWANATH D. The critical layer in pipe flow at high Reynolds number[J]. Philosophical Transactions of the Royal Society A, 2009, 367(1888): 561-576. DOI:10.1098/rsta.2008.0225 |
| [174] |
MOEHLIS J, ECKHARDT B, FAISST H. Fractal lifetimes in the transition to turbulence[J]. Chaos, 2004, 14(4): S11. DOI:10.1063/1.1821751 |
| [175] |
HOF B, WESTERWEEL J, SCHNEIDER T M, et al. Finite lifetime of turbulence in shear flows[J]. Nature, 2006, 443(7107): 59-62. DOI:10.1038/nature05089 |
| [176] |
ECKHARDT B, SCHNEIDER T M, HOF B, et al. Turbulence transition in pipe flow[J]. Annual Review of Fluid Mechanics, 2007, 39: 447-468. DOI:10.1146/annurev.fluid.39.050905.110308 |
| [177] |
DEGUCHI K. Self-sustained states at Kolmogorov microscale[J]. Journal of Fluid Mechanics, 2015, 781: R6. DOI:10.1017/jfm.2015.514 |
| [178] |
CHERUBINI S, DE PALMA P, ROBINET J C, et al. A purely nonlinear route to transition approaching the edge of chaos in a boundary layer[J]. Fluid Dynamics Research, 2012, 44(3): 031404. DOI:10.1088/0169-5983/44/3/031404 |
| [179] |
PRINGLE C C T, KERSWELL R R. Using nonlinear transient growth to construct the minimal seed for shear flow turbulence[J]. Physical Review Letters, 2010, 105(15): 1-4. |
| [180] |
CHERUBINI S, DE PALMA P, ROBINET J C, et al. Rapid path to transition via nonlinear localized optimal perturbations in a boundary-layer flow[J]. Physical Review E, 2010, 82(6): 066302. DOI:10.1103/PhysRevE.82.066302 |
| [181] |
CHERUBINI S, DE PALMA P, ROBINET J C, et al. The minimal seed of turbulent transition in the boundary layer[J]. Journal of Fluid Mechanics, 2011, 689: 221-253. DOI:10.1017/jfm.2011.412 |
| [182] |
MONOKROUSOS A, BOTTARO A, BRANDT L, et al. Nonequilibrium thermodynamics and the optimal path to turbulence in shear flows[J]. Physical Review Letters, 2011, 106(13): 134502. DOI:10.1103/PhysRevLett.106.134502 |
| [183] |
BIAU D, BOTTARO A. An optimal path to transition in a duct[J]. Philosophical Transactions of the Royal Society A, 2009, 367(1888): 529-544. DOI:10.1098/rsta.2008.0191 |
| [184] |
FARANO M, CHERUBINI S, ROBINET J C, et al. Hairpin-like optimal perturbations in plane Poiseuille flow[J]. Journal of Fluid Mechanics, 2015, 775: R2. DOI:10.1017/jfm.2015.320 |
| [185] |
KERSWELL R R. Nonlinear nonmodal stability theory[J]. Annual Review of Fluid Mechanics, 2018, 50: 319-345. DOI:10.1146/annurev-fluid-122316-045042 |
| [186] |
LUNDBLADH A, JOHANSSON A V. Direct simulation of turbulent spots in plane Couette flow[J]. Journal of Fluid Mechanics, 1991, 229: 499-516. DOI:10.1017/S0022112091003130 |
| [187] |
LEVIN O, HENNINGSON D S. Turbulent spots in the asymptotic suction boundary layer[J]. Journal of Fluid Mechanics, 2007, 584: 397-413. DOI:10.1017/S0022112007006544 |
| [188] |
WU X, MOIN P, WALLACE J M, et al. Transitional-turbulent spots and turbulent-turbulent spots in boundary layers[J]. Proceedings of the National Academy of Sciences, 2017, 114(27): E5292-E5299. DOI:10.1073/pnas.1704671114 |
| [189] |
TUCKERMAN L S, BARKLEY D. Patterns and dynamics in transitional plane Couette flow[J]. Physics of Fluids, 2011, 23(4): 041301. DOI:10.1063/1.3580263 |
| [190] |
TUCKERMAN L S, KREILOS T, SCHROBSDORFF H, et al. Turbulent-laminar patterns in plane Poiseuille flow[J]. Physics of Fluids, 2014, 26(11): 114103. DOI:10.1063/1.4900874 |
| [191] |
DUGUET Y, SCHLATTER P. Oblique laminar-turbulent interfaces in plane shear flows[J]. Physical Review Letters, 2013, 110(3): 034502. DOI:10.1103/PhysRevLett.110.034502 |
| [192] |
CHANTRY M, TUCKERMAN L S, BARKLEY D. Turbulent-laminar patterns in shear flows without walls[J]. Journal of Fluid Mechanics, 2016, 791: R8. DOI:10.1017/jfm.2016.92 |
| [193] |
GIBSON J F, BRAND E. Spanwise-localized solutions of planar shear flows[J]. Journal of Fluid Mechanics, 2014, 745: 25-61. DOI:10.1017/jfm.2014.89 |
| [194] |
ZAMMERT S, ECKHARDT B. A spotlike edge state in plane Poiseuille flow[J]. Proceedings in Applied Mathematics and Mechanics, 2014, 14(1): 591-592. DOI:10.1002/pamm.201410283 |
| [195] |
ZAMMERT S, ECKHARDT B. Streamwise decay of localized states in channel flow[J]. Physical Review E, 2016, 94(4): 041101. |
| [196] |
DUGUET Y, SCHLATTER P, HENNINGSON D S. Localized edge states in plane Couette flow[J]. Physics of Fluids, 2009, 21(11): 111701. DOI:10.1063/1.3265962 |
| [197] |
SCHNEIDER T M, GIBSON J F, BURKE J. Snakes and ladders:Localized solutions of plane Couette flow[J]. Physical Review Letters, 2010, 104(10): 104501. DOI:10.1103/PhysRevLett.104.104501 |
| [198] |
SCHNEIDER T M, MARINC D, ECKHARDT B. Localized edge states nucleate turbulence in extended plane Couette cells[J]. Journal of Fluid Mechanics, 2010, 646: 441-451. DOI:10.1017/S0022112009993144 |
| [199] |
BRAND E, GIBSON J F. A doubly localized equilibrium solution of plane Couette flow[J]. Journal of Fluid Mechanics, 2014, 750: R3. DOI:10.1017/jfm.2014.285 |
| [200] |
REETZ F, KREILOS T, SCHNEIDER T M. Exact invariant solution reveals the origin of self-organized oblique turbulent-laminar stripes[J]. Nature Communications, 2019, 10(1): 1-6. DOI:10.1038/s41467-018-07882-8 |
| [201] |
RITTER P, ZAMMERT S, SONG B, et al. Analysis and modeling of localized invariant solutions in pipe flow[J]. Physical Review Fluids, 2018, 3(1): 013901. DOI:10.1103/PhysRevFluids.3.013901 |
| [202] |
DUGUET Y, WILLIS A P, KERSWELL R R. Slug genesis in cylindrical pipe flow[J]. Journal of Fluid Mechanics, 2010, 663: 180-208. DOI:10.1017/S0022112010003435 |
| [203] |
AVILA M, MELLIBOVSKY F, ROLAND N, et al. Streamwise-localized solutions at the onset of turbulence in pipe flow[J]. Physical Review Letters, 2013, 110(22): 1-4. |
| [204] |
BUDANUR N B, HOF B. Heteroclinic path to spatially localized chaos in pipe flow[J]. Journal of Fluid Mechanics, 2017, 827: 1-13. DOI:10.1017/jfm.2017.421 |
| [205] |
CHERUBINI S, DE PALMA P, ROBINET J C, et al. Edge states in a boundary layer[J]. Physics of Fluids, 2011, 23(5): 051705. DOI:10.1063/1.3589842 |
| [206] |
DUGUET Y, SCHLATTER P, HENNINGSON D S, et al. Self-sustained localized structures in a boundary-layer flow[J]. Physical Review Letters, 2012, 108(4): 044501. DOI:10.1103/PhysRevLett.108.044501 |
| [207] |
KHAPKO T, KREILOS T, SCHLATTER P, et al. Localized edge states in the asymptotic suction boundary layer[J]. Journal of Fluid Mechanics, 2013, 717: R6. DOI:10.1017/jfm.2013.20 |
| [208] |
KHAPKO T, DUGUET Y, KREILOS T, et al. Complexity of localised coherent structures in a boundary-layer flow[J]. European Physical Journal E, 2014, 37(32): 1-12. |
| [209] |
MELLIBOVSKY F, MESEGUER A, SCHNEIDER T M, et al. Transition in localized pipe flow turbulence[J]. Physical Review Letters, 2009, 103(5): 054502. DOI:10.1103/PhysRevLett.103.054502 |
| [210] |
AVILA K, MOXEY D, DE LOZAR A, et al. The onset of turbulence in pipe flow[J]. Science, 2011, 333(6039): 192-196. DOI:10.1126/science.1203223 |
| [211] |
MOXEY D, BARKLEY D. Distinct large-scale turbulent-laminar states in transitional pipe flow[J]. Proceedings of the National Academy of Sciences, 2010, 107(18): 8091-8096. DOI:10.1073/pnas.0909560107 |
| [212] |
SONG B, HOF B. Deterministic and stochastic aspects of the transition to turbulence[J]. Journal of Statistical Mechanics:Theory and Experiment, 2014, 2014(2): P02001. DOI:10.1088/1742-5468/2014/02/P02001 |
| [213] |
BARKLEY D. Theoretical perspective on the route to turbulence in a pipe[J]. Journal of Fluid Mechanics, 2016, 803: P1. DOI:10.1017/jfm.2016.465 |
| [214] |
KAWAHARA G. Laminarization of minimal plane Couette flow:Going beyond the basin of attraction of turbulence[J]. Physics of Fluids, 2005, 17(4): 041702. DOI:10.1063/1.1890428 |
| [215] |
LI W, XI L, GRAHAM M D. Nonlinear travelling waves as a framework for understanding turbulent drag reduction[J]. Journal of Fluid Mechanics, 2006, 565: 353-362. DOI:10.1017/S0022112006002138 |
| [216] |
IBRAHIM J I, YANG Q, DOOHAN P, et al. Phase-space dynamics of opposition control in wall-bounded turbulent flows[J]. Journal of Fluid Mechanics, 2019, 861: 29-54. DOI:10.1017/jfm.2018.905 |
 2019, Vol. 38
2019, Vol. 38