迎风格式被广泛用于可压缩流计算流体力学的有限差分法和有限体积法中守恒型方程的通量计算。由于迎风格式固有的耗散性质,它能够有效地进行包含激波等流场间断的超声速、高超声速流动的计算,这也就是激波捕捉法;而迎风格式对应的解析精确Jacobian矩阵也是提高隐式时间离散格式收敛性和稳定性的关键[1-2]。但是,部分迎风格式在含激波的多维流场中出现数值激波不稳定现象,这一问题在高超声速计算中尤为突出[3],并对计算精度与稳定性都造成了不利影响。
分析表明,经典的通量矢量分裂(Flux Vector Splitting, FVS)型迎风格式计算效率高,稳定性好,能够可靠地计算激波。但是,经典的FVS格式不能够准确模拟线性波,导致流场中的接触间断[4]被抹平,进而影响摩阻或热流等黏性效应主导的问题的计算精度[5]。而通量差分分裂(Flux Difference Splitting, FDS)型格式能够有效地计算定常激波与接触间断,但是需要熵修正[6-7]或存在数值激波不稳定[8]等问题。
激波捕捉法具有使用灵活与编程简易的优点,因此,为了改善迎风格式的性能,国内外都进行了大量研究工作。其中,AUSM格式[9]将流动中的对流机制与压力传播机制分别进行处理,给出了新的格式构造思路。AUSM格式结合了FVS与FDS的特点,具有较好的综合性能。但是AUSM格式及其后续发展的同类格式也没有完全解决前述的激波计算不稳定问题。考虑到实际流动的多维效应,多种旋转迎风格式被构造出来[10-13],其机理也得到进一步研究[14-15]。旋转格式能够有效地抑制激波不稳定现象,但是由于对两个方向进行计算,导致计算量较大;并且由于旋转通量函数的非线性性质,为保证收敛性需要附加处理[10-12]。基于结合不同格式优点的思路,混合格式被提出并用于改善迎风格式性能[16-20]。研究表明,捕捉激波的稳定性与接触间断的分辨率是一对矛盾,单一的迎风格式难以同时在这两个方面具有良好的性能,因而需要采用耗散可调的旋转格式或混合格式。
由于非结构网格上无法保证正交性,同时网格单元与流动间断交错,导致非结构网格上的计算更易于产生非物理扰动。本文对非结构网格上的数值激波不稳定现象进行了研究,分析了不稳定现象与网格分布的关系;在此基础上,根据迎风型格式的耗散机制,研究并构造新型混合型格式;最后,通过一系列数值算例对比研究新型混合格式的性能。
1 控制方程与基本数值方法 1.1 控制方程及其离散本文控制方程采用积分形式的二维可压缩Navier-Stokes (NS)方程组:
| $ \frac{\partial }{{\partial t}}\iiint\limits_\mathit{\Omega } {\mathit{\boldsymbol{Q}}{\text{d}}V} + \iint\limits_{\partial \mathit{\Omega }} {\left[ {{\mathit{\boldsymbol{F}}_c}\left( \mathit{\boldsymbol{Q}} \right) - {\mathit{\boldsymbol{F}}_v}\left( \mathit{\boldsymbol{Q}} \right)} \right] \cdot \mathit{\boldsymbol{n}}{\text{d}}S} = 0 $ | (1) |
式中,Ω为积分域,∂Ω为积分域边界,n为积分域边界外法向;Q为方程守恒变量,Fc(Q)和Fv(Q)分别为对流通量与黏性通量。关于可压缩N-S方程的详细推导与说明可以参考文献[21]。
本文采用格心型有限体积法对上述方程进行离散求解,即以网格单元为空间离散后的积分域/控制体,从而得到方程组半离散形式如下:
| $ \frac{\partial }{{\partial t}}{\left( {\mathit{\boldsymbol{QV}}} \right)_i} = - {\left( {\sum\limits_{k = 1}^{{N_f}} {{\mathit{\boldsymbol{F}}_k}} \cdot {\mathit{\boldsymbol{n}}_k}{S_k}} \right)_i} $ | (2) |
其中:下标i表示第i个单元,Nf为该单元的表面的个数。Fk、nk和Sk分别为该单元第k个表面的通量、外法向单位矢量和面积。第i个单元内的变量分布可以描述为:
| $ \mathit{\boldsymbol{Q}} = {\mathit{\boldsymbol{Q}}_i} + {\phi _i}\nabla {\mathit{\boldsymbol{Q}}_i} \cdot \Delta \mathit{\boldsymbol{r}} $ | (3) |
此处下标i表示变量定义于单元i的形心。ϕi为限制器值,
完成空间离散求解后,可以采用显式或隐式方法对式(2)中的时间导数项进行离散求解。本文采用的方法包括显式一阶前差与隐式LU-SGS方法[22]。
1.2 通量计算式(2)中的单元表面通量包括了对流通量与黏性通量。其中,黏性通量采用Blazek的方法[21]构造面元梯度,而后采用中心差分计算通量。对流通量可以采用中心型格式或迎风型格式计算,本文仅讨论迎风型格式。
采用迎风格式计算单元表面对流通量,可以写为以下统一形式[9]:
| $ {F_{c,1/2}} = \frac{1}{2}\dot m\left( {{\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}^ + } + {\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}^ - }} \right) - \frac{1}{2}D\left( {{\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}^ - } - {\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}^ + }} \right) + \mathit{\boldsymbol{\tilde p}} $ | (4) |
其中上标+、-分别表示面元左右两侧变量。为简便,后续讨论中省略上式中的面元通量下标。在上式的形式下,对流通量被分为对流项Φ±与压力项
对于SLAU格式,其分裂的对流项与压力项分别为:
| $ \left\{ \begin{gathered} \mathit{\boldsymbol{ \boldsymbol{\varPhi} }} = {\left( {\rho \quad \rho u\quad \rho v\quad \rho h} \right)^{\text{T}}} \hfill \\ \mathit{\boldsymbol{\tilde p}} = {\left( {\begin{array}{*{20}{l}} 0&{\tilde p{n_x}}&{\tilde p{n_y}}&0 \end{array}} \right)^{\text{T}}} \hfill \\ \end{gathered} \right. $ | (5) |
式中:ρ、u、v、h分别为密度、x方向速度、y方向速度以及总焓。
对于TV格式与K-CUSP-X格式,能量方程中与压力相关的部分被移到压力项中,如式(6)所示:
| $ \left\{ \begin{gathered} \mathit{\boldsymbol{ \boldsymbol{\varPhi} }} = {\left( {\rho \quad \rho u\quad \rho v\quad \frac{1}{2}\rho {{\tilde U}_n}{{\left| \mathit{\boldsymbol{U}} \right|}^2}} \right)^{\text{T}}} \hfill \\ \mathit{\boldsymbol{\tilde p}} = {\left( {\begin{array}{*{20}{l}} 0&{\tilde p{n_x}}&{\tilde p{n_y}}&{\tilde p\frac{\gamma }{{\gamma - 1}}{{\tilde U}_n}} \end{array}} \right)^{\text{T}}} \hfill \\ \end{gathered} \right. $ | (6) |
其中,U为速度矢量,
本节仅简要介绍三种格式间的主要差异,格式实现细节限于篇幅不再介绍。数值计算表明,上述三种格式均具有低耗散性,能够准确地模拟接触间断以及黏性流动。此外,SLAU格式在低马赫数流动中耗散较小;K-CUSP-X格式具有速度扰动衰减特性,相对TV格式提高了激波计算的稳定性。
1.3 空间变量重构与限制器如前所述,采用式(3)描述变量分布时,空间离散具有二阶精度。本文采用Gauss-Green积分方法[26]计算单元内的梯度,其中积分所需格点变量可以通过多种方法计算[27],在此仅采用加权平均法。需要注意的是,在存在间断的流场中,二阶变量重构可能引起振荡,需要采用限制器确保重构变量的单调性。尤其在高超声速流动计算中,限制器对计算精度、稳定性等都有重要意义。本文在含间断流场计算的二阶格式中采用与Venkatakrishnan限制器[28]相结合的非结构网格MLP(Multi-dimensional Limiting Process)限制器[29]及其最新改进型MLP-pw限制器[30]。非结构网格的MLP限制器应用了Venkatakrishnan限制器的限制函数,通过协调考虑单元格心与格点变量分布,提出MLP条件,从而利用更多的单元模板信息以便更好地近似多维流动变量,并抑制非物理振荡。而MLP-pw限制器构造了强化和放宽的两个MLP型限制条件,分别用于提升激波捕捉的稳定性与降低光滑流场的耗散。
2 数值激波不稳定现象本节采用1.2节中的三种迎风格式计算高超声速钝体无黏绕流,测试它们在非结构网格上模拟强激波的稳定性,并且给出了应用广泛的Roe格式[31]和HLLC格式[32]的结果作为参考。为此生成了两种类型的三角形网格。其中,生成规则三角形网格时,首先将计算区域剖分为120×80的四边形网格,而后对每个四边形单元沿对角线剖分;不规则三角形网格采用Delaunay三角化方法将流场剖分为14 946个不规则分布的三角形单元,在激波附近与波后区域,最大和最小单元间的面积比小于5,单元长宽比均小于2。图 1中给出网格的示例。为了显示的清晰,图中网格边界的离散点只有实际计算网格的一半,内部网格采用与实际计算网格相同的方法生成。

|
图 1 测试网格示例 Fig.1 Schematics of computational grids |
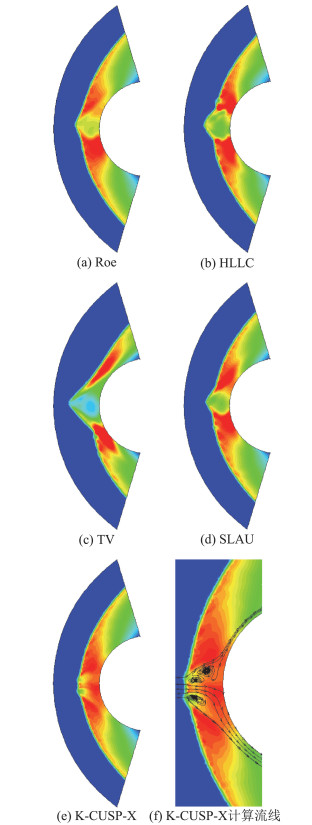
该问题的计算中,设定来流马赫数为8的单一组分均匀来流,流动受半圆形钝体阻碍形成弓形激波。本节中均采用一阶空间精度进行计算。为了突出问题,首先讨论不规则网格的计算结果。这里采用Roe格式、HLLC格式和TV格式计算,都出现了典型的“Carbuncle”现象。而后,采用SLAU格式和K-CUSP-X格式分别在TV格式得到的流场基础上继续计算,仍然存在振荡变化的异常现象。图 2(f)中给出K-CUSP-X格式异常区域附近的流线,出现了明显的分离涡。需要说明,K-CUSP-X在均匀初场条件下能够得到仅有微弱波动的流场,而SLAU格式在均匀初场或TV格式计算结果基础上继续计算都表现出类似于图 2(d)的结果。
|
图 2 激波不稳定现象(密度云图) Fig.2 Shock instabilities(density contour) |
由于网格分布不规则,难以寻找不稳定的非物理解与网格或流动之间的关系。因此在规则网格上进行计算,其它计算条件保持不变,采用均匀来流初始化流场。图 3给出SLAU格式在规则三角形网格上的计算结果。合理的流场分布应该上下对称,但是由于网格分布不同,流场下半区出现了非物理解;反之,在上半区域则获得了合理的计算结果。限于篇幅,其它格式的计算结果并未给出,但均出现不同程度的不稳定现象。TV格式的异常现象更为严重,对流场整体分布的影响更加显著;而K-CUSP-X格式的异常现象影响区域则较小。

|
图 3 SLAU格式在规则三角形网格上的不稳定现象[20] Fig.3 Shock instabilities of SLAU scheme on the regular triangular grid |
从图 3(c)中可以看出,出现激波计算异常结果区域中,流线与网格线几乎相切。关于数值激波不稳定现象,文献[33]认为具有良好接触间断分辨率的格式将出现不稳定现象,文献[34]中指出质量通量与网格切向动量通量的作用,文献[35]进一步强调穿过激波的动量扰动将导致激波不稳定的发生。在本算例中,网格穿过激波,两侧单元的动量变化剧烈;网格与流线相切又使扰动量沿网格方向传播。而SLAU格式对于接触间断的低耗散性质使动量扰动难以被耗散,导致出现激波计算的异常。反之,若采用van Leer格式[36]等无法准确捕捉接触间断的迎风格式,由于包括面元切向速度在内的接触间断被逐渐抹平,动量扰动也被抑制,因此不会在本算例中出现异常结果。值得注意的是,K-CUSP-X格式在设计时考虑了速度扰动的耗散特性,因此其稳定性相对SLAU格式和TV格式更好;但是它对密度扰动并不具备耗散能力,因此并不能完全抑制动量扰动并避免异常现象。本节结论进一步佐证了文献[33]的结论,即接触间断分辨率良好的格式倾向于出现激波不稳定现象。因此,尽管上述格式在多种问题中体现出良好的性能,其稳定性仍需要进一步提高,以改善其对复杂网格条件的适应能力。
3 混合格式鉴于迎风格式的接触间断分辨率与激波稳定性存在矛盾,因而组合具有不同特点的迎风格式,即设计混合迎风格式以改进迎风格式的综合性能。同时,考虑到动量分布的扰动被认为是激波不稳定现象的原因,混合格式的构造应当修正与动量相关的项。
以TV格式为例,借鉴对流迎风分裂格式的构造思路,将其写为式(4)的形式后,得到以下各项:
| $ \left\{ {\begin{array}{*{20}{l}} {\dot m = {{\tilde U}_n}} \\ {D = \left| {\dot m} \right|} \end{array}} \right. $ | (7) |
进一步补充式(6)中各项的定义如下:
| $ \left\{ \begin{gathered} {{\tilde U}_n} = \frac{{{C^ - }U_n^ - - {C^ + }U_n^ + }}{{{C^ - } - {C^ + }}} - \frac{2}{{{C^ - } - {C^ + }}}\left( {{p^ - } - {p^ + }} \right) \hfill \\ \tilde p = \frac{{{C^ - }{p^ + } - {C^ + }{p^ - }}}{{{C^ - } - {C^ + }}} + \frac{1}{2}\frac{{{C^ + }{C^ - }}}{{{C^ - } - {C^ + }}}\left( {U_n^ - - U_n^ + } \right) \hfill \\ {C^ + } = {\rho ^ + }\left( {U_n^ + - {A^ + }} \right),\;\;\;\;{C^ - } = {\rho ^ - }\left( {U_n^ - + {A^ - }} \right) \hfill \\ {A^ \pm } = \sqrt {U_n^ \pm + 4{{\left( {{a^ \pm }} \right)}^2}} \hfill \\ \end{gathered} \right. $ | (8) |
其中a为声速。可以发现TV格式在进行对流项与压力项的分裂后,其压力项主要由压力而不是速度决定,而压力场的椭圆型方程性质决定它的作用形式与对流项的双曲型方程扰动形式不同,因而认为压力项对激波稳定性的影响将是次要的。基于这一考虑,下面的混合格式将不考虑压力项的修正。
为了简化处理,将TV格式在式(4)中的对流项进行合并,可以恢复其在文献[24]中的形式:
| $ \left\{ \begin{gathered} \frac{1}{2}\dot m\left( {{\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}^ + } + {\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}^ - }} \right) - \frac{1}{2}D\left( {{\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}^ - } - {\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}^ + }} \right) = C\left( \mathit{\boldsymbol{ \boldsymbol{\varPhi} }} \right) = {{\tilde U}_n}\mathit{\boldsymbol{ \boldsymbol{\varPhi} }} \hfill \\ \mathit{\boldsymbol{ \boldsymbol{\varPhi} }} = \left\{ {\begin{array}{*{20}{l}} {{\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}^ + },}&{{{\tilde U}_n} > 0} \\ {{\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}^ - },}&{{{\tilde U}_n} \leqslant 0} \end{array}} \right. \hfill \\ \end{gathered} \right. $ | (9) |
由此可见,TV格式中对流项计算的关键是得到合理的速度近似,准确的速度近似使其获得了良好的接触间断分辨率[37],同时也导致了激波计算稳定性的下降[33]。
Van Leer格式具有良好的激波计算稳定性,文献[37]分析了van Leer格式对接触间断的耗散机制。混合格式借鉴van Leer格式的马赫数分裂函数[36],并通过压力权函数得到混合格式的对流项如下:
| $ \left\{ \begin{gathered} C(\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}) = \omega {{\tilde U}_n}\mathit{\boldsymbol{ \boldsymbol{\varPhi} }} + (1 - \omega )\left( {M{a^ + }{a^ + }{\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}^ + } + M{a^ - }{a^ - }{\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}^ - }} \right) \hfill \\ M{a^ \pm }(Ma) = \left\{ {\begin{array}{*{20}{l}} {\frac{1}{2}(Ma \pm |Ma|),}&{|Ma| \geqslant 1} \\ { \pm \frac{1}{4}{{(Ma \pm 1)}^2},}&{|Ma| < 1} \end{array}} \right. \hfill \\ \end{gathered} \right. $ | (10) |
其中Ma±为单元表面左右两侧法向马赫数。需要强调的是,不仅压力项的处理保持TV格式原有形式,上式中的加权混合仅对动量方程进行,而质量方程与能量方程的对流项仍保持TV格式原有形式。最后定义上式中权系数如下[20]:
| $ \left\{ {\begin{array}{*{20}{l}} {\omega = \mathop {\min }\limits_{l \in k(i) \cup k(j)} \left( {{f_l}} \right)} \\ {{f_l} = \min \left( {\frac{{{p^ + }}}{{{p^ - }}},\frac{{{p^ - }}}{{{p^ + }}}} \right)_l^3} \end{array}} \right. $ | (11) |
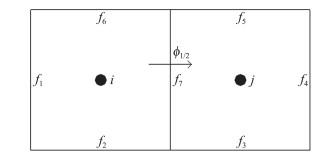
式(11)中的权系数通过计算待求通量所在的面元左右两侧单元的所有表面上的压力差得到,如图 4所示,k(i)和k(j)分别为单元i和j的所有表面。从而确保跨越激波的网格面能够随着压力差的增大切换至耗散格式。反之,在压力差较小的区域,如均匀流场或接触间断附近,混合格式完全保持TV格式的原有形式,从而保持其低耗散、高分辨率的性质。
|
图 4 混合格式权系数定义示意 Fig.4 Schematic of the definition of the weights in the hybrid scheme |
首先,为了证明混合格式引入van Leer格式的马赫数分裂函数并未降低黏性流动的计算精度,采用亚声速层流平板边界层算例考核混合格式[12]。此时,混合格式的接触间断分辨率直接影响边界层流动的计算精度。均匀来流马赫数为0.3,流场采用图 5所示的四边形网格离散,除平板前缘外,保证速度边界层内分布10~20层网格。

|
图 5 层流平板边界层流动计算网格 Fig.5 Computation grid of flat plate boundary layer flow |
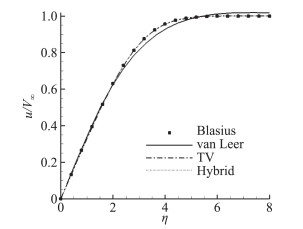
计算中采用二阶格式,由于流场中没有间断,因此不采用限制器;采用LU-SGS隐式方法计算至残差下降8个量级后认为计算收敛。给出van Leer格式、TV格式以及混合格式的计算结果与Blasius解的对比,如图 6所示。
|
图 6 层流平板边界层结果对比 Fig.6 Comparison of the results of flat plate boundary layer |
可以看到,混合格式和TV格式都获得了准确的边界层速度型分布。这是由于边界层中压力梯度较小,引入的修正耗散项的影响可以忽略不计。该结果表明混合格式并未影响接触间断的分辨率。此外,SLAU格式与K-CUSP-X格式在此问题中也能够得到准确结果。
4.2 亚声速圆柱扰流平板边界层流动较为简单,为此进一步采用圆柱的黏性绕流算例测试多维黏性流动特性的计算精度[15]。计算网格如图 7所示,圆柱附近采用200×25个四边形网格离散,外部采用13 895个三角形网格离散。计算来流马赫数为0.3,雷诺数为40。

|
图 7 亚声速圆柱绕流计算网格 Fig.7 Computation grid of subsonic flow around a cylinder |
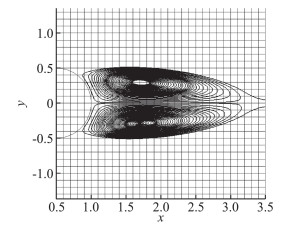
混合格式的计算结果如图 8所示,可见圆柱后形成一对稳定对称的分离涡。为进一步比较各个格式,将计算得到的分离涡长度列于表 1(圆柱直径为1)。
|
图 8 混合格式计算结果 Fig.8 Numerical result of the hybrid scheme |
| 表 1 分离涡长度 Table 1 Length of the detached eddies |
|
|
计算得到的分离涡长度同时受到网格剖分与格式耗散的影响,因此此处并不直接比较相对实验的计算结果差异。主要的结论是,在相同的网格条件下,基于TV格式的混合格式计算结果与TV格式相差不足0.5%,表明在光滑流场中增加的耗散可以忽略不计。另外Roe格式、SLAU格式、K-CUSP-X格式耗散也较小,而van Leer格式耗散较大,计算得到的分离涡最小。
4.3 高超声速钝体绕流:一阶格式采用混合格式计算第二节中的高超声速钝体绕流问题,考核其激波稳定性。分别采用规则与不规则三角形网格,计算条件不变。计算结果如图 9所示。
|
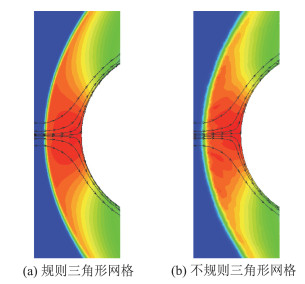
图 9 混合格式在三角形网格上的密度云图与流线(一阶) Fig.9 Density contour and streamlines of hybrid scheme on triangular grids (first-order) |
可以看到,混合格式没有出现第二节中几种迎风格式表现出的激波不稳定现象。尽管网格非对称,并且不规则三角形网格中钝体前缘亚声速区的密度分布仍与实际物理解存在差异,但是混合格式得到了基本对称的流场分布,观察流线也可以看到没有出现第二节中的非物理分离涡。因此可以认为,混合格式不仅保持了TV格式黏性流动计算的精度,也改善了强激波计算的稳定性。
4.4 高超声速钝体绕流:二阶格式空间二阶精度条件下,式(4)中的单元表面两侧变量差值减小,从而使迎风格式耗散减小,提高了流场模拟的精度。另一方面,尽管限制器的作用避免了流场变量重构的振荡,但是由于耗散减小,激波计算的不稳定现象更容易产生。因此本节在上一小节算例的基础上,采用二阶格式结合MLP限制器进行计算,检验混合格式的性能。
本节算例的计算条件和网格与上一小节相同。鉴于对高超声速流场进行计算,激波前后物理量变化剧烈,理论最大压力比超过70倍,因此MLP限制器中的Venkatakrishnan限制函数的参数K设为0.1。计算结果如图 10所示。

|
图 10 混合格式在三角形网格上的密度云图(二阶) Fig.10 Density contour of hybrid scheme on triangular grids (second-order) |
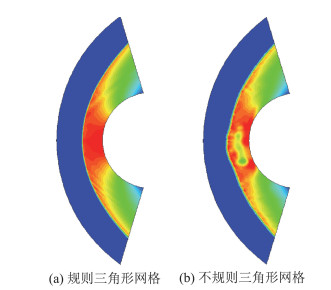
相对于一阶格式的计算结果,二阶格式中流动的对称性下降,表明随着耗散降低,对扰动的抑制能力下降。但是,计算中并未出现明显的激波不稳定现象,特别是弓形激波的位置与形态都较为准确。作为对比,给出第2节中稳定性最好的K-CUSP-X格式的计算结果,如图 11所示,可以看到在规则三角形网格上波后存在较为明显的波动,而在不规则三角形网格上计算得到的激波形态存在异常,波后亚声速区存在非定常、非物理的涡结构。上述结果表明,在二阶精度条件下采用混合格式能够有效改善计算稳定性。
|
图 11 K-CUSP-X格式在三角形网格上的密度云图(二阶) Fig.11 Density contour of K-CUSP-X scheme on triangular grids (second-order) |
若进一步对比混合格式在一阶、二阶精度空间离散中的差异,可以发现采用一阶格式得到的流场更为合理。而二阶格式在规则三角形网格上出现了类似于图 3、但更为为微弱的不合理密度分布。这主要是在二阶精度条件下耗散更低导致。文献[39]讨论了限制器对二阶格式计算稳定性的影响,并发现即使采用较为稳定的van Leer格式,也可能出现流场的异常波动。因此,在二阶空间精度格式的计算中,不仅需要考虑通量计算的影响,还需要考虑限制器的作用。特别是在非结构网格的条件下,网格的影响因素更为复杂,因此需要对限制器和迎风型格式的作用进行综合的研究。而在实际工程应用中,通过生成高质量网格或者采用网格自适应技术,避免或降低网格条件可能带来的不利影响,提高计算精度与稳定性。显然,随着网格的加密,二阶格式将更快地在光滑流场得到准确的计算结果,而激波附近的异常也会减弱。
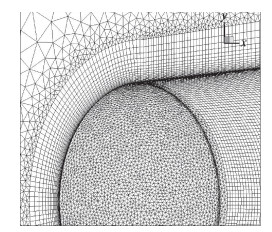
4.5 高超声速三维钝锥绕流本节对比混合格式与TV格式在三维高超声速外形含激波流场计算中的性能,采用MLP-pw限制器[30]实现二阶空间精度的激波捕捉计算。数值模拟的钝锥外形[40]半锥角为4.7°。来流马赫数为6,迎角0°。计算网格的详细参数可参考文献[41],局部网格如图 12所示。
|
图 12 钝锥绕流计算网格 Fig.12 Computation grid of hypersonic flow around a blunt cone |
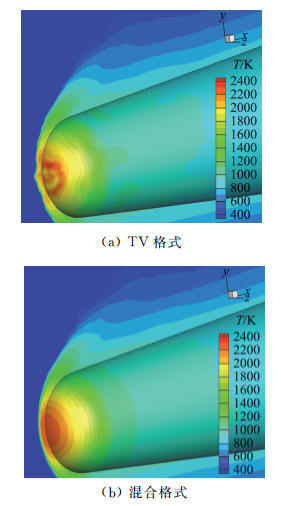
对比图 13中TV格式与混合格式计算得到的温度分布,可见混合格式有效地消除了激波不稳定现象,从而得到了更为合理的温度分布。这对于气动加热问题中的热流计算是必要的。但是必须说明的是,准确的热流计算还需要考虑黏性通量计算、流场(温度)梯度计算、网格分布乃至湍流等因素,需要进行系统的分析。本文结果仅用于说明混合格式对数值激波不稳定这一影响因素的抑制作用。
|
图 13 钝锥绕流温度云图 Fig.13 Pressure contours of the computation of hypersonic flow around a blunt cone |
本文对迎风型通量格式的激波捕捉能力进行了分析对比,得到的数值结果表明多种性能优秀的迎风格式在非结构网格上表现出数值激波不稳定现象,并且再次验证了激波横断方向的不均匀动量扰动是激波计算异常的原因。准确分辨接触间断的格式难以耗散网格切向的动量扰动,而此类扰动在非结构网格上由于网格与激波交错分布而易于产生。因此本文得出结论:修正动量方程通量中的对流项是抑制动量扰动、提高稳定性的关键。通过结合van Leer格式的马赫数分裂函数,本文构造了一种TV-van Leer混合格式,引入了van Leer格式的耗散项形式。该格式仅对TV格式对流项的动量方程分量进行修正,而压力项以及质量、能量方程保持TV格式原有形式。数值计算结果表明该混合格式保持了TV格式的黏性流动计算精度,并且改善了在非结构网格上捕捉强激波的稳定性,提高了计算高超声速流动的能力。而对于工程CFD分析中常用的二阶空间精度非结构有限体积法,其数值稳定性与计算精度的改进工作必须综合考虑限制器与计算网格的影响,展开系统的分析和研究。
| [1] |
党亚斌, 刘凯礼, 孙一峰, 等. 用隐式高精度间断伽辽金方法模拟可压层流和湍流[J]. 空气动力学学报, 2018, 36(3): 535-541. DANG Y B, LIU K L, SUN Y F, et al. Implicit high order discontinuous Galerkin method for compressible laminar and turbulent flow simulation[J]. Acta Aerodynamica Sinica, 2018, 36(3): 535-541. DOI:10.7638/kqdlxxb-2017.0183 (in Chinese) |
| [2] |
龚小权, 贾洪印, 陈江涛, 等. 基于雅可比矩阵精确计算的GMRES隐式方法在间断Galerkin有限元中的应用[J]. 空气动力学学报, 2019, 37(1): 121-132. GONG X Q, JIA H Y, CHEN J T, et al. Applications of GMRES based on exact calculations of Jacobian matrix in discontinuous Galerkin methods[J]. Acta Aerodynamica Sinica, 2019, 37(1): 121-132. DOI:10.7638/kqdlxxb-2018.0189 (in Chinese) |
| [3] |
KITAMURA K, ROE P, ISMAIL F. Evaluation of Euler fluxes for hypersonic flow computations[J]. AIAA Journal, 2009, 47(1): 44-53. DOI:10.2514/1.33735 |
| [4] |
阎超, 张智, 张立新, 等. 上风格式的若干性能分析[J]. 空气动力学学报, 2003, 21(3): 336-341. YAN C, ZHANG Z, ZHANG L X, et al. Characteristic analysis of the upwind scheme[J]. Acta Aerodynamica Sinica, 2003, 21(3): 336-341. DOI:10.3969/j.issn.0258-1825.2003.03.011 (in Chinese) |
| [5] |
李君哲, 阎超, 柯伦, 等. 气动热CFD计算的格式效应研究[J]. 北京航空航天大学学报, 2003, 29(11): 1022-1025. LI J Z, YAN C, KE L, et al. Research on scheme effect of computational fluid dynamics in aerothermal[J]. Journal of Beijing University of Aeronautics and Astronautics, 2003, 29(11): 1022-1025. DOI:10.3969/j.issn.1001-5965.2003.11.014 (in Chinese) |
| [6] |
HARTEN A. High resolution schemes for hyperbolic conservation laws[J]. Journal of Computational Physics, 1983, 49: 357-393. DOI:10.1016/0021-9991(83)90136-5 |
| [7] |
龚安龙, 刘周, 杨云军, 等. 高超声速激波/边界层干扰流动数值模拟研究[J]. 空气动力学学报, 2014, 32(6): 767-771. GONG A L, LIU Z, YANG Y J, et al. Numerical study on hypersonic double-cone separated flow[J]. Acta Aerodynamica Sinica, 2014, 32(6): 767-771. DOI:10.7638/kqdlxxb-2014.0083 (in Chinese) |
| [8] |
PEERY K, IMLAY S. Blunt-body flow simulations[R]. AIAA-88-2904, 1988.
|
| [9] |
LIOU M S, STEFFEN C J. A new flux splitting scheme[J]. Journal of Computational Physics, 1993, 107: 23-39. DOI:10.1006/jcph.1993.1122 |
| [10] |
REN Y X. A robust shock-capturing scheme based on rotated Riemann solvers[J]. Computers & Fluids, 2003, 32: 1379-1403. |
| [11] |
孙宇涛, 任玉新. 求解多维欧拉方程的二阶旋转输运格式[J]. 空气动力学学报, 2005, 23(3): 326-329. SUN Y T, REN Y X. A second-order rotational upwind transport scheme for solving multi-dimensional compressible Euler equations[J]. Acta Aerodynamica Sinica, 2005, 23(3): 326-329. DOI:10.3969/j.issn.0258-1825.2005.03.012 (in Chinese) |
| [12] |
NISHIKAWA H, KITAMURA K. Very simple, carbuncle-free, boundary-layer-resolving, rotated-hybrid Riemann solvers[J]. Journal of Computational Physics, 2008, 227: 2560-2581. DOI:10.1016/j.jcp.2007.11.003 |
| [13] |
刘友琼, 封建湖, 任炯, 等. 求解多维Euler方程的二阶旋转混合型格式[J]. 应用数学和力学, 2014, 35(5): 542-553. LIU Y Q, FENG J H, REN J, et al. A second-order rotated-hybrid scheme for solving three-dimensional compressible Euler equations[J]. Applied Mathematics and Mechanics, 2014, 35(5): 542-553. (in Chinese) |
| [14] |
ZHANG F, LIU J, CHEN B S. Numerical investigation on the dissipation property of the rotated Roe scheme[C]//Proceedings of the World Congress on Mechanical, Chemical, and Material Engineering (MCM 2015). Avestia Publishing, 2015.
|
| [15] |
ZHANG F, LIU J, CHEN B S, et al. Evaluation of rotated upwind schemes for contact discontinuity and strong shock[J]. Computers & Fluids, 2016, 134-135: 11-22. |
| [16] |
王学德, 谭俊杰, 林晓宏, 等. 基于Van Leer+AUSM混合格式超声速流场的并行数值算法研究[J]. 宇航学报, 2010, 31(4): 986-992. WANG X D, TAN J J, LIN X H, et al. Research on parallel numerical simulation of N-S equations based on Van Leer+AUSM scheme[J]. Journal of Astronautics, 2010, 31(4): 986-992. DOI:10.3873/j.issn.1000-1328.2010.04.008 (in Chinese) |
| [17] |
傅林, 高正红, 张晓东. HLL-HLLC格式的构造与应用研究[J]. 空气动力学学报, 2014, 32(1): 116-122, 135. FU L, GAO Z H, ZHANG X D. Construction and application research of HLL-HLLC scheme[J]. Acta Aerodynamica Sinica, 2014, 32(1): 116-122, 135. (in Chinese) |
| [18] |
WANG D F, DENG X G, WANG G X, et al. Developing a hybrid flux function suitable for hypersonic flow simulation with high-order methods[J]. International Journal of Numerical Methods in Fluids, 2016, 81(5): 309-327. DOI:10.1002/fld.4186 |
| [19] |
SHEN Z J, YAN W, YUAN G W. A robust HLLC-type Riemann solver for strong shock[J]. Journal of Computational Physics, 2016, 309: 185-206. DOI:10.1016/j.jcp.2016.01.001 |
| [20] |
Zhang F, Liu J, Chen B S, et al. A robust low-dissipation AUSM-family scheme for numerical shock stability on unstructured grids[J]. International Journal for Numerical Methods in Fluids, 2017, 84(3): 135-151. DOI:10.1002/fld.4341 |
| [21] |
BLAZEK J. Computational fluid dynamics:principles and applications[M]. Elsevier, 2005.
|
| [22] |
YOON S, JAMESON A. Lower-upper symmetric-Gauss-Seidel method for the Euler and Navier-Stokes equations[J]. AIAA Journal, 1988, 26(9): 1025-1026. DOI:10.2514/3.10007 |
| [23] |
SHIMA E, KITAMURA K. Parameter-free simple low-dissipation AUSM-family scheme for all speeds[J]. AIAA Journal, 2011, 49(8): 1693-1709. DOI:10.2514/1.J050905 |
| [24] |
TORO E F, VÁZQUEZ-CENDÓN M E. Flux splitting schemes for the Euler equations[J]. Computers & Fluids, 2012, 70: 1-12. |
| [25] |
谢文佳, 李桦, 潘沙, 等. 一类新型激波捕捉格式的耗散性与稳定性分析[J]. 物理学报, 2015, 64(2): 024702. XIE W J, LI H, PAN S, et al. On the accuracy and robustness of a new flux slitting method[J]. Acta Physica Sinica, 2015, 64(2): 024702. (in Chinese) |
| [26] |
BARTH T J. Numerical aspects of computing viscous high Reynolds number flows on unstructured meshes[R]. AIAA-91-0721, 1991.
|
| [27] |
张帆, 刘君, 陈飙松, 等. 格心型有限体积法格点变量重构方法研究[J]. 大连理工大学学报, 2015, 55(5): 449-456. ZHANG F, LIU J, CHEN B S, et al. Research on vertex variables reconstruction for cell-centered finite volume method[J]. Journal of Dalian University of Technology, 2015, 55(5): 449-456. (in Chinese) |
| [28] |
VENKATAKRISHNAN V. On the accuracy of limiters and convergence to steady state solutions[R]. AIAA-93-0880, 1993.
|
| [29] |
PARK J S, YOON S H, KIM C. Multi-dimensional limiting process for hyperbolic conservation laws on unstructured grids[J]. Journal of Computational Physics, 2010, 229: 788-812. DOI:10.1016/j.jcp.2009.10.011 |
| [30] |
ZHANG F, LIU J, CHEN B S. Modified multi-dimensional limiting process with enhanced shock stability on unstructured grids[J]. Computers & Fluids, 2018, 161: 171-188. |
| [31] |
ROE P L. Approximate riemann solvers, parameter vectors, and difference schemes[J]. Journal of Computational Physics, 1981, 43: 357-372. DOI:10.1016/0021-9991(81)90128-5 |
| [32] |
TORO E F, SPRUCE M, SPEARES W. Restoration of the contact surface in the HLL-Riemann solver[J]. Shock Waves, 1994, 4: 25-34. DOI:10.1007/BF01414629 |
| [33] |
PANDOLFI M, D'AMBROSIO D. Numerical instabilities in upwind methods:analysis and cures for the "Carbuncle" phenomenon[J]. Journal of Computational Physics, 2001, 166: 271-301. DOI:10.1006/jcph.2000.6652 |
| [34] |
胡立军, 袁礼. 一种治愈强激波数值不稳定性的混合方法[J]. 应用数学和力学, 2015, 36(5): 482-493. HU L J, YUAN L. Analysis of numerical shock instabilities and a hybrid curing method[J]. Applied Mathematics and Mechanics, 2015, 36(5): 482-493. (in Chinese) |
| [35] |
SHEN Z J, YAN W, YUAN G W. A stability analysis of hybrid schemes to cure shock instability[J]. Communications in Computational Physics, 2014, 15(5): 1320-1342. DOI:10.4208/cicp.210513.091013a |
| [36] |
van Leer B. Flux-vector splitting for the Euler equations[C]//Eighth International Conference on Numerical Methods in Fluid Dynamics. Springer Berlin/Heidelberg, 1982: 507-512.
|
| [37] |
LIOU M S. Mass flux schemes and connection to shock instability[J]. Journal of Computational Physics, 2000, 160: 623-648. DOI:10.1006/jcph.2000.6478 |
| [38] |
COUTANCEAU M, BOUARD R. Experimental determination of the main features of the viscous flow in the wake of a circular cylinder in uniform translation. Part 1. Steady flow[J]. Journal of Fluid Mechanics, 1977, 79(2): 231-256. DOI:10.1017/S0022112077000135 |
| [39] |
ZHANG F, YUAN Z C, Liu J. A discussion on numerical shock stability of unstructured finite volume method: Riemann solvers and limiters[C]//2017 International Conference in Aerospace for Young Scientists. Beijing, China, 2017.
|
| [40] |
RIZK Y, CHAUSSEE D, MCRAE D. Computation of hypersonic viscous flow around three-dimensional bodies at high angles of attack[R]. AIAA 1981-1261, 1981.
|
| [41] |
张帆.非结构网格有限体积法的空间离散算法研究[D].大连: 大连理工大学, 2017. ZHANG F. Research on spatial discretization schemes for finite volume method on unstructured grids[D]. Dalian: Dalian University of Technology, 2017. (in Chinese) |
 2019, Vol. 37
2019, Vol. 37

