在高性能计算机硬件技术与计算流体力学(CFD)技术的共同推动下,CFD在飞行器设计中的作用愈发凸显[1-3]。与此同时,由于空气动力学问题的复杂性和CFD理论方面的固有不足,CFD的验证和确认工作(Verification & Validation)一直是CFD研究领域的热点问题之一[4-8]。针对典型运输机巡航构型、始于2001年的AIAA阻力预测会议DPW[9-14](Drag Prediction Workshop),针对典型运输机起降构型、始于2010年的AIAA高升力预测会议HiLiftPW[15-17] (High Lift Prediction Workshop)已经成为CFD验证与确认领域最具影响力的国际合作,吸引了世界范围内空气动力学工作者的广泛参与,极大地推动了CFD验证与确认的稳步开展。
在以上研讨活动的启发下,面向国内大型客机研制的迫切需求,2017年12月,中国空气动力研究与发展中心(CARDC)计算空气动力研究所联合中国航空研究院、西北工业大学、中国商用飞机公司上海飞机设计研究院、中山大学国家超级计算广州中心成立了第一届航空CFD可信度研讨会(1st Aeronautic CFD Credibility Workshop, AeCW-1)筹备小组;2018年4月,成立了由陈作斌、马明生为顾问委员,刘刚为组长的AeCW-1组委会,通过CARDC网站(www.cardc.cn)、百度网盘(https://pan.baidu.com/s/1bburphptuo76hgcoyvspwa)发布了计算模型、基础网格和相关试验数据;2018年8月,作为首届空气动力学大会的一个研讨专题,由中国空气动力学会计算空气动力学专委会主办,在四川绵阳召开AeCW-1专题研讨会。本次活动的主要目的是评估国内CFD当前技术状态,探索CFD的发展方向,促进国内CFD验证和确认工作的开展,为大型客机的研制提供技术支撑。
本文介绍了CHN-T1模型设计与风洞试验的基本情况,总结了AeCW-1研讨会的基本情况,对国内多家单位提供的数值模拟结果进行统计分析,并与FL-26的相关风洞试验结果和部分ETW的风洞试验结果进行了对比,对CFD验证和确认工作提出了意见和建议。
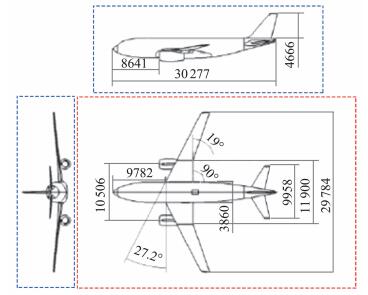
1 CHN-T1模型与风洞试验CHN-T(CHiNa-Transport)模型是CARDC自行设计的单通道运输机标模[18],主要目的是确认风洞试验品质,校对测量仪器,研究试验结果干扰修正方法、研发先进测量技术,同时为CFD的验证和确认工作提供基础数据。CHN-T模型包括了机翼、机身、平尾、立尾、挂架、短舱等部件,其中挂架、短舱两个部件可以拆卸。CHN-T模型外形及参考尺寸见图 1。CHN-T模型的设计马赫数为0.78,设计升力系数为0.50。基于目前CHN-T模型风洞试验的开展情况,AeCW-1组委会选择了机翼/机身/平尾/立尾构型(CHN-T1)作为基准研究模型。
|
图 1 CHN-T模型示意图及参考尺寸[10](单位:mm) Fig.1 Sketch of the CHN-T model with reference quantities[10](unit: mm) |
2016年9月,在CARDC 2.4m×2.4m风洞(FL-26)开展了CHN-T1模型的风洞试验[19],试验内容包括纵横航向基本特性试验、变雷诺数试验、转捩对比试验,试验马赫数范围为0.40~0.90,名义迎角为-6°~15°,侧滑角为-3°~12°,基于平均气动弦长的雷诺数为3.3×106~7.5×106。2016年12月,在德国哥廷根的2.4 m×2.0 m ETW(European Transonic Wind Tunnel)开展了CHN-T1模型的对比试验,试验内容包括纵横航向基本特性试验、转捩对比试验,试验马赫数范围为0.20~0.90,名义迎角为-6°~6°,侧滑角为-9°~9°,基于平均气动弦长的雷诺数为3.6×106~37.8×106。两期试验中,采用同一个风洞试验模型,均采用尾部支撑方式(图 2),所用尾支杆靠近模型机身尾部的外形及尺寸保持一致。CHN-T1试验模型缩比为0.052,风洞试验模型的基本参数如下:参考面积Sref=0.2578 m2,平均气动弦长cref=0.1937 m、展长b=1.5482 m、梢根比λ=0.298,展弦比AR=9.3,1/4弦线后掠角Λc/4= 25.0°。
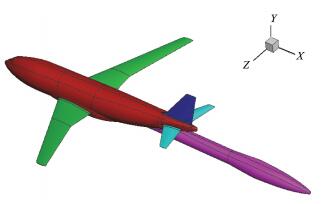
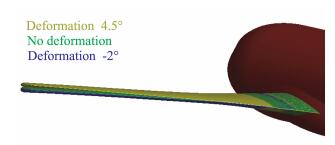
2 计算模型、研究工况与基本网格在CHN-T1风洞试验模型的基础上,AeCW-1组委会提供了三种计算模型作为研究模型,分别是CHN-T1计算模型(图 3),用于开展网格收敛性研究;包含FL-26简化支撑装置的CHN-T1模型(CHN-T1_S,图 4),用于开展风洞模型支撑装置对数值模拟结果的影响研究;基于FL-26风洞简化支撑装置和风洞变形测量数据构造的包含机翼静气动弹性的数模(CHN-T1_SA,图 5),用于开展静气动弹性变形和模型支撑装置对数值模拟结果的影响研究。与相应的风洞试验模型相比,CHN-T1、CHN-T1_S与CHN-T1_SA计算模型对风洞试验模型进行了局部光顺处理,对尾支杆与模型连接部分进行了封闭处理(试验模型在此处有缝隙),对二级尾支杆的底部进行了局部修型。

|
图 3 CHN-T1计算模型 Fig.3 Computational model of CHN-T1 |
|
图 4 CHN-T1_S计算模型 Fig.4 Computational model of CHN-T1_S |
|
图 5 CHN-T1_SA计算模型(局部) Fig.5 Computational model of CHN-T1_SA (local) |
AeCW-1组委会确定了网格收敛性研究、抖振特性研究以及雷诺数影响研究等三个工况,并将模型支撑装置影响和静气动弹性影响作为研究内容。数值模拟采用自由来流、全湍流模拟,不包括风洞洞壁。各个研究工况的计算模型、来流状态如下:
(1) Case 1—CHN-T1, grid convergence study (required): common grid convergence study at Ma=0.78, CL=0.500 (±0.001), Re=3.3×106 based on cref.
(2) Case 2—buffet study (required): 1) Case 2a,CHN-T1, medium mesh from Case 1, Ma=0.78, α= -2.0°~4.50°, Re = 3.3×106 based on cref; 2) Case 2b: CHN-T1_S, medium mesh from organizing committee, Ma=0.78, α= -2.0°~4.50°, Re=3.3×106 based on cref; 3) Case 2c: CHN-T1_SA, medium mesh from organizing committee, Ma=0.78, α= -2.0°~4.50°, Re=3.3×106 based on cref.
(3) Case 3—CHN-T1_S, Reynolds number study (optimal): Ma=0.78, CL=0.500 (±0.001), Re=3.3×106 and 15.0×106 based on cref.
为了方便与会者开展数值模拟工作,尽量避免网格因素对数值模拟结果的影响,参考DPW系列会议的网格生成规范[12],针对CHN-T1模型,AeCW-1组委会提供了三套多块对接结构网格[20]、三套非结构网格[21-22]作为基础网格,用于开展网格收敛性研究,其中,中等网格规模为工程应用上普遍采用的网格规模,CHN-T1模型的中等网格也是构造CHN-T1_S与CHN-T1_SA模型计算网格的基础。同时,AeCW-1组委会也鼓励参与者根据自身的工程经验,构造合适的计算网格。AeCW-1组委会提供的基础网格具体信息见表 1、表 2。根据网格生成规范,西北工业大学(PID:012)自行构造了粗、中、细、极细四套结构重叠网格[23],网格规模为657万、1451万、4856万和15800万。
| 表 1 CHN-T1模型的网格参数(结构网格) Table 1 Grid parameters for CHN-T1 model (structured grid) |
|
|
| 表 2 CHN-T1模型的网格参数(非结构网格) Table 2 Grid parameters for CHN-T1 model (unstructured grid) |
|
|
本次研讨活动共吸引了14家科研单位参加,其中包括7家研究所、5所高校、1家型号单位、1家商业软件公司;各参研单位共提交了26组Case 1结果、26组Case 2结果及12组Case 3结果,具体数据提交情况见表 3。表 3中给出了参研单位、姓名、软件名称、网格类型、完成的计算状态及以下统计分析中所采用的标识符号。其中,网格类型中,“S”表示结构网格、“U”表示非结构网格、“OS”表示结构重叠网格;湍流模型中,“SA”表示Spalart-Allmaras一方程湍流模型[24]、“SST”表示Menter SST k-ω两方程湍流模型[25]、“SA-QCR”表示经过Quadratic Constitutive Relation修正的S-A一方程湍流模型[26]、“RSM”表示雷诺应力模型(Reynolds Stress Model)[27-28]、“KW”表示k-ω两方程湍流模型[29]。
| 表 3 AeCW-1参与者 Table 3 AeCW-1 participants |
|
|
在Case 1的26组结果中,11组结果采用了组委会提供的多块对接结构网格,12组结果采用了组委会提供的非结构网格,3组结果采用了自行构造的重叠网格;18组结果采用了自研软件,8组结果采用了商业软件或开源软件;18组结果采用了SA湍流模型及其修正形式,7组采用了SST湍流模型,1组采用了RSM湍流模型。
在Case 2的26组结果中,10组结果采用了组委会提供的多块对接结构网格,12组结果采用了组委会提供的非结构网格,4组结果采用了自行构造的重叠网格;17组结果采用了自研软件,9组结果采用了商业软件或开源软件;17组结果采用了SA湍流模型及其修正形式,7组采用了SST湍流模型,1组采用了RSM湍流模型。
在Case 3的12组结果中,5组结果采用了组委会提供的多块对接结构网格,7组结果采用了组委会提供的非结构网格;9组结果采用了自研软件,3组结果采用了商业软件;4组结果采用了SA湍流模型及其修正形式,6组采用了SST湍流模型,1组采用了RSM湍流模型,1组采用了k-ω湍流模型。
4 Case 1计算结果统计分析Case 1是针对CHN-T1模型开展固定升力系数下的网格收敛性研究,为Case 2、Case 3的计算提供基础网格。来流条件为:马赫数Ma=0.78,基于平均气动弦长的雷诺数Re=3.3×106,升力系数CL =0.500±0.001。由于PID:007.2数据有误,PID:017数据明显异于其它计算结果,以下的分析中均不包括这两组数据。
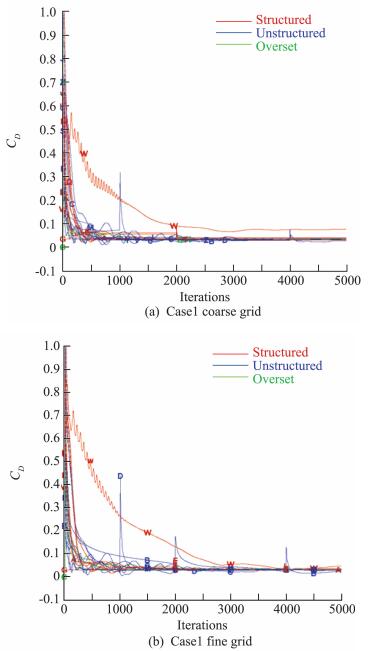
4.1 迭代收敛性图 6和图 7分别给出了Case 1采用粗网格和密网格计算结果的残差Res和阻力系数CD随迭代步数的收敛历程,按网格类型采用不同颜色的曲线进行了分类,曲线上的符号代表不同的计算结果(见表 3)。其中,PID:003.1、PID:011、PID:013.1三组结果在粗网格和密网格上的计算残差下降均小于3个量级,计算结果应进一步检查。PID:016结果在粗网格和密网格上的阻力系数收敛历程与其他计算结果明显不同。

|
图 6 残差的收敛历程 Fig.6 Convergence history of residual |
|
图 7 阻力系数的收敛历程 Fig.7 Convergence history of drag coefficient |
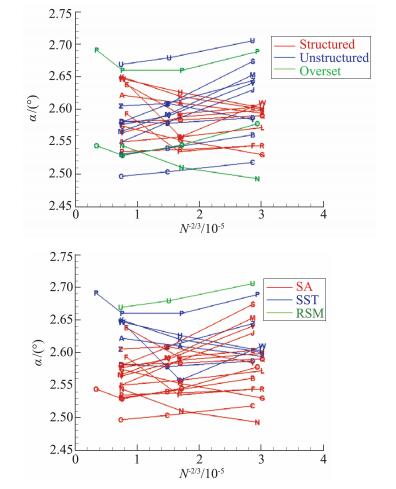
图 8、图 9和图 10分别给出了Case 1计算结果的迎角α、阻力系数CD、俯仰力矩系数Cm的网格收敛性曲线,其中横坐标为网格单元数目的-2/3次幂。图中按网格类型或湍流模型采用不同颜色的曲线进行了分类,曲线上的符号代表不同的计算结果(见表 3)。
|
图 8 迎角的网格收敛性 Fig.8 Grid convergence of angle of attack |
|
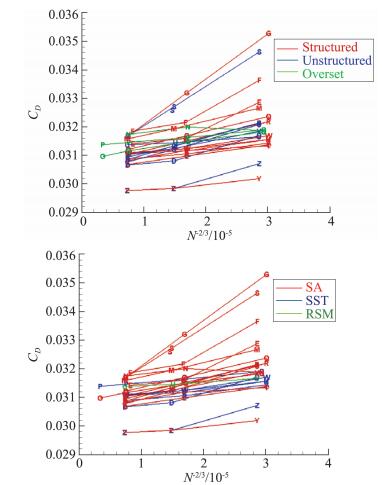
图 9 阻力系数网格收敛性 Fig.9 Grid convergence of drag coefficient |
|
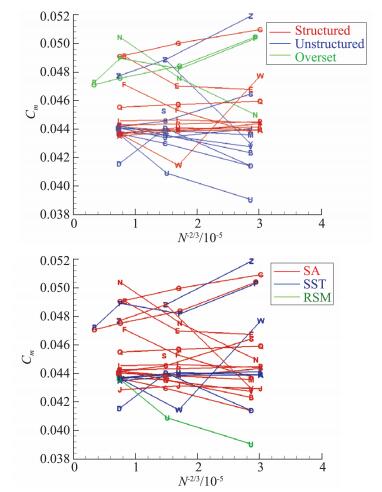
图 10 俯仰力矩系数网格收敛性 Fig.10 Grid convergence of pitch moment coefficient |
由图 8看出,采用自行构造的重叠网格,PID:012.3、PID:012.4在极细网格上的结果破坏了迎角的单调性;采用自行构造的结构网格,PID:016在细网格上的结果同样破坏了迎角的单调性。采用非结构网格,固定升力系数下的迎角随网格密度的增加单调下降;采用结构网格,固定升力系数下的迎角随网格密度的增加单调上升。相近网格规模下,采用SA湍流模型的迎角计算结果整体略低于SST湍流模型的计算结果。固定升力系数下,迎角计算结果的散布度并没有随网格密度的增加而减少。
由图 9看出,PID:019.1和PID:019.2两组阻力系数的计算结果明显低于相近网格规模下的其它计算结果。无论采用何种网格拓扑、何种湍流模型,阻力系数的计算结果基本上随网格密度的增加而单调下降;阻力系数计算结果的散布度同样随网格密度的增加而减少。
由图 10看出,PID:004、PID:012.4、PID:016和PID:019.1四组俯仰力矩系数的计算结果随网格密度的增加没有呈现单调变化。无论采用何种网格拓扑、何种湍流模型,俯仰力矩系数计算结果的散布度没有随网格密度的增加而明显减少。
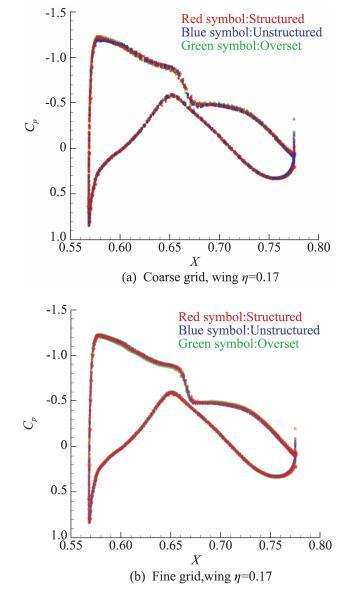
4.3 表面压力分布图 11和图 12分别给出了Case 1计算结果采用粗网格和密网格在机翼典型站位的压力Cp分布(η =0.17、η=0.95),其中横坐标X为当地弦长。
|
图 11 机翼典型站位压力分布(η=0.17) Fig.11 Pressure coefficients distribution at typical spanwise location of wing (η=0.17) |
|
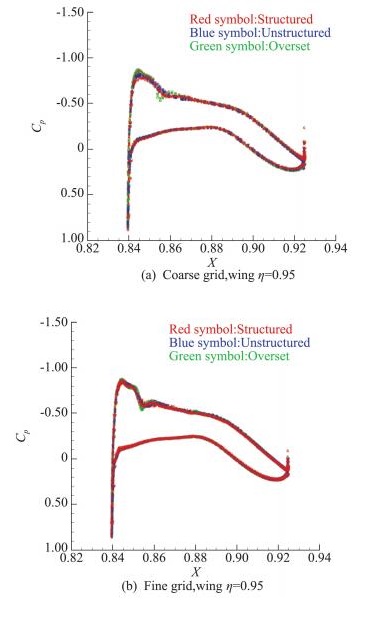
图 12 机翼典型站位压力分布(η=0.95) Fig.12 Pressure coefficients distribution at typical spanwise location of wing (η=0.95) |
在η=0.17站位(图 11),各组计算结果压力分布基本重合。在η=0.95站位(图 12),重叠网格粗网格的计算结果(PID:012.3、PID:012.4)前缘吸力峰略微过冲、吸力峰后的压力过度增加,上述现象在网格加密后有所缓解。其它结果基本重合。
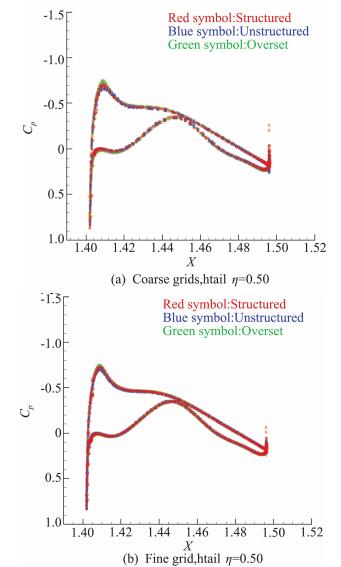
图 13给出了Case 1计算结果采用粗网格和密网格在平尾η=0.50站位的Cp分布。除了重叠网格的计算结果(PID:012.3、PID:012.4)前缘吸力峰值明显过冲外,其它各组计算结果压力分布基本重合。
|
图 13 平尾典型站位压力分布(η=0.50) Fig.13 Pressure coefficients distribution at typical spanwise location of horizontal tail (η=0.50) |
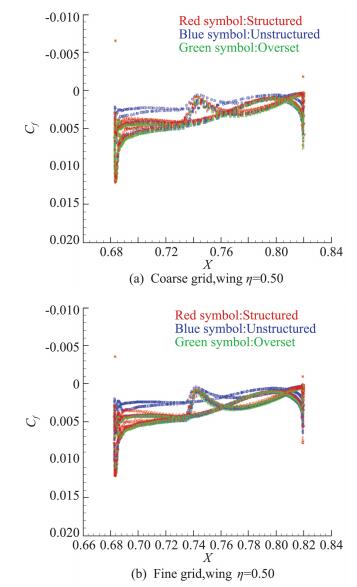
图 14和图 15分别给出了Case 1计算结果采用粗网格和密网格在机翼、平尾η=0.50站位的表面摩阻系数Cf分布,其中横坐标X为当地弦长。
|
图 14 机翼典型站位摩擦阻力分布(η=0.50) Fig.14 Friction drag coefficients distribution at typical spanwise location of wing (η=0.50) |
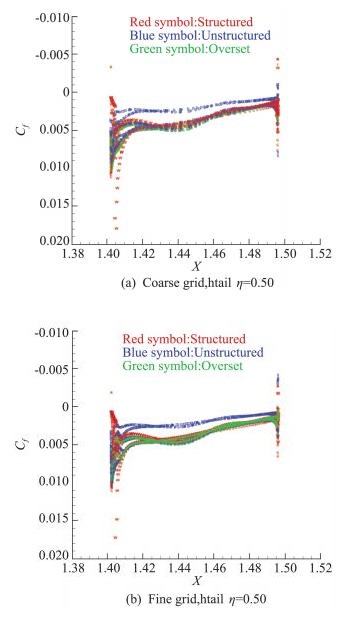
|
图 15 平尾典型站位摩擦阻力分布(η=0.50) Fig.15 Friction drag coefficients distribution at typical spanwise location of horizontal tail (η=0.50) |
在机翼的η=0.50站位上(图 14),PID:004结果明显异于其它结果。在平尾的η=0.50站位上(图 15),PID:004结果明显异于其它结果,PID:009.1、PID:016前后缘摩阻分布明显异常。以上数据异常的原因,可能是由于后置处理,也可能是计算方法本身导致的。除了以上异常的数据,其它计算结果摩阻分布彼此之间基本吻合,网格密度对摩阻分布基本没有影响。
4.5 Case 1计算结果的统计分析采用文献[30]中的统计分析方法,表 4和表 5分别给出了Case 1粗、中、细三套网格气动特性计算结果的中位数和标准误差,其中阻力系数、压差阻力系数CDp、摩擦阻力系数CDf的单位为count(1 count= 0.0001)。
| 表 4 Case 1结果中位数的比较 Table 4 Comparison of medians from Case 1 results |
|
|
| 表 5 Case 1结果标准误差比较 Table 5 Comparison of standard deviations from Case 1 results |
|
|
固定升力系数下,24组计算结果的迎角、阻力系数及压差阻力系数的中位数均随网格密度的增加而单调递减,摩擦阻力系数的中位数随网格密度的增加而略微增加,力矩系数基本不随网格密度的变化而变化。迎角的标准误差随网格密度的增加没有呈现单调变化,阻力系数及其分量、力矩系数的标准误差随网格密度的增加而减少。总体而言,网格密度增加降低了计算结果之间的数据散布度。
DPWIII选择了DLR-F6翼身组合体构型作为基本构型,该构型与AeCW-1选择的CHN-T1构型类似。DPW Ⅲ上共提交了26组网格收敛性的结果,其中20组结果完成三套网格的数值模拟工作。进一步扣除20组结果中的“outlier”结果(明显与其它计算结果不同的计算结果)还剩16组。Morrison[30]对这16组结果进行了统计分析,标准差的统计分析结果列在表 5中。由标准差的对比可以看出,除了摩阻系数的标准差外,AeCW-1计算结果的标准差小于DPW Ⅲ核心数值解的标准差。
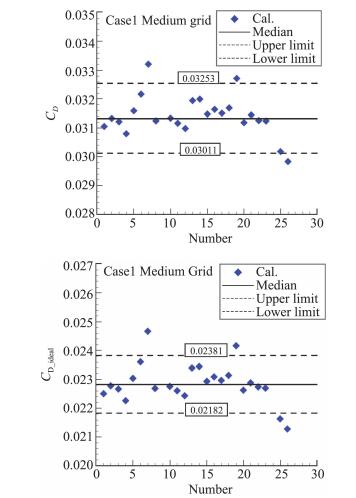
图 16和图 17分别给出了Case 1中等网格计算结果迎角、俯仰力矩系数、阻力系数、“理想阻力系数”(CD_ideal= CD-CL2/(π·AR))的统计分析结果。其中,“Median”代表计算结果的中位数,“Upper limit”和“Lower limit”代表以标准误差为参数的上下边界,横坐标为不同的计算结果(见表 3)。

|
图 16 Case 1迎角和力矩系数的统计分析 Fig.16 Statistical analysis of α and Cm for Case 1 |
|
图 17 Case 1阻力系数和理想阻力系数的统计分析 Fig.17 Statistical analysis of CD and CD_ideal for Case 1 |
迎角的统计结果中,超出标准差范围的分别是PID:003.1、PID:015.1;力矩系数的统计结果中,超出标准差范围的分别是PID:006、PID:017、PID:019.2;阻力系数及“理想阻力系数”的统计结果中,超出标准差范围的分别是PID:006、PID:014.1、PID:019.2。
5 Case 2计算结果及讨论Case 2是针对CHN-T1_S模型和CHN-T1_SA模型开展固定马赫数下的模型支撑装置和静气动弹性变形对气动特性数值模拟结果的影响研究。Case 2所采用的计算网格是在Case 1中等网格基础上构造的。AeCW-1组委会提供的Case 2多块对接结构网格规模达到了3359万、非结构网格规模达到了1916万。来流条件为:Ma=0.78,Re=3.3×106,α=-2.0°、-1.0°、0°、1.0°、2.0°、3.00°、3.50°、3.75°、4.00°、4.25°、4.50°。由于PID:007.2数据有误,以下的分析中均不包括这组数据。
5.1 气动特性随迎角的变化图 18给出了Case 2a气动特性的24组数值模拟结果,同时给出了FL-26的风洞试验结果及误差带,图中不包括PID:003.2结果(作者未提供)。
|
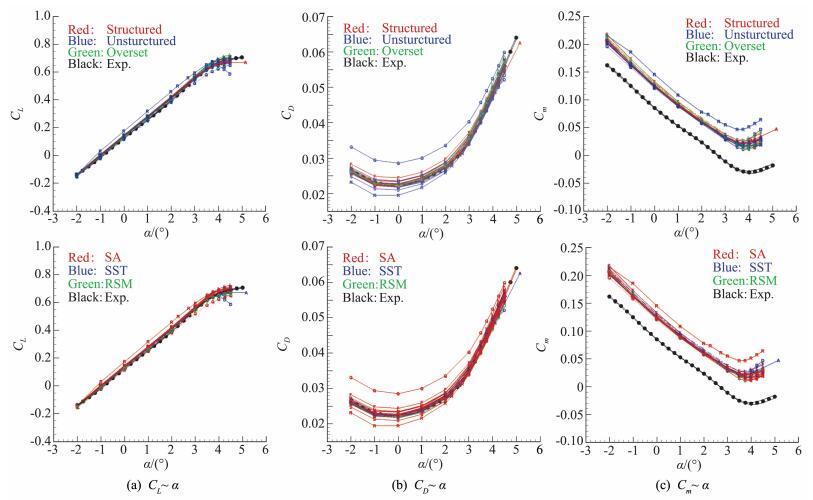
图 18 Case 2a气动特性曲线 Fig.18 Aerodynamic character curves for Case 2a |
由图 18(a)看出,PID:017计算结果略低于其它计算结果,PID:018升力系数计算结果略高于其它计算结果,PID:004计算结果出现了提前失速的情况;除了上述三组结果外,其它计算结果在计算迎角范围内,升力系数彼此之间吻合较好。总体而言,数值模拟得到的升力系数略高于相同迎角下的风洞试验结果。由图 18(b)看出,PID:017阻力系数计算结果在计算迎角范围内明显高于其它计算结果,PID:018阻力系数计算结果在小迎角范围内明显低于其它计算结果;其它计算结果在2°迎角以下的计算结果散布度明显大于2°迎角以上的计算结果散布度。总体而言,数值模拟得到的阻力系数与风洞试验结果之间尚可。由图 18(c)看出,PID:018力矩系数计算结果明显高于其它计算结果,其它计算结果之间一致性较好。总体而言,数值模拟得到的力矩系数明显高于风洞试验结果。
图 19给出了Case 2b气动特性的20组数值模拟结果,同时给出了FL-26的风洞试验结果及误差带。图中不包括PID:009.2、012.1、012.2、012.3、012.4五组计算结果(作者未提供)。
|
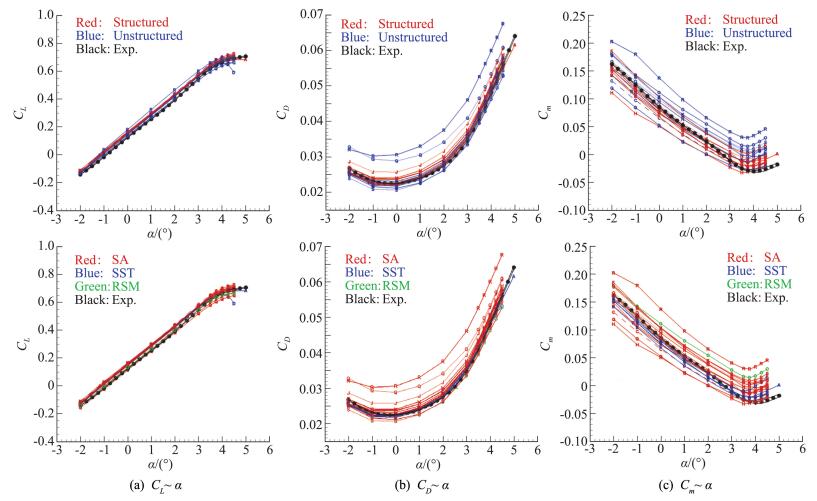
图 19 Case 2b气动特性曲线 Fig.19 Aerodynamic character curves for Case 2b |
由图 19(a)看出,除了PID:004和PID:018两组结果外,其它计算结果升力系数彼此之间吻合较好,数值模拟得到的升力系数依然略高于相同迎角下的风洞试验结果。由图 19(b)看出,PID:019.1阻力系数计算结果在小迎角范围内略低于其它计算结果,PID:017和PID:018计算结果在计算迎角范围内明显高于其它计算结果;除了上述三组结果外,其它计算结果的表现与图 18(b)相似。总体而言,数值模拟得到的阻力系数与风洞试验结果之间一致性尚可。由图 19(c)看出,PID:015.1和PID:018力矩系数计算结果明显高于其它计算结果,PID:008.1和PID:017力矩系数计算结果明显低于其它计算结果,其它计算结果之间一致性尚可,但与图 18(c)相比较,数据散布度明显增加。总体而言,计算模型考虑了风洞模型支撑以后,力矩系数计算结果与风洞试验结果的吻合程度显著提高。
图 20给出了Case 2c气动特性的19组数值模拟结果,同时给出了FL-26的风洞试验结果及误差带。图中不包括PID:009.2、011、012.1、012.2、012.3、012.4六组计算结果(作者未提供)。
|
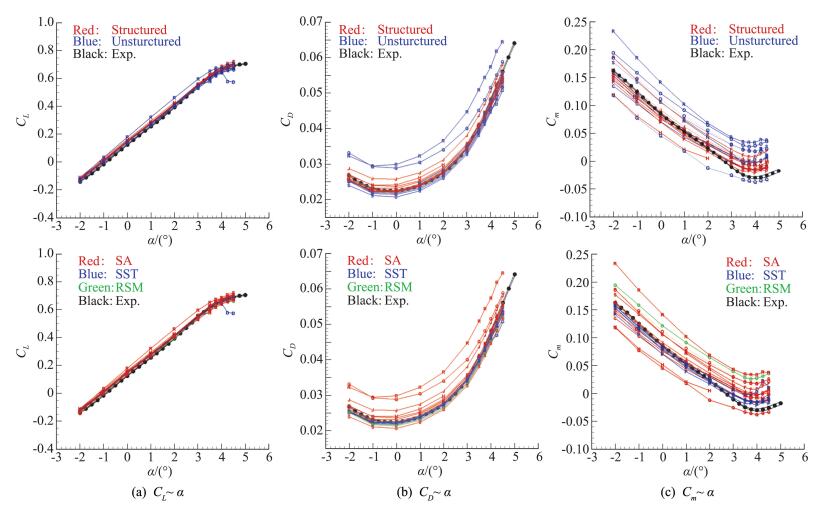
图 20 Case 2c气动特性曲线 Fig.20 Aerodynamic character curves for Case 2c |
由图 20(a)看出,除了PID:004和PID:018两组结果外,其它计算结果升力系数彼此之间吻合较好,与图 18(a)、图 19(a)相比较,数值模拟得到的升力系数与风洞试验结果的吻合程度明显提高。由图 19(b)看出,PID:010、PID:017和PID:018计算结果在计算迎角范围内明显高于其它计算结果;除了上述三组结果外,其它计算结果的表现与图 19(b)相似。总体而言,数值模拟得到的阻力系数与风洞试验结果之间一致性尚可。由图 19(c)看出,PID:015.1和PID:018力矩系数计算结果依然明显高于其它计算结果,PID:008.1和PID:017力矩系数计算结果依然明显低于其它计算结果,其它计算结果之间一致性尚可。总体而言,进一步考虑了风洞模型的静气动弹性变形后,与图 19相比较,风洞模型的静气动弹性变形对气动特性计算结果的影响不明显。这个结论与CRM构型的研究结论不同[6],CRM翼身组合体构型在Ma=0.85、α=4.0°、Re=5.0×106下,翼梢的负扭转角达到了-1.2°左右;而CHN-T1模型在Ma=0.78、α=4.0°、Re=3.3×106下,翼梢的负扭转角仅为-0.5°左右。
采用文献[17]中的统计分析方法,表 6给出了Case 2三种构型的升力线斜率CLα和力矩曲线斜率Cmα中位数,同时给出了FL-26风洞试验结果;表 7给出了Case 2三种构型气动特性导数的标准误差。
| 表 6 主要气动导数比较 Table 6 Typical aerodynamic character derivative |
|
|
由表 6、表 7看出,随着计算构型越发接近真实构型,升力线斜率的中位数逐渐降低,并更加接近试验值,标准差同时也逐步减少;力矩曲线斜率的中位数绝对值逐渐减少,并更加偏离试验值,标准差变化较大,原因有待于进一步分析。
| 表 7 气动导数标准误差 Table 7 Standard deviations of aerodynamic character derivative |
|
|
采用文献[30]中的统计分析方法,表 8给出了Case 2三种构型的零升迎角α0、零升阻力系数CD0和零升力矩系数Cm0的中位数,同时给出了FL-26风洞试验结果;表 9给出了Case 2三种构型的零升气动特性的标准误差。
| 表 8 零升气动特性中位数比较 Table 8 8 Comparison of aerodynamic character at CL=0 |
|
|
| 表 9 零升气动特性标准误差比较 Table 9 Comparison of standard deviations of aerodynamic character at CL=0 |
|
|
由表 8和表 9可以看出,对于α0而言,三种构型计算结果的中位数和计算结果的散布度随着模拟外形复杂度的增加没有呈现单调变化;对于CD0而言,三种构型计算结果的中位数单调下降,与试验结果基本吻合,但计算结果的散布度随着模拟外形复杂度的增加而增加;对于Cm0而言,计算模型中包括风洞模型支撑显著提高了Cm0计算结果与风洞试验结果的吻合程度,而风洞模型的静气动弹性变形对计算结果的影响不明显,计算结果的散布度随着模拟外形复杂度的增加而增加。
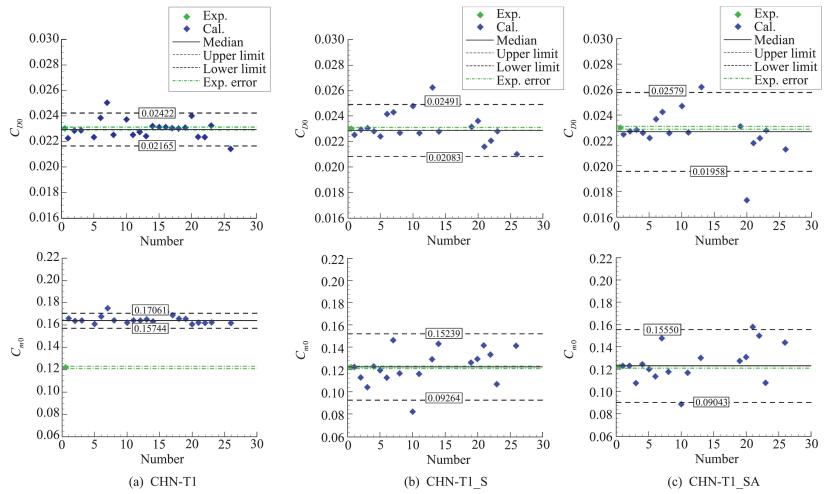
图 21给出了Case 2三种构型的零升气动特性的统计分析结果及相应的试验值(见表 3)。图中均不包含PID:017和PID:018两组数据(计算结果与其它结果误差太大)。Case 2a共22组数据,不包括PID:004(作者未提供);Case 2b共18组数据,不包括PID:009.2、PID:012.1、PID:012.2,PID_012.3、PID_012.4五组数据;Case 2c共17组数据,不包括PID:009.2、PID:011、PID:012.1、PID:012.2、PID_012.3和PID_012.4六组数据(作者未提供)。表 8和表 9中的统计分析数据与此相同。
|
图 21 Case 2零升气动特性的统计分析 Fig.21 Statistical analysis of aerodynamic character at CL=0 for Case 2 |
图 21(a)的CD0的统计分析结果中(左),超出标准差范围的结果为PID:005.1、PID:019.1;Cm0的统计分析结果中(右),超出标准差范围的结果为PID: 005.1。图 21(b)的CD0的统计分析结果中,超出标准差范围的结果为PID:010;Cm0的统计分析结果中,超出标准差范围的结果为PID:008.1。图 21(c)的CD0的统计分析结果中,超出标准差范围的结果为PID:010、PID:014.1;Cm0的统计分析结果中,超出标准差范围的结果为PID:008.1、PID:015.1。
6 Case 3计算结果及讨论Case 3是针对CHN-T1_S模型,开展固定升力系数下雷诺数对气动特性数值模拟结果的影响研究。Case 3所采用的高雷诺计算网格是在Case 2b计算网格基础上构造的。来流条件为:Ma=0.78,Re=3.3×106、15.0×106,CL =0.500±0.001。
表 10给出了12组Case 3计算得到的气动特性差量(高雷诺气动特性-低雷诺数气动特性)与试验值的比较。表 11给出了Case 3计算结果的标准误差。表 10、表 11及以下的图 22中,低雷诺数风洞试验结果来之FL-26,高雷诺数风洞试验结果来自ETW。
| 表 10 Case 3结果中位数的比较 Table 10 Comparison of medians from Case 3 results |
|
|
| 表 11 Case 3结果标准误差 Table 11 The standard deviations from Case 3 results |
|
|
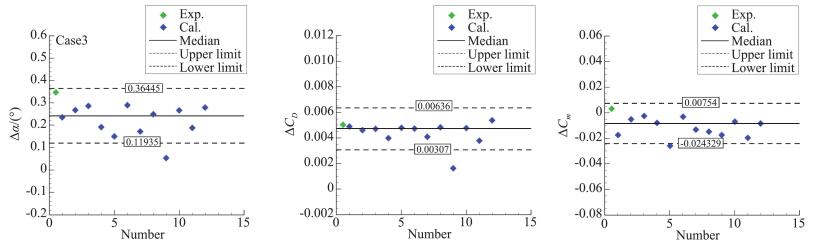
|
图 22 Case 3雷诺数影响的统计分析 Fig.22 Statistical analysis of the influence of Reynold number |
由表 10、表 11看出,计算得到的迎角差量与试验结果相差0.10°,标准差为0.07°;计算得到的阻力系数差量与试验结果相差3.1counts,但标准差达接近10 counts;计算得到的俯仰力矩系数差量与试验结果相差-0.0053,标准差达到了0.0092!总体而言,与试验结果相比,计算结果从定性上模拟了雷诺数导致的气动特性差量,定量上,尤其是力矩系数,有待于进一步提高模拟精度。
图 22给出了Case 3不同雷诺数下获得的气动特性差量的统计分析结果及相应的试验值。图 22的Δα与ΔCD的统计分析结果中,超出标准差范围的结果均为PID:014.4;ΔCm的统计分析结果中,超出标准差范围的结果为PID:008.1。
7 结论及建议基于本次AeCW-1可信度研讨活动所收集到的计算结果,基本结论如下:
(1) 国内自主研发的CFD软件与CFL3D软件计算结果精度相当;没有哪一种湍流模型、哪一种网格类型在数值模拟中呈现优势;
(2) Case 1算例:阻力网格收敛性较好,迎角及力矩网格收敛性较差;网格密度的增加并没有降低计算结果之间的散布度;典型站位上的压力分布与摩阻分布计算结果之间吻合较好;AeCW-1计算结果的标准差小于DPW Ⅲ“核心”计算结果的标准差。
(3) Case 2算例:从定性角度来看,升力与阻力计算结果之间数据散布度较小,俯仰力矩计算结果之间数据散布度较大;计算模型中包含风洞试验模型支撑装置显著改善了计算结果与风洞试验结果之间的吻合程度,静气动弹性对气动特性数值模拟结果的影响较小;零升阻力和零升力矩计算结果与试验结果之间吻合良好,零升迎角计算结果略低于试验结果;
(4) Case 2算例:从定量角度来看,比较CHN-T1_SA外形统计分析结果的中位数与纵向气动特性的试验结果,升力线斜率CLα的误差为4.7%,俯仰力矩斜率Cmα的误差为15.5%,零升阻力CD0的误差为1.3%,零升力矩Cm0的误差为0.8%;
(5) Case 3算例:与风洞试验结果相比,计算结果定性地模拟了雷诺数对气动特性的影响,定量方面,尤其是力矩系数,有待于进一步改进。
基于本次AeCW-1可信度研讨活动组织管理与数值模拟结果的统计分析,对于国内今后开展类似活动的主要建议如下:
(1) 分层次、系统地开展用于CFD可信度研究的高精度风洞试验。本次CHN-T1模型分别在FL-26和ETW开展了高精度的测力试验,为类似外形的CFD可信度研究提供了非常有价值的测力试验结果。遗憾的是缺乏测压试验、边界层测量、空间流场测量、来流湍流度测量等高精度试验结果(这也是我们现有的风洞试验结果与DPW同类试验相比的主要不足),这对于分析数值模拟结果与风洞试验结果的差异、改进计算方法和湍流模型存在诸多不便;
(2) 加强CFD方法、湍流模型和可信度分析方法研究。从本次会议的统计分析结果来看,网格规模的增加并没有明显提高计算结果之间的数据散布度,中国空气动力研究与发展中心也展示了百亿量级网格的数值模拟结果;计算结果与风洞试验结果定性方法吻合较好,定量方面距离精细化设计尚有不小的差距。这方面需要继续开展的工作包括转捩位置的影响、风洞洞壁干扰等方面,但更重要的是采用精细的、高精度的风洞试验结果,针对性的加强高阶精度计算方法、自动转捩模拟方法等方面的研究,以期为相关型号的研制提供更多的研究手段、更好的技术支持。
(3) 加强CFD知识的传承,提高从业者的软件应用能力。本次会议上,CFD数值模拟结果的提供者大多数是35岁以下的年轻人,这充分彰显了CFD研究领域持久的生命力。另一方面,从所提供的数据来看,部分年轻人CFD软件的应用能力有待于进一步提高。熟练而有经验的CFD软件使用者需要从数模处理、网格生成、流场计算、后置处理等多方面进行系统的培训并不断从工程应用中积累相关经验。
致谢: 感谢空气动力学会计算空气动力学专委会的大力支持,感谢AeCW-1组委会成员的努力工作,尤其感谢洪俊武、孟德虹、岳皓、王昊等同志在活动组织及数据处理方面付出的大量时间与精力。
| [1] |
ANTON P S, JOHNSON D J, BLOCK M, et al. Wind tunnel and propulsion test facilities: supporting analyses to an assessment of NASA's capabilities to serve national needs: RAND_TR134[R]. California: RAND, 2004.
|
| [2] |
MUJEEB R MALIK, DENNIS M BUSHNELL. Role of computational fluid dynamics and wind tunnels in aeronautics R&D: NASA/TP-2012-217602[R]. Hampton: NASA, 2012.
|
| [3] |
SLOTNICK J, KHODADOUST A, ALONSO J, et al. CFD vision 2030 study: a path to revolutionary computational aerosciences: NASA/CR-2014-218178[R]. Hampton: NASA, 2014.
|
| [4] |
OBERKAMPF W L, TRUCANOB T G. Verification and validation in computational fluid dynamics[J]. Progress inAerospace Sciences, 2002, 38: 209-272. DOI:10.1016/S0376-0421(02)00005-2 |
| [5] |
HEEG J, CHWALOWSKI P, FLORANCE J P, et al. Overview of the aeroelastic predication workshop[R]. AIAA 2013-0783, Reston: AIAA, 2013.
|
| [6] |
闫超, 席柯, 袁武力, 等. DPW系列会议述评与思考[J]. 力学进展, 2011, 41(6): 776-784. YAN C, XI K, YUAN W, et al. Review of thedrag prediction workshop series[J]. Advances in Mechanics, 2011, 41(6): 776-784. (in Chinese) |
| [7] |
王运涛. DPW Ⅳ~Ⅵ数值模拟技术综述[J]. 航空学报, 2018, 39(4): 021836. WANG Y T. An overview of DPW Ⅳ~Ⅵ numerical simulation technology[J]. Acta Aeronautica et Astronautica Sinica, 2018, 39(4): 021836. (in Chinese) |
| [8] |
王运涛. HiLiftPW-1~HiLiftPW-3数值模拟技术综述[J]. 航空学报, 2018, 39(7): 021997. WANG Y T. An overview of HiLiftPW-1 to HiLiftPW-3 numerical simulation technologies[J]. Acta Aeronautica et Astronautica Sinica, 2018, 39(7): 021997. (in Chinese) |
| [9] |
LEVY D W, VASSBERG J C, WAHLS R A, et al. Summary of data from the first AIAA CFD drag prediction workshop[J]. Journal of Aircraft, 2003, 40(5): 875-882. DOI:10.2514/2.6877 |
| [10] |
LAFLIN K R, VASSBERG J C, WAHLS R A, et al. Summary of data from the second AIAA CFD drag prediction workshop[J]. Journal of Aircraft, 2005, 42(5): 1165-1178. DOI:10.2514/1.10771 |
| [11] |
VASSBERG J C, TINOCO E N, MANI M, et al. Abridged summary of the third AIAA CFD drag prediction workshop[J]. Journal of Aircraft, 2008, 45(3): 781-798. DOI:10.2514/1.30572 |
| [12] |
VASSBERG J C, TINOCO E N, MANI M, et al. Summary of the fourth AIAA computational fluid dynamics drag prediction workshop[J]. Journal of Aircraft, 2014, 51(4): 1070-1089. DOI:10.2514/1.C032418 |
| [13] |
LEVY D W, LAFLIN K R, TINOCO E N, et al. Summary of data from the fifth computational fluid dynamics drag prediction workshop[J]. Journal of Aircraft, 2014, 51(4): 1194-1213. DOI:10.2514/1.C032389 |
| [14] |
TINOCO E N, BRODERSEN O P, KEYE S, et al. Summary of data from the sixth AIAA CFD drag prediction workshop: CRM Case 2 to 5: AIAA 2017-1208[R]. Reston: AIAA, 2017.
|
| [15] |
RUMSEY C L, LONG M, STUEVER R A, Summary of the first AIAA CFD high lift prediction workshop: AIAA 2011-0939[R]. Reston: AIAA, 2011.
|
| [16] |
RUMSEY C L, SLOTNICK J P. Overview and summary of the second AIAA high lift prediction workshop: AIAA 2014-0747[R]. Reston: AIAA, 2014.
|
| [17] |
RUMSEY C L, SLOTNICK J P, SCLAFANI A J. Overview and summary of the third AIAA high lift prediction workshop: AIAA-2018-1258[R]. Reston, VA: AIAA, 2018.
|
| [18] |
余永刚, 周铸, 黄江涛, 等. 单通道客机气动标模CHN-T1设计[J]. 空气动力学学报, 2018, 36(3): 505-513. YU Y G, ZHOU Z, HUANG J T, et al. Aerodynamic design of a standard model CHN-T1 for single-aisle passenger aircraft[J]. Acta Aerodynamica Sinica, 2018, 36(3): 505-513. DOI:10.7638/kqdlxxb-2018.0072 (in Chinese) |
| [19] |
李强, 刘大伟, 许新, 等. CHN-T1标模2.4米风洞气动特性试验研究[J]. 空气动力学学报, 2019, 37(2): 337-344. LI Q, LIU D W, XU X, et al. Experimental study of aerodynamic characteristic of CHN-T1 standard model in 2.4 m transonic wind tunnel[J]. Acta Aerodynamica Sinica, 2019, 37(2): 337-344. DOI:10.7638/kqdlxxb-2018.0099 (in Chinese) |
| [20] |
李伟, 孟德虹, 王运涛, 等. 采用TRIP3.0数值模拟CHN-T1模型[J]. 空气动力学学报, 2019, 37(2): 272-279. LI W, MENG D H, WANG Y T, et al. Numerical Simulation of CHN-T1 model with TRIP3.0[J]. Acta Aerodynamica Sinica, 2019, 37(2): 272-279. DOI:10.7638/kqdlxxb-2018.0225 (in Chinese) |
| [21] |
张耀冰, 唐静, 陈江涛, 等. 基于非结构混合网格的CHN-T1标模气动特性预测[J]. 空气动力学学报, 2019, 37(2): 262-271. ZHANG Y B, TANG J, CHEN J T, et al. Aaerodynamic characteristics prediction of CHN-T1 standard model with unstructured grid[J]. Acta Aerodynamica Sinica, 2019, 37(2): 262-271. DOI:10.7638/kqdlxxb-2018.0201 (in Chinese) |
| [22] |
王年华, 常兴华, 赵钟, 等. 基于HyperFLOW平台的客机标模CHN-T1气动性能预测及可信度研究[J]. 空气动力学学报, 2019, 37(2): 301-309. WANG N H, CHANG X H, ZHAO Z, et al. Aerodynamic performance prediction and credibility study of the transport model CHN-T1 based on HyperFLOW solver[J]. Acta Aerodynamica Sinica, 2019, 37(2): 301-309. DOI:10.7638/kqdlxxb-2018.0183 (in Chinese) |
| [23] |
杜一鸣, 庞超, 舒博文, 等. 基于嵌套网格的CHN-T1标模数值模拟[J]. 空气动力学学报, 2019, 37(2): 280-290. DU Y M, PANG C, SHU B W, et al. Numerical simulation of the standard model CHN-T1 based on overset grid[J]. Acta Aerodynamica Sinica, 2019, 37(2): 280-290. DOI:10.7638/kqdlxxb-2018.0195 (in Chinese) |
| [24] |
SPALART P R, ALLMARAS S R. A one-equation turbulence model for aerodynamic flows: AIAA-1992-0439[R]. Reston, VA: AIAA, 1992.
|
| [25] |
MENTERF R. Two-equation eddy-viscosity turbulence models for engineering application[J]. AIAA Journal, 1994, 32(8): 1598-1605. DOI:10.2514/3.12149 |
| [26] |
SPALART P R. Strategies for turbulence modelling and simulations[J]. International Journal of Heat and Fluid Flow, 2000, 21: 252-263. DOI:10.1016/S0142-727X(00)00007-2 |
| [27] |
CECORA R D, EISFELD B, PROBST A, et al. Differential Reynolds stress modeling for aeronautics[J]. AIAA Journal, 2015, 53(3): 739-755. DOI:10.2514/1.J053250 |
| [28] |
聂胜阳, 高正红, 黄江涛. 微分雷诺应力模型在激波分离流中的应用[J]. 空气动力学学报, 2012, 30(1): 52-56. NIE S Y, GAO Z H, HUANG J T. Differential Reynolds stress model for shock & separated flow[J]. Acta Aerodynamica Sinica, 2012, 30(1): 52-56. DOI:10.3969/j.issn.0258-1825.2012.01.009 (in Chinese) |
| [29] |
WILCOX D C, TRACI R M. A complete model of turbulence: AIAA-76-351[R]. Reston, VA: AIAA, 1976
|
| [30] |
MORRISON J H. Statistical analysis of the fourth drag prediction workshop computational fluid dynamics solutions[J]. Journal of Aircraft, 2014, 51(4): 1090-1100. DOI:10.2514/1.C032737 |
 2019, Vol. 37
2019, Vol. 37


