具备高升阻比外形的高超声速飞行器采用无动力助推滑翔飞行模式时因兼具速度快、射程远、精度高、机动性强的特点,一直是世界各航天大国的发展重点。从目前高超声速技术发展来看,美国代表了当前该类飞行器的最新方向,其围绕助推滑翔技术开展的研究自20世纪50年代起一直持续到现在,比较有代表性的项目包括BGRV(Boost-Glide Reentry Vehicle)、HGV(Hypersonic Glide Vehicle)、CAV(Common Aero Vehicle)、HTV-2(Hypersonic Technology Vehicle 2)等。其中HTV-2作为无动力助推滑翔式高超声速技术最具前瞻性和创新性的验证机,在2010年和2011年分别进行了两次飞行试验,但均以失败而告终。DARPA对飞行试验进行事故调查后认为目前对HTV-2所代表的非常规、创新性带乘波体特征的融合体布局而言,其在高超声速条件下的空气动力学现象依然存在认知上的盲区。而“先进高超声速武器”(Advanced Hypersonic Weapon,AHW)项目是美国陆军提出的一种类似于HTV-2但采用常规布局的助推滑翔式高超声速飞行器方案,最初该计划是作为空军常规快速全球打击计划的备份项目,关注度不及HTV-2。但HTV-2两次飞行失利,AHW在2011年11月首次进行试飞却取得了成功,并完成了4000 km的预定飞行[1-2],虽然2014年第二次飞行失败,但2017年成功进行了第三次飞行试验,完成了滑翔飞行器的综合验证评估,这也是美国首次成功真正实现了高超声速滑翔飞行的飞行试验。
考虑到HTV-2项目当前的技术困境和巨大的资金消耗以及AHW项目的试飞成功,美国当前计划利用HTV-2验证飞行试验所获得的研究成果,进一步降低气动风险,将重心转移至更加经济实用且具备可实现性的AHW项目上来,并计划在2020年附近转入技术成熟与风险降低阶段,积极推进其向武器装备转化,形成初始作战能力,因此该方案有望成为未来美国最先实现型号研制的高超声速无动力助推滑翔飞行器。AHW是以20世纪80年代美国能源部与国防部共同发展的桑迪亚国家实验室的“桑迪亚有翼赋能再入飞行器试验”(Sandia Winged Energetic Reentry Vehicle Experiment,SWERVe)计划为基础发展起来的。SWERVe是马赫数12~14的细长锥体机动再入体,锥度为10.5°,有小尺寸机翼和升降副翼,飞行高度为30~70 km,速度达马赫数20。AHW由载荷和运载器构成,其载荷为高超声速滑翔体(HGB),是在SWERVe的基础上改进而成,采用双锥十字形小尺寸弹翼的气动布局,使其能在大气中有更快的飞行速度和更远的滑翔距离,其设计指标为具有在35 min内飞行6000 km的能力。
AHW的首飞试验证明了双锥十字形小尺寸弹翼外形作为高超声速滑翔体构型的可行性,因此本文以类AHW双锥十字小尺寸弹翼布局为研究对象,探索采用该类外形作为助推滑翔飞行器时布局设计阶段所涉及的共性问题。重点进行了该类外形升阻比及容积率等关键气动特性的参数敏感性分析,利用正交设计和多目标优化设计对弹体进行了优化,并采用数值模拟方法进行了验证分析。在优化弹体基础上,探讨了尺寸约束和防热需求下该类外形的质心布置、操纵方式及弹体与控制舵面间的相互匹配问题,并对优选外形的气动特性及配平效率进行了详细设计分析,给出了布局建议。
1 参数化布局方案设计及优化本文根据公开文献资料,参考AHW的外形,利用二次曲线[4-8]及基于类型和形状函数的CST方法[9-12],生成了类AHW双锥十字形小尺寸“裙+尾翼”飞行器气动布局(见图 3)。该飞行器的横截面形状采用CST函数生成,上下表面的控制线采用二次曲线生成,以保证飞行器不同部位曲线斜率一致从而足够光滑[13]。
对于以载荷投放为目的的无动力滑翔飞行器而言,升阻比和容积率是两个很重要的关键指标。飞行器的升阻比越大,飞行器飞行的水平距离越大,其返回着陆场的可能性或迫降的范围越大,故而对于AHW无动力滑翔飞行器而言,其升阻比很大程度上决定了其总航程及横向机动能力,同时容积率则决定了其单次飞行任务的运载能力,因此在初步布局设计阶段,本文将升阻比的最大化及一定的容积率要求作为关键的设计目标。正交试验设计方法是用于多因素试验的一种设计方法,它能够用较少的试验次数得到优化过程更多的信息[14], 采用正交设计方法可以极大减少试验次数,因此可以通过该方法研究关键因素的影响,进行参数敏感性分析,得到初步的优选布局。
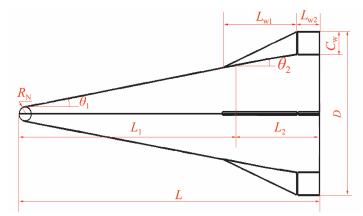
飞行器的几何外形特征和稳定的配平状态决定了飞行器的升阻比及阻力。如图 1所示,AHW外形的主要设计变量包括头部半径RN、第一锥锥角θ1、第一锥长度L1、第二锥锥角θ2、第二锥长度L2、底部直径D、边条长度Lw1、控制舵长度Lw2等。考虑到对于AHW这种轴对称外形而言,升力主要来源于主弹体,控制舵尺寸匹配主要用于提供操纵力矩,因此前期设计阶段可先不考虑对控制舵和边条尺寸的匹配设计,仅对弹体几何参数进行优化设计。而飞行器的底部直径D和总长度L等整体参数,由于受运载器限制一般是固定的。在总长和底部直径确定状态下,第一、二锥角及长度之间只有两个独立变量,为此,可使用正交表L9(34)布置头部半径、第一锥角、第二锥段起始位置三因素三水平的正交试验(表 1),建立总长L和底部直径D给定状态下,头部半径与底部直径钝度比RN/D取值范围[0.05,0.2],第一锥角θ1变化范围[5°,10°], 第一段锥与总长之比L1/L取值范围为[0.4,0.8]的正交设计优化模型,根据三变量变化范围,共设计9组不同布局外形,通过不同布局外形下升阻比和容积率的极差,分析AHW主要弹体几何参数对气动特性的影响规律,获得升阻比及容积率对几何参数的敏感性结论。
|
图 1 AHW外形布局参数示意图 Fig.1 The parameters of AHW configuration |
| 表 1 正交表L9(34)的设置及相应结果 Table 1 Experiment assignment with orthogonal table L9(34) |
|
|
在高超声速飞行器布局概念设计阶段,工程气动力预测方法因其快速有效的特点仍是不可缺少的设计工具,国外的工程气动力预测工具自20世纪60年代发展以来至今仍在不断发展和应用于高超声速飞行器设计,如S/HABP[10-11]、CBAERO[12]、ZONAIR[15]等。本文布局设计所采用的工程气动力预测方法同试验数据和数值模拟结果已进行对比验证,并且大量应用于高超声速飞行器的设计[16-21],基本能够满足布局设计阶段的要求。基于以上方法进行正交试验设计,表 1同时给出了高度30 km下,马赫数为7,迎角为10°时不同试验外形下的升阻比特性及容积率。通过极差RL/D、RVu分析可知,在当前长度和底部直径给定状态下,升阻比主要受头部半径和第一锥的角度影响较大,其中升阻比随头部半径的减小而增大,并随第一锥角的增大呈先增加后减小的趋势,此外升阻比随第一段锥长度关联较小,要实现升阻比最优,可考虑在满足防热需求下头部半径取值到最小,第一锥角在9°~12°附近进一步优化。同时由于正交试验设计固定了弹体长度和底部直径,因此容积率受三因素变化不太明显,但随头部半径的增加和第一段锥长度增加呈减小趋势,随第一锥角的增大而增大。综合分析可知,考虑升阻比和容积需求,需要减小头部半径,适当减小第一段锥长度,并在第一锥角9°~12°附近进行和第二锥角的匹配优化。
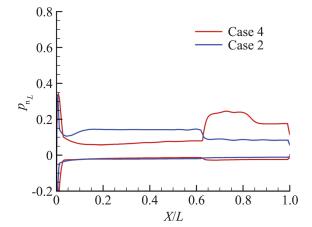
选取正交优化得到的最优外形方案2以及方案4为代表,通过数值模拟求解三维可压缩NS方程对高度30km下,马赫数为7,迎角为10°工况下工程算法的正交优化结果进行了验证分析。图 2给出了两种典型外形流场压力分布,图 3给出了两种外形子午线上压力在升力方向上的分量。

|
图 2 正交设计中方案2与方案4数值模拟压力分布对比 Fig.2 Comparison of simulated pressure contour between orthogonal experimental Case 2 and optimal Case 4 |
通过图 2及图 3的对比分析可知,在同样的长度及底部直径约束下,正交设计方案4的布局为头部半径较大且第一锥角小于第二锥角的布局,这导致了该外形头部产生阻力较大,同时在第二锥角下表面处出现了强激波,上表面压力由于压缩拐角的存在突然增加。而较优外形方案2为第一锥角大于第二锥角的布局,气流流经第一锥角到达第二锥角时有膨胀效应,因此没有强激波出现,导致第二锥角处上下表面压力均小于方案4的布局。通过子午线上压力在升力方向分量对比可知,方案2相较于方案4,第一段锥升力有所增加,而第二段锥的升力则减小。整体升阻力计算分析结果表明方案2相较于方案4,升力系数降低了6.8%,虽然升力系数有所降低,但该外形减阻效果更明显,相较于方案4阻力系数降低约37.1%,因此升阻比提升约0.6,同工程气动力方法升阻比提升0.63的预测结果基本一致。从采用工程气动力得到的正交设计结果和采用数值计算得到的结果对比来看,二者优化趋势相同,同时数值计算结果也验证了正交设计参数敏感性分析的结论:即在当前尺寸约束下具备更小的头部半径,较大的第一锥角和较小的第二锥角匹配特征的外形在升阻比方面更具优势,因此可以采用本文的工程气动力方法开展进一步布局优化研究。
|
图 3 正交设计方案4与最优外形方案2子午线压力在升力方向分量对比 Fig.3 Comparison of meridian line pressure component in the lift direction between orthogonal experimental Case 4 and optimal Case 2 |
按照正交设计结果分析(0.05,9°,0.4)应该是较优的设计组合,因此该样点可以作为多目标优化较优的初值状态。在正交设计单点定性分析基础上本文采用多目标优化方法对弹体进行进一步优化设计,采用加权和方法对多个目标进行加权处理将其转化为单目标优化问题, 同时利用罚函数法将约束优化问题转换成无约束优化问题, 并采用随机投点法和随机射线法进行求解[6]。本文给出的具体优化设计模型为求具备最大升阻比的气动布局,即:max((L/D)max)。
满足约束条件:
(1) 全长L及底部直径D保持固定不变, 即:L=L0, D=D0;
(2) 设计变量为头部半径与底部直径之比RN/D0、第一锥角θ1、第一锥长与总长度之比L1/L0,其设计域为:
| $ \begin{array}{l} \left[ {0.05, 5^\circ , 0.4} \right] \le X = [{R_{\rm{N}}}/{D_0}, {\theta _1}, {L_1}/{L_0}]\\ \le \left[ {0.2, 12^\circ , 0.8} \right]; \end{array} $ |
(3) 计算状态:Ma=7,0°≤α≤20°;
(4) 容积利用率:
(5) 设计变量初值:X0=[0.05, 9°, 0.4]。
经过优化分析,最后得到优化结果如下,可以看出,通过正交设计定性分析得到的初值结果基本已经比较接近最优值,通过多目标优化设计,最大升阻比能进一步提升6.7%,容积率提升1.4%。
| 表 3 弹体优化前后结果分析对比 Table 3 Comparison between original and optimized biconic body |
|
|
在当前优化弹体尺寸基础上,在初步给定边条和控制舵尺寸下得到的优化外形如图 4所示,后续气动布局特性分析及操纵面设计将围绕该外形展开。

|
图 4 AHW优化外形 Fig.4 Optimized configuration |
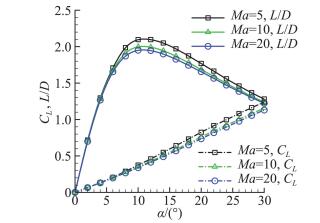
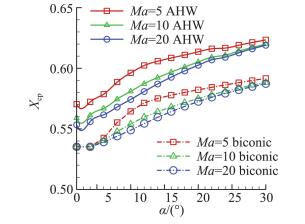
采用工程气动力方法进行优化后外形的气动特性分析, 该方法基于内伏牛顿理论[22-25],通过对干扰因子和等效迎角等概念的引入[22],考虑了舵-体、体-舵间的气动干扰, 其计算精度经过了风洞试验和数值计算进行验证[16-25]。图 5及图 6给出了本文布局外形在单独弹体不带控制及带控制舵无舵偏时Ma=5、10、20,侧滑角为0°状态下的升阻力特性及压心特性。从图 5中可以看出,不同的马赫数下升阻比特性变化规律具有相似性,最大升阻比均出现在10°~12°附近,且相同迎角下随马赫数增加升阻比略有降低。在高超声速范围内该外形最大升阻比可达2.0左右,且升力系数在0.5附近,同时升力线斜率也比较大,因此具备较好的升阻比特性。
|
图 5 不同马赫数下升力及升阻比特性 Fig.5 Lift and lift to drag ratio |
|
图 6 带边条控制舵与不带边条控制舵压心特性 Fig.6 Pressure center characteristic of AHW analog with and without control surface |
从图 6压心变化规律来看,控制舵的存在使得压心后移,且随马赫数增大,相同迎角下压心逐步前移;同时相同马赫数下压心随迎角增大逐步后移,因此符合稳定性要求,同时在最大升阻比对应的中等迎角范围内,压心变化较为明显,因此可以较为容易获得所需配平。
飞行器具备较高的控制效率时才能实现机动飞行, 这对质心/压心位置提出了要求,通常二者需要比较接近[23],以提高机动能力和减小伺服系统消耗,因此带控制舵的双锥稳定性和机动性是相互矛盾的,必须通过质心校调以及控制舵面设计进行静稳定裕度/操纵效率协调[23, 26]。
本文外形控制舵面包含边条和可活动舵面两部分,其中水平方向的固定边条可以看作附加升力面,具备一定的增升作用,在有迎角飞行下可使压心后移,有效影响力矩特性和配平特性,同时具备整流作用,有利于尾部可活动舵面的防热。由于飞行器在高超声速飞行时,外露活动控制面很难承受严重的气动加热和烧蚀,因此采用静不稳定设计使得配平状态下舵面等效迎角很小十分必要[22-23]。
尺寸相同的活动控制面,设计方式主要包括后缘舵和全动舵两种布局形式,后缘舵负舵面偏转时舵面处于飞行器背风面低压区,舵效约为相同正舵偏时的一半,且飞行末端低空高动压下舵面铰链力矩较大,可能会导致控制能力不足,但由于舵轴偏转时不会像全动舵一样存在剪刀缝,因此引起的升阻比损失较小,布局方式有利于热防护;而全动舵偏转时铰链力矩较小,对舵机载荷要求较低,同时正负舵偏时均有舵面处于高压区,因此俯仰及偏航舵效要强于后缘舵,但存在的问题是舵面偏转时,舵面前缘暴露在高压来流中,会形成比较大的升阻比损失[27]。
无论是全动舵还是后缘舵,都面临着边条-舵干扰问题,文献[27]对滑翔飞行器两种不同形式的翼-舵干扰及舵效问题进行了风洞及数值试验,结果表明全动舵在临近空间范围内作为控制舵面具有一定优势[27],因此本文作为初步布局设计考虑采用全动舵设计。控制舵面布局形式可以采用十字布局或者叉字布局,对于这两类布局开展的研究已经较多,且有定论[23, 27-28],本文不再进行讨论。由于十字布局控制回路简单,舵面偏转范围较大,本文仅讨论十字布局下边条加全动舵的操纵面匹配问题。该布局的俯仰运动由水平两舵偏转加以控制,偏航运动由垂直方向两片舵控制, 滚转运动则由逆时针或者顺时针两两差动四个舵加以控制[28]。假定上、左、下及右舵面偏转角为δ1、δ2、δ3及δ4表示, 且上下舵面前缘向左为负舵偏,左右舵面前缘向下为负舵偏, 则俯仰、偏航及滚转三个方向的操纵可以表示为[25]:
| $ {俯仰控制{\delta _\phi } = \frac{{{\delta _2} + {\delta _4}}}{{2}}{\rm{ }}, } $ |
| $ {偏航控制{\delta _\psi } = \frac{{{\delta _1} + {\delta _3}}}{2}, } $ |
| $ {滚转控制{\delta _\gamma } = {\rm{ }}\frac{{ - {\delta _1} - {\delta _2} + {\delta _3} + {\delta _4}}}{4}{\rm{。}}} $ |
此处质心位置采用静不稳定设计,选取范围为单独弹体压心之后。采用前述工程气动力方法进行气动特性分析,图 7给出了在边条长度确定条件下,不同质心和舵面尺寸时,无侧滑状态下俯仰控制舵的舵偏效率(舵面尺寸通过控制舵展向与宽度之比R尺寸调节,宽度固定)。由于该飞行器为滑翔类飞行器,为了追求更大的航程,整个飞行器过程中通常迎角需要配平在最大升阻比附近,考虑到最大升阻比在10°~12°附近,因此配平范围最好能覆盖8°~15°范围内的配平,同时在末端对地攻击时,又需要近乎垂直的落地速度,因此也需要兼顾具备大迎角配平的能力。
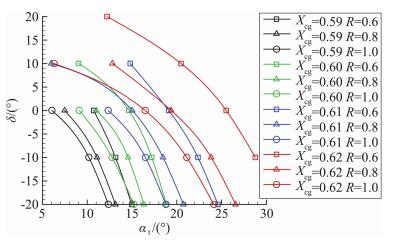
|
图 7 配平效率与舵面尺寸 Fig.7 Trimming efficiency vs. flaps size |
从图 7中可以看出,相同舵面尺寸下,随质心后移,配平迎角的最大值和最小值均增加;同时在相同的质心位置下,随舵面面积增加配平迎角的最大值和最小值均减小。质心为0.59时,因太过靠前,在不同舵面尺寸下配平范围均不太合理;当质心为0.62时,因比较靠后,在较小的舵面尺寸下也无法得到较好的配平。结合图 7分析可知,控制舵长宽比为0.6,质心位置为0.60时,能够实现9°~18°迎角配平;质心位置为0.61,舵面长宽之比为0.8时能够实现6°~21°配平及质心位置0.62,舵面长宽之比为1时能够实现6.3°~24°迎角配平可以初步满足要求。
结合图 8所示三种配置下所得到配平升阻比分析,选择质心位置0.61,控制舵展长与宽度之比为0.8时可以得到较大的配平迎角范围以及较高的配平升阻比。此时舵效较高,可以用较小的正舵偏得到想要的最大升阻比附近配平以及利用负舵偏实现大迎角配平,此时舵面等效迎角较小,对高超声速飞行下的舵面防热比较有利。
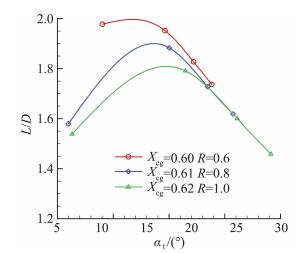
|
图 8 不同条件下的配平升阻比 Fig.8 Trimming lift to drag ratio under different conditions |
飞行器在稳定飞行时既要保证纵向稳定,又要保证其横侧向的稳定性及可控性[23]。对于AHW飞行器而言, 锥形运动是其最重要的机动动作之一,飞行器在机动飞行时其俯仰及偏航配平状态下绕飞行速度轴滚转,但飞行器并不绕体轴自转[26],因而飞行器的侧滑角和迎角将会交替变化[23]。图 9为飞行器的配平迎角αt及侧滑角βt随俯仰舵偏角δp及偏航舵偏角δy的变化规律。从图中可以看出俯仰方向配平效率较高,大于偏航方向配平效率。对偏航方向进行配平时,会对俯仰方向的配平带来影响,偏航舵偏越大,俯仰方向在相同舵偏下所能达到的配平迎角越小。另一方面, 俯仰方向配平也会使得偏航配平舵效降低,并使得配平侧滑角减小。因此锥形运动时各个控制舵面的控制效率会迎角和侧滑角的交替变化产生差异, 同时偏航控制使得偏航力矩为零的同时,不可避免会产生滚转力矩,因此在飞行时存在俯仰、偏航和滚转的较为严重的交叉耦合,需要进一步详细研究。
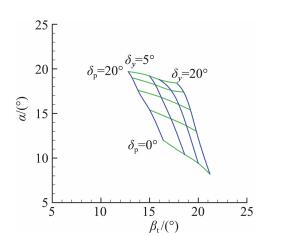
|
图 9 俯仰及偏航配平特性 Fig.9 Pitching and yawing trimming characteristic |
本文参考AHW外形,研究了此类双锥十字形小尺寸弹翼助推滑翔飞行器布局的优化设计问题。综合利用参数化外形生成方法,提出了一种类AHW气动布局运外形,采用工程气动力算法及正交设计对外形进行了参数敏感性及初步优化,并采用数值模拟进行了验证分析,在此基础上利用多目标优化方法进行了进一步优化设计及舵面设计,给出了布局建议,研究表明:
(1) 宜采用较大的第一锥角和较小的第二锥角组合设计,在匹配的质心和舵面配置下,优化后类AHW气动布局具备较高的升力、升阻比特性及较好的容积利用率,同时能够实现滑翔时最大升阻比对应的中小迎角配平以及落地攻击时大迎角配平。
(2) 考虑助推滑翔飞行器严峻的防热问题,该类外形需要采用静不稳定及较小的静稳定裕度设计使得舵面效率较高,并且实际舵面等效迎角较小。
(3) 对该类外形的俯仰和偏航配平分析表明,二者存在较强耦合,考虑飞行机动时俯仰、偏航和滚转三者的交叉耦合,还需进一步对滚转控制及飞行机动特性进行研究。
总结来看,带边条的双锥十字控制舵布局的AHW是较常规布局中能够实现高升力、高升阻比高超声速滑翔飞行的一种可行方案。但考虑到边条-舵的布局方式,缝隙干扰会引起的严峻防热问题,控制舵与边条之间的缝隙及尺寸匹配等还应作为重点要解决的问题进行更为详细的计算分析,同时考虑机动状态下俯仰、偏航和滚转下的交叉耦合,对滚转控制及机动飞行特性仍需进一步研究。
| [1] |
US Army Space and Missile Defense Command/Army Forces Strategic Command. Advanced hypersonic weapon program environmental assessment[Z]. 2011.
|
| [2] |
高清, 赵俊波, 李潜. 类HTV-2横侧向稳定性研究[J]. 宇航学报, 2014, 35(6): 657-662. GAO Q, ZHAO J B, LI Q. Study on lateral-directional stability of HTV-2 like configuration[J]. Journal of Astronautics, 2014, 35(6): 657-662. DOI:10.3873/j.issn.1000-1328.2014.06.006 (in Chinese) |
| [3] |
战培国. 美国陆军先进高超声速武器气动问题分析[J]. 航空科学技术, 2015, 26(1): 07-11. ZHAN P G. Aerodynamic analysis of US army advanced hypersonic weapon[J]. Aeronautical Science&Technology, 2015, 26(1): 07-11. (in Chinese) |
| [4] |
FENG Y, TANG W, GUI Y W. Optimization of configuration and trajectory for hypersonic vehicles[J]. Acta Aerodynamica Sinica, 2014, 32(6): 800-805. |
| [5] |
FENG Y, TANG W, GUI Y W. Aerodynamic configuration optimization by the integration of aerodynamics, aerothermodynamics and trajectory for hypersonic vehicles[J]. Chinese Science Bulletin, 2014, 59(33): 4608-4615. DOI:10.1007/s11434-014-0534-9 |
| [6] |
唐伟, 张勇, 李为吉, 等. 二次曲线截面弹身的气动设计及优化[J]. 宇航学报, 2004, 25(4): 429-433. TANG W, ZHANG Y, LI W J, et al. Aerodynamic design and optimization for vehicles with conic cross section. Optimization of configuration and trajectory for hypersonic vehicles[J]. Journal of Astronautics, 2004, 25(4): 429-433. DOI:10.3321/j.issn:1000-1328.2004.04.015 (in Chinese) |
| [7] |
KULFAN B M. Recent extensions and applications of the "CST" universal parametric geometry representation[R]. AIAA 2007-7709, 2007.
|
| [8] |
KULFAN B M. A universal parametric geometry representation method-"CST"[R]. AIAA 2007-62, 2007.
|
| [9] |
冯毅, 唐伟, 肖光明, 等. 类X37运载器气动布局概念设[J]. 空气动力学学报, 2012, 31(1): 94-98. FENG Y, TANG W, XIAO G M, et al. Aerodynamics configuration conceptual design for X-37 analog transporter[J]. Acta Aerodynamica Sinica, 2012, 31(1): 94-98. (in Chinese) |
| [10] |
GENTRY A E, SMYTH D N, OLIVER W R. The mark IV supersoic/hypersonic arbitrary-body program, Vol.I[R]. McDonnell-Douglas Corp, Technical Report AFFDL-TR-73-159, 1973.
|
| [11] |
WON H, LEVINE S, PFAENDER H, et al. Using response surface metamodels to optimize the aerodynamic performance of a high speed stand of missile within a multi-disciplinary environment[R]. AIAA 2002-5855, 2002.
|
| [12] |
MICHAEL J G, ROBERT D B. Analytic hypersonic aerodynamics for conceptual design of entry vehicles[R]. AIAA 2010-1212, 2010.
|
| [13] |
刘深深, 解静, 冯毅, 等. 一种仿HX扁平面对称类升力体气动布局分析[J]. 空气动力学学报, 2017, 35(6): 787-791. LIU S S, XIE J, FENG Y, et al. Aerodynamic characteristics analysis for HX analog lifting body[J]. Acta Aerodynamica Sinica, 2017, 35(6): 787-791. DOI:10.7638/kqdlxxb-2015.0187 (in Chinese) |
| [14] |
杨肖峰, 唐伟, 桂业伟. CSTS返回舱气动布局研究[J]. 空气动力学学报, 2014, 32(4): 493-498. YANG X F, TANG W, GUI Y W. Aerodynamics configuration study for CSTS reentry capsule[J]. Acta Aerodynamica Sinica, 2014, 32(4): 493-498. DOI:10.7638/kqdlxxb-2012.0154 (in Chinese) |
| [15] |
LIU D D, CHEN P C, TANG L, et al. Integrated hypersonic aerothermoelastic methodology for transatmospheric vehicle(TAV)/thermal protection system(TPS) structural design and optimization[R]. ZONA Technology, Inc, Technical Report AFRL-VA-WP-TR-2002-3047, 2002.
|
| [16] |
冯毅, 唐伟, 任建勋, 等. 飞行器参数化建模方法研究[J]. 空气动力学学报, 2012, 30(4): 546-550. FENG Y, TANG W, REN J X, et al. Parametric geometry representation method for hypersonic vehicle configuration[J]. Acta Aerodynamica Sinica, 2012, 30(4): 546-550. DOI:10.3969/j.issn.0258-1825.2012.04.020 (in Chinese) |
| [17] |
冯毅, 唐伟, 肖光明, 等. 类X33运载器气动特性分析[J]. 空气动力学学报, 2013, 31(4): 473-476. FENG Y, TANG W, XIAO G M, et al. Aerodynamics analysis for X-33 analog lifting body transporter[J]. Acta Aerodynamica Sinica, 2013, 31(4): 473-476. (in Chinese) |
| [18] |
肖光明, 冯毅, 唐伟, 等. 类ATLLAS_M6运输机气动布局分析与设计[J]. 空气动力学学报, 2012, 30(5): 592-596. XIAO G M, FENG Y, TANG W, et al. Aerodynamics conceptual design for ATLLAS-M6 analog transporter aircraft[J]. Acta Aerodynamica Sinica, 2012, 30(5): 592-596. (in Chinese) |
| [19] |
唐伟.新一代航天机动飞行器气动设计研究[D].博士学位论文, 西北工业大学, 2005. TANG W. Aerodynamic design study for new generation aeronautical maneuverable vehicle[D]. Northwestern Polytechnical University, 2005. (in Chinese) |
| [20] |
黄志澄. 高超声速飞行器空气动力学[M]. 北京: 国防工业出版社, 1995. HUANG Z C. Aerodynamics of hypersonic vehicle[M]. Beijing: National Defense Industry Press, 1995. (in Chinese) |
| [21] |
唐伟, 桂业伟, 方方. 新型升力再入飞船返回舱气动外形选型研究[J]. 宇航学报, 2008, 29(1): 84-88. TANG W, GUI Y W, FANG F. Aerodynamic configurations selection for lift reentry capsule. Optimization of Configuration and Trajectory for Hypersonic Vehicles[J]. Journal of Astronautics, 2008, 29(1): 84-88. DOI:10.3873/j.issn.1000-1328.2008.01.014 (in Chinese) |
| [22] |
马强, 唐伟, 张鲁民. 带控制舵双锥体工程气动力计算方法研究[J]. 宇航学报, 2003, 24(6): 552-554. MA Q, TANG W, ZHANG L M. Engineering Prediction method for aerodynamics of biconic vehicle with flaps[J]. Journal of Astronautics, 2003, 24(6): 552-554. DOI:10.3321/j.issn:1000-1328.2003.06.002 (in Chinese) |
| [23] |
唐伟, 张勇, 马强, 等. 带控制舵椭圆截面飞行器的气动设计[J]. 空气动力学学报, 2006, 24(2): 223-226. TANG W, ZHANG Y, MA Q, et al. Aerodynamics configuration design for elliptical cross section vehicle with flaps[J]. Acta Aerodynamica Sinica, 2006, 24(2): 223-226. DOI:10.3969/j.issn.0258-1825.2006.02.016 (in Chinese) |
| [24] |
唐伟, 曾磊, 冯毅, 等. 升力体机动飞行器气动布局概念设计[J]. 空气动力学学报, 2011, 29(3): 370-373. TANG W, ZENG L, XIAO G M, et al. Aerodynamic configuration conceptional design for high maneuverable lift body with flaps[J]. Acta Aerodynamica Sinica, 2011, 29(3): 370-373. DOI:10.3969/j.issn.0258-1825.2011.03.018 (in Chinese) |
| [25] |
唐伟, 张勇, 马强, 等. 带控制舵飞行器机动特性研究[J]. 空气动力学学报, 2006, 24(2): 223-226. TANG W, ZHANG Y, MA Q, et al. A study on conic maneuverability of a biconic vehicle with flaps[J]. Acta Aerodynamica Sinica, 2006, 24(1): 80-84. DOI:10.3969/j.issn.0258-1825.2006.01.015 (in Chinese) |
| [26] |
唐伟, 冯毅, 杨肖峰, 等. 非惯性弹道飞行器气动布局设计实践[J]. 气体物理, 2017, 2(1): 1-12. TANG W, FENG Y, YANG X F, et al. Practices of aerodynamic configuration design for non-ballistic trajectory vehicles[J]. Physics of Gases, 2017, 2(1): 1-12. (in Chinese) |
| [27] |
邓帆, 任怀宇, 李绪国, 等. 采用不同气动控制舵面的临近空间高超声速滑翔飞行器舵效研究[J]. 空气动力学学报, 2014, 32(2): 240-245. DENG F, REN H Y, LI X G, et al. Rudder effect of near-space hypersonic gliding vehicle with different control surfaces[J]. Acta Aerodynamica Sinica, 2014, 32(2): 240-245. (in Chinese) |
| [28] |
刘文伶, 朱广生. 浅析再入机动飞行器十字布局与叉字布局的气动特性差异[J]. 导弹与航天运载技术, 2002, 4: 33-38. LIU W L, ZHU G S. A study of the effects of cruciform configuration and bifurcate configuration on aerodynamic characteristics of maneuvering reentry vehicles[J]. Missiles and Space Vehicles, 2002, 4: 33-38. (in Chinese) |
 2019, Vol. 37
2019, Vol. 37

