飞行器气动设计涉及众多参数。当目标参数满足、飞行器整体外形或者部件外形确定后,如何通过被动/主动流动控制技术拓展和完善其在非设计状态下的气动性能成为研究者关注的焦点[1]。等离子体主动流动控制技术是基于超声速飞行器减阻的需求而产生的[2],20世纪末期被广泛用于低速和亚声速流动控制研究。研究者们从流动控制领域[2-18]和电学领域[19-21]对等离子体流动控制技术进行了很好的回顾和展望。
等离子体被定义为固体、液体、气体以外的第四种物质存在形态。在工业领域,等离子体的产生需要通过对中性气体进行加热或者施加强的电场、磁场得到[22]。当施加强电场后,中性气体会部分电离,带电粒子在顺电势电场作用下会产生漂移,进一步带动中性粒子的运动。应用电学方式产生等离子体从而进行流动控制的方式被称为电流体力学(Electrohydrodynamic, EHD)流动控制,它有着频带宽、响应迅速的特点[23]。
然而,在亚声速飞行中进行等离子体流动控制的困难在于缺乏低能耗的电源使得常压下近壁面空气电离,从而进行流动控制。美国田纳西大学Roth教授团队发明的常压辉光放电等离子电源成功解决了这一难题,该电源可以在低能耗条件下产生大面积的均匀放电等离子体。同时,该团队提出的表面介质阻挡放电(Surface Dielectric-Barrier-Discharge, SDBD)形式的等离子体激励器具有简易、成本低、性能可靠、易于大面积铺设等优点。该装置最初被用于净化去污,之后,当发现该装置在交流电压(Alternative Current,AC-)驱动下可以沿激励器表面顺电势诱导出几米每秒的诱导气流后,该团队在美国NASA Langley研究中心资助下开始致力于将其应用到流动控制领域,并从1994年开始公开发表论文[24],并于1998年有了完整的研究报告[25-26]。Roth教授团队研究成果的意义在于其提出的AC-SDBD等离子体原理将等离子体流动控制系统变得简单易操作,使得没有任何等离子体物理背景的研究者也可以很容易地制作和应用等离子体激励器进行相关研究。因此,自2000年之后,等离子体流动控制开始大量广泛地应用在空气动力学的各个研究方向,并迅速成为流动控制领域研究的热点[27-43]。
在Roth教授团队的将常压辉光放电等离子体技术应用在流动控制领域之前,也就是2000年之前,还有几个研究团队在等离子体流动控制领域做了很多的工作,法国普瓦捷大学Moreau教授团队、美国圣母大学Corke教授团队等。这些团队的工作与Roth教授团队在2000年之前是相互独立的,主要是基于直流电晕放电等离子体,并且电极形式各不相同。2000年以后,这些团队均迅速开展了利用SDBD等离子体激励器的应用研究。
典型的单SDBD激励器由裸露电极、掩埋电极及两者之间的绝缘层组成。两个电极交错放置,高电压施加在裸露电极和掩埋电极之间,其基本形式如图 1所示。诱导气流的方向由裸露电极指向掩埋电极,时均的诱导速度场不受交流电电压正负极值转换的影响。

|
图 1 SDBD等离子体激励器示意图与等离子体辉光[13] Figure 1 Schematic illustration of SDBD plasma actuator and photograph of plasma glow[13] |
大量的研究表明,表面介质阻挡放电等离子体的最大缺点是诱导的风速比较低,用于流动控制的体积力比较小。尽管Enloe等人[44]给出了单激励器诱导风速与电压之间存在以下关系式:
| $ {U_{\max }} = 0.000166{V_{p - p}}^{7/2} $ | (1) |
然而,即使是采用不同的绝缘介质(Kapton、Teflon、玻璃、陶瓷等)和不同数目的激励器,目前公开文献最大诱导速度也只能到8 m/s[45]。低的诱导速度使得基于AC-SDBD的等离子体流动控制只在低风速、较低雷诺数下有效。Christopher等[46]采用3.175 mm厚度陶瓷做绝缘介质,在30 kV、2.3 kHz电学参数下,在Ma=0.4、Re=2.3×106下进行控制实验研究,这是目前公开文献中AC-SDBD流动控制能达到的最大有效来流速度和基于翼型弦长的雷诺数。
可见,目前使用AC-SDBD等离子体激励器面临的困境就是无法在高速来流和高雷诺数条件下进行有效的流动控制。在这样的需求背景下,当莫斯科物理与科技学院Starikovskiy教授团队[47]于2009年提出基于SDBD激励器的纳秒脉冲(Nano-second Pulse,NS-)等离子体流动控制技术时,很多研究者相信这是代表了跨、超声速来流条件下等离子体流动控制的方向。该研究使用了和Roth教授团队提出的AC-SDBD等离子体流动控制同样的激励器构造(见图 1)。不同的是,其输入的电压信号不再是连续交流信号,而是纳秒级的脉冲信号(半脉宽≈5~100 ns)。该研究结果表明,纳秒脉冲等离子体激励可以在来流速度高达Ma=0.85时仍然具有有效的控制效果。该团队指出,纳秒级的脉冲电离等离子体产生的瞬时加热效应(t < 1 μs)可以产生球形压力波,该压力波在微秒级时间范围内以激波形式传播,并伴随有二次涡流效应,可以促进与主流的掺混,进而对流动产生影响。
目前,国内外很多具有SDBD等离子体研究基础的研究团队针对NS-SDBD等离子体展开了研究。本文从流动控制角度出发,从NS-SDBD等离子体激励特性、应用研究以及机理阐述等三个方面进行综述,目的是找出目前NS-SDBD流动控制的代表性成果和突破性进展,并加以总结和分析,给研究者提供NS-SDBD流动控制的研究方法、实验手段和关键技术,最终总结出纳秒脉冲等离子体流动控制的研究方向和发展趋势。
1 静止大气中NS-SDBD等离子体气动激励特性 1.1 实验研究大多数NS-SDBD流动控制研究使用的激励器与AC-SDBD激励器结构组成相同,均为长条形的表面介质阻挡放电等离子体。随着进一步的研究,研究者发现NS-SDBD的激励特点在于瞬时脉冲放电产生的热效应,故此对激励器几何参数的研究也开展起来。针对激励器几何参数的研究大多数设定在静止大气环境中进行[48-53]。
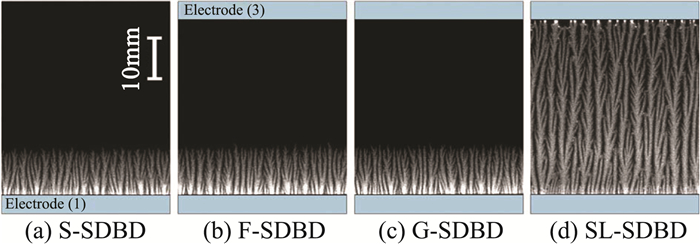
Bayoda等[48]设计了一种三电极激励器,即在掩埋电极两侧均有一条裸露电极。其中一条裸露电极接入纳秒脉冲电压信号,另外一条裸露电极可接入直流负向电压信号(SL-SDBD)、接地(G-SDBD)或空置(F-SDBD),掩埋电极接地。结果表明,SL-SDBD激励器设计使得等离子体的放电激励范围增大到整个掩埋电极长度范围(40 mm),并在掩埋电极两侧产生两条球形压力波。图 2和图 3分别给出了不同形式激励器放电和诱导压力波结构图。
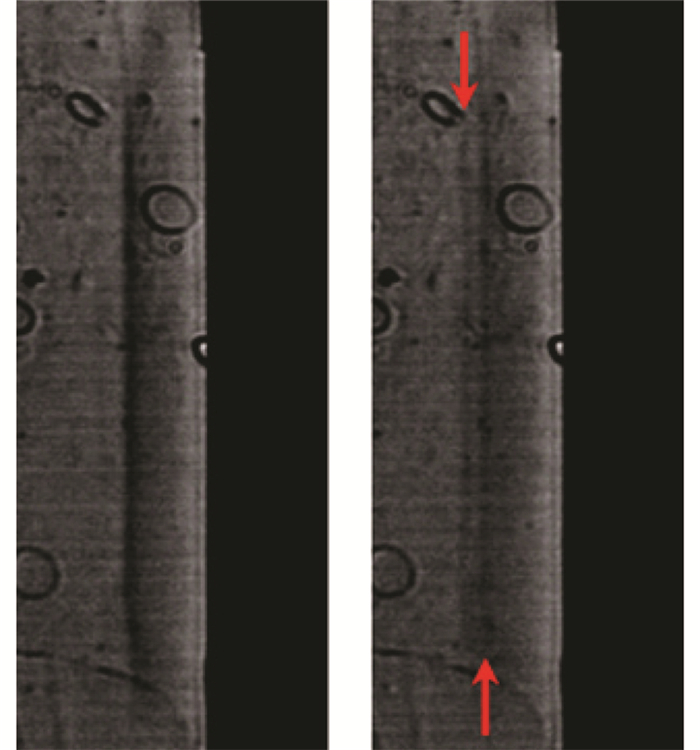
胡海洋等[49-50]等对长条形电极NS-SDBD进行了纹影观测,图 4~图 6分别给出了NS-SDBD等离子体激励的放电图、压缩波结构图、速度传播图和重复脉冲下的激励诱导纹影图。其研究结果表明:通过沿展向布置Kapton胶带可以控制球形波的数量;单脉冲激励下压力波在t < 10 μs范围内以激波形式向外传播,随后弱化为声波;重频脉冲下球形压力波中心的热效应逐渐积累,最终发展为时均的弱速度场。此研究针对NS-SDBD等离子体激励开始到发展的三个阶段给出了详细观测,首先是微秒阶段,对流场的影响表现为压缩波的传播;其次是毫秒阶段,对流场的影响表现为对气体的热扰动;最后是秒阶段,对流场的影响表现为启动涡的诱导阶段。最后阶段的流场信息可与PIV观测结果相统一,实现技术上的衔接。

|
图 6 重复脉冲激励下的诱导速度纹影图[49] Figure 6 Schlieren image of quiescent air perturbation caused by repetitive nanosecond pulse for different time delay[49] |
崔永东等人[51]在长条形电极的基础上,在裸露和掩埋电极之间等间距植入了直径为0.7 mm的印刷电铜丝,通过这种方式使得放电更加均匀,并且实现了对球形波数目的控制,图 7给出了其放电状态图。
总的来讲,静止大气中NS-SDBD等离子体气动激励特性实验的研究目的有两个:(1)探究NS-SDBD等离子体气动激励的宏观表现随时间的演化;(2)探究NS-SDBD等离子体激励器的优化准则。
对于上述研究,目前的困难在于如何细致、定量地测量纳秒级电压信号下气动激励特性。目前各研究团队使用的大多为纹影技术,主要是通过测量压力波的传播速度评价气动激励从激波发展成弱声波扰动的过程,将激波持续的时间作为衡量等离子体激励器的优化准则。而普通的纹影技术无法得到更多的定量的流场信息。基于背景纹影的密度梯度场测量技术(Background Oriented Schlieren,BOS)是值得注意的应用技术。通过发展该技术,可以对高速纹影图像进行定量计算得到密度梯度场,然后对纳秒脉冲等离子体初始扰动激波强度进行测量和评估,从而在压力波的传播速度之外增加另外一种激励器的优化准则。
另外值得注意的是,众多结果表明,脉冲等离子体的时均诱导速度几乎可以忽略不计[52],而赵子杰等[53]通过PIV技术测量,利用特殊的微距长焦镜头得到了纳秒脉冲等离子体气动激励的瞬时速度场。图 8给出了电压V=40 kV、F=100 Hz下,NS-SDBD等离子体激励的时均流场,结果显示纳秒脉冲等离子体激励下的瞬时扰动速度可以达到40 m/s。

|
图 8 脉冲激励下诱导速度场随时间的变化特性[53] Figure 8 Induced flow velocity after discharge at different times: PIV results, V=40 kV, F=100 Hz[53] |
对NS-SDBD等离子体在静止大气中的激励特性进行数值模拟研究,目前主要从以下三个方面着手:
(1) 唯象学方法[54-60]。该方法将纳秒脉冲电压下产生的瞬时作用简化为呈热功率耗散分布的热源,忽略了等离子体放电的形成和演化。
(2) 多物理场耦合方法[61-71]。该方法将中性气体的流动控制方程和描述等离子体物理过程的控制方程联立求解。其中后者考虑了较完备的化学反应及带电粒子的种类。这种方法能够对带电粒子的时间演化与空间分布以及放电过程中与中性气体粒子之间的相互作用进行较为准确的刻画和模拟。
(3) 简化的电流体模型[72-76]。该模型由多物理场模型通过极大简化而得到,在模拟带电粒子时没有考虑复杂的组分和化学过程,仅以带电属性为标准将成分复杂的带电粒子模化为少数几种组分,并以简化的漂移-扩散方程来描述其基本电学规律。
1.2.1 唯象学模型唯象学模型将NS-SDBD对流动的影响等同于一个区域内的瞬时热效应。该模型忽略了激励过程中的放电特性以及粒子的漂移扩散特性,将等离子激励的影响等效为一个热效应,探讨纳秒脉冲激励后由瞬时加热产生的压力波对流场的控制机理。该方法的优点在于研究忽略了放电阶段(t < 10 ns)粒子的漂移、扩散特性,直接从加热效应明显的时间尺度(t>10 ns)开始研究,其模拟的时间尺度同实际流动时间尺度相当。一些模型仅考虑了一个放电周期内的时均热效应,因此可对全时间尺度的流动进行模拟。
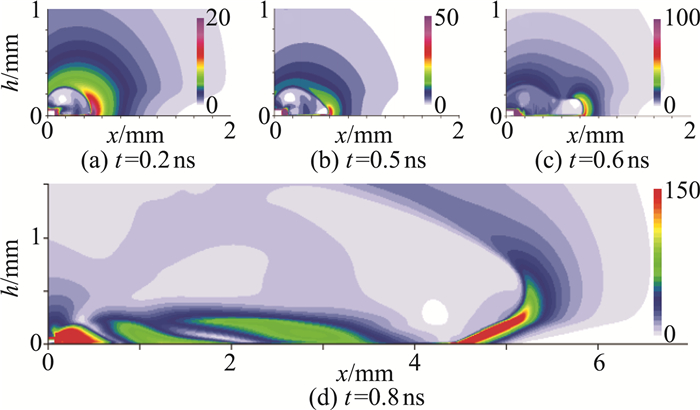
Starikovskii等[54]对初始阶段采用预电离,将高压裸露电极边缘的放电形成过程初始化为一个正弦扰动的电子浓度分布。将掩埋电极上方区域模拟为均匀加热层,选取温度和压力作为初始条件,进行后续冲击波的模拟。图 9给出了其计算的放电沿激励器表面的发展。
|
图 9 带预扰动的3D模型计算下,放电沿表面的发展[54] Figure 9 Discharge development along the surface for 3D model with initial perturbation[54] |
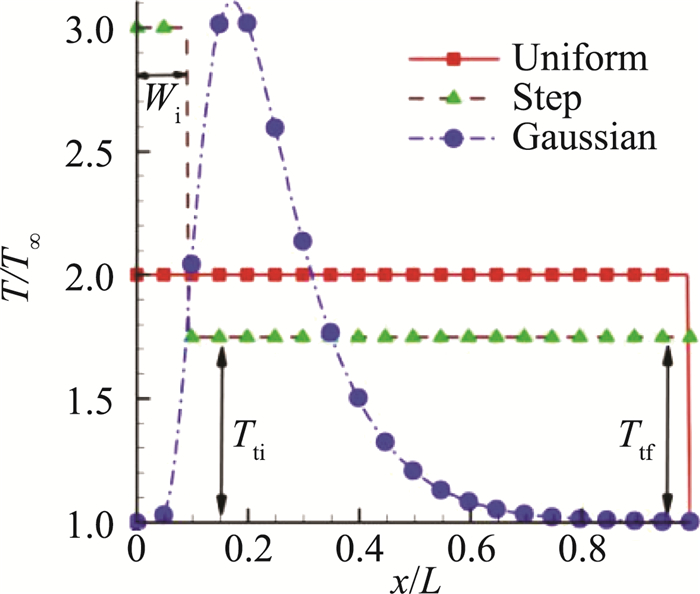
Gaitonde等[55]研究了唯象学模型耦合LES方法,模拟NS-SDBD等离子体激励效应。模型考虑了多种表面和体积热源剖面形式,模拟NS-SDBD激励的定性和定量特征,包括激波结构、速度、站位和发展过程。通过与纹影实验结果对比,调整模型参数,模拟激励开始初期激波的形状和传播速度。通过应用空间变化热分布,计算得到组合激波。图 10给出了其具有代表性的温度剖面曲线。
|
图 10 数值模拟中具有代表性的温度剖面数据[55] Figure 10 Representative computational temperature profiles considered in qualitative calibration of actuator model[55] |
陈真利等[56-58]、赵光银等[59]结合实验数据和理论分析, 建立考虑电压、频率、气压、放电能量加热率、热量释放时间等参数的NS-SDBD气动激励唯象学模型,对翼型大分离流动进行了流动控制研究。该模型通过实验数据拟合得到了放电能量的空间分布函数,并将其作为热源项耦合进N-S方程,实现了大时间尺度NS-SDBD流动控制的数值模拟。并利用上述模型对激波诱导边界层分离的NS-SDBD流动控制进行了数值模拟研究。图 11分别给出了实验结果和数值模拟在放电开始后不同时间阶段的压缩波对比图。

|
图 11 数值模拟密度梯度场与纹影实验结果对比[59] Figure 11 Comparison between numerical simulations of density gradient field and schlieren experiments[59] |
李凡玉等[60]采用关于焦耳热功率密度分布的唯象学模型,对NS-SDBD等离子体激励下静止大气流场对其的响应进行了模拟研究。结果表明:激励后在流场中形成一个高温升压区和一个低温升压区,诱导形成一强一弱两道压缩波,压缩波后存在一道稀疏波,传播速度在初始阶段大于400 m/s,初期局部诱导速度在激励器切向和法向达到60 m/s,随着压缩波减弱,诱导局部速度逐渐降至10 m/s左右(见图 12)。
1.2.2 多物理场模型化学反应动力学模型主要模拟的是纳秒脉冲等离子体在产生过程中,由于化学反应产生的各种电子、正离子和负离子的分布、发展以及运动规律。这里面包括多组分化学反应模型、三组分化学反应模型(只考虑电子、正离子、负离子),但因为其为零维特性,无法探讨空间漂移扩散、离子电流等。
Flitti等[62]在氮气-氧气混合物中,应用等离子体化学方程和能量守恒方程,模拟脉冲放电下的气体加热动态特性,主要指标包括加热率、瞬时热转化率、电子沉积能量等。模拟结果表明,电子密度越高,电场强度越大,氧气含量越高,激励对周围气体的加热率越高;另一方面,由于电子震动和自由度激发态引起的气体加热和场强大小却无明显关系。
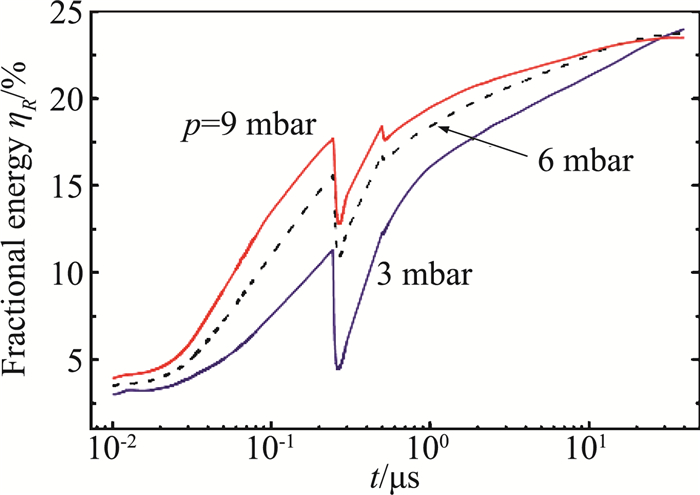
Mintoussov等[63]在环境压力3~9 mbar(1mbar=100 Pa),场强200~400 Td条件下,在实验所得电流曲线基础上,对NS-SDBD激励气体加热情况进行数值模拟研究。图 13给出了不同环境压力下的能量转化率曲线,计算得到的电场和沉积能量与实验结果基本一致。主要能量耗散为电子效应和电子激发氮分子效应引起的氮气和氧气的分解。结果表明在激励开始最初的几十微秒内,放电能量的24%被用于气体加热。
|
图 13 不同气压下能量转换率随时间的变化曲线[63] Figure 13 Fraction of discharge energy ηR versus time for different gas pressures[63] |
Popov等[64]在氮气-氧气混合气体中,数值模拟不同电场E/N下NS-SDBD激励的气体加热过程。该团队还进一步利用动力学方程模拟了激励过程中电子密度、电场、氧原子密度和气体温度随时间的变化[65]。徐双艳等[66-68]在N2-O2混合气体环境中,采用7种粒子和9种反应的化学反应方程,全时域漂移-扩散模型,电子、离子和中性粒子满足的质量(粒子数)、动量和能量守恒方程,泊松方程,对不同布局和形式电极的NS-SDBD激励放电的发展演化进行数值模拟研究。
Poggie等[69]选取对称平板为模型研究,计算选取动力学模型包含23种粒子和50个化学反应过程,捕捉能量储存和加热过程中的主要粒子和反应过程。控制方程包括电场计算的泊松方程、中性粒子的扩散方程、每种粒子的守恒方程和来流情况下的动量守恒方程。图 14给出了其数值模拟,电压为V0=5 kV和V0=27 kV下,气体激励后的速度和温度特性。

|
图 14 不同选定时间内的气体特性[69] Figure 14 Profiles of properties of bulk gas for selected times in simulation[69] |
朱益飞等[70]利用考虑16种粒子和44个化学反应过程的等离子体模型研究了NS-SDBD气动激励过程。结果表明:激励在开始后的几十个纳秒内将当地气体加热至1170 K,随后在放电结束时温度又降至310 K,30%的能耗传递给电场中的电子,但是只有20%的能量以淬火效应的形式被释放进当地气体,9%的能量以粒子碰撞的形式被消耗。基于上述效应,一个微激波在激励处产生并以声速向外扩散发展,由于高密度梯度和动态黏性效应引起的旋涡向下游发展,重复脉冲下的热效应和旋涡效应形成了一个稳定的射流。
上述研究将主要精力集中于对NS-SDBD等离子体激励放电开始之后的电场、物理场参数进行模拟,时间尺度主要集中于1×10-9~1×10-6 s尺度范围内,适合用于气动激励机理的研究。对于NS-SDBD激励影响下的大尺度流动控制问题,由于等离子物理过程与中性气体流动过程的时间尺度相差悬殊,该方法的直接应用还存在限制。
1.2.3 简化的电流体模型Likhanskii等[72],选用二维空间模型,由泊松方程得到电场分布,通过对电子、正离子和负离子分别列出连续方程和漂移-扩散方程,得到空间场中相应粒子的运动规律,最终耦合N-S方程得到诱导激波的产生和发展过程。采用正负脉冲叠加直流正电压的激励电压形式,探究了电压形式对等离子体诱导电场和速度场的影响。结果表明:负脉冲下的电子反向崩溃,使得其动量注入减小;正向脉冲耦合直流电压,提高了诱导体积力的大小,且改善了其体积力剖面形式。模型选取流量方程和连续方程,通过泊松方程确定电场分布,综合计算得到电场、电场力和动量注入。
Unfer等[73]通过对NS-SDBD激励进行数值模拟,分别得到激励诱导电场、压力场和温度场。图 15给出了不同气体加热条件下,温度随时间的变化曲线。

|
图 15 不同气体加热条件下最高温度随时间变化曲线[73] Figure 15 Maximal gas temperature as a function of time for different gas heating conditions[73] |
结果表明:电流脉冲发生在电压上升时,放电丝头部以5×107 cm/s的速度沿掩埋电极方向发展。能量堆积使得单位体积内的温度迅速上升,裸露和掩埋电极接缝处约1000 K,进而导致压力的迅速上升;温度和压力的迅速上升,引起一个微型激波的产生和发展,压力增加约1000 Pa,扰动范围约为毫米量级。简化电流体模型从一定程度上反应了带电粒子的基本演化规律,这是唯现象学模型无法做到的;其时间尺度相对于多物理场模型显著扩展,达到了毫秒量级,这使其在大尺度流场NS-SDBD流动控制数值模拟中的应用更容易实现。
车学科等[74]利用泊松方程和漂移-扩散方程,计算得到体积力和热能,带入N-S方程得到诱导流场。通过模拟气体放电过程,研究NS-SDBD激励在临近空间领域对流动的影响机制。结果表明,NS-SDBD激励产生的体积力和AC-SDBD相比很小,但由体积力引起的诱导射流在临近空间环境下范围、剖面厚度和最大速度皆比地面环境要大。在建模中,需要着重考虑激励产生的热效应、热效应产生微爆炸和压力扰动。地面环境下,微爆炸是一个点爆炸,临近空间下,微爆炸为“区域爆炸”,因此临近空间下,需要考虑能量的扩散分布。
郑建国等[75-76]通过数值模拟方法探究激励下的诱导流场的动态特性,不仅提供了激励诱导激波的基本形态,还定量给出了激波前端的站位。对NS-SDBD后气体加热、激波的产生和发展过程进行了系统描述。结果表明:压力波主要受输入电压的影响,由压力波引起了弱旋涡结构,由重复脉冲引起的多个压缩波相互作用形式并不明显。激波引起一个瞬时当地扰动,显著改变了流动的形式,扰动影响后主流流动趋于恢复原有流场;随后产生的当地热效应和激波同时作用的扰动对流动起主要的影响,表现为边界层内的扰动波序列;这个扰动十分弱,可能不是T-S波,不能激发层流到湍流的转化。它更趋于通过控制边界层稳定性,进而在控制流动分离中起到作用。
表 1给出了NS-SDBD等离子体气动激励的各数值模拟方法、所使用的方程、研究对象以及所具备模拟的时间尺度。
| 表 1 NS-SDBD气动激励数值模拟研究归纳 Table 1 NS-SDBD numerical simulations |
|
|
综上所述,NS-SDBD等离子体流动控制的数值模拟方法主要有两个发展方向:
(1) 面向流动控制工程应用需求,对现有的简化模型进行改进与完善,在保持现有模型构造简单、计算量小等特点的基础上,能更准确地模拟带电粒子向中性气体的能量传递过程,从而给研究大尺度流动控制提供有效手段。
(2) 发展全尺度范围内高效、准确模拟等离子体流动控制多物理场复杂规律与机制的数值模型与方法,从而实现放电过程、局部气动激励过程,直至主流动气动响应过程的贯通,实现对流动控制真实物理过程的一体化模拟。其中异步时间积分算法(Asynchronous Time Integration, ATI)已在简化电流体模型求解中得到应用[77],显著提高了计算效率。另一方面,基于气体动理学理论的模拟方法,可实现全尺度多物理场的数值模拟,在等离子体流动控制数值研究方面有很好的应用前景,受到国内外研究者的高度关注[78]。
2 NS-SDBD流动控制应用研究在激励机理研究的同时,针对NS-SDBD等离子体的工程应用的实验研究也多方面展开,研究者也力图从控制效果对其激励机理进行解释。NS-SDBD流动控制应用研究的流速范围很广,本节以低速/亚声速与超声速加以区分。
2.1 低速/亚声速边界层控制研究传统的AC-SDBD等离子体激励控制输出定常或周期性的动量,激发流动剪切层的不稳定性,进而影响流动。已有研究成果表明,NS-SDBD等离子体激励依靠“热”的形式对剪切层进行控制,但其基础物理原理和影响尺度目前仍处于未知状态,因此研究者们针对NS-SDBD激励与边界层的相互作用展开了细致的研究。
Lehmann等[79]探究了NS-SDBD等离子体激励对湍流剪切层的影响。实验通过吸气装置改变边界层厚度,证实NS-SDBD等离子体的激励控制效果与边界层的初始动量厚度相关。厚度越薄,控制效果越好。同时,脉冲激励产生局部大尺度扰动结构也与边界层初始状态相关。
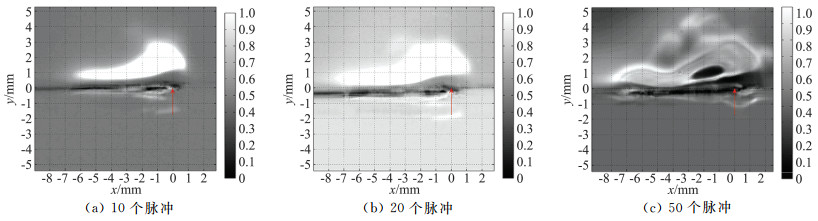
Correale等[80-81]在静止大气环境下利用纹影技术观测了多个脉冲激励下周围气体的加热情况,如图 16所示。证实激励对气体的加热是逐个脉冲激励的叠加效应,且加热区域逐渐增大。来流5 m/s风速下,在50个脉冲激励后,时间范围6~25 ms,观测到T-S波序列,波序列的长度与激励的脉冲个数成正比,同时给出了17 ms、20 ms和23 ms下流场x和y方向上的速度扰动图。该研究结论和Zheng等[75-76]的结论不相同。
|
图 16 不同脉冲下纹影的能量分布图[80] Figure 16 Schlieren images for three energy cases: 10, 20, and 50 pulsed for frames respectively[80] |
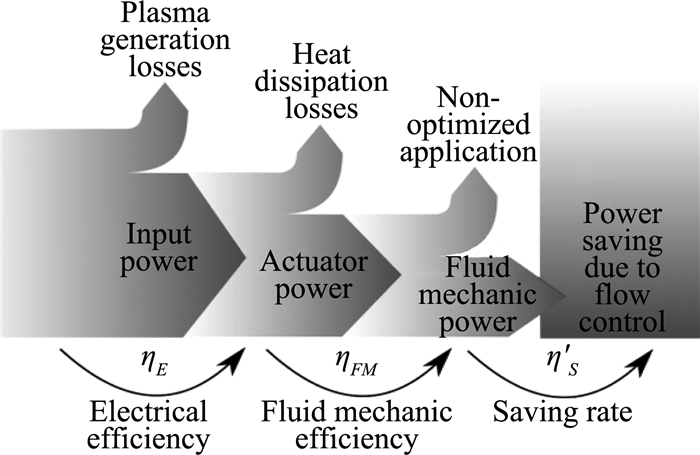
随后,该团队将NS-SDBD等离子体激励下的流动控制过程分为三个阶段——第一阶段:电学放电;第二阶段:流动控制物理机制;第三阶段:流动控制目标完成情况。针对前两个阶段,该团队提出了一种基于实验技术的NS-SDBD等离子体激励能效评估方法,见图 17[82]。第一阶段能量从脉冲发生器到等离子体放电的转化率为ηE,第二阶段能量从等离子体放电到诱导热效应的转化率为ηFM。首先测得发生器输出能量,随后根据一段时间后的输出流量和等离子体加热区域,确定转换为热效应的能量。之后应用热像技术测得激励器表面温度。上述测量得到的能量之间的差值即为能量耗损,比值即为第二阶段的能量转化率ηFM。该评定方法对NS-SDBD等离子体激励将放电与激励诱导热效应有机地结合在一起,实现了从电学参数到控制影响参数的有效转化,合理地评估激励器本身的优劣,为实现NS-SDBD等离子体激励器的实际应用提供了效能评定。
2.2 低速/亚声速分离流动控制研究在对NS-SDBD等离子体激励基本影响方式的了解基础上,其被广泛地应用于各种二维、三维的分离流动控制中。在二维分离流动的控制研究中,主要针对各种典型翼型前、后缘分离流动。
Roupassov等[83]利用NS-SDBD等离子体定常激励,在马赫数0.05~0.85范围内,实现了对NACA 0015翼型的增升减阻的有效控制。杜海等[84]在不同雷诺数下,应用NS-SDBD等离子体激励对NASASC(2)-0712翼型进行控制实验研究,图 18给出了激励器开启后机翼表面旋涡结构的变化情况。结果表明:NS-SDBD激励脉冲在瞬时表现为大尺度旋涡拟序结构,其周期性产生、运动和演化造成了分离剪切流动的动态变化过程,促进了高/低速气流的动态掺混,且激励在一个较宽的减缩频率范围内控制有效,F+= 0.4~1.3。
Kato等[85]针对Go 387翼型,采用压力测量技术,探究了NS-SDBD等离子体激励对翼型吸力面流动分离的影响。结果表明:在失速迎角之前,流动稳定,升力增量与激励频率无关,激励器关闭后升力增加的消失存在迟滞;在失速迎角之后,流动处于不稳定状态,激励频率大小对控制效果有影响。
Clifford等[86]为提升旋翼飞行器在倒飞阶段的气动性能,针对NACA 0015翼型,分别在翼型前、后缘施加NS-SDBD等离子体激励控制,探究激励频率的影响作用。实验结果表明:前缘NS-SDBD激发了流动不稳定性,产生大尺度结构,将高动量流体带进边界层,从而减小分离区,提高升力特性;后缘NS-SDBD激励控制显著减小了脱落涡结构的尺度。针对非定常激励,低减缩频率激励(F+=0.19~0.38)在分离区剪切层产生有序相干结构,改变尾迹形状、分离区域大小,从而增升减阻;F+=0.19时接近流动本身自然脱落频率,获得最佳控制效果。
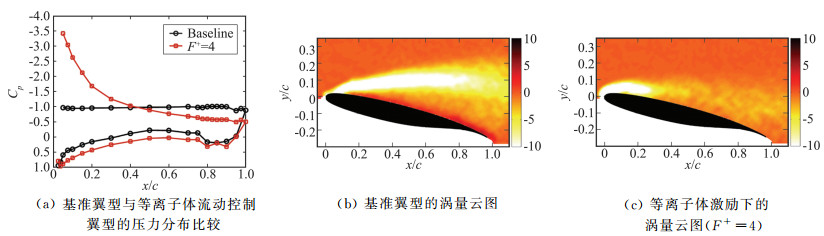
Little等[87]利用布置于NACA 0015翼型前缘的NS-SDBD等离子体激励,在雷诺数Re=1×106(62 m/s)、失速迎角12°附近,实现了对其前缘流动分离的控制;证实激励在前缘产生沿展向的相干涡结构,Fc+在4~6之间时控制效果最佳。图 19给出了激励器开、关前后压力曲线的变化及与之对应的涡量场。
|
图 19 基准翼型与等离子控制翼型时均压力分布与涡量场的比较(Re=0.75×106和α=10°)[87] Figure 19 Time-averaged pressure distributions and vorticity contours for baseline and plasma-on airfoils[87] |
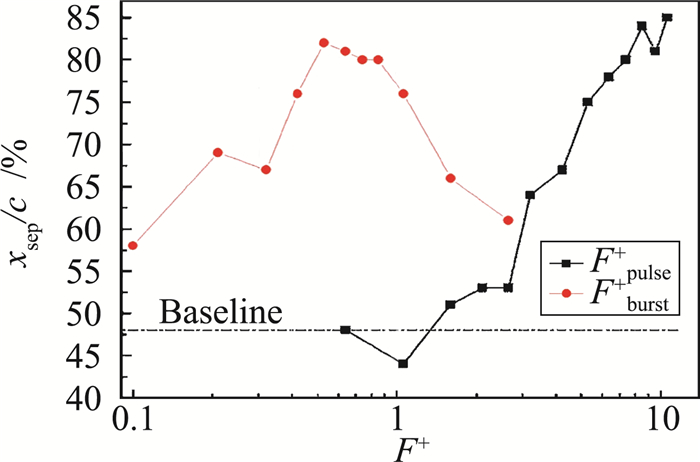
Moreau等[88]利用两种非定常激励模式对NACA 0015翼型进行流动控制研究, 实验风速40 m/s,迎角13.5°,图 20给出了翼型表面分离位置随减缩频率的变化曲线。当脉冲激励减缩频率为F+=10.06时,激励使得分离点推后至85%弦长处,且脉冲能量越高,控制效果越好;通过最佳减缩频率F+= 0.53,分离点推迟至83%弦长处,同时探究了能耗和频率对控制分离效果的影响。该研究针对NS-SDBD等离子体激励器的重点问题——频率问题,展开了详细的叙述和讨论,将激励本身频率和减缩频率区分开来分析其对流动控制作用的影响,并最终将二者统一为F+来进行比较分析。证实激励的流动频率对于分离控制的影响并不是单向性的,不能简单地认定低频或高频对流动控制的效果有积极影响。该研究成果证实在减缩低频和脉冲高频下,流动控制作用相近。
赵子杰等[89]、崔永东等[90]针对NACA 0015翼型,对其前缘分离流动进行定常和非定常控制。结果表明:定常激励脉冲产生展向涡结构,初始脉冲对流动分离的控制作用较大,将分离点推迟至下游,后续脉冲激励主要在于维持已有的流动状态;非定常低频激励在翼型表面诱导周期性涡结构,涡的演化过程对流动产生重要影响,提供额外的升力,使得最大升力提高;高激励频率下,流动较为稳定,降低了阻力;在迎角24°下,NS-SDBD激励对流动仍具有较强的控制力,但其频率依赖性降低。郑建国等[91]开展的针对NACA0015翼型流动分离控制的实验和数值模拟研究表明,纳秒脉冲放电所产生的激波只对其波及的流场产生近乎瞬态的扰动,对于流动控制没有实质性的贡献。与此相对应的是,放电所产生的残热沿边界层向下游运动时在分离点附近诱导产生的展向涡将高能量外流引入翼型上表面附近的分离区,导致流动的再附现象。因此,放电后遗留在放电区的残热才是纳秒脉冲等离子体流动控制效力的主要来源。
文献[84-85]的研究结果表明, NS-SDBD等离子体激励频率对控制效果无明显影响。然而,文献[86-90]的研究结果却表明等离子体激励的减缩频率是实现有效控制的关键性参数。因此,针对NS-SDBD等离子体激励下减缩频率对流动控制效果的影响有必要予以澄清。
在三维流动的NS-SDBD等离子体流动控制中,主要针对的是各种全机、机翼和锥柱体等流场,对流动分离、分离旋涡等进行控制研究。
Roupassov等[92]针对矩形机翼流场,在马赫数0.3~0.75下进行NS-SDBD等离子体控制,证明了其在巡航状态下的激励控制的有效性。
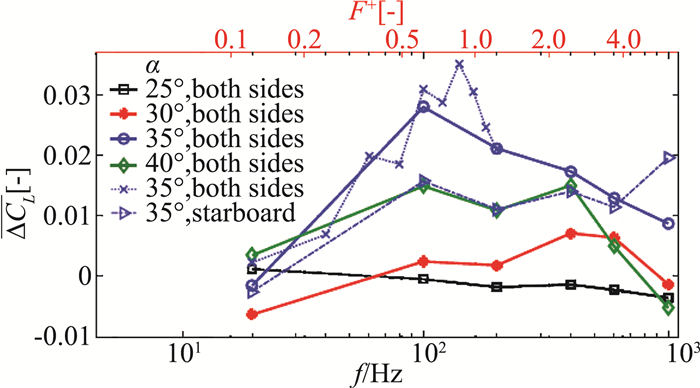
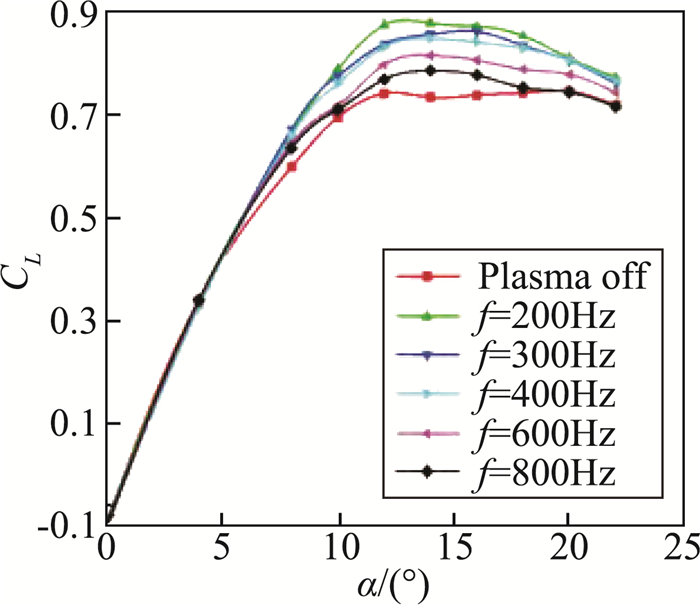
Kato等[93]等人针对NACA 65A005后掠机翼进行控制研究,雷诺数Re=6×105,激励频率范围20~1000 Hz,迎角25°~40°,图 21给出了不同迎角下升力系数的变化曲线。结果表明:激励控制后,最大升力从0.807提升至0.842,最佳减缩频率为0.86,升力提升伴随着阻力和俯仰力矩的提升,机翼前缘顺气流方向的涡量加强对增升效果显著。
化为卓等[94]针对47°后掠角的钝前缘三角翼模型,探究NS-SDBD激励控制的影响因素,结果表明当在机翼前缘施加NS-SDBD等离子体控制时,激励位置对控制效果影响较弱,激励频率对控制效果影响较大,迎角30°下最佳激励频率为200 Hz,升力系数由1.31增大到1.44, 增大9.6%, 升阻比提高3.3%。
赵光银等[95]探索了NS-SDBD对小后掠尖前缘三角翼的流动控制效果和作用机理。来流速度分别为30 m/s和45 m/s时,图 22给出了激励后升力系数的变化曲线。结果表明升力系数提升18.3%,最佳减缩频率为F+= 1~2,PIV图像证实NS-SDBD激励的作用机理为诱导分离剪切层周期性产生附体的分离涡,维持大迎角时的涡升力,从而改善上翼面旋涡结构,使分离涡附体并得到加强。
|
图 22 不同迎角下激励对升力系数的作用(U∞=45 m/s,Vp-p=14 kV)[95] Figure 22 Lift coefficient with plasma actuation at different frequencies(U∞=45 m/s, Vp-p=14 kV)[95] |
杜海等[96]、Yao等[97]对飞翼表面流场进行了NS-SDBD流动控制研究,证实激励使得旋涡聚集,分离区域减小;最佳激励位置位于前缘中、内部,最大升力提升37.8%,迎角推迟8°;最佳减缩频率为F+= 1。同时,利用激励器抑制单侧翼面流动分离产生不对称的气动力,并和常规副翼舵面滚转操控效果进行了对比,结果表明减缩频率对滚转控制效果的影响较大,与常规副翼相比,等离子体激励器在大迎角时对飞翼滚转的操控效果优于副翼。
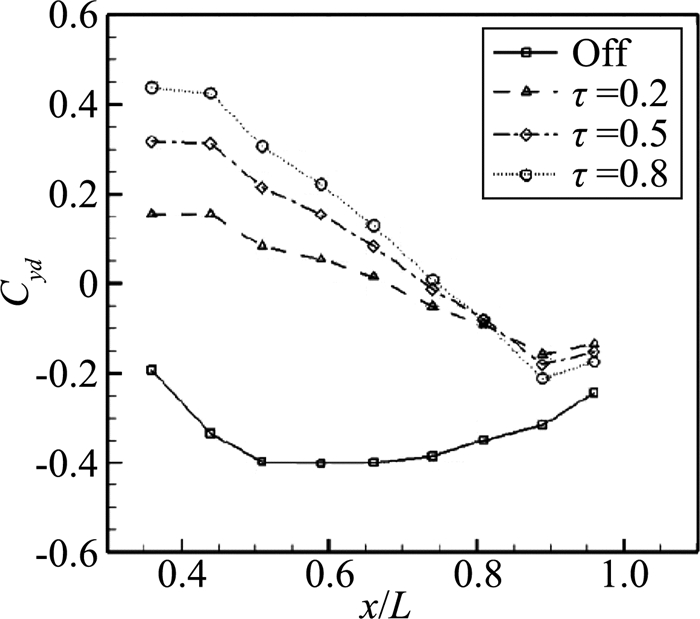
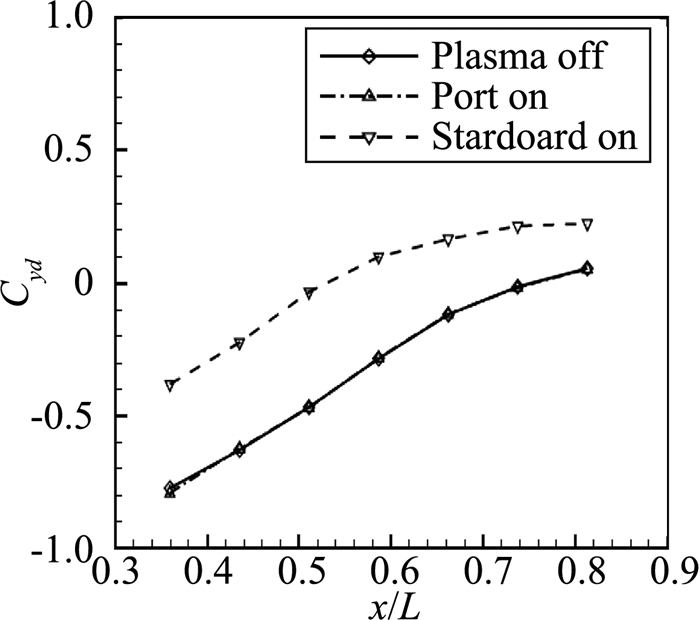
张铎等[98]、王健磊等[99]利用一对NS-SDBD等离子激励器对细长圆锥前体大迎角下的分离涡进行了控制。图 23给出了占空循环控制下的侧向力变化。图 24给出了左、右激励器开启后,模型整体侧向力的变化曲线。证实了在65 m/s来流速度下,NS-SDBD等离子体激励可以实现对圆锥截面当地侧力的线性控制。在72 m/s风速下可以有效地改变圆锥当地的压力分布。
|
图 23 NS-SDBD等离子体激励下压力与当地侧力随占空比变化(α=50°, U∞= 65 m/s)[98] Figure 23 Ensemble time-averaged Cyd vs. x/L, α=50°, U∞= 65 m/s[98] |
|
图 24 NS-SDBD激励下周向压力分布及侧向力沿轴向的变化(α=45°, U∞= 72 m/s)[99] Figure 24 Local side force vs. x/L for plasma off, port on, and starboard on at α=45° and U∞=72m/s [99] |
正如在引言中所述,NS-SDBD等离子体激励提出的初衷在于解决等离子在高速、高雷诺数下的有效性控制问题,因此,研究者在高速来流下也进行了研究和尝试。然而受制于数值模拟方法和实验条件,此类研究目前还不多见。
倪芳原等[100]通过数值模拟探究了NS-SDBD对圆柱脱体激波的控制,圆柱直径6 mm,来流马赫数Ma= 4.6。研究表明NS-SDBD激励形成的半圆形压缩波对于脱体激波有很强的干扰作用, 激波距离增加了15.7%,激波强度也有相应的减弱, 导致激波阻力减少了13%。王宇天等[101]将等离子激励简化为功率密度源项,使用不同频率和功率密度研究NS-SDBD对激波与边界层干扰流动分离控制效果,发现当激励能量过强时会加重流动的分离情况,而在合适的功率密度下可以减弱激波与边界层干扰流动分离,并在原有激波的作用下会产生一股较强的沿流向的射流。
Nishihara等[102]在高超声速下应用NS-SDBD对圆柱前端的球形激波进行控制,将控制马赫数提升至Ma=5。图 25给出了等离子体激励控制后弓形激波的位置变化纹影图。向上游发展的NS-SDBD诱导压缩波和球形激波相互作用后,激波产生25%位移。
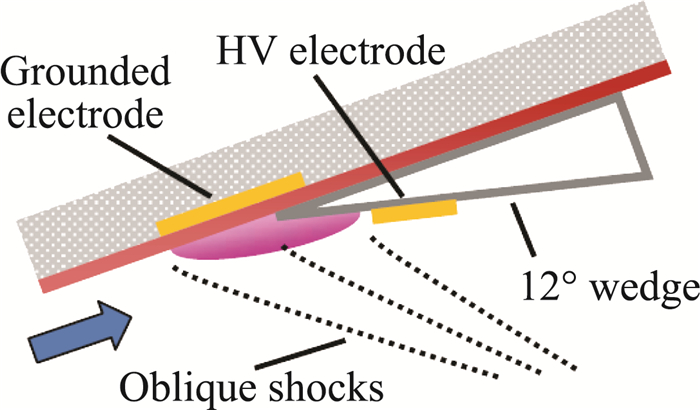
Nishihara等[103]还在来流马赫数Ma=2.2时使用NS-SDBD对斜劈产生的激波进行了控制,图 26给出了其设计原理图。将激励器暴露电极设置在激波后的斜劈上,并将覆盖电极设置在斜劈尖端前。实验结果表明可以对激波强度有所控制,但并没能改变整体激波角度。
|
图 26 斜劈上的等离子体激励器设计[103] Figure 26 Schematics of two NS-DBD surface plasma actuator configurations used with a 12° oblique shock generator model[103] |
Kinefuchi等[104]对超声速平板流动上的激波边界层干扰进行了控制。使用了多种与来流角度不同的等离子体激励器(见图 27)进行了实验。当激励器与来流方向平行时会增大分离区,还会使反射激波向上游移动。当激励器与来流成一定角度时,分离区得到了一定的抑制,同时反射激波也向下游移动。

|
图 27 两种新电极配置(两种情况下的流动方向都是从左到右的)[104] Figure 27 Two types of new electrode configurations (flow direction is from left to right in both cases)[104] |
通过上述文献的综述,可以看出NS-SDBD适用研究的领域非常广泛。总的来说,对其气动激励机理的研究集中在对纳秒脉冲激励下瞬时电场到气动激励的过程进行阐述;对其现象的研究则集中在通过精细的实验结果来表现瞬时气动激励特性及其随时间和空间的演变,为数值模拟提供准确的计算模型和为宏观的流动控制提供机理解释;对其在流动控制的研究则集中在通过有目的地设定实验参数、设计实验模型,通过流动控制效果对激励机理进行验证。
NS-SDBD流动控制研究的难点在于其激励特性集中在很短的时间量级(1×10-9 < t < 1×10-6),而控制效果却体现在宏观的流动现象(t>1×10-3),因此研究上需要跨越较大的时间尺度。另外,NS-SDBD等离子体流动控制研究往往涉及到自动控制、等离子体物理、空气动力学等多个学科,从而需要在高频、窄脉宽条件下同时对电场、密度场、温度场、速度场等多物理场进行耦合测量和诊断。
NS-SDBD流动控制研究的关键科学问题集中在电场激励-气动诱导过程的机理探索与流动控制应用机理研究两个方面,关键科学问题的解决有利于为激励器的设计、控制系统的设计提供优化准则,研究的难点在于涉及多时间尺度、多物理场耦合。注重解决多时间尺度、多物理场耦合问题的数值模拟算法与实验技术将成为解决上述科学问题的关键突破点。
NS-SDBD流动控制技术与实际工程应用之间存在的问题主要有:(1)受限于计算与实验技术,其激励机理与流动控制机理目前尚不完全清楚,从而缺乏有效的系统设计与优化准则;(2)短脉冲高电压特性产生的电磁干扰给实验室研究、飞行器的飞行验证带来了很大的挑战;(3)电源功率的提升、体积的小型化、激励器的制造工艺是进一步需要克服的关键技术。
| [1] |
Corke T C, Cavalieri D A. Controlled experiments on instabilities and transition to turbulence in supersonic boundarylayers[C]//28th Fluid Dynamics Conference, 1997.
|
| [2] |
吴云, 李应红. 等离子体流动控制研究进展与展望[J]. 航空学报, 2015, 36(2): 381-405. |
| [3] |
李应红, 梁华, 吴云, 等. 等离子体气动激励建模仿真综述[J]. 空军工程大学学报:自然科学版, 2008, 9(5): 1-5. |
| [4] |
Wang J J, Kwing-So Choi, et al. Recent developments in DBD plasma flow control[J]. Progress in Aerospace Sciences, 2013, 62(4): 52-78. |
| [5] |
Wu Y, Li Y, Liang H, et al. Nanosecond pulsed discharge plasma actuation: characteristics and flow control performance[R]. AIAA 2014-2118, 2014.
|
| [6] |
吴云, 李应红. 等离子体流动控制与点火助燃研究进展[J]. 高电压技术, 2014, 40(7): 2024-2038. |
| [7] |
罗振兵, 夏智勋, 邓雄, 等. 合成双射流及其流动控制技术研究进展[J]. 空气动力学学报, 2017, 35(2): 252-264. DOI:10.7638/kqdlxxb-2017.0053 |
| [8] |
史志伟, 杜海, 李铮, 等. 等离子体流动控制技术原理及典型应用[J]. 高压电器, 2017(4): 72-78. |
| [9] |
聂万胜, 程钰锋, 车学科. 介质阻挡放电等离子体流动控制研究进展[J]. 力学进展, 2012, 42(6): 722-734. |
| [10] |
聂超群, 李钢, 朱俊强, 等. 介质阻挡放电等离子体流动控制的研究[J]. 中国科学:E辑, 2008, 38(11): 1827-1835. |
| [11] |
杨欢, 刘汝兵, 王萌萌, 等. 等离子体射流及其发生器研究进展[J]. 机电技术, 2013, 36(90): 149-154. |
| [12] |
杨波, 白敏菂, 薛晓红, 等. 等离子体流动控制研究进展[J]. 科技导报, 2009, 27(0924): 81-85. |
| [13] |
Corke T C, Enloe C L, Wilkinson S P. Dielectric barrier discharge plasma actuators for flow control[J]. Annual Review of Fluid Mechanics, 2010, 42(1): 505-529. DOI:10.1146/annurev-fluid-121108-145550 |
| [14] |
Benard N, Moreau E. Electrical and mechanical characteristics of surface AC dielectric barrier discharge plasma actuators applied to airflow control[J]. Experiments in Fluids, 2014, 55(11): 1846. DOI:10.1007/s00348-014-1846-x |
| [15] |
Moreau E. Airflow control by non-thermal plasma Actuators[J]. Journal of Physics D:Applied Physics, 2007, 40(3): 605-636. DOI:10.1088/0022-3727/40/3/S01 |
| [16] |
Starikovskiy A, Aleksandrov N. Plasma-assisted ignition and combustion[J]. Progress in Energy and Combustion Science, 2013, 39(1): 61-110. DOI:10.1016/j.pecs.2012.05.003 |
| [17] |
赵光银, 梁华, 李应红, 等. 表面介质阻挡纳秒脉冲放电及其外流控制研究进展[J]. 力学研究, 2016, 5(2): 75-102. |
| [18] |
Cattafesta III L N, Sheplak M. Actuators for active flow control[J]. Annual Review of Fluid Mechanics, 2011, 43: 247-272. DOI:10.1146/annurev-fluid-122109-160634 |
| [19] |
邵涛, 章程, 王瑞雪, 等. 大气压脉冲气体放电与等离子体应用[J]. 高电压技术, 2016, 42(3): 685-705. |
| [20] |
卢新培, 严萍, 任春生, 等. 大气压脉冲放电等离子体的研究现状与展望[J]. 中国科学:物理学力学天文学, 2011, 41(7): 801-815. |
| [21] |
李清泉, 郝玲艳. 沿面介质阻挡放电等离子体及其应用[J]. 高电压技术, 2016, 42(4): 1079-1090. |
| [22] |
Gad-El-Hak M. Flow Control[M]. Cambridge: Cambridge University Press, 2000.
|
| [23] |
Morozov A I. Introduction to plasma dynamics[M]. CRC Press, 2012.
|
| [24] |
Liu C, Roth J R. Atmospheric glow discharge plasma for aerodynamic boundary layercontrol[C]//IEEE International Conference on Plasma Science, 1994: 97-98.
|
| [25] |
Roth J R, Sherman D M, et al. Boundary layer flow control with a one atmosphere uniform glow discharge surface plasma[R]. AIAA 98-0328.
|
| [26] |
Roth J R. Electrohydrodynamically induced airflow in aone atmosphere uniform glow discharge surface plasma[C]//IEEE International on Plasma Science, Anniversary, 1998: 291.
|
| [27] |
Huang J, Corke T C, Thomas F O. Plasma actuators for separation control of low pressure turbine blades[R]. AIAA-2003-1072.
|
| [28] |
Post M L, Corke T C. Separation control using plasma actuators:dynamic stall vortex control on oscillating airfoil[J]. AIAA Journal, 2006, 44(12): 3125-3135. DOI:10.2514/1.22716 |
| [29] |
Roth J R, Dai X. Optimization of the aerodynamic plasma actuator as an electrohydrodynamic (EHD) electrical device[R]. AIAA 2006-1203.
|
| [30] |
毛枚良, 邓小刚, 向大平, 等. 辉光放电等离子体对边界层流动控制的机理研究[J]. 空气动力学学报, 2006, 24(3): 269-274. DOI:10.3969/j.issn.0258-1825.2006.03.001 |
| [31] |
王江南, 钟诚文, 高超, 等. 基于等离子体激励器简化模型的流动分离控制[J]. 航空计算技术, 2007, 37(2): 30-34. DOI:10.3969/j.issn.1671-654X.2007.02.009 |
| [32] |
吴云, 李应红, 朱俊强, 等. 等离子体气动激励扩大低速轴流式压气机稳定性的实验[J]. 航空动力学报, 2007(12): 2025-2030. DOI:10.3969/j.issn.1000-8055.2007.12.009 |
| [33] |
Xun Huang, Sammie Chan, Xin Zhang. Atmospheric plasma actuators for aeroacoustic applications[J]. IEEE Transactions on Plasma Science, 2007, 35(3): 693-695. DOI:10.1109/TPS.2007.896781 |
| [34] |
Liu F, Luo S, Gao C, et al. Flow control over a conical forebody using duty-cycled plasma actuators[J]. AIAA J, 2008, 46(11): 2969-2973. DOI:10.2514/1.39435 |
| [35] |
孟宣市, 郭志鑫, 刘锋, 等. 细长圆锥前体非对称涡流场的等离子体控制[J]. 航空学报, 2010, 31(3): 500-505. |
| [36] |
Zhang P F, Wang J J, Feng L H, et al. Experimental study of plasma flow control on highly swept delta wing[J]. AIAA J, 2010, 48(1): 249-252. DOI:10.2514/1.40274 |
| [37] |
王万波, 章荣平, 黄宗波, 等. 等离子体激励用于两段翼型增升的试验研究[J]. 空气动力学学报, 2013, 31(1): 64-68. |
| [38] |
杜海, 史志伟, 倪芳原, 等. 基于等离子体激励的飞翼布局飞行器气动力矩控制[J]. 航空学报, 2013(9): 2038-2046. |
| [39] |
冯立好, 王晋军, Choi, 等. 等离子体环量控制翼型增升的实验研究[J]. 力学学报, 2013, 45(6): 815-821. |
| [40] |
张鑫, 黄勇, 王勋年, 等. 超临界机翼介质阻挡放电等离子体流动控制[J]. 航空学报, 2016, 37(6): 1733-1742. |
| [41] |
Cai J S, Tian Y Q, Meng X S, et al. An experimental study of icing control using DBD plasma actuator[J]. Experiments in Fluids, 2017, 58(8): 102. DOI:10.1007/s00348-017-2378-y |
| [42] |
Meng X S, Hu H Y, Yan X, et al. Lift improvements using duty-cycled plasma actuation at low Reynolds numbers[J]. Aerospace Science and Technology, 2018, 72: 123-133. DOI:10.1016/j.ast.2017.10.038 |
| [43] |
Meng X S, Long Y X, Wang J L, et al. Dynamics and control of the vortex flow behind a slender conical forebody by a pair of plasma actuators[J]. Physics of Fluids, 2018, 30(2): 024101. DOI:10.1063/1.5005514 |
| [44] |
Enloe C L, McLaughlin T E, et al. Mechanisms and responses of a single dielectric barrier plasma actuator:plasma morphology[J]. AIAA Journal, 2004, 42(3): 595-604. DOI:10.2514/1.3884 |
| [45] |
Forte M, Jolibois J, et al. Optimization of a dielectric barrier discharge actuator by stationary and instationary measurements of the induced flow velocity, application to airflow control[R]. AIAA 2006-2863.
|
| [46] |
Christopher L K, Patrick O B, et al. Leading-edge separation control using alternating current and nanosecond pulse plasma actuators[J]. AIAA Journal, 2014, 52(9): 1871-1884. DOI:10.2514/1.J052708 |
| [47] |
Roupassov D, Nikipelov A, et al. Flow separation control by plasma actuator with nanosecond pulsed-periodic discharge[J]. AIAA Journal, 2009, 47(1): 168-185. DOI:10.2514/1.38113 |
| [48] |
Bayoda K D, Benard N, et al. Elongating the area of plasma/fluid interaction of surface nanosecond pulsed discharges[J]. Journal of Electrostatics, 2015, 74: 79-84. DOI:10.1016/j.elstat.2014.12.004 |
| [49] |
Hu H Y, Li H X, et al. Phase-locked schlieren of periodic nanosecond-pulsed DBD actuation in quiescent air[R]. AIAA 2016-1696.
|
| [50] |
Hu H Y, Li H X, Meng X S, et al. Starting flow by repetitive nanosecond pulsed DBD actuation at microseconds and milliseconds in quiescent air[R]. AIAA 2015-2956.
|
| [51] |
Cui Y D, Zhao Z J, Bouremel Y, et al. Studies on the configurations of nanosecond DBD pulse plasma actuators[J]. Studies, 2014, 8: 11. |
| [52] |
李结, 李华星, 王健磊, 等. 纳秒脉冲等离子体对静止大气的激励特性[J]. 西北工业大学学报, 2014, 32(2): 176-180. DOI:10.3969/j.issn.1000-2758.2014.02.004 |
| [53] |
Zhao Z, Li J M, Zheng J, et al. Study of shock and induced flow dynamics by nanosecond dielectric-barrier-discharge plasma actuators[J]. AIAA Journal, 2014, 53(5): 1336-1348. |
| [54] |
Starikovskii A Y, Nikipelov A A, et al. SDBD plasma actuator with nanosecond pulse-periodic discharge[J]. Plasma sources Science and Technology, 2009, 18(3): 034015. DOI:10.1088/0963-0252/18/3/034015 |
| [55] |
Gaitonde D V, McCrink M H. A semi-empirical model of a nanosecond pulsed plasma actuator for flow control simulations with LES[R]. AIAA 2012-184.
|
| [56] |
Chen Z L, Hao L Z, Zhang B Q, et al. An empirical model of nanosecond pulsed SDBD actuators for separation control[R]. AIAA 2013-2743.
|
| [57] |
Chen Z L, Hao L Z, Zhang B Q. A model for nanosecond pulsed dielectric barrier discharge (NSDBD) actuator and its investigation on the mechanisms of separation control over an airfoil[J]. Sci. China Tech. Sci., 2013, 56(5): 1055-1065. DOI:10.1007/s11431-013-5179-4 |
| [58] |
Chen Z, Zhang S, Zhang B, et al. Shock-induced separation control by using nanosecond pulsed SDBD plasma actuators[R]. AIAA 2014-2368.
|
| [59] |
赵光银, 李应红, 梁华, 等. 纳秒脉冲表面介质阻挡等离子体激励唯象学仿真[J]. 物理学报, 2015, 64(1): 174-184. |
| [60] |
李凡玉, 李军, 吴云, 等. 纳秒脉冲等离子体气动激励数值仿真[J]. 航空动力学报, 2015, 30(3): 537-545. |
| [61] |
Nudnova M, Kindusheva S, Aleksahdrov N, et al. Rate of plasma thermalization of pulsed nanosecond surface dielectric barrier discharge[R]. AIAA 2010-465.
|
| [62] |
Flitti A, Pancheshnyi S. Gas heating in fast pulsed discharges in N2-O2 mixtures[J]. The European Physical Journal Applied Physics, 2009, 45: 21001. DOI:10.1051/epjap/2009011 |
| [63] |
Mintoussov E I, Pendleton S J, et al. Fast gas heating in a nitrogen-oxygen discharge plasma:Ⅱ. Energy exchange in the afterglow of a volume nanosecond discharge at moderate pressures[J]. Journal of Physics D:Applied Physics, 2011, 44(28): 285202. DOI:10.1088/0022-3727/44/28/285202 |
| [64] |
Popov N A. Fast gas heating in a nitrogen-oxygen discharge plasma:I. Kinetic mechanism[J]. Journal of Physics D:Applied Physics, 2011, 44(28): 285201. DOI:10.1088/0022-3727/44/28/285201 |
| [65] |
Popov N A. Fast gas heating initiated by pulsed nanosecond discharge in atmospheric pressure air[R]. AIAA 2013-1052.
|
| [66] |
徐双艳, 李江, 蔡晋生, 等. 二维对称结构纳秒脉冲介质阻挡放电数值模拟[J]. 高电压技术, 2015, 41(6): 2100-2107. |
| [67] |
Xu S Y, Cai J S, Li J. Modeling and simulation of plasma gas flow driven by a single nanosecond-pulsed dielectric barrier discharge[J]. Physics of plasma, 2016, 23(10): 1-84. |
| [68] |
Xu S Y, Cai J S, et al. Investigation of the electrode surfacegeometry effects driven by nanosecondpulsed surface dielectric barrier discharge[J]. Journal of Physics D:Applied Physics, 2017, 50(8): 185201. |
| [69] |
Poggie J, Adamovich I, et al. Numerical simulation of nanosecond-pulse electrical discharges[J]. Plasma Sources Science and Technology, 2013, 22(1): 015001. |
| [70] |
Zhu Y F, Wu Y, et al. Modelling of plasma aerodynamic actuation driven by nanosecond SDBD discharge[J]. J. Phys. D:Appl. Phys, 2013, 46: 355205. DOI:10.1088/0022-3727/46/35/355205 |
| [71] |
Kourtzanidis K, Raja L L. Three-electrode sliding nanosecond dielectric barrier discharge actuator:modeling and physics[J]. AIAA Journal, 2017, 55(4): 1393-1404. DOI:10.2514/1.J055473 |
| [72] |
Likhanskii A V, Shneider M N, et al. Optimization of dielectric barrier discharge plasma actuators driven by repetitive nanosecond pulses[R]. AIAA 2007-633, 2007.
|
| [73] |
Unfer T, Boeuf J P. Modelling of a nanosecond surface discharge actuator[J]. Journal of Physics D:Applied Physics, 2009, 42(42): 194017. |
| [74] |
Che X K, Shao T, et al. Numerical simulation on a nanosecond-pulse surface dielectric barrier discharge actuator in near space[J]. Journal of Physics D:Applied Physics, 2012, 45(45): 145201. |
| [75] |
Zheng J G, Zhao Z J, et al. Numerical simulation of nanosecond pulsed dielectric barrier discharge actuator in a quiescent flow[J]. Physics of fluids, 2014, 26(3): 505-529. |
| [76] |
Zheng J G, Li J, et al. Numerical study of nanosecond pulsed plasma actuator in laminar flat plate boundary layer[J]. Communications in Computation Physics, 2016, 20(5): 1424-1442. DOI:10.4208/cicp.090615.140316a |
| [77] |
Qian Y H, d'Humières D, Lallemand P. Lattice BGK models for Navier-Stokes equation[J]. EPL (Europhysics Letters), 1992, 17(6): 479. DOI:10.1209/0295-5075/17/6/001 |
| [78] |
Liu C, Xu K. A unified gas kinetic scheme for continuum and rarefied flows Ⅴ:multiscale and multi-component plasma transport[J]. Communications in Computational Physics, 2017, 22(5): 1175-1223. DOI:10.4208/cicp.OA-2017-0102 |
| [79] |
Lehmann R, Akins D, et al. Effects of nanosecond pulse driven plasma actuators on turbulent shear layers[J]. AIAA Journal, 2016, 54(2): 1-15. |
| [80] |
Correale G, Michelis T, et al. Nanosecond-pulsed plasma actuation in quiescent air and laminar boundary layer[J]. Journal of Physics D:Applied Physics, 2014, 47(10): 105201. DOI:10.1088/0022-3727/47/10/105201 |
| [81] |
Correale G, Winkel R, et al. Induced velocity and density gradients due to nanosecond plasma actuation[J]. AIAA Journal, 2016, 54(12): 3895-3901. DOI:10.2514/1.J054834 |
| [82] |
Correale G, Avallone F, et al. Experimental method to quantify the efficiency of the frst two operational stages of nanosecond dielectric barrier discharge plasma actuators[J]. Journal of Physics D:Applied Physics, 2016, 49(50): 505201. DOI:10.1088/0022-3727/49/50/505201 |
| [83] |
Roupassov D V, Nikipelov A A, et al. Flow separation control by plasma actuator with nanosecond pulsed-periodic discharge[J]. AIAA Journal, 2009, 47(1): 168-185. DOI:10.2514/1.38113 |
| [84] |
杜海, 史志伟, 程克明, 等. 纳秒脉冲等离子体分离流控制频率优化及涡运动过程分析[J]. 航空学报, 2015, 37(7): 2102-2111. |
| [85] |
Kato K, Breitsamter C, et al. Flow separation control over a Gö 387 airfoil by nanosecond pulse-periodic discharge[J]. Experiment in Fluid, 2014, 55(8): 1-19. |
| [86] |
Clifford C, Singhal C, et al. Flow control over an airfoil in fully reversed condition using plasma actuators[J]. AIAA Journal, 2016, 54(1): 141-149. DOI:10.2514/1.J054157 |
| [87] |
Little J, Takashima K, et al. Separation control with nanosecond-pulse-driven dielectric barrier discharge plasma actuators[J]. AIAA Journal, 2012, 50(2): 350-365. DOI:10.2514/1.J051114 |
| [88] |
Moreau E, Debien A, et al. Nanosecond-pulsed dielectric barrier discharge plasma actuator for airflow control along an NACA0015 airfoil at high reynolds number[J]. IEEE Transactions on Plasma Science, 2016, 44(11): 2803-2811. DOI:10.1109/TPS.2016.2603226 |
| [89] |
Zhao Z J, Cui Y D, et al. On the separated flow using nanosecond DBD plasma actuators at low reynolds number[R]. AIAA 2017-0712.
|
| [90] |
Cui Y D, Zhao Z J, et al. Flow separation control over an NACA0015 airfoil using nanosecond pulsed plasma actuator[R]. AIAA 2017-0715.
|
| [91] |
Zheng J G, Cui Y D, et al. Investigation of airfoil leading edge separation control with nanosecond plasma actuator[J]. Physical Review Fluids, 2016, 1: 073501. DOI:10.1103/PhysRevFluids.1.073501 |
| [92] |
Roupassov D V, Zavyalov I N, et al. Boundary layer separation control by nanosecond plasma actuators[R]. AIAA 2008-5067.
|
| [93] |
Kato K, Breitsamter C, Obi S. Flow control over swept wings using nanosecond-pulse plasma actuator[J]. International Journal of Heat & Fluid Flow, 2016, 61: 58-67. |
| [94] |
化为卓, 李应红, 牛中国, 等. 低速三角翼纳秒脉冲等离子体激励实验[J]. 航空动力学报, 2014, 29(10): 2331-2339. |
| [95] |
赵光银, 梁华, 李应红, 等. 纳秒脉冲等离子体激励控制小后掠三角翼[J]. 航空学报, 2015, 36(7): 2125-2132. |
| [96] |
Du H, Shi Z W, et al. Topological structures of vortex flow on a flying wing aircraft, controlled by a nanosecond pulse discharge plasma actuator[J]. Applied Physics Letters, 2016, 108(24): 246. |
| [97] |
Yao J K, Zhou D J, et al. Experimental investigation of lift enhancement for flying wing aircraft using nanosecond DBD plasma actuators[J]. Plasma Science and Technology, 2017, 19(4): 7-14. |
| [98] |
Zhang D, Meng X S, Wang J L, et al. Pressures over a conical forebody under repetitive nanosecond pulse SDBD actuations[R]. AIAA 2015-2955. https://www.researchgate.net/publication/299645286_Pressures_over_a_Conical_Forebody_under_Repetitive_Nanosecond_Pulse_SDBD_Actuations
|
| [99] |
Wang J L, Li H X, Meng X S, et al. Nanosecond-SDBD actuation over a conical forebody at wind speed 72 m/s and angle of attack 45 degree[R]. AIAA 2015-3310. https://www.researchgate.net/publication/299644448_Nanosecond-SDBD_Actuation_over_a_Conical_Forebody_at_Wind_Speed_72_ms_and_Angle_of_Attack_45_degree
|
| [100] |
倪芳原, 史志伟, 杜海. 纳秒脉冲等离子体激励器用于圆柱高速流动控制的数值模拟[J]. 航空学报, 2014, 35(3): 657-665. |
| [101] |
王宇天, 张百灵, 李益文, 等. 等离子体激励控制激波与边界层干扰流动分离数值研究[J]. 航空动力学报, 2018, 33(2): 364-371. |
| [102] |
Nishihara M, Takashima K, et al. Mach 5 bow shock control by a nanosecond pulse surface dielectric barrier discharge[J]. Physics of Fluid, 2011, 23(6): 605-622. |
| [103] |
Munetake Nishihara, Datta Gaitonde, Igor V Adamovich. Effect of nanosecond pulse discharges on oblique shock and shock wave-boundary layer interaction[R]. AIAA 2013-0461.
|
| [104] |
Kinefuchi K, Starikovskiy A Y, Miles R B. Control of shock-wave/boundary-layer interaction using nanosecond-pulsed plasma actuators[J]. Journal of Propulsion and Power, 2018, 34(4): 909-919. DOI:10.2514/1.B36530 |
 2018, Vol. 36
2018, Vol. 36