0 引言

在壁板颤振的分析过程中，需要准确计算壁板表面气动力^[1-2]，目前用到的气动力理论主要有以下四种^[3]：势流理论、活塞理论、基于Euler方程的气动力理论和基于N-S方程的气动力理论。Nydick^[4]、Bein^[5]、Selvam^[6]对比了不同气动力理论的计算结果，发现高马赫数下活塞理论、Euler方程、N-S方程得到的结果基本一致；若马赫数过高(Ma>10)，由于黏性效应的影响，N-S方程的求解结果与其余两种存在差异。在这几种气动力求解方法中，目前应用比较广泛的是活塞理论，因为在气动弹性分析中气动力的计算占据了绝大多数的计算资源。活塞理论最早由Lighthill^[7]和Ashley^[8]提出，其表达式简洁，能够兼顾计算精度、效率，经过陈劲松^[9]、杨炳渊^[10]、张伟伟^[11]等人的发展，被广泛应用于超声速及高超声速气动力、气动弹性的计算中。近年来，对活塞理论的研究多集中于根据黏性效应修正几何外形^[12-13]或者采用更高阶的数值方法^[14]，以期在更高马赫数下获得精确的气动力求解结果。根据截断误差的不同，活塞理论可分为一阶活塞理论和高阶活塞理论，阶数决定了气动载荷的求解精度。根据Cheng^[15]的总结，一阶活塞理论适应于来流条件为$\sqrt 2 $ < Ma < 5的气动力计算，而当马赫数超过5时，气动力的非线性效应增强，为满足精度要求，必须采用高阶活塞理论。可以看出，目前对活塞理论阶数的选择，更多地是基于计算结果的精度对比，这是对应用效果的经验总结而不是理论探究。要想合理地应用活塞理论，需要明确非线性项所代表的物理含义。另一方面可以注意到，在气动弹性的计算中，即使一阶活塞理论在翼面气动弹性分析中也被认为效果非常好，而在壁板颤振的分析中认为必须采用高阶活塞理论。是什么机制造成活塞理论在翼面气动弹性分析和壁板颤振计算中的差别？目前尚未见到专门的文献来分析这种气动力非线性的根源，也没有见到分析除马赫数和黏性外影响非线性效应的其他因素。因此，对活塞理论中的非线性效应进行详细分析是必要的，它可以使得对活塞理论在使用过程中的适应性有更加准确地把握。

本文对比了活塞理论、考虑激波膨胀波的活塞理论、Euler方程对气动力的计算结果，研究了在颤振计算过程中气动力非线性的主要来源，并对影响非线性效应的主要因素进行了分析。

1 考虑激波膨胀波的活塞理论

活塞理论(Piston Theory, PT)是由动量定理和等熵关系式推导得到的气动力表达式。在超声速、高超声速非定常气动力计算中，活塞理论具有良好的精度。其表达式如下：

$ p = {p_\infty }{\left( {1 + \frac{{\gamma - 1}}{2}\frac{{{v_n}}}{{{a_\infty }}}} \right)^{\frac{{2\gamma }}{{\gamma - 1}}}} $

(1)

$ {v_n} = {v_\infty }\frac{{\partial w}}{{\partial x}} + \frac{{\partial w}}{{\partial t}} $

(2)

式中，p为当地压强，p_∞、a_∞、v_∞分别为来流压强、声速、速度，v_n为非定常下洗速度，w为位移。

在超声速流场中，物面的振动变形会产生一系列的激波膨胀波，从而导致气动力计算出现非线性特征。从活塞理论的推导过程来看，并没有显式地考虑激波和膨胀波的存在，为此，本文建立了考虑激波膨胀波的活塞理论(Shock Expansion-Piston Theory, SE-PT)。

激波角β与气流偏转角θ的关系为：

$ \tan \theta = 2\cot \beta \frac{{Ma_1^2{{\sin }^2}\beta - 1}}{{Ma_1^2\left[ {\gamma + \cos \left( {2\beta } \right) + 2} \right]}} $

(3)

式中Ma₁为波前马赫数。求得β后再根据斜激波关系式可求得波后气动参数：

$ Ma_{n,2}^2 = \frac{{1 + \left[ {\left( {\gamma - 1} \right)/2} \right]Ma_{n,1}^2}}{{\gamma Ma_{n,1}^2 - \left( {\gamma - 1} \right)/2}} $

(4)

$ \frac{{{\rho _2}}}{{{\rho _1}}} = \frac{{\left( {\gamma + 1} \right)Ma_{n,1}^2}}{{2 + \left( {\gamma + 1} \right)Ma_{n,1}^2}} $

(5)

$ \frac{{{p_2}}}{{{p_1}}} = 1 + \frac{{2\gamma }}{{\gamma + 1}}\left( {Ma_{n,1}^2 - 1} \right) $

(6)

式中，Ma_{n, 1}、ρ₁、p₁为波前马赫数的垂直分量、波前密度、波前压强，Ma_{n, 2}、ρ₂、p₂为波后马赫数的垂直分量、波后密度、波后压强。

对于膨胀波来说，结合普朗特-迈耶函数v(Ma)和气流偏转角θ即可求得波后马赫数，公式可写为：

$ \theta = v\left( {M{a_2}} \right) - v\left( {M{a_1}} \right) $

(7)

$ \begin{array}{l} v\left( {Ma} \right) = \sqrt {\frac{{\gamma + 1}}{{\gamma - 1}}} \arctan \sqrt {\frac{{\gamma + 1}}{{\gamma - 1}}\left( {M{a^2} - 1} \right)} - \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\arctan \sqrt {M{a^2} - 1} \end{array} $

式中，Ma₁为波前马赫数，Ma₂为波后马赫数。再由膨胀波关系式求出波后气动参数：

$ \frac{{{\rho _2}}}{{{\rho _1}}} = {\left\{ {\frac{{1 + \left[ {\left( {\gamma - 1} \right)/2} \right]Ma_1^2}}{{1 + \left[ {\left( {\gamma - 1} \right)/2} \right]Ma_2^2}}} \right\}^{\frac{1}{{\gamma - 1}}}} $

(8)

$ \frac{{{p_2}}}{{{p_1}}} = {\left\{ {\frac{{1 + \left[ {\left( {\gamma - 1} \right)/2} \right]Ma_1^2}}{{1 + \left[ {\left( {\gamma - 1} \right)/2} \right]Ma_2^2}}} \right\}^{\frac{\gamma }{{\gamma - 1}}}} $

(9)

式中，ρ₁、p₁为波前密度、波前压强，ρ₂、p₂为波后密度、波后压强。

这样，在壁板的每一步振动中，都调用激波膨胀波关系式，得到当地的压强，并结合活塞理论计算气动力，即为考虑激波膨胀波的活塞理论(SE-PT)。

在颤振分析中，壁板模态m一般选取为如下形式：

$ m\left( {x,t} \right) = A\left( t \right)\sin \left( {i{\rm{ \mathsf{ π} }}\frac{x}{{2l}}} \right) $

(10)

式中，A表示广义位移，i表征模态阶数，2l为壁板长度。可以看到，模态振型为高阶光滑的连续函数，满足正交性，符合几何边界条件的要求。这种模态分解方法，在壁板颤振分析中取得极大成功。但对本文的研究内容来说，正弦形式的模态却不是最合适的，原因有两点：

1) 本文首先建立了考虑激波膨胀波的活塞理论，而激波膨胀波关系式不适应于求解光滑曲面的气动载荷；

2) 本文探究的是气动力的非线性效应，与壁板结构的真实模态形状无关。

因此，需要重新设计模态振型。新模态主要需考虑两点因素：便于激波膨胀波关系式的使用，满足几何边界条件。基于这样的考虑, 我们将模态振型构造为折线形状。设壁板长度为2l，模态表达式如下：

$ m\left( {x,t} \right) = \left\{ \begin{array}{l} A\left( t \right)\frac{x}{l},\;\;\;\;\;\;\;\;\;\;\;\;\;0 \le x \le l\\ A\left( t \right)\left( {2 - \frac{x}{l}} \right),\;\;\;\;\;l \le x \le 2l \end{array} \right. $

(11)

采用式(11)表征的模态，可近似应用激波膨胀波关系式计算变形后的定常气动载荷，且该模态保留了壁板结构的主要几何特征，得到的气动力分析结果是具有普遍性意义的。

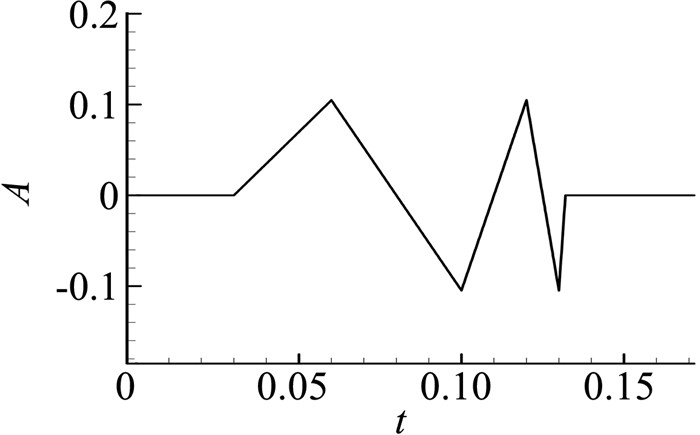
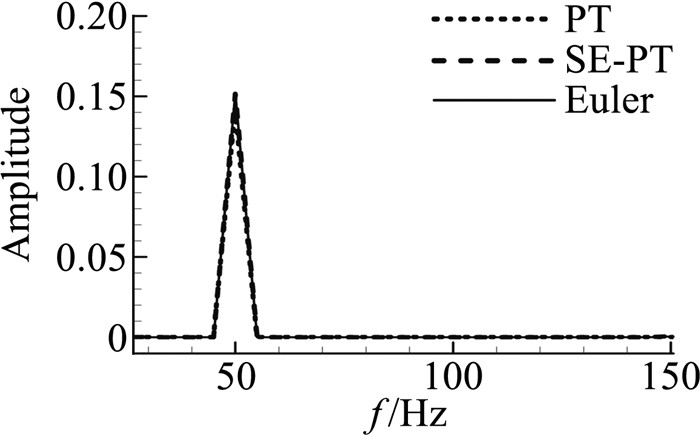
取计算状态为Ma=3，输入如图 1所示的扫频位移信号，比较SE-PT理论与Euler方程的气动力系数F求解结果，如图 2所示，可见二者符合良好，证明所采用的考虑激波膨胀波的活塞理论在气动力预测方面具有良好的精度。

2 一阶活塞理论在壁板振动中的应用

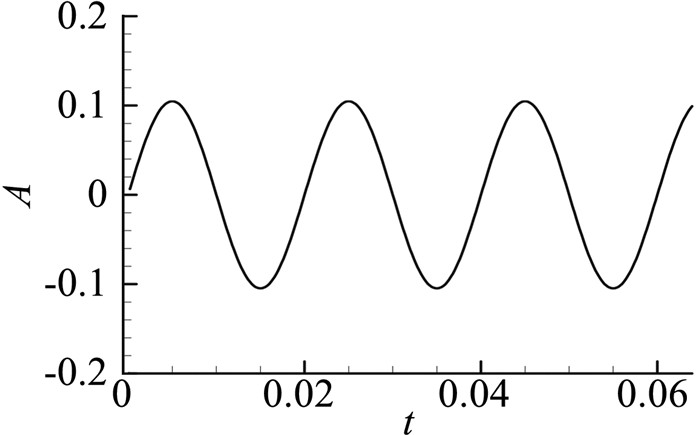
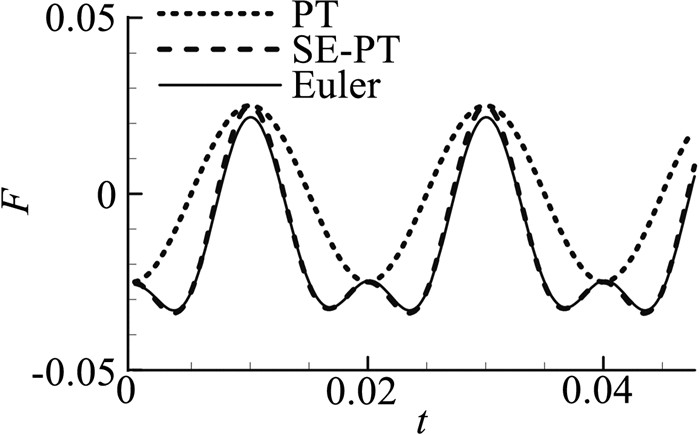
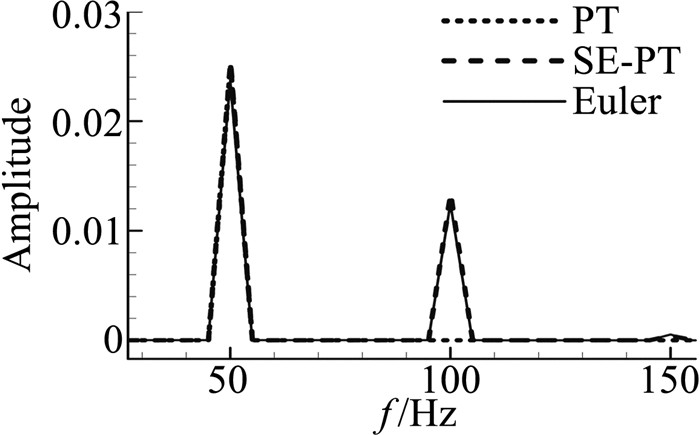
计算状态取为Ma=3，研究对象为壁板，一阶模态为前述的折线形状，输入频率50 Hz的正弦位移信号，如图 3所示。分别采用一阶活塞理论(PT)、考虑激波膨胀波的一阶活塞理论(SE-PT)、Euler方程计算气动力系数，结果如图 4所示。可以清晰地看出，SE-PT理论与Euler方程的求解结果符合良好，气动力响应的非线性特征较为明显，而一阶活塞理论只能预测气动力的线性部分。将气动力响应做频谱分析，得到的幅频特性曲线如图 5所示，从中可以看出，气动力响应的一阶谐波分量与二阶谐波分量的幅值比约为1:0.5，而一阶分量与三阶谐波分量的比值约为1:0.02，基本可以忽略。也就是说，气动力响应的非线性特征主要是出现了二阶谐波分量。

将一阶活塞理论中加入激波膨胀波关系式，得到的非定常气动力计算结果与Euler方程相同，因此得出，气动力的非线性特征是激波膨胀波带来的。

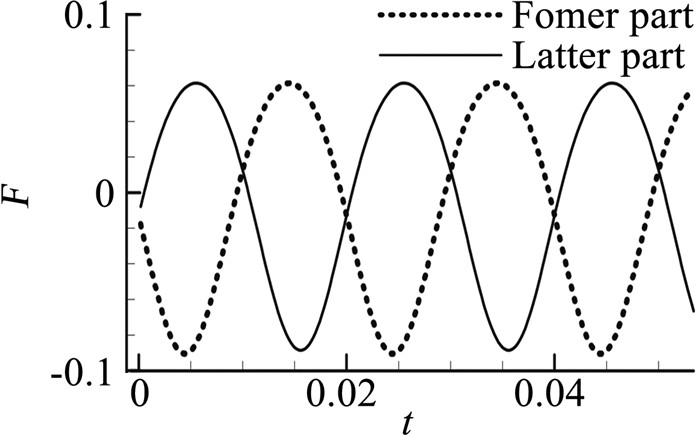
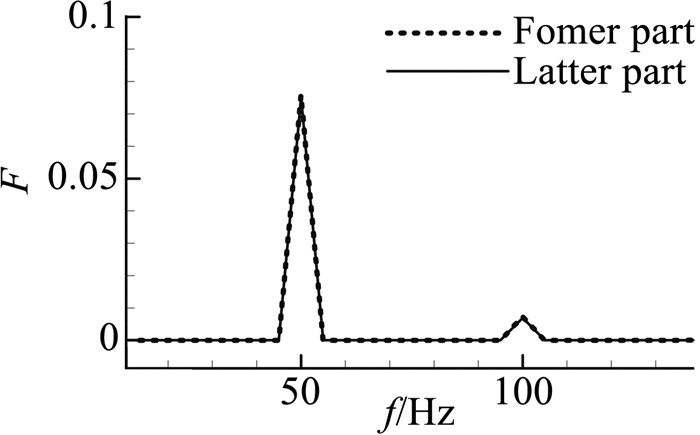
上述设计的壁板模态形状前后具有对称性，因此将壁板从中间位置分为两部分——前半部分和后半部分，同时也将壁板表面气动力分为前后两部分，分别作出两部分的气动力响应曲线以及幅频特性曲线，如图 6、图 7所示。可见，壁板前后两部分的气动力一阶、二阶谐波分量均相同，二阶分量仅占一阶分量的9%左右。而根据图 5，整个壁板的气动力二阶谐波分量约占一阶分量的50%，非线性分量占比显著增加。

表 1展示了气动力一阶、二阶谐波分量的相位大小。对一阶谐波分量来说，前后两部分的相位差较大，近似于反向，而前后表面的二阶分量几乎同相位。正是因为壁板前后部分的一阶分量反相、二阶分量同相，所以两个表面9%的非线性分量在求和后占比达到了50%，非线性效应显著增强。进一步探究一阶谐波分量反相的原因。活塞理论的一阶项可写为如下形式：

$ {p_1} = {\rho _\infty }{a_\infty }\left( {v\frac{{\partial w}}{{\partial x}} + \frac{{\partial w}}{{\partial t}}} \right) $

(12)

该式的第一项为变形分量，第二项为振动分量，由此将物面振动产生的气动力分解为变形导致的气动力分量和振动导致的气动力分量两部分，前者正比于壁板相对于来流的迎角，后者正比于壁板的横向振动速度。对于壁板的前后两部分来说，气流的迎角相反而横向振动速度相同，所以总的气动力中变形分量前后抵消，而振动分量则加强，同时在低速振动中，变形气动力分量占主导地位。因此前后部分的一阶气动力几乎是反相位的。

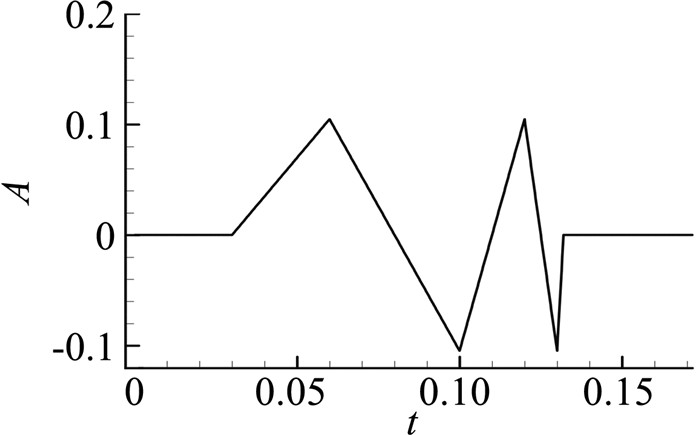
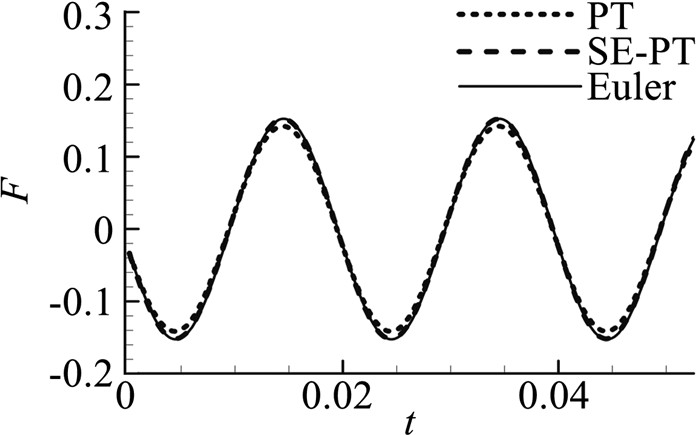
3 一阶活塞理论在具有双侧来流的物面振动中的应用

取长度为l的无厚度板，绕前端点做俯仰运动，俯仰位移如图 8所示，得到的气动力系数响应如图 9所示。一阶活塞理论的求解结果与SE-PT理论、Euler方程的结果符合良好，说明此时的气动力响应中不存在高阶谐波分量。输入单一频率(50 Hz)的广义位移，得到的气动力响应如图 10所示，频谱分析的幅频特性曲线如图 11。可见，气动力响应只有一阶谐波分量，一阶活塞理论的计算结果是准确的。

对壁板这种只有单侧来流的物面振动来说，气动力的非线性特征明显。而在双侧来流的物面振动中，却没有非线性分量。下面对这一现象做进一步的研究。把双侧来流的物面分为上表面和下表面，分别计算它们的气动力响应。图 12展示了气动力的时域响应曲线，图 13展示了气动力的幅频特性曲线。

对上、下单个表面来说，气动力出现了明显的二阶谐波分量，其与一阶谐波分量的幅值比约为9%。表 2展示了上、下表面各阶谐波分量的相位关系，可以看到，一阶分量相位相同，二阶分量相位相反，这就使得在计算总的气动力时，二阶谐波分量相互抵消，呈现出良好的线性特征。激波膨胀波带来了气动力的非线性效应，在物面振动过程中上表面出现激波时，下表面往往出现膨胀波，反之亦然。激波与膨胀波对气动力的影响相反，这是导致总的非线性效应相互抵消的物理原因。

4 高阶活塞理论

图 14对比了50 Hz广义位移输入信号下不同阶活塞理论的气动力计算结果，可见，二阶活塞理论基本能预测出气动力的非线性特征。Cheng和Mei^[15]研究了不同阶活塞理论计算壁板振动极限环幅值的区别，从计算结果来看，一阶活塞理论不够精确，二阶与三阶活塞理论的差别在0.5%以内。Fridmann^[2]对比了微幅振动下不同阶活塞理论得到的壁板表面气动力系数，发现二阶活塞理论、三阶活塞理论、Euler方程的计算结果一致。

图 15对比了不同阶考虑激波膨胀波的活塞理论气动力计算结果，由于激波膨胀波关系式的引入，一阶理论就已经能够很好地呈现出气动力的非线性特征。

对比二阶活塞理论、考虑激波膨胀波的一阶活塞理论与Euler方程在不同位移信号下的气动力求解结果，如图 16所示，三者符合良好，证明壁板颤振中气动力的非线性因素主要是由激波膨胀波带来的，而活塞理论的二阶项基本可以反映出这种非线性。

实际工程中的壁板颤振分析可能面临着很宽的结构频率范围，而活塞理论在不同的频率范围下呈现出不同的计算效果。为了澄清这方面的机制，分析了频率对气动力非线性的影响。

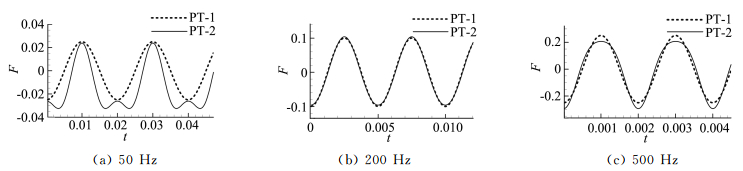
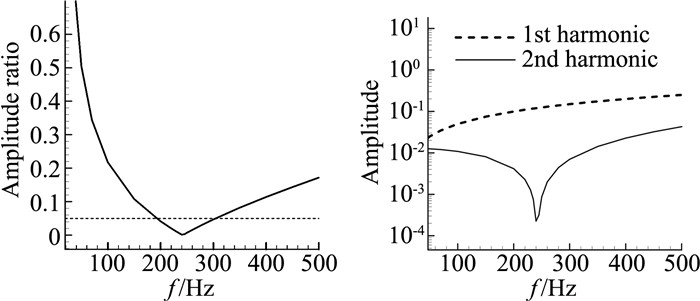
取三个不同频率(50 Hz、200 Hz、500 Hz)的位移信号，分别采用一阶、二阶活塞理论计算气动力系数。图 17是气动力的时域响应，图 18是对应的幅频特性曲线。三个频率下气动力出现了不同程度的非线性效应，二阶谐波分量与一阶谐波分量幅值比分别为0.503、0.042、0.172，可以看到，气动力的非线性程度与频率有很大关系。进一步做出二阶谐波与一阶谐波分量幅值比随频率变化的曲线图，如图 19(a)，图中另外画出了幅值比为0.05的虚线。可以看出，当振动频率较高或者较低时，气动力的非线性效应变强，而在中间某段频率(200~300 Hz)内，非线性分量占比很低，此时气动力可以近似看做是线性的。探究在中频段内气动力的非线性分量占比很低的原因。观察气动力的一阶、二阶谐波分量幅值随频率的变化(图 19b)。由前面的分析可知，一阶谐波可分为变形导致的气动力分量和振动导致的气动力分量，前者与振动频率无关，后者与振动频率成线性增大关系，二者的综合作用，使得气动力的一阶谐波分量幅值随频率线性增大。图 19(b)中的虚线展示了这一规律。实线代表的是二阶谐波分量幅值随频率的变化关系，可以看到是先减小后增大的。因此在中间频段二阶分量的占比降低，气动力的线性效应增强。

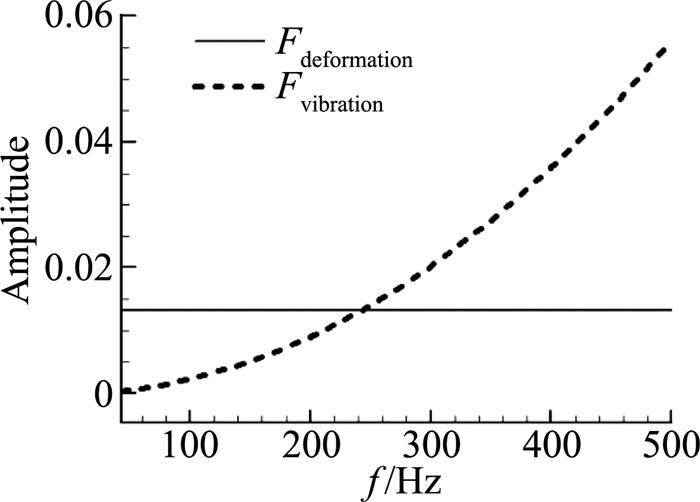
进一步探究二阶谐波的幅值随频率先减小后增大的原因。下式为活塞理论的二阶分量：

$ \begin{array}{l} {p_2} = {p_\infty }\left( {\frac{{\gamma + 1}}{4}} \right){\left( {v\frac{{\partial w}}{{\partial x}} + \frac{{\partial w}}{{\partial t}}} \right)^2}\\ \;\;\;\; = {p_\infty }\left( {\frac{{\gamma + 1}}{4}} \right)\left[ {{{\left( {v\frac{{\partial w}}{{\partial x}}} \right)}^2} + 2v\frac{{\partial w}}{{\partial x}}\frac{{\partial w}}{{\partial t}} + {{\left( {\frac{{\partial w}}{{\partial t}}} \right)}^2}} \right] \end{array} $

由于壁板模态形状的对称性，前后部分的二次交叉项$2v\frac{{\partial w}}{{\partial x}}\frac{{\partial w}}{{\partial t}}$相互抵消，气动力的二阶谐波分量可分为变形导致的气动力分量项和振动导致的气动力分量两部分，分别为含${\left( {v\frac{{\partial w}}{{\partial x}}} \right)^2}$的项和含${\left( {\frac{{\partial w}}{{\partial t}}} \right)^2}$的项。当输入正弦形式的广义位移形如h=Asin(ωt)时，变形分量正比于sin²(ωt)，振动分量正比于ω²cos²(ωt)，二者相位相反。观察气动力二阶谐波的变形分量和振动分量幅值随振动频率的变化情况，如图 20所示。频率在200~300 Hz范围时，两个分量数值相近，导致总的气动力幅值最小，低频(200 Hz以下)时变形分量远大于振动分量，高频(300 Hz以上)时恰好相反，这就导致了低频和高频范围内气动力的二阶谐波分量占比增大。

5 结论

本文选取超声速来流的计算状态，忽略壁面黏性效应，对比了活塞理论、考虑激波膨胀波的活塞理论、Euler方程的气动力计算结果，探究了壁板颤振中气动力非线性的主要来源，同时研究了具有双侧气流的物面振动气动力的线性性质，解释了振动频率影响气动力非线性效应的原因，得到的主要结论如下：

(1) 超声速物面振动过程中产生的激波膨胀波是气动力非线性的主要来源；

(2) 一阶活塞理论适应于高超声速翼面气动弹性分析，其原因是上下表面的非线性分量相互抵消，气动力的线性效应增强；而在只有单侧来流的壁板颤振分析中，模态变形量的对称性使得气动力的线性分量降低，非线性分量升高，此时需采用高阶活塞理论来模拟这种非线性效应；

(3) 活塞理论中的高阶项表征的是激波膨胀波带来的非线性效应，它随振动频率的增加先减弱后增强，其原因是非线性项中的变形气动力分量和振动气动力分量相位相反，前者幅值不随频率变化，后者随频率增加而增大，在中间某段频域内二者的幅值近似相等，非线性效用相互抵消，只有此时气动力才可以看作是线性的。