2. 国家计算流体力学实验室, 北京 100191
2. National Laboratory for Computational Fluid Dynamics, Beijing 100191, China
可回收类航天器如飞船返回舱,从空间轨道返回地球表面着陆场,先后经历在轨自由分子流,到进入、下降段稀薄过渡流,以至高空近连续滑移流,最后到达近地面连续流,是一个跨流域多尺度非平衡变化过程[1-8]。如何准确模拟返回舱以极高速度再入跨流域复杂多物理场非平衡绕流问题?特别是准确预测近连续滑移过渡流区高超声速气动力/热环境、姿态配平、升阻比、热流变化等气动特征,对航天器精细化气动设计与成功回收着陆具有至关重要作用与指导意义[8-17]。载人飞船返回着陆过程,一旦失效可能造成船毁人亡,1967年前苏联“联盟一号”载人飞船开伞失败,航天员以身殉职;2008年美国“猎户号”飞船回收系统空投测试,飞船模型发生翻滚坠毁。以美国航天飞机为例,由地面风洞模拟得到的机身体襟翼配平角为7.5°,而实际飞行试验结果为16°,导致这种极端不一致源于跨流域复杂多尺度流动稀薄非平衡效应,同样2003年2月1日美国“哥伦比亚”号航天飞机返航再入到离地面60 km高空因左翼受损解体失事,直接与高空高温稀薄非平衡流动效应相关联[11-12, 17-19]。对于具有大尺寸复杂结构的跨大气层航天飞行器,再入飞行走廊中大部分区域都为稀薄、过渡流区所覆盖(200~40 km),当航天器返回地面时,通常会在太空边缘的亚轨道状态进行推返分离、调姿配平,如飞船返回舱再入到130 km左右进行推返分离,需要在飞行高度约125 km到105 km期间根据预装的配平迎角进行调姿配平,图 1所示飞船返回舱再入过程跨流域飞行示意图;飞船返回舱一般采用横偏质心位置的方法来提供再入配平迎角和实现飞行轨迹机动控制所需的配平升阻比,因此准确预测配平迎角随再入高度变化对控制系统以及返回舱落点精度至关重要[3-8, 10-16]。

|
图 1 飞船返回舱再入跨流域高超声速绕流过程示意图 Figure 1 Sketch on hypersonic flows of reentry spacecraft covering various flow regimes |
正是由于航天器以极高超声速再入跨流域高稀薄过渡到连续流区复杂多尺度真实气体非平衡流动特点,使用空气动力学研究赖以依靠的三种手段:理论计算、风洞实验与飞行试验气动辨识,对飞船返回舱跨流域稀薄气动特性模拟揭示,特别是中间过渡流区高空配平迎角与实际飞行遥测结果差异较大。工程上通过控制系统余量设计来解决上述问题,再入返回使用姿控发动机进行轨控保守设计,造成RCS系统燃料消耗与防热结构质量大大增加,有效载荷受到限制。深空探测返回器与飞船返回舱有相似的大钝头体外形(如我国月地高速再入返回器),以近第二宇宙速度、半弹道跳跃式再入大气层[6, 12-13, 19-21],涉及稀薄、过渡、连续等多个流态,经历化学平衡、热化学电离辐射非平衡等跨尺度多物理场复杂流动状态。文献[6, 13, 19-20]综述了国内外载人登月舱的研究发展概况,对我国发展载人登月舱涉及的关键技术进行了分析。文献[12, 21]对载人登月返回的再入方式选择和再入弹道设计进行讨论,认为必须考虑升阻比等问题。文献[3-4, 7-8]分析了返回舱再入稀薄流域的配平特性和主要影响因素。文献[22-23]采用完全气体模型对几类再入返回器的气动特性进行了对比分析,需要进一步开展真实气体非平衡效应对超高速再入返回舱跨流域气动特性的影响研究。文献[15, 24-25]采用三维可压缩层流N-S方程的化学非平衡流动计算方法,分析比较了再入返回舱(器)在完全气体模型和化学非平衡/辐射加热气体模型下的流动特征与气动特性,显示出利用当前空气动力学模拟手段对返回舱(器)以第一、二宇宙速度再入极高超声速气动热环境准确预测还存在较大困难。
返回舱(器)以高超声速再入大气层时,气流被前体强扰动产生严重压缩激波,波后温度可能达10 000 K以上,飞行器周围形成高焓层,并伴随复杂的热化学非平衡过程。黏性激波层、非平衡态、化学反应及其对流动的影响等都是再入过程跨流域空气动力学必须深入研究和妥善解决的关键基础问题,急待发展相关基础理论、计算与实验模拟方法。为此,国家重点基础研究发展计划(973计划)项目“航天飞行器跨流域空气动力学与飞行控制关键基础问题研究(2014CB744100)”顶层设计制定了核心前沿基础研究方向一“返回舱跨流域非平衡气动力热绕流与姿态配平模拟”[26-27],确立了项目核心一子课题群围绕我国回收类航天器如飞船返回舱、月地高速再入返回器再入地球大气层过程,建立气动力、气动热、弹道计算分析方法与新的手段途径,致力返回舱(器)再入跨流域非平衡气动力/热绕流与姿态配平模拟,研究揭示返回舱再入跨流域真实气体非平衡绕流现象规律。
项目执行五年来,结合工程需求开展前沿基础研究与围绕核心方向子课题群集约式研究实施、深化发展。针对项目核心任务研究方向一,回收类航天器(返回舱)再入大气层跨流域飞行过程,在初步建立返回舱(器)再入跨流域气动力/热绕流模拟新的研究方法、手段途径基础上,搭建了求解Boltzmann模型方程气体动理论统一算法(GKUA)[28-32]、DSMC[21, 33-34]、N-S/DSMC[35-36]、滑移N-S解算器[37]、低密度风洞实验测试[38]等多种空气动力学模拟手段相互验证结合,返回舱再入从外层空间自由分子流到近地面连续流跨流域空气动力学一体化模拟平台框架,已初步研制形成以弹道计算为主线,耦合气动特性计算模块与动态演示,结合数据库技术与软件工程,研制返回舱再入跨流域气动模拟软件系统。本文拟在介绍考虑平动、转动、振动能激发热力学非平衡效应的Boltzmann型速度分布函数方程可计算建模气体动理论统一算法取得重要进展基础上,分析验证GKUA与DSMC、连续/近连续流区(滑移)N-S解算器、N-S/DSMC耦合算法、低密度风洞实验模拟手段途径的正确性,并简略介绍由此研发的返回舱(器)再入跨流域气动力/热绕流模拟系统特点与工程适应性。
1 Boltzmann方程可计算建模气体动理论统一算法 1.1 方法介绍将宏观流体力学与微观分子动力学连接起来的介观Boltzmann速度分布函数方程[39-40],如式(1),通过描述气体流动过程分子速度分布函数基于位置空间、速度空间任一时刻由非平衡态向平衡态的演化,将各个流域不同尺度间分子输运现象统一起来。
| $ \frac{{\partial f}}{{\partial t}} + \mathit{\boldsymbol{V}} \cdot \frac{{\partial f}}{{\partial \mathit{\boldsymbol{r}}}} = \iiint {\left( {f'{{f'}_1} - f{f_1}} \right){V_r}b{\text{d}}b{\text{d}}\varepsilon {\text{d}}{\mathit{\boldsymbol{V}}_1}} $ | (1) |
如果得到分子速度分布函数,气体动力学中感兴趣的各种宏观物理量就可以通过对分布函数乘以分子速度某种形式的函数再对整个速度空间积分而确定。然而,求解该速度分布函数方程最大的困难在于其碰撞项高度非线性、高维积分微分属性,属于复杂多尺度刚性问题,精确求解描述各流域气体流动特征的Boltzmann方程未成现实。随着流体力学发展,国际上已有众多学者基于质量、动量、能量守恒定律,由数学上较简单的统计碰撞模型代替Boltzmann方程碰撞项,提出许多表征原始Boltzmann方程碰撞松弛和统计物理特性的气体动理学理论(气体分子运动论)模型方程[41-44],特别是基于Boltzmann-BGK模型方程逐步发展起来的格子Boltzmann方法[45-46]、离散速度有限差分求解[47-50]、BGK型有限体积系列格式如GKS、UGKS、DUGKS[51-57]、线化Boltzmann方程[58-59]、矩分析法[60-63]等气体动理学理论研究途径。为了探索跨流域气体流动问题一体化模拟方法,过去近二十年来,我们从分析气体分子速度分布函数与宏观流动量依赖关系出发,使用气体分子碰撞松弛参数和当地平衡态分布函数,对Boltzmann方程碰撞积分可计算建模,先后建立起模拟各流域一维、二维、三维绕流问题气体动理论(气体运动论)统一算法(GKUA)[64-69]与复杂飞行器高超声速气动力/热问题高性能并行计算应用研究[28-32, 68-70]。下面拟在此高效并行平台基础上,进一步介绍含内能激发热力学非平衡效应Boltzmann模型方程统一算法与再入各流域绕流问题研究进展。
针对航天飞行器再入各流域多尺度绕流过程存在严重的间断粒子稀薄非平衡效应,为了表征气体黏性输运与热传导属性,这里基于气体动理论Shakhov模型[43],也可基于不同的气体动理学理论模型如Holway的椭球统计模型[30, 42]或双原子气体Rykov模型[28-29, 44]等,用以Maxwellian分布函数fM作为权函数的Hermite多项式的三阶渐近展开而得到气体分子当地平衡态分布函数fN。另一方面,为了反映跨流域气体分子相互作用、稀薄程度、分子模型与内部能量变化关系,分析推导联系于气体温度、密度、不同流区流态控制参数、分子黏性碰撞截面与扩散碰撞截面及分子相互作用规则幂指数的气体分子碰撞松弛参数ν统一模型。由此,确立可描述各流域全局马赫数复杂流动输运现象统一的Boltzmann模型速度分布函数方程(比原始Boltzmann方程要简单得多),其无量纲形式为:
| $ \frac{{\partial f}}{{\partial t}} + \mathit{\boldsymbol{V}} \cdot \frac{{\partial f}}{{\partial \mathit{\boldsymbol{r}}}} = \nu \left( {{f^N} - f} \right) $ | (2) |
| $ {f^N} = {f_M} \cdot \left[ {1 + \left( {1 - \mathit{Pr}} \right)\mathit{\boldsymbol{c}} \cdot \mathit{\boldsymbol{q}}\left( {2{c^2}/T - 5} \right)/\left( {5PT/2} \right)} \right] $ | (3) |
| $ {f_M} = n/{\left( {\pi T} \right)^{3/2}}\exp \left( { - {c^2}/T} \right) $ | (4) |
| $ \nu = \frac{{2\alpha \left( {5 - 2\omega } \right)\left( {7 - 2\omega } \right)}}{{5\left( {\alpha + 1} \right)\left( {\alpha + 2} \right)\sqrt \pi }} \cdot \frac{1}{{K{n_\infty }}} \cdot n{T^{\left( {1 - \chi } \right)}} $ |
| $ K{n_\infty } = {\lambda _\infty }/L $ | (5) |
这里,Pr是Prandtl数, Pr=μCp/K,Cp是定压比热比,μ是描述气体分子输运能力的黏性系数,K是热传导系数;n为数密度,P、T分别为压力、温度,q为热流矢量,c为气体分子热运动速度,且c=|c|。λ∞是来流气体分子平均自由程,Kn∞为基于特征长度L的来流当地Knudsen(克努森)数,是表征飞行器再入各流域流动状态控制参数;ω、α是联系于气体分子变径硬球(VHS)与变径软球(VSS)模型指数[71];χ是相关于气体分子相互作用规则常数:χ=(ζ+3)/[2(ζ-1)],ζ是联系于分子间作用力大小F与分子间距离r的负幂律指数:F=1/rζ。
方程式(2)通过描述气体流动过程中分子速度分布函数f对位置空间、速度空间和时间的变化率关系,从分子运动论一级给出气体的统计描述[39-40],通过ν和fN将不同流域流态控制参数、宏观流动物理量、气体黏性输运特性、热力学效应及气体分子相互作用规则与分子模型用统一表达式联系起来。气体动力学中感兴趣的各种宏观流动量,如气体密度、流动速度、温度、压力、应力张量、热流矢量等,均可通过速度分布函数f乘以分子速度某种形式的函数对速度空间积分的办法得到。
| $ n\left( {\mathit{\boldsymbol{r}},t} \right) = \int {f{\rm{d}}\mathit{\boldsymbol{V}}} $ | (6) |
| $ n{U_i}\left( {\mathit{\boldsymbol{r}},t} \right) = \int {{V_i}f{\rm{d}}\mathit{\boldsymbol{V}}} $ | (7) |
| $ \frac{3}{2}nT\left( {\mathit{\boldsymbol{r}},t} \right) = \int {{c^2}f{\rm{d}}\mathit{\boldsymbol{V}}} $ | (8) |
| $ {\tau _{ij}}\left( {\mathit{\boldsymbol{r}},t} \right) = 2\int {{c_i}{c_j}f{\rm{d}}\mathit{\boldsymbol{V}}} $ | (9) |
| $ {q_i}\left( {\mathit{\boldsymbol{r}},t} \right) = \int {{c^2}{c_i}f{\rm{d}}\mathit{\boldsymbol{V}}} $ | (10) |
气体分子速度分布函数实质上是一种遵从气体运动论概率统计规律的几率密度分布函数,分布函数对速度分量Vx、Vy、Vz的函数依赖关系属于指数型[73],通过发展和应用气体动理论离散速度坐标法(DVOM)[30, 48, 65, 68, 74],研制适于跨流域高超声速绕流问题模拟的离散速度坐标点自适应优化选取技术和基于离散速度分布函数适应大规模并行分布式求和的宏观流动量与物面气动力/热动态确定离散速度数值积分方法。可将单一的速度分布函数方程式(2)化为在各个离散速度坐标点处基于时间、位置空间具有非线性源项的双曲型守恒方程组,在计算位置空间(ξ, η, ζ)其守恒形式为:
| $ \frac{{\partial U}}{{\partial t}} + \frac{{\partial F}}{{\partial \xi }} + \frac{{\partial G}}{{\partial \eta }} + \frac{{\partial H}}{{\partial \zeta }} = S $ | (11) |
这里,U=Jfσ, δ, θ,F=UU,G=VU,H=WU,S=Jν(fσ, δ, θN-fσ, δ, θ)。Vxσ、Vyδ、Vzθ分别是离散速度坐标点σ、δ、θ处的气体分子速度分量。其中,U=Vxσξx+Vyδξy+Vzθξz;V=Vxσηx+Vyδηy+Vzθηz;W=Vxσζx+Vyδζy+Vzθζz;J=∂(x, y, z)/∂(ξ, η, ζ)。
根据气体分子碰撞松驰与对流运动的非定常特点,将算子分裂有限差分方法拓展应用于基于时间、位置空间与速度空间离散Boltzmann模型方程(11)数值求解,构造直接捕捉分子速度分布函数演化更新的气体动理论耦合迭代数值格式:
| $ {U^{n + 1}} = {L_S}\left( {\frac{{\Delta t}}{2}} \right){L_\zeta }\left( {\frac{{\Delta t}}{2}} \right){L_\eta }\left( {\frac{{\Delta t}}{2}} \right){L_\xi }\left( {\Delta t} \right){L_\eta }\left( {\frac{{\Delta t}}{2}} \right){L_\zeta }\left( {\frac{{\Delta t}}{2}} \right){L_S}\left( {\frac{{\Delta t}}{2}} \right){U^n} $ | (12) |
其中,LS、Lξ、Lη、Lζ分别代表式(13)~式(16)差分算子:
| $ {U^*} = {L_s}\left( {\Delta t} \right){U^n} = {U^n} + \left( {1 - \frac{\nu }{2}\Delta t} \right)\Delta t \cdot {S^n} $ | (13) |
| $ {U^{**}} = {L_\zeta }\left( {\Delta t} \right){U^*} = \left[ {1 - \bar W\Delta t{\delta _\zeta } + \frac{{{{\bar W}^2}\Delta {t^2}}}{2}{\delta _{{\zeta ^2}}}} \right]{U^*} $ | (14) |
| $ {U^{***}} = {L_\eta }\left( {\Delta t} \right){U^{**}} = \left[ {1 - \bar V\Delta t{\delta _\eta } + \frac{{{{\bar V}^2}\Delta {t^2}}}{2}{\delta _{{\eta ^2}}}} \right]{U^{**}} $ | (15) |
| $ {U^{n + 1}} = {L_\xi }\left( {\Delta t} \right){U^{***}} = \left[ {1 - \bar U\Delta t{\delta _\xi } + \frac{{{{\bar U}^2}\Delta {t^2}}}{2}{\delta _{{\xi ^2}}}} \right]{U^{***}} $ | (16) |
这里,计算网格步长只需由物理空间所要求计算精度决定,因所有宏观流动量通过离散速度分布函数积分求和动态确定,使得物理空间网格划分极为粗糙[28-32, 64-69],也能得到稳定收敛解的算法优势;计算时间步长Δt由所使用格式的差分稳定条件确定:
| $ \Delta {t_S} = \frac{{CFL}}{{\max \left( {\frac{\nu }{2},\frac{{\left| {\bar U} \right|}}{{\Delta \xi }},\frac{{\left| {\bar V} \right|}}{{\Delta \eta }},\frac{{\left| {\bar W} \right|}}{{\Delta \zeta }}} \right)}} $ | (17) |
其中,CFL为时间步长调节系数,取CFL=0.99。
一旦各个离散速度坐标点处气体分子速度分布函数被数值求解,任一时刻物理空间各点的宏观流动量如气体密度、流动速度、温度、应力张量和热流矢量等,需通过文献[65, 68, 74-76]发展的相应离散速度数值积分方法而被演化更新。由于一般大尺度高超声速飞行器外形复杂,各部位几何尺度差异很大,往返大气层跨流域高超声速飞行,会经过稀薄过渡流区和近连续滑移流区,并会在飞行器不同绕流区域因分子碰撞频率巨大差别而出现连续流、过渡流或高稀薄流共存的混合流动现象,导致物面边界条件的表述方式对气动力/热特性影响较大。基于Boltzmann模型方程的气体动理论统一算法(GKUA)需要求解的是物理空间与速度空间各个离散网格点处的气体分子速度分布函数,于是各类边界条件与物面气动热力学特性数学模型建立与计算实现[65, 68, 74-76, 78],始终通过求解气体分子速度分布函数演化更新来进行。任何固体壁面边界均具有对气体分子的不可浸透性,在任一计算时刻物面附近的分子要么撞击物面,要么未撞击物面,而所有撞击物面的分子均会反射回气体中,只是气体与壁面相互作用与固体表面层的状态有密切关系,壁面的温度、粗糙度及清洁度等直接影响气体分子与固体壁的相互作用。为了确定气体分子与固体表面相互作用数学模型,便于数值处理,这里假定撞击物面的气体分子紧接着以完全调节于壁面温度和速度的Maxwellian平衡态速度分布散射[64-69]。为此,物面边界网格在t时刻的速度分布函数可计算模型为:
若c·n≥0,则表示气体分子撞击物面并发生了反射,经物面反射的气体分子速度分布函数的数值离散形式为:
| $ \begin{array}{l} f_{\sigma ,\delta ,\theta }^w = \frac{{{n_w}}}{{{{\left( {\pi {T_w}} \right)}^{3/2}}}} \cdot \\ \exp \left[ { - \frac{{{{\left( {{V_{x\sigma }} - {U_w}} \right)}^2} + {{\left( {{V_{y\delta }} - {V_w}} \right)}^2} + {{\left( {{V_{z\theta }} - {W_w}} \right)}^2}}}{{{T_w}}}} \right] \end{array} $ | (18) |
其中,(Uw, Vw, Ww)为物面速度,一般为0。
气体分子从物面散射的数密度nw先前是未知的,将随着入射分子的速度分布及固体壁面情况而变化。本文利用物面上的质量平衡条件[65-68, 74],即在壁面处应用垂直于物面的零质量流量条件决定
| $ {n_w} = - 2{\left( {\frac{\pi }{{{T_w}}}} \right)^{1/2}}\iiint_{{C_n} < 0} {C_n^ - \cdot {f{\text{d}}}{V_x}{\text{d}}{V_y}{\text{d}}{V_z}} $ | (19) |
其中,Cn-=(Cn-|Cn|)/2,n为垂直于物面的单位外法向方向矢量。
若c·n<0,则表示气体分子未撞击物面,此时气体分子速度分布函数由流场内邻近边界的几排网格单边二阶差分实时计算确定[64-69, 74]。
由此可见,统一算法设计的壁面边界条件计算模型,避免了针对纯粹微观粒子进行随机统计模拟的DSMC方法产生统计涨落与对低Knudsen数近连续滑移过渡流难以模拟计算的问题,也避开了基于N-S方程等宏观流体力学解算器纯粹使用宏观流动量进行边界表述而不同位置的稀薄效应强弱不同、难于用固定关系式数值实现的不足。
虽然适于航天再入绕流问题Boltzmann模型方程统一算法计算空间,是由离散速度空间和位置空间组成的六维空间,并考虑内部能级分布,形成多相空间,需要大量计算机内存,使用文献[30, 77-78]发展的离散速度空间区域分解并行计算技术,结合MPI+Open MP多级并行[79],可获得求解Boltzmann模型方程高性能可扩展大规模并行算法。根据气体动理论数值格式(12)式与基于离散速度空间分布函数宏观流动取矩离散求和,对任一时刻物理空间各点的宏观流动量进行动态确定与实时演化更新,可获得位置空间各网格点处的气动力/热绕流特性。
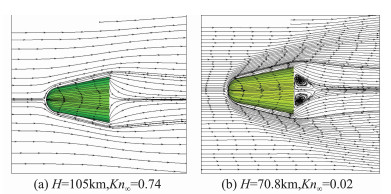
1.2 算法验证为了考验求解Boltzmann模型方程统一算法对可回收类航天器再入高稀薄流到近连续流区高超声速流动模拟能力,使用来自文献[80]相同条件下可重复使用卫星体飞行器(底部半径R=503.5 mm,飞行器总长L=1410 mm,锥身段半锥角θ=11.4°),选取飞行器底部半径为特征尺度。拟定Ma∞=5两种绕流状态H=70.8 km、Kn∞=0.002、Re∞=4074.37与H=105 km、Kn∞=0.74、Re∞=10.19,在位置空间网格51×25×31和速度空间网格60×40×40设置下,使用具有160MB/CPU的512CPU并行计算。图 2、图 3分别绘出上述两种绕流流场轴对称面内马赫数等值线与绕流场、物面流线结构,由图看出,随着飞行器飞行高度从H=105 km再入到H=70.8 km,气体绕流由强烈的稀薄效应逐渐过渡到近连续流区脱体激波、膨胀波系,飞行器绕流场受扰动区域由全场过渡到绕卫星体周围较小区域;对H=105 km、Kn∞=0.74高稀薄流,飞行器绕流并不存在激波等强间断现象与背风旋涡回流结构,而在飞行器周围形成厚厚的强扰动区域,气流附着物面流动;而对H=70.8 km、Kn∞=0.002近连续滑移流,飞行器绕流物体前面产生明晰清脆的脱体激波,罩在飞行器前面,包括驻点域、附着激波及飞行器底部出现真空区、尾涡流场结构和飞行器后部流场再压缩尾迹流动现象均能很好地捕捉;截然不同的两种流态反映了稀薄气体绕流场完全不同于近连续流区绕流面貌。

|
图 2 卫星体再入不同高度(Ma∞=5)绕流场马赫数等值线 Figure 2 Mach number contours over a sphere-cone shaped satellite spacecraft at Ma∞=5 |
|
图 3 卫星体不同高度绕流(Ma∞=5)场与物面流线结构 Figure 3 Streamlines patterns over a sphere-cone shaped satellite spacecraft at Ma∞=5 |
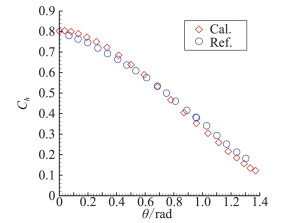
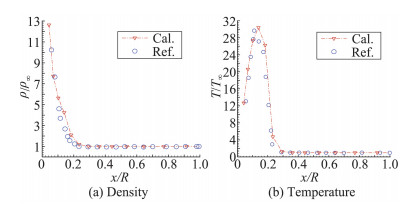
图 4绘出统一算法计算该飞行器绕流(H=105 km、Ma∞=5、Tw/T∞=1)物面热流分布与DSMC模拟值[80]定量化比较,可看出GKUA得到的结果从球头前驻点沿物面向后不同物面角热流计算值均与DSMC结果吻合较好,两种结果偏差范围0.27%~8.56%,且GKUA得到的迎风物面热流分布的非线性效应更明显。图 5绘出GKUA计算Ma∞=10上述卫星体飞行器(H=75.9 km、Kn∞=0.004、Re∞=4074.5、Tw/T∞=1.64)绕流驻点线密度、温度分布与典型文献[80]结果定量化比较,可看出GKUA计算值(带符号∇点划线表示)与文献结果(符号“○”表示)变化规律吻合很好,两种结果计算偏差0.39%~3.26%。图中显示出由于设置Tw/T∞=1.64冷壁面,在飞行器前面一定区域会出现流动高温区,整体上看GKUA对驻点线流动参数计算分辨率优于DSMC模拟值。
|
图 4 卫星体再入流(H=105 km, Kn∞=0.74, Ma∞=5)迎风物面热流分布GKUA与DSMC计算比较 Figure 4 Comparison of heat flux distribution along windward surface around SARA satellite at H=105 km, Kn∞=0.74, Ma∞=5 |
|
图 5 卫星体再入绕流(H=75.9 km, Ma∞=10, Tw/T∞=1.64)驻点线密度、温度分布GKUA与参考文献[80]结果比较 Figure 5 Comparison of stagnation line distribution around SARA satellite shape at H=75.9 km, Ma∞=10, Tw/T∞=1.64 |
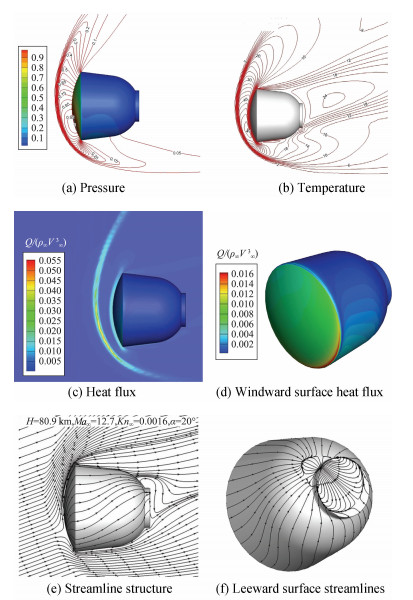
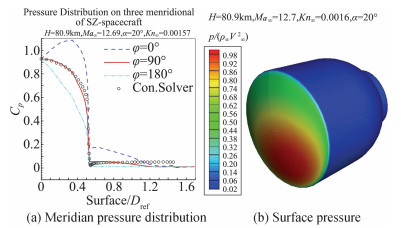
为了将求解Boltzmann模型方程统一算法应用于飞船返回舱再入近连续过渡流区绕流问题模拟,拟定H=80.9 km, Ma∞=12.7, Kn∞=0.0016, Re∞=12 175.4, Pr=0.72, α=20°绕流状态,网格布局为位置空间流向×法向×周向45×16×25和速度空间130×125×100,使用具有75.12MB/CPU分布内存的4096CPU并行计算。图 6绘出H=80.9 km, Ma∞=12.7, Kn∞=0.0016绕流流场压力、温度、热流、流线及迎风区物面热流与背风区极限流线分布。对此高超声速近连续过渡流区绕流,离返回舱驻点前端一定距离出现较清晰的脱体激波,显示出较明显的近连续流动特征。因壁温设置Tw/T0=0.5435与Tw/T∞=18.0529,从图 6(b)看出在脱体激波与驻点前端出现高温区。远前方气流跨越脱体激波改变流动方向,绕流物面,在返回舱肩部,以超声速膨胀往后流去,在返回舱尾部出现流动真空区。从图 6(c)看出在脱体激波与前驻点物面附近温度剧烈变化区域出现高热流区,而在其他部位热流影响很小。这也说明返回舱再入近连续过渡流区,因出现脱体激波,而将热流汇聚在脱体激波与驻点区物面,为此,防热设计需要考虑前体防热结构。从图 6(e, f)看出对此80.9 km高度,因空气较强的稀薄效应,回流区旋涡尚在发展中,该高超声速绕流状态Kn∞=0.0016、Ma∞=12.7、Re∞=12 175.4,因受到较强的稀薄效应影响,气流自前驻点绕流物面基本上附着物面流动,仅在后驻点背风真空区存在一定程度的回流扰动,对背风区的流动参数分布有较强的影响。为进一步分析GKUA对返回舱物面压力分布计算的正确性,图 7(a)绘出该返回舱绕流不同子午面φ=0°、90°、180°壁面压力分布,其中线段表示GKUA并行计算结果,符号“○”为N-S方程解算器计算得到子午面φ=90°的壁面压力分布,可看出两种方法得到的结果在迎风区吻合较好,跨过肩部进入背风区由于出现真空区严重稀薄效应,N-S解几乎为常数,而GKUA结果逐渐减小到返回舱后端面压力最小,两种方法在迎风区计算结果的吻合相容、背风区不一致源于在背风低压真空区出现逆压梯度、较强稀薄效应继续用连续流体力学N-S方程计算模型是产生差别的主要原因。相较N-S方程解算器,GKUA直接捕捉流场物面任意网格里的速度分布函数演化更新,所有宏观流动量均通过式(6)~式(10)的数值积分离散求和,实时表征更为客观真实,也由于在六维空间计算求解,需要大量计算内存,这是该方法的局限性,如这里使用的位置空间网格数较少。对照图 7(b)与图 6(d)分别绘出的迎风区物面压力与热流分布云图,表明对此大钝头返回舱绕流迎风物面力热分布,压力最大值发生在驻点、热流最大值集中在曲率最大的肩部,这与已开展的风洞试验与飞行测试结果相吻合一致。
|
图 6 返回舱再入H=80.9 km, Ma∞=12.7, Kn∞=0.0016, α=20°绕流场压力、温度、热流与流线结构 Figure 6 Flow field and surface streamline structures around reentry spacecraft Kn∞=0.0016, Ma∞=12.7, H=80.9 km |
|
图 7 返回舱再入H=80.9 km, Ma∞=12.7, Kn∞=0.0016, α=20°绕流物面压力分布 Figure 7 Surface pressure distribution in different meridian planes of φ=0°, 90°, 180° past reentry spacecraft (H=80.9 km) |
返回舱再入跨流域极高速、高温绕流流场中,气体分子的微观自由度(平动、转动、振动和电子态)因受到一定程度的激励,会出现能量彼此传递,使分子和原子间发生化学和电离反应。气体的宏观运动和状态变化同相应的微观物理化学过程相互影响呈现复杂的流动非平衡效应。根据表征分子微观自由度之间能量传递或组元之间进行化学反应的特征弛豫时间与流动特征时间大小尺度的不同,可将非平衡流动分为平动和转动非平衡流、振动和化学非平衡流以及电离辐射非平衡流。如果特征流动时间极小或流场的物理量变化梯度极大,平动与转动非平衡效应表现为与分子性质相关联的气体介质特性,如比热、黏性系数、热导率等不再保持常数,气体运动的基本方程就与通常气体动力学连续性质量、动量、能量方程及状态关系不同,出现黏性、热传导和扩散的非平衡变化,这是一种最基本而接近高超声速再入多尺度非平衡流动现实环境。为此,如何构造描述热力学非平衡效应的Boltzmann模型方程及数值求解途径,是气体动理学理论可计算建模在极高超声速再入空气动力学研究焦点。为了将上述求解Boltzmann模型方程统一算法推广应用于近地空间飞行环境跨流域非平衡绕流问题研究,作为这方面研究探索的第一步,我们基于对转动自由度松弛变化[81]、气体分子运动论Rykov模型[44, 82]研究,在气体分子速度分布函数演化更新求解中考虑转动自由度影响,把气体分子转动能作为分布函数的自变量,提出考虑转动非平衡效应Boltzmann模型方程数值算法[28-29, 31]。
基于转动松弛特性Rykov模型[44.82],采用转动惯量描述气体分子自旋运动,利用分子总角动量守恒作为一个新的碰撞不变量。将分子内部能量作为气体分子速度分布函数自变量,引入能量模式配分函数将能量在各自由度平均分布。基于气体分子速度分布函数f=f(r, V, t, e),这里r、V分别是位置空间和速度空间坐标、e为内能,在求解Boltzmann模型方程统一算法框架[28-32, 64-79]下,使用权因子1和e对速度分布函数依赖的速度空间无穷积分,引入能级约化速度分布函数f0与f1,去掉方程对内部能量连续依赖关系,可确立含转动非平衡效应各流域统一Boltzmann模型方程,其无量纲形式为:
| $ \left\{ \begin{array}{l} \frac{{\partial {f_0}}}{{\partial t}} + {V_i} \cdot \frac{{\partial {f_0}}}{{\partial {x_i}}} = {v_r}\left( {f_0^r - {f_0}} \right) + {v_t}\left( {f_0^t - {f_0}} \right)\\ \frac{{\partial {f_1}}}{{\partial t}} + {V_i} \cdot \frac{{\partial {f_1}}}{{\partial {x_i}}} = {v_r}\left( {f_1^r - {f_1}} \right) + {v_t}\left( {f_1^t - {f_1}} \right) \end{array} \right. $ | (20) |
| $ f_0^r = {f_M}\left( T \right)\left[ {1 + \frac{8}{{15}}{\omega _0} \cdot \frac{{q_i^t}}{P} \cdot \frac{{{c_i}}}{T}\left( {\frac{{{c^2}}}{T} - \frac{5}{2}} \right)} \right] $ |
| $ f_0^t = {f_M}\left( {{T_t}} \right)\left[ {1 + \frac{8}{{15}} \cdot \frac{{q_i^t}}{{{P_t}}} \cdot \frac{{{c_i}}}{{{T_t}}}\left( {\frac{{{c^2}}}{{{T_t}}} - \frac{5}{2}} \right)} \right] $ |
| $ \begin{array}{l} f_1^r = T \cdot {f_M}\left( T \right)\left[ {1 + \frac{8}{{15}}{\omega _0} \cdot \frac{{q_i^t}}{P} \cdot \frac{{{c_i}}}{T}\left( {\frac{{{c^2}}}{T} - \frac{5}{2}} \right) + } \right.\\ \;\;\;\;\;\;\;\;\left. {4{\omega _1}\left( {1 - \delta } \right)\frac{{q_i^r{c_i}}}{{PT}}} \right] \end{array} $ |
| $ \begin{array}{l} f_1^t = {T_r} \cdot {f_M}\left( {{T_t}} \right)\left[ {1 + \frac{8}{{15}} \cdot \frac{{q_i^t}}{{{P_t}}} \cdot \frac{{{c_i}}}{{{T_t}}}\left( {\frac{{{c^2}}}{{{T_t}}} - \frac{5}{2}} \right) + } \right.\\ \;\;\;\;\;\;\;\;\left. {4\left( {1 - \delta } \right)\frac{{q_i^r{c_i}}}{{{P_t}{T_t}}}} \right] \end{array} $ |
| $ {f_M}\left( T \right) = \frac{n}{{{{\left( {\pi T} \right)}^{3/2}}}}\exp \left( { - \frac{{{c^2}}}{T}} \right),{c_i} = {V_i} - {U_i} $ |
分析推导反映黏性与热传导属性的扩散时间与气体分子平均碰撞时间,描述含内能激发的多原子分子弹性与非弹性碰撞松弛变化统一表达式,以此表征气体分子速度分布函数趋于当地平衡态分布的碰撞松弛速率。
| $ {\nu _r} = \frac{{2\alpha \left( {5 - 2\omega } \right)\left( {7 - 2\omega } \right)}}{{5\left( {\alpha + 1} \right)\left( {\alpha + 2} \right)\sqrt \pi }} \cdot \frac{{nT_t^{1 - \chi }}}{{K{n_\infty }}} \cdot \frac{1}{Z} $ |
| $ {\nu _t} = \frac{{2\alpha \left( {5 - 2\omega } \right)\left( {7 - 2\omega } \right)}}{{5\left( {\alpha + 1} \right)\left( {\alpha + 2} \right)\sqrt \pi }} \cdot \frac{{nT_t^{1 - \chi }}}{{K{n_\infty }}} \cdot \left( {1 - \frac{1}{Z}} \right) $ | (21) |
| $ Z\left( {{T_t},{T_r}} \right) = \frac{3}{4}\pi \frac{{\varphi \left( {B{T_t}} \right)}}{{{{\left( {B{T_t}} \right)}^{1/6}}}}\frac{{9B{T_t}}}{{B{T_t} + 8}}\left( {\frac{{{T_r}}}{{{T_t}}}} \right) \cdot $ |
| $ {\left[ {0.461 + 0.5581\left( {\frac{{{T_r}}}{{{T_t}}}} \right) + 0.0358\left( {\frac{{{T_r}}}{{{T_t}}}} \right)^2} \right]}, $ |
| $ \varphi \left( t \right) = 0.767 + 0.233{t^{ - 1/6}}\exp \left[ { - 1.17\left( {t - 1} \right)} \right], $ |
| $ {\mu _t} = {\left( {{T_t}} \right)^{2/3}}\varphi \left( B \right)/\varphi \left( {B{T_t}} \right),\;\;B = {T_\infty }/{T_*} 。$ |
这里,T*与T∞一样都是有量纲值。对于氮气而言,T*=91.5 K。
速度分布函数f0、f1同样是依赖于时间t、位置空间r和速度空间V的函数,使用上节介绍的气体动理论离散速度坐标法与位置空间数值求解格式,可得到求解式(20, 21)考虑转动非平衡效应Boltzmann模型方程统一算法。
由于空气中的N2和O2分子振动特征温度远高于室温,分别为3371 K和2256 K,通常情况下气体分子振动能模态不易激发,由此建立考虑转动非平衡效应的气体动理论统一算法可在增加一个考虑转动能级约化速度分布函数f1较完全气体多一倍计算量情况下实现任意双原子气体流动问题的模拟。为了考验该计算模型实现的正确性,拟定一类返回舱外形体再入不同流域高超声速绕流问题。图 8(a, b)分别绘出了飞行高度H=105 km、Kn∞=0.091 93与H=83 km、Kn∞=0.001 95,马赫数Ma∞=8,α=0°,γ=1.4,在流动介质氮气中返回舱外形体绕流流场马赫数等值线云图与流线分布计算结果。图中可见,对于数米量级大尺度真实飞行器,即使在H=105 km气体分子平均自由程高达λ∞=0.3365 m的高度,因Kn∞=0.091 93,飞行器绕流仍表现在前端出现厚的脱体激波强扰动,远前方来流跨越脱体激波层,流动改变方向,绕流物面由于稀薄效应很严重,气体绕流完全附着物面流动;相较之下,对于图 8(b)绘出H=83 km的绕流图谱,在此高度气体分子平均自由程降低为λ∞=0.0071 m很小,Kn∞=0.001 95表现为近连续流,气体绕流出现明显的脱体激波,远前方来流跨越清脆明晰的脱体激波强间断,流动改变方向向外流去,绕流物面,跨越最高点进入倒锥区,气流产生膨胀波系,并在物体后部出现流动分离、尾涡结构等近连续绕流面貌。该图直观再现了返回舱外形体再入飞行不同流域发生的绕流现象,揭示了飞行器绕流随着Kn∞数减小由稀薄流趋近连续流的变化过程。

|
图 8 再入不同高度H=105 km与H=83 km返回舱体绕流马赫数等值线云图与流线结构分布(Ma∞=8) Figure 8 Mach number contours and streamline distribution around reentry spacecraft with Ma∞=8 |
图 9(a、b)绘出返回舱H=105 km、Ma∞=8、Kn∞=0.091 93、α=0°、γ=1.4条件下绕流流场压力p/p∞等值线云图与远场到前端驻点线密度ρ/ρ∞分布,图 9(a)上半部分、图 9(b)实线“GKUA”为统一算法结果,而下半部分及符号则是“DSMC”模拟流场分布。可见两种方法计算结果从流场结构到压力等值线、远前方来流到前驻点线密度分布均吻合很好,证实统一算法与DSMC方法适应的再入高超声速稀薄流模拟在刻画Boltzmann方程描述的客观物理过程方面具有很好的收敛一致性[83]。
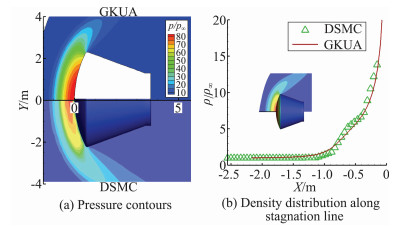
|
图 9 再入返回舱体绕流流场压力、驻点线密度分布GKUA与DSMC模拟验证(H=105 km, Ma∞=8) Figure 9 Validation of GKUA and DSMC on pressure and density distribution around reentry spacecraft with H=105 km and Ma∞=8 |
为了进一步验证统一算法用于计算返回舱再入高超声速绕流物面气动力/热特性的准确性,对H=105 km、α=0°返回舱体Ma∞=8绕流进行DSMC与GKUA结果比较分析,图 10绘出两种方法计算返回舱沿轴线方向的物面无量纲压力系数p/p∞和热流q分布对比情况,可看出,两种方法得到的表面压力和热流吻合较好,变化趋势也完全一致。分析表明,对此严重稀薄效应绕流,迎风区物面压力、热流值均远高于背风区,物面压力最大值出现在返回舱头部驻点位置;而热流最大值后移至返回舱肩部最高,过了拐点进入背风区,物面热流则迅速下降。对于物面压力分布,DSMC与GKUA结果几乎完全重合;对于物面热流分布,总体看出,GKUA在揭示具有巨大曲率过渡带的返回舱肩部最高拐点热流分布的分辨率明显优于DSMC结果,如GKUA肩部拐点热流390 W/m2,而DSMC结果低于此结果达13%,这是因为在此曲率很大的肩部拐点附近,绕流流场网格划分需要自适应加密,DSMC模拟特点决定较难像求解Boltzmann模型方程GKUA确定论数值算法易于实现,尤其在精细捕捉流动信息方面,GKUA基于物理空间与速度空间网格布局划分,直接对气体分子速度分布函数演化更新数值求解,更能刻画流动细致结构,同样在跨越肩部进入倒锥过渡背风区,GKUA仍然较DSMC有更强捕捉微弱流动传热模拟能力,显示出GKUA结果较DSMC更好地光滑过渡到背风热流极小区,且在整个倒锥、后柱段,GKUA结果均高于DSMC模拟值,通过将GKUA与经过实践广泛检验较为成熟的DSMC两种计算模型结果的比较验证,证实两种方法具有较强的工程实用互补性。通过对图 8~图 10初步分析,证实求解转动非平衡效应Boltzmann模型方程统一算法用于计算大型航天器气动力与气动热绕流问题具有较高可靠性与工程置信度,这为进一步发展复杂高超声速非平衡绕流问题统一算法解算器,开展返回舱往返大气层跨越飞行各流域绕流问题大规模并行计算,特别是近连续、过渡流区气动力/热与姿态配平绕流问题研究奠定了基础。
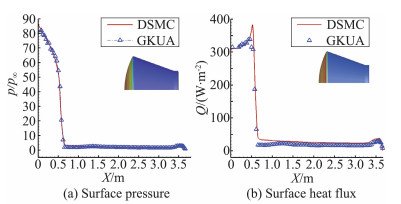
|
图 10 再入H=105 km返回舱体绕流Ma∞=8沿轴向不同位置物面无量纲压力、热流分布GKUA与DSMC模拟验证 Figure 10 Validation of GKUA and DSMC on surface pressure and heat flux distribution along with the X-axis around reentry spacecraft with H=105 km and Ma∞=8 |
返回舱再入高超声速绕流引起严重的气动加热高温非平衡效应,尤其是脱体激波与物面边界层内流动气体分子振动能将被激发,出现量子能级分布,在振动能量子效应不可忽略情况下,需要考虑如何基于描述各流域气体分子输运现象的Boltzmann方程出发,实施含平动-转动-振动能激发的热力学非平衡效应Boltzmann模型方程设计与气动力热影响问题模拟。早年王承书与Uhlenbeck提出了一种处理具有内能影响的多原子气体的半经典方法,即平动能根据自由度按经典方法处理,而内自由度按量子力学观点处理,由此得到了Boltzmann方程的推广形式—WCU方程[84-85],该方程在分子内能为非简并态时成立。Morse[86]在王承书与Uhlenbeck研究成果基础上,将弹性碰撞与非弹性碰撞解耦用于处理能量松弛过程,依此构造了一种类似BGK模型的考虑分子内能间断能级的模型方程。在这些研究中,内能作为单一模式处理,没有区分转动能和振动能。如果按量子力学观点处理分子能级跃迁,每个能级均为一个独立的分布函数,势必会加大数值处理的难度。
为此,我们在求解Boltzmann模型方程统一算法框架[64-69, 74-79]下,为了模拟高温高马赫数下多原子气体内能激发对跨流域非平衡流动的影响,将转动能、振动能分别作为气体分子速度分布函数中的自变量,把转动能和振动能处理为连续分布的能量模式,将Boltzmann方程碰撞项分解成弹性碰撞和非弹性碰撞,同时将非弹性碰撞按一定松弛速率分解为平动-转动能松弛和平动-转动-振动能松弛,构造了一类考虑振动能激发的Boltzmann模型方程,并证明其守恒性和H定理。在此基础[27-29, 31, 87]上,对分布函数基于内部能量变量无穷积分,引入三个约化速度分布函数,得到一组考虑振动能激发的约化速度分布函数控制方程组:
| $ \begin{array}{l} \;\;\;\frac{{\partial {f_i}}}{{\partial t}} + \mathit{\boldsymbol{V}} \cdot \frac{{\partial {f_i}}}{{\partial \mathit{\boldsymbol{r}}}} = \\ {\nu _{{\rm{tot}}}}\left[ \begin{array}{l} \left( {1 - \frac{1}{{{Z_{{\rm{rot}}}}}} - \frac{1}{{{Z_{{\rm{vib}}}}}}} \right)\left( {f_i^{\left( t \right)} - {f_i}} \right) + \\ \frac{1}{{{Z_{{\rm{rot}}}}}}\left( {f_i^{\left( {t,r} \right)} - {f_i}} \right) + \frac{1}{{{Z_{{\rm{vib}}}}}}\left( {f_i^{\left( {t,r,v} \right)} - {f_i}} \right) \end{array} \right] \end{array} $ | (22) |
其中,i= 1,2,3,且有
| $ f_1^{\left( t \right)} = \frac{n}{{{{\left( {\pi {T_{tr}}} \right)}^{3/2}}}}\exp \left( { - \frac{{{C^2}}}{{{T_{tr}}}}} \right),f_2^{\left( t \right)} = \frac{{{\delta _{{\rm{rot}}}}{T_{{\rm{rot}}}}}}{2}f_1^{\left( t \right)}, $ |
| $ f_3^{\left( t \right)} = \frac{{{\delta _v}\left( {{T_{{\rm{vib}}}}} \right){T_{{\rm{vib}}}}}}{2}f_1^{\left( t \right)}, $ |
| $ f_1^{\left( {t,r} \right)} = \frac{n}{{{{\left( {\pi {T^r}} \right)}^{3/2}}}}\exp \left( { - \frac{{{C^2}}}{{{T^r}}}} \right),f_2^{\left( {t,r} \right)} = \frac{{{\delta _{{\rm{rot}}}}{T^r}}}{2}f_1^{\left( {t,r} \right)}, $ |
| $ f_3^{\left( {t,r} \right)} = \frac{{{\delta _v}\left( {{T_{{\rm{vib}}}}} \right){T_{{\rm{vib}}}}}}{2}f_1^{\left( {t,r} \right)}, $ |
| $ f_1^{\left( {t,r,v} \right)} = \frac{n}{{{{\left( {\pi {T_{{\rm{rot}}}}} \right)}^{3/2}}}}\exp \left( { - \frac{{{C^2}}}{{{T_{{\rm{rot}}}}}}} \right), $ |
| $ f_2^{\left( {t,r,v} \right)} = \frac{{{\delta _{{\rm{rot}}}}{T_{{\rm{rot}}}}}}{2}f_1^{\left( {t,r,v} \right)}, $ |
| $ f_3^{\left( {t,r,v} \right)} = \frac{{{\delta _v}\left( {{T_{{\rm{rot}}}}} \right){T_{{\rm{rot}}}}}}{2}f_1^{\left( {t,r,v} \right)}, $ |
| $ {\nu _{{\rm{rot}}}} = \mathit{Pr} \cdot \frac{{2\alpha \left( {5 - 2\omega } \right)\left( {7 - 2\omega } \right)}}{{5\left( {\alpha + 1} \right)\left( {\alpha + 2} \right)}} \cdot nT_{tr}^{\left( {1 - \chi } \right)} 。$ |
在确定含振动能激发的气体动理学模型方程及离散速度坐标法可计算模型后,将其加入到气体动理论统一算法求解体系,可建立同时考虑平动、转动、振动能激发的热力学非平衡Boltzmann模型方程统一算法。相较仅考虑转动非平衡效应Boltzmann模型方程的气体动理论数值算法,通过分别相应于平动、转动、振动能松弛变化的三个约化速度分布函数f1、f2、f3的可计算表征实现,使得计算量较完全气体Boltzmann模型方程的统一算法增加了三倍,依靠所发展的Boltzmann模型方程统一算法离散速度空间区域分解多级并行MPI+OpenACC程序架构体系,可获得模拟跨流域高超声速气动力/热绕流问题的气体动理论统一算法大规模并行计算应用研究平台。
为了考察含振动能激发Boltzmann模型方程及算法实现的正确可靠性,拟定非平衡效应严重的稀薄过渡流区圆柱绕流问题进行统一算法计算检验,设置来流气体N2,Ma∞=5,T∞=Tw=500 K,n∞=1.496 6×1020/m3,Kn∞=0.01。图 11绘出含振动能激发Boltzmann模型方程统一算法计算结果(“GKUA_vibration”表示)与DSMC结果(“DSMC”表示)对比情况。两种方法得到的结果整体上符合较好,压力和等效温度分布几乎完全一致,表明含振动能激发Boltzmann模型方程及算法实现合理可行。从平动、转动、振动温度分布来看,波后驻点区域,平动温度最高,转动温度次之,振动温度最低,细致比较可看出GKUA计算的振动温度略高于DSMC结果,由此反映出DSMC方法使用常数ZrotDSMC=5、ZvibDSMC=50作为转动、振动松弛碰撞数,而本文提出根据(22)式控制转动、振动能激发的碰撞松弛数随气体分子碰撞频率、热力学输运效应实时计算确定可能更为客观真实,有待进一步研究检验,由此计算模型的不同也导致圆柱背风区低压低温区,DSMC方法使用固定碰撞松弛数计算得到较GKUA更低一些的振动温度,如图 11(f)所示。
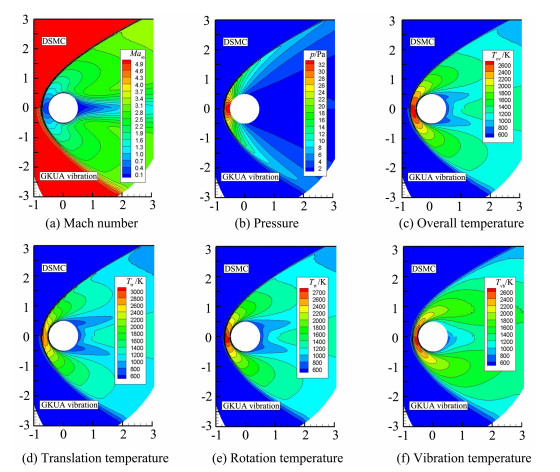
|
图 11 含振动能激发的Boltzmann模型方程GKUA计算圆柱绕流宏观流动量与DSMC方法结果对比 Figure 11 Macroscopic flow variables circular cylinder simulated by GKUA with comparison of DSMC results |
图 12绘出分别使用含平动、转动、振动非平衡效应Boltzmann模型方程GKUA与DSMC计算物面热流与压力分布对比情况,其中“GKUA-Shakhov”表示将N2作为简单气体采用基于Shakhov模型的GKUA计算值,“GKUA-ES”表示仅考虑转动能激发而基于多原子气体ES模型的GKUA结果,“GKUA-vibration”表示考虑N2振动能激发的Boltzmann模型方程GKUA结果,“DSMC-translation”表示将N2作为简单气体不考虑内能激发DSMC模拟值,“DSMC-rotation”表示仅考虑N2转动能影响的DSMC模拟值,“DSMC-vibration”表示含N2振动能激发DSMC结果。图 12(a)所示物面热流分布看出,驻点附近“DSMC-translation”结果明显高于其他几种结果,且存在严重统计波动,绕流圆柱面中部,“GKUA-vibration”偏离其他几种结果,最大偏差不超过15%;图 12(b)所示物面压力分布看出,驻点附近“DSMC-translation”结果最小,“GKUA-Shakhov”次之,其他结果几乎重合,说明内能激发热力学非平衡效应对气动力影响很小。
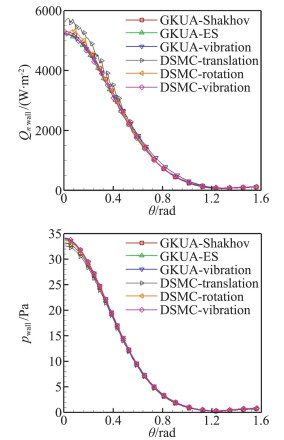
|
图 12 考虑平动、转动、振动非平衡效应的GKUA、DSMC计算圆柱绕流物面压力和热流分布, Ma∞=5, Kn∞=0.01 Figure 12 Surface heat flux and pressure around circular cylinder with different non-equilibrium effects computed by GKUA and DSMC, Ma∞=5, Kn∞=0.01 |
为了考察含振动能激发的Boltzmann模型方程统一算法对可回收类航天器再入绕流气动力热特性的影响,拟定与1.2节相同卫星体飞行器以来流马赫数5再入飞行两种绕流状态:来流Kn∞数分别为1、0.01。从前面的研究体会到,只有当温度较高时振动能的激发才会对流动产生作用,这里将来流温度和物面温度增加,研究考察振动能激发所致热力学非平衡效应对流场结构影响问题。为此设置来流温度为500 K、壁温Tw=2000 K。图 13、图 14分别绘出上述两种状态绕流场振动温度、等效温度、压力和马赫数等值线分布云图。可看出,对较高Kn∞=1稀薄气体绕流,振动温度与全场等效温度差别较大,达700 K,说明高Kn∞数气体分子数较少,能量松弛过程通过分子间碰撞完成,较少的分子数致能量松弛过程变缓,非平衡效应越发显著;另一方面,若流动趋于Kn∞=0.01近连续流,由于连续介质流中,气体分子速度分布函数呈现当地Maxwell平衡态分布,流场中平动、转动、振动温度接近或趋于与等效温度相一致的分布,这与分别考虑平动或转动非平衡的跨流域绕流现象相一致[28-29]。图中还清晰反映了从高稀薄流过渡到近连续流演变过程中流场变化规律,再入飞行器前部一定区域出现脱体强扰动逐渐演变成清晰的激波强间断、由稀薄低压过渡到高压绕流特征。
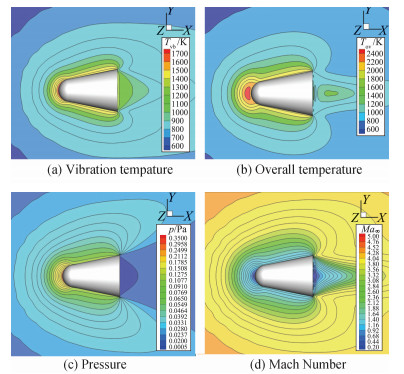
|
图 13 含振动能激发Boltzmann模型方程GKUA计算卫星体再入高稀薄绕流流场分布, Kn∞=1、Ma∞=5 Figure 13 Flow distribution in vibrational energy excitation around satellite shape with Kn∞=1, Ma∞=5 computed by GKUA |

|
图 14 含振动能激发Boltzmann模型方程GKUA计算卫星体再入近连续绕流流场分布, Kn∞=0.01、Ma∞=5 Figure 14 Flow distribution in vibrational energy excitation around satellite shape with Kn∞=0.01, Ma∞=5 computed by GKUA |
图 15、图 16分别绘出Kn∞=1、0.01两种再入非平衡绕流状态下卫星体表面压力和热流等值线分布云图。可看出,随着来流Kn∞数由1减小到0.01,来流由高稀薄流过渡到近连续流,物面压力、热流的有量纲值均急剧增大,对此卫星体再入飞行器从Kn∞=1再入到Kn∞=0.01,物面压力分布就增大了125倍、热流增大近20倍。
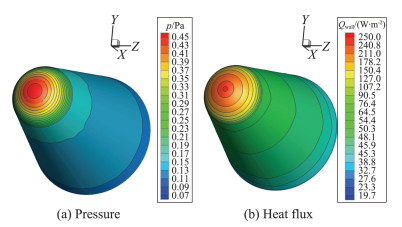
|
图 15 含振动能激发Boltzmann模型方程GKUA计算卫星体再入物面压力与热流分布, Kn∞=1、Ma∞=5 Figure 15 Pressure and heat flux distribution in vibrational energy excitation around satellite surface with Kn∞=1, Ma∞=5 computed by GKUA |

|
图 16 含振动能激发Boltzmann模型方程GKUA计算卫星体再入物面压力与热流分布, Kn∞=0.01、Ma∞=5 Figure 16 Pressure and heat flux distribution in vibrational energy excitation around satellite surface with Kn∞=0.01, Ma∞=5 computed by GKUA |
上节介绍的气体动理论统一算法作为近二十年来由Boltzmann型速度分布函数方程对完全气体到含内能激发包括转动能、振动能热力学非平衡流动一维、二维、三维直至复杂结构航天器再入过程可计算建模,发展至今,逐渐成为日趋广泛用于航天军工[26-32, 68-70]、MEMS微尺度[66-67, 88-89]行之有效的跨流域空气动力学模拟方法一种新途径,该方法将气体分子速度分布函数在位置空间和速度空间的信息保存起来进行数值求解,所需要的内存、计算量较大,仍在进一步发展中。无论是载人航天器还是跨大气层飞行器,以及各类返回器的再入过程,其飞行航迹都是采取气动方式来控制。由于在稀薄气体流域飞行的时间较长,飞行速度非常高,如2014年10月我国圆满成功完成试验任务的探月工程三期再入返回飞行试验器的再入速度达到10.6 km/s,而美国彗星探测器Stardust[5]返回再入速度更是高达12.8 km/s。如此极端速度条件下,气体分子间较高的相对运动能量足以发生化学反应和电离过程,烧蚀和所谓的“通信黑障”问题更加严重。流场稀薄气体效应影响很大,飞行器前方绕流流场,特别是前方弓形激波附近流场,气体分子状态远离平衡态,不仅气体分子的平动温度、转动温度和振动温度存在显著差别,且气体分子间的化学反应、电离辐射效应剧烈[34]。能否准确预测超高速再入导致的稀薄过渡流区严重的热化学电离非平衡效应对飞行器气动性能的影响,一直是对再入空气动力学研究的挑战。为此,本文立足既有空气动力学研究手段,发展适于返回舱(器)再入各流域相应数值模拟方法,使之形成验证结合互为补充综合分析应用研究平台。
2.1 稀薄流区DSMC方法DSMC方法用一个仿真分子代表一定数量FN的真实分子(包括分子、原子、离子和电子),计算机存储仿真分子位置坐标、速度分量和内能信息,随仿真分子运动、与边界相互作用及分子间碰撞而改变,最后统计网格内仿真分子状态实现真实气体流动的模拟,较容易引入符合物理实际的模型。方法关键是在小于当地分子平均碰撞时间步长Δt内将分子运动和碰撞解耦,即让所有分子运动一定距离并考虑边界反射,然后计算此时间段内具有代表性分子间碰撞。由于计算效率问题,DSMC方法主要用于高稀薄过渡流的模拟,为了扩展DSMC方法在近连续过渡流区模拟热化学非平衡复杂流动的能力和计算效率,根据高超声速压缩流动中连续流假设失效的判断准则,将流场区域分解为气体分子速度分布函数处于平衡态分布的连续流区和强热非平衡的稀薄流区。在连续/近连续流区域,采用限制碰撞的DSMC方法,使用网格自适应和变时间步长技术来减少数值扩散的误差。对一些流动问题,可以在保证计算精度的基础上提高计算效率。同时发展大规模并行算法[90],形成了适于模拟高超声速近连续流区气动特性的碰撞限制器DSMC混合方法[72]。文献[91]通过计算不同网格尺度、不同壁面反射模型的返回舱再入条件下表面参数分布和气动力系数随迎角变化、真实气体效应的影响,验证了算法可靠性。
稀薄气体电离现象是航天器再入速度持续增大面临的新问题,直接导致通信黑障等传统难题向稀薄区域大幅延伸。传统的再入物理通过求解含化学反应的N-S方程组[92]得到再入体绕流电子数密度分布,但是该方程组对于稀薄气体流动失效。近年来发展的稀薄气体数值模拟方法中,基于Boltzmann方程的分析和计算[28-32, 39, 40, 93, 68, 87],目前尚无法包含电离过程,只有基于粒子随机统计模拟的DSMC(Direct Simulation Monte Carlo)方法[5, 21-22, 33-34]是最有可能解决稀薄气体电离数值预测难题的手段。基于稀有组分权重格式处理稀薄气体含电离化学反应过程,对不同权重粒子之间的碰撞根据概率改变内能状态,对不同权重粒子之间的化学反应依概率删除或保留反应物粒子,同时对生成物中的稀有组分粒子进行复制。基于MPI并行环境、直角/非结构混合网格和网格自适应技术,建立了适于三维真实复杂外形航天器极高超声速再入电离热化学非平衡流动过程DSMC模拟平台[7, 21, 33-34, 72, 91]。首次计算考察了月地高速再入返回器和神舟飞船返回舱再入稀薄气体电离特性,分析了稀薄弱电离等离子体电子振动频率对应的电磁波频率,计算结果表明月地高速再入返回器和神舟飞船返回舱将分别在约85 km和80 km高度开始发生通信中断,这与飞行试验观测结果一致,证实了极高超声速再入电离热化学非平衡流DSMC模拟平台对解决国家需求的工程实用性[21, 33-34, 72, 94]。
2.2 连续/近连续流区(滑移)N-S解算器在返回舱再入近空间连续/近连续流区,为了借助N-S方程数值求解,揭示高空绕流物面稀薄非平衡效应的滑移边界模型对流场计算影响,发展了含热解烧蚀与壁面催化、滑移稀薄效应的热化学N-S方程数值方法[37, 95-97],并从完全气体和单一组分逐渐发展到考虑多组分以及振动非平衡影响的情况,实现了滑移边界修正,并用于近连续流和滑移流区飞行器气动特性的预测和模拟[100]。通过构造高温多组分混合气体物面滑移边界条件数学模型,在Gupta等[99]关于多组分滑移边界条件研究基础上,开展考虑振动能激发非平衡与物面滑移、稀薄气体间断粒子效应、黏性干扰效应可计算建模,发展了一套考虑振动非平衡、黏性干扰与稀薄气体物面滑移效应的飞行器再入近连续滑移流区高超声速非平衡绕流物面气动热特性N-S方程数值算法[37]。为了比较验证上述N-S方程数值算法对返回舱在氮气流动介质再入60公里不同来流迎角绕流实验状态:来流马赫数Ma∞=9.5、克努森数Kn∞, L=1.13×10-5、雷诺数Re∞, D=1.14×105,表 1列出来流迎角α=10°、15°、18°、20°、22°条件下,常规N-S方程解算器与考虑壁面滑移效应修正的N-S方程数值算法即表中分别备注“计算”、“滑移”的计算结果轴向力、法向力、俯仰力矩、压心、升力、阻力系数及升阻比与N2实验条件下的低密度风洞实验测量结果对比分析,可看出计算与实验总体上吻合较好,表中最后一列给出了各迎角状态下两种途径计算得到的升阻比与实验数据相对偏差范围11.97%~3.92%,考核验证了计算模型与数值方法实现的正确性。计算发现,对此H=60 km返回舱大钝头绕流,在α=20°以内,经滑移边界修正的N-S解算器结果较常规N-S计算结果更好吻合风洞实验数据,然而迎角更大,考虑壁面滑移效应修正的N-S算法结果与实验数据偏差增大,精度不如常规N-S解算器,说明滑移N-S解算器对大钝头迎风区较简单物形绕流计算具有较好适应性,然而对大迎角出现流动分离复杂结构体绕流局部物面稀薄滑移效应的表征困难而致计算局限性。从表 1反映出,针对该大钝头返回舱外形体绕流,迎角增大,会致迎风物面法向力、升力系数增大;背风区分离干扰区增大,致轴向力、阻力系数有所减小,以致升阻比随迎角增大而明显增大,为此大迎角情况下较大的升阻比计算结果与试验数据偏差绝对值与较小迎角情况下即使相当,但会出现计算结果与试验数据的相对偏差在大迎角情况比小迎角情况减小的特点。图 17(a、b)绘出上述返回舱实验模型再入60 km、α=20°条件下绕流场马赫数、压力等值线云图结构,可看出在较大迎角情况下迎风区压力远远高于背风区,稀薄效应与背风区分离多流区干扰致滑移N-S计算不适应。
| 表 1 返回舱模型绕流计算结果与试验数据对比 Table 1 Comparison of Cal. results and Exp. data forre-entry capsule |
|
|
|
图 17 返回舱试验模型绕流场结构, Ma∞=9.5, α=20° Figure 17 Hypersonic flow past re-entry capsule (Kn∞, L=1.13×10-5, Ma∞=9.5, H=60 km) |
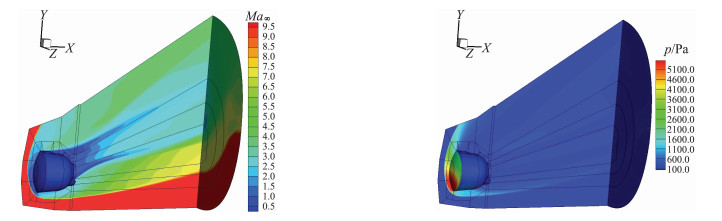
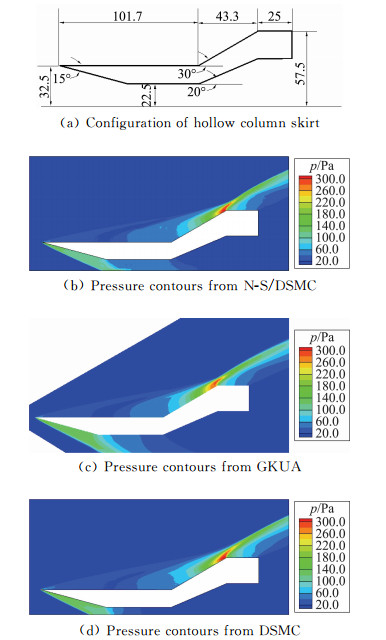
为了开展不同理论模型与数值方法间的耦合补充,通过研究连续流体力学N-S方程随着当地克努森数增大与复杂非规则物面稀薄效应增强致其失效的判断准则为基础,发展了适于近连续过渡流区高超声速绕流流场分区N-S与DSMC耦合模拟技术[35]。根据高超声速压缩流动特点,选取基于梯度变化的当地Kn∞数作为连续流方程失效判断参数,根据气体分子当地平均自由程与流动梯度定义的特征尺度比值,确定流动当地Kn∞数,利用Kn∞l≥0.02判断连续流方程失效,发展连续流方程失效界面选取法。构建MPC耦合计算模型,在统一网格系统下,N-S方程对整个流场进行计算,而DSMC只计算连续流方程失效部分区域。在分界面,两种方法进行信息交换,N-S方程结果为DSMC方法提供边界条件,DSMC模拟值替换N-S方程在DSMC区域的计算结果。构造抑制DSMC统计波动对N-S计算影响的亚松弛技术,对N-S方程和DSMC方法计算程序进行基于网格与信息交换融合分析设计,解决分区耦合计算信息传递问题,DSMC方法计算区域由计算过程中流场参数自动选取,根据N-S方程结果不断调整DSMC方法计算区域,直到流场达到稳定。建立了一套适于复杂飞行器绕流气动特性模拟的N-S/DSMC耦合算法。为了验证确认该N-S/DSMC耦合模拟技术与求解Boltzmann模型方程GKUA、DSMC方法在近连续过渡流区复杂构型绕流问题求解的可靠性,拟定来自文献[100]图 18(a)所示15°尖前缘高超声速中空柱裙流动算例:Ma∞=9.91、T∞= 51 K、p∞=6.3 Pa、Tw=293 K。流动介质N2,Lref=0.1017 m,Kn∞= 7.9135×10-4、Re∞, L=18 916,分别使用上述三种方法对该算例进行计算比较。
|
图 18 近连续过渡流区空心柱裙N-S/DSMC、GKUA、DSMC模拟流场压力等值线云图 Figure 18 Hypersonic flow past the hollow column skirt computed by the N-S/DSMC, GKUA and DSMC (Kn∞=7.9135×10-4, Ma∞=9.91, Re∞, L=18 916) |
图 18(b~d)绘出三种算法对该中空柱裙绕流流场压力分布等值线云图比较情况。在流场结构上,三种结果基本一致。在流场细节上,三种结果有一定差异,气流在尖前缘处产生斜激波,经过斜激波在压缩拐角区域形成λ波流场结构,三种算法较好地捕捉到了这种复杂结构。N-S/DSMC耦合算法与DSMC方法的结果更为接近,在远离物面与流场背风区存在一些微弱波动,而GKUA结果具有更高分辨率,更为光滑再现局部绕流结构。图 19(a)绘出该中空柱裙绕流流向位置x/L=0.6处气流密度沿横向y方向分布的三种方法计算结果比较情况,可看出三种结果变化规律总体吻合较好,特别是本项目GKUA与DSMC模拟值从边界层流动到跨越斜激波以至远场区均较为一致,N-S/DSMC耦合算法结果在壁面边界层及跨越激波过渡带较前者差别或高或低一些,反映了N-S/DSMC耦合算法在模拟稀薄非平衡效应严重的流场,存在较大的系统误差,为此我们将该方法定位于近连续过渡流区一种工程预测分析手段,能较好补充与弥补跨流域空气动力学模拟手段途径的完备性。图 19(b)绘出该中空柱裙绕流物面压力分布比较情况,看出三种方法得到的压力系数分布较为一致,物面压力最大值在斜板上部拐角处,仅在极值点上,DSMC方法模拟结果较高,GKUA与N-S/DSMC耦合算法结果相当一致,有待进一步确认造成该拐角处DSMC模拟与GKUA偏差更大的原因,是否因DSMC统计波动所致。计算表明三种方法均能获得较好的壁面压力分布,不仅证实了本文前述Boltzmann方程可计算建模GKUA用于计算复杂构型跨流区绕流非平衡相当严重的流场与物面绕流问题准确可靠性,而且反映出本项目DSMC、N-S/DSMC耦合方法用于各自所适应的流动领域复杂飞行器绕流问题模拟研究的工程可行性。

|
图 19 N-S/DSMC、GKUA、DSMC模拟流场密度物面压力 Figure 19 Comparison of density and surface pressure past the hollow column skirt computed by N-S/DSMC, GKUA and DSMC (Kn∞=7.9135×10-4, Ma∞=9.91) |
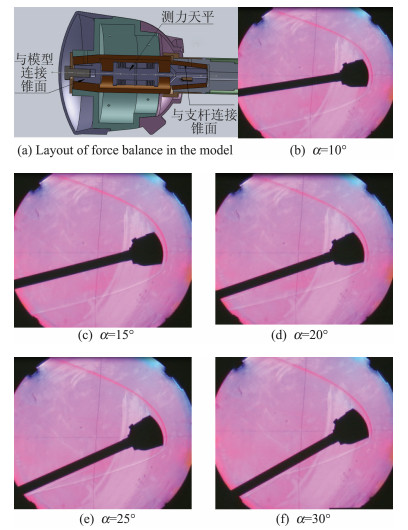
高超声速低密度风洞是模拟航天器高空、高速飞行状态的一种地面试验设备[101],在中国空气动力研究与发展中心超高速空气动力研究所新建高超声速低密度风洞喷管出口尺寸为1 m量级,可模拟带凸起物飞船返回舱真实外形,准确预测其气动力特性。为此,针对返回舱外形模型,开展了系列低密度风洞测力试验相关技术研究,包括开展小升阻比纵向三分量天平设计技术以及天平、模型防隔热技术研究,发展高温流场下高精度低升阻比测力天平设计技术,建立大钝头模型稀薄过渡流区气动力测试技术与实验方法。在此基础上,开展返回舱稀薄过渡流区不同高度、不同马赫数与迎角下气动力特性研究。设计了带凸起物(稳定翼、俯仰发动机座、分离插座板)外形试验模型,模型总长150.0 mm、最大截面直径151.02 mm。试验模型采用分段设计,主要分为头部、中段和后部等3个主要部分,如图 20(a)所示。考虑到天平元件在纵向尺寸(长度)上受到限制的现实,尽量避免天平与模型、支杆的连接锥面占用有限的模型纵向空间。将天平与模型中段的连接部分在不影响模型头部与中段装配的情况下尽量伸入模型头部内腔,同时将天平与支杆的连接锥面置于模型外的支杆内腔,使有限的模型内腔空间用来布置天平测力元件。针对天平载荷特点,天平测力元件结构尽量采取简单对称的形式进行布局。这样,一方面可有效减小热结构变形对天平测量产生的干扰影响,另一方面也便于天平机械加工和减小分量间的相互干扰影响。故在进行天平结构初步设计时,将轴向力元件布局在天平设计中心处,在天平设计中心前后处对称设置两个矩形截面梁,用来测量法向力和俯仰力矩,并尽量缩短矩形梁的长度。为减小天平的温度效应,在应变计选用上使用温度自补偿的中温应变计。对于高温流场环境下使用的小尺寸应变天平,热对天平准确测量的影响较大。天平测量梁受热产生热应力,天平加工材料弹性模量受热发生变化及天平测量梁上电阻应变片受热电阻和灵敏度系数发生变化等因素,都会对天平输出信号产生干扰。同样,天平结构不同使得天平传热途径发生变化,从而导致天平各测量梁温度分布不同,产生不同的温度影响。对高温流场条件下小尺寸应变天平技术进行深入研究时,需要考虑天平结构和传热之间的相互耦合影响。为此,需要开展天平防隔热与天平元件结构布局研究。针对天平和模型间采用简单隔热套结构的方案,在风洞来流条件下,采用有限元方法,对模型、天平及隔热套整体结构进行传热分析,获取各部件的温升分布情况,并将分析结果同试验结果进行对比,验证有限元方法对该类问题进行分析的有效性。针对不同的天平元件结构布局形式和天平测量梁几何尺寸,在天平设计载荷下,采用有限元方法,对天平的强度、刚度、灵敏度进行详细分析,选取综合性能较优的结构方案,实现天平结构优化设计[102]。
|
图 20 风洞试验模型与测力天平布局及试验纹影照片 Figure 20 Wind tunnel test model and force balance layout and test schlieren photograph for Shenzhou-type re-entry capsule |
在满足模型外形相似情况下,试验选取克努森数Kn∞作为主要模拟参数,在流场名义马赫数和前室总温确定的情况下,按照风洞试验流场的克努森数与高空飞行状态的克努森数相同的原则,得出风洞试验时的总压,以此总压值和确定的实际马赫数、总温作为风洞运行参数来模拟高空相应飞行状态:高度H=57.96 km、来流马赫数Ma∞=9.95、总压p0=1.95×106 Pa、总温T0=1070 K、来流雷诺数Re∞, D=1.7821×105、克努森数Kn∞, L=8.117×10-5。试验结果数据如表 1相关栏目所示,图 20(a)绘出试验模型及天平、模型防隔热结构示意图,图 20(b~f)绘出对应总压p0=1.95 MPa、总温T0=1100 K、来流迎角α=10°、15°、18°、20°、22°风洞试验所测纹影照片,可看出不同来流迎角所呈现的脱体激波流场结构,其相应的气动力系数与(滑移)N-S解算器比较验证情况见表 1所示,证实计算与实验模拟可靠性。
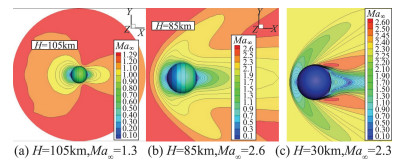
3 跨流域空气动力学模拟方法验证分析平台在研究建立求解Boltzmann模型方程气体动理论统一算法(GKUA)、DSMC、N-S/DSMC、(滑移)N-S解算器、低密度风洞实验测试多种空气动力学模拟手段基础上,为了验证确认跨流域空气动力学模拟方法计算精度与不同方法模型特点,拟定圆球再入高度H=110~30 km,Kn∞=4.43~2.48×10-5,Ma∞=0.75~3.2,Re∞=0.25~1.37×105条件下十三组状态,分别采用N-S方程解、N-S/DSMC耦合算法、DSMC与GKUA对全飞行流域不同高度气动阻力系数计算比较,表 2给出GKUA计算分别与30~60 km连续流区N-S解、65~75 km近连续过渡流区N-S/DSMC耦合算法和80~110 km高稀薄流区DSMC模拟值定量化比较,可看出两类结果吻合很好、最大偏差不超过4.5%,在连续流区GKUA与N-S偏差0.01%~4.5%、在过渡流区GKUA与N-S/DSMC偏差3.4%~3.5%、在高稀薄流区GKUA与DSMC偏差0.2%~4.4%,证实所发展不同流域计算方法模型的正确可靠性与统一算法具有全流域计算一致收敛性优势[83]。图 21绘出该球体陨落从高稀薄流H=105 km至过渡流区H=85 km以至连续流区H=30 km不同流域绕流面貌,直观揭示了气体绕流从高稀薄近自由分子流的物面附近强扰动演变为稀薄近连续过渡流区的激波过渡带,再到连续流区明晰清脆的脱体激波变化规律。
| 表 2 球体再入H=110~30 km绕流阻力系数GKUA与DSMC、N-S/DSMC、N-S计算比较 Table 2 Comparison of drag coefficients of GKUA, DSMC, N-S/DSMC and N-S solvers for re-entry sphere with H=110~30 km |
|
|
|
图 21 落球绕流马赫数等值线云图分布, H=105~30 km Figure 21 Mach No. contours around re-entry sphere with H=105~30 km computed by GKUA |
将求解Boltzmann模型方程统一算法应用于返回舱再入稀薄过渡流区配平迎角计算与实验验证,拟定相应于如下条件的绕流状态:飞行高度H=88.34 km,Kn∞=0.0063,Ma∞=15.587,Re∞=3729.15,Tw/T0=0.5435,迎角α=15°、18°、20°、22°、26°、30°,在位置空间网格设置45×16×25,使用4096CPU进行并行计算,图 22(a)绘出α=26°上述返回舱绕流轴对称面马赫数等值线计算结果,图 22(b)给出返回舱绕重心俯仰力矩系数随α变化关系,显示出GKUA计算返回舱H=88.34 km绕流配平迎角αT, Cal=25.06°,这与高超声速低密度风洞实验测得的配平迎角αT, Exp=25.39°相当一致,偏差仅1.3%,证实从介观层次Boltzmann方程可计算建模发展气体动理论统一算法用于计算返回舱再入气动力/热问题可靠性与置信度,特别是高分辨率捕捉微弱流动量模拟能力。这为进一步发展各流域复杂高超声速非平衡绕流问题统一算法解算器,开展新一代飞船返回舱再入各流域真实气体绕流问题计算,特别是近连续、滑移、过渡流区气动力/热与姿态配平绕流问题一体化模拟研究奠定了基础。

|
图 22 GKUA计算返回舱再入Kn∞=0.0063, Ma∞=15.6流场马赫数与俯仰力矩系数随迎角变化 Figure 22 Mach contours around re-entry capsule with α=26° and pitching moment coefficients vs. α computed by the GKUA |
作为跨流域空气动力学模拟方法集成升华对接工程需求与应用,构建了Boltzmann方程可计算建模气体动理论统一算法、DSMC、N-S/DSMC、滑移N-S解算器、低密度风洞实验测试多种空气动力学模拟手段相互验证结合,返回舱再入从外层空间自由分子流到近地面连续流跨流域空气动力学一体化模拟平台。以此为基础,建立跨流域气动力、气动热、弹道联合计算分析机制与数据库、图书馆式基础研究结果共享系统,研制形成返回舱(器)从高稀薄自由分子流到近地面连续流全飞行流域沿弹道再入姿态配平绕流一体化仿真与可视化软件系统,具备三大职能:1)计算执行功能;2)演示分析功能;3)存储检索“图书馆”功能。其中,计算飞行过程使用云图粒子流优化3D演示渲染效果;通过Fortran算法库接入,实时计算执行功能实现,优化计算速度等。图 23绘出飞船返回舱再入跨流域气动模拟软件系统主界面实时计算操作台与利用该平台计算得到返回舱再入120~70 km流场压力分布。
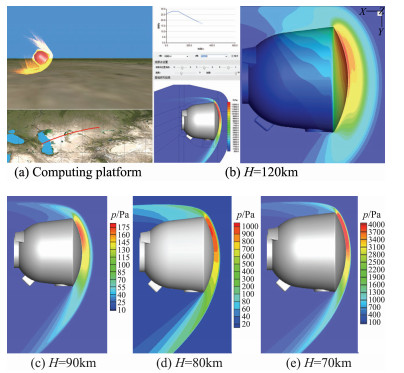
|
图 23 返回舱再入跨流域气动模拟软件系统实时计算与姿态配平绕流压力分布120~70 km Figure 23 Real-time computing pressure distribution during the spacecraft capsule re-entry with 120~70 km |
本文针对可回收类航天器,如飞船返回舱再入过程所遇跨流域多尺度非平衡变化过程绕流问题,综述了基于Boltzman方程碰撞积分物理分析与可计算建模,发展分别考虑完全气体、转动非平衡效应、含振动能激发热力学非平衡效应Boltzmann模型方程统一算法大规模并行计算研究进展与算法检验,证实统一算法在高稀薄流区,与DSMC模拟值吻合很好;在连续流区,与(滑移)N-S解算器得到的结果相一致;在中间过渡带,与N-S/DSMC耦合算法预测值相容;统一算法具有全飞行流域计算一致收敛性优势。
为克服直接对Boltzmann型速度分布函数方程在位置空间与速度空间离散数值求解计算量较大的问题,可发展适于三维复杂外形航天器极高超声速再入稀薄电离热化学非平衡流动过程DSMC方法;发展考虑振动非平衡、黏性干扰与稀薄气体物面滑移效应适于航天器再入近连续滑移流区高超声速非平衡绕流物面空气动力特性N-S方程解算器及其与DSMC耦合模拟技术,使之成为返回舱再入近连续过渡流区空气动力特性工程预测分析手段,研制基于小尺寸小载荷内式应变天平的返回舱再入稀薄过渡流区气动力测试技术与实验方法。建立基于GKUA、DSMC、N-S/DSMC、滑移N-S解算器、低密度风洞实验验证结合互为补充跨流域空气动力学模拟方法综合分析应用研究平台。将此平台用于再入H=110~30 km各流域三维球体、高超声速尖前缘中空柱裙、返回舱稀薄过渡流以至近连续流区气动力/热与姿态配平绕流问题计算与实验模拟验证,一方面证实所设计跨流域空气动力学不同模型算法实现的正确可靠性,结合软件工程、数据库,初步研制返回舱再入跨流域气动力/热沿弹道联合计算分析机制与模拟软件系统。另一方面,研究体会到,从介观层次Boltzmann方程可计算建模发展气体动理论统一算法用于计算返回舱再入气动力/热问题具有全流域计算收敛性,直接模拟客观物理过程的DSMC方法对返回舱再入稀薄热化学非平衡流动具有不可替代优越性;N-S/DSMC杂交耦合算法、滑移N-S解算器可用于较低来流迎角近连续过渡流区气动特征预测分析手段;结合低密度风洞实验,如何将此平台应用于返回(舱)器以第一、二宇宙速度再入跨流域热化学非平衡气动力热问题模拟研究,是未来进一步研究发展方向。
致谢: 本工作得到973、杰青课题组彭傲平等同志的大力帮助,部分计算在国家超级计算无锡中心、天津中心、济南中心进行,特此感谢!
| [1] |
Sarma G S R. Physico-chemical modelling in hypersonic flow simulation[J]. Progress in Aerospace Sciences, 2000, 36: 281-349. DOI:10.1016/S0376-0421(00)00004-X |
| [2] |
维特·鲁坦.宇宙飞船一号[C]//美国试验性飞机联合会第51届年会, 2004, 8.
|
| [3] |
方方. 神舟飞船返回舱气动设计综述[J]. 航天器工程, 2004, 13(1): 124-131. |
| [4] |
李志辉, 杨彦广, 梁杰, 等.飞船返回舱高空稀薄气动特性研究[C]//全国载人航天工程气动工作总结暨关键问题研讨会, 北京, 2004, 6. Li Zhihui, Yang Yanguang, Liang Jie, et al. Investigation of rarefied gas aerodynamics of spacecraft reentry capsule[C]//National Key Workshop on Aerodynamics of Spacecraft Re-entry, Beijing, June, 2004. (in Chinese). |
| [5] |
Shang J S, Surzhikov S T. Simulating stardust earth reentry with radiation heat transfer[J]. Journal of Spacecraft and Rockets, 2011, 48(3): 385-396. DOI:10.2514/1.52029 |
| [6] |
贾世锦. 载人登月返回再入有关问题初步研究[J]. 航天返回与遥感, 2011, 32(2): 18-25. Jia Shijin. Preliminary study on the return and re-entry of manned lunar landing[J]. Spacecraft Recovery & Remote Sensing, 2011, 32(2): 18-25. DOI:10.3969/j.issn.1009-8518.2011.02.003 |
| [7] |
梁杰, 李志辉, 杜波强. 飞船返回舱再入稀薄流域配平特性研究[J]. 航天返回与遥感, 2013, 34(2): 42-48. Liang Jie, Li Zhihui, Du Boqiang. Research on trim features of reentry capsule in hypersonic rarefied flow regime[J]. Spacecraft Recovery & Remote Sensing, 2013, 34(2): 42-48. DOI:10.3969/j.issn.1009-8518.2013.02.007 |
| [8] |
方方, 周璐, 李志辉. 航天器返回地球的气动特性综述[J]. 航空学报, 2015, 36(1): 24-38. Fang Fang, Zhou Lu, Li Zhihui. A comprehensive analysis of aerodynamics for spacecraft re-entery Earth's atmosphere surroundings[J]. Acta Aeronauticaet Astronautica Sinica, 2015, 36(1): 24-38. |
| [9] |
Bertin J J, et al. Fifty years of hypersonic:where we've been, where we're going[J]. Progress to Aerospace Sciences, 2003, 39. |
| [10] |
李颐黎, 戚发轫. "神舟号"飞船总体与返回方案的优化与实施[J]. 航天返回与遥感, 2011, 32(6): 1-13. Li Yili, Qi Faren. Optimigation and implementation of China Shenzhou spaceship's system and return technology scheme[J]. Spacecraft Recovery & Remote Sensing, 2011, 32(6): 1-13. DOI:10.3969/j.issn.1009-8518.2011.06.002 |
| [11] |
Raffaele Votta, Antonio Schettino, Aldo Bonfiglioli. Hypersonic high altitude aerothermodynamics of a space re-entry vehicle[J]. Aerospace Science and Technology, 2013, 25: 253-265. DOI:10.1016/j.ast.2012.02.001 |
| [12] |
Li J Y, Yang H W, Baoyin H X. Lunar exploration phase Ⅲ:Launch window and trajectory design for a lunar lander[J]. Advances in Space Research, 2015, 56: 879-892. DOI:10.1016/j.asr.2015.05.033 |
| [13] |
陆亚东, 李齐, 耿云飞, 等. 月地高速再入返回器气动设计与验证技术[J]. 中国科学:技术科学, 2015, 45(2): 132-138. Lu Yadong, Li Qi, Geng Yunfei, et al. Aerodynamic design and verification technology for the circumlunar free return and reentry flight vehicle[J]. Sci Sin Tech, 2015, 45: 132-138. |
| [14] |
Zuppardi G, Savino R, Mongelluzzo G. Aero-thermo-dynamic analysis of a low ballistic coefficient deployable capsule in Earth re-entry[J]. Acta Astronautica, 2016, 127: 593-602. DOI:10.1016/j.actaastro.2016.06.041 |
| [15] |
吕俊明, 程晓丽, 俞继军, 等. 化学非平衡效应对返回舱气动特性的影响分析[J]. 航天器环境工程, 2016, 33(4): 370-377. Lv Junming, Cheng Xiaoli, Yu Jijun, et al. The effect of chemical non-equilibrium on aerodynamic characteristics of reentry vehicles[J]. Spacecraft Environment Engineering, 2016, 33(4): 370-377. DOI:10.3969/j.issn.1673-1379.2016.04.006 |
| [16] |
徐国武, 杨云军, 周伟江. 返回舱再入过程中烧蚀影响研究[J]. 空气动力学学报, 2017, 35(1): 101-107. Xu Guowu, Yang Yunjun, Zhou Weijiang. Investigation on ablation effect of return capsule during reentry process[J]. Acta Aerodynamica Sinica, 2017, 35(01): 101-107. |
| [17] |
Kaushikh K, Arunvinthan S, Pillai S N. Aerodynamics and Aerothermodynamics of undulated re-entry vehicles[J]. Acta Astronautica, 2018, 142. |
| [18] |
Kinney D J. Development of the ORION crew exploration vehicle's aerothermal database using a combination of high fidelity CFD and engineering level methods[C]//47th AIAA Aerospace Sciences Meeting Including the New Horizons Forum and Aerospace Exposition, AIAA 2009-1100, Orlando, Florida, January 2009. https://arc.aiaa.org/doi/abs/10.2514/6.2009-1100
|
| [19] |
Korzun A M, Dubos G F, Iwata C K, et al. A concept for the entry, descent, and landing of high-mass payloads at Mars[J]. Acta Astronautica, 2010, 66(7): 1146-1159. |
| [20] |
陈金宝, 聂宏, 陈传志, 等. 载人登月舱设计及若干关键技术研究[J]. 宇航学报, 2014, 35(2): 125-136. Chen Jinbao, Nie Hong, Chen Chuanzhi, et al. Design and key techniques for lunar lander system manned lunar landing[J]. Journal of Astronautics, 2014, 35(2): 125-136. DOI:10.3873/j.issn.1000-1328.2014.02.001 |
| [21] |
梁杰, 李志辉, 杜波强, 等. 探月返回器稀薄气体热化学非平衡特性数值模拟[J]. 载人航天, 2015, 21(3): 295-302. Liang Jie, Li Zhihui, Du Boqiang, et al. Numerical simulation of rarefied gas thermochemical nonequilibrium for lunar exploration vehicle re-entering atmosphere[J]. Manned Spaceflight, 2015, 21(3): 295-302. DOI:10.3969/j.issn.1674-5825.2015.03.014 |
| [22] |
李志辉, 吴振宇. 阿波罗指令舱稀薄气体动力学特征的蒙特卡罗数值模拟[J]. 空气动力学学报, 1996, 14(2): 230-233. Li Zhihui, Wu Zhenyu. DSMC simulation on rarefied aerodynamics of Apollo-CM[J]. Acta Aerodynamica Sinica, 1996, 14(2): 230-233. |
| [23] |
詹慧玲, 陈冰雁, 刘周, 等. 典型再入返回器气动特性对比与改进研究[J]. 航天返回与遥感, 2013, 34(6): 11-20. Zhan Huiling, Chen Bingyan, Liu Zhou, et al. Comparative study and improvement design on aerodynamic characteristics of typical reentry capsules[J]. Spacecraft Recovery and Remote Sensing, 2013, 34(6): 11-20. DOI:10.3969/j.issn.1009-8518.2013.06.002 |
| [24] |
吕俊明, 潘宏禄, 苗文博, 等. 化学非平衡效应对返回舱再入气动力特性的影响[J]. 航天返回与遥感, 2014, 35(3): 11-19. Lv Junming, Pan Honglu, Miao Wenbo, et al. Impact of chemical non-equilibrium effect on aerodynamic characteristics of reentry capsules[J]. Spacecraft Recovery and Remote Sensing, 2014, 35(3): 11-19. DOI:10.3969/j.issn.1009-8518.2014.03.002 |
| [25] |
高铁锁, 江涛, 丁明松, 等. 辐射加热对返回舱气动热环境影响的数值研究[J]. 空气动力学学报, 2015, 33(1): 36-41. Gao Tiesuo, Jiang Tao, Ding Mingsong, et al. Numerical study of radiative heating influence on aerothermal environment over a reentry capsule[J]. Acta Aerodynamica Sinica, 2015, 33(1): 36-41. |
| [26] |
李志辉. "航天飞行器跨流域空气动力学与飞行控制关键基础问题研究"总体实施方案[R].绵阳: 中国空气动力研究与发展中心, 2014. Li Zhihui. General implementation scheme on study on key basic problems of aerodynamics and flight control covering flow regimes for aerospace craft[R]. Mianyang: Hypervelocity Aerodynamics Institute of the China Aerodynamics Research and Development Center, 2014. (in Chinese) |
| [27] |
李志辉, 梁杰, 唐志共, 等. "航天飞行器跨流域空气动力学与飞行控制关键基础问题研究"项目2014年度研究进展[R].国防科技报告, 2014CB744100/01, 2014.
|
| [28] |
李志辉, 吴俊林, 蒋新宇, 等. 含转动非平衡效应Boltzmann模型方程统一算法与跨流域绕流问题模拟研究[J]. 空气动力学学报, 2014, 32(2): 137-145. Li Zhihui, Wu Junlin, Jiang Xinyu, et al. The unified algorithm for various flow regimes solving Boltzmann model equation in rotational non-equilibrium[J]. Acta Aerodynamica Sinica, 2014, 32(2): 137-145. |
| [29] |
蒋新宇, 李志辉, 吴俊林. 气体运动论统一算法在跨流域转动非平衡效应模拟中的应用[J]. 计算物理, 2014, 31(4): 403-411. Jiang Xinyu, Li Zhihui, Wu Junlin. Application of gas-kinetic unified algorithm covering various flow regimes for rotational non-equilibrium effect[J]. Chinese Journal of Computational Physics, 2014, 31(4): 403-411. DOI:10.3969/j.issn.1001-246X.2014.04.004 |
| [30] |
Li Z H, Peng A P, Zhang H X, et al. Rarefied gas flow simulations using high-order gas-kinetic unified algorithms for Boltzmann model equations[J]. Progress in Aerospace Sciences, 2015, 74: 81-113. DOI:10.1016/j.paerosci.2014.12.002 |
| [31] |
Wu J L, Li Z H, Peng A P, et al. Numerical simulations of unsteady flows from rarefied transition to continuum using gas-kinetic unified algorithm[J]. Adv Appl Math Mech, 2015, 7(5): 569-596. DOI:10.4208/aamm.2014.m523 |
| [32] |
Peng A P, Li Z H, Wu J L, et al. Implicit gas-kinetic unified algorithm based on multi-block docking grid for multi-body reentry flows covering all flow regimes[J]. Journal of Computational Physics, 2016, 327: 919-942. DOI:10.1016/j.jcp.2016.09.050 |
| [33] |
梁杰, 李志辉, 杜波强, 等. 真实气体效应对MSL火星进入气动特性的影响研究[J]. 航天返回与遥感, 2017, 38(4): 8-17. Liang Jie, Li Zhihui, Du Boqiang, et al. Numerical research of real gas effect on MSL mars entry aerodynamic characteristics[J]. Spacecraft Recovery & Remote Sensing, 2017, 38(4): 8-17. DOI:10.3969/j.issn.1009-8518.2017.04.002 |
| [34] |
方明, 李志辉, 李中华, 等. 球锥钝头体再入稀薄气体电离过程三维DSMC模拟与验证[J]. 空气动力学学报, 2017, 35(01): 39-45. Fang Ming, Li Zhihui, Li Zhonghua, et al. Three dimensional DSMC simulation and validation of rarefied air ionization process for sphere-cone blunt body reentry[J]. Acta Aerodynamica Sinica, 2017, 35(01): 39-45. DOI:10.7638/kqdlxxb-2015.0086 |
| [35] |
李中华, 李志辉, 李海燕, 等. 过渡流区N-S/DSMC耦合计算研究[J]. 空气动力学学报, 2013, 31(3): 282-287. Li Zhonghua, Li Zhihui, Li Hanyan, et al. Research on CFD/DSMC hybrid numerical method in rarefied flows[J]. Acta Aerodynamica Sinica, 2013, 31(3): 282-287. |
| [36] |
Li Z H, Li Z H, Wu J L, et al. Coupled Navier-Stokes/direct simulation Monte Carlo simulation of multicomponent mixture plume flows[J]. Journal of Propulsion and Power, 2014, 30(3): 672-689. |
| [37] |
李海燕, 李志辉, 罗万清, 等. 近空间飞行环境泰氟隆烧蚀流场化学非平衡流数值算法及应用研究[J]. 中国科学:物理学力学天文学, 2014, 44(2): 194-202. Li Haiyan, Li Zhihui, Luo Wanqing, et al. Application and numerical method of chemical non-equilibrium flow for Teflon ablative flow fields in near-space flying condition[J]. Sci Sin-Phys Mech Astron, 2014, 44: 194-202. |
| [38] |
李明, 祝智伟, 李志辉. 红外热图在高超声速低密度风洞测热试验中的应用概述[J]. 实验流体力学, 2013, 27(3): 108-112. Li Ming, Zhu Zhiwei, Li Zhihui. The summarization of infrared thermography on aerodynamic heating measurement in hypersonic low density wind tunnel[J]. J Exp Fluid Mech, 2013, 27(3): 108-112. DOI:10.3969/j.issn.1672-9897.2013.03.021 |
| [39] |
Chapman S, Cowling T G. The mathematical theory of non-uniform gases[M]. 3rd ed. Cambridge Univ. Press, 1970.
|
| [40] |
Cercignani C. Kinetic theories and the Boltzmann equation[R]. Lecture Notes in Mathematics, Springer-Verlag, Berlin, 1984 https://link.springer.com/book/10.1007%2FBFb0071876
|
| [41] |
Bhatnagar P L, Gross E P, Krook M. A model collision processes in gases. Ⅰ. Small amplitude processes is charged and neutral one-component system[J]. Phys Rev, 1954, 94: 511-525. DOI:10.1103/PhysRev.94.511 |
| [42] |
Holway L H Jr. New statistical models for kinetic theory:methods of construction[J]. Physics of Fluids, 1966, 9(9): 1658-1673. DOI:10.1063/1.1761920 |
| [43] |
Shakhov E M. Generalization of the krook kinetic relaxation equation[J]. Fluid Dynamics, 1968, 3(1): 158-161. |
| [44] |
Rykov V. Model kinetic equation of a gas with rotational degrees of freedom[J]. Fluid Dynamics, 1975, 10: 959-966. |
| [45] |
Nie X, Doolen G D, Chen S. Lattice Boltzmann simulation of fluid flows in MEMS[J]. Journal of Statistical Physics, 2002, 107: 279. DOI:10.1023/A:1014523007427 |
| [46] |
Chen L, He Y L, Kang Q J, et al. Coupled numerical approach combining finite volume and lattice Boltzmann methods for multi-scale multi-physicochemical processes[J]. Journal of Computational Physics, 2013, 255: 83-105. DOI:10.1016/j.jcp.2013.07.034 |
| [47] |
Tan Z, Varghese P. The Δ-ε method for the Boltzmann equation[J]. Journal of Computational Physics, 1994, 110: 327-340. DOI:10.1006/jcph.1994.1030 |
| [48] |
Yang J Y, Huang J C. Rarefied flow computations using nonlinear model Boltzmann equtions[J]. Journal of Computational Physics, 1995, 120: 323-339. DOI:10.1006/jcph.1995.1168 |
| [49] |
Mieussens L. Discrete-velocity models and numerical schemes for the Boltzmann-BGK equation in plane and axisymmetric geometries[J]. Journal of Computational Physics, 2000, 162(2): 429-466. DOI:10.1006/jcph.2000.6548 |
| [50] |
Titarev V A, Shakhov E M. Heat transfer and evaporation from a plane surface into a half-space upon a sudden increase in body temperature[J]. Fluid Dynamics, 2002, 37(1): 126-137. DOI:10.1023/A:1015147203313 |
| [51] |
Xu K. A Gas-kinetic BGK schemes for the Navier-Stokes equations and its connection with artificial dissipation and godunov method[J]. Journal of Computational Physics, 2001, 171: 289-335. DOI:10.1006/jcph.2001.6790 |
| [52] |
Xu K, Li Zhihui. Microchannel flow in the slip regime:gas-kinetic BGK-burnett solutions[J]. Journal of Computational Physics, 2004, 513: 87-110. |
| [53] |
Xu K, Huang J C. A unified gas-kinetic scheme for continuum and rarefied flows[J]. Journal of Computational Physics, 2010, 229: 7747-7764. DOI:10.1016/j.jcp.2010.06.032 |
| [54] |
Xiong S, Zhong C, Zhuo C, et al. Numerical simulation of compressible turbulent flow via improved gas-kinetic BGK scheme[J]. Int J Numer Methods Fluids, 2011, 67(12): 1833-1847. DOI:10.1002/fld.v67.12 |
| [55] |
Chen S Z, Xu K, Lee C B, et al. A unified gas kinetic scheme with moving mesh and velocity space adaptation[J]. Journal of Computational Physics, 2012, 231: 6643-6664. DOI:10.1016/j.jcp.2012.05.019 |
| [56] |
Guo Z L, Xu K. Discrete unified gas kinetic scheme for multiscale heat transfer based on the phonon Boltzmann transport equation[J]. International Journal of Heat and Mass Transfer, 2016, 102: 944-958. DOI:10.1016/j.ijheatmasstransfer.2016.06.088 |
| [57] |
谭爽, 李诗一, 李启兵, 等. 气体动理学格式与多尺度流动模拟[J]. 计算力学学报, 2017, 34(1): 88-94. Tan Shuang, Li Shiyi, Li Qibing, et al. Gas kinetic scheme and numerical simulation of multiscale flows[J]. Chinese Journal of Computational Mechanics, 2017, 34(1): 88-94. |
| [58] |
Ohwada T. Structure of normal shock waves:Direct numerical analysis of the Boltzmann equation for hard-sphere molecules[J]. Phys. Fluids, 1993, 5: 217-234. DOI:10.1063/1.858777 |
| [59] |
Doi T. Numerical analysis of the Poiseuille flow and the thermal transpiration of a rarefied gas through a pipe with a rectangular cross section based on the linearized Boltzmann equation for a hard sphere molecular gas[J]. Journal of Vacuum Science & Technology A Vacuum Surfaces & Films, 2010, 28(4): 603-612. |
| [60] |
Balakrishnan R, Agarwal R K. Higher-order distribution functions, BGK-Burnett equations and Boltzmann's H-theorem[J]. Computational Fluid Dynamics Review, 1998, 794-832. |
| [61] |
Myong R S. A generalized hydrodynamic computational model for rarefied and microscale diatomic gas flows[J]. Journal of Computational Physics, 2004, 195(2): 655-676. DOI:10.1016/j.jcp.2003.10.015 |
| [62] |
Xiao H, Myong R S. Computational simulations of microscale shock-vortex interaction using a mixed discontinuous Galerkin method[J]. Computers & Fluids, 2014, 105: 179-193. |
| [63] |
Cai Z N, Li R. The NRxx method for polyatomic gases[J]. Journal of Computational Physics, 267: 63-91, 2014. |
| [64] |
李志辉, 张涵信. 稀薄流到连续流的气体运动论统一算法研究[J]. 空气动力学学报, 2003, 21(03): 255-266. Li Zhihui, Zhang Hanxin. Study on gas kinetic unified algorithm for flows from rarefied transition to continuum[J]. Acta Aerodynamica Sinica, 2003, 21(03): 255-266. DOI:10.3969/j.issn.0258-1825.2003.03.001 |
| [65] |
Li Z H, Zhang H X. Study on gas kinetic unified algorithm for flows from rarefied transition to continuum[J]. Journal of Computational Physics, 2004, 193: 708-738. DOI:10.1016/j.jcp.2003.08.022 |
| [66] |
李志辉, 张涵信. 基于Boltzmann模型方程的气体运动论统一算法研究[J]. 力学进展, 2005, 35(4): 559-576. Li Zhihui, Zhang Hanxin. Study on gas kinetic numerical algorithm using Boltzmann model equation[J]. Advances in Mechanics, 2005, 35(4): 559-576. DOI:10.3321/j.issn:1000-0992.2005.04.010 |
| [67] |
Li Z H, Zhang H X, Fu S. Gas kinetic algorithm for flows in poiseuille-like microchannels using Boltzmann model equation[J]. Science China, Physics, Mechanics & Astronomy, 48(4): 496-512, 2005. |
| [68] |
Li Z H, Zhang H X. Gas-kinetic numerical studies of three-dimensional complex flows on spacecraft re-entry[J]. Journal of Computational Physics, 2009, 228: 1116-1138. DOI:10.1016/j.jcp.2008.10.013 |
| [69] |
李志辉, 彭傲平, 方方, 等. 跨流域高超声速绕流环境Boltzmann模型方程统一算法研究[J]. 物理学报, 2015, 64(22): 224703-16. Li Zhihui, Peng Aoping, Fang Fang, et al. Gas-kinetic unified algorithm for hypersonic aerothermo dynamics covering various flow regimes solving Boltzmann model equation[J]. Acta Physica Sinica, 2015, 64(22): 224703-16. DOI:10.7498/aps.64.224703 |
| [70] |
李志辉, 吴俊林, 彭傲平, 等. 天宫飞行器低轨控空气动力特性一体化建模与计算研究[J]. 载人航天, 2015, 21(2): 106-114. Li Zhihui, Wu Junlin, Peng Aoping, et al. Unified modeling and calculation of aerodynamics characteristics during low-orbit flying control of the TG vehicle[J]. Manned Spaceflight, 2015, 21(2): 106-114. DOI:10.3969/j.issn.1674-5825.2015.02.002 |
| [71] |
Bird G A. Molecular gas dynamics and direct simulation of gas flows[M]. Oxford University Press, 1994.
|
| [72] |
梁杰, 李志辉, 杜波强, 等. 大型航天器再入陨落时太阳翼气动力/热模拟分析[J]. 宇航学报, 2015, 36(12): 1348-1355. Liang Jie, Li Zhihui, Du Boqiang, et al. Modeling and analysis of solar array aerothermodynamics during large-scale spacecraft reentry[J]. Journal of Astronautics, 2015, 36(12): 1348-1355. DOI:10.3873/j.issn.1000-1328.2015.12.002 |
| [73] |
Riedi P C. Thermal physics - an introduction to thermo-dynamics, statistical mechanics and kinetic theory[M]. London: The Macmillan Press LTD, 1976.
|
| [74] |
李志辉.从稀薄流到连续流的气体运动论统一数值算法研究[D].绵阳: 中国空气动力研究与发展中心, 2001.
|
| [75] |
Li Z H, Zhang H X. Gas-kinetic numerical method solving mesoscopic velocity distribution function equation[J]. Acta Mechanica Sinica, 2007, 23(3): 21-132. |
| [76] |
Li Z H, Bi L, Zhang H X, et al. Gas-kinetic numerical study of complex flow problems covering various flow regimes[J]. Computers and Mathematics with Application, 2011, 61(12): 3653-3667. DOI:10.1016/j.camwa.2010.10.046 |
| [77] |
李志辉, 张涵信. 跨流域三维复杂绕流问题的气体运动论并行计算[J]. 空气动力学学报, 2010, 28(01): 7-16. Li Zhihui, Zhang Hanxin. Gas-kinetic parallel computation for three-dimensional complex problems covering various flow regimes[J]. Acta Aerodynamica Sinica, 2010, 28(01): 7-16. DOI:10.3969/j.issn.0258-1825.2010.01.002 |
| [78] |
李志辉, 吴俊林, 蒋新宇, 等. 跨流域高超声速绕流Boltzmann模型方程并行算法[J]. 航空学报, 2015, 36(1): 201-212. Li Zhihui, Wu Junlin, Jiang Xinyu, et al. A massively parallel algorithm for hypersonic covering various flow regimes to solve Boltzmann model equation[J]. Acta Aeronauticaet Astronautica Sinica, 2015, 36(1): 201-212. |
| [79] |
李志辉, 蒋新宇, 吴俊林, 等. 求解Boltzmann模型方程高性能并行算法在航天跨流域空气动力学应用研究[J]. 计算机学报, 2016, 39(9): 1801-1811. Li Zhihui, Jiang Xinyu, Wu Junlin, et al. Study on high performance parallel algorithm for spacecraft re-entry aerodynamics in the whole of flow regimes using boltzmann model equation[J]. Chinese Journal of Computers, 2016, 39(9): 1801-1811. |
| [80] |
Sharipov F. Hypersonic flow of rarefied gas near the Brazilian satellite during its reentry into atmosphere[J]. Brazilian Journal of Physics, 2003, 33(2): 398-405. DOI:10.1590/S0103-97332003000200044 |
| [81] |
Agrwal R K, Chen R, Cheremisin F G. Computation of hypersonic shock wave flows of a diatomic using generalized Boltzmann equation[C]//39th AIAA Thermophysics Conference, Miami, 25-28 June, AIAA 2007-4541,
|
| [82] |
Rykov V A, Titarev V A, Shakhov E M. Shock wave structure in a diatomic gas based on a kinetic model[J]. Fluid Dynamics, 2008, 43(2): 316-326. DOI:10.1134/S0015462808020178 |
| [83] |
Li Z H, Fang M, Jiang X Y, et al. Convergence proof of the DSMC method and the gas-kinetic unified algorithm for the Boltzmann equation[J]. Science China, Physics, Mechanics & Astronomy, 2013, 56(2): 404-417. |
| [84] |
Boer J D, Uhlenbeck G E. Studies in statistical mechanics[M]. North-Holland, 1964.
|
| [85] |
王承书著, 应纯同, 张存镇译.气体运动论[M].原子能出版社1994, 12.
|
| [86] |
Morse T F. Kinetic model for gases with internal degrees of freedom[J]. Physics of Fluids, 1964, 7(2): 159-169. DOI:10.1063/1.1711128 |
| [87] |
彭傲平, 李志辉, 吴俊林, 等. 含振动能激发Boltzmann模型方程的气体动理论统一算法验证与分析[J]. 物理学报, 2017, 66(20): 204703. Peng Aoping, Li Zhihui, Wu Junlin, et al. Validation and analysis of gas-kinetic unified algorithm for solving Boltzmann model equation with vibrational energy excitation[J]. Acta Physica Sinica, 2017, 66(20): 204703. DOI:10.7498/aps.66.204703 |
| [88] |
Li Z H, Zhang H X, Fu S, et al. A gas kinetic algorithm for flows in microchannel[J]. International Journal of Nonlinear Sciences and Numerical Simulation, 2005, 6(3): 261-270. |
| [89] |
Hou S M, Li Z H, Jiang X Y, et al. Numerical study on two-dimensional micro-channel flows using the gas-kinetic unified algorithm[J]. Communications in Computational Physics, 2018, 23(5): 1393-1414. |
| [90] |
Wu J S, Tseng K C. Parallel DSMC method using dynamic domain decomposition[J]. Int J Numer Meth Engng, 2005, 63: 37-76. DOI:10.1002/(ISSN)1097-0207 |
| [91] |
梁杰, 李志辉, 李齐, 等. 返回舱再入跨流域气动及配平特性数值研究[J]. 空气动力学学报, 2018, 36(5): 848-855. Liang Jie, Li Zhihui, Li Qi, et al. Numerical simulation of aerodynamic and trim characteristics across different flow regimes for reentry module[J]. Acta Aerodynamica Sinica, 2018, 36(5): 848-855. DOI:10.7638/kqdlxxb-2018.0128 |
| [92] |
杨建龙, 刘猛, 阿嵘. 高超声速热化学非平衡对气动热环境影响[J]. 北京航空航天大学学报, 2017, 43(10): 2063-2072. Yang Jianlong, Liu Meng, A Rong. Influence of hypersonic thermo-chemical non-equilibrium on aerodynamic thermal environments[J]. Journal of Beijing University of Aeronautics and A, 2017, 43(10): 2063-2072. |
| [93] |
Yen S M. Numerical solution of the nonlinear Boltzmann equation for nonequilibrium gas flow problems[J]. Annual Review of Fluid Mechanics, 1984(16): 67-97. |
| [94] |
Fang M, Li Z H, Li Z H, et al. DSMC approach for rarefied air ionization during spacecraft reentry[J]. Communications in Computational Physics, 2017. |
| [95] |
程晓丽, 苗文博, 周伟江. 真实气体效应对高超声速轨道器气动特性的影响[J]. 宇航学报, 2007, 28(2): 259-264. Cheng Xiaoli, Miao Wenbo, Zhou Weijiang. Effects of real gas on aerodynamic characteristics of a hypersonic orbiter[J]. Journal of Astronautics, 2007, 28(2): 259-264. DOI:10.3321/j.issn:1000-1328.2007.02.004 |
| [96] |
高铁锁, 江涛, 丁明松, 等. 辐射加热对返回舱气动热环境影响的数值研究[J]. 空气动力学学报, 2015, 33(01): 36-41. Gao Tiesuo, Jiang Tao, Ding Mingsong, et al. Numerical study of radiative heating influence on aerothermal environment over a reentry capsule[J]. Acta Aerodynamica Sinica, 2015, 33(01): 36-41. |
| [97] |
徐国武, 杨云军, 周伟江. 返回舱再入过程中烧蚀影响研究[J]. 空气动力学学报, 2017, 35(1): 101-107. Xu Guowu, Yang Yunjun, Zhou Weijiang. Investigation on ablation effect of return capsule during reentry process[J]. Acta Aerodynamica Sinica, 2017, 35(1): 101-107. |
| [98] |
Zade A Q, Renksizbulut M, Friedman J. Slip/jump boundary conditions for rarefied reacting/non-reacting multi-component gaseous flows[J]. International Journal of Heat and Mass Transfer, 2008, 51: 5063-5071. DOI:10.1016/j.ijheatmasstransfer.2008.02.044 |
| [99] |
Gupta R N. Hypersonic low-density solutions of the Navier-Stokes equations with chemical nonequilibrium and multicomponent surface slip. AIAA-86-1349[R]. Reston: AIAA, 1986. https://arc.aiaa.org/doi/abs/10.2514/6.1986-1349
|
| [100] |
Moss J N. DSMC computations for regions of shock/shock and shock/boundary layer interaction[C]//39th AIAA Aerospace Sciences Meeting & Exhibit, Jan. 8-11, 2001, AIAA 2001-1027. https://arc.aiaa.org/doi/abs/10.2514/6.2001-1027
|
| [101] |
姜维本. 高超声速试验设备设计[M]. 国防工业出版社, 2001: 11.
|
| [102] |
李绪国, 杨彦广, 李志辉, 等. 小尺寸应变天平设计方法研究[J]. 实验流体力学, 2013, 27(4): 78-82. Li Xuguo, Yang Yanguang, Li Zhihui, et al. Design methods of the small size strain gauge balance[J]. J Exp Fluid Mech, 2013, 27(4): 78-82. DOI:10.3969/j.issn.1672-9897.2013.04.014 |
 2018, Vol. 36
2018, Vol. 36

