2. 复旦大学 航空航天系, 上海 200433
2. Department of Aeronautics and Astronautics, Fudan University, Shanghai 200433, China
近些年来,越来越多的弹性结构被应用到不同的工程领域中。而由于弹性结构大变形的存在,孤立的气动模型已经不能对这些结构的气动性能进行准确评估了,对于这些结构的气动分析需要通过引入耦合的气动弹性模型实现[1-3]。高精度的气动弹性计算需要通过耦合计算流体力学(Computational Fluid Dynamics, CFD)方法和计算结构力学(Computational Structural Dynamics, CSD)方法实现。结合不同计算精度的需求,可以在耦合CFD-CSD方法中选择不同的流体或结构求解器,而在流体和结构求解器之间需要采用合适的策略完成计算结点间的数据传递(气动载荷和结构位移的传递)。近年来,已经有很多工作投入到耦合CFD-CSD方法的研究中了[4-7]。
但是无论是采用无黏还是黏性流动的求解器,CFD方法往往要消耗大量的计算资源和计算时间。尤其在解决一些非定常气动弹性问题的时候需要与CSD方法耦合进行时间推进,其带来的计算代价更是十分巨大的。在一些工程问题中,例如在飞机概念设计阶段的气动弹性计算,有时希望通过一定程度的计算精度的牺牲来换取更高的计算效率。在过去几十年中,涡格法作为一种方便高效的定常或非定常气动计算方法被广泛应用于工程领域[8-11],有时也被用来与结构动力学方法耦合进行气动弹性计算。Wang等[12]应用非定常涡格法与非线性梁模型发展了一套气动弹性计算方法,并将该方法在一个高空长航时机翼的气弹计算上进行了验证。Palacios等[13]对于不同气动及结构计算模型组合成的气弹耦合计算方法在低速大展弦比弹性机翼的飞行模拟中的表现进行了评估。他们的研究结果表明片条模型在机翼做小幅运动时表现还可以,而对于机翼大幅运动的情况则需要通过涡格法进行模拟。Murua等人[14]综合利用涡格法、结构动力学和飞行动力学方法对大展弦比飞行器的尾迹与尾翼干扰问题进行了研究。
虽然涡格法相对CFD方法是更高效的计算方法,但要准确离散物面上的环量分布往往仍然需要几百或几千个自由度,而对于需要进行耦合迭代(气弹计算)或优化迭代(优化设计)的问题其计算量也是很大的。而通过模型降阶可以进一步提高涡格法的计算效率,从而满足各种问题的需要。近年来,本征正交分解(Proper Orthogonal Decomposition, POD)方法被人们广泛应用于降阶模型的构建。Romanowski[15]建立了一个针对二维翼型的降阶气弹计算模型。他应用降阶模型对Euler解算器求解的二维翼型非线性平衡态附近的线性动力学行为进行了模拟。Kim[16]发展出了一套针对线性动力系统的频域POD方法,并将他的方法分别应用于带阻尼的弹簧振子系统和不可压缩流动的非定常涡格法的降阶。Hall等[17]应用POD技术对二维非定常小扰动流动模型建立了降阶模型。他们应用该方法分别对单一的翼型和叶栅阵列进行了跨音速的气动和气弹计算。Pettit和Beran[18]应用基于POD方法的降阶Euler解算器对马赫数1.2下的一个振荡突起周围的流场进行了计算。他们发现基于POD技术的降阶模型可以在保有较高解算精度的同时大大降低计算自由度,同时降阶模型也增大了容许计算时间步长并提高了计算模型对不同工况计算的鲁棒性。
最近,Cao[19]提出了一种基于POD技术的降阶非定常涡格法。该方法已经在俯仰和拍动运动的刚性机翼的非定常气动计算上得到了验证。在运动刚体的计算中,非定常涡格法中的影响系数矩阵并不随时间改变,因此在整个计算过程中只需要进行一次系统降阶。因此,降阶带来的计算加速效果在运动刚体的气动计算中体现得并不明显,于是有必要在变形体的气动计算中对方法进行进一步的验证。本文利用降阶非定常涡格法耦合梁模型构建了一个高效的气弹计算模型。模型中通过引入伪时间步迭代实现了气动和结构计算的紧耦合。之后,通过针对一个具有展向弹性的振荡薄翼模型的气弹计算对该降阶计算模型进行了验证。
1 理论与方法 1.1 气动与结构建模在本研究中,选用了非定常单层涡格法对作用于薄翼(零厚度)的瞬时气动载荷进行计算。在涡格法中,物面被涡环构成的薄层所取代,而每一个涡环的环量则通过壁面无穿透条件所构成的方程进行求解,如下所示:
| $ A{\mathit{\Gamma}} = R $ | (1) |
这里A表示影响系数矩阵,可由Biot-Savart旋涡诱导定律求出,Γ表示由壁面涡环环量组成的待求解向量,而R则表示由自由来流的法向分量、尾迹涡环诱导速度、刚体运动速度和壁面变形速度所组成的右端和向量。在每个时间步上,假设壁面涡环以不变的环量由薄翼尾缘向下游尾迹中脱落。在本研究中,为了加速气弹耦合计算,忽略了尾迹面的自诱导卷起及尾迹中的环量耗散。在每个时间步上,环量未知向量Γ可由式(1)解出,之后通过如下的非定常Bernoulli方程可计算出相应的瞬时气动载荷:
| $ \begin{array}{l} \Delta {F_{n, ij}} = \rho \{ {[U\left( t \right) + {u_W}]_{ij}}\frac{{{{\mathit{\Gamma}} _{i, j}} - {{\mathit{\Gamma}} _{i - 1, j}}}}{{\Delta c}} + \\ \;\;\;\;\;\;{\left[{V\left( t \right) + {v_W}} \right]_{ij}}\frac{{{{\mathit{\Gamma}} _{i, j}} -{{\mathit{\Gamma}} _{i, j -1}}}}{{\Delta b}} + \frac{\partial }{{\partial t}}{{\mathit{\Gamma}} _{i, j}}\} \Delta b\Delta c \end{array} $ | (2) |
这里ΔFn, ij是作用在每个涡格上的气动载荷的法向分量;U、V是自由来流和刚体运动的和速度在两个方向上的分量;uW、vW是由尾迹面诱导的速度分量;Δb和Δc分别是单个涡格的展向和弦向尺寸。
在当前的研究中,假设薄翼只具有展向弹性并可由悬臂梁模型进行模化。在悬臂梁模型中应用Euler-Bernoulli假设,则结构动力学方程可以写为:
| $ EIw'''' + \mu \ddot w = p\left( {x, t} \right) $ | (3) |
这里w表示薄翼的横向变形量,撇号和头上的点分别表示空间和时间导数。p(x, t)表示作用于薄翼的瞬时分布载荷,该载荷由式(2)算出的气动载荷和由薄翼运动引起的惯性载荷两部分组成。E、I和μ分别是薄翼的杨氏模量,截面面积矩和单位长度的质量。应用模态展开,横向变形量w(x, t)可表示成以下形式:
| $ w\left( {x, t} \right) = \sum\limits_{i = 1}^\infty {{w_i}\left( x \right){\eta _i}\left( t \right)} $ | (4) |
这里wi(x)表示薄翼的第i阶模态,而ηi(t)是对应的模态广义坐标。在这项研究里,结构计算中包含了梁的前四个模态。将模态展开式(4)带入式(3),薄翼的结构运动方程的广义坐标形式可写为:
| $ \frac{{{{\rm{d}}^2}{\eta _i}\left( t \right)}}{{{\rm{d}}{t^2}}} + \omega _i^2{\eta _i}\left( t \right) = {p_i}\left( t \right) $ | (5) |
其中,
| $ \frac{{{\rm{d}}Q}}{{{\rm{d}}t}} =-BQ + P $ | (6) |
这里
本文通过双时间步迭代技术实现了上述气动和结构计算的紧耦合。在每个物理时间步上,我们引入了伪时间步并相应地在气动和结构控制方程(式(1)和式(6))中都加入了伪时间导数项:
| $ \frac{{\partial {\mathit{\Gamma}} }}{{\partial \tau }} = A{\mathit{\Gamma}}-R $ | (7) |
| $ \frac{{\partial Q}}{{\partial \tau }} + \frac{{{\rm{d}}Q}}{{{\rm{d}}t}} =-BQ + P $ | (8) |
这里用τ表示伪时间。当τ不断增加,逐渐趋近于0,而式(7)和式(8)也就收敛到式(1)和式(6)。在计算中,分别应用一阶和二阶隐式格式对伪时间步和物理时间步进行推进。于是,离散化的气动和结构方程可分别写为:
| $ \frac{{{{\mathit{\Gamma}} ^{m + 1}}-{{\mathit{\Gamma}} ^m}}}{{\Delta \tau }} = {A^m}{{\mathit{\Gamma}} ^{m + 1}}-{R^m} $ | (9) |
| $ \begin{array}{*{20}{l}} {\frac{{{Q^{m + 1}}-{Q^m}}}{{\Delta \tau }} + \frac{{3{Q^{m + 1}}-4{Q^n} + {Q^{n-1}}}}{{2\Delta t}} = }\\ {\;\; - B{Q^{m + 1}} + {P^m}} \end{array} $ | (10) |
这里Δt和Δτ分别是物理时间步和伪时间步,n和m分别表示物理时间层数和伪时间层数。
1.3 基于POD技术的模型降阶在气动弹性计算中,需要在每个伪时间迭代步上对式(9)和式(10)进行求解。如方程(9)所示,离散化的气动方程是一个N自由度的线性问题(这里N表示涡格法中涡格的数量,对于不同问题N可以是几百或几千)。根据Cao[19]之前的研究,式(9)中的未知向量Γ可以通过它的前几阶POD基向量线性叠加而很好的近似出来,如下所示:
| $ {\mathit{\Gamma}} = \sum\limits_{i = 1}^{{N_m}} {{v_i}{\phi _i}} $ | (11) |
这里ϕi是POD分析中获得的第i阶基向量,而vi是对应的广义坐标,Nm是叠加近似中所包含的POD特征模态数。应用这种POD模态叠加,离散化的气动方程式(9)可变为:
| $ {{\mathit{\Phi}} ^H}(\frac{1}{{\Delta \tau }}I-{A^m}){\mathit{\Phi}} {v^{m + 1}} = {{\mathit{\Phi}} ^H}(\frac{1}{{\Delta \tau }}{{\mathit{\Gamma}} ^m}-{R^m}) $ | (12) |
这里I表示单位矩阵,Φ表示由POD特征基向量ϕi组成的特征矩阵,而v则是由对应的特征广义坐标vi组成的向量。于是,通过这种对向量Γ的近似,气动方程的求解自由度从原来的N降到了Nm。通常来说,Nm是一个远小于N的数。例如,Cao[19]在之前的研究中显示,Nm=3时已经能够很好的近似(误差小于1%)做俯仰或拍动运动的薄翼的全气动模型了,即使在很高(k=1.2)的振荡减缩频率下。因此,这种模态分解过程可以显著的降低问题的求解自由度并加速计算。
在本文中的气弹计算中,弹性结构是一个长细的薄翼并且可以通过Euler-Bernoulli梁的前4个模态叠加进行很好的模化,因此离散结构方程式(10)的计算自由度仅为8,于是也就无需对结构方程进行降阶操作了。否则,如果我们面对的是一个复杂结构的气弹计算问题,而结构被气动载荷所激励起的特征模态数量又很多,我们当然也可以遵循类似的步骤来降低结构方程的计算自由度。
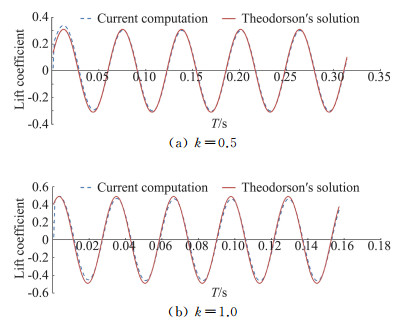
2 结果和讨论 2.1 二维刚性薄翼上的验证测试本文在进行正式的气动弹性计算之前,先在做俯仰振荡的刚性薄翼上进行了气动计算验证并与理论的Theodorsen解进行了比较。在验证测试中,为了满足薄翼二维刚性的条件,我们将计算模型中薄翼的展弦比和杨氏模量均设为了极大值。而由于在测试中对薄翼做了二维假设,因此翼面上环量分布在展向上应该是均匀的,于是在测试计算中在展向只布置了2个涡格,而在弦向为了保证一定的分辨率则布置了30个涡格。在计算中,设置薄翼的俯仰角做振幅为5°的正弦振荡,同时分别在减缩频率k=0.5和k=1.0下进行非定常升力系数计算,这里减缩频率k定义为
|
图 1 正弦俯仰振荡薄翼上的非定常升力系数比较 Figure 1 Lift coefficient calculated from unsteady vortex lattice method for harmonically pitching foil under reduced frequencies |
在气弹计算中,矩形薄翼的几何尺寸为弦长0.1 m,展长0.6 m,厚度0.001 m,薄翼的密度为1000 kg/m3,空气密度为1 kg/m3。所有气弹计算中涡格分布均设置为30(弦向)×30(展向)。计算中,在薄翼的展向中心线位置施加了一个竖向的强迫正弦振荡(幅度为0.5倍弦长),而薄翼的其它部分则根据给定的展向刚度做自由变形,如图 2所示。

|
图 2 计算获得的薄翼变形及尾涡面的示意图 Figure 2 Deformed foil and wake surface obtained from current computation |
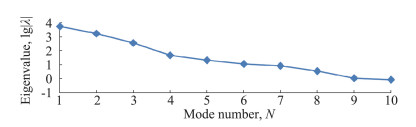
为了收集POD分析所需的样本,分别在3个不同减缩频率(k=0.2, 0.6, 1.0)和4个不同的杨氏模量E(5×109 Pa, 1×1010 Pa, 5×1010 Pa, 1×1011 Pa)下进行了计算。因此,一共在12个不同工况下进行了样本计算,并且在每次计算的第5个周期内选取了10个不同的特征时刻将对应的涡量分布作为样本提取了出来,于是样本总数为120个。经过POD分析获得的前10个特征模态如图 3所示,随着模态阶数的增大特征值下降得非常快。为了进一步评估前i阶模态对整个POD展开的贡献,计算了累积模态能量
|
图 3 前10个POD模态的特征值分布 Figure 3 Eigenvalue distribution for first 10 POD modes |

|
图 4 前10阶POD模态的累积模态能量 Figure 4 Cumulative energy of first 10 POD modes |
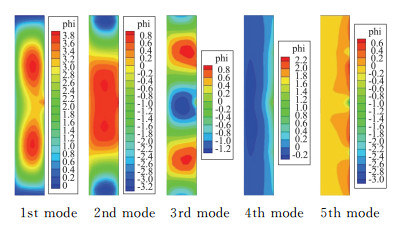
|
图 5 POD分析中获得的特征模态 Figure 5 Eigenmodes obtained from POD analysis |
在从计算样本中提取出POD模态之后,获得了一个如式(12)所示的涡格法降阶模型(reduced order model, ROM)。为了验证降阶气弹模型的计算精度,在一个不同于所有样本计算工况的条件(k=0.8, E=3×1010 Pa)下进行了降阶计算,结果如图 6所示。

|
图 6 在k=0.8, E=3×1010 Pa工况条件下的ROM计算结果和全模型计算结果比较 Figure 6 Comparison between ROM results and full-model results for the case k=0.8, E=3×1010 Pa |
在计算中,分别采用了包含不同POD模态数量的降阶模型,并分别将计算结果与全模型进行了对比。如图 6所示,只包含3个模态的降阶模型与全模型有一定的误差,包含5个模态的降阶模型结果则要准确得多,而包含7个或9个模态的降阶模型的计算结果就与全模型的结果几乎重合了。第一个测试算例的参数完全在样本参数的范围之内,即:k=0.8,在0.2~1.0范围内;E=3×1010 Pa,在5×109~1×1011 Pa范围内。为了进一步验证降阶模型的适用范围,又进行了第二个算例验证,并且将这个算例的参数设置在样本参数范围之外,结果如图 7所示。

|
图 7 在k=1.2, E=5×1011 Pa工况条件下的ROM计算结果和全模型计算结果比较 Figure 7 Comparison between ROM results and full-model results for the case k=1.2, E=5×1011 Pa |
从图 7中可以看出,在第二个验证算例中,全模型和降阶模型之间的比较结果并不比第一个算例差,只包含3个POD模态的降阶模型对全模型的近似已经比较准确了。为了进一步定量的评估降阶模型的误差,在两个算例中计算了相对百分比误差。误差定义为
| 表 1 包含不同特征模态数的降阶模型的计算百分比误差 Table 1 Percentage RMS errors for ROMs with different numbers of modes |
|
|
从表 1中可以看出,在所包含模态数从3个增加到7个的过程中,降阶模型的定量化误差迅速下降,而如果再包含更多的特征模态则降阶模型的误差下降速度就明显减慢了。对于两个不同测试算例,当降阶模型中包含7个以上模态时,降阶模型与全模型之间的误差均低于2%。因此,对于目前问题的气弹计算来说,包含7个特征模态的降阶模型是一个不错的选择。另外,十分重要的是,对于当前的计算来说包含9个特征模态的降阶模型所消耗的计算CPU时间仅仅为全模型计算所需要时间的1/10。由此可以看出,应用本文所提出的降阶计算策略,可以在损失很小计算精度的同时大大提高计算速度。
3 结论在本文中,通过应用降阶的非定常涡格法,建立了一种高效的气动弹性计算模型。模型中通过伪时间迭代方法实现了气动和结构计算的紧耦合。为了降低整个气弹计算模型的计算自由度,将未知环量向量近似展开成前几阶POD基向量的叠加形式。通过一个竖向振荡的弹性薄翼的气弹计算算例对该降阶计算模型进行了验证。计算结果显示仅仅包含前9个POD特征模态的降阶气弹模型就已经能够很准确的近似全模型计算了。另外,在验证计算中,通过降阶计算方法实现了90%的计算CPU时间节省。
本文中的方法与针对CFD方法的POD降阶模型类似,都是针对计算方法中最终形成的线性求解系统进行特征分析,再应用特征基向量对系统进行降阶近似。CFD方法不只可以对模型气动力进行计算,还同时可以解算模型周围的流场,其包含的信息量是远大于本文中应用的非定常涡格法的。但也由于其包含的信息量太大,因此要对其最终形成的线性系统进行有效的降阶重构,就需要很多阶的POD基向量。并且在构建POD基向量时,要解析系统中包含的大量信息,就需要在所关心的参数范围内保证一定的样本采集密度。而相比之下,由于涡格法所做的仅仅是对满足约束条件的壁面涡量分布的求解,因此其构成的线性求解系统中有效的信息量就小得多了,或者说只应用很少的正交特征基就可以对全系统进行较准确的重构,从本文的结果中也可以看出这点。由此看来,本文提出的方法更适合针对大量消耗计算时间的复杂耦合问题计算或优化设计计算,尤其对于需要在很大参数范围内进行大量计算的工程问题。
| [1] |
Patil M J, Hodges D H, Cesnik S, et al. Nonlinear aeroelasticity and flight dynamics of high-altitude long-endurance aircraft[J]. Journal of Aircraft, 2001, 38(1): 88-94. DOI:10.2514/2.2738 |
| [2] |
Pomin H, Wagner S. Aeroelastic analysis of helicopter rotor blades on deformable chimera grids[J]. Journal of Aircraft, 2004, 41(3): 577-584. DOI:10.2514/1.11484 |
| [3] |
Hansen M O L, Sørensen J N, Voutsinas S, et al. State of the art in wind turbine aerodynamics and aeroelasticity[J]. Progress in Aerospace Sciences, 2006, 42(4): 285-330. DOI:10.1016/j.paerosci.2006.10.002 |
| [4] |
Alonso J J, Jameson A. Fully-implicit time-marching aeroelastic solutions. AIAA-94-0056[R]. Reston: AIAA, 1994.
|
| [5] |
Bennett R M, Edwards J W. An overview of recent developments in computational aeroelasticity. AIAA-98-2421[R]. Reston: AIAA, 1998.
|
| [6] |
Kamakoti R, Shyy W. Fluid-structure interaction for aeroelastic applications[J]. Progress in Aerospace Sciences, 2004, 40(8): 535-558. DOI:10.1016/j.paerosci.2005.01.001 |
| [7] |
Farhat C, Van der Zee K G, Geuzaine P. Provably second-order time-accurate loosely-coupled solution algorithms for transient nonlinear computational aeroelasticity[J]. Computer Methods in Applied Mechanics and Engineering, 2006, 195(17): 1973-2001. |
| [8] |
Rusak Z, Wasserstrom E, Seginer A. Numerical calculation of nonlinear aerodynamics of wing-body configurations[J]. AIAA Journal, 1983, 21(7): 929-936. DOI:10.2514/3.8179 |
| [9] |
Konstadinopoulos P, Thrasher D F, Mook D T, et al. A vortex-lattice method for general, unsteady aerodynamics[J]. Journal of Aircraft, 1985, 22(1): 43-49. DOI:10.2514/3.45078 |
| [10] |
Long L N, Fritz T E. Object-oriented unsteady vortex lattice method for flapping flight[J]. Journal of Aircraft, 2004, 41(6): 1275-1290. DOI:10.2514/1.7357 |
| [11] |
Stanford B K, Beran P S. Analytical sensitivity analysis of an unsteady vortex-lattice method for flapping-wing optimization[J]. Journal of Aircraft, 2010, 47(2): 647-662. DOI:10.2514/1.46259 |
| [12] |
Wang Z, Chen P C, Liu D D, et al. Nonlinear-aerodynamics/nonlinear-structure interaction methodology for a high-altitude long-endurance wing[J]. Journal of Aircraft, 2010, 47(2): 556-566. DOI:10.2514/1.45694 |
| [13] |
Palacios R, Murua J, Cook R. Structural and aerodynamic models in nonlinear flight dynamics of very flexible aircraft[J]. AIAA Journal, 2010, 48(11): 2648-2659. DOI:10.2514/1.J050513 |
| [14] |
Murua J, Palacios R, Graham J M R. Assessment of wake-tail interference effects on the dynamics of flexible aircraft[J]. AIAA Journal, 2012, 50(7): 1575-1585. DOI:10.2514/1.J051543 |
| [15] |
Romanowski M. Reduced order unsteady aerodynamic and aeroelastic models using Karhunen-Loeve eigenmodes[C]//Proceedings 6th NASA/ISSMO Symposium on Multi-disciplinary Analysis and Optimization, 1996, AIAA-1996-3981: 96-194.
|
| [16] |
Kim T. Frequency-domain Karhunen-Loeve method and its application to linear dynamic systems[J]. AIAA Journal, 1998, 36(11): 2117-2123. DOI:10.2514/2.315 |
| [17] |
Hall K C, Thomas J P, Dowell E H. Proper orthogonal decomposition technique for transonic unsteady aerodynamic flows[J]. AIAA Journal, 2000, 38(10): 1853-1862. DOI:10.2514/2.867 |
| [18] |
Pettit C L, Beran P S. Application of proper orthogonal decomposition to the discrete Euler equations[J]. International Journal for Numerical Methods in Engineering, 2002, 55(4): 479-497. DOI:10.1002/(ISSN)1097-0207 |
| [19] |
Cao B. Development of reduced unsteady vortex lattice method using proper orthogonal decomposition technique[J]. AIAA Journal, 2015, 54(1): 366-370. |
| [20] |
Fung Y C. An introduction to the theory of aeroelasticity[M]. Courier Corporation, 2002.
|
 2018, Vol. 36
2018, Vol. 36


