工程热物理领域认为低温燃烧技术可有效解决NOX排放问题,理论上实现这一技术的关键是控制中间链式反应,为此国内外学者采用质谱仪等先进测试手段对燃烧过程进行细致研究,发现碳氢燃料的化学反应机理非常复杂,例如生物柴油包含1034组元4236反应[1]。在进行飞行器常规外流场模拟时如果不考虑湍流模型方程,基于量热完全气体假设的流动控制方程组由5个偏微分方程构成,如果对上述生物柴油的化学非平衡流动进行模拟需要增加1033个组元方程,为解决化学非平衡流的刚性问题常采用涉及到矩阵求逆的隐式算法,国外文献比较了计算量与求解变量后得出的结论是呈3次方关系[2-3],由此推算求解变量和方程数目增加到1038个所引起的计算量增加接近107倍,有理由认为采用精细化学动力学模型开展三维化学非平衡流模拟是比湍流DNS模拟具有更大的挑战。
目前解决这一难题的主要途径是在原始测量数据基础上建立简化反应机理。国家科技部2017年度“高性能计算”重点专项指南中关于“发动机数值装置原型系统—数值发动机”的指标是“构建基于国产航空燃料化学反应简化机理的燃烧模型,简化机理物种数在35个左右,模拟点火延迟预测误差不大于30%,燃烧模型能够比较准确模拟流动与化学反应相互作用”。已有的研究表明采用不同简化准则得到的模型存在着一定的迥异,其明显特征表现为预测点火延迟特性有较大差异[1]。以反应机理相对简单的H2和Air燃烧为例,通过对国内外文献调研发现,采用忽略中间链式反应的3组元2反应的单向总包反应模型[4],即使采取网格加密、时间小步长等措施提高计算精度,也无法模拟出与试验相符合的点火延迟、周期性振荡燃烧等物理现象,得到点火延迟大致结构需要采用7组元8反应[5]机理,模拟出周期性振荡燃烧需要9组元19反应[2]或13组元33反应[6-7]机理。由此看来,采用35个左右组元的简化机理实现误差不大于30%的点火延迟特性预测确实是很高的指标要求。反应简化机理缺乏普适性,如果燃料的产地和生产商改变需要重新研究。如果能够提高化学非平衡流问题的计算效率,从而可以考虑更为复杂的化学反应机理,以此来解决研制数值发动机遇到的预测精度和计算量的难题,也是一个很好的技术途径。本文主要介绍化学非平衡流问题计算方法的研究进展。
1 化学非平衡流解耦算法理论基础20世纪60年代,计算流体力学主要以显式计算格式为主,为了解决化学反应源项引起的刚性问题,采用解耦算法在空间点上把控制方程组分解为流动和化学反应两部分,为满足反应算子的计算稳定性条件需要迭代上千步才能匹配流动算子时间迭代一步,由于其计算效率偏低,难以满足工程需要。20世纪70年代,在解决航天器再入过程中遇到的热障问题推动下,化学非平衡流计算方法取得较大进展,构造出反应源项线性化的隐式算法,包括流动算子也采用隐式方法计算的全隐算法和流动算子采用显式方法计算的点隐算法。模拟点火延迟特性对不同算法存在较高的时间精度要求,全隐算法只能结合双时间步法来模拟非定常流动,由此增加的计算量难以接受。通过下面的分析可以看出点隐算法实现时间二阶精度也较为困难。
对于波动模型方程:
| $ \frac{{\partial u}}{{\partial t}} + a\frac{{\partial u}}{{\partial x}} = 0 $ | (1) |
采用显式差分格式离散,时间二阶精度的Taylor展开式:
| $ {u^{n + 1}} = {u^n} + \Delta t{\left( {\frac{{\partial u}}{{\partial t}}} \right)^n} + \frac{{\Delta {t^2}}}{2}{\left( {\frac{{{\partial ^2}u}}{{\partial {t^2}}}} \right)^n} + O\left( {\Delta {t^3}} \right) $ | (2) |
利用方程(1)把二阶时间导数转化为空间导数:
| $ \frac{{{\partial ^2}u}}{{\partial {t^2}}} = {a^2}\frac{{{\partial ^2}u}}{{\partial {x^2}}} $ | (3) |
假设空间一阶导数对应离散算子记为LxI,空间二阶导数对应算子记为LxII,得到时间二阶精度通用形式:
| $ u_i^{n + 1} = \left( {1 - \Delta taL_x^I + 0.5\Delta {t^2}{a^2}L_x^{II}} \right)u_i^n + O\left( {\Delta {t^3}} \right) $ | (4) |
化学非平衡流模型增加了源项:
| $ \frac{{\partial u}}{{\partial t}} + a\frac{{\partial u}}{{\partial x}} = f\left( u \right) $ | (5) |
点隐算法把源项在空间点线化:
| $ \begin{array}{l} f\left( u \right) = {f^n} + \Delta t\left( {\frac{{\partial f}}{{\partial u}}\frac{{\partial u}}{{\partial t}}} \right)\left| {_i^n} \right. + O\left( {\Delta {t^2}} \right)\\ \;\;\;\;\;\;\;\; = {f^n} + d_i^n\left( {u_i^{n + 1} - u_i^n} \right) + O\left( {\Delta {t^2}} \right) \end{array} $ | (6) |
源项进行线化处理以后具有时间二阶精度,将方程(6)带入到方程(4)得到点隐算法的计算格式:
| $ \begin{array}{l} \left( {1 + 0.5\Delta td_i^n} \right)u_i^{n + 1} = \\ \left( {1 - \Delta taL_x^I + 0.5\Delta {t^2}{a^2}L_x^{II} - 0.5\Delta td_i^n} \right)u_i^n\\ + \Delta t{f^n} + O\left( {\Delta {t^3}} \right) \end{array} $ | (7) |
按照截断误差分析,似乎达到时间二阶精度,但是考虑到上式中LxII是波动方程(3)进行时空变换,对于化学非平衡流模型,二阶时间导数化为空间导数准确表达式为:
| $ \frac{{{\partial ^2}u}}{{\partial {t^2}}} = {a^2}\frac{{{\partial ^2}u}}{{\partial {x^2}}} - a\frac{{\partial f}}{{\partial x}} + \frac{{\partial f}}{{\partial t}} $ | (8) |
因此,计算格式(7)达不到时间二阶精度,还没有看到按照方程(8)构造高阶格式需要处理上式中源项f(u)的时间和空间导数的算法。
采用解耦算法计算方程(5)本质是分步求解如下波动方程和常微分方程组:
| $ \left\{ \begin{array}{l} \frac{{\partial u}}{{\partial t}} + a\frac{{\partial u}}{{\partial x}} = 0\\ \frac{{\partial u}}{{\partial t}} = f \end{array} \right. $ | (9) |
常微分方程有多种成熟计算方法,采用算子形式表示为:
| $ {u^{n + 1}} = \left[ {1 + {L_f}\left( {\Delta t} \right)} \right]{u^n} $ | (10) |
不管算子Lf具体形式,时间二阶精度离散基础依然为:
| $ {L_f}\left( {\Delta t} \right) \cdot {u^n} = \Delta t \cdot {f^n} + \frac{{\Delta {t^2}}}{2}{\left( {\frac{{\partial f}}{{\partial t}}} \right)^n} + O\left( {\Delta {t^3}} \right) $ | (11) |
波动方程的时间二阶精度离散算子如前,总算子按照如下Strang形式:
| $ \begin{array}{l} u_i^{n + 1} = \left[ {1 + {L_f}\left( {\frac{{\Delta t}}{2}} \right)} \right] \cdot \left( {1 - \Delta taL_x^I + 0.5\Delta {t^2}{a^2}L_x^{II}} \right) \cdot \\ \;\;\;\;\;\;\;\;\;\left[ {1 + {L_f}\left( {\frac{{\Delta t}}{2}} \right)} \right]u_i^n + O\left( {\Delta {t^3}} \right) \end{array} $ | (12) |
上式展开以后会得到方程组(9)的时间和空间导数,可以证明对于线形算子具有时间二阶精度。因此,解耦算法易于构造时间二阶格式。
对编码为k的控制体,采用格心格式计算平均值为
包含有n个组元的化学非平衡流守恒型Euler方程组:
| $ \frac{{\partial U}}{{\partial t}} + \frac{{\partial F}}{{\partial x}} + \frac{{\partial G}}{{\partial y}} + \frac{{\partial H}}{{\partial z}} = S $ | (13) |
式中守恒变量和源项表达式:
| $ U = {\left( {\rho ,\rho u,\rho v,\rho w,E,{\rho _1}, \cdots ,{\rho _{n - 1}}} \right)^{\rm{T}}} $ | (14) |
| $ S = {\left( {0, \cdots ,0,{\sigma _1}, \cdots ,{\sigma _{n - 1}}} \right)^{\rm{T}}} $ | (15) |
其中,ρi和σi为第i个组元的密度和质量生产率,反应过程保持质量守恒,有
| $ E = 0.5\rho \left( {{u^2} + {v^2} + {w^2}} \right) + \rho \sum\limits_{i = 1}^n {{c_i}\left[ {{h_i}\left( T \right) + h_i^0} \right] - p} $ | (16) |
本文第一作者在构建新型解耦算法[10]时将热力学焓分为热焓和零点焓两部分,通过引入中间变量E′把气体微团总能量中与流场温度变化无关的零点焓hi0去掉:
| $ E' = E - \rho \sum\limits_{i = 1}^n {{c_i}h_i^0} $ | (17) |
然后用E′代替E对原始方程(13)进行改造,得到新的守恒变量和源项表达式为:
| $ {U^0} = {\left( {\rho ,\rho u,\rho v,\rho w,E',{\rho _1}, \cdots ,{\rho _{n - 1}}} \right)^{\rm{T}}} = \left( {{U^1},{U^2}} \right) $ | (18) |
| $ {S^0} = {\left( {0, \cdots , - \sum\limits_{i = 1}^n {h_i^0} \cdot {\sigma _i},{\sigma _1}, \cdots ,{\sigma _{n - 1}}} \right)^{\rm{T}}} = \left( {0, \cdots ,{S^ * }} \right) $ | (19) |
式中:U1=(ρ, ρu, ρv, ρw, E′)T,U2=(ρ1, …, ρn-1)T,
进一步引入符号γ′把E′整理成如下形式:
| $ E' = E - \rho \sum\limits_{i = 1}^n {{c_i}h_i^0} = 0.5\rho \left( {{u^2} + {v^2} + {w^2}} \right) + \frac{p}{{\gamma ' - 1}} $ | (20) |
| $ \gamma ' = \frac{p}{{\rho \sum\limits_{i = 1}^n {{c_i}{h_i}} - p}} + 1 $ | (21) |
从表达形式上看,E′与量热完全气体的总能量表达形式完全相同,称为等效能量;γ′与量热完全气体的比热比相同,称为等效比热比。这里E′和γ′不符合气体动力学中混合气体的能量和比热比定义,仅看作物理意义不明确的中间变量。通过引入等效能量和等效比热比把气体微团总能量中与流场温度变化无关的零点焓hi0提取出来构造成新的源项方程,解决了此前解耦算法存在的反应算子和流动算子时间推进步长不匹配问题,根据前面模型方程分析,证明这种计算方法具有时间二阶精度。除此之外,刘君提出的解耦算法还具有清晰的物理机理解释:求解源项方程的反应算子模拟了流体微团在当地绝热(Ea不变)、定容(ρ不变)的热力学系统内发生的化学反应过程,状态参数和组元变化耦合求解,求解流动方程的流动算子模拟组元质量分数ci保持不变的流体微团沿流线运动(冻结流),包括密度在内的状态参数随位置变化[11]。
新型解耦算法早期只能用于有限差分法,先后采用过VanLeer、HLLC、Roe、AUSM等格式进行对流项通量分裂,空间离散采用过NND2MWAF、ENO、五阶WENO等格式[12-14],时间离散包括二阶显式方法和隐式双时间法[15]。近期课题组结合解耦算法的特点和有限体积法的空间平均特性提出一种优化解耦算法,如图 1所示,流场从n时刻更新到n+1时刻,控制体k和相邻单元之间的质量交换通过求解流动算子Lf体现,流体微团在对流或者扩散作用下进出控制体过程中没有发生化学反应,组元质量分数ci保持不变,通过记录Δt时间步内进出边界的质量流量,以此计算出n+1时刻控制体中组元i的密度值。假设在Δt时间步内,流体微团从控制体单元k流出到单元3,从相邻单元1和2流入。由于U1和U2方程解耦,可以单独求解U1的方程,记录进出边界的质量流量,例如,单元1外法向速度un,流量为m1=(ρunSΔt)1,S边界面积,那么控制体k在n+1时刻i组元的密度为:
| $ \begin{array}{l} \rho _i^{n + 1} = \left( {\rho _i^n{V_k} + \sum\limits_{j = 1}^3 {{C_j}{m_j}} } \right)/{V_k}\\ \;\;\;\;\;\;\; = \rho _i^n + \frac{{{m_1} + {m_2} - {m_3}}}{{{V_k}}} \end{array} $ | (22) |

|
图 1 优化算法机理示意图 Figure 1 Schematic of optimization algorithm mechanism |
通过以上简化处理在求解过程中不需要计算U2的偏微分方程组就可以得到U2中组元的密度。即无论多少组元,流动算子只求解基本变量构成的、形式上与量热完全气体完全相似的5个方程组,目前优化算法主要完成无粘流动方程的验证,理论上通过记录相邻控制体单元边界面组元扩散引起的流量实现粘性流动计算模拟,下一步准备开展相关编程和验证工作。
本文作者在文献[11]中采用优化解耦算法对1972年Lehr[16]完成的H2/Air预混气体条件下激波诱导燃烧试验进行模拟,使用修正的Jachimowski(9组元19反应)反应机理[17],采用二维模型进行模拟,计算的工况包括马赫数M=6.46的超爆轰模态和M=4.48、4.79两种跨爆轰模态,比较计算得到的流场结构与试验数据符合很好,沿驻点流线的参数分布和文献基本一致。
3 反应算子的改进算法从方程(13)出发,描述化学反应的方程组可以表示为:
| $ \frac{{\partial {\rho _i}}}{{\partial t}} = {\sigma _i} $ | (23) |
| $ \frac{{\partial E'}}{{\partial t}} = - \sum\limits_{i = 1}^n {h_i^0} \cdot {\sigma _i} $ | (24) |
结合定容假设条件∂ρ/∂t=0可将方程(24)转化为:
| $ \frac{{\partial T}}{{\partial t}} = - \frac{{\sum\limits_{i = 1}^n {{\sigma _i}\left( {{h_i} + h_i^0 - {R_i}T} \right)} }}{{\sum\limits_{i = 1}^n {{\rho _i}\left[ {{C_{pi}}\left( T \right) - {R_i}} \right]} }} $ | (25) |
最早采用梯形公式对反应源项常微分方程组进行求解,应用中发现存在初场敏感性和收敛不稳定的缺陷,需要采取在稳定无反应流场基础再耦合反应算子Lr模块、反应剧烈需要小步长追赶等经验措施,后来改用VODE(常微分变系数方法)[18]和α-QSS(拟稳态逼近方法)[19]两种求解器解决了稳定性问题,但是计算效率明显降低。精细积分方法是由钟万勰院士[20-21]在1994年提出的,在常微分方程的求解上具有突出的优势:(1)具有极高的计算精度,(2)具有较好的计算鲁棒性。本文探索采用精细积分方法求解反应算子。
可以把方程(23)和(25)写成同一矩阵形式:
| $ \frac{{{\rm{d}}X}}{{{\rm{d}}t}} = H \cdot X $ | (26) |
其中X=(ρ1, …, ρn, T)T,H是系数矩阵,已知X(tk)时间推进一步tk+1=tk+Δt后:
| $ {X_{k + 1}} = \exp \left( {H\Delta t} \right) \cdot {X_k} $ | (27) |
为了提高Y=exp(HΔt)的计算精度,根据指数矩阵函数特性exp(HΔt)≡[exp(HΔt/m)]m,将Δt分成非常小的时间区段τ=Δt/m,其中m为任意正整数,可选用m=2N。由于下式的Ya与单位矩阵I相比非常小,容易被计算机舍入操作:
| $ \begin{array}{l} \exp \left( {H\tau } \right) \approx I + H\tau + {\left( {H\tau } \right)^2} \cdot \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\left[ {I + \frac{{\left( {H\tau } \right)}}{3} + \frac{{{{\left( {H\tau } \right)}^2}}}{{12}}} \right]/2\\ \;\;\;\;\;\;\;\;\;\;\;\;\;\; \approx I + {Y_a} \end{array} $ | (28) |
精细积分算法先将Y做分解:
| $ Y = {\left( {I + {Y_a}} \right)^{2N}} = {\left( {I + {Y_a}} \right)^{2N - 1}} \times {\left( {I + {Y_a}} \right)^{2N - 1}} = \cdots $ | (29) |
当N次循环结束后,再进行Y=I+Ya运算,这样可以保证计算精度。精细积分早期应用于结构动力学分析[22]中,由于其数值结果的高度精确,已经在优化控制[23]、偏微分方程的精细求解[24]、非线性动力系统刚性方程求解[25]等领域得到了广泛应用。
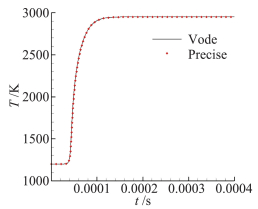
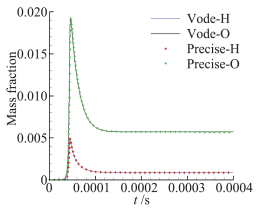
采用Jachimowski的9组元19反应机理,计算初始条件为压强P=101.325 kPa、温度T=1200 K的预混燃气爆轰过程。广泛使用的一种刚性常微分方程求解器是VODE,采用BDF(Backward Differentiation Formula)方法求解,具有高阶精度,常被用来验证其它方法的精度。采用统一时间步长Δt=1×10-8 s进行计算,两种方法得到的温度和组元质量分数随时间变化如图 2和图 3所示,几乎一致,说明采用精细积分方法求解化学动力学方程组具有较高的精度。
|
图 2 温度分布时程曲线 Figure 2 Time history curve of temperature distribution |
|
图 3 H原子和O原子质量分数时程曲线 Figure 3 Time history curves of mass fraction of H and O |
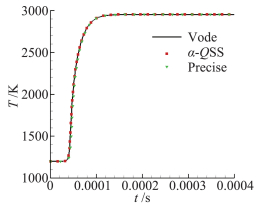
VODE是一种隐式方法,求解过程涉及到矩阵运算,在化学组元较多、矩阵维数较大时,会导致计算量较大,难以用于复杂反应机理的化学非平衡流动模拟[26-27]。α-QSS是一种拟稳态逼近方法,对于线形问题具有二阶精度,对于非线性问题因源项局部线性化处理精度达不到二阶,理论上通过基于精度自动选择时间步长可以保持计算过程稳定,但是在应用中发现在高压环境或者没有稀释气体的情况下,α-QSS对于部分燃烧问题的求解存在不稳定现象[28]。精细积分作为一种显示方法,计算精度高,稳定性好,在选取较大的时间步长时也可以得到较高的计算精度。为此,选取较大步长Δt=5×10-7 s,比较三种方法的计算效率和精度,CPU计算时间和相对误差如表 1所示,相对误差是指计算的稳定温度与参考值之间的误差,取VODE在时间步长Δt=1×10-9 s下计算的稳定温度作为参考值。与VODE和α-QSS两种方法相比,精细积分在大时间步长情况下计算用时最短。此外,由图 4可看出精细积分计算结果与前两种方法几乎一致,说明精细积分方法在大步长的情况下,具有较高的计算效率。
| 表 1 不同计算方法在相同步长条件下的结果对比 Table 1 Comparision of the results of different calculation methods under the condition of the same step size |
|
|
|
图 4 不同计算方法在Δt=5×10-7s下的温度分布时程曲线 Figure 4 Time history curve of temperature distribution with different calculation methods at Δt=5×10-7s |
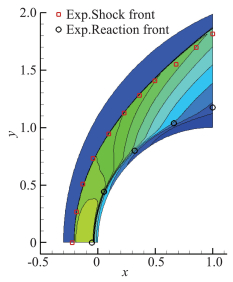
结合流动算子模拟Lehr试验,对于马赫数Ma=6.46的超爆轰模态和Ma=4.79跨爆轰模态,精细积分方法的计算结果与文献[11]中采用α-QSS的计算结果完全一致,在此不再展示。下面给出马赫数Ma=3.55亚爆轰模态的计算结果。弹丸以1892 m/s飞行速度进入H2/O2(2H2+O2)的预混气体,当地环境温度和压力分别为T=293K,p=24793Pa,相应的爆轰速度为2550m/s。采用250×200的四边形网格、Evan(7组元8反应)机理[29]模拟。密度云图中激波阵面和燃烧阵面位置与试验结果比较如图 5所示,过激波后形成的诱导区和燃烧阵面等结构符合较好,在二维情况下,控制方程组不包含w,因此图 6所示为求解4个偏微分方程的优化算法和求解10个偏微分方程的原算法得到的密度云图对比,从以上结果的对比中可以验证优化算法对于稳定爆轰的流场具有较好的空间分辨率。
|
图 5 计算结果与试验结果对比 Figure 5 Comparison between the simulation and experimental results |

|
图 6 亚爆轰密度云图比较 Figure 6 Comparison of density contour of the subdetonation case |
诱导区长度对应于激波波后的点火延迟时间。经过诱导区以后,驻点流线上的压力几乎保持恒定,而温度开始上升,密度下降。这种现象也可以清晰地从主要组元在驻点流线上的分布曲线中得到,如图 7所示,相应的计算结果在文献[30]也有所提及。从图中可以看出,在诱导区相对应的范围内,H2O组元质量分数保持为0,说明没有明显的H2O产生;经过燃烧阵面以后,H2O组元的质量分数逐渐增加伴随着O2和H2组元质量分数迅速降低,这种现象说明经过燃烧阵面以后急剧上升的温度促使化学反应更加剧烈,最终产生大量的H2O组元。

|
图 7 组元质量分数沿驻点流线分布 Figure 7 Distribution of mass fraction along the stagnation streamline |
采用精细积分方法与α-QSS方法的CPU计算时间对比如图 8所示。在相同迭代步数条件下,流动算子的CPU计算时间几乎保持一致;当N=20时精细积分方法所用的CPU计算时间最长,要高于α-QSS方法;随着N取值的逐渐降低,计算效率逐渐提高。表 2列出了反应算子在不同迭代步数条件下的CPU时间对比,当N=10时精细积分方法与α-QSS方法的CPU计算用时非常接近,当N=5时精细积分方法的计算用时只相当于α-QSS方法的79%左右,说明精细积分方法可以进一步提高计算效率,同时针对刚性问题的求解,由精细积分方法构造的反应算子求解器具有更好的稳定性。

|
图 8 计算步数与CPU时间对比曲线 Figure 8 Calculated step number and CPU time curve |
| 表 2 反应算子CPU时间对比 Table 2 Comparison of CPU time |
|
|
本文从求解化学非平衡流问题的难点入手,结合刘君解耦算法和有限体积法的平均特性,提出一种新型的优化算法,针对经典的激波诱导燃烧算例进行数值模拟,通过与不同文献和试验的结果相对比,验证了该优化算法的时空精度。同时,基于精细积分方法构造了一种刚性问题求解器,其模拟结果与传统的VODE方法和α-QSS方法的计算结果对比分析,适当的选取时间步长,可以充分发挥精细积分方法的计算优势。
| [1] |
Chang Y C. Investigation of skeletal chemical mechanisms for diesel and biodiesel surrogate fuel based on decoupling methodology[D]. Dalian University of Technology, 2016. (in Chinese) 常亚超. 基于解耦法的柴油和生物柴油表征燃料骨架反应机理研究[D]. 大连理工大学, 2016. http://cdmd.cnki.com.cn/Article/CDMD-10141-1016203674.htm (  0) 0) |
| [2] |
Choi J Y, Jeung I S, Yoon Y, et al. Computational fluid dynamics algorithms for unsteady shock-induced combustion, part 1:validation[J]. AIAA Journal, 2000, 38(7): 1179-1187. DOI:10.2514/2.1112 (  0) 0) |
| [3] |
Choi J Y, Jeung I S, Yoon Y. Computational fluid dynamics algorithms for unsteady shock-induced combustion, part 2:comparison[J]. AIAA Journal, 2000, 38(7): 1188-1195. DOI:10.2514/2.1087 (  0) 0) |
| [4] |
Liang J H, Wang C Y. 3D numerical simulation of supersonic reaction flows in scramjet combustor[J]. Journal of Propulsion Technology, 1997(4): 1-4. (in Chinese) 梁剑寒, 王承尧. 超燃冲压发动机燃烧室三维化学反应流场的数值模拟[J]. 推进技术, 1997(4): 1-4. DOI:10.3321/j.issn:1001-4055.1997.04.001 (  0) 0) |
| [5] |
Evans J S, Schexnayder C J. Influence of chemical kinetics and unmixedness on burning in supersonic hydrogen flames[J]. AIAA Journal, 1980, 18(2): 188-193. DOI:10.2514/3.50747 (  0) 0) |
| [6] |
Wilson G J, Sussman M A. Computation of unsteady shock-induced combustion using logarithmic species conservation equations[J]. AIAA Journal, 1993, 31(2): 294-301. DOI:10.2514/3.11667 (  0) 0) |
| [7] |
Liu J. Numerical study on chemical mechanism in supersonic H2/air mixture gas flow[J]. Journal of Propulsion Technology, 2003, 24(1): 67-70. (in Chinese) 刘君. 化学动力学模型对H2/air超燃模拟的影响[J]. 推进技术, 2003, 24(1): 67-70. DOI:10.3321/j.issn:1001-4055.2003.01.018 (  0) 0) |
| [8] |
Liu Y, Liu J, Bai X Z. Numerical simulation of shock-induced combustion with a new uncoupled algorithm in unstructured finite volume method[J]. Journal of National University of Defense Technology, 2011, 33(6): 139-144. (in Chinese) 刘瑜, 刘君, 白晓征. 基于新型非结构有限体积解耦算法的激波诱导燃烧数值模拟[J]. 国防科技大学学报, 2011, 33(6): 139-144. DOI:10.3969/j.issn.1001-2486.2011.06.025 (  0) 0) |
| [9] |
Liu Y, Liu J, Tang L Y, et al. A novel uncoupled algorithm for solving chemical nonequilibrium flows[J]. Chinese Journal of Theoretical and Applied Mechanics, 2015, 47(1): 82-94. (in Chinese) 刘瑜, 刘君, 唐玲艳, 等. 一种求解化学非平衡流动的新型解耦算法[J]. 力学学报, 2015, 47(1): 82-94. DOI:10.7638/kqdlxxb-2013.0002 (  0) 0) |
| [10] |
Liu J. Numerical simulation of complex freejet flowfields for supersonic perfect gas and non-equilibrium gas of H2/O2 combustion[D]. China Aerodynamics Research and Development Center, 1993. (in Chinese) 刘君. 超音速完全气体和H2/O2燃烧非平衡气体的复杂喷流流场数值模拟[D]. 中国空气动力研究与发展中心, 1993. (  0) 0) |
| [11] |
Dong H B, Zhang F, Xu C G, et al. An improved unvoupled finite volume solver for simulation unsteaely shock-induced combustion[J]. Computers and Fluids, 2018, 167: 146-157. DOI:10.1016/j.compfluid.2018.03.001 (  0) 0) |
| [12] |
Liu J, Zhou S B, Xu C G. The numerical simulation method of supersonic flow and its application[M]. National University of Defense Technology Press, 2008. (in Chinese) 刘君, 周松柏, 徐春光. 超声速流动中燃烧现象的数值模拟方法及应用[M]. 国防科学技术大学出版社, 2008. (  0) 0) |
| [13] |
Zhou S B, Liu J, Gou Z, et al. Numerical simulation for shock induced interfacial instabilities of heterogeneous gases[J]. Journal of National University of Defense Technology, 2009, 31(1): 1-4. (in Chinese) 周松柏, 刘君, 郭正, 等. 激波诱导异质气体界面失稳的数值模拟[J]. 国防科技大学学报, 2009, 31(1): 1-4. DOI:10.3969/j.issn.1001-2486.2009.01.001 (  0) 0) |
| [14] |
Liu Y. Numerical research of ALE finite volume method for calorically perfect gas/chemical nonequilibrium gas flow[D]. National University of Defense Technology, 2014. (in Chinese) 刘瑜. 量热完全气体/化学非平衡气体流动ALE有限体积计算方法研究[D]. 国防科学技术大学, 2014. http://www.wanfangdata.com.cn/details/detail.do?_type=degree&id=D675553 (  0) 0) |
| [15] |
Wang H B, Sun M B, Liang J H, et al. An uncoupled method with dual time-step for chemical nonequilibrium flows[J]. Chinese Journal of Computational Physics, 2010, 27(5): 685-691. (in Chinese) 汪洪波, 孙明波, 梁剑寒, 等. 含双时间步法的化学非平衡流解耦算法[J]. 计算物理, 2010, 27(5): 685-691. DOI:10.3969/j.issn.1001-246X.2010.05.008 (  0) 0) |
| [16] |
Lehr H F. Experiments on shock-induced combustion[J]. Astronautica Acta, 1972, 17: 589-597. (  0) 0) |
| [17] |
Matsuo A, Fujii K, Fujiwara T. Flow features of shock-induced combustion around projectile traveling at hypervelocities[J]. AIAA Journal, 1995, 33(6): 1056-1063. DOI:10.2514/3.12527 (  0) 0) |
| [18] |
Brown P N, Byrne G D, Hindmarsh A C. VODE:a variable-coefficient ODE solver[J]. Siam Journal on Scientific & Statistical Computing, 1989, 10(5): 1038-1051. (  0) 0) |
| [19] |
Mott D R, Oran E S, Leer B V. A quasi-steady-state solver for the stiff ordinary differential equations of reaction kinetics[J]. Journal of Computational Physics, 2000, 164(2): 407-428. DOI:10.1006/jcph.2000.6605 (  0) 0) |
| [20] |
Zhong W X. On precise time-integration method for structural dynamics[J]. Journal of Dalian University of Technology, 1994(2): 131-136. (in Chinese) 钟万勰. 结构动力方程的精细时程积分法[J]. 大连理工大学学报, 1994(2): 131-136. DOI:10.3321/j.issn:1000-8608.1994.02.015 (  0) 0) |
| [21] |
Zhong W X, Williams F W. A precise time step integration method[J]. ARCHIVE Proceedings of the Institution of Mechanical Engineers Part C Journal of Mechanical Engineering Science 1989-1996(vols 203-210), 1994, 208(63): 427-430. (  0) 0) |
| [22] |
Zhong W X. Precise computation for transient analysis[J]. Computational Structural Mechanics and Applications, 1995, 12(1): 1-6. (in Chinese) 钟万勰. 暂态历程的精细计算方法[J]. 计算结构力学及其应用, 1995, 12(1): 1-6. (  0) 0) |
| [23] |
Zhong W X. The precise integration for matrix riccati equations[J]. Computational Structural Mechanics and Applications, 1994, 11(2): 113-119. (in Chinese) 钟万勰. 矩阵黎卡提方程的精细积分法[J]. 计算结构力学及其应用, 1994, 11(2): 113-119. (  0) 0) |
| [24] |
Zhong W X. Subdomain precise integration method and numerical solution of partial differential equations[J]. Computational Structural Mechanics and Applications, 1995, 12(3): 253-260. (in Chinese) 钟万勰. 子域精细积分及偏微分方程数值解[J]. 计算结构力学及其应用, 1995, 12(3): 253-260. (  0) 0) |
| [25] |
Kong X D, Zhong W X. Precise time integration algorithm of stiff equationin nonlinear dynamic system[J]. Journal of Dalian University of Technology, 2002, 42(6): 654-658. (in Chinese) 孔向东, 钟万勰. 非线性动力系统刚性方程精细时程积分法[J]. 大连理工大学学报, 2002, 42(6): 654-658. DOI:10.3321/j.issn:1000-8608.2002.06.005 (  0) 0) |
| [26] |
Liu Y. Numerical study of chemical nonequilibrium flow and its' application in shock-induced combustion[D]. National University of Defense Technology, 2008. (in Chinese) 刘瑜. 化学非平衡流的计算方法研究及其在激波诱导燃烧现象模拟中的应用[D]. 国防科学技术大学, 2008. http://cdmd.cnki.com.cn/Article/CDMD-90002-2009213254.htm (  0) 0) |
| [27] |
Liu J, Liu Y, Zhou C B. Simulation of shock induced combustion based on a novel uncoupled method[J]. Chinese Journal of Theoretical and Applied Mechanics, 2010, 42(03): 572-578. (in Chinese) 刘君, 刘瑜, 周松柏. 基于新型解耦算法的激波诱导燃烧过程数值模拟[J]. 力学学报, 2010, 42(03): 572-578. (  0) 0) |
| [28] |
Terashima H, Morii Y, Koshi M. A robust multi-time scale method for stiff combustion chemistry[J]. International Journal of Energetic Materials & Chemical Propulsion, 2015, 14(3). (  0) 0) |
| [29] |
Evans J S, Schexnayder C J. Influence of chemical kinetics and unmixedness on burning in supersonic hydrogen flames[J]. AIAA Journal, 1980, 18(2): 188-193. DOI:10.2514/3.50747 (  0) 0) |
| [30] |
Soetrisno M, Imlay S. Simulation of the flow field of a ram accelerator[C]//27th Joint Propulsion Conference, 1991.
(  0) 0) |
 2018, Vol. 36
2018, Vol. 36

