2. 中国空气动力研究与发展中心 空气动力学国家重点实验室, 四川 绵阳 621052
2. State Key Laboratory of Aerodynamics, China Aerodynamics Research and Development Center, Mianyang 621000, China
近20年来,随着高精度数值方法概念的提出和发展,众多学者提出和构造了诸多高精度数值格式。目前高精度方法主要可以分为三大类:有限差分型(Finite Difference, FD)高精度方法,有限体积型(Finite Volume, FV)高精度方法和有限元型(Finite Element, FE)高精度方法。间断伽辽金方法(Discontinuous Galerkin method, DG)是有限元高精度方法的一种,最先是由Reed和Hill[1]提出,经过一些学者的研究已经能够用于RANS的计算[2-5],但是RANS求解时的稳定性问题成了目前DG方法研究的难点。
DG方法有诸多优点[4-6]:1)能够保持单元平均值意义下的守恒性,且具有良好的稳定性和收敛性;2)可以简单通过提高单元内分片多项式次数来提高精度;3)可以通过使用任意网格来灵活的处理复杂的物理边界和几何区域;4)具有紧致性,易于实施大规模并行;5)容易实现hp自适应。与此同时,DG方法也有一些不足之处,还需要进一步解决的问题有如下几点:1) DG方法使用TVD或TVB限制器抑制数值振荡,然而TVD限制器在光滑的极值点附近会降低格式精度,TVB限制器虽然修正了TVD限制器的这一缺陷,却增加了与问题相关的参数,而且对于实际问题这些参数只能通过具体问题和相关经验获得;2) DG方法在如何有效地推广到NS方程,特别是RANS方程仍然是一个值得探索的问题,目前,很多学者依然在探索间断有限元方法高效处理黏性项的方法和RANS的计算方法;3) DG方法相对于传统有限体积方法计算量较大,对计算机计算效率和存储空间都提出了更高的要求。
DG方法在处理双曲守恒律方程和可压缩无黏Euler方程组是成功而有效的。然而,对于处理扩散问题或者含有黏性项的NS方程时,则带来了一定的难度。本质问题在于,如何构造单元界面的间断问题,即如何构造含有间断的高阶黏性数值通量求解格式。针对这一问题,学者们提出了各种有效的数值格式,诸如型罚函数格式(Symmetric IP, SIP)[7]、局部间断有限元方法(Local DG, LDG)[8]、(Second Bassi-Rebay scheme, BR2)[3]、BR2格式、LDG的升级版紧致间断伽辽金格式(Compact DG, CDG)[9]、直接间断伽辽金格式(Direct DG, DDG)[10-12]。
值得注意的是,很多学者提出并发展了一类重构型和混合型的间断有限元方法。这一类方法的基本思想是在DG方法的框架下,借鉴DG方法的优势,通过重构方式在原有DG解函数自由度的基础上,重构高阶自由度从而达到高阶精度的目的。Dumbser等人将DG方法和高精度有限体积方法统一到同一PnPm框架下,提出了一类PnPm方法[13]。Luo提出并发展了一类重构型DG方法(reconstruction DG, rDG)[6],并将这种方法应用到求解Euler方程组、NS方程组和RANS方程组,并取得了很好的效果。Van Leer等人提出并发展了另一类重构DG方法(Recovery DG, RDG)[14]。Zhang等人提出并发展了一类混合DG/FV方法[15],通过DG方法和有限体积方法结合在一起,取得了很好的效果。
采用DG方法求解RANS方程是目前DG方法研究领域的挑战性问题。虽然国内外诸多学者尝试将RANS方程组和Spalart-Allmaras (SA)湍流模型耦合在一起[3-4, 16],采用统一的数值方法进行求解,取得了一些研究进展,但是采用DG进行RANS计算依然不够成熟。影响DG进行RANS稳定求解的因素主要包括以下几个方面:(1)湍流模型的稳定性。一方程和两方程湍流模型在数值求解中难免会出现求解物理量负值的情况,这对于高精度算法的稳定性影响非常大。因此,Allmaras[17]和Oliver[18]等人分别采用不同的方法对Spalart-Allmaras模型进行了修正,使得SA模型的稳定性大大提高,能够用于高精度算法的求解。(2)隐式时间格式的稳定性。在DG求解过程中,由于显式格式时间步长受限,易导致计算效率低下。因而隐式格式自然变成了一种可以依赖的高效计算方法。传统的隐式格式一般采用LU-SGS求解。近年来,有些学者采用GMRES求解线化后的系统方程组,并利用LU-SGS进行预处理,这样做的好处是使线性方程组的Jacobian矩阵刚性有所降低,有利于收敛。但是对于黏性计算,如果采用不精确的无黏通量Jacobian矩阵进行预处理,由于无黏Jacobian矩阵和黏性控制方程数值格式所对应的Jacobian矩阵相差太远,必然导致隐式格式的稳定性下降,计算CFL数降低。在隐式格式进行计算时,Jacobian矩阵的处理方式有三种:1)无黏Jacobian矩阵,不考虑对流通量数值格式的数值耗散、边界通量和黏性通量的影响;2)通过解析数值格式获得近似精确的无黏Jacobian矩阵,通常用黏性谱半径代替黏性通量的贡献;3)通过解析数值通量格式(包括黏性通量)获得与数值格式相对应的解析精确Jacobian矩阵,对于诸如DG方法的紧致格式,可以通过链式法则获得与数值离散格式相对应的解析精确Jacobian矩阵。前两种处理方法对于常规二阶有限体积方法是稳定的,但是对于高精度数值格式而言,Jacobian矩阵的精确性直接决定了隐式数值格式的稳定性和收敛性,因而采用与数值格式相对应的精确Jacobian矩阵进行隐式GMRES计算意义重大。
为了提高DG方法在采用隐式时间推进格式进行黏性计算的稳定性和收敛性,本文提出了一种基于链式法则解析求解与数值格式相对应的精确Jacobian矩阵的GMRES隐式方法,该方法不仅有利于提高DG隐式求解的稳定性,而且还能够大幅度提高计算效率。与此同时,在RANS方程求解中,针对SA湍流模型源项隐式化时出现的非物理解,对模型的生成源项进行修正,并给出合理的隐式化方式。文中通过层流和湍流算例验证了本文发展方法的有效性。
1 控制方程笛卡尔坐标系下耦合修正的负SA湍流模型的RANS方程组为[17]:
| $ \frac{{\partial \mathit{\boldsymbol{U}}}}{{\partial t}} + \frac{{\partial {\mathit{\boldsymbol{F}}_i}}}{{\partial {x_i}}} - \frac{{\partial {\mathit{\boldsymbol{F}}_{vi}}}}{{\partial {x_i}}} = S $ | (1) |
其中,U是守恒变量、Fi是无黏通量、Fvi是黏性通量和S是源项。
2 间断伽辽金有限元方法式(1)在弱积分下的DG方法可表示为:
| $ \begin{array}{l} \frac{{\rm{d}}}{{{\rm{d}}t}}\int_{{\mathit{\Omega }_e}} {{\mathit{\boldsymbol{U}}_h}{B_i}{\rm{d}}\mathit{\Omega }} + \int_{{\mathit{\Gamma }_e}} {{\mathit{\boldsymbol{F}}_k}\left( {\mathit{\boldsymbol{U}}_h^L,\mathit{\boldsymbol{U}}_h^R} \right){B_i}{\mathit{\boldsymbol{n}}_k}{\rm{d}}\mathit{\Gamma }} - \\ \int_{{\mathit{\Omega }_e}} {{\mathit{\boldsymbol{F}}_k}\left( {{\mathit{\boldsymbol{U}}_h}} \right)\frac{{\partial {B_i}}}{{\partial {x_k}}}{\rm{d}}\mathit{\Omega }} = \\ \;\;\;\;\;\;\;\int_{{\mathit{\Gamma }_e}} {{\mathit{\boldsymbol{G}}_k}\left( {\mathit{\boldsymbol{U}}_h^L,\nabla \mathit{\boldsymbol{U}}_h^L,\mathit{\boldsymbol{U}}_h^R,\nabla \mathit{\boldsymbol{U}}_h^R} \right){B_i}{\mathit{\boldsymbol{n}}_k}{\rm{d}}\mathit{\Gamma }} - \\ \;\;\;\;\;\;\;\int_{{\mathit{\Omega }_e}} {{\mathit{\boldsymbol{G}}_k}\left( {{U_h}} \right)\frac{{\partial {B_i}}}{{\partial {x_k}}}{\rm{d}}\mathit{\Omega }} + \int_{{\mathit{\Omega }_e}} {S\left( {{\mathit{\boldsymbol{U}}_h},\nabla {\mathit{\boldsymbol{U}}_h}} \right){B_i}{\rm{d}}\mathit{\Omega }} \end{array} $ | (2) |
黏性通量离散采用BR2格式[2],该格式的形式如下:
| $ \begin{array}{l} \int_{{\mathit{\Gamma }_e}} {{\mathit{\boldsymbol{G}}_k}{B_i}{\mathit{\boldsymbol{n}}_k}{\rm{d}}\mathit{\Gamma }} - \int_{{\mathit{\Omega }_e}} {{\mathit{\boldsymbol{G}}_k}\frac{{\partial {B_i}}}{{\partial {x_k}}}{\rm{d}}\mathit{\Omega }} =\\ \;\;\;\;\;\;\;\;\frac{1}{2}\int_{{\mathit{\Gamma }_e}} {\left[ {\mathit{\boldsymbol{G}}_k^L\left( {\mathit{\boldsymbol{U}}_h^L,\nabla \mathit{\boldsymbol{U}}_h^L + \eta \mathit{\boldsymbol{r}}_h^L} \right) + } \right.} \\ \;\;\;\;\;\;\;\;\left. {\mathit{\boldsymbol{G}}_k^R\left( {\mathit{\boldsymbol{U}}_h^R,\nabla \mathit{\boldsymbol{U}}_h^R + \eta \mathit{\boldsymbol{r}}_h^R} \right)} \right]{B_i}{\mathit{\boldsymbol{n}}_k}{\rm{d}}\mathit{\Gamma } - \\ \;\;\;\;\;\;\;\;\int_{{\mathit{\Omega }_e}} {{\mathit{\boldsymbol{G}}_k}\left( {{\mathit{\boldsymbol{U}}_h},\nabla {\mathit{\boldsymbol{U}}_h} + {\mathit{\boldsymbol{R}}_h}} \right)\frac{{\partial {B_i}}}{{\partial {x_k}}}{\rm{d}}\mathit{\Omega }} \end{array} $ | (3) |
为了保证格式的稳定性,h取1~6。r为局部算子,R是全局算子,定义如下:
| $ \int_{{\mathit{\Omega }_e}} {{\mathit{\boldsymbol{r}}_h}{B_i}{\rm{d}}\mathit{\Omega }} = \int_{{\mathit{\Gamma }_e}} {\frac{1}{2}\left( {\mathit{\boldsymbol{U}}_h^R - \mathit{\boldsymbol{U}}_h^L} \right){B_i}{\mathit{\boldsymbol{n}}_j}{\rm{d}}\mathit{\Gamma }} $ | (4) |
| $ {\mathit{\boldsymbol{R}}_h} = \sum\limits_{\mathit{\Gamma } \in \mathit{\Omega }} {{\mathit{\boldsymbol{r}}_h}} $ | (5) |
这两种算子的离散形式为:
| $ \begin{array}{l} \mathit{\boldsymbol{r}}_{{x_i}}^L = {M^{ - 1}}\sum\limits_{i = 1}^N {\frac{1}{2}\left( {\mathit{\boldsymbol{U}}_h^R - \mathit{\boldsymbol{U}}_h^L} \right)B_i^L{\mathit{\boldsymbol{n}}_{{x_i}}}{\mathit{\Gamma }_e}} ,\\ \mathit{\boldsymbol{r}}_{{x_i}}^R = {M^{ - 1}}\sum\limits_{i = 1}^N {\frac{1}{2}\left( {\mathit{\boldsymbol{U}}_h^R - \mathit{\boldsymbol{U}}_h^L} \right)B_i^L{\mathit{\boldsymbol{n}}_{{x_i}}}{\mathit{\Gamma }_e}} \end{array} $ | (6) |
则
| $ \begin{array}{l} \mathit{\boldsymbol{\hat U}}_{{x_i}}^L = \sum\limits_{i = 1}^N {\left( {\mathit{\boldsymbol{U}}_i^L\frac{{\partial B_i^L}}{{\partial {x_i}}} + \eta \mathit{\boldsymbol{x}}_{{x_i}}^LB_i^L} \right)} = \mathit{\boldsymbol{U}}_{{x_i}}^L + \tilde r_{{x_i}}^L,\\ \mathit{\boldsymbol{\hat U}}_{{x_i}}^R = \sum\limits_{i = 1}^N {\left( {\mathit{\boldsymbol{U}}_i^R\frac{{\partial B_i^R}}{{\partial {x_i}}} + \eta \mathit{\boldsymbol{r}}_{{x_i}}^LB_i^L} \right)} = \mathit{\boldsymbol{U}}_{{x_i}}^R + \tilde r_{{x_i}}^R \end{array} $ | (7) |
| $ 其中,{{\tilde r}_{{x_i}}} = \sum\limits_{i = 1}^N {\eta \mathit{\boldsymbol{r}}_{{x_i}}^LB_i^L} $ | (8) |
| $ {\mathit{\boldsymbol{R}}_{{x_i}}} = \sum\limits_{\mathit{\Gamma } \in \mathit{\Omega }} {{\mathit{\boldsymbol{r}}_{{x_i}}}} $ | (9) |
Uh可近似为:
| $ {\mathit{\boldsymbol{U}}_h} = \sum\limits_{i = 1}^N {{\mathit{\boldsymbol{U}}_i}\left( t \right){B_i}\left( x \right)} $ | (10) |
基函数Bi(x)采用Luo提出来的Taylor基函数[6]。需要说明的是文中的BR2P1是二阶DG格式,BR2P2是三阶DG格式。
3 隐式时间推进格式式(4)写成半离散形式为:
| $ \mathit{\boldsymbol{M}}\frac{{{\rm{d}}\mathit{\boldsymbol{U}}}}{{{\rm{d}}t}} + R = 0 $ | (11) |
其中,M是质量矩阵, U是解矢量,R是右端残值。R包括了无黏通量、黏性通量和它们对应的域积分项。这里无黏通量的求解采用HLLC格式[19],黏性通量的求解采用BR2格式[2]。
| $ \begin{array}{l} R = \sum\limits_{\mathit{\Gamma } \in \mathit{\Omega }} {{\mathit{\boldsymbol{F}}_k}{B_i}{n_k}{\mathit{\Gamma }_e}} - \sum\limits_{\mathit{\Gamma } \in \mathit{\Omega }} {{\mathit{\boldsymbol{G}}_k}{B_i}{n_k}{\mathit{\Gamma }_e}} - \\ \;\;\;\;\;\;{\mathit{\boldsymbol{F}}_k}\frac{{\partial {B_i}}}{{\partial {x_k}}}{\mathit{\Omega }_e} + {\mathit{\boldsymbol{G}}_k}\frac{{\partial {B_i}}}{{\partial {x_k}}}{\mathit{\Omega }_e} \end{array} $ | (12) |
式(11)线化后可以表示为:
| $ A\Delta \mathit{\boldsymbol{U}} = - {\mathit{\boldsymbol{R}}^n},A = \frac{M}{{\Delta t}}\mathit{\boldsymbol{I + }}\frac{{\partial {\mathit{\boldsymbol{R}}^n}}}{{\partial \mathit{\boldsymbol{U}}}},\Delta \mathit{\boldsymbol{U}} = {\mathit{\boldsymbol{U}}^{n + 1}} - {\mathit{\boldsymbol{U}}^n} $ | (13) |
其中∂Rn/∂U是Jacobian矩阵,Δt是当地时间步长。当Δt趋于无穷大时,系统方程的求解就变成了典型的牛顿迭代。
3.1 GMRES方法GMRES在求解线性方程组时具有较高计算效率。由于本文计算所求解的控制方程非线性非常强,需要在GMRES求解时进行预处理,本文采用LU-SGS进行预处理[20],具体如下:
| $ {\mathit{\boldsymbol{P}}^{ - 1}}\mathit{\boldsymbol{A}}\Delta \mathit{\boldsymbol{U}} = {\mathit{\boldsymbol{P}}^{ - 1}}{\mathit{\boldsymbol{R}}^n} $ | (14) |
P是预处理矩阵,
| $ \mathit{\boldsymbol{P}} = \left( {\mathit{\boldsymbol{L}} + \mathit{\boldsymbol{D}}} \right){\mathit{\boldsymbol{D}}^{ - 1}}\left( {\mathit{\boldsymbol{U}} + \mathit{\boldsymbol{D}}} \right) $ | (15) |
其中,L、U和D分别是下三角、上三角和对角矩阵。
在GMRES的求解过程中,和Jacobian矩阵密切相关的两个步骤是预处理和矩阵矢量生成。预处理可以采用近似的Jacobian进行计算,而矩阵矢量生成则需要精确计算AΔU。传统的处理方式是考虑到黏性通量和其数值格式的复杂性,通常采用无黏Jacobian矩阵,或者考虑到黏性通量的影响采用谱半径代替黏性Jacobian矩阵进行预处理。在矩阵矢量生成时必须采用有限差分进行AΔU计算,具体如下:
| $ \mathit{\boldsymbol{A}}\Delta \mathit{\boldsymbol{U}} = \frac{\mathit{\boldsymbol{M}}}{{\Delta t}}\Delta \mathit{\boldsymbol{U + }}\frac{{\mathit{\boldsymbol{R}}\left( {\mathit{\boldsymbol{U}} + \varepsilon \Delta \mathit{\boldsymbol{U}}} \right) - \mathit{\boldsymbol{R}}\left( \mathit{\boldsymbol{U}} \right)}}{\varepsilon } $ | (16) |
其中ε是个小量,决定了式(16)的计算精度。如果能够获得与数值通量离散格式相对应的精确Jacobian矩阵L、U和D,不但可以采用精确Jacobian矩阵进行预处理,而且还可以采用精确Jacobian矩阵获得更为精确的AΔU,即有:
| $ \mathit{\boldsymbol{A}}\Delta \mathit{\boldsymbol{U}} = \frac{\mathit{\boldsymbol{M}}}{{\Delta t}}\Delta \mathit{\boldsymbol{U + }}\left( {\mathit{\boldsymbol{L}} + \mathit{\boldsymbol{D}} + \mathit{\boldsymbol{U}}} \right)\Delta \mathit{\boldsymbol{U}} $ | (17) |
对比近似Jacobian矩阵预处理加有限差分矩阵矢量生成与精确Jacobian矩阵进行预处理和矩阵矢量生成,如果Jacobian矩阵不精确,虽然可以进行预处理,但是无法直接进行矩阵矢量生成,必须采用有限差分进行矩阵矢量生成,这种方式一方面预处理的不精确影响GMRES的稳定性和系统方程的收敛性,另一方面有限差分的计算精度取决于ε,容易影响AΔU的计算精度,与此同时采用有限差分增加了内存存储R(U+εΔU)。而采用精确Jacobian矩阵进行计算只需要在求解GMRES之前计算一次L、U和D矩阵,且采用精确Jacobian矩阵预处理降低了系统刚性,提高了AΔU的计算精度,从而大幅度提高了GMRES的稳定性和系统方程的收敛性。
3.2 解析精确Jacobian矩阵像DG这类紧致格式任意高阶数值通量所对应的Jacobian矩阵都可以精确求出。对于采用HLLC格式求解无黏通量所对应的解析精确Jacobian矩阵可以写成:
| $ {\mathit{\boldsymbol{A}}_{{\rm{inv}}}} = \left\{ \begin{array}{l} {\mathit{\boldsymbol{L}}_{{\rm{inv}}}} = \sum\limits_{I < J}^{{\rm{face}}} {\frac{{\partial \mathit{\boldsymbol{F}}_k^{{\rm{HLLC}}}}}{{\partial {\mathit{\boldsymbol{U}}^I}}}B_i^J{\mathit{\boldsymbol{n}}_k}{\mathit{\Gamma }_e}} \\ {\mathit{\boldsymbol{D}}_{{\rm{inv}}}} = \sum\limits_{I = J}^{{\rm{face}}} {\frac{{\partial \mathit{\boldsymbol{F}}_k^{{\rm{HLLC}}}}}{{\partial {\mathit{\boldsymbol{U}}^I}}}B_i^I{\mathit{\boldsymbol{n}}_k}{\mathit{\Gamma }_e}} - \frac{{\partial {\mathit{\boldsymbol{F}}_k}}}{{\partial \mathit{\boldsymbol{U}}}}\frac{{\partial {B_i}}}{{\partial {x_k}}}{\mathit{\Omega }_e} + \frac{\mathit{\boldsymbol{M}}}{{\Delta t}}\\ {\mathit{\boldsymbol{U}}_{{\rm{inv}}}} = \sum\limits_{I > J}^{{\rm{face}}} {\frac{{\partial \mathit{\boldsymbol{F}}_k^{{\rm{HLLC}}}}}{{\partial {\mathit{\boldsymbol{U}}^I}}}B_i^J{\mathit{\boldsymbol{n}}_k}{\mathit{\Gamma }_e}} \end{array} \right. $ | (18) |
对于采用BR2格式求解黏性通量所对应的解析精确Jacobian矩阵可以写成为:
| $ {\mathit{\boldsymbol{A}}_{{\rm{vis}}}} = \left\{ \begin{array}{l} {\mathit{\boldsymbol{L}}_{{\rm{vis}}}} = \sum\limits_{I < J}^{{\rm{face}}} {\frac{{\partial {\mathit{\boldsymbol{G}}_k}}}{{\partial {\mathit{\boldsymbol{U}}^I}}}B_i^J{\mathit{\boldsymbol{n}}_k}{\mathit{\Gamma }_e}} + \sum\limits_{I < J}^{{\rm{face}}} {\frac{{\partial {\mathit{\boldsymbol{G}}_k}}}{{\partial {\mathit{\boldsymbol{U}}^I}}}\frac{{\partial {B_i}}}{{\partial {x_k}}}{\mathit{\Omega }_e}} \\ {\mathit{\boldsymbol{D}}_{{\rm{vis}}}} = \sum\limits_{I = J}^{{\rm{face}}} {\frac{{\partial {\mathit{\boldsymbol{G}}_k}}}{{\partial {\mathit{\boldsymbol{U}}^I}}}B_i^J{\mathit{\boldsymbol{n}}_k}{\mathit{\Gamma }_e}} + \frac{{\partial {\mathit{\boldsymbol{G}}_k}}}{{\partial \mathit{\boldsymbol{U}}}}\frac{{\partial {B_i}}}{{\partial {x_k}}}{\mathit{\Omega }_e} + \frac{\mathit{\boldsymbol{M}}}{{\Delta t}}\\ {\mathit{\boldsymbol{U}}_{{\rm{vis}}}} = \sum\limits_{I > J}^{{\rm{face}}} {\frac{{\partial {\mathit{\boldsymbol{G}}_k}}}{{\partial {\mathit{\boldsymbol{U}}^I}}}B_i^J{\mathit{\boldsymbol{n}}_k}{\mathit{\Gamma }_e}} + \sum\limits_{I > J}^{{\rm{face}}} {\frac{{\partial {\mathit{\boldsymbol{G}}_k}}}{{\partial {\mathit{\boldsymbol{U}}^I}}}\frac{{\partial {B_i}}}{{\partial {x_k}}}{\mathit{\Omega }_e}} \end{array} \right. $ | (19) |
其中face为总交界面, I和J代表界面左右的单元标号。式(18)和式(19)中L和U矩阵以edge形式存储信息,D矩阵则以element的形式存储。式(18)和(19)的求解可以采用链式法则求解:
| $ \frac{{\partial \mathit{\boldsymbol{F}}}}{{\partial \mathit{\boldsymbol{U}}}} = \frac{{\partial \mathit{\boldsymbol{F}}}}{{\partial \mathit{\boldsymbol{U}}}}\left( {\frac{{\partial \mathit{\boldsymbol{F}}}}{{\partial {\mathit{\boldsymbol{U}}_h}}}\frac{{\partial {\mathit{\boldsymbol{U}}_h}}}{{\partial \mathit{\boldsymbol{U}}}}} \right) $ | (20) |
| $ \frac{{\partial \mathit{\boldsymbol{G}}}}{{\partial \mathit{\boldsymbol{U}}}} = \frac{{\partial \mathit{\boldsymbol{G}}}}{{\partial \mathit{\boldsymbol{U}}}}\left( {\frac{{\partial \mathit{\boldsymbol{G}}}}{{\partial \mathit{\boldsymbol{\sigma }}}}\frac{{\partial \mathit{\boldsymbol{\sigma }}}}{{\partial {\mathit{\boldsymbol{Q}}_x}}}\frac{{\partial {\mathit{\boldsymbol{Q}}_x}}}{{\partial {\mathit{\boldsymbol{U}}_x}}}\frac{{\partial {\mathit{\boldsymbol{U}}_x}}}{{\partial \mathit{\boldsymbol{U}}}},\frac{{\partial \mathit{\boldsymbol{G}}}}{{\partial \mathit{\boldsymbol{\sigma }}}}\frac{{\partial \mathit{\boldsymbol{\sigma }}}}{{\partial \mathit{\boldsymbol{Q}}}}\frac{{\partial \mathit{\boldsymbol{Q}}}}{{\partial {\mathit{\boldsymbol{U}}_h}}}\frac{{\partial {\mathit{\boldsymbol{U}}_h}}}{{\partial \mathit{\boldsymbol{U}}}}} \right) $ | (21) |
其中∂Uh/∂U和∂Ux/∂U分别是B和Bx的对角阵。有关式(18)和(19)的详细求解可见参考文献[11]。需要说明的是,解析精确Jacobian的求解完全按照数值格式进行链式法则离散求解,中间没有任何假设,从数值离散角度讲,解析精确Jacobian矩阵精确地对应了相应的∂R/∂U,因而在每一步迭代计算中Jacobian矩阵是精确的。
3.3 SA湍流模型对于SA模型而言,在源项中由于涡量容易为0,从而导致式(9)中的分母为0,因此对其进行了修正,即:
| $ \begin{array}{l} r = \left\{ \begin{array}{l} 10,\;\;\;\;\;\;\;\;\;\;{\rm{if}}\;\;\;S \equiv 0\\ {r_1},\;\;\;\;\;\;\;\;\;\;\;\text{else} \end{array} \right.\\ {r_1} = \left\{ \begin{array}{l} 10,\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;{\rm{if}}\;\;\;\frac{{{\mu _l}{\rm{ \mathsf{ χ} }}}}{{\tilde S\rho k_T^2{d^2}}} > 10\\ \frac{{{\mu _l}{\rm{ \mathsf{ χ} }}}}{{\tilde S\rho k_T^2{d^2}}},\;\;\;\;\;\;\text{else} \end{array} \right. \end{array} $ | (22) |
因此,对应的导数为:
| $ \begin{array}{l} \frac{{\partial r}}{{\partial \rho \tilde v}} = \left\{ \begin{array}{l} 0,\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;{\rm{if}}\;\;\;S \equiv 0.0\\ \frac{{\partial {r_1}}}{{\partial \rho \tilde v}},\;\;\;\;\;\;\;\;\;\;\;\;{\rm{else}} \end{array} \right.\\ \frac{{\partial {r_1}}}{{\partial \rho \tilde v}} = \left\{ \begin{array}{l} 0,\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;{\rm{if}}\;\;\;\frac{{{\mu _l}{\rm{ \mathsf{ χ} }}}}{{\tilde S\rho k_T^2{d^2}}} > 10\\ \partial \left( {\frac{{{\mu _l}{\rm{ \mathsf{ χ} }}}}{{\tilde S\rho k_T^2{d^2}}}} \right)/\partial \rho \tilde v,\;\;\;\;\;\;\;\;{\rm{else}} \end{array} \right. \end{array} $ | (23) |
修正后既保证了湍流生成源项P中涡量为0时不产生非物理解,又限制了湍流生成项在求解Jacobian矩阵时因分母为0而导致的计算失败。
4 算例分析 4.1 层流圆柱绕流层流圆柱绕流的计算条件为Ma=0.2、雷诺数Re=40。计算网格采用二阶曲线三角形和四边形混合网格,总共有8046个三角形单元和4568个四边形单元,网格如图 1所示。网格离壁面最近距离为0.0338倍直径,其中圆柱直径为1。
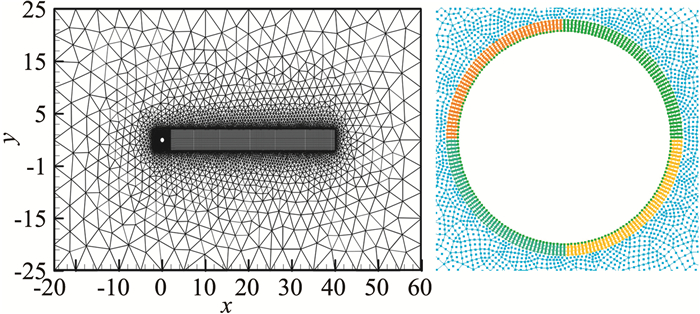
|
图 1 圆柱绕流二阶曲线混合网格 Figure 1 Second order hybrid mesh for a viscous flow past a cylinder |
图 2给出了CFL在30步之内从1增加到1×1010时BR2P1和BR2P2的残值收敛曲线。从图可知,采用精确Jacobian矩阵进行计算,在有限的计算步数内CFL数可以取到很大的数,且BR2P1在迭代25步时残值下降10个量级,相比而言BR2P2需要迭代32步。就计算时间而言,BR2P2的CPU耗时约是BR2P1的3倍以上。
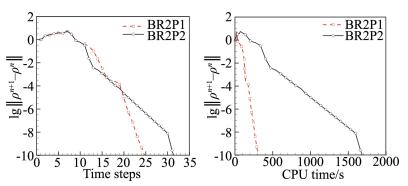
|
图 2 BR2P1和BR2P2格式的残值收敛曲线(CFLmax=1×1010) Figure 2 Convergence histories of BR2P1 and BR2P2 schemes (CFLmax=1×1010) |
图 3给出了层流圆柱的流线图,从图可知本文计算方法能够准确地捕捉到层流圆柱的一对尾涡,这和相关文献结果[2]吻合。表 1给出了计算的层流圆柱阻力系数和回流区长度与文献值的对比。从表 1可知本文计算结果和文献值吻合较好。

|
图 3 层流圆柱绕流流线和等压线图 Figure 3 Stream lines and pressure contours for laminar flow past a cylinder |
| 表 1 层流圆柱绕流的阻力系数和回流区长度的对比 Table 1 Comparison of drag coefficients and the recirculation lengths for laminar flow past a cylinder |
|
|
为了验证本文发展方法计算精度的网格收敛性,算例选择零压力梯度平板湍流绕流。计算条件为:马赫数Ma=0.2,雷诺数Re=6×106。这一算例是NASA TMR网站[22]上的湍流模型验证算例,网格取自该网站,计算采用的三套网格大小分别为35×25,69×49和137×97,如图 4所示。

|
图 4 零压力梯度平板计算网格 Figure 4 Mesh for zero pressure gradient flat plate |
图 5给出了CFL在200步之内从1增加到1×1010 时BR2P1和BR2P2格式的残值收敛曲线。由图 5可知,残值下降10个量级,就迭代步数而言,BR2P2的迭代步数是BR2P1的1/3;就计算效率而言,BR2P2格式的CPU耗时是BR2P1格式的近3倍。图 6给出了两种不同精度DG方法计算的阻力系数随网格量的收敛状况。由图 6可知本文发展的DG方法有较高的计算精度,在较粗的网上就能取得收敛解,特别是BR2P2格式能够在最粗网格上获得收敛解。与传统的成熟CFD软件CFL3D和FUN3D的计算结果相比较,本文发展DG方法的精算精度要明显高于CFL3D和FUN3D,能够在较稀的网格上得到收敛解,虽然最终收敛解的值有所差别,但是这种差别不超1%。
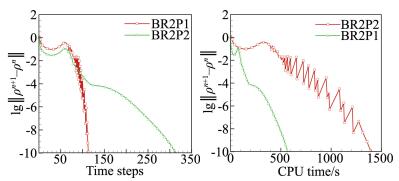
|
图 5 BR2P1和BR2P2格式的残值收敛曲线(中等网格) Figure 5 Convergence histories of BR2P1 and BR2P2 schemes (medium mesh) |
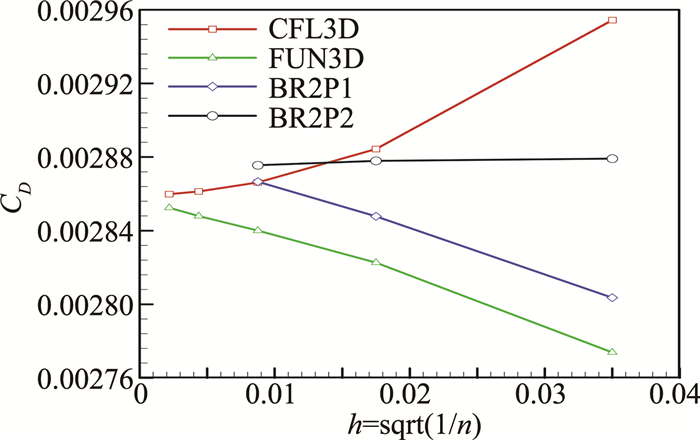
|
图 6 阻力系数随网格数收敛曲线 Figure 6 Drag coefficient convergence with grid sizes |
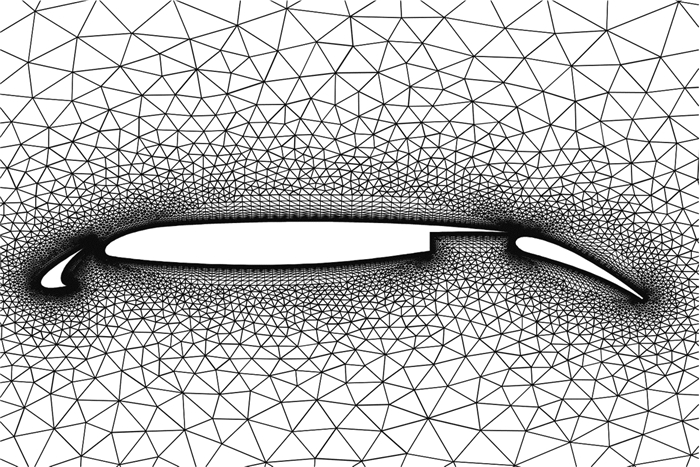
30P30N多段翼型湍流绕流是具有挑战性的算例,这是由于在前缘缝翼缝道内和襟翼舱内有分离涡,加之在缝翼前缘存在跨声速区,这些复杂的流动导致了计算的不稳定。计算条件为:马赫数Ma=0.2,迎角α=16°,雷诺数Re=9.0×106。计算网格采用二阶曲线三角形和四边形混合网格,总共有20 461个三角形单元和10 160个四边形单元,第一层离壁面距离为5.0×10-6,远场距离为500倍弦长。网格示意图如图 7所示。
|
图 7 30P30N多段翼型湍流绕流二阶混合网格 Figure 7 Second order hybrid mesh for turbulent flow past a 30P30N multi-element airfoil |
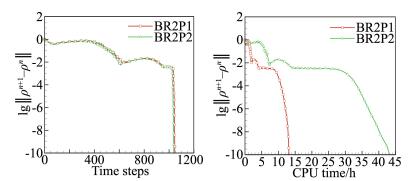
由于30P30N多段翼型构型和流动均非常复杂。为了提高计算的稳定性和计算效率,先采用较小CFL数进行计算使流场达到稳定后再采用快速增加CFL数到1×1010。所以计算CFL数设定遵从如下方式:首先在1000步以内CFL数从1增大到1000,当残值下降2.5个量级时CFL数在接下来的100步以内从当前值增大到1×1010。图 8给出了计算的残值收敛曲线。由图 8可以看出,两种不同精度的BR2格式残值收敛历程大体相同,BR2P2的CPU耗时是BR2P1的3倍。需要指出的是BR2P2计算时的初始值是以自由来流且没有采用限制器和人工耗散,计算依然能够在大CFL数下稳定并且残值最终下降了10个量级。这进一步验证了本文发展的高精度方法具有较高的稳定性,能够用于解决诸如30P30N这样复杂构型的气动计算。
|
图 8 30P30N多段翼型湍流绕流的残值收敛曲线 Figure 8 Convergence histories for turbulent flow past a 30P30N multi-element airfoil |
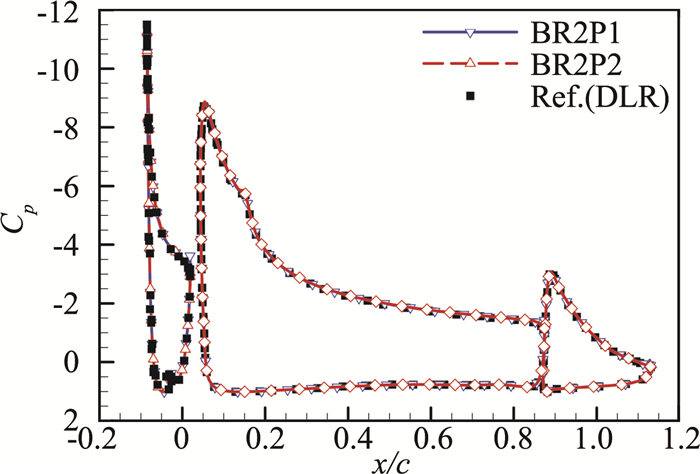
图 9给出了BR2P1和BR2P2计算的30P30N多段翼型表面压力系数分布和DLR结果[23]的对比。由图 9可知,本文计算结果和DLR的计算值吻合较好。表 2给出了BR2P1和BR2P2计算的升阻力系数和文献值[24]的对比(其中Ndof为自由度个数),可以看出,然本文的网格单元更少,但是本文的计算结果和文献结果吻合度较高。
|
图 9 30P30N多段翼型的表面压力系数 Figure 9 Pressure coefficient for 30P30N multi-element airfoil |
| 表 2 30P30N多段翼湍流绕流升阻力系数的对比 Table 2 Comparison of lift and drag coefficients for turbulent flow past a 30P30N multi-element airfoil |
|
|
为了解决DG在RANS计算中的稳定性问题,本文发展了一种基于精确Jacobian矩阵的高效隐式间断伽辽金方法,用于求解可压缩流动问题。通过层流和湍流算例验证了发展的方法的有效性。典型算例结果表明:
1) 发展的基于链式法则求解精确Jacobian矩阵的隐式GMRES方法,不仅能够提高计算的稳定性,而且还能够提高计算效率,可以实现超大CFL数的计算。
2) 针对SA湍流模型生成源项的修正较为有效,能够改善RANS-SA系统方程在采用隐式方法计算时的稳定性。
3) 发展的高精度间断伽辽金方法不仅能够用于层流流场的计算,而且还能够用于复杂湍流流场的数值模拟,结果和国际上相关成熟软件吻合较好。这表明所发展的高精度间断伽辽金方法能够用于求解复杂二维流动问题,具有较为广阔应用前景。
| [1] |
Reed W H, Hill T R. Triangular mesh methods for the neutron transport[R]. Los Alamos Scientific Laboratory Report, LAUR-73-479, 1973.
(  0) 0) |
| [2] |
Cockburn B, Hou S, Shu C W. TVD Runge-Kutta local projection discontinuous Galerkin finite element method for conservation laws Ⅳ:the multidimensional case[J]. Mathematics of Compution, 1990, 54(190): 545-581. (  0) 0) |
| [3] |
Bassi F, Rebay S. Discontinuous Galerkin solution of the Reynolds-averaged Navier-Stokes and k-ε turbulence model equations[J]. Computers & Fluids, 2005, 34: 507-540. (  0) 0) |
| [4] |
Yang X Q, Cheng J, Liu X D, et al. A Reconstructed direct discontinuous Galerkin method for compressible turbulent flows on Hybrid Grids[R]. AIAA 2016-3332, 2016.
(  0) 0) |
| [5] |
Cheng J, Yang X Q, Liu T G, et al. The direct discontinuous Galerkin method for 2D compressible Navier-Stokes equations on arbitrary grid[R]. AIAA 2016-1334, 2016.
(  0) 0) |
| [6] |
Luo H, Luo L Q, Nourgaliev R. A reconstructed discontinuous Galerkin method for the compressible Euler equations on arbitrary grids[J]. Communication in Computational Physcis, 2012, 12: 1495-1519. DOI:10.4208/cicp.250911.030212a (  0) 0) |
| [7] |
Arnold D N. An interior penalty finite element method with discontinuous elements[J]. SIAM Journal on Numerical Analysis, 1982, 19(4): 742-760. DOI:10.1137/0719052 (  0) 0) |
| [8] |
Cockburn B, Shu C W. The local discontinuous Galerkin method for time dependent convection diffusion systems[J]. SIAM Journal on Numerical Analysis, 1998, 35(6): 2440-2463. DOI:10.1137/S0036142997316712 (  0) 0) |
| [9] |
Peraire J, Persson P O. The compact discontinuous Galerkin (CDG) method for elliptic problems[J]. SIAM J Sci Comput, 2008, 30: 1806-1824. DOI:10.1137/070685518 (  0) 0) |
| [10] |
Liu H L. Optimal error estimates of the direct discontinuous Galerkin method for convection-diffusion equations[J]. Math Comput, 2015, 84: 2263-2295. (  0) 0) |
| [11] |
Yang X Q, Cheng J, Wang C J, et al. A fast, implicit discontinuous Galerkin method based on analytical jacobians for the compressible Navier-Stokes equations[R]. AIAA 2016-1326, 2016.
(  0) 0) |
| [12] |
Cheng J, Yang X Q, Liu T G, et al. A direct discontinuous Galerkin method for 2D compressible Navier-Stokes equations on arbitrary grid[J]. Journal of Computational Physics, 2016, 327: 484-502. DOI:10.1016/j.jcp.2016.09.049 (  0) 0) |
| [13] |
Dumbser M, Valsara D S, Toro E F, et al. A unified framework for the construction of one-step finite volume and discontinuous Galerkin schemes on unstructured meshes[J]. Journal of Computational Physics, 2008, 227: 8209-8253. DOI:10.1016/j.jcp.2008.05.025 (  0) 0) |
| [14] |
Van L B, Nomura S. Discontinuous Galerkin method for diffusion[R]. AIAA 2005-5108, 2005.
(  0) 0) |
| [15] |
Li M, Liu W, Zhang L P, et al. Applications of high order hybrid DG/FV methods for 2D viscous flows[J]. Acta Aerodynamica Sinica, 2015, 33(1): 17-24. (in Chinese) 李明, 刘伟, 张来平, 等. 高阶精度DG/FV混合方法在二维黏性流动模拟中的推广[J]. 空气动力学学报, 2015, 33(1): 17-24. (  0) 0) |
| [16] |
Yang X Q, Yang A, Sun G. An efficient numerical method for coupling the RANS equations with Spalart-Allmaras turbulence model equation[J]. Acta Aeronautica et Astronautica Sinica, 2013, 34(9): 2007-2018. (in Chinese) 杨小权, 杨爱明, 孙刚. 一种强耦合Spalart-Allmaras湍流模型的RANS方程的高效数值计算方法[J]. 航空学报, 2013, 34(9): 2007-2018. (  0) 0) |
| [17] |
Allmaras S R, Johnson F T, Spalart P R. Modifications and clarifications for the implementation of the Spalart-Allmaras turbulence model[C]//Seventh International Conference on Computational Fluid Dynamics, 2012.
(  0) 0) |
| [18] |
Todd A O. A high-order, adaptive, discontinuous Galerkin——nite element method for the Reynolds averaged Navier-Stokes equations[D]. Massachusetts Institute of Technology, 2008.
(  0) 0) |
| [19] |
Toro E F. Riemann solvers and numerical methods for fluid dynamics[M]. Verlag, Beilin: Springer Press, 1999.
(  0) 0) |
| [20] |
Luo H, Baum J D, Löhner R. A fast, matrix-free implicit method for compressible flows on unstructured grids[J]. J Comput Phys, 1998, 146: 664-690. DOI:10.1006/jcph.1998.6076 (  0) 0) |
| [21] |
Tseng Y H, Ferziger J H. A ghost-cell immersed boundary method for flow in complex geometry[J]. Journal of Computational Physics, 2003, 192: 593-623. DOI:10.1016/j.jcp.2003.07.024 (  0) 0) |
| [22] | |
| [23] | |
| [24] |
Peraire J, Persson P O. The compact discontinuous Galerkin (CDG) method for elliptic problems[J]. SIAM Journal on Scientific Computing, 2008, 30(4): 1806-1824. DOI:10.1137/070685518 (  0) 0) |
 2018, Vol. 36
2018, Vol. 36


