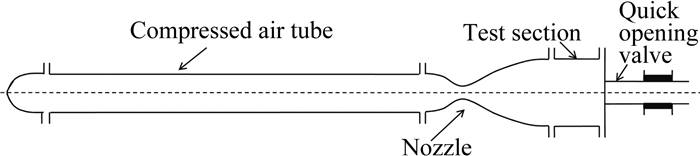
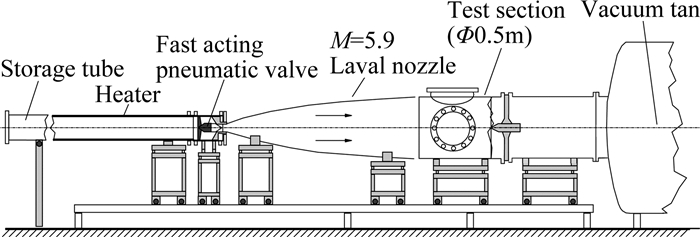
作为21世纪航空航天研究领域的制高点,超声速及高超声速飞行器及其相关技术一直是世界各大国重点发展的对象。但是,超声速及高超声速的相关技术的发展很大程度上取决于诸多基础学科的研究。在空气动力学方面,目前还存在诸多未解决的难题,比如高超声速流动的边界层稳定性、层流/湍流边界层转捩问题、流动分离及再附、真实气体效应、激波/边界层干扰问题等,这些都直接影响了超声速及高超声速飞行器的气动、控制和热防护设计[1-2]。虽然大量的相关研究工作一直在开展,但是所取得的效果甚微,很多问题并未得到实质性的解决。从目前的状况来看,学术界研究超声速及高超声速流动现象主要是通过数值模拟和实验测量。由于在高速流动下的特殊流动情况,比如真实气体效应、高温非平衡气体效应、化学反应等,已有的数值计算模型并不能普遍适用[3-4]。例如,德国宇航院的Longo认为在使用CFD进行高超声速空气动力学设计过程中的诸多关键技术,比如真实气体效应、热流问题、湍流、以及黏性的相互作用,仅仅是被CFD较低程度地模拟。因此,基于地面设备的风洞实验在高速空气动力研究中仍不可或缺。但是,常规超声速及高超声速风洞设备建设成本高昂,风洞的运行和操作也较为复杂,实验测量所需的各类仪器昂贵。以上因素提高了科研机构开展超声速及高超声速实验空气动力学基础研究的门槛。针对该问题,德国Hubert Ludwieg教授于1955年提出了Ludwieg管风洞的设计方案[5]。Ludwieg教授指出,常规下吹式高超声速风洞的费用基本与实验段设计马赫数成正比,但是如果风洞的运行时间可以降低到1 s甚至更少的话,可以采用长管形的储气段代替常规下吹式风洞的高压罐,这样避免了复杂的压力管路及阀门控制结构,风洞的建设成本也因此会大幅下降。传统的Ludwieg管风洞由储气段、Laval喷管、实验段、真空罐和快速控制阀组成,见图 1[6]。该风洞通过开合快速控制阀门来控制风洞的运行,运行成本低廉,可获得的来流单位雷诺数高,来流品质好;另外,与传统的高超声速风洞不同,Ludwieg管风洞的建造无需使用复杂的大型控制阀门以及稳定段,对空气压缩机、加热设备以及储气罐的要求也相对降低,这样导致Ludwieg管风洞的整体建设成本相对低廉。但是由于其运行时间短暂(约为百ms量级),同时代的测量设备性能尚不能与之匹配,故Ludwieg管高超声速风洞在概念提出后相当一段时间内并未得到广泛应用。
Hubert Ludwieg教授在1955年建造了世界上首座Ludwieg管高超声速风洞后,于1969年在德国宇航院再建一座大型超声速Ludwieg管风洞[8]。与此同时,美国NASA Marshall中心也建设一座口径为0.9m的超声速Ludwieg管风洞,其最高马赫数可达2.2[9]。随着现代电子测量技术的迅猛发展,百毫秒量级的风洞运行时间对于现代测量仪器,如PCB、Kulite、ALTP、热线风速仪、PIV等,已足够进行实验数据采样。此外,国内外对先进超声速及高超声速飞行器的需求一直推动着相关基础科学问题的研究,如高速边界层转捩、激波/边界层干扰等。作为经济型高速风洞的代表,Ludwieg管高超声速风洞结构简单,无需使用复杂的阀门控制系统,从而保证优良的来流品质,从20世纪90年代该类型风洞迅速进入了实验流体研究人员的视野。于此同时,德国宇航院Koppenwallner教授提出使用快速控制阀门取代之前广泛采用的压力膜片[10],极大程度上提升了Ludwieg管风洞的运行效率,降低了风洞的运行成本。欧洲以德国高校为代表,如不伦瑞克工业大学[11]、斯图加特工业大学[12]以及不莱梅大学[13],均建设了不同口径的Ludwieg管高超声速风洞,其设计马赫数主要以6以上为主;此外,荷兰代尔夫特理工大学也建设了高马赫数Ludwieg管风洞,其马赫数涵盖9、10和11[14]。在美国,Ludwieg管高超声速风洞在同时期也得到较快发展,加州理工Hornung教授设计了Caltech Ludwieg Tube,该风洞可以以马赫数4(中心轴对称)和2.3(二维)运行[15];普渡大学Schneider教授基于Ludwieg管风洞更是分别建成了NASA马赫数4的静风洞[16]和普渡大学马赫数6的静风洞[17-18];马里兰大学Laurence教授团队目前也在设计一座自由活塞式Ludwieg高超声速风洞,其设计马赫数为6.5;田纳西大学则计划在未来的4年内建设3座不同Ludwieg管风洞,预期涵盖的马赫数范围为4~6[19];美国空军实验室最近也从德国Hyperschall- und Stroemungstechnik GmbH公司采购了一座马赫数6的Ludwieg式风洞,用于高超声速基础流动问题研究[4, 20];美国圣母玛利亚大学则正在设计一座马赫数6大型Ludwieg式管静风洞[21],其实验段的口径可达0.6m,以研究高速飞行器表面边界层的自然转捩现象。此外,根据本文作者了解,德国Hyperschall-und Stroemungstechnik GmbH公司于2014年向韩国大田防务发展中心出售了一座口径为0.5m的马赫数6 Ludwieg式管高超声速风洞。
综合来看,Ludwieg管高超声速风洞具备以下几个优点:1) Ludwieg管风洞依靠膨胀波可产生定常的驻点压力和温度;2)由于无需复杂的控制阀门,总压损失小,该风洞的实验段可模拟雷诺数相比常规的下吹式风洞更高;3)该风洞的建设成本为同雷诺数的常规高超声速风洞1/3甚至1/4,根据不伦瑞克工业大学Radespiel教授估算,一座实验段口径为0.5m的Ludwieg管高超声速风洞的建造成本约为1百万美元[8];4)运行该风洞仅需1名实验人员即可,动力方面仅需使用电力间歇式的运行真空泵和空气压缩机,故风洞单趟试车成本约为数美元甚至更低。得益于上述优点,Ludwieg管风洞近些年在欧洲和美国得到了极大的应用。根据Cummings等人2012年的统计,全世界在使用的Ludwieg管风洞大概有18座[20]。加上目前美国、韩国以及我国正在建设中的数座Ludwieg管高超声速风洞,预期未来的5年Ludwieg管高超声速风洞将超过25座。可见,Ludwieg管风洞可以作为一种成熟的实验平台,极其适合用于高超声速空气动力学实验研究。
综上所述,可以得知Ludwieg管风洞的设计对象主要为高超声速流动,而非常规超声速风洞[5]。单独基于Ludwieg管风洞原理设计一座超声速风洞并不存在技术上的难题。众所周知,高超声速风洞的设计马赫数取决于实验段与喉道的面积比,以较为常见的实验段尺寸0.5m为例,如果风洞设计马赫数为6,其喉道直径约为70mm,储气段对应直径约为210mm(如果保持储气段的马赫数为0.058[8]);如果保持风洞的实验段尺寸不变来设计一座马赫数为3的Ludwieg管风洞,其喉道直径约为0.24m;在相同的储气段马赫数下,为了满足喉部的声速条件,储气段的直径则为0.76m。如此大型的高压储气段及其对应控制阀门部件,会极大增加风洞的建设成本,因而失去了Ludwieg管风洞的初始设计意义。考虑到超声速流域作为任何高超声速飞行器无法逾越的一个区间,对高超声速飞行器气动设计的影响至关重要;此外,超声速民用客机以及战斗机的先进气动布局设计也离不开超声速风洞的实验测量。如果可以基于常规的Ludwieg式高超声速管风洞,在保证实验段口径尺寸的前提下拓展其实验能力到常规超声速流域,对于开展超声速实验空气动力学研究意义重大。为了充分利用Ludwieg管风洞的优势,使其具备常规超声速实验能力,Wu和Radespiel采用了串列式Laval喷管布局的方式[22]——通过在常规Ludwieg管风洞的基础上引入一个额外的Laval喷管和稳定段,并重新设计风洞实验段对应的第二段Laval喷管,最后获得低于原风洞流动马赫数的超声速流。由于该改建的风洞沿着流向使用了两个Laval喷管,且使用了Ludwieg管产生定常总温和总压的原理,所以也称为串列式喷管Ludwieg式超声速风洞[22-23]。串列式喷管Ludwieg式超声速风洞最大限度地保留了原Ludwieg高超声速管风洞的基础平台,如储气段、快速控制阀门、实验段、扩张段和真空罐,其改建成本低廉,根据本文作者的经验,在不考虑人工成本的前提下,基于口径为0.5m的马赫数6 Ludwieg管风洞改建马赫数3串列式喷管超声速风洞的成本仅约10万欧元。实际上,串列式喷管Ludwieg式超声速风洞的设计方案最早被应用在荷兰代尔夫特理工大学Ludwieg管风洞上,旨在将原有来流为马赫数9~10的高超声速风洞拓展到马赫数6~8的流动,但是该Ludwieg管风洞改建过程中所涉及到的具体技术并未见到公开报道[23]。由于Ludwieg管风洞在向超声速流域拓展的过程中需要额外引入一些部件,从而改变了原有风洞的流场结构与分布,因此需要重新了解流动在风洞里的发展与演变。为了更好地认识串列式喷管Ludwieg式超声速风洞的设计原理,本文将以德国不伦瑞克工业大学马赫数6 Ludwieg管风洞为例,阐述将其拓展到马赫数3 Ludwieg管风洞的相关设计技术。
1 空气动力学设计原理 1.1 Ludwieg式高超声速管风洞目前常用的Ludwieg管风洞广泛采用将快速控制阀门安置在风洞的Laval喷管喉道处,通过控制快速反应阀门的闭合来控制风洞的运行,现代典型的Ludwieg管风洞布局见图 2[24]。相比Ludwieg教授最早提出的将控制阀门放置于实验段下游的方案,该设计可以更便捷地更换实验模型,以及更合理控制储气段的压力消耗,从而进一步提高了风洞的整体运行效率。根据作者的经验,图 2所示Ludwieg式高超声速管风洞在加热状态下每天可以运行60车次。
|
图 2 德国不伦瑞克工业大学马赫数6 Ludwieg式高超声速管风洞[24] Figure 2 Sketch of the hypersonic Ludwieg tube tunnel Braunschweig[24] |
Ludwieg管风洞的运行原理见图 3。风洞的高压储气段与Laval喷管通过快速控制阀门分开。在风洞启动前,储气段内储存着高温高压空气,而控制阀门下游的部分则通过真空泵抽成了真空。在开启快速控制阀门的瞬间,会产生一系列的非定常膨胀波,该膨胀波以声速向储气段的上游行进,图 3的CD段分别表示该膨胀波的波头和波尾;与此同时,该膨胀波驱动管内的气体,达到对应的储气段启动马赫数,马赫数值取决于储气段与Laval喉道部分的面积比。当膨胀波到达储气段的低端后,再次被反射回来(AE和BF)。当反射回来的膨胀波到达快速控制阀附近时快速控制阀门关闭,风洞的运行也同时结束。在快速控制阀的下游,受膨胀波驱动的高压气体会沿着Laval喷管膨胀加速,到达实验段时达到设计马赫数的高超声速气流。
储气段在风洞未启动时的状态用下角标0表示,风洞启动后的状态为下角标1。储气段产生膨胀波前、后的流动状态可以通过简单波理论描述[25]:
| $ {u_1} + \frac{{2{a_1}}}{{\gamma-1}} = \frac{{2{a_0}}}{{\gamma-1}} $ | (1) |
其中,储气段内的速度u1可以通过下式求解获得:
| $ \frac{{{u_1}}}{{{a_0}}} = \frac{{M{a_1}}}{{1 + \frac{{\gamma-1}}{2}M{a_1}}} $ | (2) |
a0为储气段初始状态的声波速度,Ma1则为产生膨胀波后储气段内的马赫数。值得注意的是该膨胀波产生为非定常过程,储气段的总温和总压变化满足下面的关系式[14, 23]:
| $ \frac{{{T_{t, 1}}}}{{{T_0}}} = \frac{{1 + \frac{{\gamma-1}}{2}Ma_1^2}}{{{{\left( {1 + \frac{{\gamma-1}}{2}M{a_1}} \right)}^2}}} $ | (3) |
| $ \frac{{{P_{t, 1}}}}{{{P_0}}} = {\left[{\frac{{1 + \frac{{\gamma-1}}{2}Ma_1^2}}{{{{\left( {1 + \frac{{\gamma-1}}{2}M{a_1}} \right)}^2}}}} \right]^{\frac{\gamma }{{\gamma -1}}}} $ | (4) |
其中下角标t表示驻点的流动情况,T为静温,P为静压,Ma1则由储气段和喷管喉道的面积比来决定,具体见式(5)[27]:
| $ {\left( {\frac{D}{{{D^*}}}} \right)^2} = \frac{1}{{M{a_1}}}{\left[{\frac{2}{{\gamma + 1}}\left( {1 + \frac{{\gamma-1}}{2}Ma_1^2} \right)} \right]^{\frac{{\gamma + 1}}{{2\left( {\gamma -1} \right)}}}} $ | (5) |
其中, D为储气段的直径,上角标*表征的是Laval喷管喉道处的声速条件。
受储气段内向上游行进的膨胀波驱动,储气段产生风洞初始启动流动,该流动沿着Laval喷管向风洞的下游加速,并在实验段得到超声速流动。
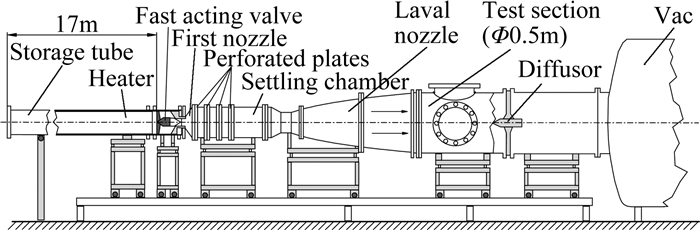
1.2 串列式喷管Ludwieg式超声速风洞为了合理应用Ludwieg管高超声速风洞产生定常总温和总压的优势,在串列式超声速风洞设计的过程中尽量保留原Ludwieg管风洞的基础设施。通过额外引入一个Laval喷管和稳定段,并重新设计第二段Laval喷管,以此来取代原高超声速Laval喷管,进而可以保留实验段以及下游的部件。图 4为基于马赫数6的Ludwieg管风洞改建而成的马赫数3串列式超声速风洞[22]。相比原Ludwieg管风洞,流场的差异主要从快速控制阀门下游开始。流动在第一段Laval喷管的喉道处首先达到声速,之后膨胀扩张到稳定段;通常由于受到第二段喉道流量的限制,第一段Laval喷管或者稳定段内会产生严重的流动分离,因此需要在稳定段采用不同的阻尼材料进行匀流;在稳定段通过匀流后,经过第二段Laval喷管再次进行加速,最终在实验段得到设计马赫数的超声速流动。
|
图 4 德国不伦瑞克工业大学马赫数3串列式喷管超声速风洞 Figure 4 Sketch of tandem nozzle supersonic wind tunnel |
在串列式超声速风洞中,由于风洞流向各截面处的流量一致,在假设Laval喷管喉道处均达到声速流动的前提下,根据式(6)可以首先得知第二喉道的总压[28]:
| $ \frac{{P_{t, 1}^*}}{{P_{t, 2}^*}} = {\left( {\frac{{D_2^*}}{{D_1^*}}} \right)^2} $ | (6) |
其中下角标1和2分别表示第一和第二Laval喷管喉道处的情况。根据式(6)可见,第一与第二喷管之间的总压压差取决于对应的喉道处面积比,由于两个Laval喷管的喉道面积不同,该总压差需要在第一喷管与稳定段之间耗散。一方面,受到第二段Laval喷管堵塞流的限制,第一段Laval喷管或者稳定段内会出现较强的背压,在第一段Laval喷管或者稳定段内会产生激波/边界层干扰,这样会承担一部分总压的损失;另外一方面,考虑到激波/边界层干扰所产生的流动分离以及激波尾迹流,稳定段通常需要使用阻尼材料,也会承担一部分总压的消耗。
根据以上介绍,可知第一段Laval喷管主要起引流作用,因此对于喷管管形的要求并不高;稳定段则起稳流作用,需要合理地布置阻尼设备;第二段Laval喷管负责产生均匀超声速气流,其管形则需要仔细设计与优化。相关工作可参考文献[22, 29-32]。
2 串列式喷管Ludwieg式超声速风洞设计技术基于常规Ludwieg管高超声速风洞设计串列式Laval喷管超声速风洞,需要首先确定实验段的设计马赫数,且该马赫数通常低于原高超声速风洞的马赫数,如德国不伦瑞克工业大学将Ludwieg式风洞由马赫数6变为了马赫数3[22],荷兰代尔夫特理工大学将马赫数9~11变为了马赫数6~8范围[23]。在保留原风洞实验段的前提下,当设计马赫数降低后,第二段Laval喷管的喉道口径增大。根据式(6),在两个Laval喉道之间必然会产生总压的损失,需要合理地设计第一段Laval喷管以及稳定段。基于空气动力学理论,可以获得串列式喷管Ludwieg式超声速管风洞的大致布局,但是考虑到实际的情况,通常需要对风洞整体进行优化设计。以德国不伦瑞克工业大学的Ludwieg高超声速管风洞改建为例,其使用德国宇航院开发的二阶有限体积求解器DLR-TAU Code[33-34]对串列式喷管Ludwieg式超声速风洞进行了局部以及整体的数值优化设计。其整体思路如下:首先求解Euler方程,对核心部件(第二段Laval喷管)的参数进行了优化设计;在确定了第二段Laval喷管参数后,分别对第一段Laval喷管以及稳定段进行设计,该部分主要以定常及非定常的RANS求解为主;最后,基于各部件优化的结果,对串列式喷管超声速风洞整体进行了数值优化,并分别采用了不同的数值预测模型,以确保数值计算的可靠性。需要说明的是,常规的Ludwieg管风洞为了追求较大的实验段面积通常采用中心轴对称设计[8, 21],所以本文所介绍串列式喷管Ludwieg式风洞设计将以中心轴对称风洞为主。
2.1 第二段Laval喷管优化设计第二段Laval喷管作为串列式喷管Ludwieg式超声速风洞的核心部件,对风洞的流场质量有重要影响。超声速Laval喷管由收缩段、喉道和扩张段组成。其中,收缩段可以采用多种方法生成对应的曲面管形,如Witozinsky法、五次样条曲线和双三次曲线法[35-37];至于喉道,一般可采用圆弧曲线[38];而扩张段则通常使用特征线法生成,以保证超声速气流的膨胀加速不会产生多余的激波[39],该部分同时也可以使用简单的线性设计,尤其是在静风洞设计过程中为了避免Laval喷管提前出现由Görtler涡引起的转捩[17]。关于超声速及高超声速喷管设计,已有较多的参考文献,如Sivells[40-41]、易仕和等[42],但是针对具体的Laval喷管参数优化设计则很是少见。整体上而言,影响Laval喷管的主要参数包括喉道的曲率、收缩段管形以及喷管整体的长度。在实际设计超声速及高超声速Laval喷管的过程中,则需要综合考虑实验场地需求、风洞预期达到的流场质量等诸多因素。
这里以德国不伦瑞克工业大学马赫数3 Laval喷管的数值优化为例,介绍常规超声速及高超声速Laval喷管设计需要具体考虑的问题。由于在Laval喷管的设计过程中黏性的影响相对较小,考虑到需要优化的参数较多,所以通常采用求解Euler方程进行优化,待具体确定了优化参数后,进而考虑黏性效应并使用NS方程求解。
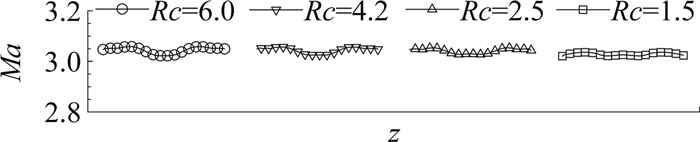
Laval喷管的第一个优化参数是喉道曲率半径Rc(Rc=曲率半径/喷管喉道半径),其大小直接影响喉道处超声速流动的发展。如在Wu和Radespiel的设计中,他们首先根据经验选择了几个比较典型的曲率半径值Rc值[43]。在保持其它流场参数不变的前提下,对相应的流场进行数值求解,流场马赫数云图的比较见图 5。从云图分布可见,当Rc=1.5时,实验段内流场分布无明显的马赫数梯度,表现最为均匀(注:图 5下端注释的0.5 m为实验段长度)。为了更直观地展示不同喉道曲率半径下的流场区别,对实验段入口处的马赫数进行了纵向的提取和比较,见图 6。通过比较,发现喉道曲率半径为1.5时实验段入口处的马赫数分布最为平坦,表明其对应的流场质量更高。该现象与Laval喷管喉道的设计经验相反。根据超声速喷管设计经验,较大的喉道曲率半径对应较为平缓的喉部流动过渡。图 5与图 6所显示的数值结果可能是由于该Laval喷管收缩段的收缩比较小,此时喉道曲率对流场的影响相对弱化所导致。
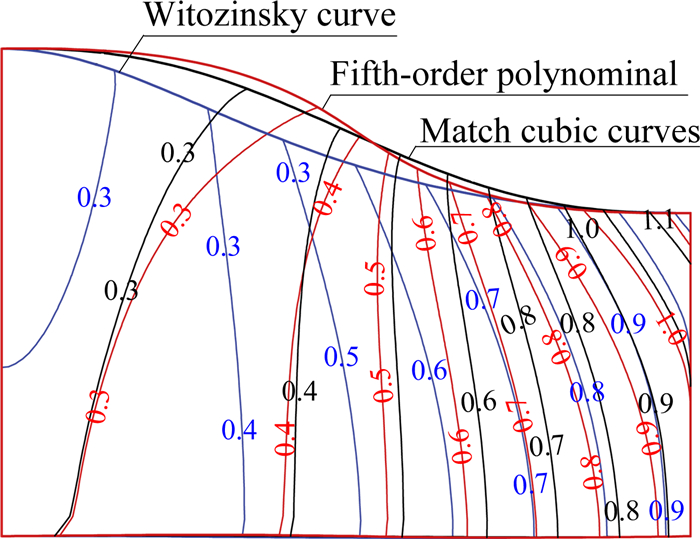
在确定了喉道的曲率半径后,Wu和Radespiel依次对喷管的收缩段进行数值优化[22]。收缩段的设计缺陷可能会导致流动分离,并影响到实验段的流场品质。在该Laval喷管的设计中,比较了常用的三种不同收缩段设计方法,即Witozinsky法、五次样条曲线和双三次曲线法。按照同样的方式对收缩段的流场进行数值求解,对应的结果以等值马赫数线显示,见图 7。Witozinsky曲线在收缩段入口处收缩较快,而在趋近喉道时流动加速较为缓和,确保了喉部流动的稳定性。通过等马赫数线的分布比较,三种方法所产生的喉部流动都相似,但是Witozinsky法对应的声速线更平直,该现象表征Witozinsky法所产生的喉部声速流动更为均匀,因此收缩段采用了该设计方法。
|
图 7 不同收缩段设计方法下的收缩段流场等马赫数线分布[22] Figure 7 Comparison of sonic line at throat under different contraction designs[22] |
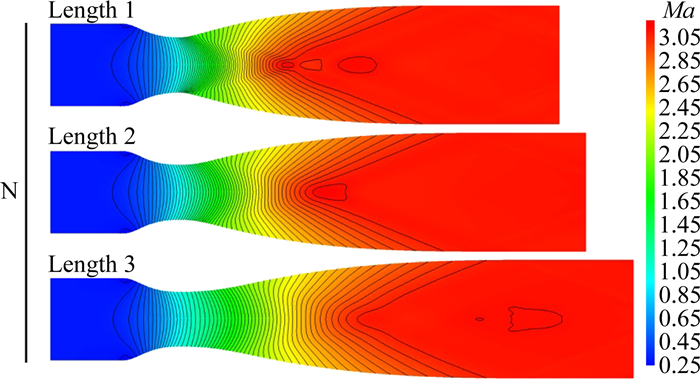
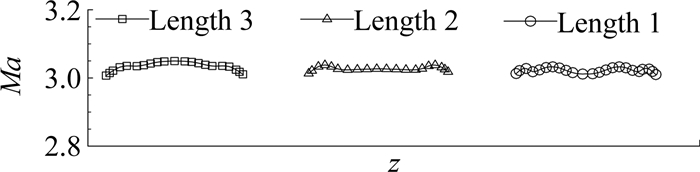
第二段Laval喷管的最后一个优化参数是喷管的长度。在喷管的收缩段和喉部设计确定的情况下,需要优化的主要对象为扩张段。考虑到大型Laval喷管的机械加工难度大,在设计中不宜过长,否则扩张段的任何微小瑕疵极都会引入多余的激波干扰,影响到实验段的流场质量;同时,Laval喷管的长度也不宜过短,否则气流膨胀过于迅速,会产生较大的流场脉动。综合考虑到实验室的空间条件,一般设计人员会对不同长度的喷管进行综合比较,如图 8所显示的马赫数3 Laval喷管在三种不同长度时的流场马赫数云图分布。通过图 8可见,在不同的扩张段长度下,实验段并无明显的反射马赫数波,马赫数的分布也很均匀。超声速喷管出口处的马赫数分布见图 9,当喷管长度为居中情况(Length 2)时实验段入口马赫数分布更为平直;长喷管情况虽然有少量马赫数的波动,但是整体分布也较为平直。综合考虑喷管的实际制造难度和成本,最终选择了Length 2作为该Laval喷管的最终设计。更多关于该部分的讨论可见文献[6, 22]。
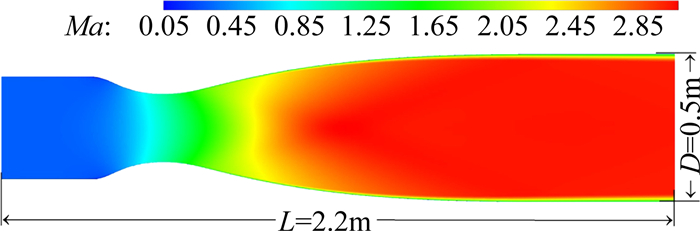
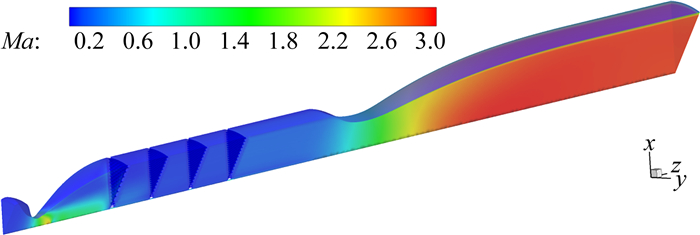
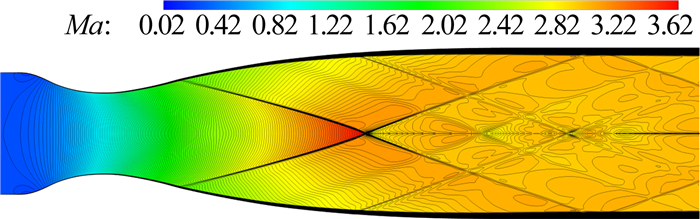
通过以上的优化,可以确定第二段喷管的外形参数。考虑到之前的数值优化均基于求解Euler方程,为了准确了解超声速Laval喷管上的真实流动发展,对该Laval喷管的流场进行了NS方程求解,对应的流场马赫数分布见图 10。
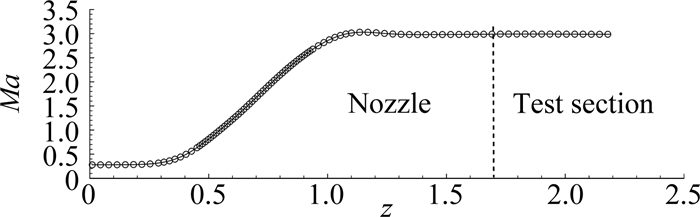
为了评估该Laval喷管所产生超声速流场的质量,图 11和图 12分别显示了沿Laval喷管中心轴以及实验段入口处的马赫数分布。由图 11可知,该Laval喷管的流动沿流向发展平缓,在达到设计马赫数后基本保持常数;实验段纵向的马赫数分布虽然出现微弱波动,但是相对偏差仅为0.33%,可以忽略不计。

|
图 12 第二段Laval喷管实验段入口处的马赫数分布[6] Figure 12 Mach number distribution in vertical direction |
在完成Laval喷管的优化设计后,接下来需要进行机械加工。大口径Laval喷管由于其纵深长度大,喷管内表面粗糙度要求高,一次性加工成型难度大。以0.5m口径的Laval喷管为例,其整体长度约为1.7m,考虑到喷管内表面的低粗糙度要求以及喉部尺寸的限制,通过数控机床一次性加工难度极高。工程上通常采用的做法是将Laval喷管分成多段分别加工,如图 13所示为德国不伦瑞克工业大学马赫数3喷管与普渡大学马赫数6喷管的加工图。在分段加工完喷管后再将各分段进行合成,此时需要对接口处进行特别处理,避免出现明显台阶以及缝隙,否则会产生多余的激波,严重影响到风洞实验段的流场分布,如图 14所示。因此,笔者建议在大型Laval喷管加工完成后有必要对喷管的内部管型进行独立的检测与测量,并基于所测量的管型数据再次开展数值计算,与之前的设计管型的流场进行对比,确保Laval喷管所产生流动的准确性。
|
图 14 马赫数3 Laval喷管分段连接处处理不当所产生的激波干扰 Figure 14 Unwanted shock waves induced by inappropriate connections between Laval nozzle segments |
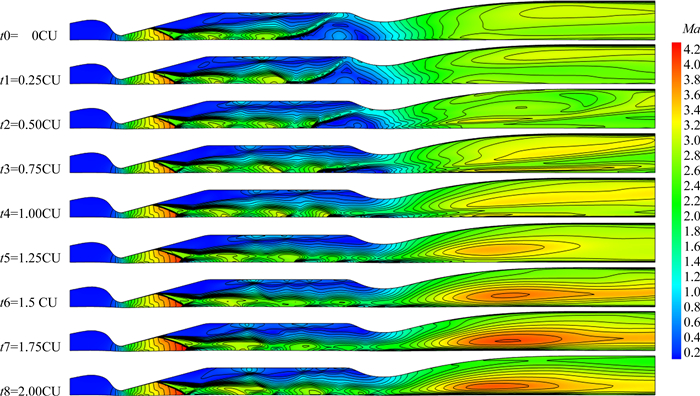
虽然同是Laval喷管,但是在串列式Laval喷管超声速风洞设计中,第一段与第二段Laval喷管的作用并不相同。根据前文的讨论,受到第二段Laval喉道流量的限制,第一段Laval喷管和稳定段需要耗散较大总压,由此可预测在第一段Laval喷管或者稳定段会出现较强的激波/边界层干扰。图 15展现了当稳定段不采取任何阻尼材料时串列式Laval喷管超声速风洞的非定常流场变化。根据流场的马赫数分布云图可见,在第一段Laval喷管上发生了严重的激波/边界层干扰,该干扰作用进一步产生流动分离区以及激波尾迹。由于稳定段没有阻尼设备进行匀流,激波的尾迹流破坏了第二段Laval喷管中的均匀超声速流动的发展。
|
图 15 串列式喷管Ludwieg式超声速风洞非定常流场马赫数云图分布 Figure 15 Unsteady flow field of the tandem nozzle supersonic wind tunnel |
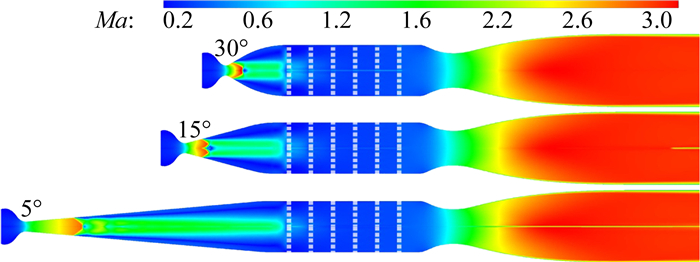
为了开展对第一段Laval喷管的优化设计,需要在稳定段采取相应的措施来消除激波尾迹及流动分离等现象。考虑到第一段喷管产生的激波尾迹流气动力较大,常规的阻尼装置如蜂窝网和阻尼网难以胜任。经过权衡,这里采用了金属多孔板来进行匀流。为了保证实验段可以得到均匀的超声速流动,首先使用了6块多孔板。第一段Laval喷管的主要优化对象是张角大小——当喷管张角较小时,喷管较长,这样加工成本高,占地面积更大。为了验证第一段Laval喷管张角的影响,在德国不伦瑞克工业大学串列式喷管超声速Ludwieg风洞中分别对5°、15°以及30°半张角的情况进行了流场模拟,对应的流场马赫数云图分布见图 16。
|
图 16 第一段Laval喷管不同张角下的流场马赫数云图[6] Figure 16 RANS simulations of wind tunnel with different opening angles of the 1st nozzle[6] |
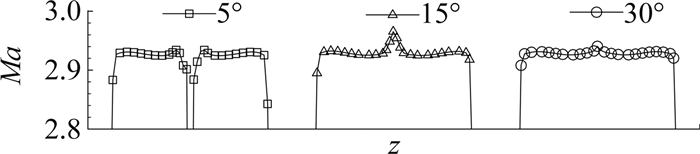
由图 16可见,第一段Laval喷管内的流场结构略有不同,但是气流在稳定段和实验段都很相似。值得注意的是在5°和15°喷管的中心轴附近均有马赫数异常分布,这个现象是中心轴对称网格由非结构向结构网格过渡引起的,属于数值现象[22]。三种不同张角下的实验段入口处的马赫数分布比较见图 17。根据比较可见,除了靠近中心轴附近的数值曲解,纵向马赫数的分布基本持平。因此,可以得出结论,当稳定段使用了6块多孔板时,第一段Laval喷管的张角对于实验段的流场影响并不大。为了降低风洞的建设成本,减小实验室空间需求,第一段Laval喷管采取半张角为30°的设计方案。
|
图 17 第一段Laval喷管不同张角下实验段入口马赫数分布[6] Figure 17 Ma slices comparison between different opening angles of the 1st nozzle[6] |
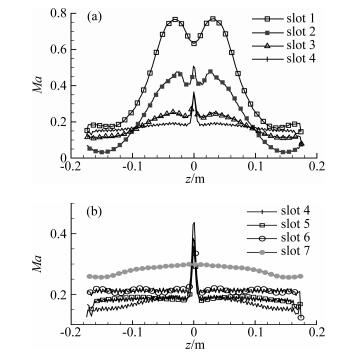
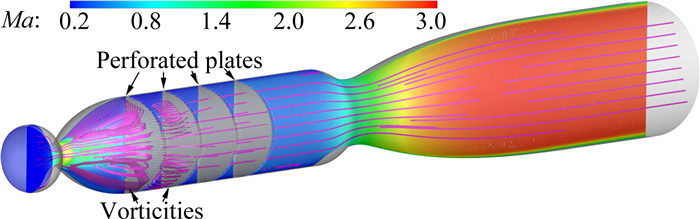
在第一段Laval喷管的设计过程中,可以得知稳定段对串列式喷管Ludwieg式超声速风洞流场的质量起着决定性的作用。由于目前世界上采用串列式喷管的Ludwieg式风洞并不常见,除了Wu和Radespiel等人围绕串列式喷管Ludwieg式超声速风洞的稳定段设计开展过的相关研究工作[29-30, 32, 45],其他可以参考的资料也较少。根据Wu和Radespiel[29, 45-46]对串列式喷管Ludwieg式超声速风洞流场的数值分析,他们认为在第一段Laval喷管所产生的强烈激波与流动分离极易损坏传统的阻尼材料,如阻尼网、蜂窝器以及消声棉等[47-48],为了消除激波与流动分离的影响,Wu等人重点对铝制多孔板进行流场匀流开展了研究。在第一段喷管的优化过程中,为了保证实验段可以获得均匀气流,Wu和Radespiel在设计稳定段时初步使用了6块多孔板[22]。一方面考虑到铝制多孔板加工昂贵,另一方面为了缩短稳定段的整体长度以延长风洞的有效运行时间,因此先对多孔板的数目进行优化。基于之前的30°半张角的工况的流场模拟结果,对稳定段多孔板上、下游的马赫数分布进行了提取及比较,见图 18和图 19(a)、(b),来了解多孔板对激波尾迹流和流动分离的作用效果。
由图 19(a)可见,在第一块多孔板之前(slot 1),靠近中心轴附近激波尾迹流马赫数高达0.8,而靠近壁面附近流动的马赫数较低;经过第一块和第二块多孔板后,纵向马赫数的分布逐渐趋于均匀;当流动发展到第三块多孔板后,马赫数的纵向分布方趋于均匀(靠近中心轴处的数值曲解无需考虑)。随着多孔板数目的逐渐增多,稳定段纵向马赫数分布的均匀性并未得到较大改善,见图 19(b)。根据上述分析可见,在经过三块多孔板后,风洞稳定段的流场已经基本不受上游的激波尾迹流和流动分离的影响。更多关于第一段Laval喷管内的激波/边界层干扰以及激波尾迹流与多孔板交互的问题可参考文献[29]。为了进一步探明多孔板的数目对于流场质量的影响,Wu和Radespiel分别对稳定段安置2块、3块、4块和6块多孔板下整体风洞的流场进行了数值模拟和比较,见图 20[6, 29]。为了进一步比较其区别,对实验段入口处的马赫数纵向分布进行了比较,见图 21。通过比较可以,当多孔板的数目达到4块以上后,纵向马赫数的分布基本持平。因此,在串列式喷管Ludwieg式风洞的实际设计中首先采用了4块多孔板作为匀流设备。

|
图 20 稳定段不同多孔板数目下的流场马赫数云图[6] Figure 20 RANS simulation of wind tunnel with different numbers of perforated plates[6] |

|
图 21 稳定段不同多孔板数目下实验段入口处的纵向马赫数分布[6] Figure 21 Mach slices comparison with different numbers of perforated plates[6] |
Wu等人对该串列式喷管Ludwieg式超声速风洞后期的流场脉动校核结果显示,单独使用多孔板虽然可以一定程度上移除在第一段Laval喷管以及稳定段内的激波和流动分离,但是风洞的流场脉动极高[30, 46]。因此,Wu等人根据数值分析以及来流扰动模态分解[29, 46],推测该风洞的声波扰动主要来源于第一段喷管内的激波/边界层干扰和超声速Laval喷管的湍流边界层;涡流扰动模态则主要来源于稳定段的多孔板。高超声速静风洞设计中为了保证流场质量,常用喉道吸气控制以及Laval喷管镜面打磨,以上方法固然可以降低声波扰动,但是其成本较高,设计相对复杂[17, 49-51]。Wu等人重点对串列式喷管Ludwieg式超声速风洞的稳定段设计进行了实验研究,主要测试不同阻尼材料对实验段流场的影响。图 22显示了Wu等人[46]以及Wu和Radespiel[45]在稳定段所使用过的阻尼材料,主要包括多层金属编织网、金属滤网、消声棉以及金属多孔板。关于具体的稳定段阻尼材料配置可以详见文献[31, 45],这里将重点介绍重新布置阻尼材料后实验段对应的流场变化。

|
图 22 风洞稳定段优化过程中使用的阻尼材料 Figure 22 Damping materials employed in the experimental investigation |
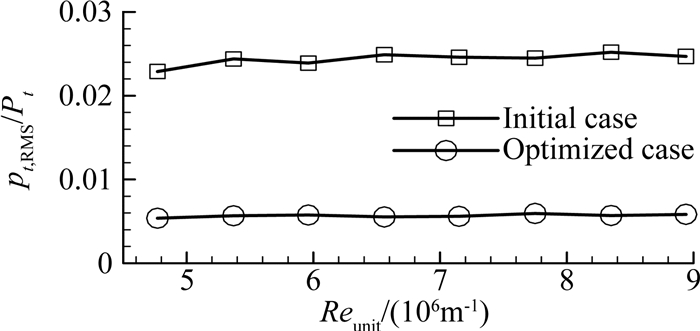
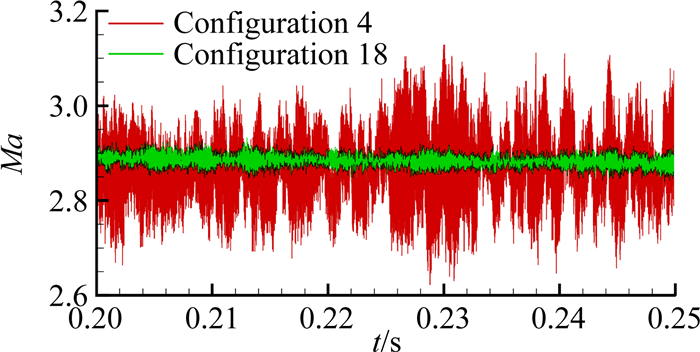
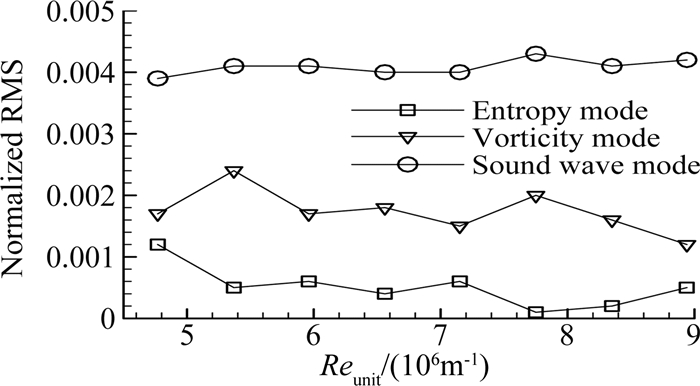
为了比较串列式喷管Ludwieg式超声速风洞在优化稳定段设计前后的流场变化情况,Wu等人创新性地采用Pitot管和热线结合的方式对实验段的自由来流进行了来流扰动模态测量,对应的结果见图 23和图 24。由图 23可见,经过合理优化稳定段的阻尼配置后,实验段的Pitot总压脉动幅值从2.3%降低到了0.58%。由图 24可见,实验段的各种不同扰动模态的幅值也极大降低,如声波扰动降到了0.4%,涡流模态为0.2%,熵模态则为0.05%。由此可见,优化后风洞的噪声度相对较低,接近甚至优于常规超声速风洞[52-53]。此外,相比最初4块多孔板的稳定段设计方案,经过优化的稳定段设计则引入了大量的阻尼材料,为了保证实验段的均值流动,Wu等人[46]以及Wu和Radespiel[45]对实验段的马赫数瞬态分布进行了测量,如图 25所示,可见实验段的来流马赫数均值并未发生变化。
|
图 24 优化后的实验段的扰动脉动模态[46] Figure 24 Disturbance modal analysis of the optimized settling chamber set-up[46] |
虽然以上的阻尼材料可以较好地应用在串列式喷管Ludwieg式超声速风洞的稳定段,但是在一定程度上缩短了风洞的有效运行时间;此外,以上阻尼材料在大雷诺数下也容易损坏,需要定期的修复与更换,这样容易导致风洞运行车次间流场的不均匀性[45]。最近,Wu等人尝试将硬质多孔介质材料,如烧结材料,应用在串列式喷管Ludwieg式超声速风洞的稳定段设计上。尝试通过使用不同开孔率压力损失的多孔介质板以取代原有的铝制多孔板,以最大程度地降低涡波扰动的幅值;此外,多孔介质板对于第二段Laval喷管上游的噪声消除也有显著效果[32]。图 26显示了稳定段使用不同数目多孔介质板后的流场分布。

|
图 26 稳定段使用不同数目的多孔介质板下风洞流场马赫数云图[32] Figure 26 Ma contours of tunnel with different numbers of porous plates in the settling chamber[32] |
由于常规的Ludwieg管风洞为中心轴对称形状,在数值优化的过程中通常使用中心轴对称的边界层条件。尽管该数值模型在优化参数阶段效率高,但是当风洞中存在大的流动分离以及激波干扰等三维流动现象时,中心轴对称数值模型所预测的流场并不完全可靠;此外,对于稳定段的阻尼设备,如多孔板及蜂窝网等结构,也很难通过中心轴对称的数值方法进行模拟。为了了解不同的数值模拟方法对流场预测的准确性,Wu等人基于德国不伦瑞克工业大学的串列式喷管Ludwieg式超声速风洞,分别对30°楔角以及全三维的风洞模型进行了RANS求解,见图 27和图 28[29]。其中,图 27所使用的计算网格约为600万,而图 28所示的全三维的网格量则高达7600万。
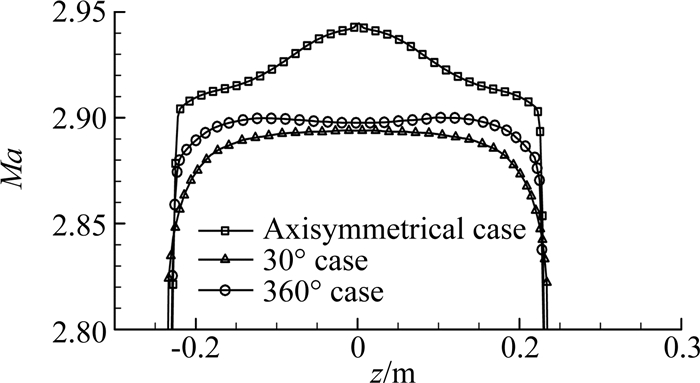
图 29显示了不同数值计算方法下风洞切面的马赫数分布云图。通过比较发现,使用30°以及360°模拟时,第一段喷管内的激波强度比中心轴对称模型时低。此外,稳定段多孔板也呈现不同的阻尼效果:在中心轴对称模型中,需要至少三块多孔板来消除激波尾迹的影响;但是在30°以及360°风洞模拟时,一块多孔板似乎已足够(具体更多细节的讨论可见文献[29])。再者,实验段的流动均匀性也略有差异,具体见实验段60 mm处纵向马赫数的分布比较(图 30)。相比较而言,30°以及360°数值模拟的流场结构基本相同,而中心轴对称法所呈现的结果略微偏高,但是并不影响使用中心轴对称模型来对该串列式超声速风洞的部件及整体进行初步的优化设计。综合权衡数值计算结果的准确性,Wu等人更推荐采用30°楔角的数值计算方法对此类中心轴对称管风洞进行数值设计。
|
图 30 实验段入口60 mm处纵向马赫数分布[29] Figure 30 Ma slices comparison for three different numerical methods[29] |
串列式喷管Ludwieg式超声速风洞在传统的Ludwieg管风洞基础上改建而成。在继承了传统Ludwieg管风洞优点的基础上,也存在诸多需要改进的问题。传统的Ludwieg管风洞的运行时间通常在百ms量级,通过加入额外的Laval喷管与稳定段后,风洞的有效运行时间会降低大概15~20 ms。为了进一步延长Ludwieg管风洞的有效运行时间,通常采取的做法是将储气段的长管进行延长,但是随着储气段长度的增加,靠近Laval喉道处的边界层厚度急剧增加,导致Ludwieg管风洞运行的总压损失增大[5]。在受到空间限制的条件下,代尔夫特理工大学采用了U形弯管的设计方式,如图 31所示,但是所采用U形管的半径对储气段的气流影响目前还不确定。
此外,超声速及高超声速边界层不稳定性研究的需求迫切,为了确保地面高超声速实验的准确性以及天地实验的数据相关性,我国发展适用于生产与研究的大型超声速或高超声速静风洞迫在眉睫。基于传统的高超声速风洞布局所设计的静风洞,除了建造与维护成本极其昂贵之外,实验段口径也很难达到较大的尺寸。据了解,目前世界上尺寸最大的静风洞由我国国防科技大学设计,该风洞采用传统高超声速风洞布局设计,实验段出口直径为300 mm[51]。该风洞采用了传统的静风洞设计技术:1) Laval喉道喷管上游采取吸气控制技术;2)风洞的稳定段采取复杂的阻尼材料;3)精密的Laval喷管加工技术。普渡大学Schneider教授则早在1995年基于Ludwieg管设计了一座马赫数4静风洞,其实验段尺寸为97×109 mm[16];之后,Schneider教授再次基于Ludwieg管风洞原理设计了Boeing/AFOSR马赫数6静风洞,其实验段口径为240 mm[54]。相比于之前设计的马赫数4静风洞,Boeing/AFOSR马赫数6静风洞采用了喉部吸气技术。但是,以上两座Ludwieg管风洞均采用了压力膜片分离风洞里的高低压力,而没有采用Koppenwallner教授提出的快速控制阀门[10]。这样一方面导致了Ludwieg式静风洞运行的效率低、更换风洞模型与测量仪器不便(模型处于高压区域)等缺陷;另外一方面,由于传统的Ludwieg管风洞没有稳定段,很难对熵波与涡波扰动进行消除,一定程度上限制了静风洞的实验段尺寸。作为Ludwieg管风洞的变种,串列式喷管Ludwieg式超声速风洞,由于额外引入了一段稳定段,则可以应用常规静风洞的设计方法,所以串列式喷管Ludwieg式风洞极有可能成为未来发展大型超声速及高超声速静风洞的研究方向。
在实验能力方面,串列式喷管Ludwieg式超声速风洞与常规的Ludwieg管风洞基本相似,可以承担常规的超声速及高超声速实验项目,如边界层稳定性与转捩[43, 55]、激波/边界层干扰[14]、后台阶流动[56]、激波/湍流干扰等[8]。另外,由于串列式喷管Ludwieg式超声速风洞的来流马赫数较低,对于驻点温度的要求并不如常规的Ludwieg管风洞高,无需对储气段的气体进行加热,这样一方面提高了风洞可模拟的雷诺数,另一方面也提高了风洞的运行效率。根据Wu等人改建Ludwieg风洞的经验,在马赫数3状态下,风洞每天可以运行100车次以上[6]。
4 结论本文介绍了传统Ludwieg管风洞向超声速流域拓展的一种风洞设计方法。该设计基于Ludwieg管风洞的基础,通过额外引入一段Laval喷管与稳定段,并重新设计第二段Laval喷管,最终获得对应的超声速流动。文章重点以德国不伦瑞克工业大学马赫数6 Ludwieg管风洞向马赫数3流域拓展为例,回顾了串列式喷管Ludwieg超声速风洞第一段Laval喷管、稳定段和第二段Laval喷管的设计要求与方法。该风洞设计方法以极低的改建成本成功将传统的Ludwieg管风洞的实验能力拓展到超声速流域,并且继承了原Ludwieg管风洞的优点,如运行成本低廉、风洞操作简单高效。此外,串列式喷管Ludwieg超声速风洞相比原Ludwieg管风洞多出了稳定段,更是提供了提升Ludwieg管风洞流场质量的空间,为发展我国大口径静风洞设计提供了新思路。该类串列式喷管Ludwieg超声速风洞在实验能力上可以胜任常规的超声速实验任务,如高速边界层稳定性与转捩、激波/边界层干扰等,为研究超声速空气动力学的基础问题提供了实验平台。整体上而言,该风洞设计方法对于已有Ludwieg管风洞设备的研究单位意义重大,可以依托已有的设备直接向超声速流域进行拓展,方便从事超声速实验空气动力学研究。
| [1] |
Bertin J J, Cummings R M. Critical hypersonic aerothermodynamic phenomena[J]. Annu Rev Fluid Mech, 2006, 38: 129-157. DOI:10.1146/annurev.fluid.38.050304.092041 (  0) 0) |
| [2] |
Anderson J D. Hypersonic and high temperature gas dynamics[M]//AIAA Education Series, 2000.
(  0) 0) |
| [3] |
Bertin J J, Cummings R M. Fifty years of hypersonics:where we've been, where we're going[J]. Progress in Aerospace Sciences, 2003, 39(6): 511-536. (  0) 0) |
| [4] |
Cummings R M. Numerical simulation of hypersonic flows[J]. Journal of Spacecraft and Rockets, 2015, 52(1): 15-16. DOI:10.2514/1.A33030 (  0) 0) |
| [5] |
Ludwieg H. Der rohrwindkanal[J]. Zeitschrift für Flugwissenschaften, 1955, 3(7): 206-216. (  0) 0) |
| [6] |
Wu J. Boundary-layer instability experiments in a tandem nozzle supersonic wind tunnel[M]. Germany: Shaker Verlag GmbH, 2015.
(  0) 0) |
| [7] |
Pope A, Goin K. High-speed wind tunnel testing[M]. New York, London, Sydney: John Wiley & Sons Inc, 1965.
(  0) 0) |
| [8] |
Radespiel R, Estorf M, Heitmann D, et al. Hypersonic Ludwieg tube[J]. Experimental Methods of Shock Wave Research, 2016, 433-458. (  0) 0) |
| [9] |
Warmbrod J D. A theoretical and experimental study of unsteady flow processes in a Ludweig tube wind tunnel[R]. NASA TN-D-5469, 1969.
(  0) 0) |
| [10] |
Koppenwallner G, Müller-Eigner R, Friehmelt H. HHK Hochschul-hyperschall-kanal: Ein 'Low-Cost' windkanal für forschung und ausbildung[R]. DGLR-Jahrbuch, 1993, (2): 887-896.
(  0) 0) |
| [11] |
Estorf M, Wolf T, Radespiel R. Experimental and numerical investigations on the operation of the Hypersonic Ludwieg Tube braunschweig[C]//Proceedings of the Fifth European Symposium on Aerothermodynamics for Space Vehicles, 2005. http://adsabs.harvard.edu/abs/2005ESASP.563..579E
(  0) 0) |
| [12] |
Weiss J. Experimental determination of the free stream disturbance field in the short duration supersonic wind tunnel of Stuttgart University[D]. Institute für Aerodynaik und Gasdynamik, University of Stuttgart, 2002.
(  0) 0) |
| [13] |
Renken H, Oelze H W, Rath H J. Application of a digital high speed camera and image processing system for investigations of short-term hypersonic fluids[M]//Digital Solid State Cameras: Designs and Applications. San Jose, California, 1998.
(  0) 0) |
| [14] |
Schrijer F. Experimental investigation of re-entry aerodynamic phenomena[D]. Technische Universtiteit Delft, 2010. https://www.narcis.nl/publication/RecordID/oai%3Atudelft.nl%3Auuid%3Acad92d3e-b8e3-48ed-a23e-e0fecd2a8133
(  0) 0) |
| [15] |
Hornung H, Parziale N. Spectral characteristics of pitot noise[C]//29th International Symposium on Shock Waves. Springer, 2015: 409-414. https://link.springer.com/chapter/10.1007%2F978-3-319-16835-7_64
(  0) 0) |
| [16] |
Schneider S P, Haven C E. Quiet-flow Ludwieg tube for high-speed transition research[J]. AIAA Journal, 1995, 33(4): 688-693. DOI:10.2514/3.12434 (  0) 0) |
| [17] |
Schneider S P. Development of hypersonic quiet tunnels[J]. Journal of Spacecraft and Rockets, 2008, 45(4): 641-664. DOI:10.2514/1.34489 (  0) 0) |
| [18] |
Schneider S P. Hypersonic laminar-turbulent transition on circular cones and scramjet forebodies[J]. Progress in Aerospace Sciences, 2004, 40(1-2): 1-50. DOI:10.1016/j.paerosci.2003.11.001 (  0) 0) |
| [19] |
Lindörfer S A, Anusonti-Inthra P, Combs C S, et al. An investigation of the role of an upstream burst diaphragm on flow quality within a Ludwieg tube using RANS[R]. AIAA 2016-3801, 2016.
(  0) 0) |
| [20] |
Cummings R M, McLaughlin T E. Hypersonic Ludwieg tube design and future usage at the US air force academy[R]. AIAA 2012-734, 2012.
(  0) 0) |
| [21] |
Jewell J S, Huffman C C, Juliano T J. Transient startup simulations for a large Mach 6 quiet Ludwieg tube[R]. AIAA 2017-0743, 2017.
(  0) 0) |
| [22] |
Wu J, Radespiel R. Tandem nozzle supersonic wind tunnel design[J]. International Journal of Engineering Systems Modelling and Simulation, 2013, 5(1): 8-18. (  0) 0) |
| [23] |
Schrijer F F, Bannink W J. Description and flow assessment of the Delft Hypersonic Ludwieg tube[J]. Journal of Spacecraft and Rockets, 2010, 47(1): 125-133. DOI:10.2514/1.40773 (  0) 0) |
| [24] |
Stephan S, Wu J, Radespiel R. Propulsive jet influence on generic launcher base flow[J]. CEAS Space Journal, 2015, 1-21. (  0) 0) |
| [25] |
Liepmann H W, Roshko A. Elements of gasdynamics[M]. Courier Dover Publications, 1957.
(  0) 0) |
| [26] |
Rathakrishnan E. Instrumentation, measurements and experiments in fluids[M]. CRC PressI Llc, 2007.
(  0) 0) |
| [27] |
Anderson Jr J D. Fundamentals of aerodynamics[M]. McGraw-Hill Education, 1985.
(  0) 0) |
| [28] |
Anderson J D. Modern compressible flow with historical perspective[M]. New York: Mc Graw-Hill Book Company, 2003.
(  0) 0) |
| [29] |
Wu J, Liu X, Radespiel R. RANS simulations of a tandem nozzle supersonic wind tunnel[J]. Aerospace Science and Technology, 2016, 49: 215-224. DOI:10.1016/j.ast.2015.11.041 (  0) 0) |
| [30] |
Wu J, Radespiel R. Experimental investigation of a newly designed supersonic wind tunnel[J]. Progress in Flight Physics, 2015(7): 123-147. (  0) 0) |
| [31] |
Wu J, Zamre P, Radespiel R. Flow quality experiment in a tandem nozzle wind tunnel at Mach 3[J]. Experiments in Fluids, 2015, 56(1): 1-18. DOI:10.1007/s00348-014-1876-4 (  0) 0) |
| [32] |
Wu J, Li R. Numerical investigation of the application of porous material in tandem nozzle supersonic wind tunnels[R]. AIAA 2017-2125, 2017.
(  0) 0) |
| [33] |
Gerhold T. Overview of the hybrid RANS code TAU[M]. Springer: MEGAFLOW-Numerical Flow Simulation for Aircraft Design, 2005, 81-92.
(  0) 0) |
| [34] |
Mack A, Hannemann V. Validation of the unstructured DLR-TAU-code for hypersonic flows[R]. AIAA 2002-3111, 2002.
(  0) 0) |
| [35] |
Su Y X. Flow analysis and design of three-dimensional wind tunnel contractions[J]. AIAA Journal, 1991, 29(11): 1912-1920. DOI:10.2514/3.10818 (  0) 0) |
| [36] |
Mehta R D, Bell J H. Boundary-layer predictions for small low-speed contractions[J]. AIAA Journal, 1989, 27(3): 372-374. DOI:10.2514/3.10122 (  0) 0) |
| [37] |
Morel T. Comprehensive design of axisymmetric wind tunnel contractions[J]. Journal of Fluids Engineering, 1975, 97(2): 225-233. DOI:10.1115/1.3447255 (  0) 0) |
| [38] |
Hall I. Transonic flow in two-dimensional and axially-symmetric nozzles[J]. Quarterly Journal of Mechanics and Applied Mathematics, 1962, 15(4): 487-508. DOI:10.1093/qjmam/15.4.487 (  0) 0) |
| [39] |
Wu J, New T H. An investigation on supersonic bevelled nozzle jets[J]. Aerospace Science & Technology, 2017, 63: 278-293. (  0) 0) |
| [40] |
Sivells J C. Aerodynamic design of axisymmetric hypersonic wind-tunnel nozzles[J]. Journal of Spacecraft and Rockets, 1970, 7(11): 1292-1299. DOI:10.2514/3.30160 (  0) 0) |
| [41] |
Sivells J C. A computer program for the aerodynamic design of axisymmetric and planar nozzles for supersonic and hypersonic wind tunnels[R]. Arnold Engineering Development Center, Arnold TR-78-63, 1978.
(  0) 0) |
| [42] |
易仕和, 赵玉新, 何霖. 超声速与高超声速喷管设计[M]. 北京: 国防工业出版社, 2013.
(  0) 0) |
| [43] |
Wu J, Radespiel R. Investigation of instability waves in a Mach 3 laminar boundary layer[J]. AIAA Journal, 2015, 53(12): 3712-3725. DOI:10.2514/1.J054040 (  0) 0) |
| [44] | |
| [45] |
Wu J, Radespiel R. Damping insert materials for settling chambers of supersonic wind tunnels[J]. Experiments in Fluids, 2017, 58(3): 19. DOI:10.1007/s00348-017-2310-5 (  0) 0) |
| [46] |
Wu J, Zamre P, Radespiel R. Flow quality experiment in a tandem nozzle wind tunnel at Mach 3[J]. Experiments in Fluids, 2015, 56(1): 20. DOI:10.1007/s00348-014-1887-1 (  0) 0) |
| [47] |
Beckwith I E. Comments on settling chamber design for quiet, blowdown wind tunnels[R]. NASA TM-81948, 1981.
(  0) 0) |
| [48] |
Beckwith I E, Chen F J, Creel Jr T. Design requirements for the NASA Langley supersonic low-disturbance wind tunnel[R]. AIAA 86-0763, 1986.
(  0) 0) |
| [49] |
Zhang C H, Tang Q, Lee C B. Hypersonic boundary-layer transition on a flared cone[J]. Acta Mechanica Sinica, 2013, 29(1): 48-54. DOI:10.1007/s10409-013-0009-2 (  0) 0) |
| [50] |
周勇为, 常熹钰, 易仕和, 等. 超声速静风洞的气动设计[J]. 流体力学实验与测量, 2002, 16(1): 61-66. (  0) 0) |
| [51] |
陆小革, 易仕和, 周勇为, 等. Φ300 mm高超声速静风洞的设计[C]//第九届全国实验流体力学学术会议论文集(下册), 2013.
(  0) 0) |
| [52] |
Zuccher S, Saric W S. Infrared thermography investigations in transitional supersonic boundary layers[J]. Experiments in Fluids, 2008, 44(1): 145-157. (  0) 0) |
| [53] |
Knauss H, Riedel R, Wagner S. The shock wind tunnel of Stuttgart University-a facility for testing hypersonic vehicles[R]. AIAA 99-4959, 1999.
(  0) 0) |
| [54] |
Schneider S P. Mach-6 quiet-flow Ludwieg tube[R]. AIAA 2000-2592, 2000.
(  0) 0) |
| [55] |
Muñoz F, Heitmann D, Radespiel R. Instability modes in boundary layers of an inclined cone at Mach 6[J]. Journal of Spacecraft and Rockets, 2014, 51(2): 442-454. DOI:10.2514/1.A32564 (  0) 0) |
| [56] |
Stephan S, Radespiel R, Müller-Eigner R. Jet simulation facility using the Ludwieg tube principle[C]//5th EUCASS. Munich, 2013. https://docplayer.net/50036191-Jet-simulation-facility-using-the-ludwieg-tube-principle.html
(  0) 0) |
 2018, Vol. 36
2018, Vol. 36