2. 中国空气动力研究与发展中心 计算空气动力研究所, 四川 绵阳 621000
2. Computational Aerodynamics Instatitiute of China Aerodynamics Research and Development Center, Mianyang 621000, China
高超声速情况下湍流的摩阻和热流通常是层流的3-5倍[1],湍流/层流转捩问题严重影响高超声速飞行器的气动特性和热防护系统。高超声速情况下边界层流动容易经历层流/湍流转捩[2],发展高超声速边界层转捩控制方法,推迟边界层流动从层流转捩成湍流,对减阻和热防护具有重要意义。但是高超声速边界层转捩现象非常复杂,影响因素众多,转捩控制极为困难。在转捩被动控制方法中,国外的研究表明,多孔表面、微槽道和超声波吸声材料或许可用来推迟转捩[3-7]。但是,这类控制方法的风洞实验难度大成本高,数值模拟也面临着算法、网格和计算量等方面的诸多困难。因此,通过简化模型、采用线性稳定性理论(LST)从转捩机理的角度对这类控制方法开展研究是目前少数可用的快速且低成本的技术途径之一。Fedorov[3]和Kozlov[4]等通过声波在无穷长管道中的传播关系对多孔表面的扰动边界条件进行了简化,Sandham[5]和Wartemann[6]等通过时间模式的直接数值模拟验证了这种简化方法是可行的。我们采用Fedorov[3]和Kozlov[4]多孔表面边界处理方法,分析了开孔率和孔半径对第二模态扰动波的影响,得到了抑制扰动波幅值增长的最优开孔率和孔半径。
1 线性稳定性理论在边界层稳定性和转捩研究中,LST被广泛用于研究边界层中小扰动演化情况(比如幅值增长率),然后可通过半经验eN方法预测转捩。
设流动可用基本流叠加扰动构成,如
| $ \tilde \phi = {\phi _0} + \phi ' $ | (1) |
其中ϕ0=[ρ0, u0, v0, w0, T0]T为基本流,ϕ′=[ρ′, u′, v′, w′, T′]T为小扰动。把叠加了扰动的流场代入Navier-Stokes方程,减去基本流满足的部分,略去二阶及高阶, 得到线化扰动方程:
| $ \begin{array}{l} \mathit{\boldsymbol{ \boldsymbol{\varGamma} }}\frac{{\partial \phi '}}{{\partial t}} + \mathit{\boldsymbol{A}}\frac{{\partial \phi '}}{{\partial x}} + \mathit{\boldsymbol{B}}\frac{{\partial \phi '}}{{\partial y}} + \mathit{\boldsymbol{C}}\frac{{\partial \phi '}}{{\partial z}} + \mathit{\boldsymbol{D}}\phi ' = \\ \;\;\;\;\;{\mathit{\boldsymbol{V}}_{xx}}\frac{{{\partial ^2}\phi '}}{{\partial {x^2}}} + {\mathit{\boldsymbol{V}}_{yy}}\frac{{{\partial ^2}\phi '}}{{\partial {y^2}}} + {\mathit{\boldsymbol{V}}_{zz}}\frac{{{\partial ^2}\phi '}}{{\partial {z^2}}} + {\mathit{\boldsymbol{V}}_{xy}}\frac{{{\partial ^2}\phi '}}{{\partial xy}}\\ \;\;\;\;\; + {\mathit{\boldsymbol{V}}_{xz}}\frac{{{\partial ^2}\phi '}}{{\partial xz}} + {\mathit{\boldsymbol{V}}_{yz}}\frac{{{\partial ^2}\phi '}}{{\partial yz}} \end{array} $ | (2) |
其中系数矩阵Γ、A、B、C、D、Vxx等为线性系数矩阵,只与雷诺数、基本流场及其一阶和二阶导数有关。在推导过程中进行了无量纲处理,参考压力为ρ∞*u∞*2,参考长度2 mm(在本文计算工况下约等于x=235 mm处的边界层排移厚度),其他参考量采用来流参数。
并假定基本流是平行流(即v=0),并进一步假设扰动可表示成如下行波的线性叠加。
| $ \phi ' = \hat \phi \left( y \right){{\rm{e}}^{{\rm{i}}\left( {\alpha x + \beta z - \omega t} \right)}} + {\rm{c}}.{\rm{c}}. $ | (3) |
式中c.c.表示对应的复共轭。把式(3)代入线化扰动方程,可得到常微分方程:
| $ \left[ {{\mathit{\boldsymbol{C}}_2}\frac{{{{\rm{d}}^2}}}{{{\rm{d}}{y^2}}} + {\mathit{\boldsymbol{C}}_1}\frac{{\rm{d}}}{{{\rm{d}}y}} + {\mathit{\boldsymbol{C}}_0}} \right]\hat \phi = 0 $ | (4) |
其中系数矩阵
| $ \begin{array}{l} {\mathit{\boldsymbol{C}}_0} = \mathit{\boldsymbol{D}} - {\rm{i}}\omega \mathit{\boldsymbol{ \boldsymbol{\varGamma} }} + {\rm{i}}\alpha \mathit{\boldsymbol{A}} + {\rm{i}}\beta \mathit{\boldsymbol{C}} + {\alpha ^2}{\mathit{\boldsymbol{V}}_{xx}} + \\ \;\;\;\;\;\;\;\;{\beta ^2}{\mathit{\boldsymbol{V}}_{zz}} + \alpha \beta {\mathit{\boldsymbol{V}}_{xz}} \end{array} $ |
| $ {\mathit{\boldsymbol{C}}_1} = \mathit{\boldsymbol{B}} - {\rm{i}}\alpha {\mathit{\boldsymbol{V}}_{xy}} - {\rm{i}}\beta {\mathit{\boldsymbol{V}}_{yz}} $ |
| $ {\mathit{\boldsymbol{C}}_2} = - {\mathit{\boldsymbol{V}}_{yy}} $ |
可见C0~C2与流向波数α、展向波数β、圆频率ω、和式(2)的线性系数矩阵Γ、A、B等有关。当给定基本流场后,式(2)的线性系数矩阵就已知了,式(4)所表达的是一个特征值问题,只有当α、β和ω满足一定关系时才有特征解,这个关系被称为色散关系式。稳定性分析时可给定其中两个参数,只需求解剩下的一个。实际求解通常分时间模式和空间模式两种情况:对于时间模式的扰动,α和β为实数,ω=ωr+iωi为复数;对于空间模式,ω为实数,α和β为复数。由于时间模式比空间模式求解更方便,本文仅考虑了时间模式,ωi表示扰动波的幅值随着时间按eωi指数型增长/衰减情况。
通过合适的边界条件(下文讨论),便可求解式(4)。求解时可以把它转化成单变量的8次方程,也可直接求解,通常采用高阶精度方法。本文采用Chebychev点配置法对式(4)进行离散。
2 边界条件对于光滑壁面,壁面取无滑移边界和等温边界,即:
| $ u' = v' = w' = T' = 0 $ | (5) |
对于远场,施加速度及温度扰动等于零的条件。
对于多孔介质表面,远场边界条件与光滑壁面相同,但是壁面条件需要考虑孔壁对扰动波的干扰作用。假设多孔介质的孔径远远小于边界层厚度,对边界层宏观流动(基本流场)无影响,但对声波、T-S波等的影响不可忽略。同时假设孔的深度远大于半径,于是扰动在孔中的传播可以简化为声波在无穷长管道中的传播,根据Fedorov[3]和Kozlov[4]等的研究,壁面上的边界条件为:
| $ \hat u = \hat w = 0,\;\;\;\;\hat v = A\hat p,\;\;\;\;\hat T = B\hat p $ | (6) |
其中系数A和B通过声波在无穷长管道中的传播关系来确定,
| $ \left\{ \begin{array}{l} A = - \frac{n}{{{Z_0}}}\tanh \left( {\mathit{\Lambda }h} \right)\\ B = - n\left( {\gamma - 1} \right)M_e^2{T_w}\frac{{{J_2}\left( {{k_t}} \right)}}{{{J_0}\left( {{k_t}} \right)}} \end{array} \right. $ | (7) |
其中,
| $ \mathit{\Lambda = }\frac{{{\rm{i}}\omega {M_e}}}{{\sqrt {{T_w}} }}\sqrt { - \frac{{{J_0}\left( {{k_v}} \right)}}{{{J_2}\left( {{k_v}} \right)}}\left[ {\gamma + \left( {\gamma - 1} \right)\frac{{{J_2}\left( {{k_t}} \right)}}{{{J_0}\left( {{k_t}} \right)}}} \right]} , $ |
| $ {Z_0} = \frac{1}{{{M_e}\sqrt {{T_w}} }}\sqrt {\frac{{ - {J_0}\left( {{k_v}} \right){J_0}\left( {{k_t}} \right)}}{{{J_2}\left( {{k_v}} \right)\left[ {\gamma {J_0}\left( {{k_t}} \right) + \left( {\gamma - 1} \right){J_2}\left( {{k_t}} \right)} \right]}}} , $ |
| $ {k_v} = r\sqrt {\frac{{{\rm{i}}\omega {\rho _w}\mathit{Re}}}{{{\mu _w}}}} ,{k_t} = {k_v}\sqrt {\mathit{Pr}} 。$ |
上面各式中:n为开孔率,定义为控制区域内孔面积所占总面积的比例(由于孔的间距不能小于孔的直径,所以最大开孔率为π/4);r为孔的半径,在给定开孔率的情况下,孔半径越小,表示单位面积上孔的个数越多;h为孔的深度;J0和J2为第一类Bessel方程;Me为边界层外缘马赫数;Re为雷诺数;Pr为普朗特数;γ为比热比;下标“w”表示物面。
ω既是时间模式的解,又是边界条件的输入参数,采用迭代方法求解ω,当迭代误差小于1×10-8时,认为结果已经收敛。
由于高超声速平板边界层中第二模态扰动波占主导作用,且第二模态扰动波中的二维扰动增长最快,所以我们仅分析二维扰动波,即展向波数β=0。
3 多孔表面对马赫数6平板边界层稳定性的影响 3.1 基本流场和方法考核边界层基本流动的参数与Sandham等[5]相同,马赫数为6.0,来流温度216.65 K,壁面温度1522.44 K。但是,本文获取基本流的方法与Sandham等的方法不同。Sandham等在边界层相似解的假设下采用Blasius解,而本文采用基于WCNS格式[8]的高阶精度CFD方法[9-10]求解Navier-Stokes方程。本文方法的优点是更接近实际情况,因为实际流动中,平板前缘因边界层开始生成,会出现一道微弱的斜激波(图 1),而Blasius相似解忽略了这道斜激波。
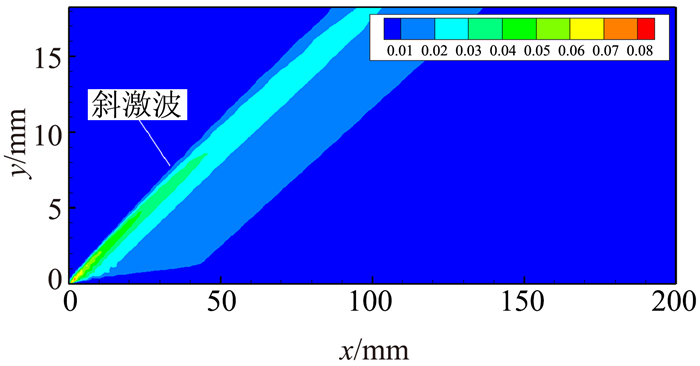
|
图 1 边界层法向速度云图 Figure 1 Wall-normal velocity of the boundary layer |
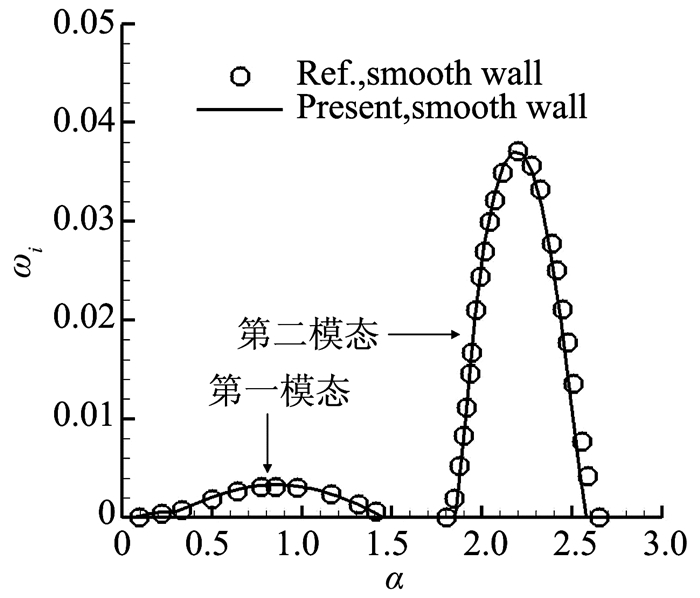
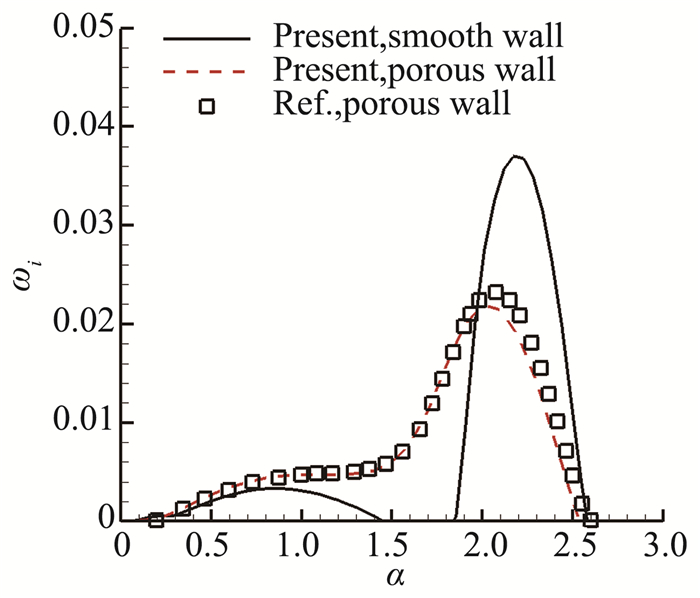
为了便于与文献比较,取排移厚度等于2 mm的边界层剖面进行稳定性分析,并以此尺度作为全文计算的参考长度。由于文献没有考虑法向速度,本文首先强制法向速度为零,通过与文献比较考察本文方法的正确性。图 2给出了流向波数为α=2π/3的扰动波形状函数,可见与文献[5]非常一致。图 3在光滑壁面上比较了本文计算的扰动增长率和文献[6](文献[5]和文献[6]为同一边界层)的结果,可见二者基本一致。图 4比较了光滑表面和多孔介质表面上的扰动波幅值增长率,还同时给出了文献[6]的计算结果,可见本文结果与文献结果一致,都表明:多孔介质能大大降低第二模态的最大增长率;多孔介质对第一模态有轻微的放大作用。

|
图 2 α=2π/3扰动波的形状函数 Figure 2 Shape function of the α=2π/3 wave |
|
图 3 光滑表面上扰动波的增长率 Figure 3 Increase rates of disturbances in the boundary layer of smooth wall |
|
图 4 多孔介质表面与光滑表面的比较 Figure 4 Comparison between the porous wall and smooth wall |
仔细观察图 3和图 4可以发现,当流向波数较小时,本文结果与文献结果几乎完全一致;当流向波数较大时(比如α>2)时,本文结果与文献有轻微差别,这种差别可能是由基本流速度剖面的细微差别引起的。文献中的速度剖面采用的是Blasius相似解,而本文采用的是DNS结果(但在LST分析时法向速度强制赋零)。由于法向速度很小,所以对波长较长(即波数较小)的扰动波的影响非常小,仅对波长较短(即波数较大)的扰动波有轻微影响。下文还将进一步讨论基本流的法向速度对多孔介质控制效果的影响。
3.2 最优开孔率和孔半径文献[6]研究表明,当孔深超过0.8倍边界层排移厚度时,控制效果基本上不再随着孔的深度变化。本文不研究孔深的影响,而是给定孔深为2 mm(等于x=235 mm处的边界层排移厚度),研究开孔率和孔半径的影响。
我们早期的考察结果表明[11],并不是开孔率越大越好,最不稳定扰动波的增长率并不是随着开孔率单调变化,而是存在最优开孔率。早期考察还表明,控制效果随孔半径的变化趋势也不是单调的,而是存在最优孔半径。为了寻找最优的控制策略,我们在较为广泛的控制参数范围内全局寻优,其中开孔率n的范围为0.05~0.75;孔半径r的范围为0.01~0.3 mm。图 5给出了距离平板前缘235 mm处最不稳定第二模态扰动增长率ωi随开孔率n和孔半径r的变化情况。可见最优控制的组合参数是n≈0.35,r≈0.20 mm。此时最不稳定时间模式扰动波的增长率仅为光滑平板情况下的38%,失稳扰动波的增长率大幅减小,有利于推迟转捩。
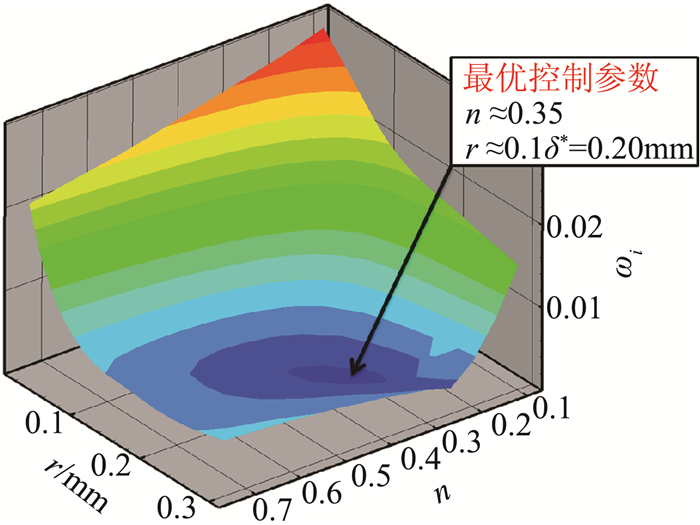
|
图 5 x=235 mm处最不稳定第二模态扰动波增长率ωi与开孔率n和孔半径r的关系 Figure 5 Increase rates of the most unstable mode-2 waves in the porosity n and pore radius r coordinates |
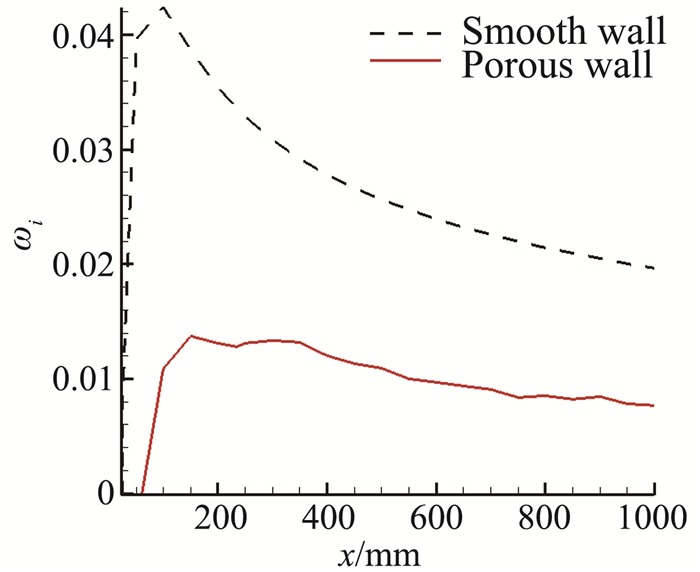
图 6比较了多孔介质表面和光滑表面的最不稳定第二模态扰动波的幅值增长率。通过采用多孔介质,扰动波开始增长的位置(中性点)从距离平板前缘24 mm推迟到了50 mm的地方,推迟比例约1倍。不仅如此,扰动波的幅值增长率也大幅减小。在所考察的1000 mm长的平板范围内,扰动波的幅值增长率不超过光滑平板的40%。图 6还表明,除了头部区域,多孔平板情况下最不稳定扰动波增长率沿流向单调降低,与光滑平板类似。在头部区域,扰动波增长率被抑制的比例更大,这说明把多孔介质安装在扰动波增长最快的区域可达到最佳控制效果。
|
图 6 最不稳定第二模态扰动波增长率沿流向比较 Figure 6 Increase rates of the most unstable mode-2 waves along the wall |
图 7给出了不同流向位置上的最优开孔率和孔半径。在x<600 mm的地方,开孔率沿流向并不是单调变化,在x=450 mm的地方达到最大值0.66左右。最优孔半径的变化范围比较小,最大值为0.22,最小值为0.19,大部分都在0.21 mm左右,这对设计多孔壁非常有利。

|
图 7 最优开孔率和孔半径沿流向变化 Figure 7 The optimal porosity and pore radius along the wall |
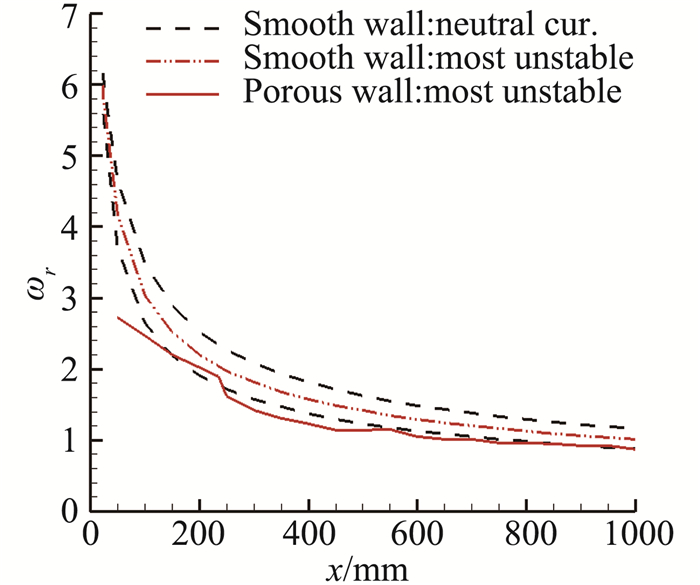
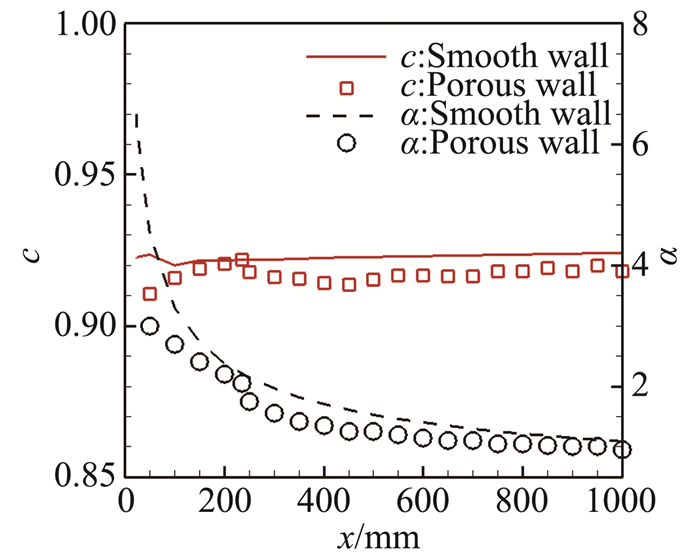
在最优多孔控制参数情况下,最不稳定扰动波的圆频率有所降低,接近光滑壁第二模态中性曲线的下支(图 8)。从图 9可以看出,多孔壁使最不稳定第二模态扰动波的相速度和流向波数轻微减小。
|
图 8 第二模态扰动波圆频率沿流向分布 Figure 8 Circular frequencies of mode-2 waves along the wall |
|
图 9 最不稳定第二模态的相速度c和流向波数α Figure 9 Phase speeds and stream-wise wavenumbers of most unstable mode-2 waves |
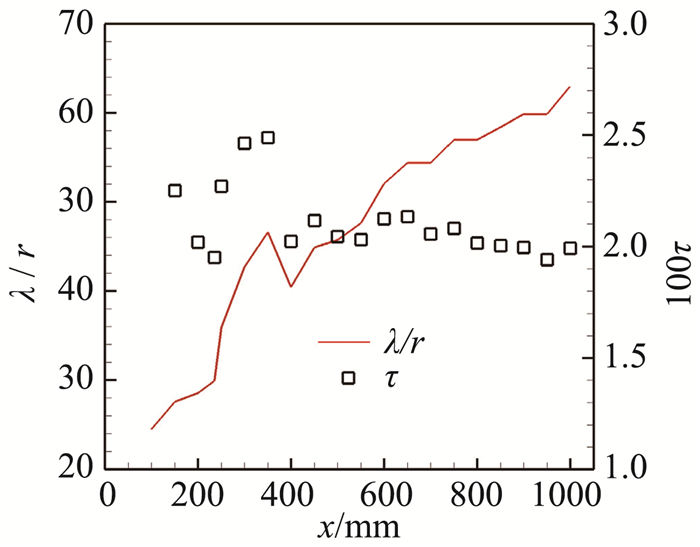
图 10给出了扰动波长与最优孔半径的关系,可见最不稳定扰动波长为最优孔半径的20倍以上,且随着下游发展,扰动波长与最优孔半径之比持续增加,这可能是由边界层增厚引起的。边界层越厚,最不稳定扰动波的波长越长。定义如下衡量扰动波波长与孔半径的无量纲参数:
| $ \tau = \mathit{Re}_x^{ - 1/2}\frac{\lambda }{r} $ | (8) |
|
图 10 最优孔半径与最不稳定扰动波长之间的关系 Figure 10 Optimal pore radius vs. stream-wise wavelength |
其中, λ为扰动波波长,r为孔半径,Rex为当地雷诺数(参考量长度为当地至前沿的距离,其他参考量为边界层外缘参数)。从图 10可以看出,除头部区域外,τ为0.02左右。
3.3 当地基本流法向速度的影响边界层流动大多不是严格的平行流,但是上述分析采用了平行流假设(v0=0),这会带来一定的误差;另外,多孔壁的扰动边界条件(6)中法向扰动不等于零,所以有必要分析基本流非平行性的影响。我们保留高阶精度CFD计算得到的基本流的法向速度(v0≠0)。即对基本流的速度进行如下扩展:
| $ {U_0} = \left[ \begin{array}{l} {u_0}\left( y \right)\\ 0\\ {w_0}\left( y \right) \end{array} \right] \to {U_0} = \left[ \begin{array}{l} {u_0}\left( y \right)\\ {v_0}\left( y \right)\\ {w_0}\left( y \right) \end{array} \right] $ | (9) |
从严格意义上理解,在非平行流假设下并不能把小扰动表示成式(3)的行波解形式。幸运的是大部分边界层的法向速度相对于流向速度是一个小量,式(3)仍然近似可行,且在实验中已经普遍证明了边界层确实存在行波(比如第一、二模态扰动波)。这说明仍然可在LST框架下保留法向速度。如果忽略形状函数和空间波数的流向变化,则仍然可以把扰动方程化为与式(4)类似的常微分方程,其边界条件和求解方法与传统LST一样。这样处理的优点是可以直接借用传统LST的分析方法和经验,缺点是仅能考虑当地非平行性的影响,而不能体现上下游的关系,是介于传统LST和抛物化稳定性分析方法之间的一种分析方法。抛物化稳定性分析方法保留了法向速度和流向1/Re量级的变化量。
图 11比较了法向速度对控制效果的影响。法向速度对最优开孔率和孔半径的影响非常小,除了头部区域,对最优开孔率的影响小于10%,对最优孔半径的影响小于5%。法向速度对控制效果有一定的影响,在头部区域,扰动波增长率可减小超过30%,但是随着向下游发展,考虑法向速度与不考虑法向速度的差异逐渐减小。总之,基于平行流假设得到的最优开孔率和孔半径仍然有效,对控制效果的估计偏保守。
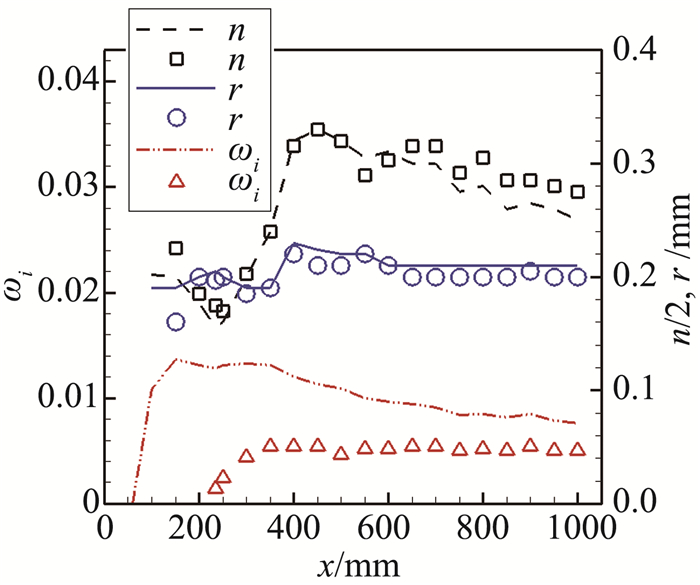
|
图 11 基本流法向速度对控制效果的影响(图中线条表示不考虑法向速度的结果,符号表示考虑法向速度的结果) Figure 11 Comparison between the results with and without wall-normal velocity of base flow (The symbols are results with wall-normal velocity; the lines are results without wall-normal velocity.) |
当参数合适时,多孔介质表面对第二模态扰动波的幅值增长率具有抑制作用。多孔介质的关键参数有三个:开孔率、孔半径和孔深。文献中采用时间模式DNS对马赫数6平板边界层的分析表明,当孔深超过边界层排移厚度的0.8倍时,控制效果基本不再随孔深变化。但是文献还未研究开孔率和孔半径对控制效果的影响。我们采用时间模式的线性稳定性理论,在孔深为2 mm的情况下,分析了开孔率和孔半径对控制效果的影响。在分析时,通过声波在无限长管道中的传播关系来确定LST的多孔壁面条件。
研究发现,采用多孔介质表面可以大大推迟第二模态扰动波的中性点,对于本文的马赫数6平板边界层,中性点距离平板前缘的位置从24 mm推迟到了50 mm。最优开孔率与流向位置紧密相关,大致变化范围是0.31至0.66之间。最优孔半径与流向位置关系不大,基本在0.2 mm左右波动。通过最不稳定扰动波长、最优孔半径和当地雷诺数组成的无量纲参数τ约等于0.02。
我们还考察了基本流的法向速度对扰动波的影响。与平行流假设相比,法向速度对最优开孔率和孔半径的影响较小,对控制效果的影响仅在头部区域比较明显,但是随着下游发展,影响趋势逐渐减弱。
上述结果是在多孔表面对基本流的影响可以忽略的假设下采用时间模式LST得到的。当开孔率较大时,多孔表面对基本流的影响将变得重要起来;另外,当孔半径较大时,多孔介质本身还会诱导声波;当孔半径较小时,需要考虑稀薄气体效应,文献[12]发现稀薄效应可以增强多孔介质的控制效果,但本文还未开展相关研究。由于空间模式LST与真实流动更一致,建议后续采用空间模式LST开展研究。
致谢:在研究过程中得到了天津大学曹伟教授、刘建新博士和赵磊博士的指点和帮助,对他们表示感谢。
| [1] |
Li F, Xie S F, Bi Z X. Experimental study of several on aerodynamicproblems on hypersonic vehicles[J]. Modern Defence Technology, 2014, 42(5): 1-7. (in Chinese) 李锋, 解少飞, 毕志献, 等. 高超声速飞行器中若干气动难题的实验研究[J]. 现代防御技术, 2014, 42(5): 1-7. (  0) 0) |
| [2] |
Chen J Q, Tu G H, Zhang Y F, et al. Hypersnonic boundary layer transition:what we know, where shall we go[J]. Acta Aerodynamics Sinica, 2017, 35(3): 311-337. (in Chinese) 陈坚强, 涂国华, 张毅锋, 等. 高超声速边界层转捩研究现状与发展趋势[J]. 空气动力学学报, 2017, 35(3): 311-337. (  0) 0) |
| [3] |
Alexander V Fedorov. Stabilization of hypersonic boundary layers by porous coatings[J]. AIAA J, 2001, 39(4): 605-610. DOI:10.2514/2.1382 (  0) 0) |
| [4] |
Kozlov V F, Fedorov A V, Malmuth N D. Acoustic properties of rarefied gases inside pores of simple geometries[J]. J. Acoustical Society of America, 2005, 117(6): 3402-3412. DOI:10.1121/1.1893428 (  0) 0) |
| [5] |
Neil D Sandham, Heinrich Lüdeke. Numerical study of Mach 6 boundary-layer stabilization by means of a porous surface[J]. AIAA J, 2009, 47(9): 2243-2252. DOI:10.2514/1.43388 (  0) 0) |
| [6] |
Wartemann W, Lüdeke H, Sandham N D. Numerical investigation of hypersonic boundary-layer stabilization by porous surfaces[J]. AIAA Journal, 2012, 50(6): 1281-1290. DOI:10.2514/1.J051355 (  0) 0) |
| [7] |
Nicola DeTullio, Neil D Sandham. Direct numerical simulation of breakdown to turbulence in a Mach 6 boundary layer over a porous surface[J]. Physics of Fluids, 2010, 22: 094105. DOI:10.1063/1.3481147 (  0) 0) |
| [8] |
Deng X G, Mao M L, Tu G H, et al. Extending weighted compact nonlinear schemes to complex grids with characteristic-based interface conditions[J]. AIAA Journal, 2010, 48(12): 2840-2851. DOI:10.2514/1.J050285 (  0) 0) |
| [9] |
Tu G H, Deng X G, Min Y B, et al. Method for evaluating spatial accuracy order of CFD and applications to WCNS scheme on four typically distorted meshes[J]. Acta Aerodynamica Sinica, 2014, 32(04): 425-432. (in Chinese) 涂国华, 邓小刚, 闵耀兵, 等. CFD空间精度分析方法及4种典型畸形网格中WCNS格式精度测试[J]. 空气动力学学报, 2014, 32(4): 425-432. (  0) 0) |
| [10] |
Tu G H, Deng X G, Mao M L. Spectral property comparison of fifth-order nonlinear WCNS and WENO difference schemes[J]. Acta Aerodynamica Sinica, 2012, 30(6): 709-712. (in Chinese) 涂国华, 邓小刚, 毛枚良. 5阶非线性WCNS和WENO差分格式频谱特性比较[J]. 空气动力学学报, 2012, 30(6): 709-712. (  0) 0) |
| [11] |
Tu G H, Chen J Q, Yuan X X, et al. Stabilizing a Mach 6 flat plate boundary layer by porous wall[C]//The 17th national conference on CFD, 2017, Hangzhou, China, CARS-2017-03-165, 141-146. (in Chinese) 涂国华, 陈坚强, 袁先旭, 等. 多孔介质对马赫6平板边界层稳定性的影响[C]//第十七届全国计算流体力学会议, 2017, 杭州: CARS-2017-03-165, 141-146. (  0) 0) |
| [12] |
Fedorov A, Kozlov V, Shiplyuk A, et al. Stability of hypersonic boundary layer on porous wall with regular microstructure[J]. AIAA J, 2006, 44(8): 1866-1871. DOI:10.2514/1.21013 (  0) 0) |
 2018, Vol. 36
2018, Vol. 36


