2. 中国工程物理研究院 流体物理研究所, 四川 绵阳 621900;
3. 天津市现代工程力学重点实验室, 天津 300072
2. Institute of Fluid Physics, China Academy of Engineering Physics, Mianyang 621900, China;
3. Tianjin Key Laboratory of Modern Engineering Mechanics, Tianjin 300072, China
高超声速扁平形升力体的气动力和气动热问题是当前航空航天领域遇到的重要问题,其短轴处的转捩位置和热流明显与两侧不同[1-2]。这是由于短轴处基本流存在流向涡[3-6],与两侧的基本流有本质的区别,导致短轴处稳定性与两侧有本质区别,最终导致转捩位置和热流不同。为了预测短轴处的转捩和热流,可以椭圆锥作为模型,研究其短轴处的稳定性。该处基本流沿展向和法向的变化同量级,而沿流向的变化要小得多,所以是二维全局稳定性问题。
人们认识到短轴处是二维全局稳定性问题,经历了一个过程。20世纪90年代中期,人们开始注意到短轴处的不稳定性[7],但一直用一维剪切层不稳定性来考虑问题[8-9],所得计算结果始终无法得到实验数据[10]的支持。直至2009年,Choudhari等[11]才明确指出该处的稳定性与两侧完全不同,需要用全局稳定性分析研究。直到最近,Paredes和Theofilis[12-13]才在长短轴比为2:1椭圆锥,来流马赫数7,单位雷诺数分别为8×105/m和1.89×106/m的短轴处找到了不稳定的外模态,其特征是特征函数峰值位置远离壁面,靠近边界层外缘,相速度较高。除了外模态,Zhang和Luo[14]在不可压展向局部型自由湍流带条纹边界层中还找到过内模态,其特征是特征函数峰值位置靠近壁面,相速度较低。
在Paredes和Theofilis[12-13]研究的基础之上,有以下几个更深入的具体问题需要回答:(1)是否有不稳定的内模态;(2)有哪些不稳定的外模态;(3)同一流向位置,不稳定模态随波数(频率)的变化规律;(4)不稳定模态沿流向的演化规律;(5)不稳定模态的物理本质,是否都由无粘的拐点不稳定性造成的。本文正是针对这几个问题进行研究。
1 数值计算方法本文使用Arnoldi方法和Rayleigh商迭代法计算椭圆锥短轴处二维全局稳定性问题,Arnoldi方法能够求解指定范围的全部特征值,能够很方便的用来寻找特征模态的种类[14]。Rayleigh商迭代法,对于追踪某一特定模态随着某一参量的演化更为方便。
1.1 基本流求解方法椭圆锥基本流是通过直接数值模拟求解三维守恒型可压缩N-S方程得到的,控制方程如下:
| $ \frac{{\partial \mathit{\boldsymbol{U}}}}{{\partial t}} + \frac{{\partial \mathit{\boldsymbol{E}}}}{{\partial x}} + \frac{{\partial \mathit{\boldsymbol{F}}}}{{\partial y}} + \frac{{\partial \mathit{\boldsymbol{G}}}}{{\partial z}} = \frac{{\partial {\mathit{\boldsymbol{E}}_v}}}{{\partial x}} + \frac{{\partial {\mathit{\boldsymbol{F}}_v}}}{{\partial y}} + \frac{{\partial {\mathit{\boldsymbol{G}}_v}}}{{\partial z}} $ | (1) |
式中,(x, y, z)表示空间坐标,t表示时间变量,U=(ρ, ρu, ρv, ρw, ρe)T为守恒变量,ρ为密度,e=cvT+(u2+v2+w2)/2,cv为比定容热容,T为温度;u、v、w分别表示x、y、z方向的速度分量,E、F、G分别为x、y、z方向的对流项通量,Ev、Fv、Gv分别为x、y、z方向的粘性项通量。
本文采用Sutherland公式计算粘性系数及热传导系数,即:
| $ \mu = {\mu _\infty }{\left( {\frac{T}{{{T_\infty }}}} \right)^{3/2}}\frac{{{T_\infty } + {C_\mu }}}{{T + {C_\mu }}} $ | (2) |
| $ \kappa = {\kappa _\infty }{\left( {\frac{T}{{{T_\infty }}}} \right)^{3/2}}\frac{{{T_\infty } + {C_\kappa }}}{{T + {C_\kappa }}} $ | (3) |
其中,Cκ、Cμ为参考温度,本文均取为110.4 K。在实际情况中,因为椭圆锥模型较为复杂,使得计算网格具有不规则性和复杂性,在一般曲线坐标系计算更为方便。通过坐标变换,得到一般曲线坐标系下的控制方程:
| $ \frac{{\partial \mathit{\boldsymbol{\hat U}}}}{{\partial t}} + \frac{{\partial \mathit{\boldsymbol{\hat E}}}}{{\partial \xi }} + \frac{{\partial \mathit{\boldsymbol{\hat F}}}}{{\partial \eta }} + \frac{{\partial \mathit{\boldsymbol{\hat G}}}}{{\partial \zeta }} = \frac{{\partial {{\mathit{\boldsymbol{\hat E}}}_v}}}{{\partial \xi }} + \frac{{\partial {{\mathit{\boldsymbol{\hat F}}}_v}}}{{\partial \zeta }} + \frac{{\partial {{\mathit{\boldsymbol{\hat G}}}_v}}}{{\partial \zeta }} $ | (4) |
式中:
| $ \begin{array}{l} \mathit{\boldsymbol{\hat U}} = J\mathit{\boldsymbol{U}}\\ \mathit{\boldsymbol{\hat E}} = J\left( {{\xi _x}\mathit{\boldsymbol{E}} + {\xi _y}\mathit{\boldsymbol{F}} + {\xi _z}\mathit{\boldsymbol{G}}} \right)\\ {{\mathit{\boldsymbol{\hat E}}}_v} = J\left( {{\xi _x}{\mathit{\boldsymbol{E}}_v} + {\xi _y}{\mathit{\boldsymbol{F}}_v} + {\xi _z}{\mathit{\boldsymbol{G}}_v}} \right)\\ \mathit{\boldsymbol{\hat F}} = J\left( {{\eta _x}\mathit{\boldsymbol{E}} + {\eta _y}\mathit{\boldsymbol{F}} + {\eta _z}\mathit{\boldsymbol{G}}} \right)\\ {{\mathit{\boldsymbol{\hat F}}}_v} = J\left( {{\eta _x}{\mathit{\boldsymbol{E}}_v} + {\eta _y}{\mathit{\boldsymbol{F}}_v} + {\eta _z}{\mathit{\boldsymbol{G}}_v}} \right)\\ \mathit{\boldsymbol{\hat G}} = J\left( {{\zeta _x}\mathit{\boldsymbol{E}} + {\zeta _y}\mathit{\boldsymbol{F}} + {\zeta _z}\mathit{\boldsymbol{G}}} \right)\\ {{\mathit{\boldsymbol{\hat G}}}_v} = J\left( {{\zeta _x}{\mathit{\boldsymbol{E}}_v} + {\zeta _y}{\mathit{\boldsymbol{F}}_v} + {\zeta _z}{\mathit{\boldsymbol{G}}_v}} \right) \end{array} $ | (5) |
二维全局稳定性分析方法(Bi-Global),是一维线性稳定性理论的扩展,是在当地求解特征值问题。无量纲化后的非守恒型N-S方程如下:
| $ \begin{array}{l} \frac{{D\rho }}{{Dt}} + \rho \left( {\nabla \cdot \mathit{\boldsymbol{V}}} \right) = 0\\ \rho \frac{{D\mathit{\boldsymbol{V}}}}{{Dt}} = - \nabla P + \frac{1}{{\mathit{Re}}}\left\{ {\nabla \left[ {\lambda \left( {\nabla \cdot \mathit{\boldsymbol{V}}} \right)} \right] + } \right.\\ \;\;\;\;\;\;\;\;\;\;\;\left. {\nabla \cdot \left[ {\mu \left( {\left( {\nabla \mathit{\boldsymbol{V}}} \right) + {{\left( {\nabla \mathit{\boldsymbol{V}}} \right)}^{\rm{T}}}} \right)} \right]} \right\}\\ \rho {C_V}\frac{{DT}}{{Dt}} + P\nabla \cdot \mathit{\boldsymbol{V}} - \frac{1}{{\mathit{RePr}}}\frac{1}{{\left( {\gamma - 1} \right){M^2}}}\nabla \cdot \left( {\kappa \nabla T} \right)\\ = \frac{1}{{\mathit{Re}}}\left\{ {\lambda {{\left( {\nabla \cdot \mathit{\boldsymbol{V}}} \right)}^2} + \frac{\mu }{2}{{\left[ {\left( {\nabla \mathit{\boldsymbol{V}}} \right) + {{\left( {\nabla \mathit{\boldsymbol{V}}} \right)}^{\rm{T}}}} \right]}^2}} \right\} \end{array} $ | (6) |
式中:
将瞬时物理量写成基本流和扰动量之和,消去基本流满足的方程,忽略二阶及以上扰动量,得到非守恒形式的线性扰动方程。通过链式求导法则,将直角坐标系的导数转化到一般曲线坐标系下,得到一般曲线坐标系下的线性扰动方程:
| $ \begin{array}{l} \mathit{\boldsymbol{ \boldsymbol{\varGamma} }}\frac{{\partial \phi }}{{\partial t}} + \mathit{\boldsymbol{\tilde A}}\frac{{\partial \phi }}{{\partial \xi }} + \mathit{\boldsymbol{\tilde B}}\frac{{\partial \phi }}{{\partial \eta }} + \mathit{\boldsymbol{\tilde C}}\frac{{\partial \phi }}{{\partial \zeta }} + \mathit{\boldsymbol{D}}\phi \\ = {\mathit{\boldsymbol{V}}_{\xi \xi }}\frac{{{\partial ^2}\phi }}{{\partial {\xi ^2}}} + {\mathit{\boldsymbol{V}}_{\eta \eta }}\frac{{{\partial ^2}\phi }}{{\partial {\eta ^2}}} + {\mathit{\boldsymbol{V}}_{\zeta \zeta }}\frac{{{\partial ^2}\phi }}{{\partial {\zeta ^2}}} + \\ {\mathit{\boldsymbol{V}}_{\xi \eta }}\frac{{{\partial ^2}\phi }}{{\partial \xi \partial \eta }} + {\mathit{\boldsymbol{V}}_{\xi \zeta }}\frac{{{\partial ^2}\phi }}{{\partial \xi \partial \zeta }} + {\mathit{\boldsymbol{V}}_{\eta \zeta }}\frac{{{\partial ^2}\phi }}{{\partial \eta \partial \zeta }} \end{array} $ | (7) |
椭圆锥短轴附近的流向涡,在展向变化剧烈,不能像LST一样设成行进波形式,但流向变化依然较为缓慢,因此流向引入局部平行假设,设成行进波:
| $ \phi \left( {\xi ,\eta ,\zeta ,t} \right) = \hat \phi \left( {\eta ,\zeta } \right){{\rm{e}}^{{\rm{i}}\left( {\alpha \xi - \omega t} \right)}} + {\rm{c}}{\rm{.c}}{\rm{.}} $ | (8) |
代入上式,即可以得到二维线性稳定性方程:
| $ \mathit{\boldsymbol{\hat B}}\frac{{\partial \hat \phi }}{{\partial \eta }} + \mathit{\boldsymbol{\hat C}}\frac{{\partial \hat \phi }}{{\partial \zeta }} + \mathit{\boldsymbol{\hat D}}\hat \phi = {\mathit{\boldsymbol{V}}_{\eta \eta }}\frac{{{\partial ^2}\hat \phi }}{{\partial {\eta ^2}}} + {\mathit{\boldsymbol{V}}_{\zeta \zeta }}\frac{{{\partial ^2}\hat \phi }}{{\partial {\zeta ^2}}} + {\mathit{\boldsymbol{V}}_{\eta \zeta }}\frac{{{\partial ^2}\hat \phi }}{{\partial \eta \partial \zeta }} $ | (9) |
其中:
| $ \begin{array}{l} \mathit{\boldsymbol{\hat B}} = \mathit{\boldsymbol{\tilde B}} - {\rm{i}}\alpha {\mathit{\boldsymbol{V}}_{\xi \eta }}\\ \mathit{\boldsymbol{\hat C}} = \mathit{\boldsymbol{\tilde C}} - {\rm{i}}\alpha {\mathit{\boldsymbol{V}}_{\xi \zeta }}\\ \mathit{\boldsymbol{\hat D}} = \mathit{\boldsymbol{D}} - {\rm{i}}\omega \mathit{\boldsymbol{ \boldsymbol{\varGamma} }} + {\rm{i}}\alpha \mathit{\boldsymbol{\tilde A}} + {\alpha ^2}{\mathit{\boldsymbol{V}}_{\xi \xi }} \end{array} $ | (10) |
计算采用的是HIFiRE-5飞行试验的38.1%缩比模型,模型为长短轴比2:1的椭圆锥,短轴所在平面头半径1 mm,半锥角7°。考虑出口对基本流的影响,模型计算域长度延长到380 mm。模型的示意图如图 1所示,基本流计算的来流条件,参考了Juliano实验[2]的工况, 如表 1所示。

|
图 1 HIFiRE-5模型 Figure 1 Sketch of HIFiRE-5 model |
| 表 1 基本流计算的来流条件 Table 1 Flow condition for the basic flow calculation |
|
|
模型零攻角工况下流场具有对称性,为节省计算资源,只取1/4模型进行计算,网格数601×251× 201,为了得到一个更好的流场,计算网格在模型头部、边界层内和激波处适当加密了网格。特征长度取1 mm,数值计算中,时间推进采用具有TVD性质的三阶Runge-Kutta格式,对流项采用AUSM+格式进行通量分裂。流场中含有激波,采用2阶NND格式捕捉激波。展向采用对称边界条件,极轴处存在奇点,采用极轴边界条件,出口采用线性外推边界条件。外边界采用远场边界条件,壁面采用无滑移等温条件。具体格式以及各控制方程具体系数矩阵可以参见张绍龙博士论文[15]。
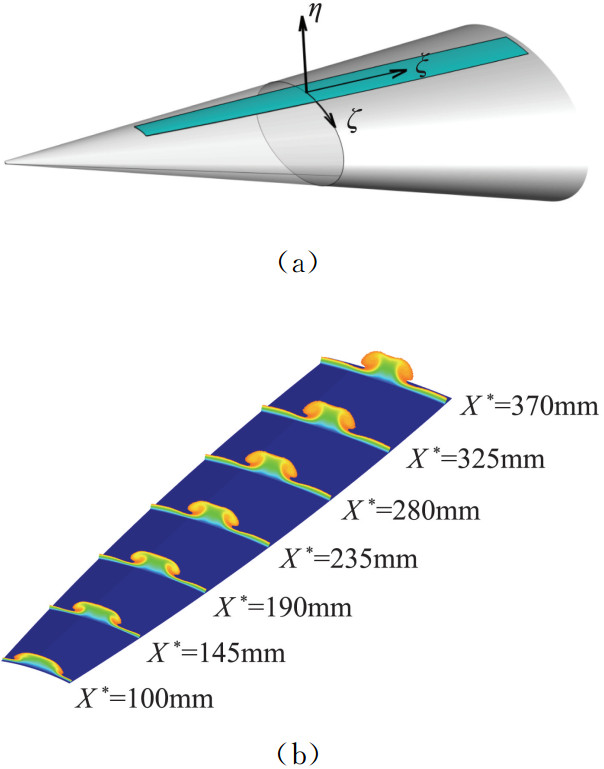
HIFiRE-5模型由于在长轴子午面和短轴子午面之间存在压力梯度,导致边界层内流线的弯曲,基本流在短轴附近存在一个“蘑菇”状的流向涡,该涡结构沿流向变化缓慢,且缓慢抬升,沿展向和法向变化较为剧烈。图 2给出了短轴附近流向涡的稳定性分析计算域选取范围示意图以及流向涡沿流向演化数值计算结果。
|
图 2 (a) 全局稳定性分析选取计算域和(b)椭圆锥短轴流向涡 Figure 2 (a)The computational domain of global stability analysis; (b) Streamwise vortices near minor-axis meridian of hypersonic elliptic cone. |
为了验证二维全局稳定性分析的程序,与一维线性稳定性方法Muller法(LST)和直接数值模拟计算结果进行了对比。
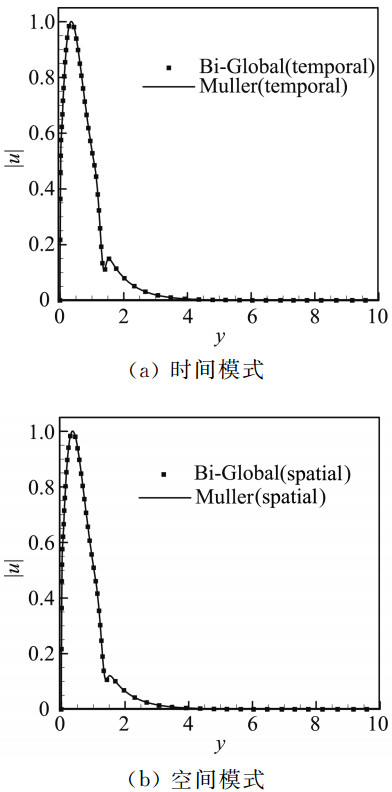
2.2.1 与Muller法对比二维全局稳定性分析与一维线性稳定性分析的最主要区别体现在考虑了基本流沿展向变化,因此扰动在展向不能设成波动形式。但当基本流展向均匀的时候,二维全局稳定性分析仍有效,且与一维线性稳定性计算结果应该是一致的。选取平板边界层,具体参数见表 2,全局稳定性分析与用Muller法求解一维线性稳定性分析的特征值结果对比如表 3所示,所得特征函数如图 3所示,可见两种方法所得结果一致,程序是可靠的。需要指出,这里我们计算了时间模式和空间模式两种情况。
| 表 2 验证Bi-Global程序所用基本流的工况 Table 2 Basic flow freestream condition for verifying of Bi-Global program |
|
|
| 表 3 Bi-Global方法和Muller法计算的平板边界层特征值的比较 Table 3 Flat plate boundary layer eigenvalues comparison between Bi-Global and Muller |
|
|
|
图 3 Bi-Global方法和Muller方法计算的平板边界层特征函数的比较 Figure 3 Flat plate boundary layer eigenfunction, Bi-Global and Muller comparison |
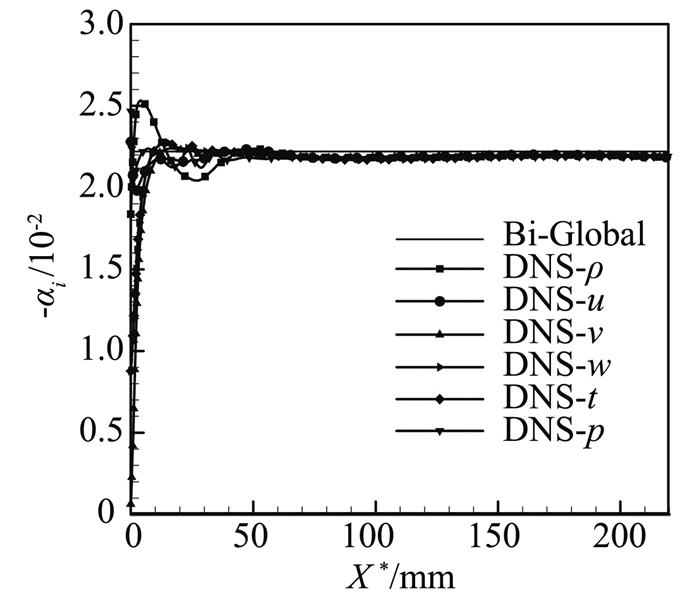
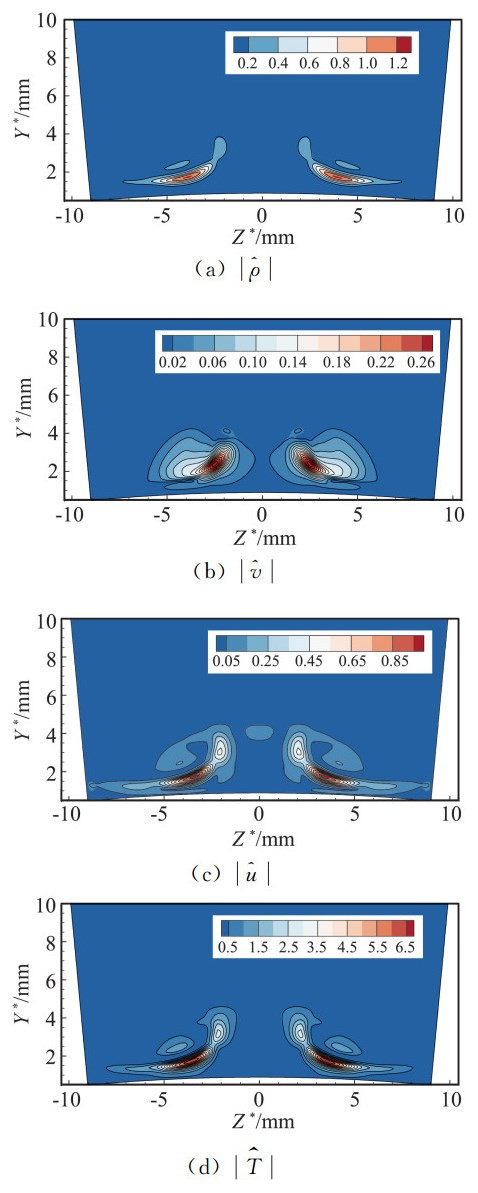
为了验证基本流沿展向变化较大时, 全局稳定性程序的计算是否可靠,与直接数值模拟做了对比。基于全局稳定性分析基本流,以X*=192mm处的流场剖面,沿着流向均匀延拓,构造了计算域为20倍波长的平行流。将全局稳定性分析结果作为直接数值模拟的入口条件,向下游进行计算。图 4是用密度、速度、温度和压力不同参量得到的增长率,可见,经过入口附近的调整,增长率最终都与全局稳定性分析(空间模式)吻合。DNS所得特征值见表 4,特征函数见图 5,都与全局稳定性分析的结果吻合。
|
图 4 全局稳定性与直接数值模拟得到的扰动增长率 Figure 4 Perturbation growth rate obtained by global stability and direct numerical simulation |
| 表 4 全局稳定性分析与直接数值模拟对比:特征值 Table 4 Comparison between global stability analysis and direct numerical simulation: eigenvalues |
|
|
|
图 5 全局稳定性分析与直接数值模拟对比:特征函数(等值线为全局稳定性分析结果,彩色云图为直接数值模拟结果) Figure 5 Comparison between global stability analysis and direct numerical simulation:eigenfunction (The contour is the global stability analysis result, the color cloud image is the direct numerical simulation result) |
Parades和Theofilis[12-13]在短轴处找到了不稳定的外模态。而在不可压二维全局稳定性分析中,既发现了外模态,也发现了有不稳定的内模态,且内模态的增长率较大[14, 17]。因此,本文认为有必要在短轴处观察是否有内模态。
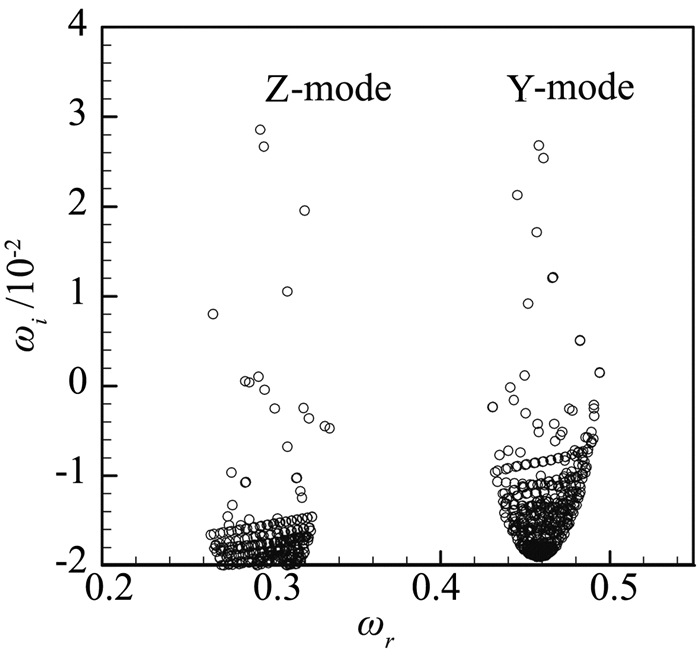
在X*=192mm处做全局稳定分析,所得特征值分布如图 6所示。
|
图 6 全局稳定性分析结果:特征值分布 Figure 6 Globalstability analysis result: the distrbution of eigenfuction |
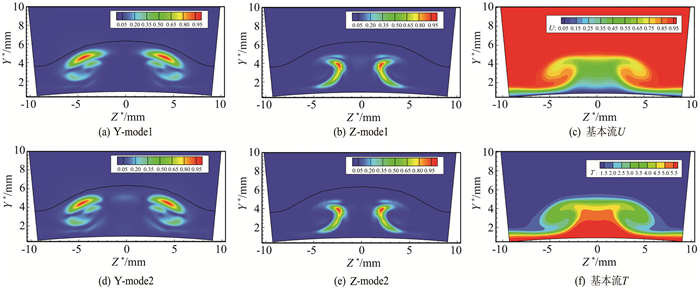
图中有两个分支,都是外模态,没有内模态的结果。图 6中两个分支上的特征函数如图 7所示,都是典型的外模态。其它流向位置结果与之类似,不再赘述。
|
图 7 全局稳定性分析结果:特征函数|û|(黑实线表示边界层外缘) Figure 7 Globalstability analysis result:eigenfunction |û|(the black solid lines refer to the outer edge of the boundary layer) |
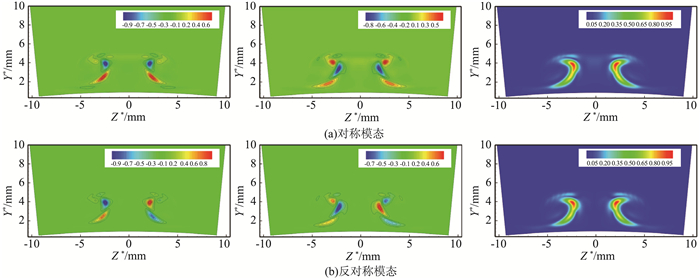
在X*=192 mm处做全局稳定分析,图 6中有两个分支,都是外模态,分别为Y模态和Z模态(Y、Z模态见文献[15-16]),其特征函数如图 7所示。Y模态特征函数在蘑菇状慢速区的“两肩”,沿展向伸展成条带状,表明该模态主要由法向剪切造成。Z模态特征函数在蘑菇状慢速区的“腰部”,为沿法向伸展成条带状,表明该模态主要由展向剪切造成。Y模态又分为两种,分别为对称和反对称模态,特征函数的实部和虚部如图 8所示。Z模态也分为对称和反对称模态两种,特征函数如图 9所示。

|
图 8 对称和反对称的Y模态特征函数:ûr(左),ûi(中),|û|(右) Figure 8 Eigenfunction of symmetric and anti-symmetric Y-modes:ûr(left), ûi(middle), |û|(right) |
|
图 9 对称和反对称的Z模态特征函数:ûr(左),ûi(中),|û|(右) Figure 9 Eigenfunction of symmetric and anti-symmetric Z-modes:ûr(left), ûi(middle), |û|(right) |
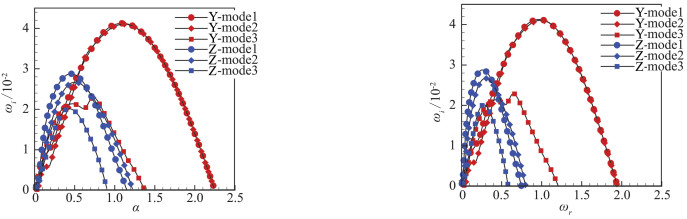
在X*=192 mm处做全局稳定分析,改变波数α,观察不稳定模态随其变化,结果如图 10所示,图中画出了三个最不稳定的Y模态和三个最不稳定的Z模态。可见,Y模态的最大增长率高于Z模态,但是在低波数(低频率)段,Z模态增长率略高于Y模态。我们在X*=175mm处也做了计算,结果与之类似,如图 11所示。
|
图 10 X*=192mm处增长率随波数α和频率ωr的变化 Figure 10 Growth rate varies with wave-number and frequency at X*=192mm |
|
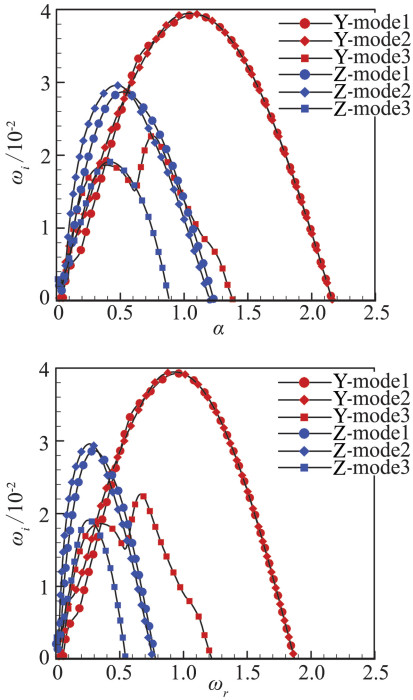
图 11 X*=175 mm处增长率随波数α和频率ωr的变化 Figure 11 Growth rate varies with wave-number and frequency at X*=175 mm |
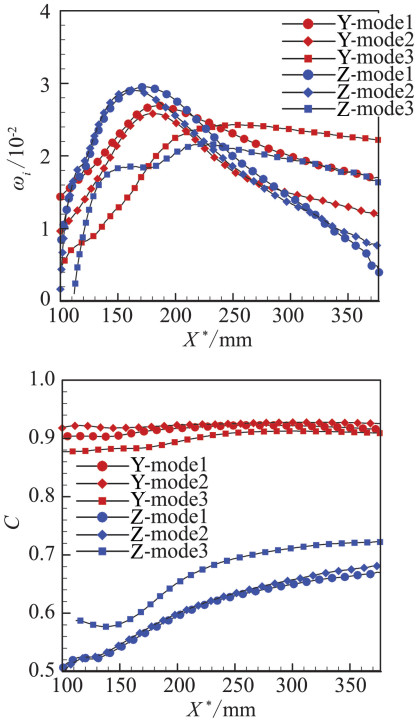
为研究模态沿流向的演化,取固定波数α=0.5,观察不稳定模态沿流向的变化,结果如图 12所示,图中画出了三个最不稳定的Y模态和三个最不稳定的Z模态。可见,几个模态一直在相互竞争,没有一个模态始终是最不稳定的。从相速度随流向演化的曲线来看,Y模态相速度较高,主要分布在0.9左右,Z模态相速度与Y模态有明显差别,比其小很多。值得注意的是,在流向X*=210 mm附近,有很多不稳定的模态在此站位交汇,很可能会引起模态间的转换,具体转换机理还得做深入的研究。我们又取波数α=0.7做了计算,结果与之类似,如图 13所示。
|
图 12 不稳定模态沿流向的变化(α=0.5):增长率ωi和相速度C Figure 12 Variation of unstable modes along streamwise(α=0.5): the growth rate ωi and phase velocity C |
|
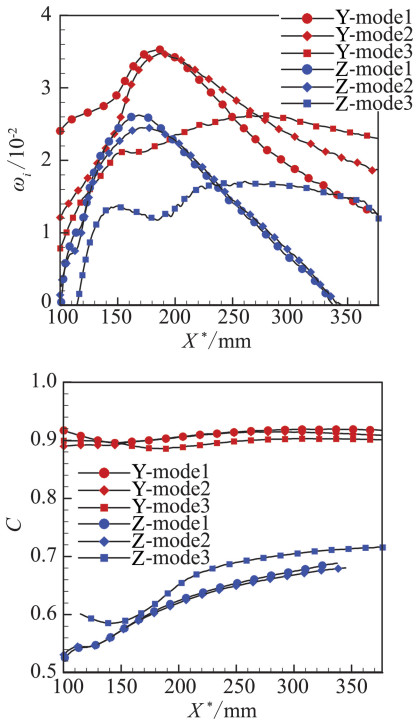
图 13 不稳定模态沿流向的变化(α=0.7):增长率ωi和相速度C Figure 13 Variation of unstable modes along streamwise (α=0.7): the growth rate ωi and phase velocity C |
Y模态和Z模态的特征函数在形式上有所区别,但都是由于基本流的剪切造成。由一维基本流的稳定性理论可知,无粘的拐点不稳定性需要满足Fjortoft拐点条件。椭圆锥短轴处基本流流向速度分布是二维的,在Y*-Z*平面内既沿Y*方向有变化,又沿Z*方向有变化。而变化最剧烈的方向,即为基本流流向速度在Y*-Z*平面内的梯度方向,基本流沿这个方向变化最剧烈,即剪切最强。所用Fjortoft拐点条件为:
| $ \frac{\partial }{{\partial l}}\left( {\rho \frac{{\partial {U_I}}}{{\partial l}}} \right) = 0 $ | (11) |
| $ \frac{\partial }{{\partial l}}\left( {\rho \frac{{\partial {U_I}}}{{\partial l}}} \right)\left( {U - {U_I}} \right) < 0 $ | (12) |
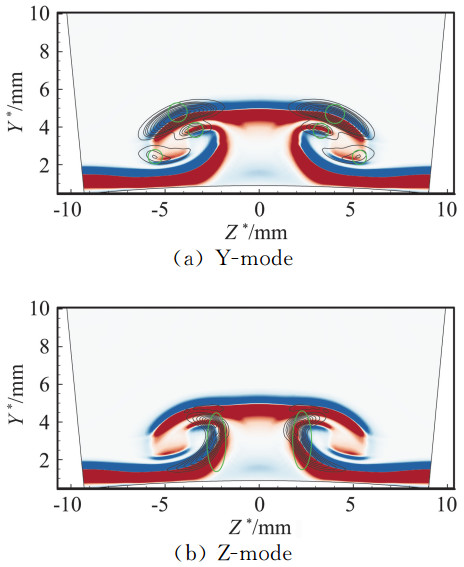
其中∂/∂l为当地基本流在Y*-Z*平面内沿流向速度梯度方向的导数。对X*=192mm处的基本流,将Fjortoft拐点位置用绿色圆圈标记在图 14中,相应的Y模态和Z模态的流向速度特征函数也画在图中。可见,特征函数集中的位置与Fjortoft拐点吻合。这表明它们都具有相同的产生机理,即由基本流剪切的无粘拐点不稳定性造成。
|
图 14 流向速度在梯度方向的Fjortoft拐点与特征函数|û| Figure 14 Fjortoft inflection point at the gradient direction of streamwise velocity and eigenfuction |û| |
由图 14还可以看出,“蘑菇”所在区域没有符合内模态特性的Fjortoft拐点,这就解释了为什么我们找不到内模态。图 4中红色云图表示梯度方向二阶导数大于零;蓝色表示小于零;白色表示等于零;绿色圆圈表示Fjortoft拐点位置;黑色等值线为特征函数。
4 结论找到了不稳定的外模态,尚未发现不稳定的内模态。外模态有两个分支,即Y模态和Z模态,二者都存在对称和反对称两种模态。在同一流向位置,Y模态最大增长率高于Z模态,但在低波数段,Z模态增长率略高于Y模态。观察不稳定模态沿流向的演化,发现几个模态一直在相互竞争,没有一个模态始终是最不稳定的。所找到的不稳定模态都出现在基本流沿其梯度方向的Fjortoft拐点处,这表明它们都具有相同的产生机理,即由基本流剪切的无粘拐点不稳定性造成。因为没有符合内模态特性的Fjortoft拐点,所以没有内模态。
致谢:感谢国家重点研发计划“大科学装置前沿研究”重点专项“高超声速边界层转捩机理、预测及控制方法研究”(2016YFA0401200)提供资助。
| [1] |
Wheaton M B, Juliano J T, Berridge C D, et al. Instability and transition measurements in the Mach-6 Quiet Tunnel[R]. AIAA 2009-3559.
(  0) 0) |
| [2] |
Juliano J Thomas. Instability and transition on the HIFiRE-5 in a Mach-6 quiet tunnel[D]. Purdue University. Indiana, US, 2010.
(  0) 0) |
| [3] |
Schmisseur J, Schneider S, Collicott S. Receptivity of the Mach-4 boundary-layer on an elliptic cone to laser-generated localized free stream perturbations[R]. AIAA-98-0532, 1998.
(  0) 0) |
| [4] |
Schmisseur J, Schneider S, Collicott S. Response of the Mach-4 boundary layer on an elliptic cone to laser-generated free stream perturbations[R]. AIAA-99-0410, 1999.
(  0) 0) |
| [5] |
Poggie J, Kimmel R. Traveling instabilities in elliptic cone boundary-layer transition at Ma=8[R]. AIAA-98-0435, 1998.
(  0) 0) |
| [6] |
Huntley M, Smits A. Transition studies on an elliptic cone in Mach 8 flow using filtered Rayleigh scattering[J]. European Journal of Mechanics B-Fluids, 2000, 19(5): 695-706. DOI:10.1016/S0997-7546(00)00130-8 (  0) 0) |
| [7] |
Lyttle I, Reed H. Use of transition correlations for three-dimensional boundary layers within hypersonic flows[R]. AIAA-95-2293, 1995.
(  0) 0) |
| [8] |
Kimmel R, Klein M, Schwoerke S. Three-dimensional hypersonic laminar boundary-layer computations for transition experiment design[J]. Spacecraft Rockets, 1997, 34(4): 409-415. DOI:10.2514/2.3236 (  0) 0) |
| [9] |
Gosse R, Kimmel R. CFD study of three-dimensional hypersonic laminar boundary layer transition on a Mach 8 ellipticcone[R]. AIAA 2009-4053, 2009.
(  0) 0) |
| [10] |
Poggie J, Kimmel R, Schwoerke S. Traveling instability waves in a Mach 8 ow over an elliptic cone[J]. AIAA J, 2000, 38(2): 251-258. DOI:10.2514/2.979 (  0) 0) |
| [11] |
Choudhari M, Chang C, Jentink T, et al. Transition analysis for the HIFiRE-5 vehicle[R]. AIAA 2009-4056, 2009.
(  0) 0) |
| [12] |
Paredes P, Theofilis V. Spatial linear global instability analysis of the HIFiRE-5 elliptic cone model flow[R]. AIAA 2013-2880.
(  0) 0) |
| [13] |
Paredes P, Theofilis V. Traveling global instabilities on the HIFiRE-5 elliptic cone model flow[R]. AIAA 2014-0075, 2014.
(  0) 0) |
| [14] |
Zhang Y M, Luo J S. Application of Arnoldi method to boundary layer instability[J]. Chinese Physics B, 2015, 24(12): 124701. DOI:10.1088/1674-1056/24/12/124701 (  0) 0) |
| [15] |
Zhang S L. The instability and wave propagation in the hypersonic 2: 1 elliptic cone boundary layer[D]. Tianjin University, 2016. (in Chinese) 张绍龙. 高超声速2: 1椭圆锥边界层的稳定性特征及扰动演化[D]. 天津大学, 2016. (  0) 0) |
| [16] |
Li F, Choudhari M M, Duan L, et al. Nonlinear development and secondary instability of traveling crossflow vortices[J]. Phys Fluids, 2014, 26: 064104. DOI:10.1063/1.4883256 (  0) 0) |
| [17] |
Zhang Yongming, Zaki Tamer, Sherwin Spencer, et al. Nonlinear response of a laminar boundary layer to isotropic and spanwise localized free-stream turbulence. AIAA 2011-32[R]. Reston: AIAA, 2011.
(  0) 0) |
 2018, Vol. 36
2018, Vol. 36


