2. 中国空气动力研究与发展中心 计算空气动力研究所, 四川 绵阳 621000
2. Computational Aerodynamics Institute of China Aerodynamics Research and Development Center, Mianyang 621000, China
层流过渡至湍流的转捩问题被认为是经典物理遗留的难题之一,该问题尚未完全解决并将长期作为现代流体力学重点关注的前沿领域而存在。转捩研究不仅具有重要的基础理论意义,还具有重要的工程应用价值,因为转捩起始位置及区域会影响航空航天飞行器表面的气动力、热分布,进而对飞行器的操纵特性以及热防护设计等带来影响。在能够准确预测转捩位置的前提下,可以通过优化外形、改变壁面条件等多种手段延迟转捩的发生,从而有效实现飞行器减阻以及热防护设计的优化。
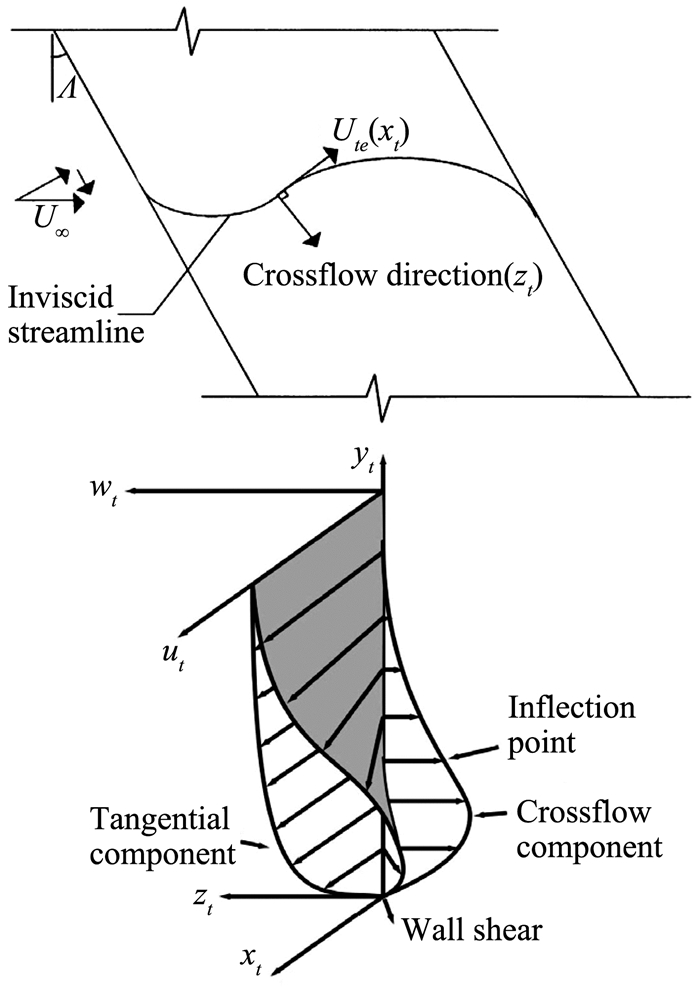
转捩过程受诸多因素的影响,转捩机制亦多种多样。在真实飞行器的三维边界层中,受压力梯度和后掠角的共同作用,边界层内近壁区往往会出现与边界层外势流平面内流线方向垂直的流动分量,称为横流流动,如图 1所示。由横流速度拐点导致的横流失稳机制在三维边界层中普遍存在,常常成为三维边界层转捩的主导因素。
目前,横流转捩的预测方法主要有两类。一类是基于线性稳定性理论以及非线性稳定性理论的稳定性分析方法,能够预测横流转捩中的首次失稳[2-3]、横流涡的饱和以及二次失稳[4]。另一类是基于雷诺平均方程(RANS)的转捩模型,该类方法与现代CFD相结合,从转捩的统计特性出发,能够以较低的计算条件、较少的计算资源获得转捩预测结果。本文主要介绍现阶段横流转捩模型的研究进展,结合横流判据对横流转捩模型进行分析与讨论,并对横流转捩模型的发展进行了展望。
1 横流转捩判据由于压力梯度、后掠角等因素综合作用,在边界层内部垂直于势流区流线方向形成横流速度剖面,相应地会产生横流涡。横流不稳定波的增长率比T-S波增长率大得多[5],相应的,在相同来流条件与相同迎角下,后掠翼绕流相比平直翼绕流其转捩位置更靠前,湍流区域也更大。横流失稳模态可以分为定常模态与非定常模态,对应定常横流涡与非定常横流涡,也称之为驻波扰动与行波扰动,通常定常横流涡由壁面粗糙度引起,非定常横流涡由来流湍流度引起[6]。一般来讲,后掠翼的行波扰动比驻波扰动的增长率要高[7],但哪种扰动占主导地位则与具体情况有关,如表面粗糙程度以及自由来流扰动幅值等。在不可压流动中,定常横流涡在多数情况下均主导转捩,只有在高湍流度条件下横流转捩由非定常横流涡主导[7]。超声速可压流中,何种扰动占主导地位还在研究当中[8]。
构建转捩模型的核心是转捩判据的建立。最早的后掠翼转捩实验[9]于1952年进行,同年Owen和Randall[10]提出了横流不稳定性的判定标准,其主要判据是基于当地壁面法线方向最大横流速度的横流雷诺数。其后一种应用较多的判据由Kohama和Davis[11]提出,将横流失稳与Görtler失稳类比,构造了基于势流流线曲率半径的Kohama数作为横流转捩判据,称为Kohama准则。Arnal等[12]根据风洞实验数据提出并标定了横流转捩位移厚度雷诺数ReδCF*,该判据称为C1准则。Grabe和Krumbein[13]根据Falkner-Skan-Cooke(FSC)方程的三维边界层相似解对类比γ-Reθt转捩模型的流向转捩判据进行当地化,构造了横流转捩判据。Müller和Herbst[14]则针对横流涡的辨识提出了横流涡强度的判定标准。本节将对各类判据的构造和相关研究进行介绍。
1.1 横流雷诺数通过构造横流雷诺数并寻找临界值作为横流转捩判据是传统的横流判据研究思路。早期横流雷诺数由Owen和Randall[10]基于英国皇家空军实验室的飞行试验数据[9]提出,其横流雷诺数构造如下
| $ \mathit{R}{\mathit{e}_{{\rm{crossflow}}}} = \frac{{{W_{\max }}{\delta _{10\% }}}}{\nu } $ | (1) |
其中最大横流速度Wmax为沿当地壁面法向寻找的横流速度最大值,是横流速度为最大横流速度10%且更靠近边界层外缘的位置所对应的壁面距离。该判据采用亚声速实验标定,横流涡生成和由横流涡导致转捩的临界雷诺数分别约为125和175。由于该判据需要全场搜寻Wmax和δ10%,因此效率较低[1]。
关于横流雷诺数的进一步工作,Boltz等[15]以及Scott等[16]分别进行了亚声速和超声速的实验补充。Dagenhart[17]采用小扰动理论计算后掠翼绕流发现横流扰动增长率正比于最大横流速度,并指出临界横流雷诺数是横流边界层形状因子H12的函数。Arnal等[12]将横流位移厚度雷诺数与转捩起始位置的形状因子进行拟合得到横流转捩位移厚度雷诺数Reδ-C1*,作为后掠翼前缘附近加速区域的转捩重要判据,称为C1准则:
| $ \begin{array}{*{20}{c}} {\mathit{Re}_{\delta - {\rm{C1}}}^ * = \frac{{300}}{{\rm{ \mathsf{ π} }}}\arctan \left[ {\frac{{0.106}}{{{{\left( {{H_{12}} - 2.3} \right)}^{2.05}}}}} \right],}\\ {2.3 \le {H_{12}} < 2.7} \end{array} $ | (2) |
| $ \mathit{Re}_{\delta - {\rm{C1}}}^ * = 150.0,{H_{12}} < 2.3 $ | (3) |
C1准则的局限在于其只适用于计算后掠翼前缘附近的加速区域[1]。Chapman[18]验证了Owen和Randall[10]的横流判据在亚声速至超声速较大马赫数范围内钝前缘后掠翼绕流中的适用性,并基于实验数据和二维边界层近似假设提出了针对翼型的圆柱形前缘横流雷诺数的简化计算方法。Boltz等[15]通过风洞实验研究低速无尖梢后掠翼的后掠角对边界层稳定性的影响,认为后掠角、压力梯度和流向雷诺数的综合效应可以用横流雷诺数来表述,给出了临界雷诺数,并提出了在后掠翼算例中已知压力梯度时快速计算横流雷诺数的方法。
迄今为止,多数横流转捩判据研究局限于低速流动,关于高超声速流动横流转捩判据的研究还很少,同时各种来流参数对高超声速下横流失稳的影响还没有严格定论[19]。Reed和Haynes[20]开展了带迎角的高超声速圆锥实验,提出了高超声速条件下考虑可压缩效应和壁温效应的横流雷诺数RCF(new)。新定义的横流雷诺数为:
| $ {R_{{\rm{CF}}\left( {{\rm{new}}} \right)}} = HL{R_{{\rm{CF}}}} = HL{W_{\max }}{\delta _{10\% }}/{\upsilon _e} $ | (4) |
压缩性修正因子H定义为:
| $ H = \eta \left( {{\delta _{10\% }}} \right)/\int_0^{\eta \left( {{\delta _{10\% }}} \right)} {\left( {T/{T_{\rm{e}}}} \right){\rm{d}}\eta } $ | (5) |
壁温修正因子L定义为:
| $ \begin{array}{l} L = {\left( {{C^ * }/C_{{\rm{ad}}}^ * } \right)^{0.5}}\left[ {3.279 + 1.721\left( {{T_w}/{T_{{\rm{ad}}}}} \right)\left( {1 + A} \right)} \right.\\ \;\;\;\;\;\;\left. {\left. { + 0.664A} \right]} \right)/\left( {5 + 2.385A} \right) \end{array} $ | (6) |
其中,Te、Tw、Tad分别是边界层外缘温度、当地壁温和当地绝热壁温。C*和Cad*是基于参考温度和参考绝热壁温度的Chapman-Rubesin参数。
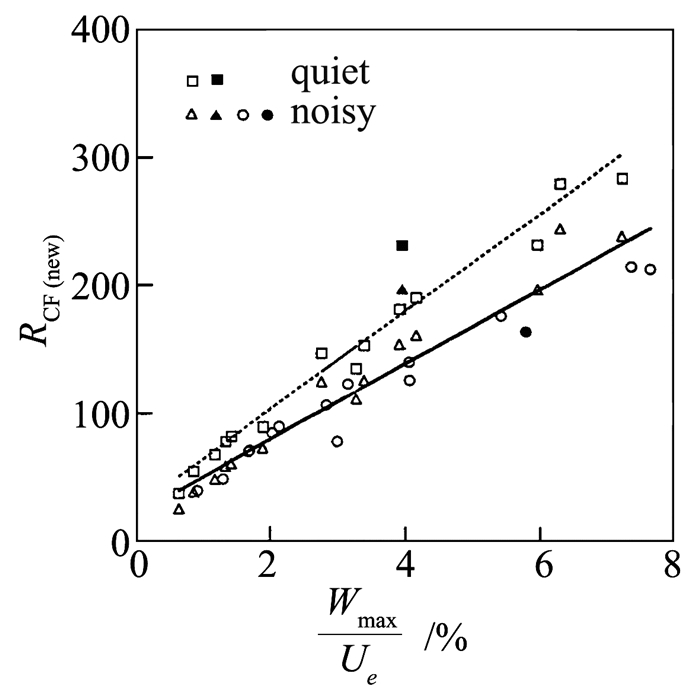
如图 2,Reed等采用上述实验数据拟合得到新横流雷诺数转捩判据:
| $ R = {R_{{\rm{CF}}\left( {{\rm{new}}} \right)}}{U_e}/{W_{\max }} = \left\{ \begin{array}{l} 44.0,\;\;\;\;{\rm{quiet}}\\ 33.7,\;\;\;\;{\rm{noisy}} \end{array} \right. $ | (7) |
|
图 2 带侧滑角圆锥实验数据最小二乘法拟合[20] Figure 2 Linear least-squares fit through the experimental yawed-cone data[20] |
该判据适用于高超声速流动,并且在不可压条件下退化到传统横流雷诺数。但如图 2所示,依靠经验拟合构造的新横流雷诺数的横流强度范围有限,当横流强度大于8%以后,RCF(new)-Wmax/Ue是否满足线性关系目前未知。
1.2 Kohama参数在Kohama参数提出前,横流转捩判据研究工作基本上围绕横流雷诺数展开。横流雷诺数虽然有多种定义形式,但始终未摆脱单纯依靠实验标定、受外形参数影响而适用范围受限以及因需要全场寻找边界层特定厚度和特定速度导致计算效率低等问题。基于此,Kohama和Davis[11]根据横流涡和Görtler涡的相似性提出了仅与无粘流区域相关而不需要边界层全场信息的Kohama参数作为横流转捩判据。Kohama等认为横流不稳定性和Görtler不稳定性主要区别仅在于离心力的方向不同,可以用相似的参数来判断转捩发生,类比Görtler数提出了Kohama参数,定义如下:
| $ {C_k} = \frac{{{U_e}\theta }}{\nu }\sqrt {\frac{\theta }{r}} $ | (8) |
其中:Ue是边界层外的势流流速,r是平行于壁面平面内的势流流线曲率半径,θ是横流方向边界层动量厚度,
Kohama参数的局限在于具有较强的几何相关性[1]。在该横流转捩判据提出以后,Watanabe等[21]对Kohama参数进行改进以减弱其受边界条件几何特性影响,并将改进后的判据应用到γ-Reθt转捩模型中,构造了基于当地量的横流转捩模型,详细介绍见2.2节。
1.3 横流强度一般后掠角越大,横流效应越明显。Müller和Herbst[14]采用流向涡强度用于指示边界层内的横流信息,将无量纲的速度矢量与涡矢量点乘以获得流线方向的涡量大小,又称为Helicity参数。当用壁面距离y对流向涡量无量纲化,得到横流强度的判定标准Hcrossflow:
| $ \begin{array}{l} \mathit{\boldsymbol{U}} = \left( {\frac{u}{{\sqrt {{u^2} + {v^2} + {w^2}} }},\frac{v}{{\sqrt {{u^2} + {v^2} + {w^2}} }},} \right.\\ \;\;\;\;\;\;\left. {\frac{w}{{\sqrt {{u^2} + {v^2} + {w^2}} }}} \right) \end{array} $ | (9) |
| $ \mathit{\boldsymbol{ \boldsymbol{\varOmega} }} = \left( {\frac{{\partial w}}{{\partial y}} - \frac{{\partial v}}{{\partial z}},\frac{{\partial u}}{{\partial z}} - \frac{{\partial w}}{{\partial x}},\frac{{\partial v}}{{\partial x}} - \frac{{\partial u}}{{\partial y}}} \right) $ | (10) |
| $ {\mathit{\Omega }_{{\rm{streamwise}}}} = \left| {\mathit{\boldsymbol{U}} \cdot \mathit{\boldsymbol{ \boldsymbol{\varOmega} }}} \right| $ | (11) |
| $ {H_{{\rm{crossflow}}}} = \frac{{y{\mathit{\Omega }_{{\rm{streamwise}}}}}}{{\left| \mathit{\boldsymbol{U}} \right|}} $ | (12) |
Hcrossflow具有如下特点:无横流时,在展向速度为零的近似二维流动中值为0;在横流效应很强的三维流动当中,横流强度越大,该值越大。
Hcrossflow的取值与后掠角和速度相关,可以用来指示横流转捩。需说明,Hcrossflow并不是像传统横流雷诺数或者Kohama参数直接作为横流转捩判据,而是参与转捩判据的构造,如Langtry等[22]提出的定常横流雷诺数ReSCF,见2.3节。Müller和Herbst[14]也根据Helicity参数提出了横流转捩模型,国内史亚云等[23]对其进行了改进。
1.4 类比γ-Reθt模型的横流转捩判据目前横流转捩预测模型研究的热点与难点在于模型参数的完全当地化以及提高模型在复杂构型下的适用性[23]。Kohama准则[11]和流向涡判据[14]都是将当地求解作为判据构造要求之一。而三维边界层方程相似解是实现横流模型参数当地化的又一有效途径。
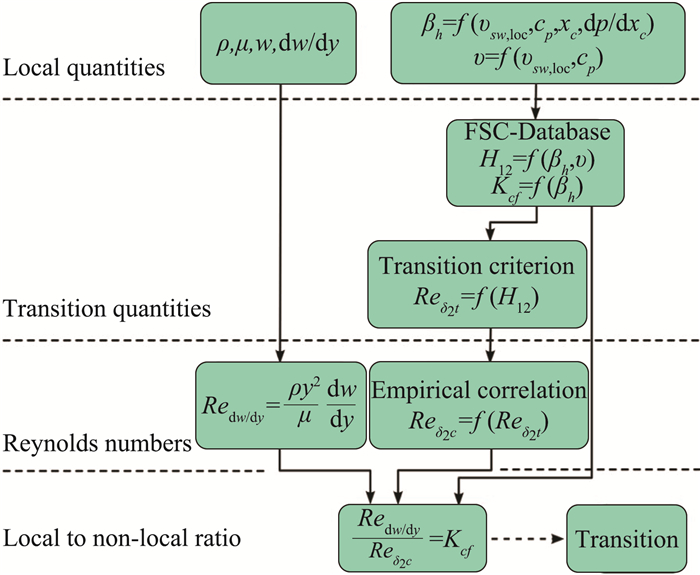
Grabe和Krumbein [13, 24]针对γ-Reθt转捩模型不适合计算三维横流转捩的问题,对模型进行了拓展,增加了横流转捩判据。如图 3所示,该判据核心是基于速度梯度的横流雷诺数Redω/dy与横流临界位移厚度雷诺数Reδ2c的比值达到临界值Kcf时,即认为转捩发生:
| $ \mathit{R}{\mathit{e}_{{\rm{d}}w/{\rm{d}}y}} = \mathit{R}{\mathit{e}_{\delta 2c}} = {K_{cf}} $ | (13) |
由于横流方向不存在类似二维边界层方程中涡雷诺数Rev与动量厚度雷诺数Reθ之间的线性关系,因此Kcf不是常数而是Hartree压力梯度因子的函数。临界横流位移厚度雷诺数Reδ2c是通过经验拟合而成的压力梯度因子βh和当地后掠角ϑ的函数。该函数通过不同压力梯度下FSC方程的解来确定。该判据未涉及动量厚度雷诺数Reδ2t输运方程求解,并且通过FSC数据库实现了Reδ2c的当地化,因而具有当地求解特性。
以上对目前常用的四类转捩判据进行了介绍,基于这些判据出现了多种边界层横流转捩模型,下面逐一进行分析讨论。
2 横流转捩模型湍流模型中工程应用较普遍的是涡粘模型,如S-A模型[25]、k-ω SST剪切应力输运模型[26]等。时至今日,各类湍流模型依然在不断改进与发展中。湍流模型与间歇因子、层流脉动动能、转捩经验关系式、放大因子等相结合形成了各种转捩模型[27],进而通过各类横流转捩判据构造出多种横流转捩预测模型。
Medida和Baeder[1]模化了横流雷诺数并以其为判据引入到γ-Reθt模型中。王亮[5]等基于Warren和Hassan[28]的时间尺度,构建了新型k-ω-γ湍流/转捩模型,模型包含横流时间尺度。周玲等[29]基于Owen和Randall[10]提出的横流雷诺数,对k-ω-γ转捩模型进行了横流改进。张毅锋等[30]采用了考虑可压缩效应和壁温效应的横流雷诺数[20],初步实现了γ-Reθt模型对高超声速横流转捩的预测。在Kohama参数[11]提出之后,Watanabe等[21]以其为判据在γ-Reθt模型中添加了横流模块,并尝试对Kohama参数进行模化。Langtry等[22]根据Müller和Herbst[14]提出的Helicity参数,引入粗糙度影响,构建了横流判据与模型。Grabe和Krumbein [13, 24]基于FSC方程相似解构建了当地化横流模型,在此基础上Choi和Kwon[31-32]引入T-S不稳定性和横流不稳定性相互作用机制。徐家宽等[33-34]以不同压力梯度下FSC方程解为数据库类似地构建了当地化横流判据与模型。独立的横流模型方面,Vizinho等[35]针对三维边界层转捩基于S-A一方程模型构造了唯象的横流转捩模型。
2.1 基于横流雷诺数的横流转捩模型横流雷诺数作为横流转捩的判据之一,可以被直接应用于横流转捩模型中,多数横流模型的转捩触发都体现为其定义的横流雷诺数ReCF大于某个临界值ReCF-threshold。
2.1.1 时间尺度转捩模型Warren和Hassan[28]将不稳定扰动波的影响νnt引入到有效涡粘系数中,记作ν=(1-γ)νnt+γνt。并假设νnt的形式与湍流粘性系数的形式相似,νnt=Cμkτnt,其中τnt对应各模态不稳定波的时间尺度,也包括横流时间尺度。他们采用横流时间尺度后能够准确预测多种表面粗糙度下变雷诺数的亚声速NLF(2)-0415后掠翼的一系列转捩位置[28]。
同样,基于时间尺度,王亮等提出了新型k-ω-γ湍流/转捩模型[5],他们通过定义当地相对马赫数实现第一、二模态时间尺度的切换,并引入了以Reed等[20]横流雷诺数R=44为横流转捩判据的横流时间尺度:
| $ {\tau _{nt}} = {\tau _{nt,2d}} + {\tau _{{\rm{crossflow}}}} $ | (14) |
| $ \begin{array}{l} {\tau _{{\rm{crossflow}}}} = {C_7} \cdot \left( {4\zeta /{U_e}} \right) \cdot \\ \;\;\;\left\{ { - \exp \left[ { - {C_8}{{\left( {\zeta {U_e}/{\nu _e} - 44} \right)}^2}} \right]} \right\} \cdot {\left( {W/{U_e}} \right)^{{C_9}}} \end{array} $ | (15) |
该模型未考虑表面粗糙度因素对横流转捩的影响,在对不可压后掠翼、后掠平板以及带迎角的高超声速圆锥边界层的转捩预测中,与实验值符合较好。该模型只采用了当地量,避免了在边界层内进行参数积分,提高了计算效率[36]。模型中R=44的横流判据是基于静音风洞带迎角尖锥的实验数据拟合得到,针对不同的风洞设备或不同来流噪声条件,该判据可能需要重新标定。
周玲等[29]基于传统横流雷诺数判据对k-ω-γ[5]转捩模型进行了改进,构造了新的横流时间尺度τcross,增大了横流预测的适用性,并在高超声速算例中进行了测试。横流时间尺度τcross包含了横流速度、横流雷诺数等横流相关物理量:
| $ {\tau _{{\rm{cross}}}} = {C_7} \cdot {\xi _{{\rm{eff}}}}/{U_e} \cdot 100 \cdot f\left( w \right) \cdot f\left( {\mathit{R}{\mathit{e}_{{\rm{CF}}}}} \right) $ | (16) |
| $ f\left( w \right) = 0.5\left[ {{\rm{sign}}\left( {{{\left| {w/{U_e}} \right|}_{{\rm{local}}}} - {{\left| {w/{U_e}} \right|}_{{\rm{crit}}}}} \right) + 1} \right]{\left| {w/{U_e}} \right|_{{\rm{local}}}} $ | (17) |
| $ f\left( {\mathit{R}{\mathit{e}_{{\rm{CF}}}}} \right) = 1 - \exp \left[ { - \max {{\left( {\mathit{R}{\mathit{e}_{{\rm{CF,local}}}}/\mathit{R}{\mathit{e}_{{\rm{CF,crit}}}} - 1,0} \right)}^2}} \right] $ | (18) |
其中,横流雷诺数采用Owen和Randall [10]等的定义,横流时间尺度大于0视作横流转捩的启动,该模型采用双重判据,即横流雷诺数和横流速度同时超过临界值时,横流时间尺度为正值。图 4为该模型对马赫数6、迎角0°、HIFiRE-5椭锥外形的转捩位置进行预测的结果,基本可以模拟出双肺叶状转捩阵面。模型需要确认边界层范围并需要沿壁面法向搜寻横流速度最大值,非当地量的求解使模型在大规模并行计算中受到限制。
2.1.2 γ-Reθt转捩模型γ-Reθt转捩模型是Menter等提出的一种经验关系式转捩模型,该模型中的间歇因子触发函数和有效间歇因子可以被用来实现横流转捩模拟。
考虑到势流区无粘流线弯曲是横流流动的重要特征,Medida和Baeder[1]以横流曲率半径为长度尺度,并将曲率半径矢量引入速度尺度中,基于不同横流速度的定义构造了两种横流雷诺数,其作为判据引入γ-Reθt-SA转捩模型当中:
| $ \mathit{R}{\mathit{e}_{{\rm{MCF1}}}} = \frac{{{U_{{\rm{CF1}}}}\left| \mathit{\boldsymbol{R}} \right|}}{\upsilon } $ | (19) |
| $ \mathit{R}{\mathit{e}_{{\rm{MCF2}}}} = \frac{{{U_{{\rm{CF2}}}}\left| \mathit{\boldsymbol{R}} \right|}}{\upsilon } $ | (20) |
| $ {U_{{\rm{CF1}}}} = \left| {u \cdot {r_1} + v \cdot {r_2} + w \cdot {r_3}} \right| $ | (21) |
| $ {U_{{\rm{CF2}}}} = \left| {u \cdot {r_1}} \right| + \left| {v \cdot {r_2}} \right| + \left| {w \cdot {r_3}} \right| $ | (22) |
| $ \mathit{\boldsymbol{R}} = \left( {{r_1},{r_2},{r_3}} \right) $ | (23) |
其中R是边界层边缘平行于壁面平面的横流曲率半径矢量,转捩判据为:
| $ {F_{{\rm{BL}}}} \cdot \max {\left[ {\mathit{R}{\mathit{e}_{{\rm{MCF1}}}}} \right]_{{\rm{BL}}}} > 0.7 $ | (24) |
| $ {F_{{\rm{BL}}}} \cdot \max {\left[ {\mathit{R}{\mathit{e}_{{\rm{MCF2}}}}} \right]_{{\rm{BL}}}} > 2.0 $ | (25) |
Medida等研究发现第一种判据ReMCF1在非定常流动以及动边界问题中的适用性较差,因此他们将第二种判据用于γ-Reθt模型中触发函数:
| $ {F_{{\rm{onsetl}}}} = \max \left( {\frac{{\mathit{R}{\mathit{e}_\upsilon }}}{{2.193\mathit{R}{\mathit{e}_{\theta c}}}},\frac{{{F_{{\rm{BL}}}} \cdot \mathit{R}{\mathit{e}_{{\rm{MCF2}}}}}}{{2.0}}} \right) $ | (26) |
该模型的标定仅采用了不考虑表面粗糙度因素的NLF(2)-0415后掠翼实验数据,其判据ReMCF1和ReMCF2的临界值的选取则是采用了该后掠翼算例上表面实验转捩位置处层流计算得到的最大值。模型的标定和判据临界值的选取都过于单一,造成该模型过于经验化,普适性较差。
虽然该模型判据未实现完全当地化[1](R是非当地变量),受到非并行求解的限制,但在湍流模型中可实现性强,并且由于转捩判据基于平均量,能够添加至各类湍流模型中。Medida和Baeder[1]采用横流模型对ONERA M6机翼转捩位置预测结果见图 5,横流模型(Crossflow)与未添加横流判据模型(Streamwise)相比,预测结果更接近实验值。

|
图 5 采用模化横流雷诺数准则的转捩模型与传统转捩模型间歇因子云图对比[1] Figure 5 Transition onset prediction with new crossflow transition criterion[1] |
张毅锋等[30]对Langtry和Menter提出的γ-Reθt模型[37-38]进行改进以模拟高超声速边界层转捩,并且根据Reed等的高超声速横流转捩实验结果[20],采用以横流雷诺数ReCF(new)为基础的转捩准则,通过有效间歇因子的形式在γ-Reθt转捩模型中实现横流转捩预测:
| $ {\gamma _{{\rm{eff}}}} = \min \left( {\gamma ,{\gamma _{{\rm{sep}}}},{\gamma _{{\rm{CF}}}}} \right) $ | (27) |
| $ {\gamma _{{\rm{CF}}}} = \max \left[ {\min \left( {\frac{R}{{{R_{{\rm{threshold}}}}}},1} \right),0} \right]{F_{\theta t}} $ | (28) |
| $ R = \mathit{R}{\mathit{e}_{{\rm{CF}}\left( {{\rm{new}}} \right)}}{U_e}/{W_{\max }} $ | (29) |
其中Ue是边界层外缘速度,Wmax是最大横流速度。ReCF(new)作为新定义的横流雷诺数,相比于Owen等[10]提出的传统横流雷诺数更适合作为高超声速流场中的横流判别标准。张毅锋等[30]采用该模型对HIFiRE-5椭锥马赫数6的风洞实验状态进行了数值计算。计算前首先对R值进行了数值标定,在噪声条件下取R=45。标定后,该模型在不同雷诺数下都取得了与噪声风洞实验比较吻合的计算结果,图 6给出了其中一组单位雷诺数Re=4.1×106/ft的壁面热流分布,预测的转捩位置与测量结果符合较好。与周玲等方法相类似,该方法需要沿法向搜索边界层最大横流速度及相关的物理量,不属于完全的局部计算。

|
图 6 HIFiRE-5壁面热流分布[30] Figure 6 Distribution of heat flux distribution on HIFiRE-5 surface [30] (上:风洞试验,下:计算结果) |
横流转捩的当地化预测一直是横流模型的主要发展方向。构建当地求解的横流转捩模型的有效方法之一是在现有转捩模型中添加基于当地量的横流判据。Watanabe等[21]提出了计算边界层内Kohama参数CK的方法,并对CK进行了模化改进以尝试解决CK受物体边界几何外形影响较大的问题,将转捩判据CK以有效间歇因子γeff的形式在
| $ {\gamma _{{\rm{eff}}}} = \max \left( {\gamma ,{\gamma _{{\rm{sep}}}},{\gamma _{{\rm{CF}}}}} \right) $ | (30) |
| $ {\gamma _{{\rm{CF}}}} = \min \left[ {\max \left( {\frac{{{C_K}}}{{{C_{{\rm{threshold}}}}}},1} \right),0} \right]{F_{\theta t}} $ | (31) |
| $ {C_K} = \frac{{{U_e}\theta }}{\nu }\sqrt {\frac{\theta }{r}} $ | (32) |
| $ {C_{K{U_e}}} = {C_K}\mathit{R}{\mathit{e}_{{U_e}}} $ | (33) |
其中Ue是边界层边缘速度,r是平行于壁面平面的势流区流线曲率半径,θ是横流方向边界层动量厚度,ReUe是基于边界层边缘速度的雷诺数。
原始定义的CK为非当地参数,对应的转捩模型无法完全当地求解。Watanabe等[21]指出CK不应定义在壁面边界层外,应定义为当地参数。其中动量厚度θ可由
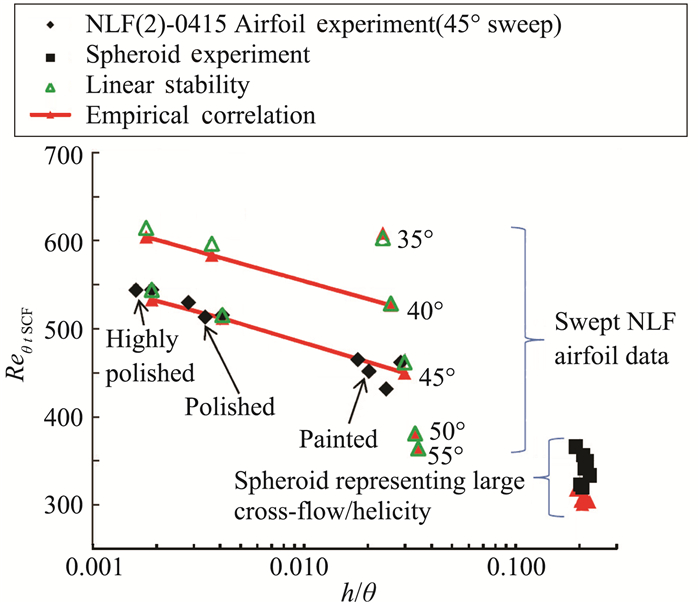
流向涡强度常被用来表示横流的强度,例如Hcrossflow是横流涡强度的指示方法之一。Langtry等[22]根据45°NLF(2)-0415后掠翼变粗糙度实验结果,借助线性稳定性分析,拟合了新的定常横流经验关系式ReSCF-h-Hcorssflow,其中包含壁面粗糙度信息[39]和Müller & Herbst [14]构造的横流涡强度。将该经验公式应用于γ-Reθt转捩模型,实现了完全基于局部变量的横流转捩预测。该横流模型与一般横流转捩模型在间歇因子生成项上增加转捩开关控制的方法不同,Langtry等通过在γ-Reθt模型中Reθt输运方程的右端增加衰减项DSCF来实现粗糙度引起的横流转捩预测。
| $ \begin{array}{*{20}{l}} {\frac{{\partial \left( {\rho \overline {R{e_{\theta t}}} } \right)}}{{\partial t}} + \frac{{\partial \left( {\rho {U_j}\overline {R{e_{\theta t}}} } \right)}}{{\partial {x_j}}} = {P_{\theta t}} + {D_{{\rm{SCF}}}} + }\\ {\;\;\;\;\frac{\partial }{{\partial {x_j}}}\left[ {{\sigma _{\theta t}}\left( {\mu + {\mu _t}} \right)\frac{{\partial \overline {R{e_{\theta t}}} }}{{\partial {x_j}}}} \right]} \end{array} $ | (34) |
| $ {D_{{\rm{SCF}}}} = {c_{\theta t}}\frac{\rho }{t}{c_{{\rm{crossflow}}}}\min \left( {\mathit{R}{\mathit{e}_{{\rm{SCF}}}} - \overline {\mathit{R}{\mathit{e}_{\theta t}}} ,0} \right){F_{\theta 2}} $ | (35) |
| $ \begin{array}{l} \mathit{R}{\mathit{e}_{{\rm{SCF}}}} = \frac{{{\theta _t}\rho \left( {\frac{U}{{0.82}}} \right)}}{\mu } = - 35.088Ln\left( {\frac{h}{{{\theta _t}}}} \right) + 319.51 + \\ \;\;\;\;f\left( { + \Delta {H_{{\rm{crossflow}}}}} \right) - f\left( { - \Delta {H_{{\rm{crossflow}}}}} \right) \end{array} $ | (36) |
公式(36)为定常横流雷诺数ReSCF与粗糙度h和Hcrossflow的拟合关系式。拟合关系的数据点来自不同后掠角和粗糙度下的ReSCF实验值和稳定性计算结果,如图 7所示。定常横流雷诺数ReSCF与对数坐标系下表面粗糙高度h/θt呈线性关系。±ΔHcrossflow为横流强度偏移量,用来反映不同横流强度效应。当边界层中ReSCF小于输运Reθt值时衰减项DSCF开始起作用。
Langtry等[22]采用该模型对NLF(2)-0415机翼、6:1椭球体和Sickle机翼进行了模拟,机翼的计算结果较准确地再现了横流转捩位置,与实验值符合较好。如图 8,转捩模型能够准确预测镰刀翼面上沿展向不规则分布的转捩位置。该模型优点是转捩预测完全基于当地量,合理的考虑了壁面粗糙度的影响,并适用于非结构网格和大规模并行计算。但Hcrossflow以及速度标量不具有伽利略不变性,并且修改后的衰减项DSCF具有较大的网格相关性。
Müller和Herbst以γ-Reθt转捩模型为基础,在动量厚度雷诺数输运方程中添加源项PCF以考虑横流效应对转捩的影响,采用Helicity参数
| $ \begin{array}{l} {P_{{\rm{CF}}}} = - \min \left\{ {\max \left[ {0,\frac{\rho }{{1000t}} \cdot {{\left( {\frac{{\mathit{R}{\mathit{e}_H}}}{6}} \right)}^{c1}} \cdot } \right.} \right.\\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\left. {\left. {{{\left( {\mathit{R}{\mathit{e}_\mathit{\Omega }}} \right)}^{c2}} \cdot {{\left( {\frac{{12\theta }}{y}} \right)}^{c3}} \cdot {c_4}} \right],{c_5}} \right\} \end{array} $ | (37) |
式(37)各项定义详见文献[14, 23],其中
史亚云等[23]在横流源项PCF中添加了横流速度并与Helicity参数相结合来指示横流信息,修改后的横流源项PCF, improved为:
| $ \begin{array}{l} {P_{{\rm{CF}},{\rm{improved}}}} = - \min \left[ {\max \left( {0,\frac{\rho }{{1000t}} \cdot } \right.} \right.\\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\left. {\left. {\mathit{Re}_H^{{c_1}} \cdot \mathit{Re}_\mathit{\Omega }^{{c_2}} \cdot {\theta ^{{c_3}}}{{\left( {\frac{\omega }{U}} \right)}^{{c_6}}} \cdot {c_4}} \right),{c_5}} \right] \end{array} $ | (38) |
其参数c1~c6都进行了重新标定。
改进后的模型提升了对6:1椭球横流转捩的预测能力,如图 9。同时在对DLR-F5机翼的数值模拟中,捕捉到翼根处的横流转捩现象,与风洞实验测量符合较好。
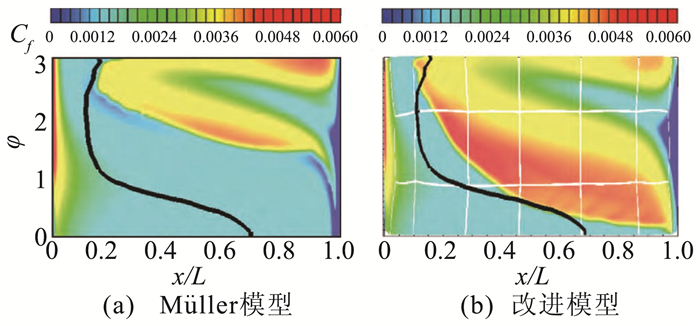
|
图 9 椭球数值模拟同实验转捩位置对比[23] Figure 9 Comparison between model and experiment data for transition localtion of prolate spheriod[23] |
采用三维边界层相似解实现横流转捩判据和横流转捩模型的当地化求解是目前横流转捩模型研究的一个重要方向。Grabe和Krumbein [13, 24]基于FSC三维边界层相似解首先提出了类比γ-Reθt模型中转捩判据的横流转捩判据。Choi和Kwon[31-32]在此基础上采用该判据,在数值模拟中引入了T-S不稳定性和横流不稳定性相互作用的机制,拓宽了模型适用范围,明显提升了模型对椭球迎风面的横流转捩预测能力。徐家宽等[33-34]以不同压力梯度FSC方程的解为数据库,类似地构造当地化的横流转捩判据与模型。
FSC方程的解是二维Falkner-Skan方程拓展到三维Falkner-Skan-Cooke方程的相似解,二维边界层(FS方程)沿垂直于前缘的弦向,拓展的横向流动方程(Cooke方程)沿前缘展向。通过引入流函数和无量纲化壁面距离,在边界层外缘速度满足一定条件下推导可得FSC方程[40]。采用FSC方程对横流判据和模型当地化的基本思想是:横流转捩的判断是用当地横流雷诺数Redω/dy与横流位移厚度雷诺数Reδ2c的比值来实现,该比值与压力梯度相关。通过数值求解FSC方程获得不同压力梯度因子βH下典型流场的横流速度型作为数据库,进而获得所需横流位移厚度雷诺数及比值判据函数。
Grabe和Krumbein[13, 24]以不同后掠角和压力梯度因子下FSC方程解作为数据库,构建了横流涡粘雷诺数Redω/dy与横流临界位移厚度雷诺数Reδ2c比值形式的判据函数和对应模型。由于FSC方程的限制以及采用的C1准则仅适用于翼型类流动,该类模型适用范围受限[24],主要适用于后掠翼计算,不适合带迎角的旋成体计算。
Choi和Kwon[31-32]对采用FSC方程的横流模型进行了详细阐述[31],并引入了T-S不稳定性和横流不稳定性相互作用的机制[32]。他们在转捩模型的实现过程中,主要是对γ-Reθt模型间歇因子输运方程的Flength和Fonset进行了修改。Flength采用了带迎角椭球实验数据进行重新标定[32],Fonset引入了上文提到的由FSC方程解得到的横流转捩判据。
保留了γ-Reθt模型中原始的触发函数:
| $ {F_{{\rm{onset1}}}} = \frac{{\mathit{R}{\mathit{e}_v}}}{{2.193\mathit{R}{\mathit{e}_{\theta c}}}} $ | (39) |
横流触发函数为:
| $ {F_{{\rm{onset1}}\_{\rm{CF}}}} = \frac{{\mathit{R}{\mathit{e}_{{\rm{d}}w/{\rm{d}}y}}}}{{\mathit{Re}_{\delta 2t}^ * \cdot {K_{cf}}}} $ | (40) |
| $ {F_{{\rm{onset1}}\_{\rm{3D}}}} = \max \left( {{F_{{\rm{onset1}}}},{F_{{\rm{onset1}}\_{\rm{CF}}}}} \right) $ | (41) |
其中Reδ2t*由形状因子H12决定[24],其它项构造与γ-Reθt模型的形式一致。
| $ {F_{{\rm{onset2}}}} = \min \left( {\max \left( {{F_{{\rm{onset1}}\_{\rm{3D}}}},F_{{\rm{onset1}}\_{\rm{3D}}}^4} \right),2} \right) $ | (42) |
| $ {F_{{\rm{onset3}}}} = \max \left( {1 - {{\left( {\frac{{{R_T}}}{{2.5}}} \right)}^3},0} \right);{R_T} = \frac{{\rho k}}{{\mu \omega }} $ | (43) |
| $ {F_{{\rm{onset1}}\_{\rm{3D}}}} = \max \left( {{F_{{\rm{onset2}}}} - {F_{{\rm{onset3}}}},0} \right) $ | (44) |
最终间歇因子输运方程的生成项定义为:
| $ {P_\gamma } = {F_{{\rm{length}}\_3{\rm{D}}}}{c_{a1}}\rho S{\left[ {\gamma {F_{{\rm{onset}}\_{\rm{3D}}}}} \right]^{0.5}}\left( {1 - {c_{e1}}\gamma } \right) $ | (45) |
上述转捩模型基于转捩完全由T-S不稳定性或者完全由横流不稳定性主导的假设,而实验数据显示两种不稳定性的相互作用会导致转捩提前[41],Choi和Kwon[32]进一步引入了T-S不稳定性和横流不稳定性相互作用的机制,对原触发函数进行线性组合:
| $ {F_{{\rm{onset1}}\_{\rm{3D}}}} = \max \left( {{F_{{\rm{onset1}}}},{F_{{\rm{onset}}\_{\rm{CF}}}},{F_{{\rm{onset}}\_{\rm{inter}}}}} \right) $ | (46) |
其中,当Fonset1>0.5 & Fonset_CF>0.15时
| $ {F_{{\rm{onset1}}\_{\rm{inter}}}} = \frac{{34}}{{37}}{F_{{\rm{onset1}}}} + \frac{{20}}{{37}}{F_{{\rm{onset}}\_{\rm{CF}}}} $ | (47) |
其它情况下,Fonset1_inter=0。
图 10是各类方法计算的椭球体表面截面摩擦系数分布,引入不稳定性相互作用机制的横流转捩模型[32]在椭球体迎风面(50°≤ψ≤90°)转捩预测中的表现明显优于其它方法。
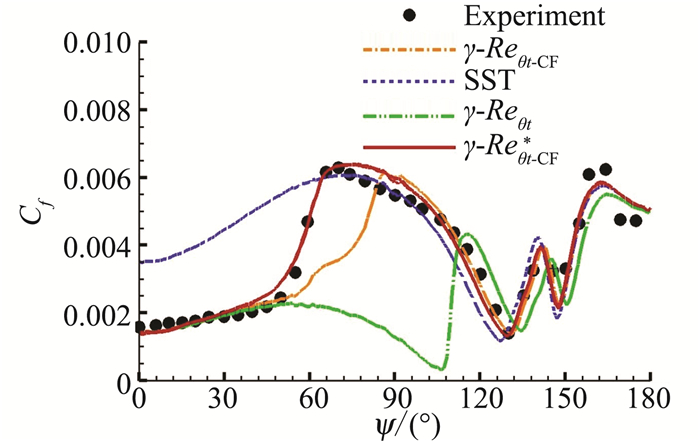
|
图 10 6:1椭球体表面x/a=0.48截面各方法摩擦系数分布[32](Re=7.2×106, 迎角30°) Figure 10 Skin friction coefficient distributions at x/a=0.48 on a 6:1 prolate spheroid [32] |
徐家宽等[33-34]详细介绍了采用三维边界层相似解求解压力梯度因子βH和形状因子H12的方法并采用C1准则最终建立当地求解的横流不稳定转捩判据,将判据与γ-Reθt转捩模型耦合,进行了椭球体、后掠翼转捩位置的预测,取得了良好结果。图 11为椭球算例,其中黑点为实验转捩位置,白点为eN方法转捩位置,云图为转捩模型计算值,与实验测量符合较好。

|
图 11 椭球体表面摩阻系数云图与试验数据的对比[34] Figure 11 Comparison of skin friction coefficients contour of prolate spheroids between transition model and test data[34] |
目前,横流转捩模型普遍是在现有转捩模型(如k-ω-γ或者γ-Reθt)基础上根据某一横流判据对转捩模型输运方程进行修改来实现的,直接在湍流模型基础上构建横流转捩模型较为困难,相关研究亦较少。Vizinho等的工作[35]则是上述研究方向的典型代表,为构造不显含横流判据的独立横流模型提供了思路。
该横流转捩模型是基于层湍流发展过程中的动力学近似,从唯象的角度用
| $ \frac{{D{k_p}}}{{Dt}} = \mathit{Pro}{\mathit{d}_{{k_p}}} - Des{t_{{k_p}}} + \frac{\partial }{{\partial {x_j}}}\left[ {\left( {\nu + {\nu _T}} \right)\frac{{\partial {k_p}}}{{\partial {x_j}}}} \right] $ | (48) |
其中生成项:
| $ \mathit{Pro}{\mathit{d}_{{k_p}}} = - C{p_k} \cdot S \cdot \overline {u'v'} $ | (49) |
| $ \overline {u'v'} = 0.5\left( {r_{{\rm{avg}}}^2{\omega ^2}\cos \alpha \cdot {F_S}} \right) $ | (50) |
关于每一项的具体定义见文献[35],该模型称为“V-model”,不依赖现有的转捩模型,通过在SA一方程生成项中增加控制函数实现“V-model”与一方程湍流模型的耦合:
| $ \begin{array}{l} \frac{{D{{\tilde \nu }_T}}}{{Dt}} = {C_{b1}}S{{\tilde \nu }_T} \cdot \exp \left( { - {C_{{\nu _T}}} \cdot {\rm{ratio}}} \right) - \\ \;\;{C_{w1}}{f_w}{\left( {\frac{{{{\tilde \nu }_T}}}{d}} \right)^2} + \frac{\partial }{{\partial {x_j}}}\left[ {\left( {{{\tilde \nu }_T} + \frac{\nu }{\sigma }} \right)\frac{{\partial {{\tilde \nu }_T}}}{{\partial {x_j}}}} \right] \end{array} $ | (51) |
该模型在6:1椭球体亚声速绕流以及跨声速DLR-F5机翼绕流算例中进行了测试。跨声速三维机翼绕流算例中,能够较准确预测上翼面转捩位置及各截面压力系数分布。椭球体算例中大迎角下能准确预测转捩位置,但在迎角5°下,存在转捩过早、转捩区域过短的问题,如图 12所示。Vizinho等[35]认为原因是V-model输运方程中耗散项在边界层内偏大导致的,但是Grabe和Krumbein[24]指出迎角5°实验状态下的转捩是由T-S不稳定性和横流不稳定性共同主导的。Vizinho等[35]并未指出V-model是否具备T-S不稳定性导致转捩的预测能力,也并未考虑T-S不稳定性与横流不稳定性的相互作用。关于该模型适用范围,即是否适用于除横流之外的转捩预测,还需要进一步研究与讨论。
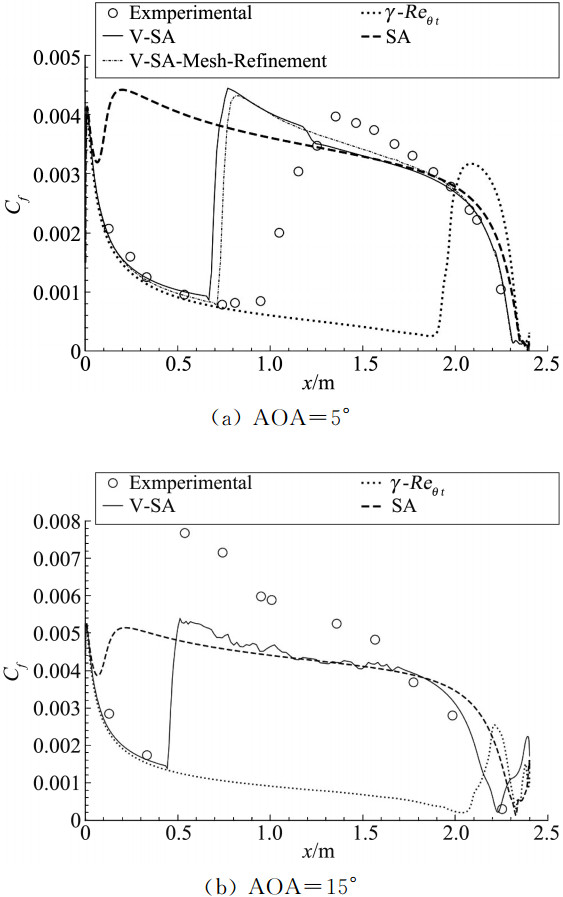
|
图 12 迎角5°和15°椭球体x-z截面摩擦系数分布图[35] Figure 12 Skin-friction coefficient along the x-z cutting plane over the 6:1 prolate-spheroid with AOA 5° and 15°[35] |
横流转捩模型的相关研究起步较晚,主要受限于基础转捩模型的发展。随着各种横流转捩判据的提出,目前已形成多种横流转捩模型,其预测的流动速域主要集中在亚跨声速范围,横流判据主要针对后掠翼,模型参数需要通过数值试验进行标定,经验性较强,这使得横流转捩模型在使用过程中出现以下主要困难:转捩判据几何通用性较差、不同流动问题的普适性较差、非当地量求解在多块并行计算中的实现比较复杂、多数模型不适用于超声速或高超声速流动。因此,未来横流转捩模型研究将有以下发展方向:
1) 以更系统广泛的实验数据为基础,构造物理意义更强、经验性更低、适用范围更广的横流转捩判据作为横流转捩模型的基础。
2) 在现有横流转捩模型中实现模型的完全当地化计算,或脱离现有基础转捩模型,直接构造独立的横流转捩模型。
3) 针对航空航天工程中的迫切需求,发展适合于超声速、高超声速横流流场和对应几何外形的横流转捩判据和模型。
| [1] |
Medida S, Baeder J D. A new crossflow transition onset criterion for RANS turbulence models[R]. AIAA 2013-3081.
(  0) 0) |
| [2] |
Reed H, Saric W, Arnal D. Linear stability theory applied to boundary layers[J]. Annual Review of Fluid Mechanics, 1996, 28: 389-428. DOI:10.1146/annurev.fl.28.010196.002133 (  0) 0) |
| [3] |
Balakumar P, Malik M. Discrete modes and continuous spectra in supersonic boundary layer[J]. Journal of Fluid Mechanics, 1992, 239: 631-656. DOI:10.1017/S0022112092004555 (  0) 0) |
| [4] |
Malik M R, Li F, Chang C L. Crossflow disturbances in three-dimensional boundary layers:nonlinear development, wave interaction and secondary instability[J]. Journal of Fluid Mechanics, 1994, 268: 1-36. DOI:10.1017/S0022112094001242 (  0) 0) |
| [5] |
Wang L. Modelling flow transition in hypersonic boundary layer[D]. Beijing: Tsinghua University, 2008. (in Chinese) 王亮. 高超音速边界层转捩的模式研究[D]. 北京: 清华大学, 2008. (  0) 0) |
| [6] |
Bippes H. Basic experiment on transition in three-dimensional boundary layers dominated by crossflow instability[J]. Progress in Aerospace Sciences, 1999, 35: 363-412. DOI:10.1016/S0376-0421(99)00002-0 (  0) 0) |
| [7] |
Bippes H, Nitschke-Kowsky P. Experimental study of instability modes in a three-dimensional boundary layer[R]. AIAA 1987-1336.
(  0) 0) |
| [8] |
Balakumar P, King R A. Receptivity and transition of supersonic boundary layers over swept wings[C]//48th AIAA Aerospace Science Meeting Including the New Horizons Forum and Aerospace Exposition, 2010. 1, 1454: 1-23.
(  0) 0) |
| [9] |
Gray W E. The effect of wing sweep on laminar flow[R]. RAE TM Aero 256, 1952
(  0) 0) |
| [10] |
Owen P R, Randall D J. Boundary-layer transition on a swept-back wing[R]. RAE TM Aero 277, 1952.
(  0) 0) |
| [11] |
Kohama Y, Davis S S. A new parameter for predicting crossflow instability[J]. JSME International Journal, Fluids and Therman Engineering, 1993, 36-B: 80-85. (  0) 0) |
| [12] |
Arnal D, Habiballah M, Coutols E. Theory of laminar instability and transition criteria in two and three dimensional flow[J]. The Aerospace Research, 1984, 33(2): 125-143. (  0) 0) |
| [13] |
Grabe C, Krumbein A. Extension of the  0) 0) |
| [14] |
Müller C, Herbst F. Modelling of crossflow-induced transition based on local variables[C]//6th European Conference on Computational Fluid Dynamics, 2014.
(  0) 0) |
| [15] |
Boltz F W, Kenyon G C, Allen C Q. Effects of sweep angle on the boundary-layer stability characteristics of an untapered wing at low speeds[R]. NASA TND-338, 1960.
(  0) 0) |
| [16] |
Scott-Wilson J B, Capps D S. Wind tunnel observation of boundary layer transition on two sweptback wings at a wach number of 1. 61[R]. RAE, Technical Note Aero 2347, 1954
(  0) 0) |
| [17] |
Dagenhart J R. Amplified crossflow disturbances in the laminar boundary layer on swept wings with suction[R]. NASA TP-1902, 1982.
(  0) 0) |
| [18] |
Chapman G T. Some effects of leading-edge sweep on boundary-layer transition at supersonic speeds[R]. NASA TND-1075, 1999.
(  0) 0) |
| [19] |
Chen J Q, Tu G H, Zhang Y F, et al. Hypersonic boundary layer transition:what we know, where shall we go[J]. Acta Aerodynamica Sinica, 2017, 35(3): 311-337. (in Chinese) 陈坚强, 涂国华, 张毅锋, 等. 高超声速边界层转捩研究现状与发展趋势[J]. 空气动力学学报, 2017, 35(3): 311-337. (  0) 0) |
| [20] |
Reed H L, Haynes T S. Transition correlation in 3-D boundary layers[J]. AIAA Journal, 1994, 32(5): 923-945. DOI:10.2514/3.12075 (  0) 0) |
| [21] |
Watababe Y, Misaka T, Obayashi S, et al. Application of crossflow transition criteria to local correlation-based transition model[R]. AIAA 2009-1145.
(  0) 0) |
| [22] |
Langtry R B, Sengupta K, Yeh D T, et al. Extending the  0) 0) |
| [23] |
Shi Y Y, Bai J Q, Hua J, et al. Study and modification of cross-flow induced transition model based on local variables[J]. Acta Aeronautica et Astronautica Sinica, 2016, 37(3): 780-789. (in Chinese) 史亚云, 白俊强, 华俊, 等. 基于当地变量的横流转捩预测模型的研究与改进[J]. 航空学报, 2016, 37(3): 780-789. (  0) 0) |
| [24] |
Grabe C, Krumbein A. Correlation-based transition transport modeling for three-dimensional aerodynamic configurations[J]. Journal of Aircraft, 2013, 1533-1539. (  0) 0) |
| [25] |
Spalart P R, Allmaras S R. A one-equation turbulence model for aerodynamic flows[R]. AIAA-92-0439, 1992.
(  0) 0) |
| [26] |
Menter F R. Zonal two-equation k-ω turbulence model for aerodynamic flows[R]. AIAA-93-2906, 1993.
(  0) 0) |
| [27] |
Fu S, Wang L. Progress in turbulence/transition modeling[J]. Advances in Mechanics, 2007, 37(3): 409-416. (in Chinese) 符松, 王亮. 湍流转捩模式研究进展[J]. 力学进展, 2007, 37(3): 409-416. DOI:10.6052/1000-0992-2007-3-J2006-159 (  0) 0) |
| [28] |
Warren E S, Hassan H A. Transition closure model for predicting transition onset[J]. Journal of Aircraft, 1998, 35(5): 769-775. DOI:10.2514/2.2368 (  0) 0) |
| [29] |
Zhou L, Yan C, Hao Z H, et al. Transition model; and transition criteria for hypersonic boundary layer flow[J]. Acta Aeronautica et Astronautica Sinica, 2016, 37(4): 1092-1102. (in Chinese) 周玲, 阎超, 郝子辉, 等. 转捩模式与转捩准则预测高超声速边界层流动[J]. 航空学报, 2016, 37(4): 1092-1102. (  0) 0) |
| [30] |
Zhang Yifeng, Zhang Yirong, Chen Jianqiang, et al. Numerical simulations of hypersonic boundary layer transition based on the flow solver chant 2. 0[R]. AIAA 2017-2409.
(  0) 0) |
| [31] |
Choi J H, Kwon O J. Recent improvement of a correlation-based transition turbulence model for simulating three-dimensional boundary layers[R]. AIAA 2015-2762.
(  0) 0) |
| [32] |
Choi J H, Kwon O J. Enhancement of a correlation-based transition turbulence model for simulating crossflow instability[R]. AIAA 2014-1133.
(  0) 0) |
| [33] |
Xu J K, Bai J Q, Qiao L, et al. Prediction model of cross-flow instability transition in swept wing boundary layers[J]. Journal of Aerospace Power, 2015, 30(4): 927-935. (in Chinese) 徐家宽, 白俊强, 乔磊, 等. 后掠翼边界层横流不稳定转捩预测模型[J]. 航空动力学报, 2015, 30(4): 927-935. (  0) 0) |
| [34] |
Xu J K, Bai J Q, Qiao L, et al. Transition model for predicting crossflow instabilities[J]. Acta Aeronautica et Astronautica Sinica, 2015, 36(6): 1814-1822. (in Chinese) 徐家宽, 白俊强, 乔磊, 等. 横流不稳定性转捩预测模型[J]. 航空学报, 2015, 36(6): 1814-1822. (  0) 0) |
| [35] |
Vizinho R, Morgado J, Pascoa J, et al. Analysisi of transitional flow in 3D geometries using a novel phenomenological model[J]. Aerospace Science and Technology, 2015, 45: 431-441. DOI:10.1016/j.ast.2015.06.018 (  0) 0) |
| [36] |
Tu G H, Deng X G, Mao M L. Validation of a RANS transition model using a high-order weighted compact nonlinear scheme[J]. Science China, Physics (Mechanics & Astronomy), 2013, 56(4): 1-7. (  0) 0) |
| [37] |
Langtry R B, Menter F R. Transition modeling for general CFD applications in aeronautics[R]. AIAA 2005-522.
(  0) 0) |
| [38] |
Langtry R B, Menter F R. Correlation-based transition modeling for unstructured parallelized computational fluid dynamics codes[J]. AIAA Journal, 2009, 47(12): 2894-2906. DOI:10.2514/1.42362 (  0) 0) |
| [39] |
Radeztsky R H, Reibert M S, Saric W S, et al. Effect of micron-sized roughness on transition in swept-wing flows[R]. AIAA 1993-0076.
(  0) 0) |
| [40] |
章梓雄, 董曾南. 粘性流体力学[M]. 北京: 清华大学出版社, 1998, 129-134.
(  0) 0) |
| [41] |
Stock H W. eN transition prediction in three-dimensional boundary layers on inclined prolate spheroids[J]. AIAA Journal, 2006, 44(1): 108-118. DOI:10.2514/1.16026 (  0) 0) |
 2018, Vol. 36
2018, Vol. 36