自然界的鸟、昆虫等飞行生物具有高超的飞行技巧,翅膀的大幅扑动是其奥秘所在,是其克服尺寸小、速度低引起的低雷诺数空气动力问题的重要方式。受自然界飞行生物启发,仿生扑翼在微型飞行器上获得成功并重新引起学界的广泛关注。通过实验和数值模拟研究,国际、国内学者在飞行原理、气动机理、飞行力学以及与之相关的实验和数值模拟方法等方面开展了大量的工作,揭示了多种扑翼高升力气动机理,增进了对扑翼飞行原理的了解和掌握,为仿生飞行器的设计提供了原理依据,相关研究进展和成果可参见Shyy[1]、孙茂[2]、Sane[3]、Wang[4]、杨文青等[5]的综述文献和著作。基于对扑翼空气动力学原理的认识,近年来,多种形式的仿生飞行器相继被研发问世。但航空界普遍认为,当前仿生飞行器的进一步发展和应用遇到了新的技术瓶颈。
一方面,现阶段仿生飞行器的设计仍是对飞行生物的简单模仿,效率低,性能远不及自然界飞行生物,在空气动力方面亟待进一步精细设计优化。受非定常气动设计优化理论与方法不足的制约,现有仿生飞行器的设计主要沿用简单的估参数-预分析的单向设计思路;通过实验或数值模拟,研究扑动运动参数或形状外形参数对气动的影响,以此获得气动特性随设计变量的变化规律,并据此来确定仿生扑翼的设计参数(或大概的设计范围),由于设计参数众多且设计范围较大,这种逐个分析参数的方法需要的计算量巨大;更严重的问题是,该方法常常割裂各个设计参数之间的内在联系,并不能实现真正的最佳设计。
另一方面,仿生扑翼流场具有强烈的非定常效应、涡流动复杂、粘性效应强,且除气动外形之外,翼的复杂大幅扑动运动也是其重要的气动措施,两者耦合使得设计变量众多,属大参数设计问题。扑翼气动问题的特殊性给气动建模和设计优化理论与方法带来了极大的挑战,常规定常气动设计方法已不能适应非定常仿生飞行器这类新问题。仿生扑翼这一新型飞行器技术的发展迫切需要基础的设计优化理论方法有大的革新和新的突破。
基于仿生飞行器的发展需要,仿生扑翼的非定常气动设计优化问题逐渐受到重视,近年,国内外学者针对扑翼气动优化设计问题,从气动建模、设计优化理论方法和应用研究等角度开展工作,构建了不同保真度的优化设计方法和模型用于扑翼气动的优化设计,取得了较大的进展;但鉴于扑翼非定常流动问题的复杂性和特殊性,仿生扑翼非定常气动优化设计仍面临很大的困难和挑战。本文拟从气动建模、优化方法策略等方面,对当前仿生飞行器的非定常气动优化设计研究取得的进展、面临的困难和挑战进行分析、评述和总结,以与同行交流。为方便起见,本文按照气动模型的保真度和优化方法策略的不同,将现有仿生扑翼气动优化设计的研究工作归纳为基于传统方法和基于现代新型方法两个大类进行论述。
1 运用传统方法的仿生扑翼气动优化设计这一类的仿生扑翼气动优化设计研究,按照气动模型的保真度从低到高归纳为基于叶素理论气动建模、基于快速数值方法气动建模、基于非定常N-S方程气动建模和实验测量几种。
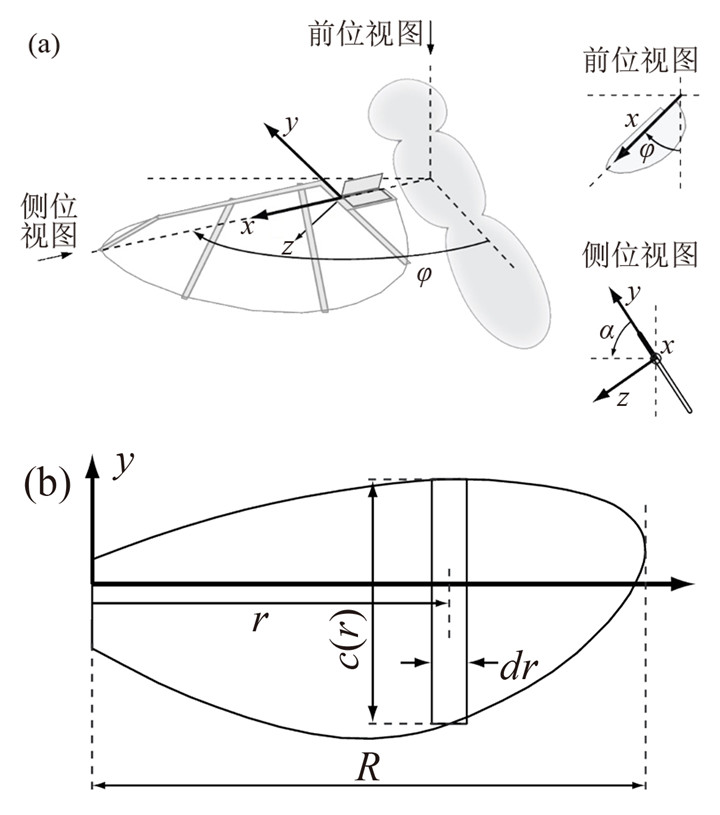
1.1 基于叶素理论气动建模的仿生扑翼气动优化设计叶素理论原来主要用于螺旋桨或旋翼的气动计算,即将桨叶按展向分成若干微元,每个微元按照二维定常情况根据当地气流条件计算其气动力,累加即得到整个桨叶的气动力。基于此理论,仿生扑翼也可建立类似的准定常气动模型。以悬停状态的扑翼为例,其扑动运动参数和平面形状示意如图 1所示,扑翼展长为R,展向截面的弦长为c(r),扑动角度定义为φ。扑翼扑动过程中,认为气动力总是垂直于翼面。考虑扑动运动引起的气动力,对扑翼某个展向位置处的微元段dr,其当地瞬时速度为
| $ d{{F}_{\rm{aero}}}=\underbrace{1/2\rho {{{\dot{\varphi }}}^{2}}{{r}^{2}}}_{{{p}_{\rm{dyn}}}}\underbrace{{{C}_{F}}\left( \alpha \right)}_{{{C}_{F}}}\underbrace{c\left( r \right)\rm{d}\mathit{r}}_{\rm{d}\mathit{A}~} $ | (1) |
|
图 1 基于叶素理论的扑翼气动建模示意图[8] Figure 1 Schematics of aerodynamic model of flapping wing based on blade element theory[8] |
其中,
| $ {{F}_{\rm{aero}}}=\frac{1}{2}\rho {{{\dot{\varphi }}}^{2}}{{C}_{F}}\left( \alpha \right)\bar{c}{{R}^{3}}\underbrace{\int_{0}^{1}{{{\left( {\hat{r}} \right)}^{2}}\hat{c}\left( {\hat{r}} \right){\rm{d}}\hat{r}}}_{\equiv \hat{r}_{2}^{2}} $ | (2) |
式中,
Berman和Wang等[7]即基于这类准定常模型,运用遗传全局优化和Nelder-Mead单纯形的梯度局部优化相结合的组合算法,对昆虫扑翼悬停状态的11个扑动运动参数进行优化设计。以周期平均升力等于重力为约束、以平均功率消耗(气动力+惯性力)最小为目标,先用遗传算法进行大范围寻优,后用梯度优化算法进行局部优化,最终优化设计得到的扑翼运动轨迹与对自然界生物的观测结果相似。Kurdi等[9]运用同样的气动模型,采用梯度优化方法对昆虫翼悬停状态的30个扑动运动变量进行优化,扑动运动规律采用样条函数拟合使其光滑连续,优化设计模型甚至考虑了弹性影响。Ke和Zhang等[10]同样基于准定常模型,运用遗传算法和梯度优化方法,以扑翼的平面几何外形和扑动运动参数为设计变量,以功耗最小为目标进行优化设计,分析认为扑翼外形参数和运动参数之间通过展弦比和雷诺数建立有较强的耦合关系而共同影响着目标函数。Yan和Taha等[11]对悬停状态的扑翼运动参数进行优化设计以使功耗最小,优化过程采用了几种基于叶素理论建立的精度不一的气动模型,包括上述准定常模型和Haithen等[12]建立的考虑前缘涡等非定常效应的全非定常气动模型;研究认为准定常模型较高估计了升力系数,使得最小功耗值比全非定常模型优化结果更小,论文通过综合比较建议扑翼的非定常气动优化设计应该采用较高精度的非定常气动模型。
Gogulapati等[13-14]完成了悬停状态柔性扑翼的优化设计,气动模型采用基于叶素理论的结合势流求解器的非定常气动模型[15],即叶素模型的微元气动力通过求解二维速势方程得到,速势方程的求解假定分离从前缘开始,涡强度由强化的前缘滞止条件和后缘库塔条件决定,同时计及前缘涡高升力;优化设计也包括了非线性结构有限元模型;由于气动模型和结构有限元模型计算量相对较大,作者通过Kriging插值建立时均推力和时均功率的代理模型;设计变量为扑动和俯仰运动参数以及柔性翼的刚度共13个设计变量;优化算法是全局优化和梯度优化的组合算法;优化结果表明在一定扑动幅度和频率下,扑动与俯仰运动的相位差对效率影响很大,柔性翼的效率峰值出现于较小俯仰运动角度情况,在若干设计变量区间,柔性翼相比刚性翼并不占优。
基于叶素理论气动模型的优化设计可快速地在全局范围内寻得最优解,但气动模型本身的问题决定了优化设计的精度不会很高;原因是,叶素理论模型从原理上就不考虑展向流动和翼尖涡,而实际上由于扑翼展弦比一般不大,且强烈的展向流动是扑翼延迟失速的重要机理;因此,从设计精度角度来说,这类优化设计只适合初步概念设计阶段大量参数的粗略分析和筛选。
1.2 基于快速数值方法的仿生扑翼气动优化设计扑翼非定常气动的快速数值方法主要是非定常涡格法(Unsteady Vortex-Lattice Method, UVLM)。UVLM在运动的升力面上进行涡格划分,并在每个涡格上布置马蹄涡和控制点,通过在控制点处满足升力面法向无穿透的边界条件来进行求解。相对叶素理论气动模型,该方法具有较高的精度,同时计算量又远小于N-S方程的求解,在扑翼非定常气动力计算分析上得到较多应用,同时也在不断改进发展中[16-17]。
目前有少数学者运用UVLM进行气动建模用于仿生扑翼的气动优化设计。Stanford等[18]将UVLM气动模型嵌入梯度优化器,在升力、阻力约束条件下以气动功率最小为目标,对前飞状态的主动变形仿鸟扑翼的弦向扭转和展向弯曲进行优化,与Kurdi[9]类似,运动规律采用样条函数拟合以保证其光滑连续;优化结果表明,在低缩减频率下,展向弯曲变形对增加时均推力、提高效率起主导作用,在较高缩减频率下,弦向扭转变形则在减少功耗上更为重要,该研究也表明增加设计变量数量可获得更优的设计和更高的计算效率。Ghommen等[19]基于非定常涡格法结合确定全局优化方法,建立基于三角函数和样条函数的两种扑翼运动规律的参数化模型,对主动变形仿鸟扑翼的运动规律进行优化设计,设计参数仅4-8个;结果表明样条函数的参数化建模由于三角函数模型,翼变形对效率有益,且扭转和弯曲中的二阶模态对效率提升有明显作用。之后,Ghommen等[19]又对扑翼外形(包括展弦比、弯度、前缘后缘弯曲形状等)进行基于全局优化和梯度优化结合的优化设计,表明合理配置展弦比、弯度和前后缘外形,对改善尾涡结构(如图 2所示)、提高推进效率有积极意义,其结果可为仿鸟扑翼的工程设计提供有价值的参考。Stewart等[21]将UVLM和平板有限元模型结合,运用局部优化方法,对柔性扑翼的外形和结构进行了多目标的优化设计,结果显示增强结构弹性变形,有利于提高推力但也增加了功率消耗。贺红林等[22]运用非定常涡格法建立气动模型,结合模式搜索算法,以升力和推力最大化为目标,对扑动和俯仰运动相位差、扑动频率和柔性扭转角进行优化设计,对三者的配匹给出了一定的建议。

|
图 2 优化设计展弦比及前后缘外形对扑翼尾涡的形状和强度影响[19] Figure 2 Optimal shape on the wake patterns and vorticity strength of a bird-like flapping wing[19] |
总的来说,基于ULVM气动模型的扑翼优化设计,计算量适中,用于仿中大型鸟类扑翼这类较弱或中等强度非定常气动设计,也能取得较高的精度;但用于非定常效应更严重的仿昆虫扑翼的优化设计,则还需ULVM方法的进一步发展和完善。
1.3 基于非定常N-S方程和实验测量的仿生扑翼气动优化设计对非定常效应强烈、涡流动复杂、粘性效应强的仿生扑翼流场,基于非定常N-S方程的气动模型能获得相对较高的保真度,但N-S方程求解复杂,动态网格处理繁琐,计算量大,若按照传统思路,采用全局优化或常规梯度优化算法,对扑翼尤其三维复杂扑翼的气动优化设计将由于超大的计算量而难以实现。目前只有极少数工作进行了尝试,但也仅限于二维或简单三维情况,且设计变量数目非常有限。
Tuncer等[23]基于前向模式差分的梯度优化算法,建立二维N-S方程的优化设计模型,对在自由来流中做俯仰和沉浮运动的翼型进行推力和推进效率最大化的优化设计;揭示了扑动运动与流场结构、进而与气动效率的因果关系,表明能产生前缘涡的扑动运动可增加升力但降低了推进效率,而不产生前缘涡的扑动运动则有利于提高推进效率。Soueid等[24]通过建立基于敏感度方程和二维不可压N-S方程气动模型的优化设计模型,完成了NACA0012翼型扑动运动规律(沉浮、俯仰和相位差)的设计。Culbreth等[25]运用有限差分的梯度优化方法和三维N-S方程气动模型,分析了矩形扑翼的4个展向扭转参数对推进效率的敏感度。
最近也有个别学者尝试通过实验测量或基于有限的实验数据,利用相关的优化算法,以扑翼气动性能参数为目标进行扑动运动参数的优化,Milano[26]、Chaudhuri[27]、Nan[28]等的工作是其中的主要代表。但基于实验测量的优化设计,成本高、难度大,不易掌控,应用于工程实际问题存在比较大的困难。
1.4 传统优化设计面临的问题虽然仿生飞行器的发展备受关注,但目前对仿生扑翼的非定常气动设计优化方法仍缺乏系统的研究。现有研究大多数都沿用传统的优化设计理论,利用遗传算法等全局寻优技术或利用常规的基于梯度的局部寻优方法,构建仿生扑翼的优化设计模型,这一思路在初步设计或少量设计参数问题上可发挥一定的作用,但用于非定常仿生飞行器会面临很大的问题和挑战。正如前文所述,仿生扑翼流动具有强非定常、低雷诺数特点,涡流动复杂,粘性效应强,其气动的计算分析需采用基于N-S方程的高保真度数值方法,计算量大;另一方面,仿生扑翼的设计变量,包括气动外形参数和扑动运动参数,数量可达数十甚至上百个。传统优化设计方法的计算量与设计变量数量相关,因此,用于仿生飞行器问题,要么以牺牲精度为代价,气动分析采用较低精度的模型,如准定常气动模型、涡格法等;或者气动模型采用高阶模型,但严格限制设计变量数量,即使采用代理模型技术构建响应面,其设计参数数量也相当有限。可以说,基于传统优化设计理论的思路很难实现有效的高精度的优化设计,对仿生飞行器问题,要另辟蹊径,需在适于大参数非定常气动问题的优化设计理论和方法研究上寻求突破。
2 仿生扑翼气动的非定常伴随优化设计近年来,航空界新发展一种基于控制理论的伴随优化方法,代表着当前国际先进的设计优化理论和发展趋势。该方法将设计问题当作最优控制问题,通过引入并求解一个伴随方程系统实现设计目标对设计变量的灵敏度分析,一轮优化,只需求解一次流动控制方法和一次伴随方程,其计算量与设计变量数量无关,成为解决大参数气动设计优化问题技术瓶颈的重要措施和发展方向。目前,对伴随优化理论和方法的研究已经在多个领域的气动外形设计优化上(如叶轮机械[29]、翼型和三维机翼[30]、气动噪声[31]等)取得了很多成果,国内的北京大学刘峰团队[32-33]、西安交通大学丰镇平团队[34-35]、西北工业大学[36-38]、上海交大[31]以及北京理工大学[29, 39]、中国空气动力研究与发展中心[40-41]、兰州理工[42]和南京航空航天大学[43-45]等,在该领域的研究都相当出色。但需要指出的是,上述研究的重点主要针对定常流动的气动外形设计优化。
随着非定常流动及其设计优化问题日益受到重视,为其发展有效的优化设计理论与方法也迫在眉睫。对非定常问题,时均性能参数通常是受关心的量,理论上来说,非定常流场的优化设计问题,也可以看成是受非定常流体控制方程和动网格方程约束的时均目标函数的最小值优化问题,同样可以运用最优控制理论求解。对某段物理时间,通过建立与时均目标函数和非定常流动控制方程求解相容的非定常伴随方程,在前向积分求解出流场后,再逆时间积分求出各物理时间步的伴随变量,从而实现该段时间内时均目标函数对设计变量的敏感度分析,这一思路为解决大参数非定常设计优化问题提供了可能,在仿生扑翼非定常气动问题上也具有可行性。
对仿生飞行器而言,时均气动参数是衡量性能的重要指标。我们将仿生飞行器的非定常气动优化设计问题,当成是受非定常流体控制方程和动态网格方程约束的时均目标函数最小值优化问题,即:
| $ \left\{ \begin{align} &{\rm{min}}{{\mathit{F}}_{\rm{obj}}}\left( \mathit{\boldsymbol{D}} \right), {{F}_{\rm{obj}}}\left( \mathit{\boldsymbol{D}} \right)=\sum\limits_{n={{N}_{b}}}^{{{N}_{e}}}{{{f}^{n}}\left( {{\mathit{\boldsymbol{Q}}}^{n}}, {{\mathit{\boldsymbol{X}}}^{n}}, \mathit{\boldsymbol{D}} \right)}\Delta t \\ &{\rm{subject}}\ {\rm{to}}:\frac{3{{V}^{n}}{{\mathit{\boldsymbol{Q}}}^{n}}-4{{V}^{n-1}}\mathit{\boldsymbol{Q}}{{~}^{n-1}}~+{{V}^{n-2}}~{{\mathit{\boldsymbol{Q}}}^{n-2}}}{~2\Delta t}~ \\ &\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ +{{\mathit{\boldsymbol{R}}}^{n}}+\mathit{\boldsymbol{R}}_{\rm{GCL}}^{n}{{\mathit{\boldsymbol{Q}}}^{n-1}}=0 \\ &\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \mathit{\boldsymbol{G}}\left( {{\mathit{\boldsymbol{X}}}^{0}}, {{\mathit{\boldsymbol{X}}}^{n}}, \mathit{\boldsymbol{D}} \right)=0 \\ \end{align} \right. $ | (3) |
式中fn为第n时间步跟流场变量Q、网格X和设计变量D有关的目标函数值;式(3)中第二行为基于二阶时间精度的非定常流体离散求解方程,Rn、RGCLn分别为流场残值和动网格下的几何守恒定律项;第三行为动态网格方程,G为其残值。对周期性的扑翼运动,Ne=Nb+M(M为一个周期的时间步数)。
基于最优控制理论,可找到适当的Q和D使得受约束的目标函数值最小,达到解决式(3)最小值优化问题的目的。通过拉格朗日乘子Λf, Λg将式(3)中的约束引入到目标函数中,形成新的拉格朗日函数L,即:
| $ \begin{array}{l} L\left( {\mathit{\boldsymbol{D}}, \mathit{\boldsymbol{Q}}, \mathit{\boldsymbol{X}}, {\mathit{\boldsymbol{ \boldsymbol{\varLambda} }}_f}, {\mathit{\boldsymbol{ \boldsymbol{\varLambda} }}_f}} \right) = \sum\limits_{n = 1}^M {{f^n}\Delta t + } \\ \sum\limits_{n = 1}^M {{{\left[{\mathit{\boldsymbol{ \boldsymbol{\varLambda} }}_f^n} \right]}^{\rm{T}}}\left( {\frac{{3{V^n}{\mathit{\boldsymbol{Q}}^n} - {}4{V^{n - 1}}\mathit{\boldsymbol{Q}}{^{n - 1}} + {}{V^{n - 2}}{\mathit{\boldsymbol{Q}}^{n - 2}}}}{{2\Delta t}} + } \right.} \\ \left. {{\mathit{\boldsymbol{R}}^n} + \mathit{\boldsymbol{R}}_{{\rm{GCL}}}^n{\mathit{\boldsymbol{Q}}^{n - 1}}} \right)\Delta t + \\ \sum\limits_{n = 1}^M {{{\left[{\mathit{\boldsymbol{ \boldsymbol{\varLambda} }}_f^n} \right]}^{\rm{T}}}} {\mathit{\boldsymbol{G}}^n}\Delta t \end{array} $ | (4) |
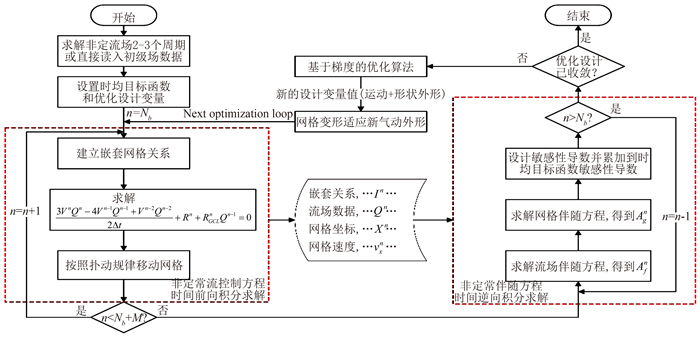
运用链式法则推导出拉格朗日函数对设计变量的敏感性导数式,为避开计算量巨大的
|
图 3 非定常气动离散伴随优化设计思路和流程 Figure 3 Flow chart of unsteady discrete adjoint optimization for flapping wings |
目前已有少数学者开展了这方面的研究。如Nielsen[46-47]、Mavriplis[48]、Alonso[49]等在非定常离散伴随和非定常连续伴随优化理论及求解方法上开展了开拓性的研究工作,并在旋翼、动态失速翼型等的气动外形设计上进行了初步应用研究;北京理工大学雷娟棉[50-51]发展了非定常离散伴随方法并在二维跨声速俯仰翼型和低雷诺数翼型的外形优化上进行了验证;上海应用数学力学研究所[52]研究了二维沉浮翼型的连续伴随优化方法;清华大学[53]初步探索了基于非定常流动控制方程瞬态解和非定常伴随方程瞬态解的动态演化伴随方法,以达到提高定常气动外形优化效率的目的,其思路和优势在二维翼型外形设计算例上得到验证。
对仿生扑翼的非定常气动问题,伴随优化方法也表现出良好的应用前景,近两年逐渐受到关注。Lee和Liou[54-55]对伴随优化在仿生扑翼问题上的应用进行了初步尝试,分别研究了二维扑动翼型的外形及简单运动轨迹的优化设计,由于伴随方法的计算量与设计变量数目无关,该方法才有可能将高精度N-S方程的气动模型用于较多设计变量的非定常气动优化。Jones等[56]则将应用对象扩展到三维情况,分别对仿昆虫扑翼的扑动运动参数、几何外形参数进行了优化设计,并尝试了将运动参数和外形参数联立,构成统一的设计空间进行设计,其结果也表明两者对优化目标而言存在较强的非线性耦合关系。Xu等[57]针对扑翼问题的特殊性,发展了一种新的伴随方法中动态边界的处理办法,并将其应用到刚性、柔性平板扑翼的优化设计,表明柔性对推力特性和推进效率都有帮助;对三维矩形扑翼悬停状态的运动参数和柔性变形参数的优化设计结果证实,非定常伴随优化方法能找到最佳的运动参数和柔性变形,使得前缘涡更大,下洗流动更强,柔性变形能更好地捕捉尾涡,而这些特征是低阶气动模型无法做到的,显示了伴随优化在仿生飞行器上的良好愿景。就目前而言,仿生扑翼的非定常离散伴随优化设计的研究不多,但已有工作发挥了良好的推动作用。
3 仿生飞行器非定常气动优化设计的问题与展望仿生扑翼流场具有强烈的非定常效应,流动机理复杂多样,雷诺数低、粘性效应强;同时,气动外形和翼的复杂大幅扑动运动都是其重要的气动措施,两者相互耦合,设计变量数目众多;仿生扑翼的复杂性和特殊性给仿生飞行器的气动优化设计带来很大的困难和挑战。
针对仿生飞行器发展的需要,现阶段已经从不同途径,或基于传统方法,或发展新的技术,发展了若干不同精度的气动模型或气动评估方法,运用不同优化设计策略进行了仿生飞行器气动的优化设计。这些气动模型或方法各有优势,从实际工程来说,不必片面强调高精度而忽略其他。对于仿生飞行器的具体设计,从概念设计到详细设计,不同阶段需要不同精度的气动优化模型和策略,发展并应用分层次、分阶段的多保真度仿生扑翼非定常气动优化设计方法和模型,将是仿生飞行器领域值得考虑的问题。
对仿生飞行器非定常气动的优化设计,未来以下几个方面的问题需要重点关注和寻求解决。
1) 仿生扑翼的低阶气动模型可在仿生飞行器的概念设计阶段发挥重要作用,未来应结合扑翼非定常气动机理、相关空气动力学原理和理论,发展和完善计算模型,充分计及前缘涡、延迟失速、旋转效应等高升机制和展向流动、翼尖涡等在气动力产生方面的作用或影响,形成一套效率好、精度高的仿生飞行器非定常气动快速优化设计的技术方案。
2) 基于传统方法的优化设计因为模型精度与计算量的矛盾而不能满足仿生飞行器这一复杂问题的精细设计需要,伴随优化是解决这一问题的有效途径,但非定常伴随优化理论和方法的研究刚刚起步,在仿生飞行器上应用还不成熟,在非定常伴随方程构造、高效求解、初边值条件(空间的和时间的)以及与仿生飞行器特殊问题相关的适定性、目标泛函选取原则、设计准则等方面,其理论和方法的发展完善还需要学者持续深入研究;此外,仿生扑翼的大幅扑动运动常常要求流场解算基于动态嵌套网格进行,在动态嵌套网格上,非定常伴随方程的构造求解理论与方法及其扩展迁移也是仿生飞行器非定常伴随优化研究需要解决的问题。
3) 就仿生扑翼气动优化设计本身来说,现有研究,无论是基于传统优化方法还是应用新型伴随优化方法的,大多数将气动外形和扑动运动参数分开,单一地就某一方面进行设计,较少将运动或轨迹参数与外形参数耦合构建一个统一的设计空间;而对仿生飞行器而言,外形与扑动运动的耦合又十分重要,如何将复杂非连续扑动运动(如翼翻转、往返非对称等)参数化并与外形参数联合,构造连续光顺的利于优化设计收敛的设计空间,是仿生飞行器非定常气动优化设计值得探讨的问题。
4) 对仿生扑翼的优化设计,目前多数研究工作也主要集中在悬停状态,前飞状态、机动飞行状态甚至阵风状态下的扑翼气动优化设计也应该是下一步要解决的问题;此外,翼的柔性是影响气动效率的重要因素,翼的结构柔性也应是其气动优化设计的变量,柔性扑翼的气动建模及优化设计、甚至柔性扑翼气动-结构多学科耦合的优化设计,都将是仿生飞行器领域的重要课题。
总的来说,仿生飞行器非定常空气动力的优化设计仍是一个具有挑战性的课题,需要从基础理论到工程技术研究的全面推动和发展。
4 结论仿生扑翼是一种新型的飞行器技术,由于其扑翼流场强烈的非定常特征和低雷诺数效应、外形与扑动运动耦合的大量设计变量,仿生飞行器的气动优化设计存在很大的难度,是一个非常复杂的不同于定常气动问题的研究课题。由于缺乏成熟有效的设计方法和工具,目前仿生扑翼的优化设计大多数按照传统的优化设计思路,存在精度低或计算量大的缺陷,较难取得良好的优化设计效果。伴随优化方法是仿生飞行器非定常气动高精度高效率优化设计的有效途径,但该方法仍有待完善发展。对仿生扑翼气动的优化设计,需耦合外形参数和扑翼运动参数,建立联合的设计空间;前飞状态、机动飞行状态或阵风状态下的扑翼气动优化设计也是未来工作关注的重点。对仿生飞行器设计来说,采用不同保真度模型,分层次、分阶段地进行气动优化设计是从概念设计走向详细设计的有效策略。
| [1] |
Shyy W, Aono H, Kang C K, et al. An introduction to flapping wing aerodynamics[M]. Cambridge University Press, 2013.
(  0) 0) |
| [2] |
孙茂. 昆虫飞行的空气动力学[J]. 力学进展, 2015, 45: 1-28. (  0) 0) |
| [3] |
Sane S P. The aerodynamics of insect flight[J]. Journal of Experimental Biology, 2003, 206: 4191-4208. DOI:10.1242/jeb.00663 (  0) 0) |
| [4] |
Wang Z J. Dissecting insect flight[J]. Annual Review of Fluid Mechanics, 2005, 37: 183-210. DOI:10.1146/annurev.fluid.36.050802.121940 (  0) 0) |
| [5] |
杨文青, 宋笔锋, 宋文萍. 仿生微型扑翼飞行器中的空气动力学问题研究进展与挑战[J]. 实验流体力学, 2015, 29: 1-10. DOI:10.11729/syltlx20140132 (  0) 0) |
| [6] |
Sane S P, Dickinson M H. The aerodynamic effects of wing rotation and a revised quasi-steady model of flapping flight[J]. The Journal of Experimental Biology, 2002, 205: 1087-1096. (  0) 0) |
| [7] |
Berman G J, Wang Z J. Energy-minimizing kinematics in hovering insect flight[J]. Journal of Fluid Mechanics, 2007, 582: 153. DOI:10.1017/S0022112007006209 (  0) 0) |
| [8] |
Whitney J P, Wood R J. Conceptual design of flapping-wing micro air vehicles[J]. Bioinspiration & Biomimetics, 2012, 7: 36001. (  0) 0) |
| [9] |
Kurdi M, Stanford B, Beran P. Optimal kinematics of hovering insect flight for minimum mechanical power[C]//48th AIAA Aerospace Sciences Meeting Including the New Horizons Forum and Aerospace Exposition, Reston, Virigina: American Institute of Aeronautics and Astronautics, 2010.
(  0) 0) |
| [10] |
Ke X, Zhang W, Cai X, et al. Wing geometry and kinematic parameters optimization of flapping wing hovering flight for minimum energy[J]. Aerospace Science and Technology, 2017, 64: 192-203. DOI:10.1016/j.ast.2017.01.019 (  0) 0) |
| [11] |
Yan Z, Taha H E, Hajj M R. Effects of aerodynamic modeling on the optimal wing kinematics for hovering MAVs[J]. Aerospace Science and Technology, 2015, 45: 39-49. DOI:10.1016/j.ast.2015.04.013 (  0) 0) |
| [12] |
Haithem E Tahaa, Muhammad R Hajja, Philip S Beranb. State-space representation of the unsteady aerodynamics of flapping flight[J]. Aerospace Science and Technology, 2014, 34: 1-11. DOI:10.1016/j.ast.2014.01.011 (  0) 0) |
| [13] |
Gogulapati A, Friedmann P P, Martins J R R A. Optimization of flexible flapping-wing kinematics in hover[J]. AIAA Journal, 2014, 52: 2342-2354. DOI:10.2514/1.J053083 (  0) 0) |
| [14] |
Gogulapati A, Friedmann P P, Martins J R R. Optimization of the kinematics of a flapping wing MAV in hover for enhanced performance[C]//54th AIAA/ASME/ASCE/AHS/ASC Structures, Structural Dynamics, and Materials Conference, Boston, Massachusetts: 2013.
(  0) 0) |
| [15] |
Gogulapati A, Friedmann P P, Kheng E, et al. Approximate aeroelastic modeling of flapping wings in hover[J]. AIAA Journal, 2013, 51: 567-583. DOI:10.2514/1.J051801 (  0) 0) |
| [16] |
Gardiner J, Razak N A, Dimitriadis G, et al. Simulation of bird wing flapping using the unsteady vortex lattice method[C]//IFASD 2013-International Forum on Aeroelasticity and Structural Dynamics, 24-27 June, Bristol, 2013: 1-14.
(  0) 0) |
| [17] |
Nguyen A T, Kim J K, Han J S, et al. Extended unsteady vortex-lattice method for insect flapping wings[J]. Journal of Aircraft, 2016, 53(6): 1709-1718. DOI:10.2514/1.C033456 (  0) 0) |
| [18] |
Stanford B K, Beran P S. Analytical sensitivity analysis of an unsteady vortex-lattice method for flapping-wing optimization[J]. Journal of Aircraft, 2010, 47: 647-662. DOI:10.2514/1.46259 (  0) 0) |
| [19] |
Ghommem M, Collier N, Niemi A H, et al. On the shape optimization of flapping wings and their performance analysis[J]. Aerospace Science and Technology, 2014, 32: 274-292. DOI:10.1016/j.ast.2013.10.010 (  0) 0) |
| [20] |
Ghommem M, Hajj M R, Mook D T, et al. Global optimization of actively morphing flapping wings[J]. Journal of Fluids and Structures, 2012, 33: 210-228. DOI:10.1016/j.jfluidstructs.2012.04.013 (  0) 0) |
| [21] |
Stewart E C, Patil M J, Canfield R A, et al. Aeroelastic shape optimization of a flapping wing[J]. Journal of Aircraft, 2016, 53: 636-650. DOI:10.2514/1.C033278 (  0) 0) |
| [22] |
贺红林, 周翔, 朱保利, 等. 基于非定常涡格法的扑翼飞行器气动特性优化[J]. 空气动力学学报, 2012, 30(1): 74-79. (  0) 0) |
| [23] |
Tuncer I, Kaya M. Optimization of flapping airfoils for maximum thrust and propulsive efficiency[J]. AIAA Journal, 2005, 43: 2329-2336. DOI:10.2514/1.816 (  0) 0) |
| [24] |
Soueid H, Guglielmini L, Airiau C, et al. Optimization of the motion of a flapping airfoil using sensitivity functions[J]. Computers and Fluids, 2009, 38: 861-874. DOI:10.1016/j.compfluid.2008.09.012 (  0) 0) |
| [25] |
Culbreth M, Allaneau Y, Jameson A. High-fidelity optimization of flapping airfoils and wings[C]//29th AIAA Applied Aerodynamics Conference, 2011.
(  0) 0) |
| [26] |
Milano M, Gharib M. Uncovering the physics of flapping flat plates with artificial evolution[J]. Journal of Fluid Mechanics, 2005, 534: 403-409. DOI:10.1017/S0022112005004842 (  0) 0) |
| [27] |
Chaudhuri A, Haftka R T, Ifju P G, et al. Experimental flapping wing optimization and uncertainty quantification using limited samples[J]. Structural and Multidisciplinary Optimization, 2014, 51: 957-970. (  0) 0) |
| [28] |
Nan Y, Karásek M, Lalami M E, et al. Experimental optimization of wing shape for a hummingbird-like flapping wing micro air vehicle[J]. Bioinspiration & Biomimetics, 2017, 12: 26010. (  0) 0) |
| [29] |
季路成, 李伟伟, 伊卫林. 伴随方法用于叶轮机优化设计的回顾与展望[J]. 航空发动机, 2011, 37(5): 53-57+62. (  0) 0) |
| [30] |
Osusky L, Buckley H, Reist T, et al. Drag minimization based on the navier-stokes equations using a Newton-Krylov approach[J]. AIAA Journal, 2015, 53: 1555-1577. DOI:10.2514/1.J053457 (  0) 0) |
| [31] |
邱昇. 基于伴随方法的涡扇发动机涵道的气动噪声优化设计研究[D]. 上海交通大学博士学位论文, 2013. http://cdmd.cnki.com.cn/Article/CDMD-10248-1014077473.htm
(  0) 0) |
| [32] |
Luo J, Zhou C, Liu F. Multipoint design optimization of a transonic compressor blade by using an adjoint method[J]. Journal of Turbomachinery, 2013, 136: 51005-51005-10. DOI:10.1115/1.4025164 (  0) 0) |
| [33] |
Luo J, Xiong J, Liu F. Aerodynamic design optimization by using a continuous adjoint method[J]. Science China-Physics, Mechanics & Astronomy, 2014, 57: 1363-1375. (  0) 0) |
| [34] |
张朝磊, 卢娟, 丰镇平. 基于离散伴随方法的透平叶栅反设计[J]. 工程热物理学报, 2012, 33(4): 583-586. (  0) 0) |
| [35] | |
| [36] |
王龙, 宋文萍, 杨旭东. 一种基于伴随方程迎角不变的多目标优化减阻方法[J]. 西北工业大学学报, 2012, 30(1): 68-72. (  0) 0) |
| [37] |
白俊强, 陈颂, 华俊. 基于伴随方程和自由变形技术的跨声速机翼气动设计方法研究[J]. 空气动力学学报, 2014, 32(6): 820-826+833. (  0) 0) |
| [38] |
左英桃, 苏伟, 高正红. 基于离散共轭方法的高超声速导弹气动外形优化设计[J]. 计算力学学报, 2012, 29(2): 284-289. (  0) 0) |
| [39] |
李伟伟, 季路成, 伊卫林. 基于伴随方法的多级叶轮机三维叶片优化设计[J]. 工程热物理学报, 2014, 35(11): 2164-2167. (  0) 0) |
| [40] |
李彬, 邓有奇, 唐静, 等. 基于三维非结构混合网格的离散伴随优化方法[J]. 航空学报, 2014, 35(3): 674-686. (  0) 0) |
| [41] |
吴文华, 范召林, 陈德华, 等. 基于伴随算子的大飞机气动布局精细优化设计[J]. 空气动力学学报, 2012, 30(6): 719-724+760. (  0) 0) |
| [42] |
张人会, 刘宜, 郭苗, 等. 基于伴随方法的离心泵叶轮优化设计[J]. 排灌机械工程学报, 2014, 32(11): 943-947+954. DOI:10.3969/j.issn.1674-8530.14.0033 (  0) 0) |
| [43] |
徐兆可, 夏健, 高宜胜. 基于三维非结构网格的连续伴随优化方法[J]. 南京航空航天大学学报, 2015, 47(1): 145-152. (  0) 0) |
| [44] |
高宜胜, 伍贻兆, 夏健. 基于非结构网格离散型伴随方法的翼型优化[J]. 空气动力学学报, 2013, 31(2): 244-265. (  0) 0) |
| [45] |
Tang Z, Dong J. Couplings in multi-criterion aerodynamic optimization problems using adjoint methods and game strategies[J]. Chinese Journal of Aeronautics, 2009, 22: 1-8. DOI:10.1016/S1000-9361(08)60062-X (  0) 0) |
| [46] |
Nielsen E J, Diskin B, Yamaleev N K. Discrete adjoint-based design optimization of unsteady turbulent flows on dynamic unstructured grids[J]. AIAA Journal, 2010, 48: 1195-1206. DOI:10.2514/1.J050035 (  0) 0) |
| [47] |
Nielsen E J, Diskin B, Yamaleev N K. Discrete adjoint-based design optimization of unsteady turbulent flows on dynamic unstructured grids[J]. AIAA Journal, 2013, 51: 1355-1373. DOI:10.2514/1.J051859 (  0) 0) |
| [48] |
Mani K, Mavriplis D. Geometry optimization in three-dimensional unsteady flow problems using the discrete adjoint[C]//51st AIAA Aerospace Sciences Meeting including the New Horizons Forum and Aerospace Exposition, Grapevine (Dallas/Ft. Worth Region), Texas: 2013.
(  0) 0) |
| [49] |
Economon T D, Palacios F, Alonso J J. An unsteady continuous adjoint approach for aerodynamic design on dynamic meshes[J]. AIAA Journal, 2015, 53: 2437-2453. DOI:10.2514/1.J053763 (  0) 0) |
| [50] |
何建东, 雷娟棉. 基于伴随方法的动态非定常气动外形优化设计[J]. 北京理工大学学报, 2015, 35(2): 127-132. (  0) 0) |
| [51] |
Lei J, He J. Adjoint-based aerodynamic shape optimization for low reynolds number airfoils[J]. Journal of Fluids Engineering, Transactions of the ASME, 2016, 138: 21401-21401-6. (  0) 0) |
| [52] |
Fang L, Li X. Design optimization of unsteady airfoils with continuous adjoint method[J]. Applied Mathematics and Mechanics, 2015, 36: 1329-1336. DOI:10.1007/s10483-015-2010-9 (  0) 0) |
| [53] |
高莹莹, 何树沈, 孟育. 非定常动态演化伴随优化设计方法[J]. 物理学报, 2012, 61(20): 200206-1-200206-11. (  0) 0) |
| [54] |
Lee B J, Padulo M, Liou M, et al. Non-sinusoidal trajectory optimization of flapping airfoil using unsteady adjoint approach[C]//49th AIAA Aerospace Sciences Meeting including the New Horizons Forum and Aerospace Exposition, Orlando, Florida: 2011.
(  0) 0) |
| [55] |
Lee B J, Liou M S. Unsteady adjoint approach for design optimization of flapping airfoils[J]. AIAA Journal, 2012, 50: 2460-2475. DOI:10.2514/1.J051663 (  0) 0) |
| [56] |
Jones M, Yamaleev N K. Adjoint-based optimization of flapping-wing flows[J]. AIAA Journal, 2015, 53: 934-947. DOI:10.2514/1.J053239 (  0) 0) |
| [57] |
Xu M, Wei M. Using adjoint-based optimization to study kinematics and deformation of flapping wings[J]. Journal of Fluid Mechanics, 2016, 799: 56-99. DOI:10.1017/jfm.2016.351 (  0) 0) |
 2018, Vol. 36
2018, Vol. 36

