2. 西北工业大学, 陕西 西安 710072
2. Northwestern Polytechnical University, Xi'an 710072, China
基于流动变分思想的分析手段以其独有的优势,在气动设计、网格误差修正领域等扮演着重要角色,针对不同形式的主控方程,CFD学者们发展出了连续伴随、离散伴随方程[1-5],并进行了相应的求解方式研究,以期高效地获得气动特性对设计变量的梯度信息,由于该项技术求解梯度信息的工作量几乎与设计变量个数无关,因此,倍受CFD研究人员以及气动优化设计研究人员的重视。其中,由于离散伴随方程与NS方程清晰的导数关系,实现起来比较方便,梯度信息更为准确等优点,在伴随系统研究领域最为关注,也是国内外空气动力学研究机构重点发展的研究方向,大多研究机构均基于自身研发的大型并行CFD计算代码发展了离散伴随优化系统,例如NASA Langley研究中心利用自动微分工具开发了基于结构化求解器CFL3D、非结构化求解器FUN3D的离散伴随优化系统[6-7];德宇航基于结构化求解器Flower、非结构化求解器TAU发展了离散伴随优化系统[8],法宇航基于CFD代码elsA开发了离散伴随优化[9], 英国谢菲尔德大学覃宁[10]开展了基于结构化网格的并行离散伴随优化。
国内在离散伴随方程求解器自主研发方面也取得了一定的进展,例如西北工业大学左英桃、高正红基于结构化网格求解器开展了M6机翼离散伴随优化[11];熊俊涛[12]等基于显式时间推进实现了离散伴随方程的求解;屈崑等利用Tapenade自动微分工具进行通量变分,按照矩阵模式组装到全局稀疏矩阵,实现了稳态CFD的伴随系统求解[13];西安交通大学张朝磊等基于离散伴随理论和自动微分技术构建离散伴随系统,应用于透平叶栅的气动优化[14];南京航空航天大学高宜胜、伍贻兆、夏健等基于非结构求解器进行了翼型离散伴随优化[15];中国空气动力研究与发展中心李彬等基于非结构求解器实现了离散伴随系统的开发[16]。
对于离散伴随优化设计系统的研究,大部分研究侧重点处于气动优化问题本身,而对于离散伴随系统构造的关键问题归纳整理较少,本文将系统地对离散伴随方程求解梯度信息的若干问题开展研究;另一方面,离散伴随优化多点设计的方式是加权平均,设计结果依赖于权系数的选择,需要对权系数进行多次尝试,由于结构化网格求解器在相同资源条件下计算效率、精度更高,更利于变权系数的多点分布式优化设计,比较适合于工程型号设计。因此,本文基于中国空气动力研究与发展中心自主研发的大型并行结构化网格RANS求解器PMB3D[17],开展了离散伴随系统构造的关键问题研究。
1 基于伴随思想的梯度计算方法简介对于气动优化设计问题:
| $ \mathop {{\rm{min}}}\limits_{w.r.t.D} I\left( {W,X,D} \right) $ | (1) |
及其残差约束R(W, X, D)=0,可以构造以下目标函数:
| $ L = I + {\mathit{\Lambda} ^T}R $ | (2) |
对式(2) 进行求导,
| $ \begin{array}{l} \frac{{{\rm{d}}I}}{{{\rm{d}}X}} = \frac{{\rm{d}}}{{{\rm{d}}X}}I\left( {W,X} \right) + {\mathit{\Lambda} ^T}R\left( {W,X} \right)\\ \;\;\;\;\;\; = \left\{ {\frac{{\partial I}}{{\partial W}}\frac{{{\rm{d}}W}}{{{\rm{d}}X}} + \frac{{\partial I}}{{\partial X}}} \right\} + {\mathit{\Lambda} ^T}\left\{ {\frac{{\partial R}}{{\partial W}}\frac{{{\rm{d}}W}}{{{\rm{d}}X}} + \frac{{\partial R}}{{\partial X}}} \right\}\\ \;\;\;\;\;\; = \left\{ {\frac{{\partial I}}{{\partial W}} + {\mathit{\Lambda} ^T}\frac{{\partial R}}{{\partial W}}} \right\}\frac{{{\rm{d}}W}}{{{\rm{d}}X}} + \left\{ {\frac{{\partial I}}{{\partial X}} + {\mathit{\Lambda} ^T}\frac{{\partial R}}{{\partial X}}} \right\} \end{array} $ | (3) |
从式(3) 可以看出,若找到合适的Λ使得右端第一项为0,可完全消除
| $ \frac{{\partial I}}{{\partial W}} + {\mathit{\Lambda} ^T}\frac{{\partial R}}{{\partial W}} = 0 $ | (4) |
式(4) 就是流场伴随方程,通过迭代方法求解Λ之后,可以通过式(6) 进行梯度信息快速求解。
| $ \frac{{{\rm{d}}I}}{{{\rm{d}}X}} = \left\{ {\frac{{\partial I}}{{\partial X}} + {\mathit{\Lambda} ^T}\frac{{\partial R}}{{\partial X}}} \right\} $ | (5) |
| $ \begin{array}{l} \frac{{\partial I}}{{\partial X}} \approx \frac{{I(W,X + \Delta X) - I\left( {W,X} \right)}}{{\Delta X}}\\ \frac{{\partial R}}{{\partial X}} \approx \frac{{R(W,X + \Delta X) - R\left( {W,X} \right)}}{{\Delta X}} \end{array} $ | (6) |
显然,离散伴随方程构造核心是对Navier-Stokes方程右端残差项进行变分推导,涉及到对流项、人工黏性项、黏性项部分,以及边界条件的处理。对各项的变分可以进行手工推导,也可以借助自动微分工具(如Tapenade、ADIFOR等)的后向模式来完成,前者的优点是程序运行效率较高、不依赖于第三方库支持,缺点是工作繁琐,容易出错;后者的特点是简捷方便,依赖于第三方库支持、计算效率略低以及内存需求偏大等问题。本文采用手工推导方式。
2.1 离散伴随方程对流项的处理离散伴随方程对流项的构造的主要依赖于空间离散格式、插值精度的选择,不同的空间离散格式以及插值精度会产生不同的模板需求,尤其对于高精度格式来讲,其无黏项的离散伴随构造将及其复杂。本文采用二阶精度的中心格式,该格式构造简单,在亚、跨、超声速流场数值模拟中表现鲁棒,在实际工程应用较多。
对于式(4) 中的
| $ {\mathit{\Lambda} ^T}\frac{{\partial R}}{{\partial W}} = {\mathit{\Lambda} ^T}\frac{{\partial {R_c}}}{{\partial W}} - {\mathit{\Lambda} ^T}\frac{{\partial {R_D}}}{{\partial W}} - {\mathit{\Lambda} ^T}\frac{{\partial {R_v}}}{{\partial W}} $ | (7) |
式(7) 右端分别代表无黏项、人工黏性项和物理黏性项。此时,需要构造的就是离散伴随方程无黏项部分
| $ \delta L = \delta I + \sum\limits_{j,k,l = 2}^{j2,k2,l2} {\mathit{\Lambda} _{_{j,k,l}}^{^T}} \delta R\left( {j,k,l} \right) $ | (8) |
对于l方向,式(8) 的右端第二项中δR(j, k, l)可以表达为:
| $ \begin{array}{l} \delta R\left( {j,k,l} \right) = \delta {f_{l + 1/2}} - \delta {f_{l - 1/2}}\\ = {({f_1}\delta {\xi _x})_{l + 1/2}} + {({\xi _x}\delta {f_1})_{l + 1/2}} + \\ {({f_2}\delta {\xi _y})_{l + 1/2}} + {({\xi _y}\delta {f_2})_{l + 1/2}} + \\ {({f_3}\delta {\xi _z})_{l + 1/2}} + {({\xi _z}\delta {f_3})_{l + 1/2}} - \\ [{({f_1}\delta {\xi _x})_{l - 1/2}} + {({\xi _x}\delta {f_1})_{l - 1/2}}] - \\ [{({f_2}\delta {\xi _y})_{l - 1/2}} + {({\xi _y}\delta {f_2})_{l - 1/2}}] - \\ [{({f_3}\delta {\xi _z})_{l - 1/2}} + {({\xi _z}\delta {f_3})_{l - 1/2}}] \end{array} $ | (9) |
其中,f1、f2、f3分别为无黏通量在笛卡尔坐标系下三个方向的分量,对于定常问题,式(9) 中忽略对几何参数的变分后转化为:
| $ \begin{array}{l} \delta R\left( {j,k,l} \right) = \delta {f_{l + 1/2}} - \delta {f_{l - 1/2}}\\ = {({\xi _x}\delta {f_1})_{l + 1/2}} + {({\xi _y}\delta {f_2})_{l + 1/2}} + {({\xi _z}\delta {f_3})_{l + 1/2}} - \\ [{({\xi _x}\delta {f_1})_{l - 1/2}} + {({\xi _y}\delta {f_2})_{l - 1/2}} + {({\xi _z}\delta {f_3})_{l - 1/2}}] \end{array} $ | (10) |
将上式代入式(9) 并考虑以下关系式:
| $ {f_{l + 1/2}} = f{(\bar W)_{l + 1/2}},\delta \bar W = \delta (\frac{1}{2}({W_l} + {W_{l + 1}})) $ |
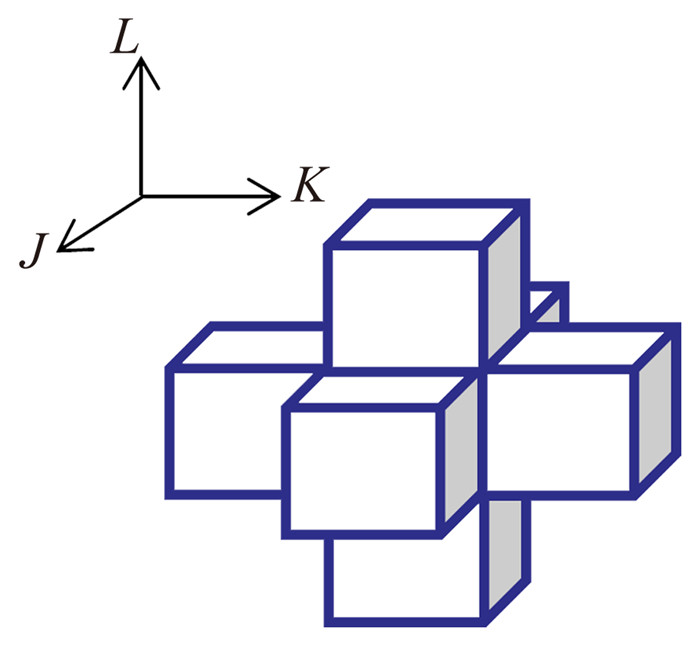
整理包含δWl的项,可以看到,对l单元伴随无黏通量有贡献的模板单元有l-1,l,l+1,拓展到三维问题,对(j, k, l)单元伴随无黏通量有贡献的模板单元有:(j, k, l),(j-1, k, l),(j+1, k, l),(j, k-1, l),(j, k+1, l),(j, k, l-1),(j, k, l+1) 共七个单元,如图 1所示。综合式(8)、式(10) 可以推导出离散伴随方程的对流项:
|
图 1 离散伴随无黏项模板单元 Figure 1 Template unit of discrete adjoint inviscid term |
| $ \begin{array}{l} {R_c}{\left( \lambda \right)_{j,k,l}} = \frac{1}{2}(\frac{{\partial {F_c}(\bar W)}}{{\partial {W_{j,k,l}}}})_{j,k,l - 1/2}^{\rm{T}}({\lambda _{j,k,l - 1}} - {\lambda _{j,k,l}}) + \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\frac{1}{2}(\frac{{\partial {F_c}(\bar W)}}{{\partial {W_{j,k,l}}}})_{_{j,k,l + 1/2}}^T({\lambda _{j,k,l}} - {\lambda _{j,k,l + 1}}) + \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\frac{1}{2}(\frac{{\partial {F_c}(\bar W)}}{{\partial {W_{j,k,l}}}})_{_{j - 1/2,k,l}}^T({\lambda _{j + 1,k,l}} - {\lambda _{j,k,l}}) + \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\frac{1}{2}(\frac{{\partial {F_c}(\bar W)}}{{\partial {W_{j,k,l}}}})_{_{j + 1/2,k,l}}^T({\lambda _{j + 1,k,l}} - {\lambda _{j,k,l}}) + \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\frac{1}{2}(\frac{{\partial {F_c}(\bar W)}}{{\partial {W_{j,k,l}}}})_{_{j,k - 1/2,l}}^T({\lambda _{j,k - 1,l}} - {\lambda _{j,k,l}}) + \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\frac{1}{2}(\frac{{\partial {F_c}(\bar W)}}{{\partial {W_{j,k,l}}}})_{_{j,k + 1/2,l}}^T({\lambda _{j,k,l}} - {\lambda _{j,k + 1,l}}) \end{array} $ | (11) |
由于对单元(j, k, l)的伴随人工黏性通量有贡献的模板单元较多,因此,人工黏性的变分比较复杂,文中固定人工黏性系数前提下,给出了两种处理方式,一种是直接变分推导,另外一种是对四阶耗散项进行简化处理,在梯度验证部分给出了两种处理方式的可行性对比。
第一种方式~直接变分推导,首先仅考虑j方向:
| $ \begin{array}{l} \delta {R_D}\left( {j,k,l} \right) = \delta {f_{d,}}_{j + 1/2} - \delta {f_{d,j - 1/2}}\\ = \mathit{\Lambda} _{_{j + 1/2}}^{^{(2)}}(\delta {W_{j + 1}} - \delta {W_j}) - \\ \mathit{\Lambda} _{_{j + 1/2}}^{^{(4)}}(\delta {W_{j + 2}} - 3\delta {W_{j + 1}} + 3\delta {W_j} - \delta {W_{j - 1}}) - \\ \mathit{\Lambda} _{_{j - 1/2}}^{^{(2)}}(\delta {W_j} - \delta {W_{j - 1}}) + \\ \mathit{\Lambda} _{_{j - 1/2}}^{^{(4)}}(\delta {W_{j + 1}} - 3\delta {W_j} + 3\delta {W_{j - 1}} - \delta {W_{j - 2}}) \end{array} $ | (12) |
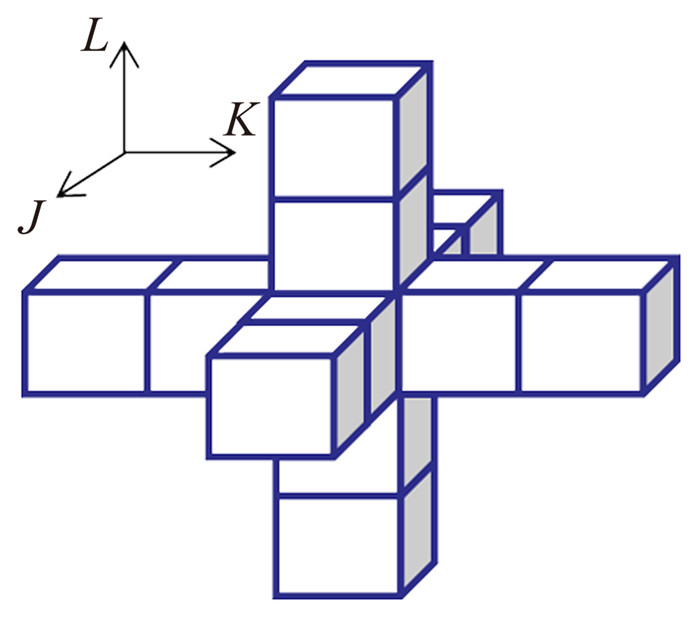
由式(12) 可以看出,一维方向上对单元(j, k, l)的伴随人工黏性通量有贡献的模板单元有5个,推广到三维问题,模板单元有13个,如图 2所示。
|
图 2 离散伴随人工黏性项模板单元 Figure 2 Template unit of discrete adjoint artificial viscous term |
第二种方式~四阶耗散项简化处理[18],仅考虑j方向:
| $ \begin{array}{l} \delta {R_D}\left( {j,k,l} \right) = \delta {f_{d,}}_{j + 1/2} - \delta {f_{d,j - 1/2}}\\ = {\rm{max}}(\mathit{\Lambda} _{_{j + 1/2}}^{^{(2)}},\sigma \mathit{\Lambda} _{_{j + 1/2}}^{^{(4)}})(\delta {W_{j + 1}} - \delta {W_j}) - \\ {\rm{max}}(\mathit{\Lambda} _{_{j - 1/2}}^{^{(2)}},\sigma \mathit{\Lambda} _{_{j - 1/2}}^{^{(4)}})\mathit{\Lambda} _{_{j - 1/2}}^{^{(2)}}(\delta {W_j} - \delta {W_{j - 1}}) \end{array} $ | (13) |
上述简化,降低了推导难度,且虚网格单元的伴随变量能够利用边界条件做到简单处理(见边界条件部分),由式(13) 可以看出,一维方向上对单元(j, k, l)的伴随人工黏性通量有贡献的模板单元有3个,推广到三维问题,模板单元有7个,如图 1所示。
2.3 离散伴随方程黏性项的处理离散伴随方程黏性项的推导是最为复杂的一项,其核心是对速度导数项变分,如果直接采用完全NS方程进行推导,将涉及速度导数交叉项,所需要的模板更多,推导将更加繁琐,因此,本文采用黏性项薄层近似进行变分。
曲线坐标系下,采用如下薄层近似方式:
| $ \begin{array}{l} \frac{{\partial u}}{{\partial x}} \approx \frac{{\partial u}}{{\partial \xi }}\frac{{\partial \xi }}{{\partial x}} = {\xi _x}\frac{{\partial u}}{{\partial \xi }}\\ \frac{{\partial u}}{{\partial y}} \approx \frac{{\partial u}}{{\partial \xi }}\frac{{\partial \xi }}{{\partial y}} = {\xi _y}\frac{{\partial u}}{{\partial \xi }}\\ \frac{{\partial u}}{{\partial z}} \approx \frac{{\partial u}}{{\partial \xi }}\frac{{\partial \xi }}{{\partial z}} = {\xi _z}\frac{{\partial u}}{{\partial \xi }} \end{array} $ | (14) |
类似2.1部分的推导,从式(14) 可以看出对单元(j, k, l)的伴随黏性通量有贡献的模板单元。
在式(14) 的条件下,曲线坐标系下的黏性通量可以表达为:
| $ \begin{array}{l} {f_v} = \frac{{{M_\infty }\mu }}{{R{E_L}J}}\left[ \begin{array}{l} 0\\ {\phi _1}\frac{{\partial u}}{{\partial \xi }} + {\xi _x}{\phi _2}\\ {\phi _1}\frac{{\partial v}}{{\partial \xi }} + {\xi _y}{\phi _2}\\ {\phi _1}\frac{{\partial w}}{{\partial \xi }} + {\xi _z}{\phi _2}\\ {\phi _1}\frac{{\partial p/\rho }}{{\partial \xi }}\frac{1}{{\gamma - 1}}\\ + u{f_{v2}} + v{f_{v3}} + w{f_{v4}} \end{array} \right]\\ {\phi _1} = \xi _{_x}^{^2} + \xi _{_y}^{^2} + \xi _{_z}^{^2},\\ {\phi _2} = ({\xi _x}\frac{{\partial u}}{{\partial \xi }} + {\xi _y}\frac{{\partial v}}{{\partial \xi }} + {\xi _z}\frac{{\partial w}}{{\partial \xi }})/3 \end{array} $ | (15) |
实际上,黏性通量伴随方程变分的主要工作就是对速度矢量导数的变分,由于速度矢量导数计算文中采用了前向差分的方式,因此在进行fvj+1/2、fvj-1/2对单元变分时,要考虑梯度变号问题,对于
| $ \frac{{\partial {f_{{v_{j - 1/2}}}}}}{{\partial {Q_j}}} = \left[ {\begin{array}{*{20}{c}} 0&0&0&0&0\\ 0&{{\phi _1} + \xi _{_x}^{^2}/3}&{{\xi _x}{\xi _y}/3}&{{\xi _x}{\xi _z}/3}&0\\ 0&{{\xi _x}{\xi _y}/3}&{{\phi _1} + \xi _{_y}^{^2}/3}&{{\xi _y}{\xi _z}/3}&0\\ 0&{{\xi _x}{\xi _z}/3}&{{\xi _y}{\xi _z}/3}&{{\phi _1} + \xi _{_z}^{^2}/}&0\\ {\frac{{{\phi _1}}}{{\gamma - 1}}\frac{p}{{{\rho ^2}}}}&{\frac{{\partial {f_{v5}}}}{{\partial u}}}&{\frac{{\partial {f_{v5}}}}{{\partial v}}}&{\frac{{\partial {f_{v5}}}}{{\partial w}}}&{\frac{{{\phi _1}}}{{\gamma - 1}}\frac{1}{\rho }} \end{array}} \right] $ | (16) |
其中,
| $ \begin{array}{l} \frac{{\partial {f_{v5}}}}{{\partial u}} = {u_{j - 1/2}}\frac{{\partial {f_{v2}}}}{{\partial u}} + {v_{j - 1/2}}\frac{{\partial {f_{v3}}}}{{\partial u}} + {w_{j - 1/2}}\frac{{\partial {f_{v4}}}}{{\partial u}} + \frac{1}{2}{f_{v2}}\\ \frac{{\partial {f_{v5}}}}{{\partial v}} = {u_{j - 1/2}}\frac{{\partial {f_{v2}}}}{{\partial v}} + {v_{j - 1/2}}\frac{{\partial {f_{v3}}}}{{\partial v}} + {w_{j - 1/2}}\frac{{\partial {f_{v4}}}}{{\partial v}} + \frac{1}{2}{f_{v3}}\\ \frac{{\partial {f_{v5}}}}{{\partial w}} = {u_{j - 1/2}}\frac{{\partial {f_{v2}}}}{{\partial w}} + {v_{j - 1/2}}\frac{{\partial {f_{v3}}}}{{\partial w}} + {w_{j - 1/2}}\frac{{\partial {f_{v4}}}}{{\partial w}} + \frac{1}{2}{f_{v4}} \end{array} $ | (17) |
进一步利用原始变量对守恒变量的转换矩阵,求出对守恒变量的导数矩阵:
| $ \frac{{\partial {f_{{v_{j - 1/2}}}}}}{{\partial {W_j}}} = \frac{{\partial {f_{{v_{j - 1/2}}}}}}{{\partial {Q_j}}}\frac{{\partial {Q_j}}}{{\partial {W_j}}} = \frac{{\partial {f_{{v_{j - 1/2}}}}}}{{\partial {Q_j}}}M_{_j}^{^{ - 1}} $ | (18) |
其中,Mj-1是原始变量对守恒变量的转换矩阵。对于
需要指出的是,伴随黏性通量中W对求导不再具有使用意义,W仅在黏性项第5项变分中起到作用,且需要边界特殊处理。
2.4 离散伴随方程时间项隐式化将上述推导结果进行整合,并加入伪时间项可以得到离散伴随主控方程:
| $ \begin{array}{l} {R_c}{\left( \lambda \right)_{j,k,l}} - {R_D}{\left( \lambda \right)_{j,k,l}} - {R_v}{\left( \lambda \right)_{j,k,l}} = 0\\ {V_{j,k,l}}\frac{{\partial \lambda }}{{\partial t}} + {R_c}{\left( \lambda \right)_{j,k,l}} - {R_D}{\left( \lambda \right)_{j,k,l}} - {R_v}{\left( \lambda \right)_{j,k,l}} = 0 \end{array} $ | (19) |
对式(19) 的迭代求解,可以采用显式经典四步龙格-库塔推进,也可以采用隐式时间推进,这里我们将重点介绍LU-SGS方法,由于(19) 在形式上与NS方程一致,因此,LU-SGS方法及其最大特征值分裂方法可以用于离散伴随求解:
| $ \begin{array}{l} {A^ \pm } = \frac{A \pm \beta {\gamma _A}I}{2},{\gamma _A} = {\rm{max}}\left[ {\left| {\lambda \left( A \right)} \right|} \right]\\ {B^ \pm } = \frac{B \pm \beta {\gamma _B}I}{2},{\gamma _B} = {\rm{max}}\left[ {\left| {\lambda \left( B \right)} \right|} \right]\\ {C^ \pm } = \frac{C \pm \beta {\gamma _C}I}{2},{\gamma _C} = {\rm{max}}\left[ {\left| {\lambda \left( C \right)} \right|} \right] \end{array} $ | (20) |
| $ \begin{array}{l} \left[ {\frac{V}{{\Delta \tau }} + \beta ({\gamma _A} + {\gamma _B} + {\gamma _C})} \right]\Delta \bar Q = \\ - \frac{1}{\omega }RHS + (A_{_{i - 1/2}}^{^ + } + B_{_{j - 1/2}}^{^ + } + C_{_{k - 1/2}}^{^ + })\Delta \bar Q \end{array} $ | (21) |
| $ \begin{array}{l} \Delta Q = \Delta \bar Q - {D^{ - 1}}(A_{_{i + 1/2}}^{^ + } + B_{_{j + 1/2}}^{^ + } + C_{_{k + 1/2}}^{^ + })\Delta \bar Q\\ {Q^{n + 1}} = {Q^n} + \Delta Q \end{array} $ |
由于离散伴随方程雅克比矩阵转置的原因,上式中对应的矩阵均需要进行转置处理,且无矩阵算法不再适用,右端项必须严格按照矩阵相乘进行运算,这是伴随方程求解单步耗时、内存需求高于NS方程的一个主要原因。流场时间推进采用的隐式边界条件在离散伴随方程中依然可用:
| $ \begin{array}{l} \Delta {Q^*} = 0,\Delta Q = 0\\ \Delta {\lambda ^*} = 0,\Delta \lambda = 0 \end{array} $ | (22) |
对流项边界条件、人工黏性项边界条件、黏性项边界条件、加速收敛技术、复杂项的简化方式、对离散伴随方程求解来讲至关重要,直接影响到梯度计算精度以及求解效率,为此,该部分将对上述关键环节进行研究讨论,探讨对不同流动问题的影响程度。
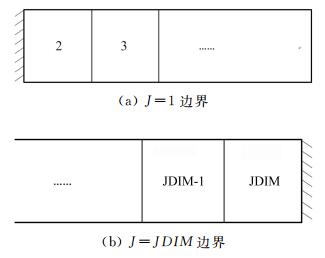
3.1 离散伴随方程对流项的边界条件离散伴随无黏通量计算在边界处的模板单元与内部点的个数不一样,因此在边界处的变分需要特殊处理,由于ξ, η, γ三个方向上的独立性,对于ξ, η, γ=1, JKLDIM不同的边界,可以分开处理,显然,对于任意曲线坐标方向,边界单元无黏通量计算模板将减少一个,如图 3所示。
|
图 3 边界单元的无黏通量模板单元 Figure 3 Inviscid flux template unit on boundary |
以J=1边界紧邻的J=2单元通量计算为例,式(11) 将改写为(其他方向类似):
| $ \begin{array}{l} {R_c}{\left( \lambda \right)_{j,k,l}} = \frac{1}{2}(\frac{{\partial {F_c}(\bar W)}}{{\partial {W_{j,k,l}}}})_{_{j,k,l - 1/2}}^T({\lambda _{j,k,l - 1}} - {\lambda _{j,k,l}}) + \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\frac{1}{2}(\frac{{\partial {F_c}(\bar W)}}{{\partial {W_{j,k,l}}}})_{_{j,k,l + 1/2}}^T({\lambda _{j,k,l}} - {\lambda _{j,k,l + 1}}) + \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\frac{1}{2}(\frac{{\partial {F_c}(\bar W)}}{{\partial {W_{j,k,l}}}})_{_{j - 1/2,k,l}}^T( - {\lambda _{j,k,l}}) + \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\frac{1}{2}(\frac{{\partial {F_c}(\bar W)}}{{\partial {W_{j,k,l}}}})_{_{j + 1/2,k,l}}^T({\lambda _{j + 1,k,l}} - {\lambda _{j,k,l}}) + \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\frac{1}{2}(\frac{{\partial {F_c}(\bar W)}}{{\partial {W_{j,k,l}}}})_{_{j,k - 1/2,l}}^T({\lambda _{j,k - 1,l}} - {\lambda _{j,k,l}}) + \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\frac{1}{2}(\frac{{\partial {F_c}(\bar W)}}{{\partial {W_{j,k,l}}}})_{_{j,k + 1/2,l}}^T({\lambda _{j,k,l}} - {\lambda _{j,k + 1,l}}) \end{array} $ | (23) |
不仅通量表达式需要特殊处理,根据边界性质的不同,雅克比
| $ \frac{{\partial {F_c}(\bar W)}}{{\partial {W_2}}} = \frac{{\partial {F_c}(\bar W)}}{{\partial \bar Q}}\frac{{\partial \bar Q}}{{\partial {Q_2}}}\frac{{\partial {Q_2}}}{{\partial {W_2}}} = \bar A\frac{{\partial \bar Q}}{{\partial {Q_2}}}{M_2} $ | (24) |
其中,A、M2分别对应雅克比矩阵及原始变量对守恒变量的转换矩阵。从式(24) 可以看出,边界条件的处理的核心就是求出边界条件矩阵
| $ \frac{{\partial \bar Q}}{{\partial {Q_2}}} = \frac{1}{2}\frac{{\partial ({Q_1} + {Q_2})}}{{\partial {Q_2}}} = \frac{1}{2}({M_{BC}} + E) $ | (25) |
式(25) 中E, MBC分别对应单位矩阵以及边界条件矩阵,可以看出,离散伴随无黏项的不同边界条件变分,只需替换对应边界条件矩阵MBC,很容易实现不同边界类型、以及内外流伴随之间的转换、匹配,且这对于模块化编程也十分有利。需要指出的是,由于离散伴随无黏项的主导作用,该项边界条件处理很大程度直接影响梯度的计算精度。
3.2 离散伴随方程人工黏性的边界条件离散伴随人工黏性通量计算模板单元较多,在边界处的变分处理比较繁琐,为此,而文中考察了2.2节的两种处理方式,与2.1节一样,其核心问题仍然是推导边界条件矩阵MBC,由于推导过程较长,本节仅给出了简化推导方式[19],其他方式类似:
| $ \begin{array}{l} \delta {R_D}\left( {j,k,l} \right) = \delta {f_{d,}}_{j + 1/2} - \delta {f_{d,j - 1/2}}\\ = {\rm{max}}(\mathit{\Lambda} _{_{j + 1/2}}^{^{(2)}},\sigma \mathit{\Lambda} _{_{j + 1/2}}^{^{(4)}})(\delta {W_{j + 1}} - \delta {W_j}) - \\ \;\;\;{\rm{max}}(\mathit{\Lambda} _{_{j - 1/2}}^{^{(2)}},\sigma \mathit{\Lambda} _{_{j - 1/2}}^{^{(4)}})\mathit{\Lambda} _{_{j - 1/2}}^{^{(2)}}(\delta {W_j} - \delta {W_{j - 1}})\\ = {\rm{max}}(\mathit{\Lambda} _{_{j + 1/2}}^{^{(2)}},\sigma \mathit{\Lambda} _{_{j + 1/2}}^{^{(4)}})(\delta {W_{j + 1}} - \delta {W_j}) - \\ \;\;\;{\rm{max}}(\mathit{\Lambda} _{_{j - 1/2}}^{^{(2)}},\sigma \mathit{\Lambda} _{_{j - 1/2}}^{^{(4)}})\mathit{\Lambda} _{_{j - 1/2}}^{^{(2)}}(\delta {W_j} - {M_{BC}}\delta {W_j}) \end{array} $ | (26) |
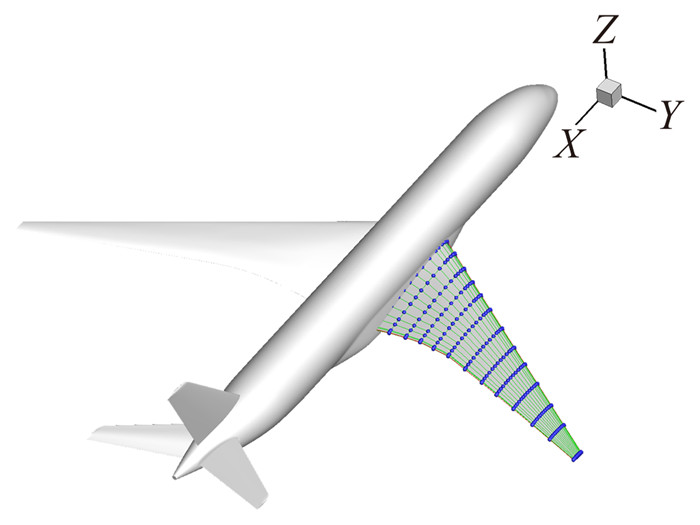
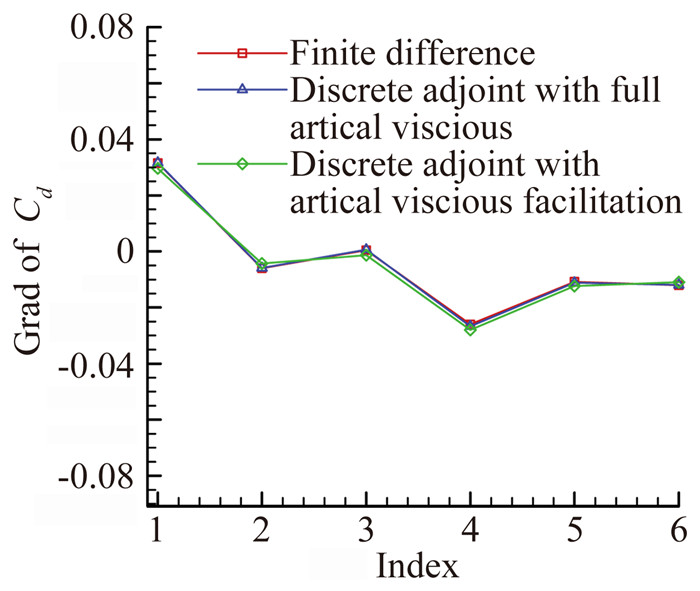
图 4、图 5分别给出了某型飞机参数化及人工黏性处理方法对梯度计算精度影响比较。
|
图 4 某型客机FFD参数化 Figure 4 FFD lattice for wide body airplane |
|
图 5 人工黏性处理方式对梯度计算精度影响比较 Figure 5 Effect on gradient calculation of different artificial viscous processing method |
离散伴随黏性通量的模板单元也将在边界处发生变化。从式(16) 的推导不难看出,黏性项的边界条件需要考虑对虚网格的变分关系,实质上仍然是推导边界条件矩阵MBC。这样,无论是无黏项、人工黏性项还是物理黏性项的边界条件均转化为一个矩阵推导,大大简化了程序设计框架,式(26)~式(29) 给出了几类典型的边界条件矩阵。
广义对称边界与无黏物面条件矩阵:
| $ {M_{BC}} = \left[ {\begin{array}{*{20}{c}} 1&0&0&0&0\\ 0&{1 - 2n_{_x}^{^2}}&{ - 2{n_y}{n_x}}&{ - 2{n_z}{n_x}}&0\\ 0&{ - 2{n_x}{n_y}}&{1 - 2n_{_y}^{^2}}&{ - 2{n_z}{n_y}}&0\\ 0&{ - 2{n_x}{n_z}}&{ - 2{n_y}{n_z}}&{1 - 2n_{_z}^{^2}}&0\\ 0&0&0&0&1 \end{array}} \right] $ | (27) |
黏性物面条件矩阵:
| $ {M_{BC}} = \left[ {\begin{array}{*{20}{c}} 1&0&0&0&0\\ 0&{ - 1}&0&0&0\\ 0&0&{ - 1}&0&0\\ 0&0&0&{ - 1}&0\\ 0&0&0&0&1 \end{array}} \right] $ | (28) |
超声速入流/出流边界条件矩阵:
| $ \begin{array}{l} {M_{BC}} = \left[ {\begin{array}{*{20}{c}} 1&0&0&0&0\\ 0&1&0&0&0\\ 0&0&1&0&0\\ 0&0&0&1&0\\ 0&0&0&0&1 \end{array}} \right]\\ {M_{BC}} = \left[ {\begin{array}{*{20}{c}} 0&0&0&0&0\\ 0&0&0&0&0\\ 0&0&0&0&0\\ 0&0&0&0&0\\ 0&0&0&0&0 \end{array}} \right] \end{array} $ | (29) |
其他类型边界条件矩阵同样可以依据边界类型进行求导。
3.4 离散伴随方程的时间推进不同时间推进方式,同样也对离散伴随方程产生不同的收敛效果,比如GMRES、BLU-SGS时间推进方式,综合考虑内存需求与计算效率,文中进行了BLU-SGS与LU-SGS收敛历程以及计算结果的对比,在伴随方程求解中依然有效。
与式(20) 不同的是,BLU-SGS隐式推进中,
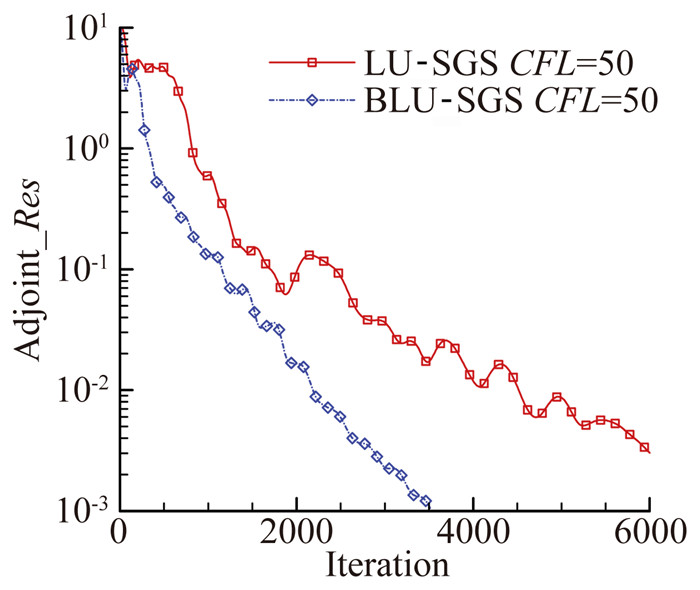
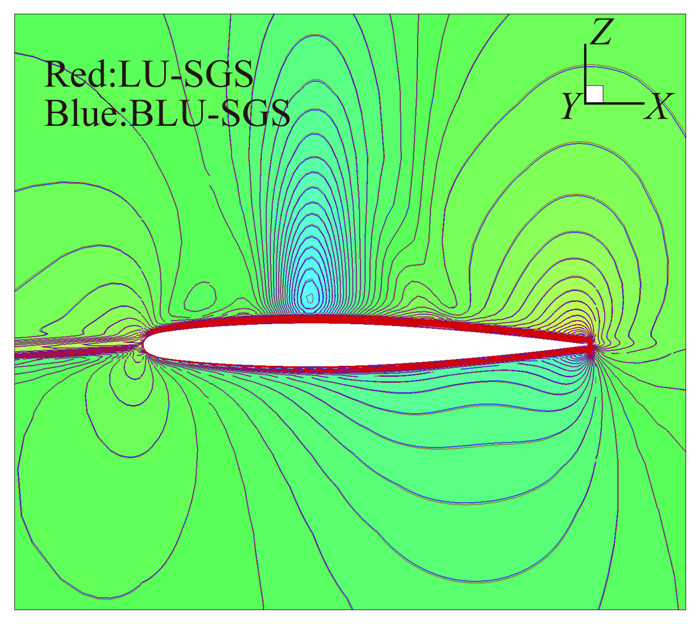
图 6、图 7分别给出了不同的时间推进方式对收敛速度及计算结果的对比。
|
图 6 LU-SGS、BLU-SGS收敛速度比较 Figure 6 Convergence rate comparison of LU-SGS and BLU-SGS |
|
图 7 LU-SGS、BLU-SGS第一伴随变量计算结果 Figure 7 The calculation result of fist adjoint variable of LU-SGS and BLU-SGS |
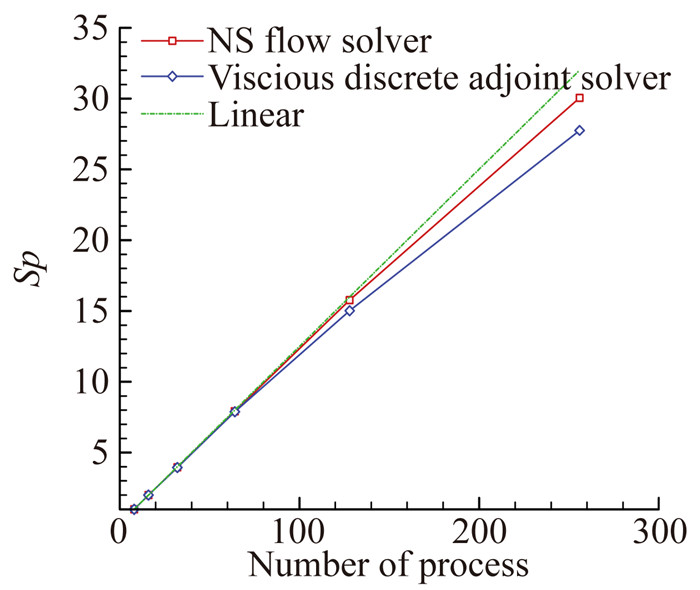
与流场并行计算一样,离散伴随方程求解时,并行机制依然采用单元数衡量的负载平衡、对等式计算以及MPI消息传递模式,对于伴随方程来讲,依赖于求解器的构架,通过MPI进行传递的信息可以是雅克比矩阵,也可以是伴随变量本身。本文求解器采用了多块对接网格技术,与对接面边界信息一样,MPI传递的信息是各个进程分割面上的两层虚网格上的伴随变量信息,这样离散伴随求解的并行效率特性与流场的基本一致,由于存在矩阵运算,略低于流场并行效率。图 8给出了NS方程与离散伴随方程并行效率比较。
|
图 8 离散伴随/NS方程并行效率 Figure 8 Parallel efficiency of discrete adjoint and NS equation |
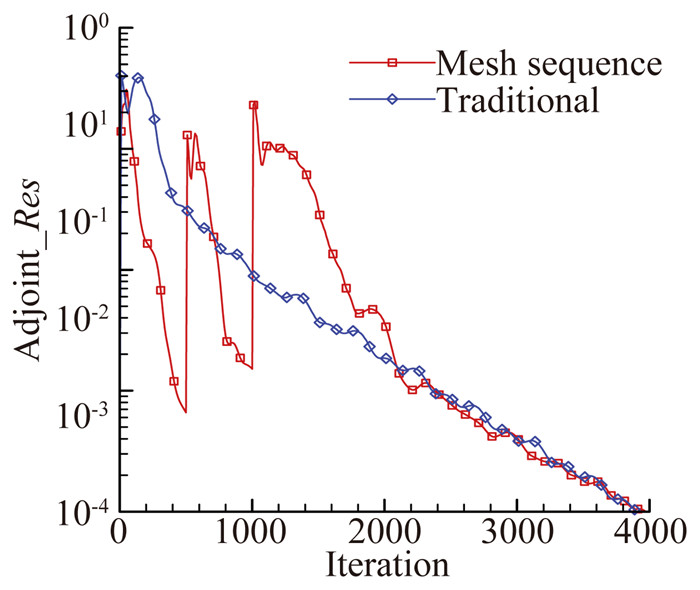
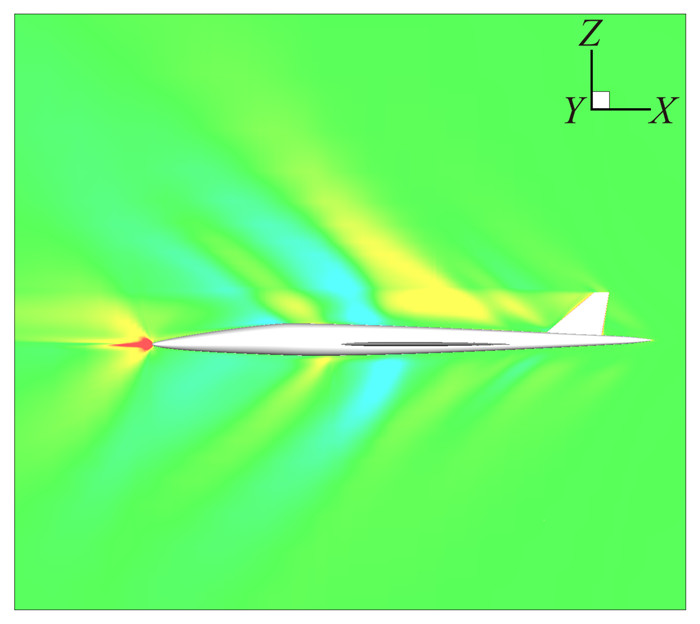
在流场计算中采用的当地时间步长、多重网格、网格序列法等加速收敛技术,在离散伴随方程求解中使用仍然能够起到加速作用。无论是多重网格方法,还是网格序列法,均要涉及粗网格残差计算方法,本文在粗网格上的残差计算采用二阶格式且不考虑黏性项,而对于伴随变量本身的插值、限制方式仍与流场变量一致;当地时间步长取值与流场计算相同,不同的是,求解离散伴随方程时是基于流场收敛解进行的,因此,稳定性更好,CFL可以取得更大(图 9)。图 10为超声速低声爆客机第一伴随变量云图,在黏性流场计算时CFL≤10.0取值基本保证稳定收敛,离散伴随计算时CFL=50依然能够稳定收敛。
|
图 9 网格序列法加速收敛(CFL=50无黏伴随) Figure 9 Convergence accelerated method based on grid sequence method(Inviscid adjoint) |
|
图 10 超声速低声爆客机第一伴随变量云图(目标函数:阻力CFL=50) Figure 10 The first adjoint variable contour of supersonic low sonic boom airplane |
求解方法对梯度计算的影响经过讨论之后,进一步采用本文的方法开展不同流动问题梯度计算精度验证,采用了两种构型:某型客机全机巡航构型和外压式超声速进气道。
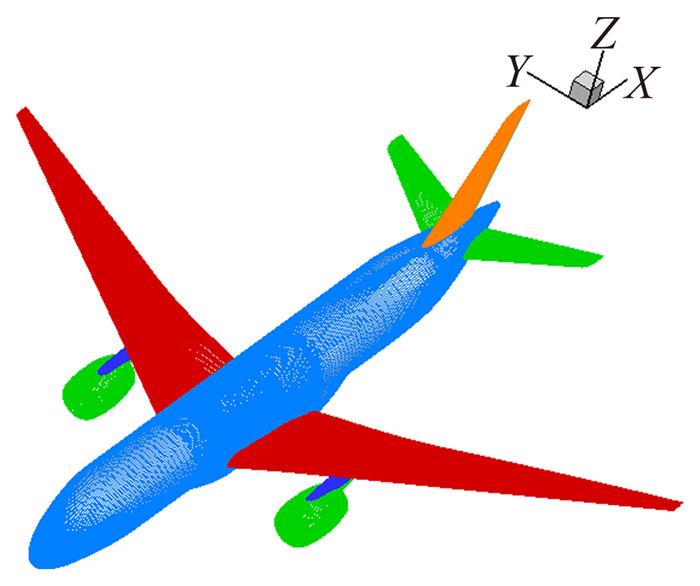
4.1 外部黏性绕流问题——某型客机全机巡航构型以某型某型客机全机巡航构型外部绕流为算例,主要部件包含机翼、机身、挂架、短舱内外涵道、平尾以及立尾。半模网格划分为526块,网格规模2500万量级,如图 11所示。采用SST湍流模型,128核进行并行计算。
|
图 11 表面网格分布 Figure 11 Grid distribution on surface |
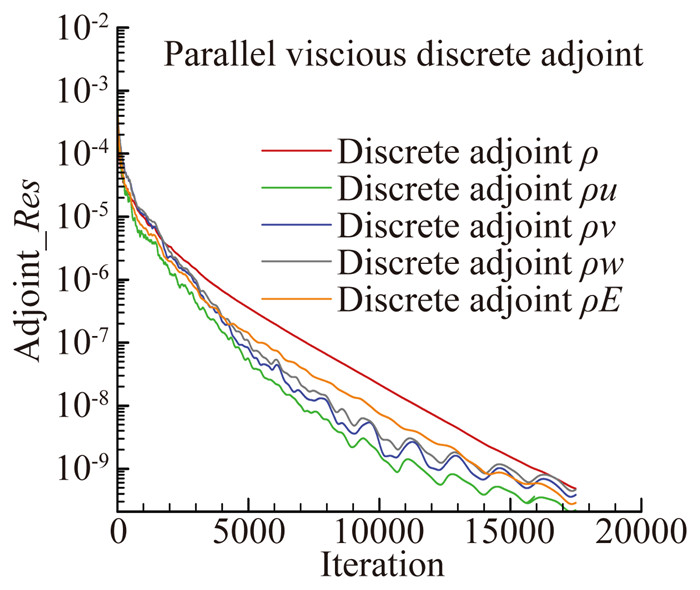
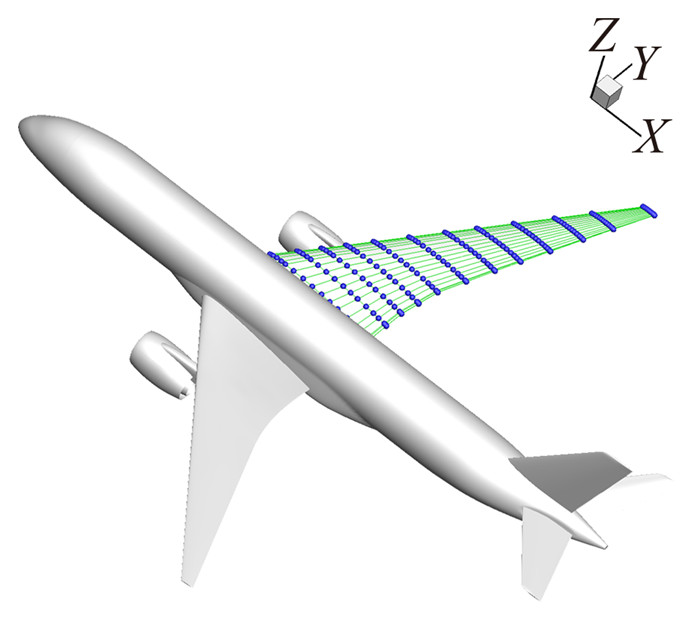
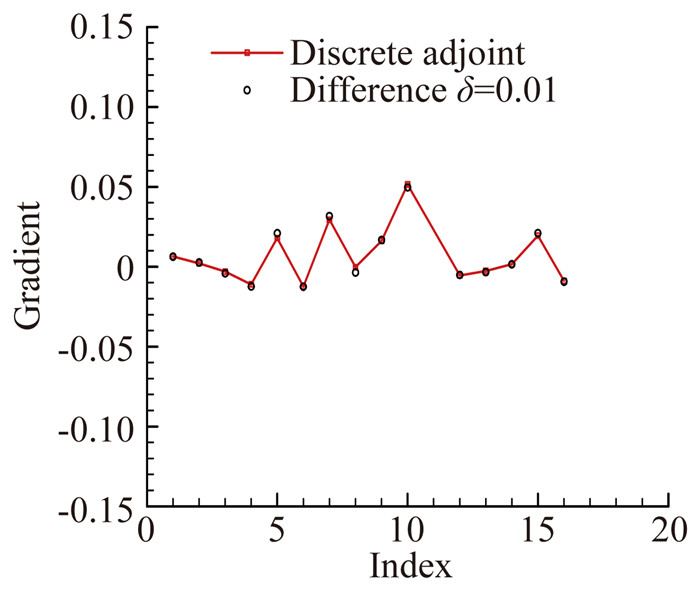
图 12给出了黏性离散伴随方程的收敛历程,可以看出文中的求解方法对于复杂外形也非常稳定。图 13、图 14分别为物面第一伴随变量云图与参数化示意图。图 15给出了任意选取的几个控制顶点的导数值对比,梯度幅值以及梯度方向一致,平均误差为6%,可以看出,在外部黏性扰流问题中,基于薄层近似的黏性离散伴随导数计算精度较高,完全满足工程气动设计要求。
|
图 12 离散伴随方程收敛历程 Figure 12 Convergence process of discrete adjoint equation |

|
图 13 物面第一伴随变量云图 Figure 13 Contour of the first adjoint variable on surface |
|
图 14 机翼参数化FFD lattice示意图 Figure 14 FFD lattice for wing parameterized |
|
图 15 黏性离散伴随梯度计算与差分对比 Figure 15 Comparison of gradient calculation of viscous discrete adjoint and difference |
该算例为超声速无附面层隔道进气道内外流一体化数值模拟,涉及超声速入口、超声速出口、黏性物面以及风扇入口(质量流流场出口)四类边界条件。
需要指出的是,流场计算直接采用质量出口边界条件,带来收敛速度慢、边界条件矩阵推导困难等问题,因此本文采用了压力特征出口—质量流调节的方法,即给定初始反压,计算程序依据流量特征进行自动调节,该方法可以提高管道内“激波外推”速度,加速收敛。流场收敛后风扇入口流场仍然保持亚声速压力特征出口边界,有利于其边界条件矩阵推导。
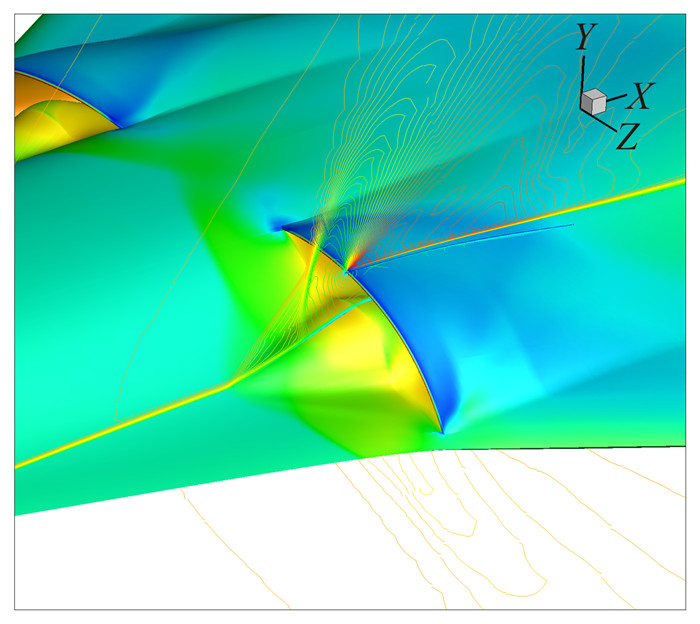
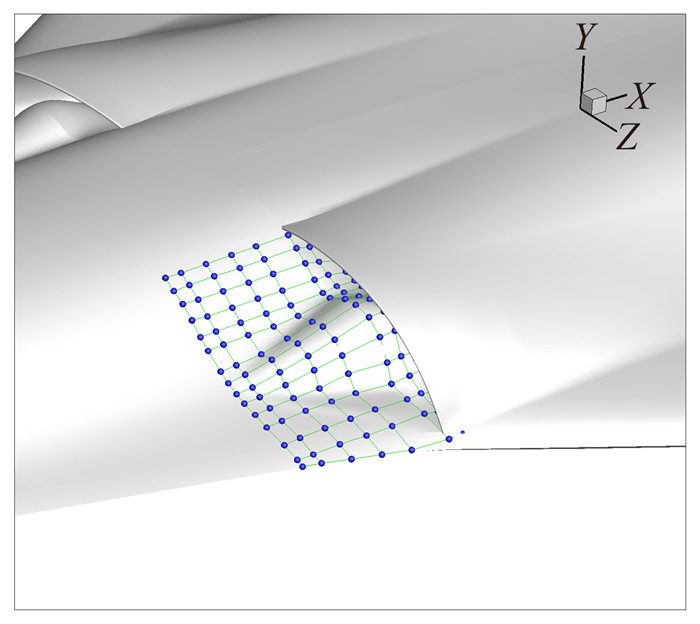
图 16给出了设计状态进气道波系状态分布,该模型的初始鼓包依据三维乘波理论设计,图 17给出了鼓包FFD参数化示意图,沿进气方向选取5个控制点,进行总压恢复系数梯度测试,这里给出总压对守恒变量的变分推导方法:
|
图 16 无附面层隔道进气道波系分布 Figure 16 Wave system distribution of DSI |
|
图 17 DSI进气道鼓包参数化 Figure 17 The parameterized DSI inlet bump |
| $ \frac{{\partial {p_0}}}{{\partial W}} = \frac{{\partial {p_0}}}{{\partial Q}}\frac{{\partial Q}}{{\partial W}} = \frac{{\partial {p_0}}}{{\partial Q}}{M^{ - 1}} $ | (30) |
其中
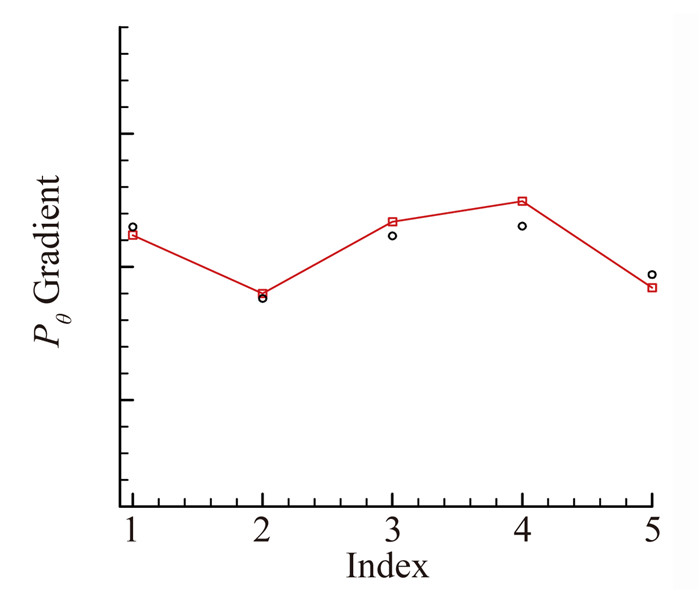
图 18给出了鼓包上任意选取几个控制点,计算风扇入口总压对控制点的导数,由于内外流一体化问题流动黏性效应较强,而文中黏性离散伴随计算采用了薄层近似,本文将对此进一步开展研究,消除这些因素带来的误差。综上所述,文中采用的方法误差较为明显,但依然较好地反映了梯度幅值变化趋势,且梯度方向一致,能够应用于气动优化。
|
图 18 黏性离散伴随梯度计算与差分对比 Figure 18 Comparison of gradient calculation of viscous discrete adjoint and difference method |
基于自主研发的大规模并行结构化网格RANS求解器PMB3D,开展了黏性离散伴随方程构造、求解方法的研究与讨论:
1) 以矩阵的形式体现离散伴随方程的边界条件,有利于程序的简捷化、模块化。
2) 人工黏性的简化处理虽然降低了的梯度求解精度,但仍然能够较好地反映梯度变化趋势,可以应用于气动优化。
3) 结构化求解器网格中,无黏项、人工黏性项的离散推导具有方向独立性;薄层假设条件下,黏性项的离散推导能够大大简化推导过程以及实现程序模块化。
4) 由于存在大量的矩阵运算,离散伴随方程求解计算效率、并行效率均低于NS方程求解。
5) 薄层假设条件在外流问题梯度计算中精度较高,在内流问题计算中梯度精度降低,但可以较好地反映梯度变化趋势。
致谢:在本文的研究工作中,肖中云、牟斌、李彬、唐静、贾洪印等同志在大规模并行块隐式时间推进方法、进气道计算等方面给予了有益的建议,在此表示感谢!
| [1] |
Jameson A. Aerodynamic design via control theory[J]. Journal of Scientific Computing, 1988, 3: 233-260. DOI:10.1007/BF01061285 (  0) 0) |
| [2] |
Giles M B, Duta M C. Algorithm developments for discrete adjoint methods[J]. AIAA Journal, 2003, 41(2): 198-205. DOI:10.2514/2.1961 (  0) 0) |
| [3] |
Carpentieri G. An adjoint-based shape-optimization method for aerodynamic design[D]. Delft:Technische Universiteit, 2009.
(  0) 0) |
| [4] |
Amoignon O, Berggren M. Adjoint of a median-dual finite-volume scheme application to transonic aerodynamic shape optimization[R]. Technical Report 2006-3, Uppsala University, 2006. http://www.mendeley.com/research/adjoint-mediandual-finitevolume-scheme-application-transonic-aerodynamic-shape-optimization/
(  0) 0) |
| [5] |
Reuther J. Aerodynamic shape optimization using control theory[D]. Ph.D. Dissertation, University of California, Davis, Davis, CA, June 1996.
(  0) 0) |
| [6] |
Thomas A Zang, et al. Multidisplinary design optimization techniques:implications and opportunities for fluid dynamics research[C]//30th AIAA Fluid Dynamics conference, Norfolk, VA. June 28-July, 1999.
(  0) 0) |
| [7] |
Nielsen E J, Anderson W K. Recent improvements in aerodynamic design optimization on unstructrued meshes[J]. AIAA Journal, 2002, 40(6): 1155-1163. DOI:10.2514/2.1765 (  0) 0) |
| [8] |
Dwight R P, Brezillon J. Effect of various approximations of the discrete adjoint on gradient-based optimiza-tion[R]. AIAA-2006-0690, 2006.
(  0) 0) |
| [9] |
Carrier G, Destarag D, et al. Gradient-based aerodynamic optimization with the elsA software[R]. AIAA 2014-0568.
(  0) 0) |
| [10] |
Qin N, Wong W S, Moigne A L. Three-dimensional contour bumps for transonic wing drag reduction[J]. Proceedings of the Institution of Mechanical Engineers, Part G:Journal of Aerospace Engineering, 2008, 222(5): 619-629. DOI:10.1243/09544100JAERO333 (  0) 0) |
| [11] |
Zuo Yingtao, Gao Zhenghong, Zhan Hao. Aerodynamic design method based on N-S equations and discrete adjoint approach[J]. Acta Aerodynamica Sinica, 2009, 27(1): 67-72. (in Chinese) 左英桃, 高正红, 詹浩. 基于N-S方程和离散共轭方法的气动设计方法研究[J]. 空气动力学学报, 2009, 27(1): 67-72. (  0) 0) |
| [12] |
Xiong Juntao, Qiao Zhide, Yang Xudong, et al. Optimum aerodynamic design of transonic wing based on viscous adjoint method[J]. Acta Aeronautica et Astronautica Sinica, 2007, 28(2): 281-285. (in Chinese) 熊俊涛, 乔志德, 杨旭东, 等. 基于黏性伴随方法的跨声速机翼气动优化设计[J]. 航空学报, 2007, 28(2): 281-285. (  0) 0) |
| [13] |
Qu Kun, Li Jichao, Cai Jinsheng. Method of linearizing computational fluid dynamics model and its applications[J]. Acta Aeronautica et Astronautica Sinica, 2015, 36(10): 3218-3227. (in Chinese) 屈崑, 李记超, 蔡晋生. CFD数学模型的线性化方法及其应用[J]. 航空学报, 2015, 36(10): 3218-3227. (  0) 0) |
| [14] |
Zhang Chaolei, Li Haitao, Feng Zhenping. Aerodynamic optimization design of turbomachinery cascade based on discrete adjoint method[J]. Journal of Engineering Themophics, 2012, 33(1):47-50.(in Chinese) 张朝磊, 等.基于离散伴随方法的透平叶栅气动优化[J].工程热物理学报, 2012, (33):47-50. http://www.cnki.com.cn/Article/CJFDTOTAL-GCRB201201013.htm (  0) 0) |
| [15] |
Gao Yisheng, Wu Yizhao, Xia Jian. A discrete adjoint-based approach for airfoil optimization on unstructured meshes[J]. Acta Aerodynamica Sinica, 2013, 31(2): 244-249. (in Chinese) 高宜胜, 伍贻兆, 夏健. 基于非结构网格离散型伴随方法的翼型优化[J]. 空气动力学学报, 2013, 31(2): 244-249. DOI:10.7638/kqdlxxb-2011.0306 (  0) 0) |
| [16] |
Li Bin, Deng Youqi, Tang Jing, et al. Discrete adjoint optimization method for 3d unstructured grid[J]. Acta Aeronautica et Astronautica Sinica, 2014, 35(3): 674-686. (in Chinese) 李彬, 邓有奇, 唐静, 等. 基于三维非结构混合网格的离散伴随优化方法[J]. 航空学报, 2014, 35(3): 674-686. (  0) 0) |
| [17] |
Liu Gang, Xiao Zhongyun, Wang Jiantao, Liu Fan. Numerical simulation of missile air-launching process under rail slideway constraints[J]. Acta Aerodynamica Sinica, 2015, 33(02):192-197.(in Chinese) 刘刚, 肖中云, 王建涛, 等.考虑约束的机载导弹导轨发射数值模拟[J].空气动力学学报, 2015, 33(02):192-197. http://www.kqdlxxb.com/CN/abstract/abstract11650.shtml (  0) 0) |
| [18] |
Nadarajah Siva K, Jameson Antony. A comparison of the continuous and discrete adjoint approach to automatic aerodynamic optimization[C]//38th AIAA Aerospace Sciences Meeting and Exhibit Reno-NV-Jan. 10-13-2000.
(  0) 0) |
| [19] |
Chen R F, Wang Z J. Fast, block lower-upper symmetric gauss-seidel scheme for a artributrary grids[J]. AIAA Journal, 2000, 38(12): 2238-2245. DOI:10.2514/2.914 (  0) 0) |
 2017, Vol. 35
2017, Vol. 35


