倾转旋翼机具有常规直升机不具备的高速巡航能力,又具有固定翼飞机不具备的垂直起降和悬停能力,这些独特的性能都得益于其特有的倾转旋翼构型。[1]悬停状态,倾转旋翼轴垂直于机身,倾转旋翼作用相当于普通直升机的旋翼;前飞状态,倾转旋翼向前倾转,起到固定翼飞机螺旋桨的作用。悬停状态的倾转旋翼提供升力以克服飞行器的重力;前飞状态的倾转旋翼仅提供克服飞行器高速前飞所受到的阻力,升力主要由固定翼的机翼提供,此时良好的巡航效率要求低型阻和小的压缩性影响,这就要求桨叶面积和桨尖速度要小。此外,桨叶扭转也是倾转旋翼设计中必须加以考虑的重要因素之一:悬停状态下低的桨叶扭转可以提高失速裕度,但巡航状态则需要采用大的桨叶扭转来保证飞行器在高速下充分的可控性和低速时足够的机动性能。由此可见,倾转旋翼的气动设计要综合考虑直升机与固定翼的不同工作模式对其不同的要求,应该是直升机旋翼和固定翼螺旋桨两种类型气动外形的折中。
在常规旋翼气动特性分析及桨叶外形优化设计方法方面,早期的模拟方法[2-6]主要是采用升力线模型、动量叶素理论或者涡尾迹方法。近期,Johnson等[7]基于均匀入流假设,采用升力线法结合多学科优化方法开展了倾转旋翼的设计,主要针对倾转旋翼悬停性能和巡航效率进行了优化。Stahlhut等[8]在对倾转旋翼进行参数化分析和优化设计研究的过程中,采用动量/叶素理论(BEMT)分析了不同桨叶构型参数对倾转旋翼性能的影响特性。薛立鹏等[9]选取悬停和巡航效率为目标函数,以旋翼功率和桨叶重量为约束条件,采用自由尾迹分析方法建立了倾转旋翼的气动模型,通过选取弦长、预扭角、厚度以及翼型分布位置和旋翼转速为设计参数,对桨叶气动外形进行了优化设计。这些方法虽然可以高效地计算(倾转)旋翼的气动性能,但很难应用于复杂气动外形的精细化设计。
随着数值方法和计算机水平不断提高,高精度的CFD方法已经被引入到旋翼的气动外形优化设计之中。法国的Pape等[10]通过耦合CFD方法和梯度方法的优化策略,尝试对悬停状态下旋翼平面外形进行了优化设计,获得了高悬停效率的旋翼气动外形。Potsdam等[11]基于结构运动嵌套网格方法和RANS方程,较好地预测了悬停状态倾转旋翼的气动性能,但未能深入分析倾转旋翼桨叶气动载荷分布特征,也未开展优化设计研究。随后,Dumot等[12]引入离散伴随方法,对旋翼气动外形进行了优化设计,设计出具有桨尖下反等特性的先进气动外形方案。王博等[13]基于代理模型并采用CFD方法进行旋翼流场的分析,建立了耦合桨叶优化策略,主要针对旋翼的负扭转进行优化设计。李鹏等[14-15]采用CFD方法分别针对倾转旋翼/机翼气动干扰及过渡状态的非定常气动特性进行了数值模拟,但未进一步开展倾转旋翼桨叶气动优化设计。
综合来看,已经开展的工作主要是针对常规直升机旋翼桨叶平面形状、弦长等某一方面展开分析研究,但对倾转旋翼桨叶的三维外形优化设计相对较少,CFD在该方面的应用尚处于起步阶段。对于倾转旋翼的设计要满足悬停和巡航状态的不同性能要求,已开展的工作中也未见能够综合描述倾转旋翼的悬停和巡航性能的设计评价指标。
鉴于此,本文将高精度CFD方法与优化方法相结合,建立了一套适合倾转旋翼气动外形优化设计的方法,并提出了能够同时描述悬停和巡航性能的综合性能评价指标。发展了高效的动量/叶素组合方法以模拟倾转旋翼悬停和巡航状态的气动特性,建立了针对倾转旋翼悬停/巡航工作状态的操纵配平方法,并采用遗传算法对拉丁超立方方法进行优化,以径向函数为基函数,通过线性叠加构造的模型为代理模型,开展倾转旋翼桨叶构型参数对倾转旋翼气动性能的影响研究。最后,选取一种包含前后掠以及尖削等组合变化外形的倾转旋翼作为原始构型,采用本文建立的优化方法进行倾转旋翼的综合优化,获得了一种高性能的倾转旋翼气动外形优化方案,并获得了该方案的典型特征。
1 网格生成方法采用CFD方法进行旋翼桨叶气动外形优化设计时往往需要计算大量不同气动外形参数的旋翼流场,为了兼顾模拟精度,对网格质量有较高要求,这势必导致整个优化过程的计算量很大。鉴于此,本文建立了一套适合于桨叶气动外形优化的高效网格生成技术。主要思想是根据桨叶外形特征,将桨叶气动外形分解为翼型、扭转、弦长及1/4气动弦线位置四种独立变量进行参数化描述。通过对桨叶进行参数化分解,可以将桨叶三维网格的生成转化为沿桨叶展向分布的独立二维网格生成问题。相对而言,二维网格的生成简单易行,网格贴体性和正交性更容易控制,网格生成的难度和计算量明显低于三维网格,这都有利于生成高质量的网格和节省三维网格的生成时间。此外,考虑到桨叶根部和尖部是出现明显的涡流动的部位,且存在复杂的三维非定常绕流,为了能够精确的模拟上述流动特性,在桨根和桨叶尖部特征剖面外采用了O型网格生成方法,保证了端部的光滑过渡。
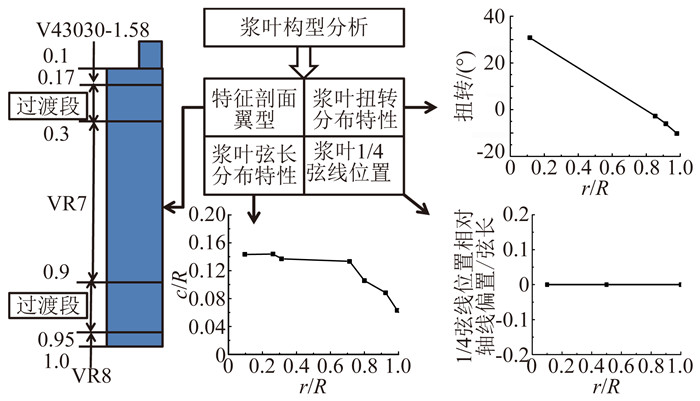
下面以ATB(复合材料的XV-15的桨叶)倾转旋翼为研究对象来表述网格生成过程,图 1给出了ATB倾转旋翼的桨叶外形特性分布,整套网格生成方法主要可分为五部分:
|
图 1 ATB倾转旋翼桨叶特性 Figure 1 Characters of ATB tiltrotor blade |
第一步,对目标桨叶进行参数化分解,将桨叶特性(翼型、扭转、弦长及气动弦线位置)表述为沿展向分布的特征函数。为了描述桨叶外形参数的分布,需要在特征函数的表述过程中引入插值函数,在优化领域较常见的插值函数有Bezier曲线[16]、NURBS曲线[17]等。相对于NURBS曲线,Bezier曲线较为高效且拟合精度较高。因此,采用Bezier曲线插值函数来描述桨叶外形参数的详细分布。n阶的Bezier曲线由n+1个给定点确定,曲线的参数方程如下:
| $ \begin{array}{l} B\left( t \right) = \mathop \sum \limits_i^n \left( \begin{array}{l} n\\ i \end{array} \right){\mathit{\boldsymbol{P}}_i}{\left( {1 - t} \right)^{n - i}}{t^i}\\ \;\;\;\;\;\;\; = {\mathit{\boldsymbol{P}}_0}{\left( {1 - t} \right)^n} + \left( \begin{array}{l} n\\ 1 \end{array} \right){\mathit{\boldsymbol{P}}_1}{\left( {1 - t} \right)^{n - 1}}t + \cdots \\ \;\;\;\;\;\;\; + {\mathit{\boldsymbol{P}}_n}{t^n},t \in \left[ {0,1} \right] \end{array} $ | (1) |
式中,Pi为第i+1个给定点。
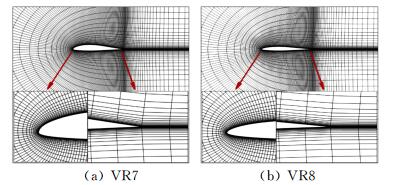
第二步,根据桨叶构造特征,确定特征剖面,并按照数值模拟要求生成对应剖面的二维初始网格,图 2给出了该桨叶的典型特征剖面翼型网格。
|
图 2 特征剖面翼型网格 Figure 2 Airfoil grids of typical profile |
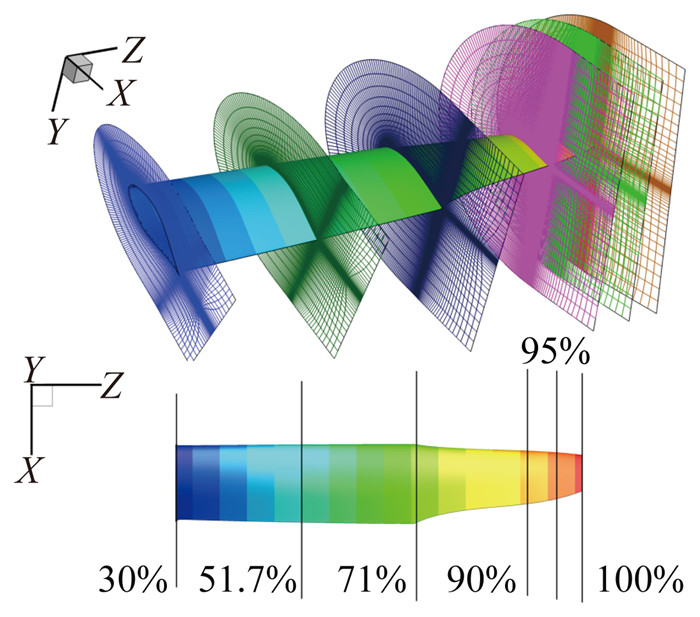
第三步,依据桨叶的扭转、弦长及1/4弦线位置分布特性,对特征剖面的翼型网格进行平移、旋转等变换得出真实桨叶特征剖面所对应的翼型网格,图 3给出了围绕倾转旋翼桨叶的初始网格模板示意图。
|
图 3 初始桨叶特征剖面网格 Figure 3 Typical profile grids of initial blade |
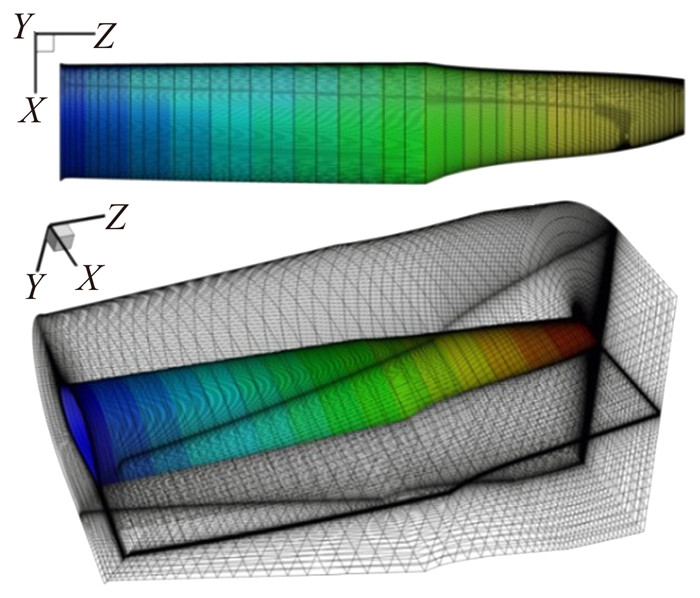
第四步,以第三步中的特征剖面网格为基准,对特征剖面之间的翼型网格按照桨叶外形特性进行插值填充,同时针对可能出现的非线性扭转、变翼型、大尖削等复杂三维构型变化剧烈的位置进行局部展向加密来提高旋翼桨叶整体网格生成质量,图 4给出了围绕桨叶的物面网格和外边界网格示意图。
|
图 4 桨叶表面及外边界网格 Figure 4 Grids of blade surface and outer boundary |
第五步,对第四步网格在桨根和桨尖位置进行合理的O型翻折封闭处理,如图 5所示。
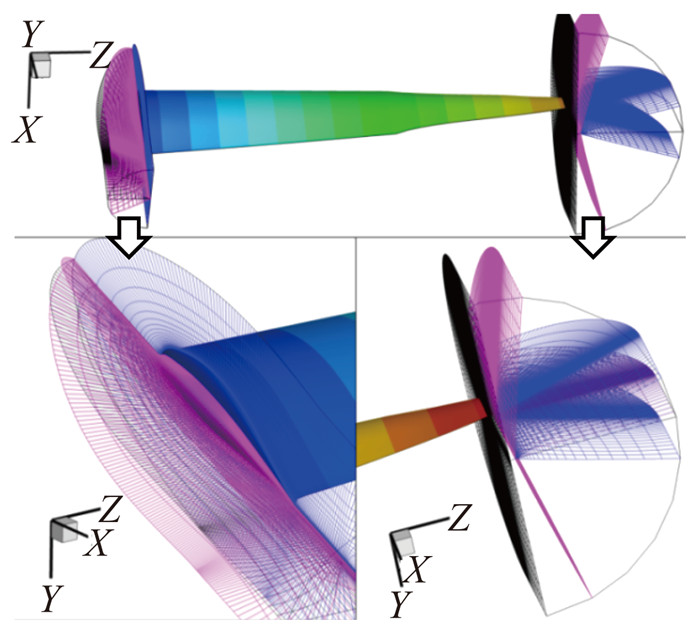
|
图 5 桨叶端部O型网格翻折示意图 Figure 5 Schematic diagram of O-type grid turning over at the end of the blade |
为了能够开展相同拉力状态下倾转旋翼气动性能的对比,需要合理分析出相应运行状态下的旋翼操纵量。因此,本节针对倾转旋翼悬停/巡航工作状态分别建立了相应的操纵量配平方法。
准确的翼型来流角是确定不同飞行状态下的翼型升力系数的关键。本文对不同飞行状态下入流分布进行了简化,由动量理论可得旋翼的拉力系数为:
| $ {C_T} = 2\frac{{{V_n}{v_n}}}{{{{\left( {\omega R} \right)}^2}}} = 2\frac{{{V_n}}}{{\left( {\omega R} \right)}}\frac{{{v_n}}}{{(\omega R)}} $ | (2) |
| $ {V_h} = \omega R\cdot\sqrt {\frac{{{C_T}}}{2}} $ | (3) |
式中,ω为旋翼转速,R为桨叶半径,Vn、vn、Vh分别为桨盘处入流速度、轴向诱导速度和平均下洗速度。
由方程(2) 和(3) 得桨叶展向剖面r处的轴向流入比:
| $ {\lambda _r} = \frac{{V_{_n}^{^\infty } + {v_n}}}{{\omega r}} = \frac{{V_{_n}^{^\infty }}}{{2\omega r}} + \frac{1}{{\omega r}}\sqrt {{{\left( {\frac{{V_{_n}^{^\infty }}}{2}} \right)}^2} + {{({V_h})}^2}} $ | (4) |
式中,Vn∞为无穷远处法向速度。
在悬停和巡航状态下的倾转旋翼工作状态有明显的周向对称性,因此由叶素理论计算出旋翼拉力系数为:
| $ \begin{array}{l} {C_T} = \int_{{{\bar r}_0}}^1 {d{C_T}} \\ \;\;\;\;\; = \sigma \int_{{{\bar r}_0}}^1 {\frac{1}{2}\sqrt {\xi _{_r}^{^2} + \lambda _{_r}^{^2}} } ({C_l}{\xi _r} - {C_d}{\lambda _r})d\bar r \end{array} $ | (5) |
式中,σ、ξr、λr、Cl、Cd和r0分别为旋翼实度、周向诱导流入比、轴向诱导流入比、微元拉力系数、阻力系数和根切比。
综合式(2) 和式(5),采用Newton迭代方法求解,由于扭转角已给定,可得出目标拉力下旋翼总距操纵量θ0。
2.2 综合气动性能指标倾转旋翼同时具有直升机旋翼和固定翼螺旋桨两种飞行模式,因此,对应不同的飞行状态有两种飞行性能评价标准,而过多的参数定义会增加了数据处理以及分析的困难,因此,本文将气动性能参数进行了综合,得出倾转旋翼的前进比(μ)、拉力系数(CT)、功率系数(CQ)、悬停效率(Figure of Merit, FM)和巡航效率(η)分别为:
| $ \left\{ \begin{array}{l} {\mu _{t/n}} = {V_{t/n}}/\left( {\omega R} \right)\\ {C_T} = T/(\rho \pi {\omega ^2}{R^4})\\ {C_Q} = P/(\rho \pi {\omega ^3}{R^5})\\ FM = \sqrt {{C_T}/2.0} \times {C_T}/{C_Q}\\ \eta = {\mu _n} \times {C_T}/{C_Q} \end{array} \right. $ | (6) |
式中,t表示切向,n表示法向。
悬停效率FM是衡量直升机旋翼桨叶气动外形设计在悬停状态下的气动性能指标,巡航效率η是衡量螺旋桨在巡航状态下的气动性能指标,而倾转旋翼同时具有直升机旋翼和固定翼螺旋桨的双重功能。因此,为了能在旋翼优化设计的过程中同时描述倾转旋翼的悬停和巡航性能,本文提出了倾转旋翼/螺旋桨综合气动性能设计评价指标,具体为:
| $ {P_O} = \frac{{{\rm{sgn}}(FM - F{M_O}) + {\rm{sgn}}(\eta - {\eta _O})}}{2}\left( {\frac{{FM}}{{F{M_O}}} + \frac{\eta }{{{\eta _O}}}} \right) $ | (7) |
式中,下标O表示为设计目标值,
| $ {\rm{sgn}}\left( x \right) = \left\{ \begin{array}{l} 1\;\;\;\;x > 0\\ 0\;\;\;\;x = 0\\ - 1\;\;x < 0 \end{array} \right.。$ |
采用相对坐标系,以绝对物理量为参数的守恒积分形式的可压N-S方程作为主控方程:
| $ \frac{\partial }{{\partial t}}\int_{_\mathit{\Omega} } {W{\rm{d}}\mathit{\Omega} } + \oint_{\partial \mathit{\Omega} } {{Q_C}} \cdot\mathit{\boldsymbol{n}}{\rm{d}}s - \oint_{\partial \mathit{\Omega} } {{Q_V}} \cdot\mathit{\boldsymbol{n}}{\rm{d}}s = \int_{_\mathit{\Omega} } {\mathit{\boldsymbol{F}}{\rm{d}}\mathit{\Omega} } $ | (8) |
其中,
| $ {Q_V} = \left[ {\begin{array}{*{20}{c}} 0\\ {{\tau _{xx}}{\mathit{\boldsymbol{n}}_x} + {\tau _{xy}}{\mathit{\boldsymbol{n}}_y} + {\tau _{xz}}{\mathit{\boldsymbol{n}}_z}}\\ {{\tau _{yx}}{\mathit{\boldsymbol{n}}_x} + {\tau _{yy}}{\mathit{\boldsymbol{n}}_y} + {\tau _{yz}}{\mathit{\boldsymbol{n}}_z}}\\ {{\tau _{zx}}{\mathit{\boldsymbol{n}}_x} + {\tau _{zy}}{\mathit{\boldsymbol{n}}_y} + {\tau _{zz}}{\mathit{\boldsymbol{n}}_z}}\\ {{\mathit{\Phi} _x}{\mathit{\boldsymbol{n}}_x} + {\mathit{\Phi} _y}{\mathit{\boldsymbol{n}}_y} + {\mathit{\Phi} _z}{\mathit{\boldsymbol{n}}_z}} \end{array}} \right],\boldsymbol{F} = \left\{ {\begin{array}{*{20}{c}} 0\\ {\rho \omega w}\\ 0\\ { - \rho \omega u}\\ 0 \end{array}} \right\} $ |
式中,Ω、∂ Ω、ρ、p、(Vx,Vy,Vz)、Vb、E、H、ω分别表示为体积、面积、密度、压强、绝对速度在笛卡尔坐标系下的分量、旋转速度、总能、总熵、角速度。
湍流模型采用一方程S-A模型来模拟气体的粘性影响,相对于两方程湍流模型,S-A模型的计算量较小,并具有较好的中等分离流动模拟能力。S-A湍流模型因其精度和效率较高,在工程实践中得到了越来越广泛的运用。
时间推进采用隐式LU-SGS格式,空间离散采用有限体积法,采用中心差分格式计算交界面上的通量。
2.4 近似模型验证在设计倾转旋翼时,涉及多次迭代计算的多学科设计优化,若全部采用高精度的数值模拟方法开展桨叶的气动分析,则需要花费大量的时间。因此本文采用代理模型方法,通过选取少量样本桨叶气动外形和模拟得到的气动特性参数,建立能得到与数值分析或物理试验结果相近的数学模型,从而在保证计算精度的同时大幅度减少计算量。
这里采用具有生成样本点数量少、生成简单等优点的拉丁超立方设计(Latin Hypercube Sampling, LHS)方法,但LHS样本点为随机产生,因此生成结果随机性较大,容易出现局部过密或过疏的情况。鉴于此,采用遗传算法方法对拉丁超立方方法进行优化,形成了PermGA LHS方法。从图 6中可以看出生成相同样本点时,采用PermGA LHS生成的样本点分布较为均匀。
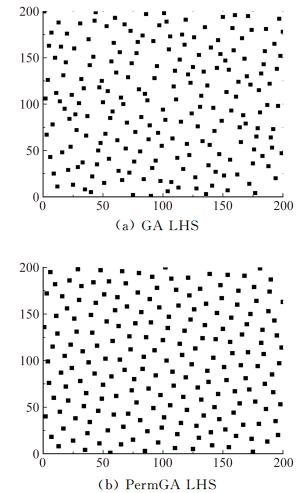
|
图 6 设计空间内的样本点(2变量,200水平) Figure 6 Sample points in design space (2 variables, 200 levels) |
代理模型技术的主体是建立用于数据拟合的预测模型,本文采用的是径向基函数(Radial Basis Function)模型。该模型是以待测点与样本点之间的欧氏距离为自变量的函数,以径向函数为基函数,通过线性叠加构造出来的模型。
为检查所建立模型的拟合能力,预测误差运用百分比均方根差(RMSE%)来衡量,计算方法如下:
| $ RMSE = \frac{{\sqrt {\frac{1}{m}\sum\limits_{m = 1}^m {{{\left( {f(x) - \hat f(x)} \right)}^2}} } }}{{\frac{1}{m}\sum\limits_{m = 1}^m {|f(x)|} }} $ | (9) |
其中,f(x)为真实值,
首先,采用PermGA LHS设计方法选取了100个样本点,建立样本点范围。然后,基于目标函数计算出样本点的响应,并以此为空间运用径向基函数方法进行函数拟合。图 7给出了测试函数与拟合函数的对比,从中可以看出,在拟合范围内,所有的极值点及其所在位置都吻合较好,最大误差值为1.51%,表明本文采用的径向基函数方法具有较好的拟合效果。
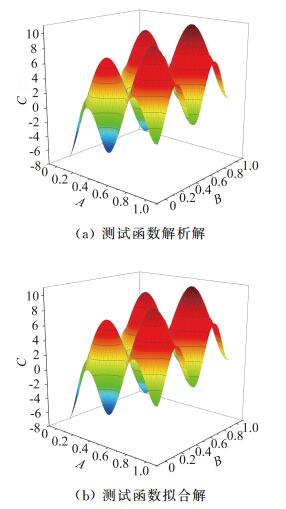
|
图 7 测试函数解析解与拟合解的对比 Figure 7 Comparisons of analytic solution and fitting solution of the test function |
选择XV-15倾转旋翼桨叶为研究对象来开展本文CFD方法的算例验证。图 8给出了XV-15旋翼悬停状态和巡航状态(555km/h)气动性能的计算结果,并与试验值[18]进行对比,表明建立的CFD方法能够有效地计算悬停和巡航状态倾转旋翼的气动性能。
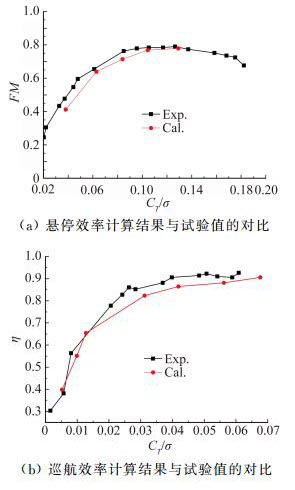
|
图 8 XV-15倾转旋翼气动性能计算值与试验值的对比 Figure 8 Comparisons of calculated aerodynamic performance of the rotor with experimental results |
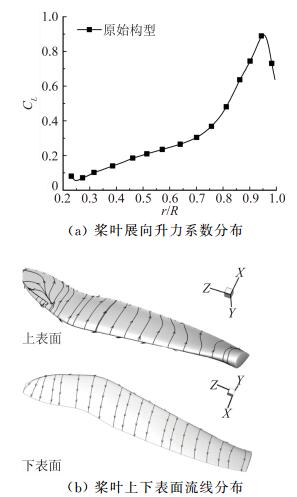
工作状态为:Mtip=0.68,CT=0.017,该状态下的倾转旋翼悬停效率计算结果为FM=0.625。图 9(a)给出了原始构型旋翼桨叶展向升力系数分布,可以看出,展向内段的升力系数较小,且沿展向向尖部的分布变化剧烈,且尖部的升力系数峰值较高,表明桨尖上下表面的压力差较大,会形成更强烈集中的桨尖涡,这些将对其气动性能造成一定的不利影响。为了揭示上述倾转旋翼气动特性分布的原因,图 9(b)进一步给出了该悬停状态下的倾转旋翼上下表面流线分布,可以看出,此时倾转旋翼桨叶尖部上表面前缘出现了明显的气流分离现象,说明气流沿桨叶展向流动遇到了较大的逆压梯度,导致桨尖局部的升力能力下降。因此,在悬停状态下减弱前缘的气流分离、继而进一步改善桨尖局部升力系数的合理分布,可能在一定程度上提高倾转旋翼的悬停气动性能。
|
图 9 悬停状态原始构型倾转旋翼的气动特性 Figure 9 Aerodynamic characteristics of tiltrotor of initial configuration in hover |
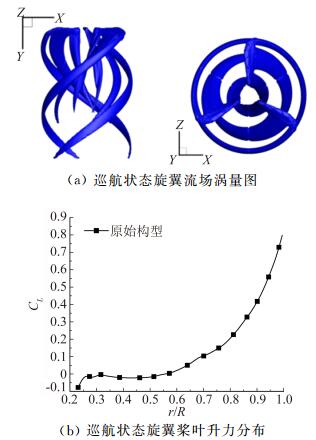
工作状态为:μn=0.703,Mtip=0.58,CT=0.006,该状态下的倾转旋翼巡航效率为η=0.805。图 10(a)给出了在该工作条件下倾转旋翼的流场涡量图,此时的倾转旋翼桨叶后缘拖出的涡比较复杂,除了强烈的桨尖涡外,在桨叶中段还有较强的尾随涡出现。图 10(b)给出了巡航状态下桨叶展向升力系数分布,可以看出桨叶尖部气动力变化较为剧烈,并且桨叶内侧存在负拉力区域。因此,改善桨叶尖部的升力分布特征,并使桨叶根部产生一定的正拉力,有可能提高倾转旋翼的巡航气动性能。
|
图 10 巡航状态原始构型倾转旋翼的气动特性 Figure 10 Aerodynamic characteristics of tiltrotor of initial configuration in cruise |
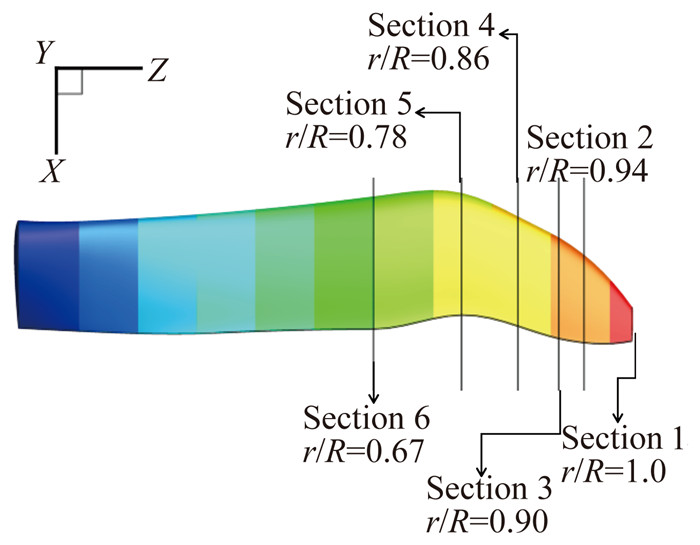
原始构型桨叶的外形没有三维特征变化,且桨尖存在气流分离现象,而且升力沿展向的分布也不理想。为此,本文将通过对模型桨叶尖部进行三维曲面造型优化,旨在提高倾转旋翼的悬停和巡航气动性能。通过对桨叶尖部剖面进行特征分析,确定了如图 11所示的六个优化特征翼型剖面位置,分别对应桨叶展向0.67r/R(剖面6)、0.78r/R(剖面5)、0.8r/R(剖面4)、0.90r/R(剖面3)、0.94r/R(剖面2) 和1.0r/R(剖面1)。为减少潜在的结构动力学问题,仅在桨叶特征剖面处引入扭转、弦长、上下反等优化参数,以桨叶外段为主,并且对1/4弦线位置进行了约束限制,具体实施方案如下:
|
图 11 桨叶优化特征剖面示意图 Figure 11 Schematic diagram of optimized blade section |
第一步,关于桨叶扭转及其弦长参数的选择。维持桨叶展向剖面6的气动参数不变,对桨叶展向剖面4的扭转和弦长进行参数选择,并且桨叶展向剖面4的扭转/弦长变化范围处于展向剖面6和剖面2的对应值之间,桨叶展向剖面2的扭转分布范围处于展向剖面4和剖面1的对应值之间。
第二步,关于三维桨尖外形参数的选择。对桨叶展向剖面1、剖面2和剖面5的上下反位置进行了布置,以桨叶展向剖面6为基准,上述三个剖面上反角最大为5°,下反角最大为10°。
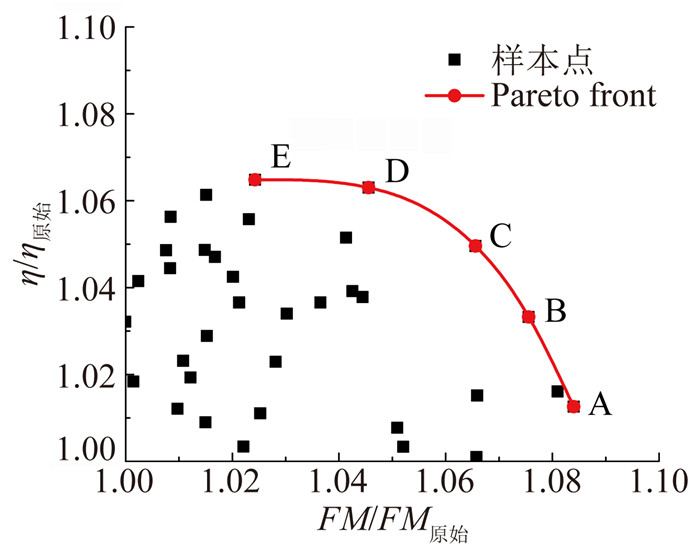
3.3 优化倾转旋翼的气动性能图 12给出了不同优化构型下倾转旋翼综合气动效率与原始构型的对比,悬停和巡航气动性能均得到了较好的提高。表 1给出了Pareto前缘上五种优化构型倾转旋翼的气动性能结果,从表中可以看出,优化出的桨叶相对于原始构型气动性能在悬停和巡航状态下均有更明显的提高,优化倾转旋翼最大悬停效率提高了8.4%(A构型),最优巡航效率提高了6.48%(E构型)。基于前文所提出的综合效率评价方法,得出了悬停/巡航状态倾转旋翼气动性能综合最优的为C构型,综合性能指标提高5.7%以上,其中最大悬停效率提高6.5%,最大巡航效率提高4.9%以上。
|
图 12 倾转旋翼综合气动效率分布 Figure 12 Distribution of the comprehensive aerodynamic efficiency of tiltrotor |
| 表 1 不同构型的气动性能对比 Table 1 Comparison of aerodynamic performance of different configurations |
|
|
图 13给出了气动性能较优的倾转旋翼桨叶与原始构型桨叶的气动外形参数对比。
|
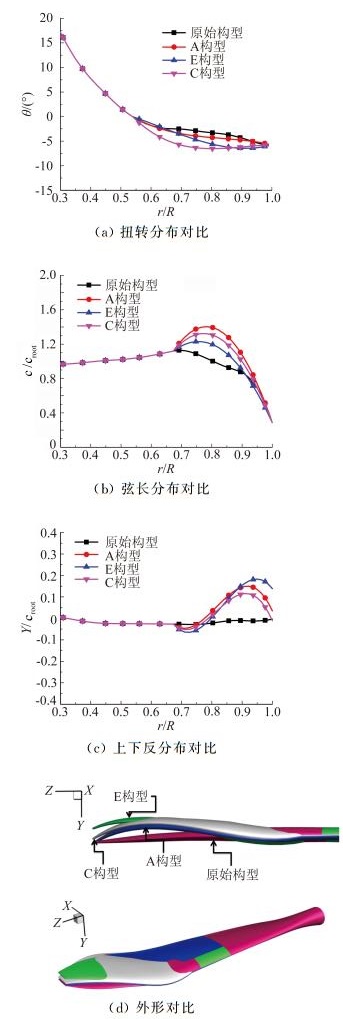
图 13 不同倾转旋翼构型外形特征对比 Figure 13 Comparisons of shape characters of different tiltrotor configurations |
从图 13(a)的桨叶扭转分布对比看出,与原始构型相比,优化构型在桨叶展向外侧均存在比原始构型更加明显的负扭转,C构型的变化最为明显,在三种优化构型中获得最优悬停性能。
从图 13(b)的桨叶的弦长分布对比看出,与原始构型相比,优化倾转旋翼桨叶弦长在桨叶外段有明显增加,悬停气动性能改变最显著的A构型桨叶弦长变化最大,表明桨叶实度增加最多;巡航气动性能改变最大的E构型桨叶弦长变化相对小些。这些变化有助于桨叶升力沿展向的合理分布,综合气动性能最优的C构型弦长分布介于两者之间。
从图 13(c)的桨叶上下反分布对比看出,与原始构型相比,优化倾转旋翼桨叶在尖部都有了明显的上下反组合变化,先上反后下反。巡航效率最优的E构型相对于原构型在尖部出现了更大的上反,综合性能最优的C构型具有相对较缓和的上下反组合变化特点。
从图 13(d)给出了三种优化倾转旋翼构型与原始构型外形的对比,与原始构型相比,综合气动性能最优的倾转旋翼桨叶扭转角变化曲线最为平滑,在外侧存在较大负扭转;外侧弦长有显著增加、尖部大尖削;尖部内侧上反和外侧下反组合变化。
图 14给出了悬停状态下优化构型与原始构型的展向升力系数分布对比,从图 14(a)中可以看出,与原始构型相比,优化倾转旋翼升力分布在桨叶内侧有一定的增量,桨叶沿展向的整体升力分布更加均匀,且桨叶尖部的升力峰值位置向外发生了明显的移动,同时升力峰值有所减小,这在一定程度上反映了优化构型削弱了原始构型前缘的气流分离;同时为了弥补升力下降的可能,与原始构型相比,此处优化桨叶外形的弦长加大。这些桨叶展向升力分布特征的改善提高了倾转旋翼的悬停性能。

|
图 14 不同构型倾转旋翼气动特性分布对比 Figure 14 Comparisons of aerodynamic characteristics of different tiltrotor configurations |
从图 14b中可以看出,优化构型E和C相对于原始构型桨叶,在内侧的升力均得到了一定程度的提高,且优化构型(A至E)桨叶尖部的拉力峰值均有明显的降低,表明桨尖上下表面的压力差减小,不易形成强烈集中的桨尖涡,桨叶内、外侧展向升力的优化分布显著提高了巡航状态倾转旋翼的气动性能。
图 14c给出了悬停状态下优化构型倾转旋翼桨叶表面流动特性的对比,从图中可以看出,A构型倾转旋翼桨叶上表面气流分离得到了很好的抑制,这令A构型倾转旋翼获得了最优悬停性能。
图 14d给出了巡航状态下优化构型倾转旋翼桨叶表面流动特性对比,A和E构型倾转旋翼均能较好的缓解桨叶尖部前缘的激波气流分离,从而相对于原始构型倾转旋翼进一步提高了巡航效率。
综合分析表明,在原始构型基础上,加入三维特征、弦长及扭转等组合优化出的倾转旋翼综合气动性能更优。最优构型扭转角变化内陡外缓;外侧弦长相比内侧明显增加并且在尖部有大尖削和上下反的组合构型特征。
4 结论1) 根据倾转旋翼桨叶构造特征,将桨叶气动外形分解为翼型、扭转、弦长及1/4弦线位置四种独立变量进行参数化描述,从而桨叶三维网格可以通过沿其展向生成特征剖面二维网格生成、展向拉伸、局部加密分布和端部翻折处理相结合得到,提高了桨叶三维网格的生成效率并保证了网格正交性。
2) 基于代理模型建立的优化设计方法适用于倾转旋翼气动外形的优化设计与分析,能够设计出悬停和巡航综合气动效率较高的倾转旋翼方案。
3) 通过对三维桨叶尖部的综合气动外形(扭转/弦长/上下反)进行优化设计,可有效地改善桨尖部位的气流分离现象,提升桨叶升力沿展向分布的均匀性,能明显提高倾转旋翼的综合气动效率。
4) 综合气动性能较好的桨叶构型特征为:桨叶扭转角变化内陡外缓;桨叶外侧弦长有显著增加,且尖部大尖削;桨叶尖部内侧上反和外侧下反组合变化。
| [1] |
Poling D R, Rosenstein H, Rajagopalan G. Use of a Navier-Stokes code in understanding tiltrotor flowfields in hover[J]. Journal of the American Helicopter Society, 1998, 43(2): 103-109. DOI:10.4050/JAHS.43.103 (  0) 0) |
| [2] |
Joanne L Walsh, Gene J Bingham, Michael F Riley. Optimization methods applied to the aerodynamic design of helicopter rotor blades[J]. Journal of the American Helicopter Society, 1987, 32(4): 39-44. DOI:10.4050/JAHS.32.39 (  0) 0) |
| [3] |
Lim J W, Chopra I. Aeroelastic optimization of a helicopter rotor[J]. Journal of the American Helicopter Society, 1989, 34(1): 52-62. (  0) 0) |
| [4] |
Rocchetto A, Poloni C. A hybrid numerical optimization technique based on genetic and feasible direction algorithms for multipoint helicopter rotor blade design[C]//21st European Rotorcraft Forum, St. Petersburg, Russia. 1995. https://link.springer.com/chapter/10.1007/978-3-7091-2658-5_11
(  0) 0) |
| [5] |
Zibi J. An optimization method applied to the aerodynamics of helicopter rotor blades[C]//The 21st European Rotorcraft Forum, St. Petersburg, Russia. 1995.
(  0) 0) |
| [6] |
Leishman J G, Ananthan S. Aerodynamic optimization of a coaxial proprotor[C]//The 62nd Annual Forum of AHS, 2006.
(  0) 0) |
| [7] |
Yeo H, Johnson W. Aeromechanics analysis of a heavy lift slowed-rotor compound helicopter[J]. Journal of Aircraft, 2012, 44(2): 501-508. (  0) 0) |
| [8] |
Stahlhut C W. Aerodynamic design optimization of proprotors for convertible-rotor concepts[D]. Doctor thesis. University of Maryland, 2012.
(  0) 0) |
| [9] |
Xue Lipeng, Zhang Chenglin. The aerodynamic optimization design to tilt-rotor[J]. Acta Aerodynamica Sinica, 2011, 29(4): 453-458. (in Chinese) 薛立鹏, 张呈林. 倾转旋翼气动优化设计[J]. 空气动力学学报, 2011, 29(4): 453-458. (  0) 0) |
| [10] |
LePape A, Beaumier P. Numerical optimization of helicopter rotor aerodynamic performance in hover[J]. Aerospace Science and Technology, 2005, 9(3): 191-201. DOI:10.1016/j.ast.2004.09.004 (  0) 0) |
| [11] |
Potsdam M A, Strawn R C. CFD simulations of tiltrotor configurations in hover[J]. Journal of the American Helicopter Society, 2005, 50(1): 82-94. DOI:10.4050/1.3092845 (  0) 0) |
| [12] |
Dumont A, Le Pape A, Peter J, et al. Aerodynamic shape optimization of hovering rotors using a discrete adjoint of the reynolds-averaged Navier-Stokes equations[J]. Journal of the American Helicopter Society, 2011, 56(3): 1-11. (  0) 0) |
| [13] |
Wang Bo, Zhao Qijun, Xu Guohua. Numerical optimization of helicopter rotor twist distribution in hover[J]. Acta Aeronautica et Astronautica Sinica, 2012, 33(7): 1163-1172. (in Chinese) 王博, 招启军, 徐国华. 悬停状态直升机桨叶扭转分布的优化数值计算[J]. 航空学报, 2012, 33(7): 1163-1172. (  0) 0) |
| [14] |
Li Peng, Zhao Qijun. CFD calculations on the interaction flowfield and aerodynamic force of tiltrotor/wing in hover[J]. Acta Aeronautica et Astronautica Sinica, 2014, 02(2): 361-371. (in Chinese) 李鹏, 招启军. 悬停状态倾转旋翼/机翼干扰流场及气动力的CFD计算[J]. 航空学报, 2014, 02: 361-371. (  0) 0) |
| [15] |
Li Peng, Zhao Qijun, Zhu Qiuxian. CFD calculations on the unsteady aerodynamic characteristics of a tilt-rotor in a conversion mode[J]. Chinese Journal of Aeronautics, 2015, 06: 1593-1605. (  0) 0) |
| [16] |
Talbert J A, Parkinson A R. Development of an automatic, two-dimensional finite element mesh generator using quadrilateral elements and bezier curve boundary definition[J]. International Journal for Numerical Methods in Engineering, 1990, 29(7): 1551-1567. DOI:10.1002/(ISSN)1097-0207 (  0) 0) |
| [17] |
Piegl L. On NURBS:a survey[J]. IEEE Computer Graphics and Applications, 1991, 1: 55-71. (  0) 0) |
| [18] |
Johnson W, Lau B H, Bowles J V. Calculated performance, stability, and maneuverability of high-speed tilting-prop-rotor aircraft[J]. Vertica, 1986, 11: 317-339. (  0) 0) |
 2017, Vol. 35
2017, Vol. 35


