2. 中国科学院力学研究所 高温气体动力学国家重点实验室, 北京 100190
2. Institute of Mechanics, Chinese Academy of Sciences, Beijing 100190, China
高超声速飞行方式正由传统的弹道式飞行和太空返回向近空间大气层内做长时间高速机动飞行的方向发展。以美国的“HTV-2”为代表的高超声速滑翔飞行器是其典型代表之一,该类飞行器以单级或多级火箭为动力,助推到一定高度和马赫数后箭体分离,之后滑翔器在近空间进行高超声速滑翔机动飞行。美国国防预先研究局对“HTV-2”进行过两次试飞,均发生了飞行器因横航向动态失稳而坠毁[1-2]。
乘波体的概念由Nonweiler[3]在1959年提出,近30年来得到了广泛发展。其原理是在乘波体的前缘产生附体激波,阻止了下表面的高压气体上溢,使波后高压气体都限制在下表面,从而获得在相同攻角下比普通外形更高的升力以及升阻比。乘波体的高升阻比优势,使其成为高超声速滑翔飞行器的一种非常理想的潜在构型。
与HTV-2类似,乘波体非轴对称、扁平、大长细比的几何外形特点也决定了乘波体飞行器将面临类似的横航向稳定性问题。首先,侧滑对横向滚转力矩的影响不可忽略,同时大长细比外形使其横向转动惯量相比纵向和航向要小的多,因而在出现侧滑时会引起明显的横滚效应;第二,具有尖前缘特征的乘波体飞行器在高超声速飞行时同样可能出现由于气动烧蚀引起防热层脱落,进而诱导出激波引起附加的横航向气动力/力矩,乘波体下表面可能出现的非对称转捩会引发下游流动的不对称,形成横向的环流和横航向的非对称气动力[4],这些影响因素难以通过计算或实验进行评估,因而对飞行器本身的横航向稳定性提出了更苛刻的要求;第三,扁平的几何外形使得其由侧滑产生的侧向力较小,难以通过直接侧滑拐弯方式直接获得较大的侧向加速度,所以通常采用倾斜拐弯方式,也会面临横航向运动耦合问题[5];第四,飞行器在高超声速飞行时气动阻尼很小,横航向稳定性较低,容易发生失稳现象,由于飞行速度极快,即使平静、缓慢发展的耦合不稳定也可能演化成迅速发展的耦合不稳定,使飞行器产生强烈的不可控运动[6]。综上,横航向稳定性问题是高超声速乘波体飞行器设计过程中面临的一个严峻考验。
研究高超声速飞行器横航向耦合运动机理的最常用方法是对横航向小扰动线化模型进行简化,获得各个模态的近似表达式,进而分析影响各个模态的主要气动参数。已有文献[7-12]对飞行器在亚、跨、超声速的横航向模态进行了简化分析,但是高超声速飞行器所处的高空高马赫数飞行条件、大后掠气动布局特点以及惯量沿纵轴集中的质量分布特点,与传统飞行器有很大不同,因而无法通过传统结论来直接分析高超声速飞行器的横航向运动模态。例如,传统上认为荷兰滚模态仅包含偏航和侧滑运动,忽略滚转运动的物理量,即忽略与滚转角速度p和滚转角φ相关项,只保留与偏航角速度r和侧滑角β相关项。Phillips[13]通过推导指出,这种传统上忽略滚转运动的荷兰滚近似是滚转阻尼无穷大时的渐近解,实际上大多数情况滚转阻尼没有大到可以忽略荷兰滚模态中的滚转运动。在高超声速飞行条件下,滚转阻尼较小,滚转运动在荷兰滚模态中甚至起主导作用,传统的荷兰滚模态分析将得到明显错误的结论。针对上述问题,近年来已有少量文献对高超声速飞行时的横航向耦合模态机理进行了研究。
Heller和Breitsamter等[14-15]推导了高超声速飞行器HYTEX R-A3的模态近似表达式,分析了横航向模态随马赫数和质心的变化规律,并推导了滚转和螺旋模态耦合为横向长周期模态的条件,最后指出滚转阻尼小、荷兰滚不稳定和滚转-偏航耦合度高是导致高超声速飞行器面临飞行品质缺陷的主要原因。
Yin等[16]推导了荷兰滚模态中滚转角速度与偏航角速度振幅比值|p/r|的表达式,结果表明由于高超声速飞行器较大的飞行攻角和细长体的外形特征,该比值一般较大,使得传统荷兰滚阻尼比近似失效。同时由于|p/r|较大,因而他们忽略了r的相关项得到了荷兰滚阻尼比的近似表达式,结果表明其大小主要受滚转阻尼导数和横向静导数的影响。
从目前对高超声速飞行器横航向模态的少量研究来看,还存在几个方面的不足:1) 对荷兰滚模态频率的分析理论较为完善,但缺乏对荷兰滚阻尼有效而简洁的近似表达式,因而难以分析荷兰滚阻尼特性的主要影响因素;2) 已有研究大多数针对某一个而不是某一类飞行器来研究,结论缺乏普适性;3) 缺乏对高超声速乘波体类飞行器横航向耦合运动机理性研究。
针对上述问题,本文尝试对高超声速乘波体飞行器横航向耦合动稳定模态中最为复杂的荷兰滚模态特性进行研究。建立几何特征可参数化描述的乘波体模型,通过CFD定常/非定常气动力计算和代理模型获得整个样本设计空间内所有乘波体的静/动导数,结合横航向线化小扰动模型及模态简化,得到荷兰滚模态频率和阻尼特性随外形参数的变化规律及主要影响因素。
1 研究对象和计算方法 1.1 幂次乘波体乘波体是从已知流场中通过反设计方法获得的一种高升阻比飞行器。由于乘波体前缘线附着在激波面上,将波后高压气体限制在下表面,从而在小攻角下即可获得较高升力。通过幂次轴对称流场获得的幂次乘波体是一种容易设计成纵向静稳定的构型[17],因而本文以幂次乘波体为研究对象, 其外形由幂次曲线y=Cxn中的参数C和n决定,此处选用的外形参数为:C=1,n=0.7;设计马赫数选为15,绕幂次轴对称体的基准流场通过CFD求解Euler方程获得。
乘波体通常可通过前缘在底面的投影进行定义。在底面上定义一条前缘线的基准曲线,将该曲线沿自由来流方向在激波面上投影所获得的交线即为乘波体前缘线,对前缘线上的点进行流线追踪即可获得乘波体,生成过程如图 1所示。
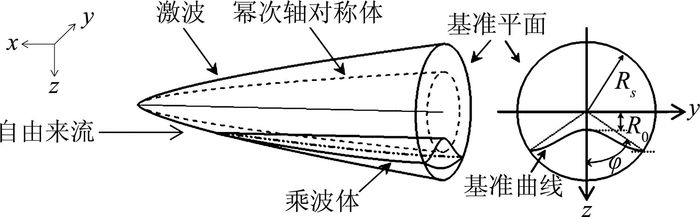
|
| 图 1 乘波体生成示意图 Fig. 1 Generation of waverider |
采用三次多项式定义基准曲线:
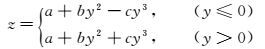
|
(1) |
令基准曲线与激波圆的交点处斜率为0,设激波圆半径为Rs,基准曲线纵截距绝对值为R0,方位角为φ,令参数kw= R0/Rs,化简可得:
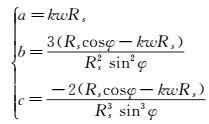
|
(2) |
选取距离幂次体顶点200m处的平面为基准面,则根据幂次曲线方程可确定Rs,然后给定设计参数kw和φ的值即可确定基准曲线方程,从而生成幂次乘波体。
1.2 数值模拟方法采用格心格式有限体积法求解RANS (Reynolds-Averaged Navier-Stokes)方程,空间离散采用AUSM+格式,时间离散采用隐式LU-SGS方法。在计算非定常气动力时,采用双时间法求解控制方程,对子迭代采用四阶龙格-库塔法进行推进,使用基于RBF内插的网格变形技术[18]。选用层流和完全气体模型,忽略真实气体效应的影响。
文献[19]采用上述计算方法获得了高空高马赫数条件下航天飞机“OV-102”的升阻比,并与试飞结果进行对比,表明了计算程序在强粘性干扰飞行条件下的可靠性;文献[20]对比了跨音速条件下NACA0012翼型的非定常气动力计算与实验结果,验证了求解器对非定常气动力计算的可靠性,此处不再赘述。
1.3 横航向耦合飞行力学模型本文通过求解线化横航向小扰动方程特征矩阵的特征根,来获得乘波体的开环横航向耦合动稳定模态特性[21]。在体轴系下的方程为:
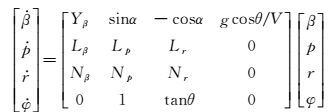
|
(3) |
其中Yβ=CyβqS/(mV),Lβ=ClβqSb/Ix,Nβ=CnβqSb/Iz,Li=CliqSb2/(2IxV),Ni=CniqSb2/(2IzV),i∈{p, r}。式中α、θ、β、p、r、φ分别表示攻角、俯仰角、侧滑角、滚转角速度、偏航角速度和滚转角;Y、L、N分别表示侧向力、滚转力矩和偏航力矩,Yβ、Lβ、Nβ为相应气动力对侧滑角的静导数;Lp、Np、Lr、Nr为相应气动力对相应角速度的动导数,此处不考虑航迹角,因而有α=θ。
静导数通过求解静态气动力即可获得,动导数采用简谐振荡法进行计算[22]。所有外形采用相同的质量(m=500kg)和惯量(Ix=75kg·m2,Iz=750kg·m2,忽略Ixz),乘波体长度L=4m,质心位置为(0.59L,-0.05L,0),其中坐标原点位于乘波体头部顶点处。研究的飞行工况为:Ma=15,H=50km。
1.4 代理模型由于需要研究乘波体横航向动稳定模态特性在一定设计参数空间内的分布,而对于每个点都通过CFD求得其相应的静/动导数是不现实的。为了解决该问题,采用Kriging代理模型,在求得采样点的静/动导数后,其他点通过代理模型插值获得相应的静/动导数。
表征乘波体外形的设计参数kw和φ的取值范围分别选为[0.3, 0.5],[35°, 55°]。为了提高插值精度,对于每个研究工况,采用全析因试验设计方法对kw和φ各取9个水平。通过CFD获得81个设计样本点的横航向静/动导数,设计空间内其它点通过代理模型插值获得。
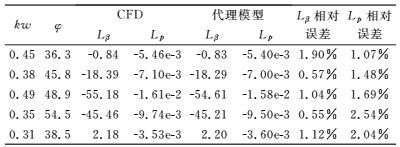
为了验证所构建代理模型计算静/动导数的精度,在设计空间随机选取五个样本点,通过CFD求解气动力获得静/动导数作为基准值,与通过代理模型获得的静/动导数进行对比。以零攻角的Lβ和Lp为例,相对误差如表 2所列,最大误差仅为2.54%。可见,由于训练样本点取得较密,构建的代理模型有着较高的精度。
2 横航向静稳定性
在获得横航向耦合模态特性分布之前,根据CFD计算和代理模型的结果,我们首先可以得到横航向静稳定性随参数的分布规律。
对无尾飞行器来说,影响横向静稳定性的主要几何特征为上反角和后掠角。由于乘波体外形的特殊性,无法按照常规飞机那样精确定义其上反角Γ和后掠角Λ,为此我们将其按图 2所示定义为:
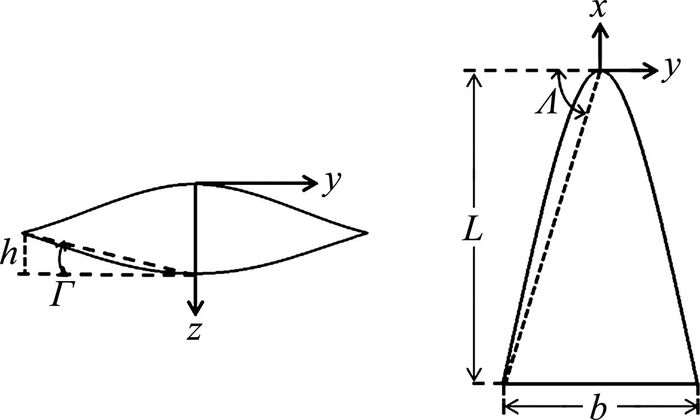
|
| 图 2 上反角和后掠角示意图 Fig. 2 Sketch of dihedral and sweep angle |
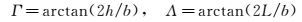
|
(4) |
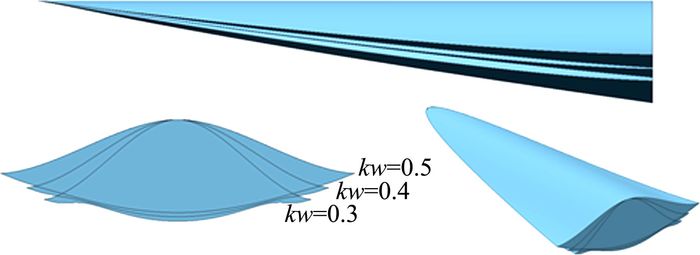
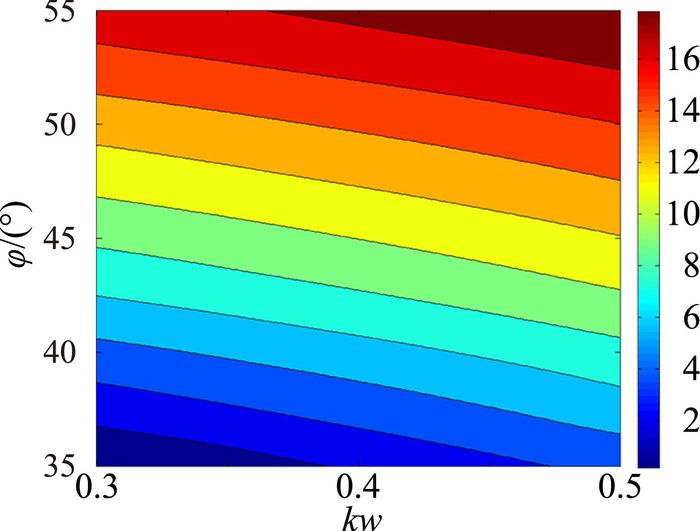
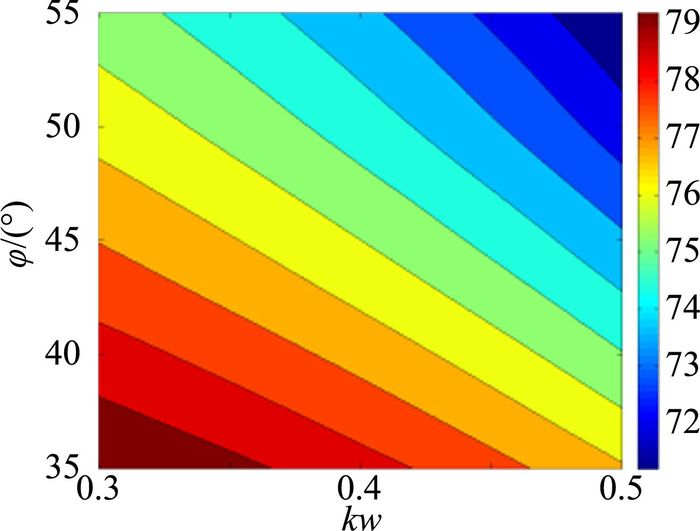
乘波体三维外形随kw和φ的变化特征如图 3和图 4所示,其上反角和后掠角分布如图 5和图 6所示。结合图 3~图 6可知,上反角随着kw和φ的增大而增大,后掠角随着kw和φ的增大而减小。
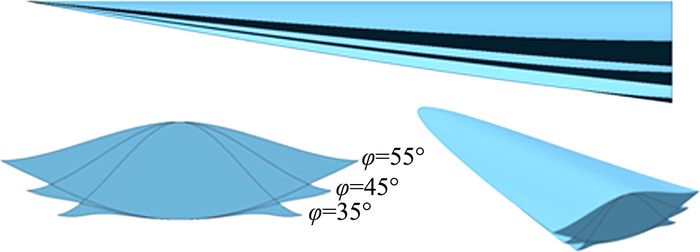
|
| 图 3 外形随φ变化示意图,kw=0.4 Fig. 3 Variation of shape with φ, kw=0.4 |
|
| 图 4 外形随kw变化示意图,φ=45° Fig. 4 Variation of shape with kw, φ=45° |
|
| 图 5 上反角分布 Fig. 5 Distribution of dihedral angle |
|
| 图 6 后掠角分布 Fig. 6 Distribution of sweep angle |
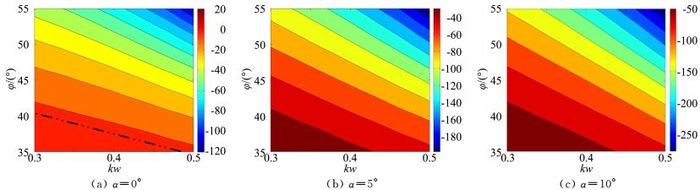
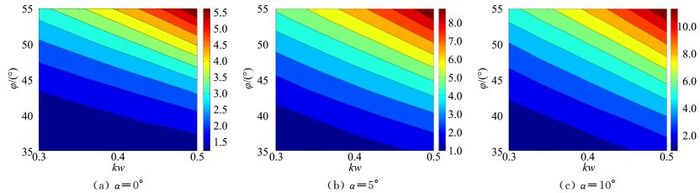
图 7和图 8分别给出了三个攻角的横航向静导数分布。可以看到在靠近参数空间区域的右上角,横向和航向静稳定性都较强,靠近左下角则较弱。
|
| 图 7 横向静导数Lβ分布 Fig. 7 Distribution of Lβ |
|
| 图 8 航向静导数Nβ分布 Fig. 8 Distribution of Nβ |
对于横向静稳定性来说,随着攻角的增加,稳定性都逐渐增强,且分布规律与上反角一致,其可能原因是乘波体本身后掠角已经很大,其随参数变化的相对变化幅度较小,因而影响横向静稳定性的主要几何特征为上反角;0°攻角时靠近左下角虚线以下区域Lβ>0,即横向静不稳定,其主要原因是上反角较小;增加攻角可以起到上反作用,因而随攻角增加横向静稳定性显著增强。
对于航向静稳定性来说,三个攻角所有区域都是静稳定的。在定常侧滑直线飞行时,偏航力矩主要取决于机身侧面积的大小以及航向压心与质心的距离。乘波体的下表面由流线追踪而成,上表面与自由来流平行,因此乘波体靠近尾部的侧面积比靠近头部的侧面积明显要大,其接近尾部的侧向力就大,只要质心位置不是过于靠后,是容易实现航向静稳定性的。
3 横航向耦合动稳定特性横航向耦合动稳定性一般可以由三个模态表征:螺旋模态、滚转模态和荷兰滚模态。其中荷兰滚模态是运动形式最复杂、控制难度最大的模态。目前对高超声速飞行器的横航向模态研究很少,且已有的研究一般在0°攻角下进行,不能考虑攻角的影响;同时对荷兰滚阻尼的近似较为复杂,不易分析影响阻尼特性的主要因素。因而,本文结合高超声速乘波体类飞行器静/动导数的特点,通过模态简化来获得荷兰滚模态特性随外形参数的分布规律及主要影响因素。
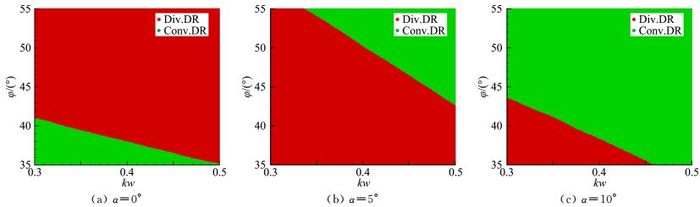
图 9所示为三个攻角荷兰滚模态的分布,红色区域表示模态发散,绿色区域表示模态收敛。可见,不同攻角下荷兰滚模态呈现出明显不同的发散/收敛特性。
|
| 图 9 荷兰滚模态分布 Fig. 9 Distribution of Dutch roll |
3.1 荷兰滚阻尼 3.1.1 模态简化
我们根据各个模态特征根的特点,对特征方程进行分解以获得各个模态特征根的近似表达式。将式(3) 中特征矩阵(用A表示)的特征方程展开可得:
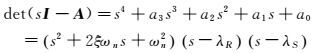
|
(5) |
其中:
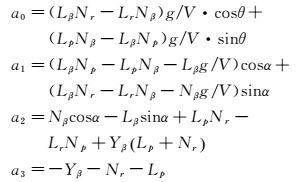
|
(6) |
式中ξ和ωn分别表示荷兰滚阻尼和无阻尼自振频率,λR和λS分别为滚转和螺旋模态特征根。
对于高超声速乘波体飞行器来说,荷兰滚模态特征根的虚部远大于其实部以及滚转与螺旋模态的实根大小,因而可以只保留特征方程的二阶及更低阶数项来获得滚转和螺旋模态的近似表达式,然后将式(5) 展开,根据对应项相等即可得
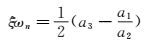
|
(7) |
进而可得荷兰滚实部η和虚部ω的表达式
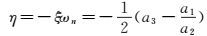
|
(8) |
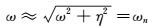
|
(9) |
荷兰滚实部表征荷兰滚的阻尼大小,通过式(8) 所求η几乎与精确值完全相等。但是,由于a1、a2和a3所包含的物理量较多,通过式(8) 仍然难以直观地获得定性的结论。因此,需要对a1、a2和a3进一步简化,以损失一定程度的精度为代价来获得更简洁的表达式,进而分析荷兰滚阻尼的主要影响因素。
以10°攻角时点(0.4, 45°)所对应的幂次乘波体为例,其静/动导数如表 3所列。
对于a1,
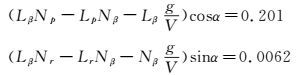
|
两项值的大小相差很大,忽略第二项,即:
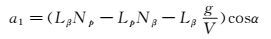
|
(10) |
对于a2,Lβ和Nβ远大于其他导数大小,因而可简化为:
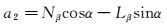
|
(11) |
对于a3,Yβ+Nr与Lp相差接近一个数量级,可做如下近似:
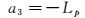
|
(12) |
根据上述简化,可得:
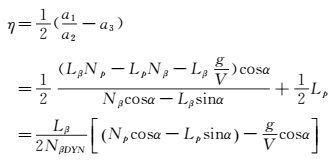
|
(13) |
其中
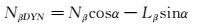
|
(14) |
NβDYN即为有量纲形式的荷兰滚静稳定性导数[23]。参考荷兰滚静稳定性导数的定义,此处定义一个荷兰滚动稳定性导数的概念——NpDYN,其表达式为:
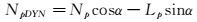
|
(15) |
则有
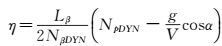
|
(16) |
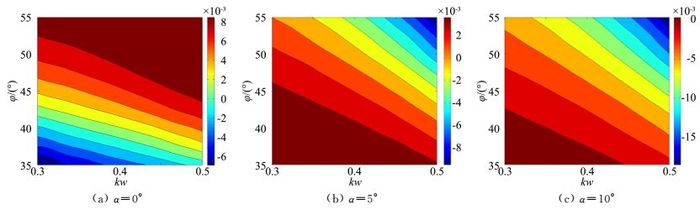
根据式(16) 得到的三个攻角下近似荷兰滚阻尼如图 10所示,根据特征根得到的精确荷兰滚阻尼如图 11所示。从图中可以看到,三个攻角下的荷兰滚阻尼近似解与精确解的分布趋势几乎完全一致,仅仅在定量上存在较小的误差,因而通过简化后的式(16) 可以较准确的对荷兰滚阻尼进行定性分析。
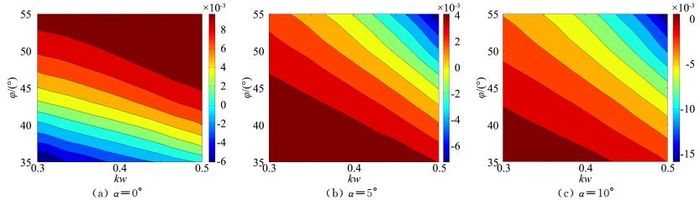
|
| 图 10 近似荷兰滚阻尼分布 Fig. 10 Distribution of approximate Dutch roll damping |
|
| 图 11 荷兰滚阻尼分布 Fig. 11 Distribution of the Dutch roll damping |
3.1.2 荷兰滚模态边界判断
通过式(16) 可以直接判断荷兰滚模态是否稳定,而对于具有横航向静稳定性的乘波体,荷兰滚模态收敛的近似条件可进一步简化为:
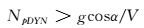
|
(17) |
荷兰滚模态边界如图 12所示。图中“DR”表示通过求解特征矩阵获得的与图 9对应的荷兰滚精确边界,“DR_Approx.”表示通过式(16) 得到的荷兰滚近似边界,“A”表示攻角。可见,每个攻角下的荷兰滚模态近似边界与精确边界都比较接近,表明通过式(16) 来近似判断荷兰滚模态的发散/收敛特性是可靠的。
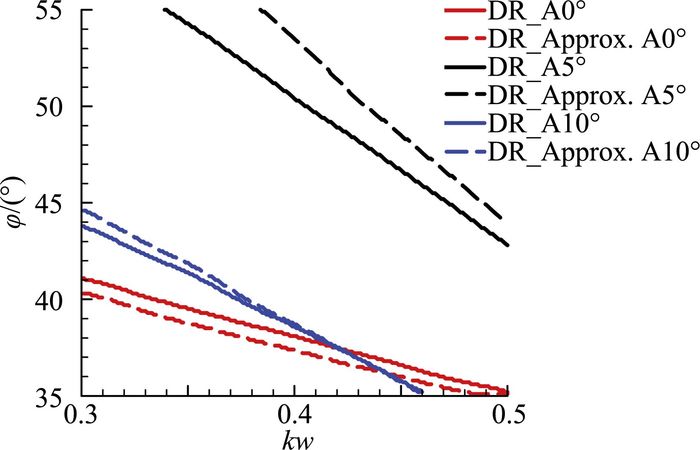
|
| 图 12 荷兰滚模态发散/收敛边界 Fig. 12 Boundaries of the Dutch roll mode |
接下来根据式(16) 来分析三个攻角荷兰滚模态发散/收敛的原因。荷兰滚动稳定性导数NpDYN在三个攻角下设计参数空间内的分布如图 13所示。对于Ma=15、H=50km的飞行工况,g/V=0.002。
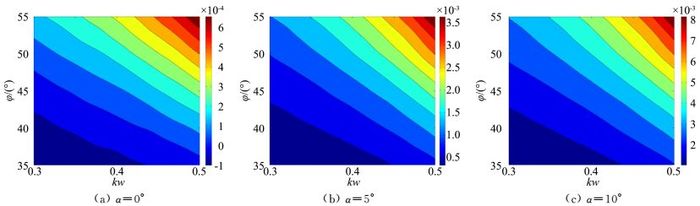
|
| 图 13 NpDYN分布 Fig. 13 Distribution of NpDYN |
当α=0°时,整个区域都有NpDYN<gcosα/V和NβDYN>0(因为Nβ>0),此时荷兰滚模态边界由Lβ的正负决定:当Lβ>0时,荷兰滚模态收敛;反之,荷兰滚模态发散。由图 7(a)可知,图中虚线左下角区域横向静不稳定,即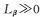
当α=5°时,整个区域横航向都是静稳定的,即Lβ/NβDYN<0。在靠近右上角的部分区域,NpDYN>gcosα/V,因而此区域荷兰滚模态收敛,其余区域荷兰滚模态发散。
当α=10°时,整个区域同样为横航向静稳定的,靠近左下角的小部分区域NpDYN较小,有NpDYN<gcosα/V,因而该区域荷兰滚模态发散,其余部分荷兰滚模态收敛。
3.1.3 荷兰滚阻尼分布规律对荷兰滚模态来说,当特征根实部为负且绝对值越大时,飞行器受扰后越能够快速地回复到平衡状态,荷兰滚阻尼特性越好,反之则越差。
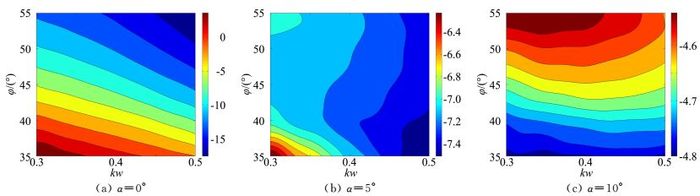
在0°攻角时,由图 13和图 14(Lβ/NβDYN在参数设计空间内的分布)可知,Lβ/NβDYN与NpDYN两项在整个参数空间内的变化范围都比较大,二者共同作用导致荷兰滚阻尼特性越靠近左下角越好,越靠近右上角越差,如图 11所示。
|
| 图 14 Lβ/NβDYN分布 Fig. 14 Distribution of Lβ/NβDYN |
在5°和10°攻角时,参数kw和φ越大,荷兰滚阻尼特性越好,而且每个点的阻尼也随攻角增大而增大,其原因可以通过式(16) 来解释。在两个攻角下,整个参数空间的Lβ/NβDYN的相对变化范围较小,阻尼特性的变化主要由NpDYN决定:参数kw和φ越大,NpDYN越大,荷兰滚阻尼特性越好;攻角越大,NpDYN越大,因而荷兰滚阻尼特性越好。
根据上述分析,对于高超声速乘波体飞行器来说,荷兰滚动稳定性导数NpDYN对荷兰滚模态的阻尼特性起着关键作用。在飞行器初步设计与控制律设计时,应着重考虑NpDYN的影响。
3.1.4 横航向耦合运动的CFD/RBD数值模拟采用计算流体动力学方程和刚体动力学方程(CFD/RBD)的耦合求解来模拟受扰后的横航向方程可参考文献[21],由于此处只针对横航向耦合运动进行数值模拟,因而不考虑与飞行器纵向运动相关的自由度,只考虑与横航向运动相关的自由度,即只保留绕x轴滚转、绕z轴偏航和沿y轴平动三个自由度上的位移和气动力。非定常计算的物理时间步长取0.0004s。
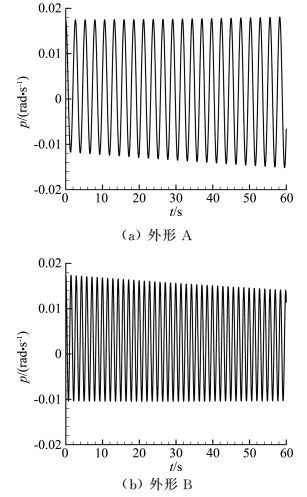
以10°攻角为例,选取两个典型外形,对应的(kw, φ)分别为:外形A (0.3, 35°),外形B (0.3, 50°)。根据图 9和图 12(c)可知,两个外形对应的荷兰滚模态分别为发散和收敛。两个外形受扰后的横航向耦合运动的CFD/RBD数值模拟结果(以滚转角速度p为例)如图 15所示。由于荷兰滚模态特征根实部很小,因而荷兰滚模态的发散或者收敛速度较为缓慢,但仍然可以看出外形A呈现出荷兰滚模态发散特性,而外形B呈现出荷兰滚模态收敛特性,与小扰动理论和判据式(17) 的结果相吻合。
|
| 图 15 CFD/RBD数值模拟结果,α=10° Fig. 15 Simulation results of CFD/RBD, α=10° |
3.2 荷兰滚频率
荷兰滚虚部ω表征荷兰滚频率,由于其值明显大于η、λR和λS,因而可忽略特征矩阵中的重力项和阻尼项,根据式(5) 可得:
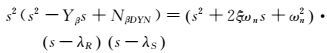
|
(18) |
此时两个零根对应滚转模态和螺旋模态[16],则根据对应项相等可得:
|
(19) |
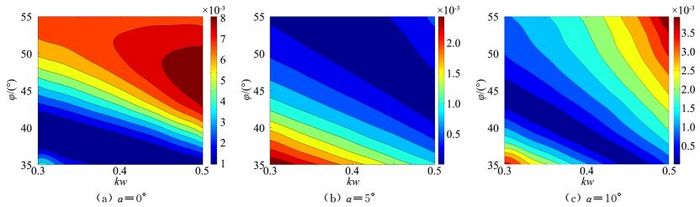
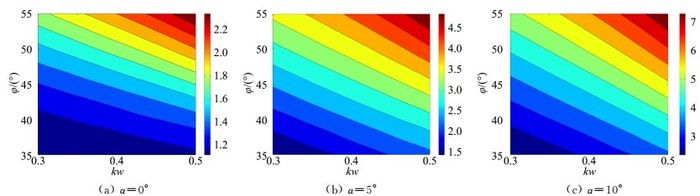
图 16所示为该式计算所得的荷兰滚频率相对误差,可见误差几乎为0。由此可知,荷兰滚频率特性由荷兰滚静稳定性导数NβDYN决定。荷兰滚频率和NβDYN分布分别如图 17和图 18所示。从图中可见,同一攻角下,kw和φ越大,荷兰滚频率越大;随攻角增大,每个参数点的荷兰滚频率也越大。因而,在飞行攻角较大时,乘波体会面临荷兰滚振荡速度较快的不利现象,需要在飞行器设计初期合理选择外形参数和适当的控制律设计来解决这一飞行品质问题。
|
| 图 16 荷兰滚频率误差(%) Fig. 16 Error of the Dutch roll frequency |
|
| 图 17 荷兰滚频率分布 Fig. 17 Distribution of the Dutch roll frequency |
|
| 图 18 NβDYN分布 Fig. 18 Distribution of NβDYN |
4 结论
横航向静/动稳定性分析是飞行器设计中的关键一步,本文引入参数kw和φ对幂次乘波体外形进行参数化处理,结合CFD计算和代理模型得到了三个攻角下横航向静稳定性和荷兰滚模态随参数的分布规律,主要内容和结论如下:
1) 乘波体横向静稳定性主要受上反角影响,随着设计参数kw和φ的增大,上反角变大,横向静稳定性增强;乘波体的外形特点使其容易设计成航向静稳定的。
2) 得到了三个攻角下的荷兰滚模态分布,不同攻角下呈现出明显不同的发散/收敛特性。
3) 推导了荷兰滚阻尼的近似表达式,定义了一个新的概念——荷兰滚动稳定性导数NpDYN。分析表明,NpDYN对荷兰滚阻尼随参数和攻角的变化规律起着主导作用;根据阻尼近似表达式,可以清晰地分析出荷兰滚模态发散/收敛的主要成因。
4) 荷兰滚静稳定性导数NβDYN对荷兰滚频率起决定性作用。设计参数kw和φ越大,荷兰滚频率越大;攻角越大,荷兰滚频率也越大,因而在较大攻角时会面临荷兰滚振荡较快的不利现象。
5) 在实际工程应用中,需要对原始乘波体进行局部修型以满足工程需求来获得最终的高超声速滑翔飞行器方案,但是经过合理得修型,对原有的乘波气动布局特征不会产生较大的影响。因而,本文关于荷兰滚阻尼和频率的研究结论对乘波布局高超声速滑翔飞行器的开环稳定性设计、评估及闭环控制律设计有一定参考价值。
| [1] | DARPA concludes review of falcon HTV-2 flight anomaly[OL]. http://www.darpa.mil/WorkAera/DownloadAsset.aspx?id=2147484134 |
| [2] | Engineering review board concludes review of HTV-2 second test flight[OL]. http://www.darpa.mil/NewsEvents/Releases/2012/04/20.aspx |
| [3] | Nonweiler T R F. Aerodynamic problems of manned space vehicles[J]. Journal of Royal Aeronautical Society, 1959, 63(585): 521–528. DOI:10.1017/S0368393100071662 |
| [4] |
Zhu L G, Wang Y F, Zhuang F G, et al. The derivation, development of weissman chart and applications on configuration design of reentry vehicle[J].
Journal of Astronautics, 2009, 30(1): 13–17.
(in Chinese) 祝立国, 王永丰, 庄逢甘, 等. Weissman图的产生、发展及其在再入航天飞行器气动布局设计中的应用[J]. 宇航学报, 2009, 30(1): 13–17. |
| [5] |
Gao Q, Li Q, Chen N, et al. The influence of asymmetric transition on stability of hypersonic aircrafts[J].
Tactical Missile Technology, 2012(6): 12–15.
(in Chinese) 高清, 李潜, 陈农, 等. 高超声速飞行器非对称转捩对稳定性的影响[J]. 战术导弹技术, 2012(6): 12–15. |
| [6] | 高 清, 李 潜. 美国高超声速飞行器横侧向稳定性研究[J]. 飞航导弹, 2012(12): 14–18. |
| [7] | Nelson R C. Flight stability and automatic control[M].New York: McGraw-Hill, 1990. |
| [8] | Livneh R. Improved literal approximation for lateral-directional dynamics of rigid aircraft[J]. Journal of Guidance, Control, and Dynamics, 1995, 18(4): 925–927. DOI:10.2514/3.56682 |
| [9] | Lutze F H, Durham W C, Mason W H. Unified development of lateral-directional departure criteria[J]. Journal of Guidance, Control, and Dynamics, 1996, 19(2): 489–493. DOI:10.2514/3.21644 |
| [10] | Schmidt L V. Introduction to aircraft flight dynamics[M].New York: AIAA Education Series, AIAA, 1998. |
| [11] | Chakravarty M K. Prediction, modeling, and mechanism of aircraft wing rock[D]. Indian Inst. Of Technology. Bombay, India, 1999. |
| [12] | Ananthkrishnan N, Unnikrishnan S. Literal approximations to aircraft dynamic modes[J]. Journal of Guidance, Control, and Dynamics, 2001, 24(6): 1196–1203. DOI:10.2514/2.4835 |
| [13] | Phillips W F. Improved closed form approximation for dutch roll[J]. Journal of Aircraft, 2000, 37(3): 484–490. DOI:10.2514/2.2623 |
| [14] | Heller M, Holzapfel F, Sachs G. Robust lateral control of hypersonic vehicles[R]. AIAA 2000-4248, 2000. |
| [15] | Breitsamter C, Cvrlje T, Laschka B, et al. Lateral-directional coupling and unsteady aerodynamic effects of hypersonic vehicles[J]. Journal of Spacecraft and Rockets, 2001, 38(2): 159–167. DOI:10.2514/2.3689 |
| [16] | Yin L L, Huang Y, Sun C Z, et al. Improved dutch roll approximation for hypersonic vehicle[J]. Sensors & Transducers, 2014, 173(6): 28–33. |
| [17] | 贾子安, 张陈安, 王柯穆, 等. 乘波布局高超声速飞行器纵向静稳定特性分析[J]. 中国科学:技术科学, 2014, 44(10): 1114–1122. |
| [18] | Boer A, Schoot M S, Faculty H B. Mesh deformation based on radial basis function interpolation[J]. Computers & Structures, 2007, 85: 784–795. |
| [19] | Liu W, Zhang C A, Han H Q, et al. Local piston theory with viscous correction and its application[J]. AIAA Journal, 2017, 55(3): 942–954. DOI:10.2514/1.J055207 |
| [20] | Kou J Q, Zhang W W. An approach to enhance the generalization capability of nonlinear aerodynamic reduced-order models[J]. Aerospace Science and Technology, 2015, 49: 197–208. |
| [21] | 方振平, 陈万春, 张曙光. 航空飞行器飞行动力学[M].北京: 北京航空航天大学出版社, 2005. |
| [22] |
Liu W. Nonlinear dynamics analysis for mechanism of slender wing rock and study of numerical simulation method[D]. National University of Defense Technology, 2004. 刘伟. 细长机翼摇滚机理的非线性动力学分析及数值模拟方法研究[D]. 国防科学技术大学, 2004. |
| [23] | Moul M T, Paulson J. Dynamic lateral behavior of high performance aircraft[R]. NACA RML58E16, 1958. |