乘波体设计是当前国际上高超声速飞行器气动布局研究的重点和热点之一。乘波体构型在设计状态将激波附着于下表面前缘,阻止了气流泄露,具有很高的升阻比。升阻比是反应高超声速飞行器气动特性非常重要的一个参数,升阻比很大程度上决定了高超声速飞行器能够实现哪一种飞行轨道。对于滑翔式和巡航式高超声速飞行器的气动设计,升阻比往往是非常重要的一个技术指标,因为升阻比直接关系到飞行器能够达到的航程、横向机动能力等关键战技术指标。因此,乘波体往往被选择为高超声速飞行器气动布局的基础构型。
乘波体的设计要素包括两点:带激波的流场与沿流线追踪生成型面。本文定义生成激波流场的外形为“导波体”,与在流场中追踪流线得到的外形“乘波体”相对应。传统的乘波体设计方法均可以据此定义导波体,例如楔形流场乘波体[1]的导波体为二维楔形,锥导乘波体[2-3]对应圆锥,密切锥方法[4-5]的流场是由已知激波形状反推得到,基准流场为锥形流,导波体也可以认为是锥体的一种。基准流场对乘波体的性能有着根本性的影响,选择导波体就是选择基准流场,是乘波体设计过程的重要环节,也是保证乘波体满足气动、装载等设计要求的基础。
圆锥的激波流场一般通过求解Taylor-Maccoll方程数值[6],在乘波体设计中应用较多,但这也限制了导波体的选择范围,设计空间不大,同时流场模拟不够准确[7]。为了规避传统乘波体设计方法的局限性,相关学者提出使用三维流场进行乘波体设计[8-9]。求解三维流场时,激波曲面的准确分辨是一个难题,Marcu使用激波捕捉法计算了圆锥流场,并沿流线根据压力梯度确定激波位置,这一方法计算量较大,激波曲面的光滑性难以保证,推广到复杂外形存在困难。激波装配法[10]可以准确定位激波曲面,为寻找性能更优的流场进行乘波体设计提供了良好的工具。前期工作中笔者使用三维流线追踪技术[11],探索了三维流场乘波体快速设计方法,在扩大设计空间方面具有优势。
在三维流场乘波体设计中,随着设计空间的扩大,合理选择流场变得越来越重要。如果能找到乘波体与导波体外形间的对应关系,就可以先根据乘波体的要求寻找导波体,再用所得的导波体设计外形,从而提高乘波体设计的灵活性。本文使用激波装配法计算带激波的流场,固定流线追踪(FCT,Flow Capture Tube)初始线为水平直线,投影到激波作为流线追踪的起始点,即“平切”激波,正向追踪流线生成乘波体外形。研究几类导波体生成乘波体的算例,指出乘波体与导波体之间存在一定程度上的对应关系,可作为未来设计中导波体外形选择的参考依据。
1 激波装配法带激波的超声速流场通常采用激波捕捉法数值求解。激波捕捉法无需将激波作为未知边界进行求解,因此所得到的激波边界实际上是一个流动量连续急剧变化的狭小区域,给激波的分辨带来了困难,难以用于乘波体设计。
与激波捕捉法不同,激波装配法则将流场的外激波作为未知外边界同流场一起求解(图 1)。为此引入三维非定常激波的求解方程,包括Rankine-Hugoniot激波关系式及描述激波边界处特征波传播特性的特征相容关系式。将上述方程联立数值求解,可求得波后流动量及激波速度。由于外激波边界在求解过程中是移动的,因此求解过程需在动网格中进行。当方程解收敛时,激波速度趋近于零,非定常激波收敛为定常激波,即得到流场外激波的准确外形,所得激波面可直接用于乘波体设计。
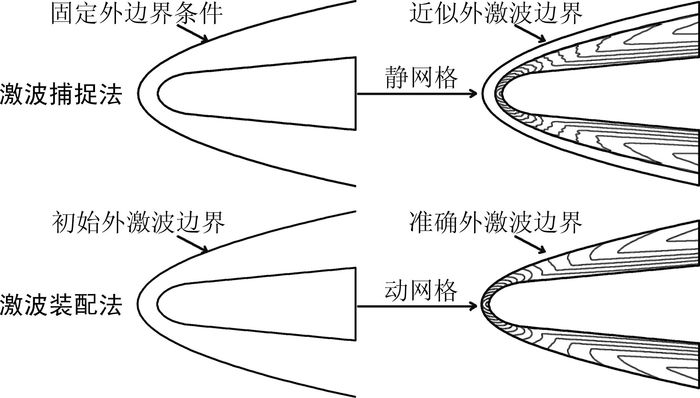
|
| 图 1 激波捕捉法及装配法比较 Fig. 1 Comparison between shock-capturing method and shock-fitting method |
采用超声速Euler方程激波装配法数值计算程序求解导波体激波及流场。选择文献[12]所给物形作为测试算例,其中Ma=6,α=15°, 图 2为计算得到的激波,图 3和图 4分别为激波位置rs和激波斜率rsx与文献[12]数据的比较,可以看出两者非常吻合。
|
| 图 2 激波外形计算结果 Fig. 2 Shock simulation results using shock-fitting method |
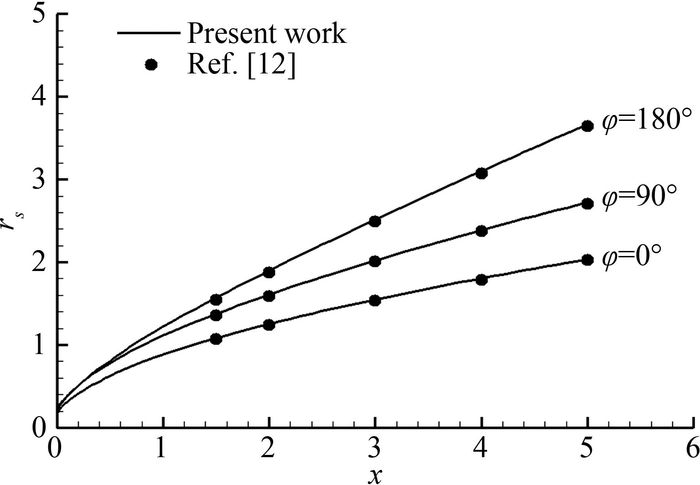
|
| 图 3 激波位置计算结果比较 Fig. 3 Comparison of shock locations |
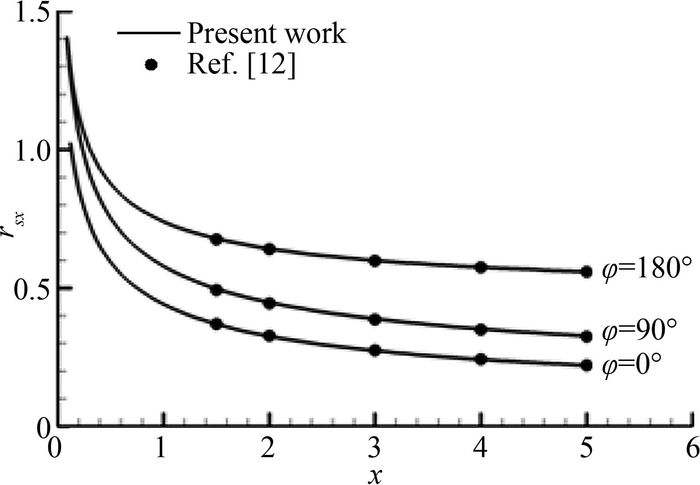
|
| 图 4 激波斜率计算结果比较 Fig. 4 Comparison of shock wave slope |
2 导波体 2.1 外形基本特征描述方法
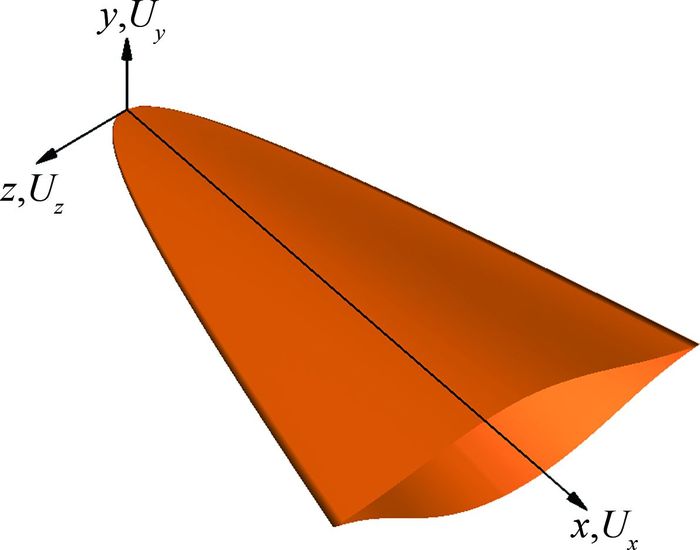
在描述乘波体和导波体外形时采用如图 5所示的坐标系,其中Ux、Uy、Uz表示流场速度分量。
|
| 图 5 坐标系定义 Fig. 5 Definition of coordinate system |
在此坐标系下,乘波体和导波体由三个坐标面上的外形描述:1) xy方向上描述纵向截面外形;2) yz方向对应横截面外形;3) xz方向描述前缘外形。
固定流线追踪初始线时,决定乘波体外形基本特征的因素包括:纵向截面外形与导波体流场速度Uy/Ux沿纵向(x向)分布特性相关;横截面与Uy/Ux、Uz/Ux沿展向(z向)的分布特性相关;前缘外形及长宽比与激波形状和流线追踪初始线切割激波的位置等因素相关。因此乘波体外形的基本特征可以通过改变导波体的激波外形及速度分布得到。
下面给出两类可改变激波外形及流场速度沿纵向及展向分布的导波体——锥形导波体和双锥导波体,作为重点研究对象。
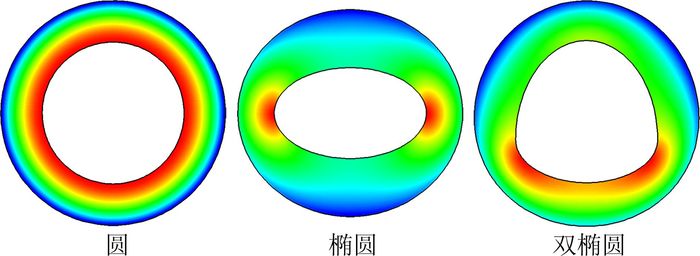
2.2 锥形导波体锥形导波体的外形为尖头,母线为直线,横截面可为任意外形。图 6给出了几种典型的横截面形状,其中截面为圆的外形即为锥导乘波体中的圆形尖锥导波体。
|
| 图 6 锥形导波体的横截面外形 Fig. 6 Cross sections of conical SGBs |
锥形流的流场特性与长度无关,即沿纵向分布的各横截面具有相同的流场特性。改变横截面外形,可以改变锥形导波体流场的速度Uy/Ux和Uz/Ux沿z向的分布特性,进而改变乘波体的横截面外形。
2.3 双锥导波体双锥导波体的外形特征是尖头锥形前体、后接扩张或收缩的后锥体,横截面为任意外形。过前体的流场为锥形流场,当后体收缩时,存在沿纵向传播的膨胀波,后体扩张时,存在激波。
通过后体出现的膨胀波或激波,可以改变流场速度Uy/Ux、Uz/Ux沿纵向的分布特性,从而改变乘波体纵向截面外形;俯视外形前后锥体的长度、角度决定激波外形,进而决定乘波体的前缘外形;改变横截面外形,可以改变流场速度沿展向的分布特性,从而改变乘波体横截面外形。
3 乘波体与导波体外形对应关系 3.1 纵向截面外形对应关系分析乘波体外形通过追踪流线生成,纵向截面流场对于乘波体性能影响很大,目前常用的锥导乘波体等使用圆锥流动,流场分布较简单,不存在激波膨胀波等现象,但也限制了设计空间。而增加波系则可以使外形具有更好的特性,比如吕侦军等[13]提出了多级压缩锥导乘波体的概念,使用多波系充分发挥前体的预压缩作用,为进气道的正常工作提供均匀流场。本文使用准确的三维流场进行设计,可以方便地构造流场内激波或膨胀波,提高了设计灵活性及精度。
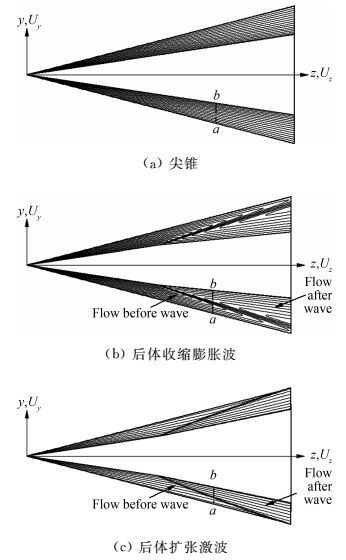
3.1.1 流场内波系对速度分布的影响导波体流场内存在激波或膨胀波时,由于波前波后速度的明显变化,流线穿过这些波时走向会发生明显改变。分析三个典型外形:尖锥、后体收缩的双锥、后体扩张的双锥,考察波系对速度的分布。
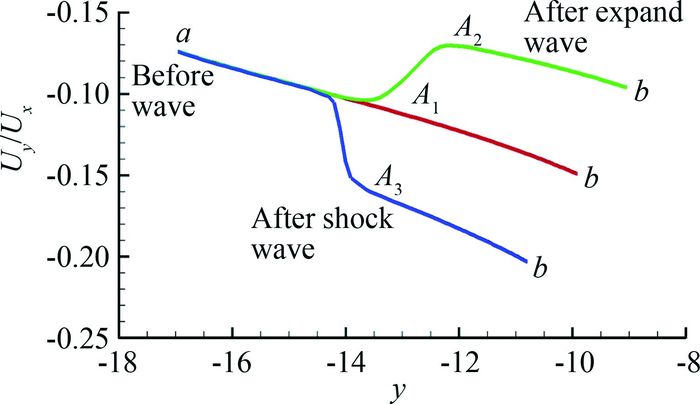
图 7给出了尖锥和后体收缩、扩张的双锥导波体流场内Uy/Ux的分布特性。图 8给出了取定导波体流场内的同一位置截面ab,查看速度分布的特性。可以看到收缩后体产生膨胀波,波后Ux大于波前值,而Uy小于波前值,因此膨胀波波后Uy/Ux小于波前值;扩张双锥内存在激波,激波波后速度分布与膨胀波相反,Uy/Ux大于波前值。
|
| 图 7 双锥导波体流场的Uy/Ux分布特性 Fig. 7 Uy/Ux distribution characteristics of double-conical flow |
|
| 图 8 双锥导波体流场ab截面的Uy/Ux分布特性 Fig. 8 Uy/Ux distribution characteristics at ab cross section |
根据波前波后速度分布Uy/Ux的变化特性,流线穿过内膨胀波及内激波的趋势可以大体确定,如果双锥导波体后体收缩,所生成的乘波体边界后段也向上收缩;双锥导波体后体扩张,所生成的乘波体边界后段也向下扩张。
3.1.2 具体算例分析考虑三个导波体生成流场进行乘波体设计,设计状态为Ma=6,攻角α=0°,其中外形1为8.5°半锥角的尖锥外形;外形2为后体收缩的双锥外形(10°半锥角转7°);外形3为后体扩张的双锥外形(7°半锥角转10°)。横截面均为圆,图 9所示为三个导波体外形流场的Uy/Ux云图。
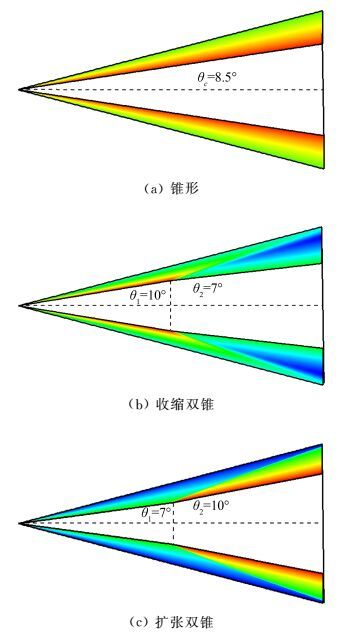
|
| 图 9 导波体外形的流场速度Uy/Ux云图 Fig. 9 Velocity Uy/Ux contour of SGB flowfield |
构造乘波体外形,下表面使用追踪流线得到,上表面则考虑扩充容积设计[14],截面形状用三次函数表示,形状为“凸”。在不同乘波体的构造过程中保持长宽比不变,得到的乘波体外形为W1、W2和W3,对应于图 9中的导波体外形1、2和3,其纵向截面、横截面及前缘外形的比较如图 10所示。可见三个乘波体的前缘外形和横截面外形均相差不大,主要区别是在纵向截面外形。
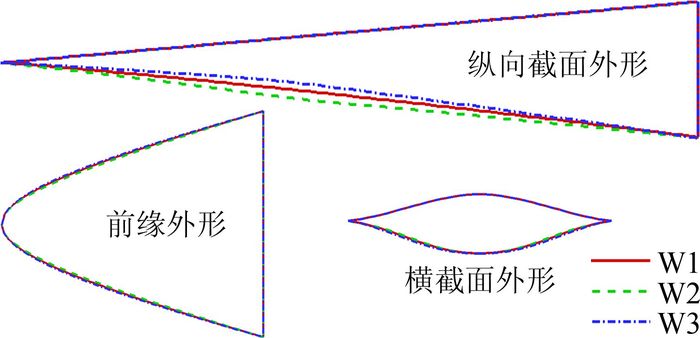
|
| 图 10 乘波体W1、W2和W3外形特征比较 Fig. 10 Configurations of W1, W2 and W3 |
使用CFD方法计算乘波体的流场,图 11给出了三个乘波体外形纵向截面和迎风面表面的压力分布云图。三个外形的压力分布差别很大:W1的压力分布比较均匀;W2由于膨胀波的影响后体表面压力明显低于前体;W3则由于激波的影响后体表面压力明显高于前体。这种不同的压力分布特性对乘波体的纵向稳定特性有着显著的影响。
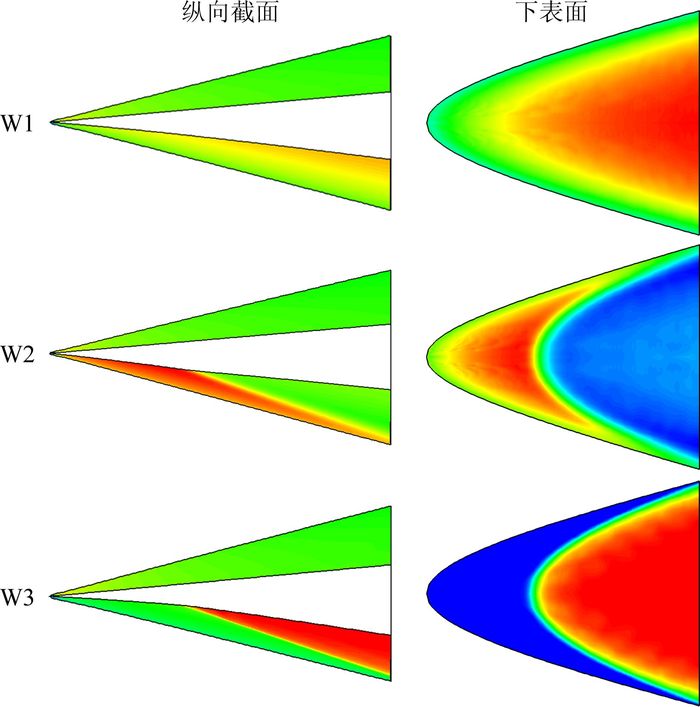
|
| 图 11 乘波体压力云图对比 Fig. 11 Pressure contour of the waveriders |
图 12给出了三个乘波体的升阻及纵向压心特性,即升力CL·S (CL为升力系数,S为参考面积),升阻比L/D和纵向压心系数Xcp的比较。由图 11给出的乘波体迎面压力云图可以看出,内激波的存在导致W3的迎风面高压区较大,迎风面压力高于W1,而膨胀波流场得到的外形迎风面压力低于W1,因此W3的升力最大,W2升力最小。与升力特性相对应,在设计点(α=0°)附近,W3的L/D最大而W2最小,但是随着攻角增大,W3的阻力迅速增加,导致其升阻比低于W1和W2。此外,由于W3迎风面高压区集中在后部,导致压心靠后,W2迎风面低压区集中在后部,导致压心靠前。
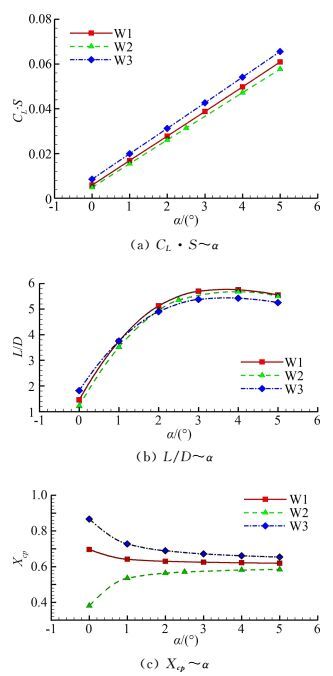
|
| 图 12 乘波体气动性能比较 Fig. 12 Aerodynamic properties via angle-of-attack |
上述分析可知,双锥体在后体产生的激波或膨胀波能有效地改变导波体流场内速度沿纵向分布的特性,利用该特性可以设计不同纵向截面外形的乘波体,从而实现在俯视平面形状受约束的情况下对乘波体构型纵向稳定性的按需设计,而这种乘波体性能设计的灵活性正是常规乘波体设计方法所难以提供的。
本节算例导波体采用了双锥轴对称外形,实际应用中只要求物形在纵向截面的迎风面存在收缩或扩张即可。
3.2 横截面外形对应关系分析乘波体的横截面外形与导波体流场内速度Uy/Ux、Uz/Ux沿展向的分布特性有关,此速度特性可由导波体外形的横截面确定。分析三个导波体外形:尖锥A0、双椭圆锥D1、双椭圆锥D2,如图 13所示,这三个导波体外形的纵向截面外形完全一致,横截面不同——A0横截面为圆,D1和D2横截面为两个椭圆的组合,D2的下部份外形(迎风面)比D1分布较为平坦。
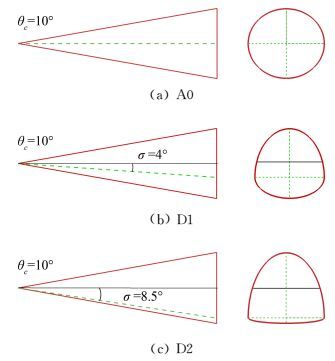
|
| 图 13 双椭圆锥导波体与尖锥导波体 Fig. 13 Double elliptical cone SGB |
图 14给出了导波体A0、D1和D2的横截面比较,并给出了迎风面处沿cd位置流场速度Uy/Ux、Uz/Ux沿展向分布的比较。导波体在相同迎风面锥角条件下,横截面迎风面越平,Uy/Ux的负值越大,而且在整个cd段都保持这一特性。Uz/Ux的分布特性有所不同,在cd前段,随着导波体迎风面逐渐变平,Uz/Ux逐渐变小,而在cd后端,Uz/Ux快速增大。上述特性导致乘波体横截面外形及气动特性差别明显。
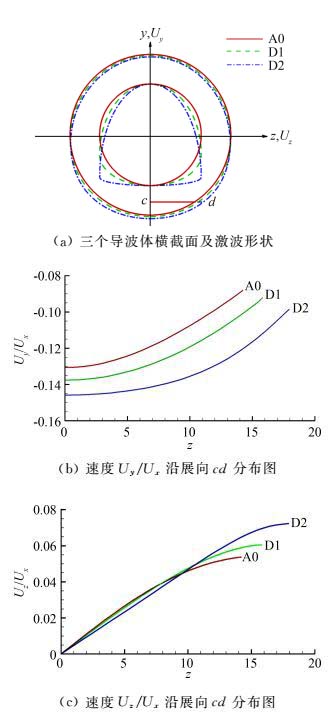
|
| 图 14 导波体流场的横截面速度分布 Fig. 14 Velocity on cross section of different SGBs |
在要求长宽比相同的条件下,由导波体A0、D1和D2生成的乘波体W-A0、W-D1和W-D2的外形如图 15所示。三个乘波体的纵向截面外形和前缘外形基本不变,区别主要在横截面外形。由前面给出的速度沿展向分布特性可以得出,导波体迎风面越平,生成的乘波体越平,内侧厚度越大,而展向外缘则较薄。这种横截面特征的对应关系可以在对乘波体外形的迎风面进行扩容设计时获得应用。
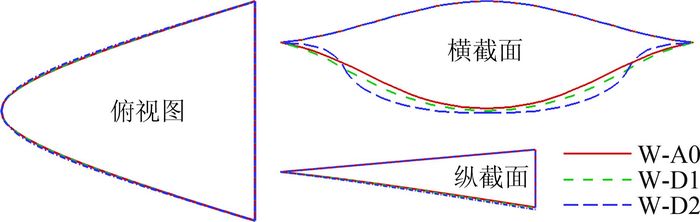
|
| 图 15 乘波体三视图比较 Fig. 15 Waverider configurations with different cross section profiles |
3.3 前缘外形对应关系分析
乘波体前缘由导波体流场的激波曲面决定,由于锥形流导波体的激波外形为锥形或近似锥形,采用FCT为直线平切激波曲面时,其生成的乘波体前缘形状一般为近似抛物线,如图 16所示。
|
| 图 16 典型类锥导流场生成的乘波体外形 Fig. 16 Conical flow waverider |
而我们扩大设计空间,则可以得到前缘线具有特殊性质的乘波体外形,比如双后掠外形等,这为我们改善乘波体低速阶段的性能缺陷提供了一种新的思路。如果需要得到双后掠外形的乘波体,则需采用俯视图为双前缘的导波体。如图 17所示的两个导波体外形,Y1横截面为双椭圆,Y2为椭圆,纵向截面外形均为锥形,锥角为8°;俯视平面外形均为后体扩张的双锥,锥角分别为7°和18°。
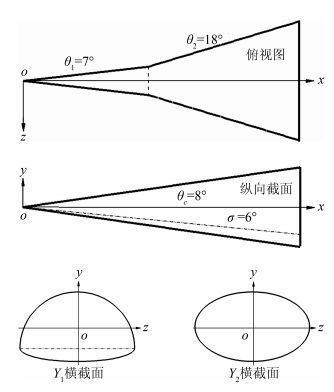
|
| 图 17 双前缘导波体外形 Fig. 17 Double swept conical SGB |
从图 18看到,导波体Y1、Y2的激波的俯视图为扩张的双前缘形状,可生成前缘为双后掠的乘波体外形,同时由于Y1、Y2的横截面不同,生成的乘波体WY1的横截面比WY2更平(图 19所示)。
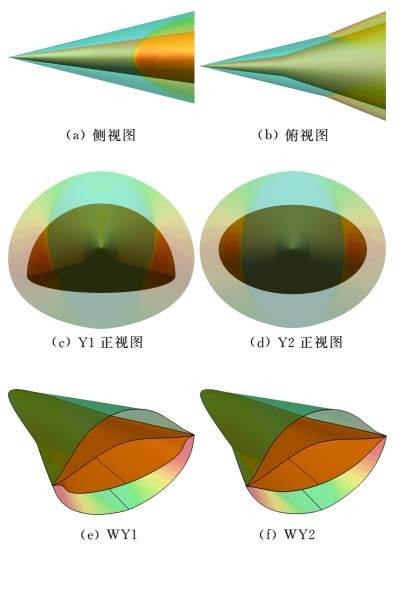
|
| 图 18 双锥导波体激波流场及乘波体外形 Fig. 18 Shock wave from double conical SGBs |
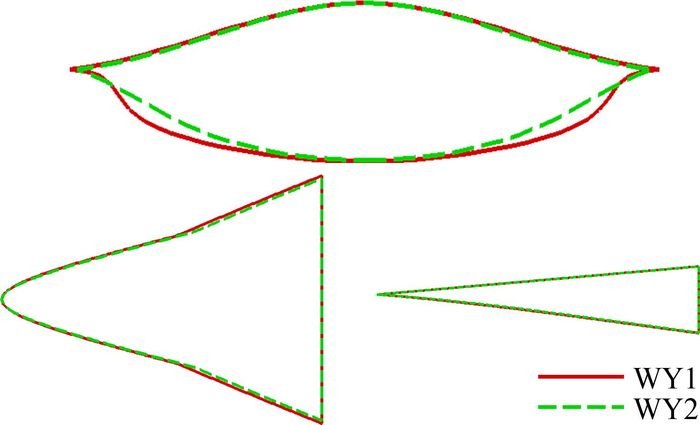
|
| 图 19 双后掠乘波体外形 Fig. 19 Views of the double swept waverider |
图 20为乘波体WY1和WY2气动特性的比较。与其他乘波体类似,升力呈线性增长,升阻比在α=4°左右取得最大,同时压心靠后,并随攻角增大压心逐步前移。虽然WY1和WY2的纵向对称面外形及前缘外形相差不大,但由于WY1横截面下表面更平,横截面积比WY2大,导致两者气动特性不同。
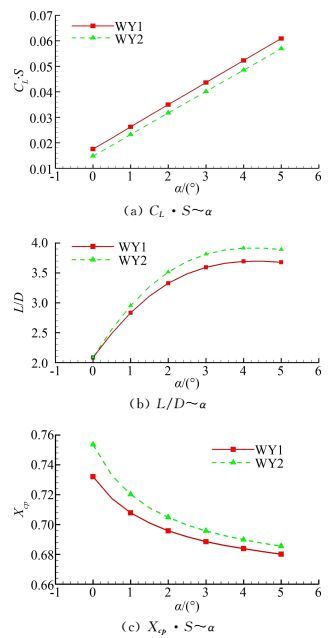
|
| 图 20 双后掠乘波体气动特性对比 Fig. 20 Aerodynamic performances of the double swept waverider |
4 结论
通过引入激波装配法建立了普适于一般三维流场的乘波体设计方法,突破了导波体外形的限制。采用平切导波体激波及正向跟踪流线生成乘波体,通过锥形流导波体和双锥导波体生成乘波体的算例分析了导波体与乘波体在纵向截面外形、横截面外形、前缘外形方面的对应关系。分析表明,双锥体在后体产生的激波或膨胀波能有效地改变导波体速度沿纵向分布特性,利用该特性可实现在俯视平面形状受约束的情况下对乘波体构型纵向稳定性的按需设计;通过改变导波体横截面外形,可以改变速度沿展向的分布特性,从而实现乘波体横截面外形改变;乘波体前缘外形主要与导波体激波在俯视面上的外形相关,通过后体扩张的双锥外形能够生成双前缘乘波体外形。
| [1] | Nonweiler T R. Aerodynamic problem of manned space vehicles[J]. Journal of the Royal Aeronautical Society, 1959, 63: 521–530. DOI:10.1017/S0368393100071662 |
| [2] | Rasmussen M L. Waverider configurations derived from inclined circular and elliptic cones[J]. Journal of Spacecraft and Rockets, 1980, 17(6): 537–545. DOI:10.2514/3.57771 |
| [3] | Jones J G, Moore K C, Pike J, et al. A method for designing lifting configurations for high supersonic speeds using axisymmetric flow field[J]. Archive of Applied Mechanics, 1968, 37(1): 56–72. |
| [4] | Center K, Sobieczky H, Dougherty F. Interactive design of hypersonic waverider geometries[R]. AIAA 1991-1697, 1991. |
| [5] | Sobieczky H, Dougherty F C, Jones K. Hypersonic waverider design from given shock wave[C]//The First International Waverider Symposium. Maryland: University of Maryland, 1990. |
| [6] | Anderson J D. Fundamentals of aerodynamics[M].3rd edition. McGraw-Hill Companies, 2001. |
| [7] | Mark J L, Maire L C. Shock-based waverider design with pressure gradient corrections and computational simulations[J]. Journal of Aircraft, 2005, 42(5): 1350–1352. DOI:10.2514/1.13027 |
| [8] | Marcu A. L, Kojiro S. Experimental investigation of a Mach 3.5 waverider designed using computational fluid dynamics[J]. AIAA Journal, 2015, 53(6): 1590–1601. DOI:10.2514/1.J053458 |
| [9] |
Le G G, Ma D W, Li Z Y. Computation of hypersonic flowfields for elliptic-cone-derived waverider[J].
Journal of Nanjing University of Science and Technology(Natural Science), 2006, 30(3): 257–260.
(in Chinese) 乐贵高, 马大为, 李自勇. 椭圆锥乘波体高超声速流场数值计算[J]. 南京理工大学学报(自然科学版), 2006, 30(3): 257–260. |
| [10] | Moretti G. Thirty-six years of shock fitting method[J]. Computers & Fluids, 2002, 31: 719–723. |
| [11] |
Liu C Z, Bai P, Chen BY, et al. Rapid design and optimization of waverider from 3D flow[J].
Journal of Astronautics, 2016, 37(5): 535–543.
(in Chinese) 刘传振, 白鹏, 陈冰雁, 等. 三维流场乘波体快速设计方法及多目标优化[J]. 宇航学报, 2016, 37(5): 535–543. |
| [12] | Любимов А Н, Русанов В В. Течения газа около тупых тел[M].НАУКА. МОСКВА, 1970. |
| [13] |
Lyu Z J, Wang J F, Wu Y Z, et al. Design and analysis of multistage compression cone-derived waverider configuration[J].
Journal of Astronautics, 2015, 36(5): 518–523.
(in Chinese) 吕侦军, 王江峰, 伍贻兆, 等. 多级压缩锥导乘波体设计与分析[J]. 宇航学报, 2015, 36(5): 518–523. |
| [14] | Bowcutt K G. Optimization of hypersonic waveriders derived from cone flows including viscous effects[D]. University of Maryland, 1986. |



