2. 中国空气动力研究与发展中心 计算空气动力研究所, 四川 绵阳 621000;
3. 中国空气动力研究与发展中心 低速空气动力研究所, 四川 绵阳 621000
2. Computational Aerodynamics Instatitiute of China Aerodynamics Research & Development Center, Mianyang 621000, China;
3. Low Speed Aerodynamics Institute of China Aerodynamics Research & Development Center, Mianyang 621000, China
边界层转捩通常是指边界层流动由层流状态发展为湍流状态的过程,是一个多因素耦合影响的强非线性复杂流动物理现象。转捩问题是经典力学遗留的少数基础科学问题之一,与湍流问题一起被称为“百年(或世纪)难题”。边界层转捩在工业部门具有广泛的应用背景,这主要是因为层流流动和湍流流动在摩擦阻力、噪声、热交换和掺混等方面有巨大差别,比如湍流摩阻和热流通常是层流的3-5倍[1],且随着马赫数增加,热流增加量更为可观。转捩对飞行器设计的影响是多方面的,可带来有利影响和不利影响[2]。有利的一面是,湍流有利于克服流动分离,能够增强流体掺混,因而能够用来提高燃烧效率,提高发动机性能。例如超燃冲压发动机入口前添加转捩装置可以促进流动从层流转捩成湍流,进而提高发动机效率、防止发动机不启动。转捩的不利影响包括引起摩阻增加,产生气动光学效应,降低飞行器稳定性(比如横侧稳定性[3-5]),引起热流成倍增加等。因此,开展转捩机理以及转捩预测与控制等方面的研究,不仅对飞行器、发动机、舰艇等设计具有重大工程实际意义,同时也有十分重要的学术意义。
航空航天工程对转捩预测的需求十分迫切,不幸的是这一直是CFD的巨大缺陷[6]。在美国“CFD远景2030”中,转捩被列为第一类急需解决的物理模型问题[7]。2009年3月,NASA成立了三个高超研究中心,其中一个即为“国家高超声速层流/湍流转捩研究中心”[8]。高超声速飞行器的飞行雷诺数范围正好容易出现边界层转捩[9-10],比如美国X-33在飞行马赫数6~18时,基于飞行器长度的雷诺数范围为2.5×106~1.3×107,刚好处于自然转捩和粗糙壁转捩的参数范围内。在X-33返回地面过程中,随着高度和速度降低、大气密度增加等,边界层流动会经历转捩、层流化和再次转捩的过程[11]。与转捩有关的研究虽然不少,但是目前还没有能在较广飞行条件下精确预测转捩的半经验关系式或模型[9]。这严重制约了先进可重复使用高速飞行器、高速导弹、再入航天器等的研制。
高超声速边界层转捩研究伴随高超声速的概念自20世纪50年代就已经开始,并且取得了一系列研究成果。关于这些研究成果,国内外有不少文献进行了综述。周恒等[12]在其专著中详细介绍了转捩问题起源、转捩机理、转捩预测eN方法、抛物化稳定性方程(PSE)及应用、感受性问题等。周恒[13]还分析了国外流行的转捩预测方法及湍流计算模型中存在的问题,介绍了一些改进方法。罗纪生[14]在其综述中描述了边界层转捩的基本过程,介绍了可压缩边界层不同于不可压缩边界层的失稳特征、转捩机理与感受性特征以及高超声速三维边界层中预测转捩的常用方法,并着重介绍了可用于工程实际的eN方法以及对eN方法的改进,同时列举了在高超声速三维边界层中应用eN方法预测转捩的多个实例,最后分析并总结了高超声速边界层转捩预测所存在的困难及需要解决的问题。解少飞等[15]从扰动波演化的角度回顾了高超声速边界层感受性、线性稳定性和非线性作用的国内若干研究进展,并介绍了他们在转捩机理和转捩控制方面的研究成果。近些年,越来越多的研究人员采用直接数值模拟方法研究转捩,详见周恒等[12]和傅德薰等[16]的专著。本文侧重介绍高超声速边界层转捩认知概况,转捩机理、预测与控制研究,以及飞行试验等方面的最新研究进展,所述内容尽可能不与已有的专著和综述文献重复,侧重介绍他们未涉及或未详细介绍的内容。
1 国外投入情况在基础研究方面,美欧日等都启动了多个大型基础研究计划。美国国家高超声速基础研究计划(NHFRP)[17]由NASA和桑迪亚(Sandia)国家实验室发起,边界层转捩物理机理是6项研究内容之一,其2020-2030中长期规划更将高超声速边界层转捩列为首要研究对象。美国还通过STAR(STablilty Analysis for Reentry[17])项目使转捩基础研究成果向工程应用成果转化,以支持HTV-2、X43和X-51等大型高超声速工程项目。美国普渡大学的马赫6静音风洞(也译成静风洞)[18]专门为边界层转捩研究设计,配备了高灵敏度高频响压力脉动传感器、高精度热流传感器、红外热图测量仪等先进配套测试技术与仪器,开展了大量转捩基础研究。欧洲针对未来高超声速概念飞行器和高超声速双模态发动机等也开展了大量转捩研究工作。日本也不甘落后,近年来,日本JAXA和NASA联合开展了阿波罗返回舱转捩试验研究,他们在高焓风洞中发现高焓情况下转捩带的控制效率较低[19]。
与高超声速转捩有关的飞行试验项目也有多个,比如美国的HyBoLT(Hypersonic Boundary Layer Transition)、Pegasus、FLARE等,美国与澳大利亚合作项目HIFiRE(Hypersonic International Flight Research Experimentation),欧洲的EXPERT(European eXPErimental Reentry Testbed),法国的LEA等,下文还将详细介绍。
除了专门的基础研究项目,基本上所有的高超声速工程项目中都设置有与边界层转捩相关的基础研究内容。美国典型的工程项目有HTV、Hyper-X/X-43A、X-33、X-37B、X-51、SR-72等,其中不乏涉密计划。欧盟和日本也都启动了高超声速运输机项目,比如欧洲的先进长时推进概念及技术(LAPCAT,Long Term Advanced Propulsion Concepts and Technologies)和高速实验飞行器(HEXAFLY,High-Speed Experimental Fly Vehicles)、高超声速试验飞行器(LEA)、欧洲和日本的合作研究项目未来高速空运关键技术研究与创新合作计划(HIKARI,HIgh speed Key technologies for future Air transport Research & Innovation cooperation scheme)等。HIKARI项目组提出的发展目标是2045年前后完成100座量级马赫数5的高超声速客机研制,2055年前后完成200座量级的研制。
2 研究难度和静音风洞 2.1 高超声速边界层转捩研究难度高超声速边界层转捩现象非常复杂,影响转捩的因素众多,且不同因素在飞行器不同位置和不同飞行阶段的影响效果也不同。
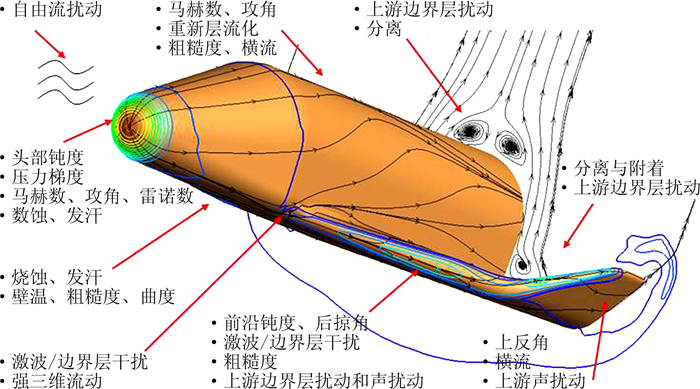
典型高超声速飞行器边界层转捩的影响因素如图 2所示。Anderson[20]把高超声速边界层转捩雷诺数表示成如下包含近20个因素的函数
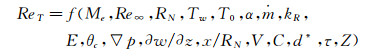
|
(1) |
|
| 图 2 影响转捩因素示意图 Fig. 2 Factors affecting laminar-turbulent transition |
其中Me为边界层外沿的马赫数,Re∞为自由来流的单位雷诺数,RN为头部曲率半径,Tw为物面温度,T0为来流总温,α为攻角,ṁ为物面质量流量(比如吹/吸或烧蚀),kR代表物面粗糙度,E代表环境因素(比如噪声),θc代表物面外形特征(比如圆锥的半锥角),▽p为压力梯度,əw/əz是横流速度梯度,x/RN为熵层吞并边界层的位置,V代表物体振动,C代表物体表面曲率,d*代表物体特征尺寸,τ和Z分别代表化学反应特征时间和程度。对于不同的外形和流动,上述影响因素所起的作用大小不同。各类研究方法手段如风洞实验、飞行试验、稳定性分析和数值模拟等,都仅能从一个或少数几个方面开展研究。
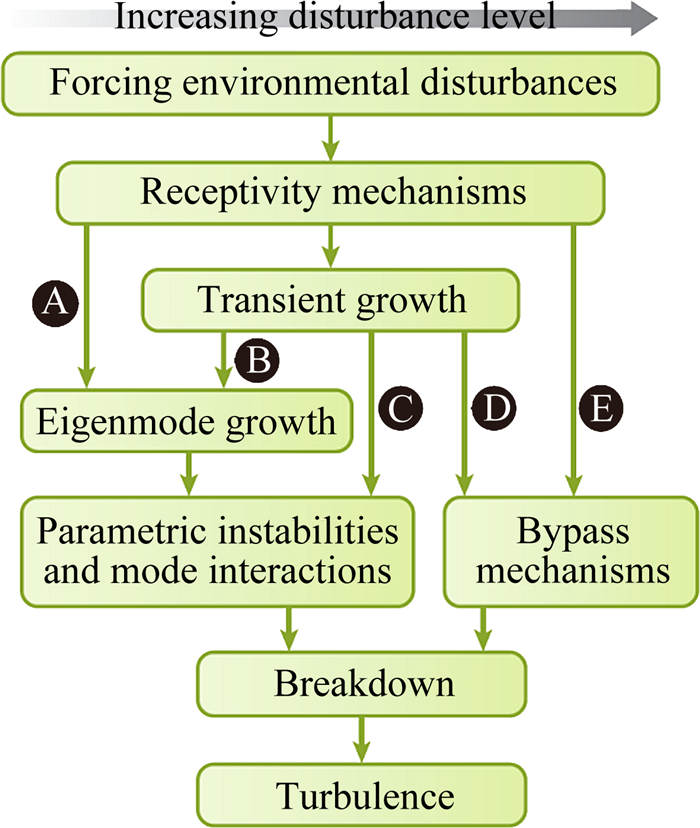
转捩的历程通常是自由流扰动、壁面扰动和粗糙度等通过感受性机制激发边界层内的不稳定波,通过一种或多种失稳模态导致边界层转捩。Morkovin[21]指出,随着初始扰动幅值的增加,转捩过程可能经历5条不同的路径(图 3),这5条路径中有多种失稳形式,比如模态增长(第一、二模态、横流失稳等)、瞬态增长、多参数不稳定、模态干扰、旁路转捩等。当扰动发展到一定阶段会出现饱和,同时平均流被修正,比如出现横流涡或Görtler涡,此时边界层稳定性特征发生变化,通常会出现二次失稳,扰动与平均流以及不同扰动之间也会出现干扰,这些非线性机制都会导致多参数不稳定和模态干扰,边界层中出现马蹄涡或Λ涡等,转捩开始发生。低速边界层流中常有第一模态、Görtler模态、横流失稳等。高超声速转捩研究的另一难点是,高超声速边界层中还有以第二模态为代表的Mack模态以及弓形激波导致的熵模态(或熵层影响)等。第二模态的扰动频率比第一模态高,增长速度快,但是失稳的频率范围通常比第一模态窄。熵模态存在于弓形激波后的熵层中,可以对边界层稳定性和转捩产生影响。高超声速边界层中各种失稳模态的特征频率之间通常没有特别明显的分界线,比如第一模态的频率可能与横流失稳的频率有重叠,也可能与第二模态有重叠,这也加大了研究难度。由于特征模态不是正交,有可能出现两个或多个斜交的特征模态是衰减的,但是其综合效果是增长的,这种情况可归为瞬态增长。高超声速流动中很可能还有我们没有认识到的模态和不稳定机制[18, 22]。
不管是何种情况下的转捩,背景扰动影响都十分重要。但是,目前对高超声速风洞流场和高超声速实际飞行条件下的背景扰动的了解都极其有限。转捩本身是一个过程,其形成的历史与外界扰动有关,并敏感地依赖于外界扰动。由于对外界干扰进行充分预测存在难度,由此导致转捩精确预测的困难[14]。迄今为止,还没有一种被普遍接受的转捩预测方法,各种转捩预测方法都有其适用范围和局限性,现有的科学技术储备还很难在较广的范围内精确预测转捩位置。
直接数值模拟(DNS)是研究边界层转捩机理的重要手段之一,但数值模拟面临对强激波的精细且鲁棒的捕捉能力、对小扰动的高精度高分辨率刻画能力这两个几乎矛盾的要求。近些年,DNS在认识转捩机理方面虽然发挥了重要的作用,但因其计算量巨大,能模拟的实例有限,且通常仅能模拟特定流场在特定扰动条件下的转捩情况,在认识参数影响规律方面的能力仍显不足。
高超声速风洞实验受条件限制,能测量的物理量有限,通常只能测量有限点位上的压力、压力脉动、热流、表面温度,和少数几个切面的阴影/纹影图像等,还不足以研究转捩的全过程。风洞实验中转捩位置测量也有很大的不确定性,不同的测量手段可以得到不同的转捩位置。比如基于热流的转捩位置通常是把热流偏离层流的位置作为转捩开始位置,而纹影测到的是转捩过程(中期)各阶段的破碎过程。
高超声速转捩研究另一大难点是风洞实验和飞行试验的重复性较差。在40多年前,Owen等发现高超声速风洞实验和飞行试验转捩数据散度较大,可出现一个数量级的差异,该状况至今也并没有改善许多[10, 23]。悲观者认为不管是风洞实验还是飞行试验都不能正确认识和预测高超声速边界层转捩。Bushnell[24]在总结历史上的转捩研究时发现在预测高超声速转捩方面非常不成功,以X-15为例,风洞实验显示大部分流动应该是层流,但是飞行试验表明大部分流动都是湍流。美国航天飞机的数据也表明,即使是同一架飞行器在相同弹道多次飞行时,转捩雷诺数也会出现非常大的变化[9, 25]。
2.2 静音风洞及其重要性静音风洞通过尽量保持洞壁边界层为层流状态,减小洞壁噪声等实现“静音”条件。Schneider[18, 26]指出风洞噪声可使大部分(如果不是全部)风洞实验中的高超声速转捩数据失效,建议采用静音风洞。他进一步指出,风洞噪声至少对以下四个方面有显著影响:1) 由孤立粗糙元引起的转捩;2) 第二模态扰动的初始幅值;3) 第二模态的非线性破碎;4) 横流失稳及转捩。美国普渡大学的静音风洞对深入研究高超声速边界层转捩机理起到了至关重要的作用。在国内,北京大学和国防科技大学的静音风洞也已经建成并投入使用[27-31]。北京大学李存标教授等[27-29]把高频响脉动压力测量技术(PCB)、瑞利散射成像技术(RSI)、激光纹影技术和萤光温敏漆(TSP)技术等成功用于高超声速边界层转捩研究。国防科技大学易仕和教授等[30-31]发展的纳米粒子示踪平面激光散射技术(NPLS)也被用于转捩问题研究。
遗憾的是,美国以及国内的静音风洞因喷管口径不够大、实验雷诺数不够高,在静音实验条件下还不足以使尖锥边界层发生转捩,需要采用特殊措施比如粗糙带或具有逆压梯度的实验模型[27, 32]。所有静音风洞的实验条件都非常有限,仅能复现有限的飞行条件,非常有必要利用飞行试验开展转捩研究与验证,在本文最后一节将重点介绍。
3 高超声速边界层转捩的认知现状Bertin和Cummings[9]在综述高超声速技术进展时把对高超声速研究现状分为4种情况:已知的已知现象(What we know we know),已知的未知现象(What we know we don’t know),有人知道但是我们还没有发现的现象(What someone knows, but that we haven’t found yet)以及未知的未知现象(What we don’t know we don’t know)。Schneider[10, 33-36]对过去50多年高超声速边界层转捩数据进行了汇总,得到了一些规律,并发现了许多问题或相互矛盾的地方。这些数据主要是在平板和圆锥(尖锥或钝锥)外形上得到的,也有部分太空返回舱和航天飞机的转捩数据。此处借鉴Bertin和Cummings的分类方式,把高超声速转捩研究现状分为3种情况:1) 已知主要原因的现象与规律;2) 已知部分原因(不一定是主要原因)的现象与规律;3) 未知或矛盾的现象。需要指出的是,这些现象与规律是基于平板和圆锥得到的,当把它们推广到更普遍的外形时可能会出现不一致的情况。
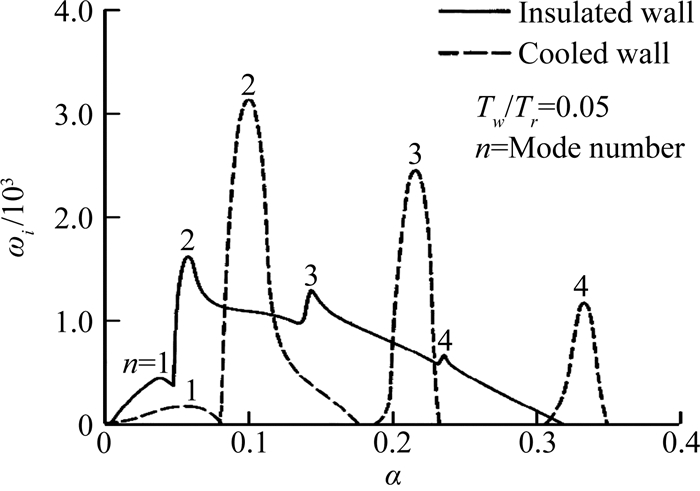
3.1 已知主要原因的现象与规律 3.1.1 壁温的影响规律早期,特别是20世纪70年代,有人在高超声速实验时观察到转捩位置随着壁温降低向后移动的现象,也有人观察到转捩前移的现象,还有人观察到壁温对转捩的影响有些时候大、有些时候小、有些时候不明显。于是对温度影响规律存在很强的争论,这种争论直到Mack[37]和Stetson等[38]的工作,才渐渐取得了较为一致的观点。
与低速流动的转捩情况不同,高超声速情况下,第二模态不稳定起重要作用。壁温越低,第二模态扰动增长越快。壁面冷却还可以促进更多高频的Mack模态失稳,所以在高超声速情况下降低壁温可导致转捩提前。由于Mack模态都是高频模态,Stetson等猜测,如果环境扰动不能在边界层内激发Mack模态,边界层仍然可能是第一模态主导,降低壁温则可能推迟转捩,因为冷壁对第一模态具有稳定作用[38]。在马赫数4左右,第二模态可能存在,也可能不存在,壁温的影响规律就变得非常不明朗。再后来的理论分析和风洞实验等还发现,增加壁面温度可以放大横流行波,但对扰动频率的影响非常有限。壁温对Görtler模态的影响规律与第二模态类似,但在高超声速情况下还需要进一步确认。以上壁温影响规律只是针对各种失稳模态得到的,由于高超声速情况下有多种模态或路径可导致转捩,在确定壁温对转捩位置的影响规律前,需要先确认是何种失稳模态导致的转捩。特别需要注意,当壁温影响被风洞噪声和粗糙度等其他因素掩盖时,也可能得到壁温对转捩几乎没有影响的假结论,比如文献[33]中引用的一些文献。
3.1.2 马赫数影响规律
边界层外沿马赫数Me对边界层稳定性和转捩有重要影响。通常,在马赫数4以上时,随着马赫数增加,可压缩效应等因素导致边界层更加稳定,转捩位置推迟,转捩雷诺数增加。一些典型外形(比如平板、圆锥和返回舱)的风洞实验和飞行试验都显示,转捩雷诺数与边界层外沿马赫数呈现近似线性的正相关。稳定性理论分析也显示随着马赫数增加,边界层失稳雷诺数增大,失稳速率变慢。
|
| 图 6 转捩位置与马赫数的关系 Fig. 6 Transition location vs. boundary edge Mach number |
3.1.3 噪声影响规律
半个多世纪以来,研究人员都认为,自由流扰动对转捩有重要影响。风洞喷管壁上的边界层通常为湍流,湍流产生高噪声并影响到实验模型上。除了噪声,风洞流场还包括熵波和涡波等,但常规高超声速风洞中噪声影响占主导,且导致转捩提前[40]。基于风洞实验和飞行试验的转捩数据,研究人员对来流扰动的影响进行了关联并取得了较好的效果,如Dougherty等[41]针对圆锥的噪声关联公式:
|
(2) |
最近20多年来的相关研究主要关注噪声的影响机理。在高噪声环境中,边界层通过感受性机理获得的扰动波初始幅值增加,线性增长阶段变短,甚至可能改变扰动波的传播特性和转捩机理,或越过线性增长阶段[18, 40]。但噪声的影响机理远不止如此,目前已经发现噪声对转捩的影响机理还有[14, 18]:噪声与粗糙元或粗糙壁面相互作用诱发边界层的不稳定波;噪声与涡波或熵波相互作用产生新的扰动(其频率和波速与边界层色散关系有可能匹配)并激发边界层失稳;噪声可以诱导横流失稳;噪声可加速扰动波的非线性失稳。
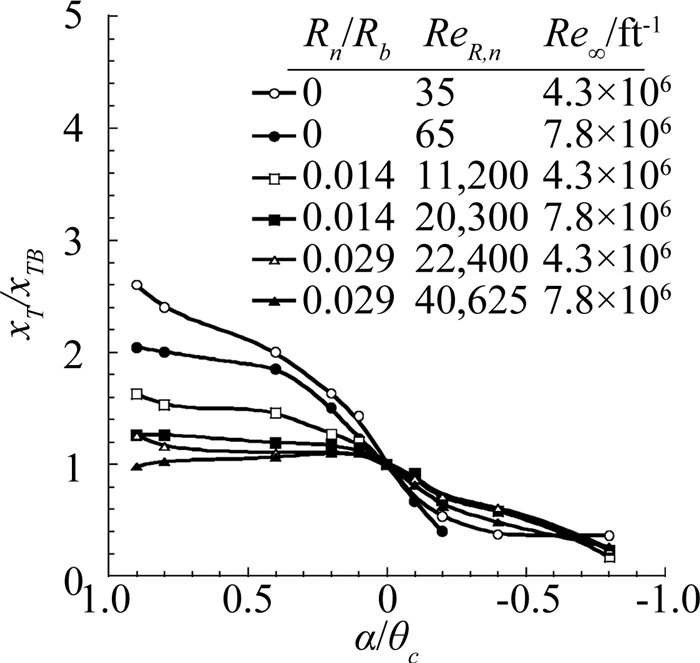
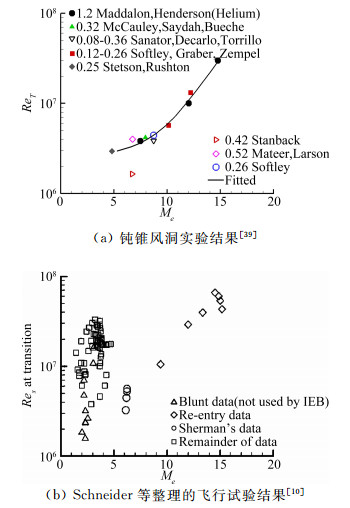
3.2 已知部分原因的现象与规律 3.2.1 圆锥头部钝度的影响规律高超声速流动的头部热流与头部半径的平方根呈现逆相关,对热防护来说采用钝头体是非常必要的。但是,头部钝度对转捩有重要影响且存在着影响趋势反转的现象。当头部钝度增加时,转捩位置推迟,极端情况下可把转捩位置推迟约10倍。但是,当头部钝度超过某个临界值大小时,转捩位置提前,严重时可把转捩位置提前约4/5。所以,常以临界钝度为参考,小于临界值称为小钝度,大于临界值称为大钝度。实际研究中通常以钝度半径为参考长度定义钝度雷诺数。从公开文献(如文献[39, 42])的数据观察可发现转捩趋势反转的临界钝度雷诺数大约为1×10-5,前后波动范围可能超过2倍,典型结果如图 7。
头部钝度不仅对高超声速圆锥或返回舱的边界层转捩有非常明显影响,而且对非常简单的二维钝锲也有明显影响。造成头部钝度影响趋势反转的原因可能有多种,至今还没有一个统一的认识。Reshotko[43]认为瞬态增长理论是解释这个现象有效方法。也有研究者认为头部钝度影响趋势反转现象与风洞实验时低温结冰有关,有的认为与头部粗糙度有关,有的认为头部钝度影响了边界层的感受性强度,有的认为头部钝度增加了壁温的影响效果,而更多人认为是熵层影响[18, 44-45]。早期研究发现头部钝度导致边界层失稳的临界雷诺数增大、失稳范围和扰动增长率变小[46]。最近,Schneider[18]猜测头部大钝度可使边界层对头部粗糙度的敏感度增加,从而导致转捩提前。有很多风洞实验结果显示头部钝度影响趋势反转与熵层的关系比较密切,但是依然不知道是否还有其他原因。
在钝度影响规律上,实验、计算和理论分析的结果可能会不一致。迄今为止,还没有稳定性分析发现头部钝度影响趋势反转现象,比如随着头部钝度增加,第二模态扰动总是变得越来越稳定[47]。已有的公开研究还无法定量预测头部钝度导致的转捩位置前/后移动距离。
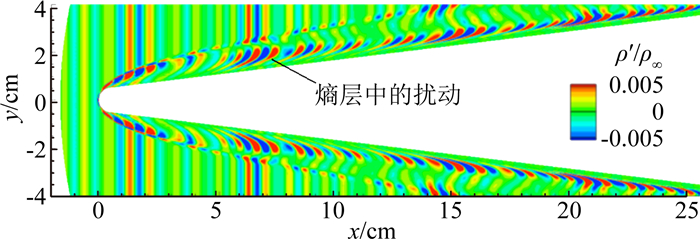
3.2.2 熵层影响与尖形前缘的贴体斜激波不同,钝体前缘的脱体弓形激波存在熵层。熵层本身可能存在无粘不稳定,且表现形式与边界层第一模态类似,这些扰动经轻微衰减/增长后可能进入边界层,然后迅速增长[42, 48]。
有不少文献认为熵层与边界层相互作用改变了边界层稳定性特性,这很可能是头部钝度影响趋势反转的原因,但是还需要更多的分析来验证这种现象。Chynoweth等[49]在静音风洞中开展钝头体转捩研究时,通过热线观察到一种特殊扰动,这种扰动存在于边界层外的熵层中,随着向下游发展,该扰动波向边界层靠近,在流向方向先增长、再衰减,然后再增长。Chynoweth等认为该现象是熵层进入边界层引起的。其实早在20世纪80年代,Stetson等[50]在马赫数8的7°半锥角平头锥(比球形头部更钝)转捩实验中就已经观察到类似扰动。这种扰动起先位于熵层,然后通过熵层与边界层干扰进入边界层,并迅速增长。Stetson等没有在熵层中找到广义拐点,但是在马赫数分布上找到有拐点,且熵层中扰动极大值点与马赫数的拐点在位置上比较一致,熵层中大部分的扰动频率都低于100kHz。后来,他们还发现,随着头部锥角增加,该扰动的频率降低、强度增加。Stetson等还观察到,与尖锥相比,钝锥边界层的稳定性特征出现较大差别,除了熵层存在,钝锥边界层失稳的临界雷诺数比尖锥高,但是失稳后扰动波的增长速度比尖锥快。Stetson[42]通过系列实验研究把头部钝度对平头锥转捩影响效果分为三种情况:(1) 如果熵层与边界层的干扰位置在转捩点附近,头部钝度起稳定的作用,即转捩雷诺数增加,转捩推迟;(2) 如果干扰位置比转捩位置靠后10倍左右,那么可能有多种机制起作用(可能未知),导致转捩雷诺数减小,Stetson猜测头部钝度引起的压力梯度也起重要作用;(3) 如果干扰位置远在转捩点之后(比如30倍以后),转捩雷诺数同样是减小,但这时转捩对头部流动和头部粗糙度非常敏感,转捩区较长,风洞实验的重复性变差,甚至在0°攻角时也会出现非对称转捩。
Fedorov等[44]研究超声速熵层时发现,头部钝度较小时,边界层在较大的当地雷诺数下都是稳定的,边界层对外界扰动的感受性也被抑制或减弱;头部钝度较大时,熵层本身非常容易发生无粘失稳,来流扰动经过头部弓形激波后在熵层产生较大扰动,扰动幅值甚至可以比来流扰动大好几倍,这些扰动随着熵层向下游缓慢发展,增长并不明显,但是,随着熵层与边界层干扰,熵层中的扰动进入边界层后,扰动迅速增长,哪怕边界层当地雷诺数相对较小,也能促进边界层失稳。
最近,Balakumar等[45]的数值计算表明,外界声波通过激波后可以在熵层中产生扰动,这些扰动沿着熵层向下游发展,并对边界层产生影响,熵层中扰动发展情况与边界层中的扰动发展情况是不同的。与尖锥相比,钝锥可以减小边界层对声波的感受性,但是还没有得到趋势反转现象。
3.2.3 攻角对圆锥边界层转捩的影响规律
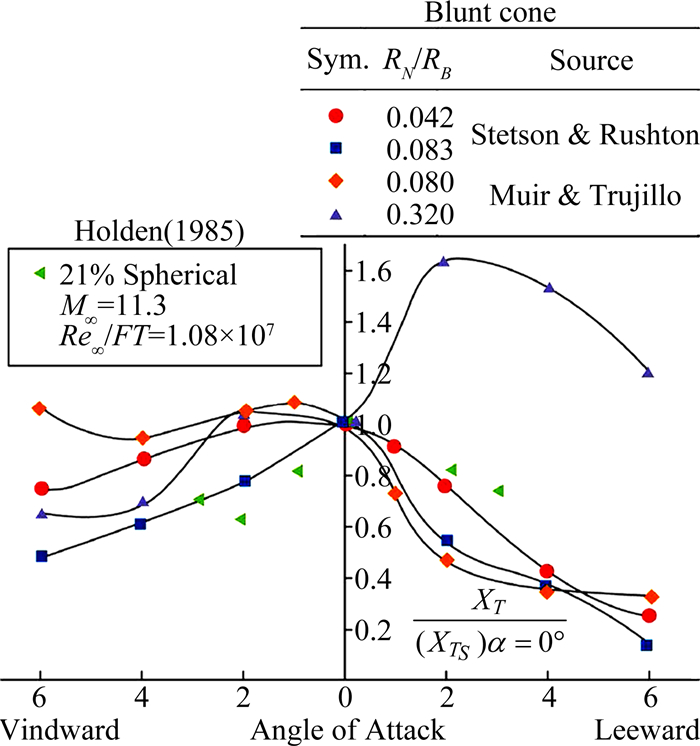
早期,当有人在风洞实验中观察到迎风面转捩靠后、背风面转捩靠前时,大家几乎不相信这些结果。因为,随着攻角增加,迎风面马赫数减小,当地雷诺数增加,如果从0°攻角得到的经验判断,迎风面转捩应该提前。后来稳定性分析和更多风洞实验都显示迎风面比背风面稳定、转捩位置靠后(比如文献[51-53]),人们才逐渐接受这个事实。在有攻角时,侧面的转捩情况比迎风面和背风面更复杂,侧面某些地方的转捩位置可以比背风面更靠前,现有的研究结果表明侧面主要是受横流失稳影响,迎风面主要是第二模态,背风面主要有第二模态和从侧面汇集而来的失稳扰动。不管是哪种情况,第一模态在转捩过程中都可能起重要作用[12]。刘建新等[54]采用数值模拟和线性稳定性理论研究了5°半锥角钝锥在攻角1°、马赫数6时的转捩问题,发现转捩位置沿周向的分布与入口不稳定波的频率和幅值有关。他们认为背面先转捩迎风面后转捩的原因在于:背风面最不稳定波的频率较低,迎风面的最不稳定波的频率较高,而流场的背景扰动中频率低的扰动幅值大,频率高的扰动幅值小。当攻角在0° < α < θc范围内变化时,迎风面转捩位置通常是单调推迟,背风面转捩位置先是提前,当提前到一定程度时,转捩位置随攻角的变化不再明显。小攻角情况下迎风面转捩位置推迟现象在风洞实验和数值模拟中都得到了广泛证实,推迟原因之一很可能是第二模态失稳被极大抑制[55]。
特别需要留意的是,当头部钝度较大时,随着攻角增加,迎风面转捩位置可能先推迟然后提前(如图 10),在有的情况下甚至出现迎风面转捩提前,背风面转捩推迟,还有的情况下迎风面和背风面的转捩位置都提前(甚至小钝度情况下也可能出现[56]),这些特殊现象的原因至今未知[18, 33]。Lin等[5]猜测迎风面转捩提前与头部钝度或头部粗糙度有很大关系,但是还需要更多研究来确认该猜测。
以上现象或规律都是基于尖锥或小钝锥得到的,且攻角都小于圆锥的半锥角。当攻角大于半锥角时,背风面可能出现低温低密度(接近真空)区域和流动分离,热流和摩阻不再显著,但是迎风面激波增强、横流增强、当地马赫数减小,温度和热流增加。目前对大攻角转捩问题的研究还非常少。
3.2.4 攻角对椭圆锥和升力体的影响规律对于HIFiRE-5椭圆锥[57]或X-33[11]之类的升力体,在0°攻角或小攻角情况下,由于两侧的激波强度大,波后压力高,壁面附近的流线从两侧向中心线汇拢,导致中心对称面附近的边界层增厚,严重时出现蘑菇状结构,转捩分析非常困难。但是当攻角较大时,迎风面上的横向压力梯度会出现反转,即中心对称面附近压力高,两侧压力低,壁面附近流线向两侧分开,转捩趋势可能发生本质变化。对于HIFiRE-5椭圆锥,当攻角在0°~4°之间变化时,增大攻角还可减小横流失稳,从而推迟迎风面转捩[57]。
3.3 未知或矛盾现象 3.3.1 单位雷诺数影响规律
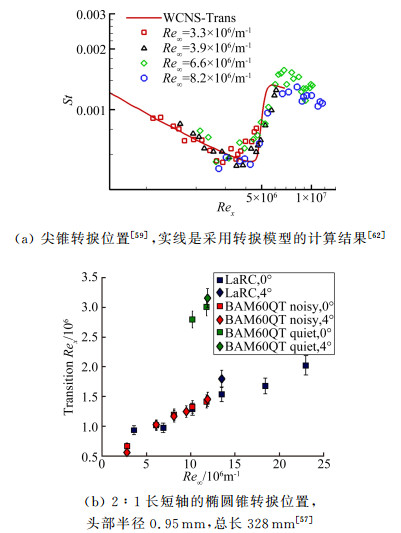
关于单位雷诺数对转捩雷诺数是否有影响的争论一直没有停止。单位雷诺数与转捩雷诺数都是无量纲参数,当保证其他相似参数相同时,单位雷诺数理应对转捩雷诺数没有影响。有少部分风洞实验[39, 59]观测到单位雷诺数对转捩雷诺数的确没有明显影响,这也符合从物理角度出发的直观认识。
但是,更多的常规风洞实验、静音风洞实验和飞行试验结果显示单位雷诺数对转捩雷诺数有影响,甚至有较大影响,比如文献[20, 23, 56-57, 60],典型趋势如图 12所示。随着单位雷诺数增加,直观看法是转捩位置应该按比例前移(即保证转捩雷诺数不变),但实际情况是转捩位置前移比例通常小于单位雷诺数增加比例,于是出现转捩雷诺数增加的现象。线性稳定性分析表明,随着单位雷诺数增加,最不稳定扰动波的频率增加,但这不足以解释单位雷诺数影响规律。有不少人试图解释单位雷诺数影响原因。Stetson等[61]进行了如下猜测:在有的情况下转捩雷诺数随单位雷诺数增加而增加,这或许是因为自由流中的压力波动随单位雷诺数增加而减小;在有的情况下转捩雷诺数基本上不随单位雷诺数变化,这或许是因为当单位雷诺数变化时,自由流中的压力波动仍然基本保持不变。但是,这些解释仍然不能让大部分人接受,只能期待未来能给出更合理解释。
|
| 图 12 单位雷诺数对转捩雷诺数的影响 Fig. 12 Unit Reynolds number vs. transition Reynolds number |
在研究单位雷诺数影响时需要注意到,当单位雷诺数变化时,背景噪声、壁温与总温之比、头部钝度雷诺数、表面粗糙雷诺数、模型连接处的缝隙和台阶的特征雷诺数等都极可能发生变化,如果这些变化掩盖了单位雷诺数的影响效果,就很可能得到错误的结论。
3.3.2 转捩区长度高超声速与低速的另一个不同现象是高超声速边界层转捩区长度较长。早在20世纪70年代,Ownen等[23]就发现转捩区可占层流至完全湍流之间的一半或1/3。后来发现转捩区长度受头部钝度、马赫数、噪声、单位雷诺数等影响。一般情况下,头部钝度越大,转捩区越长。随着马赫数增加,转捩区长度可能更长。定义转捩开始位置与结束位置的比值k=xend/xbegin(参考点为前沿驻点),其变化大概有如下规律:1) 一般超声速:飞行试验k=1.1~1.2,低噪声风洞实验k=1.1~1.2;常规风洞实验k=1.3~1.6。2) 高超声速:飞行试验k=1.5~1.9;常规风洞实验k=1.6~2.5。可见飞行试验的转捩区长度比风洞实验短,这可能暗示转捩区长度随着背景扰动增加而增加。风洞实验数据还表明,迎风面的转捩区比背风面长(至少对尖锥如此)[20]。但是,造成上述转捩区长度变化的物理原因还不清楚。
目前的大量计算以及实验表明,在全层流和全湍流区域,对热流和摩擦的预测,计算和实验比较一致。但是对于转捩流动,转捩位置、转捩区长度等,计算与实验、不同计算之间、不同实验之间的差别还较大[63]。高超声速转捩区域非常长,对转捩区的研究也应该重视。
3.3.3 转捩过程中摩阻和热流增长-衰减-再增长现象
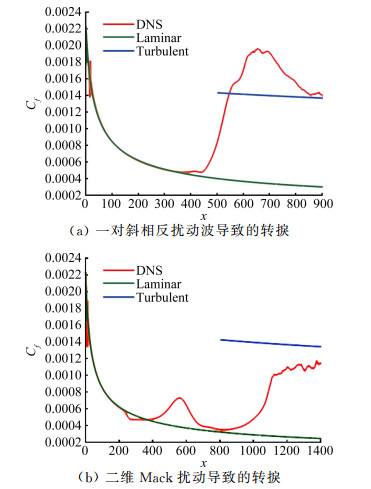
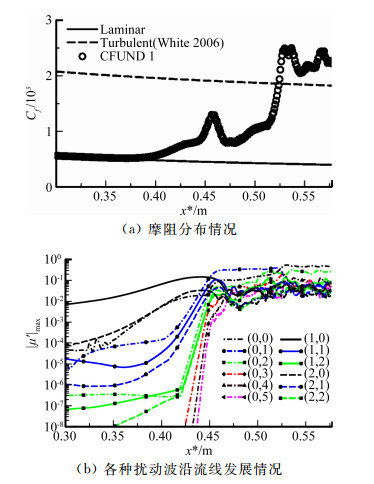
转捩后期摩擦阻力和热流都会出现过冲现象,即摩阻和热流都高于全湍流的相应值,如图 14(a)所示。随着流动向下游发展,摩阻和热流逐渐向全湍流的相应值靠近。转捩位置越靠近上游,这种过冲现象越严重。有人把这种过冲现象归因为边界层的二次失稳,二次失稳导致流向涡出现,流向涡把高速流动带到边界层内部,把低速流动带到边界层外部,在形成高速条纹和低速条纹的同时,加大了壁面速度剪切和热交换[64]。
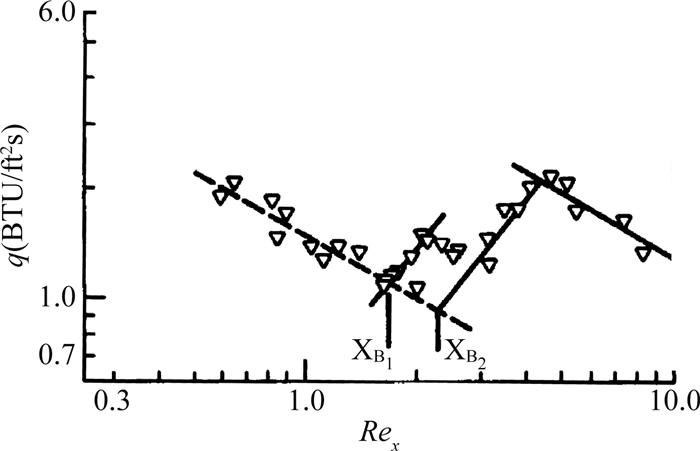
图 14(b)显示了一种与图 14(a)不同的转捩过程,在这个过程中,摩阻出现了增长-衰减-再增长现象,这种异常的分布形态也存在于表面热流。其实,早在1969年,Softley[39]就在马赫10常规风洞实验中观察到转捩过程中的异常现象:热流出现了先增长,再减小,然又增长的情况,如图 15。但是这个异常现象仅在一种风洞实验参数情况下出现过,在别的情况都没有出现,直到现在都没有引起人们太多注意。这个现象为转捩位置定义带来麻烦,因为很多文献都把热流(或摩阻)最小值点作为转捩开始点。
最近几年关于转捩的精细实验和DNS结果让我们重新审视转捩过程。北京大学在马赫6的锥-裙外形的边界层转捩实验中观察到第二模态失稳过程中存在一个“安静区”,即第二模态增长到一定阶段变得“安静”了,随后出现了流场结构破碎,如图 16所示[27-28]。普渡大学在马赫6静音风洞中研究分布式粗糙元促进小攻角尖锥的横流转捩时,也观察到表面热流在转捩过程中也存在增长-衰减-再增长现象(图 17)[49]。Sivasubramanian等[65]采用DNS研究尖锥和锥-裙边界层转捩时也观察到热流增长-衰减-再增长过程(图 18a)。在有的情况下,热流的第一个高点甚至可以超过全湍流的热流值,详情可参考文献[60, 64]和文献[65]等。现在仍不清楚在何种情况下会出现增长-衰减-再增长现象,这很可能与流动参数和扰动形式有关。文献[64]和文献[65]的DNS都是在马赫6情况下,通过壁面吹吸诱导第二模态扰动和一对小的斜波来促进转捩。文献[27]是静音风洞在噪声运行模式下的第二模态失稳导致的转捩。
北京大学朱一丁等[28]认为“安静区”是由涨量波与涡波共同作用促使扰动能量从高频扰动(第二模态)向低频扰动(第一模态)迅速转移所导致的。但是,Sivasubramanian和Fasel[65]的直接数值模拟结果与朱一丁等[28]的风洞实验观察并不完全一致。第一个热流(或摩阻)增长区域很可能是基本模态的一次失稳造成的。当边界层发展到中性点之后时,最初只有一个或少数几个扰动波增长,其他扰动波都是衰减的。当这些失稳扰动波增长到一定幅值时(通常>1%),非线性作用会导致其他原本衰减的扰动波开始增长,这时,热流和摩阻有可能开始增长,流场中可能出现条纹结构,热流和摩阻在展向分布很可能是不均匀的。当这些扰动增长到较高水平时会出现非线性饱和,这时热流和摩阻都达到一个最大值。但是,流场中的大尺度结构并没有立即破碎,而是沿流向维持一段距离,该阶段或许存在“安静”区域,热流和摩阻开始下降。当发展到下游一定距离,大尺度流场结构无法继续保持,其结构开始破碎,湍流斑或间隙性湍流出现,热流和摩阻再次增加,出现第二个峰值;再往下游,边界层完成转捩,热流和摩阻逐渐与全湍流一致。以上转捩过程中的扰动发展情况如图 18(b)所示。
4 转捩机理研究周恒等[12]在其专著中对转捩机理进行了详细介绍,此处尽量避免与文献[12]重复,对Bypass转捩、PSE等不作详细介绍,对感受性、第一、二模态等仅做补充,着重介绍文献[12]很少涉及的全局稳定性、横流模态、Görtler模态、瞬态增长等。
4.1 感受性最初人们认为外部扰动和边界层中的扰动大小相当,但实际研究发现边界层内外扰动的频谱特征和幅值都有较大差别,那么外部扰动是怎样在边界层中产生扰动的,这就是感受性问题,它是自然转捩过程的起始阶段。
感受性的研究方法有三种:实验研究,理论研究和数值计算。实验研究时必须保证两个基本条件:一是风洞的环境噪声必须很小;二是要能够产生可以控制频率、振幅和波数的扰动波。这两个条件在高超声速风洞中都不易实现,因而关于高超声速边界层的感受性实验非常少,通常需要在静音风洞中进行。理论研究主要采用渐近方法和求解抛物化稳定性方程(Parabolized Stability Equation,PSE)。渐近方法是根据流动特性将边界层划分成不同的区域,对各区域应用不同的近似处理及相应的控制方程,不同区域间的衔接采用渐近展开方法,它可以解释自由流声波扰动如何进入边界层并产生Tollmien-Schlichting波(TS),比较典型的是三层理论(Triple-Deck Theory)[66]。PSE是将扰动方程中流向方向上扰动导数的高阶小量略去,使扰动方程抛物化,并采用流向推进的方法来计算空间扰动,这种方法能够考虑非平行流和部分非线性效应,可用来研究感受性[67-68]。近年来,基于高精度算法的DNS越来越多地应用于感受性研究。DNS虽然计算量较大,但能设定扰动环境,同时能够获得扰动场的细节。
4.2 全局稳定性线性稳定性(LST)和求解PSE是研究转捩机理的主要方法,有很多文献都进行了详细介绍。近年来,大涡模拟也被用来研究高超声速边界层转捩机理,比如潘宏禄[69]、赵晓慧[70]等。对于复杂高超声速流动,本文想强调一下全局稳定性分析方法。全局稳定性[71-72]与LST及PSE一样,都是在小扰动假设下进行的,全局稳定性的优越性在于适合流动在多个方向都存在剧烈变化的情况。LST由于平行流或近似平行流假设,只能是一个方向剧烈变化、另外的方向必须相同或缓慢变化。PSE对基本流平行性的要求没有LST那么强烈,能通过流向推进快速求解,但是其缺点是基本流在流向上必须是缓慢变化的。
全局稳定性分析方法目前还不及LST和PSE成熟,比如缺少基于理论的入口/出口边界条件,也不清楚边界条件对模态的形态以及增长率的影响。传统全局稳定性分析方法的另一个典型缺点是需要求解巨型矩阵的特征值问题[73]。这个巨型矩阵通常为稀疏矩阵,二维问题的矩阵大小通常为1×104量级;三维问题的矩阵更大。传统全局稳定性分析方法除了基于小扰动假设外,还需要一个基本流场,这也与LST和PSE一样。在很多情况下,比如大攻角流动、台阶流动、圆柱绕流等,获得基本流场并不是一件容易的事。
全局稳定性发展的一个新趋势是结合高精度数值计算方法和动态模分解方法(DMD)。DMD[74-76]基于一系列瞬时流场或流场切片,通过Arnoldi过程,采用Koopman算子构造有限空间,获得原巨型矩阵的近似矩阵或一个小的伴随矩阵,通过求解近似矩阵或伴随矩阵的特征值和特征向量来近似求解原巨型矩阵的特征值和特征向量。可用PIV等手段测得瞬时流场,也可采用高精度数值模拟求得瞬时流场或流场切片。如果对一片区域或整个流场进行DMD分解,则求得的DMD模态与全局稳定性分析得到的特征模态等价,所对应的特征值体现了该模态增长/衰减情况。如果特征值在单位圆内,则是增长的,反之则是衰减的。为了减小误差,采用高阶精度高分辨率计算格式精细模拟流场中各种细小扰动的发展演化是相当必要的。这种全局稳定性分析方法的优点是:1) 不需要事先准备基本流场;2) 不需要小扰动假设;3) 特征矩阵比较小。如果流场中的扰动量比较小,扰动发展过程为线性过程,那么Arnoldi过程中带来的误差基本可以忽略,DMD得到的是全局线性稳定性的结果;如果流场中扰动量比较大,DMD得到的是主要模态或饱和模态,其特征值非常接近单位圆。我们建议把DMD与正交模态分解(POD)结合,不仅找到最易失稳的DMD模态,而且找到能量最大的DMD模态。能量最大的DMD模态应该能体现线性和非线性情况下的全局稳定性特征。POD也是对一系列瞬时流场或空间切片进行分析,它可以得到能量从大到小的一系列流场结构,但是该结构中可能包含多个频率/波数[77]。DMD得到的模态是单个频率/波数。我们在这方面进行了尝试,物理模型是一个悬浮于马赫数1.5边界层中的微型圆柱(图 19a),首先通过5阶精度计算程序[78-80]模拟圆柱对边界层的干扰,然后进行DMD和POD分析现流场的全局稳定性特征,且是全局稳定性类似卡门涡的形式,是微型圆柱的卡门涡脱落造成的,该DMD模态与流场含能结构有非常强的关联。
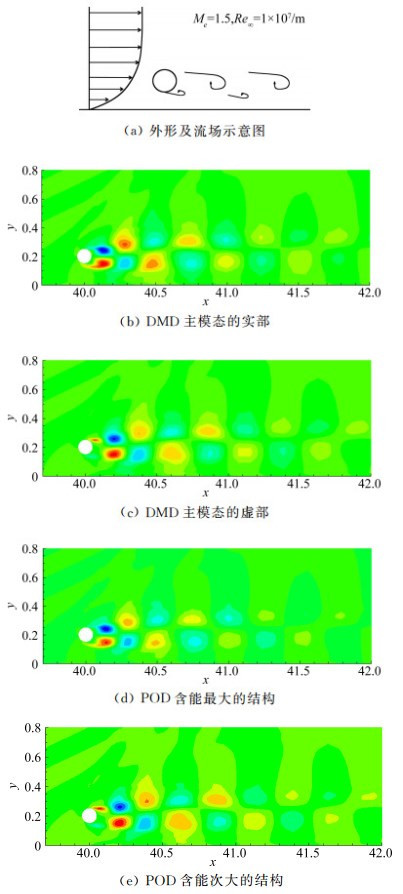
|
| 图 19 外形、DMD和POD分析结果 Fig. 19 Configuration, DMD and POD analysis |
4.3 第一、二模态
Reed等[81]回顾了线性稳定性理论在边界层流动中的运用,这也是关于线性稳定性理论比较权威的总结。在文章中他们回顾了二维、三维、可压缩、不可压缩边界层流动稳定性相关问题。周恒等[12]对可压缩流中第一、二模态在转捩过程中所起的作用进行了比较深入的研究。我们仅补充一点,第一、二模态在0°攻角圆锥和平板边界层中通常有所差异。圆锥边界层比平板边界层薄,厚度沿流向增长比平板缓慢,圆锥边界层中的第一、二模态扰动频率较高,失稳的频率范围较小,增长速率也较缓慢。所以,圆锥边界层转捩位置比平板靠后,在可压缩情况下,二者的差异有所加大,比如低速时靠后1.2倍左右,在马赫数6时可达2倍左右。另外,小钝锥边界层中的第二模态扰动比尖锥边界层中的幅值小[82]。
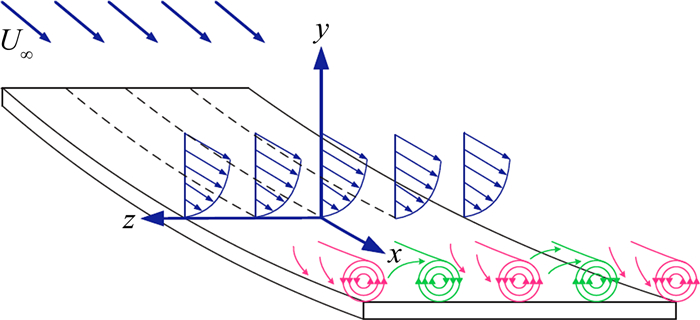
4.4 横流失稳三维边界层与二维边界层存在明显不同,以后掠机翼流动为例,由于压力梯度与后掠角共同作用,使得在边界层内部垂直于无粘流线的方向产生一个横流剖面。由于横流剖面的存在,三维边界层流动与二维边界层流动失稳机制不同。在低速流情形,已经发现了许多横流失稳的现象和规律。三维边界层由横流失稳产生横流涡,在低湍流度来流条件下,一般由定常横流涡主导层流转捩,而在高湍流度来流条件下,则由非定常横流涡主导层流转捩。由于低来流湍流度环境与飞行器外部飞行环境类似,并且后掠机翼、升力体等又是飞行器常见的气动外形,因此针对三维边界层流动主要研究由定常横流涡导致的转捩。粗糙度是定常横流模态的主要扰动源,而来流湍流度是非定常横流模态的主要扰动源[83]。
横流失稳会导致横流涡,横流涡的二次失稳是横流研究中的重要内容。横流涡饱和以后,通过饱和横流涡所谓的“上抛下扫”使得低速流体向边界层外运动而高速流体向壁面运动,强烈扭曲了边界层背景流动,产生了具有非常强烈剪切和拐点的新的背景流动。这个新的背景流动对扰动非常敏感,产生二次失稳。通常,横流涡导致的二次失稳比层流边界层首次失稳最不稳定模态的频率高一个量级。Malik等[85]从扰动能量生成项的角度出发定义了横流涡的两种二次失稳模:类型Ⅰ(也称为‘z’模态)态和类型Ⅱ(也称为‘y’模态)。类型Ⅰ的生成项主要为-〈u2w2〉əU2/ə2,类型Ⅱ模态生成项主要为-〈u2v2〉əU2/əz2,其中下标2表示在涡轴坐标系下。类型Ⅰ主要由横流涡在展向拐点的无粘失稳产生,而类型Ⅱ主要由横流涡在壁面法向拐点产生。其中类型Ⅰ的能量主要分布在横流涡的边部,而类型Ⅱ的能量主要分布在横流涡的顶部,且频率通常比类型Ⅰ高。
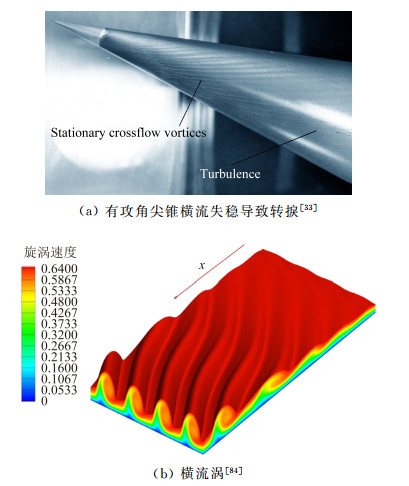
|
| 图 20 横流失稳 Fig. 20 Crossflow unstable |
以上都是基于低速流动得到的研究结果,在高超声速情况下可能出现差异。近些年来,由于高超声速飞行器的快速发展,高超声速情况下的横流失稳研究呈现井喷趋势。美国和澳大利亚等在HIFiRE项目资助下,以小攻角圆锥和椭圆锥为主要研究对象,开展了一系列高超声速转捩研究,横流转捩是重点研究内容之一。在对椭圆锥进行转捩研究过程中,发现其边界层中既存在Mack模态也存在横流涡模态,这与低速边界层不同。静音风洞条件下椭圆锥边界层同时存在定常和非定常横流扰动,而在噪声来流条件下,却未能发现非定常横流扰动,前缘附近布置粗糙单元确实可以有效地激发横流失稳[86]。高超声速情况下增加壁面温度可以放大横流行波,与第一模态趋势相同、第二模态趋势相反。Chynoweth等[49]在实验中观察到横流驻波与横流行波之间的干扰现象,比如通过粗糙元激发横流驻波,结果横流行波得到了抑制,但是其物理机制还不清楚。Borg等[86]对HIFiRE-5椭圆锥进行了静音风洞实验,发现在多次吹风情况下,最不稳定横流扰动频率的重复性较好,但是扰动幅值的重复性很差,差别可达一个数量级。Borg等猜测可能是不同模型温度引起的,后来Chynoweth等[49]在圆锥的实验中观察到壁面温度增加3.9%,横流扰动幅值增加了2.5倍,但是扰动频率基本不受壁温影响。Borg等[87]在静音风洞中开展椭圆锥转捩实验时发现,噪声情况下即使没有观察到定常和非定常横流扰动,但边界层仍然可能转捩。这种转捩如果是流向失稳(主要为第一、二模态)引起的,那么即使在有横流的情况下,第一、二模态等流向失稳模态仍然非常重要。椭圆锥中心线上很可能是第二模态失稳导致转捩,也可能存在其它模态;侧面很可能是横流失稳导致转捩;当攻角从0°~4°之间增加时,迎风面的横流转捩被推迟[57]。高超声速情况下也观察到类型Ⅰ的横流涡二次失稳,但是有的情况下观察不到类型Ⅱ的二次失稳[22]。线性稳定性并不能预测横流涡的饱和过程,也不能预测饱和横流涡的二次失稳,需要采用一些非线性算法来预测横流涡的非线性发展和饱和横流涡二次失稳,比如非线性PSE和DNS等。
总之,目前对高超声速三维边界层横流失稳问题的研究还不够,来流噪声、单位雷诺数、马赫数等是否对横流失稳有影响以及有多大影响等方面还没有严格的定论。
4.5 Görtler模态1941年,Görtler在研究凹面边界层流动的稳定性问题时,得出解的形式为涡轴沿流向反向旋转的涡列。因此,这种形式的失稳被称为Görtler失稳,产生的涡结构称为Görtler涡。Görtler失稳本身并不足以引发转捩,但其形成的高低速条带结构的二次失稳被认为是导致凹面边界层转捩的关键[88],这与横流模态类似。对于不可压缩Görtler涡流动,其二次失稳得到了较为充分的研究,反对称及对称模态被发现[89-90],并被通过能量平衡方法进行分析[91-92]。对于可压缩边界层Görtler涡的失稳,其研究较为欠缺。手段主要包括线性稳定性理论(LST)、渐近方法和DNS方法。Whang等[93]进行了来流马赫数15情况下凹面边界层的DNS,发现相对于反对称模态,演化为马蹄涡的对称模态占主导地位。而在来流马赫数6情况下,Li等[94]发现最危险的模态是反对称模态。Spall和Malik[95]研究了超声速和高超声速边界层中的Görtler涡,他们发现速度和温度扰动都会导致Görtler涡失稳,壁面冷却和逆压梯度具有促进失稳的作用,压缩性则具有增强稳定的效果,这种性质与第二模态失稳类似。以上研究主要针对Görtler基本模态,而对于Görtler高阶模态却罕有报告。近年来,清华大学任杰和符松[88]利用Floquet理论开展了不同流向位置可压缩效应对于Görtler涡二次失稳影响的系统性研究(Ma=0.015~6)。他们深入阐述了Görtler涡二次失稳多种模态的竞争机制,并且发现沿边界层下游发展,二次失稳模态的顺序依次为反对称模态Ⅰ、对称模态以及反对称模态Ⅱ,这些失稳模态在适当条件下均有可能成为增长率最大的不稳定模态。任杰和符松[96]还采用LST和PSE研究了Görtler流动(马赫数4.5) 的离散特征谱。
4.6 瞬态增长
瞬态增长理论(也有人称为非模态增长理论)近年来在可压缩边界层流动方面的应用越来越多。时间模式方面,Hanifi[97]和Bitter[98]等采用正则模态迭加和奇异值(SVD,Singular Value Decomposition)相结合的方法[99]研究了自相似可压缩边界层速度型以及高超声速平板边界层的时间瞬态增长特性,前者发现可压缩边界层最优扰动(在特定时间扰动能量相对于初始时刻增长最大的扰动)初始时刻为流向涡形式,其随时间发展演化为流向条带,因此可压缩边界层扰动瞬态增长的机制与不可压缩情形类似,同样为“抬升”机制,且瞬态增长的量级随马赫数增大而增大。后者发现对于高超声速平板边界层,存在最优的壁面冷却温度使得扰动瞬态增长最小。空间模式方面,Bitter[98]和Tempelmann[100]等进行了可压缩边界层(包括高超声速边界层)扰动空间瞬态增长特性的研究。他们的主要贡献在于基于空间瞬态增长理论、依据扰动能量重新定义了扰动增长因子
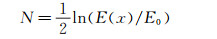
|
(3) |
此处E(x)是流向位置x处的扰动能量,E0是初始位置x0处扰动能量。他们考察了增长因子随马赫数、壁面温度等参数的变化规律,并分析了瞬态增长机制和正则模不稳定机制对于转捩发生过程的影响。Bitter等[98]发现对于高焓平板边界层流动,当扰动放大水平较小时(N=3~4),正则模不稳定相对于瞬态增长机制占优,而当扰动放大量级较大且为流向涡形式时,瞬态增长机制更易引发转捩。Tempelmann等[100]计及了非平行流效应的影响,发现对于带横流的三维边界层,随着马赫数增加(Ma=0.01~1.5),温度扰动和密度扰动对扰动能量以及最优扰动能量增长率的贡献都变大;壁面冷却会引起三维扰动瞬态增长变大,也就是说即使在正则模稳定的情况下,壁面冷却可能因为引起非正则模失稳从而导致转捩提前发生。Reshotko[101]认为瞬态增长在有的情况下可导致Bypass转捩。以上这些工作为基于瞬态增长理论发展eN转捩预测方法打下一定基础。
5 转捩预测与建模 5.1 eN方法周恒[12]、罗纪生[14]和苏彩虹[102-103]等对eN方法进行了详细的介绍,包括方法详情、近期改进以及应用实例,此处仅做补充。早期的eN方法忽略了感受性、自由流噪声和所有非线性效应等影响。而今,eN方法正逐渐完善,开始考虑更多影响因素。
在高超声速情况下,三维边界层的横流失稳模态和第一模态存在重叠的失稳频率范围,第一模态和第二模态也可能存在重叠频率范围,导致模态之间不容易区分,这对eN方法在积分求解N值时造成一定麻烦[104]。Juliano等[57]在静风洞中考察了噪声对HIFiRE-5椭圆锥转捩的影响,发现在有噪声情况下N=3.5,在静音情况下N=8。在外形相同的情况下,N值随着单位雷诺数增加而增加,比如对于马赫数10、头部半径0.152mm、半锥角为7°的尖锥,在单位雷诺数2.03×106/m时N=4.0,单位雷诺数16.25×106/m时N=6.7[45](需注意这是风洞实验结果)。这可能是随着单位雷诺数增加,引起转捩的频率带向高频移动,但是风洞噪声中高频扰动的能量比低频扰动小。但是,我们还需要注意到,随着单位雷诺数变化,尖锥(虽然头部半径很小)头部半径所对应的钝度雷诺数也在变化。总之,eN基于稳定性理论得到主要扰动的增长率,通过经验参数N判断转捩,其估算转捩位置和范围的技术水平取决于我们对所涉及的物理机理的了解程度[18]。
5.2 经验关联式对于低速流动,目前有许多基于转捩数据的经验关联式,但是对于高超声速流动,经验关系式非常少,文献中常把转捩雷诺数与边界层外缘马赫数关联起来,常见的两个关联式如下:
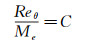
|
(4) |
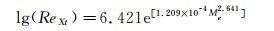
|
(5) |
Reθ为当地边界层动量厚度雷诺数,Me为当地边界层外沿马赫数,ReXt为转捩雷诺数。其中式(4) 主要基于类航天飞机和返回舱的转捩数据,参数C根据情况不同可以取100~500;式(5) 主要基于圆锥的转捩数据,有人也用它来预测乘波体转捩[20]。目前公开文献还能查到粗糙元引起转捩的经验关联式,将在下文的转捩控制中介绍。需要特别注意的是,这些经验公式都没有物理基础,仅仅是在数值上对已有的数据进行关联,且没有一种经验关联式能普遍关联目前已有的数据[9-10]。采用不同转捩关联式得到的边界层动量厚度雷诺数可差3倍,而转捩雷诺数(参考长度为距离前缘驻点的曲边长度)可差异一个数量级;任何一种关联式都仅能在其基础数据内的情况下运用,在此范围之外的预测精准度很难保证[10, 20]。这些经验关联式大都需要用到边界层外缘参数和动量厚度雷诺数,而这些变量的获得并不是一件容易的事。因为高超声速情况下同时存在速度边界层和温度边界层,边界层外缘不好定义,而且需要一种沿壁面法向的搜索方法,对于非结构网格和多块结构网格来说困难更大。对于并行计算来说,由于边界层可能由不同的CPU来计算,通常需要通讯才能完成搜索。
5.3 基于RANS框架张雯等[105]将转捩模型分成了4种类型,分别回顾了其发展背景和构建思路,并在此基础上进行了讨论。经过多年的发展,转捩模型的准确性和实用性已经明显提高,普遍具有以下几个特点:1) 借助经验公式全面考虑环境对转捩的影响因素;2) 一定程度上体现转捩的物理机制;3) 附加方程以计算额外的转捩相关变量;4) 使用“当地变量”进行计算;5) 模块化设计、可移植性好。我们非常认同张雯等人对转捩模型发展特点的总结。基于经验关联式的预测模型和基于层流脉动的预测模型基本上都具备上述4至5个特点,本文重点介绍这两类预测模型。
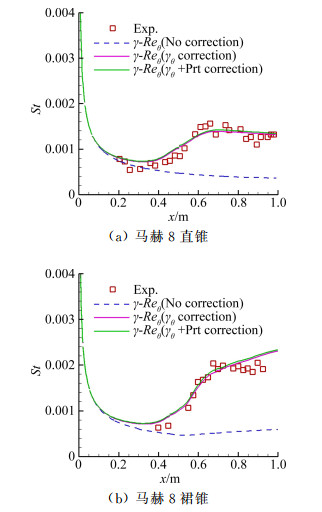
5.3.1 基于经验关联式的预测模型最有代表性的经验预测模型是Menter和Langtry等的γ-Reθ转捩模型[106-108]。该模型没有考虑转捩过程的物理机理,而是依据转捩实验数据将局部湍流度和压力梯度等物理量与转捩动量厚度雷诺数相关联,根据局部涡量雷诺数和临界动量厚度雷诺数的比值判断转捩,在流场中任意一个涡量雷诺数超过局部转捩雷诺数的地方,间歇方程源项被激活并产生湍流。该模型优点是:严格意义上基于局部变量的转捩模型,与现代CFD方法(如非结构网格和大规模并行计算)兼容,可以方便地植入于一般数值模拟软件中。目前主流CFD软件,如Ansys CFX、Fluent、CFD++、CFL3D和OVERFLOW等都有γ-Reθ模型计算模块。
γ-Reθ转捩模型包含三个关键经验关系式:转捩动量厚度雷诺数Reθt、转捩区长度Flength、临界动量厚度雷诺数Reθc。其中Reθt关系式是通过依据风洞实验、飞行试验等得来的转捩动量雷诺数与湍流度、压力梯度等的关联关系。而Flength和Reθc的具体形式曾被作为商业秘密直到2009年才公开[108]。实际上,这两个函数对数值模拟平台的依赖性很高,CFD计算平台的数值特性不同,Flength和Reθc的具体形式和参数也会有所不同。例如张玉伦[109]、牟斌[110]、Medida[111]等都在各自软件平台上进行专门的模型校准。
γ-Reθ模型已在低速边界层转捩流动模拟中获得了成功的应用,许多学者开始将该模型用于高超声速边界层转捩模拟。例如,Krause等[112]考虑来流湍流度构造了Flength和Reθc关系式,较好地模拟了马赫数8.3的双楔壁面压力分布。Cheng等[113]对压力梯度和转捩长度关系式进行修正,对马赫数8的尖锥进行了轴对称计算,研究了来流湍流度和网格间距对转捩模拟结果的影响。Bensassi等[114]模拟了高超声速轴对称圆锥转捩流动,转捩区热流和实验值符合较好。国内,张晓东等[115]重新构造了转捩模型的两个关键函数,并在马赫数8.1尖头双楔平板流动计算中得到应用,较好地预测激波/边界层干扰引起的流动分离。颜培刚等[116]将γ-Reθ模型和PSE方法结合模拟了高超声速圆锥边界层转捩和激波边界层干扰。张毅锋等[117-118]基于原始γ-Reθ模型,对模型经验关系式进行了低速标定、高马赫数修正以及普朗特修正,在高超声速平板、尖锥等一系列转捩流动模拟中取得了较好的计算结果。
除了γ-Reθ转捩模型,还有一些其他转捩预测方法也是基于经验关联式建立起来的。孔维萱等[119]基于雷诺数和马赫数发展了转捩预测准则f(Re, Me),通过间隙因子γ连接层流区和湍流区,通过结合湍流模型便可实现层流/湍流一体化计算。
5.3.2 基于层流脉动和转捩机理的预测模型
层流脉动是指层流边界层中的各种脉动。根据边界层稳定性理论,一些特定的扰动在边界层中可增长,而其他扰动是衰减的。Warren等[120]以层流涡粘系数的形式把层流脉动并入雷诺平均(可压缩时也称Favré平均)Navier-Stokes方程,通过间隙因子将层流涡粘系数和湍流涡粘系数统一起来,得到等效涡粘系数为:
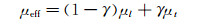
|
(6) |
其中μl是层流涡粘系数,μt是湍流涡粘系数,γ是间隙因子。μt可以通过常用的湍流模型求得,μl可以根据第一、二模态和横流模态等的特点构造求解公式。在求解μl时通常需要用到层流脉动动能,可以专门构造层流脉动方程,比如Mayle[121]、Walters[122]和宋博[123]等人的做法。也可以对湍流模型的湍动能输运方程适当修改,使其在层流区能代表层流脉动动能,比如符松等人的方法[124-127]。符松和王亮等基于SST湍流模型和间隙因子输运方程建立起来的k-ω-γ三方程模型,能够考虑不同模态的转捩,也可用于高超声速流动情况。最近,他们针对高超声速横流转捩和来流噪声对模型进行了改进[127]。宋博和李椿萱[123]在Favré平均的框架下推导了可压缩层流脉动动能输运方程,并根据一定的假设和尺度分析封闭了该方程,构造了可用于高马赫数的转捩模型。放大因子可以间接体现层流脉动发展。史亚云等[128]构造了放大因子输运方程,基于放大因子来预测转捩,通过结合间隙因子输运方程和SA湍流模型,实现了对低速流动的转捩预测。
网格光滑程度、网格粗细及配置、模态参数设置等都会对转捩计算结果产生较大影响[129]。转捩预测模型通常需要用到流场变量的一阶导数,有的还需要用到二阶导数。我们在使用符松等人k-ω-γ三方程模型时发现,采用高阶精度格式可以提高流场一、二阶导数的求解精度,从而有效降低对网格密度的依赖[62]。
6 转捩控制实际工程中可能需要促进或推迟转捩。按是否需要能量输入可分为被动控制方法和主动控制方法。被动控制方法由于不需要额外添加控制能量,倍受国内外同行重视。转捩控制相关研究非常丰富,本文仅给出国内外高超声速边界层转捩被动控制研究进展。
6.1 促进转捩高超声速情况下转捩位置比低速流动靠后,转捩过程漫长,为了防止流动分离、促进燃烧等,通常采用促进转捩的控制装置。粗糙元阵列是使用最为普遍的一种方法,典型的如X-43A,其下表面采用斜坡型转捩装置促进转捩以克服分离并增加发动机入口流量,但上表面因没有采用转捩装置,流动仍然处于层流状态[130]。国内外已经针对粗糙元选型、高度和布阵等方面开展了大量研究。朱德华等[131]通过数值模拟,从边界层稳定性和拓扑结构稳定性角度分析了钻石型粗糙元的主要转捩机理。段志伟等[132-133]采用数值模拟对粗糙单元和阵列的参数和转捩机理进行了考察。涂国华[134-135]等研究发现在超声速边界层中布置悬空的细丝可促进边界层失稳,他们还针对高超声速强制湍流提出了一种湍流模型修正方法。战培国[136]归纳总结了各风洞在超燃冲压发动机前体边界层强制转捩实验中采用的主要测量和显示技术,介绍了美国开展Hyper-X前体边界层强制转捩研究风洞设备的选择依据和选用的主要风洞,分析了强制转捩装置设计过程中,风洞实验研究采用的方法。赵慧勇等[137]介绍了强制转捩装置设计的5个主要问题:转捩装置的转捩机理、安装位置、选型和几何参数优化、装置对进气道性能的影响规律、天地相关性。并针对强制转捩建议了3个未来主要研究方向:静音风洞与常规风洞的强制转捩差异;风洞实验和飞行试验的转捩差异及对进气道性能影响;缩比模型到全尺寸模型上的控制装置参数差异。他们还认为转捩装置的效果最终还需要飞行试验,且需要通过多次飞行试验才能得到比较全面的验证。
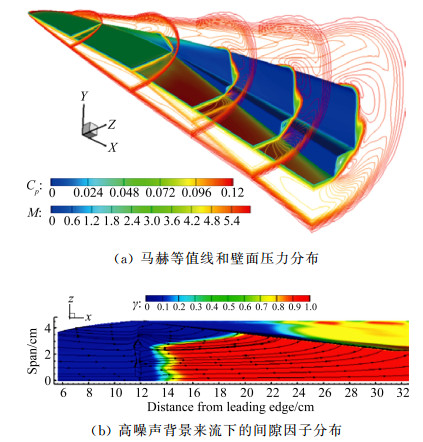
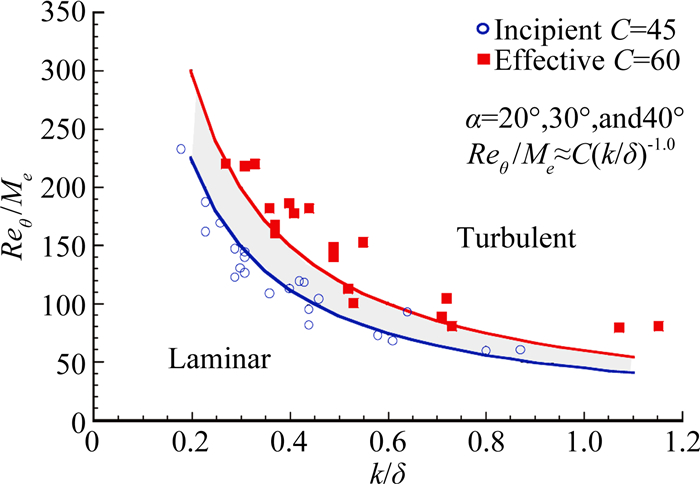
高度是粗糙元控制的主要敏感参数,边界层当地参数非常适合用来评估粗糙元高度是否能有效促进转捩。图 24显示通过k/δ(粗糙元高度/当地边界层厚度)和Reθ/Me (边界层动量厚度雷诺数/外缘马赫数)的比值能较好判断转捩[138]。迎风面中心线上粗糙元的控制效果可以用式(7) 来关联。
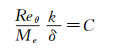
|
(7) |
后来发现这种关联式对迎风面其他位置上的粗糙元也适合,甚至对于凹腔也合适[11, 139]。
为了防止粗糙单元或凹腔引起转捩以致热流增加,当粗糙单元高度或凹腔长度超过一定大小时需要处理,比如美国航天飞机就曾经专门进行过一次太空行走以消除隔热瓦缝隙中突出的填充材料。为了保险起见,防止转捩的关联系数要比促进转捩的关联系数小许多。McGinley等[140]根据航天飞机的风洞实验数据,取关联系数C=27;如果把k换成凹腔的深度,则取C=100;如果取凹腔的长度,则取C=900。
也有人用粗糙元高度与边界层排移厚度的比值来关联[5]。
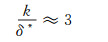
|
(8) |
以上两个经验公式都没有考虑壁温的影响,如果考虑壁温影响,则
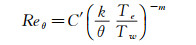
|
(9) |
系数C′=200~750,m=0.7~1.5。值得注意的是,美国用这个公式来预测烧蚀头部对转捩的影响[5]。
在使用上述三个粗糙元高度关联式需要注意:式(7) 和式(8) 没有考虑壁面温度的影响;式(8) 和式(9) 没有考虑马赫数的影响;这三个关联式都没有考虑单位雷诺数和攻角影响。同一粗糙高度,在不同飞行马赫数、攻角、单位雷诺数等情况下对转捩控制的效果可能差别非常大,比如0.005in高的钻石型粗糙单元在攻角20°对转捩仅有轻微影响,但当其他条件不变,把攻角增加到30°时,能迅速促进转捩[11]。所以,结合风洞实验和飞行试验对粗糙元控制效果进行验证是非常必要的。
高超声速情况下烧蚀导致的壁面粗糙增加会影响转捩,甚至可能产生非定常波动[141]。壁面烧蚀产物会进入边界层,风洞实验与弹道靶实验表明会导致转捩位置前移,且烧蚀对边界层注入的产物越多,提前情况越严重。烧蚀产生的气流是高温的,地面实验通过冷喷流来模拟烧蚀不能体现烧蚀的全部影响,也不能体现真实气体效应、化学反应等。烧蚀对转捩影响的实验研究、计算研究和机理分析都非常困难,相关研究还非常少。
6.2 推迟转捩在被动控制方法中主要是通过控制飞行器的型面来推迟转捩,型面控制的主要思想是增大顺压梯度的面积、减小逆压梯度的面积和强度。波纹壁、多孔壁[142-145]等在适当条件下也可用来增强边界层稳定性和推迟转捩。微槽道、多孔介质或超声波吸声材料在高超声速边界层中对第二模态扰动具有抑制作用,对第一模态扰动具有轻微放大作用,整体效果体现为推迟转捩[142-143]。一些特定的条带结构也可以对第一、二模态扰动波失稳起抑制作用[146]。粗糙元不仅可以用于促进转捩,当参数合适时,也可以抑制快/慢模态的增长。Fong等[147-148]发现粗糙元与边界层共振点的相对位置对扰动波的发展非常关键。边界层感受到快/慢声波后,产生所谓的快/慢模态扰动,快模态的相速度比慢模态快。在扰动波向下游发展过程中,快模态的相速度变慢、慢模态的相速度变快,快慢模态相速度相同的点被称为共振点。如果粗糙元安装位置在共振位置,那么高于共振频率的扰动将会衰减,低于共振频率的扰动将会被放大。如果粗糙元安装在共振点之后,那么会抑制慢模态;如果粗糙元安装在共振点之前,则会放大慢模态。与粗糙元的宽度相比,高度对放大/抑制作用的影响更明显,越高效果越好(在扰动线性阶段)[148]。
三维流动的横流失稳控制是转捩控制研究的主要内容之一。精心设计的粗糙元也可以起到抑制横流不稳定的效果[149-150],其主要机理被认为是通过合适布置粗糙元高度和位置,可激发次不稳定的横流波、避免最不稳定的横流波,从而抑制或推迟横流扰动增长。Saric等[149]通过粗糙带、等离子体等对超临界机翼的横流不稳定现象进行了控制,通过改变基本流的形状,使得次不稳定的横流波代替最不稳定的横流波出现,从而可以抑制流动失稳。Schuele等[151]采用风洞实验研究了马赫数3.5来流条件下小攻角圆锥边界层转捩情况,采用亚临界粗糙单元阵列激发次不稳定定常横流涡使得转捩位置延迟了35%。
7 飞行试验飞行试验是唯一能在真实飞行环境下开展高超声速边界层转捩研究的手段,最近十多年来,与转捩有关的飞行试验越来越多[32]。与可搭载在某些飞机平台上的中低马赫数飞行试验不同,高超声速情况下没有通用的飞行器可供搭载,目前和今后很长一段时间都仅能依靠火箭发射[32]。下面我们列出国外一些与高超声速边界层转捩有关的飞行试验,总结飞行试验发展趋势和注意事项。
7.1 国内外飞行试验简介 7.1.1 MF-1我国由于多方面的原因,在航天模型飞行试验手段的建设以及飞行试验的开展上,与美国等航天强国具有很大的差距。2015年12月,由中国空气动力研究与发展中心自主开发的航天模型飞行试验平台顺利完成代号为MF-1的首次飞行并取得圆满成功,这也是我国高超声速模型飞行试验历史上首次以空气动力学基础研究为目的的飞行试验。MF-1为“锥-柱-裙-柱”构型(图 25a),通过火箭助推的形式达到高超声速,在下降段采用无控自主飞行。MF-1的锥段长1180.6mm,半锥角7°,头部半径为5mm。第一个圆柱段直径300mm,第二个圆柱段半径400mm,中间通过33°张角的裙段连接。

|
| 图 25 MF-1飞行试验模型 Fig. 25 Flight test model of MF-1 |
通过58个温度测量点(绿色)和59个压力测量点(红色)获取飞行试验数据(图 25b)。MF-1主要开展边界层转捩和激波/边界层干扰研究,在上升阶段和下降阶段都成功获取了全部测量点上的数据。上升阶段的试验窗口内,模型表面转捩位置向后移动,并最终变成全层流。在下降阶段的试验窗口内,转捩位置从模型底部向前移动。在同一高度同一马赫数下,模型表面转捩位置不同,下降阶段的转捩位置偏后。
7.1.2 HIFiREHIFiRE由美国空军研究实验室(AFRL)和澳大利亚国防科技组织(DSTO)共同发起,目的是发展和验证下一代航空航天飞行系统的关键技术,并侧重研究地面设备和数值计算难以分析的现象,强调飞行试验、地面实验和数值计算最大限度的结合。HIFiRE计划飞行10次,其中两次主要为边界层转捩研究服务,包括圆锥外形(HIFiRE-1) 和椭圆锥外形(HIFiRE-5)[152]。Kimmel等[153]详细介绍了HIFiRE飞行试验情况。该计划2007年启动,2010年3月22日HIFiRE-1首飞,在上升和下降阶段都成功获得了转捩数据。HIFiRE-1圆锥的半锥角为7°,头部半径2.5mm,底部连接两段直径不同的圆柱,圆柱之间通过裙过渡。飞行时通过喷流控制以尽可能保证0°攻角飞行,但是在返回阶段控制不是非常成功,攻角大致在8°~12°。在HIFiRE每次飞行前,都进行了大量地面实验、数值计算和理论分析,以尽可能认识飞行试验中可能会遇到的问题。虽然HIFiRE-1在第一次飞行就取得了非常大的成功,但也发现了一些问题,比如应该提高数据采集系统性能以提高数据质量,在模型设计上也需要改进。
另一个以转捩研究为主要目的的是HIFiRE-5椭圆锥外形,该椭圆锥截面为长/短轴之比为2:1的椭圆。对于该外形,即使是0°攻角情况下也存在很强的横流,在短轴附近边界层还会加厚[58],出现蘑菇形状结构。目前已经对HIFiRE-5开展了大量风洞实验、数值计算和理论分析工作,飞行试验也于2016年5月完成,后续研究还正在继续。
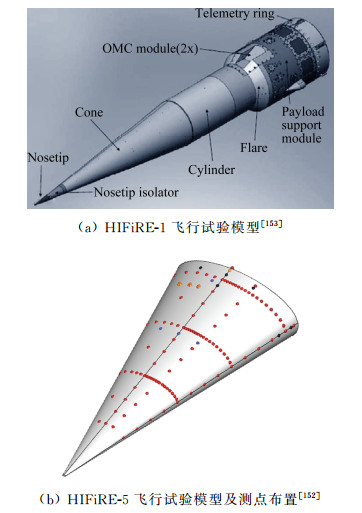
|
| 图 26 HIFiRE-1和HIRiRE-5飞行试验模型 Fig. 26 Flight test model of HIFiRE-1 and HIFiRE-5 |
但是,HIFiRE-5的飞行试验颇为波折。2012年4月的转捩飞行试验Flight-5(注意编号不是按时间排序)因第二级火箭点火失败,导致没有达到预定的飞行速度和高度,仅获得了马赫数3以下的部分数据[152]。另外,HIFiRE-5还遇到了难以克服的其它技术困难,该计划曾经几度调整目标,2015年又不得不延期,这已经是该项目自启动以来的第3次调整。HIFiRE-5的再次飞行试验延迟到2016年5月才完成(代号为HIFiRE-5B)。HIFiRE-5B的飞行高度达到了278km,速度达到了马赫数7.5。造成HIFiRE计划不断调整和延期的原因,主要是由于高超声速相关研究仍然采用传统的方法,很多实验还是在风洞中进行。风洞实验不论是实验时间还是模拟实际飞行条件都有一定的局限性,这也是长期以来困扰高超声速探索研究的主要问题。
7.1.3 HYFIRE[32]HYFIRE从1988年开始,最初计划了10次飞行试验,试验模型包括10°锥、14°平头锥、双锥、凹面锥/发动机入口模型锥等。飞行采用火箭助推,其中两次为助推后自由旋转飞行,另外8次在助推后仍然进行控制以实现预定的飞行姿态。HYFIRE研究高超声速边界层转捩中的多种机理,包括逆压梯度影响、Görtler模态、第一模态、第二模态和横流失稳等,也研究大气环境、测试飞行试验技术等。但是由于美国在20世纪90年度初消减航空航天方面的经费,后续飞行试验研究被迫停止。
7.1.4 FLARE/HYFLEX
始于1991年的FLARE飞行试验主要用于获得马赫数15飞行高度25km的具有压力梯度和横流影响的转捩数据,同时研究激波/边界层干扰和冲压发动机唇口热流[32]。飞行模型是锥裙结构,头部半径为0.15in(3.81mm), 前体为5°锥,后体扩展成9°的裙,总长度14ft(4.27m)。该项目研究在1993年后被归入NASA的HYFLEX项目。但是HYFLEX项目没有获得资助。1996年,日本启动了一个项目也称为HYFLEX(Hypersonic Flight Experiment),该项目是为了给日本HOPE-X(可重复使用太空穿梭飞行器)项目提供技术支撑,获得飞行气动力和气动热数据,考察热防护系统、发展飞行试验技术和地面测试技术等[154]。
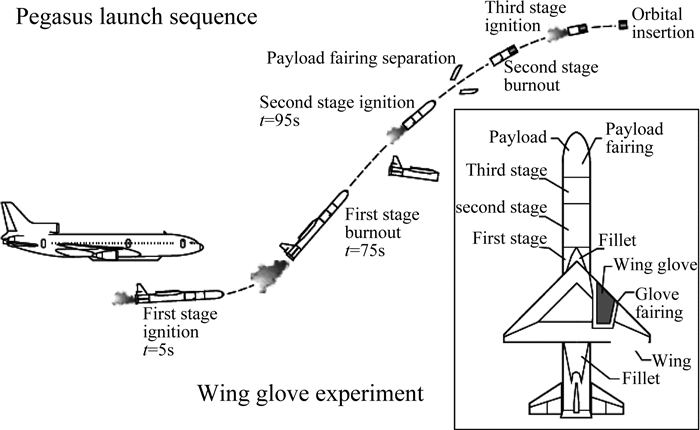
7.1.5 Pegasus机翼蒙皮Pegasus(飞马)机翼蒙皮飞行试验1992年启动,1998年飞行成功。此为搭载试验,基于Pegasus发射系统,搭载在某高超声速三角翼试验模型上,三角翼右侧中段部分采用特殊蒙皮以研究横流转捩。该飞行试验原计划在马赫6、高度80~100kft的飞行条件下获得横流转捩数据。但是,事后数据分析表明,该试验在马赫数4~4.5时发生了湍流的层流化现象(逆转捩),在马赫数6时全部为层流。这与飞行前地面预测结果不一致,猜测是因为对单位雷诺数估计错误造成的,飞行前预估单位雷诺数为2.74×105 /ft,实际飞行为1.62×105/ft。该飞行试验是第一次在马赫数4以上的飞行条件下测得横流失稳,并发现壁面冷却对横流失稳有抑制作用,但是,并没获得有用的边界层扰动频谱特征。
7.1.6 EXPERT
欧洲航天局(European Space Agency, ESA)的EXPERT项目2004年启动,采用弹道再入的形式,飞行模型长1.6m,重436kg。该项目的主要目的是:通过飞行试验获得飞行器高超声速气动力以及气动热的关键数据,比如边界层转捩、激波/边界层干扰、真实气体效应;验证CFD和风洞实验数据和数据库,发展天地关联式,减小设计边缘和不确定度;为工业部门发展再入飞行器提供高超声速热防护技术、试验技术和相关经验等。EXPERT计划搭载18种载荷,获得各种飞行试验数据,以达到不同的研究目的,并且针对这些载荷的研制,联合欧洲众多部门,安排了多项技术攻关,开展了大量的风洞实验、数值模拟和理论分析工作[155-157]。2012年6月完成飞行模型组装,原计划2013年通过俄罗斯退役的SLBM Volna发射。但是由于DLR HEG风洞模型加工问题和ONERA F4风洞的严重电气失败,导致该项目推迟[157],2013年后与该项目有关的文献突然大幅减少。
7.1.7 LEA
LEA项目[158-159]2003年启动,是法国莫当中心和ONERA联合研制的一种以双模态超燃冲压发动机为动力装置高超声速试验飞行器,而前体近壁层流/湍流转捩的预测是LEA设计过程中需要解决的重要问题之一。LEA飞行试验项目经理Laurent Serre说,该飞行器的概念将在Ma=4~8的条件下得到验证。LEA原计划2013年结束,但是公开文献中可以查到LEA飞行试验计划在2014和2015年进行,前期已开展大量风洞实验和数值计算。LEA计划由俄罗斯Tu-22M3“逆火”轰炸机进行空射试验,然后4.2m长的飞行器将由俄罗斯Kh-22(AS-4) 反舰导弹的助推器进行加速。该组合体长度将达到12m、重达5.6T。目标投放高度为13000m,分离速度为马赫数1.7。助推器将推动LEA飞行器在20~30s的时间内达到Ma=4~8,其中将至少有10s是由飞行器的双模态亚燃/超燃冲压发动机单独提供动力。如果分离成功,LEA将在燃料用完前自主控制飞行40km,最后在俄罗斯境内结束飞行试验。但是,公开文献中很难看到后续进展情况。
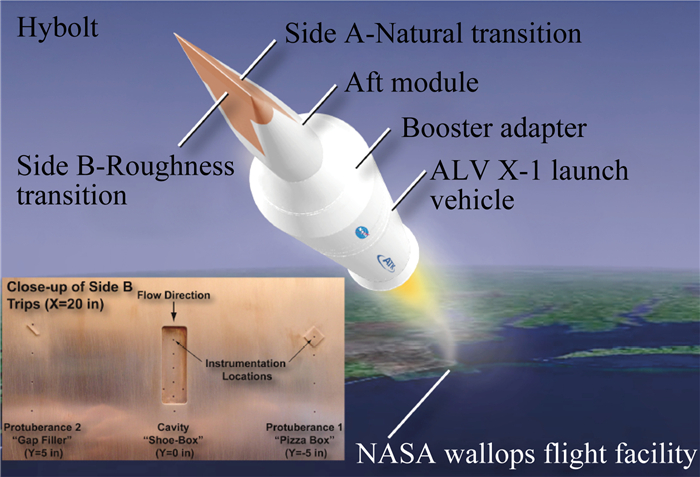
7.1.8 HyBoLT
HyBoLT计划始于2005年,主要研究集中在2006~2008年期间进行。HyBoLT飞行试验想要在锲状模型两个侧面上实现两种目标:一面是研究光滑壁面转捩,另一面是研究离散粗糙元转捩。
试验模型是头部半径为0.15in的锲状构型,后段有12°的压缩拐角。模型宽24in,长度90in,计划获得马赫数5~7,高度33.5km左右的转捩数据。但是在2008年8月的飞行试验中,起飞后助推器出现偏离,试验被迫中断,花费1700万美元(不包含发射火箭的费用)的研究以失败告终。此次教训深重,项目启动和实施匆忙,没有足够时间对测试仪器进行充分调试、仅设计一次飞行试验而没有辅助飞行试验都加大了风险。后来,Hyper-X吸取了该教训,比如X-43就制定了多次飞行计划,即使是第一次飞行失败,后面两次飞行成功也确保了项目的整体成功。
7.2 飞行试验的经验教训
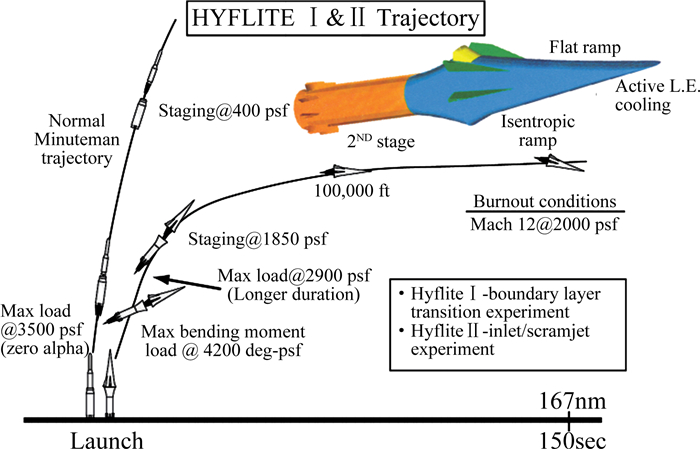
除了上述飞行试验,美欧还有许多飞行试验计划由于经费和难度等原因没有获得资助,其中包括一些制定了详细飞行试验方案、甚至开展了部分地面测试和CFD计算的飞行试验计划,比如HYFLITE(图 32)和HySTP(图 33)等。飞行试验成本高、难度大、风险大,应该想方设法保证每次飞行试验成功。为此,飞行试验前必须进行充分的论证,尽可能考虑一切可能出现的状况,要地面实验、数值计算和理论分析相结合指导做好飞行方案。测试仪器、元器件及测试方案最好能有备份。飞行试验前要对飞行模型进行详尽的地面实验和数值模拟。早在1976年,美国边界层转捩研究组就针对边界层转捩风洞实验给出了4点建议,然后在1990年,又针对飞行试验补充了4点建议,这些建议对后续研究产生了很大影响[32]。4点风洞实验建议如下[161]:(1) 要了解实验设备(风洞)任何可能的特殊附加效应,并尽可能避免。(2) 应该注意到模型表面、材料和结构等造成的扰动,并在实验研究中注明。(3) 应该通过理论和实验来认识边界层不同类型扰动的耦合效应,以便确定它们在飞行环境下的敏感程度。(4) 尽量在多种设备开展实验,且实验条件/参数有重叠,并尽可能保证转捩测试元器件有工作余量。针对飞行试验的4点建议如下[162]:(1) 环境扰动测量必须在模型设计阶段就考虑,并作为模型的一部分。(2) 要注意维持和监控飞行条件和姿态,比如测量窗口的马赫数、雷诺数、攻角、侧滑角、表面温度等。(3) 要注意在每次飞行时都维持和监控模型表面条件,包括发射前对模型表面进行保护,在下一次飞行前对模型表面进行检查和修复。(4) 由于超声速和高超声速边界层失稳现象发生在数百kHz频率范围,这需要数据采集频率非常高、特别是多通道监测更是如此。这对数据采集和压缩提出了特殊的问题,需要重量轻体积小并且可靠的遥测装置。
Berry等[32]从飞行试验中总结出6点经验教训。(1) 飞行试验必须制定清晰目标,该目标不可能在地面设备中实现。由于多目标的飞行试验需要更多经费、更多设计时间、且常常需要在多个目标之间折中,以至于减小了某些特定目标的试验能力,所以飞行试验的目标最好比较单一。多个目标应该通过一系列飞行,每次试验实现一个目标的方式来实现。(2) 转捩研究团队的指导是非常有帮助的,应该尽可能遵照他们的指导。(3) 对转捩有洞察力的专家应该对转捩装置的安装设计进行评审。(4) 不要对飞行流场进行任何假设,而是应该维持姿态和监测试验条件,比如速度、攻角、侧滑角等,同时应该测量环境扰动。(5) 在高超声速边界层转捩试验中,测试元器件对获得高质量数据非常关键,只要有可能,都应该采用适合飞行环境的测试元器件。飞行试验对测试元器件有特殊的要求,比如耐高温。大部分地面实验用的元器件都不是针对天上的状态设计的,需要特别注意。(6) 应该在项目预算中专列资金支持数据分析和原因分析。
Berry等[32]还建议在飞行试验中对转捩的多种物理机理进一步进行评估,包括马赫数6以上的第二模态、马赫数5以上的横流模态、Görtler模态等,还应该对分布式粗糙元、化学反应、烧蚀等定量测量。建议飞行马赫数范围为6~10,高度为24.4km(80kft)左右。Berry等[32]还对助推火箭选择、姿态控制、测试方案设计等都提出了建议。美国系列飞行试验数据、以及针对飞行试验开展的地面实验与数值计算等数据,为HTV、Hyper-X、X-51、X-33、X-37B、SR-72、HyFly、SED等高超声速工程项目提供了较好技术支持,但仍远远不能满足工程研制的需要,比如无法精确预测转捩位置和热流,采取保守的热防护设计策略,转捩导致的不确定甚至可能导致飞行失败。
转捩飞行试验昂贵,基于已有的高超声速飞行器开展转捩搭载试验或许是有效降低成本的一种方法。美国曾经在航天飞机返回阶段多次开展转捩研究,他们在航天飞机返回地面前对航天飞机表面进行扫描,以发现防热瓦的凸起物和凹槽等,然后在返回阶段通过红外图像观察转捩位置,据此来判断表面凸起物/凹槽等对转捩的影响。我国能否借鉴美国的经验,在不影响安全的前提下,在载人飞船和货运飞船的返回阶段或其他高超声速飞行试验过程中开展高超声速边界层转捩研究,值得我们探索。
8 结束语
由于高超声速飞行技术在民用航天航空和国防事业中的战略地位,世界各大国都非常重视。虽然经过了60多年研究,但高超声速边界层转捩仍然还处于盲人摸象阶段,仅有一些局部或片面的认识,研究的深度、成果的综合性和系统性都不够,对先进高超声速飞行器研制的支撑作用不显著。
影响高超声速边界层转捩的因素很多,目前仅对壁面温度、马赫数和噪声的影响规律和机理比较了解;对头部钝度、熵层和攻角仅知道部分影响规律和原因;对单位雷诺数效应和转捩区域的了解还非常不足。在转捩机理研究方面,第一、二模态研究比较充分,负曲率流动Görtler失稳的研究也有不少,但是感受性、横流失稳、瞬态增长等研究较少。由于实际飞行器多为三维边界层,需要特别关注三维边界层的横流失稳和模态相互作用。对于各向异性的三维边界层,全局稳定性分析方法是一种比较好的机理分析方法。
预测转捩是转捩研究的主要目的之一。eN方法是基于稳定性理论和经验参数N建立起来的,在很多典型流动,比如平板和圆锥的转捩预测中取得了较好的效果。但是需要改进eN方法对三维边界层的适应性,提高对非对称转捩的预测能力。第二种转捩预测方法是基于经验关联式,这些经验关联式通常是基于大量转捩数据总结而来,在其基础数据范围内的效果较好,但在基础数据范围外的误差可能较大,甚至可能出现趋势性错误。也有不少人把经验关联式融入RANS方法,并取得了较好的效果,但缺点也是明显的,即在经验关联式适用范围外的精度较差。在RANS框架下还有一种比较流行的方法是基于层流脉动、扰动增长因子等来建立转捩预测模型,该方法可以在一定程度上体现转捩机理,但还需要完善。
转捩控制是转捩研究的另一主要目的。高超声速情况下主要采用粗糙元阵列来促进转捩。推迟转捩比促进转捩困难,初步研究表明精心设计的粗糙元(或阵列)或许可以推迟转捩;还有研究表明微槽道、多孔介质或超声波吸收材料可以抑制第二模态失稳,从而推迟转捩。未来高超声速转捩控制研究应重点关注高效、低阻、低热的转捩控制方法。
飞行试验是唯一能在真实飞行条件下开展转捩研究的手段。为了尽可能保证飞行试验成功,飞行前需充分论证、并通过风洞实验、数值计算和机理分析预测天上一切可能发生的情况。飞行试验结束后,还应开展事后分析与研究,比如数据处理、异常现象研究、补充风洞实验和数值计算等。
总之,高超声速边界层转捩的机理和规律尚不完全清楚。由于高超声速转捩问题的复杂性、影响因素的多样性、研究难度大等特点,期望在短期内全面掌握其机理和规律是不现实的。在今后的转捩研究中,建议把单个影响因素独立出来单独研究,尽量避免多因素相互干扰。未来研究还应是理论分析、风洞实验、数值模拟和飞行试验相结合,发挥各种研究手段的优点,避免其缺点,互为补充。
| [1] |
Li F, Xie S F, Bi Z X, et al. Experimental study of several on aerodynamic problems on hypersonic vehicles[J].
Modern Defence Technology, 2014, 42(5): 1–7.
(in Chinese) 李锋, 解少飞, 毕志献, 等. 高超声速飞行器中若干气动难题的实验研究[J]. 现代防御技术, 2014, 42(5): 1–7. |
| [2] |
Shen Q, Yang W B, Zhuang F G. Turbulence of aerospacecraft[J].
Modern Defence Technology, 2012, 40(1): 21–25.
(in Chinese) 沈清, 杨武兵, 庄逢甘. 航天飞行器中的湍流问题[J]. 现代防御技术, 2012, 40(1): 21–25. |
| [3] |
Gao Q, Li Q, Chen N, et al. The influence of asymmetric transition on stability of hypersonic aircrafts[J].
Tactical Missile Technology, 2012(6): 12–15.
(in Chinese) 高清, 李潜, 陈农, 等. 高超声速飞行器非对称转捩对稳定性的影响[J]. 战术导弹技术, 2012(6): 12–15. |
| [4] |
Xu G W, Li F, Gong A L, et al. Effect of asymmetric transition on lateral departure stability[J].
Journal of Astronautics, 2015, 36(9): 994–1001.
(in Chinese) 徐国武, 李锋, 龚安龙, 等. 非对称转捩对横向偏离稳定的影响[J]. 宇航学报, 2015, 36(9): 994–1001. |
| [5] | Lin T C. The Influence of laminar boundary layer transition on entry vehicle design and its performance[R]. AIAA 2007-309, 2007. |
| [6] |
Yuan C, Yu J, Xu J L, et al. On the achievements and prospects for the methods of computational fluid dynamics[J].
Advances in Mechanics, 2011, 41(5): 562–589.
(in Chinese) 阎超, 于剑, 徐晶磊, 等. CFD模拟方法的发展成就与展望[J]. 力学进展, 2011, 41(5): 562–589. DOI:10.6052/1000-0992-2011-5-lxjzJ2010-082 |
| [7] | Slotnick J, Khodadoust A, Alonso J, et al. CFD vision 2030 study: a path to revolutionary computational aerosciences[R]. NASA CR-2014-218178, 2014. |
| [8] | 陈英硕, 叶蕾. 美国建立国家高超声速中心[J]. 飞航导弹, 2009(6): 10–11. |
| [9] | Bertin J J, Cummings R M. Fifty years of hypersonics: where we've been, where we're going[J]. Progress in Aerospace Sciences, 2003, 39: 511–536. DOI:10.1016/S0376-0421(03)00079-4 |
| [10] | Schneider S P. Flight data for boundary-layer transition at hypersonic and supersonic speeds[J]. Journal of Spacecraft Rockets, 1999, 36(1): 8–20. DOI:10.2514/2.3428 |
| [11] | Berry S A, Horvath T J, Hollis B R, et al. X-33 hypersonic boundary layer transition[R]. AIAA 99-3560, 1999. |
| [12] | 周恒, 苏彩虹, 张永明. 超声速/高超声速边界层的转捩机理及预测[M].北京: 科学出版社, 2015. |
| [13] |
Zhou H. Transition prediction and turbulence computation of hypersonic boundary layers[J].
Morden Defence Technology, 2014, 42(4): 1–9.
(in Chinese) 周恒. 高超声速边界层转捩和湍流计算问题[J]. 现代防御技术, 2014, 42(4): 1–9. |
| [14] |
Luo J S. Transition and prediction for hypersonic boundary layers[J].
Acta Aeronautica et Astronautica Sinica, 2015, 36(1): 357–372.
(in Chinese) 罗纪生. 高超声速边界层的转捩及预测[J]. 航空学报, 2015, 36(1): 357–372. |
| [15] |
Jie S F, Yang W B, Shen Q. Review of progresses in hypersonic boundary layer transition mechanism and its applications[J].
Acta Aeronautica et Astronautica Sinica, 2015, 36(3): 714–723.
(in Chinese) 解少飞, 杨武兵, 沈清. 高超声速边界层转捩机理及应用的若干进展回顾[J]. 航空学报, 2015, 36(3): 714–723. |
| [16] | 傅德薰, 马延文, 李新亮, 等. 可压缩湍流直接数值模拟[M].北京: 科学出版社, 2010. |
| [17] | Schmisseur J D. Hypersonics into the 21st century: a perspective on AFOSR-sponsored research in aerothermo-dynamics[J]. Progress in Aerospace Sciences, 2015, 72: 3–16. DOI:10.1016/j.paerosci.2014.09.009 |
| [18] | Schneider S P. Developing mechanism-based methods for estimating hypersonic boundary-layer transition in flight: the role of quiet tunnels[J]. Progress in Aerospace Sciences, 2015, 72: 17–29. DOI:10.1016/j.paerosci.2014.09.008 |
| [19] | Kirk L C, Lillard R P. Boundary layer transition trip effectiveness on an apollo capsule in JAXA high enthalpy shock tunnel(HIEST) facility[R]. AIAA 2015-0209, 2015. |
| [20] | Anderson J D. Hypersonic and high temperature gas dynamics[M].McGraw-Hill Book Company: 1989. |
| [21] | Morkovin M V. Transition in open flow systems-a reassessment[J]. Bulletin of the American Physical Society, 1994, 39(9): 1882. |
| [22] | Carig S A, Saric W S. Experimental study of crossflow instability on a Mach 6 yawed cone[R]. AIAA 2015-2774, 2007. |
| [23] | Owen F K, Horstman C C, Stainback P C, et al. Comparison of wind tunnel transition and freestream disturbances measurements[J]. AIAA Journal, 1975, 13(3): 266–269. DOI:10.2514/3.49691 |
| [24] | Bushnell D M. Hypersonic flight experimentation-status and shortfalls[C]//Symposium on Future Technology in Service to the Alliance. AGARD CP-6000, 1997. |
| [25] | Bouslog S A, An M Y, Hartmann L N, et al. Review of boundary layer transition flight data on the space shuttle orbiter[R]. AIAA 91-0741, 1991. |
| [26] | Schneider S P. Effects of high-speed tunnel noise on laminar-turbulent transition[J]. Journal of Spacecraft Rockets, 2001, 38: 323–333. DOI:10.2514/2.3705 |
| [27] | Zhang C H, Tang Q, Lee C B. Hypersonic boundary-Layer transition on a flared cone[J]. Acta Mechanica Sinica, 2013, 29(1): 48–53. DOI:10.1007/s10409-013-0009-2 |
| [28] | Zhu Y, Zhang C, Chen X, et al. Transition in hypersonic boundary layers: role of dilatational waves[J]. AIAA Journal, 2016, 54(10): 3039–3049. DOI:10.2514/1.J054702 |
| [29] | Zhang C, Lee C. Rayleigh-scattering visualization of the development of second-mode waves[J]. Journal of Visualization, 2017, 20(1): 7–12. DOI:10.1007/s12650-016-0384-4 |
| [30] |
Yi S H, Tian L F, Zhao Y X. The new advance of the experimental research on compressible turbulence based on the NPLS technique[J].
Advances in Mechanics, 2011, 41(4): 379–389.
(in Chinese) 易仕和, 田立丰, 赵玉新. 基于NPLS技术的可压缩湍流机理实验研究新进展[J]. 力学进展, 2011, 41(4): 379–389. DOI:10.6052/1000-0992-2011-4-lxjzJ2010-028 |
| [31] |
Zhao Y F, Liu W, Gang D D, et al. Study of surface roughness induced supersonic boundary layer transition[J].
Journal of Astronautics, 2015, 36(6): 739–746.
(in Chinese) 赵云飞, 刘伟, 冈敦殿. 粗糙物面引起的超声速边界层转捩现象研究[J]. 宇航学报, 2015, 36(6): 739–746. |
| [32] | Berry S A, Kimmel R, Reshotko E. Recommendations for hypersonic boundary layer transition flight testing[R]. AIAA 2011-3415, 2011. |
| [33] | Schneider S P. Hypersonic laminar-turbulent transition on circular cones and scramjet forebodies[J]. Progress in Aerospace Sciences, 2004, 40(1-2): 1–50. DOI:10.1016/j.paerosci.2003.11.001 |
| [34] | Schneider S P. Laminar-turbulent transition on reentry capsules and planetary probes[J]. Journal of Spacecraft and Rockets, 2006, 44(2): 1153–1173. |
| [35] | Schneider S P. Effects of roughness on hypersonic boundary-layer transition[J]. Journal of Spacecraft and Rockets, 2008, 45(2): 193–209. DOI:10.2514/1.29713 |
| [36] | Schneider S P. Summary of hypersonic boundary-layer transition experiments on blunt bodies with roughness[J]. Journal of Spacecraft and Rockets, 2008, 45(6): 1090–1105. DOI:10.2514/1.37431 |
| [37] | Mack L M. Boundary layer linear stability theory[R]. AGARD-709, 1984. |
| [38] | Stetson K F, Thompson E R, Donaldson J C, et al. Hypersonic layer boundary layer stability experiments on a cone at Mach 8, part 5: tests with a cooled model[R]. AIAA 89-1985, 1985. |
| [39] | Softley E J. Boundary layer transition on hypersonic blunt slender cones[R]. AIAA 69-705, 1969. |
| [40] | Pate S R. Effects of wind tunnel disturbances on boundary-layer transition with emphasis on radiated noise: a review[R]. AIAA 80-0431, 1980. |
| [41] | Dougherty N S, Fisher D F. Boundary-layer transition on a 10 degree cone: wind tunnel/flight data correlation[R]. AIAA 80-0154, 1980. |
| [42] | Stetson K F. Hypersonic laminar boundary layer transition, part I: nosetip bluntness effects on cone frustum transition; part Ⅱ: Mach 6 experiments of transition on a cone at angle of attack[R]. AFWAL-TR-86-3089, 1986. |
| [43] | Reshotko E. Transition issues at hypersonic speeds[R]. AIAA 2006-707, 2006. |
| [44] | Fedorov A, Tumin A. Evolution of disturbances in entropy layer on blunted plate in supersonic flows[J]. AIAA Journal, 2004, 42(1): 89–94. DOI:10.2514/1.9033 |
| [45] | Balakumar P, Chou A. Transition prediction in hypersonic boundary layers using receptivity and freestream spectra[R]. AIAA 2016-0847, 2016. |
| [46] | Stetson K F. Effect of bluntness and angle of attack on boundary layer transition on cones and biconic configurations[R]. AIAA 79-0269. 1979. |
| [47] | Lei J, Zhong X. Linear stability analysis of nose bluntness effects on hypersonic boundary layer transition[J]. Journal of Spacecraft and Rockets, 2012, 49(1): 24–37. DOI:10.2514/1.52616 |
| [48] | Fedorov A, Tumin A. Evolution of disturbances in entropy layer on blunted plate in supersonic flow[J]. AIAA Journal, 1971, 42(1): 89–94. |
| [49] | Chynoweth B C, Ward C A C, Henderson R O, et al. Transition and instability measurements in a Mach 6 hypersonic quiet wind tunnel[R]. AIAA 2014-0074, 2014. |
| [50] | Stetson K F, Thompson E R, Donaldson J C, et al. Hypersonic layer boundary layer stability experiments on a cone at Mach 8, part 2: blunt cone[R]. AIAA 84-0006, 1984. |
| [51] | Stetson K F, Thompson E R, Donaldson J C, et al. Hypersonic layer boundary layer stability experiments on a cone at Mach 8, part 3: sharp cone at angle of attack[R]. AIAA 85-0492, 1985. |
| [52] | Muir J F, Trujillo R A. Experimental Investigation of the effect of nose bluntness, free-stream unit Reynolds number, angle of attack on cone boundary layer transition at a Mach number of 6[R]. AIAA 72-216, 1972. |
| [53] | Horvath T J, Berry S A, Hollis B R, et al. Boundary layer transition on slender cones in conventional and low disturbance Mach 6 wind tunnels[R]. AIAA 2002-2743, 2002. |
| [54] | Liu J, Luo J. Effect of disturbances at inlet on hypersonic boundary layer transition on a blunt cone at small angle of attack[J]. Applied Mathematics & Mechanics(English Edition), 2010, 31(5): 535–544. |
| [55] | Li X, Fu D, Ma Y. Direct Numerical simulation of hypersonic boundary layer transition over a blunt cone with a small angle of attack[J]. Physics of Fluids, 2010, 22: 025105. DOI:10.1063/1.3313933 |
| [56] |
Chang Y, Chen S Y, Zhang K L. Experimental investigation of hypersonic boundary layer transition[J].
Journal of Astronautics, 2015, 36(11): 1318–1323.
(in Chinese) 常雨, 陈苏宇, 张扣立. 高超声速边界层转捩特性试验探究[J]. 宇航学报, 2015, 36(11): 1318–1323. DOI:10.3873/j.issn.1000-1328.2015.11.014 |
| [57] | Juliano T J, Borg M P, Schneider S P. Quiet tunnel measurements of HIFiRE-5 boundary-layer transition[J]. AIAA Journal, 2015, 53(4): 832–846. DOI:10.2514/1.J053189 |
| [58] | Li F, Choudhari M, Chang C L, et al. Stability analysis for HIFiRE experiments[R]. AIAA 2012-2961, 2012. |
| [59] | Kimmel R L. The effect of pressure gradients on transition zone length in hypersonic boundary layers[J]. Journal of Fluids Engineering, 1997, 119: 36–41. DOI:10.1115/1.2819115 |
| [60] | Sivasubramanian J, Fasel H F. Direct numerical simulation of laminar-turbulent transition in a flared cone boundary layer at Mach 6[R]. AIAA 2016-0846. |
| [61] | Stetson K F, Thompson E R, Donaldson J C, et al. Hypersonic layer boundary layer stability experiments on a cone at Mach 8, part 4: on unit Reynolds number and environmental effects[R]. AIAA 86-1087, 1986. |
| [62] | Tu G, Deng X, Mao M. Validation of a RANS transition model using a high-order weighted compact nonlinear scheme[J]. Science ChinaPhysics Mechanics and Astronomy, 2013, 56: 1–7. DOI:10.1007/s11433-012-4972-6 |
| [63] | Hollis B R, Hollingsworth K E. Laminar, transitional, and turbulent heating on Mid lift-to-drag ratio entry vehicles[R]. AIAA 2012-3063, 2012. |
| [64] | Franko K J, Bhaskaran R, Lele S K. Direct numerical simulation of transition and heat-transfer overshoot in a Mach 6 flat plate boundary layer[R]. AIAA 2011-3874, 2011. |
| [65] | Sivasubramanian J, Fasel H F. Direct numerical simulation of transition in a sharp cone boundary layer at Mach 6: fundamental breakdown[J]. Journal of Fluid Mechanics, 2015, 768: 175–218. DOI:10.1017/jfm.2014.678 |
| [66] | Qin F, Wu X. Response and receptivity of the hypersonic boundary layer past a wedge to free-stream acoustic, vortical and entropy disturbances[J]. Journal of Fluid Mechanics, 2016, 797: 874–915. DOI:10.1017/jfm.2016.287 |
| [67] | Tempelmann D, Schrader L U, Hanifi A, et al. Swept wing boundary-layer receptivity to localized suface roughness[J]. Journal of Fluid Mechanics, 2012, 711: 516–544. DOI:10.1017/jfm.2012.405 |
| [68] | Herbert T. Studies of boundary-layer receptivity with parabolized stability equations[R]. AIAA 93-0353, 1993. |
| [69] |
Pan H L, Ma H D, Wang Q. Large eddy simulation of transition in a hypersonic blunt-wedge boundary layer[J].
Acta Aeronautica et Astronautica Sinica, 2007, 28(2): 269–774.
(in Chinese) 潘宏禄, 马汉东, 王强. 高超声速钝楔边界层转捩大涡模拟[J]. 航空学报, 2007, 28(2): 269–774. |
| [70] |
Zhao X H, Deng X B, Mao M L, et al. Large eddy simulation for forced transition flow at hypersonic inlet[J].
Acta Aeronautica et Astronautica Sinica, 2016, 37(8): 2445–2453.
(in Chinese) 赵晓慧, 邓小兵, 毛枚良, 等. 高超声速进气道强制转捩流动的大涡模拟[J]. 航空学报, 2016, 37(8): 2445–2453. |
| [71] | Theofilis V. Global linear instability[J]. Annual Review of Fluid Mechanics, 2011, 43: 319–352. DOI:10.1146/annurev-fluid-122109-160705 |
| [72] | Theofilis V. Advances in global linear instability of nonparallel and three-dimensional flows[J]. Progress in Aerospace Sciences, 2003, 39(4): 249–315. DOI:10.1016/S0376-0421(02)00030-1 |
| [73] | Gómez F, Clainche L, Paredes P, et al. Four decades of studying global linear instability: problems and challenges[J]. AIAA Journal, 2012, 50(12): 2371–2383. |
| [74] | Rowley C W, Mezic' I, Bagheri S, et al. Spectral analysis of nonlinear flows[J]. Journal of Fluid Mechanics, 2009, 641: 115–127. DOI:10.1017/S0022112009992059 |
| [75] | Schmid P J. Dynamic mode decomposition of numerical and experimental data[J]. Journal of Fluid Mechanics, 2010, 656: 5–28. DOI:10.1017/S0022112010001217 |
| [76] | Schmid P J, Li L, Juniper M, et al. Applications of the dynamic mode decomposition[J]. Theoretical and Computational Fluid Dynamics, 2011, 25: 249–259. DOI:10.1007/s00162-010-0203-9 |
| [77] | Rowley C W, Colonius T, Murray R M. Model reduction for compressible flows using POD and Galerkin projection[J]. Physica D: Nonlinear Phenomena, 2004, 189(1-2): 115–129. DOI:10.1016/j.physd.2003.03.001 |
| [78] | Tu G H, Deng X B, Mao M L. Implementing high-order weighted compact nonlinear scheme on patched grids with a nonlinear interpolation[J]. Computers and Fluids, 2013, 77: 181–193. DOI:10.1016/j.compfluid.2013.02.015 |
| [79] |
Tu G H, Deng X B, Mao M L. A staggered non-oscillatory finite difference method for high-order discretization of viscous terms[J].
Acta Aerodynamica Sinica, 2011, 29(1): 10–15.
(in Chinese) 涂国华, 邓小刚, 毛枚良. 消除粘性项高阶离散数值振荡的半结点-结点交错方法[J]. 空气动力学学报, 2011, 29(1): 10–15. |
| [80] | Tu G H, Zhao X, Mao M L, et al. Evaluation of Euler fluxes by a high-order CFD scheme: shock instability[J]. International Journal of Computational Fluid Dynamics, 2014, 28(5): 171–186. DOI:10.1080/10618562.2014.911847 |
| [81] | Reed H, Saric W, Arnal D. Linear stability theory applied to boundary layers[J]. Annual Review of Fluid Mechanics, 1996, 28: 389–428. DOI:10.1146/annurev.fl.28.010196.002133 |
| [82] | Maslov A. Experimental study of stability and transition of hypersonic boundary layer around blunted cone[R]. Final Project Technical Report of ISTC 1863-2000, 2001. |
| [83] | Muller B, Bippes H. Experimental study of instability modes in a three-dimensional boundary layer[C]//Proceedings AGARD Symposium on Fluid Dynamics of 3D-turbulent shear flows and transition. AGARD CP-438. Cesme, Turkey, 1988. |
| [84] |
Xu G L, Fu S. The instability and control of compressible cross flows[J].
Advances in Mechanics, 2012, 42(3): 1–12.
(in Chinese) 徐国亮, 符松. 可压缩横流失稳及其控制[J]. 力学进展, 2012, 42(3): 1–12. |
| [85] | Malik M R, Li F, Choudhari M M, et al. Secondary instability of crossflow vortices and swept-wing boundary layer transition[J]. Journal of Fluid Mechanics, 1999, 399: 85–115. DOI:10.1017/S0022112099006291 |
| [86] | Borg M P, Kimmel R, Stanfield S. Crossflow instability for HIFiRE-5 in a quiet hypersonc wind tunnel[R]. AIAA 2012-2821, 2012. |
| [87] | Borg M P, Kimmel R L. Simultaneous infrared and pressure measurements of crossflow instability modes for HIFiRE-5[R]. AIAA 2016-0356, 2016. |
| [88] | Ren J, Fu S. Secondary instabilities of Görtler vortices in high-speed boundary layer flows[J]. Journal of Fluid Mechanics, 2015, 781: 388–421. DOI:10.1017/jfm.2015.490 |
| [89] | Hall P, Horseman N J. The linear inviscid secondary instability of longitudinal vortex structures in boundary layers[J]. Journal of Fluid Mechanics, 1991, 232: 357–375. DOI:10.1017/S0022112091003725 |
| [90] | Yu X, Liu J T C. The secondary instability in Görtler flow[J]. Phys. Fluids, 1991, A3(8): 1845–1847. |
| [91] | Liu W, Domaradzki J A. Direct numerical simulation of transition to turbulence in Görtler flow[J]. Journal of Fluid Mechanics, 1993, 246: 267–299. DOI:10.1017/S0022112093000126 |
| [92] | Yu X, Liu J T C. On the mechanism of sinuous and varicose modes in three-dimensional viscous secondary instability of nonlinear Görtler rolls[J]. Phys. Fluids, 1994, 6(2): 736–750. DOI:10.1063/1.868312 |
| [93] | Whang C, Zhong X. Secondary Görtler instability in hypersonic boundary layers[C]//39th Aerospace Sciences Meeting & Exhibit. AIAA 2001-0273, 2001. |
| [94] | Li F, Choudhari M, Chang C L, et al. Development and breakdown of Görtler vortices in high speed boundary layers[C]//50th Aerospace Sciences Meeting Including the New Horizons Forum and Aerospace Exposition. AIAA 2010-0705, 2010. |
| [95] | Spall R E, Malik M R. Görtler vortices in supersonic and hypersonic boundary-layers[J]. Physics of Fluids A: Fluid Dynamics, 1989, 1(11): 1822–1835. DOI:10.1063/1.857508 |
| [96] | Ren J, Fu S. Study of the discrete spectrum in a Mach 4.5 Görtler flow[J]. Flow Turbulence Combust, 2015, 94: 339–357. DOI:10.1007/s10494-014-9575-z |
| [97] | Hanifi A, Schmid P J, Henningson D S. Transient growth in compressible boundary layer flow[J]. Physics of Fluids, 1996, 8(3): 826–837. DOI:10.1063/1.868864 |
| [98] | Bitter N P, Shepherd J E. Transient growth in hypersonic boundary layers[R]. AIAA 2014-2497. |
| [99] | Schmid P J. Nonmodal stability theory[J]. Annual Review of Fluid Mechanics, 2007, 39: 129–162. DOI:10.1146/annurev.fluid.38.050304.092139 |
| [100] | Tempelmann D, Hanifi A, Henningson D S. Spatial optimal growth in three-dimensional compressible boundary layers[J]. Journal of Fluid Mechanics, 2012, 704: 251–279. DOI:10.1017/jfm.2012.235 |
| [101] | Reshotko E. Transient growth: a factor in bypass transition[J]. Physics of Fluids, 2001, 13(5): 1066–1075. |
| [102] | Su C H, Zhou H. Transition prediction of a hypersonic boundary layer over a cone at a small angle of attack-with the improvement of eN method[J]. Science in China(Series G: Physics, Mechanics & Astronomy), 2009, 52(1): 115–123. |
| [103] | Su C, Zhou H. Transition prediction for supersonic and hypersonic boundary layers on a cone with an angle of attack[J]. Science in China(Series G: Physics, Mechanics & Astronomy), 2009, 352(8): 1223–1232. |
| [104] | Orlik E, Davidenko D. Boundary-layer transition on a hypersonic forebody: experiments and calculations[J]. Journal of Spacecraft and Rockets, 2011, 48(4): 545–555. DOI:10.2514/1.51570 |
| [105] |
Zhang W, Liu P Q, Guo H, et al. Review of transition prediction methods[J].
Journal of Experiments in Fluid Mechanics, 2014, 28(6): 1–12, 38.
(in Chinese) 张雯, 刘沛清, 郭昊, 等. 湍流转捩工程预报方法研究进展综述[J]. 实验流体力学, 2014, 28(6): 1–12, 38. |
| [106] | Menter F R, Langtry R B, Likki S R, et al. A correlation-based transition model using local variables—part I: model formulation[J]. Journal of Turbomachinery, 2006, 128: 413–422. DOI:10.1115/1.2184352 |
| [107] | Langtry R B, Menter F R, Volker S. Transition Modeling for general purpose CFD codes[J]. Flow Turbulence Combust, 2006, 77: 277–303. DOI:10.1007/s10494-006-9047-1 |
| [108] | Langtry R B, Menter F R. Correlation-based transition modeling for unstructured parallelized computational fluid dynamic codes[J]. AIAA Journal, 2009, 47(12): 2894–2906. DOI:10.2514/1.42362 |
| [109] |
Zhang Y L, Wang G X, Meng D H, et al. Calibration of γ-Reθ transition model[J].
Acta Aerodynamica Sinica, 2011, 29(3): 295–301.
(in Chinese) 张玉伦, 王光学, 孟德虹, 等. γ-Reθ转捩模型的标定研究[J]. 空气动力学学报, 2011, 29(3): 295–301. |
| [110] |
Mou B, Jiang X, Xiao Z Y, et al. Implementation and caliberation of γ-Reθ transition model[J].
Acta Aerodynamica Sinica, 2012, 31(1): 103–109.
(in Chinese) 牟斌, 江雄, 肖中云, 等. γ-Reθ转捩模型的标定与应用[J]. 空气动力学学报, 2012, 31(1): 103–109. |
| [111] | Medida S, Baeder J D. Application of the correlation-based γ-Reθt transition model to the Spalart-Allmaras turbulence model[R]. AIAA 2011-3979, 2011. |
| [112] | Krause M, Behr B, Ballmann J. Modeling of transition effects in hypersonic intake flows using a correlation-based intermittency model[R]. AIAA 2008-2598, 2008. |
| [113] | Cheng G, Nichols R, Neroorkar K D, et al. Validation and assessment of turbulence transition models[R]. AIAA 2009-1141, 2009. |
| [114] | Bensassi K, Lani A, Rambaud P. Numerical investigations of local correlation-based transition model in hypersonic flows[R]. AIAA 2012-3151, 2012. |
| [115] |
Zhang X D, Gao Z H. Numerical discuss to complete empirical correlation in Langtry's transition model[J].
Applied Mathematics and Mechanics, 2010, 31(5): 544–552.
(in Chinese) 张晓东, 高正红. 关于补充Langtry的转捩模型经验修正式的数值探讨[J]. 应用数学和力学, 2010, 31(5): 544–552. |
| [116] | Yan P, Mao R, Qiang X. Application of PSE analysis method with transitional turbulence model on hypersonic flows[R]. AIAA 2011-3981, 2011. |
| [117] |
Zhang Y, Lei J, Zhang Y, et al. Calibration of transition model for hypersonic numerical simulation platform[J].
Acta Aerodynamica Sinica, 2015, 33(1): 42–47.
(in Chinese) 张毅锋, 雷净, 张益荣, 等. 高超声速数值模拟平台转捩模型的标定[J]. 空气动力学学报, 2015, 33(1): 42–47. |
| [118] |
Zhang Y F, He K, Zhang Y R, et al. Improvement and validation of Menter's transition model for hypersonic flow simulation[J].
Journal of Astronautics, 2016, 37(4): 397–402.
(in Chinese) 张毅锋, 何琨, 张益荣, 等. Menter转捩模型在高超声速流动模拟中的改进及验证[J]. 宇航学报, 2016, 37(4): 397–402. |
| [119] |
Kong W X, Zhang H, Yan C. Transition criterion prediction method for hypersonic boundary layer[J].
Missiles and Space Vehicles, 2013, 328: 54–58.
(in Chinese) 孔维萱, 张辉, 阎超. 适用于高超声速边界层的转捩准则预测方法[J]. 导弹与航天运载技术, 2013, 328: 54–58. |
| [120] | Warren E S, Harris J E, Hassan H A. Transition model for high-speed flow[J]. AIAA Journal, 1995, 33(8): 1391–1397. DOI:10.2514/3.12687 |
| [121] | Mayle R E, Schulz A. The path to predicting bypass transition[J]. Journal of Turbomachinery, 1997, 119: 405–411. DOI:10.1115/1.2841138 |
| [122] | Walters D K, Cokljat D. A three-equation eddy-viscosity model for Reynolds-averaged Navier-Stokes simulations of transitional flow[J]. Journal of Fluids Engineering, 2008, 130(12): 121401. DOI:10.1115/1.2979230 |
| [123] | Song B, Lee C H. A Favré averaged transition prediction model for hypersonic flows[J]. Science China Technological Sciences, 2010, 53: 2049–2056. DOI:10.1007/s11431-010-3173-7 |
| [124] | Fu S, Wang L. RANS modeling of high-speed aerodynamic flow transition with consideration of stability theory[J]. Progress in Aerospace Sciences, 2013, 58(2): 36–59. |
| [125] | Wang L, Fu S. Modelling flow transition in a hypersonic boundary layer with Reynolds-averaged Navier Stokes approach[J]. Science in China(Series G: Physics, Mechanics & Astronomy), 2009, 52(5): 768–774. |
| [126] | Wang L, Liu Z, Fu S. Numerical aspects of including crossflow effects in the recently proposed transition models[R]. AIAA 2016-3492, 2014. |
| [127] | Wang L, Xiao L, Fu S. A modular RANS approach for modeling hypersonic flow transition on a scramjet-forebody configuration[J]. Aerospace Science and Technology, 2016, 56: 112–124. DOI:10.1016/j.ast.2016.07.004 |
| [128] |
Shi Y Y, Bai J Q, Hua J, et al. Transition prediction based on amplification factor and Spalart-Allmaras turbulence model[J].
Journal of Aerospace Power, 2005, 30(7): 1670–1677.
(in Chinese) 史亚云, 白俊强, 华俊, 等. 基于放大因子与Spalart-Allmaras湍流模型的转捩预测[J]. 航空动力学报, 2005, 30(7): 1670–1677. |
| [129] | Langel C M, Chow R, van Dam C P. A comparison of transition prediction methodologies applied to high Reynolds number external flows[R]. AIAA 2016-0551, 2016. |
| [130] | Berry S, Daryabeigi K, Wurster K, et al. Boundary-layer transition on X-43A[J]. Journal of Spacecraft and Rockets, 2010, 47(6): 922–934. DOI:10.2514/1.45889 |
| [131] |
Zhu D H, Yuan X J, Shen Q, et al. Numerical simulation and mechanism analysis of hypersonic roughness induced transiton[J].
Chinese Journal of Theoretical and Applied Mechanics, 2015, 47(3): 381–388.
(in Chinese) 朱德华, 袁湘江, 沈清, 等. 高超声速粗糙元诱导转捩的数值模拟及机理分析[J]. 力学学报, 2015, 47(3): 381–388. DOI:10.6052/0459-1879-14-217 |
| [132] | Duan Z, Xiao Z, Fu S. Direct numerical simulation of hypersonic transition induced by isolated cylindrical roughness element[J]. Science China-Physics, Mechanics & Astronomy, 2014, 57(12): 2330–2345. |
| [133] | Duan Z, Xiao Z. Direct numerical simulation of geometrical parameter effects on the hypersonic ramp-induced transition[R]. AIAA 2014-2495, 2014. |
| [134] | Tu G, Hu Z, Sandham N D. Enhanced instability of supersonic boundary layer using passive acoustic feedback[J]. Physics of Fluids, 2016, 28: 024103. DOI:10.1063/1.4940324 |
| [135] |
Tu G H, Yan Z G, Zhao X H, et al. SA and SST turbulence models for hypersonic forced boundary layer transition[J].
Acta Aerodynautica et Astronautica Sinica, 2015, 36(5): 1471–1479.
(in Chinese) 涂国华, 燕振国, 赵晓慧, 等. SA和SST湍流模型对高超声速边界层强制转捩的适应性[J]. 航空学报, 2015, 36(5): 1471–1479. |
| [136] |
Zhan P G. Wind tunnel test methods for boundary layer transition on scramjet engine forebody[J].
Aeronautical Science & Technology, 2012, 6: 22–25.
(in Chinese) 战培国. 超燃冲压发动机前体边界层转捩风洞试验方法[J]. 航空科学技术, 2012, 6: 22–25. DOI:10.3969/j.issn.1007-5453.2012.01.007 |
| [137] |
Zhao H Y, Yi M R. Review of design for forced-transition trip of hypersonic inlet[J].
Acta Aerodynamica Sinica, 2014, 32(5): 623–627.
(in Chinese) 赵慧勇, 易淼荣. 高超声速进气道强制转捩装置设计综述[J]. 空气动力学学, 2014, 32(5): 623–627. DOI:10.7638/kqdlxxb-2014.0095 |
| [138] | Thompson R A, Hamilton H H, Berry S A, et al. Hypersonic boundary layer transition for X-33 phase Ⅱ vehicle[R]. AIAA 98-0867, 1998. |
| [139] | Reda D C. Review and synthesis of roughness-dominated transition correlations for reentry applications[J]. Journal of Spacecraft and Rockets, 2002, 39(2): 161–167. DOI:10.2514/2.3803 |
| [140] | McGinley C B, Berry S A, Kinder G R, et al. Review of orbiter flight boundary layer transition data[R]. AIAA 2006-2921, 2006. |
| [141] | Schneider S P. Hypersonic boundary-layer transition with ablation and blowing[J]. Journal of Spacecraft and Rockets, 2010, 47(2): 225–237. DOI:10.2514/1.43926 |
| [142] | Sandham N D, Lüdeke H. Numerical study of Mach 6 boundary-layer stabilization by means of a porous surface[J]. AIAA Journal, 2009, 47(9): 2243–2252. DOI:10.2514/1.43388 |
| [143] | Tritarelli R C, Lele S K, Fedorov A. Stabilization of a hypersonic boundary layer using a felt-metal porous coating[J]. Journal of Fluid Mechanics, 2015, 769: 729–739. DOI:10.1017/jfm.2015.156 |
| [144] |
Zhu D H, Liu Z L, Yuan X J. Mechanism of transition delay by porous surface in hypersonic boundary layers[J].
Chinese Journal of Computational Physics, 2016, 33(2): 163–169.
(in Chinese) 朱德华, 刘智勇, 袁湘江. 多孔表面推迟高超声速边界层转捩的机理[J]. 计算物理, 2016, 33(2): 163–169. |
| [145] | Wang X, Zhong X. The stabilization of a hypersonic boundary layer using local sections of porous coating[J]. Physics of Fluids, 2012, 24: 034105. DOI:10.1063/1.3694808 |
| [146] | Ren J, Fu S, Hanifi A. Stabilization of the hypersonic boundary layer by finite-amplitude steaks[J]. Physics of Fluids, 2016, 28: 024110. DOI:10.1063/1.4941989 |
| [147] | Fong K D, Wang X, Zhong X. Numerical simulations of roughness effect on the stability of a hypersonic boundary layer[J]. Computers & Fluids, 2014, 96: 350–367. |
| [148] | Fong K D, Zhong X. DNS and PSE study on the stabilization effect of hypersonic boundary layer waves using 2-D surface roughness[R]. AIAA 2016-3347, 2016. |
| [149] | Saric W, Reed H, White E. Stability and transition of three-dimensional boundary layers[J]. Annual Review of Fluid Mechanics, 2003, 35: 413–440. DOI:10.1146/annurev.fluid.35.101101.161045 |
| [150] | Schuele C Y. Control of stationary cross-flow modes in a Mach 3.5 boundary layer using patterned passive and active roughness[D]. Ph. D. thesis, University of Notre Dame, South Bend, Indiana, 2011. |
| [151] | Schuele C Y, Corke T C, Matlis E. Matlis E. Control of stationary cross-flow modes in a Mach 3.5 boundary layer using patterned passive and active roughness[J]. Journal of Fluid Mechanics, 2013, 718: 5–38. DOI:10.1017/jfm.2012.579 |
| [152] | Juliano T J, Adamczak D, Kimmel R. HIFiRE-5 flight test results[J]. Journal of Spacecraft and Rockets, 2015, 52(3): 650–663. DOI:10.2514/1.A33142 |
| [153] | Kimmel R L, Borg M P, Jewell J S. HIFiRE-5 boundary layer transition and HIFiRE-1 shock boundary layer interaction[R]. AFRL-RQ-WP-TR-2015-0151, 2015. |
| [154] | Shirouzu M, Yamamoto M. Overview of the HYFLEX project[R]. AIAA, 96-4524, 1996. |
| [155] | Barrio A M, Sudars M, Aulisio R, et al. EXPERT-the ESA experimental re-entry test-bed trajectory and mission design[R]. AIAA 2011-6342, 2011. |
| [156] | Clemente M D, Trifoni E, Walpot L, et al. Aerothermal rebuilding of plasma wind tunnel tests on the EXPERT capsule open flap[R]. AIAA 2012-3003, 2012. |
| [157] | Brazier J P, Schramm J M, Paris S, et al. An overview of HyFIE technical research project: cross testing in main european hypersonic wind tunnels on EXPERT body[J]. CEAS Space Journal, 2016, 8(3): 167–176. DOI:10.1007/s12567-016-0117-5 |
| [158] | Fedioun I, Orlik E. Boundary layer transition on the LEA hypersonic vehicle forebody[R]. AIAA 2012-5864, 2012. |
| [159] | Falempin F, Serre L. French flight testing program LEA-status in 2011[R]. AIAA 2011-2200, 2011. |
| [160] | Fedioun I, Orlik F. Boundary layer transition on the LEA hypersonic vehicle forebody[R]. AIAA 2012-5864, 2012. |
| [161] | Reshotko E. Boundary layer stability and transition[J]. Annual Review of Fluid Mechanics, 1976, 8: 311–349. DOI:10.1146/annurev.fl.08.010176.001523 |
| [162] | Reshotko E. Transition research using flight experiments[M]//Hussaini M Y, Voigt R G. Instability and Transition Vol.I. Springer-Verlag, 1990: 88-90. |