边界条件处理是CFD计算中极其重要的一个环节,直接关系到计算能否收敛、收敛速度快慢等方面。通常,边界条件的处理可以分为强边界条件和弱边界条件。强边界条件直接给定边界上的数值,而弱边界条件则是通过通量的方式间接引入边界贡献。在当前的Navier-Stokes方程数值计算中,物面边界为无滑移边界,一般采用强边界条件处理,即直接指定物面的速度。强边界条件概念直观,实现方便,是目前应用最多的Navier-Stokes方程物面边界条件处理方式。
近年来,物面弱边界条件也逐渐得到了研究和应用[1-4]。这是因为相比传统的强边界条件,弱边界条件具有以下优势:(1) 在有限差分方法中,弱边界条件配合分部求和算子(summation-by-parts operators),能够实现数学上可证明的稳定格式[5],而基于强边界条件尚无相应的结果;(2) Eliasson等人利用非结构网格求解器Edge研究了弱边界条件和强边界条件对于定常问题收敛性的影响,发现弱边界条件能够改善收敛性,并提高多重网格的收敛速度[6];(3) 在实现流场全隐式求解或者推导离散伴随方程的时候,需要推导Jacobian矩阵(或者其转置形式),由于强边界条件下物面点的残值和流场变量无关,因此Jacobian矩阵(或者其转置矩阵) 需要特别处理[7];而在弱边界条件下,可以直接推导相应的Jacobian矩阵,简化了物面边界的处理;(4) 最近,Stück发现在强边界条件下,传统的力计算公式不满足通量一致关系(flux consistency),因此强边界条件下计算力函数需要新的计算公式[8]。正因为具有上述优点,弱边界条件正逐步得到应用[9]。而目前国内关于物面弱边界条件的研究尚属空白。
本文提出了一种基于物面弱边界条件的非结构网格并行全隐式流场求解方法。首先,实现了非结构网格格点格式有限体积法的物面弱边界条件并推导了相应的Jacobian矩阵。与强边界条件相比,Jacobian矩阵可以直接从黏性通量表达式推导得到而无需特别处理。为了稳定求解湍流问题,改进了Shende等人的Spalart-Allmaras (S-A) 模型无条件保正性收敛方法(unconditionally positive-convergent implicit scheme,UPC)[10],提出了弱边界条件下的UPC方法,保证弱边界条件下S-A模型的收敛性和湍流工作变量的正值。采用多色高斯-塞德尔迭代法(multicolor Gauss-Seidel iteration,MCGS) 求解由流场方程全隐式时间推进和UPC方法所建立的线性方程组,并利用MPI实现并行计算。通过若干算例研究了弱边界条件的计算结果,并通过与强边界条件结果的对比,说明了弱边界条件所具有的优点。
1 物面弱边界条件的实现和Jacobian矩阵推导 1.1 物面弱边界条件的具体实现首先采用Eliasson等的方法[6]构造物面弱边界条件。对于Navier-Stokes方程的绝热物面边界,其对流通量的处理和Euler方程滑移物面边界的处理一致,因此只考虑其黏性通量。物面边界的黏性通量可以表示为:

|
(1) |
式中,下标0表示物面点,如图 1所示,μ表示有效黏性系数,u表示速度矢量,n0表示物面边界的单位外法向矢量,|S0|表示物面边界的面积,下标tl表示薄黏性层。需要注意的是,一般情况下薄黏性层表示的黏性通量和全NS黏性通量是不同的,但在物面边界上,由于动量方程没有切向的黏性通量贡献,因此两者相同,可以采用薄黏性层的黏性通量表示完整的黏性通量。
参考文献[11]提供了多种计算式(1) 中物面速度法向梯度∂u/∂n的表达式,这里选用其中的第一种,其表示为:

|
(2) |
式中,σ是罚系数,为了保证稳定性需要σ≥1/4[6],下标1表示沿物面法向的相邻内场点,如图 1所示,|x1-x0|是两点的距离,u0是物面点0的速度矢量,u1是流场内部点1的速度矢量。值得注意的是,由于式(2) 采用物面点和内场点的差分来近似计算物面速度法向梯度∂u /∂n,为了计算准确,需要流场内部点1位于物面点0的法向方向上,所以在网格生成的时候需沿着物面法向生成网格点,即要求二维情况下边界层内使用四边形单元,而在三维情况下使用三棱柱或者六面体单元。
1.2 物面弱边界条件的Jacobian矩阵推导为了实现流场全隐式求解,需要推导相应的Jacobian矩阵。在强边界条件下,由于物面边界点的速度直接设置为零,物面点的动量方程不起作用,物面点的残值和流场变量没有直接联系,因此需要采用类似有限元中Dirichlet边界条件的处理方式,将全局Jacobian矩阵中物面点的动量方程所对应的行消去,再将对应的对角项设为1,并将对应的右端项设为零。而在弱边界条件下,物面无滑移边界条件是利用式(1) 计算黏性通量的方式引入的,因此其Jacobian矩阵可以直接通过式(1) 的求导得到。这里给出二维情况下的推导,并只考虑对角项即物面点对自身黏性通量的贡献。
设W为守恒变量,直接推导黏性通量对守恒变量的Jacobian矩阵∂G0/∂W较为复杂,所以先考虑黏性通量对原始变量的Jacobian矩阵∂G0/∂Q,其中Q=[ρ u v p]T表示原始变量。设∂u/∂n=[∂u/∂n ∂v/∂n]T, 对式(2) 求导,可以得到:

|
(3) |
对式(1) 求导,并代入式(3) 的结果,有:

|

|
(4) |
式中,nx,ny为n0的分量。根据式(4) 可以得到:

|
(5) |
式中,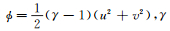
湍流模型的求解是CFD计算中一个较为复杂的问题。因为网格质量不好、数值离散误差等原因会造成计算过程中S-A模型的工作变量变为负值,使得计算失败。为了避免这个问题,可以直接用max函数进行截断,但是这样往往会造成不连续而影响收敛。针对这个问题,Mor-Yossef等人在两方程模型上提出了无条件保正性收敛方法(UPC),通过构造特别的迭代矩阵使得每一步的工作变量都是非负值,并且能够保证湍流模型计算的收敛[12-13]。随后,Shende等人又将其发展到S-A模型上,实现了强边界条件下S-A模型的稳定计算[11]。本文改进了该方法,提出了弱边界条件下的UPC方法,用于湍流的稳定求解。
S-A模型的控制方程表达式为:

|
(6) |
式中,ν表示湍流工作变量,v表示运动粘度,uj表示j方向的速度分量,d表示物面距离,其它各项和相关常数定义可见参考文献[14]。根据物理特性,可以将式(6) 各项分为对流项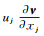
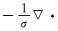
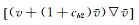
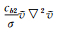
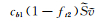
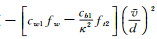
对于每个控制体i,空间离散后的半离散形式S-A模型可以写为:

|
(7) |
式中,Ri表示控制体i的对流项、扩散项和反扩散项综合起来的残值,Ωi表示控制体i的体积,Si表示由生成项和消耗项组成的源项。采用一阶后向Euler差分离散时间项,则得到全局线性方程组:

|
(8) |
考虑构造具有良好数值特性的矩阵M来近似湍流模型方程的Jacobian矩阵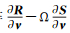
(a) M是M矩阵[15];
(b) -Rn+ΩSn+ Mνn是非负矢量,即每个分量都是非负值。
参考文献[13]证明了如果矩阵M满足上述2个条件,则全隐式时间推进

|
(9) |
具有无条件收敛性和保正性,即ν始终为非负矢量。
基于这个结果,需要构造M矩阵并且使其同时满足条件(b)。参考文献[15]对于构造M矩阵提供了一个充分条件:如果一个矩阵满足下面3个要求,则该矩阵为M矩阵:(1) 矩阵的所有对角线元素大于零;(2) 矩阵的所有非对角线元素非正;(3) 对角占优,即每行的对角线元素大于该行所有非对角元素的绝对值之和。根据这个充分条件,下面分别考虑式(6) 中对流项、扩散项、反扩散项、源项的近似Jacobian矩阵构造。
令Rinv表示对流项的残值,由于对流项采用一阶逆风格式进行离散,那么得到

|
(10) |

|
(11) |

|
(12) |

|
(13) |
这里,J表示控制体i和控制体j的交界面,SJ表示交界面面积,ui, j,vi, j,wi, j表示控制体i/j的速度分量,nx、ny、nz为单位法向矢量。根据式(10)~(13),可以得到:

|
(14) |
因为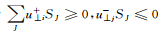

|
(15) |
即对角线元素大于零,非对角线元素非正,但无法满足对角占优的要求。为了使得对角占优,令:

|
(16) |

|
(17) |
则式(14) 可以写为:

|
(18) |
那么

|
(19) |
式(19) 表示对流项的近似Jacobian矩阵。可知:

|
(20) |

|
因此对流项的近似Jacobian矩阵满足上述的充分条件的要求。
对于扩散项,其离散形式为:

|
(21) |

|
(22) |
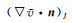

|
(23) |
这里,lij表示边ij的长度,rij表示边ij的单位边矢量,nJ控制体界面J的单位法向矢量。因此有:

|
(24) |
根据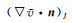

|
(25) |
式(25) 表示扩散项的近似Jacobian矩阵。考虑到整体Jacobian矩阵中还包括对流项和反扩散项的矩阵构造,所以扩散项的矩阵构造只要求对角项大于零而非对角项小于零,而不要求对角占优。
对于反扩散项,其离散形式为:

|
(26) |

|
(27) |
采用类似耗散项的处理,有

|
(28) |
考虑到

|
(29) |
令

|
(30) |
这里反耗散项的矩阵构造本身也不满足M矩阵的充分条件,但是综合对流项、耗散项和反耗散项的矩阵构造以后仍然满足M矩阵的充分条件。
接着考虑边界点对近似Jacobian矩阵的贡献。对于远场边界,由于远场工作变量梯度较小,所以其耗散项和反耗散项较小,忽略它们的贡献,只考虑远场边界对流项的贡献。远场边界的对流项残值可表示为

|
(31) |

|
(32) |

|
(33) |

|
(34) |
这里,ufar,vfar,wfar为远场边界的速度,由流场的特征边界条件得到,Sfar为远场边界面积。相应的矩阵构造为:

|
(35) |
对于对称边界,由于对称边界的法向速度为零,并且工作变量的法向梯度为零,因此没有通量贡献,也没有Jacobian矩阵贡献。
对于物面边界,由于物面上工作变量为零,因此没有对流项和反扩散项的贡献,只有扩散项的贡献。弱边界条件可以按照类似式(2) 的方式计算工作变量的法向梯度:

|
(36) |
这里,ϕ为S-A模型弱边界条件的罚系数。那么物面边界的扩散项对残值的贡献为:

|
(37) |
式中,Swall为物面边界面积。相应的矩阵构造为:

|
(38) |
对于源项,将其表示为:

|
(39) |
对应的矩阵构造为:

|
(40) |
这里采用类似参考文献[14]中源项的处理方法,用max函数限制源项Jacobian矩阵为非负值。
综合对流项、扩散项、反扩散项和源项的矩阵构造,得到:

|

|
(41) |
式(41) 中的近似矩阵构造满足了UPC的条件(a),但由于实际求解的是非线性方程组,每个伪时间步迭代中式(41) 的右端项都会改变,所以条件(b) 不一定能满足。令

|
(42) |
如果Φ < 0,令:

|
(43) |
系数1.5考虑了计算机采用浮点数表示实数而带来数值精度影响。将式(43) 加入式(41) 的对角项,得到:

|
(44) |
由于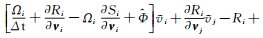
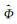
需要说明的是,由于UPC方法采用了特别的矩阵构造,为了保证UPC特性,在式(44) 的求解过程中必须保证矩阵不发生改变,所以不能使用LU-SGS这类引入矩阵分解误差的求解方法。为此,本文采用多色高斯-塞德尔迭代法求解线性方程组,这是因为高斯-塞德尔迭代中矩阵保持不变,因此保证了UPC特性。其具体过程在下节详细叙述。
3 多色高斯-塞德尔迭代法流场的全隐式时间推进和上一节介绍的UPC方法都需要在每个伪时间步中求解大型稀疏线性方程组。同时考虑到上文所述的UPC求解不能引入矩阵分解误差的要求,因此采用多色高斯-塞德尔迭代法(MCGS) [17]求解线性方程组,并利用MPI实现了该方法的分布式并行计算。
待求解的线性方程组可以表示为:

|
(45) |
这里,A表示(大型稀疏) 矩阵,x为解向量,b为已知
右端列向量。传统的高斯-塞德尔迭代法可以写为:

|
(46) |
式中,i表示点的编号,对应矩阵的第i行,上标m表示迭代计数,aii为矩阵第i行的对角项,bi为第i行对应的右端项,Adj(i) 表示点i的相邻点,aij为矩阵第i行的非对角项,n为点数,即解向量的维数。为了实现并行求解,首先对网格进行染色。非结构网格点周围存在数量不一的相邻点,需要多种颜色进行染色,来保证每个点和周围相邻点的颜色不同,如图 2所示的网格就需要6种颜色进行染色。本文采用最常用的贪心染色算法[18],其流程如图 3所示。数值测试显示,非结构网格染色所需的颜色数量大致在5~13之间。染色完成后,染成同一种颜色的点相互之间不相邻,没有数据依赖,因此可以按照颜色顺序进行并行更新。整个并行MCGS迭代法的计算过程如图 4所示。图中在Loop3循环完成以后,采用MPI非阻塞通信更新分区边界上相应颜色的ghost点的值,就实现了并行求解。

|
| 图 2 多色染色 Fig. 2 Multicoloring |

|
| 图 3 贪心染色算法 Fig. 3 Greedy multicoloring algorithm |

|
| 图 4 并行多色高斯-塞德尔迭代法 Fig. 4 Parallel multicolor Gauss-Seidel iteration |
4 计算结果 4.1 NACA0012翼型的层流流动
首先考虑二维层流流动的结果。计算网格如图 5所示,物面附近采用四边形单元而其它部分采用三角形单元,网格单元数为13156,网格点数为8741。计算状态为马赫数Ma=0.5,迎角α=1°,Reynolds数Re=5000。对流通量采用JST (Jameson-Schmidt-Turkel) 格式计算[19]。而在黏性通量的计算中,先由Green-Gauss公式得到原始变量的梯度,再采用基于边修正的方法计算控制体边界的梯度[20]。前10步CFL数从10线性增长至10000,然后维持为10000。MCGS迭代次数为15次。计算平台为MacBook Pro 15(2013 Later),编译器为GFortran 4.9,采用串行方式运行。

|
| 图 5 NACA0012翼型层流流动网格 Fig. 5 NACA0012 airfoil mesh for laminar flow |
图 6给出了弱边界条件下物面罚系数σ分别取1、10、100时的翼型表面压强系数Cp的分布情况,同时为了与强边界条件的结果进行对比,还给出了开源CFD代码SU2[21]在相同状态下采用强边界条件计算的结果(需要说明的是,SU2的对流通量计算同样采用JST格式,但黏性通量计算方法和边界条件处理与本文方法不同)。可以看到4条曲线在除了后缘的位置以外几乎完全重合。图 7给出了后缘部分的放大图,可以看到随着罚系数的增大,弱边界条件的结果将趋向于强边界条件的结果。

|
| 图 6 NACA0012翼型层流流动表面压强系数Cp分布 Fig. 6 Cp distribution for NACA0012 airfoil laminar flow |

|
| 图 7 后缘Cp分布 Fig. 7 Cp distribution at the trailing edge |
图 8给出了物面罚系数σ分别取1、10、100时以及SU2计算的翼型表面摩擦力系数Cf的分布情况,可以看出4条曲线几乎完全重合,而图 9给出了后缘部分的放大图,4条曲线仍然重合得很好。表明采用弱边界条件可以得到和强边界条件一致的结果。

|
| 图 8 NACA0012翼型层流流动表面摩擦力系数Cf分布 Fig. 8 Cf distribution for NACA0012 airfoil laminar flow |

|
| 图 9 后缘Cf分布 Fig. 9 Cf distribution at the trailing edge |
图 10显示了物面罚系数σ分别取1、10、100时翼型上表面一点以及附近点的速度矢量和速度大小。从图中可以看出,由于使用了弱边界条件,壁面点的速度不再为零,但是其数值大小比其法向点小的多,而且随着罚系数的增大将更加趋近于零,因此其对流场计算的影响可以忽略,表明了弱边界条件可用于黏性流动计算。

|
| 图 10 不同罚系数下物面点和附近点的速度矢量方向和大小 Fig. 10 Velocity vector directions and magnitudes of a wall node and near nodes at different penalty coefficients |
图 11给出了物面罚系数σ分别取1、10、100时密度的收敛历史,可以看到不同的罚系数对于收敛影响很小,为了更接近实际的无滑移条件,计算中可以采用较大的罚系数。

|
| 图 11 不同罚系数下密度收敛历史 Fig. 11 Convergence histories of density at different penalty coefficients |
4.2 RAE2822翼型的湍流流动
本算例说明本文方法用于二维湍流计算的情况。计算网格如图 12所示,物面附近采用四边形单元捕捉湍流边界层,而其余部分采用三角形单元,网格单元数为22842,网格点数为13937。计算状态为马赫数Ma=0.729,迎角α=2.31°,Reynolds数Re=6.5×106。对流通量和黏性通量计算方法同上。流场方程和湍流模型方程的CFL数在前10步从10线性增长至1000,然后维持为1000。MCGS迭代次数均为15次。物面罚系数均取100。计算平台和上例一样,同样采用串行计算。

|
| 图 12 RAE2822翼型湍流流动网格 Fig. 12 RAE2822 airfoil mesh for turbulent flow |
图 13给出了本文采用弱边界条件和SU2采用强边界条件计算的表面压强系数以及和实验数据[22]的对比。可以看到,本文的计算结果和SU2的结果几乎重合,与实验数据也吻合较好,表明本文基于弱边界条件的求解体系能够有效地计算湍流流动,得到与传统强边界条件一致的结果。

|
| 图 13 RAE2822翼型湍流流动表面压强系数Cp分布 Fig. 13 Cp distribution for RAE2822 airfoil turbulent flow |
下面利用该算例来说明不同边界条件处理对力计算的影响。对于力的计算,可以采用基于物面或者基于远场的方法,如图 14所示,左图表示对整个物面积分计算力,右图表示对整个远场积分计算力。其标准计算公式可以表示为[8]:

|
(47) |
这里dk为单位矢量,对于阻力取来流方向,对于升力取与来流垂直方向,Γ0根据不同的力计算方法表示远场边界或者壁面边界,可见图 14,δkl为克罗内克符号,nl为单位外法向矢量,ΔΓ为表面单元面积。由于流场中没有额外的力源,理论上基于物面或者基于远场这两种方法计算得到的力应该是完全一样的。但最近Stuck[8]发现,在强边界条件下,两种方法使用式(47) 计算出来的力是不一样的,存在着通量不一致(flux inconsistency) 的问题。这是因为强边界条件直接给定物面点的速度,动量方程不起作用,使得物面处没有严格考虑通量项的贡献,而在远场边界,特征边界条件是一种弱边界条件处理,是通过通量的方式引入的,因此远场处的所有通量项对于力的计算都是有贡献的,这样造成了整个计算区域的通量贡献不守恒。而采用了弱边界条件以后,物面边界条件也是以通量的方式引入的,同时整个流场采用守恒形式有限体积法离散,因此整个流场区域保持通量守恒,自动满足了通量一致关系。表 1给出了强边界条件和弱边界条件下由基于物面和基于远场方法所得到的升力系数和阻力系数的值。可以看到,在强边界条件下,基于物面和基于远场的方法计算得到的升力系数和阻力系数是不同的,表现出了通量不一致的问题,这与Stuck的结论一致。为了使得强边界条件下两种方法计算的力相同,必须采用参考文献[8]提出的公式而不能使用式(47)。而在弱边界条件下,基于物面和基于远场方法计算得到的升力系数和阻力系数在机器精度的范围内一致,自动满足通量一致关系,无需任何特别处理,表明弱边界条件相比强边界条件在计算力的时候更加方便可靠。
| strong farfield-based | strong wall-based | weak farfield-based | weak wall-based | |
| CL | 0.7311326188 | 0.7308915699 | 0.7311326187 | 0.7311326187 |
| CD | 0.0134902824 | 0.0133283580 | 0.0134902824 | 0.0134902824 |
4.3 ONERA M6机翼的湍流流动
接下来研究本文方法应用于三维湍流流场求解的情况。计算采用非结构混合网格,如图 15所示,边界层内采用三棱柱单元,远场采用四面体单元,过渡部分采用金字塔单元。网格单元数为915923,网格点数为2323893。计算状态为马赫数Ma=0.8395,迎角α=3.06°,Reynolds数Re=11.72×106。对流通量和黏性通量计算方法同上。流场方程和湍流模型方程的CFL数在前10步从10线性增长至500,然后维持为500。MCGS迭代次数均为15次。物面罚系数均取10000。计算环境为天津超级计算中心天河1A的2个计算节点。每个节点拥有2个Intel Xeon X5670处理器,每个处理器拥有6个核心,主频为2.93GHz,操作系统为RHEL,编译器为Intel Fortran 11.1,MPI环境为天河自主实现的MPI。计算采用24核并行计算。

|
| 图 15 ONERA M6机翼湍流流动网格 Fig. 15 ONERA M6 wing mesh for turbulent flow |

|
| 图 16 ONERA M6机翼湍流流动展向不同位置表面压强系数Cp分布 Fig. 16 Cp distribution at different spanwise sections for ONERA M6 wing turbulent flow |
图 16给出了本文和SU2计算的机翼展向44%和65%这两个位置的压强系数分布以及同实验数据[23]的对比。本文的计算结果与SU2的结果非常接近,因此在各展向位置的压强系数分布曲线几乎完全重合,并且和实验数据也吻合得很好,说明本文的弱边界条件适用于三维湍流流动的计算。
表 2给出了该算例中采用强边界条件和弱边界条件时由基于物面和基于远场方法所得到的升力系数和阻力系数的值。可以看到,和二维情况类似,强边界条件下同样出现了通量不一致的问题,而弱边界条件计算得到的力系数一致,自动满足通量一致关系。
| strong farfield-based | strong wall-based | weak farfield-based | weak wall-based | |
| CL | 0.2007443436 | 0.2012650319 | 0.2007443722 | 0.2007443089 |
| CD | 0.0143444907 | 0.0132698254 | 0.0143444568 | 0.0143444081 |
图 17对本文方法的并行加速比和理想加速比进行了对比。可以看出当CPU核心数较少时,并行效率较高,而当CPU核心数达到24核时并行效率约为77%。因为本文采用的MCGS迭代,在每次循环一种颜色时都需要通信一次,通信量较大,如果需要进一步改进并行效率,后续将考虑通信和计算重叠的方法或者采用通信量更小的迭代方法。

|
| 图 17 ONERA M6机翼湍流流动计算并行加速比 Fig. 17 Parallel speedup for ONERA M6 wing turbulent flow |
5 结论
本文基于近年来逐步发展起来的物面弱边界条件,建立了并行全隐式流场求解方法。在非结构网格格点格式有限体积法中实现了物面弱边界条件,并推导了相应的Jacobian矩阵。其Jacobian矩阵可以直接由黏性通量表达式推导得到,简化了流场全隐式计算的推导处理。在此基础上,提出了弱边界条件下S-A模型的无条件保正性收敛方法,能够保证弱边界条件下S-A模型求解的收敛性和湍流工作变量的正值,实现了湍流流动的稳定求解。采用多色高斯-塞德尔迭代法求解全隐式时间推进和S-A模型无条件保正性收敛方法所得到的线性方程组,并利用MPI实现并行计算。对二维、三维条件下的若干层流和湍流问题进行了计算分析,结果表明:(1) 随着物面罚系数的增大,弱边界条件下的结果趋向于强边界条件的结果;(2) 对于力的计算,弱边界条件保证了整个流场的通量守恒,自动满足通量一致关系,无需特别的处理,因而比传统的强边界条件更加方便可靠。
后续研究工作将深入以下几个方面:(1) 力计算的通量一致问题与对偶一致问题(dual consistency)[24]密切相关,近年来正得到越来越多的重视,对于计算结果的影响需要进一步研究;(2) 本文目前的并行效率在CPU数量增多以后下降较为明显,需要研究提高并行效率的策略,比如通信和计算重叠的方法,以便用于更大规模的问题。
| [1] | NORDSTROM J, ERIKSSON S, ELIASSON P. Weak and strong wall boundary procedures and convergence to steady-state of the Navier-Stokes equations[J]. Journal of Computational Physics, 2012, 231(14):4867–4884. DOI:10.1016/j.jcp.2012.04.007 |
| [2] | BAZILEVS Y, MICHLER C, CALO VM, HUGHES TJR. WeakDirichlet boundary conditions for wall-bounded turbulent flows[J]. Computer Methods in Applied Mechanics and Engineering, 2007, 196(49-52):4853–4862. DOI:10.1016/j.cma.2007.06.026 |
| [3] | BAZILEVS Y, HUGHES TJR. Weak imposition of Dirichlet boundary conditions in fluid mechanics[J]. Computers & Fluids, 2007, 36(1):12–26. |
| [4] | CHANDRASHEKAR P. Finite volume discretization of heat equation and compressibleNavier-Stokes equations with weak Dirichlet boundary condition on triangular grids[J]. International Journal of Advances in Engineering Sciences and Applied Mathematics, 2016, 8(3):174–193. DOI:10.1007/s12572-015-0160-z |
| [5] | FISHER TC, CARPENTER MH. High-order entropy stable finite difference schemes for nonlinear conservations laws:Finite domains[J]. Journal of Computational Physics, 2013, 252:518–557. DOI:10.1016/j.jcp.2013.06.014 |
| [6] | ELIASSON P, ERIKSSON S, NORDSTROM J. The influence of weak and strong solid wall boundary conditions on the convergence to steady-state of the Navier-Stokes equations. AIAA 2009-3551[R]. Reston:AIAA, 2009. |
| [7] | GILES MB, DUTA MC, MULLER J-D, PIERCE NA. Algorithm developments for discrete adjoint methods[J]. AIAA Journal, Reston:AIAA, 2009, 41(2):198–205. |
| [8] | STUCK A. Anadjoint view on flux consistency and strong wall boundary conditions to the Navier-Stokes equations[J]. Journal of Computational Physics, 2015, 301:247–264. DOI:10.1016/j.jcp.2015.08.022 |
| [9] | LAKSHMINARAYAN V, SITARAMAN J, ROGET B, WISSINK A. Development and validation of a multi-strand solver for complex aerodynamic flows. AIAA 2016-1581[R]. Reston:AIAA, 2016. |
| [10] | SHENDE N, MOR-YOSSEF Y. Robust implementation of the Spalart-Allmaras turbulence model for unstructured grid[C]. European Conference on Computational Fluid Dynamics 2010, 2010. |
| [11] | ELIASSON P, NORDSTROM J. The influence of viscous operator and wall boundary conditions on the accuracy of the Navier-Stokes equations. AIAA 2013-2956[R]. Reston:AIAA, 2013. |
| [12] | MORYOSSEF Y, LEVY Y. Unconditionally positive implicit procedure for two-equation turbulence models:Appliciation to k-ω turbulence models[J]. Journal of Computational Physics, 2006, 220(1):88–108. DOI:10.1016/j.jcp.2006.05.001 |
| [13] | MOR-YOSSEF Y, LEVY Y. The unconditionally positive-convergent implicit time integration scheme for two-equation turbulence models:Revisited[J]. Computers & Fluids, 2007, 38(10):1984–1994. |
| [14] | SPALART P, ALLMARAS S. A one-equation turbulence model for aerodynamic flows. AIAA 92-0439[R]. Reston:AIAA, 1992. |
| [15] | BERMAN A, PLEMMONS R. Nonnegative matrices in the mathematical sciences[M]. New York: Academic Press, 1979. |
| [16] | SVARD M, NORDSTROM J. Stability of finite volume approximations for the Laplacian operator on quadrilateral and triangular grids[J]. Applied Numerical Mathematics, 2004, 51(1):101–125. DOI:10.1016/j.apnum.2004.02.001 |
| [17] | SATO Y, HINO T, OHASHI K. Parallelization of an unstructured Navier-Stokes solver using a multi-color ordering method for OpenMP[J]. Computers & Fluids, 2013, 88(1):496–509. |
| [18] | SAAD Y. Iterative methods for sparse linear systems, second edition[M]. Philadelphia: Society for Industrial and Applied Mathematics, 2003. |
| [19] | JAMESON A, SCHMIDT W, TURKEL E. Numerical solution of the Euler equations by finite volume methods using Runge-Kutta time-stepping schemes. AIAA 1981-1259[R]. Reston:AIAA, 1981. |
| [20] | HASELBACHER A, BLAZEK J. Accurate and efficient discretization of Navier-Stokes equations on mixed grids[J]. AIAA Journal, Reston:AIAA, 2000, 38(11):2094–2102. DOI:10.2514/2.871 |
| [21] | ECONOMON TD, PALACIOS F, COPELAND SR, LUKACZYK TW, ALONSO JJ. SU2:an open-source suite for multiphysics simulation and design[J]. AIAA Journal, Reston:AIAA, 2016, 54(3):828–846. DOI:10.2514/1.J053813 |
| [22] | COOK P, MCDONALD M, FIRMIN M.Aerofoil RAE 2822-pressure distributions, and boundary layer and wake measurements. AGARD Report AR 138[R]. AGARD, 1979. |
| [23] | SCHMITT V, CHARPIN F. Pressure distribution on the ONERA-M6-Wing at transonic Mach numbers. AGARD Report AR 138[R]. AGARD, 1979. |
| [24] | HICKEN JE, ZINGG DW. Dual consistency and functional accuracy:a finite-difference perspective[J]. Journal of Computational Physics, 2014, 256:161–182. DOI:10.1016/j.jcp.2013.08.014 |





