在吸气式高超声速飞行器关键难题攻关中,激波-激波干扰带来的高热、力载荷是需要予以关注的重要一环。飞行器前体压缩激波与进气道唇口弓形激波干扰是一类非常典型的问题,激波干扰在唇口局部区域产生极高的热、力载荷,这对飞行器部件的使用寿命和飞行安全都提出了严峻的考验。1967年X-15飞行器虽然实现了大气层内的载人高超声速飞行,但在飞行试验中也暴露出飞行器因激波干扰而产生的严重烧蚀问题[1]。之后,Edney[2]系统地研究了激波-激波干扰,归纳出六类激波干扰,其中第Ⅳ类激波干扰以其产生超声速射流,引起壁面局部区域压力和热流剧增而广受关注。针对第Ⅳ类激波干扰,国内外学者做了大量的实验[3-8]和数值[9-16]研究工作。Keyes & Hains[3],Wieting & Holden[4],Boldyrev et al.[7]通过风洞实验和激波-膨胀波理论分析了激波干扰流场结构,对壁面压力、热流进行了预测,为数值计算提供了丰富的实验数据。Wieting & Holden[4]指出第Ⅳ类激波干扰具有非定常性,实验条件下流动振荡频率在3~10kHz之间。Gaitonde & Shang[9]采用改进的Steger-Warming格式求解了第Ⅳ类激波干扰的非定常流场,计算的振荡频率为32kHz。Zhong[12]、Chu & Lu[13]采用高阶格式求解二维Navier-Stokes方程,分析和探讨了相关非定常流场的特征。上述数值模拟是基于Wieting & Holden[4]的实验展开的,但计算得到的振荡频率与实验所得到的3~10kHz相差很大。
大量的实验与数值结果向我们展示了第Ⅳ类激波干扰的流动特征,但其非定常振荡的机理并没有完全弄清楚。振荡反馈机制的形成机理,振荡频率和幅值的影响因素仍需要深入的研究,而找寻合理的流动控制方法来避免或者抑制第Ⅳ类激波干扰振荡现象是很有意义同时极富挑战性的工作。受限于实验上流动显示方面的精细刻画以及传感器的时空分辨能力,现有的实验结果中尚未见到令人满意的非定常振荡的数据。相比实验研究,数值模拟更容易获得激波干扰的流场细节,更适合做非定常激波干扰的参数研究。
本文以高超声速飞行器前体激波与进气道唇口激波可能发生的第Ⅳ类激波干扰为关注对象,着重对其中超声速射流的非定常特性、关键影响因素及规律进行数值考察,分析入射激波位置、入射激波强度、钝头体外形等因素对第Ⅳ类激波干扰非定常特性和壁面压力、热流分布的影响,加深对其流动机理的认识,并力图为相关工程应用提供有价值的参考。
1 数值方法及验证本文采用VAS2D程序[17](two-dimensional & axisymmetric vectorized adaptive solver) 计算第Ⅳ类激波干扰非定常振荡问题。该程序基于有限体积方法,采用自适应的非结构四边形网格和MUSCL-Hancock格式求解二维可压缩Navier-Stokes方程,在时间和空间上具有二阶精度。在流场参数变化剧烈的区域自适应加密网格(如图 1所示),减小因网格尺度带来的数值耗散,达到精确刻画流场的效果。

|
| 图 1 计算网格 Fig. 1 Computational meshes |
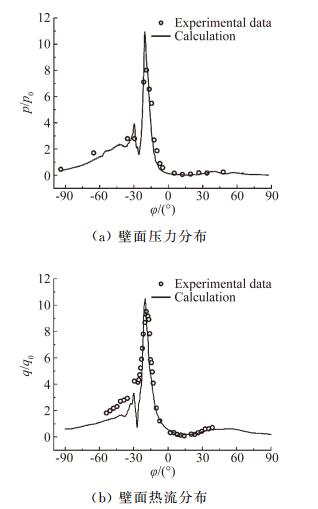
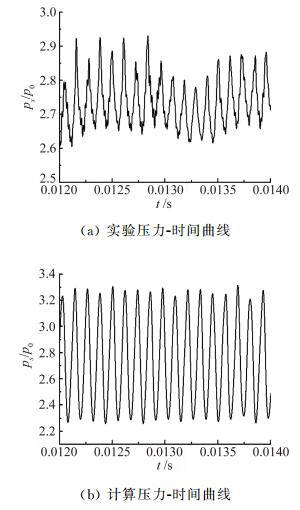
为了验证该数值方法在计算第Ⅳ类激波干扰问题上的可靠性,分别参照Wieting & Holden[4]和笔者前期工作[18]中的实验进行了模拟。文献[4]中实验条件马赫数M∞=8.03,静温T∞=111.56K,静压p∞=985.06Pa,圆柱半径R=38.1mm。计算与实验结果对比如图 2所示,圆柱壁面压力和热流分布吻合较好,图中p0和q0分别表示无干扰时圆柱驻点压力和热流。文献[18]为笔者前期开展的一种非定常振荡实验,实验条件马赫数M∞=6.0,静温T∞=115K,静压p∞=800Pa,圆柱半径R=15mm。如图 3所示,计算的压力-时间曲线与实验结果吻合也较好,图中ps为监测点压力,经过FFT变换,实验压力信号频率为8.90kHz,计算压力信号频率为8.44kHz,说明该数值方法在计算第Ⅳ类激波干扰非定常振荡问题上是可信的。
2 数值模拟条件
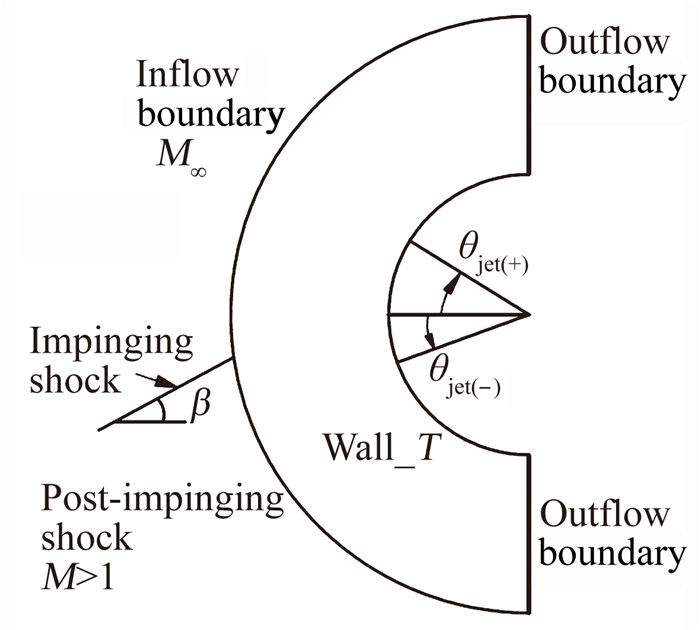
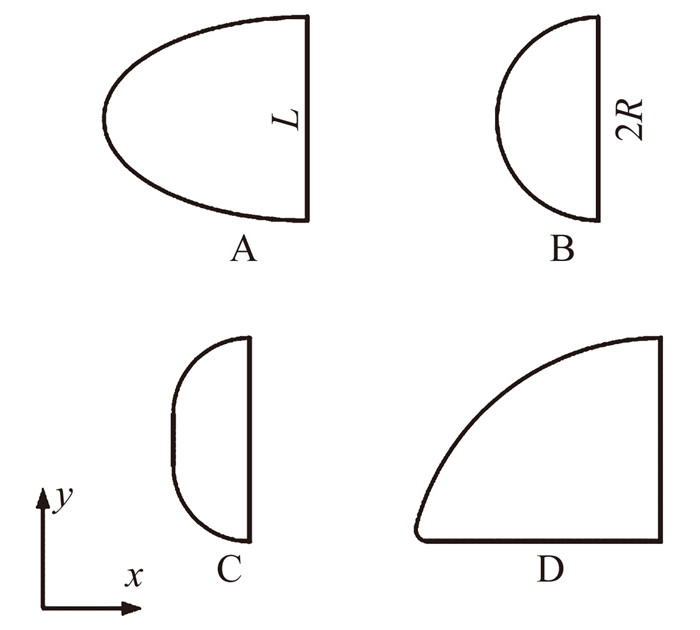
来流条件(见表 1) 参照文献[4]中的实验条件设置,计算域和边界条件如图 4所示,入射斜激波由Rankine-Hugoniot关系引入,A点为斜激波入射点,β为激波角,出口边界条件为无反射边界,壁面取等温无滑移条件。图 5给出了4种典型的钝头体外形,包括对称和非对称外形[19],各个外形在Y方向上的特征长度均为L=2R,外形A为椭圆,长短轴之比为2,B为圆形,C由2个半径0.75R的圆弧和与之相切的直线段连接而成,D由相切的两段圆弧和直线段组成,大圆弧半径为2.5R,大小圆弧半径比为21.5。
|
| 图 4 边界条件 Fig. 4 Boundary conditions |
|
| 图 5 四种钝头体外形 Fig. 5 Four different geometries used in this paper |
| Mach number | 8.03 |
| Temperature, K | 111.56 |
| Pressure, Pa | 985.06 |
| Wall temperature, K | 294.44 |
| Cylinder radius (R), mm | 38.1 |
选取这四种几何外形的目的是期望在相同的参考迎风面积条件下,考察驻点区域钝度及对称性的改变对激波干扰结果的影响,其中圆柱形B作为基准构型。此外,计算时还通过改变入射激波入射点的位置、入射激波强度来分别探讨这些因素对第Ⅳ类激波干扰壁面压力、热流分布和非定常特性的影响规律。
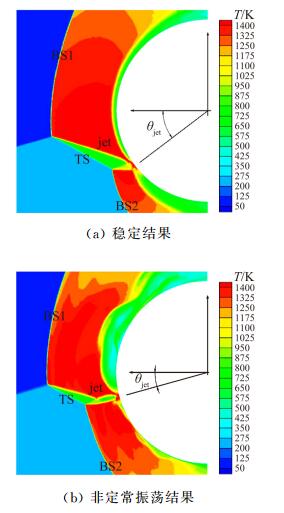
3 结果与分析 3.1 激波干扰流场结构计算时,通过改变激波入射点的位置得到不同的干扰结果,随着激波入射点位置下移,射流冲击点位置也下移,射流冲击角度减小。对于基准B外形,图 6为不同射流冲击角度的激波干扰的温度云图,其中θjet(对应图 4中θjet) 表示射流冲击角度,BS1、BS2为弓形激波上、下部分,透射激波TS波后为超声速射流Jet。图 6(a)为稳定结果,流场波系结构稳定,亚声速区域的温度等值线光滑;图 6(b)为非定常振荡结果,剪切层不稳定性和射流冲击壁面产生的扰动在弓形激波波后亚声速区域中传播,流场结构周期性波动,温度等值线起伏明显。
|
| 图 6 第Ⅳ类激波干扰温度云图 Fig. 6 Flow features shown by the temperature contours for the type Ⅳ shock interaction |
3.2 入射激波位置和强度的影响
选取3组不同强度的入射激波,激波角分别为16.0°、17.1°和18.1°。计算时,固定入射激波强度,在Y方向上改变激波入射点位置从而得到不同入射激波位置下的壁面压力,采用Strouhal数对干扰流场的非定常特性进行描述(St=fL/U,f、L和U分别表示振荡频率、钝头体特征长度和来流速度)。
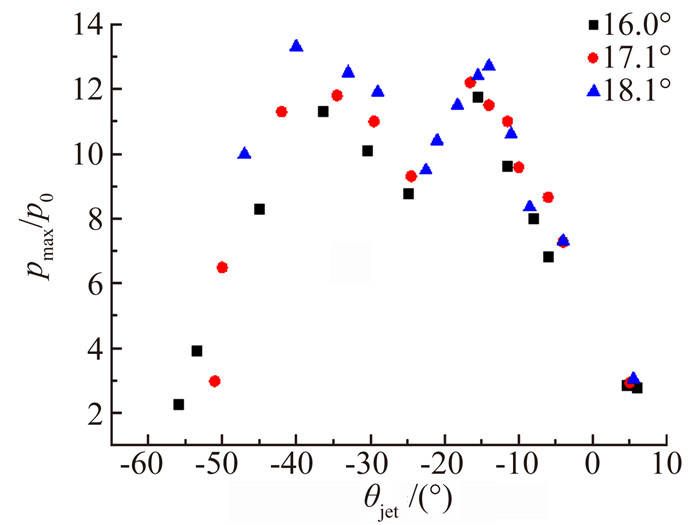
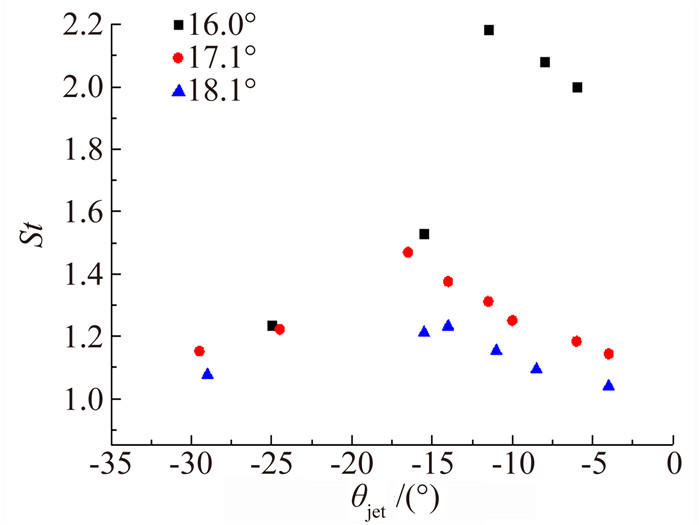
图 7和图 8分别给出了3组不同强度的入射激波与圆形钝头体弓形激波干扰后壁面压力峰值均值以及Strouhal数分布规律,横轴表示超声速射流冲击角度θjet,p0为无干扰时圆柱驻点处压力,pmax为壁面压力峰值平均值(即超声速射流冲击点位置的压力)。
|
| 图 7 入射激波条件对壁面压力峰值分布影响 Fig. 7 Effect of impinging shock on the peak pressure amplification |
|
| 图 8 入射激波条件对Strouhal数分布影响 Fig. 8 Effect of impinging shock on the Strouhal number |
对于入射激波角为16.0°、17.1°和18.1°这3组算例,随着射流冲击点下移,射流角度θjet减小,压力峰值均值经历上升-下降-上升-下降的过程,出现两个明显的峰值,Strouhal数则呈现先增大后减小的趋势。随着入射激波强度增大,pmax/p0略有上升,Strouhal数则明显减小。可以看到,超声速射流冲击壁面角度不同,第Ⅳ类激波干扰的流动特征明显不同。根据射流冲击角度的大小对第Ⅳ类激波干扰进行分类:当θjet大于0°时射流未接触或者擦过壁面流向下游,流动基本呈现稳定特征;θjet在0°~-15°之间时,流动具有非常明显的非定常振荡特征;θjet在-15°~-30°之间为过渡区域,流动可能稳定也可能是非定常的;θjet小于-30°,流动呈现稳定状态。
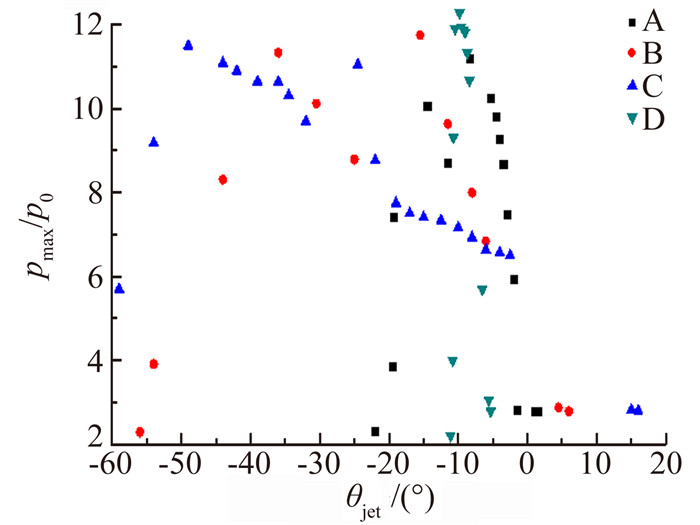
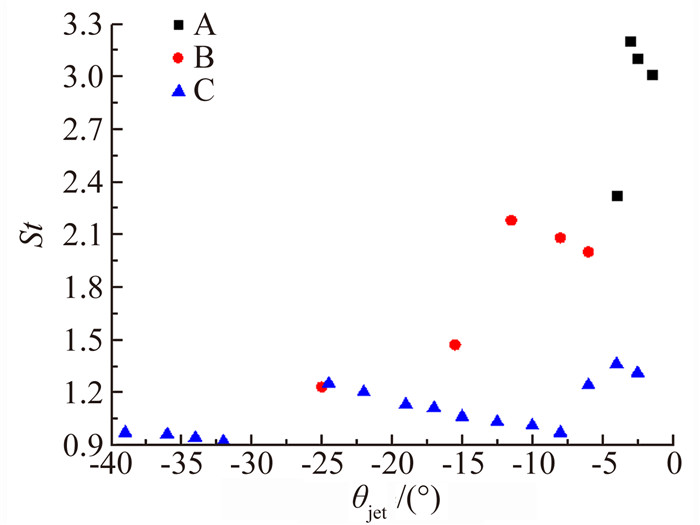
3.3 钝头体外形的影响鉴于基准构型B在16.0°激波角时的非定常特性更为显著,在16.0°激波角下对不同外形钝头体的激波干扰进行了计算。从图 9、10(A、B、C和D分别代表图 5中4种外形) 可知,钝头体外形对第Ⅳ类激波干扰引起的壁面压力和Strouhal数有显著的影响。对于A、B和C三种对称外形,随着入射点位置下移,射流角度θjet减小,压力峰值均值都会经历上升-下降-上升-下降的过程,压力峰值均值的最大值区别不大。对于D这种非对称外形,壁面压力峰值均值在入射激波位置移动过程中只经历了先上升后下降的过程,而且最大值略大于其他三种外形。图 10表明随着外形变钝(A→B→C),Strouhal数有减小的趋势。也就是说,在来流条件相同的情况下,钝头体外形越尖锐,第Ⅳ类激波干扰非定常振荡的频率越高。这主要是因为激波干扰产生的扰动在弓形激波与钝头体壁面之间传播,钝头体越尖锐弓形激波脱体距离越小,从而导致频率升高。值得注意的是,对于外形D,计算时并没有出现非定常振荡现象。
|
| 图 9 钝头体外形对壁面压力峰值分布影响 Fig. 9 Effect of geometry on the peak pressure |
|
| 图 10 钝头体外形对Strouhal数分布的影响 Fig. 10 Effect of geometry on the Strouhal number |
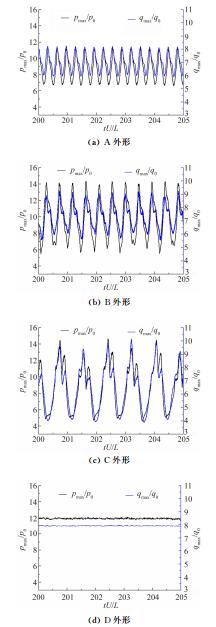
图 11表示4种外形钝头体壁面压力、热流峰值随时间变化规律,对于每种外形选取的是峰值均值最大的一组结果。可以看出随着外形变钝,流动非定常振荡加剧,脉动压力和热流峰值有增大的趋势,压力和热流振幅增大,对于非对称外形D来说,虽然压力和热流平均值大于圆形外形B,但因为外形D的第Ⅳ类激波干扰未出现非定常振荡,其所能达到的压力和热流峰值均小于圆形的情况。也就是说,减小钝头体外形的钝度或者采用不会出现非定常振荡的非对称外形都能够有效地降低第Ⅳ类激波干扰带来的脉动热、力载荷。
|
| 图 11 4种外形壁面压力、热流峰值随时间变化规律 Fig. 11 Time variation of the peak pressure and heat flux amplicication for the four different geometries |
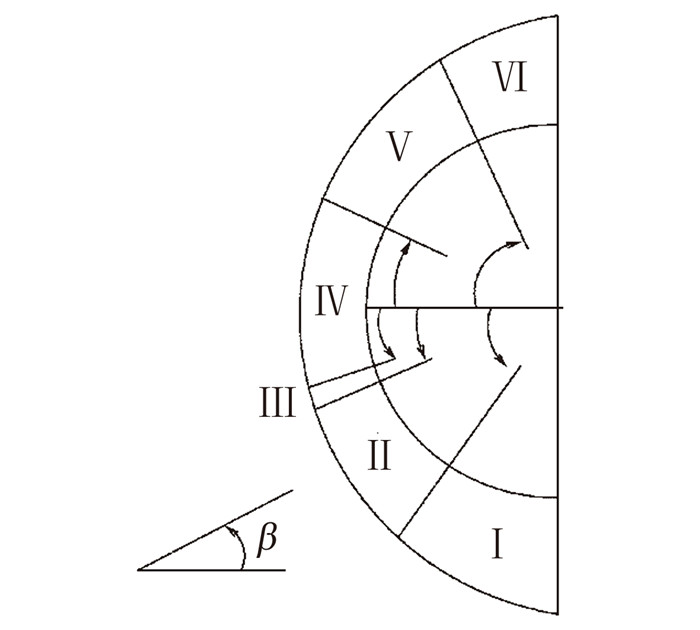
入射斜激波位置不同,激波干扰类型不同,图 12为六类激波干扰分布的示意图。不同的钝头体前缘外形,第Ⅳ类激波干扰区域的范围也不同,外形越钝,弓形激波接近正激波强度的区域就越大,第Ⅳ类激波干扰所占的区域也就越大。
|
| 图 12 六类激波干扰分布示意图 Fig. 12 Edney's classification of shock-shock interaction |
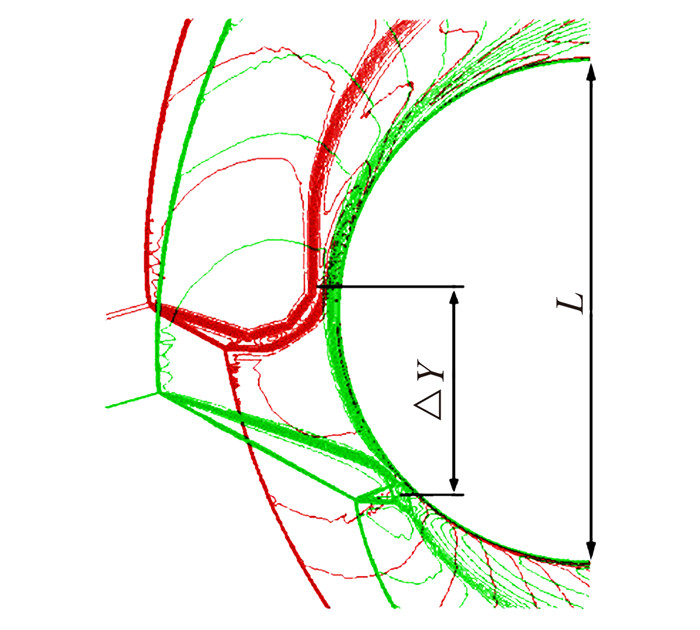
引入η表示可能出现第Ⅳ类激波干扰的比率,η=ΔY/L,如图 13所示,ΔY表示随着激波入射点位置下移,超声速射流壁面冲击点在Y方向下移的最大距离,L表示钝头体特征长度。由表 2可知,对于外形D和外形A,钝头体弓形激波强度接近正激波的区域较小,可能出现第Ⅳ类激波干扰的区域也就较小,η值也就较小。所以,采用这种外形能够很有效地降低出现第Ⅳ类激波干扰的可能性,尤其是外形D。
|
| 图 13 第Ⅳ类激波干扰温度等值线图 Fig. 13 Flow features shown by the temperature contours for the type Ⅳ shock interaction |
| Geometry | A | B | C | D |
| η | 0.335 | 0.468 | 0.550 | 0.065 |
4 结束语
本文以吸气式高超声速飞行器前体激波与进气道唇口激波可能发生的第Ⅳ类激波干扰为关注对象,着重对其中超声速射流的非定常特性、关键影响因素及规律进行了数值考察,研究结果表明:
1) 第Ⅳ类激波干扰可能出现非定常振荡,也可能呈现稳定状态。对圆柱形钝头体来说,在入射激波强度不大的情况下,基于超声速射流冲击壁面的角度对流动类型进行了划分:θjet>0°或者θjet < -30°,流动稳定;-15° < θjet < 0°,流动出现非常明显的非定常特性;-30° < θjet < -15°,流动则呈现稳定和非定常的过渡特征。
2) 入射激波强度和钝头体外形对第Ⅳ类激波干扰非定常特性和热、力载荷有显著影响。在本文计算条件下,入射激波强度增大或钝头体外形变钝,脉动热、力载荷峰值有增大的趋势,Strouhal数则会减小。对于非对称外形D,第Ⅳ类激波干扰则没有出现非定常振荡,热流和压力峰值小于圆形基准外形B。由此推断,合理选择钝头体外形可望有效地降低第Ⅳ类激波干扰带来的脉动热、力载荷。
| [1] | Watts J D. Flight experience with shock impingement and interference heating on the X-15-2 research airplane[R]. NASA TMX-1669, 1968. |
| [2] | Edney B. Anomalous heat transfer and pressure distributions on blunt bodies at hypersonic speeds in the presence of an impinging shock[R]. Aeronautical Research Inst of Sweden, FFA Rept. 115, Stockholm, Sweden, 1968. |
| [3] | Keyes J W, Hains F D. Analytical and experimental studies of shock interference heating in hypersonic flows[R]. NASA TN D-7139, 1973. https://engineering.purdue.edu/~aae519/classnotes/keyes-shock-interaction-images.pdf |
| [4] | Wieting A R, Holden M S. Experimental shock-wave interference heating on a cylinder at Mach 6 and 8[J]. AIAA Journal, 1989, 27(11):1557–1565. DOI:10.2514/3.10301 |
| [5] | Kolly J M. An investigation of aerothermal loads generated in regions of hypersonic shock interference flows[D]. New York:State University of New York at Buffalo, 1996. |
| [6] | Sanderson S R. Shock wave interaction in hypervelocity flow[D]. California:California Institute of Technology, 1995. http://adsabs.harvard.edu/abs/1995PhDT.......355S |
| [7] | Boldyrev S M, Borovoy V Y, Chinilov A Y, et al. A thorough experimental investigation of shock/shock interference in high Mach number flows[J]. Aerospace Science and Technology, 2001, 5(3):167–178. DOI:10.1016/S1270-9638(01)01094-X |
| [8] | Grasso F, Purpura C, Chanetz B, et al. Type Ⅲ and type Ⅳ shock/shock interferences:theoretical and experimental aspects[J]. Aerospace Science and Technology, 2003, 7(2):93–106. DOI:10.1016/S1270-9638(02)00005-6 |
| [9] | Gaitonde D, Shang J S. On the structure of an unsteady type Ⅳ interaction at Mach 8[J]. Computers & Fluids, 1995, 24(4):469–485. |
| [10] | Lind C A. Effect of geometry on the unsteady type Ⅳ shock interaction[R]. AIAA-95-3157, 1995. http://arc.aiaa.org/doi/pdfplus/10.2514/6.1995-3157 |
| [11] | Lind C A, Lewis M J. Computational analysis of the unsteady type Ⅳ shock interaction of blunt body flows[J]. Journal of Propulsion and Power, 1996, 12(1):127–133. DOI:10.2514/3.24000 |
| [12] | Zhong X. Application of essentially nonoscillatoryshemes to unsteady hypersonic shock-shock interference heating problems[J]. AIAA Journal, 1994, 32(8):1606–1616. DOI:10.2514/3.12150 |
| [13] | Chu Y B, Lu X Y. Characteristics of unsteady type Ⅳ shock/shock interaction[J]. Shock Waves, 2012, 22(3):225–235. DOI:10.1007/s00193-012-0366-y |
| [14] |
Deng Xiaogang, Zhang Hanxin. Computations and analysis of viscous hypersonic shock-on-shock interferences[J].
Acta Aerodynamica Sinica, 1994, 12(1):1–7.
(in Chinese) 邓小刚, 张涵信. 粘性高超声速激波-激波碰撞的计算和分析[J]. 空气动力学学报, 1994, 12(1) : 1–7. |
| [15] |
Yan Chao, Tu zhengguang, Yu Xiaohong, et al. Numerical research on unsteady effect of shock-shock interference flow[J].
Journal of Beijing University of Aeronautics and Astronautics, 2003, 29(3):214–217.
(in Chinese) 阎超, 涂正光, 于晓红, 等. 激波碰撞干扰流动非定常效应的数值模拟[J]. 北京航空航天大学学报, 2003, 29(3) : 214–217. |
| [16] |
Tian Zhengyu, Li Hua, Fan Xiaoqiang. Numerical investigation for six types of hypersonic turbluent shock-shock interaction[J].
ActaAerodynamica Sinica, 2004, 22(3):361–364.
(in Chinese) 田正雨, 李桦, 范晓樯. 六类高超声速激波-激波干扰的数值模拟研究[J]. 空气动力学学报, 2004, 22(3) : 361–364. |
| [17] | Sun M, Takayama K. Conservative smoothing on an adaptive quadrilateral grid[J]. Journal of Computational Physics, 1999, 150(1):143–180. DOI:10.1006/jcph.1998.6167 |
| [18] |
Xiao Fengshou, Li Zhufei, Zhu Yujian, et al. Influence of forward-facing cavity on the behaviors of type Ⅳ shock interaction of blunt body flows[J].
Journal of Propulsion Technology, 2016, 37(1):1–7.
(in Chinese) 肖丰收, 李祝飞, 朱雨建, 等. 带凹腔钝头体第Ⅳ类激波干扰特性研究[J]. 推进技术, 2016, 37(1) : 1–7. |
| [19] | Wang W X, Guo R W. Influence of hypersonic inlet cowl lip on flowfield structure and thermal load[J]. Journal of Propulsion and Power, 2014, 30(5):1175–1182. DOI:10.2514/1.B35138 |