2. 重庆理工大学 车辆工程学院, 重庆 400054
2. School of Automobile Engineering, Chongqing University of Technology, Chongqing 400054, China
高速气动悬浮列车(Aero-train) 是一种利用空气动力原理的创新型高速列车,即利用带侧翼的列车行驶在距离地面或水面上方一定空间时所产生的地面效应即WIG (Wing-In-Ground) 现象而悬浮飞行的列车。图 1是气动悬浮列车概念图[1]。气动悬浮列车首先由日本东北大学提出,并在日本政府的支持下开展着相关研究。

|
| 图 1 气动悬浮列车概念图 Fig. 1 Aero-train concept image |
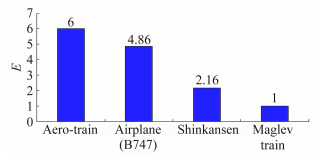
通过日本东北大学前期试验及调研得到几种常用交通运输工具(波音747飞机、日本新干线、上海磁悬浮列车) 的运载经济效率E如图 2所示。运载经济效率E定义如式(1) 所示:
|
| 图 2 运载经济效率的对比 Fig. 2 Comparision of economic efficiency |
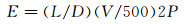
|
(1) |
其中,L为气动升力,D为气动阻力,V为交通运输工具的巡航速度(km/h),P为载荷率,表示载荷质量与总质量的比值[2, 3]。国内只有重庆理工大学赖晨光研究团队在与日本东北大学合作进行气动悬浮列车相关研究。日本东北大学在气动悬浮列车研究过程中选用现有标准翼型作为气动悬浮列车机翼,本文利用遗传算法结合CFD技术对特定地面效应下翼型进行优化设计并得出在该条件下更优的气动悬浮列车翼型。
气动悬浮列车研究关键在于其地面效应对机翼翼型气动特性的影响程度。本文在优化翼型时以初始模型中的翼型LA203A为基础,利用遗传算法与CFD技术相结合的方法优化设计出气动特性更佳的翼型以满足气动悬浮列车的设计要求。分别对基础翼型和优化翼型及安装这两种机翼后的整车进行地面效应数值分析。利用风洞实验方法对安装有优化翼型的气动悬浮列车初始研究模型(AERO-1) 整车气动特性进行研究。
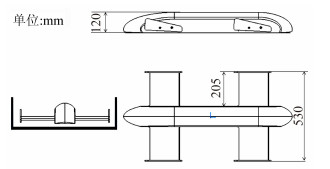
1 气动悬浮列车AERO-1研究模型结构图 3为气动悬浮列车的初始模型结构图,该研究模型仅保留了列车部分主要特征,简化了列车动力装置及车轮。在AERO-1的车身底部安装有两副机翼。AERO-1的行驶轨道截面形状为U形。
|
| 图 3 初始研究模型 Fig. 3 Initial research model |
机翼两端安装有端板,端板的截面形状为矩形。当气动悬浮列车高速行驶时,机翼由于地面效应产生的升力将使气动悬浮列车悬浮于地面一定高度飞行。机翼的迎角为α,离地间隙为H,机翼有效展长为Ld,弦长为L。AERO-1的主要尺寸参数如图 3。
2 AERO-1单向翼翼型优化设计AERO-1单向翼机翼弦长为L=1000mm,有效展长Ld=1000mm。将AERO-1初始翼型LA203A作为优化设计的基础翼型,利用解析函数线性叠加方法[5]对机翼翼型几何形状进行描述并利用遗传算法对翼型进行气动优化设计,并通过CFD技术对基础翼型和优化翼型的地面效应分别进行模拟分析。
2.1 翼型的几何表达翼型的形状由基准翼型、型函数及其系数来定义。
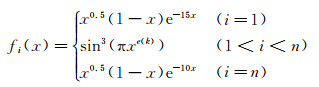
|
(2) |
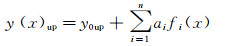
|
(3) |

|
(4) |
式中, y0表示基础翼型,
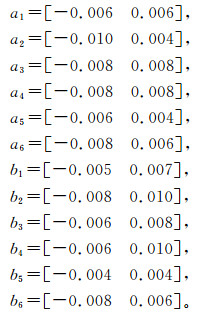
|
计算域为方槽形,机翼初始迎角为迎角α=5°,初始离地高度为1/2L(L为机翼弦长,值为1000mm)。整体网格布局采用非结构网格和棱柱网格相结合的形式。机翼局部网格如图 4所示。利用FLUENT软件计算设计翼型的阻力系数、升力系数,以得到在相对应条件上的升阻比,计算初始状态为速度Ma=0.3, 迎角α=5°,初始离地高度为1/2L,雷诺数Re=1.04×107[6]。升力系数、阻力系数通过在FLUENT中选择Spalart-Allmaras (1 eqn) 模型求解N-S方程得到。

|
| 图 4 翼型局部计算域网格 Fig. 4 Grid around the airfoil |
2.3 响应面模型及遗传算法
通过U12-120的均匀设计方法[7]建立翼型升力系数、阻力系数、升阻比和翼型设计变量之间的响应面。根据均匀设计矩阵表给定的翼型设计参数, 计算速度Ma=0.3, 迎角α=5°, 雷诺数Re=1.04×107时翼型的气动特性值并用其建立Kriging响应面[8]。目标函数为f=CL/Cd,约束条件主要包括翼型的参数变化范围。优化设计中取翼型上下面的12个控制参数作为设计变量(上下翼面各6个), 并与固定的前后缘一起作为翼型的控制参数来确定翼型形状。
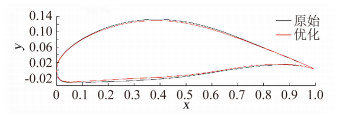
对于运用遗传算法对一个具体问题优化来说,优化结束时具有最大适应值的个体所对应的设计变量值便是优化问题的最优解[9]。通过建立响应面模型了解个体区间及总体规模,得到群体由120个随机个体组成即群体规模。通过基于赌轮法的选择算子,使父代的优良个体以较大的概率在子代中得到继承的遗传。杂交和变异可以避免局部优化从而保证收敛的全局搜索性。定义交叉概率为0.9、变异率为0.01,得到交叉个体数目为108[10]。表 1给出了优化前后翼型的升力系数、阻力系数和升阻比。图 5给出了初始翼型和优化设计后的翼型形状。LA203A翼型属于高升力翼型, 优化后的翼型前沿变薄,后沿弯度增大, 整体厚度变小,翼型的最大厚度位置后移, 其升阻比相对基准翼型LA203A增大30%左右。
|
| 图 5 基准翼型及优化翼型形状 Fig. 5 The initial airfoil and optimized airfoil shapes |
| CL | CD | CL/CD | |
| Initial value | 1.30 | 0.037 | 35.14 |
| Optimized value | 1.48 | 0.031 | 47.74 |
3 翼型地面效应分析
当有正弯度机翼贴近地面飞行时,机翼下表面由于堵塞效应使流速加快,机翼上下表面压力差增大,因而机翼升力增加,诱导阻力减少,从而使机翼的升阻比提高的现象称为机翼的地面效应[11, 12]。本文通过对优化翼型及基础翼型做地面效应对比分析,得出优化翼型在地效区的气动特性(升力系数、阻力系数、升阻比) 要优于基础翼型。运用实验数据法得出各设计变量(离地间隙和迎角) 与目标变量(阻力系数、升力系数、升阻比) 之间的数值关系,其中迎角变化范围为-10°到13°、离地间隙变化范围为1/4L到2.3L(L为机翼弦长,值为1000mm),并在变量变化范围内生成变量矩阵,共50组变量参数。由于变量只有两个,因此,同一个角度对应了多个离地间隙。之后建立翼型升力系数、阻力系数、升阻比和设计变量(离地间隙、迎角) 之间的关系,计算初始状态为速度Ma=0.3,迎角α=5°,初始离地间隙为1/4L,雷诺数Re=1.04×107时翼型的升力系数、阻力系数, 并得出其升阻比。
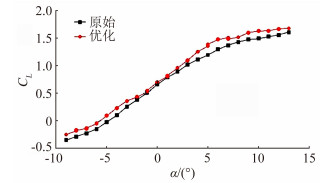
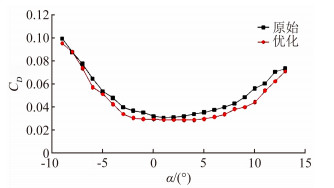
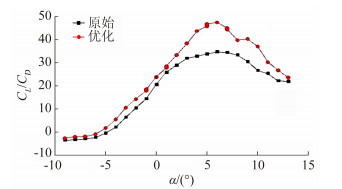
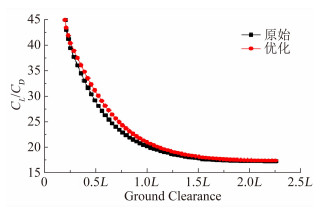
基础机翼和优化机翼气动特性分析结果如图 6、图 7、图 8和图 9。从图 6可以看出优化后翼型升力系数对于原始翼型升力系数有较大的提升,其中两幅翼型在迎角范围为-2°至2°时升力系数差异较小,迎角在4°至6.5°范围内有较大的变化,特别是在迎角为6°的情况下,优化后的翼型升力系数(1.48) 明显大于原始翼型升力系数(1.3)。图 7所示为阻力随迎角的变化趋势,优化翼型与原始翼型阻力系数在迎角范围5°至7°的情况下阻力系数明显降低,并在-1°至4°范围内变化较为平坦。两幅翼型升阻比变化如图 8所示,优化翼型升阻比线斜率明显增加,在迎角范围为5°至6.5°时升阻比有明显提升,相对于原始翼型升阻比提升约26%左右。从图 9可以看出随着离地间隙扩大升阻比降低,在离地间隙范围大于1L(L为机翼弦长,值为1000mm) 时升阻比变化幅度很小,并且趋于平缓,表明离地间隙已经不再是影响升阻比的主要因素, 优化前后翼型升阻比随离地间隙的变化趋势基本相同,但在离地间隙为1/4L至1L范围内优化翼型相对于原始翼型有一定提高,最大提高达18%。
|
| 图 6 不同迎角的升力系数 Fig. 6 Lift coefficient values with diffirent angles of attack |
|
| 图 7 不同迎角的阻力系数 Fig. 7 Drag coefficient values with diffirent angles of attack |
|
| 图 8 不同迎角的升阻比 Fig. 8 CL/CD values with diffirent angles of attack |
|
| 图 9 不同离地间隙的升阻比 Fig. 9 CL/CD values with diffirent ground clearances |
4 AERO-1整车地面效应风洞实验研究
本次研究风洞实验在吉林大学风洞实验中心进行,风洞为开口、回流式低速风洞。最大风速为50m/s。风洞实验模型AERO-1整车尺寸参数见图 3所示。实机翼有效弦长L为150mm,H为离地间隙,α为机翼迎角。验段地面放置2200mm×4100mm的黑色平板以模拟固定地面,轨道侧壁面尺寸为220mm×3100mm。气动悬浮列车采用底部支撑方式,并与三分力传感器相连接,数据采集时,仅采集z方向、x方向的数值(其中z方向为气动悬浮列车升力、x方向为气动悬浮列车阻力)。由于风洞设施风速最高50m/s的限制,本次实验来流速度为35m/s。轨道侧壁面与气动悬浮列车翼端之间距离和气动悬浮列车离地间隙均为为1/5L(30mm)。迎角分别为0°、5°、10°。如图 10所示。利用FLUENT软件计算AERO-1实验模型的阻力、升力,以得到在相对应条件上的升阻比,为了使数值计算与实验结果阻力误差小于5%、升力误差小于10%, 机翼最小网格尺度设置为2mm、车身网格尺度为8mm,整体网格数量在500W~600W之间。图 11、图 12、图 13为在实验工况下气动特性值对比。

|
| 图 10 AERO-1实验模型 Fig. 10 AERO-1 research mode |
|
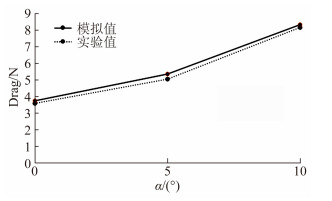
| 图 11 不同迎角的阻力 Fig. 11 Drag values with diffirent angles of attack |
|
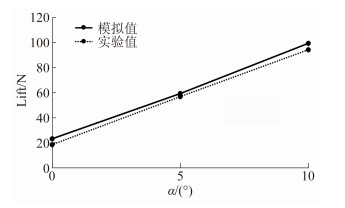
| 图 12 不同迎角的升力 Fig. 12 Lift values with diffirent angles of attack |
|
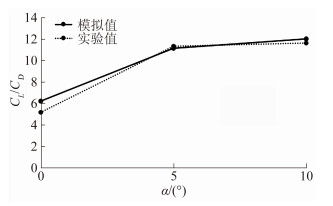
| 图 13 不同迎角的升阻比 Fig. 13 CL/CD values with diffirent angles of attack |
图 11、图 12、图 13为在实验工况下气动特性值对比。数值计算时,通过对网格、边界层以及计算模型等的调整,使得数值计算值与实验值之间的误差在允许误差范围内。图 14为机翼迎角为5°,离地间隙为30mm时车头右侧机翼及车尾左侧机翼上表面的表面流动状况。车身侧向扰流及机翼端板扰流加剧了气流在机翼上表面的分离趋势[13-15]。气流流过前端翼后,使得后端翼处于前端翼气流尾流湍流区,紊乱的来流使得后端翼上表面流动状态更为复杂。由于前端翼来流相对均匀,因此对气动特性的主要影响因素为车身的侧向扰流及端板扰流。但后端机翼流场处于车身侧向扰流、前端机翼尾部紊流和端板侧向扰流混合影响,特别是前端机翼尾部紊流导致了后端机翼来流流速变化和来流分离加剧。前后端机翼周围流动的不均匀性使得其气动特性有所不同,将导致列车在运行时前后机翼产生升力差,严重者将诱导列车以及机翼振动。

|
| 图 14 机翼上表面表面流动 Fig. 14 Surface flow on the wing surface |
5 结束语
通过对高升力翼型LA203A在地面效应存在的情况下进行了气动优化设计并对基础翼型与优化翼型进行了对比分析,最后利用数值模拟机风洞实验的方法通过对整车的地面效应进行了地效分析对比,得出以下结论:
与基准翼型相比, 新翼型的升阻比有明显提高,特别是在迎角范围5°至6.5°、离地间隙在1/2至3/4倍气动弦长的情况下,翼型气动特性(升力系数、阻力系数、升阻比) 有较大提升。翼型升阻比随离地间隙的增加而减少,离地间隙变化范围在大于等于一倍弦长时升阻比变化趋于平缓,表明此时离地间隙不再是影响升阻比的变化主要因素。
利用遗传算法进行高升力翼型的气动优化设计研究及对优化前后翼型地面效应分析研究, 对气动悬浮列车的气动设计研究具有一定的指导意义。
利用数值模拟及风洞实验的方法对保留气动悬浮列车大部分特征的实验车型的地面效应的分析得出,优化后翼型满足气动悬浮列车的气动要求(高升低阻)。通过油流法对机翼上表面流动分析,后端机翼处于前端机翼尾部湍流区,不均匀的来流使得后端机翼气动特性产生不稳定影响,该不稳定的影响可能导致列车在运行时出现前后升力的变化差及机翼颤振。该点需要继续研究从而找出降低相互影响同时又满足气动悬浮列车升力需求的最优距离及迎角范围。
| [1] | Kohama Y. Mechanical civilization induced earth pollution problem, and Aero-Train[J]. Trans. of the Japan Soc. of Mechanical Engineers, B, 2005, 71(707):1733–1737. DOI:10.1299/kikaib.71.1733 |
| [2] | Tomaru H, Kohama Y. Wind-tunnel investigation of aerofoil for wing in ground effect[J]. Nagare, 1991, 10:47–60. |
| [3] | Mohammed Rafiuddin AHMED, Yasuaki KOHAMA. Experimental investigation on the aerodynamic characteristics of a tandem wing configuration in close ground proximity[J]. Jsme International Journal, 1999, 42(4):612–618. DOI:10.1299/jsmeb.42.612 |
| [4] | Kohama Y. An application of ACV to railway transportation[C]//25th Aircraft Symp, 1987. (in Japanese) |
| [5] | Hicks R, Henne P. Wing design by numerical optimization[J]. Jounnal of Aircraft, 1978, 15(7):407–413. DOI:10.2514/3.58379 |
| [6] | 王福军. 计算流体动力学分析[M]. 北京: 清华大学出版社, 2004. |
| [7] | 方开泰, 马长兴. 正交设计与均匀设计[M]. 北京: 科学出版社, 2001. |
| [8] |
Li P F, Zhang B Q, Chen Y C. An effective transonic airfoil optimization method using Response Surface Model (RSM)[J].
Journal of Northwestern Polytechnical University, 2012, 30(3):395–401.
(in Chinese) 李沛峰, 张彬乾, 陈迎春. 基于响应面和遗传算法的翼型优化设计方法研究[J]. 西北工业大学学报, 2012, 30(3) : 395–401. |
| [9] |
Wang X P, Gao Z H. Aerodynamic optimization design of airfoil based on genetic algorithm[J].
Acta Aerodynamica Sinica, 2000, 21(3):70–75.
(in Chinese) 王晓鹏, 高正红. 基于遗传算法的翼型气动优化设计[J]. 空气动力学学报, 2000, 21(3) : 70–75. |
| [10] |
Wang X P. Study of genetic algorithm for aerodynamic optimization and design[J].
Acta Aerodynamica Sinica, 2001, 19(2):129–134.
(in Chinese) 王晓鹏. 气动优化设计中的遗传算法研究[J]. 空气动力学学报, 2001, 19(2) : 129–134. |
| [11] |
Qin X G, Liu P Q, Qu Q L, et al. Numerical simulation and analysis on aerodynamics of three-element airfoil in ground effect[J].
Journal of Aerospace Power, 2011, 26(4):890–896.
(in Chinese) 秦绪国, 刘沛清, 屈秋林, 等. 多段翼型地面效应数值模拟与分析[J]. 航空动力学报, 2011, 26(4) : 890–896. |
| [12] | Sobieczky H. Parametric airfoils and wings[M]. . |
| [13] | Chen S, Hang F, Khalid M. Aerodynamic optimization for a high-lift airfoil/wing configuration[R]. AIAA 2004-5078. |
| [14] | Jung S, Moon B R. Toward minimal restriction of genetic en-coding and crossovers for the two-dimensional euclidean TSP[J]. IEEE Transactions on Evolutionary Computation, 2011, 6(12):557–565. |
| [15] | Jens Madsen. Response surface techniques for diffuser shape optimization[J]. AIAA Journal, 2000, 38(9):1512–1518. DOI:10.2514/2.1160 |



