2. China Aeronautical Establishment, Beijing 100012, China
2. 中国航空研究院, 北京 100012
Flutter is a typical dynamic aeroelastic phenomenon, which could cause catastrophic results. Transonic flutter prediction is greatly important for the design of transport aircrafts and fighters. Nowadays, Computational Fluid Dynamics (CFD) has been widely applied in transonic flutter predictions[1]. However, it is still very time-consuming to calculate instantaneous response of aeroelastic system by time-marching methods.
However, it is still very time-consuming to calculate instantaneous response of aeroelastic system by time-marching methods.
To improve analysis efficiency, reduced order model has been widely applied in flutter analysis.Weiwei Zhang et al[2] applied ARX reduced order model to construct aeroelastic equation in state space form, which shows similar results with CFD/CSD simulation, except for transonic condition. Walter A. Silva[3] created multiple-input multiple-output reduced order aeroelastic system based on Volterra series, which established the relationship between modal inputs and generalized aerodynamic forces (GAFs). However, the precision of unsteady aerodynamic forces based on Volterra series is very sensitive to amplitude of input signals and time steps[4]. Weiwei Zhang et al[5] also predicted flutter boundary by nonlinear ROM based on RBF neural network model.
Except for the time domain method, frequency domain method is another important approach of flutter analysis[6]. Aerodynamic describing functions can be obtained by exciting aeroelastic system with harmonic disturbance of small amplitudes. Then, flutter velocity and frequency of different structural parameters can be obtained by V-g or P-K method, which shows great efficiency, comparing with time-marching methods[7]. However, it takes excessive computational costs to calculate harmonic responses of aeroelastic system, because it needs to carry on unsteady flow simulation for each structural mode every harmonic frequency.
In addition, harmonic balance (HB) method shows superior efficiency in the simulation of periodic unsteady flow[8-10], which is widely applied in the simulation of turbomachines[11-12], helicopter rotors[13-14], dynamic derivations[15], et al. Therefore, a frequency domain flutter analysis method based harmonic balance is proposed in this paper, which takes efficiency and precision into account.
1 Time-marching methodReynolds-Averaged Navier-Stokes (RANS) equation is the highest-fidelity flow solver in current engineering applications, which can be written as:
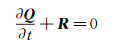
|
(1) |
where Q and R are the vectors of flow variables and residuals respectively. Third-order Roe scheme is applied in spatial discretization, while approximate factorization scheme is used in implicit time-marching method. And S-A turbulence model is adopted.
Two-degree-of-freedom structural dynamic equation can be written as:

|
(2) |
where
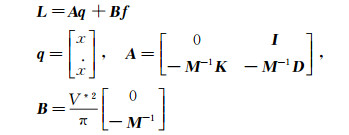
|
Eq.(2) can be transferred into state space form:
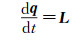
|
(3) |
where
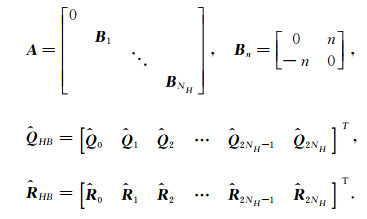
|
Eq.(3) can be solved by second-order Euler prediction-correction method:
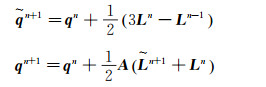
|
(4) |
The flow chart of time-marching approach of aeroelastic system is shown in Fig. 1.
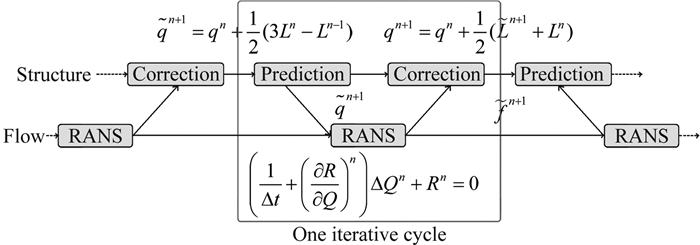
|
| 图 1 气动弹性系统时间推进求解的流程 Fig. 1 Flow chart of time-marching method of aeroelastic system |
2 Harmonic balance method
Harmonic balance method is an efficient approach of periodic unsteady flow field. Because of the periodicity, the vector of flow variables and residuals can be deployed by Fourier series:

|
(5) |
The time derivation of Q is:
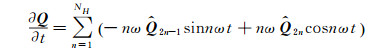
|
(6) |
Substituting Eq.(5) into Eq.(1) and rearranging, we can get a pair of algebraic equations:
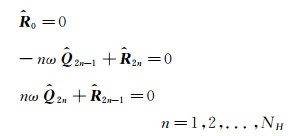
|
(7) |
Eq.(7) can be written into matrix form:
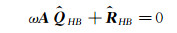
|
(8) |
where
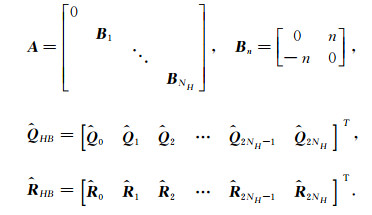
|
Eq.(8) is the governing equation of original harmonic balance method. In this method, the calculation of residual terms by Fourier transformation is very complex and tedious, which is as follows:
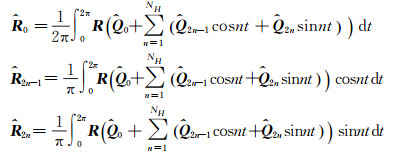
|
(9) |
To resolve this problem, sub-time levels were introduced by Hall et al[11] to convert Q back to time domain through Fourier transformation:
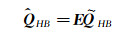
|
(10) |
where
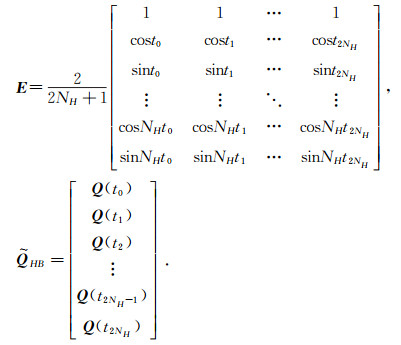
|
{ti, i=1, 2, ..., 2NH} are equally distributed sub-time levels in a cycle, and ti=2π(i-1)/2NH.
Substituting Eq.(10) into Eq.(8):
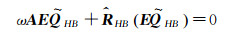
|
(11) |
Both sides in Eq.(11) are multiplied by E -1:
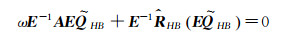
|
(12) |
To achieve an easy approach, the residual terms are simplified by:

|
(13) |
where

|
In this step, nonlinear residual terms can produce terms whose frequencies are higher that NHω, which are included in low-frequency terms by Eq.(13). This rough simplification may produce non-physical solutions in strong nonlinear problems[16]. Therefore, the number of harmonics should be chose adequately to guarantee that high-frequency harmonic terms approach zero. Finally the governing equation of harmonic balance method can be obtained:
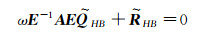
|
(14) |
In order to solve Eq.(14) by time-marching method, pseudo time derivation is added:
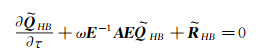
|
(15) |
Eq.(15) is the same as original RANS Eq.(1), except for its middle term (which is also called harmonic balance source term). Therefore, harmonic balance solver can be obtained from original steady RANS solver.
Then the harmonic balance method is validated by NACA64A010 airfoil under forced harmonic motion[17]. The angle of attack changes as follows:

|
(16) |
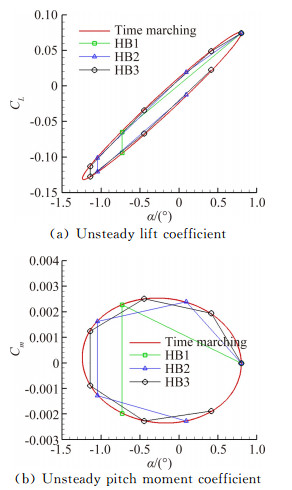
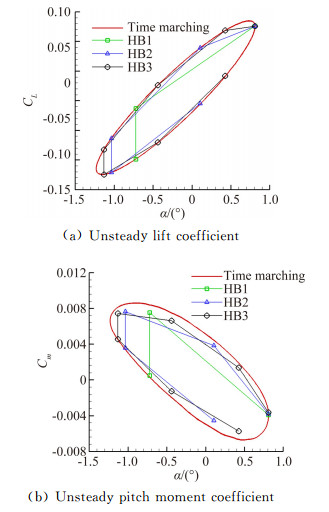
The flow conditions of two test cases are shown in Table 1. The comparison of unsteady aerodynamic forces between harmonic balance and time-marching methods are illustrated in Fig. 1 and Fig. 3. It is demonstrated that the unsteady forces calculated by harmonic balance and time-marching methods coincide with each other, which validates the precision of harmonic balance method. The time costs of time-marching and harmonic balance methods are shown in Table 2.
| Case | Ma | Re/106 | α0 | αm | f | xα/c |
| CT2 | 0.502 | 9.98 | -0.22 | 1.02 | 10.8 | 0.269 |
| CT5 | 0.789 | 12.56 | -0.21 | 1.02 | 17.2 | 0.248 |
|
| 图 2 CT2算例时间推进和谐波平衡方法计算结果对比 Fig. 2 Comparison of unsteady aerodynamic forces between time-marching and harmonic balance methods in CT2 case |
|
| 图 3 CT5算例时间推进和谐波平衡方法计算结果对比 Fig. 3 Comparison of unsteady aerodynamic forces between time-marching and harmonic balance methods in CT5 case |
| Case | Time-marching | HB1 | HB2 | HB3 |
| CT2 | 1770 | 140 | 260 | 397 |
| CT5 | 2223 | 189 | 355 | 487 |
3 Frequency domain solver
When the aeroelastic system is undergoing single harmonic motion, the plunge and pitch displacements can be written as:
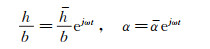
|
(17) |
The corresponding lift and pitch moment coefficients can be written as:
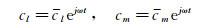
|
(18) |
Therefore, the structural Eq.(2) can be transferred into frequency domain:
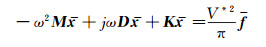
|
(19) |
Through aerodynamic describing function matrix F, the aerodynamic forces can be easily obtained by:
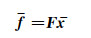
|
(20) |
where

|
The aerodynamic describing functions can be obtained through exciting aeroelastic system by harmonic disturbance of small amplitude. Harmonic Balance method is applied to acquired aerodynamic describing functions efficiently.
However, the aeroelastic systemmay exhibit different behaviors (convergent oscillation, simple harmonic or divergent oscillation) in different freestream conditions. Therefore, an artificial damping coefficient j g K can be added into the aeroelastic system (19) to maintain harmonic motion:
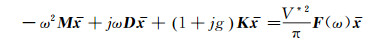
|
(21) |
The stability of aeroelastic system can be judged by the sign of artificial damping coefficient. Eq.(21) can be rearranged into a generalized complex eigenvalue problem:
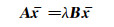
|
(22) |
where
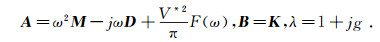
|
At a fixed frequency ω, the matrix A will only change with freestream velocity. Different eigenvalue λ can be obtained in various velocity. When the real part of eigenvalue λRe is equal to 1.0, the imaginary part of eigenvalue λIm is the damping coefficient at a certain velocity. Thus we can get the relationship between damping coefficients and frequencies (or velocities). When damping coefficient is equal to 0, the frequency and velocity is flutter frequency and velocity respectively.
The procedure of frequency domain flutter analysis is as follows:
1) Calculate aerodynamic forces when the system are undergoing harmonic motionsat different frequencies;
2) Obtain aerodynamic transfer function matrix;
3) Construct generalized complex eigenvalue problem by aerodynamic transfer function matrix and structural dynamic equation;
4) Get the freestream velocity which makes the real part of eigenvalue λRe=1;
5) Obtain the relationship between damping coefficients and frequencies/velocities;
6) Acquire the flutter velocity and frequency.
4 Flutter analysis of Isogai wingThe Isogai Case A wing[18-19] is a standard configuration of flutter analysis. The structural parameters of this case are: xα=1.8, rα2=3.48, a=-2.0, ωh=ωα=100rad/s, μ=60. The inviscid flutter velocity boundary shows a "S" shape in transonic Mach number, while the viscous flutter velocity boundary does not.
4.1 Aerodynamic describing function matrixThe aerodynamic describing function matrix is calculated byharmonic balance method to improve efficiency. Take h -/b=0.001 and ω=0.10 as an example. Tables 3 and 4 are the lift describing functions ( CL h/b= CLRe+j C LIm ) and pitch moment describing functions ( Cmḣ /b= CmRe+j C mIm ) at two Mach number (Ma=0.60 and Ma=0.87) respectively.
| Case | Real(CL) | Imag(CL) | Real(Cm) | Imag(Cm) |
| HB1 | -0.16131 | -0.52874 | 0.11794 | 0.40315 |
| HB2 | -0.16131 | -0.52874 | 0.11794 | 0.40315 |
| Case | Real(CL) | Imag(CL) | Real(Cm) | Imag(Cm) |
| HB1 | -5.89447 | -2.20604 | 7.56041 | 3.02303 |
| HB2 | -0.27076 | -0.41057 | 0.32760 | 0.40627 |
| HB3 | -0.27951 | -0.40340 | 0.33830 | 0.39749 |
| HB4 | -0.27429 | -0.41099 | 0.33226 | 0.40688 |
It is illustrated that first-order harmonic is enough for subsonic case and more harmonics are necessary for transonic case to ensure the precision of aerodynamic describing functions.
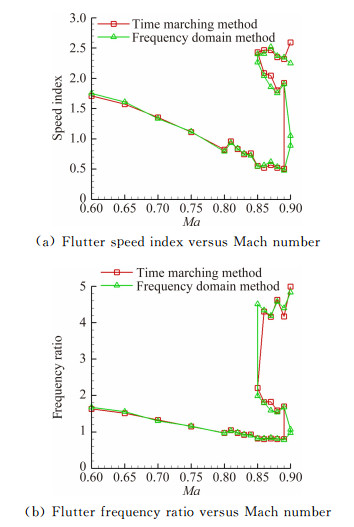
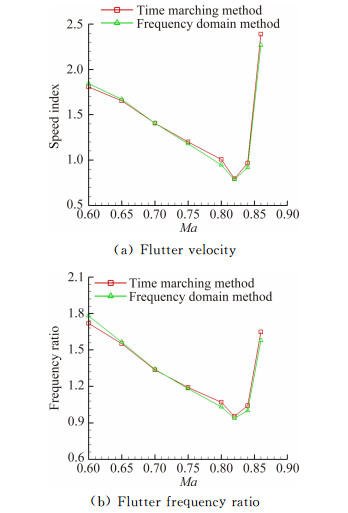
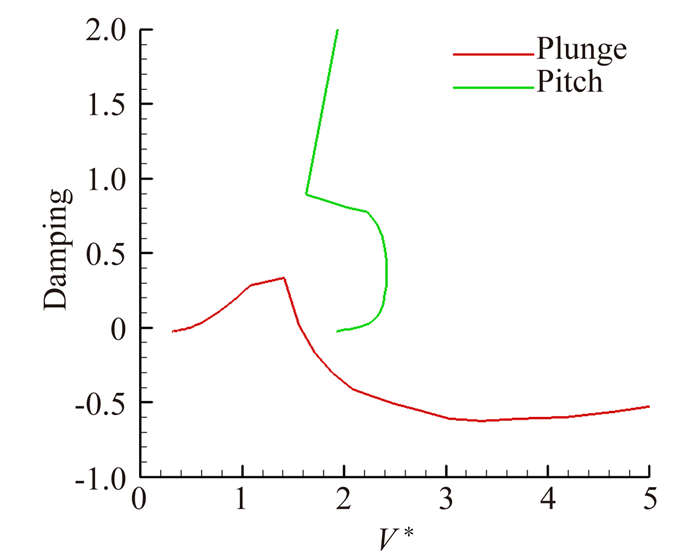
4.2 Flutter boundaryThe inviscid and viscous flutter boundaries are shown in Figs. 4 and 5. It is demonstrated that the difference between time-marching and frequency domain methods is insignificant, even in trmansonic range. The inviscid damping coefficient at Ma=0.88 is exhibited in Fig. 6, from which we can obtain the reason of "S" shape flutter boundary. The damping coefficient of plunge mode exceeds zero at a low flow velocity. But as the velocity increases, the damping coefficient returns back and falls below zero at a moderate velocity. Then the damping coefficient of pitch mode exceeds zero at a high velocity.
|
| 图 4 时间推进方法和频域法得到的无粘颤振边界对比 Fig. 4 Comparison of inviscid flutter boundaries between time-marching and frequency domain methods |
|
| 图 5 时间推进方法和频域法得到的粘性颤振边界对比 Fig. 5 Comparison of viscous flutter boundaries between time-marching and frequency domain methods |
|
| 图 6 Ma=0.88时无粘阻尼系数随来流速度的变化趋势 Fig. 6 Inviscid damping coefficient versus speed index at Ma=0.88 |
4.3 Influence of structural parameters
If the structural parameters undergo some change, flutter boundary can be easily obtained by generalized eigenvalue analysis in frequency domain method, other than time-marching method, which must carry on numerous CFD/CSD simulations. Therefore, the influences of mass ratio and frequency ratio on viscous flutter boundary are investigated below, based on the frequency domain method.
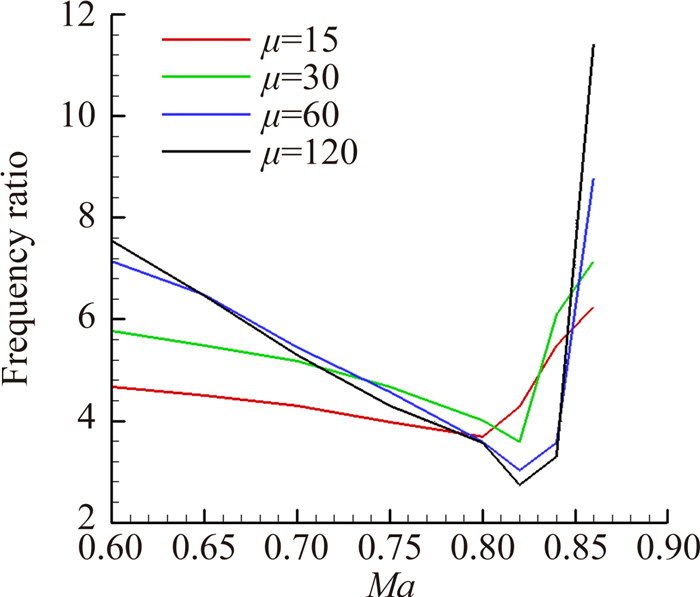
The influences of mass ratio μ and frequency ratio ωh /ωα are shown in Fig. 6 and 8 respectively. It is illustrated that higher mass ratio is preferable in subsonic region, while lower mass ratio is better in transonic region of Isogai A case. The frequency ratio also has a great impact on flutter boundary. When the frequency ratio is close to 1.0, the flutter velocity decreases significantly.
|
| 图 7 质量比对颤振速度的影响 Fig. 7 Influence of mass ratio on flutter velocity |

|
| 图 8 频率比对颤振速度的影响 Fig. 8 Influence of frequency ratio on flutter velocity |
5 Conclusion
1) Comparing with time-marching method, harmonic balance method is an efficient approach of periodic unsteady flow;
2) A frequency domain flutter analysis method based on harmonic balance is proposed, which shows high efficiency and precision;
3) When the structural parameters undergo some change, new flutter boundary can be obtained quickly by generalized eigenvalue analysis in the proposed frequency domain method, other than time-marching method, which must carry on a series of CFD/CSD coupled simulations.
| [1] | Schuster D M, Liu D D, Huttsell L J. Computational aeroelastic:success, progress, challenge[J]. Journal of Aircraft, 2003, 40(5):843–856. DOI:10.2514/2.6875 |
| [2] | Zhang Weiwei, Ye Zhengyin. Effect of control surface on airfoil flutter in transonic flow[J]. Acta Astronautica, 2010, 66:999–1007. DOI:10.1016/j.actaastro.2009.09.016 |
| [3] | Silva W A. Simultaneous excitation of multiple-input multiple-output CFD-based unsteady aerodynamic systems[C]//48th AIAA/ASME/AS-CE/AHS/ASC Structures, Structural Dynamics, and Materials Conference. Honolulu, Hawaii. AIAA 2007-1988. |
| [4] | Raveh D E. Reduced-order models for nonlinear unsteady aerodynamics[J]. AIAA Journal, 2001, 39(8):1417–1429. DOI:10.2514/2.1473 |
| [5] | Zhang Weiwei, Wang Bobin, Ye Zhengyin, et al. Efficient method for limit cycle flutter analysis by nonlinear aerodynamic reduced-order models[J]. AIAA Journal, 2012, 50(5):1019–1028. DOI:10.2514/1.J050581 |
| [6] | Ueda T, Dowell E H. Flutter analysis using nonlinear aerodynamic forces[C]//Proceedings of the 23rd AIAA/ASME/ASCE/AHS Structures, Structural, Dynamics, and Materials Conference, New Orleans, LA. AIAA 82-0728-CP. |
| [7] | He S, Yang Z, Gu Y. Transonic limit cycle oscillation analysis using aerodynamic describing functions and superposition principle[J]. AIAA Journal, 2014, 52(7):1393–1403. DOI:10.2514/1.J052559 |
| [8] | Woodgate M A, Badcock K J. Implicit harmonic balance solver for transonic flow with forced motions[J]. AIAA Journal, 2009, 47(4):893–901. DOI:10.2514/1.36311 |
| [9] | Im D, Kwon J, Park S. Periodic unsteady flow analysis using a diagonally implicit harmonic balance method[J]. AIAA Journal, 2012, 50(3):741–745. DOI:10.2514/1.J051178 |
| [10] | Blanc F, Roux F X, Jouhaud J C. Harmonic-balance-based code-coupling algorithm for aeroelastic systems subjected to forced excitation[J]. AIAA Journal, 2010, 48(11):2472–2481. DOI:10.2514/1.45444 |
| [11] | Hall K C, Thomas J P, Clark W S. Computation of unsteady nonlinear flows in cascades using a harmonic balance technique[J]. AIAA Journal, 2002, 40(5):879–886. DOI:10.2514/2.1754 |
| [12] | Weiss J M, Subramanian V, Hall K C. Simulation of unsteady turbomachinery flows using an implicitly coupled nonlinear harmonic balance method[C]//Proceedings of ASME Turbo Expo 2011. Vancouver, British Columbia. GT 2011-46367. |
| [13] | Ekici K, Hall K C, Dowell E H. Computationally fast harmonic balance methods for unsteady aerodynamic predictions of helicopter rotors[C]//46th AIAA Aerospace Sciences Meeting and Exhibit. Reno, Nevada. AIAA 2008-1439. |
| [14] |
Xu Jianhua, Song Wenping, Wang Long. Application of harmonic balance method in forward flight simulation for helicopter rotors[J].
Acta Aerodynamica Sinica, 2013, 31(5):546–553.
(in Chinese) 许建华, 宋文萍, 王龙. 谐波平衡法在旋翼前飞绕流数值模拟中的应用研究[J]. 空气动力学学报, 2013, 31(5) : 546–553. |
| [15] | Ronch A D, McCracken A J, Badcock K J. Linear frequency domain and harmonic balance predictions of dynamic derivatives[J]. Journal of Aircraft, 2013, 50(3):694–707. DOI:10.2514/1.C031674 |
| [16] | Liu L, Thomas J P, Dowell E H, et al. A comparison of classical and high dimensional harmonic balance approaches for a Duffing oscillator[J]. Journal of Computational Physics, 2006, 215:298–320. DOI:10.1016/j.jcp.2005.10.026 |
| [17] | Davis S S. NACA64A010(NASA AMES model) oscillatory pitching[R]. AGARD Report No. 702. |
| [18] | Isogai K. On the transonic-dip mechanism of flutter of a sweptback wing[J]. AIAA Journal, 1979, 17(7):793–795. DOI:10.2514/3.61226 |
| [19] | Alonso J J, Jameson A. Fully-implicit time-marching aeroelastic solutions[C]//32nd Aerospace Sciences Meeting & Exhibit. Reno, NV. AIAA-94-0056. |



