栅格翼作为一种特殊的气动控制面,由外部框架和内部若干栅格布置而成的一个空间多升力面系统,自1985年开始,美国航空与导弹研究与发展中心就对栅格翼布局展开了相关研究[1-2]。与传统的平板翼相比,栅格翼有其固有的优点,体现在:1)由于弦长较小,翼面上的压力中心距铰链轴很近且受迎角变化影响较小,因此舵面铰链力矩较小,降低了对作动装置的要求,允许采用较轻和较小的转向机构;2)便于折叠,在不需要翼面时可以贴在主体表面,而不影响主体的外形,减小了栅格翼布局的空间体积;3)栅格翼的流动分离晚于平板翼,具有同平板翼不一样的失速特性,有利于在大迎角下保持升力[3-6]。
另一方面,与常规平板翼相比,栅格翼布局的阻力较大,可以说减少阻力,提高升阻比是栅格翼空气动力特性研究的关键[7]。
在减小栅格翼阻力的研究进程中,国内外学者主要关注的是降低超声速条件下栅格翼的阻力,主要措施是改变栅格翼边框剖面形状、减小边框和格栅条的厚度等[8-10],这些措施对亚、跨声速栅格翼阻力的影响较小。另外,在布局形式的研究方面,近年来比较典型的是:新加坡国立大学Jinsheng Cai等[11-12]设计了一种后掠形栅格翼布局,Daniel Guyton等[13]设计了带有局部掠角的栅格翼布局(Locally Swept Lattice Wings)。这些栅格翼布局形式与常规的栅格翼布局相比在超声速条件下都有一定的减阻效果[14-15],但结构较为复杂。
为减小栅格翼翼元内部气流的壅塞,降低栅格翼的阻力,本文设计了一种曲面形栅格翼布局。在结构上这种栅格翼布局在类似旋成体弹身上能够很好的折叠,在不需要翼面时可以贴在弹体表面,缩小了主体的外形尺寸,而且结构简单,易于实现,在内埋武器系统上有很好的应用前景。
本文通过数值模拟方法,在亚、跨、超声速条件下,研究了曲面形栅格翼布局的减阻效果和减阻机理,对比了曲面形栅格翼和常规后掠形栅格翼布局的减阻效果,并对不同迎风方式的曲面形栅格翼气动特性进行了分析。
1 计算外形和计算方法 1.1 计算外形本文以已有试验结果的典型常规蜂窝式单栅格翼布局[16](如图 1所示),作为数值模拟方法有效性验证的基准栅格翼外形。图 2给出了基准栅格翼布局框架图,在此栅格翼外形的基础上保持弦长c、格宽t等几何参数不变,改变栅格翼布局的曲率半径r使得曲率半径与展长的比为r/l=1.1(如图 3所示),作为本文研究的曲面形栅格翼布局,保持有效后掠角θ一致,生成了常规后掠栅格翼外形。图 3从左到右分别为基准栅格翼布局上视图、曲面形栅格翼布局上视图、后掠形栅格翼布局上视图。图 4给出了三种栅格翼布局三维建模效果图。
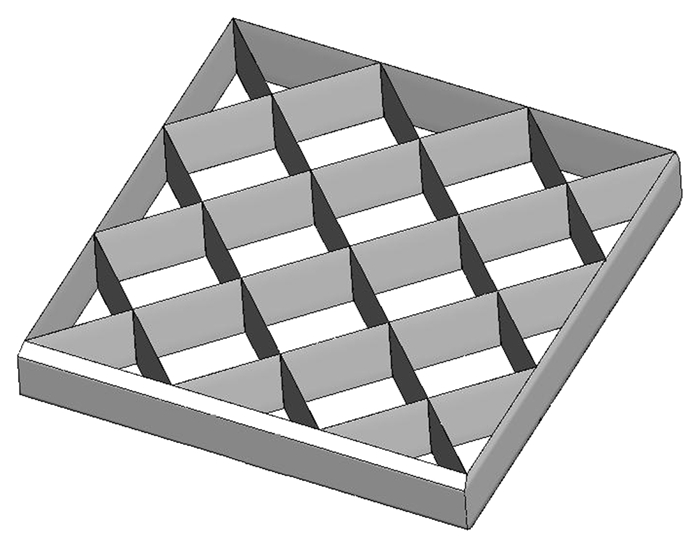
|
| 图 1 典型栅格舵示意图 Fig. 1 Typical sketch of grid fin |

|
| 图 2 栅格翼框架图 Fig. 2 Schematic of the baseline grid fin |
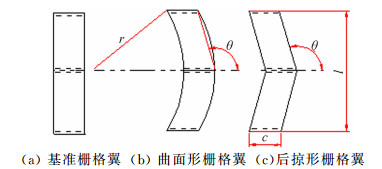
|
| 图 3 栅格翼布局上视图 Fig. 3 Top view of the grid fin configurations |
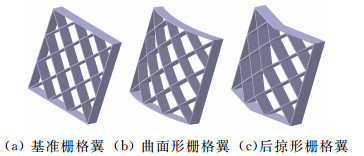
|
| 图 4 栅格翼布局示意图 Fig. 4 Sketch of the grid fin configurations |
1.2 计算方法
本文流场的控制方程采用雷诺平均的N-S方程,采用有限体积法进行空间离散,空间无粘通量采用ROE格式进行离散,粘性通量采用二阶中心差分格式离散,时间项采用隐式LU-SGS方法求解,为了加快收敛速度,采用了局部时间步长和多重网格技术。湍流模型是两方程k-ω SST模型。计算网格采用多块对接结构网格,空间和物面均采用“H”型网格。附面层第一层网格y+≈1,变化率约为1.2。网格量为620万,图 5给出了基准栅格翼布局网格拓扑。
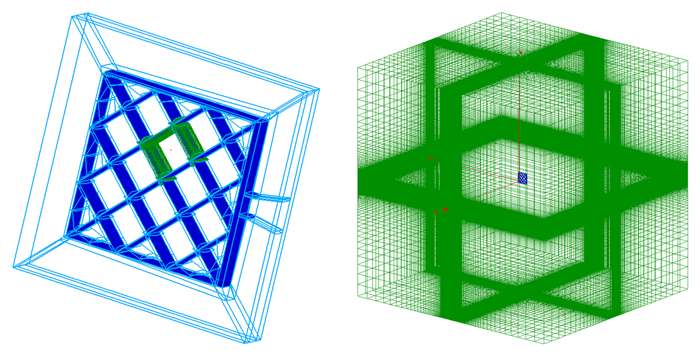
|
| 图 5 基准栅格翼布局计算网格 Fig. 5 Computational grid for baseline grid fin configuration |
1.3 计算方法验证
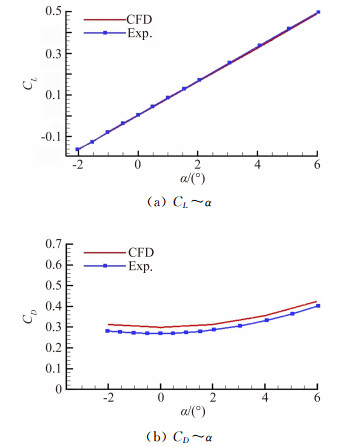
采用基准栅格翼布局在马赫数1.5条件下升力和阻力系数的试验结果对本文的数值模拟方法和网格划分的有效性进行验证,计算雷诺数与试验雷诺数保持一致,M=1.5基于弦长的雷诺数为1.6×107。
从图 6所示基准栅格翼布局升力和阻力系数计算结果和试验值的对比曲线中可以看出,升力系数的计算结果与试验值吻合的较好,阻力系数也模拟出了相同的趋势,但有约10%左右的增量,这主要与湍流模型的选取有关,考虑到栅格翼的弦长较小,栅格翼翼面上部分区域的流动应该是层流,那么全湍流模型的计算势必造成摩阻的计算值较试验值偏大。鉴于本文主要是考察不同栅格翼布局气动特性的差异,因此在相同网格划分和计算方法条件下(统一采用收敛性较好的k-ω SST湍流模型)开展此项研究是可行的。
|
| 图 6 M=1.5,基准栅格翼布局升力和阻力系数与试验值的对比 Fig. 6 Lift and drag coefficients of the baseline grid fin(M=1.5) |
2 计算结果与分析 2.1 不同构型栅格翼减阻效果对比
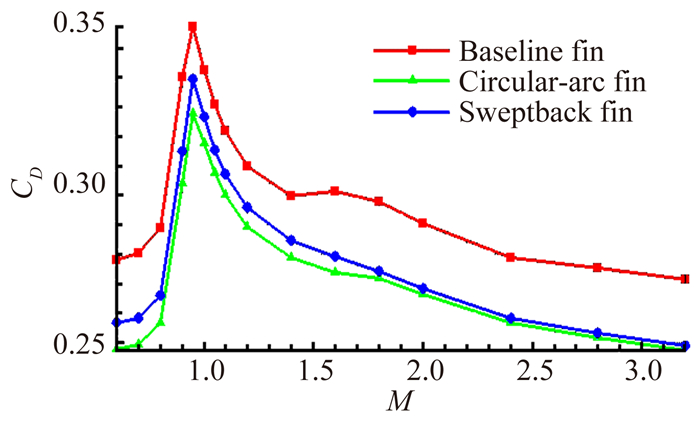
采用曲面形和后掠形栅格翼布局的凸平面迎风的方式进行数值计算。首先在迎角为0°,马赫数0.6~3.6条件下对曲面形和后掠形栅格翼布局的减阻效果进行了对比研究。
图 7所示为迎角为0°,三种栅格翼布局阻力系数随马赫数变化的曲线图,从图中可以看出,在所计算的马赫数范围内,曲面形栅格翼布局的阻力系数有明显的降低,降低量在7%~13%之间。后掠形栅格翼布局也有一定的减阻效果,但在第三临界马赫数(激波不在栅格壁之间来回反射对应的来流马赫数,本文基准栅格翼布局的第三临界马赫数Mcr≈1.8)之前与曲面形栅格翼布局相比其减阻效果略差。在第三临界马赫数之后曲面形栅格翼布局和后掠形栅格翼布局的减阻效果相当。
|
| 图 7 α=0°,不同栅格翼布局阻力系数随马赫数的变化 Fig. 7 Comparison of drag coefficients(α=0°) |
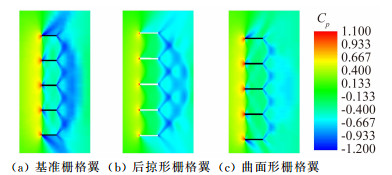
从图 8所示M=1.0,α=0°时不同栅格翼布局纵向对称剖面压力云图的对比中可以看出,相比曲面形栅格翼布局来说,基准栅格翼布局前缘激波波系和后缘膨胀波波系明显较强,造成的能量损失以及带来的阻力增量明显较大。对于基准栅格翼布局来说,栅格翼翼元通道的固壁长度是相同的,那么每个翼元通道内的加速情况是相似的,都存在较强的壅塞现象,而曲面形栅格翼布局相邻壁面的前后缘都有一定的距离,从而减小了翼元通道的等固壁长度,翼元通道内气流的壅塞现象要弱于基准栅格翼布局。与基准栅格翼相比,后掠形栅格翼布局的波系强度也有一定程度的减弱。
|
| 图 8 不同栅格翼布局对称剖面压力云图的变化(M=1.0,α=0°) Fig. 8 Comparison of pressure counters on the symmetry plane(M=1.0, α=0°) |
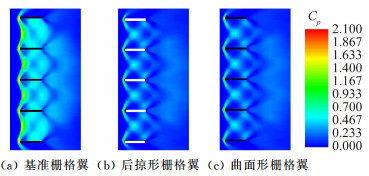
图 9给出了M=2.4,α=0°时不同栅格翼布局对称剖面压力云图的对比,从图中不难看出曲面形栅格翼布局和基准栅格翼布局对称剖面的流态是相似的,不同的是基准栅格翼布局翼元内部波系较强,能量损失较大,而此时曲面形栅格翼布局和后掠形栅格翼布局的翼元内部流态基本相同,这也是超声速下两种栅格翼布局减阻效果较为一致的原因。
|
| 图 9 不同栅格翼布局对称剖面压力云图的变化(M=2.4,α=0°) Fig. 9 Comparison of pressure counters on the symmetry plane(M=2.4, α=0°) |
2.2 不同迎风方式曲面形栅格翼气动特性对比
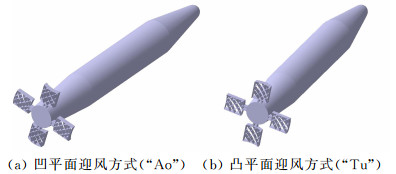
如图 10所示,曲面形栅格翼在弹身上有两种安装形式,即凹平面迎风方式和凸平面迎风方式。凹平面迎风安装,在不需要翼面时,栅格翼向前折叠贴于弹身表面,在投放后栅格翼可以靠气动力作用自动打开;而凸平面迎风安装,栅格翼向后折叠,投放后需要一定的作动装置来打开栅格翼布局。
|
| 图 10 曲面形栅格翼布局在弹体上的安装形式 Fig. 10 Two windward forms of the circular-arc fin |
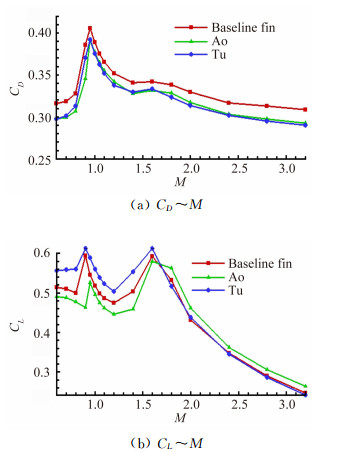
图 11给出了α=6°,基准栅格翼布局和两种迎风方式曲面形栅格翼布局升力和阻力系数随马赫数的变化。从图中可以看出两种迎风方式的曲面形栅格翼布局都具有明显的减阻效果,跨声速范围凹平面迎风布局的减阻效果略大于凸平面迎风布局,但在第三临界马赫数之前,凹平面迎风布局相比常规和凸平面迎风布局升力系数有一定程度的降低,凸平面迎风布局的升力系数较基准栅格翼布局增大7%左右,较凹平面迎风布局增大15%左右,超过第三临界马赫数之后,凹平面迎风布局的升力系数略大于其它两种布局。
|
| 图 11 α=6°,不同迎风形式栅格翼布局升力和阻力系数的对比 Fig. 11 Lift and drag coefficients of different wind ward-form grid fins(α=6°) |
升力系数随马赫数变化出现的两个下降凹坑也反映了栅格翼流动的三个典型状态,对于基准布局来说当来流马赫数M=0.8(对应于第一临界马赫数)时,栅格翼翼元之间最窄截面处气流速度等于声速,通道内的流动发生壅塞而在截面前出现了溢流,导致栅格翼升力的减小和阻力增加,随着来流马赫数的继续增加,通道最小截面后出现超声速区和激波系,栅格翼的升力系数导数将由于空气的可压缩性影响而增大。当来流马赫数为低超声速时,通道前出现脱体激波,随着来流M数的增加,脱体激波向通道前缘靠拢,当来流马赫数M=1.2(对应于第二临界马赫数)时,脱体激波正好移至通道前缘处,此时,栅格翼的阻力急剧上升,升力降低至最低点。当来流马赫数继续增加,M>1.8(对应于第三临界马赫数)时,翼元前缘发出的斜激波不再落到相邻的翼元上,通道内的波系不存在相互干扰,栅格翼的气动特性基本上与超声速下单翼面的气动特性一样,翼元周围的流场不再出现实质性的变化,升力系数导数随马赫数增加逐渐降低。
3 结 论通过上文的计算分析,得出如下结论:
1) 在亚、跨、超声速范围,曲面形栅格翼布局与常规栅格翼布局相比具有明显的减阻效果;
2) 在有效后掠角相同时,第三临界马赫数之前,曲面形栅格翼布局的减阻效果优于后掠形栅格翼布局,第三临界马赫数之后,两者减阻效果相当;
3) 在第三临界马赫数之前,凸平面迎风布局的升、阻特性优于凹平面迎风布局,第三临界马赫数之后两种迎风方式的曲面形栅格翼阻力系数相当,凹平面迎风布局升力特性略优。
| [1] | Miller M S, Washington W D. An experimental investigation of grid fin drag reduction techniques[R]. AIAA-94-1914. 1994: 800-808. |
| [2] | Brooks R A, Burkhalter J E. Experimental and analytical analysis of grid fin configurations[J].Journal of Aircraft, 1989, 26(9):885–557.DOI:10.2514/3.45856 |
| [3] | James Despirito. CFD investigation of canard-controlled missile with planar and grid fins in supersonic flow[R]. AIAA 2002-4509. |
| [4] | Abate G, Winchenbach G, Hathaway W. Transonic aerodynamic and scaling issues for lattice fin projectiles tested in a ballistic range[C]//19th International Symposium of Ballistics, May 2001. |
| [5] |
Wu X J, CHEN H Q, DENG Y Q, et al. CFD analysis of grid fins[J].Acta Aerodynamica Sinica, 2009, 27(1):78–82. (in Chinese) 吴晓军, 陈红全, 邓有齐, 等. 栅格扰流数值模拟研究[J]. 空气动力学学报, 2009, 27(1) : 78–82. |
| [6] | Lin H, Huang, Huang J C, Chieng C. Navier-Stokes computations for body/cruciform grid fin configuration[J].Journal of Spacecraft and Rockets, 2003, 40(1):30–38.DOI:10.2514/2.3912 |
| [7] | Ravindra K, Nikhil V, Shende N Balakrishnan. CFD simulation of the grid fin flows[R]. AIAA 2002-2722. |
| [8] | Theerthamalai P. Effect of geometric parameters on the aerodynamic characteristics of grid-fin cells at supersonic speeds[R]. AIAA 2007-690. |
| [9] | Berner C, Dupuis A. Wind tunnel tests of a grid finned projectile configuration[R]. AIAA 2000-0105. |
| [10] | Brooks R A, Burkhalter J E. Experimental and analytical analysis of grid fin configurations[J].Journal of Aircraft, 1989, 26(9):885–557.DOI:10.2514/3.45856 |
| [11] | Zing Y, Cai J S, Debiasi M. Numerical study on drag reduction for grid-fin configurations[R]. AIAA 2009-1105. |
| [12] | Marco Debaser, Zeng Yan. Swept-back grid fins for transonic drag reduction[R]. AIAA 2010-4244. |
| [13] | Daniel Guyton, Erich Chilean. Novel locally swept lattice wings for missile control at high speeds[R]. AIAA 2007-63. |
| [14] |
Deng Fan, Chen Shaosong, Tao Gang. CFD analysis of roll damping derivatives for missile with grid fins at supersonic speeds[J].Acta Aerodynamica Sinica, 2012, 30(2):151–156. (in Chinese) 邓帆, 陈少松, 陶钢. 带栅格翼导弹超声速阶段滚转阻尼导数的数值研究[J]. 空气动力学学报, 2012, 30(2) : 151–156. |
| [15] |
Deng Fan, Chen Shaosong. The investigations of windward swept grid fin's lift and drag characterization[J].Acta Aerodynamica Sinica, 2012, 30(5):628–633. (in Chinese) 邓帆, 陈少松. 前缘后掠式栅格翼升阻特性研究[J]. 空气动力学学报, 2012, 30(5) : 628–633. |
| [16] |
Chen Jianzhong, Zhang Zhao, Huang Guochuan. Numerical simulation about grid fin's dynamic characteristic by patched mesh[J].Acta Aerodynamica Sinica, 2013, 31(5):652–656. (in Chinese) 陈建中, 张兆, 黄国川. 基于拼接网格的栅格舵动态特性数值模拟研究[J]. 空气动力学学报, 2013, 31(5) : 652–656. |


